| Емкость в цепи переменного тока

Из сказанного следует, что ток в цепи и э. д. с. самоиндукции не совпадают по фазе. Ток опережает э. д.с. самоиндукции по фазе на  четверть периода или на угол  = 90°. Необходимо также иметь в виду, что в цепи с индуктивностью, не содержащей г, в каждый момент времени электродвижущая сила самоиндукции направлена навстречу напряжению генератора U. В связи с этим напряжения и э. д. с. самоиндукции ес также сдвинуты по фазе друг относительно друга на 180°.

Из изложенного следует, что в цепи переменного тока, содержащей только индуктивность, ток отстает от напряжения, вырабатываемого генератором, на угол ==90о (на четверть периода) и опере­жает э. д.с. самоиндукции на 90°. Можно также сказать, что в  индуктивной цепи напряжение опережает по фазе ток на 90°.

Построим векторную диаграмму тока и напряжения для цеь переменного тока с индуктивным сопротивлением. Для этого отложим вектор тока I по горизонтали в выбранном нами масштаба (рис.

54,6.)

Чтобы на векторной диаграмме показать, что напряжение опережает по фазе ток на угол  = 90°, откладываем вектор напряжения  вверх под углом 90°. Закон Ома для цепи с индуктивностью можно выразить так:

Следует подчеркнуть, что имеется существенное отличие между индуктивным и активным сопротивлением переменному току.

Когда к генератору переменного тока подключена активная на­грузка, то энергия безвозвратно потребляется активным сопротив­лением.

Если же к источнику переменного тока присоединено индуктив­ное сопротивление r= 0, то его энергия, пока сила тока возрастает, расходуется на возбуждение магнитного поля. Изменение этого поля вызывает возникновение э. д. с. самоиндукции. При уменьше­нии силы тока энергия, запасенная в магнитном поле, вследствие возникающей при этом э. д.с. самоиндукции возвращается обратно генератору.

В первую четверть периода сила тока в цепи с индуктивностью возрастает и энергия источника тока накапливается в магнитном поле. В это время э. д.с. самоиндукции направлена против напря­жения.

Когда сила тока достигнет максимального значения и начинает во второй четверти периода убывать, то э. д.с. самоиндукции, изме­нив свое направление, стремится поддержать ток в цепи. Под дей­ствием э. д.с. самоиндукции энергия магнитного поля возвращается к источнику энергии — генератору. Генератор в это время работает в режиме двигателя, преобразуя электрическую энергию в механи­ческую.

В третью четверть периода сила тока в цепи под действием э. д. с. генератора увеличивается, и при этом ток протекает в противопо­ложном направлении. В это время энергия генератора вновь накап­ливается в магнитном поле индуктивности.

В четвертую четверть периода сила тока в цепи убывает, а на­копленная в магнитном поле энергия при воздействии э. д.с. само­индукции вновь возвращается генератору.

Таким образом, в первую и третью четверть каждого периода генератор переменного тока расходует свою энергию в цепи с ин­дуктивностью на создание магнитного поля, а во вторую и четвер­тую четверть каждого периода энергия, запасенная в магнитном поле катушки в результате возникающей э.

д. с. самоиндукции, воз­вращается обратно генератору.

Из этого следует, что индуктивная нагрузка в отличие от актив­ной в среднем не потребляет энергию, которую вырабатывает гене­ратор, а в цепи с индуктивностью происходит «перекачивание» энер­гии от генератора в индуктивную нагрузку и обратно, т, е. возни­кают колебания энергии.

Из сказанного следует, что индуктивное сопротивление является Реактивным. В цепи, содержащей реактивное сопротивление, происходят колебания энергии от генератора к нагрузке и обратно.

§ 54. ЕМКОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА

В главе I § 10 был объяснен процесс заряда и разряда конденсатора, включенного в цепь постоянного тока. 

Рассмотрим теперь цепь переменного тока (рис. 55,а), в кото­рую включена электрическая емкость (конденсатор). Активным сопротивлением этой цепи пренебрегаем (r = 0).

Полярность зажимов генератора переменного тока, включенного  в цепь с емкостью, меняется с частотой

В первую четверть периода (рис.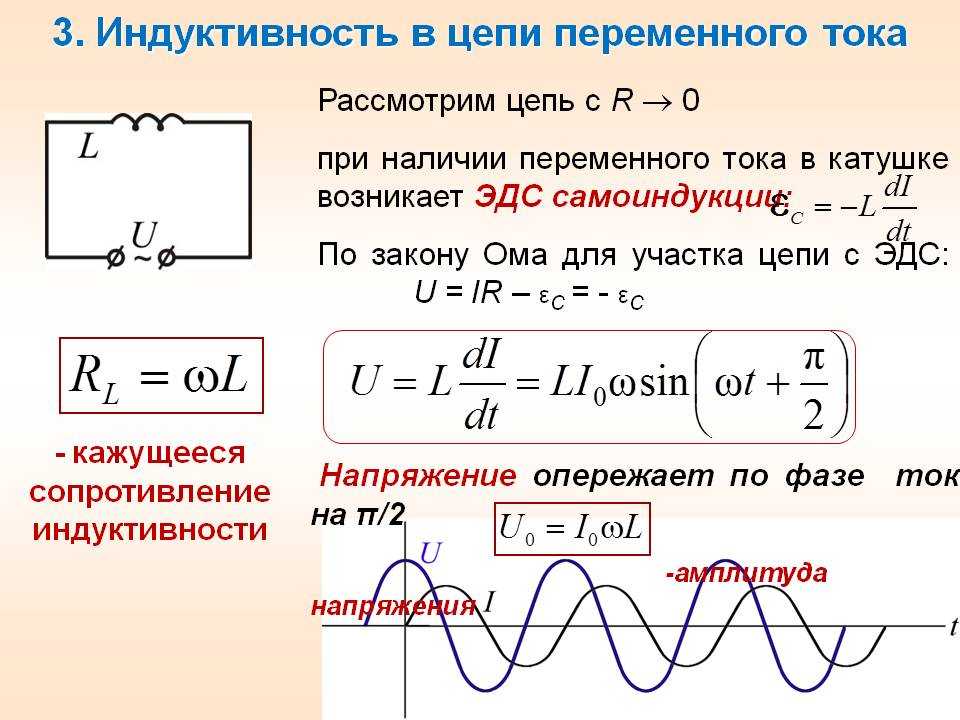 55, в) конденсатор заряжаете  и на его пластинах появляются противоположные по знаку электрические заряды (на левой пластине плюс, на правой — минус).

При заряде конденсатора по проводам, соединяющим генератор с пластинами, перемещаются электрические заряды, следовательно, протекает зарядный ток, измеряемый миллиамперметром. Через диэлектрик конденсатора ток не проходит. Как видно на волновой диаграмме, в первую четверть периода во время заряда конденса­тора напряжение на пластинах конденсатора возрастает от нуля до максимального значения, сила тока, наоборот, в начале заряда будет максимальной, а в конце заряда, когда напряжение на конден­саторе (Uс) окажется равным напряжению генератора (Ur,), она станет равной нулю.

За вторую четверть периода напряжение генератора постепенно убывает и становится равным нулю. В это время конденсатор раз­ряжается. При этом разрядный ток, протекающий по проводам, имеет направление, противоположное направлению тока заряда.

За третью четверть периода полярность на зажимах генератора изменится и напряжение возрастет от нуля до наибольшего значе­ния. В это время конденсатор вновь зарядится, но полярность на его пластинах изменится. На левой пластине будет отрицательный заряд, на правой — положительный заряд. По проводам пройдет за­рядный ток, сила которого к концу заряда конденсатора, когда Uс = Ur, станет равной нулю.

В четвертую часть периода напряжение генератора убывает и становится равным нулю. Конденсатор в это время вторично разря­жается, и по проводам, соединяющим генератор с пластинами кон­денсатора, вновь протекает разрядный ток.

Из сказанного следует, что за один период изменения перемен­ного напряжения дважды происходит процесс заряда и разряда конденсатора и при этом в его цепи протекает переменный ток. Кроме того, при заряде и разряде конденсатора ток в цепи и напря­жение не совпадают по фазе. Ток опережает по фазе напряжение на четверть периода, т. е. на 90°.

Построим векторную диаграмму для цепи переменного тока с емкостью (рис. 55,

б). Для этого отложим вектор тока I в выбран­ном масштабе по горизонтали. Чтобы на векторной диаграмме по­казать, что напряжение отстает от тока на угол  = 90°, отклады­ваем вектор напряжения Uс вниз под углом 90°.

Выясним, от чего зависит сила тока в цепи с емкостью. Обозна­чим сопротивление цепи Хс и назовем его емкостным сопротивле­нием. Тогда закон Ома для цепи с емкостью можно выразить так:

где U —напряжение генератора, в;

   Хc — емкостное сопротивление, ом;

   I — сила тока, а.

Известно, что сила тока в цепи определяется количеством элек­трических зарядов, проходящих через поперечное сечение провод­ника в единицу времени:

Если в единицу времени по проводам протекает большое количество зарядов, то сила тока будет большой, и наоборот, когда по проводам в каждую секунду протекает малое количество зарядов,
то сила тока оказывается незначительной. 

Допустим, что частота переменного тока, вырабатываемого генератором, большая. В этом случае в каждую секунду конденсатор много раз (часто) заряжается и разряжается. В проводах, идущих от генератора к пластинам конденсатора, будет перемещаться в каждую секунду большое количество электрических зарядов. По  этому можно сказать, что в рассматриваемой цепи возникает боль­шая сила тока и в данном случае, согласно закону Ома, емкостное  сопротивление цепи Хс оказывается малой величиной.

Если же частота переменного тока генератора будет мала, то конденсатор в каждую секунду зарядится и разрядится меньшее количество раз: В связи с этим по проводам цепи в каждую секунду пройдет незначительное количество зарядов и сила тока будет мала, а следовательно, емкостное сопротивление цепи, наоборот,  будет большим.

Из сказанного можно сделать вывод, что емкостное сопротивление обратно пропорционально частоте переменного тока.

Емкостное сопротивление зависит не только от частоты переменного тока, но и от величины емкости, включенной в цепь.

Допустим, что в цепь включен конденсатор большой емкости. Количество электричества, которое накапливает конденсатор при заряде и отдает при разряде, прямо пропорционально его емкости:

Чем больше емкость конденсатора, включенного в цепь перемен­ного тока, тем большее количество электричества переместится при заряде и разряде, по проводам, идущим от генератора к его пластинам. Поэтому в проводах возникает ток большой силы и в данном случае, согласно закону Ома, емкостное сопротивление цепи Хc будет мало. Если же включенная в цепь емкость мала, то при заряде и разряде по проводам пройдет меньшее количество электрических зарядов и  сила тока  будет  незначительной,  следовательно, емкостное сопротивление цепи, наоборот, будет большим.

цепь переменного тока содержащая емкость индуктивность и сопротивление



цепь переменного тока содержащая емкость индуктивность и сопротивление

38)

ЦЕПЬ ПЕРЕМЕННОГО ТОКА, СОДЕРЖАЩАЯ ЕМКОСТЬ

Если в цепь постоянного, тока включить конденсатор (идеаль­ный — без потерь), то в течение очень короткого времени после включения по цепи потечет зарядный ток. После того как конден­сатор зарядится до напряжения, равного напряжению источника, кратковременный ток в цепи прекратится. Следовательно, для постоянного тока конденсатор представляет собой разрыв цепи, или, иными словами, бесконечно большое сопротивление.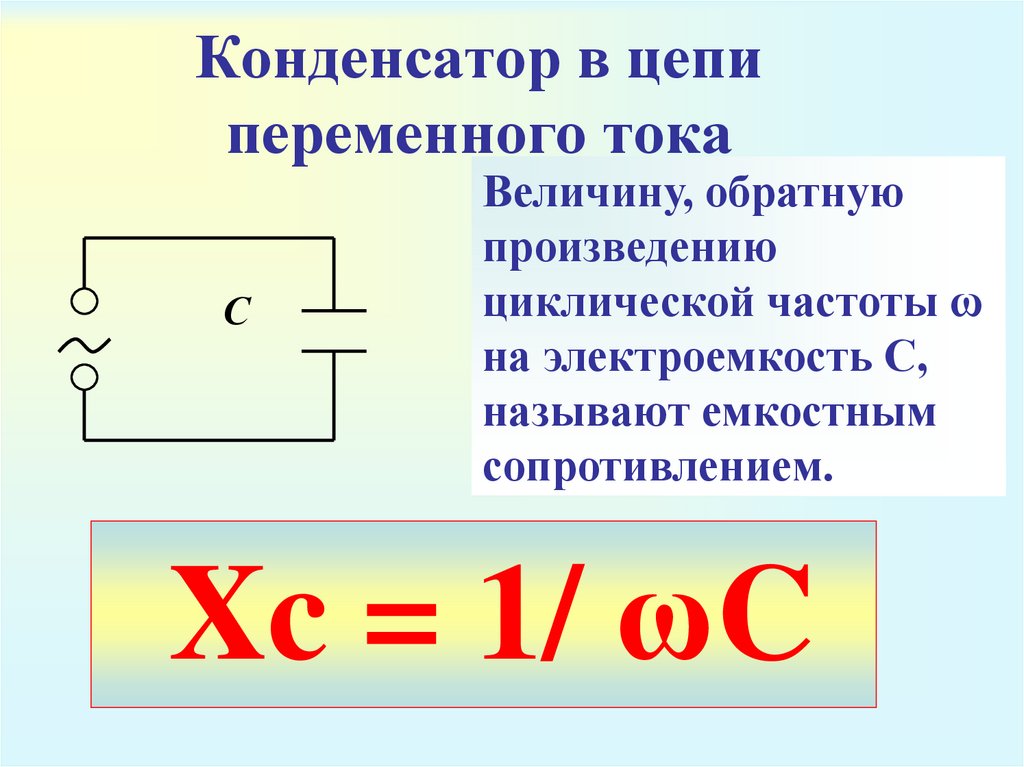

Если же конденсатор включить в цепь переменного тока, то он будет заряжаться попеременно то в одном, то в другом направлении.

При этом в цепи будет проходить переменный ток. Рассмотрим это явление подробнее.

В момент включения напряжение на конденсаторе равно нулю. В течение первой четверти периода, когда напряжение сети будет возрастать (рис. 143), конденсатор будет заряжаться.

По мере накопления зарядов на обкладках конденсатора напря­жение конденсатора увеличивается. Когда напряжение сети к концу первой четверти периода достигнет максимального значения  Um, напряжение конденсатора также станет равным Um, заряд конден­сатора прекращается и ток в цепи становится равным нулю. Ток в цепи конденсатора можно определить по формуле

где ∆q — количество электричества, протекающее по цепи за время ∆t.

 Из электростатики известно:

где   С — емкость конденсатора;

u — напряжение сети;

uc — напряжение конденсатора. Окончательно для тока имеем

Из последнего выражения видно, что, когда  ∆u/∆t   максимально (положения a, в, d),  i также максимально.

 

Когда  ∆u/∆t   = 0 (положения   б, г на рис. 143), то i также равно нулю.

Во вторую четверть периода напряжение сети будет уменьшать­ся, и конденсатор начнет разряжаться. Ток в цепи меняет свое направление на обратное.

В следующую половину периода напряжение сети меняет свое направление и наступает перезаряд конденсатора и затем снова его разряд.

Из рис. 143 видно, что ток I в цепи с емкостью в своих изменениях опережает по фазе напряжение конденсатора на 1/4 периода, или 90°.

Сравнивая векторные диаграммы цепей с индуктивностью и емкостью, мы видим, что индуктивность и емкость на фазу тока влияют прямо противоположно.

Пользуясь высшей математикой, можно доказать, что ток в цепи с емкостью пропорционален напряжению Uc, приложенному к конденсатору, угловой частоте w и величине емкости конденсатора  C:

Обозначим

Величина Хс называется емкостным сопротивле­нием, или реактивным сопротивлением ем­кости, и измеряется в омах.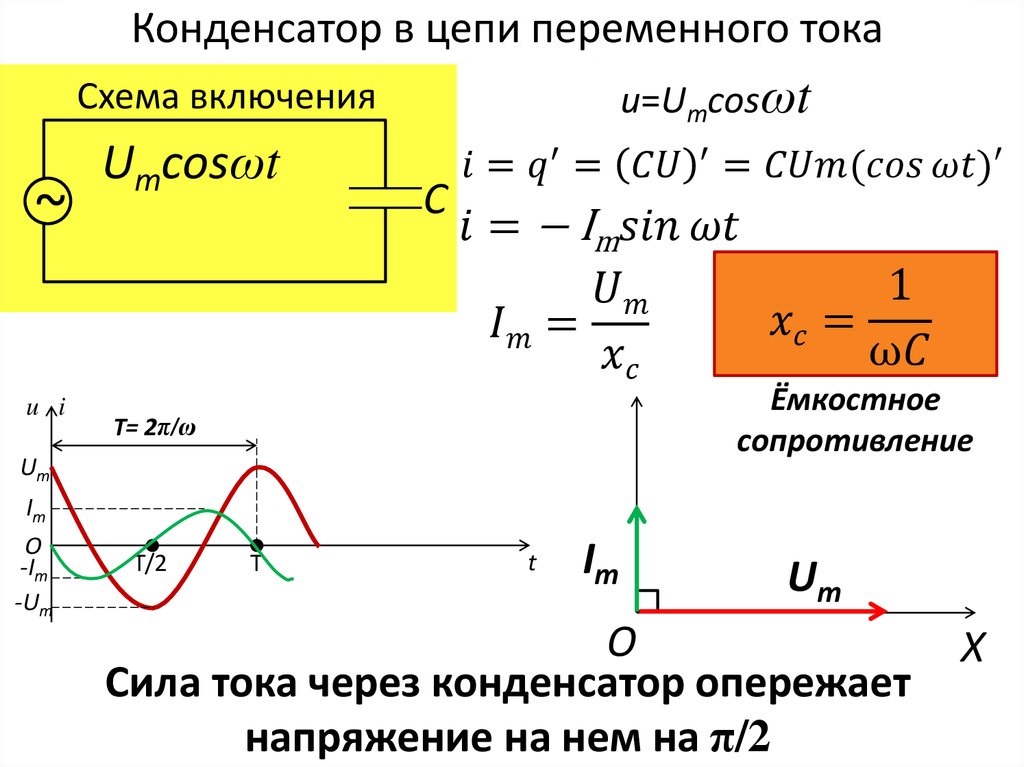 Выражение закона Ома для цепи переменного тока, содержащей емкость, имеет вид

Та часть напряжения сети, которая приложена к конденсатору, называется емкостным падением напряжения (или   реактивной   слагающей   напряжения)   и   обозначается   Uc:

Емкостное сопротивление Хс, так же как индуктивное сопро­тивление xL, зависит от частоты переменного тока.

Но если с увеличением частоты индуктивное сопротивление увеличивается, то емкостное сопротивление, наоборот, будет умень­шаться.

Пример 6. Определить сопротивление конденсатора емкостью 5 мкф при частоте 50 гц:

при частоте 400 гц:

 

На рис. 144 показана кривая мгновенной мощности в цепи с емкостью. Из чертежа видно, что в первую четверть периода цепь с емкостью забирает из сети энергию, которая запасается в электрическом поле конденсатора.

Энергию, запасаемую конденсатором к моменту, когда напряже­ние на нем равно максимальному значению, можно определить по известной формуле CU2м/2.

В следующую четверть периода конденсатор разряжается на сеть, отдавая ей ранее запасенную в нем энергию.

За вторую половину периода явление колебаний энергии пов­торяется. Таким образом, в цепи с емкостью происходит лишь обмен энергией между сетью и конденсатором без ее потерь.

Поэтому средняя за период мощность, или активная мощность, цепи с емкостью равна нулю, как и в цепи с индуктивностью.

Из графика, изображенного на рис. 144, видно, что мгновенная мощность в цепи с емкостью два раза в течение каждого периода (когда wt = 45°, 135° и т. д.) достигает максимального значения, равного

 

Этой величиной принято характеризовать количественно про­цесс обмена энергии между источником и электрическим полем конденсатора. Ее также называют реактивной мощностью и обозначают буквой Q.

Учитывая,, что в рассматриваемой цепи U = IХc, получим сле­дующее выражение для реактивной мощности:

Емкость в цепях переменного тока — Цепи переменного тока

Цепи переменного тока

Изменение напряжения на конденсаторе вызывает ток, равный пропорциональна как скорости изменения напряжения, так и емкости.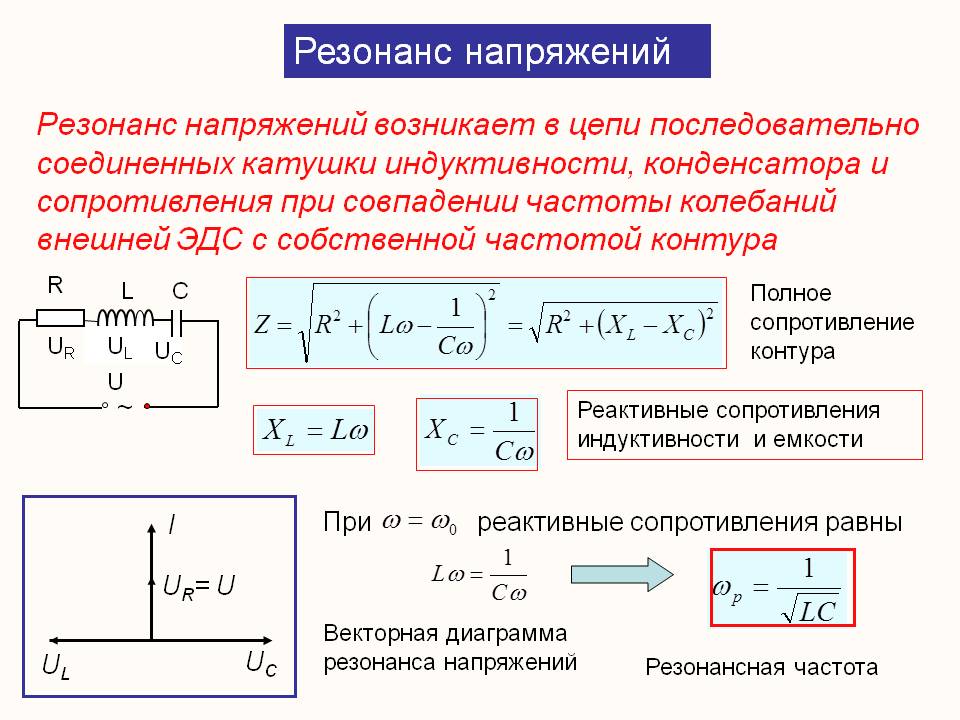 отношения задаются уравнением

Чисто емкостная схема.

К конденсатору в цепи рисунка приложено синусоидальное напряжение. выше. График зависимости тока от времени относительно напряжения v на рисунке ниже.

Текущее опережение напряжения на 90° (π/2) — отношение тока к напряжению в чисто емкостной цепи.

График напряжения на рисунке выше увеличивается с t ₀ до т ₁ . Напряжение растет с убывающей скоростью, и при t ₁ скорость изменения напряжения равна нулю. Вовремя t ₁ , тогда ток должен быть равен нулю. От времени т ₁ до т ₂ , напряжение снижается, и при t ₂ напряжение изменяется с максимальной скоростью. Электрический ток отрицательно от t ₁ до t ₃ и максимум отрицательный при t ₂ . При t ₃ скорость изменения напряжение мгновенно равно нулю, следовательно, ток равен нулю. От t ₃ до t ₄ напряжение увеличивается с возрастающей скоростью, а максимальная мгновенная скорость изменения возникает при т ₄ . Поэтому я максимально при т ₄ .

Из осциллограмм на рисунке выше видно, что максимальный положительный ток возникает на 90 градусов впереди максимального положительного напряжения. Электрический ток Говорят, что в чисто емкостной цепи опережает напряжение на 90°. Это фазовое соотношение выводится математически путем применения исчисления.

Используя уравнение

а также

Путем дифференцирования находится дв / дт .

Следовательно,

По общему виду периодической функции

а также

Поскольку отношение вольта к амперу определяется как противодействие току в омах, величина 1/ωC ​​выражена в омах. Величина 1/ωC ​​называется емкостное сопротивление и обозначается символами X _C .

X _C можно показать как отношение эффективных значений тока и напряжения таким же образом, как показано для X _L в предыдущем разделе.

Величина, обратная емкостному реактивному сопротивлению, называется емкостной проводимостью . и обозначен B _C . Единица емкостной проводимости это mho (или сименс S), когда частота в Гц и емкость в фарадах.

Пример 1 : Напряжение, имеющее эффективное значение 220 вольт и частота 20 кГц подается на конденсатор емкостью 0,08 мкФ. (1) Рассчитать эффективное значение тока. (2) Рассчитайте максимальное значение Текущий. (3) Напишите периодические функции, представляющие ток и напряжение.

Решение:

1.

2.

3. Если напряжение взято за эталон,

Ток опережает напряжение на 90° в емкостной цепи.

Эти периодические функции также могут быть записаны относительно тока.

По отношению к току напряжение отстает на 90°.

Пример 2 : Когда 250 вольт подается на конденсатор емкостью 0,05 мкФ, измеряется ток 0,6 А. Найдите частоту.

Решение: можно найти величину X _C .

Теперь можно рассчитать частоту

Соотношение мощностей в емкостной цепи можно проанализировать с помощью уравнение P = VI на основе мгновенных значений. Продукт v и i рисунка выше нанесены на рисунок ниже. Это то же самое, что было сделано в предыдущем разделе для мгновенного мощность в чисто индуктивной цепи. Полезная мощность в чисто емкостном цепь равна нулю, как это было в чисто индуктивной цепи.

Мощность в чисто емкостной цепи.

Это соотношение оправдывается тем, что из t ₀ до t ₁ напряжение растет, заряд сохраняется, и энергия запасается конденсатором. От т ₁ до t ₂ , напряжение снижается, зарядка возвращается конденсатором, а энергия возвращается к источнику.

Полезная мощность снова определяется уравнением P = VI cos θ

Емкость переменного тока и емкостное реактивное сопротивление

Введение

Как и в случае катушек индуктивности, электрические характеристики конденсаторов также зависят от характера источника: постоянного или переменного тока. В этом руководстве мы увидим, что в некотором смысле конденсатор можно рассматривать как противоположность катушки индуктивности с точки зрения функционирования частоты.

Как и для резисторов и катушек индуктивности, мы представляем в первом разделе концепцию емкости , которая поможет нам понять, почему конденсаторы ведут себя по-разному в режиме постоянного и переменного тока и за счет каких механизмов они это делают.

Во втором разделе мы говорим о емкостном реактивном сопротивлении, чтобы точно понять, как конденсаторы реагируют на увеличение частоты.

В последнем разделе показано, как работают ассоциации резисторов и конденсаторов или катушек индуктивности и конденсаторов, и их можно использовать для приложений фильтрации.

Презентация

Емкость

Емкость (C) является основным понятием для понимания того, как работает конденсатор. Он описывает напряжение (В), которое компонент будет генерировать при зарядке электрические заряды (Q) на своих клеммах. Таким образом, наиболее общий и естественный способ выражения емкости C=Q/V выражается в фарадах (F).

Прежде чем проиллюстрировать и дать более подробную информацию о емкости, стоит кратко описать, что такое электрический заряд. Как и понятия массы и времени, заряд трудно описать простыми словами, его легко почувствовать, но сложно определить. Это внутреннее свойство элементарных частиц, таких как электроны или протоны.

Когда заряд движется, он создает ток, заряд электронов равен -е , а протонов +е , противоположные заряды притягиваются друг к другу: вот почему электроны вращаются вокруг атомов, не покидая их. Официальной единицей измерения заряда является кулонов (единица C) и e≅1,6×10 ^-19 C .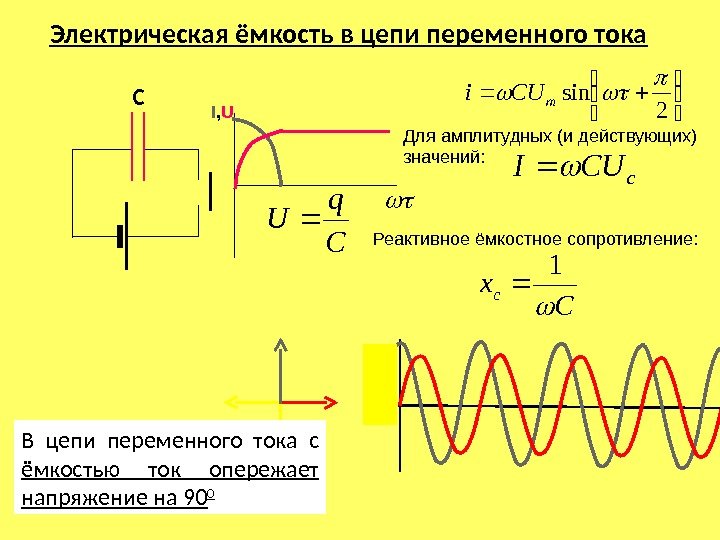

Однако измерение заряда и метод, используемый для определения емкости конкретного компонента, непрост. К счастью, емкость можно выразить с помощью другой формулы, представленной ниже.

В отличие от удельного сопротивления и индуктивности емкость сильно зависит от рассматриваемой геометрии. Наиболее простым примером конденсатора является топология с параллельными пластинами, представленная на рис. 1 . Он состоит из двух проводящих пластин, разделенных тонким слоем изоляционного материала (зеленый).

рис. 1 : Конфигурация конденсатора с параллельными пластинами

Если между пластинами через клеммы подается разность потенциалов, то в пластине 1 (соответственно -Q) образуется заряд +Q (соответственно -Q). Емкость в этом случае может быть выражена следующей формулой:

экв. 1 : Емкость конфигурации с параллельными пластинами

ε является абсолютной диэлектрической проницаемостью и может быть разложена на два коэффициента: -12 Ф/м — диэлектрическая проницаемость вакуума, а ε _r — относительная диэлектрическая проницаемость изоляционного материала. Материалы с более высокими изоляционными свойствами имеют более высокую относительную диэлектрическую проницаемость, что увеличивает емкость.

Чтобы лучше понять эти концепции и то, как работают конденсаторы, мы можем определить гидравлический аналог с эластичной мембраной внутри трубы, как показано на рис. 2 . Гидравлические аналогии — это распространенный способ установить корреляцию между абстрактными понятиями в электричестве с более простым подходом в области гидравлики.

рис. 2 : Гидравлическая аналогия конденсатора

В этой аналогии труба представляет собой электрический провод, поток воды представляет собой электричество, а мембрана представляет собой конденсатор. Кроме того, жесткость мембраны представляет собой емкость.

Как и в конденсаторе, вода не может пройти через мембрану, но ее давление (аналог потенциала) вызывает смещение мембраны. Если давление воды поддерживается постоянным в одном и том же направлении, мембрана толкается в том же направлении с той же кривизной, и молекулы воды не двигаются. Однако если подать переменный поток воды, то мембрана попеременно толкается в противоположных направлениях и молекулы воды движутся вокруг нее.

Режимы постоянного и переменного тока

Теперь, когда мы более глубоко знаем, из чего состоит емкость, нам нужно понять, почему ее поведение отличается при подаче постоянного или переменного напряжения, что мы кратко объяснили с помощью гидравлической аналогии. Рассмотрим ту же архитектуру емкости C, что и в . Рисунок 1 при подаче постоянной разности потенциалов V-V _{ЗАЗЕМЛЕНИЕ} :

рис. 3: Конфигурация с параллельными пластинами в режиме постоянного тока

Из-за электростатического эффекта приложение положительного напряжения V притягивает заряды +q к пластине 1 и -q к пластине 2. Сумма положительных зарядов (соответственно отрицательных зарядов) равна +Q (соответственно -Q). Такое распределение зарядов создает напряжение V _C =Q/C в конденсаторе.

Пока конденсатор держит заряд, напряжение V _C остается стабильным, и мы описываем это конкретное состояние как заряженный . Для идеальных конденсаторов напряжение V _C может сохраняться даже при отключении источника постоянного тока. Однако в реальности мы наблюдаем разряд , когда заряды перераспределяются и V _C уменьшается по экспоненциальному закону.

Кроме временного тока, который можно наблюдать при разряде конденсатора (если источник выключен), I _C =0 в режиме постоянного тока .

Однако это поведение отличается в режиме переменного тока, Рис. 4 ниже накладывают характеристики напряжения и тока вместе с распределением зарядов в конденсаторе:

рис. 4: Циклы заряда и разряда в режиме переменного тока

При подаче напряжения переменного тока к конденсатору наблюдаются циклы зарядки и разрядки, которые генерируют ток, сдвинутый по фазе на 90 236 на -90 ° 90 237, что известно как квадратура 90 236 фазы 9.0237 задержка .

Еще один более математический способ понять появление тока при увеличении частоты — использовать общее соотношение C=Q/V, которое можно переписать как V=Q/C.

Это соотношение является дифференцируемым, как показано в следующем уравнении:

По определению dQ/dt=I, следовательно, ток (I), напряжение (V) и емкость (C) связаны следующим уравнением:

eq 2 : Текущее уравнение емкостной составляющей

С Уравнение 2 , мы можем видеть, что ток не может наблюдаться, если нет изменения напряжения. Более того, ток увеличивается, если изменения происходят быстрее, т.е. если увеличивается частота.

Частотная характеристика

Так же, как и для катушек индуктивности, концепция реактивного сопротивления также может быть применена для конденсаторов. Он отмечен X _C и описывает противодействие емкостной составляющей при изменении напряжения. Емкостное сопротивление представляет собой мнимую часть комплексного импеданса Z _C емкостного компонента: Z _C =R _C +j×X _C .

В действительности импеданс конденсатора уменьшается до – мк _C , так как мы видели ранее, что фазовый сдвиг, наблюдаемый в емкостном компоненте, составляет -90°.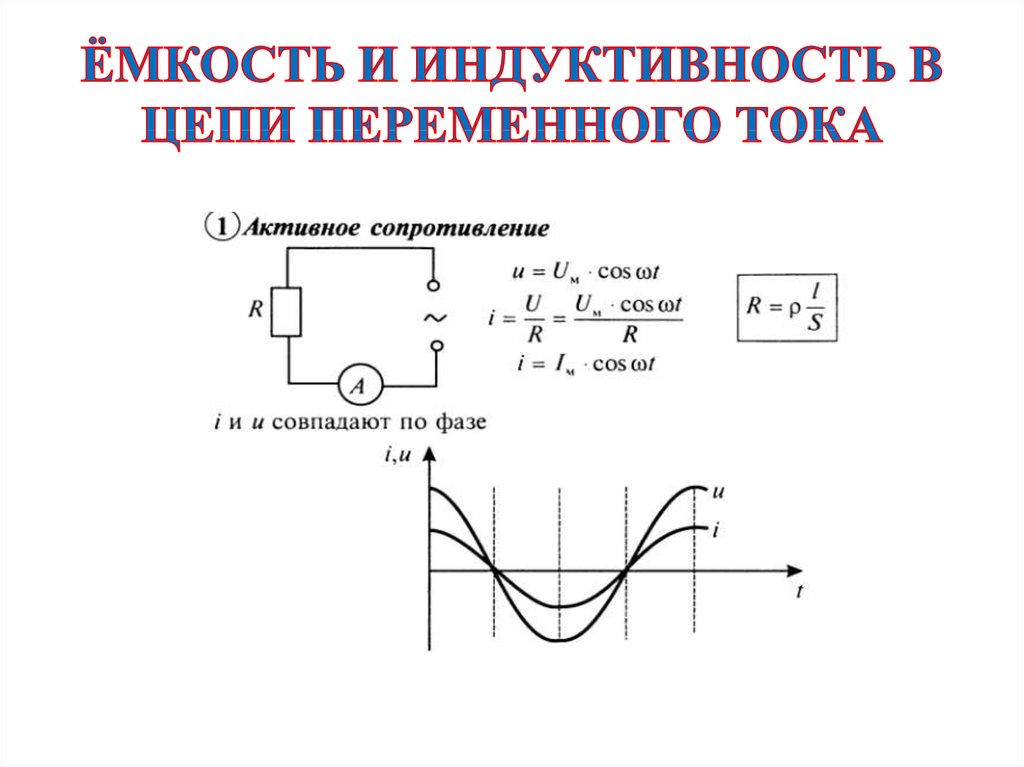 Мы можем обратиться к учебнику по комплексным числам, чтобы понять, что такой фазовый сдвиг возможен только в том случае, если комплексный импеданс является чисто мнимым числом, что дает, следовательно, R _C =0.

Емкостное реактивное сопротивление удовлетворяет следующему уравнению 3 :

уравнение 3 : Реактивное сопротивление конденсатора

В отличие от катушек индуктивности, мы можем понять с помощью этого уравнения, что сопротивление переменному напряжению уменьшается обратно пропорционально увеличению частоты. При f=0 X _C →+∞, что означает, что конденсатор ведет себя как разомкнутая цепь на низкой частоте. Когда f→+∞, X _C =0, это означает, что конденсатор становится короткозамкнутым.

Фильтры

Различные свойства трех основных электрических компонентов (R, L и C) могут быть связаны в одной цепи для создания фильтров. В этом разделе мы кратко представляем фильтры RC и LC .

RC-фильтр

Рассмотрим следующую схему на . учебник по индуктивности, чтобы получить коэффициент усиления и фазовый сдвиг схемы с передаточной функцией.

Применяя формулу делителя напряжения, мы получаем следующую передаточную функцию T _V :

eq 4 : Передаточная функция RC-цепи

И, наконец, коэффициент усиления и фазовый сдвиг RC-фильтра определяется выражением |T _V | и Φ :

eq 7 : Коэффициент усиления и фазовый сдвиг цепи RL

Мы можем нанести эти две величины на диаграмму Боде, выбрав, например, R = 100 Ом и C = 1 мкФ :

рис. 6 : Диаграмма Боде серии RC цепь

На диаграмме Боде мы можем видеть, что последовательная цепь RC представляет собой ФНЧ т.к. на низких частотах коэффициент усиления равен 1 а при увеличении частоты коэффициент усиления стремится к 0.

LC фильтры

Объединение дросселя с конденсатором более интересно потому что совершенно противоположное поведение появляется при последовательном или параллельном подключении, что не относится к RC-фильтру.

Давайте прежде всего рассмотрим последовательную цепь, как показано на рис. 7 :

рис. 7 : последовательная цепь LC

Общий импеданс Z определяется как Z=Z _C +Z _L =jLω+(1/jCω) . Мы можем переписать это выражение с общим знаменателем, и, определив величину ω ₀ = 1/√(LC), получим:

eq 8 : Импеданс последовательной LC-цепи

Мы можем видеть, что Z(ω ₀ )=0 , по этой причине ω ₀ называют резонансной частотой . При подключении к нагрузке LC-схема будет вести себя как полосовой фильтр вокруг ω ₀ .

Параллельная цепь, представленная на рис. 8 , ведет себя точно противоположно последовательной цепи.

рис. 8: параллельный LC-контур

Используя тот же метод, что описан ранее, полное сопротивление можно записать следующим образом:

eq 9: импеданс LC-параллельного контура

Однако здесь Z(ω ₀ )→+∞ , что означает, что на резонансной частоте цепь ведет себя как разомкнутая. При подключении к нагрузке параллельный фильтр LC действует как режекторный фильтр около ω ₀ .

Заключение

Сначала мы представили понятие емкости, чтобы лучше понять, как работают конденсаторы. Емкость отражает противодействие тока, которое компонент создает из-за изменения напряжения. Мы видели, что в режиме постоянного тока конденсатор просто накапливает энергию в виде зарядов, при этом ток не наблюдается. Однако заряды могут быть сняты, если произойдет изменение напряжения: это имеет место в режиме переменного тока.

Описывая емкостное сопротивление, мы видели, что сопротивление току конденсатора обратно пропорционально частоте. В режиме постоянного тока конденсатор представляет собой разомкнутую цепь, и по мере увеличения частоты происходит короткое замыкание.

Наконец, объединение резисторов и катушек индуктивности с конденсаторами может создать интересные фильтры. Цепь серии RC представляет собой фильтр нижних частот : он ослабляет высокие частоты.