Список логических символов — frwiki.wiki
В логике для выражения логического представления обычно используется набор символов . В следующей таблице перечислены многие символы с их именами, возможные способы их чтения и связанные области математики . Кроме того, третий столбец содержит неформальное определение, четвертый столбец дает краткий пример, пятый дает их код Unicode, а шестой и седьмой — числовые или текстовые ссылки, используемые в документах HTML (см. Сущность HTML ). Последний столбец содержит символ LaTeX .
Резюме
- 1 Основные логические символы
- 2 Продвинутые и редко используемые логические символы
- 3 Статьи по теме
- 4 Примечания и ссылки
- 4.1 Примечания
- 4.2 Ссылки
Основные логические символы
| Символ | Фамилия | Объяснение | Примеры | Юникод (шестнадцатеричный) | (десятичный) | HTML (текст) | Латекс |
|---|---|---|---|---|---|---|---|
| Чтение | |||||||
| Категория | |||||||
| Участие | A ⇒ B истинно, только если либо A ложно, либо B истинно. → означает то же, что и ⇒ Означает то же, что и ⇒ | Пусть x будет действительным числом: | U + 21D2 U + 2192 U + 2283 | & # 8658; & # 8594; & # 8835; | & rArr; & rarr; & Как дела; | ⇒{\ displaystyle \ Rightarrow} \ Правая стрелка →{\ displaystyle \ to} \ к ⊃{\ displaystyle \ supset} \ supset ⟹{\ displaystyle \ implies} \ подразумевает | |
| вовлеченный если так является достаточным условием для | |||||||
| Логическая эквивалентность | A ⇔ B истинно, если A и B ложны или если A и B истинны. | х + 5 знак равно у + 2 ⇔ х + 3 = у | U + 21D4 U + 2261 U + 2194 | & # 8660; & # 8801; & # 8596; | & hArr; & Equiv; & harr; | ⇔{\ displaystyle \ Leftrightarrow} \ Leftrightarrow ≡{\ Displaystyle \ Equiv} \ Equiv ↔{\ displaystyle \ leftrightarrow} \ leftrightarrow ⟺{\ Displaystyle \ iff} \ iff | |
| если и только если равно означает то же, что и | |||||||
| Логика высказываний | |||||||
| Отрицание | Утверждение ¬ A истинно тогда и только тогда, когда A ложно. | ¬ (¬ А ) ⇔ А х ≠ у ⇔ ¬ ( х = у ) | U + 00AC U + 0021 | & # 172; & # 732; & # 33; | & нет; & тильда; & искл; | ¬{\ displaystyle \ neg}\ lnot или \ neg ∼{\ displaystyle \ sim} \ sim | |
| Не Нет | |||||||
| Логика высказываний | |||||||
| Соединение | Утверждение A ∧ B истинно, если истинны A и B ; в противном случае это ложь.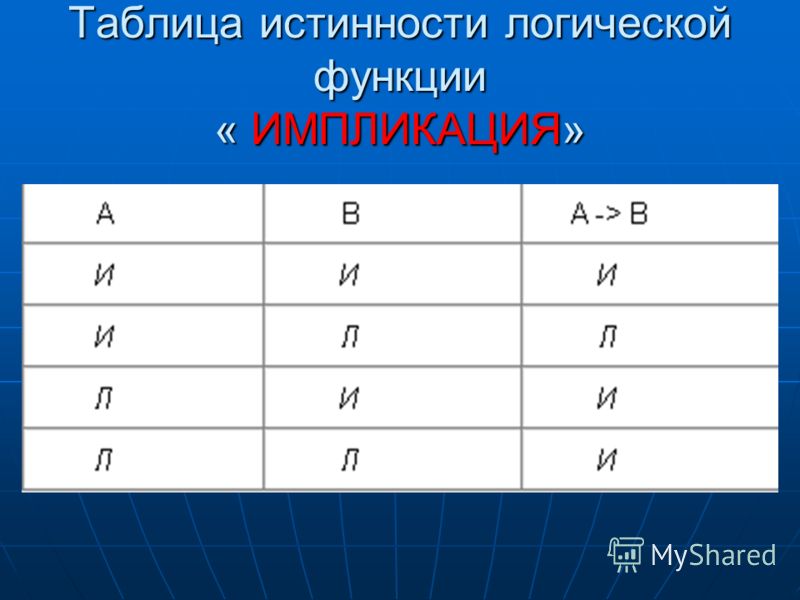 | n <4 ∧ | U + 2227 U + 00B7 U + 0026 | & # 8743; & # 183; & # 38; | & а также; & middot; & amp; | ∧{\ Displaystyle \ клин}\ клин или \ земля &{\ Displaystyle \ &} \ & | |
| а также | |||||||
| Логика высказываний , булева алгебра | |||||||
| Инклюзивная дизъюнкция | Утверждение A ∨ B истинно, если истинны A или B , или оба; если оба ложны, утверждение ложно. | n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3, когда n — целое число . | U + 2228 U + 002B U + 2225 | & # 8744; & # 43; & # 8741; | &золото; | ∨{\ displaystyle \ lor}\ lor или \ vee | |
| или же | |||||||
| Логика высказываний , булева алгебра | |||||||
⊕ | Исключительная дизъюнкция | Утверждение A ⊕ B истинно, когда истинно либо A, либо B, только одно или другое. | (¬ A ) ⊕ A всегда верно, A ⊕ A всегда ложно. | U + 2295 U + 22BB | & # 8853; & # 8891; | & oplus; | ⊕{\ displaystyle \ oplus} \ oplus ⊻{\ displaystyle \ veebar} \ veebar |
| xor | |||||||
| Логика высказываний , булева алгебра | |||||||
| Тавтология | Утверждение ⊤ безусловно верно. | A ⇒ ⊤ всегда верно. | U + 22A4 | & # 8868; | ⊤{\ displaystyle \ top} \вершина | ||
| Высокая Правда | |||||||
| Логика высказываний , булева алгебра | |||||||
| Противоречие | Утверждение ⊥ безусловно ложно.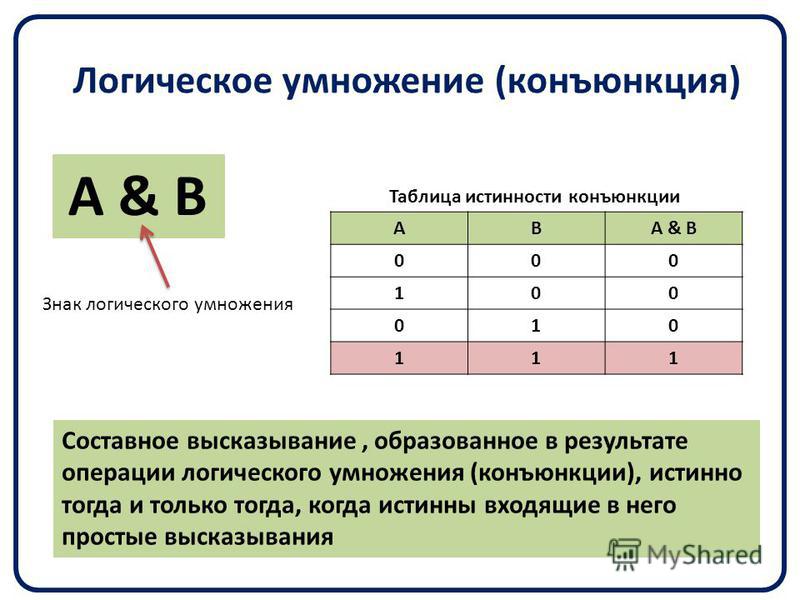 (Символ ⊥ также может относиться к перпендикулярным линиям .) | U + 22A5 | & # 8869; | & perp; | ⊥{\ displaystyle \ bot} \ бот | ||
| Низкий Ложь | |||||||
| Логика высказываний , булева алгебра | |||||||
| Универсальный квантификатор | ∀ x : P ( x ) или ( x ) P ( x ) означает, что P ( x ) истинно для всех x . | ∀ n ∈ ℕ: n 2 ≥ n . | U + 2200 | & # 8704; | ∀{\ displaystyle \ forall} \ для всех | ||
| За все Для всех Для каждого | |||||||
| вычисление предикатов | |||||||
∃ | Экзистенциальный квантификатор | ∃ x : P ( x ) означает, что существует хотя бы один x такой, что P ( x ) истинно. | ∃ n ∈ ℕ: n положительно. | U + 2203 | & # 8707; | &существовать; | ∃{\ Displaystyle \ существует} \ существуют |
| Это существует | |||||||
| вычисление предикатов | |||||||
∃! | Уникальный экзистенциальный квантификатор | ∃! x : P ( x ) означает, что существует ровно один x такой, что P ( x ) истинно. | ∃! n ∈ ℕ: n + 5 = 2 n . | U + 2203 U + 0021 | & # 8707; & # 33; | ∃!{\ displaystyle \ существует!} \ существуют! | |
| Есть ровно один | |||||||
| вычисление предикатов | |||||||
≔ ≡ : ⇔ | Определение | x ≔ y или x ≡ y означает, что x определяется как другое имя для y, но обратите внимание, что ≡ также может означать что-то еще, например конгруэнтность .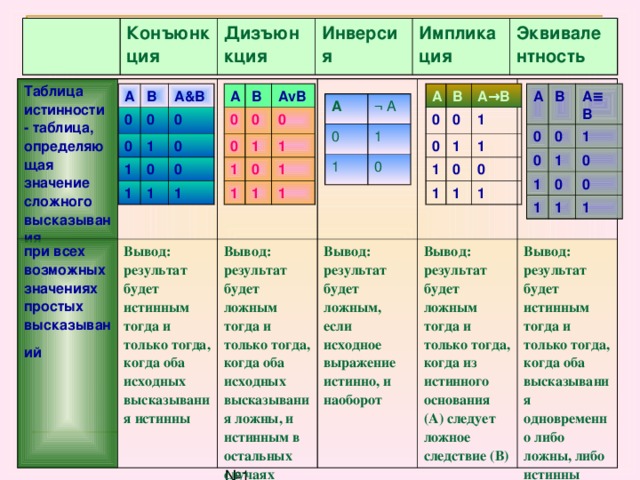 Р : ⇔ Q означает , что Р определяется как логически эквивалентны с Q . | cosh x ≔ (ехр х + ехр (- х )) / 2 Исключающее ИЛИ Б : ⇔ ( ∨ B ) ∧ ¬ ( ∧ B ) | U + 2254 (U + 003A; U + 003D) U + 2261 U + 003A; U + 229C | & # 8788; (& # 58; & # 61;) & # 8801; & # 8860; | & Equiv; & hArr; | знак равно{\ displaystyle: =} знак равно ≡{\ Displaystyle \ Equiv} \ Equiv : ⇔{\ displaystyle: \ Leftrightarrow} : \ Leftrightarrow |
| определяется как | |||||||
| Всюду | |||||||
() | Порядок операций | Операции в круглых скобках имеют приоритет. | (8 ÷ 4) ÷ 2 = 2 ÷ 2 = 1, но 8 ÷ (4 ÷ 2) = 8 ÷ 2 = 4. | U + 0028 U + 0029 | & # 40; & # 41; | ( ){\ Displaystyle (~)} () | |
| круглые скобки, скобки | |||||||
| Всюду | |||||||
⊢ | Удержание | x ⊢ y означает, что y доказуемо относительно x (в определенной формальной системе ). | A → B ⊢ ¬ B → ¬ A | U + 22A2 | & # 8866; | ⊢{\ displaystyle \ vdash} \ vdash | |
| доказуемо ( стопор ) | |||||||
| Логика высказываний , исчисление предикатов | |||||||
⊨ | Моделирование | x ⊨ y означает, что x семантически влечет y . | A → B ⊨ ¬ B → ¬ A | U + 22A8 | & # 8872; | ⊨{\ displaystyle \ vDash} \ vDash | |
| Включает | |||||||
| Логика высказываний , исчисление предикатов |
Продвинутые и редко используемые логические символы
- Монеты Куайна
Статьи по Теме
- Юзеф Мария Бохенский
- Таблица математических символов
- Логический разъем
- Инфиксные, префиксные, польские и постфиксные обозначения
- Таблица истинности
- Логический квадрат
- Логический шестиугольник
Примечания и ссылки
Заметки
- (ru) Эта статья частично или полностью взята из статьи в англоязычной Википедии под названием « Список логических символов » ( см.
 список авторов ) .
список авторов ) .
Рекомендации
- ↑ (in) « Ссылки на именованные символы » в HTML 5.1 Nightly , W3C (по состоянию на 9 сентября 2015 г. )
- ↑ Этот персонаж доступен в LaTeX, но не в системе TeX от MediaWiki .
Типографские символы | |
|---|---|
| Пунктуация | Скобы ({}) · Круглые скобки (()) · шевроны (<> или <> или ⟨⟩) · Крючки ([]) · Половина крючки (⸢ ⸣ ⸤ ⸥) · кавычки ( «» или «» или » или «» или » или » » или ») · Апостроф (‘ или ‘) · запятая (,) · косая черта (/) · обратная косая черта (\) · косое пропускание (⸍ ⸌) · Пробел () · Точка () . · многоточие (… или …) · запятой (;) · двоеточие (:) · восклицательный знак ! () · восклицательный знак переворачивается (¡) · Точка Вопросительный знак ? () · Выброс знак вопроса (¿ ) · Восклицательный знак (‽) · Знак иронии (moins) · Коммерческий знак минус (⁒) · Дефис (- или -) · Дефис (- или — или -) · Другая пунктуация |
| Диакритический знак (от латинского алфавита ) | Акут (◌) · Двойной ударения (◌̋) · апостроф (◌) · Двойной апостроф (◌̏) · Каре (◌) · Caret подписался (◌̭) · Бар включен (◌̶) · Краткая (◌ ̆) · Обратный бриф (◌̑) · Подписанный бриф (◌̮) · Подписанный обратный бриф (◌̯) · Caron (◌̌) · Cédille (◌̧) · Рог (◌ ̛) · Крючок в голове (◌̉) · вертикальная линия (◌̍) · вертикальная линия , на которые подписан (◌̩) · Macron (◌̄) · Macron подписался (◌) · Огонек (◌̨) · Огонек suscrit (◌᷎) · Точка подписки (◌̣) · Точка suscrit (◌̇) · Главный раунд (◌̊) · Круглый подписался (◌̥) · Тильда (◌) · Тильда подписался (◌̰) · линия suscrit (◌̅) · Двойной Overline (◌̿) · черта подписываемый (◌) · Двойной функция подписываемый (◌̳) · Умляут (◌̈) · Умляут подписался (◌̤) · Умляут (◌̈) · разделенные по подписчикам (◌̦) · запятой верхний индекс (◌̓) |
| Типографский символ | Ampersand (&) · В знаке (@) · Звездочка (*) · Астеризм (⁂) · Вертикальная черта (| или |) · Пунктирного круг (◌) · Copyright (©) · Фонографические авторские права (℗) · Товарный знак (® или ?) · Товарный знак (™ или ?) · знак обслуживания (℠) · Флажок (✓) · Паук (#) · Пунктирные крест (⁜) · Референтная метка (※) · Степень (°) · Цельсия (° C) · Фаренгейта (° F) · Количество ( Et ) · и Tironian (icule) · Manicule (☞) · Obele († и ‡) · Prime: минута, второй и третий ( » » ‘) · Пункт (§) · Поэтому (∴ ) · из (∵) · пестрой-де-Муш (¶) · Midpoint (·) · Чип (•) · Подчеркивание (_) · Ведущий дефис (~) · Конец знак статьи (◼) · х бюллетеней для голосования (✘ ) · Пояснительный символ (ɔ 🙂 |
| Математический символ | Больше (+) · Меньше (-) · Плюс или минус (±) · Крест (x) или точка (⋅) умножения · Двоеточие (:) или Obelus (÷) деления · Равно (=) · Отличается от (≠ ) · Меньше или больше (<, ≤,>, ≥, ≮ и ≯) · приближение (≈) · дробная черта (/ или /) · процент (%) · до тысячи (‰) · Через десять миль (‱ ) · Квадрат , куб и экспонирование ( 2 3 . .. n ) · Радикал (√) · Интеграл (∫) · Сумма (Σ) · индексированный продукт (Π) · Микро (μ) · Вся партия (⌊ ⌋ ⌈ ⌉) .. n ) · Радикал (√) · Интеграл (∫) · Сумма (Σ) · индексированный продукт (Π) · Микро (μ) · Вся партия (⌊ ⌋ ⌈ ⌉) |
| Логический символ | И и или логическое (∧ ∨) · Экзистенциальные и универсальные кванторы (∃ ∀) · Отрицание (¬) · Пустое множество (∅) · Пересечение и объединение (∩ ∪) · Подмножество и надмножество (⊆ ⊇) · Принадлежность (∈ ∋) · Дополнительные (∁) · Монеты Куайн (⌜ ⌝ ⌞ ⌟) |
| Символ валюты | Валюта (¤) · Бат (฿) · Биткойн (₿) · Седи (₵) · Цент (¢) · Двоеточие (₡) · Доллар ($) · Донг (₫) · Драм (֏) · Евро (€) · Гуарани (₲) · гривна (₴) · Кип (₭) · Фунт стерлингов (£) · Турецкая лира (₺) · Азербайджанский манат (₼) · Найра (₦) · Филиппинское песо (₱) · Риель (៛) · Рубль Русский (₽) · Индийская рупия (₹) · Шекель (₪) · тенге (₸) · Тугрик (₮) · Вон (₩) · Йена или юань (¥) |
<img src=»https://fr.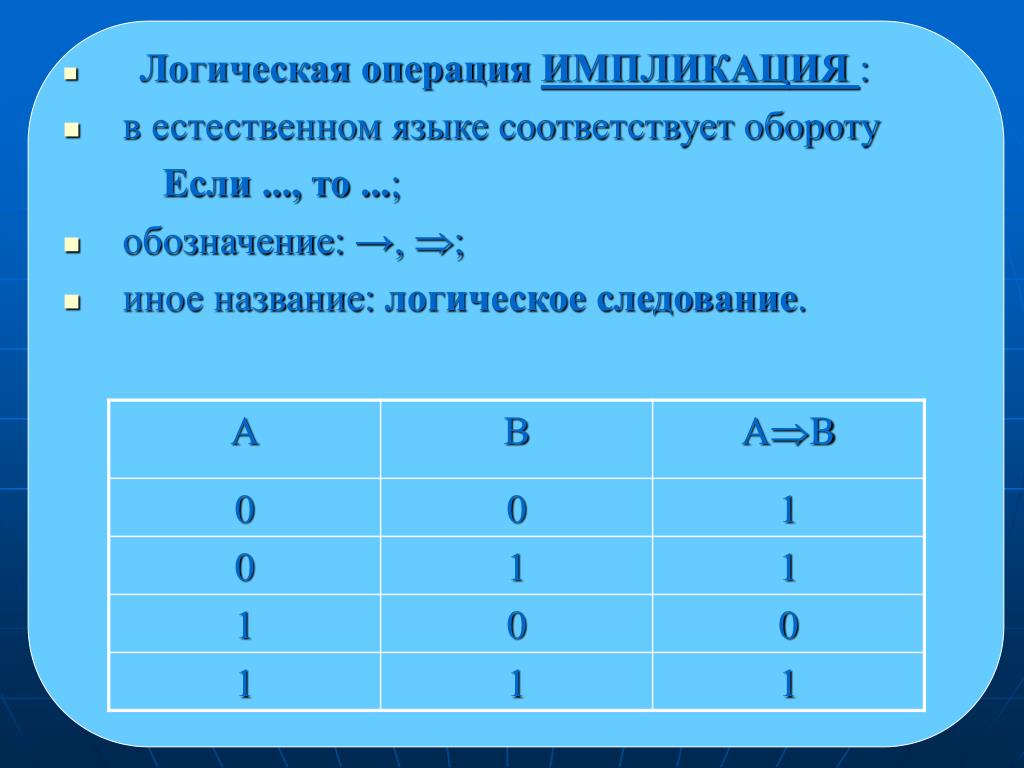 wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
Основы алгебры логики
8
3.2. Основы алгебры логики
В цифровых устройствах (сокращённо ЦУ) используются только два символа 0 и 1, поэтому алгебра логики использует логические переменные и функции от них, которые также принимают только два значения — 0 и 1. В логике символы 0 и 1 не цифры. Единица обозначает истину, символ 0 — ложь. Основы алгебры логики придумал в середине XIX века ирландский математик Джон Буль, поэтому алгебра логики иногда называется булева алгебра.
В
алгебре логики операции сложения и
умножения заменяют операцией логического
умножения,
которую называют конъюнкция,
и операцией логического
сложения (дизъюнкция).
Для обозначения операций сложения и
умножения используют специальные
символы: \/ — логическое сложение, /\ — логическое умножение, но для простоты
можно обозначать привычными «+» и
«х», «х» — это знак умножения.
Операция логического сложения обозначается союзом «ИЛИ«.
Выражение a + b означает «или a или b«. т. е. если и a, и b равно нулю, то и результат равен нулю. Результат равен единице, если хотя бы одна из переменных равна единице. Результат также будет единицей, если обе переменных равны единице.
Логическое умножение обозначается союзом «И».
Выражение a x b означает «a и b», т. е. если a и b равны нулю, то и результат равен нулю. Если одна из переменных равна единице, другая нулю, то результат все равно равен нулю. Результат равен единице, если обе переменных равны единице.
В двух словах: для логического сложения результат равен нулю только при совпадении нулей, для логического умножения результат равен единице только при совпадении единиц.
Есть
еще операция отрицания,
обозначаемое «НЕ«.
Обозначается отрицание чертой над
обозначением переменной или символом ¬,
стоящим перед переменной. Например, ā означает отрицание a.
По-другому это отрицание называется инверсией.
То есть, если a
= 1, то ā = 0 и наоборот. Отрицание может быть не
только одной переменной, но и целого
выражения.
Например, ā означает отрицание a.
По-другому это отрицание называется инверсией.
То есть, если a
= 1, то ā = 0 и наоборот. Отрицание может быть не
только одной переменной, но и целого
выражения.
Понятие двоичной переменной, логических операций И, ИЛИ, НЕ образуют систему аксиом алгебры логики.
Аналогично обычной алгебре, в булевой действительны свойства перестановки, сочетательности и распределительности:
a + b = b + a |
a x b = b x a |
a + (b + c) = (a + b) + c |
a x (b x c) = (a x b) x c |
a x (b + c) = a x b + a x c |
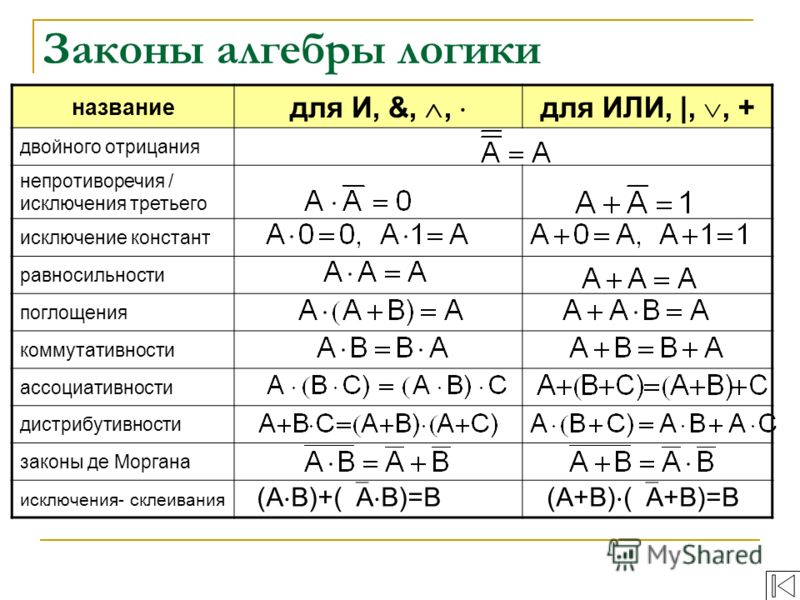
Помимо этих есть и другие, свойственные только алгебре логики, законы:
Законы одинарных элементов |
a x 1 = a |
a + 1 = 1 |
a x 0 = 0 |
a + 0 = a |
Законы отрицания (правила де Моргана) |
a x ā = 0 |
a + ā = 0 |
= ā + |
= ā + |
Распределительность дизъюнкции |
a + (b x c) = (a x b) + (a x c) |
Правила поглощения |
a + (a x b) = a |
a x (a + b) = a |
Эти
правила и законы позволяют упростить
логические уравнения и функции. Рассмотрим
логические элементы, реализующие
логические функции.
Рассмотрим
логические элементы, реализующие
логические функции.
Схема «И»
Изображение логического элемента «И» на схемах ЦУ:
Таблица истинности:
x2 | x1 | y |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Таблица
поясняет, как работает логический
элемент, т. е. какой сигнал есть на его
выходе при определенных сигналах на
входе. Таблицы истинности присущи всем ЦУ.
В этой таблице символы x1 и
x2означают
входные сигналы, y —
выходные. Причем входы принято обозначать
слева (это касается любых устройств),
выходы — справа. Переменная х1 обозначает младший разряд, x2 —
старший. Судя по таблице, единица будет
на выходе только тогда, когда на обоих
входах будут единицы. Символ & говорит
о том, что это элемент «И».
е. какой сигнал есть на его
выходе при определенных сигналах на
входе. Таблицы истинности присущи всем ЦУ.
В этой таблице символы x1 и
x2означают
входные сигналы, y —
выходные. Причем входы принято обозначать
слева (это касается любых устройств),
выходы — справа. Переменная х1 обозначает младший разряд, x2 —
старший. Судя по таблице, единица будет
на выходе только тогда, когда на обоих
входах будут единицы. Символ & говорит
о том, что это элемент «И».
Схема «ИЛИ»
Изображение логического элемента «ИЛИ» на схемах ЦУ:
Таблица истинности:
x2
x1
y
0
0
0
0
1
1
1
0
1
1
1
1
То
есть, единица на выходе тогда, когда
хотя бы на одном из входов присутствует
единица. Символ 1 говорит
о том, что это элемент «ИЛИ«.
Символ 1 говорит
о том, что это элемент «ИЛИ«.
2курс Схема «НЕ»
Изображение логического элемента «НЕ», иначе инвертора:
Таблица истинности:
x | y |
0 | 1 |
1 | 0 |
Видно,
этот элемент проще всех. О том, что это
инвертор, говорит кружок на выходе
элемента. В электронике принято кружком
обозначать инверсию сигнала, т. е.
переворот фазы на 180 градусов. Вспомните
операционный усилитель (ОУ),
неинвертирующий вход как обычно,
инвертирующий с кружком, т. к. на выходе ОУ при
подаче сигнала на инвертирующий вход
сигнал переворачивается по фазе на 180
градусов, т. е. инвертируется.
е. инвертируется.
Теперь рассмотрим еще пару элементов, имеющих некоторые особенности.
Базисные элементы
Базисом называется совокупность элементов, с помощью которых схемотехнически можно реализовать устройство любой сложности. Простым языком базис — это те элементы, при помощи которых можно сделать любое устройство цифровой техники. Интересно, что этих базисных элементов всего 2.
Базис «И-НЕ»
И-НЕ — это схема И и схема НЕ, сложенные вместе. Операция, которую производит такой элемент называется инверсией логического умножения или отрицанием логического умножения, или инверсией конъюнкции и еще штрих Шеффера. Штрихом она называется потому, что в виде формулы операция И-НЕ записывается так: y = x1 | x2. Вертикальная черта между иксами и есть штрих.
Логический элемент И-НЕ на схемах ЦУ изображается так:
Таблица истинности:
x2 | x1 | y |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Сначала
как бы умножаем (логически), а потом все
это отрицаем (логически). Если к элементу И (см.
выше) прицепить на выход инвертор, то
получим такой вот элемент И-НЕ.
Ну и если к элементу И-НЕ прицепить на выход инвертор, то получим
элемент И.
Если у элемента И-НЕ замкнуть входы, то получится тот самый
инвертор.
Если к элементу И (см.
выше) прицепить на выход инвертор, то
получим такой вот элемент И-НЕ.
Ну и если к элементу И-НЕ прицепить на выход инвертор, то получим
элемент И.
Если у элемента И-НЕ замкнуть входы, то получится тот самый
инвертор.
Базис ИЛИ-НЕ
Здесь все по аналогии с элементом И-НЕ. Операция, выполняемая элементом ИЛИ-НЕ, называется инверсией логического сложения или инверсией дизъюнкции и еще стрелка Пирса. Стрелка потому, что в виде формулы функция записывается так: y = x 1↓ x2. Символ между иксами и есть стрелка Пирса.
Логический элемент ИЛИ-НЕ на схемах ЦУ изображается так:
Таблица истинности:
x2 | x1 | y |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 0 |
Аналогично,
если к выходу элемента ИЛИ-НЕ прицепить инвертор, то получится элемент ИЛИ.
Существуют и другие элементы. Они представляют собой комбинацию перечисленных.
Рассмотрим Элемент “ИСКЛЮЧАЮЩЕЕ-ИЛИ”
Операция, выполняемая таким элементом, называется сложение по модулю два и обозначается плюсом в кружочке, т. е. символом . В виде уравнения функция записывается так: X1X2. Читается это, как «либо икс один, либо икс два».
Изображение элемента ИСКЛЮЧАЮЩЕЕ-ИЛИ на схемах ЦУ:
Таблица истинности:
x2 | x1 | y |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Этот элемент можно заменить логическими элементами И, ИЛИ, НЕ, так как
Для
иллюстрации составим схему этой функции
из базисных элементов.
Таким образом, зная свойства цифровых устройств и основы булевой алгебры, любой логический элемент можно заменить другими логическими элементами. Этот метод имеет и обратное направление. Если в какой-то схеме стоит изображенная на нашем рисунке её часть, в виде подсхемы, она легко заменяется на один элемент ИСКЛЮЧАЮЩЕЕ-ИЛИ. Следуя этому принципу можно менять элементную базу проектируемого цифрового устройства. Главное, чтобы в этом был смысл, чтобы улучшались характеристики устройства – функциональные или конструктивные, производственные или экономические.
Элементы алгебры логики (8 класс, информатика)
4.4
Средняя оценка: 4.4
Всего получено оценок: 332.
4.4
Средняя оценка: 4.4
Всего получено оценок: 332.
Одним из направлений теоретической информатики является алгебра логики. Основы алгебры логики изучаются в школьном курсе информатики в 8 классе. Кратко об элементах алгебры логики можно прочитать в данной статье.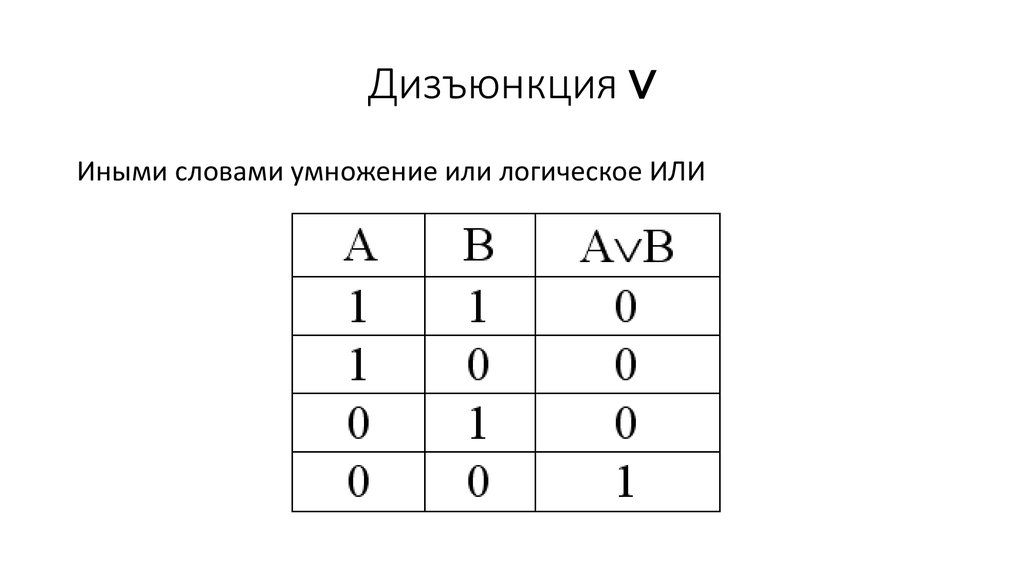
Элементы алгебры логики
Одним из разделов теоретической информатики является алгебра логики. Некоторые элементы алгебры логики доступны для понимания уже на школьном уровне.
Первые элементы алгебры логики были описаны в 19 веке в работах английского математика Джорджа Буля. Он первый высказал мысль о связи логики с математикой.
Высказывания
Объектом изучения алгебры логики являются высказывания, которые представляют собой повествовательные предложения, которые могут быть однозначно оценены как истинные или ложные. Истинность высказывания обозначают единицей, ложность – нулем. Примером высказывания может быть предложение «Москва столица Российской федерации».
Высказывания принято обозначать латинскими буквами.Не все предложения, несущие ту или иную информацию можно назвать высказываниями. Например, вопросительные или побудительные предложения – это не высказывания. Также не являются высказываниями математические выражения с переменными.
Например, не являются высказываниями следующие предложения:
- Сколько весит слон?
- Летайте самолетами Аэрофлота!
- 5*х + 8*y = 24
- Этот фильм самый лучший.

Алгебра логики изучает методы работы с высказываниями.
Действия над высказываниями
Высказывания как объекты могут быть операндами следующих логических действий
- Пересечение.
- Объединение.
- Инверсия.
Наглядно логические операции поясняют круги Эйлера или диаграммы Венна.
Пересечение
Пересечение – это действие над высказываниями, в результате которого будет получено новое высказывание истинное только в том случае, когда и исходные высказывания одновременно истинны.
Например, для высказываний «На каникулах я поеду в Волгоград» и «Выходные я проведу у бабушки» результатом операции пересечения будет новое высказывание «На каникулах я поеду в Волгоград и выходные я проведу у бабушки», которое является истиной только в том случае, когда истины оба исходных утверждения одновременно
Пересечение также называют логическим умножением, конъюнкцией или логическим И.
Обозначают знаками И, & или ∩.
На диаграмме операция пересечения выглядит как закрашенная область – представляющая собой общую для каждого операнда часть.
Объединение
Объединение – представляет собой действие над двумя высказываниями, в результате которого будет получено новое высказывание, ложное в том случае, когда одно из двух исходных операндов ложно.
Например, для исходных высказываний «На каникулах я поеду в Волгоград» и «На каникулах я поеду в Питер» результатом операции объединения будет высказывание «На каникулах я поеду в Волгоград или на каникулах я поеду в Питер», которое ложно только в том случае, когда ложны оба исходных высказывания. Если хотя бы одно из первоначальных высказываний является правдой, то и результат будет иметь значение «Истина».
Объединение также называют логическим сложением, дизъюнкцией, логическим ИЛИ.
Для ее обозначения используются знаки: ИЛИ, +, U.
Рис. 2. Диаграмма Венна для операции объединенияНа диаграмме Венна операция объединения представляет собой всю область, относящуюся и к первому и ко второму операнду.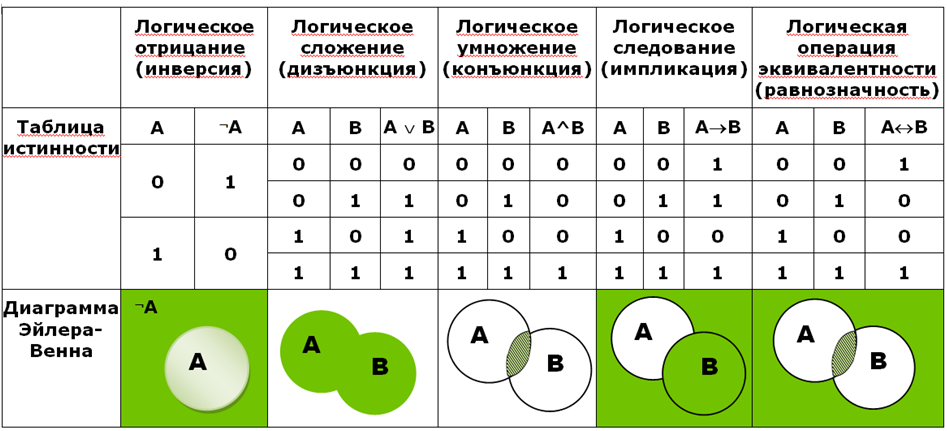
Инверсия
Инверсия – унарная логическая операция, заключающаяся в изменении на противоположное значение.
Например, высказывание «На каникулах я поеду в Волгоград» в инверсной форме будет выглядеть так «На каникулах я не поеду в Волгоград».
Инверсию обозначают знаками НЕ, ¬, ¯.
Инверсия на диаграмме Венна выглядит как область, не относящаяся к операнду.
Рис. 3. Диаграмма Венна для операции инвертированияАксиомы алгебры логики
В математике есть понятие аксиома – постулат, не требующий доказательств.
В математической логике также есть бездоказательные утверждения, касающиеся логических операций над высказываниями.
Для объединения справедливы аксиомы:
- А + 0 = А
- А + 1 = 1
- А + А = А
- А + НЕ(А) = 1
Для пересечения характерны такие аксиомы:
- А & 0 = 0
- А & 1 = А
- А & А = А
- А & НЕ(А) = О
Для операции инверсии применима аксиома двойного отрицания НЕ (НЕ (А)), когда дважды проинвертировав операнд получают в итоге само исходное значение.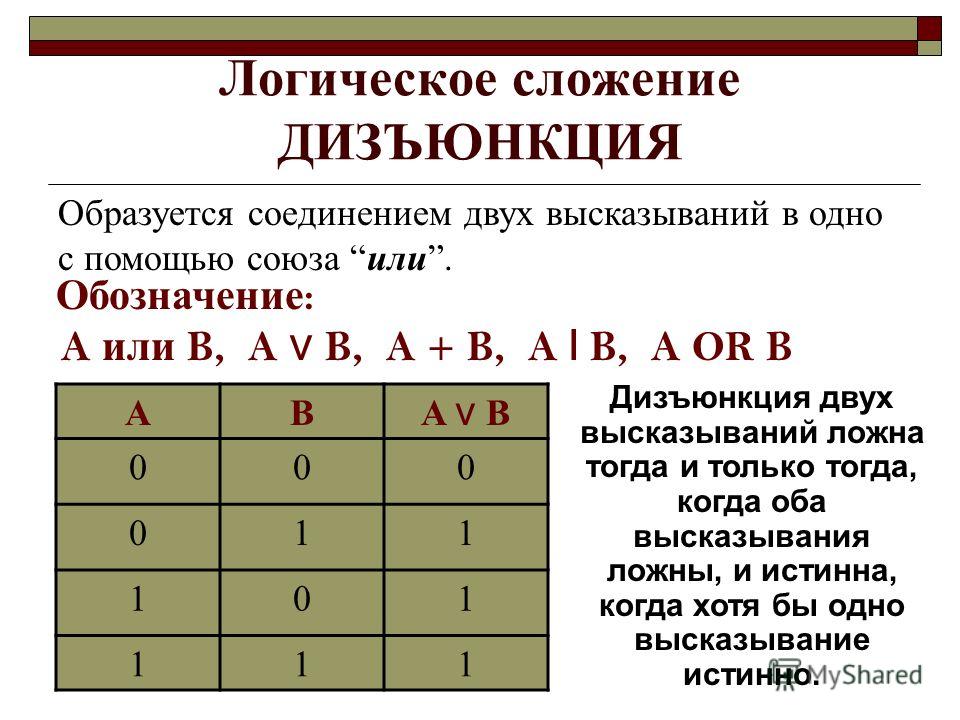
Что мы узнали?
Алгебра логики стоит на стыке математики и информатики и составляет теоретическую базу, на основе которой строятся методы работы с информацией. Объектом изучения этого направления является высказывания. Основными логическими операциями являются пересечение, объединение и инверсия. В алгебре логики действуют ряд аксиом.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Некит Розводовский
9/10
Алиса Волк
6/10
Оценка статьи
4.4
Средняя оценка: 4.4
Всего получено оценок: 332.
А какая ваша оценка?
Элементы алгебры логики. Логические операции
На этом уроке мы с вами познакомимся с такими логическими операциями, как инверсия, конъюнкция и дизъюнкция. А также научимся решать задачи с использованием этих операций.
Мы с вами уже знаем, что высказывание
– это предложение на любом языке, содержание которого можно однозначно
определить, как истинное или ложное.
Высказывания бывают простыми и сложными.
Простое высказывание – это высказывание, в котором никакая его часть сама не является высказыванием.
К примерам простых высказываний можно отнести следующие предложения:
«Минск – столица Беларуси.»
«Монитор является устройством хранения информации».
Первое простое высказывание истинно, а второе – ложно.
Сложные или же составные высказывания – это высказывания, которые строятся из простых с помощью логических операций.
Примером сложного высказывания будет следующее предложение:
«В интернете можно найти много полезной информации и пообщаться с друзьями». Это высказывание истинно.
Оно высказывание состоит из двух: «В интернете можно найти много полезной информации.», «В интернете можно пообщаться с друзьями». В данном случае оба простых высказывания истинны.
А сейчас давайте узнаем,
какие существуют основные логические операции. Для этого рассмотри таблицу.
Для этого рассмотри таблицу.
В первом столбце у нас указаны названия логических операций, а во втором – логические связки.
Логическая связка – это союзы или выражения, которые употребляются в естественном языке для соединения простых высказываний в сложные.
Итак, первая логическая операция – инверсия. Ей соответствуют следующие логические связки: «не», «неверно, что». Вторая – конъюнкция и соответственно её логические связки: «и», «а», «но», «хотя». И последняя, третья логическая операция – дизъюнкция. У неё всего одна логическая связка «или».
Прежде чем приступить к рассмотрению всех логических операций, давайте рассмотрим таблицу, в которой указаны способы обозначения истинности и ложности логических высказываний. Существуют различные способы, но все они являются верными.
То есть мы можем написать
просто словами на русском языке: Истинна или Ложь. Или же сократить их до
первых букв. Также можно писать на английском языке:
True или False.
Или также сократить до первых букв. И последнее обозначение — это 1 и 0, где 1
– это истина, а 0 – ложь. Мы с вами будем использовать числа ноль и один.
Также можно писать на английском языке:
True или False.
Или также сократить до первых букв. И последнее обозначение — это 1 и 0, где 1
– это истина, а 0 – ложь. Мы с вами будем использовать числа ноль и один.
А теперь давайте подробнее познакомимся с логическими операциями.
Итак, конъюнкция – это логическая операция, которая объединяет два высказывания в одно новое, которое будет являться истинным тогда и только тогда, когда оба исходных высказывания истинны. Слово конъюнкция произошло от латинского «Conjunctio», которое обозначает «союз, связь».
Давайте разберёмся на примере. Нам даны два высказывания А и B. А = «У квадрата четыре стороны». B = «У ромба четыре стороны.».
Значит новое высказывание будет звучать следующим образом: «У квадрата четыре стороны и у ромба четыре стороны». Так как высказывания А и В истинны, то новое высказывание также будет истинно.
Давайте узнаем, как
обозначается знак конъюнкции в различных сферах его применения.
Итак, в естественном языке конъюнкция соответствует союзу «И». В алгебре конъюнкция может обозначаться с помощью нескольких знаков: знака амперсанда, знака конъюнкции (он похож на крышу дома, а, чтобы набрать его на клавиатуре, нужно нажать на клавиши слэш и бэкслэш (обратный слэш)), а также знака умножения.
В языках программирования для обозначения конъюнкции используется английский союз «And». Также в некоторых языках программирования может использоваться одинарный или двойной знак амперсанда.
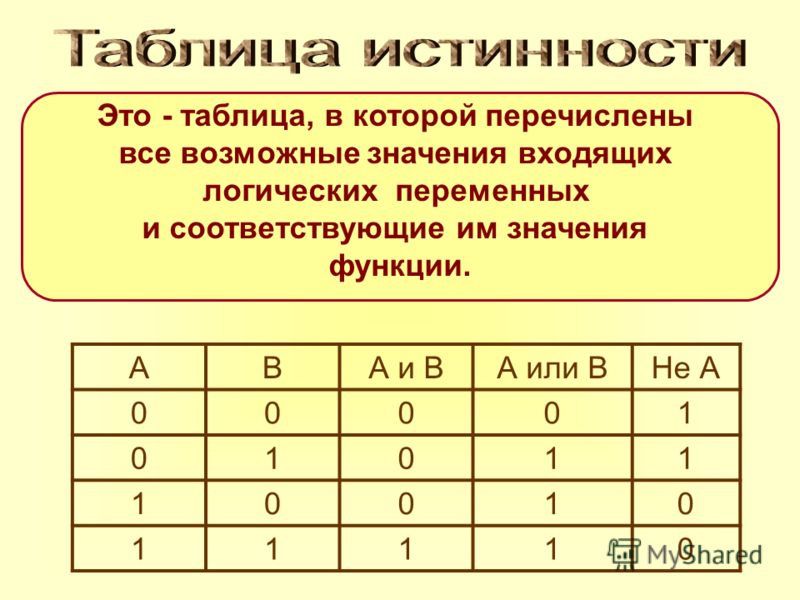
А сейчас мы с вами составим таблицу истинности для конъюнкции.
Пусть у нас есть два высказывания А и B. Они будут заголовками первого и второго столбца. А новое выражение, которое образуется с помощью конъюнкции обозначим А и B – и это будет являться заголовком для третьего столбца.
Далее, вспомним, что если высказывание истинно, то ему соответствует число 1, а если ложно – 0.
Допустим, высказывания А
и B – оба ложны. Занесём нули в соответствующие
ячейки.
Занесём нули в соответствующие
ячейки.
Из определения мы знаем, что новое высказывание будет истинно тогда и только тогда, когда истинны исходные высказывания. А так как у нас два высказывания ложны, значит и при их соединении мы получим новое ложное высказывание.
Далее, пусть А будет ложным, а B – истинным. Новое высказывание будет ложным, так как высказывание А – ложно.
Теперь сделаем наоборот, пусть А – истинно, B – ложно. И снова новое высказывание будет ложным.
А если высказывания А и B будут истинными, то новое высказывание также будет истинно. Так как в определение сказано, что новое высказывание будет истинно тогда и только тогда, когда истинны исходные высказывания.
Мы с вами рассмотрели все возможные значения исходных высказываний А и B.
Так же очень легко
запомнить таблицу истинности для конъюнкции, если представить её в виде
электрической цепи с двумя последовательными выключателями.
Лампочка загорится только в том случае, если два выключателя будут включены (замкнуты).
То есть тогда новое высказывание будет истинно.
Конъюнкцию также называют логическим умножением. Давайте посмотрим ещё раз на таблицу истинности.
Какие числа мы получим в результате перемножение первого и второго столбцов? В первых трёх строках третьего столбца будут нули, так как любое число при умножении на 0 даёт 0. А вот 1 на 1 равно 1. То есть мы получили такие же данные, как и при первом построении таблицы истинности.
А теперь переходим к дизъюнкции.
Дизъюнкция – это логическая операция, которая объединяет два высказывания в одно новое, которое будет являться ложным тогда и только тогда, когда ложны оба исходных высказывания. Слово дизъюнкция произошло от латинского «Disjunctio», которое обозначает «разобщение».
Рассмотрим пример. Нам
даны два высказывания А и B. А = «У квадрата три стороны». B =
«У
ромба две стороны.».
А = «У квадрата три стороны». B =
«У
ромба две стороны.».
Значит новое высказывание будет звучать следующим образом: «У квадрата три стороны или у ромба две стороны». Так как высказывания А и B ложны, то новое высказывание также будет ложно.
В различных сферах применения, дизъюнкция обозначается по-разному.
В естественном языке это слово «ИЛИ». В алгебре высказываний используется следующий знак: «V». Или знак «+». В программировании в основном используется английское «OR». Но в некоторых языках программирования дизъюнкция обозначается следующими знаками: «|», «||».
А теперь давайте составим таблицу истинности для дизъюнкции. Нам даны два высказывания А и B. Их значения мы будем вносить в первых два столбца. А в третий будем вносить обозначения, которые получаются при образовании нового высказывания с использованием дизъюнкции.
Итак, пусть наши два
высказывания ложны. В определении сказано, что новое высказывание будет ложно
тогда и только тогда, когда ложны два высказывания. Значит в нашем случае новое
высказывание будет ложно.
В определении сказано, что новое высказывание будет ложно
тогда и только тогда, когда ложны два высказывания. Значит в нашем случае новое
высказывание будет ложно.
Далее, пусть А будет ложным, а B – истинным. Новое высказывание будет истинным. Так как высказывание B – истинно.
Теперь сделаем наоборот, пусть А – истинно, B – ложно. И снова новое высказывание будет истинным.
А если высказывания А и B будут истинными, то новое высказывание снова будет истинно. Так как в определение сказано, что новое высказывание будет ложно тогда и только тогда, когда ложны исходные высказывания.
И снова для запоминания таблицы истинности можно использовать электрическую цепь с двумя параллельными выключателями.
То есть лампочка загорится в том случае если будет включён (замкнут), хотя бы один выключатель.
Дизъюнкцию ещё называют логическим
сложением.
Давайте сложим данные из первого и второго столбцов. В результате мы получим такие же данные, как и при первом построении таблицы истинности. Обратим внимание на последнюю строку таблицы. При сложении двух логических единиц всё равно получается логическая единица. Алгебра логики оперирует только двумя значениями – ложью (логический ноль) и истиной (логическая единица). Истина не может быть двойной, тройной или истиной в квадрате, поэтому при сложении двух истин результатом будет просто истина, то есть цифра один.
И последняя логическая операция, которую мы с вами рассмотрим – это инверсия.
Инверсия – это логическая операция, которая преобразует исходное высказывание в новое, значение которого противоположно исходному. Слово инверсия произошло от латинского «Inversio», которое обозначает «переворачивание, перестановка».
Здесь всё очень просто.
Если исходное высказывание было истинно, то после инверсии оно становится
ложным, а если исходное высказывание было ложным, то после операции инверсии
оно становится истинным.
Для примера возьмём высказывание «Я знаю английский язык». После операции инверсии мы получим новое высказывание «Я не знаю английский язык».
Давайте посмотрим, как обозначается инверсия в различных сферах её применения.
В естественном языке инверсии соответствуют речевой оборот «неверно, что» и частица «не». В алгебре высказывания инверсия обозначается следующими знаками: «¬», «ˉ». А вот в сфере программирования используется английское слово «NOT».
Нам осталось составить таблицу истинности для инверсии. Нам дано исходно высказывание А. Его значения будем записывать в первый столбик таблицы. А вот значение высказывания, которое получается после инверсии, будем записывать во второй столбик.
Итак, если наше высказывание А ложно, то новое высказывание будет истинно.
А если А – истинно, то новое высказывание после инверсии будет ложно.
Инверсию также называют логическим
отрицанием.
Из вышесказанного можно сделать вывод, что, при применении к высказыванию логического отрицания, в него добавляется речевой оборот «неверно, что» или же частица «не». Частица «не» прибавляется к глаголу.
Также любое сложное высказывание можно записать в виде логического выражения.
Логическое выражение – это выражение, которое содержит переменные, знаки логических операций и скобки.
Как и в математики, при выполнении логических операций в логическом выражении существует свой порядок действий. Сначала выполняется инверсия, затем конъюнкция, а после дизъюнкция. То есть, если записать все действия математическими знаками, то получим, что в начале выполняется действие отрицания (число меняется на противоположное), затем конъюнкция (умножение), а после всего дизъюнкция (сложение). Порядок выполнения действий можно изменять с помощью скобок.
А теперь давайте
рассмотрим пример. На доске нарисованы точки и круги. Пусть А = «Внутри круга А
находятся 190 точек» и В = «Внутри круга В находятся 230 точек». Всего на доске
нарисовано 500 точек. На пересечении обоих кругов одновременно нарисовано 70
точек. Для какого количества точек будут истины следующие выражения:
Пусть А = «Внутри круга А
находятся 190 точек» и В = «Внутри круга В находятся 230 точек». Всего на доске
нарисовано 500 точек. На пересечении обоих кругов одновременно нарисовано 70
точек. Для какого количества точек будут истины следующие выражения:
1. НЕ А.
2. А V В.
3. НЕ (А V В)?
Переходим к решению. Нам даны два высказывания А = «Внутри круга А находятся 190 точек» и B = «Внутри круга B находятся 230 точек». То есть высказывание А верно для 190 точек, а B – для 230 точек. Давайте для начала решим задачу с использованием кругов Эйлера. Рисуем один большой круг, который будет обозначать доску. Внутри этого круга рисуем ещё два – А и B.
А сейчас изобразим графически множества точек, для которых истины вышеприведённые выражения. Первое: НЕ А. То есть будет закрашено всё пространство, кроме круга А.
Во втором случае, А V
B, будут закрашены два круга А и B.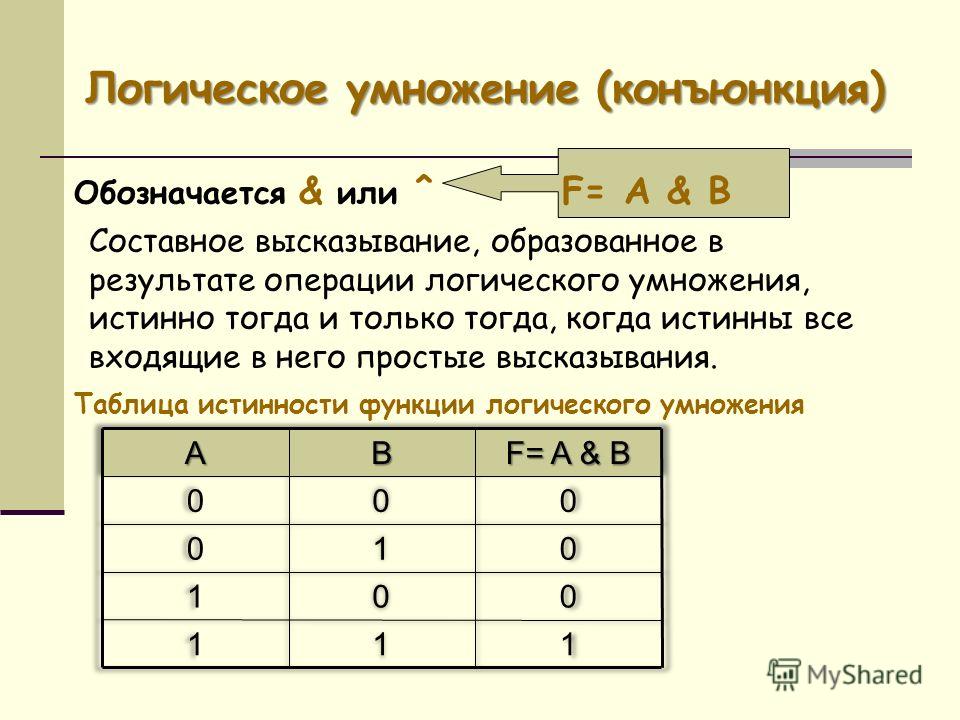
А в третьем – всё пространство, кроме кругов А и B.
Данные изображения помогут нам решить задачу.
Итак, нам нужно найти количество точек, для которых будет истинно выражение «НЕ А». Смотрим на наш круг.
Это все точки, кроме тех, которые входят в круг А.
500 – 190 = 310.
Таким образом для 310 точек истинно выражение «НЕ А».
Второе: А V B. Смотрим на графическое представления для этого выражения.
Это все точки, которые входят в круги А и B. Для того, чтобы найти количество точек, давайте те точки, которые входят только в круг А обозначим буквой x, а которые входят только в B – буквой y. А точки, которые входят и в А и в Бэ обозначим буквой z. В круг А входят 190 точек, но в них есть точки z, которые входят и в А и в B.
z = 70.
Значит то наш x будет вычисляться следующим образом:
x
=
190 – 70 = 120.
Аналогично и с кругом B, в который входят 230 точек.
y = 230 – 70 = 160.
Для того, чтобы вычислить точки, которые входят в А или B, нам нужно сделать следующее:
70 + 120 + 160 = 350.
То есть для 350 точек истинно выражения А V B.
Ну и последнее выражение «НЕ (А V B)».
Это все точки, которые не входят в круги А и B. Для их нахождения нужно:
500 – 350 = 150.
То есть для 150 точек истинно выражение «НЕ (А V B)».
Задача решена. И сейчас мы с вами подошли к подведению итогов урока.
Сегодня мы с вами узнали, что такое сложные высказывания, познакомились с такими логическими операциями, как конъюнкция, дизъюнкция и инверсия. Построили таблицы истинности для трёх логических операций, а также решили задачу с использованием кругов Эйлера и логических операций.
Логические выражения в Python 3
24 декабря, 2016 12:21 пп 31 413 views | 1 комментарийPython | Amber | 1 Comment
Логический тип данных (или Boolean) – это примитивный тип, который принимает одно из двух возможных значений: истину (True) или ложь (False). Этот тип используется во многих языках программирования для построения алгоритмов и управления поведением программ.
Этот тип используется во многих языках программирования для построения алгоритмов и управления поведением программ.
Примечание: Название этого типа данных (Boolean) всегда пишется с заглавной буквы, поскольку он назван в честь математика Джорджа Буля, который занимался исследованиями математической логики. Значения True и False тоже пишутся с большой буквы – в Python они являются специальными значениями.
Данное руководство ознакомит вас с основами булевой логики в Python: операторами сравнения, логическими операторами, таблицами истинности и т.п.
Операторы сравнения
В программировании операторы сравнения используются при оценке и сравнении значений для последующего сведения их к одному логическому значению (True или False).
Операторы сравнения Python 3 представлены в этой таблице:
| Оператор | Значение |
| == | Проверяет равенство между компонентами; условие истинно, если компоненты равны. |
| != | Проверяет равенство между компонентами; условие истинно, если компоненты НЕ равны. |
| < | Оценивает значение левого компонента; условие истинно, если он меньше, чем правый. |
| > | Оценивает значение левого компонента; условие истинно, если он больше, чем правый. |
| <= | Оценивает значение левого компонента; условие истинно, если он меньше или равен правому компоненту. |
| >= | Оценивает значение левого компонента; условие истинно, если он больше или равен правому компоненту. |
Попробуйте поработать с этими операторами, чтобы понять, как они действуют. Для начала создайте пару переменных:
x = 5
y = 8
Теперь сравните значения переменных с помощью вышеперечисленных операторов.
x = 5
y = 8
print("x == y:", x == y)
print("x != y:", x != y)
print("x < y:", x < y)
print("x > y:", x > y)
print("x <= y:", x <= y)
print("x >= y:", x >= y)
x == y: False
x != y: True
x < y: True
x > y: False
x <= y: True
x >= y: False
Следуя математической логике, Python оценивает соотношения между значениями переменных так:
- 5 равно 8? Ложь
- 5 не равно 8? Истина
- 5 меньше 8? Истина
- 5 больше 8? Ложь
- 5 меньше или равно 8? Истина
- 5 больше или равно 8? Ложь
Также операторы сравнения можно применять к числам с плавающей точкой и строкам.
Примечание: Строки чувствительны к регистру; чтобы отключить такое поведение, нужно использовать специальный метод.
Читайте также: Методы строк в Python 3
Попробуйте сравнить две строки:
Hello = "Hello"
hello = "hello"
print("Hello == hello: ", Hello == hello)
Hello == hello: False
Строки Hello и hello содержат одинаковый набор символов, однако они не равны, поскольку одна из них содержит символы верхнего регистра. Попробуйте добавить ещё одну переменную, которая также будет содержать символы верхнего регистра, а затем сравните их.
Hello = "Hello"
hello = "hello"
Hello_there = "Hello"
print("Hello == hello: ", Hello == hello)
print("Hello == Hello_there", Hello == Hello_there)
Hello == hello: False
Hello == Hello_there: True
Также для сравнения строк можно использовать операторы > и <. Python выполнит лексикографическое сравнение строк на основе значений символов ASCII.
Операторы сравнения можно применять к логическим значениям True и False:
t = True
f = False
print("t != f: ", t != f)
t != f: True
Обратите внимание на разницу между операторами = и ==.
x = y # Оператор присваивания. Устанавливает равенство между x и y (то есть присваивает x значение y).
x == y # Оператор сравнения. Проверяет равенство между x и y и оценивает выражение как истинное или ложное. Выражение истинно, если x и y равны.
Логические операторы
Для сравнения значений используется три логических оператора, которые сводят результат к логическому значению True или False.
| Оператор | Значение |
| and | Оператор «и»: выражение истинно, если оба его компонента истинны. |
| or | Оператор «или»: выражение истинно, если хотя бы один из его компонентов истинен. |
| not | Оператор «не»: изменяет логическое значение компонента на противоположное. |
Логические операторы обычно используются для оценки двух или больше выражений. Например, их можно использовать в программе, которая проверит:
- сдал ли студент экзамен
- и зарегистрирован ли он.
Если оба значения истинны, студент будет переведён на следующий курс.
Другой пример: программа с логическими операторами может проверять активность пользователя в онлайн-магазине:
- использовал ли он кредит магазина
- или заказывал ли он товары в течение последних 6 месяцев.
Для примера попробуйте сравнить три выражения:
print((9 > 7) and (2 < 4)) # Оба выражения истинны (True)
print((8 == 8) or (6 != 6)) # Одно из выражений истинно (True)
print(not(3 <= 1)) # Выражение ложно (False)
True
True
True
В первом случае оба выражения истинны, потому оператор and возвращает True.
Во втором случае истинно только значение 8 == 8. Поскольку хотя бы одно из предложенных условий истинно, оператор or возвращает True. Оператор and в таком случае выдал бы False.
Поскольку хотя бы одно из предложенных условий истинно, оператор or возвращает True. Оператор and в таком случае выдал бы False.
В третьем случае выражение 3 <= 1 ложно. Оператор not изменяет полученное логическое значение на противоположное: not False = True.
Теперь попробуйте сравнить числа с плавающей точкой.
print((-0.2 > 1.4) and (0.8 < 3.1)) # Одно из выражений ложно (False)
print((7.5 == 8.9) or (9.2 != 9.2)) # Оба выражения ложны (False)
print(not(-5.7 <= 0.3)) # Выражение истинно (True)
- Поскольку в первом примере одно из выражений ложно, and вернёт False. Оператор and оценивает выражение как истинное только тогда, когда оба компонента истинны.
- Поскольку оба выражения ложны, оператор or выдаст False.
- Поскольку выражение истинно, оператор not вернёт False (not True = False).
Примечание: Если вы не понимаете, как это работает, вам помогут разобраться таблицы истинности. Эту тему мы рассмотрим далее в этом руководстве.
Эту тему мы рассмотрим далее в этом руководстве.
Логические операторы можно объединять в составные выражения:
not((-0.2 > 1.4) and ((0.8 < 3.1) or (0.1 == 0.1)))
Выражение (0.8 < 3.1) or (0.1 == 0.1) истинно, поскольку оба математических выражения, из которых оно состоит, истинны. Оператор or вернёт True.
Полученное значение True становится компонентом следующего выражения: (-0.2 > 1.4) and (True). Оператор and выдаст False, потому что выражение -0.2 > 1.4 ложно. (False) and (True) = False.
Далее оператор not заменит полученное значение False на обратное ему логическое значение: not(False) = True. Значит, результат будет таким:
True
Таблицы истинности
Математическая логика – очень полезная в программировании область знаний. В данном руководстве мы ознакомимся с основными её аспектами.
Ниже представлены таблицы истинности для оператора сравнения == и всех логических операторов. Ими можно пользоваться при написании логических выражений. В таблицах перечислены общие случаи использования оператора, потому их рекомендуется выучить наизусть.
В таблицах перечислены общие случаи использования оператора, потому их рекомендуется выучить наизусть.
Таблица истинности оператора ==
| x | == | y | Результат |
| True | == | True | True |
| True | == | False | False |
| False | == | True | False |
| False | == | False | True |
Таблица истинности оператора AND
| x | and | y | Результат |
| True | and | True | True |
| True | and | False | False |
| False | and | True | False |
| False | and | False | False |
Таблица истинности оператора
OR| x | or | y | Результат |
| True | or | True | True |
| True | or | False | True |
| False | or | True | True |
| False | or | False | False |
Таблица истинности оператора NOT
| not | x | Результат |
| not | True | False |
| not | False | True |
Таблицы истинности – общие математические таблицы, которые используются в логике. Их полезно выучить наизусть, чтобы затем применять при построении алгоритмов и написании программ.
Их полезно выучить наизусть, чтобы затем применять при построении алгоритмов и написании программ.
Использование логических операторов для управления потоком
Для управления результатом и потоками данных программы можно использовать условные операторы (condition) с выражениями (clause).
Условные операторы оценивают значение как истинное или ложное.
Выражение – это блок кода, который идёт после условного оператора и определяет результат программы.
Ниже приведён блок кода, который показывает, как объединить условные операторы для управления потоком программы Python.
if grade >= 65: # условие
print("Passing grade") # выражение
else:
print("Failing grade")
Эта программа оценивает результат каждого студента и определяет, сдал он экзамен или нет. К примеру, если студент набрал 83, первое условие будет иметь значение True, и программа выведет на экран строку:
Passing grade
Если же студент набрал 59 баллов, первое условие будет ложно, потому программа выдаст:
Failing grade
Читайте также: руководство PEP 8
Заключение
Данное руководство охватывает основы работы с логическими данными Python.
Читайте также:
Типы данных в Python 3
Условные операторы в Python 3
Tags: Python, Python 3Полный список символов алгебры
Алгебра — это раздел математики, относящийся к манипулированию символами и их правилам. Ниже приводится подборка из символов из различных разделов алгебры, включая базовую алгебру, теорию чисел, линейную алгебру и абстрактную алгебру.
Для удобства чтения эти символы разбиты по функциям и темам на диаграммы и таблицы . Другие полные списки символов — с разбивкой по темам и типам — также можно найти на соответствующих страницах ниже (или на панели навигации).
Содержание
Предпочитаете версию в формате PDF?
Получите основную сводку математических символов в форме электронной книги — вместе с использованием каждого символа и кодом LaTeX.
Да. Это было бы полезно.
Константы
В алгебре константы — это символы, используемые для обозначения ключевых математических элементов и наборов. В следующих таблицах описаны наиболее распространенные из них — вместе с названием каждого символа, его использованием и примером.
В следующих таблицах описаны наиболее распространенные из них — вместе с названием каждого символа, его использованием и примером.
(Общие общие константы см. в разделе Общие математические константы.) 92 + 1 = 0$
Ключевые математические наборы
В алгебре одни наборы чисел (или другие более сложные объекты) встречаются чаще, чем другие. Эти наборы часто обозначаются некоторыми вариантами букв алфавита , многие из которых набраны жирным шрифтом на доске.
| Символ Название | Пояснение | Пример |
|---|---|---|
| $ \ mathbb {p} $ | Набор Prime Numbers | $ 127 \ in \ mathbb {p} $ |
| $ \ \ числа (начиная с $0$) | $0 \in \mathbb{N}_0$ | |
| $\mathbb{N}_1$ | Набор из натуральных чисел (начиная с $04$) | $0 \notin \mathbb{N}_1$ |
| $\mathbb{Z}$ | Набор из целых чисел | Для всех $x, y \in \mathbb{N}$, $x-y \in \mathbb{Z}$. |
| $\mathbb{Z}_+$ | Набор из натуральных чисел | $\mathbb{Z}_+ = \mathbb{N}_1$ |
| $\mathbb | Набор из рациональных чисел | $3.\overline{73} \in \mathbb{Q}$ |
| $\mathbb{Q}_p$ | Набор из p-адических чисел 54 9 $\mathbb{Q}_{10}$, $-1 = …999$ (как $1 + …999 = 0$). | |
| $\mathbb{A}$ | Набор из алгебраических чисел | $\sqrt{5} + 3 \in \mathbb{A}$ |
| $\mathbb 4 $\mathbb 4 Набор из действительных чисел | $i \notin \mathbb{R}$ | |
| $\mathbb{R}_+$ | Набор из положительных действительных чисел | Для всех $x, y \in \mathbb{R}_+$, $xy \in \mathbb{R}_+$. |
| $\mathbb{R}_-$ | Набор из отрицательных действительных чисел | Если $a, b \in \mathbb{R}_-$, то $a+b \in \mathbb{R}_-$. |
| $\mathbb{R}-\mathbb{Q}$ | Набор из иррациональных чисел | $\log 2 \in \mathbb{R}-\mathbb{Q}$ | Набор из мнимых чисел | $5i \in \mathbb{I}, 2+3i \notin \mathbb{I}$ |
| $\mathbb{C}$ | Набор из комплексных чисел | Существует число $x \in \mathbb{C}$ такое, что $x^2 + 2x + 3 = 0$. 92 + 2x +1$ 92 + 2x +1$ $\in \mathbb{Z}[x]$ |
Переменные
Поскольку алгебра занимается оперированием математическими символами, она часто использует широкий диапазон переменных как заполнители для различных объектов и количеств. В следующей таблице описаны наиболее распространенные из них, а также их соответствующее использование и пример.
| Название символа | Используется для | Пример |
|---|---|---|
| $m, n, p, q$ | Натуральные числа и целые числа | $m+n-2p = q$ |
| $a, b, c$ | 30 Коэффициент функции 9045 900 и уравнения | Линейное уравнение имеет общий вид $ax+by+c = 0$. |
| $x, y, z$ | Неизвестные в функциях и уравнениях | Если $14x + 2y = 4$, то $y = 2-7x$. |
| $\Delta$ | Дискриминант 9{(3,5)} \frac{i + j}{2}$ | |
| $z$ | Комплексные числа | $ |z_1 z_2| = |z_1| |z_2|$ |
| $f(x)$, $g(x, y)$, $h(z)$ | Функции | $g(f(x), 3) = h( x)$ |
| $\mathbf{u}, \mathbf{v}, \mathbf{w}$ (или $\vec{u}, \vec{v}, \vec{w}$) | Векторы | $2\mathbf{u} + 3\mathbf{v} = 5\mathbf{w}$ |
| $U, V, W$ | Векторные пространства | $U$ — подпространство векторного пространства $V$. |
| $ A, B, C $ | MATRICES | $ ab \ ne ba $ |
| $ \ lambda $ | eigenvalues | $ $. mathbf{v_0}$, $3$ — собственное значение $A$. |
| $G, H$ | Группы | Существует элемент $e \in G$ такой, что для всех $x \in G$ $x \circ e = x$. |
Разделители
В математике разделители — это символы, используемые для обозначения разделения между независимыми математическими объектами. В следующей таблице представлены некоторые из наиболее распространенных разделителей в алгебре. Общие общие разделители см. в разделе Общие разделители.
| Имя символа | Объяснение | Пример |
|---|---|---|
| \begin{bmatrix} x & y \\ w & z\end{bmatrix}$ | Индикаторы векторов/матриц | $\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + \begin{pmatrix} 4 \\ 5 \\ 6 \end{pmatrix} = \\ \ begin{pmatrix} 5 \\ 7 \\ 9 \end{pmatrix} $ |
| $\{ \}$ | Построитель наборов | $\{ -1, 3. \overline{5}, \ pi \} \in \mathbb{R}$ \overline{5}, \ pi \} \in \mathbb{R}$ |
| $\bigg\{$ | Кусочно-функциональный индикатор | $|x| = \begin{cases} x & x \ge 0 \\ -x & x<0 \end{cases}$ |
| $:$, $\mid$ | Маркер «такой, что» | $\mathbb{Q} =$ $\displaystyle \left\{ \frac{x}{y} \,\ middle|\, x \in \mathbb{Z}, y \in \mathbb{N} \right\}$ |
Символы, связанные с функциями
В качестве основного компонента алгебры функция играет ключевую роль роль в установлении правил, касающихся манипулирования символами. В следующей таблице описаны некоторые из наиболее распространенных операторов и обозначений, связанных с функциями, а также их значение и примеры. 93$ переводит число в свой куб.

Операторы
В алгебре операторов можно рассматривать как особый тип функции, отображающей одну или несколько математических единиц в другую, и часто получают специальные имена или обозначения из-за их повторения.
В частности, эти операторы часто связаны с числами , ключевыми функциями , линейной алгеброй и абстрактной алгеброй — подавляющее большинство из которых можно найти в таблицах ниже. Общие операторы см. в разделе Общие операторы.
Операторы, связанные с номером,
| Название символа | Объяснение | Пример | ||
|---|---|---|---|---|
| $ \ GCD (x, y) $ | 9003 GESTEM AMPARIOD DIVISIS DIVISISISISIOR $ | 9003 9003 GESTEM AMPARISIS DIVISISISIS DIVISISISISISISISIST $ $9003 GESTER Common DIVISISISISIS $ $ | 9003 GESTER AMPISOR. | $\gcd (20, 15) = 5$ |
| $\mathrm{lcm} (x, y)$ | Наименьшее общее кратное чисел $x$ и $y$ | $\mathrm{lcm } (x, y) = \dfrac{xy}{\gcd (x, y)}$ | ||
| $x \bmod y$ | Остаток от $x$ при делении на $y$ | $23 \bmod 4 = 3$ | ||
| $|x|$ | Абсолютное значение от $x$ | $|-| = |5| = 5 $ | ||
| $ \ lfloor x \ rfloor $ | Пол $ x | $ \ lfloor 5,999 \ rfloor = 5 $ | ||
| $ \ lceil x \ rceil $ | ||||
| $ \ lceil x \ rceil $ | ||||
| $ \ lceil x \ rceil $ | ||||
| $ \ lceil x \ rceil $ | ||||
| $ \ $x$ | Для всех $x \in \mathbb{R}$ $\lceil x \rceil-1 < x \le \lceil x \rceil$. 9y $ | |||
| $ \ ln x $ | Натуральная логарифмическая функция | $ \ ln 10 = \ ln 2 + \ ln 5 $ | ||
| $ \ x $ | ||||
| $\log 1000000 = 6$ | ||||
| $\log_b x$ | Логарифмическая функция по основанию $b$ | $\log_{11} 23 = \dfrac{\ln 23}{\ln 11} $ | ||
| $\sin x$, $\cos x$, $\tan x$, $\sec x$, $\csc x$, $\cot x$ | 6 92 \cdot 3 \cdot 5$, $\omega(60)=3$. | |||
| $\mathrm{id}_A (x)$ | Функция тождества на множестве $A$ | Для всех множеств $A$ $\mathrm{id}_A$ взаимно однозначно и на. | ||
| $\mathbf{1}_A(x)$, $\chi_A(x)$ | Индикаторная/характеристическая функция множества $A$ | $\mathbf{1}_{\mathbb{Q }}(x) = \\ \begin{case} 1 & x \in \mathbb{Q} \\ 0 & x \notin \mathbb{Q} \end{cases}$ | ||
| $\delta_{ij }$ | Дельта-функция Кронекера | Для каждой единичной матрицы $I$ $I_{ij}=\delta_{ij}$. |
Операторы, связанные с комплексными номерами
| Название символа | Объяснение | Пример |
|---|---|---|
| $ \ bar {z} $ | ||
| $ \ bar {z} $ | ||
| $ \ bar {z} $ | ||
| $ \ $ $ $ | ||
| $ \ $ $ | ||
. \overline{5 + 6i}= \\ 5-6i$ \overline{5 + 6i}= \\ 5-6i$ | ||
| $\Re(z)$ | Действительная часть комплексного числа $z$ 9{\pi i}$ |
Operators in Linear Algebra
| Symbol Name | Explanation | Example |
|---|---|---|
| $-\mathbf{v}$ | Аддитивное обратное число вектора $\mathbf{v}$ | $\mathbf{v} + (-\mathbb{v}) = \mathbf{0}$ |
| $k\mathbf{v}$ | Скалярное произведение вектора $\mathbf{v}$ на скаляр $k$ | $(-1)\mathbf{v}=-\mathbf{v}$ |
| $\mathbf{u} + \mathbf{v}$ | Сумма векторов $\mathbf{u}$ и $\mathbf{v}$ | $\mathbf{u} + \mathbf{0} = \mathbf{u}$ |
| $\mathbf{u}-\mathbf{v}$ | Разница векторов $\mathbf{u}$ и $\mathbf{v}$ | $(5, 7, 1)-(3, 2, 5)=$ $(2, 5, -4)$ |
| $\mathbf{u} \cdot \mathbf{v}$ | Скалярное произведение векторов $\mathbf{u}$ и $\mathbf{v}$ | $(5\mathbf{u}) \cdot (7\mathbf{v}) = 35 (\mathbf{u} \cdot \mathbf{v})$ |
| $\mathbf{u} \times \mathbf{v}$ | Перемножение векторов $\mathbf{u}$ и $\mathbf{v}$ | $\mathbf{v} \times \mathbf{u} =\, – ( \ mathbf{u} \times \mathbf{v} )$ |
| $\mathbf{u} \wedge \mathbf{v}$ | Произведение клиньев векторов $\mathbf{u}$ и $\mathbf {v}$ | $\mathbf{u} \клин \mathbf{v} =\, – (\mathbf{v} \клин \mathbf{u})$ |
| $\langle \mathbf{u}, \mathbf{v} \rangle$ | Скалярное произведение векторов $\mathbf{u}$ и $\mathbf{v}$ | В евклидовом пространстве , $\langle \mathbf{u}, \mathbf{v} \rangle = \mathbf{u} \cdot \mathbf{v}$ |
| $\mathbf{u} \otimes \mathbf{v}$ | Внешний продукт векторов $\mathbf{u}$ и $\mathbf{v}$ | $(1, 2) \otimes (3, 4) =$ $\begin{pmatrix} 1 \cdot 3 & 1 \cdot 4 \\ 2 \cdot 3 & 2 \cdot 4 \end{pmatrix}$ |
| $\| \mathbf{v} \|$ | Норма вектора $\mathbf{v}$ | $\| к \mathbf{v} \| = |к| \| \mathbf{v} \|$ |
| $\| \mathbf{v} \|_p$ | P-норма вектора $\mathbf{v}$ | $\| \mathbf{v} \|_1 =$ $|v_1|+ \cdots + |v_n|$ |
| $\hat{\mathbf{v}}$ | Единичный вектор в направлении вектора $ \mathbf{v}$ | $\hat{\mathbf{v}} = \dfrac{\mathbf{v}}{\| \mathbf{v} \|}$ |
| $\mathrm{proj}_{\mathbf{u}}\mathbf{v}$ | Проекция вектора $\mathbf{v}$ на вектор $\mathbf{u}$ | $ \ mathrm {proj} _ {\ mathbf {u}} \ mathbf {v} = \ dfrac {\ mathbf {v} \ cdot \ mathbf {u}} {\ mathbf {u} \ cdot \ mathbf {u}} \ , \mathbf{u}$ |
| $\mathrm{oproj}_{\mathbf{u}} \mathbf{v}$ | Ортогональная проекция вектора $\mathbf{v}$ на вектор $\ mathbf{u}$ | $\mathrm{proj}_{\mathbf{u}} \mathbf{v} + \mathrm{oproj}_{\mathbf{u}} \mathbf{v} = \mathbf{v }$ |
Операторы, связанные с матрикой,
| Название символа | Пояснение | $ |
|---|---|---|
| $ | ||
| $ | ||
| $ | ||
| $ | ||
| $ | ||
| $ | ||
| $ | ||
| $kA$ | Скалярное произведение матрицы $A$ на скаляр $k$ | $5(3B)=(5 \cdot 3)B$ |
| Сумма матриц $A$ и $B$ | $A + B = B+A$ | |
| $A-B$ | Разность матриц $A$ и $B$ | $\begin{pmatrix} 2 & 5 \\ 3 & 1 \end {pmatrix}-\begin{pmatrix} 1 & 5 \\ 2 & 4 \end{pmatrix} =$ $\begin{pmatrix} 1 & 0 \\ 1 & -3 \end{pmatrix} $ |
| $ AB$ | Произведение матриц $A$ и $B$ | $(AB)_{ij} = (i\mathrm{th \ row \ of \ }A)$ $\cdot \, (j\ mathrm{th\column\of\}B)$ | 9{-1} = A$
| $\mathrm{tr}(A)$ | След матрицы $A$ | $\mathrm{tr}(I_n)=n$ |
| |A|$, $\det (A)$ | Определитель матрицы $A$ | $\begin{vmatrix} 4 & 3 \\ 2 & 5 \end{vmatrix} = \\ 4 \cdot 5 -3 \cdot 2$ |
| $\|A\|$ | Норма матрицы $A$ | $\| А + Б \| \le$ $\| А \| + \| В \|$ |
| $\| А \|_p$ 9{\mathrm{T}})=\mathrm{rank}(A)$ |
| Symbol Name | Explanation | Example |
|---|---|---|
| $\ ker(f)$ | Ядро линейного отображения $f$ | $\mathbf{v} \in \ker(f) \iff$ $f(\mathbf{v})=\mathbf{0} $ |
| $\mathrm{span}(S)$ | Span набора векторов $S$ | $\mathrm{span} \left( \{ (1, 2), (4, 5) ) \} \справа)$ 92$ |
| $\dim(V)$ | Размерность векторного пространства $V$ | $\dim(W) \le \dim(V)$ |
| $W_90$ 6 | Сумма подпространств $W_1$ и $W_2$ | Для всех $\mathbf{w_1} \in W_1$ и $\mathbf{w_2} \in W_2$, $\mathbf{w}_1+\mathbf{w }_2$ $\in W_1 + W_2$.  |
| $W_1 \oplus W_2$ | Прямая сумма подпространств $W_1$ и $W_2$ | Если $W_1 + W_2 = V$ и $W_1 \cap W_2 = \{\mathbf{0}\ }$, то $W_1 \oplus W_2 = V$. |
| $V_1 \times V_2$ | Прямое произведение векторных пространств $V_1$ и $V_2$ | Если $\mathbf{v_1} \in V_1$ и $\mathbf{v}_2 \in V_2 $, затем $(\mathbf{v}_1, \mathbf{v}_2) \in V_1 \times V_2$. |
| $V_1 \otimes V_2$ | Тензорное произведение векторных пространств $V_1$ и $V_2$ | $\dim (V_1 \otimes V_2) =$ $\dim(V_1) \times \times \dim(V_2)$ |
| $V/W$ | Частное пространство 9{\!*}) = \ dim (v) $ |
Операторы в абстрактной алгебре
| Название символа | Объяснение | |
|---|---|---|
| $ | . класс элемента $a$ класс элемента $a$ | В $\mathbb{Z}_5$, $[2] =$ $\{ 2 + 5m \mid m \in \mathbb{Z} \}$. |
| $\deg(p(x))$ | Степень многочлена $p(x)$ | $\deg (p(x) q(x)) =$ $\deg(p (х)) + \deg(q(x))$ |
| $\langle S \rangle$ | Подгруппа , порожденная элементами множества $S$ | Если $G=\langle S \rangle$, то $S$ является генератором $G$. |
| $ H_1 \ Oplus H_2 $ | Прямая сумма из подгрупп $ H_1 $ и $ H_2 $ | $ g = H_1 \ toplus H_2 $ |
| $ G_1 \ Times G_2 $ | ||
| $ G_1 \ Times G_2 $ | ||
| $ G_1 \ Times G_2 $ | ||
| . групп $G_1$ и $G_2$ | $(e_{G_1}, e_{G_2}) \in \\ G_1 \times G_2$ | |
| $ST$ | Произведение групповых подмножеств $S$ и $T$ | Если $S, T \subseteq G$, то $ST$ $=\{st \mid s \in S \ земля t \in T \}.  $ $ |
| $N \rtimes H$ | Полупрямое произведение подгрупп $N$ и $H$ | $G = N \rtimes H$ |
| $G_1 \wr G_2$ | Сплетение групп $G_1$ и $G_2$ | $\mathbb{Z}_2 \wr \mathbb{Z}$ |
| $G/N$ | Факторгруппа группы $G$ по подгруппе $N$ | $\mathbb{Z}/3\mathbb{Z} = \\ \{[0], [1], [2]\}$ |
| $R/I$ | Факторкольцо кольца $R$ по идеалу $I$ | Существует естественный гомоморфизм из $R$ в $R/I$. |
| $\mathrm{ker}(f)$ | Ядро гомоморфизма $f$ | $x_1, x_2 \in \mathrm{ker}(f) \implies$ $x_1 \circ x_2 \in \mathrm{ker}(f)$ |
| $\overline{\mathbb{F}}$ | Алгебраическое замыкание поля $\mathbb{F}$ | $\overline{\mathbb {R}} = \mathbb{C}$ |
Символы отношения
В алгебре символа отношения используются для выражения отношения между двумя математическими объектами и часто связаны с такими понятиями, как равенство, сравнение, делимость и другие отношения более высокого порядка. В следующих таблицах описаны наиболее распространенные из них, а также их использование и значение. 92 \примерно 7,4$
В следующих таблицах описаны наиболее распространенные из них, а также их использование и значение. 92 \примерно 7,4$
$xRy$
Основанные на номере реляционные символы
| Название символа | Объяснение | $ |
|---|---|---|
| $ $ | ||
| $ $ | ||
| $ $ | ||
| $ | ||
| $m \nmid n$ | Целое число $m$ не делится на целое число $n$ | $34 \nmid 90$ |
| $m \perp n$ | Целые числа $m$ и $n$ являются взаимно простыми | Если $n \pq $n \perp p$, затем $n \mid q$. |
Реляционные символы в абстрактной алгебре
| Название символа | Объяснение | Пример |
|---|---|---|
| $ n \ varstrian | $ varstrian | $ varstrian $ $ varstrian $ varstrian $ $ varstrian.
Основной список символов см. в разделе математические символы. Списки символов, классифицированных по типу и предмету , см. на соответствующих страницах ниже.
Предпочитаете версию в формате PDF?
Получите основную сводку математических символов в форме электронной книги — вместе с использованием каждого символа и кодом LaTeX.
Да. Это было бы полезно.
Дополнительные ресурсы
- Полное руководство по изучению высшей математики : Система из 10 принципов для эффективного обучения математике, мышления и решения задач
- Полное справочное руководство по LaTeX : Полное справочное руководство по LaTeX, позволяющее сделать процесс LaTeX более рациональным, эффективным и менее болезненным
- Электронная книга по линейной алгебре Серия : четыре бесплатных электронных книги по различным подтемам вводной линейной алгебры
- 10 заповедей высшего математического обучения : иллюстрированное веб-руководство по 10 масштабируемым правилам для изучения высшей математики
Таблица логических математических символов | Justfreetools
Имейте в виду, что вне логики разные символы имеют одно и то же значение, а один и тот же символ имеет, в зависимости от контекста, разные значения.
Чтение логических символов пугает многих людей больше, чем следовало бы. Сам термин «символическая логика» звучит устрашающе, и наличие даже небольшой доли символизма может отпугнуть многих читателей от текстов, которые в противном случае были бы вполне понятны. Следующее объяснение знакомит с символикой, используемой в этой работе, и перечисляет некоторые вариации, которые могут встречаться в других работах. Следует отметить, что технические термины, используемые в этом приложении, также объясняются под их собственными заголовками в основной части словаря, и там, где это уместно, даны перекрестные ссылки.
Строчные курсивные буквы из этой части алфавита: p , q , r …, используются как пропозициональные переменные. Это означает, что они обозначают предложения или утверждения. Некоторым логикам не нравятся эти категории, и они предпочитают называть их буквами предложения или сентенциальными переменными. В любом случае они возникают там, где можно заменить предложение, так же как x и y в алгебре стоят там, где можно заменить выражение для числа.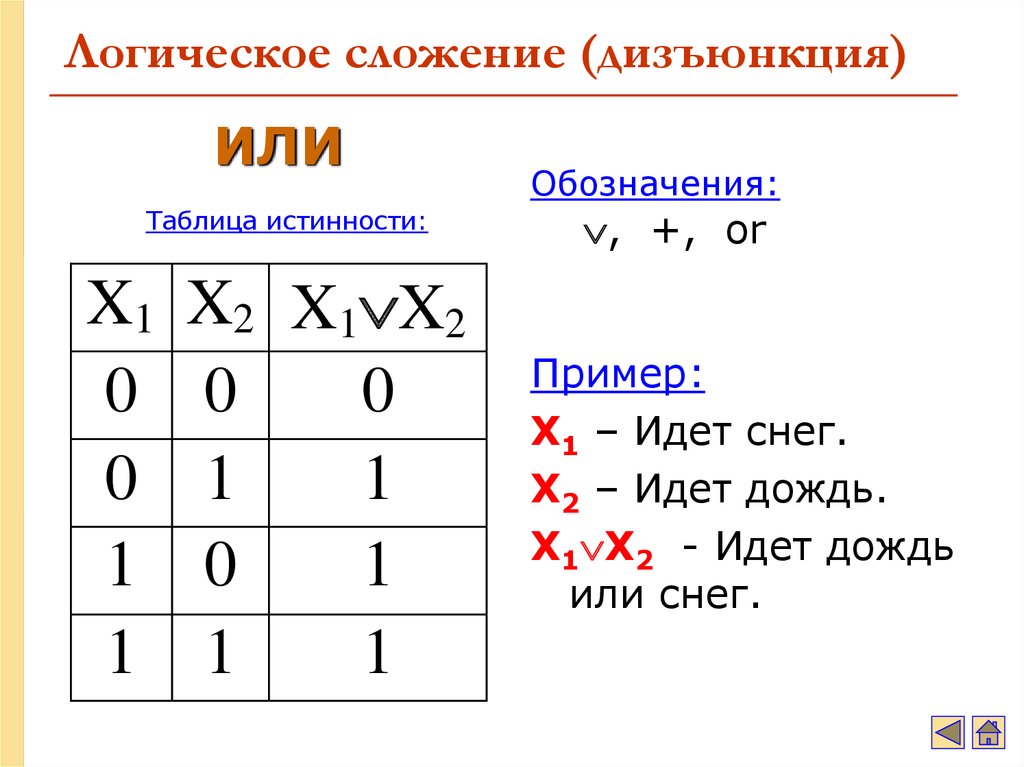 Утверждение типа «Если кто-то считает, что p и q тогда он считает, что p ‘ говорит, что в любом случае, когда кто-то верит в соединение (например, «Идет дождь и ветрено», тогда этот человек верит в его отдельные части (что это встречаются заглавные буквы (P, Q,…) или курсивные заглавные P , Q ,…
Утверждение типа «Если кто-то считает, что p и q тогда он считает, что p ‘ говорит, что в любом случае, когда кто-то верит в соединение (например, «Идет дождь и ветрено», тогда этот человек верит в его отдельные части (что это встречаются заглавные буквы (P, Q,…) или курсивные заглавные P , Q ,…
Строчные курсивные буквы с конца алфавита: x , y , z …, используются как объектные переменные. Это означает, что они стоят там, где может иметь место ссылка на человека, вещь или число. Используя такую переменную, приведенный выше пример можно было бы сформулировать так: «Если x полагает, что p и q , затем x полагает, что p ’, где x обозначает любого человека. Это обозначение является практически универсальным, хотя типографский вид переменных различается.
Как и в обычной математике, строчные латинские буквы, особенно n, k, j…, используются в контексте для обозначения определенных чисел. С самого начала алфавита a, b, c… также являются отдельными константами или терминами, используемыми в контексте для обозначения определенных вещей или людей. Фа означает, что некоторая конкретная вещь, а, есть F и, следовательно, является самостоятельным предложением, истинным или ложным, в зависимости от обстоятельств. Ф x 92 124 – нет, поскольку переменная 92 123 x ничего не выбирает.
С самого начала алфавита a, b, c… также являются отдельными константами или терминами, используемыми в контексте для обозначения определенных вещей или людей. Фа означает, что некоторая конкретная вещь, а, есть F и, следовательно, является самостоятельным предложением, истинным или ложным, в зависимости от обстоятельств. Ф x 92 124 – нет, поскольку переменная 92 123 x ничего не выбирает.
Заглавные латинские буквы F, G, R обозначают предикаты и выражения отношений. Конкретные их примеры являются стандартными: например, тождество (=), неидентичность (≠), больше и меньше (>, <) и другие математические отношения. По обычному соглашению сказуемые буквы стоят перед терминами, к которым они применяются. Fn означает, что n равно F; Rab означает, что a имеет отношение R к b. В некоторых работах это будет написано aRb.
Наиболее простыми отношениями между предложениями, изучаемыми в логике, являются функции истинности. К ним относятся:
Не . Не- р является отрицанием р.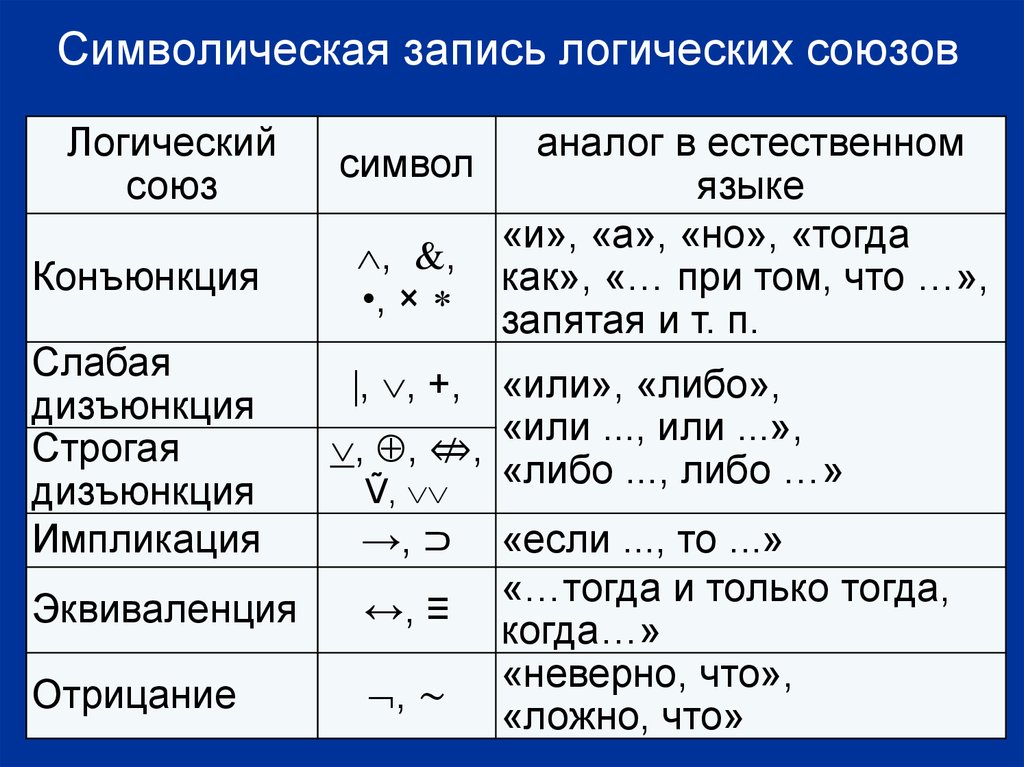 В классическом понимании ложным является утверждение, когда p истинно, и наоборот. В этой работе пишется не- p в неформальном контексте, а ¬ p в более формальном контексте. Это означает то же самое. Встречающиеся варианты включают — p и ~ с.
В классическом понимании ложным является утверждение, когда p истинно, и наоборот. В этой работе пишется не- p в неформальном контексте, а ¬ p в более формальном контексте. Это означает то же самое. Встречающиеся варианты включают — p и ~ с.
А. p и q является конъюнкцией двух предложений. Это истинно тогда и только тогда, когда они оба истинны. В этой работе написано p и q . Встречающиеся варианты включают p · q и, чаще, p ∧ q .
или . p или q — это дизъюнкция двух предложений. Оно истинно тогда и только тогда, когда истинно хотя бы одно из них. В этой работе написано p ∨ q , и это стандарт. Исключительная дизъюнкция, означающая, что одно из p , q является истинным, но не оба, иногда встречается, пишется p ⊻ q.
Значение . Логика изучает различные виды следствий. Самый простой из них называется материальной импликацией. Здесь написано p → q . Наиболее распространенный вариант – p ⊃ q .
Самый простой из них называется материальной импликацией. Здесь написано p → q . Наиболее распространенный вариант – p ⊃ q .
Эквивалент . Если p → q и q → p , то p и q называются эквивалентными (у них одинаковое истинностное значение). Неофициально это часто выражается как p iff q . Написано p ↔ q . Наиболее распространенная альтернатива: p ≡ q .
Это основной набор функций истинности, в терминах которых обычно определяются другие. В исчислении предикатов изучается внутренняя структура предложений, а также отношения между ними. Ключевыми понятиями являются два квантификатора:
Универсальный квантор . В этой работе это написано ∀. (∀ x )F x означает, что все является F. Возможные варианты включают (A x )F x и ( x )F x .
Квантор существования . В данной работе это написано ∃. (∃ x )F x означает, что что-то есть F. Основное изменение, которое может встречаться, это (E x )F x .
В данной работе это написано ∃. (∃ x )F x означает, что что-то есть F. Основное изменение, которое может встречаться, это (E x )F x .
В исчислении предикатов могут быть определены числовые кванторы, например (∃n x )(F x ) означает, что существует n x таких, что F x. Основным вариантом является (∃! x )F x (называемый Э-визг x), что означает, что существует ровно одно x такое, что x является F.
Термины могут быть определены из определенных описаний . Основные встречающиеся примеры: (1 x )F x (уникальное x такое, что x является F) и (µ x )F x (наименьшее x такое, что x равно F).
Модальная логика изучает понятие необходимости или возможности предложений. Основные обозначения:
Обязательно p . Написано □ стр . Основная вариация N p .
Возможно стр .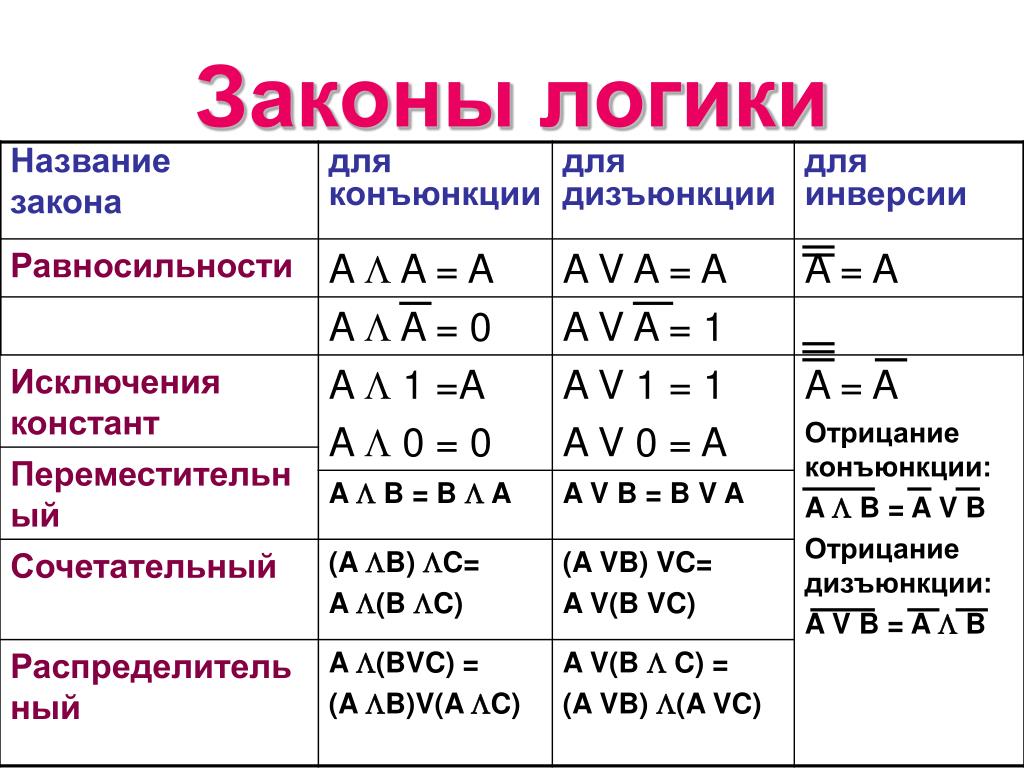 Написано ⋄ стр . Основная вариация М р .
Написано ⋄ стр . Основная вариация М р .
В *метатеории или теории логических систем предметом обсуждения становятся формулы и их отношения. В этой работе заглавные буквы A, B являются переменными для формул, где A1…An относится к последовательности формул. В других произведениях может встречаться греческий язык в различных формах (α, β…). Основные отношения, которые имеют значение:
Существует доказательство B из A. Стандартно это записывается как A ⊦ B.
B истинно во всех интерпретациях, в которых A истинно. Обычно это записывается A ⊧ B.
В традиционной или аристотелевской логике не существует такого же набора понятий. Предполагается, что предложения состоят из терминов, таких как подлежащее и сказуемое, или среднего термина силлогизма. В этой работе для них используются заглавные латинские буквы (S, P, M). Теория множеств вводит небольшой новый набор фундаментальных терминов:
{ x : F x } относится к набору вещей, x , которые соответствуют условию F. Теперь это стандарт. На множество также можно ссылаться, перечисляя его элементы («расширенно»): {a, b, c} — это множество, элементами которого являются a, b и c.
Теперь это стандарт. На множество также можно ссылаться, перечисляя его элементы («расширенно»): {a, b, c} — это множество, элементами которого являются a, b и c.
Набор без элементов или нулевой набор записывается как ∅. Более старая вариация — ∧.
Сами наборы обозначаются заглавными буквами S, T и т. д. Возможны различные типографские варианты.
∈ обозначает принадлежность к множеству. x ∈ S означает, что x является элементом множества S.
x ∈ { y : G y } означает, что x является элементом множества G .
<…> относится к упорядоченному n-кортежу.
Основные понятия, используемые для построения множеств, включают:
Пересечение . S Союз . S ∪ R — это множество вещей, принадлежащих либо S, либо R. Это тоже стандартно.
Дополнение . S̄ — множество вещей, не принадлежащих S.
Декартово произведение . S×R — это множество упорядоченных пар, первый член которых принадлежит S, а второй — R.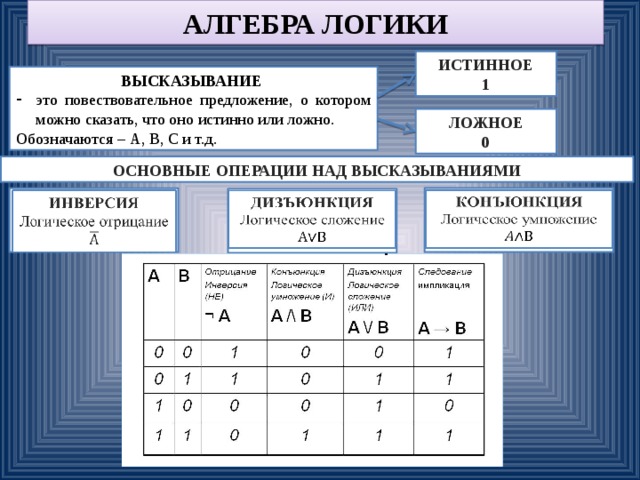
Отношения между множествами включают: что S ⊆ S).
Собственное подмножество : S ⊂ R означает, что S включено в R (это подмножество, но не идентичное R).
Основные нестандартные обозначения, с которыми можно столкнуться, – это польские обозначения, которые объясняются в основной части словаря, а также подстановочная квантификация и ее обозначения.
В настоящее время у нас есть около 5611 калькуляторов, таблиц преобразования и полезных онлайн-инструментов и программных функций для студентов, преподавателей и преподавателей, дизайнеров и просто для всех.
Вы можете найти на этой странице финансовые калькуляторы, ипотечные калькуляторы, калькуляторы для кредитов, калькуляторы автокредита и калькуляторы лизинга, калькуляторы процентов, калькуляторы выплат, пенсионные калькуляторы, калькуляторы амортизации, инвестиционные калькуляторы, калькуляторы инфляции, калькуляторы финансов, калькуляторы подоходного налога , калькуляторы сложных процентов, калькулятор зарплаты, калькулятор процентной ставки, калькулятор налога с продаж, калькуляторы фитнеса и здоровья, калькулятор ИМТ, калькуляторы калорий, калькулятор жировых отложений, калькулятор BMR, калькулятор идеального веса, калькулятор темпа, калькулятор беременности, калькулятор зачатия беременности, срок родов калькулятор, математические калькуляторы, научный калькулятор, калькулятор дробей, калькулятор процентов, генератор случайных чисел, калькулятор треугольника, калькулятор стандартного отклонения, другие калькуляторы, калькулятор возраста, калькулятор даты, калькулятор времени, калькулятор часов, калькулятор среднего балла, калькулятор оценок, конкретный калькулятор, подсеть калькулятор, генератор паролей калькулятор преобразования tor и многие другие инструменты, а также для редактирования и форматирования текста, загрузки видео с Facebook (мы создали один из самых известных онлайн-инструментов для загрузки видео с Facebook). Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других сайтов социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все видео, которые вы загружаете, загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, ALT-кодах для Mac, Windows и Linux и других полезных советах и инструментах (как написать смайлики онлайн и т. д.)
Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других сайтов социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все видео, которые вы загружаете, загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, ALT-кодах для Mac, Windows и Linux и других полезных советах и инструментах (как написать смайлики онлайн и т. д.)
Есть много очень полезных бесплатных онлайн-инструментов, и мы будем рады, если вы поделитесь нашей страницей с другими или пришлете нам какие-либо предложения по другим инструментам, которые придут вам на ум. Также, если вы обнаружите, что какой-либо из наших инструментов не работает должным образом или нуждается в лучшем переводе, сообщите нам об этом. Наши инструменты сделают вашу жизнь проще или просто помогут вам выполнять свою работу или обязанности быстрее и эффективнее.
Ниже приведены наиболее часто используемые многими пользователями по всему миру.
- Бесплатные онлайн-калькуляторы и инструменты
- Калькуляторы часовых поясов/часов/дат
- Бесплатные онлайн-калькуляторы перевода единиц
- Бесплатные онлайн-инструменты для веб-дизайна
- Бесплатные онлайн-инструменты для электричества и электроники
- Математика
9 Онлайн-инструменты
9
- Инструменты PDF
- Код
- Экология
- Прочее
- Бесплатные онлайн-загрузчики для социальных сетей
- Номера
- Algebra
- Trigonometry
- Probability & Statistics
- Calculus & analysis
- Mathematical symbols
- Algebra symbols
- Asterisk sign
- Basic math symbols
- Calculus symbols
- Division sign
- Equals sign
- Geometry symbols
- Греческий алфавит
- Символ бесконечности
- Символ бесконечности ALT-код
- Символ бесконечности в MS Word
- Символ бесконечности на Facebook
- Символ бесконечной бесконечности на клавиатуре
- Символ бесконечности на MAC
- — это бесконечность.
 Реальное число
Реальное число - Логические символы
- Минус Знак
- Символ. Статистические символы
- Знак времени
И мы все еще развиваемся. Наша цель — стать универсальным сайтом для людей, которым нужно быстро рассчитать или найти быстрый ответ для основных конверсий.
Кроме того, мы считаем, что Интернет должен быть источником бесплатной информации. Поэтому все наши инструменты и сервисы абсолютно бесплатны и не требуют регистрации. Мы кодировали и разрабатывали каждый калькулятор индивидуально и подвергали каждый из них строгому всестороннему тестированию. Однако, пожалуйста, сообщите нам, если вы заметите малейшую ошибку — ваш вклад чрезвычайно ценен для нас. Хотя большинство калькуляторов на Justfreetools.com предназначены для универсального использования во всем мире, некоторые из них предназначены только для определенных стран.
Логические символы — Citizendium
- Содержание этой страницы создано в Википедии и еще не было значительно улучшено.
 Авторам предлагается заменить и добавить материал, чтобы сделать эту статью оригинальной.
Авторам предлагается заменить и добавить материал, чтобы сделать эту статью оригинальной.
В логике базовый набор из логических символов используется как сокращение для логических конструкций. Поскольку эти символы часто считаются знакомыми, они не всегда объясняются. Для удобства в следующей таблице перечислены некоторые распространенные символы вместе с их названиями, произношением и соответствующими областями математики. Кроме того, в третьем столбце содержится неформальное определение, а в четвертом столбце приведен краткий пример.
Имейте в виду, что вне логики разные символы имеют одно и то же значение, а один и тот же символ имеет, в зависимости от контекста, разные значения.
| Примечание : Эта статья содержит логические символы. Без надлежащей поддержки рендеринга вы можете увидеть вопросительные знаки, прямоугольники или другие символы вместо логических символов. |
Символ | Имя | Пояснение | примеров | Значение Юникода | HTML Сущность | Символ LaTeX |
|---|---|---|---|---|---|---|
| Следует читать как | ||||||
| Категория | ||||||
| материальное значение | A ⇒ B означает, что если A верно, то B также верно; если A ложно, то о B ничего не говорится. → может означать то же, что и ⇒ (символ может также указывать домен и домен функции; см. таблицу математических символов). ⊃ может означать то же, что и ⇒ (символ также может означать надмножество). | x = 2 ⇒ x 2 = 4 верно, но x 2 = 4 ⇒ x = 2 в общем случае может быть -3 x 9212 -3 x 9212. | U+21D2 U+2192 U+2283 | ⇒ → &up; | ⇒ {\ displaystyle \ Rightarrow} \ Rightarrow | |
| подразумевает; если .. то | ||||||
| логика высказываний, алгебра Гейтинга | ||||||
| Эквивалентность материалов | A ⇔ B означает, что A истинно тогда и только тогда, когда B истинно. | x + 5 = y +2 ⇔ x + 3 = y | U+21D4 U+2261 U+2194 | ⇔ экв. ↔ | ⇔ {\ Displaystyle \ Leftrightarrow} \ Leftrightarrow | |
| тогда и только тогда, когда; если | ||||||
| пропозициональная логика | ||||||
| отрицание | Утверждение ¬ A истинно тогда и только тогда, когда A ложно. Косая черта, помещенная через другой оператор, аналогична «¬», помещенной впереди. | ¬(¬ A ) ⇔ A x ≠ y ⇔ ¬( x = y ) | U+00AC U+02DC | &нет; &тильда; ~ | ¬{\ displaystyle \ lnot} \ lnot | |
| нет | ||||||
| пропозициональная логика | ||||||
| логическое соединение | Заявление А ∧ B истинно, если A и B оба истинны; иначе это ложь. | n < 4 ∧ n >2 ⇔ n = 3, когда n — натуральное число. | и+2227 и+0026 | &и; &ампер; | ∧ {\ Displaystyle \ клин} \ клин или \ земля \ & [1] | |
| и | ||||||
| пропозициональная логика | ||||||
| логическая дизъюнкция | Утверждение A ∨ B истинно, если A или B (или оба) верны; если оба ложны, утверждение ложно. | n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3, когда n — натуральное число. | U+2228 | &или; | ∨{\ Displaystyle \ лор} \ лор | |
| или | ||||||
| пропозициональная логика | ||||||
| | исключительная дизъюнкция | Утверждение A ⊕ B истинно, когда либо A, либо B, но не оба, истинны. A ⊻ B означает то же самое. A ⊻ B означает то же самое. | (¬ A ) ⊕ A всегда верно, A ⊕ A всегда ложно. | U+2295 U+22BB | + | ⊕ {\ displaystyle \ oplus} \ oplus ⊻ {\ displaystyle \ veebar} \ veebar |
| хор | ||||||
| логика высказываний, булева алгебра | ||||||
| | Тавтология | Утверждение ⊤ безусловно истинно. | A ⇒ ⊤ всегда верно. | У+22А4 | Т | ⊤ {\ displaystyle \ top} \ top |
| верх | ||||||
| логика высказываний, булева алгебра | ||||||
| | Противоречие | Утверждение ⊥ безусловно ложно.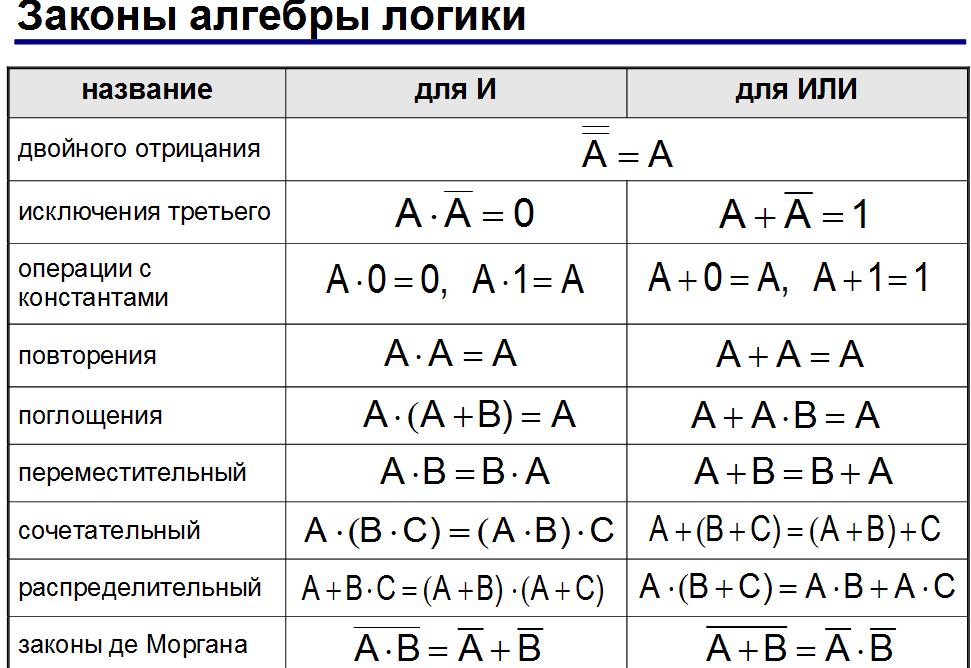 | ⊥ ⇒ Число всегда истинно. | У+22А5 | % Ф | ⊥{\ Displaystyle \ бот} \ бот |
| снизу | ||||||
| логика высказываний, булева алгебра | ||||||
∀ | универсальный количественный анализ | ∀ x : P ( x ) означает P ( x ) верно для всех х . | ∀ n ∈ N : n 2 ≥ n . | U+2200 | ∀ | ∀{\ displaystyle \ forall} \ forall |
| для всех; для любого; для каждого | ||||||
| логика предикатов | ||||||
∃ | экзистенциальная квантификация | ∃ x : P ( x ) означает, что есть хотя бы одно x , так что P ( x ) истинно. | ∃ n ∈ N : n четно. | U+2203 | &существует; | ∃ {\ Displaystyle \ существует} \ существует |
| существует | ||||||
| логика первого порядка | ||||||
∃! | количественная оценка уникальности | ∃! x : P ( x ) означает, что существует ровно одна x , так что P ( x ) верно. | ∃! n ∈ N : n + 5 = 2 n . | U+2203 U+0021 | &существует; ! | ∃! {\ Displaystyle \ существует!} \ существует! |
| существует ровно один | ||||||
| логика первого порядка | ||||||
| определение | x := y или x ≡ y означает, что x определяется как другое имя для y (но обратите внимание, что ≡ может также означать другие вещи, такие как конгруэнтность). P :⇔ Q означает, что P определен как логически эквивалентный Q . | COSH x : = (1/2) (exp x + exp ( — x )) A xor B : ⇔ ( A ∨ B : ⇔ A ∨ B : ⇔ A ∨ B : ⇔ A ∨ B : ⇔ A ∨ B : ⇔ A ∨ B : ⇔ A a B : ⇔ A . ∧ Б ) | U+2254 (U+003A U+003D) U+2261 U+003A U+229C | := : &эквивалент; ⇔ | : = {\ Displaystyle: =}: = | |
| определяется как | ||||||
| везде | ||||||
( ) | группировка по приоритету | Сначала выполните операции внутри скобок.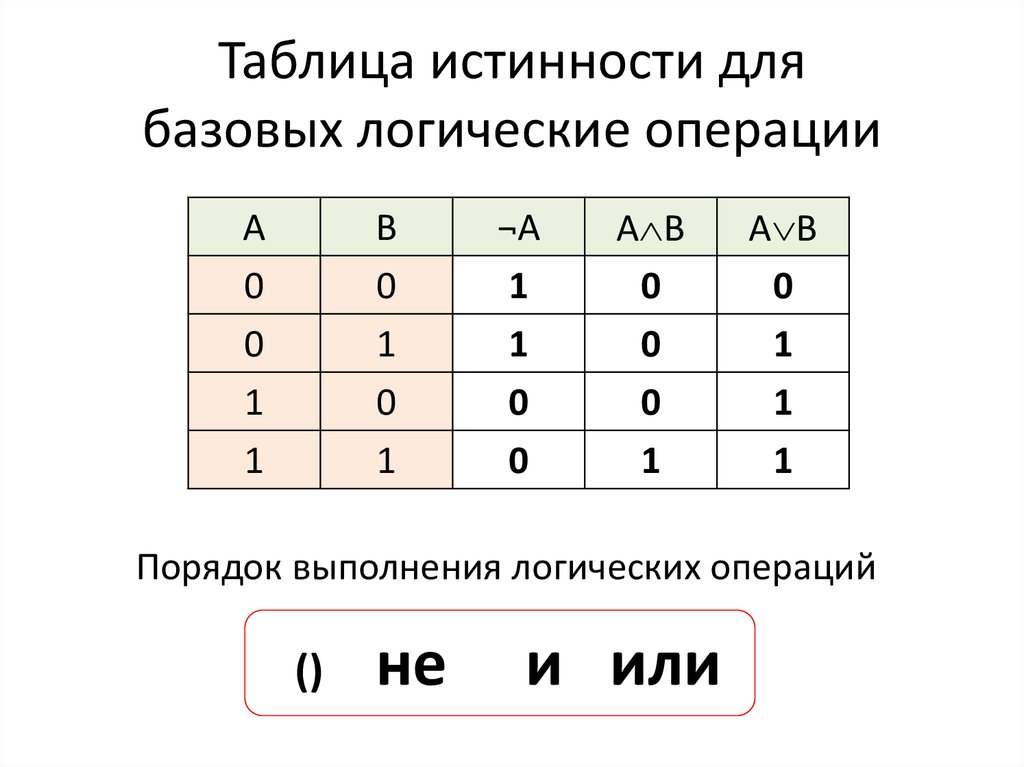 | (8/4)/2 = 2/2 = 1, но 8/(4/2) = 8/2 = 4. | U+0028 U+0029 | ( ) | ( ) {\ Displaystyle (~)} ( ) |
| везде | ||||||
⊢ | вывод | x ⊢ y означает, что y получено из x . | А → В ⊢ ¬ В → ¬ А | У+22А2 | ⊢{\ Displaystyle \ vdash} \ vdash | |
| предполагает или является производным от | ||||||
| логика высказываний, логика первого порядка |
- ↑ Хотя этот символ доступен в LaTeX, система Mediawiki TeX не поддерживает этот символ.
Математические символы — список символов, примеры решений
Математика — это числа, символы и формулы. Математические символы используются для разных целей в разных областях математики. Использование символов для представления математической информации облегчает понимание выражений, поскольку эти символы показывают взаимосвязь между величинами. В этой статье давайте рассмотрим общие, которые мы используем в разных областях математики.
Математические символы используются для разных целей в разных областях математики. Использование символов для представления математической информации облегчает понимание выражений, поскольку эти символы показывают взаимосвязь между величинами. В этой статье давайте рассмотрим общие, которые мы используем в разных областях математики.
| 1. | Общие математические символы |
| 2. | Константы, используемые в качестве математических символов |
| 3. | Математические символы, используемые в логике |
| 4. | Диаграмма Венна и символы теории множеств |
| 5. | Цифровые символы |
| 6. | Символы геометрии и алгебры |
| 7. | Греческие алфавиты и символы комбинаторики |
| 8. | Решенные примеры |
| 9. | Практические вопросы |
10. | Часто задаваемые вопросы о математических символах |
Общие математические символы
Если мы напишем несколько раз слова «прибавление 4 к 2 дает 6», это может усложнить ситуацию. Эти слова также занимают больше места и требуют времени для написания. Вместо этого мы можем сэкономить время и место, используя символы. Язык и словарный запас математики содержат большое количество символов, и этот список бесконечен — некоторые из них более технические, чем другие. У нас есть как минимум 10 000+ символов, и некоторые из них мы редко используем. Наиболее распространенные символы перечислены в следующей таблице:
| Символы | Значение | Примеры математических символов |
|---|---|---|
| + | Добавить | 5 + 4 = 9 |
| — | Вычесть | 5 — 4 = 1 |
| = | Равно | 1+1 = 2 |
| \(\экв\) | Тождественно равно | (а+б) 2 \(\экв\) а 2 + 2аб +б 2 |
| \(\примерно\) | Приблизительно равно | \(\пи \приблизительно 3,14\) |
| \(\neq\) | Не равно | 5 + 4 \(\neq\) 1 |
| \(\раз\) | Умножить | 5 \(\раз\) 4 = 20 |
| \(\дел\) | Разделить | 10 \(\дел\) 2 = 5 |
| \(<\) | Менее | 10 \(<\) 20 |
| \(>\) | Больше | 20 \(>\) 10 |
| \(\leq\) | Меньше или равно | х + у \(\leq\) г |
| \(\geq\) | Больше или равно | x +y \(\geq\) z |
| \(\%\) | Процент | 50% = \(\begin{align}\frac{50}{100}\end{align}\) |
\(.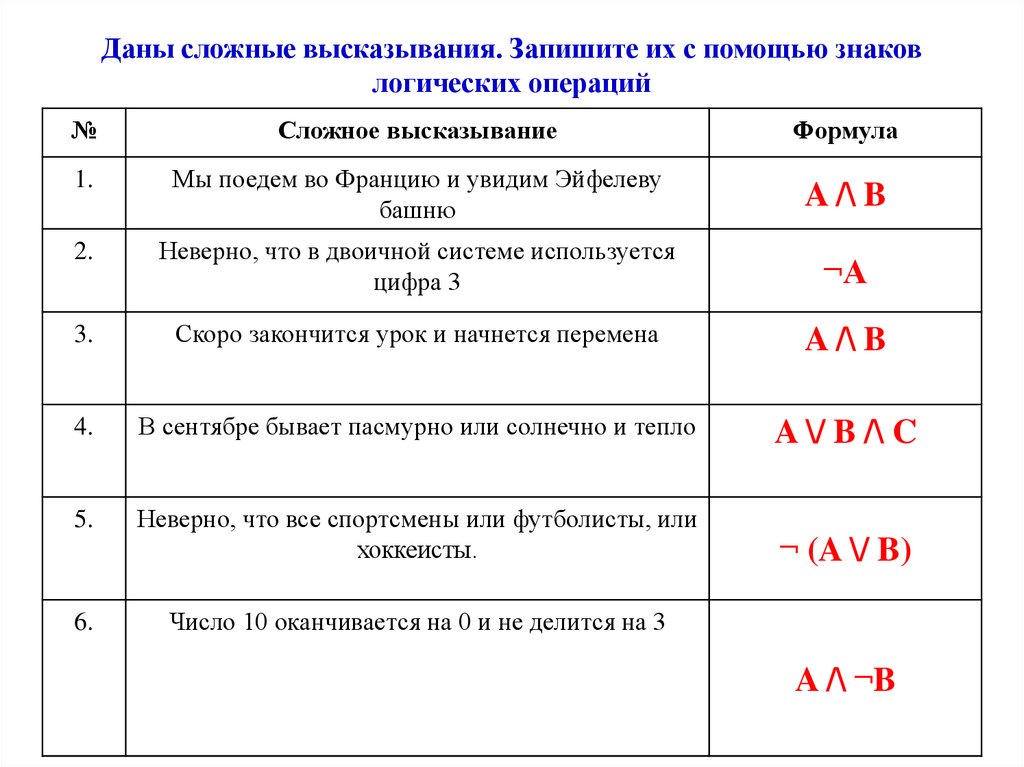 \) \) | Десятичная точка или период | \(\begin{align}\frac{1}{2} = 0,5\end{align}\) |
| \(-\) | Винкулум Разделяет числитель и знаменатель | \(\begin{align}\frac{2}{3}\end{align}\) |
| \(\sqrt{} \) | Квадратный корень | \(\sqrt{4} = 2\) |
| \(\sqrt[3]{х}\) | Кубический корень из x | \( \sqrt[3]{ 27} = 3\) |
| \( \sqrt[n]{x}\) | n th корень \(x\) | \( \sqrt[4]{16} = 2\) |
| \(()\) | Скобки | \(2+(5-3) = 2 +2 = 4\) |
| \([\:\:]\) | Квадратные скобки | \(\ начало {выравнивания} &3\раз[2 +(5 -2)] +1 \\ &3 \раз[2+3] +1 \\ &3 \times5+1\\ &16 \конец{выравнивание}\) |
| \(\{\}\) | Кронштейн для цветов | \(\ начало {выравнивания} &16 \div \{3\times[2 +(5 -2)] +1\} \\ &16 \дел \{3 \раз[2+3] +1\} \\ &16 \дел \{3 \times5+1\}\\ &16 \дел \{16\} \\ &1 \конец{выравнивание}\) |
| \(\в\) | Принадлежит | 0 \(\in\) Целое число |
| \(\нет\в\) | Не принадлежит | \(\frac{1}{2} \not\in\) Натуральные числа |
| \(\поэтому\) | Поэтому | \(х+1 = 2 \следовательно, х = 1\) |
| \(\потому что\) | Потому что | \(\begin{align}\frac{1}{2} \!\div\! 0.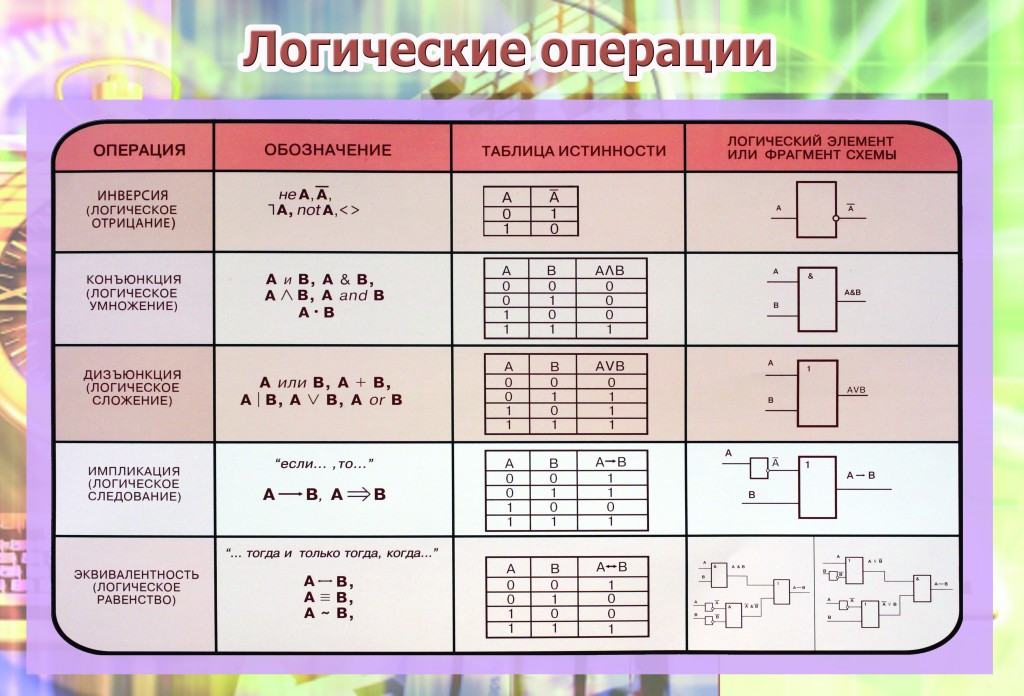 5 \!= \!1 (\потому что\! \frac{1}{2} \!=\! 0.5)\ конец{выравнивание}\) 5 \!= \!1 (\потому что\! \frac{1}{2} \!=\! 0.5)\ конец{выравнивание}\) |
| \(\infty\) | Бесконечность | Бесконечность бесчисленна, \(\begin{align}\frac{1}{3}\end{align}\) при записи в десятичной форме, бесконечно \(0,333…..\) |
| \(!\) | Факториал | \( 5!\ \!\!=\! 5 \!\раз\! 4 \!\раз\!3 \!\раз\! 2\! \раз\! 1\) |
Константы, используемые в качестве математических символов
Мы используем константы в математике для обозначения неизменных объектов. Эти константы могут включать в себя ключевые математические наборы, ключевые числа, ключевые математические бесконечности и другие ключевые математические объекты (например, единичную матрицу). Эти математические константы чаще всего принимают форму буквы алфавита или ее производной. В следующей таблице перечислены некоторые наиболее часто используемые константы, а также их имена, значения и использование.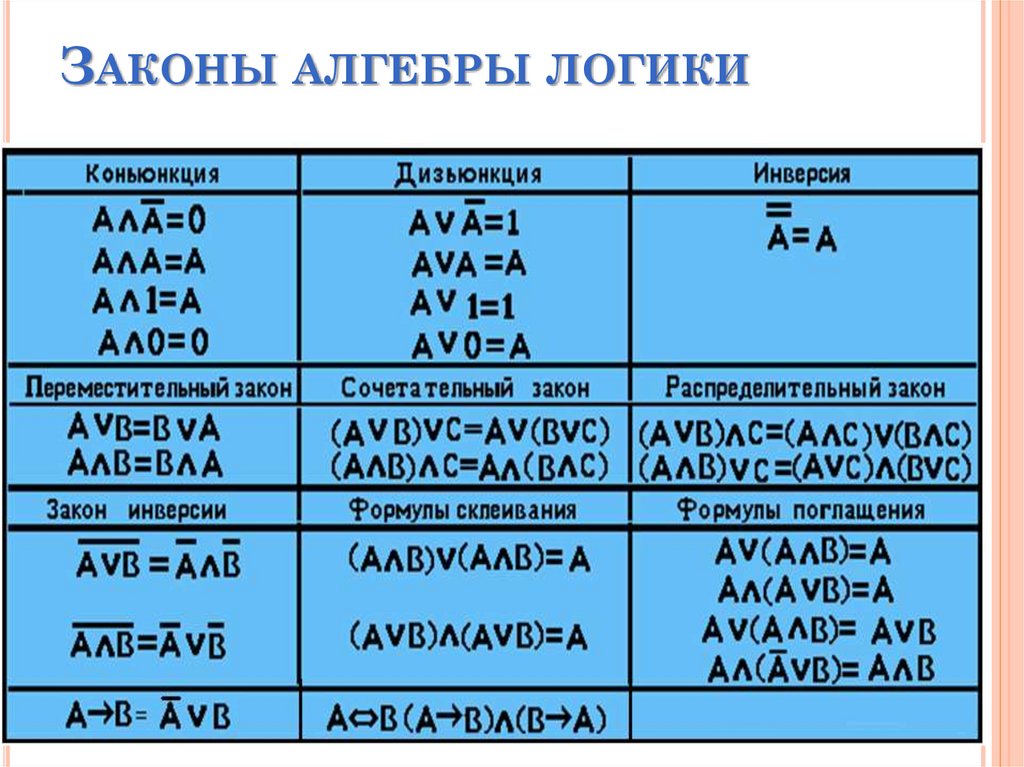
| Имя символа | Пояснение |
|---|---|
| 0 (ноль) | Аддитивная идентичность общих чисел |
| 1 (один) | Мультипликативная идентичность обычных чисел |
| √2 (квадратный корень из 2) | Положительное число, квадрат которого равен 2. Приблизительно равно 1,41421. |
| e (постоянная Эйлера) | Основание натурального логарифма. Предел последовательности (1 + (1/n) n ). Приблизительно равно 2,71828 |
| \(\pi\) (Pi, постоянная Архимеда) | Отношение длины окружности к ее диаметру. Половина окружности единичного круга. Приблизительно равно 3,14159 |
| \( \phi\) (Phi, золотое сечение) | Отношение между большим числом и p меньшим числом q, когда (p+q)/p = p/q. Положительное решение уравнения y 2 -y-1 = 0 . |
| i (Воображаемая единица) | Главный корень из -1. Основной компонент комплексного числа. |
Математические символы, используемые в логике
В следующей таблице показаны математические символы, используемые в логике.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| \(\существует\) | Существует по крайней мере один | ∃ х: Р(х)∃ х: F(х) Существует хотя бы один элемент p(x), \(x\), , такое что F(x) равно True. |
| \(\существует!\) | Существует один и только один | ∃! х: Ф(х) означает, что существует ровно один \(x\) такое, что F(x) истинно. 92 > 1\) |
| \(\отрицательный\) | Логический Не | Утверждение A истинно, только если \(\neg\) ложно \(х \neq y \iff\neg(x=y)\) |
| \(\лор\) | Логическое ИЛИ | Утверждение A \(\lor\) B истинно , если A или B верно; , если оба ложны, утверждение неверно. |
| \(\земля\) | Логический И | Утверждение A \(\land\) B истинно , если A и B оба верны; иначе это ложь. |
| \(\подразумевается\) | Подразумевает | х = 2 \(\подразумевается\) x 2 = 4 |
| \(\если\) | Если и только если | х +1 = у +1 \(\ тогда и только тогда) х = у |
| \(\text{|}\) или \(\text{:}\) | Такой, что | { \(х\) | \(х\) > 0} = {1,2,3,…} |
Диаграмма Венна и символы теории множеств
В следующей таблице показаны математические символы, используемые в диаграммах Венна и теории множеств.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| \(\крышка\) | Перекресток | А = {2,3,4} Б = {4,5,6} А \(\заглавная\) В = {4} |
| \(\чашка\) | Союз | А = {2,3,4} В = {4,5,6} А \(\чашка\) В = {2,3,4,5,6} |
| \(\ничего\) | Пустой набор | Набор без элементов \(\varnothing\) = { } |
| \(\в\) | Является членом | 2 \(\в\) \(\mathbb{N}\) |
| \(\нотин\) | не является членом | 0 \(\нетин\) \(\mathbb{N}\) |
| \(\подмножество\) | Является подмножеством | \(\mathbb{N} \подмножество \mathbb{I}\) |
| \(\расстроен\) | Является надмножеством | .\(\mathbb{R} \supset \mathbb{W}\) |
| \(\текст{П(А)}\) | Силовой набор А | P({1,2}) = {{}, {1}, {2}, {1,2}} |
| \(А=В\) | Равенство (одинаковые элементы в наборе А и наборе В) | А = {1,2}; В = {1,2} \(\ подразумевает \) А = В |
| \( А \раз В\) | Декартово произведение Набор заказанных пар от A и B | А ={5,6}; В = {7,8} \(\ подразумевает \)\( A \times B\) = {(5,7),(5,8),(6,7),(6,8)} |
| \(\текст{|А|}\) | Количество элементов в множестве A | |{1,2,3,4}| = 4 |
Цифровые символы
Цифровые символы с их примерами и соответствующие индийско-арабские цифры перечислены здесь, в таблице.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| Римская цифра I | Значение = 1 | I = 1 , II = 2 , III = 3 |
| Римская цифра V | Значение = 5 | IV = 4 (5-1) ВИ = 6 (5+1) VII = 7 (5+2) VIII = 8 (5+3) |
| Римская цифра X | Значение = 10 | IX = 9 (10-1) |
| Римская цифра L | Значение = 50 | XLIX = 49 (50-1) |
| Римская цифра C | Значение = 100 (столетие) | СС = 200 (100+100) CCLIX = 259 (100+100+50+9) |
| Римская цифра D | Значение = 500 | DCLI = 651 (500+100+50+1) DCCIV = 704 (500+100+100+4) |
| Римская цифра М | Значение = 1000 | мм = 2000 (1000+1000) |
| R или \(\mathbb{R}\) | Вещественные числа | \(\frac{1}{2} , \frac{1}{4}, 0,5\)\(\sqrt{2},\sqrt{3}\) |
| Z или \(\mathbb{Z}\) | Целое число | -100,-20,5,10,. … … |
| N или \(\mathbb{N}\) | Натуральные числа | 1,2,3,…500,… |
| Q или \(\mathbb{Q}\) | Рациональные числа | \(-\frac{1}{2}, \frac{1}{4}, 0,5\) |
| P или \(\mathbb{P}\) | Иррациональные числа | \(\sqrt{2},\sqrt{3}\) |
| C или \(\mathbb{C}\) | Комплексные числа | 5+2i |
Символы геометрии и алгебры
В приведенной ниже таблице показаны наиболее часто используемые геометрические символы. Математические символы с названиями и примерами также приведены в таблице.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| \(\угол\) | Укажите угол | \(\угол ABC\) |
| \(\Дельта\) | Символ треугольника | \(\Дельта\текст{PQR}\) |
| \(\конг\) | соответствует | \(\Delta \text{PQR} \cong \Delta \text{ABC}\) 9\цирк\) |
| \(\overline{\rm AB}\) | Отрезок линии AB | Линия из точки А в точку Б |
| \(\overrightarrow{\rm AB}\) | Рэй AB | Линия, начинающаяся из точки А и продолжающаяся через точку В |
| \(\overleftrightarrow{\rm AB}\) | Линия AB | Бесконечная линия, проходящая через точки A и B | 9в\)
Алгебраические символы
В следующей таблице показаны наиболее часто используемые алгебраические символы. 2 \)
2 \)
\(\пропто\)
Греческие алфавиты и символы комбинаторики
В таблице ниже показаны греческие алфавиты, используемые в качестве математических символов. Их имена, использование и примеры также перечислены в таблице.
| Символы | Значение | Примеры математических символов |
|---|---|---|
| \(\альфа\) | Альфа | Используется для обозначения углов, коэффициентов |
| \(\бета\) | Бета | Используется для обозначения углов, коэффициентов |
| \(\гамма\) | Гамма | Используется для обозначения углов, коэффициентов |
| \(\Дельта\) | Дельта | Дискриминантный символ |
| \(\варепсилон\) | Эпсилон | Используется для обозначения универсального набора | .
| \(\йота\) | Йота | Представляет мнимое число |
| \(\лямбда\) | Лямбда | Представляет константу |
| \(\пи\) | Пи | \(\пи \примерно 3,14\) |
| \(\Сигма\) | Сигма | Представляет сумму |
| \(\тета\) | Тета | Представляет углы |
| \(\ро\) | Ро | Статистическая константа |
| \( \фи\) | Фи | Обозначение диаметра |
Символы комбинаторики
В таблице ниже показаны наиболее часто используемые символы комбинаторики. 96{P_4} &= 6 \times 5 \times 4 \times 3 = 360\end{align}
Похожие статьи о математических символах
Ознакомьтесь со следующими страницами, посвященными математическим символам.
- Арифметика
- Алгебраические выражения
- Правила делимости
- Векторы
Важные примечания
Вот несколько моментов, которые следует помнить при изучении математических символов:
- Использование символов для представления информации облегчает понимание математических выражений.

- У нас есть как минимум 10 000+ символов, и некоторые из них мы редко используем.
- Мы используем константы в математике для обозначения неизменных объектов.
Часто задаваемые вопросы о математических символах
Что такое U в математических символах?
Математический символ U используется для обозначения множества, состоящего из элементов двух множеств. Следовательно, объединение двух множеств P и Q будет множеством элементов P и Q. Для обозначения множества используется специальный символ ∪, который выглядит как «U».
Сколько существует математических символов?
Более 10000 математических символов. Некоторые из основных: =,+,−,≠,±, * и так далее. Есть сложные символы, такие как \(\alpha\), \(\varepsilon\) и так далее.
Какой математический символ используется для обозначения периода волны?
Математический символ, который используется для обозначения периода волны, — λ. Он также известен как длина волны, которая измеряется в единицах расстояния.
Каково использование символа сложения?
Символ сложения (+) обычно используется при сложении двух и более чисел, например, 5 + 5. Кроме того, символ (+) также может использоваться для обозначения положительного числа, например, +7.
Перечислите некоторые распространенные арифметические математические символы.
Некоторые из распространенных арифметических математических символов: знак плюс (+), используемый для сложения, знак минус (-), используемый для вычитания, знак звездочки (*) или знак умножения (×), используемый для умножения, и знак деления (÷). или знак косой черты (/), используемый для деления. 9Обозначение 0005
. По каким причинам некоторые символы в математической логике не стандартизированы?
$\begingroup$
Почему так трудно найти стандартизацию в отношении символики и/или терминологии в математической логике?
Мы снова и снова видим, как студенты спрашивают, например, $\rightarrow$ и $\implies$ означают одно и то же: кто-то отвечает: «да», кто-то отвечает: «нет».
То же самое происходит с «тавтологией» и «достоверностью», с «логическим следствием» и «логически следует» и так далее…
Почему эта проблема все еще с нами и что мы можем с этим поделать?
- логика
- нотация
- история математики
- условность
$\endgroup$
15
$\begingroup$
Думаю, этому есть несколько причин. Мои идеи:
- Символическая логика все еще относительно новая область. (Вопреки вашему мнению, символическая логика началась не с древних греков, а с Begriffsschrift Фреге в 1879 г., даже не 150 лет назад, и даже не пытайтесь следовать его обозначениям.)
- Некоторые философы думали, что они уже все знают о логике, но даже не изучали ее и поэтому никогда не сталкивались со стандартной системой обозначений.
- Некоторые логики нуждались в других видах импликации (релевантной, строгой, материальной), отрицании (минимальной, субминимальной, конструктивной) или следования (стандартной, нечеткой, квази-, степени) для своей собственной логики и создавали для нее свои новые символы.

- Некоторые логики сравнивали разные логики и решили использовать другой набор связок, чтобы не запутаться совсем.
- Пара ввела свои собственные обозначения, потому что их не устраивала старая: польская запись, точечная запись, сжатая точечная запись, лямбда-нотация…
А может быть, кто-то хотел всех запутать 🙂
Добавлю немного:
Даже в таблицах истинности встречаются публикации, где $0$ соответствует истине, а другие — где $1$ соответствует истине. И это только при двузначной логике. Если вам повезет, у вас есть книга, в которой используются $T$ и $F$ или $\top$ и $\bot$. В любом случае $T$ или $\top$ означают истину, а $F$ или $\bot$ — ложь. Но даже в этом случае будьте осторожны: всегда сначала проверяйте значение.
$\endgroup$
3
$\begingroup$
Почему так трудно найти стандартизацию символизма.
.. в математической логике?
Ну, если вы сравните ситуацию с (скажем) пятьдесят-шестьдесят лет назад — время, когда были написаны книги, которые я просматривал, когда был студентом, — я бы сказал, что произошла довольно значительная стандартизация в символизме, по крайней мере, в основных книгах/статьях по математической логике. И одной из причин этого, безусловно, стало повсеместное внедрение LaTeX, который позволяет так легко набирать 9 символов.0003 \land [для ‘логического и’] и всегда получать ‘$\land$’ (а не ‘&’, точку и т. д.) и набирать \forall x и получать ‘$\forall x$ ‘ (а не, например, ‘$(x)$’ или ‘$\Pi x$’). Итак, давайте будем должным образом благодарны за всю стандартизацию, которая сейчас существует!
Правда есть досадное дело с $\to$ vs $\implies$. Я думаю, это тоже частично связано с LaTeX, поскольку \ подразумевает, что дает второе. Теперь «A подразумевает B» используется в неформальной беседе и как вариант «если A, то B», и как вариант «A логически влечет B», то есть как то, что я мог бы классифицировать как $A \to B$, так и как $ A \vDash B$ [или $A \vDash B$].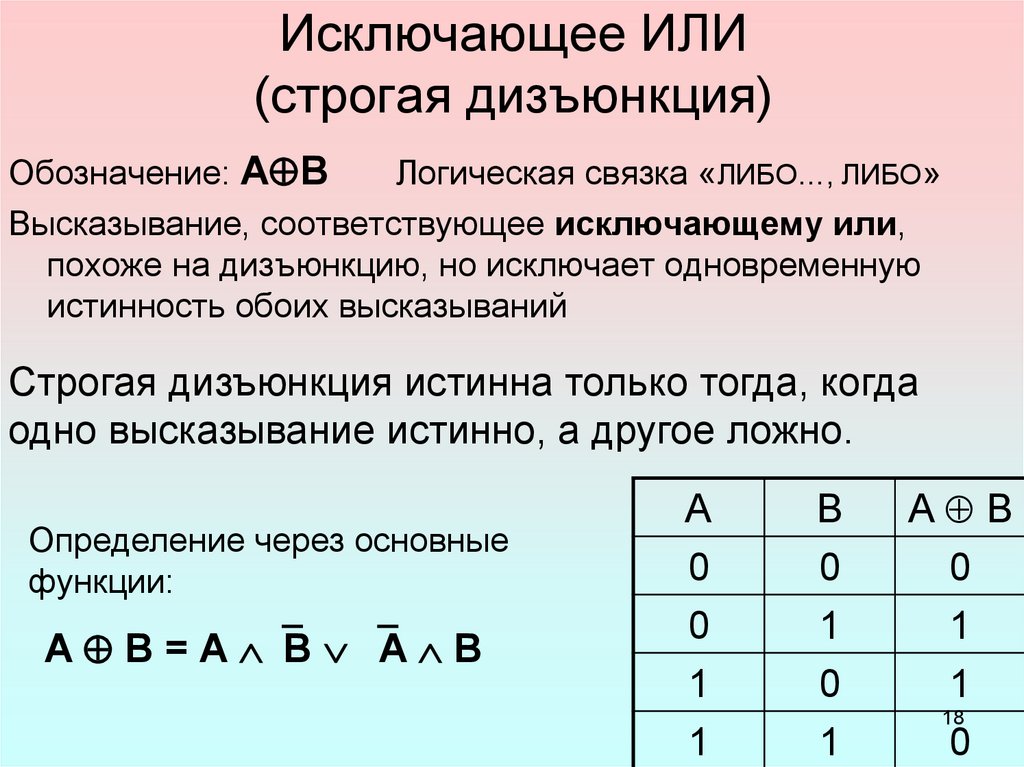 И вот, мы обнаруживаем, что $\implis$ используется в обоих смыслах [в объектном языке или в метаязыке]. Консерватизм в символизме — это хорошо, поэтому я думаю, что использование $\implies$ должно быть осуждено: я бы сказал, используйте $\to$ для условного объектного языка и соответствующий турникет в метаязыке. Исключение может быть в последовательном исчислении. [Действительно, только когда я начал регулярно посещать math.se, я действительно заметил, что двойная стрелка так широко использовалась в непоследовательных исчислениях за пределами очень узкого логического сообщества, с которым я был наиболее знаком, — хотя это может просто показать Я действительно не обращал внимания!]
И вот, мы обнаруживаем, что $\implis$ используется в обоих смыслах [в объектном языке или в метаязыке]. Консерватизм в символизме — это хорошо, поэтому я думаю, что использование $\implies$ должно быть осуждено: я бы сказал, используйте $\to$ для условного объектного языка и соответствующий турникет в метаязыке. Исключение может быть в последовательном исчислении. [Действительно, только когда я начал регулярно посещать math.se, я действительно заметил, что двойная стрелка так широко использовалась в непоследовательных исчислениях за пределами очень узкого логического сообщества, с которым я был наиболее знаком, — хотя это может просто показать Я действительно не обращал внимания!]
$\endgroup$
6
$\begingroup$
Перефразируя Билла Терстона, математика — это всего лишь способ организовать человеческое мышление. Цель математических обозначений — помочь нам понять друг друга.
Одна из причин использования различных обозначений заключается в том, что одно и то же понятие может потребоваться сравнить или сопоставить с разными вещами в разных ситуациях. Например, недавно я обсуждал с кем-то различные символы деления:
Обозначение дроби $\frac{a}{b}$ наиболее полезно при упрощении уравнений вручную.
Полное деление наиболее удобно при вычислении точных значений.
Косая черта / отлично подходит для компьютеров, так как работает с обычной клавиатурой.
«Обелус» ÷ используется в калькуляторах, потому что другие обозначения отличаются от +, — и x.
Я чувствую, что попытка стандартизировать деление была бы контрпродуктивной.
Математическая логика отличается от арифметики, но верны те же истины. Рассел и Уайтхед использовали нотацию, наиболее удобную для чисто символических вычислений, но она может оказаться не лучшей для записи на доске или написания компьютерной программы.
TL;DR Математические обозначения предназначены для максимально ясного выражения мыслей, и строгая стандартизация затрудняет это.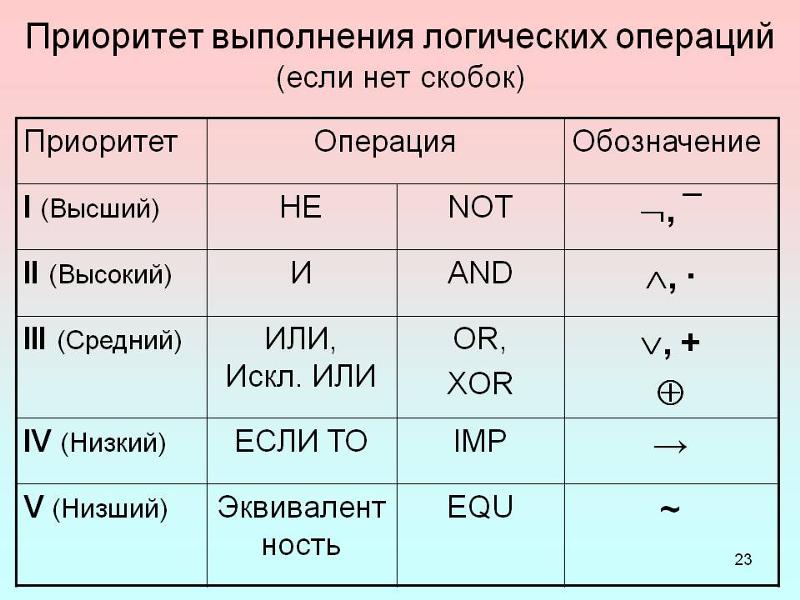
$\endgroup$
1
$\begingroup$
Другие ответы, похоже, не затрагивали напрямую вопрос об импликации $\rightarrow$ или $\implies$, поэтому я укажу, что математики (нелогики) в основном используют $\implies$, тогда как логики чаще используют $\стрелка вправо$. Возможно, это связано с тем, что логики используют его гораздо чаще, так что в конце концов каждый улавливает, что бессмысленно проводить две линии, когда можно провести одну. Поскольку речь идет о двух разных научных культурах, разница в обозначениях может остаться с нами в обозримом будущем. Для сравнения заметим, что физики часто используют разные обозначения (чем привыкли математики) для различных математических понятий.
$\endgroup$
1
$\begingroup$
Что касается неоднозначности между импликацией $\rightarrow$ и следствием $\Rightarrow$, проблема, конечно, заключается в том, что большинство теорий имеют теорему вывода, следствием которой является эквивалентность следующих суждений.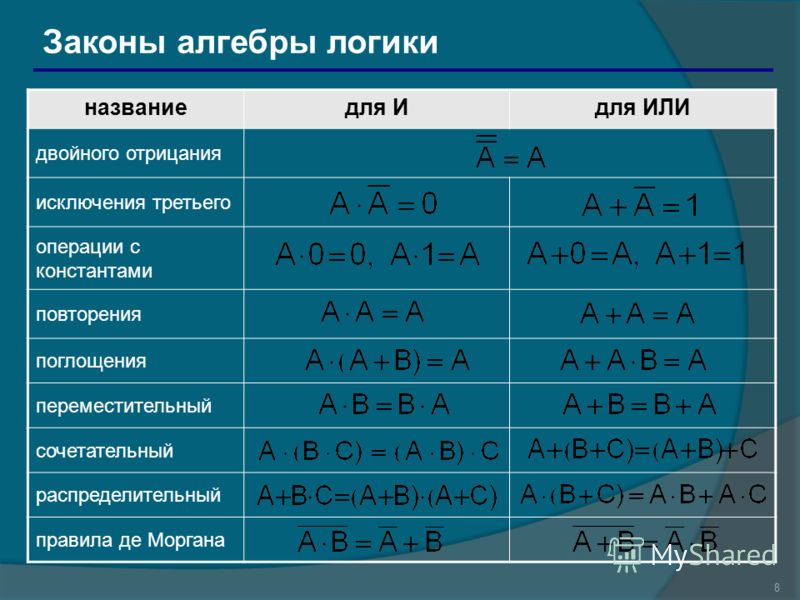
$$\varphi \Rightarrow \psi,\quad\quad \Rightarrow \varphi \rightarrow \psi$$
Кроме того, каждую формулу $\alpha$ можно рассматривать как сокращение для суждения $\Rightarrow \alpha$. Так что в некотором смысле (как бы мне это ни было больно) следующие утверждения эквивалентны.
$$\varphi \Rightarrow \psi,\quad\quad \varphi \rightarrow \psi$$
Это, вероятно, является причиной многих неясностей, но также предполагает, что нам не о чем беспокоиться; утверждать, что эти строки символов «истинно» означают примерно одно и то же значение, поэтому двусмысленность не слишком проблематична. (С другой стороны, утверждение, что первая строка символов ложна, сильно отличается от утверждения, что вторая строка символов ложна.)
$\endgroup$
$\begingroup$
Это часть эволюции и изменения языка. А математика, кроме того, что она метафизична, еще и язык.
Определенные части языка, часто используемые и широко используемые, имеют тенденцию к стандартизации. Например, я не думаю, что мы увидим новые символы для натуральных чисел.
Например, я не думаю, что мы увидим новые символы для натуральных чисел.
Менее интенсивно используемые, как правило, имеют варианты, которые могут использоваться различными частями сообщества.
Что может быть полезно, так это комитет по стандартам. Но только в ограниченной степени.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Почему знак + обычно используется как логический оператор ИЛИ?
\$\начало группы\$
Несколько дней назад меня спросили, почему довольно часто используется + вместо символа v в качестве логического оператора ИЛИ в цифровой логике.
Его аргумент заключался в том, что совершенно нелогично использовать + для ИЛИ, потому что это, скорее всего, будет интерпретировано как И из общего использования/контекста.
Из Wiki: В логике и математике или — это функциональный оператор истинности, также известный как (включительно) дизъюнкция и чередование. Логическая связка, представляющая этот оператор, также известна как «или» и обычно записывается как 9.4629 против или
+.
Я провел небольшое исследование и выяснил происхождение знака и .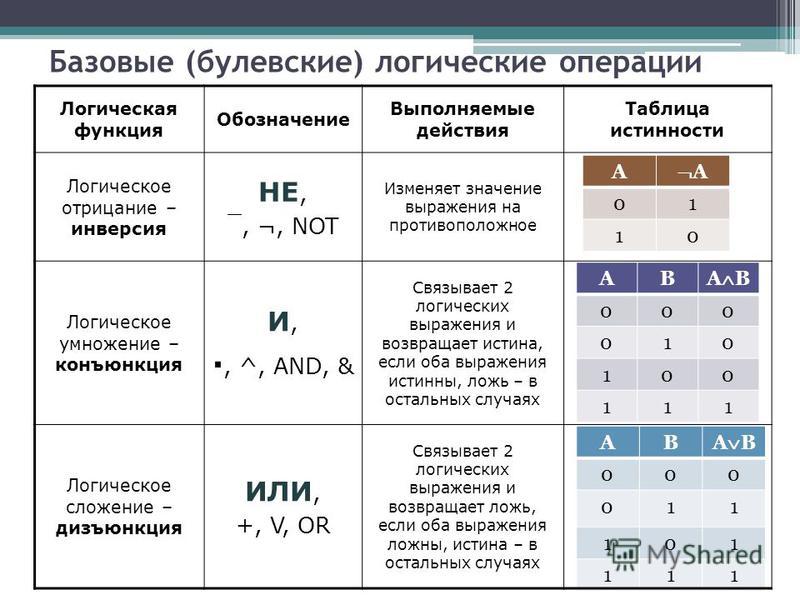 Оно происходит от латинского слова «vel», что означает «или».
Оно происходит от латинского слова «vel», что означает «или».
Одна вещь, которая добавляет путаницы, заключается в том, что + означает «и» с исторической точки зрения. Согласно этому и этому было изобретено около 1360 г. как и аббревиатура от латинского «et» («и»), напоминающая знак «плюс».
Однако я понятия не имею, кто придумал + в булевой алгебре и почему он предпочтительнее против в контексте цифровой логики/инженерии.
- цифровая логика
- логические вентили
- булева алгебра
\$\конечная группа\$
9
\$\начало группы\$
Одно слово: Дистрибутивность
Умножение является дистрибутивным над сложением, и поэтому логическое И дистрибутивное над логическим ИЛИ.
С другой стороны, умножение часто используется без символа ( 2a вместо 2*a ), и логическое И очень похоже. Если и A, и B должны быть истинными, написать AB просто и интуитивно понятно.
Если и A, и B должны быть истинными, написать AB просто и интуитивно понятно.
Очень удобен при построении таблиц истинности и алгоритмов на их основе.
$$f = A + BC$$
даже человек с небольшим опытом с первого взгляда заметит, что f может иметь место, когда верно A, или когда оба B и C верны.
Сравните это с $$f = A \vee B \wedge C$$ Если вы не используете это в течение нескольких дней, вам придется снова задаться вопросом, было ли 9 И или наоборот? Даже если вы их не забудете, читать будет намного понятнее и легче, если использовать только символы умножения и сложения, тем более что их невозможно спутать. В булевой логике нет ни сложения, ни умножения, поэтому их символы можно использовать повторно.
Тот факт, что 1 * 0 = 0 и 1 + 0 = 1 , и в булевой алгебре мы выбрали 1 как истину, а 0 как ложь, также помогает определить, какой оператор есть какой. Символы в математике — это просто символы. У них есть значение, потому что мы присвоили им значение, поэтому лучше, если мы выберем символы, которые легко запомнить, и их использование в других областях аналогично.
Символы в математике — это просто символы. У них есть значение, потому что мы присвоили им значение, поэтому лучше, если мы выберем символы, которые легко запомнить, и их использование в других областях аналогично.
\$\конечная группа\$
2
\$\начало группы\$
Один из аргументов, который я всегда использовал для логических знаков И и ИЛИ, — это их отношение к математическим операциям, которые они представляют.
Начнем с логического И. Его часто представляют в виде знака умножения, например *. Итак, если у вас есть длинное выражение, такое как s1*s2*s3*s4…. и одна из переменных принимает значение 0 или логическую ложь, тогда все выражение примет значение 0, что вполне нормально для умножения. , потому что 1*1*0*1… равно 0,
С другой стороны, когда мы используем знак +, который обычно обозначает сложение для представления логического ИЛИ, мы имеем аналогичный случай. Если у нас есть несколько переменных, объединенных ИЛИ, то мы снова имеем случай s1+s2+s3+s4… Если хотя бы одна из переменных отлична от нуля, то результат также будет ненулевым, т.е. логично (ИМХО), когда мы сравниваем ИЛИ с дополнением. Например, 0+0+1+0… равно 1. Одна точка, где это прерывается, заключается в том, что у нас больше единиц, результат все еще один. Один из способов мышления, который я использовал для этого, состоит в том, чтобы просто помнить, что один представляет существование, так что если что-то существует, и вы добавляете к этому больше существования, оно все равно будет существовать.
Если у нас есть несколько переменных, объединенных ИЛИ, то мы снова имеем случай s1+s2+s3+s4… Если хотя бы одна из переменных отлична от нуля, то результат также будет ненулевым, т.е. логично (ИМХО), когда мы сравниваем ИЛИ с дополнением. Например, 0+0+1+0… равно 1. Одна точка, где это прерывается, заключается в том, что у нас больше единиц, результат все еще один. Один из способов мышления, который я использовал для этого, состоит в том, чтобы просто помнить, что один представляет существование, так что если что-то существует, и вы добавляете к этому больше существования, оно все равно будет существовать.
\$\конечная группа\$
2
\$\начало группы\$
Майкл Шредер «Краткая история обозначений алгебры Буля», Nordic Journal of Philosophical Logic 2 (1): 41-62 (1997), приписывает использование + для представления включительно-или Лейбницу в его «Элементах исчисления» и обсуждает использование Булем обозначений, а также некоторые другие обозначения.


 список авторов ) .
список авторов ) .
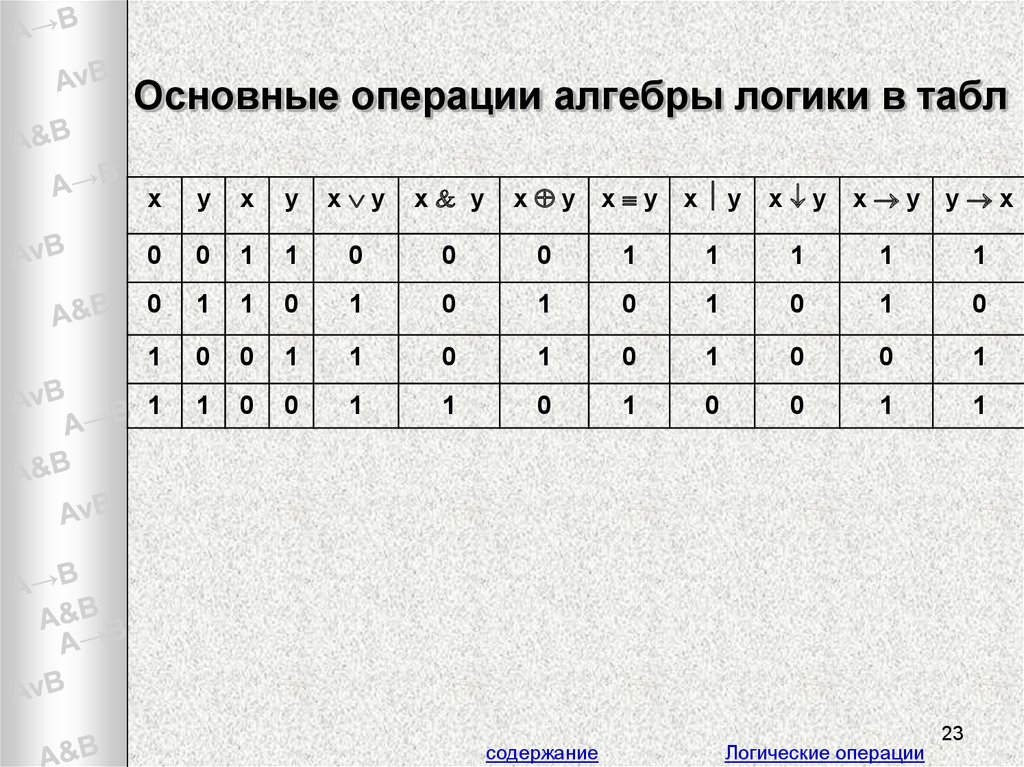
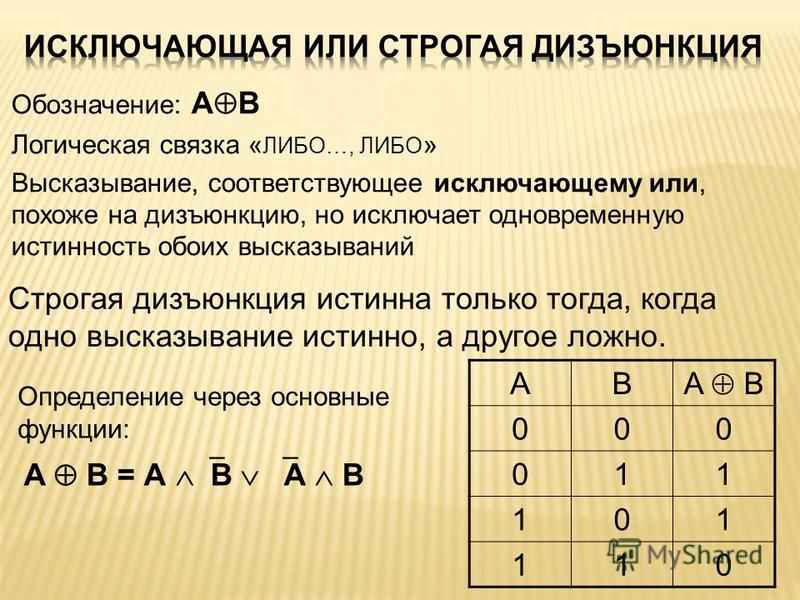 = O$
= O$ 4$
4$ Реальное число
Реальное число Авторам предлагается заменить и добавить материал, чтобы сделать эту статью оригинальной.
Авторам предлагается заменить и добавить материал, чтобы сделать эту статью оригинальной. 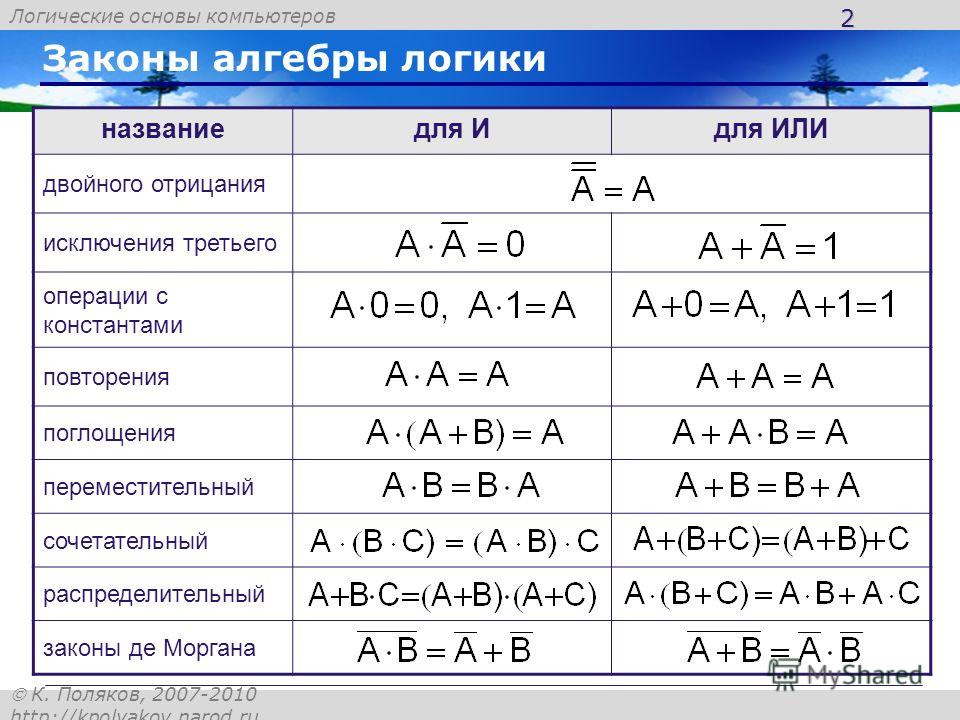


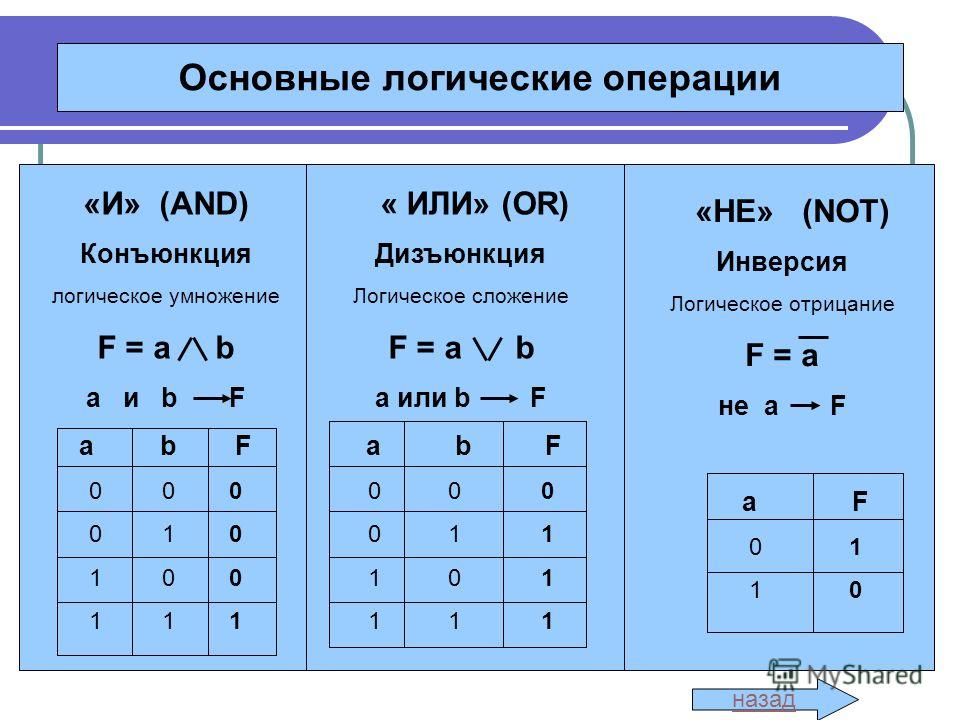

 .. в математической логике?
.. в математической логике?