Глава 12 Двоичный сумматор . Код. Тайный язык информатики
Сложение — простейшая арифметическая операция. Если мы хотим создать компьютер (а именно в этом заключается цель этой книги), сначала нужно найти способ создания устройства, складывающего два числа. По сути, компьютеры выполняют только операцию сложения. Если нам удастся сконструировать механизм, умеющий складывать, мы окажемся способны создать устройство, использующее операцию сложения для того, чтобы вычитать, умножать, делить, рассчитывать платежи по ипотеке, отправлять ракеты на Марс, играть в шахматы и вносить путаницу в наши телефонные счета.
Сумматор, который мы построим, будет большим, нескладным, медленным и шумным по сравнению с современными калькуляторами и компьютерами. Самое интересное заключается в том, что мы соберем эту машину из простых электрических устройств, о которых говорили в предыдущих главах, — переключателей, лампочек, проводов, батарейки и реле, объединенных в различные логические вентили. Этот сумматор будет состоять исключительно из деталей, которые уже были изобретены 120 лет назад. Особенно хорошо то, что нам не нужно ничего собирать в своей гостиной; вместо этого мы можем конструировать на бумаге и в уме.
Этот сумматор будет состоять исключительно из деталей, которые уже были изобретены 120 лет назад. Особенно хорошо то, что нам не нужно ничего собирать в своей гостиной; вместо этого мы можем конструировать на бумаге и в уме.
Эта машина будет работать исключительно с двоичными числами, в ней будут отсутствовать некоторые современные функции. Вы не сможете использовать клавиатуру для ввода чисел, подлежащих сложению; вместо этого будет ряд переключателей. Роль дисплея для отображения результатов в этом сумматоре исполнит ряд лампочек.
Однако машина сумеет сложить два числа, и она сделает это фактически как компьютер.
Сложение двоичных чисел похоже на сложение десятичных. Если хотите сложить два десятичных числа, например 245 и 673, вы разбиваете задачу на более простые этапы. На каждом этапе складываете две десятичные цифры. В данном примере начинаете со сложения 5 и 3. Эта задача решается быстрее, если вы знаете таблицу сложения.
Большая разница между сложением десятичных и двоичных чисел заключается в том, что в случае с двоичными числами используется более простая таблица.
Если вы выросли среди дельфинов, вероятно, вы в школе учили эту таблицу, громко произнося:
0 плюс 0 равно 0,
0 плюс 1 равно 1,
1 плюс 0 равно 1,
1 плюс 1 равно 0, 1 в уме.
Вы можете добавить в эту таблицу нули так, чтобы каждый результат представлял 2-битное значение.
Таким образом, результатом сложения пары двоичных чисел являются два бита, которые называются разрядом суммы и разрядом переноса (1 плюс 1 равно 0, 1 в уме). Теперь мы можем разделить таблицу сложения двоичных чисел на две таблицы. Первая — для разряда суммы.
Вторая — для разряда переноса.
Сложение двоичных чисел удобно рассматривать так, поскольку наш сумматор выполняет операции суммирования и переноса отдельно. Для создания двоичного сумматора потребуется сконструировать схему, выполняющую эти операции. Работа исключительно в двоичной системе счисления значительно упрощает задачу, поскольку все части схемы — переключатели, лампочки и провода — могут представлять двоичные цифры.
Как и при сложении десятичных чисел, мы складываем двоичные числа столбец за столбцом, начиная с крайнего правого.
Обратите внимание: при сложении значений в третьем столбце справа 1 переносится в следующий столбец. Это происходит снова в шестом, седьмом и восьмом столбцах справа.
Какого размера двоичные числа мы хотим сложить? Поскольку мы создаем сумматор прямо в уме, то можем сделать так, чтобы он складывал очень длинные числа. Однако давайте будем благоразумными и ограничимся двоичными числами длиной до восьми бит, то есть будем складывать двоичные числа в диапазоне от 0000 0000 до 1111 1111 (десятичные от 0 до 255). Сумма двух 8-битных чисел может достигать двоичного значения 1 1111 1110 (десятичного значения 510).
Пульт управления нашим двоичным сумматором может выглядеть так.
На этом пульте есть два ряда по восемь переключателей. Этот набор переключателей — устройство ввода, которое мы будем использовать для ввода двух 8-битных значений.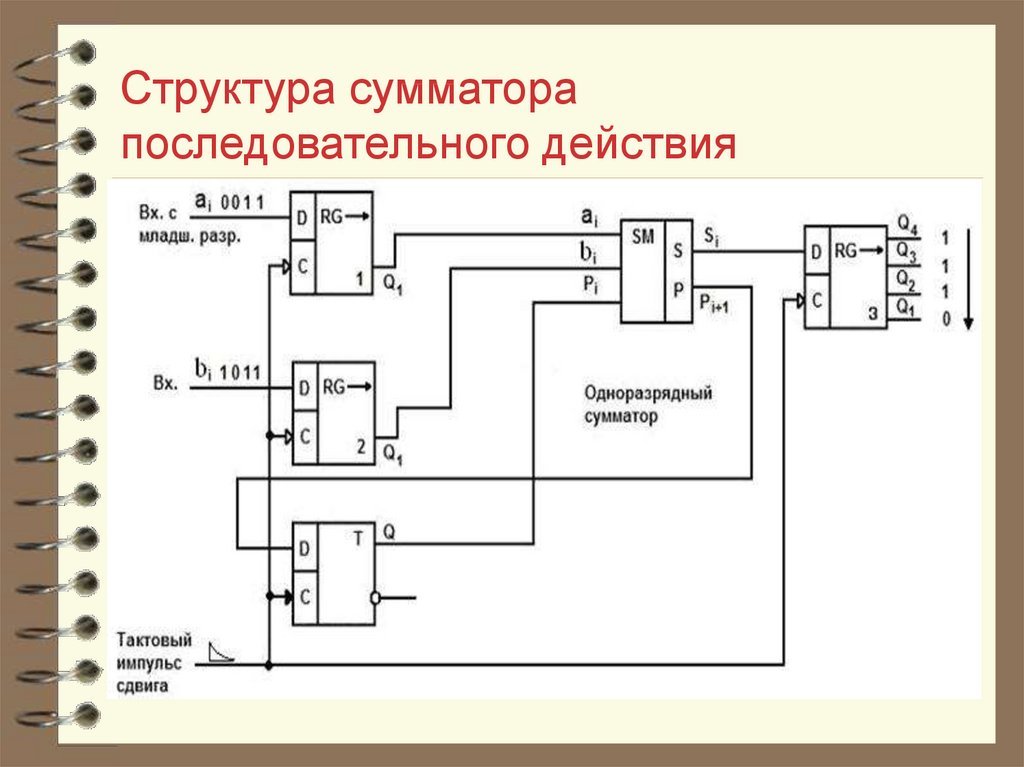
В остальном сумматор будет состоять из логических вентилей, соединенных различными способами. Переключатели будут активировать реле в логических вентилях, которые, в свою очередь, будут зажигать нужные лампочки. Например, если мы хотим сложить числа 0110 0101 и 1011 0110 (из предыдущего примера), включаем соответствующие переключатели.
Загоревшиеся лампочки показывают результат: 1 0001 1011. По крайней мере, мы на это надеемся. Мы ведь еще не собрали устройство!
В предыдущей главе я упомянул, что в этой книге буду использовать множество реле.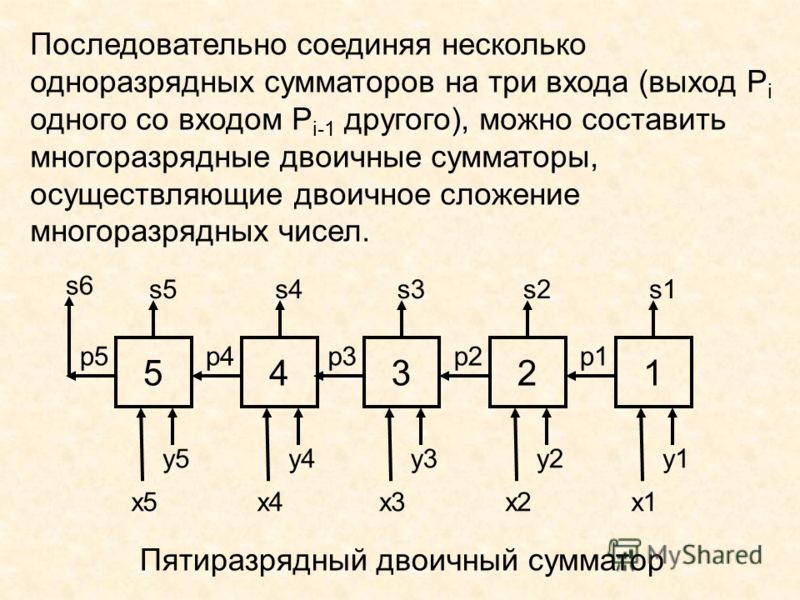 Для 8-битного сумматора, который мы создаем, требуется не менее 144 реле — по восемнадцать для каждой из восьми пар битов, которые складываем. Если бы я показал готовую схему, вы бы наверняка испугались. Никому не под силу разобраться в схеме, состоящей из ста сорока четырех хитро соединенных реле. Вместо этого мы будем решать такую задачу поэтапно, используя логические вентили.
Для 8-битного сумматора, который мы создаем, требуется не менее 144 реле — по восемнадцать для каждой из восьми пар битов, которые складываем. Если бы я показал готовую схему, вы бы наверняка испугались. Никому не под силу разобраться в схеме, состоящей из ста сорока четырех хитро соединенных реле. Вместо этого мы будем решать такую задачу поэтапно, используя логические вентили.
Возможно, вы сразу заметили связь между логическими вентилями и сложением двоичных чисел, когда увидели таблицу для разряда переноса, который возникает в результате сложения двух однобитных чисел.
Вероятно, вы узнали в ней результат работы вентиля И.
Таким образом, вентиль И вычисляет значение разряда переноса при сложении двух двоичных цифр.
Ага! Мы определенно делаем успехи. Наш следующий шаг, похоже, заключается в том, чтобы убедить некоторые реле вести себя так:
Это вторая часть задачи при сложении пары двоичных цифр.
Первое, что нужно понять, — это то, что результат работы вентиля ИЛИ близок к тому, что нам нужно, за исключением значения в правом нижнем углу.
Результат работы вентиля И-НЕ также близок к тому, что нам требуется, за исключением значения в верхнем левом углу:
Итак, давайте подключим вентили ИЛИ и И-НЕ к одним и тем же входам.
В следующей таблице представлены выходные сигналы вентилей ИЛИ и И-НЕ и их сравнение с тем, что мы хотим получить от сумматора.
Заметьте, что мы хотим получить значение 1, только если выходные сигналы обоих вентилей ИЛИ и И-НЕ равны 1. Это говорит о том, что эти два выходных сигнала могут являться входными сигналами для вентиля И.
То, что нужно.
Обратите внимание: во всей этой схеме по-прежнему есть только два входа и один выход.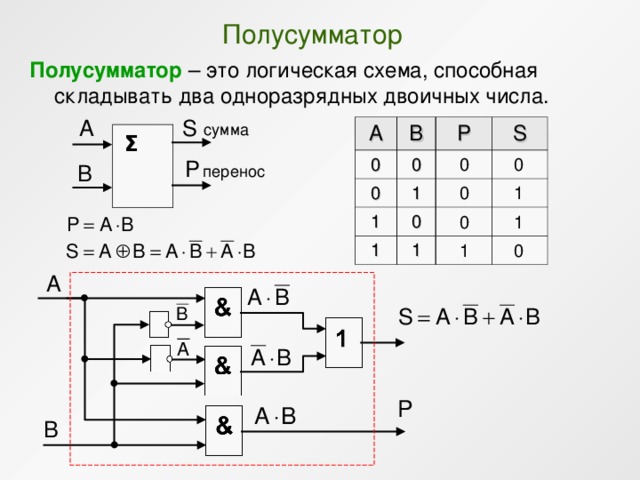 Два входа относятся к обоим вентилям ИЛИ и И-НЕ. Выходные сигналы вентилей ИЛИ и И-НЕ подаются на вход вентиля И, и это дает именно тот результат, к которому мы стремимся.
Два входа относятся к обоим вентилям ИЛИ и И-НЕ. Выходные сигналы вентилей ИЛИ и И-НЕ подаются на вход вентиля И, и это дает именно тот результат, к которому мы стремимся.
На самом деле у этой схемы есть название: вентиль исключающее ИЛИ (Искл-ИЛИ, оно же — сложение по модулю 2). Она называется так потому, что выход равен 1, если вход A равен 1 или вход B равен 1, но не оба одновременно. Вместо того чтобы рисовать вентили ИЛИ, И-НЕ и И, мы можем использовать обозначение, которым инженеры-электрики показывают вентиль Искл-ИЛИ.
Это обозначение очень похоже на обозначение вентиля ИЛИ, но имеет дополнительную кривую линию со стороны входа.
Вентиль Искл-ИЛИ — это последний логический элемент, который будет подробно описан в этой книге. Иногда в электротехнике используется шестой вентиль, называющийся вентилем совпадения или 
Давайте повторим все, что уже знаем. При сложении двух двоичных чисел получается бит суммы и бит переноса.
Для получения этих результатов можно использовать следующие два вентиля.
Разряд суммы двух двоичных чисел задается выходом вентиля Искл-ИЛИ, а разряд переноса — выходом вентиля И, поэтому можно комбинировать вентили И и Искл-ИЛИ для сложения двух двоичных цифр A и B.
Вместо многократного перерисовывания вентилей И и Искл-ИЛИ можно просто нарисовать схему, подобную следующей.
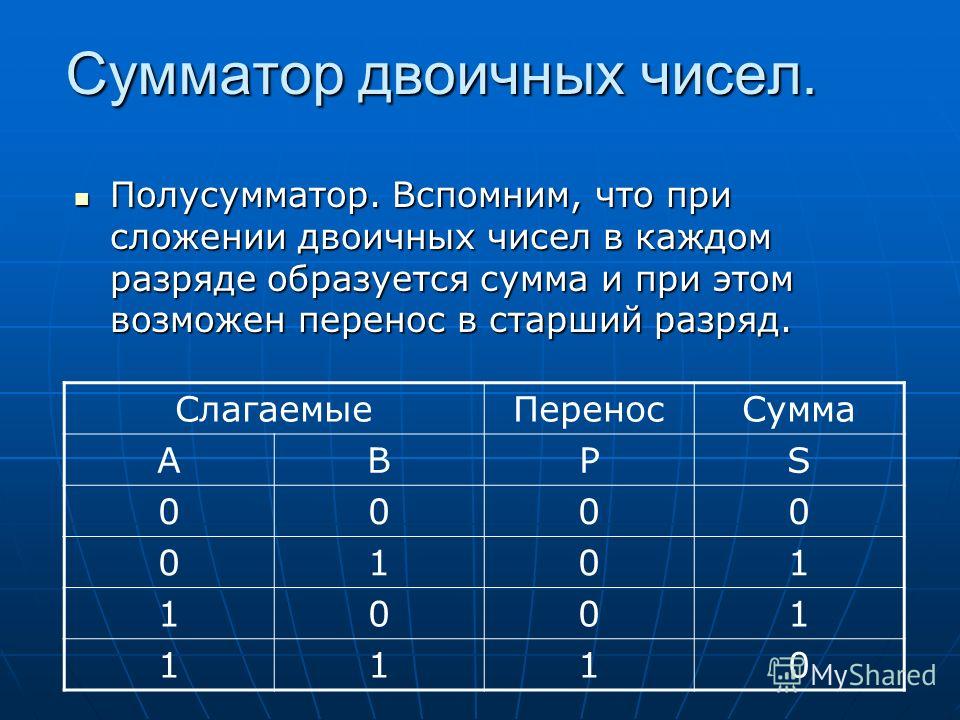
Существует причина, по которой эта схема называется полусумматором. Разумеется, она складывает две двоичные цифры и выдает бит суммы и бит переноса. Однако длина подавляющего большинства двоичных чисел превышает один бит. То, что полусумматор не может сделать, так это прибавить возможный бит переноса, получившийся в результате предыдущей операции сложения. Представьте, что складываем два двоичных числа.
Мы можем использовать полусумматор только для сложения цифр в правом крайнем столбце: 1 плюс 1 равно 0, 1 переносится.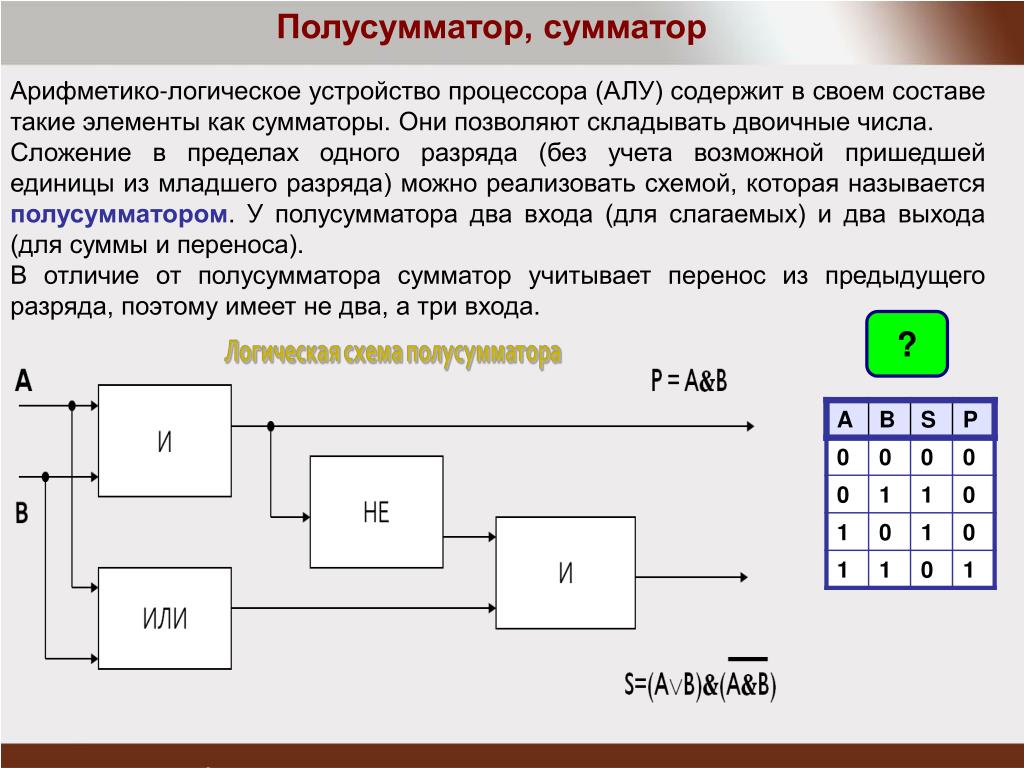 В случае со вторым столбцом справа нам, по сути, нужно сложить три двоичные цифры из-за переноса. И это касается всех остальных столбцов. Каждая последующая операция сложения двух двоичных цифр может включать бит переноса из предыдущего столбца.
В случае со вторым столбцом справа нам, по сути, нужно сложить три двоичные цифры из-за переноса. И это касается всех остальных столбцов. Каждая последующая операция сложения двух двоичных цифр может включать бит переноса из предыдущего столбца.
Для сложения трех двоичных цифр понадобятся два полусумматора и вентиль ИЛИ, соединенные следующим образом.
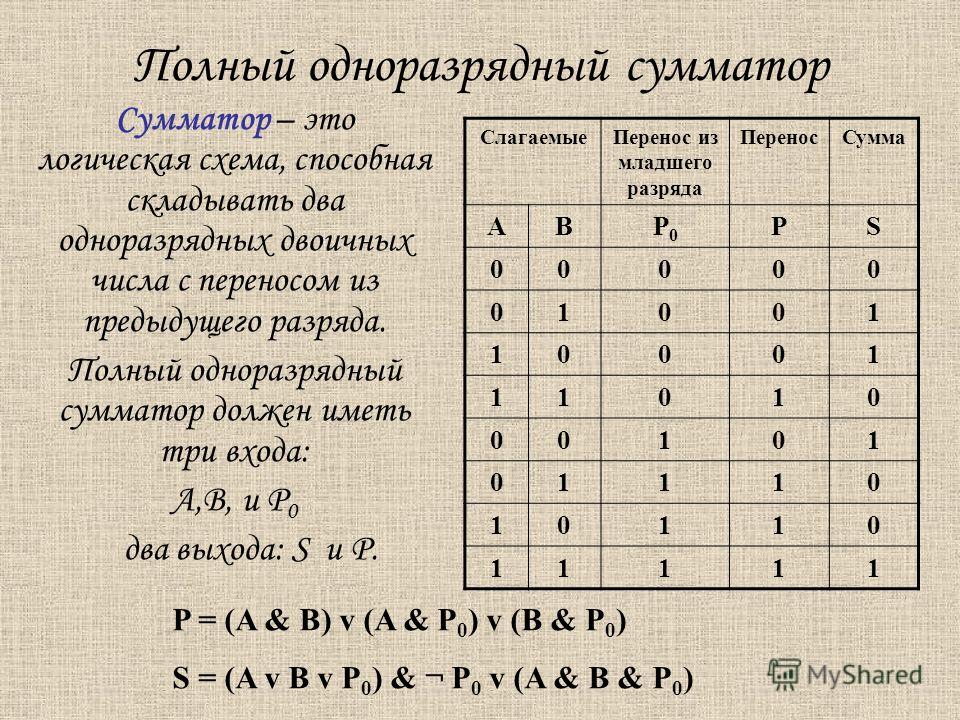
Чтобы разобраться в этой схеме, начнем со входов A и B первого полусумматора слева. Результат — бит суммы и бит переноса. Эта сумма должна быть добавлена к переносу из предыдущего столбца, поэтому они являются входами для второго полусумматора. Сумма, полученная от второго полусумматора, — окончательная. Два переноса из полусумматоров — входы для вентиля ИЛИ. Может показаться, что здесь нужен второй полусумматор, и такая схема, безусловно, сработала бы. Однако если вы проанализируете все возможности, то обнаружите, что оба переноса из двух полусумматоров никогда не равны 1. Вентиля ИЛИ достаточно для их сложения, поскольку он действует так же, как вентиль Искл-ИЛИ, если оба входных сигнала одновременно не равны 1.
Вместо многократного перерисовывания этой схемы можем просто назвать ее полным сумматором.
В следующей таблице представлены все возможные комбинации входов для полного сумматора и результирующие выходы.
В начале этой главы я сказал, что для создания сумматора потребуются 144 реле. Вот как я это понял: для каждого вентиля И, ИЛИ и И-НЕ требуются по два реле. Таким образом, вентиль Искл-ИЛИ состоит из шести реле. Полусумматор — это вентиль Искл-ИЛИ и вентиль И, поэтому для его создания необходимы восемь реле. Каждый полный сумматор — два полусумматора и вентиль ИЛИ, то есть 18 реле. Нам нужны восемь полных сумматоров для создания 8-битной машины, или 144 реле.
Вспомните наш исходный пульт управления с переключателями и лампочками.
Теперь мы можем начать присоединять переключатели и лампочки к полному сумматору.
Сначала подключим два крайних правых переключателя и крайнюю правую лампочку к полному сумматору.
Когда вы начинаете складывать два двоичных числа, первый столбец цифр отличается от остальных тем, что не может содержать бит переноса из предыдущего столбца. В первом столбце нет бита переноса, поэтому вход для переноса полного сумматора соединяется с землей, то есть его значением является 0 бит. Разумеется, в результате сложения первой пары двоичных цифр может получиться бит переноса. Этот выход переноса — вход для следующего столбца.
Для следующих двух цифр и лампочки вы используете полный сумматор, подключенный так.
Выход переноса, полученный от первого полного сумматора, является входом для второго полного сумматора. Каждый последующий столбец цифр складывается по той же схеме. Каждый разряд переноса из одного столбца подается на вход для переноса следующего столбца.
Наконец, восьмая и последняя пара переключателей подключена к последнему полному сумматору.
Здесь последний выход для переноса подключен к девятой лампочке.
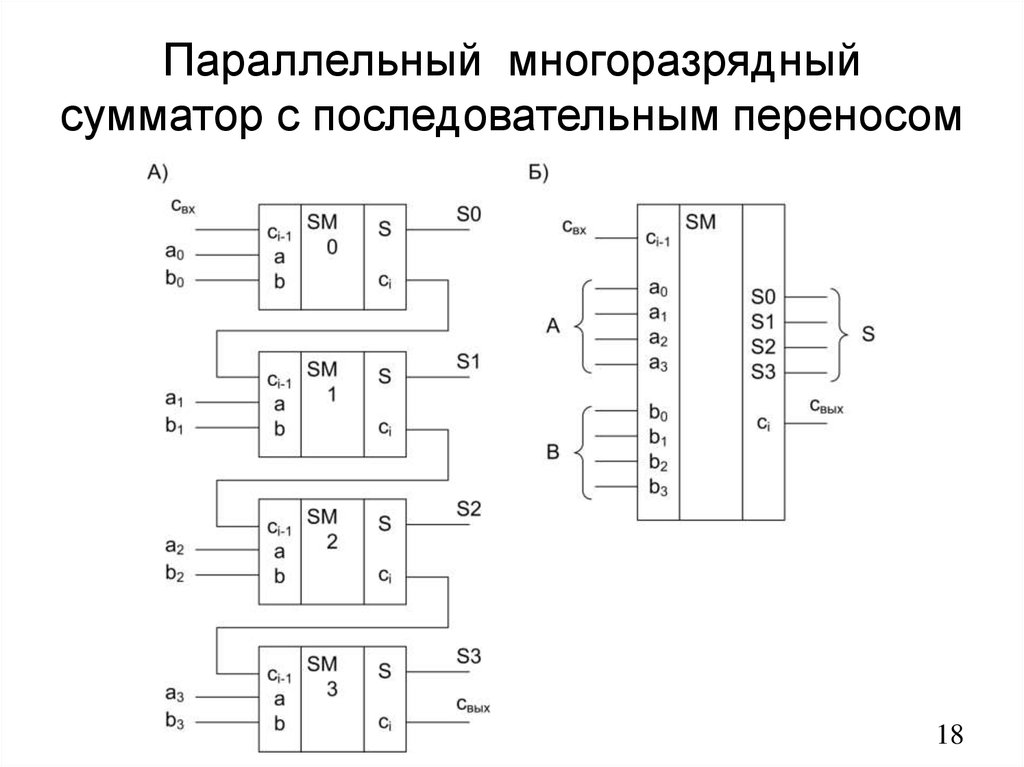
Вот еще один способ изобразить схему из восьми полных сумматоров (full adder, FA), в которой каждый выход для переноса (CO) подключен к следующему входу для переноса (CI).
Представим единое обозначение 8-битного сумматора, входы обозначим буквами от A0 до A7 и от B0 до B7, выходы — буквами от S0 до S7 (от sum — «сумма»).
Это распространенный способ обозначения отдельных битов многобитного числа. Биты A0, B0 и S0 являются младшими, а биты A7, B7 и S7 — старшими. Например, вот как с помощью этих букв с индексами можно было бы представить двоичное число 0110 1001.
Индексы начинаются с 0 и увеличиваются по мере перехода ко все более значимым цифрам, поскольку они соответствуют показателю степени двойки.
Если вы умножите каждую степень двойки на цифру, расположенную под ней, и сложите результаты, получите десятичный эквивалент числа 0110 1001, который равен 64 + 32 + 8 + 1, или 105.
По-другому 8-битный сумматор можно изобразить так.
Восьмерки внутри стрелок указывают на то, что каждая из них — это группа из восьми отдельных сигналов. Индексы символов A7 … A0, B7 … B0 и S7 … S0 также обозначают восьмиразрядность числа.
Как только соберете один 8-битный сумматор, вы сможете создать второй. Их легко расположить каскадом, чтобы сложить два 16-битных числа.
Выход для переноса правого сумматора связан со входом для переноса левого. Левый сумматор в качестве входных значений принимает самые старшие восемь цифр двух слагаемых и в качестве выходного значения выдает самые старшие восемь цифр.
Теперь вы можете спросить: «Неужели компьютеры действительно складывают числа именно так?»
В принципе да. Но не совсем.
Во-первых, сумматоры могут быть быстрее тех, которые мы описали. Если вы посмотрите на то, как работает эта схема, то поймете, что выход переноса от младшей пары цифр необходим для сложения со следующей парой, выход переноса от второй пары цифр — для сложения с третьей парой и т. д. Общая скорость сумматора равна количеству битов, умноженному на скорость одного полного сумматора. Это называется сквозным переносом. Быстрые сумматоры используют дополнительные схемы ускоренного переноса.
д. Общая скорость сумматора равна количеству битов, умноженному на скорость одного полного сумматора. Это называется сквозным переносом. Быстрые сумматоры используют дополнительные схемы ускоренного переноса.
Во-вторых (и это самое главное), компьютерам больше не нужно реле! Однако первые цифровые компьютеры, созданные в начале 1930-х годов, использовали реле, позднее — вакуумные лампы. Современные компьютеры создаются на основе транзисторов. Транзисторы в основном функционируют так же, как и реле, однако (как мы увидим далее) они намного быстрее, компактнее, тише, дешевле и потребляют гораздо меньше энергии. Для построения 8-битного сумматора по-прежнему требуются 144 транзистора (или больше, если вы хотите заменить сквозной перенос схемой ускоренного переноса), однако при этом размер схемы микроскопический.
StudyPort.
 Ru — Десятично-двоичный сумматор
Ru — Десятично-двоичный сумматорДесятично-двоичный сумматор
Введение.
В настоящее время интегральные микросхемы (ИМС) широко применяются в радиоэлектронной аппаратуре, в вычислительных устройствах, устройствах автоматики и т.д. Цифровые методы и цифровые устройства, реализованные на интегральных микросхемах разной степени интеграции, в том числе на микропроцессорных средствах, имеют широкие перспективы использования в цифровых системах передачи и распределения информации, в телевизионной, радиовещательной и другой аппаратуре связи. Современный этап развития научно – технического процесса характеризуется широкими применением электроники и микроэлектроники во всех сферах жизнедеятельности человека. Важную при этом сыграло появление и быстрое совершенствование ИМС – основной элементной базы современной электроники. С внедрением ИМС значительно снизилась себестоимость радиоэлектронных приборов, они стали более доступными и более компактными и расширилось внедрение радиоэлектроники в развитие науки и техники.
В отличии от цифровых устройств некоторые импульсные устройства, например формирователи и генераторы импульсов различной формы производить серийно в виде интегральных схем (ИС) экономически невыгодно. Перспективен другой путь – построение импульсных устройств на ИС широкого применения т.е на логических элементах, операционных усилителях и других ИС совместно с навесными элементами. Это способствует унификации элементной базы, эффетивному использованию и комплексной миниатюризации радиоэлектронной аппаратуры – высокая надёжность, малые габариты и масса, низкая стоимость и потребляемая мощность.
1. Общая часть.
1.1. Назначение арифметически — логических интегральных схем.
Арифметически – логические интегральные микросхемы, являются неотъемлемой частью микроэлектронных цифровых вычислительных устройств и предназначены для выполнения арифметических и логических операций над числами, представленными в двоичном, двоично– десятичном и других кодах.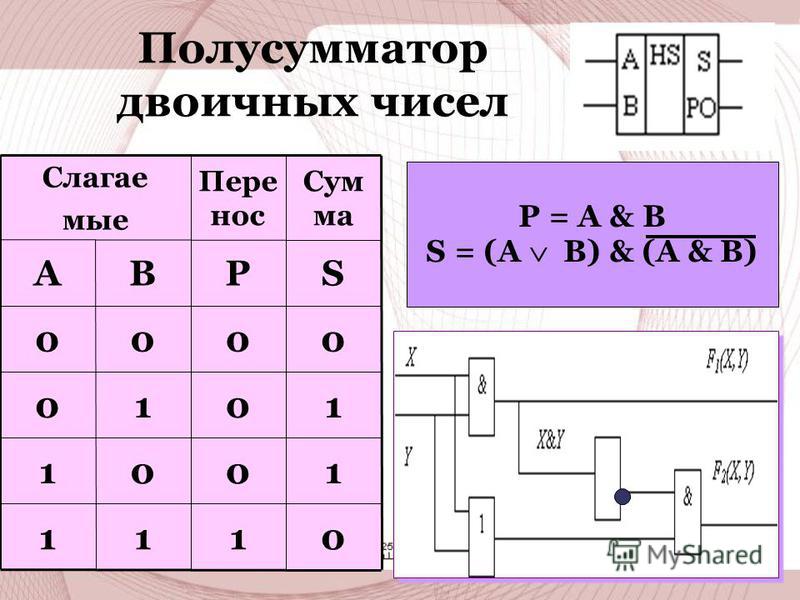 Для выполнения арифметических операций АЛУ строят на сумматорах.
Для выполнения арифметических операций АЛУ строят на сумматорах.
Сумматором называется устройство, выполняющее арифметическое сложение двух чисел, представленных сигналами на его входах. При необходимости сумматоры с помощью некоторых вспомогательных операций (сдвига числа, обращения кода числа) могут выполнять алгебраическое сложение, вычитание, умножение, деление, сравнение и другие действия с числами.
1.2. Классификация сумматоров.
Сумматоры классифицируются по следующим признакам.
По основанию системы исчисления чисел, с которыми оперирует сумматор ( двоичные, двоично –десятичные и другие ) .
По способу обработки многоразрядных чисел. Передача числа из одного места ЭЦВМ в другое может выполнятся последовательно или параллельно. В устройствах последовательного действия цифры какого – либо числа, начиная с младшего разряда, последовательно передаются в канал, обладающий емкостью в одну цифру.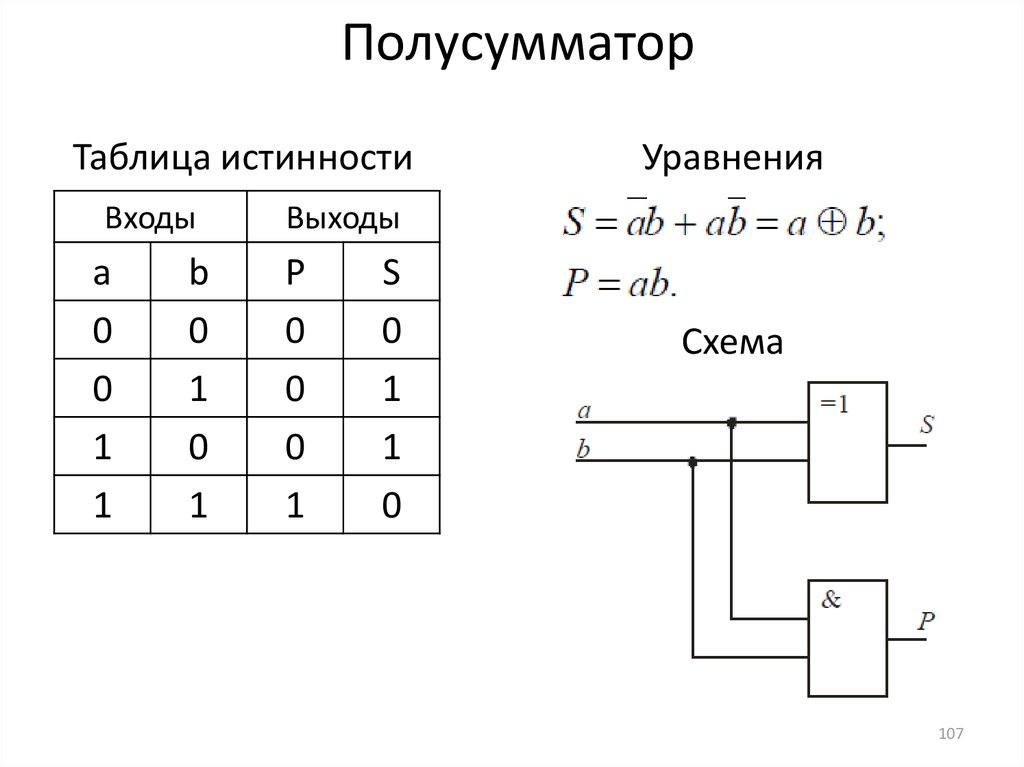 В устройствах параллельного действия все цифры числа передаются одновременно, поэтому емкость канала должна быть N цифр. В таком устройстве передача всего числа осуществляется за такое же время как у последовательного одна цифра. Суммирование может так же осуществляться последовательно – параллельно и параллельно – последовательно.
В устройствах параллельного действия все цифры числа передаются одновременно, поэтому емкость канала должна быть N цифр. В таком устройстве передача всего числа осуществляется за такое же время как у последовательного одна цифра. Суммирование может так же осуществляться последовательно – параллельно и параллельно – последовательно.
По способу организации цепей переноса.
По способу организации процесса суммирования одноразрядной суммирующей схемы ( комбинационный или накапливающий типы ).
1.3. Выбор и обоснование функциональной схемы.
Последовательно – параллельный тип сумматора. ( Смотри рисунок 1)
Количество одноразрядных суммирующих схем в таком сумматоре меньше количества разрядов в суммируемых числах. Эти схемы соединены между собой в цепочку в порядке последовательного возрастания разрядов. На входы сумматора поступает группа цифр младших разрядов слагаемых, причем перенос образующийся на входе старшей одноразрядной суммирующей схемы, запоминается соответствующим устройством. Затем на входы сумматора поступает следующая группа слагаемых. Одновременно на соответствующий вход младшей одноразрядной суммирующей схемы поступает перенос, который хранится в запоминающей схеме.
Затем на входы сумматора поступает следующая группа слагаемых. Одновременно на соответствующий вход младшей одноразрядной суммирующей схемы поступает перенос, который хранится в запоминающей схеме.
Элементная база.
В качестве элементной базы для построения арифметического устройства использованы ИМС серии К155ТМ2, К155ИР1, К155ИМ1.
К155ТМ2.
ИМС серии К155ТМ2 (рис1) содержат два независимых D-триггера имеющих общую цепь питания
У каждого триггера есть входы D, S и R, а так же комплиментарные выходы Q и Q. Входы R и S – асинхронные, потому что они работают независимо от сигнала на тактовом входе. Напряжение питания +5В подаётся на контакт 14, а питание 0В на контакт 7.
Для защиты схемы от электрических помех на выходы питания ставится электролитический конденсатор К–53–14-1,6В-6,8 мкФ. Для защиты от низкочастотных помех, между контактами питания и заземления, ставятся керамические конденсаторы типа КМ-5б-Н90-0,047 мкФ.
Электрические характеристики конденсаторов.
К-53-14-1,6в-6,8мкФ
ТАБЛИЦА 4
Параметры | Значение |
Uном | 6,6В |
Предельно допустимая температура | + 80ос |
Рабочая температура | + 20ос |
КМ-5б-Н90-0,47мкФ
ТАБЛИЦА 5
Параметры | Значение |
Uном | 16В |
Предельно допустимая температура | + 80ос |
Рабочая температура | + 20ос |
2. Специальная часть.
Специальная часть.
2.1. Описание работы принципиальной схемы.
На входы А и В сумматора ( ДД3 ) последовательно начиная с младшего разряда подаются числа из четырехразрядных регистров ( ДД1 и ДД2 ). Полученная сумма с выхода сумматора записывается в регистр ( ДД4 ). Полученный в результате перенос записывается Д – триггером ( ДД5 ), с выхода которого он поступает на вход входного переноса сумматора, для сложения его со следующими разрядами.
2.2.Расчет параметров.
2.2.1.Расчет потребления мощьности.
ТИП ИМС | I потребления mВт | P потребления mВт |
К 155 ТМ 2 | 31.5 | 157.5 |
К 155 ИМ 1 | 80 | 400 |
К 155 ИР 1 | 82 | 410 |
Потребляемая мощность.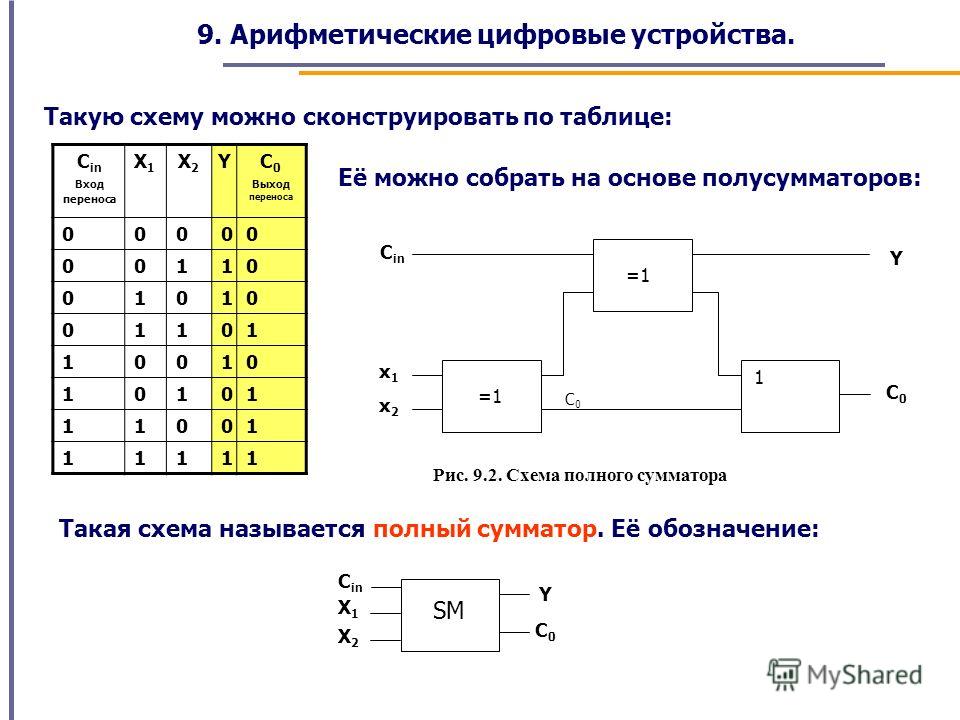
2.2.2.Расчет быстродействия.
ТИП ИМС | T задержки ср. н.с. |
К 155 ТМ 2 | 25 |
К 155 ИМ 1 | 34 |
К 155 ИР 1 | 35 |
2.2.3 Расчёт надёжности.
Надёжность – это свойство объекта выполнять заданные функции, сохраняя значения эксплуатационных параметров в допустимых приделах в соответствии с установленными нормами его эксплуатации, ремонта, технического обслуживания и транспортировки.
Расчёт параметров надёжности ведётся в два этапа:
1. Предварительный расчёт надёжности изделия проводят на этапе эскизного проектирования.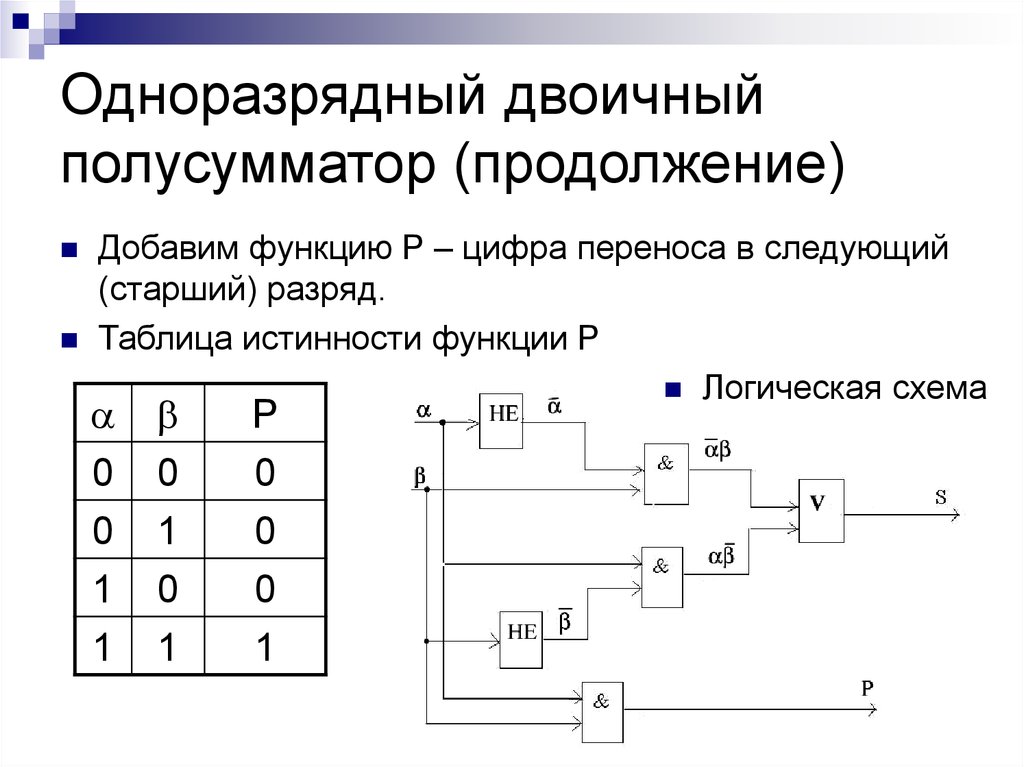 В результате предварительного расчёта определяются все основные параметры:
В результате предварительного расчёта определяются все основные параметры:
а) Интенсивность отказа изделий. Определяется по формуле 9.
Где N – число группы “компонентов надёжности”, имеющие разные интенсивности отказов.
io – интенсивность отказа элементов в i – ой группе.
ni – количество элементов в i – ой группе.
б) Время наработки на отказ определяется по формуле 10.
в) Вероятность безотказной работы определяется по формуле 11.
где t – время работы изделия.
В таблице 8 приведены показатели надёжности изделий.
ТАБЛИЦА 8
Группа элементов | Интенсивность атказа 1/час | Количество элементов 1/час | io ni 1/час |
ИМС. Конденсаторы: а)Керамические. б)Электролитические. Контактные разводы. Пайка. Печатная плата. | 0.01.10-5 0.062 . 10-5 0.035 . 10-5 0.02 . 10-5 0.01 . 10-5 0.1 . 10-5 | 4 3 2 1 6 41 1 | 0.04 . 10-5 0.124 . 10-5 0.035 . 10-5 0. 0.41 . 10-5 0.1 . 10-5 |
По формуле 9 получим интенсивность отказов для всего изделия:
По формуле 10 определим время наработки на отказ:
По формуле 11 определим вероятность безотказной работы для 100 часов, 1000 часов и 10000 часов.
P (100) = 0.9991
P(1000) = 0.9917
P(10000) = 0.9209
2. Окончательный расчёт надёжности.
Ведётся на этапе техниического проектирования. Формулы для расчёта показателей те же, но следует учитывать электрический режим работы схемы и условия эксплуатации, вибрации и т.д.
В рамках курсового проекта для учёта влияния режима работы расчитывается коэффициент нагруски Кн по формуле 12, а температурный коэффициент берётся равный 1. Коэффициент нагрузки для ИМС определяется по нагрузочной способности (через коэффициент разветвления).
Коэффициент нагрузки для ИМС определяется по нагрузочной способности (через коэффициент разветвления).
где Кр.р – коэффициент разветвления рабочий (вычисляется).
Кр.н – коэффициент разветвления наминальный.
Для конденсаторов коэффициент нагрузки через напряжение по формуле 13.
В таблице 9 приведены паказатели надёжности всего изделия
ТАБЛИЦА 9
ИМС | Интенсивность отказа | Кн | io. ni .Кн |
К155ТМ2. К155ИМ1. К155ИР1. К155ИР1. К155ИР1. Керомический конденсатор. Электролитический конденсатор Плата. Контактные разъёмы. Пайка. | 0.01 . 10-5 0.01 . 10-5 . 10-5 0.01 . 10-50.01 . 10-5 0.062 . 10-5 0.035 . 10-5 0.1 . 10-5 0.02 . 10-5 0.01 . 10-5 | 0.1 0.1 0.5 0.5 0.5 1 1 1 1 1 | 0. 0.001 . 10-5 0.05 . 10-5 0.05 . 10-5 0.05 . 10-5 0.062 . 10-5 0.035 . 10-5 0.1 . 10-5 0.02 . 10-5 0.01 . 10-5 |
P (100) = 0.9991
P(1000) = 0.9912
P(10000) = 0.9156
2.4 Конструкционный расчёт печатной платы.
На рис.6 показана двухсторонняя печатная плата с металлизированными отверстиями.
Рис 6
d – диаметр отверстия.
dкп – диаметр контактной площадки.
S – расстояние между контактными площадками или контактной площадкой и проводником.
t – ширина печатного проводника.
H – ширина печатной платы.
Диаметр металлизированных монтажных отверстий, выбирается в зависимости от диаметра вставляемого в него выхода и от толщины ПП.
В схеме два различных вида диаметров выводов. У ИМС и керамических конденсаторов диаметры выводов составляют 0.5мм.
У электрического конденсатора диаметр выводов составляет 0.6мм.
Для обеспечения высокого качества пайки и надёжности соединения, различие диаметров выводов и металлизированного отверстия не должно быть больше 0.4 мм.
При разработке конструкции ПП решают задачу размещения элементов на ПП, трассировки печатных проводников, выбора метода изготовления ПП.
2.4.1 Расчёт геометрических размеров.
Выбираем ПП второго класса.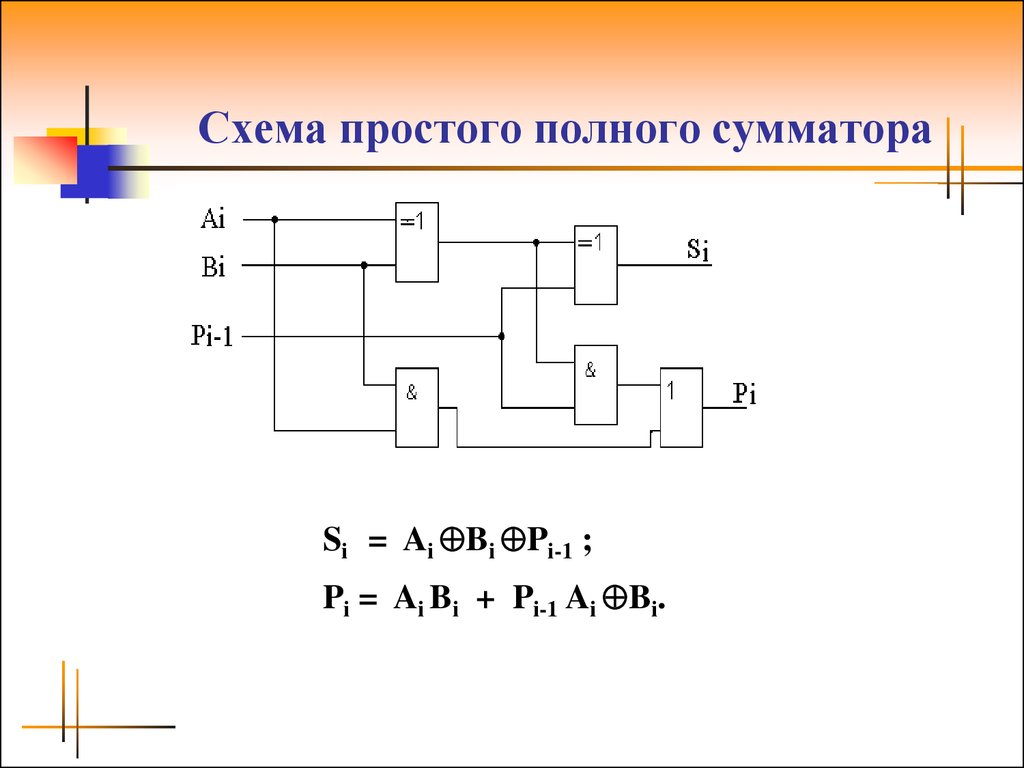 Расчёт геометрических размеров ПП по оси X:
Расчёт геометрических размеров ПП по оси X:
Lx = x1 + x2 + lx + tx (nx. 1)
Размер ПП по оси Y:
Ly = y1 + y2 + ly + ty (ny. 1)
Шаг размещения ИМС по оси X:
tx = Lx + rx R
Шаг размещения ИМС по оси Y:
ty = Ly + ry R
где: x1 и x2 – краевые технологические поля.
y1 и y2 – краевые защитные поля.
Lx и Ly – длинна и ширина ИМС.
nx и ny – число ИМС в ряду по осям “X” и “Y”.
rx и ry – количество шагов по осям “X” и “Y”.
Формула для расчёта прокладки в узком месте требуемого количества проводников.
Ширина печатного проводника выбирается из следуемых показателей:
0.45 в свободных местах платы
0.40 в узких местах платы.
Unit 6 Дополнительные проекты, стр. 2
Unit 6 Дополнительные проекты, стр. 2На этой странице вы исследуете, как можно комбинировать логические вентили для выполнения арифметических действий (в частности, сложения) с двоичными значениями.
Вспомните, что при сложении двух чисел (в базе 10) вы найдете сумму каждого столбца , включая любое переносимое значение из предыдущего столбца.
Та же процедура используется для сложения двух чисел по основанию 2.
Для выполнения сложения любой алгоритм должен учитывать значения, переносимые из младших разрядов в старшие разряды.
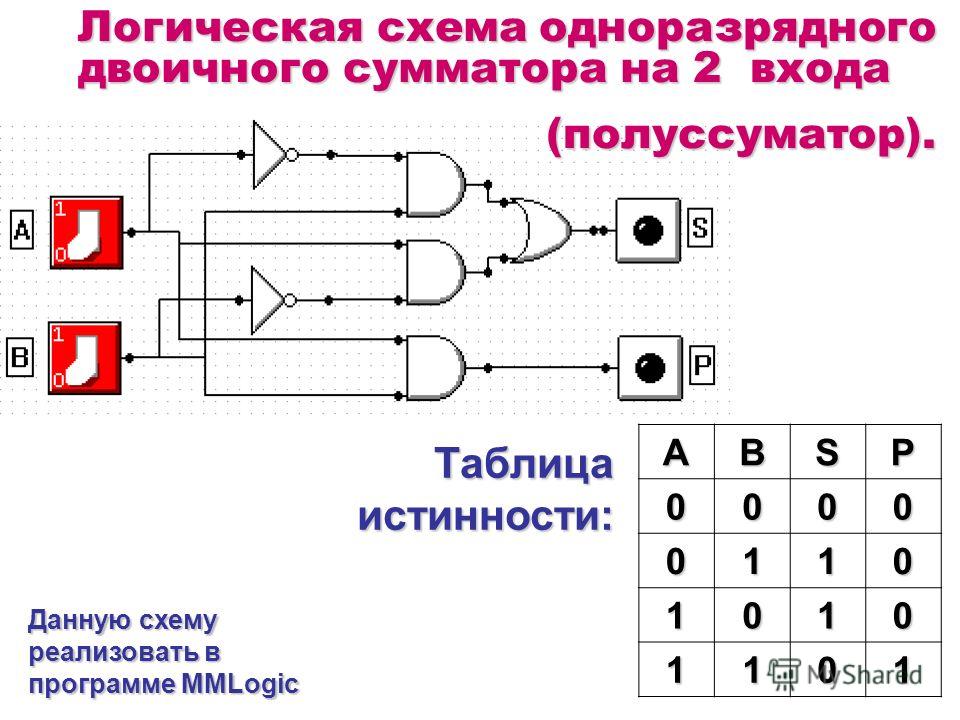
Полусумба
Логические операторы принимают два логических значения ( true или false ) в качестве входных данных и сообщают один бит (одно логическое значение) в качестве выходных данных. Это в отличие от основных операций, используемых в математике. Например, кроме того, сумма двух однобитовых значений может иметь два -битных результата: 1 + 1 = 10 в двоичном виде. Таким образом, такие вещи, как арифметические схемы, построены из логических схем.
Это в отличие от основных операций, используемых в математике. Например, кроме того, сумма двух однобитовых значений может иметь два -битных результата: 1 + 1 = 10 в двоичном виде. Таким образом, такие вещи, как арифметические схемы, построены из логических схем.
Полусумматор складывает две двоичные цифры (без переноса в ) и сообщает сумму, а значение выполняет . Если вы посмотрите на столбец «SUM», вы заметите, что он идентичен выходному столбцу XOR, а если вы посмотрите на столбец «CARRY», вы заметите, что он идентичен выходному столбцу AND.
Если вам трудно разобраться в этой таблице, рассмотрите возможность добавления двоичных цифр:
0+0=0
0+1=1
1+0=1
1+1=2, что равно 10 в двоичном виде с суммой единиц 0 и переносом 1.
- Осмотрите оснастку ! и все его спрайты. Для спрайтов
SUMиCARRYсоберите несколько блоков кода для имитации полусумматора.
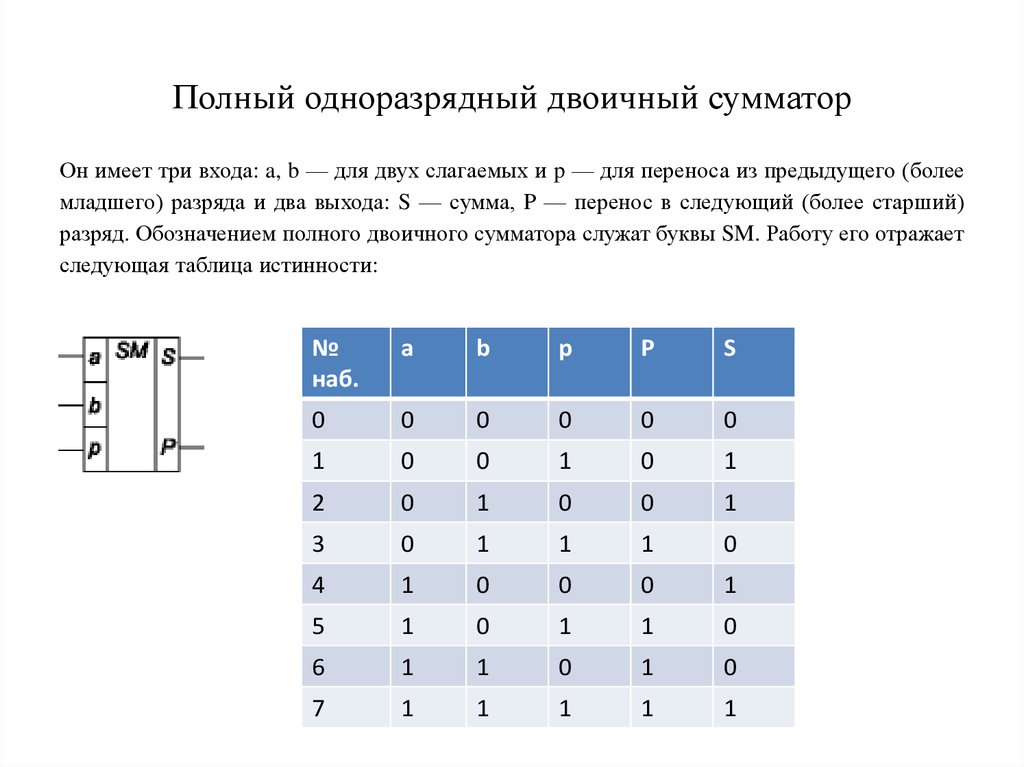
Полный сумматор
Если у вас возникли трудности с пониманием этой таблицы, рассмотрите возможность добавления трех двоичных цифр:
Например, 1+1+1=3, что равно 11 в двоичном формате с цифрой единиц 1 и значением переноса 1.
Полный сумматор использует два полусумматора для полного сложения двоичных цифр, вмещающих перенос в значение . Он сообщает сумму и выполняет значение .
- Изучите приведенную выше таблицу и схему полного сумматора, чтобы объяснить, как полный сумматор выполняет сложение двух двоичных чисел с числом 9.0007 перенесите с помощью двух полусумматоров и вентиля ИЛИ.
- Осмотрите оснастку ! и все его спрайты. Код для спрайтов
CARRY IN,AиB, был написан для вас. Для спрайтов
Для спрайтов SUM1,CARRY1,SUM OUT,CARRY2,CARRY OUTсоберите несколько блоков кода для имитации полного сумматора.
- Узнайте о сумматорах с неравномерным переносом и объясните, как они используют полные сумматоры для сложения многозначных двоичных чисел. Собери снап ! программа для имитации сложения двух 4-значных двоичных чисел с помощью сумматора с неравномерным переносом .
Изображение предоставлено пользователем Википедии Cburnett. - Узнайте, как компьютеры вычитают и умножают двоичные числа с помощью логических вентилей, и создайте Snap ! программ для эмуляции этих операций.
Бинарное дополнение: Мне кажется, это как-то отстало. Он вводит «выполнение» и «перенос» как технические термины, прежде чем указать, почему они важны, а именно добавить больше чем однобитовые числа.1. Сделайте сложение с основанием 10, которое включает в себя переноску, и расскажите о том, что например, «вынос» из столбца десятков - это «перенос» в сотни столбец. 2. Сделайте то же самое в двоичном формате, с той разницей, что сигналы переноса шириной всего в один провод. 3. Покажите однобитовый срез сложения, чтобы показать, что + схема нуждается /три/ входа и /два/ выхода. 4. Нарисуйте сумматор пульсаций, чтобы показать, как перенос из одного битового среза становится Carry In для следующего левого битового фрагмента. 5. Теперь вы готовы сказать, что традиционный способ построения однобитового сумматор должен начинаться со схемы, называемой полусумматор, которая имеет перенос, но нет переноски. 6. Нарисуйте эту картинку: +----------+ А ----->| |-----> Сумма |полусумматор| Б ----->| |-----> Выполнить +----------+ а затем / пусть ученики построят его! / Не водить их за кольцо в носу. Если у вас должна быть /скрытая/ подсказка, которая просто говорит: «Нарисуйте таблицу истинности для суммы и еще одна таблица истинности для Carry Out».
7. Покажите рисунок с двумя каскадными полусумматорами, но без вентиля ИЛИ. и три выходные метки. Предложите учащимся нарисовать остальную часть схемы, напомнив им, что они должны выдать два результата: Sum и Исполняйте. Также напомните им, что /каждый полусумматор/ имеет выходы, называемые Sum и Выполнить, и что полный сумматор имеет свои одноименные выходы, и все три различны. Я думаю, где-то должно быть сказано, что компьютеры сегодня на самом деле не используют эти простые цепи пульсации, потому что они слишком медленные; каждый бит должен ждать бит справа от него, прежде чем он сможет определить свой собственный вывод. Итак, ТИФ А: Как компьютеры /действительно/ добавляют двоичные целые числа? TIF B состоит из двух частей, в каждой из которых есть подводные камни. Чтобы сделать вычитание, вам действительно нужно сначала понять два дополнения. Что касается умножения, как я сказал ранее, есть простой способ (сдвинуть и добавить), а есть реальный способ (много более сложный, включающий, я думаю, поиск в таблице фрагментов из четырех или восьми биты).

Полусумматор
Полусумматор складывает две двоичные цифры и выводит сумму и переносимое значение. Если вы посмотрите на столбец «SUM», вы заметите, что он идентичен выходному столбцу XOR, а если вы посмотрите на столбец «CARRY», вы заметите, что он идентичен выходному столбцу AND.
Если у вас возникли трудности с пониманием этой таблицы, рассмотрите возможность добавления двоичных цифр:
0+0=0
0+1=1
1+0=1
1+1=2, что равно 10 в двоичном формате с цифрой единиц сумма 0 и перенос 1,
- Осмотрите оснастку ! и все его спрайты. Для спрайтов
SUMиCARRYсоберите несколько блоков кода для имитации полусумматора.
Полный сумматор
Если у вас возникли трудности с пониманием смысла этой таблицы, рассмотрите возможность сложения трех двоичных цифр:
Например, 1+1+1=3, что равно 11 в двоичной системе с суммой единиц 1 и переносом 1.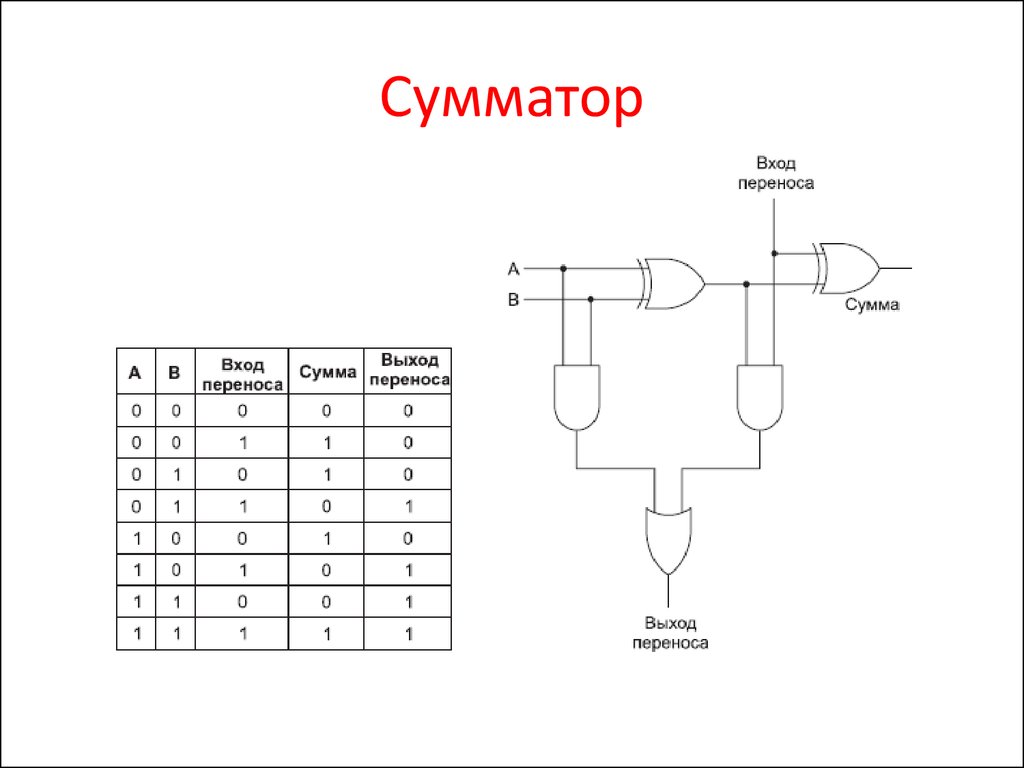
Полный сумматор использует два полусумматора для выполнения полного сложения двоичных цифр с переносом значения. Он сообщает сумму и выполняет значение.
- Изучите приведенную выше таблицу и схему полного сумматора, чтобы объяснить, как полный сумматор выполняет сложение двух двоичных чисел с переносом, используя два полусумматора и вентиль ИЛИ.
- Осмотрите оснастку ! и все его спрайты. Код для спрайтов
CARRY IN,AиB, был написан для вас. Для спрайтовSUM1,CARRY1,SUM OUT,CARRY2,ВЫПОЛНИТЕ, соберите несколько блоков кода для эмуляции полного сумматора.
- Узнайте о сумматорах с неравномерным переносом и объясните, как они используют полные сумматоры для сложения многоразрядных двоичных чисел. Собери снап ! программа для имитации сложения двух 3-значных двоичных чисел с помощью сумматора с неравномерным переносом .

- Узнайте, как компьютеры вычитают и умножают двоичные числа с помощью логических вентилей, и создайте Snap ! программ для эмуляции этих операций.
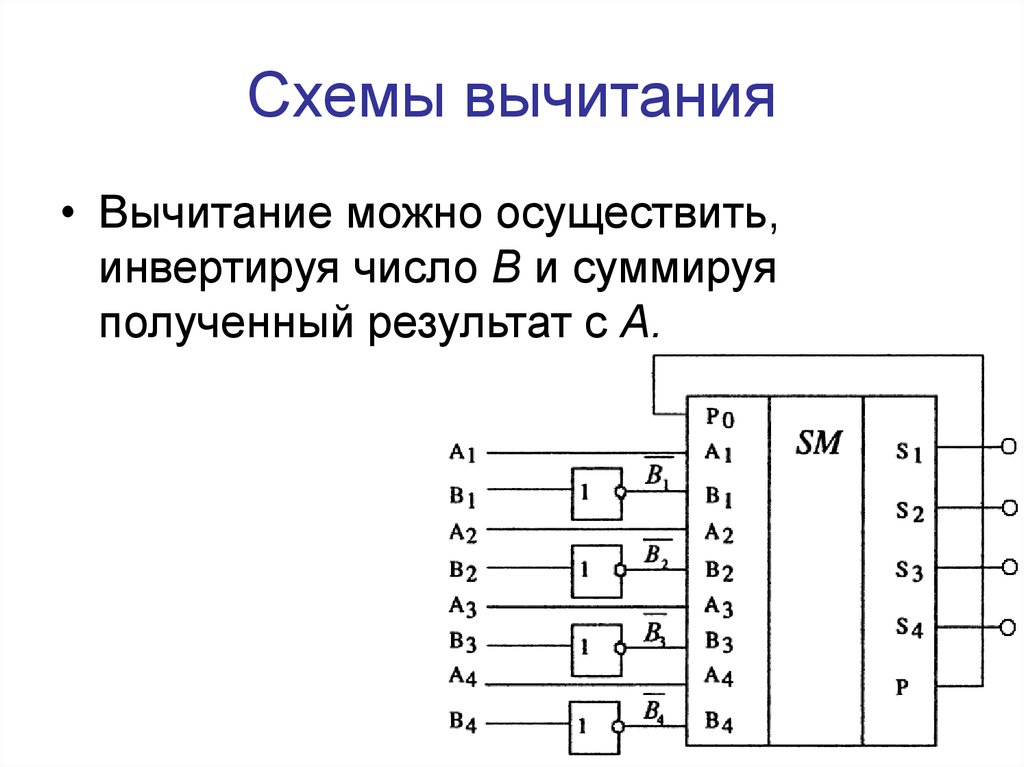
Двоичный сумматор-вычитатель — Javatpoint
следующий → ← предыдущая Двоичный сумматор-вычитатель — это особый тип схемы, который используется для выполнения обеих операций, т. е. сложения и вычитания. Операция, которая будет использоваться, зависит от значений, содержащихся в управляющем сигнале. В арифметико-логическом устройстве это один из важнейших компонентов. Для работы с бинарным сумматором-вычитателем требуется знание вентиля XOR, полного сумматора, двоичного сложения и вычитания. Например, мы возьмем два 4-битных двоичных числа «X» и «Y» для операции с цифрами. X 0 X 1 X 2 X 3 для X Двоичный сумматор-вычитатель представляет собой комбинацию из 4 полных сумматоров, которые могут выполнять сложение и вычитание 4-битных двоичных чисел. На приведенной выше диаграмме линии управления первого полного сумматора напрямую поступают на его вход (входной сигнал C0). X 0 является младшим значащим битом A, который непосредственно вводится в полный сумматор. Результат, полученный в результате выполнения операции XOR Y 0 и K, является третьим входом двоичного сумматора-вычитателя. Сумма/разность (S 0 ) и перенос (C 0 ) являются двумя выходными данными первого полного сумматора. Если значение K равно true или 1, Y 0 ⨁K производит дополнение Y 0 в качестве вывода. Таким образом, операция будет выглядеть так: X+Y 0 ‘, что представляет собой вычитание X и Y в дополнении до 2. Это означает, что когда значение K равно 1; операция вычитания выполняется двоичным сумматором-вычитателем. Таким же образом, когда значение K установлено на 0, Y 0 ⨁K производит Y 0 в качестве выхода. Таким образом, операция будет выглядеть так: X+Y 0 , что представляет собой двоичное сложение X и Y. Это означает, что когда значение K равно 0; операция сложения выполняется бинарным сумматором-вычитателем. Перенос/заимствование C 0 обрабатывается как ввод переноса/заимствования для второго полного сумматора. Сумма/разность S 0 определяет младший значащий бит суммы/разности чисел X и Y. Как и X 0 , X 1 , X 2 и X 3 затухают напрямую. к 2 nd , 3 rd и 4 th Full-Adder в качестве входа. Выходы после выполнения операции XOR Y 1 , Y 2 и Y 3 входы с K являются третьими входами для 2 nd , 3 rd и 4 th Full-Adder. Перенос C 1 , C 2 передается в качестве входных данных для Full-Adder. |



 12 . 10-5
12 . 10-5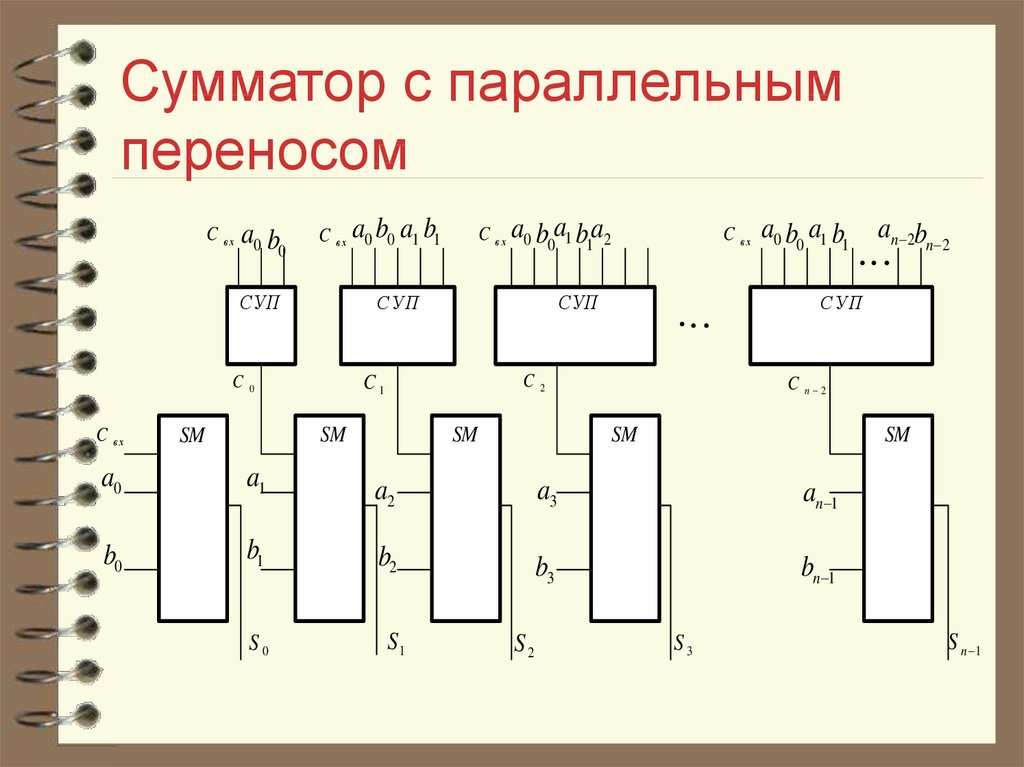
 001 . 10-5
001 . 10-5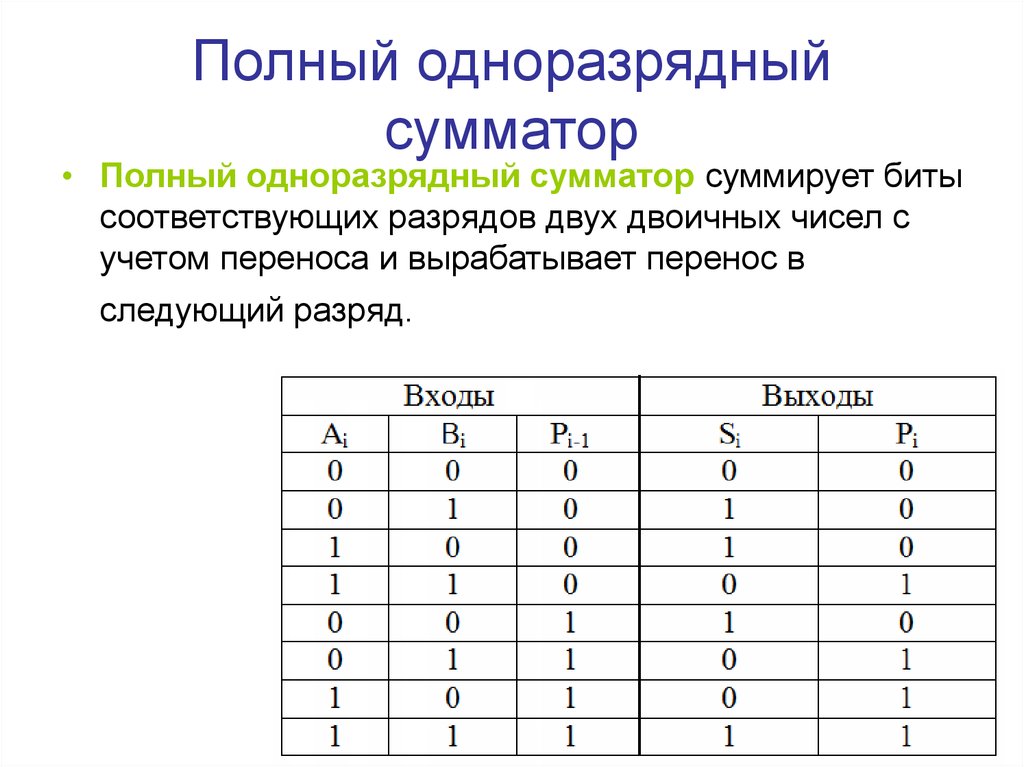
 Для спрайтов
Для спрайтов 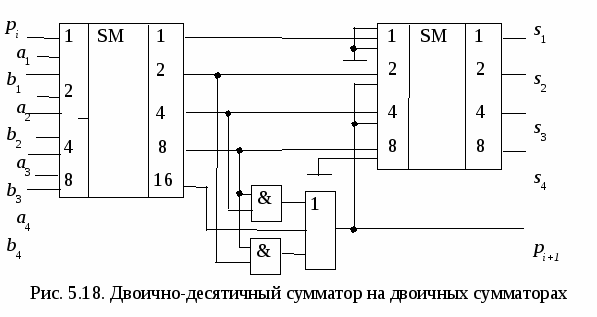 1. Сделайте сложение с основанием 10, которое включает в себя переноску, и расскажите о том, что
например, «вынос» из столбца десятков - это «перенос» в сотни
столбец.
2. Сделайте то же самое в двоичном формате, с той разницей, что сигналы переноса
шириной всего в один провод.
3. Покажите однобитовый срез сложения, чтобы показать, что + схема нуждается
/три/ входа и /два/ выхода.
4. Нарисуйте сумматор пульсаций, чтобы показать, как перенос из одного битового среза становится
Carry In для следующего левого битового фрагмента.
5. Теперь вы готовы сказать, что традиционный способ построения однобитового
сумматор должен начинаться со схемы, называемой полусумматор, которая имеет перенос, но
нет переноски.
6. Нарисуйте эту картинку:
+----------+
А ----->| |-----> Сумма
|полусумматор|
Б ----->| |-----> Выполнить
+----------+
а затем / пусть ученики построят его! / Не водить их за кольцо в носу. Если
у вас должна быть /скрытая/ подсказка, которая просто говорит: «Нарисуйте таблицу истинности для суммы и
еще одна таблица истинности для Carry Out».
1. Сделайте сложение с основанием 10, которое включает в себя переноску, и расскажите о том, что
например, «вынос» из столбца десятков - это «перенос» в сотни
столбец.
2. Сделайте то же самое в двоичном формате, с той разницей, что сигналы переноса
шириной всего в один провод.
3. Покажите однобитовый срез сложения, чтобы показать, что + схема нуждается
/три/ входа и /два/ выхода.
4. Нарисуйте сумматор пульсаций, чтобы показать, как перенос из одного битового среза становится
Carry In для следующего левого битового фрагмента.
5. Теперь вы готовы сказать, что традиционный способ построения однобитового
сумматор должен начинаться со схемы, называемой полусумматор, которая имеет перенос, но
нет переноски.
6. Нарисуйте эту картинку:
+----------+
А ----->| |-----> Сумма
|полусумматор|
Б ----->| |-----> Выполнить
+----------+
а затем / пусть ученики построят его! / Не водить их за кольцо в носу. Если
у вас должна быть /скрытая/ подсказка, которая просто говорит: «Нарисуйте таблицу истинности для суммы и
еще одна таблица истинности для Carry Out». 7. Покажите рисунок с двумя каскадными полусумматорами, но без вентиля ИЛИ.
и три выходные метки. Предложите учащимся нарисовать остальную часть схемы,
напомнив им, что они должны выдать два результата: Sum и
Исполняйте. Также напомните им, что /каждый полусумматор/ имеет выходы, называемые Sum и
Выполнить, и что полный сумматор имеет свои одноименные выходы, и
все три различны.
Я думаю, где-то должно быть сказано, что компьютеры сегодня на самом деле не используют эти
простые цепи пульсации, потому что они слишком медленные; каждый бит должен ждать
бит справа от него, прежде чем он сможет определить свой собственный вывод. Итак, ТИФ А: Как
компьютеры /действительно/ добавляют двоичные целые числа?
TIF B состоит из двух частей, в каждой из которых есть подводные камни. Чтобы сделать вычитание, вам действительно нужно
сначала понять два дополнения. Что касается умножения, как я сказал ранее,
есть простой способ (сдвинуть и добавить), а есть реальный способ (много
более сложный, включающий, я думаю, поиск в таблице фрагментов из четырех или восьми
биты).
7. Покажите рисунок с двумя каскадными полусумматорами, но без вентиля ИЛИ.
и три выходные метки. Предложите учащимся нарисовать остальную часть схемы,
напомнив им, что они должны выдать два результата: Sum и
Исполняйте. Также напомните им, что /каждый полусумматор/ имеет выходы, называемые Sum и
Выполнить, и что полный сумматор имеет свои одноименные выходы, и
все три различны.
Я думаю, где-то должно быть сказано, что компьютеры сегодня на самом деле не используют эти
простые цепи пульсации, потому что они слишком медленные; каждый бит должен ждать
бит справа от него, прежде чем он сможет определить свой собственный вывод. Итак, ТИФ А: Как
компьютеры /действительно/ добавляют двоичные целые числа?
TIF B состоит из двух частей, в каждой из которых есть подводные камни. Чтобы сделать вычитание, вам действительно нужно
сначала понять два дополнения. Что касается умножения, как я сказал ранее,
есть простой способ (сдвинуть и добавить), а есть реальный способ (много
более сложный, включающий, я думаю, поиск в таблице фрагментов из четырех или восьми
биты).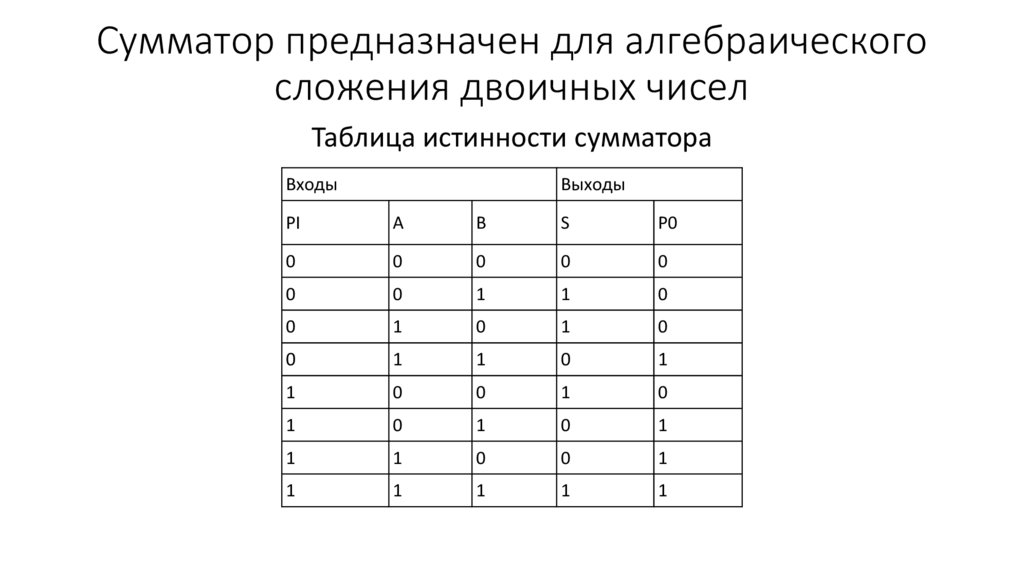
 Контрольная линия определяет, является ли выполняемая операция вычитанием или сложением. Это определение осуществляется с помощью двоичных значений 0 и 1, которые содержатся в K.
Контрольная линия определяет, является ли выполняемая операция вычитанием или сложением. Это определение осуществляется с помощью двоичных значений 0 и 1, которые содержатся в K.