Информатика ЕГЭ 5 задание разбор и объяснение
Урок посвящен тому, как решать 5 задание ЕГЭ по информатике
Кодирование информации
5-я тема характеризуется, как задания базового уровня сложности, время выполнения – примерно 2 минуты, максимальный балл — 1
- Кодирование — это представление информации в форме, удобной для её хранения, передачи и обработки. Правило преобразования информации к такому представлению называется кодом.
- Кодирование бывает равномерным и неравномерным:
- при равномерном кодировании всем символам соответствуют коды одинаковой длины;
- при неравномерном кодировании разным символам соответствуют коды разной длины, это затрудняет декодирование.
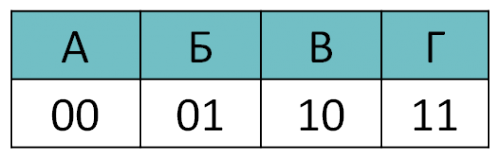
Таким образом, мы получили равномерный код, т.к. длина каждого кодового слова одинакова для всех кодов (2).
Кодирование и расшифровка сообщений
Декодирование (расшифровка) — это восстановление сообщения из последовательности кодов.
Для решения задач с декодированием, необходимо знать условие Фано:
Условие Фано: ни одно кодовое слово не должно являться началом другого кодового слова (что обеспечивает однозначное декодирование сообщений с начала)
Префиксный код — это код, в котором ни одно кодовое слово не совпадает с началом другого кодового слова. Сообщения при использовании такого кода декодируются однозначно.
- если сообщение декодируется с конца, то его можно однозначно декодировать, если выполняется обратное условие Фано:
- условие Фано – это достаточное, но не необходимое условие однозначного декодирования.
Обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова
Постфиксный код — это код, в котором ни одно кодовое слово не совпадает с концом другого кодового слова. Сообщения при использовании такого кода декодируются однозначно и только с конца.
Однозначное декодирование обеспечивается:
Однозначное декодирование

Декодирование
Егифка ©:

Решение 5 заданий ЕГЭ
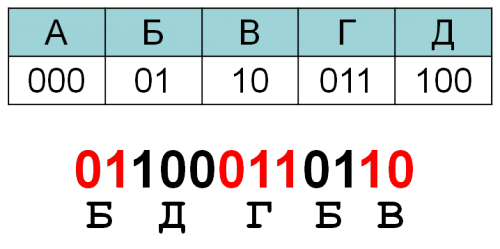
ЕГЭ 5.1: Для кодирования буквО, В, Д, П, А решили использовать двоичное представление чисел 0, 1, 23 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления).Закодируйте последовательность букв ВОДОПАД таким способом и результат запишите восьмеричным кодом.
✍ Решение:
- Переведем числа в двоичные коды и поставим их в соответствие нашим буквам:
О -> 0 -> 00 В -> 1 -> 01 Д -> 2 -> 10 П -> 3 -> 11 А -> 4 -> 100
ВОДОПАД:010010001110010
010 010 001 110 010 ↓ ↓ ↓ ↓ ↓ 2 2 1 6 2
Результат: 22162
Решение ЕГЭ данного задания по информатике, видео:
Рассмотрим еще разбор 5 задания ЕГЭ:
| a | b | c | d | e |
|---|---|---|---|---|
| 000 | 110 | 01 | 001 | 10 |
Какой набор букв закодирован двоичной строкой 1100000100110?
✍ Решение:
110 000 01 001 10 ↓ ↓ ↓ ↓ ↓ b a c d e
Результат: b a c d e.
✎ 2 вариант решения:
- Этот вариант решения 5 задания ЕГЭ более сложен, но тоже верен.
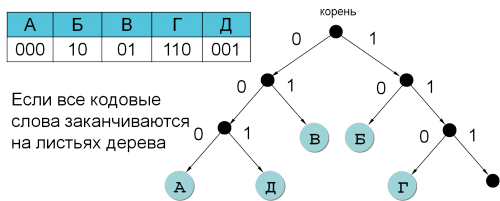
- Сделаем дерево, согласно кодам в таблице:
- Сопоставим закодированное сообщение с кодами в дереве:

110 000 01 001 10
Результат: b a c d e.
Решим следующее 5 задание:
Для передачи чисел по каналу с помехами используется код проверки четности. Каждая его цифра записывается в двоичном представлении, с добавлением ведущих нулей до длины
4, и к получившейся последовательности дописывается сумма её элементов по модулю 2 (например, если передаём 23, то получим последовательность 0010100110).Определите, какое число передавалось по каналу в виде
✍ Решение:
- Рассмотрим пример из условия задачи:
Было2310 Стало00101001102
0010100110 (0010 - 2, 0011 - 3)
01100 01010 01001 00110
0110 0101 0100 0011
0110 0101 0100 0011 ↓ ↓ ↓ ↓ 6 5 4 3
Ответ: 6 5 4 3
Вы можете посмотреть видео решения этого задания ЕГЭ по информатике:
ЕГЭ 5.4:
Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Н использовали кодовое слово 0, для буквы К — кодовое слово 10.
Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?
Подобные задания для тренировки
✍ Решение: ✎ 1 вариант решения основан на логических умозаключениях:
- Найдём самые короткие возможные кодовые слова для всех букв.
- Кодовые слова 01 и 00 использовать нельзя, так как тогда нарушается условие Фано (начинаются с 0, а 0 — это Н).
- Начнем с двухразрядных кодовых слов. Возьмем для буквы Л кодовое слово 11. Тогда для четвёртой буквы нельзя подобрать кодовое слово, не нарушая условие Фано (если потом взять 110 или 111, то они начинаются с 11).
- Значит, надо использовать трёхзначные кодовые слова. Закодируем буквы Л и М кодовыми словами 110 и 111. Условие Фано соблюдается.
- Суммарная длина всех четырёх кодовых слов равна:
(Н)1 + (К)2 + (Л)3 + (М)3 = 9
✎ 2 вариант решения:
- Будем использовать дерево. Влево откладываем 0, вправо — 1:
- Теперь выпишем соответствие каждой буквы ее кодового слова согласно дереву:
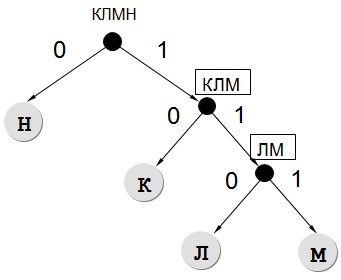
(Н) -> 0 -> 1 символ (К) -> 10 -> 2 символа (Л) -> 110 -> 3 символа (М) -> 111 -> 3 символа
(Н)1 + (К)2 + (Л)3 + (М)3 = 9
Ответ: 9
5.5: ЕГЭ по информатике 5 задание 2017 ФИПИ вариант 2 (под редакцией Крылова С.С., Чуркиной Т.Е.):
По каналу связи передаются сообщения, содержащие только 4 буквы: А, Б, В, Г; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв А, Б, В используются такие кодовые слова:
А: 101010, Б: 011011, В: 01000
Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Подобные задания для тренировки
✍ Решение:
- Наименьшие коды могли бы выглядеть, как 0 и 1 (одноразрядные). Но это не удовлетворяло бы условию Фано (А начинается с единицы — 101010, Б начинается с нуля — 011011).
- Следующим наименьшим кодом было бы двухбуквенное слово 00. Так как оно не является префиксом ни одного из представленных кодовых слов, то Г = 00.
Результат: 00
5.6: ЕГЭ по информатике 5 задание 2017 ФИПИ вариант 16 (под редакцией Крылова С.С., Чуркиной Т.Е.):
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приемной стороне канала связи. Использовали код:
А - 01 Б - 00 В - 11 Г - 100
Укажите, каким кодовым словом должна быть закодирована буква Д. Длина этого кодового слова должна быть наименьшей из всех возможных. Код должен удовлетворять свойству однозначного декодирования. Если таких кодов несколько, укажите код с наименьшим числовым значением.
✍ Решение:
- Так как необходимо найти кодовое слово наименьшей длины, воспользуемся деревом. Влево будем откладывать нули, а вправо — единицы:
- Поскольку у нас все ветви завершены листьями, т.е. буквами, кроме одной ветви, то остается единственный вариант, куда можно поставить букву Д:
- Перепишем сверху вниз получившееся кодовое слово для Д: 101
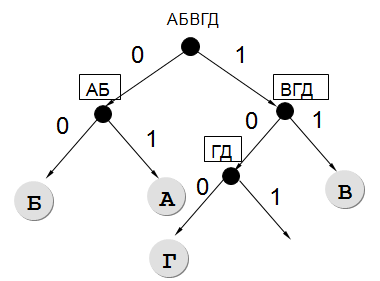
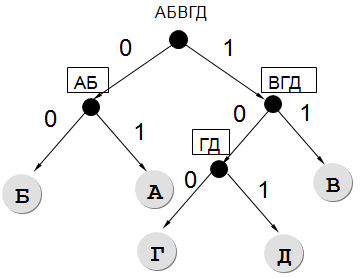
Результат: 101
Подробней разбор урока можно посмотреть на видео ЕГЭ по информатике 2017:
5.7: 5 задание. Демоверсия ЕГЭ 2018 информатика (ФИПИ):
По каналу связи передаются шифрованные сообщения, содержащие только десять букв: А, Б, Е, И, К, Л, Р, С, Т, У. Для передачи используется неравномерный двоичный код. Для девяти букв используются кодовые слова.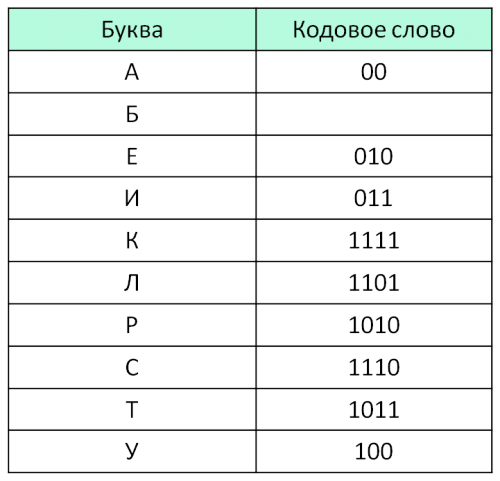
Укажите кратчайшее кодовое слово для буквы Б, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Похожие задания для тренировки
✍ Решение:
- Для решения будем использовать дерево. Ветви, соответствующие нулю, будем откладывать влево, единице — вправо.
- При рассмотрении дерева видим, что все ветви «закрыты» листьями, кроме одной ветви — 1100:
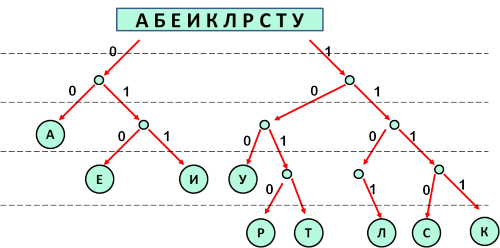
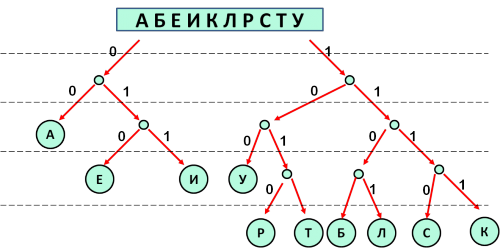
Результат: 1100
Подробное решение данного 5 задания из демоверсии ЕГЭ 2018 года смотрите на видео:
5.8: Задание 5_9. Типовые экзаменационные варианты 2017. Вариант 4 (Крылов С.С., Чуркина Т.Е.):
По каналу связи передаются шифрованные сообщения, содержащие только четыре букв: А, Б, В, Г; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв А, Б, В используются кодовые слова:
А: 00011 Б: 111 В: 1010
Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
✍ Решение:
- Для решения будем использовать дерево. Ветви, соответствующие нулю, будем откладывать влево, единице — вправо.
- Поскольку в задании явно не указано о том, что код должен удовлетворять условию Фано, то дерево нужно построить как с начала (по условию Фано), так и с конца (обратное условие Фано).
- Получившееся числовое значение кодового слова для буквы Г — 01.
- Получившееся числовое значение кодового слова для буквы Г — 00.
- После сравнения двух кодовых слов (01 и 00), код с наименьшим числовым значением — это 00.
Дерево по условию Фано (однозначно декодируется с начала):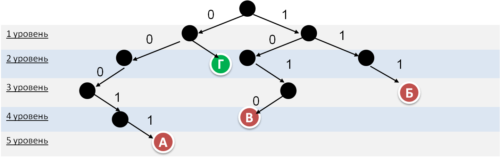
Дерево по обратному условию Фано (однозначно декодируется с конца):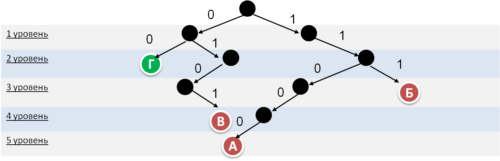
Результат: 00
5.9: Тренировочный вариант №3 от 01.10.2018 (ФИПИ):
По каналу связи передаются сообщения, содержащие только буквы: А, Е, Д, К, М, Р; для передачи используется двоичный код, удовлетворяющий условию Фано. Известно, что используются следующие коды:
Е – 000 Д – 10 К – 111
Укажите наименьшую возможную длину закодированного сообщения ДЕДМАКАР.
В ответе напишите число – количество бит.
✍ Решение:
- С помощью дерева отобразим известные коды для букв:
- В результирующем слове — ДЕДМАКАР — вде буквы А. Значит, для получения наименьшей длины необходимо для буквы А выбрать наименьший код в дереве. Учтем это и достроим дерево для остальных трех букв А, М и Р:
- Расположим буквы в порядке их следования в слове и подставим их кодовые слова:
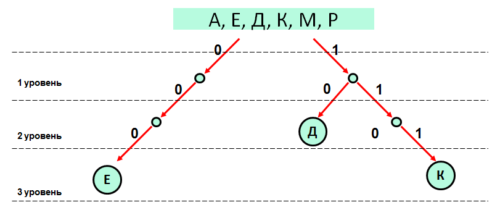
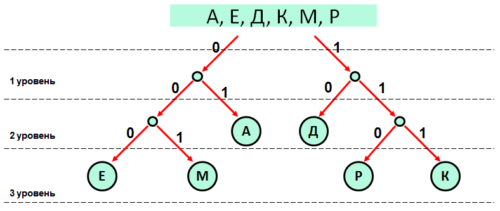
Д Е Д М А К А Р 10 000 10 001 01 111 01 110
Результат: 20
Смотрите виде решения задания:
Двоичный код алфавит русский. §1.5. Двоичное кодирование
При передаче сообщений по линиям связи всегда приходится пользоваться тем или иным кодом, т. е. представлением сообщения в виде ряда сигналов. Общеизвестным примером кода может служить принятая в телеграфии для передачи словесных сообщений азбука Морзе. С помощью этой азбуки любое сообщение представляется в виде комбинации элементарных сигналов: точка, тире, пауза (пробел между буквами), длинная пауза (пробел между словами).
Вообще кодированием называется отображение состояния одной физической системы с помощью состояния некоторой другой. Например, при телефонном разговоре звуковые сигналы кодируются в виде электромагнитных колебаний, а затем снова декодируются, превращаясь в звуковые сигналы на другом конце линии. Наиболее простым случаем кодирования является случай, когда обе системы и (отображаемая и отображающая) имеют конечное число возможных состояний. Так обстоит дело при передаче записанных буквами сообщений, например, при телеграфировании. Мы ограничимся рассмотрением этого простейшего случая кодирования.
Пусть имеется некоторая система (например, буква русского алфавита), которая может случайным образом принять одно из состояний . Мы хотим отобразить ее (закодировать) с помощью другой системы , возможные состояния которой . Если (число состояний системы меньше числа состояний системы ), то нельзя каждое состояние системы закодировать с помощью одного-единственного состояния системы . В таких случаях одно состояние системы приходится отображать с помощью определенной комбинации (последовательности) состояний системы . Так, в азбуке Морзе буквы отображаются различными комбинациями элементарных символов (точка, тире). Выбор таких комбинаций и установление соответствия между передаваемым сообщением и этими комбинациями и называется «кодированием» в узком смысле слова.
Коды различаются по числу элементарных символов (сигналов), из которых формируются комбинации, иными словами — по числу возможных состояний системы . В азбуке Морзе таких элементарных символов четыре (точка, тире, короткая пауза, длинная пауза). Передача сигналов может осуществляться в различной форме: световые вспышки, посылки электрического тока различной длительности, звуковые сигналы и т. п. Код с двумя элементарными символами (0 и 1) называется двоичным. Двоичные коды широко применяются на практике, особенно при вводе информации в электронные цифровые вычислительные машины, работающие по двоичной системе счисления.
Одно и то же сообщение можно закодировать различными способами. Возникает вопрос об оптимальных (наивыгоднейших) способах кодирования. Естественно считать наивыгоднейшим такой код, при котором на передачу сообщений затрачивается минимальное время. Если на передачу каждого элементарного символа (например 0 или 1) тратится одно и то же время, то оптимальным будет такой код, при котором на передачу сообщения заданной длины будет затрачено минимальное количество элементарных символов.
Предположим, что перед нами поставлена задача: закодировать двоичным кодом буквы русской азбуки так, чтобы каждой букве соответствовала определенная комбинация элементарных символов 0 и 1 и чтобы среднее число этих символов на букву текста было минимальным.
Рассмотрим 32 буквы русской азбуки: а, б, в, г, д, е, ж, з, и, й, к, л, м, н, о, п, р, с, т, у, ф, х, ц, ч, ш, щ, ъ, ы, ь, э, ю, я плюс промежуток между словами, который мы будем обозначать «–». Если, как принято в телеграфии, не различать букв ъ и ь (это не приводит к разночтениям), то получится 32 буквы: а, б, в, г, д, е, ж. з, и, й, к, л, м, н, о, п, р, с, т, у. ф, х, ц, ч, ш, щ, (ъ, ь). ы. э, ю, я, «–».
Первое, что приходит в голову — это, не меняя порядка букв, занумеровать их подряд, приписав им номера от 0 до 31, и затем перевести нумерацию в двоичную систему счисления. Двоичная система — это такая, в которой единицы разных разрядов представляют собой разные степени двух. Например, десятичное число 12 изобразится в виде
и в двоичной системе запишется как 1100.
Десятичное число 25 —
Запишется в двоичной системе как 11001.
Каждое из чисел может быть изображено пятизначным двоичным числом. Тогда получим следующий код:
В этом коде на изображение каждой буквы тратится ровно 5 элементарных символов. Возникает вопрос, является ли этот простейший код оптимальным и нельзя ли составить другой код, в котором на одну букву будет в среднем приходиться меньше элементарных символов?
Действительно, в нашем коде на изображение каждой буквы — часто встречающихся «а», «е», «о» или редко встречающихся «щ», «э», «ф» — тратится одно и то же число элементарных символов. Очевидно, разумнее было бы, чтобы часто встречающиеся буквы были закодированы меньшим числом символов, а реже встречающиеся — большим.
Чтобы составить такой код, очевидно, нужно знать частоты букв в русском тексте. Эти частоты приведены в таблице 18.8.1. Буквы в таблице расположены в порядке убывания частот.
Таблица 18.8.1.
Дискретная форма представления информации
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 7 классы | Планирование уроков на учебный год (ФГОС) | Дискретная форма представления информации
Содержание урока
1.5.1. Преобразование информации из непрерывной формы в дискретную
1.5.2. Двоичное кодирование
1.5.3. Универсальность двоичного кодирования. 1.5.4. Равномерные и неравномерные коды
Вопросы и задания
Электронное приложение к учебнику
Единая коллекция цифровых образовательных ресурсов
Практическая часть урока
1.5.2. Двоичное кодирование
В общем случае, чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка. Таких языков тысячи. Каждый язык имеет свой алфавит.
 Алфавит — конечный набор отличных друг от друга символов (знаков), используемых для представления информации. Мощность алфавита — это количество входящих в него символов (знаков).
Алфавит — конечный набор отличных друг от друга символов (знаков), используемых для представления информации. Мощность алфавита — это количество входящих в него символов (знаков).
Алфавит, содержащий два символа, называется двоичным алфавитом (рис. 1.11). Представление информации с помощью двоичного алфавита называют двоичным кодированием. Закодировав таким способом информацию, мы получим её двоичный код.
Рассмотрим в качестве символов двоичного алфавита цифры 0 и 1.
Покажем, что любой алфавит можно заменить двоичным алфавитом. Прежде всего, присвоим каждому символу рассматриваемого алфавита порядковый номер. Номер представим с помощью двоичного алфавита. Полученный двоичный код будем считать кодом исходного символа (рис. 1.12).
Если мощность исходного алфавита больше двух, то для кодирования символа этого алфавита потребуется не один, а несколько двоичных символов. Другими словами, порядковому номеру каждого символа исходного алфавита будет поставлена в соответствие цепочка (последовательность) из нескольких двоичных символов.
Правило получения двоичных кодов для символов алфавита мощностью больше двух можно представить схемой на рис. 1.13.
Двоичные символы (0,1) здесь берутся в заданном алфавитном порядке и размещаются слева направо. Двоичные коды (цепочки символов) читаются сверху вниз. Все цепочки (кодовые комбинации) из двух двоичных символов позволяют представить четыре различных символа произвольного алфавита:
Цепочки из трёх двоичных символов получаются дополнением двухразрядных двоичных кодов справа символом 0 или 1. В итоге кодовых комбинаций из трёх двоичных символов получается 8 — вдвое больше, чем из двух двоичных символов:
Соответственно, четырёхразрядный двоичный код позволяет получить 16 кодовых комбинаций, пятиразрядный — 32, шестиразрядный — 64 и т. д.
Длину двоичной цепочки — количество символов в двоичном коде — называют разрядностью двоичного кода.
Обратите внимание, что:
4 = 2-2, 8=2 2-2, 16 = 2 2 2 2, 32 = 2-2-2-2-2 и т. д.
Здесь количество кодовых комбинаций представляет собой произведение некоторого количества одинаковых множителей, равного разрядности двоичного кода.
Если количество кодовых комбинаций обозначить буквой N, а разрядность двоичного кода — буквой i, то выявленная закономерность в обшем виде будет записана так:
В математике такие произведения записывают в виде:
N = 2 i.
Запись 2i читают так: «2 в i-й степени».
Зядача. Вождь племени Мульти поручил своему министру разработать двоичный код и перевести в него всю важную информацию. Двоичный код какой разрядности потребуется, если алфавит, используемый племенем Мульти, содержит 16 символов? Выпишите все кодовые комбинации.
Решение. Так как алфавит племени Мульти состоит из 16 символов, то и кодовых комбинаций им нужно 16. В этом случае длина (разрядность) двоичного кода определяется из соотношения: 16 = 2 i. Отсюда i = 4.
Чтобы выписать все кодовые комбинации из четырёх 0 и 1, воспользуемся схемой на рис. 1.13: 0000, 0001, 0010, ООН, 0100, 0101, 0110, 0111,1000,1001,1010,1011,11Q0,1101,1110,1111.
На сайте http://sc.edu.ru/ размещена виртуальная лаборатория «Цифровые весы» (135009). С её помощью вы можете самостоятельно открыть метод разностей — ещё один способ получения двоичного кода целых десятичных чисел.
«Двоичное кодирование. Двоичный алфавит. Двоичный код. Разрядность двоичного кода. Связь длины двоичного кода и количества кодовых комбинаций. Практическая работа №1. Кодирование информации»
Тема урока: «Двоичное кодирование. Двоичный алфавит. Двоичный код. Разрядность двоичного кода. Связь длины двоичного кода и количества кодовых комбинаций.
Практическая работа №1. Кодирование информации»
Цели: сформировать у учащихся понимание процесса обмена информацией; показать различные виды кодирования информации; выявить преимущества двоичного кодирования различных видов информации.
Требования к знаниям и умениям:
Учащиеся должны знать:
что такое «код», «кодирование», «двоичное кодирование», бит;
почему в вычислительной технике используется двоичное кодирование информации;
как кодируются различные виды информации в вычислительной технике.
Учащиеся должны уметь:
— кодировать информацию;
— восстанавливать информацию по ее кодовому представлению.
Ход урока
Орг. Момент
Актуализация
Визуальная проверка выполнения домашнего задания.
Опрос по теме знаковая система
Заполнить таблицы
Естественные языки (носят национальный характер): речь и письменность | Формальные языки (интернациональны, понятны всем) | |||||
Примеры | -русский язык; — английский язык; -и т.д. | — язык математики; — язык химии; — языки программирования — командные языки опера — и т.д. | ||||
Алфавит — набор основных символов, различимых по их начертанию | — кириллица — 33 буквы; — латиница — 26 букв; — иероглифы и др | Алфавит жестко зафиксирован. — арабские цифры; — ноты; — дорожные знаки; — точки и тире; — изображения элементов | ||||
Синтаксис — правила для образования предложений языка | Формируется из большого числа правил, из которых существуют исключения | Наличие строгих правил | ||||
Грамматика — правила правописания | ||||||
Физическая природа знаков | Изображения на бумаге, звуки (фонемы), электрические импульсы и т.д. | |||||
| Естественный язык | Формальный язык | ||||
Нахождение площади прямоугольника | ||||||
Правило дорожного движения | ||||||
Призыв о помощи | ||||||
3. Изложение нового материала
1. Кодирование информации
Когда человек или какой-либо другой живой организм или какое-то устройство участвуют в информационном процессе, то все они представляют информацию в той или иной форме. При выполнении домашнего задания вы также представляли информацию в различных формах.
Когда мы представляем информацию в разных формах или преобразуем ее из одной формы в другую, мы информацию кодируем.
Код — это система условных знаков для представления информации.
Кодирование — это операция преобразования символов или группы символов одного кода в символы или группы символов другого кода.
Человек кодирует информацию с помощью языка.
Язык — это знаковая форма представления информации.
В процессе обмена информацией кроме кодирования информации происходит и ее декодирование.

Теоретически и экспериментально было показано, что с технической точки зрения самым удобным и эффективным является использование двоичного кода, то есть набора символов, алфавита, состоящего из пары чисел {0,1}. Поскольку двоичный код используется для хранения информации в вычислительных машинах, его еще называют машинным кодом.
Цифры 0 и 1, образующие набор {0,1}, обычно называют двоичными цифрами, потому что они используются как алфавит в так называемой двоичной системе счисления. Система счисления представляет собой совокупность правил и приемов наименования и записи чисел, а так же получения значения чисел из изображающих их символов. Количество знаков в алфавите системе счисления обычно отражается в ее исчислении: двоичная, восьмеричная, десятичная, шестнадцатеричная и т.д.
Элементарное устройство памяти компьютера, которое применяется для изображения одной двоичной цифры, называется двоичным разрядом или битом.
Слово «бит» произошло от английского термина bit, представляющего собой сокращение словосочетания Binary digit – двоичная цифра.
1 бит кодирует 2 понятия или сообщения (0 или 1).
2 бита — 4 разных сообщения (11 или 00 или 01 или 10).
3 бита — 8 разных сообщений.
4 бита — 16 сообщений и т.д.
Почему именно двоичное кодирование используется в вычислительной технике? Оказывается такой способ кодирования легко реализовать технически: 1 — есть сигнал, 0 — нет сигнала. Для человека такой способ кодирования неудобен тем, что двоичные последовательности получаются достаточно длинными. Но технике легче иметь дело с большим числом однотипных элементов, чем с небольшим числом сложных.
Как разные виды информации кодируются в компьютере?
2. Кодирование чисел
В двоичной системе счисления для записи чисел используется всего две цифры — 1 и 0. С их помощью можно записать любое число. Во всем остальном эта система счисления не отличается от привычной для вас десятичной системы. Она обладает всеми теми же свойствами, в ней соблюдаются все основные законы выполнения арифметических операций.
3. Кодирование текстовой информации
Для кодирования текстовой информации в компьютере также применяется двоичное кодирование, т.е. представление текста в виде последовательности 0 и 1. Каждому символу алфавита сопоставили определенное целое число, которое и принято считать кодом этого символа.
Бит – это очень маленькая порция информации. Поэтому, так же как и при записи десятичных чисел, используется несколько десятичных разрядов – разряд единиц, разряд десятков, сотен и т.д., так и для записи двоичных чисел используется несколько двоичных разрядов, несколько битов.
Для хранения двоичных чисел в компьютере используется устройство, которое принято называть ячейкой памяти. / Память компьютера можно образно представить себе как автоматическую камеру хранения, состоящую из отдельных ячеек, в каждую из которых можно положить некоторое число./
Ячейки образуются из нескольких битов, так же как двоичные числа образуются из двоичных разрядов. В общем случае ячейки различных компьютеров могут состоять из различного количества битов. Поэтому, начиная с машин третьего поколения, стандартными являются те ячейки, которые состоят из восьми битов.
Элемент памяти компьютера, состоящий из восьми битов, называется байтом.
а) б)Сколько же бит необходимо для кодирования символов?
Чтобы ответить на этот вопрос, нужно определить их количество. Ограничений на количество символов теоретически не существует. Однако есть количество, которое можно назвать достаточным.
Запись двоичного кода легко спутать с аналогичным по записи десятичным числом. В таких случаях справа от двоичного числа записывают индекс 2, а около десятичного числа указывают индекс 10. Например: 101100112 – двоичное число, 1011001110 – десятичное.
Так как байт состоит из восьми двоичных разрядов, то количество различных кодов, различных комбинаций из восьми нулей и единиц, записываемых в один байт, равно 28=256. (00000001, 00000010,…, 11111111).
С помощью 1 байта можно закодировать 256 различных символов.
Система счисления — способ записи чисел с помощью набора специальных знаков, называемых цифрами.
Система счисления | Основание | Алфавит цифр |
Десятичная | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
Двоичная | 2 | 0, 1 |
Восьмеричная | 8 | 0, 1, 2, 3, 4, 5, 6, 7 |
Шестнадцатеричная | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Десятичная система счисления — позиционная система счисления по основанию 10. Предполагается, что основание 10 связано с количеством пальцев рук у человека. Наиболее распространённая система счисления в мире. Для записи чисел используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называемые арабскими цифрами.
Двоичная система счисления — позиционная система счисления с основанием 2. Используются цифры 0 и 1. Двоичная система используется в цифровых устройствах, поскольку является наиболее простой.
Двоичная система счисления обладает такими же свойствами, что и десятичная, только для представления чисел используются не 10 цифр, а всего две. Соответственно и разряд числа называют не десятичным, а двоичным.
Перевод из десятичной системы счисления в систему счисления с основанием p осуществляется последовательным делением десятичного числа и его десятичных частных на p, а затем выписыванием последнего частного и остатков в обратном порядке.
Переведем десятичное число 20 в двоичную систем счисления (основание системы счисления p=2).
 В итоге получили 2010 = 101002.
В итоге получили 2010 = 101002.
Обратный перевод осуществляется операцией умножение. Умножаем на p в n-1 степени
1*24+0*23+1*22+0*21+0*20=20
4. Закрепление пройденного
1. Каким образом информация добирается от источника информации до приемника
2. Как информация кодируется в компьютере. Почему?
Практическая работа №1. Кодирование информации
Перевести
ИЗ 10-ной в 2-ную
27, 48, 64, 115, 57
ИЗ 2-ной в 10-ную
1011, 11011,1111, 10000
5. Итоги урока
Выставление оценок.
Беседа: что понятно, что – нет, что нового…
Домашнее задание
Уровень знания: выучить, что такое код, кодирование, бит, байт и формулу, связывающую количество разных сообщений и количество бит.
§ 1.5 чит.
Уровень понимания:
Перевести
ИЗ 10-ной в 2-ную
47, 28, 92, 18, 103
ИЗ 2-ной в 10-ную
1001, 111,1100, 1110


 Информация
Информация