Длина вектора — как найти? Формулы и примеры

Поможем понять и полюбить математику

Начать учиться

Сегодня мы поговорим с вами о таких понятиях, как вектор и его длина. Эти термины достаточно популярны в алгебре, геометрии и физике. С их помощью можно решать как очень легкие задачи, так и комплексные с разными физическими величинами и математическими правилами. Сложная ли эта тема? Нет, совсем несложная, но очень и очень важная, поэтому мы посвятим сегодняшнюю статью ей. Приятного чтения!

Что такое векторы и какими они бывают

Как обычно, мы начнем с самого важного: с определения.

Вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.

Вектор обозначают знаком →, например . Как вы заметили, вектор можно выразить одной латинской буквой, а можно — сочетанием двух букв, которыми мы назовем точками начала и конца вектора.

Нулевой вектор — вектор, начало которого совпадает с его концом. Обозначается он так: .

Как вы уже знаете, векторы бывают коллинеарными и неколлинеарными, сонаправленными и противоположно направленными. Теперь давайте подумаем, что объединяет все виды векторов без исключения. Правильно, у всех есть длина! О том, что это такое, мы и поговорим дальше.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Длина вектора

Длиной или модулем вектора называется длина направленного отрезка, определяющего вектор.

Иногда в математике длину вектора называют модулем. Это легко запомнить, так как длина вектора обозначается с помощью знака | |. Например: . Альтернативное название длины вектора дает нам отличную подсказку: она не может быть отрицательной, в какую бы сторону вектор ни был направлен. А вот нулевой — пожалуйста!

Длина нулевого вектора всегда равна нулю.

Здесь вам может стать интересно, зачем нам нужно знать, как найти длину вектора, и это очень хороший вопрос. Причин может быть множество, но мы выделим несколько главных:

1. Чтобы определить равенство векторов, необходимо знать их длины. Векторы являются равными, если равны их длины, и сами векторы — сонаправленные.

2. Вычислив модуль вектора, мы можем рассчитать другие величины.

3. Например, в физике сила — это векторная величина, т. е. имеет направление. Если вычислить модуль силы, мы можем рассчитать массу тела, его ускорение и т. д.

4. В геометрии с помощью длины векторов мы можем определить угол между ними, их скалярное произведение.

Достаточно весомые аргументы для нахождения этой величины, правда? Самое время перейти от слов к делу: давайте научимся вычислять длину вектора через свои координаты!

Как можно найти длину вектора по его координатам

Используя прямоугольную систему координат, нарисуем вектор АВ (х, у) из точки (0; 0). Тогда его можно будет считать радиус-вектором для векторов АВ₁ и АА₁.

Давайте обозначим длину вектора |АВ₁| = у, длину вектора |АА₁| = х. Треугольники АА₁В и АВ₁В являются прямоугольными, где АВ — гипотенуза. Теперь вспомните, как можно найти длину гипотенузы, зная длины катетов. Верно, через теорему Пифагора! Составим выражение для АВ:

Это значит, чтобы найти длину вектора нужно взять квадратный корень из суммы квадратов его координат. В общем виде эту формулу для длины вектора записывают так — длина вектора :

Если мы будем рассматривать векторы в трехмерном пространстве, формулу нахождения длины вектора можно рассчитать так:

Давайте разберемся, как работают эти формулы для нахождения длины вектора, на примерах. Вы можете решать задания самостоятельно, а потом свериться с нами: так будет еще эффективнее!

Пример № 1

Найдите модуль вектора .

Решение:

Ответ:

Пример № 2

Проведите вычисление длины вектора по его координатам {-2; 0; 5}.

Решение:

Ответ:

Пример № 3

Определите координату х вектора , если его координата по у равна 6, а длина вектора 10.

Решение:

,

,

,

.

,

,

,

.

Ответ: .

Уверены, что у вас все блестяще получилось!

Как найти длину вектора по двум точкам

Давайте подумаем, как решать задачи, если нам не даны координаты вектора. Для этого нужно понять, как найти длину вектора по двум точкам — координатам начала и конца. Вспомним: координаты вектора с точкой А (х_а; у_а) и В (х_в; у_в) можно рассчитать так: (х_в – х_а; у_в – у_а). А значит, длину вектора мы определим, если подставим эти выражения в формулу для ее нахождения:

Пример № 4

Найти длину вектора , если В (4; 6), С (-2; 0).

Решение:

Ответ:

Как найти длину вектора по теореме косинусов

Пришло время разобраться, как длина вектора связана с теоремой косинусов. К сожалению, не во всех задачах дано нужное количество информации, чтобы определить длину вектора — тут-то нам и поможет теорема. Вспомним ее!

Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Итак, чтобы определить длину стороны треугольника, нужно сложить квадраты двух других сторон, вычесть удвоенное произведение длин сторон на косинус угла между ними и взять корень из полученного числа. Так мы получим формулу нахождения длины вектора через теорему косинусов.

Предположим, что нам необходимо узнать длину вектора или . Тогда, чтобы воспользоваться теоремой косинусов, нам нужно найти длину векторов и и угол между ними.

Пример № 5

Длины векторов и равны 5 и 12 соответственно, а угол между ними равен π/3. Проведите вычисление длины вектора .

Решение:

Ответ:

Сегодня мы обсудили с вами все основные моменты, которые касаются длины вектора: изучили теорию и дополнили ее базовыми задачами. Дело осталось за малым — выучить весь материал и практиковаться! В этом вам помогут курсы по профильной математике в школе Skysmart. Уникальная платформа, учителя-профессионалы, индивидуальная программа — уроки просто созданы для того, чтобы стать уверенными в математике. Ждем вас на занятиях и до новых встреч!

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Дарья Вишнякова

К предыдущей статье

Плоскость

К следующей статье

Компланарность векторов

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Как найти длину (модуль) вектора: формула, пример задачи

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

В данной публикации мы рассмотрим, что такое длина вектора, как она находится, а также приведем пример задачи для демонстрации применения теоретических знаний на практике.

• Определение длины вектора
• Нахождение длины вектора
• Пример задач

Определение длины вектора

Длина (или модуль) вектора AB – это неотрицательное число, которое равно расстоянию между его началом и концом. Другими словами, это длина соответствующего отрезка AB.

Для рассматриваемого вектора длина обозначается как |AB|, т.е. по бокам добавляются вертикальные черточки.

Примечания:

• Длина нулевого вектора 0, соответственно, равняется нулю.
• Длина единичного вектора e равна единице.

Нахождение длины вектора

Допустим, у нас есть вектор a, который задан своими координатами:

a = (a_x; a_y; a_z).

В этом случае длина вектора вычисляется по формуле:

Таким образом, длина вектора, заданная определенными координатами, равняется квадратному корню из суммы квадратов этих координат.

Пример задач

Дан вектор a = (2; -5; 6). Найдем его длину.

Решение

Все, что нам нужно сделать – это воспользоваться приведенной выше формулой, подставив в нее известные значения.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

4.

4: длина вектора

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

14520

• Кен Каттлер
• Университет Бригама Янга via Lyryx

9{2}} \метка{расстояние1}\]

Теперь рассмотрим случай \(n=2\), показанный на следующем рисунке.

Рисунок \(\PageIndex{1}\)

Есть две точки \(P =\left( p_{1},p_{2}\right)\) и \(Q = \left(q_{1},q_ {2}\справа)\) в плоскости. Расстояние между этими точками показано на рисунке сплошной линией. Обратите внимание, что эта линия является гипотенузой прямоугольного треугольника, который составляет половину прямоугольника, показанного пунктирными линиями. Мы хотим найти длину этой гипотенузы, которая даст расстояние между двумя точками.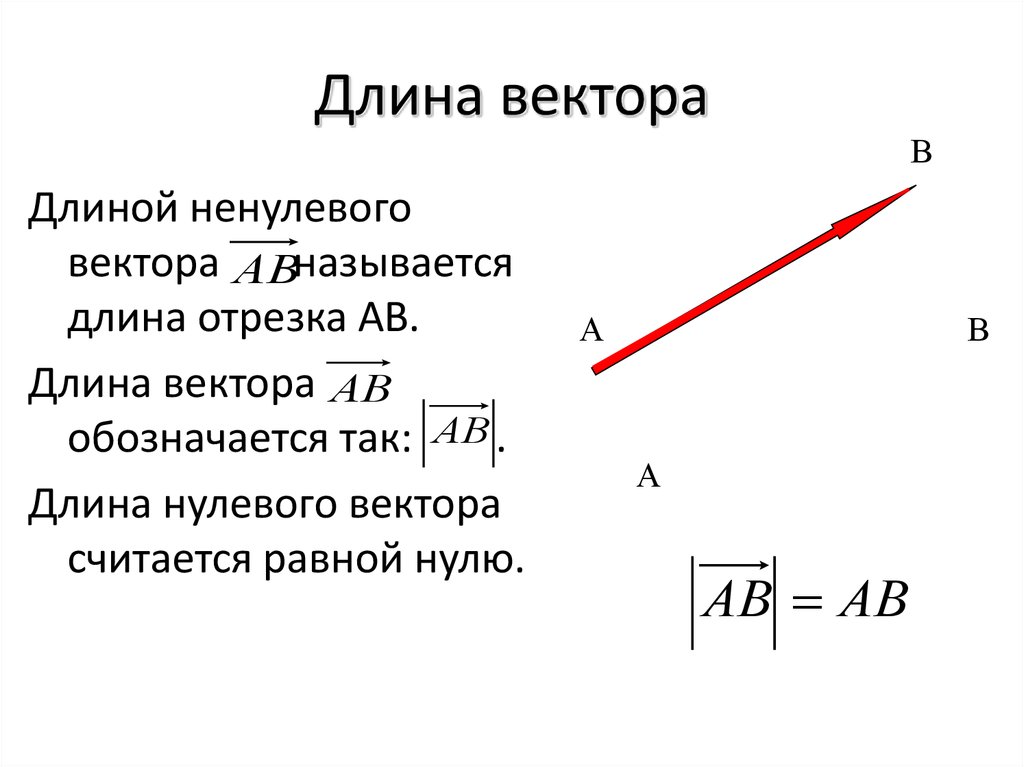 {1/2} \label{distance3}\] 9n\), и пусть расстояние между ними \(d( P, Q)\) задано, как в определении \(\PageIndex{1}\). Тогда выполняются следующие свойства.

• \(d(P, Q) = d(Q, P)\)
• \(d( P, Q) \geq 0\), и равен 0 точно, когда \(P = Q.\)

Концепция расстояния имеет множество применений. Например, имея две точки, мы можем спросить, какой набор точек находится на одинаковом расстоянии между данными точками. Это исследуется в следующем примере.

9{2}-4p_3\nonumber \] Упрощая, получается \[-2p_1+14-4p_2-6p_3=-2p_2+5-4p_3\nonumber \], что можно записать как \[2p_1+2p_2+2p_3=-9 \ label{distanceplane}\] Таким образом, точки \(P = \left( p_1,p_2,p_3\right)\), находящиеся на одинаковом расстоянии от каждой из заданных точек, образуют плоскость, уравнение которой задается выражением \(\eqref {расстояние}\).

Теперь мы можем использовать наше понимание расстояния между двумя точками, чтобы определить, что понимается под длиной вектора. Рассмотрим следующее определение. 92}\nonumber \]

Это определение соответствует определению \(\PageIndex{1}\), если вы считаете, что вектор \(\vec{u}\) имеет хвост в точке \(0 = \left ( 0, \cdots ,0 \right)\) и его кончик в точке \(U = \left(u_1, \cdots, u_n \right)\). Тогда длина \(\vec{u}\) равна расстоянию между \(0\) и \(U\), \(d(0,U)\). В общем, \(d(P,Q)=||\vec{PQ}||\).

Рассмотрим пример \(\PageIndex{1}\). По определению \(\PageIndex{2}\) мы также можем найти расстояние между \(P\) и \(Q\) как длину соединяющего их вектора. Следовательно, если бы мы нарисовали вектор \(\overrightarrow{PQ}\) с хвостом в \(P\) и точкой в ​​\(Q\), этот вектор имел бы длину, равную \(\sqrt{47 }\). 9{н}\). Тогда вектор \(\vec{u}\), который имеет то же направление, что и \(\vec{v}\), но длина равна \(1\), является соответствующим единичным вектором вектора \(\vec{v} \). Этот вектор задается \[\vec{u} = \frac{1}{\| \vec{v} \|} \vec{v}\номер\]

Мы часто используем термин нормализовать для обозначения этого процесса. Когда мы нормализуем вектор, мы находим соответствующий единичный вектор длины \(1\). Рассмотрим следующий пример.

Пример \(\PageIndex{3}\): поиск единичного вектора 9T\end{aligned}\]

С помощью определения \(\PageIndex{1}\) можно проверить, что \(\| \vec{u} \| = 1\).

---

Эта страница под названием 4.4: Длина вектора распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Кеном Каттлером (Lyryx) с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Кен Каттлер

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Показать страницу TOC

   нет

2. Теги

   1. Формула расстояния
   2. источник@https://lyryx. com/first-course-linear-алгебра

Величина вектора Определение, формулы и задачи

Что такое Величина вектора?

Как мы знаем, вектор — это объект, который имеет как величину, так и направление. Чтобы найти величину вектора, нам нужно вычислить длину вектора. Такие величины, как скорость, перемещение, сила, импульс и т. д., являются векторными величинами. Но скорость, масса, расстояние, объем, температура и т. д. являются скалярными величинами. Скаляр имеет единственную величину, тогда как векторы имеют и величину, и направление.

Величина векторной формулы используется для вычисления длины заданного вектора (например, v ) и обозначается как | против |. Таким образом, эта величина представляет собой длину между начальной и конечной точками вектора. Чтобы вычислить величину вектора, мы используем формулу расстояния, которую мы обсудим здесь. 2}\end{массив} \) 92}\конец{массив} \)

Направление вектора

Направление вектора есть не что иное, как измерение угла с горизонтальной линией. Один из способов найти направление вектора

\(\begin{array}{l}\vec{AB}\end{array} \)

это;

тангенс α = у/х; конечная точка 0.

Где x — изменение горизонтальной линии, а y — изменение вертикальной линии.

Или tan α =

\(\begin{array}{l}\frac{y_1 – y_0}{x_1 – x_0}\end{массив} \)

; где (x _{0 ,} y ₀ ) — начальная точка и (x ₁ , y ₁ ) — конечная точка.

Задачи на величину вектора

Задача 1: Найдите модуль вектора

\(\begin{array}{l}\vec{AB}\end{array} \)

, начальная точка которого A равна (1, 2), а конечная точка , В равно (4, 3).

Решение: Дано, A равно (1, 2) и B равно (4, 3) в качестве начальной и конечной точки соответственно.

Следовательно, х 92}\конец{массив} \)

|

\(\begin{array}{l}\vec{AB}\end{array} \)

| =

\(\begin{массив}{l}\sqrt{9 + 1}\end{массив} \)

|

\(\begin{array}{l}\vec{AB}\end{array} \)

| =

\(\begin{массив}{l}\sqrt{10}\конец{массив} \)

|

\(\begin{array}{l}\vec{AB}\end{array} \)

| ≈ 3,2

Величина

\(\begin{array}{l}\vec{AB}\end{array} \)

≈ 3,2

Если нам нужно вычислить величину трехмерного вектора 92}\конец{массив} \)

Рассмотрим трехмерный объект.