Как измерить уровень сигнала в децибелах на вашем мобильном телефоне?

Почему мощность сигнала измеряется в децибелах?

Прежде чем мы углубимся в посторонние подробности того, как вы можете измерить уровень сигнала в децибелах на своем мобильном телефоне, давайте разберем эту тему на более простые термины и поймем, что это значит. Давайте сначала разберемся, что такое «децибел» и как он связан с измерением уровня сигнала. Но прежде чем мы углубимся в эти детали, давайте вкратце попытаемся понять, что означает «мощность сигнала». Уровень сигнала покажет вам, насколько сильна связь между вашим мобильным телефоном и базовой станцией оператора сотовой связи, как быстро вы сможете передавать данные или насколько четко вы сможете совершать звонки, не прерывая их. Итак, дБ и дБм — популярные термины, о которых вы, вероятно, слышали когда-то, либо при покупке нового сотового телефона, либо при ремонте маршрутизатора Wi-Fi.

В этой статье мы расскажем, что означают эти термины и как вы можете измерить уровень сигнала в децибелах на своем мобильном телефоне. В двух словах, вы можете думать о дБм как о мощности, которую способен производить усилитель или антенна, или о том, сколько сигнала присутствует на сайте. В то время как дБ — это относительное число увеличения или уменьшения сигнала. дБм является абсолютной мерой мощности сигнала. Это аббревиатура для децибел милливатт и рассчитывается как десятикратное логарифмическое значение мощности сигнала в милливаттах. дБм является важным показателем качества при измерении мощности внешнего сигнала. Обычно мы думаем о внешнем сигнале как о сильном, когда он составляет -70 дБм, или как о плохом, когда он составляет -100 дБм.

дБм также полезен для оценки зоны покрытия внутри помещения, которую мы можем ожидать от системы усилителя. Например, комнатная антенна, излучающая -20 дБм, может эффективно покрыть около 900 квадратных метров. дБ, с другой стороны, является относительной цифрой и просто сокращением от децибел. Мы используем дБ, чтобы описать, насколько увеличивается или уменьшается мощность сигнала в нашей системе. Например, если мы измеряем внешний сигнал на крыше -90 дБм, а наша система усилителя имеет общее усиление +70 дБ, то наш внутренний излучаемый сигнал будет -20 дБм. Имейте в виду, что, поскольку дБ и дБм являются логарифмическими величинами, обычные способы, которыми мы привыкли думать о величинах, здесь неприменимы. Например, сигнал -30 дБм в два раза мощнее сигнала -33 дБм. А сигнал -84 дБм в четыре раза мощнее сигнала -90 дБм. Это означает, что уровень сигнала удваивается каждый дБ. Эта тема намного сложнее, и о ней нужно знать намного больше, но знания этих основ достаточно, чтобы прочитать эту статью.

Как перевести телефон в режим Test Mode, чтобы измерить уровень сигнала в децибелах?

Теперь, если вы хотите проверить уровень своего сигнала на телефоне, то, конечно, вы можете взглянуть на «полоски» и увидеть уровень принимаемого сигнала от оператора мобильной связи, но этих визуальных индикаторов недостаточно, если вы хотите узнать точный сигнал вашего мобильного телефона. Но для этого вы должны установить режим отображения уровня сигнала вашего телефона в дБ (децибел), чтобы вы могли проверить мощность дБ рейтинга сигнала дБм. Вы, должно быть, замечали, что иногда у вас есть 3 или, может быть, даже 5 баров, но вы не можете сделать звонок по какой-то причине. Это связано с тем, что визуальный индикатор сигнала не всегда очень точен, и, следовательно, вы должны знать, как проверить уровень сигнала в децибелах на вашем мобильном телефоне. Попросту говоря, если вы хотите измерить уровень сигнала на своем телефоне в децибелах, вам нужно перевести телефон в режим Test Mode. Для этого потребуется другой шаг настройки, учитывая, является ли ваш телефон Android или Apple, работающим на iOS 11. Если у вас есть телефон Android, перейдите к настройкам, мобильным сетям и уровню сигнала. В разделе «Сила сигнала» вы увидите показания в дБ. Если ваш iPhone работает под управлением IOS 11, позвоните по номеру *3001#12345#*, выберите измерение обслуживающей ячейки и выберите Измеренный RSSI. Для iPhone, не работающего на IOS 11, позвоните по тому же номеру, указанному выше. После звонка по указанному выше номеру и выбора указанной выше опции, если вы нажмете на полоски уровня сигнала на своем мобильном телефоне, вы сможете переключить их на цифры. Эти цифры не что иное, как мощность сигнала вашей сотовой связи в децибелах. Если вы хотите, вы можете сохранить эту настройку в своем мобильном телефоне и всегда видеть мощность сигнала в децибелах на своем мобильном телефоне, но если нет, то вы можете вернуть обычные настройки обратно, перезагрузив телефон. Цифры, которые вы видите на экране, подскажут вам, достаточно ли хороший у вас сигнал для совершения звонка или нет. Чем ближе число к нулю, тем выше мощность сигнала. Чтобы измерить уровень сигнала в децибелах на телефоне Android, нажмите кнопку настроек на главном экране вашего телефона. Там вы найдете раздел состояния, в котором вы увидите уровень сигнала. Здесь сигнал будет записан в децибелах. Опять же, здесь применяются те же правила: чем ближе число к нулю, тем лучше сигнал. Если вы видите отрицательный знак вместе с показаниями вашего сигнала, вам не о чем беспокоиться, с вашим сигналом все в порядке. Это просто стандартный метод представления сигналов по шкале децибел. Идеальный уровень телефонного сигнала находится в диапазоне от -50 дБ до -80 дБ.

Если вы не хотите самостоятельно заниматься измереними для решения вопроса слабого сигнала, предлагаем обратиться к специалистам нашей компании, которые проанализируют ситуацию, сделают соответствующие замеры и помогут решить проблему со связкой с помощью установки и использования дополнительного оборудования — системы усиления сотового сигнала, которая решит проблему слабого сигнала и некачественной связи для вас раз и навсегда.

вместо умножения, деления, возведения в степень

Для применения децибелов и оперирования логарифмами вместо процентов или долей есть ряд причин:

•Удивительно, но характер отображения в органах чувств человека и животных изменений течения многих физических и биологических процессов пропорционален не амплитуде входного воздействия, а логарифму входного воздействия (живая природа живёт по логарифму).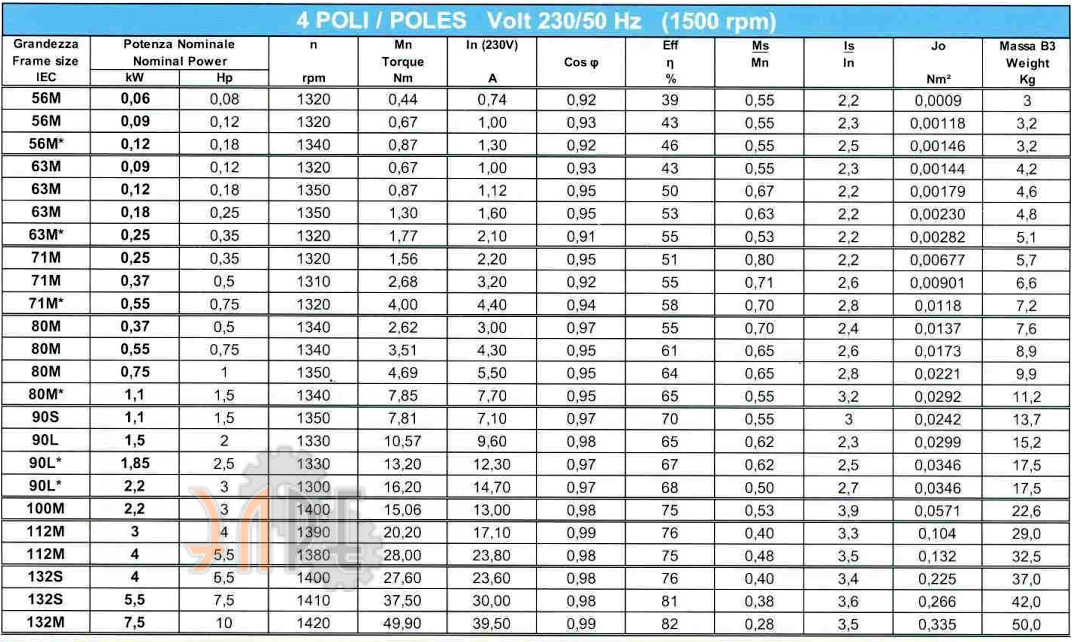 Например, музыкальная равномерно темперированная шкала частот является одной из таких логарифмических шкал

•удобство логарифмической шкалы в тех случаях, когда в одной задаче приходится оперировать одновременно величинами, различающимися не во втором знаке после запятой, а в разы и, тем более, различающимися на много порядков (примеры: задача выбора графического отображения уровней сигнала, частотных диапазонов радиоприемников, расчет частот для настройки клавиатуры фортепьяно)

•удобство отображения и анализа величины, изменяющейся в очень широких пределах (примеры — диаграмма направленности антенны, амплитудно-частотная характеристика электрического фильтра)

•Децибел служит для определения отношения двух величин. Но нет ничего удивительного в том, что децибел используют и для измерения абсолютных значений. Для этого достаточно условиться, какой уровень измеряемой физической величины будет принят за опорный уровень.

•Строго говоря, должно быть однозначно определено, какая именно физическая величина

и какое именно её значение используются в качестве опорного уровня. Опорный уровень указывается в виде добавки, следующей за символами «дБ» (например, дБм), либо опорный уровень должен быть ясен из контекста (например, «дБ относительно 1 мВт»).

•dBm (русское дБм) — опорный уровень — это мощность в 1 мВт. Например, «выходная мощность усилительного каскада составляет 13 дБм» (то есть мощность, выделяющаяся на номинальной для этого усилительного каскада нагрузке, составляет 20 мВт).

•dBV (русское дБВ) — опорное напряжение 1 В на номинальной нагрузке

•dBm0 (русское дБм0) — опорная мощность в дБм в точке нулевого относительного уровня. «Абсолютный уровень мощности относительно 1 мВт в точке линии передачи с нулевым уровнем»

•dBrn — опорное напряжение соответствует тепловому шуму идеального резистора сопротивлением 50Ω при комнатной температуре в полосе 1Гц.

•dBFS (англ. Full Scale — «полная шкала») — опорное напряжение соответствует полной шкале прибора

•dBSPL (англ. Sound Pressure Level — «уровень звукового давления») — опорное звуковое давление 20мкПа, соответствующее порогу слышимости; например, «громкость 100dBSPL».

•dBPa — опорное звуковое давление 1Па

•dBA, dBB, dBC, dBD — опорные уровни выбраны в соответствии с частотными характеристиками «весовых фильтров» в соответствии с кривыми равной громкости.

•dBc (русское дБн) — опорным является уровень излучения на частоте несущей или уровень

основной гармоники в спектре сигнала.

•dBi (русское дБи) — изотропный децибел (децибел относительно изотропного излучателя). Характеризует коэффициент направленного действия(а также коэффициент усиления) антенны относительно коэффициента направленного действия изотропного излучателя. Как правило, если не оговорено специально, характеристики усиления реальных антенн даются именно относительно усиления изотропного излучателя. То есть, когда вам говорят, что коэффициент усиления какой-то антенны равен 12 децибел, подразумевается 12 дБи.

•dBd (русское дБд) — децибел относительно диполя («относительно полуволнового вибратора»). Характеризует коэффициент направленного действия (а также коэффициент усиления) антенны относительно коэффициента направленного действия полуволнового вибратора, размещенного в свободном пространстве.

•Поскольку коэффициент направленного действия указанного полуволнового вибратора приближённо равен 2,15 дБи, то коэффициент направленного действия, измеряемый в дБд, всегда меньше коэффициента направленного действия, измеряемого в дБи, на фиксированную величину, равную 2,15 дБ.

•dBsm — децибел относительно одного квадратного метра. Характеризует эффективную поверхность рассеяния рассеивателя в радиолокации.

•dBm (русское дБм)

•dBV (русское дБВ)

•dBm0 (русское дБм0)

•dBrn

•dBFS (англ. Full Scale — «полная шкала»)

•dBSPL (англ. Sound Pressure Level — «уровень звукового давления»)

•dBPa (англ. Pascale,Pa – паскаль, единица измерения давления)

•dBA, dBB, dBC, dBD

•dBc (русское дБн)

•dBi (русское дБи)

•dBd (русское дБд)

•dBsm (англ. Square meters – квадратные метры)

•Усилитель в своём основном значении относится к преобразованию (увеличению, усилению) одной из характеристик исходного входного сигнала, при этом вид сигнала остаётся неизменным. В то же время, термин «усилитель» не вполне корректно, но традиционно употребляется для устройств управления мощными электрическими нагрузками, например, «релейный усилитель.

Усилитель

•Аттенюатор — устройство для плавного, ступенчатого или фиксированного понижения интенсивности электрических или электромагнитных колебаний.

•В радиотехнике аттенюатор называется электронным устройством, которое уменьшает амплитуду или мощность сигнала без

существенного искажения его формы.

•С точки зрения работы, аттенюатор является противоположностью усилителя, хотя оба эти устройства имеют различные принципы работы. В то время как усилитель обеспечивает усиление, аттенюатор обеспечивает ослабление или усиление в меньше, чем 1 раз.

•Аттенюаторы используются в случаях, когда необходимо ослабить сильный сигнал до приемлемого уровня, например, во избежание перегрузки входа какого-либо прибора чрезмерно мощным сигналом. Полезным побочным эффектом является то, что использование аттенюатора между линией и нагрузкой улучшает коэффициент бегущей волны и коэффициент стоячей волны в подводящей линии в

случае, когда нагрузка плохо согласована с линией.

Аттенюат

ор

дБ-калькулятор

дБ-калькулятор

На этой странице есть несколько различных калькуляторов звука и децибел.

Сложение или вычитание значений в децибелах

Добавьте или вычтите значения дБ (или дБА): результат: Доступные операторы: + —

Вариант использования: Вычесть фоновый шум

Измерьте уровень звука в дБ или дБА при работающем источнике звука и наличии фонового шума. Вы измеряете, например, 80 дБА. Теперь выключите источник звука и измерьте в том же месте. просто фоновый шум. Вы измеряете, например, 75 дБА. Фоновый шум должен быть более или менее постоянным.
Введите в калькулятор 80-75 и нажмите рассчитать. Результат 78,3 дБА
Это означает, что источник звука производит 78,3 дБА в точке измерения без фонового шума.

Вариант использования: добавление источников звука

Измерьте 3 источника звука отдельно в одном месте (на одном расстоянии) а затем вычислить, каким будет результирующее значение дБ, если все они бежали одновременно.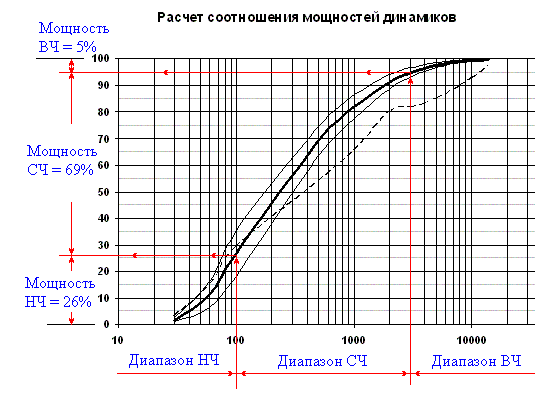
38 + 40 + 29 = 42,3 дБА

Формула, используемая вышеприведенным калькулятором

Вычислить xdB + ydB: 9Результат 0013=10*Log(10 ^x/10 +10 ^y/10 ) Просто расширьте формулу, чтобы добавить/вычесть больше значений.

---

Падение звука на расстоянии, дБ на расстоянии

Этот калькулятор использует закон обратных квадратов, который позволяет вам оценить уменьшение звука на расстоянии. Его можно применять в ситуациях, когда звук может распространяться свободно и не ограничивается стенами или другими крупными объектами. Уровень звука падает на 6 дБ, когда вы удваиваете расстояние до источника звука. 10-кратное увеличение расстояния снижает уровень звука на 20 дБ. Введите 3 значения, и калькулятор рассчитает для вас 4-е значение. L = уровень звука в дБ или дБА, d = расстояние в м (метрах) или футах (футах). Не смешивайте единицы. Используйте футы или м.

Пример использования: измерение вблизи источника и расчет уровня звука на расстоянии

Измерьте уровень звука L1 в дБ или дБА на расстоянии d1 от источника. Вы хотите знать, каким будет уровень звука на расстоянии d2.
Пример: L1=80 дБА при d1=1,5 м. Каков уровень звука при d2=4,5 м?
Введите значения 80 (L1), 1,5 (d1) и 4,5 (d2) в калькулятор и он рассчитает L2 = 70,5 дБА.
Не подходите слишком близко к источнику при измерении L1, но достаточно близко, чтобы фоновым шумом можно было пренебречь. Общие хорошие значения: 1,5 метра или 2 метра для d1.

Пример использования: измерение звука в удаленной точке и расчет уровня звука вблизи источника

Измерьте уровень звука L2 в дБ или дБА на расстоянии d2 от источника. Вы хотите знать, каким будет уровень звука на расстоянии d1.
Пример: L2=50 дБА при d2=100 м. Каков уровень звука при d1=1,5 м?
Введите значения 50 (L2), 100 (d2) и 1,5 (d1) в калькулятор и он рассчитает L1 = 86,5 дБА.

Формула, используемая вышеуказанным калькулятором

i2/i1=(d1/d2) ²
ΔL=10*Log(i2/i1)
, где ΔL — разница уровней звука (L1-L2) в дБ (или дБА).
Отношение i2/i1 представляет собой отношение интенсивности звука.

Эта формула работает до тех пор, пока у вас есть сферические волновые фронты. Некоторые источники звука например, большой вентилятор может создавать параллельные волновые фронты непосредственно на вентиляторе и они становятся сферическими только по мере того, как вы уходите дальше. d1 поэтому не должно быть слишком маленький. Общие хорошие значения для d1 составляют от 1 м (3 фута) до 2 м (6 футов) в зависимости от размера объект, излучающий звук.

---

дБ к коэффициенту

Единица дБ — это просто логарифмическое отношение между двумя числами. С звук также используется как абсолютное значение, и в этом случае это настроен на самый низкий уровень звука, который может слышать человеческое ухо.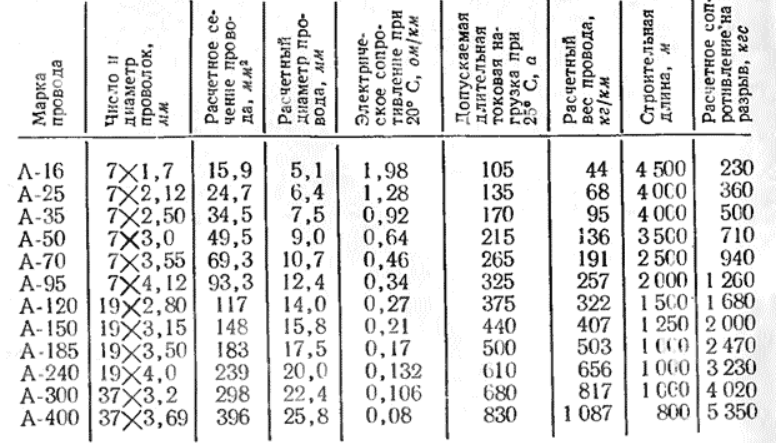

Самый слабый слышимый звук 0 дБ, а тихий разговор в 100000 раз интенсивнее или на 50 дБ выше.

Пояснения:
Интенсивность звука: Интенсивность — это количество энергии, передаваемой в секунду по площади. Измеряется в ватт/м ²
Звуковое давление: Звуковое давление измеряется микрофонами в форме амплитуды. Он пропорционален квадратному корню интенсивности (P=sqrt(I) или I = P ² ).

---

Звуковые концепции и определения

• Шум:
  Шум – это нежелательный звук, который может быть опасен для здоровья, мешать речи и устному общению или иным образом мешать, раздражать или раздражать.
• Звук:
  Звук — это любое изменение давления в газе или жидкости, которое может быть обнаружено человеческим ухом.
• Длина волны: длина волны
  = скорость/частота
  Скорость звука в воздухе равна 340 м/с .
• дБ против дБА:
  Люди не одинаково слышат все частоты. Для этого были созданы различные весовые коэффициенты. Взвешенные уровни звука «А» относятся к дБА. См. https://en.wikipedia. org/wiki/A-weighting.

Пожалуйста, включите JavaScript!

© Guido Socher, версия 2019-08-07
Вы можете установить этот калькулятор на свой компьютер, просто сохранив эту веб-страницу на рабочем столе. (Firefox->правый клик->Сохранить страницу как)

История: 05.07.2017 — первая версия, 20.05.2018 — код очистки для лучшей совместимости, 07.08.2019 — исправлена ​​опечатка

децибел — Biamp Cornerstone

1. Последнее обновление

2. Сохранить как PDF

Децибелы — это основной способ измерения различных электрических и акустических величин, связанных со звуком. Тем не менее, децибелы часто неправильно понимают, потому что они не особенно интуитивны, а математика, лежащая в основе децибелов, — это не просто повседневная арифметика. Эта статья призвана описать децибелы в простой для понимания форме и помочь избежать распространенных недоразумений, связанных с децибелами.

История

В то время как децибелы чаще всего используются для описания громкости звука, можно удивиться, узнав, что происхождение децибелов восходит к измерению потерь электроэнергии в кабелях передачи на большие расстояния. В конце 19-го и начале 20-го веков телеграфные и телефонные линии быстро опоясывали земной шар. Прогнозирование и измерение производительности и эффективности этих линий передачи на большие расстояния требовало сложных расчетов, особенно при суммировании потерь мощности на нескольких сегментах кабелей передачи на большие расстояния.

Чтобы упростить эти расчеты, Bell Telephone Labs изобрела децибел для описания величины потери мощности. Эта единица децибел позволила инженерам отказаться от ранее необходимых сложных расчетов и вместо этого использовать простое сложение. Изобретенная ими единица первоначально называлась единицей передачи (TU), но вскоре была переименована в децибел (дБ) в честь пионера телекоммуникаций Александра Грэма Белла. Официальной единицей является бел, который является порядком величины или степенью десяти, единственной единицей в логарифмической системе счисления. Он почти никогда не используется, поскольку децибел (1/10 бела, поскольку «деци» — это префикс системы СИ, означающий «одна десятая») гораздо удобнее.

Децибел – это не единица измерения

Первое, что нужно понять о децибелах, это то, что они не являются единицами измерения. Стандартные единицы измерения (например, метры, галлоны, градусы Цельсия, секунды) всегда измеряют физические величины относительно постоянной ссылки. Напротив, децибелы — это просто способ сравнения двух произвольных значений в логарифмической шкале.

Несмотря на то, что децибелы обычно используются для измерения уровня звука, их можно использовать для сравнения любых двух значений. Следующие утверждения совершенно справедливы:

• «Расстояние от Нью-Йорка до Токио на 5,9 дБ больше, чем расстояние от Чикаго до Лос-Анджелеса».
• «Бобу требуется на 3 дБ больше времени, чтобы пробежать милю, чем Джилл».
• «У Билла Гейтса денег на 59 дБ больше, чем у меня».

Конечно, эти сравнения несколько бессмысленны, и вы никогда не услышите, чтобы они использовались в реальном сценарии. Но это подтверждает, что децибелы неявно не измеряют какую-либо физическую величину, они только сравнивают два значения в логарифмической шкале. Мы привыкли сравнивать значения на линейная шкала , которая гораздо более интуитивно понятна. Линейным эквивалентом единицы децибела является единица «х» или «умножение». Например, «Моя машина в 2 раза быстрее, чем машина Джима» или «Мой компьютер загружается в раза в 3 раза дольше, чем ваш». Обратите внимание, что единица «x» или «times» также не является единицей измерения; он сравнивает только два произвольных значения на линейной шкале

.

Линейная и логарифмическая шкалы

Измерение величин на линейной шкале имеет смысл для вещей, которые комбинируются аддитивно. Например, если расстояние от точки А до точки В равно 10 метрам, а расстояние от точки В до точки С равно 100 метрам, имеет смысл сказать, что «общее расстояние от А до точки В и С равно 110 метрам». Также имеет смысл сказать, что «расстояние от B до C в 10 раз больше, чем от A до B».

Линейные величины, такие как расстояние, увеличиваются арифметически (1, 2, 3, 4, 5…). Другими словами, разница между 1 метром и 2 метрами такая же, как разница между 100 метрами и 101 метром. Большинство величин, с которыми мы привыкли иметь дело изо дня в день, увеличиваются арифметически и комбинируются аддитивно, поэтому линейные сравнения для них имеют смысл. Однако не все величины ведут себя так хорошо. Некоторые величины увеличиваются геометрически (1, 2, 4, 8, 16…) и объединяются путем умножения. Другими словами, разница между 1 паскалем (единицей давления) и 2 паскалями воспринимается так же, как разница между 2 паскалями и 4 паскалями.

На изображении ниже показана линейная шкала сверху и логарифмическая шкала снизу:

Обратите внимание, что на линейной шкале расстояние от 0 до 10 равно расстоянию от 10 до 20. На логарифмической шкале масштабе расстояние между 1 и 10 такое же, как расстояние между 10 и 100. Это связано с тем, что линейные шкалы сравниваются аддитивно, тогда как логарифмические шкалы сравниваются путем умножения. Это видно на шкалах выше: на линейной шкале, чтобы перейти от одной из больших решеток к следующей, нужно прибавить или вычесть на 10. На логарифмической шкале, чтобы перейти от одной из больших решеток к следующее, нужно умножить или разделить на 10.

Примеры логарифмических шкал

Например, люди воспринимают высоту музыкальной ноты в логарифмической шкале. Разница между частотой 100 Гц и частотой 200 Гц воспринимается так же, как разница между частотой 1000 Гц и частотой 2000 Гц; оба интервала считаются одной октавой. Единица Гц является линейной, но другие единицы, такие как октавы и шаги, являются логарифмическими. Как и уровни звукового давления (измеряемые в паскалях), частота (измеряемая в Гц) является линейной, но ее восприятие человеком (описанное в октавах и шагах) является логарифмическим; изменение относится к целому. Чтобы найти разницу между двумя величинами, воспринимаемыми логарифмически (например, частотой), я бы разделил их друг на друга.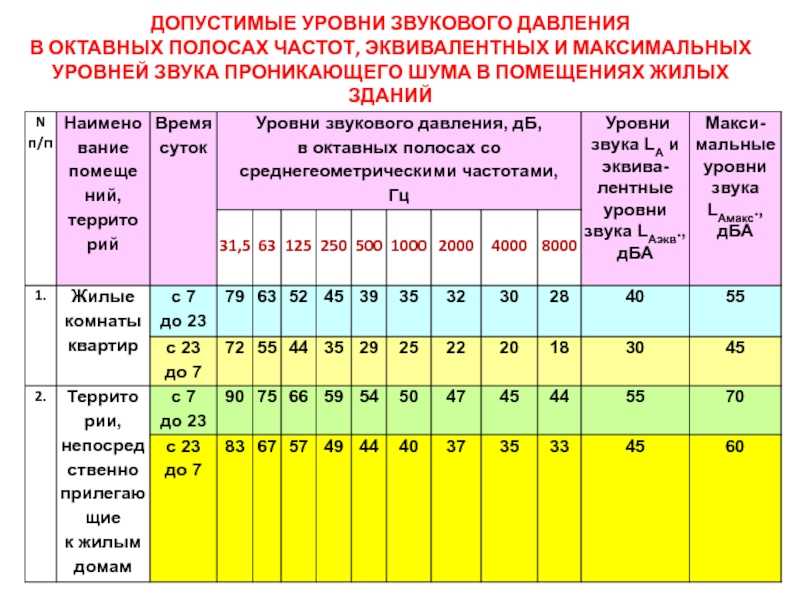 Чтобы найти разницу между двумя величинами, воспринимаемыми линейно (например, расстоянием), я бы вычел их друг из друга.

Звук вызывается колебаниями атмосферного давления, а воспринимаемая громкость звука зависит от того, насколько уровень его давления отличается от нормального атмосферного давления. Стандартной единицей давления является паскаль. Однако уровни звукового давления также не линейно воспринимаются людьми. Например, разница в громкости между двумя звуками, воспроизводимыми при давлении 1 паскаль и 2 паскалях, составляет 90 152, а не 90 153, и воспринимается так же, как разница в громкости между двумя звуками, воспроизводимыми при давлении 100 паскалей и 101 паскаль. На самом деле, чтобы получить ту же воспринимаемую разницу в объеме, вам нужно перейти от 100 паскалей к 200 паскалям. Точно так же вы получите одинаковую разницу в громкости между двумя звуками, воспроизводимыми при 0,001 паскалях и 0,002 паскалях.

Логарифмы

Чтобы полностью понимать децибелы, вы должны понимать логарифмы. Логарифмы — это просто операция, обратная возведению в степень, точно так же, как вычитание — операция, обратная сложению, а деление — операция, обратная умножению:

	Операция	Обратная операция
Сложение/вычитание	7 + 3 = 10	10 — 7 = 3
Умножение/Деление	5 * 4 = 20	20 ÷ 5 = 4
Экспонента/логарифм	10 3 = 1000	журнал 10 (1000) = 3

Основание b , возведенное в степень степени y , дает число x . Логарифмирование меняет эту операцию на обратную: логарифмирование по основанию

b числа x дает показатель степени y .

B ^Y = x log _B ( x ) = Y

Logarith. Однако при работе с децибелами основание всегда равно 10. Поэтому в этом контексте часто используется сокращение log ₁₀ (x) как просто log (x).

Определение в децибелах

Бел определяется как логарифм (по основанию 10) отношения двух значений. Другими словами:

бел = log ₁₀ (значение1 ÷ значение2)

Поскольку децибел составляет 1/10 бела, у вас всегда будет в 10 раз больше децибел по сравнению с белами. Таким образом, определение децибела:

децибел = 10 * log ₁₀ (значение1 ÷ значение2)

Децибел используется гораздо чаще, чем бел, потому что он предлагает более широкий диапазон значений для работы. .

Примеры расчета в децибелах

Чтобы довести до конца эту мысль, давайте сделаем несколько примеров расчета в децибелах для величин, которые вообще не имеют ничего общего со звуком. Если вы хотите попробовать это сами, многие калькуляторы могут вычислять логарифмы, или вы также можете использовать встроенный калькулятор Google.

Если я могу пробежать милю за 16 минут, а вы можете пробежать милю за 8 минут, на сколько децибел я медленнее?

10 * log(16 ÷ 8) = 10 * log(2) = 3,01029995664 ≈ 3 дБ

на сколько децибел я дальше от этого объекта, чем вы?

10 * log(300 ÷ 150) = 10 * log(2) = 3,01029995664 ≈ 3 дБ

Уже сейчас мы видим, что разница между 16 и 8 такая же, как разница между 300 и 150: они’ re оба около 3 децибел друг от друга. Как вы скоро увидите, 3 дБ обычно представляют собой удвоение значения. Вот другой пример:

Если у меня есть пол-литровая бутылка воды, а у вас есть двухлитровая бутылка воды, то насколько меньше у меня воды, чем у вас?

10 * log(0,5 ÷ 2) = 10 * log(0,25) = -6,02059991328 ≈ -6 дБ

увеличения), значение в децибелах становится отрицательным. Еще один пример:

Если состояние Джеффа Безоса составляет 114 миллиардов долларов, а ваш собственный капитал составляет 5700 долларов, то на сколько децибелов Джефф Безос богаче вас?

10 * log(114 000 000 000 ÷ 5700 долл. США) = 10 * log(20000000) = 73,0102999566 ≈ 73 дБ

Здесь мы также видим, что еще одно замечательное свойство децибелов заключается в том, что они могут уменьшать большие числа до управляемых. Тот, у кого денег в 20 миллионов раз больше, чем у вас, богаче всего на 73 дБ.

Сокращения в децибелах

Как мы видели в некоторых из приведенных выше примеров, удвоение значения равносильно увеличению его на (примерно) 3 дБ. Соответственно, уменьшение значения вдвое равносильно уменьшению его (примерно) на 3 дБ. Это легко запомнить. Если что-то увеличилось в четыре раза, это то же самое, что удвоить вдвое, то есть оно увеличилось на 3 дБ дважды, то есть на 6 дБ. Если что-то увеличилось в 8 раз, это то же самое, что удвоить это, затем удвоить, а затем снова удвоить; что то же самое, что 3дБ + 3дБ + 3дБ = 9дБ.

Другим упрощением является то, что увеличение чего-либо в 10 раз равносильно увеличению на 10 дБ. В приведенных ниже таблицах показаны оба этих ярлыка:

Фактор	Децибел
1/64x	-18дБ
1/32x	-15дБ
1/16x	-12 дБ
1/8x	-9дБ
1/4x	-6 дБ
1/2x	-3дБ
1x	0 дБ
2x	3 дБ
4x	6 дБ
8x	9дБ
16x	12 дБ
32x	15 дБ
64x	18 дБ

Коэффициент	Децибел
1/1 000 000x	-60 дБ
1/100 000x	-50 дБ
1/10 000x	-40 дБ
1/1000x	-30 дБ
1/100x	-20дБ
1/10x	-10 дБ
1x	0 дБ
10x	10 дБ
100x	20 дБ
1000x	30 дБ
10 000x	40 дБ
100 000x	50 дБ
1 000 000x	60 дБ

Применение теории на практике

Теперь, когда мы изучили теорию децибелов, давайте разберемся, как они используются в реальном мире. Во-первых, мы рассмотрим, почему децибелы полезны:

Зачем нужны децибелы?

Как мы видели в приведенных выше примерах, децибелы обеспечивают два основных преимущества:

1. Они позволяют легко манипулировать величинами, которые ведут себя или воспринимаются логарифмически.
2. Они могут сократить очень большие диапазоны чисел до более управляемых чисел.

Как эти преимущества помогают нам при измерении более важных величин, таких как электрическая мощность или уровень звукового давления (SPL)? В случае SPL единицами измерения давления являются паскали. Человеческое ухо может воспринимать поразительно широкий диапазон уровней давления. Самый низкий звук, который может уловить средний человек, составляет 0,00002 паскаля или 20 микропаскалей (также называемый порогом слышимости), что соответствует звуку комара, летящего на расстоянии 10 футов от вас. Самые громкие звуки становятся болезненными, когда они достигают около 200 паскалей (это также называется порогом боли). Это может показаться не таким уж большим, но представляет собой десятимиллионную разницу между разницей давлений на пороге слышимости и порогом боли. К счастью, мы не слышим его в десять миллионов раз громче, потому что наше чувство слуха тоже логарифмическое.

Кроме того, люди воспринимают уровень звукового давления в логарифмической шкале (это означает, что мы воспринимаем каждое удвоение давления как ту же разницу; от 0,0001 до 0,0002 паскаля такая же разница, как от 50 до 100 паскалей). Другими словами, если вы посмотрите на это на логарифмическом графике, «расстояние» от 0,0001 до 0,0002 паскаля будет таким же, как расстояние от 50 до 100 паскалей. Таким образом, сравнение значений SPL с использованием логарифмической шкалы имеет гораздо больше смысла, чем использование линейной шкалы. Ведь без этой шкалы было бы трудно интуитивно понять разницу в громкости для звуков, скажем, 0,00355 паскалей, 0,714 паскалей и 71,5 паскалей (45 дБУЗД, 91 дБ УЗД и 131 дБ УЗД соответственно).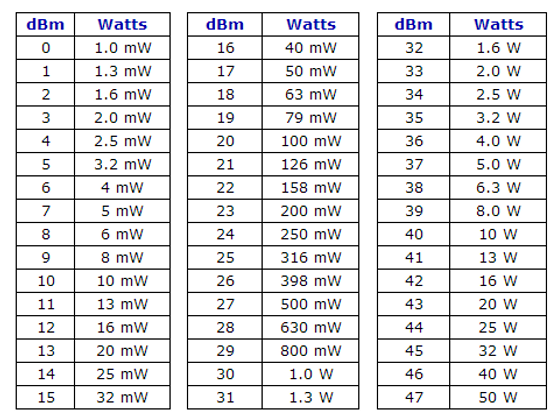

Самый громкий неискаженный звук, возможный в атмосфере Земли, составляет 101 325 паскалей, что примерно в 5 миллиардов раз выше человеческого порога слышимости. Децибелы помогают нам легче справляться с такими большими диапазонами отношений. Разница в dBSPL между порогом слышимости и самым громким неискаженным звуком, возможным на Земле, составляет около 194 дБ, несмотря на то, что последнее давление в 5 миллиардов раз выше, чем первое.

А теперь давай нарушим правила

В следующих разделах рассматриваются аспекты использования децибел в реальных сценариях. И, как вы скоро увидите, некоторые правила, которые мы узнали о децибелах, на практике нарушаются. В частности:

Правило: Децибелы не являются единицами измерения.
Реальность: Хотя это правило технически верно, есть способы преобразовать децибелы в фактические единицы измерения. Мы обсудим это в следующем разделе о единицах децибел.

Правило: 3 дБ всегда представляет собой удвоение базовых значений.
Реальность: Хотя это верно для чистых децибелов, все становится немного сложнее, когда мы начинаем вводить единицы децибел. В разделах ниже мы узнаем, что 3 дБ по-прежнему представляют собой удвоение для некоторых типов единиц измерения, но для других типов единиц 6 дБ представляют собой удвоение.

Децибелы

Выше мы узнали, что децибелы не являются единицами измерения; они не измеряют какую-либо конкретную физическую величину, они представляют собой просто логарифмическое сравнение двух чисел. Это верно для необработанных, чистых децибелов. Однако для различных целей было создано множество «единиц измерения децибел». Это шкалы в децибелах, которые сравнивают значения с согласованным эталонным значением. В этих случаях децибелы могут фактически стать единицами измерения и могут делать больше, чем просто сравнивать два числа.

При использовании чистых децибелов используется сокращение «дБ». При использовании единиц децибел к концу единицы дБ добавляется одна или несколько букв. Например, dBu, dBV, dBW, dBFS, dBSPL и т. д. Каждая из этих единиц децибел предназначена для измерения реальной физической величины по сравнению с эталонным значением для этой величины. Таким образом, новое уравнение для децибелов принимает вид:

Единицы децибела = 10 * log ₁₀ (значение1 ÷ эталонное значение)

эталонное значение  всегда остается неизменным для данной единицы децибел, поэтому мы всегда сравниваем значения с известным стабильным эталонным значением.

Ниже приведены лишь несколько примеров распространенных единиц децибел, но имейте в виду, что существуют десятки, если не сотни различных единиц децибел, которые были определены для различных целей.

дБУЗД

дБУЗД — хороший пример единицы децибел. dBSPL позволяет нам сравнивать уровни звукового давления (SPL) в паскалях, используя шкалу децибел. Эталонное значение для dBSPL составляет 0,00002 паскаля, что является порогом слышимости. Это означает, что при использовании dBSPL мы всегда рассчитываем, насколько данный звук громче порога слышимости в децибелах.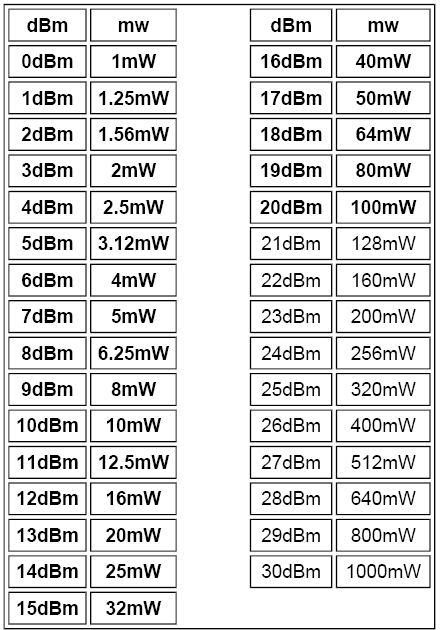 Уравнение для dBSPL будет следующим:

Единицы децибела = 20 * log ₁₀ (SPLValue ÷ 0,00002)

Вы могли заметить, что dBSPL использует уравнение 20*логарифм вместо обычного уравнения 10*логарифм. Придержите эту мысль пока, скоро мы узнаем об этом больше.

dBu

dBu — это децибел, который позволяет нам измерять электрические напряжения. Эталонное значение для dBu составляет 0,775 В. Это может показаться странным значением, но оно было выбрано по уважительной причине (которая выходит за рамки этой статьи). Таким образом, dBu позволяет нам измерять среднеквадратичное напряжение по сравнению с 0,775 В по шкале децибел.

дБм

дБм — это децибел, который позволяет нам измерять электрическую мощность. Эталонное значение для дБм составляет 1 мВт или 0,001 Вт. Следовательно, дБм позволяет нам измерять значения электрической мощности по сравнению с 0,001 Вт по шкале децибел.

дБ(А), дБ(В), дБ(С)

дБ(А), дБ(В) и дБ(С) немного отличаются от приведенных выше единиц в децибелах.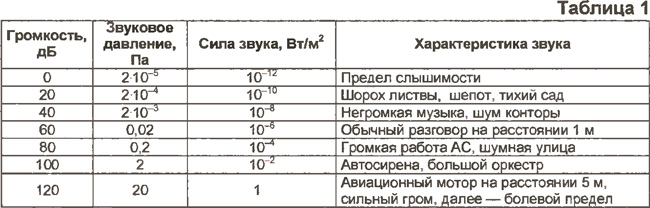 Все эти значения на самом деле все еще измеряют дБ УЗД; то есть они измеряют давление в паскалях по сравнению с 0,00002 паскалями по шкале децибел. Однако каждое из этих устройств применяет различные «взвешивания» к значениям SPL в зависимости от их частоты. Таким образом, мы получаем чистое значение dBSPL, применяем к нему взвешивание для изменения значений, а затем вычисляем новое взвешенное значение dBSPL. Чтобы указать, какая схема взвешивания использовалась, мы используем дБ(А), дБ(В), дБ(С) (иногда обозначаемые как дБА, дББ, дБС) или несколько других доступных схем взвешивания.

Взвешивание используется для изменения частотной характеристики измерения в различных целях. Например, человеческое ухо не воспринимает все частоты с одинаковой громкостью. Если вы воспроизведете тон 50 Гц и тон 2000 Гц с одинаковым значением dBSPL, тон 2000 Гц будет восприниматься намного громче. Следовательно, A-взвешивание пытается применить веса к уровням различных частот таким образом, чтобы они приближались к уровню, который фактически воспринимает средний человек. Это может быть полезно при измерении уровня окружающего шума. Если присутствует шум на частоте, которую люди не очень хорошо воспринимают, то этот шум не так важен и не должен так сильно влиять на общее значение дБА, как шум на частоте, которую человеческое ухо воспринимает хорошо.

dBFS

dBFS — еще одна аббревиатура децибел, которая немного отличается от остальных. На самом деле dBFS на самом деле не является единицей децибел, потому что она не привязана к стабильному значению. «FS» в dBFS означает «полная шкала», что является еще одним способом описания точки отсечения цифрового аудиоустройства. Таким образом, dBFS относится к точке отсечения цифрового аудиоустройства, что означает, что 0dBFS равно точке отсечения этого устройства.

Поскольку значения dBFS обычно измеряют расстояние до сигнала  ниже  точка отсечения устройства (поскольку обычно не так полезно знать, насколько выше точки отсечения находится сигнал), значения dBFS обычно отрицательны. -10dBFS означает на 10 дБ ниже точки отсечки. Поскольку точка отсечки различных устройств часто может быть разной, dBFS не привязан к стабильному значению и, следовательно, не является единицей измерения.

10 log против 20 log, 3 дБ или 6 дБ на удвоение?

Возможно, вы заметили выше, что формула для dBSPL равна 9.0228 20 * log ₁₀ (Value ÷ RefValue) вместо обычного 10 * log ₁₀ (Value ÷ RefValue). И, если вы раньше работали с децибелами, вы, возможно, знаете, что иногда удвоение значения представлено увеличением на 3 дБ, а в других случаях удвоение представлено увеличением на 6 дБ. Этот раздел объяснит это явление децибел.

Децибелы как отношение двух степеней

Когда в Bell Telephone Labs изобрели децибелы, они в основном занимались измерением потерь в мощность  по линиям электропередачи на большие расстояния. Поэтому они начали использовать соглашение, согласно которому децибелы всегда формулируются для описания изменения мощности, или, точнее, логарифмического отношения двух мощностей. Эта условность сохранилась и по сей день. Это означает, что когда мы используем децибелы для измерения количества энергии, ничего не меняется. Формула все та же:

10 * log ₁₀ (мощность1 ÷ мощность2)

Ты всегда в итоге говоришь о смене власти. Для этого мы должны использовать 20 * log ₁₀ (Value1 ÷ Value2)  для расчета значений этих величин в децибелах. Это связано с тем, что мощность пропорциональна квадрату напряжения и тока, о чем свидетельствует закон Ома:

P = V ²  ÷ R
P = I ²  * R

Показан вывод значения напряжения в децибелах. ниже. Обратите внимание, что хотя мы измеряем напряжение, мы начинаем с уравнения, в котором используется отношение мощностей, и манипулируем им, чтобы получить напряжение.

дБ(Мощность) = 10 * log ₁₀ (Power1 ÷ Power2)
дБ (мощность) = 10 * log ₁₀ ((V ₁ ² ÷ r) ÷ (V ₂ ² ÷ R)) 1 2 9 ² ÷ R)) 1. V ²  ÷ R
дБ(Мощность) = 10 * log ₁₀ (V ₁ ²  ÷ V ₂ ² ) 9013 дБ(1 *Мощность) = 20 (02 9013 дБ(1 *Мощность) ₁  ÷ В ₂ ) ² )
дБ(мощность) = 10 * (2 * log ₁₀ (В ₁  ÷ В ₂ ))                                                                     0152, поскольку log(x ² ) = 2 * log(x)
дБ(мощность) = 20 * log ₁₀ (V ₁ ÷ V ₂ )

давно используется с децибелами, но в некоторых случаях это соглашение может упростить задачу. Например, когда инженеры Bell Laboratories захотели измерить потери мощности в линии передачи на большие расстояния, они не смогли напрямую измерить мощность в линии. Вместо этого они измерили потери напряжения в кабеле с помощью вольтметра и использовали потери напряжения и сопротивление для расчета потерь мощности. Используя это соглашение, они могли легко измерить потери напряжения в дБ и сразу узнать потери мощности в дБ без каких-либо дополнительных расчетов.

Аналогичным образом, при описании аудиоустройств, таких как усилители, это соглашение позволяет нам игнорировать различия между типами устройств при указании уровней. Например, можно описать усилитель как имеющий усиление «40 дБ», не указывая, является ли это усилением по напряжению или усилением по мощности. Это соглашение гарантирует, что 40 дБ усиления по напряжению (измеряется при 20*log) всегда приводит к 40 дБ прироста мощности (измеряется при 10*log).

Иными словами, это соглашение дает нам роскошь просто сказать «этот сигнал на 6 дБ громче», не уточняя, говорим ли мы о мощности, напряжении, токе или давлении. Все единицы выравниваются таким образом, что увеличение на 6 дБ является увеличением на 6 дБ, независимо от используемой базовой единицы измерения. Без этого соглашения мы всегда должны были бы быть осторожны, говоря: «напряжение этого сигнала на 3 дБ выше» или «напряжение этого сигнала на 10 дБ ниже».

Какие единицы 10log, а какие 20log?

Когда мы говорим об электрических единицах, таких как напряжение, сила тока и мощность, довольно легко запомнить, какие единицы используют уравнение 10log, а какие используют 20log: любые единицы измерения мощности используют 10log, а остальные используют 20log. Однако с другими единицами, такими как уровень звукового давления, все не так очевидно. Ниже приведен список общих единиц измерения и того, используют ли они 10 log или 20 log при использовании единиц децибел. Также обратите внимание, что любые единицы, использующие 10log , увеличиваются на 3 дБ за удвоение, тогда как любые единицы, использующие 20log, увеличиваются на 6 дБ за удвоение.

10 логарифмических единиц — 3 дБ на удвоение

Любые единицы измерения, прямо пропорциональные мощности, используют уравнение 10 логарифмических единиц. Их часто называют «величинами мощности».

• Мощность, Вт (дБм)
• Уровень силы звука, Вт на м ²  (dBSIL)

Единицы измерения 20 log — 6 дБ на удвоение

Любые единицы измерения, которые прямо пропорциональны квадратному корню из мощности, используют уравнение 20 log. Их часто называют «величинами корневой мощности».

• Напряжение, вольт (dBu, dBV)
• Уровень звукового давления, в паскалях (dBSPL, дБ(A), дБ(B), дБ(C))

Психоакустика

Чтобы еще больше усложнить ситуацию, люди обычно не воспринимают увеличение громкости на 3 дБ как удвоение громкости.