Что такое ГАРМОНИЧЕСКИЙ, определение термина в Словарь иностранных слов
Все словариБольшой юридический словарьОднотомный большой юридический словарьСправочник лекарственных средствЭнциклопедия БиологияФинансовый словарьЭкономический словарьБольшой бухгалтерский словарьМедицинский словарьМорской словарьСоциологический словарьСексологический словарьАстрономический словарьБизнес словарьПолитический словарьСловарь литературных терминовМедицинский большой словарьЭнциклопедический словарьСловарь ЕфремовойЭнциклопедия КольераЭнциклопедия Брокгауза и ЕфронаТолковый словарь УшаковаСловарь ОжеговаСловарь ДаляСловарь наркотического сленгаСловарь воровского жаргонаСловарь молодёжного слэнгаСловарь компьютерного жаргонаМеталлы и сплавы. СправочникТолковый строительно-архитектурный словарьАрхитектурный словарьДжинсовый словарьСловарь по ландшафтному дизайнуАвтомобильный словарьКулинарный словарьСтроительный словарьПолиграфический словарьСловарь модыYoga Vedanta DictionaryСловарь йогиСловарь терминов Йоги и ведантыСозвездия, латинские названияСловарь музыкальных терминовБиографический словарьСловарь эпитетовСловарь курортовСловарь русских технических сокращенийЭтимологический словарь ФасмераСловарь иностранных словСловарь фразеологизмовСловарь географических названийСловарь символовСловарь синонимовСловарь нумизматаСловарь имёнСловарь мерСловарь русских фамилийЭтнографический словарьСловарь лекарственных растенийСловарь народовИсторический словарьРелигиозный словарьСловарь по мифологииБиблейская энциклопедияСловарь по искусствуФилософский словарьСловарь логикиПсихологический словарьВсё о вине, энциклопедический словарьКнига о вкусной и здоровой пищеКулинарный словарьПищевые добавкиСловарь алкогольных напитковЭнциклопедия трезвого образа жизни
-
ГАРМОНИЧЕСКИЙ — ая, ое Исполненный гармонии, основанный на гармонии.
Гармонические колебания ( физ. ) — колебания, при которых сила, возвращающая колеблющееся тело к положению равновесия, возрастает пропорцио-нально отклонению от положения равновесия; противоп. а н г а р м о н и ч е с к и е к о л е б а н и я (см. АНГАРМОНИЧЕСКИЙ ).
Гармонические колебания ( физ. ) — колебания, при которых сила, возвращающая колеблющееся тело к положению равновесия, возрастает пропорцио-нально отклонению от положения равновесия; противоп. а н г а р м о н и ч е с к и е к о л е б а н и я (см. АНГАРМОНИЧЕСКИЙ ).Ivanov Alex
гармония, полнота,
Выберите букву
А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я
- Значение слова ГАРМОНИЧЕСКИЙ в других словарях:
-
- Значение слова гармонический — Толковый словарь Ушакова
- Что такое Гармонический Анализ — Энциклопедический словарь
- Определение термина Гармонический прил.
- Что означает слово Гармонический Ряд — Энциклопедический словарь
Популярные слова
РУТИНА КЛИФ ФИСКАЛ ЕПАНЧА БАЛЕТМЕЙСТЕР ТОМПАК ОКСИГЕН БАЛЕТ ТОН ВАТИКАН РУЛЬ ДИАГОНАЛЬ ГЕРОЙ МОЛ АМПУЛА ДАМА ФРАНШИЗА ТЕФТЕЛИ ТУФ МАДРИГАЛ
Гармонический ряд
В математике гармонический ряд — это дивергентный бесконечный ряд:
∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{1}{n}=1+{\frac {1}{2}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots }
Расхождение означает, что по мере того, как вы добавляете больше терминов, сумма никогда не перестает увеличиваться.
Она не переходит к одному конечному значению.
Бесконечность означает, что вы всегда можете добавить еще один термин. Финального термина в серии не существует.
Ее название происходит от идеи гармоник в музыке: длина волны обертонов вибрирующей струны составляет 1/2, 1/3, 1/4 и т.д. от фундаментальной длины волны струны. Кроме первого термина, каждый термин серии является гармоническим значением терминов по обе стороны от него. Фраза «гармоническое значение» также происходит от музыки.
История
Тот факт, что гармонические серии расходятся, впервые был доказан в 14 веке Николь Оресме, но был забыт. Доказательства были даны в 17 веке Пьетро Менголи, Иоганном Бернулли и Якобом Бернулли.
Архитекторы использовали гармоничные последовательности. В эпоху барокко архитекторы использовали их в пропорциях поэтажных планов, возвышенностей и во взаимоотношениях между архитектурными деталями церквей и дворцов.
Расхождение
Существует несколько известных доказательств расхождения гармонических рядов.
Некоторые из них приводятся ниже.
Тест на сравнение
Одним из способов доказать расхождение является сравнение гармонического ряда с другим дивергентным рядом, в котором каждый знаменатель заменяется на следующий по величине — два:
1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\displaystyle {\begin{подпись} &{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots [12pt] \geq {}&1+{\frac {1}{2}+{\frac {1}{\color {red}{\mathbf {4} }}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}++{\frac {1}{\color {red}{\mathbf {8} }}++{\frac {1}{\color {red}{\mathbf {8} }}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}+\cdots \end{aligned}}}
Каждый член ряда гармоник больше или равен соответствующему члену второго ряда, и поэтому сумма ряда гармоник должна быть больше или равна сумме второго ряда. Однако сумма второго ряда бесконечна:
1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\displaystyle {\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}!+!{\frac {1}{4}}\right)+\left({\frac {1}{8}}!+!{\frac}{1}{8}}!+!{\frac}{1}{8}}!+!{\frac {1}{8}\right)+\left({\frac {1}{16}}!+!\cdots !+!!!!{\frac {1}{16}}\right)+\cdots [12pt]={}&1+{\frac {1}{2}+{\frac {1}{2}+{\frac {1}{2}+\frac {1}{2}+\cdots =\infty \end{aligned}}}
Из этого (по результатам сравнительного теста) следует, что сумма ряда гармоник также должна быть бесконечной.
{k}}{\frac {1}{n}\geq 1+{\frac {k}{2}}}
на каждое положительное целое число k.
Это доказательство, предложенное Николь Оресме примерно в 1350 году, считается вершиной средневековой математики. Это по-прежнему является стандартным доказательством, преподаваемым на уроках математики сегодня.
Интегральный тест
Можно доказать, что гармонический ряд расходится, сравнивая его сумму с неправильным интегралом. Рассмотрим расположение прямоугольников, показанных на рисунке справа. Каждый прямоугольник имеет ширину 1 единицы и высоту 1/n единиц, поэтому общая площадь бесконечного числа прямоугольников является суммой гармонического ряда:
площадь прямоугольников = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle {\begin{array}{c}{\text{area of}}{\text{rectangles}}\end{array}}=1+{\frac {1}{2}+{\frac {1}{3}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots }
Общая площадь под кривой y = 1/x от 1 до бесконечности задается расходящимся неправильным интегралом:
область под кривой = ∫ 1 ∞ 1 x d x = ∞ .
{k}{\frac {1}{n}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1}
где γ — константа Эйлера-Маскерони и εk ~ 1/2k, которая приближается к 0 по k, переходит в бесконечность. Леонхард Эйлер доказал как это, так и то, что сумма, которая включает только обратные связи праймов, также расходится, то есть:
∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . {\displaystyle \sum _{p{\text{ prime }}}{\frac {1}{p}={\frac {1}{2}+{\frac {1}{3}+{\frac {1}{5}}+{\frac {1}{7}+{\frac {1}{11}}+{\frac {1}{13}+{\frac {1}{17}}+\cdots =\infty . }
Частичные суммы
Первые тридцать гармонических чисел | ||||||||||||||||||||||||||||||||||||||||||||
n | Частичная сумма гармонического ряда, Hn |
| ||||||||||||||||||||||||||||||||||||||||||
выраженный в виде дроби | десятичная дробь | относительный размер |
| |||||||||||||||||||||||||||||||||||||||||
1 | 1 | ~1 | 1
|
| ||||||||||||||||||||||||||||||||||||||||
2 | 3 | /2 | ~1. | 1.5
|
| |||||||||||||||||||||||||||||||||||||||
3 | 11 | /6 | ~1.83333 | 1.83333
|
| |||||||||||||||||||||||||||||||||||||||
4 | 25 | /12 | ~2.08333 | 2.08333
|
| |||||||||||||||||||||||||||||||||||||||
5 | 137 | /60 | ~2.28333 | 2.28333
|
| |||||||||||||||||||||||||||||||||||||||
6 | 49 | /20 | ~2.45 | 2.45
|
| |||||||||||||||||||||||||||||||||||||||
7 | 363 | /140 | ~2.59286 | 2.59286
|
| |||||||||||||||||||||||||||||||||||||||
8 | 761 | /280 | ~2. | 2.71786
|
| |||||||||||||||||||||||||||||||||||||||
9 | 7129 | /2520 | ~2.82897 | 2.82897
|
| |||||||||||||||||||||||||||||||||||||||
10 | 7381 | /2520 | ~2.92897 | 2.92897
|
| |||||||||||||||||||||||||||||||||||||||
11 | 83711 | /27720 | ~3.01988 | 3.01988
|
| |||||||||||||||||||||||||||||||||||||||
12 | 86021 | /27720 | ~3.10321 | 3.10321
|
| |||||||||||||||||||||||||||||||||||||||
13 | 1145993 | /360360 | ~3.18013 | 3.18013
|
| |||||||||||||||||||||||||||||||||||||||
14 | 1171733 | /360360 | ~3. | 3.25156
|
| |||||||||||||||||||||||||||||||||||||||
15 | 1195757 | /360360 | ~3.31823 | 3.31823
|
| |||||||||||||||||||||||||||||||||||||||
16 | 2436559 | /720720 | ~3.38073 | 3.38073
|
| |||||||||||||||||||||||||||||||||||||||
17 | 42142223 | /12252240 | ~3.43955 | 3.43955
|
| |||||||||||||||||||||||||||||||||||||||
18 | 14274301 | /4084080 | ~3.49511 | 3.49511
|
| |||||||||||||||||||||||||||||||||||||||
19 | 275295799 | /77597520 | ~3.54774 | 3.54774
|
| |||||||||||||||||||||||||||||||||||||||
20 | 55835135 | /15519504 | ~3. | 3.59774
|
| |||||||||||||||||||||||||||||||||||||||
21 | 18858053 | /5173168 | ~3.64536 | 3.64536
|
| |||||||||||||||||||||||||||||||||||||||
22 | 19093197 | /5173168 | ~3.69081 | 3.69081
|
| |||||||||||||||||||||||||||||||||||||||
23 | 444316699 | /118982864 | ~3.73429 | 3.73429
|
| |||||||||||||||||||||||||||||||||||||||
24 | 1347822955 | /356948592 | ~3.77596 | 3.77596
|
| |||||||||||||||||||||||||||||||||||||||
25 | 34052522467 | /8923714800 | ~3.81596 | 3.
|
| |||||||||||||||||||||||||||||||||||||||
26 | 34395742267 | /8923714800 | ~3.85442 | 3.85442
|
| |||||||||||||||||||||||||||||||||||||||
27 | 312536252003 | /80313433200 | ~3.89146 | 3.89146
|
| |||||||||||||||||||||||||||||||||||||||
28 | 315404588903 | /80313433200 | ~3.92717 | 3.92717
|
| |||||||||||||||||||||||||||||||||||||||
29 | 9227046511387 | /2329089562800 | ~3.96165 | 3.96165
|
| |||||||||||||||||||||||||||||||||||||||
30 | 9304682830147 | /2329089562800 | ~3.99499 | 3. где sn являются независимыми, идентично распределенными случайными переменными, принимающими значения +1 и -1 с равной вероятностью 1/2, является известным примером в теории вероятностей для ряда случайных переменных, сходящихся с вероятностью 1. Факт такого сходства является легким следствием либо теорем Колмогорова трех серий, либо близкородственным Колмогорову максимальным неравенством. Байрон Шмуланд из Университета Альберты дополнительно изучил свойства случайного ряда гармоник и показал, что сходящийся ряд является случайной переменной с некоторыми интересными свойствами. В частности, функция плотности вероятности этой случайной величины, оцененная при +2 или -2, принимает значение 0,124999999999999999999999999999764…, отличающееся от 1/8 менее чем на 10-42. В работе Шмуланда объясняется, почему эта вероятность так близка к 1/8, но не совсем точна. Точное значение этой вероятности дает бесконечный косинусный интеграл С2, разделенный на π. Испорченный ряд гармоникОбедненная гармоническая серия, в которой все термины, в которых цифра 9 появляется в любом месте знаменателя, удалены, может быть показана как сходящаяся, и ее значение меньше 80. Фактически, при удалении всех терминов, содержащих какую-либо определенную строку цифр (в любом основании), серия сходится. Первые четырнадцать частичных сумм чередующихся гармонических рядов (сегменты черной линии) показаны сходящимися с натуральным логарифмом 2 (красная линия). ЗаявленияСерия гармоник может быть интуитивно понятной. Это объясняется тем, что это расходящаяся серия, несмотря на то, что сроки серии становятся меньше и идут к нулю. Расхождение ряда гармоник является источником некоторых парадоксов.
1 100 ∑ k = 1 n 1 k . Поскольку серия становится произвольно большой по мере того, как n становится больше, в конце концов это соотношение должно превысить 1, что означает, что червь достигает конца резиновой ленты. Однако значение n, при котором это происходит, должно быть чрезвычайно большим: примерно e100, число, превышающее 1043 минуты (1037 лет). Несмотря на то, что гармонический ряд действительно расходится, он делает это очень медленно.
| ||||||||||||||||||||||||||||||||||||||||
5
7178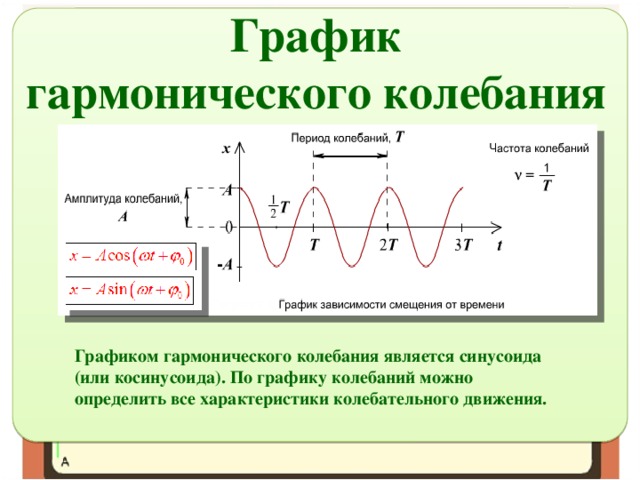6
25156
59774
81596
{\infty }{\frac {s_{n}}{n},}
{n}{\frac {1}{k}}. }
{n}{\frac {1}{k}}. }
д. от основной длины волны струны.
stat.ualberta.ca — «Random Harmonic Series»- doi.org — 10.2307/3647827- mathworld.wolfram.com — Infinite Cosine Product Integral- www.qbyte.org — «Nick’s Mathematical Puzzles: Solution 72»- www.pme-math.org — «Problem 52: Overhanging dominoes»
9n_{i=1}\frac{w_i}{x_i}}}
∑i=1nxiwi∑i=1nwi
Технически это определяется как « nth корневой продукт n чисел.» Среднее геометрическое необходимо использовать при работе с процентами, которые получены из значений, в то время как стандартное среднее арифметическое работает с самими значениями.
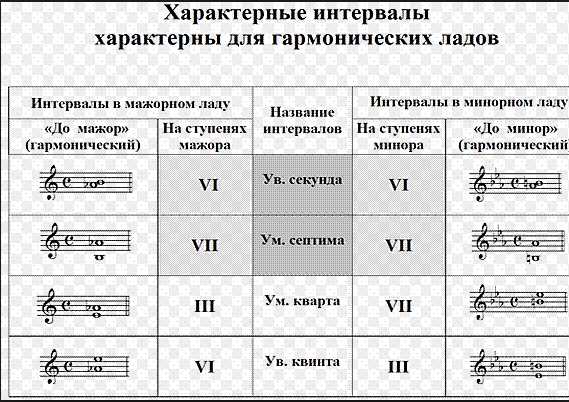Среднее гармоническое можно вычислить для ряда, включающего отрицательные значения, хотя его невозможно вычислить, если ряд включает нулевое значение. По сравнению со средним арифметическим и средним геометрическим среднее гармоническое дает более прямую кривую.
Это одно из трех пифагорейских средств. Оставшиеся два — среднее арифметическое и среднее геометрическое. Эти три средних значения очень важны, поскольку они широко используются в области геометрии и музыки. Если нам дан ряд данных или набор наблюдений, то среднее гармоническое может быть определено как величина, обратная среднему значению обратных членов. т. е. это величина, обратная среднему арифметическому обратных величин.
Чтобы найти его, мы делим количество членов в ряду данных на сумму всех обратных членов. Он всегда будет наименьшим по сравнению со средним геометрическим и средним арифметическим.
Таким образом, формула среднего гармонического определяется как
Это будет н.
Скажем, у нас есть 2 числа a и b.
Ниже приведены достоинства и недостатки гармонического среднего:
{n}\frac{f_{i}}{x_{i}}}\)
Кроме того, если есть определенные веса, связанные с каждым наблюдением, мы можем вычислить взвешенное среднее гармоническое. 9{n}\frac{w_{i}}{x_{i}}}\).
