Векторно-векторное произведение векторов — это… Что такое Векторно-векторное произведение векторов?
- Векторно-векторное произведение векторов
Тройно́е ве́кторное произведе́ние (другое название: двойное векторное произведение)
![\left[ \vec{a}, \vec{b}, \vec{c} \right]](//rc74.ru/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) векторов
векторов  — векторное произведение вектора
— векторное произведение вектора  на векторное произведение векторов
на векторное произведение векторов  и
и 
В литературе этот тип произведения трёх векторов называется как тройным[1] (по числу векторов), так и двойным[2] (по числу операций умножения).
Свойства
Формула Лагранжа
Для тройного векторного произведения справедлива формула Лагранжа,
которую можно запомнить по мнемоническому правилу «бац минус цаб».
Доказательство
Тождество Якоби
Для тройного векторного произведения выполняется тождество Якоби
которое доказывается раскрытием скобок по формуле Лагранжа
Примечания
- ↑ См., например, Weisstein, Eric W. Vector Triple Product на сайте Wolfram MathWorld.(англ.).
- ↑ См., например, М. Я. Выгодский, Справочник по высшей математике, М., 1977, стр. 156.
См. также
Wikimedia Foundation. 2010.
- Вектор (персонаж Battle Angel)
- Векторно-полевой анализ
Смотреть что такое «Векторно-векторное произведение векторов» в других словарях:
Векторное произведение векторов — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства … Википедия
Векторное произведение — в трёхмерном пространстве. Векторное произведение это псевдовектор, перпендикулярный плоскости, построенной по двум … Википедия
Векторное умножение — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства … Википедия
Оператор набла — (оператор Гамильтона) векторный дифференциальный оператор, обозначаемый символом (набла) (в Юникоде U+2207, ∇). Для трёхмерного евклидова пространства в прямоугольных декартовых координатах[1] оператор набла определяется следующим образом … Википедия
Момент силы — Размерность L2MT−2 Единицы измерения СИ Ньютон метр … Википедия
Вращательный момент — Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) физическая величина, характеризующая вращательное действие силы на твёрдое тело. Момент силы приложенный к гаечному ключу Отношение между векторами силы, момента силы … Википедия
Вращающий момент — Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) физическая величина, характеризующая вращательное действие силы на твёрдое тело. Момент силы приложенный к гаечному ключу Отношение между векторами силы, момента силы … Википедия
Крутящий момент — Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) физическая величина, характеризующая вращательное действие силы на твёрдое тело. Момент силы приложенный к гаечному ключу Отношение между векторами силы, момента силы … Википедия
Механический момент — Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) физическая величина, характеризующая вращательное действие силы на твёрдое тело. Момент силы приложенный к гаечному ключу Отношение между векторами силы, момента силы … Википедия
Момент сил — Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) физическая величина, характеризующая вращательное действие силы на твёрдое тело. Момент силы приложенный к гаечному ключу Отношение между векторами силы, момента силы … Википедия
векторное произведение — с русского на английский
Векторное произведение — в трёхмерном пространстве. Векторное произведение это псевдовектор, перпендикулярный плоскости, построенной по двум … Википедия
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ — вектора a на вектор b вектор p=ВЕКТОРНОЕ ПРОСТРАНСТВО математическое понятие, обобщающее понятие совокупности всех векторов 3 мерного пространства на случай произвольного числа измерений … Большой Энциклопедический словарь
векторное произведение — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN cross productvector product … Справочник технического переводчика
векторное произведение — вектора а на вектор b, вектор р = [а, b], или а×b, равный по длине площади параллелограмма, построенного на векторах а и b, перпендикулярный плоскости этого параллелограмма; направление векторного произведения р зависит от выбора координатной… … Энциклопедический словарь
векторное произведение — vektorinė sandauga statusas T sritis fizika atitikmenys: angl. outer product; vector product; vectorial product vok. Kreuzprodukt, n; äußeres Produkt, n; vektorielles Produkt, n; Vektorprodukt, n rus. векторное произведение, n; внешнее… … Fizikos terminų žodynas
векторное произведение — vektorinė sandauga statusas T sritis automatika atitikmenys: angl. cross product; vector product; vectorial product vok. Kreuzprodukt, n; äußeres Produkt, n; Vektorprodukt, n rus. векторное произведение, n pranc. produit vectoriel, m … Automatikos terminų žodynas
Векторное произведение — вектора а на вектор b вектор, обозначаемый [а, b] и определяемый так: 1) длина вектора [а, b] равна произведению длин векторов а и b на синус угла φ между ними (берётся тот из двух углов между а и b, который не превосходит π), 2) вектор… … Большая советская энциклопедия
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ — вектора . навек т о р вектор , обозначаемый символом или и удовлетворяющий условиям: длина вектора равна произведению длин векторов на синус угла, между ними, т. е. вектор … Математическая энциклопедия
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ — вектора а на вектор b, вектор р = [а, b], или aхb, равный по длине площади параллелограмма, построенного на векторах a и b, перпендикулярный плоскости этого параллелограмма; направление В. п. р зависит от выбора координатной системы i, j, k; из… … Естествознание. Энциклопедический словарь
Векторное произведение векторов — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства … Википедия
Векторное произведение в семимерном пространстве — В математике, векторное произведение в семимерном пространстве билинейная операция над векторами в семимерном пространстве. Оно назначает для любых двух векторов a, b в 7 вектор a × b 7. В семи измерениях существует и векторное произведение с… … Википедия
векторное произведение — это… Что такое векторное произведение?
- 1. adj
math. Kreuzprodukt, Vektorprodukt
2. n1) eng. vektorielles Produkt
2) electr. äußeres Produkt
Универсальный русско-немецкий словарь. Академик.ру. 2011.
- векторное прерывание
- векторное пространство
Смотреть что такое «векторное произведение» в других словарях:
Векторное произведение — в трёхмерном пространстве. Векторное произведение это псевдовектор, перпендикулярный плоскости, построенной по двум … Википедия
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ — вектора a на вектор b вектор p=ВЕКТОРНОЕ ПРОСТРАНСТВО математическое понятие, обобщающее понятие совокупности всех векторов 3 мерного пространства на случай произвольного числа измерений … Большой Энциклопедический словарь
векторное произведение — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN cross productvector product … Справочник технического переводчика
векторное произведение — вектора а на вектор b, вектор р = [а, b], или а×b, равный по длине площади параллелограмма, построенного на векторах а и b, перпендикулярный плоскости этого параллелограмма; направление векторного произведения р зависит от выбора координатной… … Энциклопедический словарь
векторное произведение — vektorinė sandauga statusas T sritis fizika atitikmenys: angl. outer product; vector product; vectorial product vok. Kreuzprodukt, n; äußeres Produkt, n; vektorielles Produkt, n; Vektorprodukt, n rus. векторное произведение, n; внешнее… … Fizikos terminų žodynas
векторное произведение — vektorinė sandauga statusas T sritis automatika atitikmenys: angl. cross product; vector product; vectorial product vok. Kreuzprodukt, n; äußeres Produkt, n; Vektorprodukt, n rus. векторное произведение, n pranc. produit vectoriel, m … Automatikos terminų žodynas
Векторное произведение — вектора а на вектор b вектор, обозначаемый [а, b] и определяемый так: 1) длина вектора [а, b] равна произведению длин векторов а и b на синус угла φ между ними (берётся тот из двух углов между а и b, который не превосходит π), 2) вектор… … Большая советская энциклопедия
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ — вектора . навек т о р вектор , обозначаемый символом или и удовлетворяющий условиям: длина вектора равна произведению длин векторов на синус угла, между ними, т. е. вектор … Математическая энциклопедия
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ — вектора а на вектор b, вектор р = [а, b], или aхb, равный по длине площади параллелограмма, построенного на векторах a и b, перпендикулярный плоскости этого параллелограмма; направление В. п. р зависит от выбора координатной системы i, j, k; из… … Естествознание. Энциклопедический словарь
Векторное произведение векторов — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства … Википедия
Векторное произведение в семимерном пространстве — В математике, векторное произведение в семимерном пространстве билинейная операция над векторами в семимерном пространстве. Оно назначает для любых двух векторов a, b в 7 вектор a × b 7. В семи измерениях существует и векторное произведение с… … Википедия
Векторное произведение векторов — это… Что такое Векторное произведение векторов?
Правые и левые тройки векторов
Три вектора называются упорядоченной тройкой, если указано, какой из этих векторов является первым, какой — вторым, а какой — третьим.
Тройка некомпланарных векторов 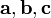 называется правой (левой), если, будучи приведёнными к общему началу, эти векторы располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки.
называется правой (левой), если, будучи приведёнными к общему началу, эти векторы располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки.
Определение
Векторным произведением вектора 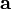 на вектор
на вектор 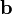 называется вектор
называется вектор 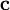 , удовлетворяющий следующим требованиям:
, удовлетворяющий следующим требованиям:
- длина вектора
 равна произведению длин векторов
равна произведению длин векторов  и
и  на синус угла
на синус угла  ; между ними
; между ними
Обозначение:
В различных учебных заведениях определение векторного произведения даётся по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах. А далее выводится данное выше определение.
Свойства
Геометрические свойства векторного произведения
Алгебраические свойства векторного произведения
Выражение для векторного произведения в декартовых координатах
Если два вектора 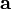 и
и 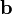 определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе
определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе
то их векторное произведение имеет вид
Для запоминания этой формулы удобно использовать определитель:
или
где 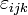 — символ Леви-Чивиты.
— символ Леви-Чивиты.
Обобщения
Кватернионы
Векторное произведение можно также записать в кватернионной форме, поэтому буквы 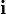 ,
, 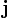 ,
, 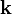 — стандартные обозначения для ортов в
— стандартные обозначения для ортов в 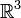 : они рассматриваются как воображаемые кватернионы.
: они рассматриваются как воображаемые кватернионы.
Заметим, что соотношения через векторное произведение между 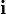 ,
, 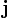 и
и 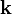 соответствуют правилам умножения для кватернионов i, j и k. Если представить вектор
соответствуют правилам умножения для кватернионов i, j и k. Если представить вектор 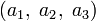 как кватернион a1i + a2j + a3k, то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.
как кватернион a1i + a2j + a3k, то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.
Преобразование к матричной форме
Векторное произведение двух векторов можно записать как произведение кососимметрической матрицы и вектора:
где
Пусть 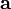 равен векторному произведению:
равен векторному произведению:
тогда
Такая форма записи позволяет обобщить векторное произведение на высшие размерности, представляя псевдовекторы (угловая скорость, индукция и т. п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь n(n − 1) / 2 независимых компонент в n-мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.
С такой формой записи также зачастую проще работать (например, в en:epipolar geometry).
Из общих свойств векторного произведения следует, что
![[\mathbf{a}]_{\times} \, \mathbf{a} = \mathbf{0}](//rc74.ru/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) и
и ![\mathbf{a}^{T} \, [\mathbf{a}]_{\times} = \mathbf{0}](//rc74.ru/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
а так как ![[\mathbf{a}]_{\times}](/800/600/https/brokgauz.academic.ru/pictures/wiki/files/100/d00b55ad4c7fdd0a1f2a424e0ca572ef.png) кососимметрична, то
кососимметрична, то
В такой форме записи легко доказывается тождество Лагранжа (правило «бац минус цаб»).
Распространение на матрицы
В 3-хмерном случае можно определить векторное произведение матриц и произведение матрицы на вектор. Это делает очевидным указанный выше изоморфизм и позволяет упростить многие выкладки. Представим матрицу A как столбец векторов, тогда
Умножение матрицы на вектор слева определяется аналогично, если представить A как строку векторов. Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот. Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например (A — матрица, 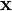 ,
, 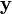 — векторы):
— векторы):
После этого можно изменить форму записи для векторного произведения:
E — единичная матрица. Отсюда очевидны существование и вид матрицы, соответствующей векторному умножению на вектор слева. Аналогично можно получить выражение для матрицы умножения на вектор справа. Распространяя операции над векторами на матрицы покомпонентно, представляя их как «векторы из векторов», стандартные соотношения для векторов легко обобщаются на матрицы. Например, теорема Стокса в  примет вид:
примет вид:
где ротор матрицы A вычисляется как векторное произведение матрицы A на оператор Гамильтона слева. В этих обозначениях очень легко доказать, например, следующие формы теоремы Стокса:
Размерности, не равные трём
Пусть D — размерность пространства.
Векторное произведение, обладающее всеми свойствами обычного трёхмерного векторного произведения, то есть бинарное билинейное антисимметричное невырожденное отображение 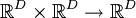 , можно ввести только для размерности 3.
, можно ввести только для размерности 3.
Однако есть простое обобщение на остальные натуральные размерности, начиная с 3, а если нужно — и на размерность 2 (последнее, правда, сравнительно специфическим образом). Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора (D − 1) векторов-сомножителей. Вполне аналогично смешанному произведению, естественно обобщаемому в D-мерном пространстве на операцию с D сомножителями. Используя символ Леви-Чивиты  с D индексами, можно явно записать такое (D − 1)-валентное векторное произведение как
с D индексами, можно явно записать такое (D − 1)-валентное векторное произведение как
Такое обобщение дает гиперплощадь размерности (D − 1).
Если нужно ввести операцию именно для двух сомножителей, имеющую геометрический смысл, предельно близкий к смыслу векторного произведения (то есть представляющую ориентированную площадь), то результат уже не будет вектором, так как при D < > 3 не найдется единственной, однозначно определённой нормали к двумерной плоскости, натянутой на множители. Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:
 .
.
Эта конструкция называется внешним произведением.
Для двумерного случая эта операция называется псевдоскалярным произведением, так как получающееся пространство одномерно и результат можно отождествить с псевдоскаляром.
Алгебра Ли векторов
Векторное произведение вводит на 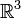 структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам — антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению
структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам — антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению  с касательной алгеброй Ли so(3) к группе Ли SO(3) ортогональных линейных преобразований трёхмерного пространства.
с касательной алгеброй Ли so(3) к группе Ли SO(3) ортогональных линейных преобразований трёхмерного пространства.
См. также
Произведения векторов
Другое
Ссылки
Литература
- Кочин Н. Е. Введение в векторный и тензорный анализ.
Wikimedia Foundation. 2010.
Что такое векторное произведение векторов и как его найти?
 Не менее полезное и широко используемое в геометрии, чем скалярное произведение векторов есть векторное произведение. Так что, и на эту тему я решил написать небольшую онлайн программку, которая будет вам помогать с вычислениями и в понимании формул.
Не менее полезное и широко используемое в геометрии, чем скалярное произведение векторов есть векторное произведение. Так что, и на эту тему я решил написать небольшую онлайн программку, которая будет вам помогать с вычислениями и в понимании формул.
Также хочу вам немножко рассказать, что такое векторное произведение и где оно используется? Векторным произведением двух векторов, является вектор, длина которого равна произведению длин этих векторов на синус угла между ними, также этот вектор должен быть перпендикулярен к плоскости, в которой лежат два других вектора, и все они должны образовывать правый репер. То есть тройка векторов {a, b, c} будет правой, если посмотреть с конца вектора c на плоскость векторов a и b, то движение от a к b по меньшему углу должна происходить против часовой стрелки.
Очень интересны и геометрические свойства векторного произведения:
- Первое сформулируем теоремой:
Векторное произведение двух векторов равно нулю тогда и только тогда, когда угол между ними ноль, то есть когда эти векторы коллинеарные.
Основываясь на эту теорему, и доводят, что векторы или прямые коллинеарные.
- Второе – это то, что длина векторного произведения равна площади параллелограмма, построенного на перемножаемых векторах. Именно это часто используют для вычисления площади параллелограмма, треугольника и некоторых других геометрических фигур.
Сама программа вычисляет двумя способами длину векторного произведения, в первом случае по определению, а во втором для ортонормированного базиса. В последнем, она также находит и координаты вектора векторного произведения. Как всегда, выводятся все формулы и матрицы с пошаговыми шагами решения. Вам надо только выбрать подходящий для вас вариант и ввести данные вашей задачи и через секунду перед вами полное решение.
Пользуйтесь программкой и вы сможете не просто проверить своё решение, но и увидеть, где вы допустили ошибку, если она будет. Всё расписано до мельчайших подробностей.
Материалы по теме:
Поделиться с друзьями:
 Загрузка…
Загрузка…векторное произведение — это… Что такое векторное произведение?
- векторное произведение
1) Engineering: external product, vectorial product
2) Construction: vector multiplication
3) Mathematics: cross product, vector product
4) Mechanics: outer product
Универсальный русско-английский словарь. Академик.ру. 2011.
- векторное прерывание
- векторное произведения
Смотреть что такое «векторное произведение» в других словарях:
Векторное произведение — в трёхмерном пространстве. Векторное произведение это псевдовектор, перпендикулярный плоскости, построенной по двум … Википедия
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ — вектора a на вектор b вектор p=ВЕКТОРНОЕ ПРОСТРАНСТВО математическое понятие, обобщающее понятие совокупности всех векторов 3 мерного пространства на случай произвольного числа измерений … Большой Энциклопедический словарь
векторное произведение — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN cross productvector product … Справочник технического переводчика
векторное произведение — вектора а на вектор b, вектор р = [а, b], или а×b, равный по длине площади параллелограмма, построенного на векторах а и b, перпендикулярный плоскости этого параллелограмма; направление векторного произведения р зависит от выбора координатной… … Энциклопедический словарь
векторное произведение — vektorinė sandauga statusas T sritis fizika atitikmenys: angl. outer product; vector product; vectorial product vok. Kreuzprodukt, n; äußeres Produkt, n; vektorielles Produkt, n; Vektorprodukt, n rus. векторное произведение, n; внешнее… … Fizikos terminų žodynas
векторное произведение — vektorinė sandauga statusas T sritis automatika atitikmenys: angl. cross product; vector product; vectorial product vok. Kreuzprodukt, n; äußeres Produkt, n; Vektorprodukt, n rus. векторное произведение, n pranc. produit vectoriel, m … Automatikos terminų žodynas
Векторное произведение — вектора а на вектор b вектор, обозначаемый [а, b] и определяемый так: 1) длина вектора [а, b] равна произведению длин векторов а и b на синус угла φ между ними (берётся тот из двух углов между а и b, который не превосходит π), 2) вектор… … Большая советская энциклопедия
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ — вектора . навек т о р вектор , обозначаемый символом или и удовлетворяющий условиям: длина вектора равна произведению длин векторов на синус угла, между ними, т. е. вектор … Математическая энциклопедия
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ — вектора а на вектор b, вектор р = [а, b], или aхb, равный по длине площади параллелограмма, построенного на векторах a и b, перпендикулярный плоскости этого параллелограмма; направление В. п. р зависит от выбора координатной системы i, j, k; из… … Естествознание. Энциклопедический словарь
Векторное произведение векторов — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства … Википедия
Векторное произведение в семимерном пространстве — В математике, векторное произведение в семимерном пространстве билинейная операция над векторами в семимерном пространстве. Оно назначает для любых двух векторов a, b в 7 вектор a × b 7. В семи измерениях существует и векторное произведение с… … Википедия
векторное произведение — это… Что такое векторное произведение?
- векторное произведение
векторное произведение
—
[Я.Н.Лугинский, М.С.Фези-Жилинская, Ю.С.Кабиров. Англо-русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.]Тематики
- электротехника, основные понятия
EN
- cross product
- vector product
Справочник технического переводчика. – Интент. 2009-2013.
- векторное прерывание
- векторное пространство
Смотреть что такое «векторное произведение» в других словарях:
Векторное произведение — в трёхмерном пространстве. Векторное произведение это псевдовектор, перпендикулярный плоскости, построенной по двум … Википедия
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ — вектора a на вектор b вектор p=ВЕКТОРНОЕ ПРОСТРАНСТВО математическое понятие, обобщающее понятие совокупности всех векторов 3 мерного пространства на случай произвольного числа измерений … Большой Энциклопедический словарь
векторное произведение — вектора а на вектор b, вектор р = [а, b], или а×b, равный по длине площади параллелограмма, построенного на векторах а и b, перпендикулярный плоскости этого параллелограмма; направление векторного произведения р зависит от выбора координатной… … Энциклопедический словарь
векторное произведение — vektorinė sandauga statusas T sritis fizika atitikmenys: angl. outer product; vector product; vectorial product vok. Kreuzprodukt, n; äußeres Produkt, n; vektorielles Produkt, n; Vektorprodukt, n rus. векторное произведение, n; внешнее… … Fizikos terminų žodynas
векторное произведение — vektorinė sandauga statusas T sritis automatika atitikmenys: angl. cross product; vector product; vectorial product vok. Kreuzprodukt, n; äußeres Produkt, n; Vektorprodukt, n rus. векторное произведение, n pranc. produit vectoriel, m … Automatikos terminų žodynas
Векторное произведение — вектора а на вектор b вектор, обозначаемый [а, b] и определяемый так: 1) длина вектора [а, b] равна произведению длин векторов а и b на синус угла φ между ними (берётся тот из двух углов между а и b, который не превосходит π), 2) вектор… … Большая советская энциклопедия
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ — вектора . навек т о р вектор , обозначаемый символом или и удовлетворяющий условиям: длина вектора равна произведению длин векторов на синус угла, между ними, т. е. вектор … Математическая энциклопедия
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ — вектора а на вектор b, вектор р = [а, b], или aхb, равный по длине площади параллелограмма, построенного на векторах a и b, перпендикулярный плоскости этого параллелограмма; направление В. п. р зависит от выбора координатной системы i, j, k; из… … Естествознание. Энциклопедический словарь
Векторное произведение векторов — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства … Википедия
Векторное произведение в семимерном пространстве — В математике, векторное произведение в семимерном пространстве билинейная операция над векторами в семимерном пространстве. Оно назначает для любых двух векторов a, b в 7 вектор a × b 7. В семи измерениях существует и векторное произведение с… … Википедия


![\left[ \vec{a}, \vec{b}, \vec{c} \right]](/800/600/https/dal.academic.ru/pictures/wiki/files/48/0e6a64ecd01d00a9fa21e04ac4c4f468.png) векторов
векторов 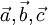 — векторное произведение вектора
— векторное произведение вектора 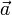 на векторное произведение векторов
на векторное произведение векторов 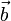 и
и 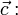
![\left[ \vec{a}, \vec{b}, \vec{c}\right] = \left[\vec{a}, \left[\vec{b}, \vec{c}\right]\right].](/800/600/https/dal.academic.ru/pictures/wiki/files/98/b4a0f2d97f92bdbf8128b5c059f22670.png)
![\left[ \vec{a}, \vec{b}, \vec{c} \right] = \vec{b} \left( \vec{a} \cdot \vec{c} \right) - \vec{c} \left( \vec{a} \cdot \vec{b} \right),](/800/600/https/dal.academic.ru/pictures/wiki/files/49/1c5e6e3f9a366e3bddb24a5f5e454705.png)
![\left[ \vec{a}, \vec{b}, \vec{c} \right]+\left[ \vec{b}, \vec{c}, \vec{a} \right]+\left[ \vec{c}, \vec{a}, \vec{b} \right] = 0,](/800/600/https/dal.academic.ru/pictures/wiki/files/52/4ca42dc4ee2810c9d98baf7332ebc7df.png)
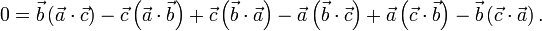
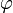 ; между ними
; между ними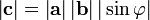
![\mathbf c = \left[ \mathbf a \mathbf b \right] = \left[ \mathbf a,\; \mathbf b \right] = \mathbf a \times \mathbf b](/800/600/https/brokgauz.academic.ru/pictures/wiki/files/101/ed09d9154faf68b1a7783004b4cbc46c.png)
![[ \mathbf a,\; \mathbf b ] = S\, \mathbf e](/800/600/https/brokgauz.academic.ru/pictures/wiki/files/50/28395f1def81662c027a8cbd7f6f8aa9.png)
![\left[ \mathbf a,\; \mathbf c \right] = \mathrm{Pr}_{ \mathbf e }\, \mathbf a \left](/800/600/https/brokgauz.academic.ru/pictures/wiki/files/48/04002beabcb294e180266aa94180d9b9.png)
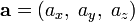
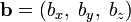
![[ \mathbf a,\; \mathbf b ] = (a_y b_z - a_z b_y,\; a_z b_x - a_x b_z,\; a_x b_y - a_y b_x).](/800/600/https/brokgauz.academic.ru/pictures/wiki/files/52/4c3df91a2cfe53408b07f333a175565a.png)
![[ \mathbf a,\; \mathbf b ] = \begin{vmatrix} \mathbf i &amp; \mathbf j &amp; \mathbf k \\ a_x &amp; a_y &amp; a_z \\ b_x &amp; b_y &amp; b_z \end{vmatrix}](/800/600/https/brokgauz.academic.ru/pictures/wiki/files/49/16ea255c911b3e4c07cc2adae3d7626e.png)
![[ \mathbf a,\; \mathbf b ]_i = \sum_{j,k=1}^3 \varepsilon_{i j k} a_j b_k,](/800/600/https/brokgauz.academic.ru/pictures/wiki/files/55/7c8e6ab7e9c7e3607e920bb75caae299.png)
![\mathbf{a} \times \mathbf{b} = [\mathbf{a}]_{\times} \mathbf{b} = \begin{bmatrix}\,0&amp;\!-a_3&amp;\,\,a_2\\ \,\,a_3&amp;0&amp;\!-a_1\\-a_2&amp;\,\,a_1&amp;\,0\end{bmatrix}\begin{bmatrix}b_1\\b_2\\b_3\end{bmatrix}](/800/600/https/brokgauz.academic.ru/pictures/wiki/files/98/bb0828317b64e54d924e3d9dabb54234.png)
![\mathbf{b} \times \mathbf{a} = \mathbf{b}^T [\mathbf{a}]_{\times} = \begin{bmatrix}b_1&amp;b_2&amp;b_3\end{bmatrix}\begin{bmatrix}\,0&amp;\!-a_3&amp;\,\,\,a_2\\\,\,\,a_3&amp;\,0&amp;\!-a_1\\-a_2&amp;\,\,a_1&amp;\,0\end{bmatrix}](/800/600/https/brokgauz.academic.ru/pictures/wiki/files/97/a1999aed4c7add8bb1d9f291beb9a7e9.png)
![[\mathbf{a}]_{\times} \stackrel{\rm def}{=} \begin{bmatrix}\,\,0&amp;\!-a_3&amp;\,\,\,a_2\\\,\,\,a_3&amp;0&amp;\!-a_1\\\!-a_2&amp;\,\,a_1&amp;\,\,0\end{bmatrix}](/800/600/https/brokgauz.academic.ru/pictures/wiki/files/52/42367ea2bfc38aaf3870e9a3aba428bb.png)
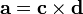
![[\mathbf{a}]_{\times} = (\mathbf{c}\mathbf{d}^T)^T - \mathbf{c}\mathbf{d}^T.](/800/600/https/brokgauz.academic.ru/pictures/wiki/files/53/55d46afc14c256de89aa56b17ef38491.png)
![[\mathbf{a}]_{\times} \, \mathbf{a} = \mathbf{0}](/800/600/https/brokgauz.academic.ru/pictures/wiki/files/98/b00e919750be3b08a60e4757f3cf9cf9.png) и
и ![\mathbf{a}^{T} \, [\mathbf{a}]_{\times} = \mathbf{0}](/800/600/https/brokgauz.academic.ru/pictures/wiki/files/55/762d1d364c16664eff7d042f99842e70.png)
![\mathbf{b}^{T} \, [\mathbf{a}]_{\times} \, \mathbf{b} = 0.](/800/600/https/brokgauz.academic.ru/pictures/wiki/files/98/b0e7a57333b3ebbdf3c81c827152e5fa.png)
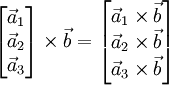
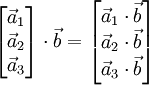
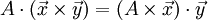
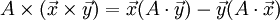
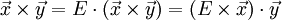
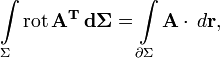
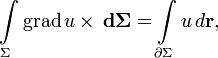
![\int\limits_{\Sigma} \left[ \mathbf{d\Sigma}; \left[ \nabla; \vec a \right] \right] = \int\limits_{\partial\Sigma} \vec a \times d \mathbf{r}.](/800/600/https/brokgauz.academic.ru/pictures/wiki/files/53/552f7432c2a90d787f641f23287017c2.png)
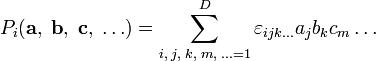
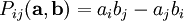 .
.