Что значит реактивное сопротивление — Значения слов

Раздел очень прост в использовании. В предложенное поле достаточно ввести нужное слово, и мы вам выдадим список его значений. Хочется отметить, что наш сайт предоставляет данные из разных источников – энциклопедического, толкового, словообразовательного словарей. Также здесь можно познакомиться с примерами употребления введенного вами слова.

Энциклопедический словарь, 1998 г.

реактивное сопротивление

величина, характеризующая сопротивление, оказываемое переменному току электрической емкостью и индуктивностью цепи (ее участка). Реактивное сопротивление синусоидальному току при последовательном соединении индуктивного и емкостного элементов цепи равно x = ?L — 1/?C, где ? угловая частота, L и C — индуктивность и емкость. Измеряется в омах.

Википедия

Реактивное сопротивление

Реакти́вное сопротивле́ние — электрическое сопротивление , обусловленное передачей энергии переменным током электрическому или магнитному полю .

Реактивное сопротивление определяет мнимую часть полного сопротивления ( импеданса ):

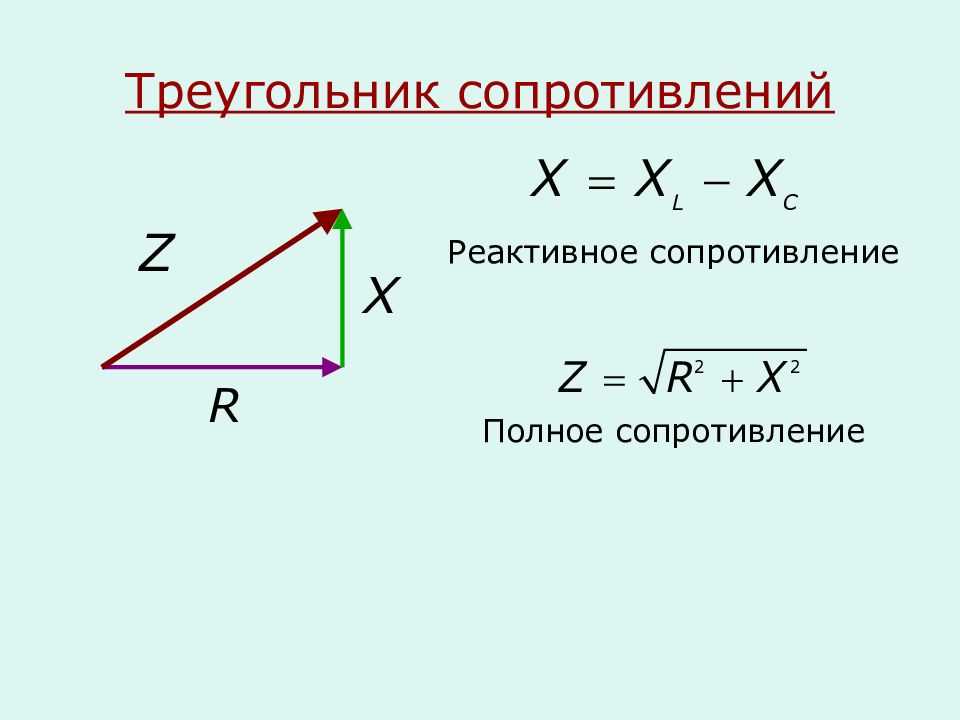
Z = R + jX, где Z — полное сопротивление или импеданс , R — величина активного сопротивления , X — величина реактивного сопротивления, j — мнимая единица .

В зависимости от знака величины X какого-либо элемента электрической цепи говорят о трёх случаях:

• X > 0 — элемент проявляет свойства индуктивности .
• X = 0 — элемент имеет чисто активное сопротивление .
• X  — элемент проявляет ёмкостные свойства.

Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений:

X = X − X

Индуктивное сопротивление (X) обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи. Изменение тока и, как следствие, изменение его магнитного поля вызывает препятствующую изменению этого тока ЭДС самоиндукции. Величина индуктивного сопротивления зависит от индуктивности L элемента и частоты ω протекающего тока:

X = ωL = 2πfL

Ёмкостное сопротивление (X). Величина ёмкостного сопротивления зависит от ёмкости элемента C и также частоты протекающего тока f:

$X_C = \frac {1} {\omega C} = \frac {1} {2\pi f C}$

Здесь ω — циклическая частота , равная 2πf.

Реактивное сопротивление (психология)

Реактивное сопротивление — мотивационное состояние, возникающее в ситуации, когда какое-либо внешнее условие ограничивает свободу или создает угрозу ограничения проявлений индивида. Главная задача такого поведения — восстановление утраченной или ограниченной свободы.

Реактивное сопротивление возникает, когда на человека оказывается сильное давление с целью изменить его поведение, точку зрения, отношение к чему-либо. Обязательным условием для возникновения данного состояния является осознание факта оказываемого воздействия. Результатом обычно становится выбор индивидом запретного или ограниченного варианта, а также повышение его устойчивости к убеждениям.

Данный феномен иногда используется некоторыми специалистами для разного рода манипуляций .

В качестве примера можно привести человека, регулярно и сознательно нарушающего общественный порядок, с целью оказывать сопротивление власти, которая запрещает этот тип действий на законодательном уровне.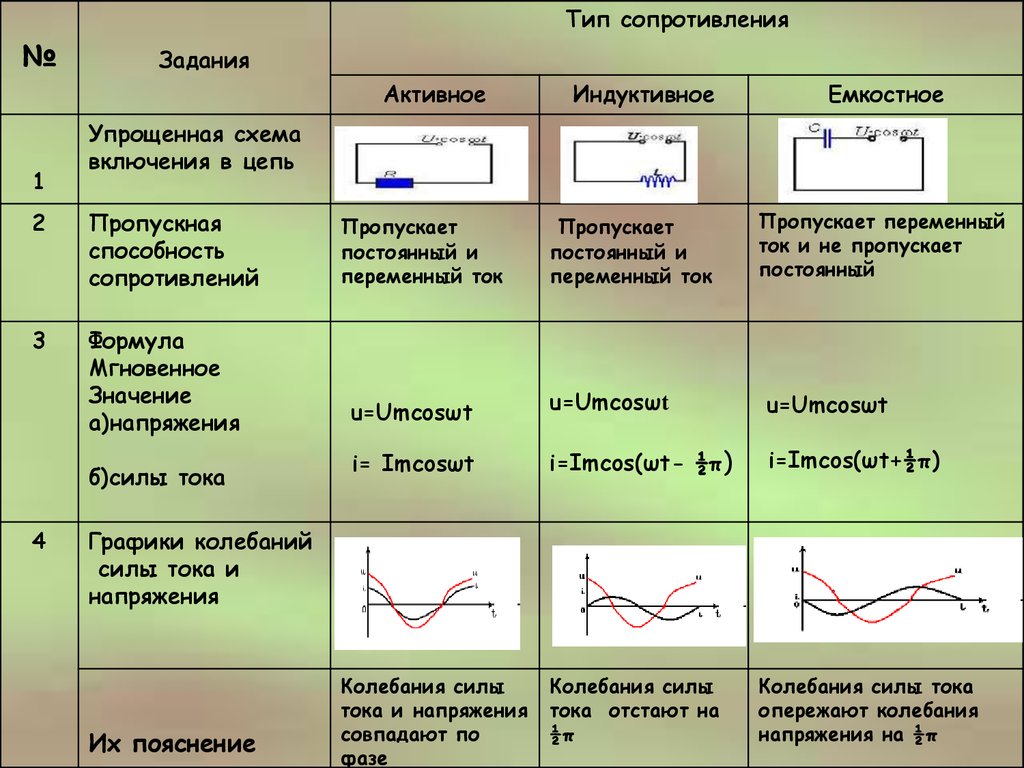

Причём этому человеку не важны выгоды, которые такое поведение может ему принести, а также он не задумывается о личных ресурсах, которые он должен будет затратить на это дело.

Сам термин «реактивное сопротивление» был заимствован из физики (см. Реактивное сопротивление ).

РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ

        1.6. Реактивное сопротивление.

    Если через обмотку катушки индуктивности с магнитопроводом (сердечником) пропустить переменный ток, изменяющийся по синусоидальному закону simt (см. рис. 3), возникнет, как мы говорили, магнитный поток, намагничивающий магнитопровод. Ток и магнитный поток в магнитопроводе будут также переменными и возбудят в обмотке ЭДС индукции. Она равна напряжению на выводах катушки, и в то же время пропорциональна скорости изменения магнитного потока. В итоге напряжение будет сдвинуто по фазе на -90° относительно тока.

Это значит, что ток отстает по фазе на 90° от напряжения.
    Ток, протекающий через катушку, называется реактивным, и в отличие от тока через активное сопротивление, он не приводит к расходованию мощности. Кроме того, напряжение на катушке при фиксированном токе пропорционально частоте, следовательно, сопротивление катушки возрастает с частотой. Напряжение на катушке может быть рассчитано по закону Ома, в который в качестве сопротивления надо подставить индуктивное сопротивление катушки: X _L = jL = j2fL (индуктивное сопротивление). Перед обозначением реактивного сопротивления ставят символ j, в математике обозначающий мнимую величину, равную квадратному корню из -1.
    Посмотрим теперь, что получится, если к пластинам конденсатора приложить переменное напряжение, изменяющееся по синусоидальному закону simt. Через конденсатор потечет переменный ток, вызванный тем, что пластины конденсатора должны будут перезаряжаться столько раз в секунду, сколько раз ток изменяет свое направление. Заряд на пластинах прямо пропорционален приложенному напряжению (q = CU), а ток пропорционален скорости изменения заряда (I = dq/dt).
    Таким образом, ток через конденсатор также реактивный, но опережает напряжение на 90°. Ток пропорционален частоте, следовательно, емкостное сопротивление конденсатора обратно пропорционально частоте: Х _с = 1/jС = -j/С (емкостное сопротивление).
    Зависимости реактивных сопротивлений от частоты показаны на рис. 6,а. В реальных электрических цепях встречаются как реактивные, индуктивные и емкостные, так и активные сопротивления. Вместе они образуют комплексные, или полные сопротивления, обозначаемые буквой Z и математически представляющие собой комплексные числа, содержащие действительную R и мнимую X части: Z = R + jX (полное сопротивление).

Рис. 6

    Как складываются активные сопротивления при последовательном и параллельном соединении, мы уже изучали (рис. 2,г), и теперь нам осталось сказать, что и полные сопротивления складываются точно так же, только не надо забывать про знак реактивного сопротивления и символ j.
    Будет очень полезно, если вы немного потренируетесь и попробуете написать полное сопротивление цепей, содержащих различным образом включенные катушки индуктивности, конденсаторы и резисторы (рис. 6, б-д). Очень скоро вы убедитесь, что одно и то же полное сопротивление на одной, заданной частоте могут иметь цепи, выполненные по-разному, и это открывает возможность их преобразования.

    Например, цепь из последовательно соединенных резистора и конденсатора можно заменить цепью, где те же элементы включены параллельно, но, разумеется, номиналы у них будут другими. Также легко убедиться, что при последовательном соединении двух катушек их индуктивности складываются, а вот емкости складываются при параллельном соединении конденсаторов. Ну а теперь перейдем к обещанному рассказу о трансформаторах.

---

Радио, 1998

Реакции резистентности проксимальных отделов артериальных сосудов, артериол и вен при реактивной гиперемии скелетных мышц и лежащие в их основе регуляторные механизмы

. 1990 г., август; 139 (4): 535-50.

doi: 10.1111/j.1748-1716.1990.tb08957.x.

Дж. Бьорнберг ¹ , У Альберт, С. Мелландер

принадлежность

• ¹ Кафедра физиологии и биофизики Лундского университета, Швеция.

• PMID: 2248033
• DOI: 10. 1111/j.1748-1716.1990.tb08957.x

Дж. Бьорнберг и соавт. Acta Physiol Scand. 1990 августа

. 1990 г., август; 139 (4): 535-50.

doi: 10.1111/j.1748-1716.1990.tb08957.x.

Авторы

Дж. Бьорнберг ¹ , У Альберт, С Мелландер

принадлежность

• ¹ Кафедра физиологии и биофизики Лундского университета, Швеция.

• PMID: 2248033
• DOI: 10.1111/j.1748-1716. 1990.tb08957.x

Абстрактный

Реактивную реакцию гиперемии скелетных мышц кошек на окклюзию артерий в течение 2-120 с анализировали в отношении амплитуды, продолжительности, «избыточного кровотока» и места дилататорного действия вдоль сосудистого русла. Последнее было оценено с помощью новой методики для всего органа, позволяющей непрерывно регистрировать сегментарное сопротивление в артериальных сосудах более 25 микрон, артериолах менее 25 микрон и венах. Пиковая амплитуда, продолжительность и избыточный поток увеличивались с увеличением длины окклюзии, при этом избыточный поток был линейно связан с длиной окклюзии. Участок активной дилатации преимущественно ограничивался артериолами менее 25 микрон, в которых полное расслабление наблюдалось уже после 20-секундной окклюзии, хотя продолжительность ответа продолжала увеличиваться при более длительных окклюзиях. Постепенное, но менее выраженное расширение происходило в артериальных сосудах размером более 25 микрон и в венах, при этом первые демонстрировали 63%-ное торможение тонуса как максимальный ответ при 120-секундной окклюзии. Фаза восстановления характеризовалась ярко выраженным активным констрикторным компонентом, по-видимому, защищающим капилляры от избыточной нагрузки давлением при освобождении артериальной окклюзии, но это сужение ослаблялось при длительных окклюзиях, тем самым пролонгируя реакцию гиперемии. Роль миогенных регуляторных механизмов в ответах оценивали по наблюдаемым сегментарным резистентным реакциям на избирательно применяемые трансмуральные стимулы давления, подобные тем, которые вызываются артериальной окклюзией/расслаблением. Сделан вывод, что только миогенные механизмы могут объяснить амплитуду реакции реактивной гиперемии при коротких (до 30 с) окклюзиях. Метаболические механизмы, по-видимому, ответственны за дальнейшее расслабление проксимальных артериальных сосудов при более длительных окклюзиях, а также за увеличение продолжительности реакции гиперемии при окклюзиях более 10 с. Блокада образования оксида азота (эндотелиальный релаксирующий фактор), по-видимому, не влияла на реактивную реакцию гиперемии.

Похожие статьи

• Метаболический контроль крупных артериальных сосудов сопротивления, артериол и вен в скелетных мышцах кошек во время физических упражнений.

  Бьёрнберг Дж., Масперс М., Мелландер С. Бьёрнберг Дж. и соавт. Acta Physiol Scand. 1989 г., февраль; 135 (2): 83–94. doi: 10.1111/j.1748-1716.1989.tb08555.x. Acta Physiol Scand. 1989. PMID: 2923003

• Миогенная сосудистая регуляция в скелетных мышцах in vivo не зависит от эндотелиального оксида азота.

  Экелунд У., Бьорнберг Дж., Гранде П.О., Альберт У., Мелландер С. Экелунд У и др. Acta Physiol Scand. 1992 г., февраль; 144(2):199-207. doi: 10.1111/j.1748-1716.1992.tb09286.x. Acta Physiol Scand. 1992. PMID: 1575052

• Роль эндотелиального оксида азота в регуляции тонуса крупных артериальных резистивных сосудов, артериол и вен в скелетных мышцах кошек.

  Экелунд У., Мелландер С. Экелунд У и др. Acta Physiol Scand. 1990 ноябрь; 140(3):301-9. doi: 10.1111/j.1748-1716.1990.tb09004.x. Acta Physiol Scand. 1990. PMID: 2082699

• Регуляция коронарного кровотока при физической нагрузке.

  Duncker DJ, Bache RJ. Дункер Д.Дж. и др. Physiol Rev. 2008 г., июль; 88 (3): 1009-86. doi: 10.1152/physrev.00045.2006. Физиол Ред. 2008. PMID: 18626066 Обзор.

• Медиаторы реактивной гиперемии.

  Монсуэз Дж.Дж. Монсуэс Дж. Arch Mal Coeur Vaiss. 2001 г., июнь; 94 (6): 591-9. Arch Mal Coeur Vaiss. 2001. PMID: 11480157 Обзор. Французский.

Посмотреть все похожие статьи

Цитируется

• Влияние кофеина на кожную постокклюзионную реактивную гиперемию.

  Мелик З., Принси Т., Гриль В., Джанкар К. Мелик З. и др. ПЛОС Один. 8 апреля 2019 г .; 14 (4): e0214919. doi: 10.1371/journal.pone.0214919. Электронная коллекция 2019. ПЛОС Один. 2019. PMID: 30958851 Бесплатная статья ЧВК. Клиническое испытание.

• Позиционные различия в реактивной гиперемии дают представление о начальной фазе гиперемии при физической нагрузке.

  Джасперс Д.Л., Шумейкер Д.К., Грей Э.Дж., Клиффорд П.С. Джасперс Дж.Л. и соавт. J Appl Physiol (1985). 1 сентября 2015 г .; 119 (5): 569–75. doi: 10.1152/japplphysiol.01253.2013. Epub 2015 2 июля. J Appl Physiol (1985). 2015. PMID: 26139221 Бесплатная статья ЧВК.

• Сосудистые эффекты пищевых конечных продуктов повышенного гликирования.

  Штирбан А., Чепе Д. Стирбан А. и др. Int J Endocrinol. 2015;2015:836498. дои: 10.1155/2015/836498. Epub 2015 18 мая. Int J Endocrinol. 2015. PMID: 26089897 Бесплатная статья ЧВК. Обзор.

• Зависимость реактивной гиперемии кожи от циклооксигеназы и синтазы оксида азота у человека.

  Медоу М.С., Танеджа И., Стюарт Дж.М. Медоу М.С. и соавт. Am J Physiol Heart Circ Physiol. 2007 г., июль; 293(1):h525-32. doi: 10.1152/ajpheart.01217.2006. Epub 2007 16 марта. Am J Physiol Heart Circ Physiol. 2007. PMID: 17369458 Бесплатная статья ЧВК.

• Влияние метилового эфира NG-нитро-L-аргинина на базальный кровоток и эндотелийзависимую вазодилатацию в задних конечностях собак.

  Уайт Д. Г., Дрю Г.М., Гурден Дж.М., Пенни Д.М., Роуч А.Г., Уоттс И.С. Уайт Д.Г. и др. Бр Дж. Фармакол. 1993 март; 108 (3): 763-8. doi: 10.1111/j.1476-5381.1993.tb12875.x. Бр Дж. Фармакол. 1993. PMID: 8467362 Бесплатная статья ЧВК.

Просмотреть все статьи «Цитируется по»

Типы публикаций

термины MeSH

Цепь серии RC (коэффициент мощности, активная и реактивная мощность)

Что касается цепи серии RC, в этой статье поясняется приведенная ниже информация.

• Коэффициент мощности \({\cos}{\theta}\) цепи серии RC
• Активная мощность \(P\), реактивная мощность \(Q\) и полная мощность \(S\) цепи Цепь серии RC

На рисунке выше показана последовательная RC-цепь с резистором \(R\) и конденсатором \(C\), соединенными последовательно.

В качестве примера, параметры последовательной цепи RC следующие.

• Напряжение питания: \({\dot{V}}=200{\;}{\mathrm{[V]}}\)
• Частота напряжения питания: \(f=60{\;}{ \mathrm{[Гц]}}\)
• Значение сопротивления резистора: \(R=50\sqrt{3}{\;}{\mathrm{[{\Omega}]}}\)
• Емкость конденсатора : \(C=53{\;}{\mathrm{[мкФ]}}\)

Коэффициент мощности \({\cos}{\theta}\), активная мощность \(P\), реактивная мощность \(Q\) и полная мощность \(S\) последовательной цепи RC могут быть полученный с помощью следующей процедуры (шаги 1-4).

Процедура

• Рассчитайте величину \(Z\) импеданса последовательной RC-цепи
• Рассчитайте величину \(I\) тока, протекающего в последовательной RC-цепи
• Рассчитайте коэффициент мощности \( {\cos}{\theta}\) цепи серии RC
• Рассчитайте активную мощность \(P\), реактивную мощность \(Q\) и полную мощность \(S\) последовательной RC-цепи

Теперь мы опишем каждую процедуру по очереди.

Дополнение

В цепи переменного тока существует три типа мощности: активная мощность \(P\), реактивная мощность \(Q\) и полная мощность \(S\).

• Активная мощность \(P\)
  • Это мощность, потребляемая резистором \(R\), также называемая потребляемой мощностью. Единица измерения [Вт].
• Реактивная мощность \(Q\)
  • Это мощность, не потребляемая резистором \(R\). Мощность, которую индуктор или конденсатор накапливает или выделяет, называется реактивной мощностью. Единица измерения [вар].
• Полная мощность \(S\)
  • Мощность представляет собой сумму активной мощности \(P\) и реактивной мощности \(Q\). Единица измерения [ВА].

Рассчитать величину \(Z\) импеданса последовательной RC-цепи

Импеданс \({\dot{Z}}_R\) резистора \(R\) и импеданс \( {\dot{Z}}_C\) конденсатора \(C\) можно выразить следующими уравнениями соответственно.

\begin{eqnarray}
{\dot{Z}_R}&=&R\tag{1}\\
\\
{\dot{Z}_C}&=&-jX_C=-j\frac{1 }{{\omega}C}\tag{2}
\end{eqnarray}

, где \({\omega}\) — угловая частота, равная \(2{\pi}f\) а \(X_C\) называется емкостным реактивным сопротивлением, которое представляет собой резистивный компонент конденсатора \(C\). {-6}}\\
\\
&{\приблизительно}&50{\;}{\mathrm{[{\Omega}]}}\tag{3}
\end{eqnarray}

Импеданс \({\dot{Z}} \) последовательной цепи RC является суммой соответствующих импедансов и выглядит следующим образом.

\begin{eqnarray}
{\dot{Z}}&=&{\dot{Z}_R}+{\dot{Z}_C}\\
\\
&=&R-jX_C\\
\ \
&=&50\sqrt{3}-j50{\;}{\mathrm{[{\Omega}]}}\tag{4}
\end{eqnarray}

Величина \(Z\) импеданс последовательной цепи RC представляет собой абсолютное значение импеданса \({\dot{Z}}\) в уравнении (4). 92}\\
\\
&=&100{\;}{\mathrm{[{\Omega}]}}\tag{5}
\end{eqnarray}

Статья по теме

Вычислить величину \( I\) тока, протекающего в последовательной цепи RC

Величина \(V\) питающего напряжения является следующей величиной.

\begin{eqnarray}
V=|{\dot{V}}|=|200|=200{\;}{\mathrm{[V]}}\tag{6}
\end{eqnarray}

Из уравнений (5) и (6) величина \(I\) тока, протекающего в последовательной цепи RC, может быть получена с помощью следующего уравнения

\begin{eqnarray}
I=\frac{V}{Z}=\frac{200}{100}=2{\;}{\mathrm{[A]}}\tag{7}
\end {eqnarray}

Поскольку это последовательная цепь, «величина \(I_R\) тока через резистор \(R\)» и «величина \(I_C\) тока через конденсатор \(C \)» равны «величине \(I\) тока через последовательную цепь RC», и верна следующая формула.

\begin{eqnarray}
I=I_R=I_C=2{\;}{\mathrm{[A]}}\tag{8}
\end{eqnarray}

Таким образом, «величина \(V_R\) напряжения на резисторе \(R\)» и «величина \(V_C\) напряжения на конденсаторе \(C\)» могут быть получены с помощью следующую формулу.

\begin{eqnarray}
V_R=I_RR=2{\;}{\cdot}{\;}50\sqrt{3}=100\sqrt{3}{\;}{\mathrm{[V]} }\tag{9}\\
\\
V_C=I_CX_C=2{\;}{\cdot}{\;}50=100{\;}{\mathrm{[V]}}\tag{10}
\end{eqnarray}

Расчет коэффициента мощности \({\cos}{\theta}\) последовательной RC-цепи

Коэффициент мощности \({\cos}{\theta}\) последовательной RC-цепи цепи представляет собой отношение величины импеданса \(Z\) к сопротивлению \(R\) и может быть получено с помощью следующего уравнения

\begin{eqnarray}
{\cos}{\theta}=\frac{R}{Z}=\frac{50\sqrt{3}}{100}=\frac{\sqrt{3}}{ 2}\tag{11}
\end{eqnarray}

Supplement

\(V_R\) напряжения на резисторе \(R\)» до «величины \(V\) напряжения питания». Можно рассчитать следующее уравнение, равное уравнению (11).

\begin{eqnarray}
{\cos}{\theta}=\frac{V_R}{V}=\frac{100\sqrt{3}}{200}=\frac{\sqrt{3}}{ 2}\тег{12}
\end{eqnarray}

Рассчитать активную мощность \(P\), реактивную мощность \(Q\) и полную мощность \(S\) последовательной RC-цепи

Найдя «величину \(V\ ) напряжения источника питания», «величина \(I\) тока, протекающего в последовательной цепи RC», и «коэффициент мощности \({\cos}{\theta}\) последовательной цепи RC, «активная мощность \(P\), реактивная мощность \(Q\) и полная мощность \(S\) могут быть рассчитаны.

[Последовательная цепь RC] Расчет полной мощности \(S\) 92}{100}=400{\;}{\mathrm{[VA]}}\tag{15}

\end{eqnarray}

[Последовательная цепь RC] Расчет активной мощности \(P\)

активная мощность \(P\) может быть получена по следующему уравнению ;}{\cdot}{\;}\frac{\sqrt{3}}{2}=200\sqrt{3}{\;}{\mathrm{[W]}}\tag{16}
\end {eqnarray}

Другое решение

Поскольку эффективная мощность \(P\) — это мощность, потребляемая резистором \(R\), ее также можно получить с помощью следующего уравнения. Результаты расчета показывают, что он равен уравнению (16). 92}{50}=200{\;}{\mathrm{[var]}}\tag{21}
\end{eqnarray}

Коэффициент мощности \({\cos}{\theta}\) Последовательная цепь RC также может быть получена путем отношения «активной мощности \ (P \)» к «полной мощности \ (S \)». Расчет дает следующее уравнение, равное уравнениям (11) и (12).

\begin{eqnarray}
{\cos}{\theta}=\frac{P}{S}=\frac{200\sqrt{3}}{400}=\frac{\sqrt{3}}{ 2}\tag{22}
\end{eqnarray}

Резюме

В этой статье описана следующая информация о «схеме серии RC».

1. Коэффициент мощности \({\cos}{\theta}\) цепи серии RC
2. Активная мощность \(P\), реактивная мощность \(Q\) и полная мощность \(S\) цепи Цепь серии RC

Спасибо за внимание.

Связанная статья

В цепях переменного тока статьи, относящиеся к коэффициенту мощности \({\cos}{\theta}\), активной мощности \(P\), реактивной мощности \(Q\) и полной мощности \( S\) перечислены ниже.