1.2.Перевод чисел из одной системы счисления в другую
Рассмотрим правила перевода чисел из одной системы счисления в другую.
Для перевода шестнадцатеричного числа в двоичную систему счисления каждый символ исходного числа заменяется соответствующим четырехразрядным двоичным числом (см. таблицу). В полученном двоичном числе удаляются незначащие нули (крайние слева в целой части и крайние справа — в дробной).
Пример 1. Перевести число 7D2,E16 из шестнадцатеричной системы счисления в двоичную.
Решение:
7 D 2, E = 011111010010,1110
0111 1101 0010, 1110
Ответ: 7D2,E16 = 11111010010,1112
Для
перевода двоичного числа в шестнадцатеричную систему
счисления поступают следующим образом:
двигаясь
от десятичной запятой сначала влево,
затем
вправо, разбивают двоичное число на
группы по четыре разряда, дополняя, при
необходимости, нулями крайние левую и
правую группы.
Пример 2. Перевести число 10111110001,0012 из двоичной системы счисления в шестнадцатеричную.
Решение:
0101 1111 0001, 0010 = 5F1,2
5 F 1, 2
Ответ: 10111110001,0012 = 5F1,216
Для перевода двоичного или шестнадцатеричного числа в десятичную систему счисления достаточно представить число в виде полинома (*), подставив в него известные коэффициенты, и вычислить сумму.
Пример 3. Перевести число 11011,112 из двоичной системы счисления в десятичную.
Решение:
11011,11 = 1*24 + 1*23 + 0*22 + 1*21 + 1*2° + 1*2-1 +1*2-2 = = 16+8+0+2+1+0,5+0,25 = 27,75
Ответ: 11011,112 = 27,7510
Пример
4. Перевести
число 4A,116 из шестнадцатеричной
системы счисления в десятичную.
Перевести
число 4A,116 из шестнадцатеричной
системы счисления в десятичную.
Решение:
4А,1 = 4*161 + 10*16° + 1*16-1 = 64+10+0062,5 = 74,0625
Ответ: 4А,116 = 74,062510
Для перевода целого десятичного числа в двоичную систему счисления необходимо делить это число, а затем получаемые частные на 2 до тех пор, пока частное не станет равным 1. Последнее частное и остатки записывают в порядке, обратном их получению.
Пример 5. Перевести число 2510 из десятичной системы счисления в двоичную:
Решение:
Ответ: 2510 = 110012
Для
перевода целого десятичного числа
в шестнадцатеричную систему счисления необходимо делить
это число, а затем получаемые частные
на 16 до тех пор, пока частное не станет
меньше 16.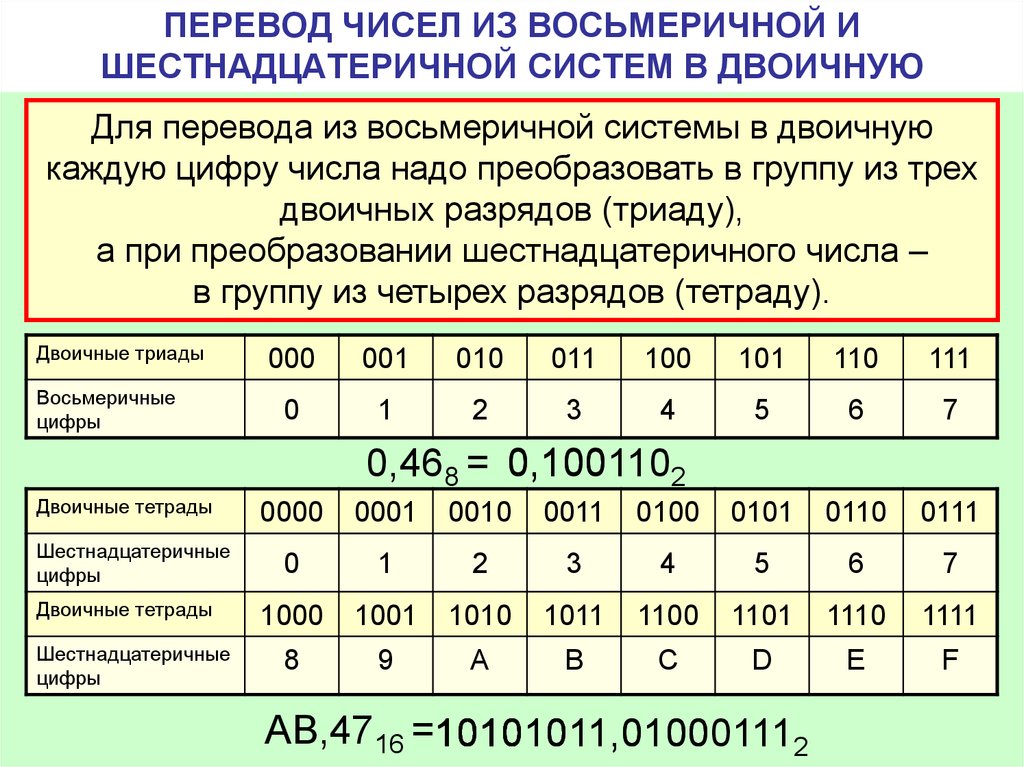
Пример 6. Перевести число 17710 из десятичной системы счисления в шестнадцатеричную:
Решение:
Ответ: 17710 = В116
Для перевода правильной десятичной дроби (целая часть равна 0) в двоичную систему счисления необходимо умножать исходную дробь и дробные части получающихся произведений на 2. Операцию умножения повторяют до тех пор, пока дробная часть произведения не станет равной 0 или не будет достигнута заданная точность (определенное количество символов). Целые части получающихся произведений дают последовательность цифр, которая является записью полученного двоичного числа.
Пример 7. Перевести правильную десятичную дробь 0,187510 в двоичную систему счисления.
Ответ: 0,187510 = 0,00112
Для
перевода правильной
десятичной дроби в шестнадцатеричную систему счисления необходимо умножать
исходную дробь и дробные части получающихся
произведений на 16.
Пример 8. Перевести правильную десятичную дробь 0,4710 из десятичной системы счисления в шестнадцатеричную с точностью до пяти знаков.
Решение.
Ответ: 0,4710 = 0,7851Е16
При переводе неправильной десятичной дроби
Пример 9. Перевести число 9,625 из десятичной системы счисления в двоичную.
Решение:
Переведем целую часть десятичного числа в двоичную систему счисления (см. пример 5):
910 = 10012
Затем
переведем
правильную
дробь (см.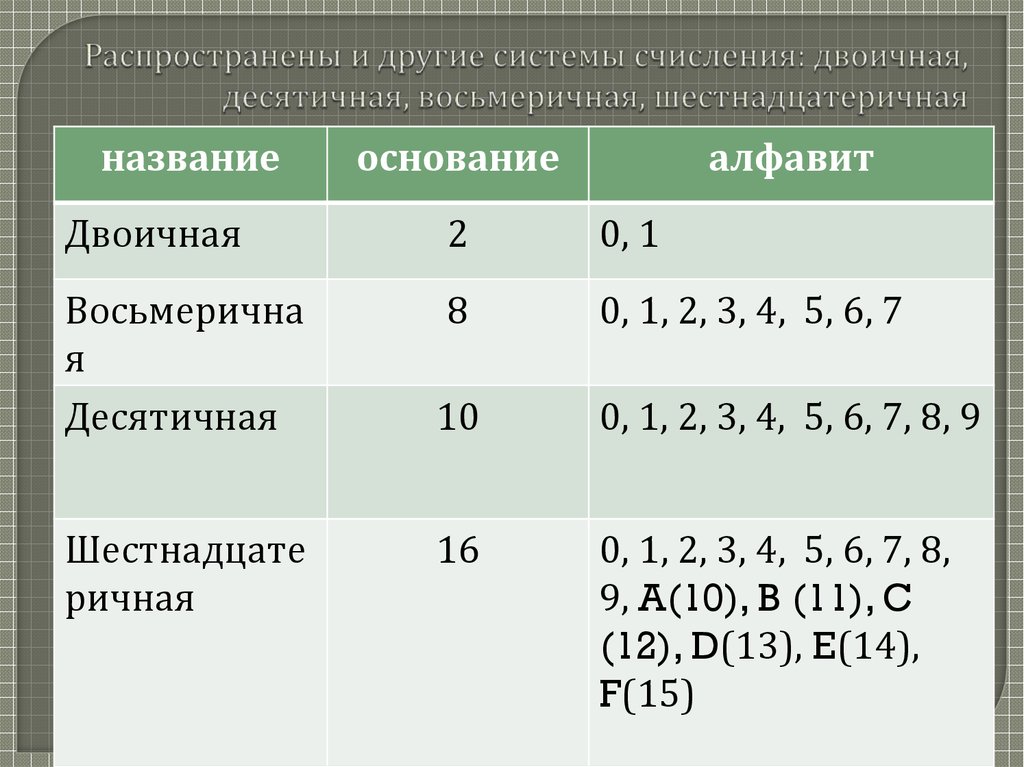 пример 7):
пример 7):
0,62510 = 0,1012
Ответ: 9,62510 = 1001,101
Пример 10. Перевести число 399,125 из десятичной системы счисления в шестнадцатеричную.
Решение:
Переведем целую часть десятичного числа в шестнадцатеричную систему счисления (см. пример 6):
39910 = 18F16
Затем переведем правильную дробь (см. пример 8):
0,12510=0,216
Ответ: 399,12510 = 18F,216
При переводе чисел из десятичной системы счисления в шестнадцатеричную и наоборот иногда применяют так называемый «двойной перевод», когда в качестве промежуточного используют двоичное число. Перевод осуществляют по схеме 10 2
Пример
11. Перевести
число 741,62510 из десятичной системы счисления в
шестнадцатеричную.
Решение:
Переведем десятичное число в двоичную систему счисления (см. пример 9):
741,62510 = 1011100101,1012
Затем переведем полученное двоичное число в шестнадцатеричную систему счисления (см. пример 2): 1011100101,1012 = 2Е5,А16
Ответ: 741,625
Пример 12. Перевести число DC,216 из шестнадцатеричной системы счисления в десятичную.
Решение:
Переведем шестнадцатеричное число в двоичную систему счисления (см. пример 1):
DC,216 = 11011100,0012
Затем полученное двоичное число переведем в десятичную систему счисления (см. пример 3):
11011100,0012 = 200,12510
Ответ: DC,216 = 200,12510
Дистанционный репетитор — онлайн-репетиторы России и зарубежья
КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?
Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!
КАК ВЫБРАТЬ
Выбрать репетитора самостоятельно
ИЛИ
Позвонить и Вам поможет специалист
8 (800) 333 58 91
* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК
ПОДАТЬ ЗАЯВКУ
Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41
Выбранные репетиторы
Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.
Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных
Вы также можете воспользоваться
расширенной формой подачи заявки
Как оплачивать и СКОЛЬКО ЭТО СТОИТ
от
800 до 5000 ₽
за 60 мин.
и зависит
ОТ ОПЫТА и
квалификации
репетитора
ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)
ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)
Оплата непосредственно репетитору, удобным для Вас способом
Почему я выбираю DisTTutor
БЫСТРЫЙ ПОДБОР
РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД
ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА
ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ
НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.
ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА
ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО
376111 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор
И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах
Владимир Александрович Кузьмин
«
Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить.
Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии.
Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype. В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!
В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!
«
Вячеслав Юрьевич Матыкин
Чулпан Равилевна Насырова
«
Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!
«
Алина Крякина
Надежда Васильевна Токарева
«
Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания. Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.
«
Эльмира Есеноманова
Ольга Александровна Мухаметзянова
«
Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.
«
Оксана Александровна
Клиентам
- Репетиторы по математике
- Репетиторы по русскому языку
- Репетиторы по химии
- Репетиторы по биологии
- Репетиторы английского языка
- Репетиторы немецкого языка
Репетиторам
- Регистрация
- Публичная оферта
- Библиотека
- Бан-лист репетиторов
Партнеры
- ChemSchool
-
PREPY.
 RU
RU
- Class
Преобразователь двоичного кода в шестнадцатеричный
Преобразователь двоичного кода в шестнадцатеричныйГлавная›Преобразование›Преобразование чисел›Двоичный код в шестнадцатеричный
От BinaryDecimalOctalHexadecimalText
Кому BinaryDecimalOctalHexadecimalText
Введите двоичное число
Шестнадцатеричный номер
Десятичное число
Группировка цифр
Расчет
Преобразователь шестнадцатеричного кода в двоичный ►
Как преобразовать двоичный код в шестнадцатеричный
Преобразовать каждые 4 двоичных разряда (начиная с бита 0) в 1 шестнадцатеричный разряд с помощью этой таблицы:
| Двоичный | Шестигранник |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | А |
| 1011 | Б |
| 1100 | С |
| 1101 | Д |
| 1110 | Е |
| 1111 | Ф |
Пример
Преобразовать двоичное число 1101100 2 в шестнадцатеричное:
Преобразовать каждые 4 двоичных бита (из бита 0) в шестнадцатеричное число:
1101100 2 = 110 1100 = 6 C = 6C 16
Преобразователь шестнадцатеричного кода в двоичный
Напишите, как улучшить эту страницу
ПРЕОБРАЗОВАНИЕ ЧИСЕЛ
- ASCII, шестнадцатеричный, двоичный, десятичный преобразователь Преобразователь текста
- ASCII в двоичный код
- Преобразователь текста ASCII в шестнадцатеричный
- Базовый преобразователь
- Двоичный преобразователь
- Преобразователь двоичного текста в текст ASCII
- Преобразователь двоичного кода в десятичный
- Преобразователь двоичного кода в шестнадцатеричный
- Преобразователь даты в римские цифры
- Преобразователь десятичных чисел в дроби
- Преобразователь десятичных чисел в проценты
- Преобразователь десятичной системы в двоичную
- Преобразователь десятичного числа в восьмеричное
- Преобразователь десятичного числа в шестнадцатеричный
- Перевод градусов в град,мин,сек
- Перевод градусов,мин,сек в градусы
- Перевод градусов в радианы
- Преобразователь дроби в десятичную дробь
- Преобразователь дробей в проценты
- Шестнадцатеричный/десятичный/восьмеричный/двоичный преобразователь
- Преобразователь текста Hex в ASCII
- Преобразователь шестнадцатеричного кода в двоичный
- Преобразователь шестнадцатеричного кода в десятичный
- Преобразователь восьмеричных чисел в десятичные
- Преобразователь процентов в десятичные числа
- Преобразователь процентов в дроби
- Конвертер процентов в ppm Конвертер
- ppm в проценты Конвертер
- ppm в ppb Конвертер
- ppm в ppt Конвертер
- ppb в ppm Конвертер
- ppt в ppm Преобразователь
- частей на миллион
- Перевод радиан в градусы
- Преобразователь римских цифр
- Преобразователь экспоненциальной записи
RAPID TABLES
- Рекомендовать сайт
- Отправить отзыв
- О
Двоичный код в шестнадцатеричный — определение, этапы преобразования, преобразование с десятичной точкой, примеры
Преобразование двоичного кода в шестнадцатеричный — это еще один тип преобразования, который происходит в системе счисления. В математике существует 4 типа системы счисления: двоичная, восьмеричная, десятичная и шестнадцатеричная. Каждая из этих форм может быть преобразована в другой тип системы счисления с помощью таблицы преобразования или метода преобразования. Давайте рассмотрим различные способы преобразования двоичных чисел в шестнадцатеричные числа и решим несколько примеров для лучшего понимания.
В математике существует 4 типа системы счисления: двоичная, восьмеричная, десятичная и шестнадцатеричная. Каждая из этих форм может быть преобразована в другой тип системы счисления с помощью таблицы преобразования или метода преобразования. Давайте рассмотрим различные способы преобразования двоичных чисел в шестнадцатеричные числа и решим несколько примеров для лучшего понимания.
| 1. | Что такое преобразование двоичного кода в шестнадцатеричный? |
| 2. | шагов для преобразования двоичного в шестнадцатеричный |
| 3. | Преобразование двоичного в шестнадцатеричное с десятичной точкой |
| 4. | Часто задаваемые вопросы о преобразовании двоичного кода в шестнадцатеричный код |
Что такое преобразование двоичного кода в шестнадцатеричный?
Преобразование двоичных чисел в шестнадцатеричные — это процесс преобразования двоичных чисел в шестнадцатеричные числа. Двоичные числа имеют базовое число 2, а базовое число шестнадцатеричных — 16. Преобразование из двоичного в шестнадцатеричное происходит с помощью базовых чисел. Существуют способы, с помощью которых выполняется преобразование, первый — путем преобразования двоичного числа в десятичное число, а затем в шестнадцатеричное число. Во-вторых, с помощью двоичной таблицы преобразования в шестнадцатеричное. Прежде чем мы перейдем к методу преобразования, давайте посмотрим, что такое двоичный и шестнадцатеричный форматы.
Двоичные числа имеют базовое число 2, а базовое число шестнадцатеричных — 16. Преобразование из двоичного в шестнадцатеричное происходит с помощью базовых чисел. Существуют способы, с помощью которых выполняется преобразование, первый — путем преобразования двоичного числа в десятичное число, а затем в шестнадцатеричное число. Во-вторых, с помощью двоичной таблицы преобразования в шестнадцатеричное. Прежде чем мы перейдем к методу преобразования, давайте посмотрим, что такое двоичный и шестнадцатеричный форматы.
Двоичная система счисления
Двоичная система счисления — одна из самых простых систем счисления, в которой цифры 0 и 1 используются только вместе с базовым числом 2. Двоичные числа в основном используются в компьютерах, которые очень удобны для инженеров, сетей и связи. специалиста, и во многих современных компьютерах. Цифры 0 и 1 называются битами, а 8 бит вместе составляют байт. Двоичная система счисления не работает с другими числами, такими как 2,3,4,5 и так далее.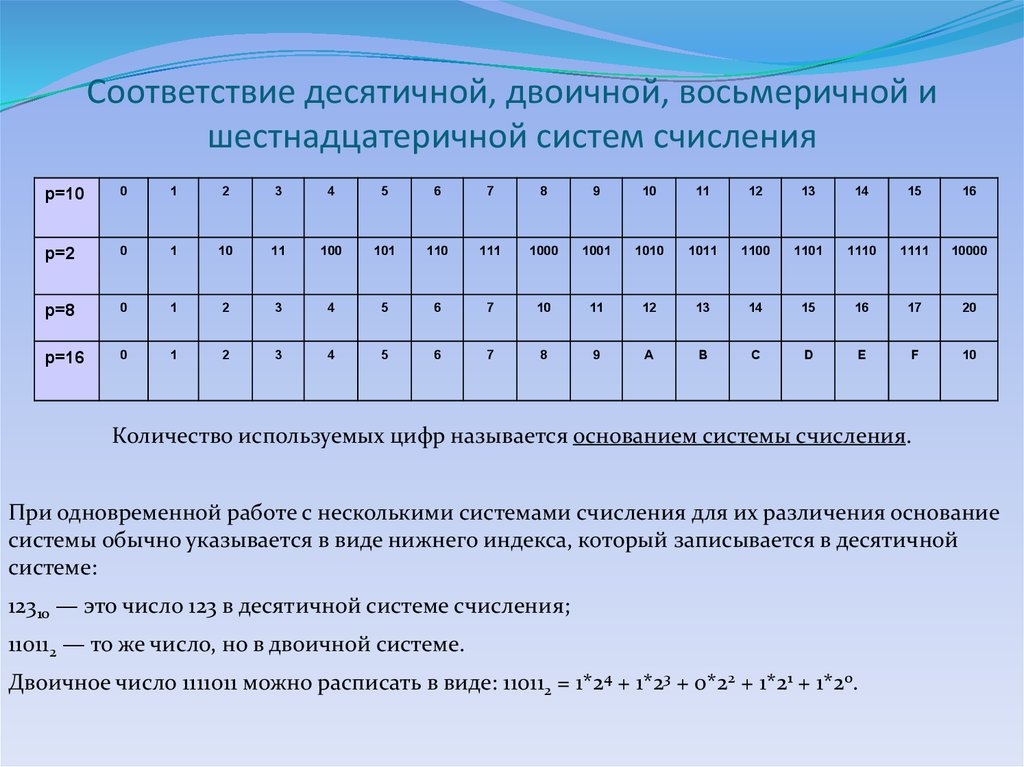 Например: \(10110001_2, 11001101_2, 1011001_2 \) — некоторые примеры чисел в двоичной системе счисления.
Например: \(10110001_2, 11001101_2, 1011001_2 \) — некоторые примеры чисел в двоичной системе счисления.
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления — это позиционная система счисления в системе счисления, в которой используется базовое число 16 вместе с шестнадцатью цифрами/алфавитами: 0, 1, 2, 3, 4, 5, 6, 7. , 8, 9 и A, B, C, D, E, F. Здесь A-F шестнадцатеричной системы счисления означают соответственно числа 10-15 десятичной системы счисления. Каждая цифра в шестнадцатеричной системе счисления представляет степень основания (16). Например: \(4E7_{16}, 3F_{16}, 6D2C_{16}\) — некоторые примеры чисел в шестнадцатеричной системе счисления.
шагов для преобразования двоичного в шестнадцатеричный
Чтобы преобразовать двоичные числа в шестнадцатеричные, нам нужно использовать оба основных числа, то есть 2 для двоичных и 16 для шестнадцатеричных. Процесс преобразования происходит двумя способами.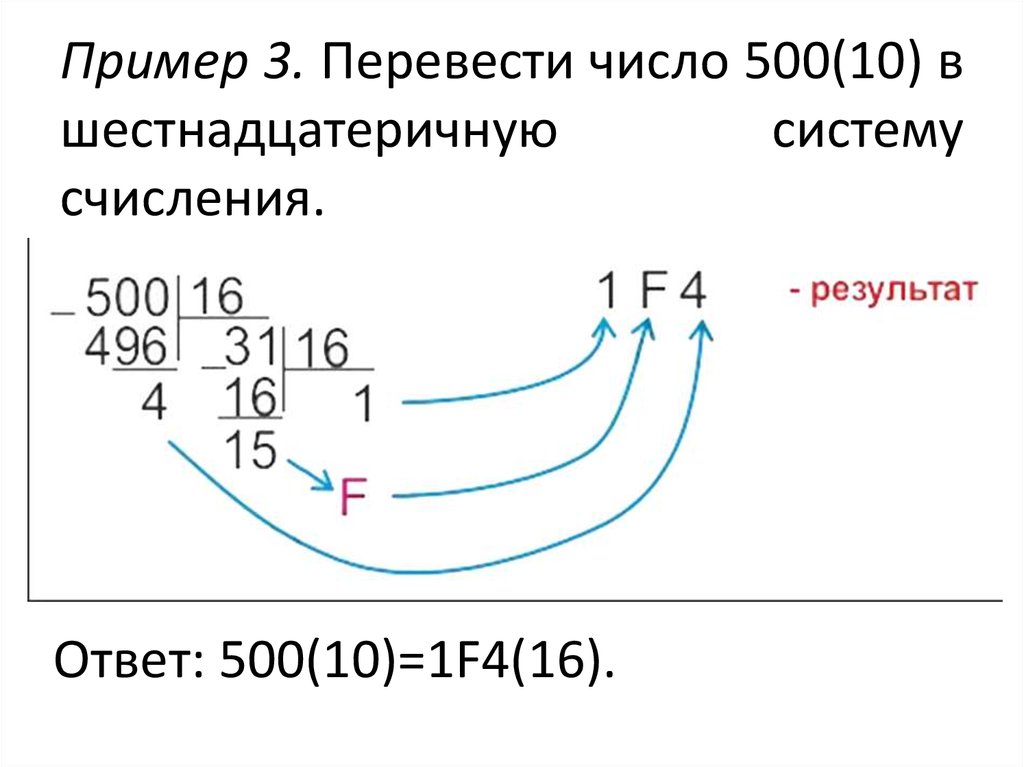 Первый метод заключается в использовании таблицы преобразования двоичного кода в шестнадцатеричный, где 1 шестнадцатеричное число эквивалентно 4 двоичным числам. Второй метод заключается в преобразовании шестнадцатеричного числа в десятичное, а затем в двоичное. Давайте рассмотрим оба метода подробно.
Первый метод заключается в использовании таблицы преобразования двоичного кода в шестнадцатеричный, где 1 шестнадцатеричное число эквивалентно 4 двоичным числам. Второй метод заключается в преобразовании шестнадцатеричного числа в десятичное, а затем в двоичное. Давайте рассмотрим оба метода подробно.
Способ 1. Преобразование двоичного в шестнадцатеричное с помощью таблицы преобразования
Один из самых простых и легких способов преобразования из двоичного в шестнадцатеричное — использование таблицы преобразования. Поскольку двоичные числа имеют только 0 и 1, которые называются битами, а шестнадцатеричные числа также являются позиционной системой счисления, каждые 4 бита или числа эквивалентны 1 шестнадцатеричному числу, которое также включает алфавиты от A до F. Таблица преобразования выглядит следующим образом:
Давайте рассмотрим пример для лучшего понимания.
Например: преобразовать \((00110110101)_{2}\) в шестнадцатеричное число.
Сначала мы группируем числа в набор из 4.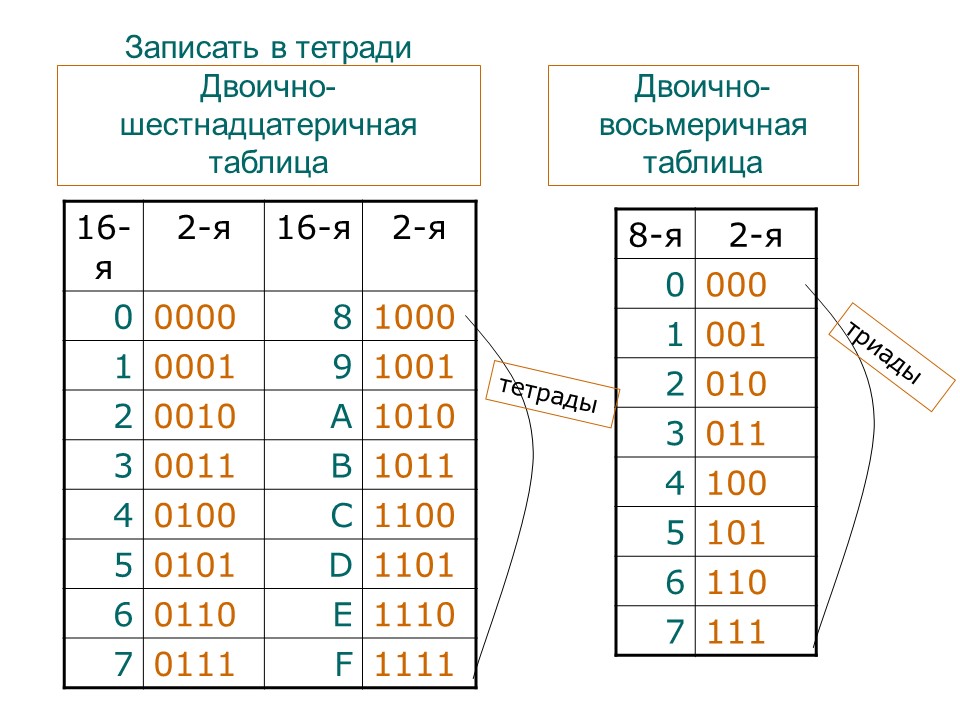 Так как каждые 4 цифры в двоичном формате становятся одной 1 цифрой в шестнадцатеричном формате. Добавьте нули слева от последней цифры, если цифр недостаточно для составления набора из четырех:
Так как каждые 4 цифры в двоичном формате становятся одной 1 цифрой в шестнадцатеричном формате. Добавьте нули слева от последней цифры, если цифр недостаточно для составления набора из четырех:
0001 1011 0101
Взглянув на таблицу преобразования, мы можем найти эквивалентное шестнадцатеричное число.
0001 = 1 , 1011 = B , 0101 = 5
Складываем числа вместе, чтобы получить окончательное число.
Следовательно, \((00110110101)_{2}\) = \((1B5)_{16}\).
Способ 2: Преобразование двоичных чисел в шестнадцатеричные без таблицы преобразования
Двоичные числа можно также преобразовать в шестнадцатеричные без использования таблицы преобразования. Двоичные числа сначала преобразуются в десятичное, а затем в шестнадцатеричное число. Здесь базовое число десятичного числа равно 10. Двоичное число можно преобразовать в десятичное число, представив каждую цифру как произведение заданного числа 1 или 0 в соответствующей степени 2. И преобразовать из десятичного числа в шестнадцатеричное делим число 16 до тех пор, пока частное не станет равным нулю. Давайте посмотрим на пример для лучшего понимания.
Давайте посмотрим на пример для лучшего понимания.
Например: преобразовать \((0111000101001)_{2}\) в шестнадцатеричное число.
Сначала мы преобразуем двоичное число в десятичное. Для этого каждая цифра умножается на соответствующую степень двойки.
\((0111000101001)_{2}\) = 0 × 2 12 + 1 × 2 11 + 1 × 2 10 + 1 × 2 9 + 0 3 8 2 90 × 2 7 + 0 × 2 6 + 1 × 2 5 + 0 × 2 4 + 1 × 2 3 + 0 × 2 2 + 0 × 2 1 + 1 × 2 0
\((0111000101001)_{2}\) = 0 × 4096 + 1 × 2048 + 1 × 1024 + 1 × 512 + 0 × 256 + 0 × 128 + 0 × 64 + 1 × 32 + 0 × 16 + 1 × 8 + 0 × 4 + 0 × 2 + 1 × 1
\((0111000101001)_{2}\) = 0 + 2048 + 1024 + 512 + 0 + 0 + 0 + 32 + 0 + 8 + 0 + 0 + 1
\((0111000101001)_{2}\) = 3625
Следовательно, \((0111000101001)_{2}\) = \((3625)_{10}\).
После получения десятичного числа мы преобразуем это десятичное число в шестнадцатеричное число.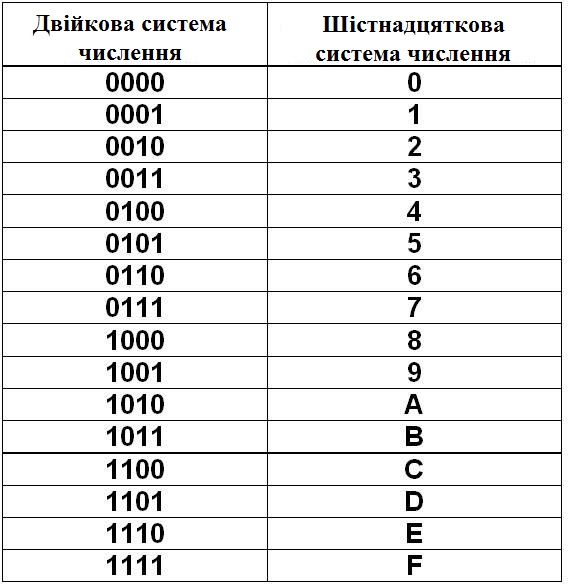 Число делится на 16 до тех пор, пока частное не станет равным нулю.
Число делится на 16 до тех пор, пока частное не станет равным нулю.
3625/16 = 226 частное, остаток 9
226/16 = 14 частное, остаток 2
14/16 = 0 частное, остаток 14
Окончательное число получается путем расположения чисел снизу вверх, то есть 1429. Поскольку шестнадцатеричная система счисления имеет дело только с 0–9 в цифрах и 10–15 в алфавитах как A–F, поэтому число равно E29.
Следовательно, \((0111000101001)_{2}\) = \((E29)_{16}\).
Преобразование двоичного в шестнадцатеричное с десятичной точкой
Чтобы преобразовать двоичное число в шестнадцатеричное с десятичной точкой, мы используем метод, аналогичный тому, что использовался в предыдущем разделе. Мы используем таблицу преобразования для преобразования двоичных чисел в шестнадцатеричные. С десятичной точкой двоичное число также будет иметь дробную часть, которая считается после десятичной точки. При преобразовании десятичная точка не влияет на положение чисел. Давайте посмотрим на пример, чтобы понять это лучше.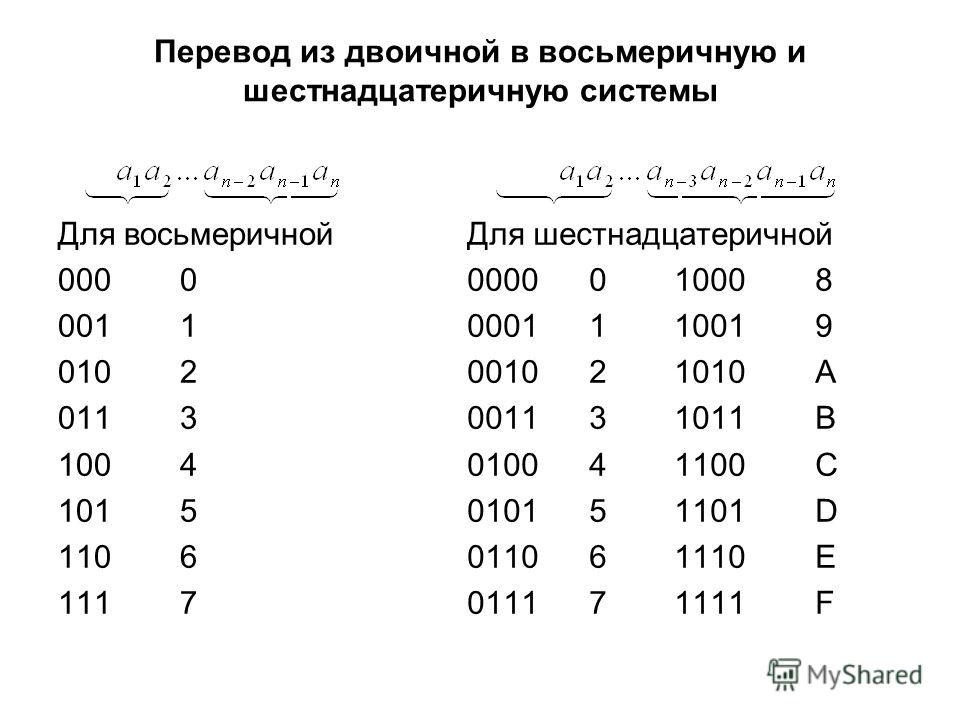
Например: \((0100110.10110110)_{2}\)
Сначала мы группируем числа в набор из 4. Так как каждые 4 цифры в двоичном формате становятся одной 1 цифрой в шестнадцатеричном. Добавьте нули слева от последней цифры, если цифр недостаточно для составления набора из четырех:
0010 0110 . 1011 0110
Глядя на таблицу преобразования, упомянутую в предыдущем разделе, мы можем найти эквивалентное шестнадцатеричное число.
0010 = 2 , 0110 = 6 , 1011 = B , 0110 = 6
Складываем числа вместе, чтобы получить окончательное число. Десятичная точка будет в том же положении, что и в двоичном числе.
Следовательно, \((0100110.10110110)_{2}\) = \((26.B6)_{16}\).
Связанные темы
Ниже перечислены несколько интересных тем, связанных с преобразованием двоичного кода в шестнадцатеричный.
- Шестнадцатеричный код в двоичный
- Десятичный в восьмеричный
- Восьмеричный в десятичный
Часто задаваемые вопросы о преобразовании двоичного кода в шестнадцатеричный
Как преобразовать двоичный код в шестнадцатеричный?
Двоичное число в шестнадцатеричное — это форма преобразования, при которой двоичное число с основанием 2 преобразуется в шестнадцатеричное число с основанием 16.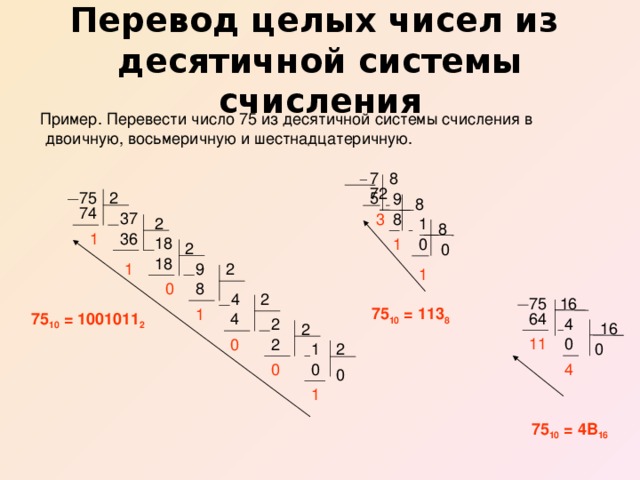


 RU
RU