Алгебра логики в программировании — Умскул Учебник
На этой странице вы узнаете- Что не так с импликацией и эквиваленцией?
- Какое применение алгебра логики может найти в программировании?
В статье «Алгебра логики» мы выучили основы этого непростого раздела математики. Разобравшись в той теме, пора пойти дальше и заговорить на понятном компьютеру языке — языке программирования.
Логические уравнения в Python| Мы говорили, что алгебра логики оперирует истиной и ложью, которым также могут соответствовать числа 1 и 0. В Python эта логика сохраняется. В нем есть логический тип данных bool, который может принимать значение True или False — истина и ложь соответственно. Последние также эквивалентны числам 1 и 0. |
Как логические операторы записываются в программе Python и в чем их отличие?
Логические операторы в Python мы уже упоминали в статье «Основы программирования. Часть 2». Давайте их вспомним:
Часть 2». Давайте их вспомним:
| Что не так с импликацией и эквиваленцией? Проблема в том, что для импликации и эквиваленции нет специальных логических операторов, но для них можно использовать математические: Но несмотря на схожесть работы, это все еще математические операторы, из-за чего нарушается привычный приоритет. Так что в программе он будет следующим: |
Самый практичный совет по записи логических уравнений в программе — не стесняйтесь использовать скобки, если используете математические операторы.
Например:
- простое логическое уравнение только из конъюнкции, дизъюнкции и инверсии в лишних скобках не нуждается (кроме тех, конечно, что уже есть в уравнении):
- при появлении импликации и эквиваленции подключаем скобки, чтобы сохранить приоритет и этих, и других логических операторов:
| Какое применение алгебра логики может найти в программировании? Между программированием и алгеброй логики установлен довольно приятный союз: — С одной стороны, в больших и запутанных программах может быть много логических зависимостей, распутать которые поможет знание алгебры логики. |
Например, очень популярная задача алгебры логики — построение таблицы истинности. Давайте попробуем предположить, что нам может понадобиться, чтобы программа смогла это сделать?
А много нам и не надо
- Нужен перебор логических переменных по совсем небольшому диапазону — от 0 до 1.
- Правильно записанное логическое уравнение, чтобы проверить его при каждом наборе истины и лжи.
Вопрос встает только о конкретной реализации. Python — очень гибкий язык. Для разных формулировок задачи он может предложить разные инструменты, при использовании которых написание кода станет еще приятнее.
Начнем с обобщенной задачи — построение таблицы истинности. На этом примере можно показать, что математические операторы путают приоритет логических. Так что давайте составим таблицу истинности для уравнения A ≡ B ∧ C ⇒ A.
Перебор устроим с помощью вложенных циклов for. Они будут перебирать отдельные переменные, которые потом будут поставляться в логическое уравнение. Для удобства будем сохранять значение уравнения в отдельную переменную, затем выводить все на экран.
print("A B C")
for A in range(0, 2):
for B in range(0, 2):
for C in range(0, 2):
result = A == ((B and C) <= A)
print(A, B, C, result)
Вывод:
A B C
0 0 0 False
0 0 1 False
0 1 0 False
0 1 1 True
1 0 0 True
1 0 1 True
1 1 0 True
1 1 1 True
Мы заранее подписали каждый столбец, так что не запутаться в выводе будет проще.
Да, промежуточных результатов при такой реализации у нас нет. 
У меня есть ощущение, что этот код не очень красивый. Он однозначно рабочий, но все-таки слишком много вложенных циклов. Как это можно решить?
В статье «Комбинаторика в информатике» мы обсуждали такую вещь, как модуль itertools, который содержит функции для работы с различными комбинациями. Как раз наш случай — мы используем различные комбинации 1 и 0.
Сейчас нам пригодится
from itertools import product
print("A B C")
d = [0, 1]
for i in product(d, repeat = 3):
A, B, C = i
result = A == ((B and C) <= A)
print(A, B, C, result)
Вывод:
A B C
0 0 0 False
0 0 1 False
0 1 0 False
0 1 1 True
1 0 0 True
1 0 1 True
1 1 0 True
1 1 1 True
Как видите, результат мы получили тот же, но смогли избавиться от некрасивого массива вложенных циклов. С еще большим количеством переменных в уравнении было бы нагляднее.
Пожалуй, стоит подробнее рассказать про строку:
A, B, C = i.
Мы точно знаем, что i — это массив с 3 элементами, так как мы изначально задали создание наборов длиной 3. Если указать перед ним ровно столько же переменных, им можно присвоить соответствующие элементы массива в одну строку.
Выше мы обсуждали, почему в этом уравнении обязательно должны быть скобки. Давайте докажем это. Построим таблицу истинности для того же уравнения, но не будем ставить скобки.
from itertools import product
print("A B C")
d = [0, 1]
for i in product(d, repeat = 3):
A, B, C = i
result = A == B and C <= A
print(A, B, C, result)
Вывод:
A B C
0 0 0 True
0 0 1 False
0 1 0 False
0 1 1 False
1 0 0 False
1 0 1 False
1 1 0 True
1 1 1 True
Не вышло: итоговые значения таблиц истинности разные. Значит, приоритет действительно нарушается.
Другая наша возможная цель — проверить, будет ли выражение истинным всегда? Получим ли мы истину при любом наборе логических переменных?
Как и в прошлый раз, у нас есть не один вариант реализации. Будем анализировать выражение А ∧ (В ∨ С) ≡ В.
Будем анализировать выражение А ∧ (В ∨ С) ≡ В.
Первый вариант:
- перебор всех наборов — вложенными циклами или с помощью product;
- сохранение всех результатов уравнения от каждого набора;
- проверка, чтобы ни одно значение не было ложным — для сохранения всех результатов можно использовать список.
from itertools import product
d = [0, 1]
all_results = []
for i in product(d, repeat = 3):
A, B, C = i
result = (A and (B or C)) == B
all_results.append(result)
if False not in all_results:
print("Функция полностью истинна")
else:
print("Функция истинна не всегда")
Вывод: Функция истинна не всегдаPython не был бы Python, если бы не дал нам возможность записать все практически в одну строку.
Второй вариант — функция all. Она возвращает True, если все значения внутри нее равны True — как раз наш случай. Чтобы записать программу максимально коротко, прямо внутри нее можно прописать и уравнение, и перебор его элементов:
from itertools import product
d = [0, 1]
result = all((A and (B or C)) == B for A, B, C in product(d, repeat = 3))
if result:
print("Функция полностью истинна")
else:
print("Функция истинна не всегда")
Здесь в переменную result записывается логическое значение True, если для всех наборов А, В, С из комбинаций d длиной 3 результат логического уравнения равен True. Если же среди всех результатов есть хоть один False — функция all даст нам False.
Если же среди всех результатов есть хоть один False — функция all даст нам False.
Для похожей задачи — чтобы не все значения уравнения были ложными — можно использовать функцию any. Синтаксис абсолютно такой же, разница есть в принципе работы. any вернет True, если среди всех переданных значений есть хоть одно истинное значение.
from itertools import product
d = [0, 1]
result = any((A and (B or C)) == B for A, B, C in product(d, repeat = 3))
if result:
print("Функция не всегда ложна")
else:
print("Функция всегда ложна")
Вывод: Функция не всегда ложна
Python — гибкий язык. Если вам важнее видеть алгоритм работы кода более явно — используйте вложенные циклы, массивы для хранения значений и будьте более, чем на 100% уверены в каждом шаге. Если же вы хотите использовать дополнительные инструменты для сокращения объема кода и, как следствие, более быстрого его написания — вам в помощь комбинации product из itertools и инструменты массовой проверки all и any.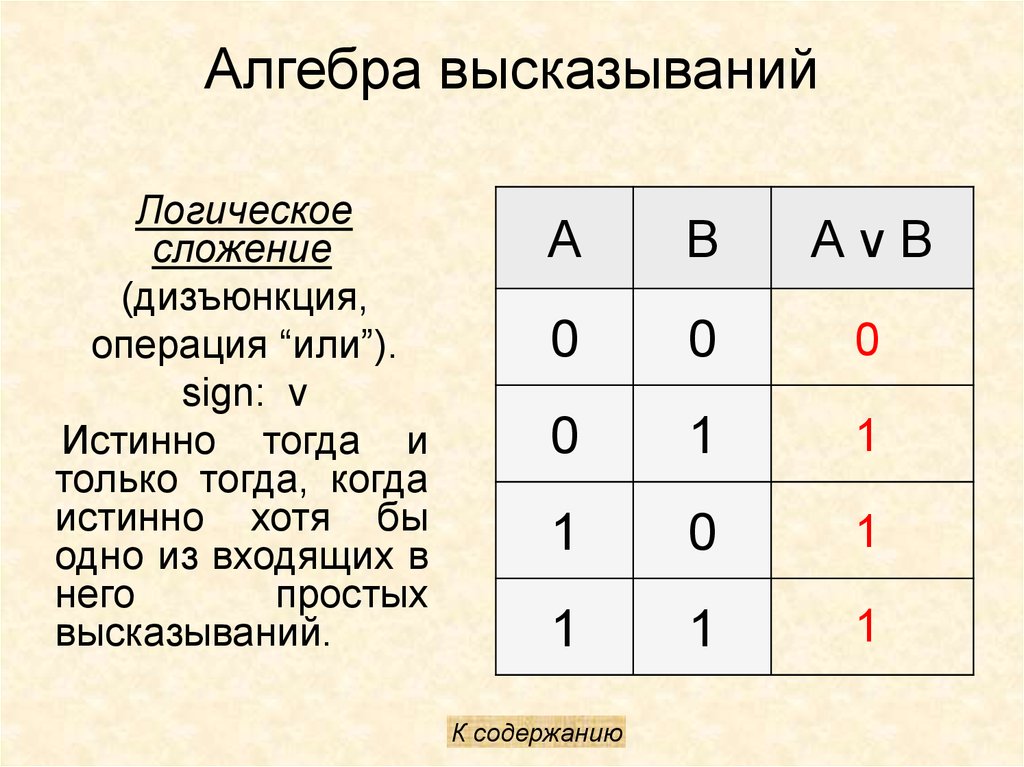
- Для импликации и эквиваленции в Python используются математические операторы сравнения, что немного нарушает их общий приоритет. Сохранить его можно с помощью скобок.
- Значения истины и лжи в Python являются логическим типом данных, который может принимать значение True или False и соответствует 1 и 0.
- Функция all проверяет, все ли переданные ей значения истинны. Функция any проверяет, есть ли среди всех переданных значений хоть одно истинное.
Задание 1.
Для выражения А ∨ В ∧ ¬(В ∧ А) выберите верную запись на языке Python (с сохранением порядка действий):
- A and B or not B or A
- A and B or not (B or A)
- A or B and not B and A
- A or B and not (B and A)
Задание 2.
Для выражения ¬А ⇒ В ≡ А ∧ В выберите верную запись на языке Python (с сохранением порядка действий):
- not (А <= В == А and В)
- not А <= В == (А and В)
- ((not A) <= B) == (A and B)
- (not А) <= (В == (А and В))
Задание 3.
Чему будет равен последний столбец таблицы истинности для уравнения:
A ∧ B ⇒ C ∧ D ∨ D ∧ A?
- 11101101
- 11101111
- 00000011
- 11000111
Задание 4.
Выберите уравнение, которое во всех случаях принимает значение истины:
- ¬(A ∧ B) ∧ ¬(C ∧ ¬A)
- ¬(A ∧ B) ∨ ¬(C ∧ ¬A)
- A ∧ B ∧ ¬(C ∧ ¬A)
- ¬(A ∧ B) ∨ ¬(C ∧ A)
Ответ: 1. — 4; 2. — 3; 3. — 1; 4. — 2.
Математические и логические основы информатики
Определение 1
Математические и логические основы информатики — это раздел математики, называемый «алгебра логики» и изучающий высказывания, которые рассматриваются с точки зрения их истинности или ложности, а также логические операции над ними.
Алгебра логики
Замечание 1
Алгеброй логики является раздел математики, который изучает высказывания с точки зрения их логических значений, то есть, истинны они или ложны, и логические операции над ними.
Логическим высказыванием считаются повествовательное предложение, про которое можно точно утверждать, что оно является истинным или ложным.
Замечание 2
Истинное высказывание принято обозначать символом единица (1), а ложное высказывание принято обозначать символом ноль (0).
Примеры логических высказываний приведены в таблице ниже:
Рисунок 1. Таблица. Автор24 — интернет-биржа студенческих работ
Математические и логические основы информатики
Используемые в повседневной речи слова и словосочетания «не», «и», «или», «если…,то», «тогда и только тогда» и другие дают возможность из стандартных высказываний формировать более сложные формы высказываний. Такого типа слова и их сочетания именуются логическими связками. Высказывания, которые были образованы при помощи логической связки, именуются составными высказываниями. Высказывания, которые не являются составными, считаются элементарными. Чтобы обозначить логическое высказывание, ему следует присвоить имя. (¬B v А)
(¬B v А)
Определение значения логического выражения выполняется слева направо согласно таблице истинности и приоритету осуществления логической операции. Ниже приведена таблица истинности:
Рисунок 3. Таблица истинности. Автор24 — интернет-биржа студенческих работ
Приоритет осуществления логической операции определяется согласно следующей таблице:
Рисунок 4. Таблица. Автор24 — интернет-биржа студенческих работ
Замечание 3
Очерёдность осуществления логических операций может быть изменена при помощи круглых скобок.
Основные правила алгебры логики
Базовые правила алгебры логики, которые позволяют выполнять тождественные преобразования логических выражений, приведены в таблице ниже:
Рисунок 5. Таблица. Автор24 — интернет-биржа студенческих работ
Математический аппарат алгебры логики является очень удобным средством для описания работы аппаратного обеспечения компьютерного оборудования, так как там применяется двоичная система счисления, где есть только две цифры нуль и единица аналогично логическим постулатам.
- Одни и те же компьютерные модули можно использовать для сохранения и переработки как числовых данных, которые представлены в двоичном формате, так и для переменных алгебры логики.
- При проектировании аппаратного обеспечения компьютеров методы алгебры логики дают возможность существенно упростить логические процедуры, которые описывают работу компьютерных схем. Это позволяет в разы сократить количество элементарных элементов логики, составляющих модули компьютера.
Формирование таблицы истинности
Как отмечалось выше, таблица истинности логического выражения отражает соответствие среди допустимых наборов значений переменных и значениями выражения (формулы). Если формула содержит только две переменные, то возможных наборов величин переменных будет четыре.
Когда в логическую формулу входят три переменные, то количество допустимых наборов значений переменных будет уже равно восьми.
Число наборов для выражений, имеющих четыре переменные, будет равняться шестнадцати и так далее.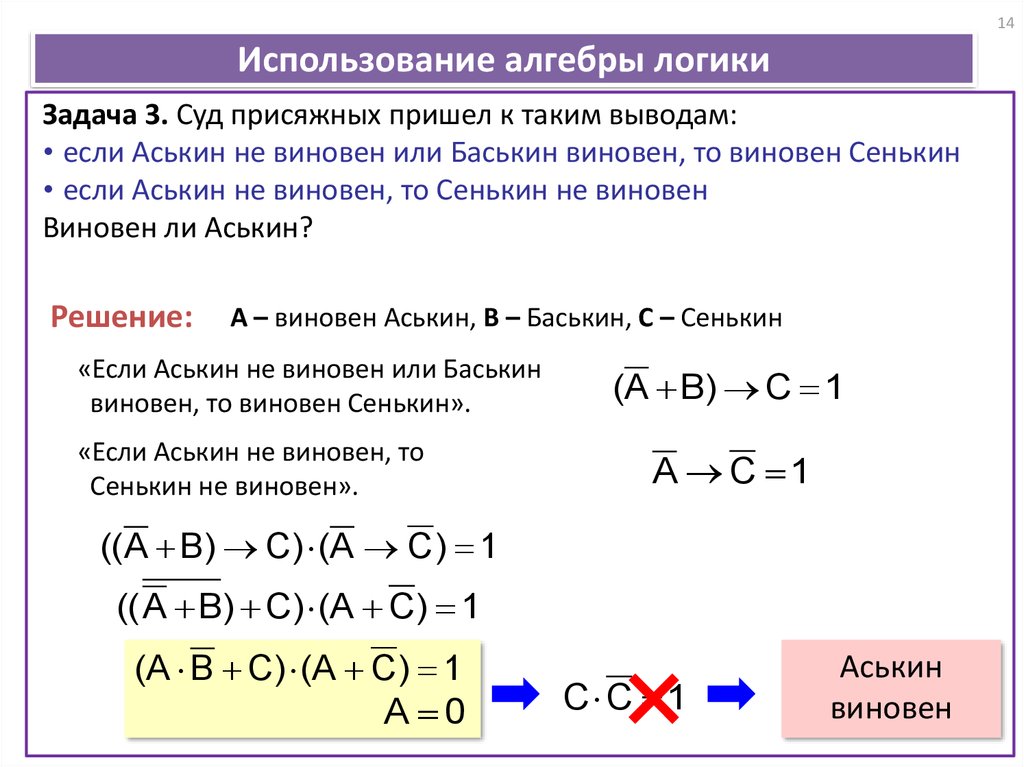
Рассмотрим пример решения конкретной задачи. Какое из приведённых ниже имён отвечает истинности следующего высказывания: «Первая из букв в имени является гласной, буква, стоящая в имени четвёртой, является согласной». Список имён следующий:
- Елена.
- Вадим.
- Антон.
- Фёдор.
Обозначим высказывания следующим образом:
A = «Гласная является первой буквой имени».
B = «В имени буква на четвёртом месте является согласной».
В таком случае исходное высказывание можно выразить так:
¬ (A → B).
Выполнив необходимые преобразования, можно определить, что условию задачи удовлетворяет только имя Антон.
Конспект по информатике на тему «Элементы алгебры логики. Высказывания. Логические операции» | План-конспект занятия по информатике и икт (10 класс):
ОБЛАСТНОЕ ГОСУДАРСТВЕННОЕ ПРОФЕССИОНАЛЬНОЕ
ОБРАЗОВАТЕЛЬНОЕ БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ
«МНОГОПРОФИЛЬНЫЙ ЛИЦЕЙ»
ОТКРЫТЫЙ УРОК
по дисциплине «Информатика и информационно-коммуникативные технологии»
Тема: «Элементы алгебры логики. Высказывания. Логические операции»
Высказывания. Логические операции»
Разработчик:
Науменко А.В.
преподаватель информатики и ИКТ
ОГПОБУ «Многопрофильный лицей»
с. Амурзет 2020
План учебного занятия по теме: Элементы алгебры логики. Высказывания. Логические операции.
Цели урока:
Образовательные:
- сформировать у обучающихся представление об алгебре высказываний и логических операций с ними.
Развивающие:
- развивать логическое мышление, память, внимание;
- формировать умения чётко и ясно излагать свои мысли.
Воспитательные:
- воспитывать интерес к предмету, настойчивость, целеустремленность;
- воспитывать уважение к предмету;
- способствовать воспитанию самоорганизации и самоконтроля.
Планируемые образовательные результаты:
- предметные – представления о разделе математики алгебре логики, высказывании как её объекте;
- метапредметные – навыки анализа логической структуры высказываний;
- личностные – понимание роли фундаментальных знаний как основы современных информационных технологий, развитие логического мышления, внимательности.

Решаемые учебные задачи:
- знакомство с понятием высказывания, истинными и ложными высказываниями.
- сформировать у обучающихся понятие “логическая операция»;
Тип урока: комбинированный урок (дискуссия, лекция (изучение нового материала), мультимедиа, практикум, самостоятельная работа).
Формируемые общие компетенции (ОК):
ОК1. Выбирать способы решения задач профессиональной деятельности, применительно к различным контекстам.
ОК2. Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности.
ОК3. Планировать и реализовывать собственное профессиональное и личностное развитие.
ОК9. Использовать информационные технологии в профессиональной деятельности.
Методы обучения: словесные (рассказ, объяснение, беседа), наглядные (иллюстрация), практические.
Форма организации: индивидуальная, фронтальная.
Оборудование: проектор, экран, компьютер, презентация.
Время на проведение занятия: 1 учебный час
План урока:
- Организация начала занятия – 2 минуты.
- Подготовка к основному этапу занятия. Мотивация учебной деятельности –3 минуты.
- Актуализация знаний обучающихся – 5 минут.
- Изложение нового материала – 20 минут.
- Закрепление учебного материала – 10 минут.
- Задание на дом – 3 минуты.
- Рефлексия – 2 минуты.
Ход урока:
Организация начала занятия (2 минуты)
Здравствуйте ребята, садитесь. Запишите тему урока. — Элементы алгебры логики. Высказывания. Логические операции.
Актуализация знаний обучающихся (5 минут)
Как вы думаете, можно ли научить техническое устройство (в частности компьютер) логически мыслить? (Только если запрограммировать варианты решений, само по себе техническое устройство принимать решения не может.- Будет хорошо, если мнения ребят разделятся)
Что по вашему является высказыванием? Что такое логика?
Давайте разбираться!
Изложение нового материала – (20минут)
Знание логики необходимо при разработке алгоритмов и программ, так как в большинстве языков программирования есть логические операции.
Алгебра логики имеет сходство с работой электрических переключательных схем. Электрический переключатель либо пропускает ток (истина), либо не пропускает (ложь).
Оперируя логическими переменными, которые могут быть равны только 0 или 1, алгебра логики позволяет свести обработку информации к операциям с двоичными данными. Именно аппарат алгебры логики положен в основу компьютерных устройств хранения и обработки данных.
Объектами алгебры логики являются высказывания.
Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. (слайд 2)
Давайте задумаемся над смыслом слова высказывание. Что означает: человек высказывает свое мнение?
Высказывание — это повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно. (слайд 2)
Например, относительно предложений «Великий русский учёный М. В. Ломоносов родился в 1711 году» и Дважды два четыре» можно однозначно сказать, что они истинны.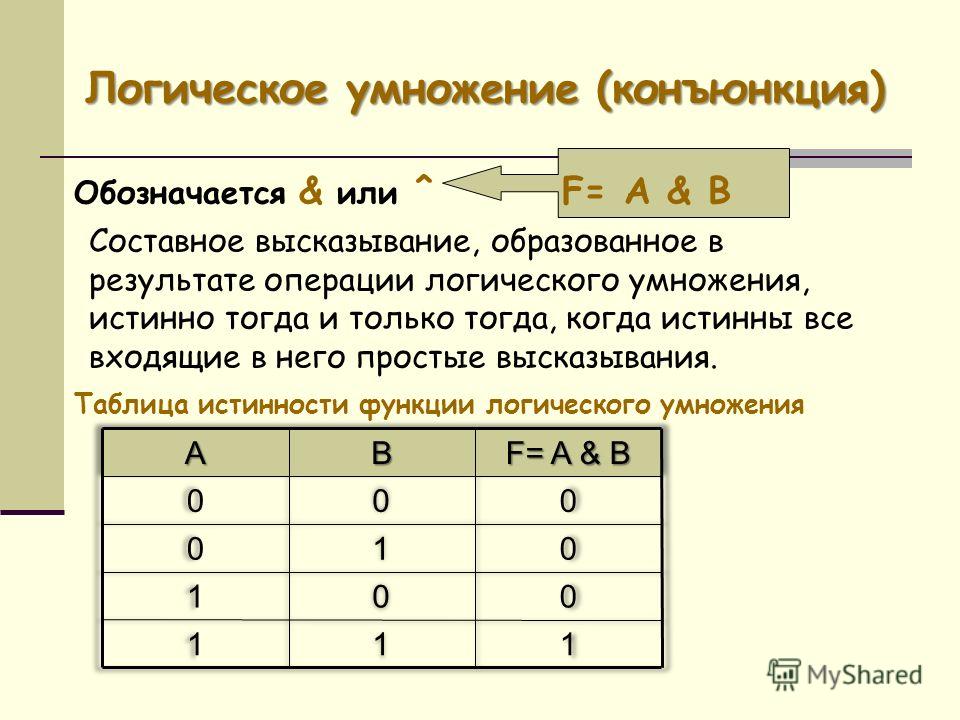 Предложение «Зимой воробьи впадают в спячку» ложно. Следовательно, эти предложения являются высказываниями.
Предложение «Зимой воробьи впадают в спячку» ложно. Следовательно, эти предложения являются высказываниями.
Побудительные и вопросительные предложения высказываниями не являются.
Например, не являются высказываниями такие предложения, как: «Запишите домашнее задание», «Как пройти в библиотеку?», «Кто к нам пришёл?».
В алгебре логики высказывания обозначают буквами и называют логическими переменными.
При этом если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей (А = 1), а если ложно — нулём (В = 0).
Из простых высказываний с помощью логических операций строятся сложные (составные) высказывания.
Логическая операция — способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний. (слайд 3)
Основные логические операции:
1. Отрицание (инверсия, логическое НЕ) (слайд 4)
Смысл операции: результат меняется на противоположный (вместо истины — ложь, вместо лжи — истина).
Обозначение: ¬.
Таблица истинности:
А | ¬А |
0 | 1 |
1 | 0 |
2. Логическое сложение (дизъюнкция, логическое ИЛИ) (слайд 5)
Смысл операции: результат — истина, если хотя бы один операнд — истина (операндом называется то значение или та переменная, над которым (которой) осуществляется операция).
Обозначения: ˅ или +.
Таблица истинности:
А | В | A ˅ В |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 1 |
3. Логическое умножение (конъюнкция, логическое И) (слайд 6)
Логическое умножение (конъюнкция, логическое И) (слайд 6)
Смысл операции: результат — истина, если оба операнда — истина.
Обозначения: ˄ или &
Таблица истинности:
А | В | A ˄ В |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
4. Исключающее ИЛИ (строгая дизъюнкция) (слайд 7)
Смысл операции: результат — истина, если операнды различны.
Обозначения: ⊕ или ≠
Таблица истинности:
А | В | A ⊕ В |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
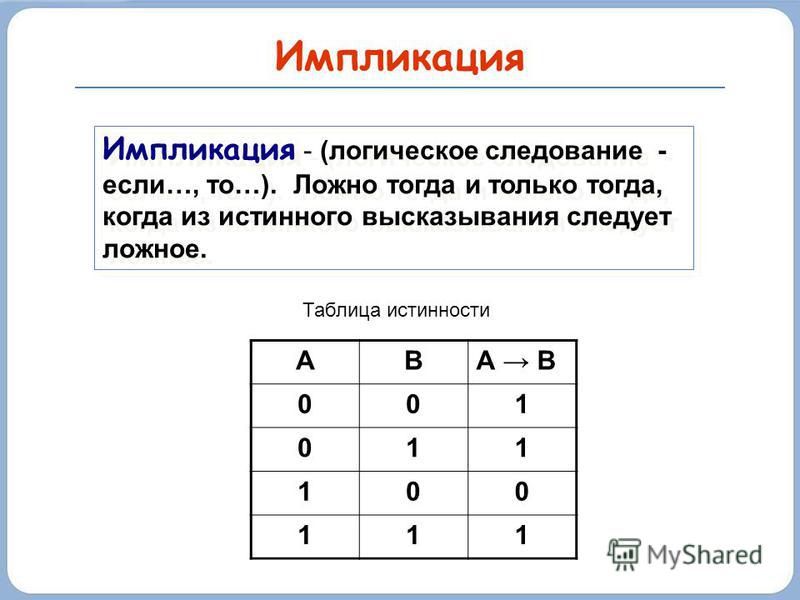
5. Следование (импликация) (слайд 8)
Смысл операции: из лжи может следовать что угодно, а из истины — только истина (если А≤В, то истина).
Обозначение: →
Таблица истинности:
А | В | A → В |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 0 |
1 | 1 | 1 |
6. Равносильность (эквиваленция) (слайд 9)
Равносильность (эквиваленция) (слайд 9)
Смысл операции: результат — истина, если операнды одинаковы.
Обозначения: ≡ или ↔
Таблица истинности:
А | В | A ↔ В |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Если в логическом выражении используется несколько логических операций, то их порядок определяется приоритетами логических операций: (слайд 10)
Выражение в скобках ( ) | ( ) | приоритет | |
Логическое НЕ (инверсия) | ¬ | ||
Логическое И (конъюнкция) | ˄ | ||
Логическое ИЛИ (дизъюнкция) | ˅ | ||
Исключающее ИЛИ (строгая дизъюнкция) | ⊕ | ||
Следование (импликация) | → | ||
Равносильность (эквиваленция) | ↔ |
Пример 1:
Какое из приведённых имён удовлетворяет логическому условию: ¬(последняя буква гласная → первая буква согласная) ˄ вторая буква согласная?
1) СТЕПАН 2) АРТЁМ 3) ИРИНА 4) МАРИЯ
Решение:
Составляется таблица.
Имя | Х1: последняя буква гласная | Х2: первая буква согласная | Х3: вторая буква согласная | Х4: Х1→Х2 | Х5: ¬Х4 | Результат: Х5˄Х3 |
СТЕПАН | 0 | 1 | 1 | 1 | 0 | 0 |
АРТЁМ | 0 | 0 | 1 | 1 | 0 | 0 |
ИРИНА | 1 | 0 | 1 | 0 | 1 | 1 |
МАРИЯ | 1 | 1 | 0 | 1 | 0 | 0 |
В таблице выделена строка, соответствующая правильному ответу (первому).
Ответ: ИРИНА (вариант ответа №1).
Пример 2:
Символом F обозначено одно из указанных ниже логических выражений от трёх аргументов X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
X | Y | Z | F |
1 | 1 | 1 | 0 |
0 | 1 | 0 | 1 |
0 | 0 | 0 | 1 |
Какое выражение соответствует F?
1) X ∨ Y ∨ Z
2) ¬X ∨ ¬Y ∨ ¬Z
3) X ∧ ¬Y ∧ Z
4) ¬X ∧ ¬Y ∧ ¬Z
Решение:
Проверяем первое вариант ответа:
X | Y | Z | F |
1 | 1 | 1 | 1 |
0 | 1 | 0 | 1 |
0 | 0 | 0 | 0 |
Проверяем второй вариант ответа:
X | Y | Z | F |
1 | 1 | 1 | 0 |
0 | 1 | 0 | 1 |
0 | 0 | 0 | 1 |
Правильный ответ – 2.
Закрепление учебного материала– 10 минут
Задача 1. Для какого имени ложно высказывание:
(Первая буква имени гласная → Четвертая буква имени согласная).
1) ЕЛЕНА
2) ВАДИМ
3) АНТОН
4) ФЕДОР
Задача 2. Дан фрагмент таблицы истинности выражения F:
X | Y | Z | F |
0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 |
1 | 1 | 1 | 1 |
Каким выражением может быть F?
- Х ˄ Y ˄ Z
- ¬X ˅ ¬Y ˅ Z
- Х ˅ Y ˅ Z
- ¬Х ˄ ¬Y ˄ ¬Z
Задача 3. Дан фрагмент таблицы истинности выражения F:
Дан фрагмент таблицы истинности выражения F:
X | Y | Z | F |
0 | 1 | 1 | 0 |
1 | 1 | 1 | 1 |
0 | 0 | 1 | 1 |
Какое выражение соответствует F?
- Х ˄ ¬Y ˄ ¬Z
- ¬X ˄ ¬Y ˄ Z
- ¬Х ˅ ¬Y ˅ Z
- Х ˅ ¬Y ˅ ¬Z
Задание на дом – 3 минуты § 18-19 учебника
Рефлексия – 2 минуты
Обобщение пройденного материала, оценивание работы активных обучающихся.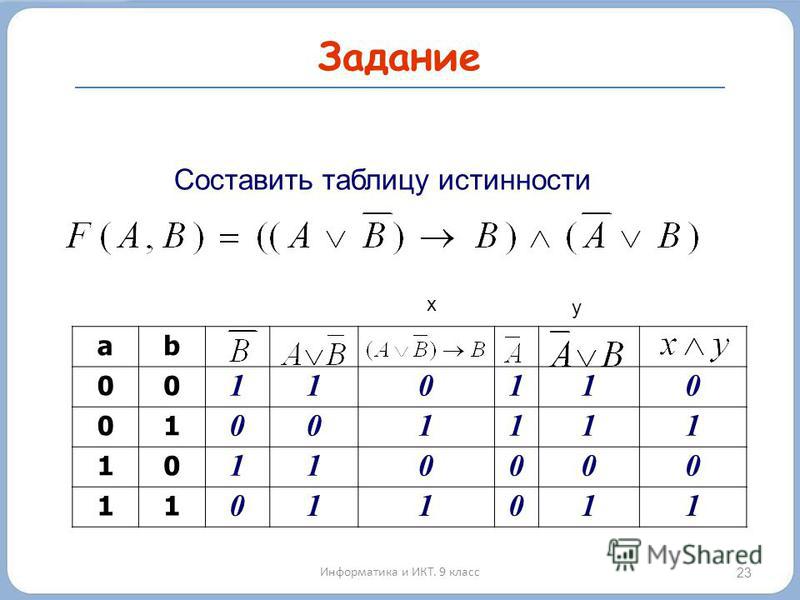
Источники:
- Информатика. 10 класс. Базовый и углубленный уровни : учебник : в 2 ч. Ч. 1 / К. Ю. Поляков, Е. А. Еремин. — М. : БИНОМ. Лаборатория знаний, 2015. — 344 с.: ил.
- Информатика и ИКТ. Задачник-практикум: в 2 т. И74 Т. 1/ Л. А. Залогова [и др.]; под ред. И. Г. Семакина, Е. К. Хеннера. – 4-е изд. – М.: БИНОМ. Лаборатория знаний, 2012. – 309 с.: ил.
Тема №1. Основные понятия алгебры логики.
В основе алгебры логики или булевой алгебры (Джордж Буль — английский математик, разработал основы алгебры,
в которой используются только 0 и 1) лежит понятие «логическое высказывание».
Логическое высказывание – это повествовательное предложение, относительно которого можно однозначно сказать, истинно оно или ложно.
Являются логическими высказываниями: Сейчас осень. Летом медведи впадают в спячку. Весной тает снег.
Не являются высказываниями: Пойдем завтра в кино? Красиво!!! В городе N проживают 4000 человек.
Обозначение высказываний
Простые высказывания:
A – Сейчас светит солнце. B – Мы идем гулять.
Любое высказывание может быть ложно (0) или истинно (1).
Составные
высказывания строятся из простых с
помощью логических связок (операций) «и», «или», «не», «если …
то», «тогда и
только тогда» и др.
Например:
А и В — Сейчас светит солнце и мы идем гулять.
А или не В — Сейчас светит солнце и мы не идем гулять.
Если А, то В — Если сейчас светит солнце, то мы идем гулять.
А тогда и только тогда, когда В — Солнце светит тогда и только тогда, когда мы идем гулять.
Операции алгебры логики
Операция НЕ (инверсия или отрицание) — Если высказывание A истинно, то «не А» ложно, и наоборот.
Обозначения: не А, ¬A, not A (Паскаль), !A (Си)
Таблица истинности:
| А | не А |
| 0 | 1 |
| 1 | 0 |
Операция И (логическое умножение, конъюнкция) — Высказывание «A и B» истинно тогда и только тогда, когда А и B истинны одновременно. B, A&B, A and B (Паскаль), A&&B (Си)
B, A&B, A and B (Паскаль), A&&B (Си)
Таблица истинности:
| A | B | A и В |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Операция ИЛИ (логическое сложение, дизъюнкция) — Высказывание «A или B» истинно тогда и только тогда, когда истинно А или B, или оба вместе.
Обозначения: А или В, А+B, AvB, A or B (Паскаль), AIIB (Си)
Таблица истинности:
| A | B | A и В |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
тест по теме №1 раздела Логика
Операция «Исключающее ИЛИ» — Высказывание
«A Е B» истинно тогда, когда истинно А или B, но не оба одновременно. B (Си)
B (Си)
Таблица истинности:
| A | B | A Е B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Операция Импликация (» Если А, то В»)- Высказывание «A ® B» истинно, если не исключено, что из А следует B.
Обозначения: A ® B
Таблица истинности:
| A | B | A ® B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Операция Эквиваленция (» А тогда и только тогда, когда В»)- Высказывание
«A « B» истинно тогда и только тогда, когда А и B равны
Обозначения: A « B
Таблица истинности:
| A | B | A « B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Порядок выполнения логических операций:
1. неВ
неВ
Использованы материалы с сайта К. Полякова. Более подробную информацию по данной теме смотреть здесь http://kpolyakov.narod.ru
Алгебра логики: Конъюнкция, Дизъюнкция, Импликация, Эквивалентность
Лада Есакова, преподаватель информатики и математики, автор книги «Информатика. Полный курс подготовки к ЕГЭ».
Ну а теперь, ребята, самая «вкусная» тема теоретической части ЕГЭ – это булева алгебра, она же алгебра логики.
Сначала я хочу задать вам вопрос: для чего вообще придумали такой аппарат как булева алгебра, кроме того, чтобы мучить маленьких детей?
Раз у нас есть такая возможность пообщаться с компьютером, поручить ему какие-то задачи на выполнение, неплохо бы нам научиться говорить с ним на одном языке. То есть перевести наши желания и намерения на его компьютерный язык.
А кто такой компьютер? Если очень упрощенно, то это некоторое устройство, у которого на проводники подается либо не подается ток. Так вот в зависимости от того, есть ток или его нет на входящих проводниках, происходят определенные действия. Обозначим это 0 и 1: 0 – нет тока, 1 – есть ток. Вот именно в таких терминах нам и надо разговаривать с компьютером.
Рассматривая задачи, в том числе и 27, сложную задачу, считаем, что мы крутые программисты, если мы написали программный код на каком-то языке программирования. А компьютер нас поймет? Нет. Он знает только 0 и 1. Как же нам тогда до него достучаться?
После программистов высокого уровня в дело вступают Боги от программирования – это люди, которые пишут компиляторы, драйверы, операционные системы и которые уже непосредственно пытаются достучаться до компьютерного железа.
Что такое уже перевод программы в машинные коды? У меня нет цели рассказать, как это работает детально, я расскажу очень упрощенно, чтобы просто было понятно, для чего это нужно.
Если на один компьютерный разъем ток не поступил, а на другой поступил, мне нужно, чтобы получился 0. Я уже говорю терминами 0 и 1, нет тока или есть ток.
Если на оба разъема ток не поступил, тоже будет 0.
Если наоборот на первый поступил, а на второй не поступил, – то я тоже хочу 0. И в случае, если на оба разъема ток поступил, тогда пусть будет у меня 1
Например, у меня другая схема, в которую входит три проводника, и, в зависимости от того, что пришло на входы, я тоже хочу какое-то значение. Например, вот так. Не буду расписывать все варианты
По сути, у меня единственный возможный способ общаться с компьютером – это завести много функций от разного числа переменных, которые могут быть только 0 и 1 и которые на выходе дают тоже 0 или 1.
Можно посмотреть функцию от двух переменных и назвать ее f(1), функцию от трех переменных назовем f(2). Будут и другие функции, которые запишем в таблицы, переплету в многотомники и поставлю на полку. В случае, если мне нужно найти какую-то схему, достаю том, листаю страницы и нахожу то, что мне нужно.
Для компьютера это будет нормально, его устроит, если я выстрою с ним такой диалог. А вот человека такая схема работы не устроит, потому что людям очень сложно оперировать большими объемами информации без логического обоснования. Нам проще понять, как это работает, чем зубрить большое количество таблиц. Поэтому человек для облегчения своей жизни ввел аналогию – истину и ложь.
Наверняка вы помните детсадовские игры, когда можно задавать только вопросы, на которые можно ответить «да» или «нет», и нужно что-то угадать. Наверное, у детей изначально подсознательно заложена склонность к двоичному коду.
Поэтому человек поставил в соответствие аппарат логических высказываний, и теперь за 0 мы принимаем ложь, за 1 – истину. И выяснилось, что если я такими операциями буду оперировать, то все операции от трех, четырех, пяти и т. д. переменных я могу свести к функциям от двух переменных. А к каким же функциям?
Первая функция – это функция отрицания. Ее можно обозначить несколькими способами — .
Посмотрим, как это работает.
Если у меня высказывание ложное (например, я показываю маркер, а говорю, что это апельсин)
| 0 | |
| 1 |
А если я показываю маркер и говорю, что это не апельсин, то это истина
| 0 | 1 |
| 1 |
Если я наоборот говорю, что это маркер и показываю его, то это истина, а если я говорю, что это не маркер, это будет ложь
| 0 | 1 |
| 1 | 0 |
Следующая операция – это логическое ИЛИ, она же записывается как .
Покажу как это работает.
Функция от двух переменных работает следующим образом: например, я говорю, что это апельсин или это яблоко (то есть два ложных высказывания), в сумме получается 0; если я говорю, что это апельсин или это маркер, в целом я сказала правду, потому что одно из утверждений является истинным, то получается 1; если я говорю, что это маркер или это банан, опять же это правда; и наконец, если я говорю, что это маркер или это маркер, то есть два верных утверждения, это тоже правда
| 00 | 0 |
| 01 | 1 |
| 10 | 1 |
| 11 | 1 |
Вот таким образом работает функция. Акцентирую ваше внимание, что мне ненужно запоминать эти наборы. Конечно, они запомнятся после несколько десятков прорешанных задач, но эту таблицу истинности не надо запоминать, это вытекает из логики.
Акцентирую ваше внимание, что мне ненужно запоминать эти наборы. Конечно, они запомнятся после несколько десятков прорешанных задач, но эту таблицу истинности не надо запоминать, это вытекает из логики.
Далее логическое И — , &, знак умножения.
Посмотрим, как оно работает. Если я говорю два ложных утверждения – это яблоко и это банан – это ложь. Если я говорю, что это яблоко и это маркер – одно высказывание истина, но я же настаиваю на том, что и то, и другое должно выполняться, поэтому это ложь. Если я говорю, что это маркер и это банан, то это тоже ложь. И если я говорю два истинных утверждения – это маркер и это маркер – да, это правда
| 00 | 0 |
| 01 | 0 |
| 10 | 0 |
| 11 | 1 |
А умножение, потому что если 1 умножить на 0 или 0 на 1, то тоже будет 0, и только в случае умножения 1 на 1 получится 1.
Вот именно к этим операциям можно свести и все остальные, но не всегда удобно, поэтому еще две функции используется в курсе школьной программы – это импликация и эквивалентность.
Импликацию можно свести к вышеперечисленным, но удобнее ее использовать по-другому.
Импликация – это логическое следование
Не будем зубрить таблицу истинности, а попробуем понять.
Если у меня есть ложное высказывание (например, 2 больше 5), могу ли я получить из него ложь разрешенными функциями? Легко! Добавлю к двум частям неравенства единицу и получу ложь: 2>5, 3>6.
То есть мы можем получить изо лжи ложь.
А могу ли я изо лживого высказывания получить истину? Тоже могу. -5 больше -3. Это ложь? Ложь. А применим-ка разрешенную операцию – возведение в квадрат. И запросто получим истину: -5>-3, 25>9. То есть изо лжи истину мы тоже можем получить.
А вот из истины получить ложь никак не получится. Из истины можно получить только истину.
Ну и из истины истину получить, конечно же, возможно.
| 00 | 1 |
| 01 | 1 |
| 10 | 0 |
| 11 | 1 |
То есть не всегда удобно приводить импликацию к другим функциям. Потому что это замечательная функция, которая 0 дает в единственном случае, когда из истины следует ложь.
Потому что это замечательная функция, которая 0 дает в единственном случае, когда из истины следует ложь.
И последняя функция, часто употребляемая, – это функция эквивалентности, обозначается логическим равенством или взаимными стрелками
Здесь все очень просто. 0 равен 0? Да. 0 = 1? Нет. 1 равна 0? Нет. 1 равна 1? Да.
| 00 | 1 |
| 01 | 0 |
| 10 | 0 |
| 11 | 1 |
Мы логически обосновали все пять функций, и это избавляет нас от необходимости зубрить таблицы истинности. Да, мы их запомним в процессе решения задач, но гораздо проще логически понять, в чем суть вопроса.
Теперь приоритеты этих функций.
Если у нас не стоят никакие скобки, то все действия, как и в математике, имеют некоторый приоритет.
Вот такая cтрока без скобок
Первый приоритет имеет отрицание , оно прямо приклеивается к тому высказыванию, рядом с которым стоит , поэтому я всегда настаиваю использовать вот такой символ, черточку сверху , потому что это гораздо понятнее, что оно относится к высказыванию.
Следующий приоритет – умножение . То есть в нашем выражении у нас будет вот так
Третий приоритет у сложения , То есть вот так .
А дальше одинаковый приоритет имеют эквивалентность и импликация , слева на право. В нашем случае сначала выполнится сравнение на эквивалентность, а потом из этого импликация .
Все видео по информатике
Алгебра логики
Алгебра логики
Из курса информатики основной школы вы знаете, что для компьютерных наук большое значение имеет математическая логика, а точнее, её часть, называемая алгеброй логики.
|
Алгебра логики — раздел математики, изучающий высказывания, рассматриваемые с точки зрения их логических значений (истинности или ложности), и логические операции над ними. |
Джордж Буль (1815-1864) — английский математик, основоположник алгебры логики. Дж. Буль изучал логику мышления математическими методами и разработал алгебраические методы решения традиционных логических задач. В 1854 году он опубликовал работу, в которой изложил суть алгебры логики, основанной на трёх операциях: and, or, not. Долгое время алгебра логики была известна достаточно узкому классу специалистов. В 1938 году Клод Шеннон применил алгебру логики для описания процесса функционирования релейноконтактных и электронно-ламповых схем.
В 1854 году он опубликовал работу, в которой изложил суть алгебры логики, основанной на трёх операциях: and, or, not. Долгое время алгебра логики была известна достаточно узкому классу специалистов. В 1938 году Клод Шеннон применил алгебру логики для описания процесса функционирования релейноконтактных и электронно-ламповых схем.
|
Высказывание — это предложение, в отношении которого можно сказать, истинно оно или ложно. |
Например, высказывание «Джордж Буль — основоположник алгебры логики» истинно, а высказывание «2 + 2 = 5» ложно.
Что вы можете сказать об истинности или ложности предложения «Данное высказывание — ложь»?
Из имеющихся высказываний можно строить новые высказывания. Для этого используются логические связки — слова и словосочетания «не», «и», «или», «если …, то», «тогда и только тогда» и др.
|
Высказывания, образованные из других высказываний, называются составными (сложными). |
Например, из двух простых высказываний «Алгебра логики является основой строения логических схем компьютеров» и «Алгебра логики служит математической основой решения сложных логических задач» можно получить составное высказывание «Алгебра логики является основой строения логических схем компьютеров и служит математической основой решения сложных логических задач».
Обоснование истинности или ложности элементарных высказываний не является задачей алгебры логики. Эти вопросы решаются теми науками, к сфере которых относятся элементарные высказывания. Такое сужение интересов позволяет обозначать высказывания символическими именами (например, А, B, С). Так, если обозначить элементарное высказывание «Джордж Буль — основоположник алгебры логики» именем А, а элементарное высказывание «2 + 2 = 5» именем B, то составное высказывание «Джордж Буль — основоположник алгебры логики, и 2 + 2 = 5» можно записать как «А и B». Здесь А, В — логические переменные, «и» — логическая связка.
Здесь А, В — логические переменные, «и» — логическая связка.
|
Логическая переменная — это переменная, которая обозначает любое высказывание и может принимать логические значения «истина» или «ложь». |
Для логических значений «истина» и «ложь» могут использоваться следующие обозначения:
Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).
|
Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний. |
Из курса информатики основной школы вам известны логические операции отрицание, конъюнкция и дизъюнкция. Их таблицы истинности представлены ниже.
Их таблицы истинности представлены ниже.
|
Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны, называется конъюнкцией или логическим умножением. Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны, называется дизъюнкцией или логическим сложением. Логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному, называется отрицанием или инверсией. При построении отрицания простого высказывания:
|
Рассмотрим несколько новых логических операций.
|
Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся ложным тогда и только тогда, когда первое высказывание (посылка) истинно, а второе (следствие) — ложно, называется импликацией или логическим следованием. |
Операция импликации обозначается символом -» и задаётся следующей таблицей истинности:
В разговорной речи импликации соответствуют предложения, содержащие связку «если …, то». Эту связку мы используем тогда, когда хотим показать наличие причинно-следственной связи, иначе говоря, зависимость одного события от другого. Например, пусть некоторый человек сказал: «Если завтра будет хорошая погода, то я пойду гулять». Ясно, что человек окажется лжецом лишь в том случае, если погода действительно будет хорошей, а гулять он не пойдёт. Если же погода будет плохой, то, независимо от того, пойдёт он гулять или нет, во лжи его нельзя обвинить: обещание пойти гулять он давал лишь при условии, что погода будет хорошей.
Если же погода будет плохой, то, независимо от того, пойдёт он гулять или нет, во лжи его нельзя обвинить: обещание пойти гулять он давал лишь при условии, что погода будет хорошей.
Результат операции импликации, как и других логических операций, определяется истинностью или ложностью логических переменных, а не наличием причинно-следственных связей между высказываниями. Например, абсурдное с житейской точки зрения высказывание «Если 2 > 3, то существуют ведьмы» является истинным с точки зрения алгебры логики.
|
Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным тогда и только тогда, когда только одно из двух высказываний истинно, называется строгой (исключающей) дизъюнкцией. |
Строгая дизъюнкция обозначается символом ⊕ и задаётся следующей таблицей истинности:
В русском языке строгой (разделительной) дизъюнкции соответствует связка «либо». В отличие от обычной дизъюнкции (связка «или») в высказывании, содержащем строгую дизъюнкцию, мы утверждаем, что произойдёт только одно событие.
В отличие от обычной дизъюнкции (связка «или») в высказывании, содержащем строгую дизъюнкцию, мы утверждаем, что произойдёт только одно событие.
Например, высказывая утверждение «На сегодняшнем матче Петя сидит на трибуне А либо на трибуне Б», мы считаем, что Петя сидит либо только на трибуне А, либо только на трибуне Б, и что сидеть одновременно на двух трибунах Петя не может.
|
Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным, когда оба исходных высказывания истинны или оба исходных высказывания ложны, называется эквиваленцией или равнозначностью. |
В логике эквиваленция обозначается символом ↔ и задаётся следующей таблицей истинности:
В разговорной речи для выражения взаимной обусловленности используется связка «тогда и только тогда, когда», а в математике — «необходимо и достаточно».
Рассмотрим высказывание «Денис пойдёт в бассейн тогда и только тогда, когда он выучит уроки».
Это высказывание истинно (договорённость соблюдается), если истинны оба элементарных высказывания («Денис пойдёт в бассейн», «Денис выучит уроки»). Высказывание истинно (договорённость не нарушается) и в том случае, если оба элементарных высказывания ложны («Денис не пойдёт в бассейн», «Денис не выучит уроки»). Если же одно из двух высказываний ложно («Денис пойдёт в бассейн, хотя и не выучит уроки», «Денис выучит уроки, но не пойдёт в бассейн»), то договорённость нарушается, и составное высказывание становится ложным.
А сейчас посмотрите внимательно на таблицы истинности строгой дизъюнкции и эквиваленции: если на некотором наборе логических переменных результатом строгой дизъюнкции является истина, то на этом же наборе результатом эквиваленции всегда будет ложь, и наоборот. Можно сделать выводы:
- операция эквиваленции есть отрицание операции строгой дизъюнкции
- операция строгой дизъюнкции есть отрицание операции эквиваленции
На сегодняшний день в алгебре логики не существует унифицированной символики для обозначения логических операций.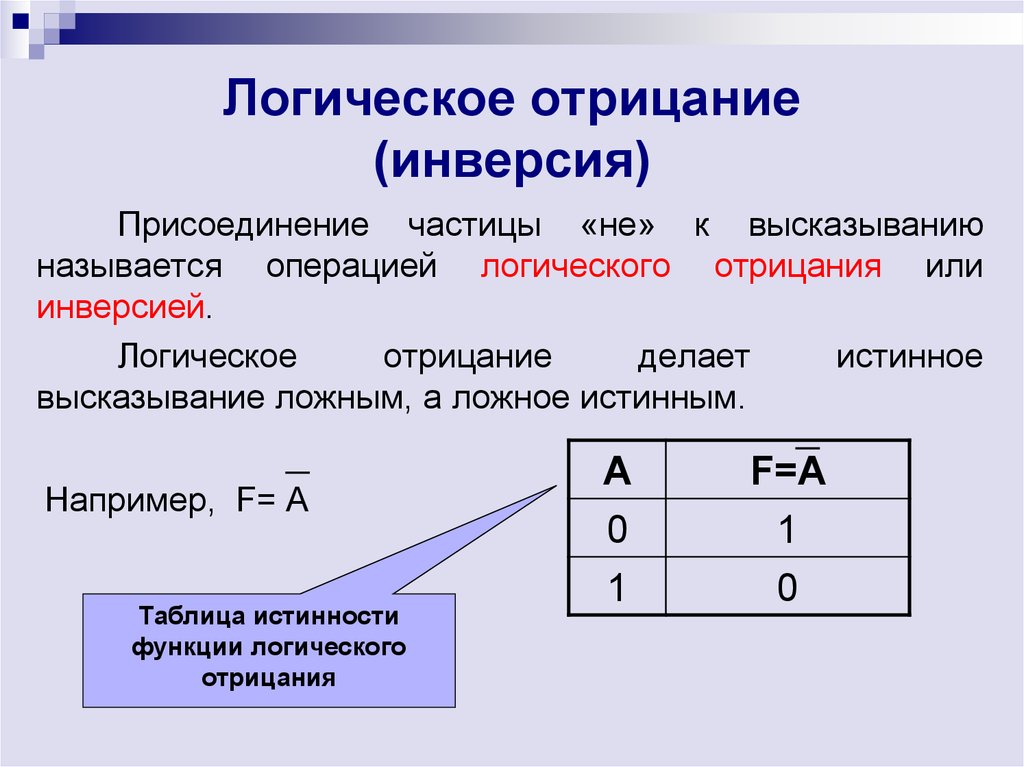 В таблице 4.1 представлены логические операции и их наиболее распространённые обозначения, используемые как в алгебре логики, так и в некоторых языках программирования. Здесь же приведены речевые обороты, соответствующие логическим операциям.
В таблице 4.1 представлены логические операции и их наиболее распространённые обозначения, используемые как в алгебре логики, так и в некоторых языках программирования. Здесь же приведены речевые обороты, соответствующие логическим операциям.
Операция отрицания выполняется над одним операндом. Такие операции называются одноместными или унарными. Все остальные логические операции, представленные в таблице 4.1, выполняются над двумя операндами и называются двуместными или бинарными.
|
Составное логическое высказывание можно представить в виде логического выражения (формулы), состоящего из логических констант (0, 1), логических переменных, знаков логических операций и скобок. |
Для логического выражения справедливо:
1) всякая логическая переменная, а также логические константы (0, 1) есть логическое выражение;
2) если А — логическое выражение, то и А — логическое выражение;
3) если А и В — выражения, то, связанные любой бинарной операцией, они также представляют собой логическое выражение.
При преобразовании или вычислении значения логического выражения логические операции выполняются в соответствии с их приоритетом:
1) отрицание;
2) конъюнкция;
3) дизъюнкция, строгая дизъюнкция;
4) импликация, эквиваленция.
Операции одного приоритета выполняются в порядке их следования, слева направо. Как и в арифметике, скобки меняют порядок выполнения операций.
Пример 1. Выясним, какие из приведённых слов удовлетворяют логическому условию (первая буква согласная → вторая буква согласная) & (последняя буква гласная → предпоследняя буква гласная):
1) ОЗОН;
2) ИГРА;
3) МАФИЯ;
4) ТРЕНАЖ.
Вычислим значение логического выражения для каждого из данных слов:
1) (0 → 1) & (0 → 1) = 1 & 1 = 1;
2) (0 → 1) & (1 → 0) = 1 & 0 = 0;
3) (1 → 0) & (1 → 1) — 0 & 1 = 0;
4) (1 → 1) & (0 → 1) = 1 & 1 = 1.
Итак, заданному условию удовлетворяют первое и четвёртое слова.
Решение логического уравнения — это один или несколько наборов значений логических переменных, при которых логическое уравнение становится истинным выражением.
Пример 2. Решим логическое уравнение
Дизъюнкция ложна в том и только в том случае, когда ложно каждое из образующих её высказываний. Иными словами, наше уравнение соответствует системе уравнений:
Таким образом, значение переменной D уже найдено. Импликация равна нулю в единственном случае — когда из истины следует ложь. Иначе говоря, в нашем случае: А = 1 и С = 0.
Подставим найденные значения переменных в уравнение Получим: или т. е. В = 1.
Ответ: А = 1, В = 1, С = 0, D = 0.
Логические уравнения могут иметь не одно, а несколько и даже очень много решений. Зачастую требуется, не выписывая все решения уравнения, указать их количество.
Пример 3. Выясним, сколько различных решений имеет логическое уравнение
Дизъюнкция истинна, если истинно хотя бы одно из образующих её высказываний.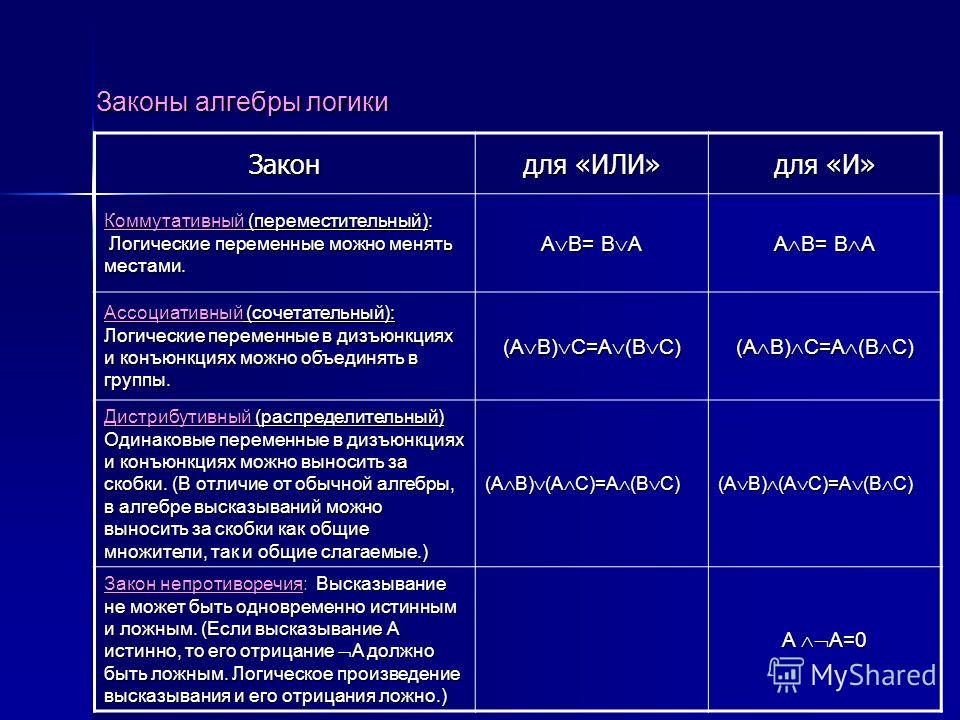 Решение данного логического уравнения равносильно совокупности, состоящей из двух уравнений:
Решение данного логического уравнения равносильно совокупности, состоящей из двух уравнений:
Первое равенство будет выполняться только при А = 1, В = 1 и С = 0. Поскольку D в этом уравнении не задействовано, оно может принимать любое из двух значений (0 или 1). Таким образом, всего первое уравнение имеет два решения.
Самостоятельно выясните, сколько решений имеет второе уравнение (из совокупности двух уравнений).
Сколько решений имеет исходное уравнение?
Пример 4. Выясним, сколько решений имеет очень простое с виду логическое уравнение х1 & х2 → х3 & х4 = 1.
Введём замену переменных. Пусть t1 = х1 & х2, t2 = х3 & х4. Тогда исходное уравнение примет вид: t1 ↔ t2 = 1.
На t1 никаких ограничений нет, эта переменная может принимать значения 0 и 1. Импликация равна 0 только в случае, когда из истины (1) следует ложь (0). Исключим этот вариант. Построим дерево решений, представив на нём значения переменных t1 и t2y при которых t1 ↔ t2 = 1.
Импликация равна 0 только в случае, когда из истины (1) следует ложь (0). Исключим этот вариант. Построим дерево решений, представив на нём значения переменных t1 и t2y при которых t1 ↔ t2 = 1.
Получаем для t1 и t2 три набора значений: 00, 01, 11. Первая двоичная цифра в каждом из этих трёх наборов — результат выражения х1 & х2, вторая — х3 & х4. Рассмотрим первый набор: существует три набора х1 и х2 таких, что х1 & х2 = 0, другими словами, первый 0 мы можем получить тремя способами. Второй 0 в этом наборе мы также можем получить тремя способами.
Из курсов информатики и математики основной школы вам известно одно из основных правил комбинаторики — правило умножения. Согласно ему, если элемент А можно выбрать n способами, и при любом выборе А элемент В можно выбрать m способами, то пару (А, В) можно выбрать n • m способами.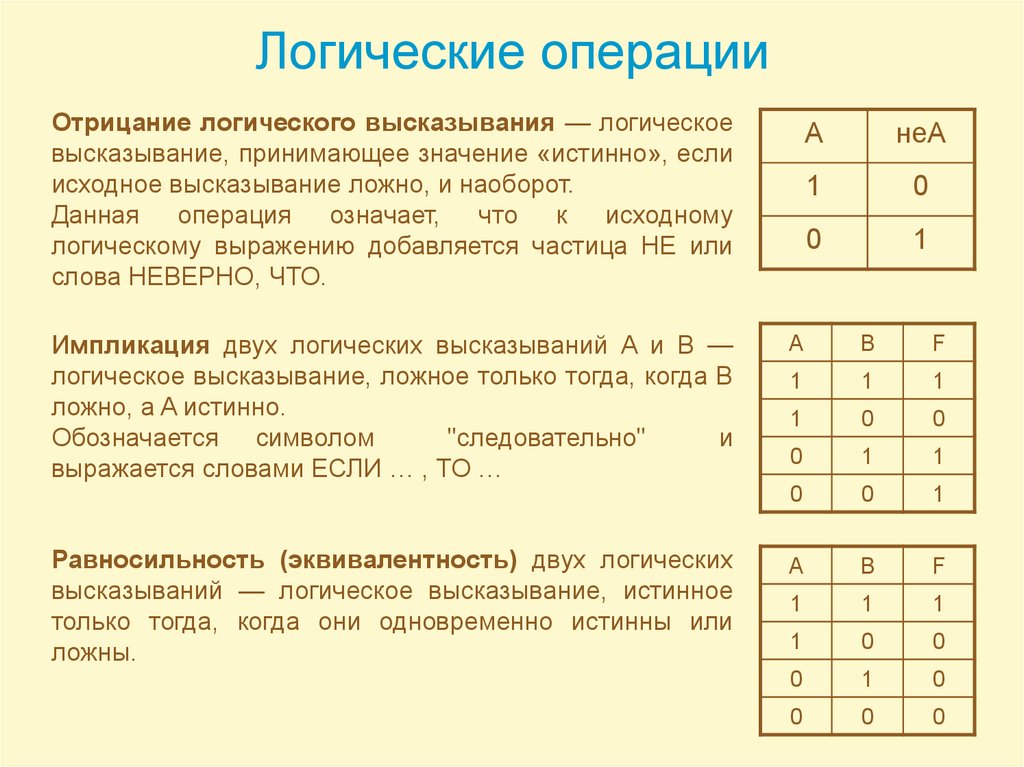
Согласно правилу умножения, пару 00 можно получить 3 • 3 = 9 способами.
Что касается пары 01, то первый 0 мы можем получить тремя способами, а для получения 1 существует единственный вариант (x3 & х4 = 1 при x3 = 1 и x4 = 1). Следовательно, есть ещё три набора переменных х1, х2, х3, х4, являющихся решением исходного уравнения.
Самостоятельно доведите решение этой задачи до конца.
Равенства, неравенства и другие предложения, содержащие переменные, высказываниями не являются, но они становятся высказываниями при замене переменной каким-нибудь конкретным значением. Например, предложение х < 12 становится истинным высказыванием при x = 5 (5 < 12 — истина) и ложным при x = 15 (15 < 12 — ложь). Предложения такого рода называют высказывательными формами или предикатами.
|
Предикет — это утверждение, содержащее одну или несколько переменных. |
Выделим некоторый предикат Р(x) и рассмотрим множество всевозможных объектов I, к которым он относится, — область определения предиката. Можно выделить такое подмножество Р множества I, что на всех его элементах предикат Р(х) будет превращаться в истинное высказывание. Определённое таким образом Р называется множеством истинности предиката Р(х).
Рассмотрим множество учеников некоторого класса. Известно, что в этом классе два отличника — Иван и Саша. Предикат «Он отличник» будет истинным высказыванием только по отношению к этим двум ученикам и ложным по отношению ко всем остальным.
Предикаты позволяют задать множество, не перечисляя всех его элементов. Например, множество истинности предиката Р(х) = (х < 0) — множество отрицательных чисел; множество истинности предиката Р(х, у) = (х2 + у2 = 1) — множество точек окружности единичного радиуса с центром в начале координат. Следует отметить, что многие задания, выполняемые вами на уроках математики, прямо связаны с предикатами.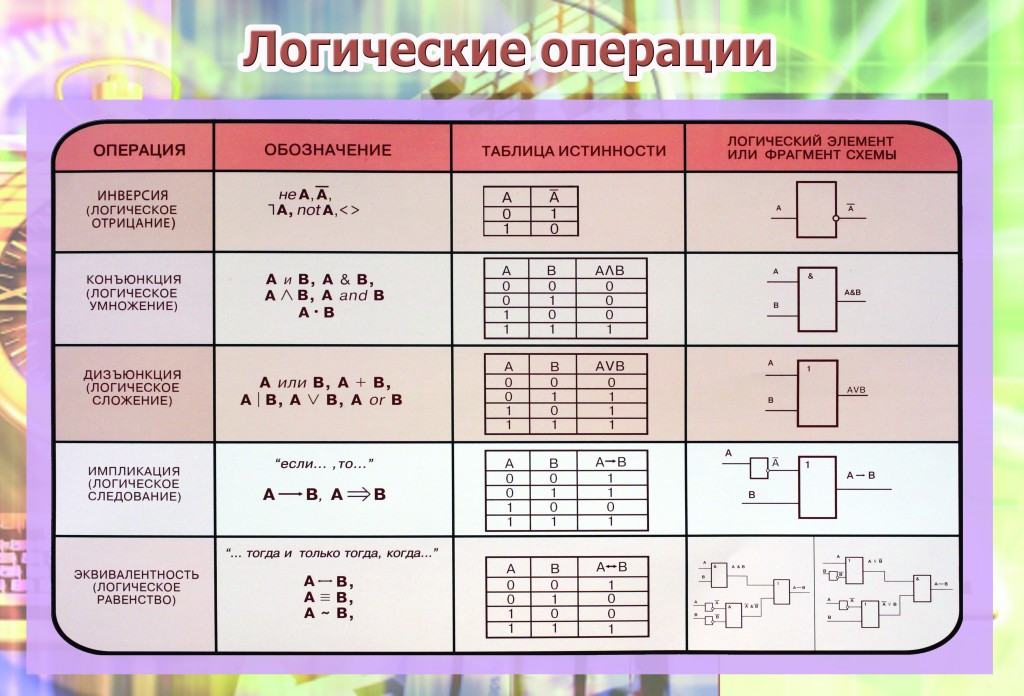 Например, стандартное задание «Решить квадратное уравнение х2 — 3х + 2 = 0» фактически означает требование найти множество истинности предиката Р(х) = (х2 — 3х + 2 = 0).
Например, стандартное задание «Решить квадратное уравнение х2 — 3х + 2 = 0» фактически означает требование найти множество истинности предиката Р(х) = (х2 — 3х + 2 = 0).
Из имеющихся предикатов с помощью логических операций можно строить новые предикаты.
Пусть А и В соответственно являются множествами истинности предикатов А(х) и В(х). Тогда пересечение множеств А и В будет являться множеством истинности для предиката А(х) & В(х), а объединение множеств А и В будет множеством истинности для предиката
Пример 5.
Найдём все целые числа 2, превращающие предикат
P(z) = (2 > 5) & (z — 2 < 15)
в истинное высказывание. Другими словами, требуется найти множество истинности предиката P(z), заданного на множестве целых чисел
Предикат P(z) состоит из двух предикатов, соединённых операцией конъюнкции: P(z) = A(z) & B(z). Рассмотрим каждый из них в отдельности.
Множеством истинности предиката A(z) = (z > 5) являются целые числа 6, 7, 8 и т.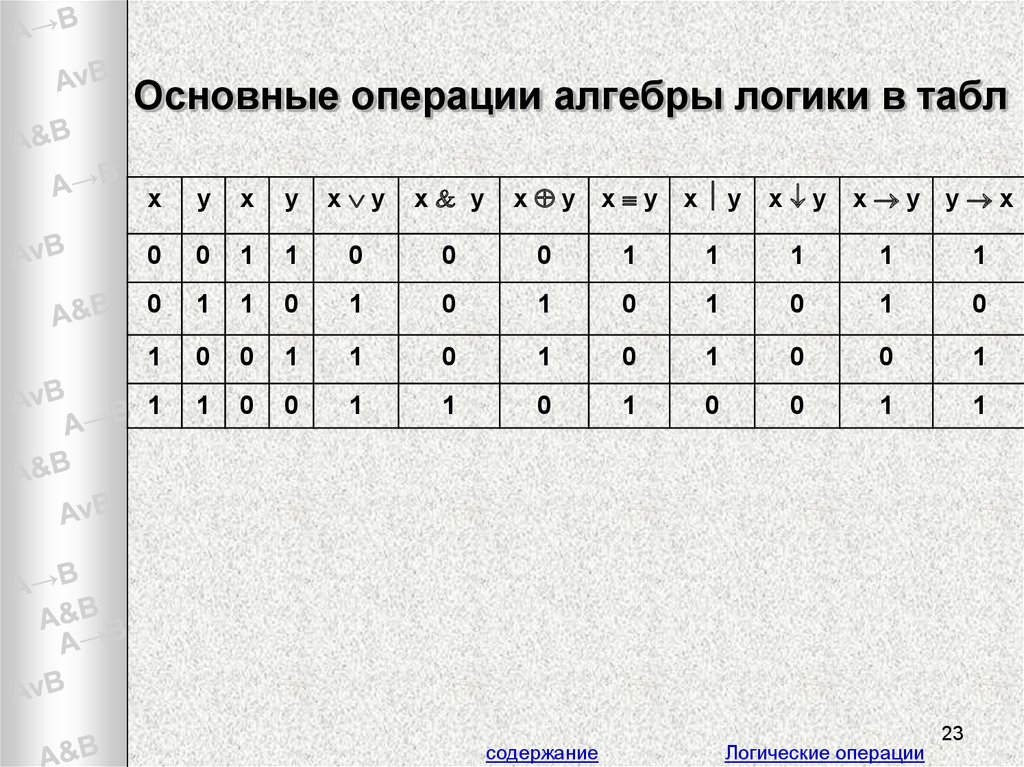 д. Множеством истинности предиката B(z) = (z — 2 < 15) являются все целые числа, меньшие 17.
д. Множеством истинности предиката B(z) = (z — 2 < 15) являются все целые числа, меньшие 17.
Множество истинности исходного предиката — пересечение (общие элементы) множеств истинности образующих его предикатов:
|P| = A ∩ B = {6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,}
Его мощность P = 11.
Пример 6. Рассмотрим предикат (50 < х2) → (50 > (х + 1)2), определённый на множестве целых чисел. Найдём множество истинности этого предиката.
|
Зачастую задания такого рода формулируют несколько иначе. Например, так: «Найдите все целые числа х, для которых истинно высказывание (50 < х2) → (50 > (х + 1)2)». |
Проанализируем отдельно каждый из элементарных предикатов (50 < х2) → (50 > (х + 1)2), решив соответствующие неравенства:
50 < х2 истинно для всех целых х ⊂ ]-∞; -8] ∪ [8; +∞[;
50 > (m + 1)2 истинно для всех целых х ⊂ [8; 6].
Определим значение исходного предиката на каждом из полученных подмножеств, причём отдельно рассмотрим значение х = -8 (оно попадает в два подмножества) и значение х = 7 (оно не попадает ни в одно подмножество):
Итак, множеством истинности исходного предиката являются целые числа, принадлежащие отрезку [-8; 7]. Наименьшим элементом этого множества является число -8, наибольшим — число 7; мощность множества равна 16.
Самое главное
Высказывание — это предложение, в отношении которого можно сказать, истинно оно или ложно. Высказывания, образованные из других высказываний, называются составными (сложными). Высказывание, никакая часть которого не является высказыванием, называется элементарным (простым). Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).
Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний.
Составное логическое высказывание можно представить в виде логического выражения (формулы), состоящего из логических констант (0, 1), логических переменных, знаков логических операций и скобок.
Логические операции имеют следующий приоритет:
1) отрицание;
2) конъюнкция;
3) дизъюнкция, строгая дизъюнкция;
4) импликация, эквиваленция.
Операции одного приоритета выполняются в порядке их следования, слева направо. Скобки меняют порядок выполнения операций.
Предикат — это утверждение, содержащее одну или несколько переменных. Из имеющихся предикатов с помощью логических операций можно строить новые предикаты.
Почему логика важна для информатики и математики
Чешский перевод этой страницы доступен по адресу Scientific и технический перевод .
Шведский перевод этой страницы доступен по адресу
Научный блог: https://www. expertoautorecambios.es/science/?p=998 .
expertoautorecambios.es/science/?p=998 .
Эстонский перевод этой страницы доступен по адресу:
https://www.espertoautoricambi.it/science/2017/11/03/miks-loogika-on-oluline-et-arvuti-teadust-ja-matemaatika/
4
7 A Португальский перевод этой страницы доступен по адресу:
https://www.homeyou.com/~edu/ciencia-da-computacao-e-matematica
Логика связана с формами рассуждений. С
рассуждение участвует в большинстве интеллектуальных действий, логика имеет отношение к
широкий круг занятий. Изучение логики необходимо для школьников.
Информатика. Это также очень ценно для студентов, изучающих математику, и других
которые используют математические доказательства, например, студенты-лингвисты. в
процесс рассуждения делает выводы. В выводе используется
совокупность утверждений, предпосылок, чтобы оправдать другое утверждение,
вывод. Наиболее надежными типами умозаключений являются дедуктивные умозаключения,
в котором заключение должно быть истинным, если посылки верны. Вспомнить элементарно
геометрия: Предполагая, что постулаты верны, мы доказываем, что другие
утверждения, такие как теорема Пифагора, также должны быть истинными. Геометрический
доказательства и другие математические доказательства обычно используют множество дедуктивных выводов.
Наиболее надежными типами умозаключений являются дедуктивные умозаключения,
в котором заключение должно быть истинным, если посылки верны. Вспомнить элементарно
геометрия: Предполагая, что постулаты верны, мы доказываем, что другие
утверждения, такие как теорема Пифагора, также должны быть истинными. Геометрический
доказательства и другие математические доказательства обычно используют множество дедуктивных выводов.
Большинство наших курсов логики включают точный анализ характеристик
дедуктивный вывод. Эти курсы вводят некоторые специальные символы в то, что
называется «формальными языками», но логика не является операцией с символами. Курсы
обучать общим понятиям и методам, которые полезны независимо от формальных
языки. Студенты узнают, как строить доказательства на английском языке, а также на
формальный язык, так что понятия и методы, которые изучены, могут быть использованы в
разнообразие контекстов. Учатся даже доказывать теоремы о формальных
языки; это особенно важно для информатики, лингвистики и
некоторые разделы математики.
Идея компьютера общего назначения, машины Тьюринга, была изобретена в
курс исследований по логике. Программы для ЭВМ пишутся на специальных,
символьные языки, например, Fortran, C++, Lisp, Prolog.
Эти языки содержат черты логического символизма, а Лисп и Пролог
производные от формальных языков для логики. Благодаря таким связям изучение
логика может помочь в разработке программ. Другие математические методы
описанные в PHL 313K, например рекурсивные определения, широко используются в программах.
Теория множеств, описанная в PHL 313K, используется в современных проектах баз данных. Но
информатика — это не только программирование. включает в себя логические и
математический анализ программ. С помощью таких анализов можно доказать
корректность процедур и оценить количество шагов, необходимых для выполнения
заданную программу. В такой работе используется современная логика, и она заложена
в программы, которые помогают построить доказательства таких результатов. Логика тоже играет роль
в разработке новых языков программирования, и это необходимо для работы в
искусственный интеллект и когнитивная наука. Некоторые части логики используются
инженеры по схемотехнике.
Некоторые части логики используются
инженеры по схемотехнике.
Понимание предметов, преподаваемых в PHL 313K, требуется для успешная специальность по информатике: 1. Так же, как исчисление используется в инженерных курсах, основы логики и теории множеств используются во многих курсы информатики. 2. Курсы CS для старших классов не являются программированием. сверла; эти курсы охватывают общие принципы и требуют математических доказательств об этих принципах. PHL 313K обучает основным принципам и методам построение и оценка доказательств.
Математики рассуждают об абстрактных понятиях, например, непрерывных
функции, алгебраические системы, такие как «кольца», и топологические пространства. Самый
студенты-математики учатся писать доказательства таких вещей, следуя примерам в
их классы. Это часть изучения математики, но она медленная и часто приводит к
к путаницам. Специалисты по математике, изучающие логику, обнаруживают, что она помогает им в их учебе.
математическое мышление. Это помогает избежать путаницы и помогает в
построение ясных, убедительных доказательств. Изучение логики необходимо для работы
в основаниях математики, которая в значительной степени связана с природой
математической истины и с обосновывающими доказательствами математических объектов,
такие как целые числа, комплексные числа и бесконечные множества. Математические специальности в UT не
необходимо пройти курс логики, но те, кто это делает, почти всегда сообщают, что это
интересно и полезно.
Это помогает избежать путаницы и помогает в
построение ясных, убедительных доказательств. Изучение логики необходимо для работы
в основаниях математики, которая в значительной степени связана с природой
математической истины и с обосновывающими доказательствами математических объектов,
такие как целые числа, комплексные числа и бесконечные множества. Математические специальности в UT не
необходимо пройти курс логики, но те, кто это делает, почти всегда сообщают, что это
интересно и полезно.
PHL 313K — введение в логику, элементарную теорию множеств, основы теории чисел и использования индукции и рекурсии. Это требует серьезного изучения, но он охватывает интересный и полезный материал. Хорошие курсы повышения квалификации, для студентов, заинтересованных в более продвинутой логике, есть PHL 344K (= M 344K) и PHL. 358.
Роберт Л. Кози
Обновление RLC: 22.09.17
Справочник по логике в компьютерных науках: Том 5.
 Алгебраические и логические структуры
Алгебраические и логические структурыИконка Цитировать Цитировать
Разрешения
- Делиться
- Твиттер
- Подробнее
Cite
Abramsky, S, Dov M Gabbay, and TS E Maibaum (eds),
Handbook of Logic in Computer Science: Volume 5. Algebraic and Logical Structures
(
Oxford,
000109 online;9 20009 edn,Oxford Academic
, 12 ноября 2020 г.
), https://doi.org/10.1093/oso/9780198537816.001.0001,
по состоянию на 27 сентября 2022 г.
Выберите формат
Выберите format. ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Фильтр поиска панели навигации Oxford Academic Handbook of Logic in Computer Science: Volume 5. Algebraic and Logical StructuresComputer Architecture and Logic DesignBooksJournals Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford Academic Handbook of Logic in Computer Science: Volume 5. Algebraic and Logical StructuresComputer Architecture and Logic DesignBooksJournals Термин поиска на микросайте
Расширенный поиск
Abstract
В настоящее время логика широко признана одной из основополагающих дисциплин вычислительной техники, и ее приложения охватывают почти все аспекты предмета, от разработки программного обеспечения и аппаратного обеспечения до языков программирования и искусственного интеллекта. Справочник по логике в компьютерных науках — это многотомный труд, охватывающий все основные области применения логики в теоретической информатике. Справочник состоит из шести томов, каждый из которых содержит пять или шесть глав, дающих углубленный обзор одной из основных тем в данной области. Это результат многолетней совместной работы некоторых из самых выдающихся передовых исследователей в этой области, и, несомненно, он станет стандартным справочником по логике и теоретической информатике на долгие годы. Том 5: Алгебраические и логические структуры охватывает все основные темы семантики в логике и вычислениях. Обширные главы являются результатом нескольких лет скоординированных исследований, и каждая из них имеет тематическую перспективу. Вместе они предлагают читателю новейшие исследовательские работы, и книга станет незаменимой
Справочник по логике в компьютерных науках — это многотомный труд, охватывающий все основные области применения логики в теоретической информатике. Справочник состоит из шести томов, каждый из которых содержит пять или шесть глав, дающих углубленный обзор одной из основных тем в данной области. Это результат многолетней совместной работы некоторых из самых выдающихся передовых исследователей в этой области, и, несомненно, он станет стандартным справочником по логике и теоретической информатике на долгие годы. Том 5: Алгебраические и логические структуры охватывает все основные темы семантики в логике и вычислениях. Обширные главы являются результатом нескольких лет скоординированных исследований, и каждая из них имеет тематическую перспективу. Вместе они предлагают читателю новейшие исследовательские работы, и книга станет незаменимой
Предмет
Компьютерная архитектура и логическое проектирование
Содержание
Передний вопрос
- Расширять Титульные страницы
- Расширять Предисловие
- Авторы
- Расширять Титульные страницы
- Расширять Теория типов Мартина-Лёфа
- Расширять Категориальная логика
- Расширять Единый метод доказательства нижних оценок вычислительной сложности логических теорий
- Расширять Алгебраическая спецификация абстрактных типов данных
- » data-targeturl=»/book/40635/chapter/3482 «/>
Конец Материи
- 525Индекс
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Нажмите Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением.
 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. - После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом.
 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. - После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.

- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
Покупка
Наши книги можно приобрести по подписке или приобрести в библиотеках и учреждениях.
Информация о покупке
Реклама
Реклама
научно-исследовательских центров
научно-исследовательских центровИсследовательские группы и центры: Европа — Северная Америка — прочие
Публикации — Блоги — Организации и конференции — Почтовое отправление списки — Программное обеспечение — Другое
Вот список исследовательских групп и отделов (и некоторых
отдельные специалисты по логике в других отделах) в
основы математики и информатики (логика, множество
теория, теория моделей, теоретическая информатика, теория доказательств,
языки программирования).
Европа
Австрия
- Линц :
- Институт Формальные модели и проверка
- Институт математических систем, основанных на знаниях (FLLL — Лаборатория нечеткой логики Линц-Хагенберг)
- Научно-исследовательский институт символьных вычислений (Institut für Symbolisches Rehnen)
- Вена
- Курт Гёдель Исследовательский центр математической логики Университета Вена
- Общество Курта Гёделя
- Группа теории и логики,
Венский технологический университет — Группа приложений
Формальная логика. Области исследования: на основе разрешения и таблиц
доказательство теорем — Неклассическая логика — Молекулярные вычисления —
Формальные языки — Обоснование уравнений и переписывание терминов —
Формальные методы спецификации и проверки.

- Группа формальных методов в системной инженерии Венского технического университета
- Алгебра (Руководитель: Мартин Голдстерн ) включает математическую логику, универсальную алгебру, приложения теории множеств и теории моделей
- Вычислительная логика группа
- Институт Граца теоретической информатики
Бельгия
Национальный центр исследований de Logique (CNRL / NCNL) стремится содействовать и координировать математические и философские исследования в области логики среди бельгийских университетские учреждения.Бельгийское общество логики и Философия науки (BSLPS) направлена на продвижение бельгийского исследований в области логики и философии науки, приглашая выдающиеся исследователи для обсуждения своей работы.
- Брюссель
- Логика mathématique (в ULB): теории множеств, теория моделей, неклассическая логика, теоретическая информатика.
- Центр по логике и философии науки, Свободный университет Брюссель
- Сентер Федере ан
Верификация (CFV) включает в себя все исследовательские группы из
Французская часть Бельгии заинтересована в компьютерных
проверка.
 Организует ежемесячные семинары.
Организует ежемесячные семинары. - Гент: Центр Логика и философия науки.
- Адаптивный Домашняя страница логики: программа адаптивной логики нацелена на разработка типа формальной логики, пригодной для объяснения много интересных динамических отношений следствий, которые происходят в человеческое мышление, но для которого нет положительного теста
- Грайфсвальд: Arbeitsgruppe Berechenbarkeitstheorie über алгебраическая структура = Исследование Групповая теория вычислимости над алгебраическими структурами
- Левен
- Центр логики и Аналитическая философия
- Группа ДТАИ (Declaratieve Talen en Artificiele Intelligentie = декларативный Языки и искусственный интеллект)
- Функциональный Программирование
- Теоретическая Информатика
- Льеж: Unité de Recherches en Métaphysique et Théorie de la connaissance, Департамент философии
- Лувен-ла-Нев :
- ЦЕНТРАЛЬНЫЙ (Centre de Traitement Informatique du Langage — Центр естественных Language Processing) — это вычислительная центр при Факультете философии и литературы и специализируется на изучении обработки естественного языка
- Теория де категории
- Монс:
- Служба де Математическая логика
- Институт Информатика
- Теоретическая Информатика
- Алгоритмы
Лабораторная работа: обучение (алгоритмы, программирование, искусственные
Интеллект и др.
 ), исследовательская деятельность (Extremal Graph
Теория и компьютерные научные открытия).
), исследовательская деятельность (Extremal Graph
Теория и компьютерные научные открытия).
Болгария
- Департамент Математическая логика и приложения, Софийский университет
- Болгарская академия наук
- Алгебра и логического отдела
- математический
Основы информатики
Чехия
- Брно
- Факультет информатики
:
- Естественный язык Процессинговый центр
- Лаборатория Формальных методов, логики и алгоритмов (Формела)
- Философский факультет
- Прозрачный Интенсивный логика
- Обучение
ресурсы по логике на чешском языке
- Острава
- Институт исследований и Приложения нечеткого моделирования
- Лаборатория Интеллекта Системы
- Пльзень (Западночешский университет)
- Институт для теоретической информатики (ITI)
- Яна
Блобнер (ультрафильтры)
- Прага
- Карлов университет
- Департамент теоретической информатики и математической логики
- Кафедра логики
на философском факультете
- Чешский технический университет в Праге: автоматизированный Reasoning Group разрабатывает проект Artificial Интеллект для крупномасштабных компьютерных рассуждений
- Академия наук
- Институт математики: математический Логика, алгебра и теоретическая информатика (MLATCS)
- автоматическое управление
- принуждение в теории множеств
- математическая логика и теория сложности
- Институт философии: Кафедра логики
- Теоретическая
Информатика
Дания
БРИКС (Фундаментальные исследования в компьютерной
Science) был исследовательским центром и школой докторантуры, финансируемой
Датский национальный исследовательский фонд с 1994 по 2006 год.
- Орхус :
- Логика и семантика
- математический Информатика
- Программирование
языки
- Копенгаген: Алгоритмы и группа языков программирования
- Копенгаген — Kongens Lyngby (Технический университет Дании):
- Алгоритмы, Логика и графики
- Формальные методы
- Роскилле: Программирование, Группа логики и интеллектуальных систем в Роскилле университет, исследует основы, инструменты и языки для разработка адаптируемого, надежного, ориентированного на человека компьютера системы.
- Южная Дания: Программирование
Языки и проверка
Эстония
- Таллин: Исследовательская группа и лаборатория логики и семантики
наук программного обеспечения, Институт кибернетики
Финляндия
- Хельсинки
- Логическая группа
: теория моделей, теория множеств, теория конечных моделей, логика и
анализ, другие темы.

- Теоретическая философия
- Вычислительный Лингвистика
- Аалто
- Алгоритмы, Логика и вычисления — Вычислительная логика
- Семантические вычисления Исследовательская группа
- Тампере: математический
Логика
- Конечная модель
теория в Финляндии
Франция
Париж и окрестности
- Мастер Parisien de Recherche en Informatique (MPRI)
- Париж
1: Логика преподавание на философском факультете
- Университет Париж 7 (Дени-Дидро)
- Эквип де Логик Математика
- Мастер
2 математической логики и основ компьютера
Наука
- Laboratoire Preuves, Programs et Systèmes, (Proofs, Программы и системы) Проектирование, изучение и внедрение языков для пруфов и программ
- INRIA — πr² аффилированные члены
- Париж 12 (Кретей): LACL (Алгоритмический, Сложность и Лаборатория логики)
- Логика, вычисления и Программирование
- ЭНС Париж: АБСТРАКЦИЯ (интерпретация abstraite et analysis statique = Аннотация Интерпретация и статический анализ) — личное дело руководителя группы веб-сайт (связанный с Paris — Rocquencourt INRIA)
- Париж, исследовательский центр INRIA
- ГАЛЛИУМ : Программирование языки, типы, составление и корректура
- Просекко
исследовательская группа: формальное и практическое исследование безопасности на
криптографические протоколы, безопасность программного обеспечения, веб-безопасность и
аппаратные защитные механизмы.

- Deducteam : Дедукция Модуль, интероперабельность и автоматическая демонстрация — Жиль Доуек (была ведущей ЛОГИЧЕСКОЙ : Логика и вычисления в INRIA)
- Институт истории и Философия науки и техники (IHPST)
- Логика, язык, философия математики
- Орсе — Сакле — Палезо — Гиф-сюр-Иветт
- ЛИКС (Лаборатория информатики Политехнической школы)
- Стандартный (Типы, логика и вычисления) (распущен в дек. 2012)
- Алгоритмы и сложность
- INRIA : Парсифаль (Preuves Automatiques et Raisonnement sur des SpécIFicAtions Logiques) работает над фундаментальными аспектами теории доказательств, а также над проектирование и внедрение систем, использующих это фундаментальная работа
- Проверенные алгоритмы VALS,
Языки и системы в LRI
(Лаборатория компьютерных наук Университета Париж-Юг).
Включает Токкату в
продвигать формальную спецификацию и компьютерное доказательство в
разработка программного обеспечения, которое требует высокой гарантии
его безопасность и его правильность по отношению к его предполагаемому
поведение (ранее ProVal :
Доказательство программ).

Другие регионы Франции
- Анже : Удача ДАРНЬЕР
- Кан
- Алгоритмическое оборудование,
Расчетные модели, Alea, Cryptographie, Complexité
- Геометрия, представления, алгебра, анализ, логика (GRAAL), команда: Пьер Агерон
работы по теории категорий (в основном на французском языке) — Патрик
Связные косы Дехорной с элементарными вложениями в
теории множеств и написал книги по логике и сложности.
- Чембери: LIMD (Логическая информатика и дискретная математика) исследования команда в отделении математики Савойского университета
- Лилль 3 Савуарс, Тексты, язык (философия): Теро Туленхеймо — Шахид Рахман
- Лион
- Группа de Logique (Институт Камиллы Джордан)
- Лаборатория d’Informatique du Parallélisme, ENS-Лион
- ПЛЮС : программы и пруфы
- Моделей де
Расчет и комплексность: дискретный и алгебраический
алгоритмы, теория сложности, комбинаторика
- Марсель-Люмини: Logique де ла Программирование
- Университет Экс-Марсель: Центр Жиля Гастона Грейнджера: Паола Канту
- Нэнси: ЛОРИЯ (Исследовательская лаборатория Лотарингии в области компьютерных технологий)
Наука и ее приложения): Формальный
Методический отдел.
 Вклад в логику и доказательство
теория, методы проверки распределенных и
реактивные системы, вирусология и безопасность. Логика, модели для
вычисления, программирование моделей, переписывание, моделирование,
спецификация…
Вклад в логику и доказательство
теория, методы проверки распределенных и
реактивные системы, вирусология и безопасность. Логика, модели для
вычисления, программирование моделей, переписывание, моделирование,
спецификация… - Ренн: Теория, Алгоритмы и системы ограничений
- София Антиполис: Марель : Mathématiques, Raisonnement et Logiciel (в Английский : Компьютерная проверка доказательств и программного обеспечения), INRIA, для изучения и использования методов проверки математические доказательства на компьютере, чтобы убедиться в правильности программного обеспечения.
Германия
немецкий Vereinigung для математической логики и фундаментальных исследований эксактов Wissenschaften (DVMLG)- Ахен: математический Основы компьютерных наук в Рейниш-Вестфалише Высшая техническая школа.
- Алгоритмический Теория моделей
- ИГРЫ
: исследовательская и учебная программа для проектирования и
верификация вычислительных систем, используя методологическую
структура, основанная на взаимодействии конечных и
бесконечные игры, математическая логика и теория автоматов.

- АлгоСин : Интеграция компьютерных и инженерных подходов. наук проект направлен на разработку методов автоматизированное проектирование программных и аппаратных средств.
- Аугсбург: теория параллельных
системы
- Берлин
- Свободный университет Берлина
- Логика и теория множеств: Сабина Коппельберг и Оливер Дейзер
- Теоретическая информатика
- Технические науки
Университет Берлина
- Кай Хаузер: Mathematische Logik und Grundlagenforschung, Erkenntnistheorie, Wissenschaftsphilosophie
- Логика и семантика Исследовательская группа
- Университет Гумбольдта в Берлине
- Логика в информатике
- Спецификация исследовательского блока, теория проверки и тестирования
- математический Логика (теория моделей), Institut für Mathematik, Humboldt-Universitaet zu Berlin (стар. страница)
- Бонн (Рейнский университет им.
 Фридриха Вильгельма)
Фридриха Вильгельма) - математический Логическая группа
- Институт Информатика
- Интеллектуальный Системы
- Теоретическая
Информатика
- Алгоритмика
- Хаусдорф
Центр математики (HCM): Алгоритмы, комбинаторика и сложность — Теоретическая Информатика (совместно с Хайко Рёглином)
- Брауншвейг: Институт Теоретическая информатика
- Бремен
- Официальный Методы разработки программного обеспечения
- Формализм,
Логика, институт — связь, перевод и структурирование
список рассылки и семинары
- Дармштадт: Логика Группа в Техническом университете Дармштадта. Применение теория доказательств, теория рекурсии, теория категорий, алгебраические и теоретико-модельные методы от математической логики до математика и информатика.
- Дортмунд : Департамент компьютерных наук
- Компьютер Наука I: логика в информатике — информация Инженерия — теория типов данных
- Компьютер Наука II: эффективные алгоритмы и Теория сложности
- Компьютер Наука VIII: искусственный интеллект
- Дрезден (Технический университет Дрездена):
- Международный Центр вычислительной логики
- институт теоретической информатики
- Алгебраический и логические основы информатики
- Фонды программирования
- Теория автоматов
- Институт Искусственный интеллект
- Вычислительный Логическая группа
- Знания
Представление и рассуждение
- Дуйсбург — Эссен Алгебра и логика
- Эрланген : Департамент компьютерных наук
- Теоретический компьютер Наука
- Адаптация знаний и обоснование контента
- Франкфурт: математический
Информатика
- Фрайбург :
- Математический
Институт — Секция математической логики,
Университет Альберта-Людвига.

- Выпускник Школа математической логики и приложений
- Фонды искусственного интеллекта
- Алгоритмы и сложность
- Хаген: Факультет для математики и информатики
- Гамбург : Берайх Математическая логика и междисциплинарные исследования Логик
- Ганновер: Факультет электротехники и информатики
- Institut für
Теоретическая информатика
- Гейдельберг: математический Рабочая группа по логике и теоретической информатике
- Ильменау : Институт теоретической информатики
- Йена: теоретический информатика : вычислительная сложность, сложность теория и логика.
- Кайзерслаутерн : Департамент информатика
- Институт Макса Планка
Системы программного обеспечения: языки программирования/верификация
(Виктор Вафиядис, Рупак Маджумдар; остальные в Саарбрюккене)
- Немецкий исследовательский центр Искусственный интеллект
- Карлсруэ
- Институт теоретической информатики
- институт криптографии и безопасности
- Киль: Arbeitsgruppe Логик, Университет Кристиана-Альбрехта: Отмар Спинас
- Кобленц : Институт компьютерных наук
- Официальный Методы и теоретическая информатика (Исследовательская группа Софроние-Стоккерманс)
- Искусственный Интеллект
- языков программного обеспечения команда
- Констанц: Модель
Теоретическая рабочая группа, состоящая из членов «Forschungsschwerpunkt
reelle Geometrie und Algebra» («Реальная геометрия и алгебра
исследовательская группа) с интересом к теории моделей.

- Лейпциг: Abteilung Logik und Wissenschaftstheorie, Институт философии, Университет Лейпцига
- Любек : Институт для теоретической информатики
- Мюнстер: Департамент по математической логике и фундаментальным исследованиям, Westfälische Университет Вильгельма
- Мюнхен (Мюнхен):
- Университет Людвига-Максимилиана
- Математика Логика: Установить теория, модель теория (нестандартный анализ), Доказательство теория, МИНЛОГ интерактивная система доказательства
- Институт Фюр Информатик
- Группа по теоретической информатике,
- Программирование и
Языки моделирования
- Центр
обработка информации и языка
- Мюнхен Центр математической философии
- Технический университет: Факультет
для исследований в области информатики
список стульев:
- Эффективные алгоритмы
- Фонды надежности программного обеспечения и теоретической информатики
- Формальный Языки, Создание компиляторов, Создание программного обеспечения
- Логика и проверка
- Теоретическая
информатика
- Институт теоретической информатики, математики и исследования операций, Университет Бундесвера
- Департамент Падерборн информатики
- Алгоритмы и сложность
- Основанный на знаниях Системы (включает математическую логику)
- Департамент Пассау кафедр информатики и математики и исследования
- Теоретическая Информатика
- Символический Вычисление
- Потсдам
- (Математический
Логическая команда была распущена, Торальф
Раш уехал в Бонн)
- Основы компьютерной лингвистики
- Саарбрюккен
- Институт Макса Планка по информатике
- Автоматика логики
- Алгоритмы
и сложность
- Саарский университет, информатика
- Вычислительный Сложность
- Исследования
Группы: Дипак Гарг (компьютерная безопасность и конфиденциальность, формальная логика, языки программирования) и Кристоф.
 Вайденбах (Автоматизация логики)
Вайденбах (Автоматизация логики) - Теоретическая Информатика
- Скопление Excellence «Мультимодальные вычисления и взаимодействие»
- Основы точных алгоритмов
- РА1: Обработка текста и речи
- РА3: Алгоритмические основы
- Институт Макса Планка Системы программного обеспечения: языки программирования/верификация (Дерек Дрейер, Ева Дарулова, Дипак Гарг)
- Зиген Математика Логика и теоретическая информатика
- Трир Теоретический Информатика
- Тюбинген, Eberhard-Karls-Universität:
- Арбайтсберайх
Mathematische Logik, Grundlagen und Geschichte der
Mathematik (Математическая логика, основание и история
математики) — группы больше не существует.
- Институт теоретической информатики
- Логик und Sprachtheorie (теория языка, профессор доктор Петер Шредер-Хейстер): основы вывода, теоретико-доказательная семантика
- ДиФоС — Диалогические основы семантики
- Гипотезы
философский проект
- Ульм
- Институт теоретической информатики
- Институт Искусственный интеллект
- Вадерн : Замок
Дагштуль — Международный центр информатики Лейбница
конференц-центр и исследовательский центр компьютерных наук.

Греция
- Национальный технический университет Афин:
- Программа магистратуры в Логика, алгоритмы и вычисления
- ΜГруппа математической логики
- Факультет компьютерных наук: вычисления и Лаборатория рассуждений
- Университет Аристотеля в Салониках: Алгебра, Теория чисел и математическая логика
- Костас Д. Кутрас, Группа алгоритмов, Криптография и вычислительная логика, кафедра информатики и Телекоммуникации, Университет Пелопоннеса, Триполис
Венгрия — Будапешт
- Математический институт им. Альфреда Реньи Венгерской академии наук.
- Теория множеств, логика и Топология.
- Университет Этвёша
- Кафедра логики, Институт философии
Ирландия
- Корк: Центр Буля
Исследования в области информатики
Италия
Итальянская ассоциация логики и ее приложений (AILA — Associazione Italiana di Logica e иск Applicazioni)
Итальянское общество логики и
Философия науки
- Флоренция
- Семинары
Логика и философия науки
- Даниэле
Mundici (Математическая логика и приложения: модели и
алгоритм для дедукции)
- Генуя
- Математика: логика: Риккардо Камерло
- Дипартименто ди Информатика, биоинженерия, робототехника и инженерия деи системы (ДИБРИС)
- Искусственный Лаборатория разведки и многоагентных систем (AIMS)
- Милан:
- Алгоритмы и основы информатики
- Падуя (Dipartimento di Matematica Pura e Applicata, Университет Падуи)
- Математическая логика
- математический Логика в Падуе
- Формальные методы обеспечения надежности программного обеспечения
- Оформление Формальная топология с помощью интерактивного средства доказательства теорем Матита
- Пиза
- Логический Фонды рационального взаимодействия в Centro di Ricerca Matematica Эннио Де Джорджи
- Формальные методы и инструменты
Лаборатория в Институте
di Scienza e Tecnologie dell’Informazione «A.
 Фаэдо»
Фаэдо» - математический
Логика: Алессандро
Берардуччи — Мауро Ди Нассо
- Эгон Бергер ранее работал над логикой и теорией сложности.
- Рим: Gruppo di Logica
e Geometria della Cognizione, кафедра философии
- Салерно: математический Логическая группа
- Сиенна: Математическая логика и общие математические системы
- Турин (Турин)
- Математика Логическая группа, отдел математики (дипартименто di Matematica «Джузеппе Пеано», Università degli Studi ди Торино)
- Тренто: математическая логика и теоретическая информатика
- Верона : Логика — Теория вычислительной техники, Университет Вероны
Латвия
- Вычислительный лингвистика
- математический основы компьютерных наук — исследования сосредоточены на теория квантовых алгоритмов
Мальта
Группа исследований семантики и верификацииНидерланды
Голландская ассоциация теоретических Информатика
- Амстердам — Институт Логика, язык и вычисления, научно-исследовательский институт в междисциплинарная область между математикой, лингвистикой, информатика, философия и искусственный интеллект
- Делфтский технологический университет: Клаас Питер Харт
- Эйндховен: Институт
для исследований в области программирования и алгоритмики
- Неймеген
- Голландский
Исследовательская школа логики Onderzoeksschool Logica (OZSL) стремится предоставить форум для
исследователи в Нидерландах, чьи исследования связаны с логикой.

- Университет Радбауд
- Математика: алгебра и топология: Себастьян А. Тервейн
- Категория Теоретический семинар
- Институт вычислительной техники и информационные науки
- Департамент Программное обеспечение
- Оформление Математика
- Тилбургский университет: Тилбург Центр логики, этики и философии науки (TiLPS) (другая страница)
- Утрехт
- Высшая школа логики Нидерландов (OZSL)
- Математический институт: Ике Мурдейк — Яап ван Остен
- Теоретическая Философия
- Центр Алгоритмические системы
Норвегия
- Осло :
- Логика группа математического факультета
- Кафедра информатики
- Pålitelige systemer (PSY) = Надежные системы (PSY)
- Спроктекнологгрупп = Язык Технологическая группа (LTG)
- Analytiske Systemer og Resonnering (ASR) = Аналитические решения и рассуждения (ASR))
Польша
- Белосток : Департамент Логика, информатика и философия науки
- Катовице : Институт математика
- Математический логика
- Комплект теория и топология
- Компьютер
Наука и дискретная математика
- Кельце : Логика
и теория множеств
- Краков
- Теоретическая информатика
- Департамент
логики в Институте философии Ягеллонского
Университет
- Лодзинский университет, Логика
и методология науки
- Познань
- Математическая логика
с небольшим
список логических команд в Польше
- Прикладное отделение
логика (лингвистика) с большим
список логических команд в Польше и еще несколько ссылок
- Варшава
- Факультет математики, Информатика и механика (МИМ)
- Математический Логика и теория категорий
- Топология и теория множеств
- Алгоритмика
- Логика в области компьютерных наук
- Теория автоматов
- Логическая группа, Институт философии
- Польская Ассоциация по логике и философии науки
- Фонд информационных технологий, логики и математики
- Институт компьютеров Наука (Польская академия наук)
Португалия
- Лиссабон (Лиссабон)
- Группа математической логики в Лиссабоне (Centro de Matemática e Aplicações Fundamentais, Universidade de Lisboa)
- Логика и вычислений на кафедре Математика, Instituto Superior Técnico
Румыния
Бухарестская логика и безопасность — семинар по логикеКафедра теоретической философии и логики
Сербия
Математический институт, Белград :- Зоран Петрич — (Коста Досен 1954 — 2017)
- Представительства логических структур и формальных языков и их применение в вычислениях
Словакия
- Братислава
- Департамент информатики
- Департамент логики и методологии науки
- институт философии, Словацкая академия наук
- Объем формальной семантики
- Департамент аналитической философии: Мариан Зухар, Лукаш Белик, Игорь Седлар
- Кошице:
- Институт
математика Университета Павла Йозефа Шафарика: Лев
Буковский заслуженный, работал над теорией множеств.

- Математический институт им. Словацкая академия наук (темы) : Мирослав Репицкий
Испания
Sociedad de Lógica, Metodología y Filosofía de la Ciencia en España Список конференций по теории моделей
Сумма Logicae : библиография и конгрессы «Инструменты для обучения логика»
- Барселона
- Неклассическая логика, кафедра философии, ЗАО
- Исследовательские проекты философского факультета — Grup de recerca en lògiques no clàssiques
- Joan Bagaria Pigrau (аксиомы теории множеств) и другие в Департаменте математики и информатики
- Департамент де Probabilitat, Lògica i Estadística семинары и исследования группы (на каталонском языке), среди которых
- Исследовательская группа по теория моделей со списком теоретиков моделей вокруг мир
- Мастер в чистоте и Прикладная логика — кандидат наук в чистой и прикладной логике
- Компьютерный факультет Наука о техническом Университет Каталонии (UPC):
- ЛОГПРОГ: Логика и программирование
- АЛЬБКОМ — Алгоритмы, биокомпьютинг, сложность и формальные методы Группа
- ВГРН — Группа обработки естественного языка
- LARCA — международная исследовательская группа, занимающаяся интеллектуальным анализом данных, машинным обучением, анализом данных и математической лингвистикой.

- Беллатерра : Искусственный Научно-исследовательский институт разведки (IIIA)
- Логика и рассуждения
- Философия Гранады: М. Дж. Фраполли
- Мадрид
- Политехнический университет Мадрида: вычислительная логика, Лаборатория реализации и параллелизма
- Департамент de Lógica y Filosofía de la Ciencia
- Donostia: Институт Логика, познание, язык и информация
- Департамент Саламанка
de Filosofía, Lógica y Estética
- Сан-Себастьян: логика и Кафедра философии науки
- Сантьяго-де-Компостела : Сосьедад
de Lógica, Metodología y Filosofía de la Ciencia
- Севилья: Dpto. de Ciencias de la Computación e Inteligencia Artificial
- Валенсия : Логика y Filosofía de la Ciencia (докторская программа) — Логика и Теория аргументов
Швеция
- Гётеборг (Гетеборг)
- Логика (философия)
- Информатика и Машиностроение
- Функциональный Программирование
- Язык
технологий, стал Центром языковых технологий.

- Формальные методы
- Стокгольм
- Стокгольмский логический семинар по логике группа, факультет математики, Стокгольмский университет
- Теоретическая Информатика
- Язык Технология
- Департамент Философия: основные научные интересы включают философию языка, философию логики и математики
- Умео Факультет информатики: Логика и приложения —
Фонды
языковой обработки
- Уппсала
- Математический Логика где-то в разделе Алгебра и Геометрия… там же есть обучение логики. Теория вычислимости, конструктивная математика, теория типов, теория предметной области, категориальная логика и модель теория.
- Департамент информационных технологий
- Алгоритмический Проверка программы — параметризованная и Системы с бесконечным состоянием
- Компьютеры Наука
- Философия: Логика и Метафизика
- Кай Бёрге Хансен
Швейцария
Швейцарское общество логики и философии науки и ее молодой ветви швейцарской Высшее общество логики и философии науки- Берн (факультет естественных наук Бернский университет)
- Институт компьютерных наук и прикладная математика: Группа логики и теории
- Математический институт: логика
- Фрибург : вездесущий и искусственный интеллект (PAI) — основы Надежные системы
- Женева, департамент
информатики
- Теоретический компьютер Научные и сенсорные сети
- Программное моделирование и Группа проверки
- Лозанна: Исследования Группа математической логики, Факультет высших коммерческих исследований (HEC)
- Невшатель: Институт философия
- Цюрих
- Институт теоретической Информатика
- Лоренц Дж.
 Халбайзен работает над бесконечной комбинаторикой и теорией множеств.
в Цюрихском университете.
Халбайзен работает над бесконечной комбинаторикой и теорией множеств.
в Цюрихском университете.
Соединенное Королевство
Британская логика
Коллоквиум
- Ванна: математическая
Основы вычислений, кафедра компьютерных наук
- Бирмингем :
- Философия языка и философии математики + доктор Сальваторе Флорио
- Информатика
- Рассуждение (включает в себя: Доказательство теорем, Планирование доказательств и Символическое Алгебра, обработка естественного языка…)
- Натуральный Языковая обработка
- Теоретическая Информатика
- Кембридж
- Компьютерная лаборатория
- Группа программирования, логики и семантики
- Кентербери: Программирование Группа языков и систем
- Бристоль :
- Математический логика и теория множеств
- Фундаментальные исследования в Бристоле, способствующие сотрудничеству между членами факультета философии и Школы математики
- Департамент философии: гомотопия Теория типов (Джеймс Ледиман, Стюарт Преснелл)
- Дарем: Алгоритмы и сложность
- Эдинбург:
- Школа информатики Эдинбургского университета
- Институт приложений искусственного интеллекта (AIAI)
- Математический Группа рассуждений
- Институт для языка, познания и вычислений
- Лаборатория по основам компьютерных наук
- Вычислительный Программа исследования мышления
- Компьютер Научные исследования, Университет Хериот-Ватт
- Надежный
Группа систем
- Интеллектуальный Системная лаборатория
- Группа ULTRA: Полезная логика, Шрифты, Рерайтинг,
Автоматизация.

- Философия
- Логика и язык
- Проекты Archelogos направлена на разработку методов электронной представления аргументов и методов электронного рассуждения, используя продвинутый искусственный интеллект методы.
- Эссекс :
- Дэвид Х. Фремлин, заслуженный деятель: теоретико-множественный анализ и мера. теория
- Глазго
- Математически Группа структурированного программирования, Университет Стратклайда
- Школа
Информатика, Университет Глазго
- Официальный Анализ, теория и алгоритмы (FATA)
- Лидс
- Лидс Логическая группа: теория вычислимости, теория моделей, множество теории и основаниях, теории доказательств и в приложениях к алгебра, анализ и теоретическая информатика.
- Школа вычислительной техники
- Алгоритмы
и сложность
- Искусственный интеллект
- Ливерпуль Компьютер Научный отдел
- Алгоритмы, теория сложности и оптимизация
- Искусственный интеллект
- Лестер : Компьютер Наука
- Основы вычислительной техники
- Валидация и проверка (КЛАПАН)
- Лондон
- Королевы Марии, Лондонский университет: теоретический Информатика — исследование логических методов для рассуждения о компьютерных системах
- Департамент вычислительной техники, Имперский колледж
- Вычислительный Логика и аргументация
- Машина Обучение
- Проверка Автономные системы
- Языки программирования
- Королевский колледж
- Системы программного обеспечения (исследования в области применения логики и математики в широкой информатике)
- Лондонский логический форум объединяет лондонских исследователей в области математики и вычислительные аспекты формальной логики
- Теория
вычислительной техники, Ройал Холлоуэй
- Департамент
философии, логики и научного метода, Лондон
Школа экономики : Дэвид
Макинсон
- Манчестер :
- Официальный
Группа методов, Школа компьютерных наук.
 Широкий
круг интересов, от разработки новой математики
вычислительного поведения, к изучению и развитию
проектирование системы и методы проверки. Есть большая группа
посвященный автоматизации логики — Манчестер является домом
двух мировых чемпионов автоматизированных систем доказательства теорем.
Широкий
круг интересов, от разработки новой математики
вычислительного поведения, к изучению и развитию
проектирование системы и методы проверки. Есть большая группа
посвященный автоматизации логики — Манчестер является домом
двух мировых чемпионов автоматизированных систем доказательства теорем. - Математические основы Группа, состоящая в основном из людей, работающих в Школе Информатика в Манчестерском университете.
- математический Логика: неопределенные рассуждения, вычисления в группах и Полугруппы, теория моделей
- Норидж: Теория моделей и Теория множеств, Университет Восточной Англии.
- Ноттингем : Фонды
программирования
- Оксфорд
- Оксфордский математический Логическая группа. Геометрическая теория устойчивости, модельная теория поля и о-минимальные структуры.
- Кафедра компьютерных наук
- Фундаменты, Логика и структуры
- Программирование Языки
- Автоматическая проверка
- Философский проект: невыразимость
и отражение в формальных науках
- Департамент Шеффилд компьютерных наук
- Обработка естественного языка
- Проверка и тестирование
- Университет Суонси, Уэльс:
- Теоретический
Информатика (вычислимость, спецификация, теория доказательств, сложность, железнодорожная проверка),
Университет Суонси.

- Дж Роджер Хиндли: Математическая логика; особенно лямбда-исчисление, комбинаторная логика и теории типов
- Сент-Эндрюс, Шотландия:
- Факультет компьютерных наук:
- Искусственный интеллект и символьные вычисления
- Языки программирования
- Арче: Философский исследовательский центр логики, языка, метафизики и эпистемология
- Стерлинг, Шотландия: вычислительная техника Естествознание и математика
- Вычислительная математика и оптимизация включает символьные вычисления
- Фонды Уорика компьютерных наук
- Йорк: Департамент информатика
- Искусственный интеллект.
Северная Америка
Канада
- Калгари (Альберта) — факультет философии, Университет Калгари.
- Монреаль (Квебек): Теория категорий Исследовательский центр
- Галифакс : Атлантика Группа теории категорий
- Гамильтон (Онтарио): математический Логика, Университет Макмастера
- Лондон (Онтарио)
- Теоретическая Информатика
- Онтарио Исследовательский центр компьютеров Алгебра: символьные вычисления
- Оттава: Логика
и Фонды вычислительной группы
- Остров Принца Эдуарда: Максим Р.
 Берк (Набор
теория, общая топология…)
Берк (Набор
теория, общая топология…) - Саскатун : Центр по алгебре, логике и вычислениям, Университет Саскачеван
- Торонто (Онтарио)
- Университет Торонто
- Департамент математика : некоторые люди работа над «теорией множеств».
- Департамент Информатика: Стивен А. Кук (доказательство сложности) — Тонианн Питасси (сложность доказательства, вероятностное рассуждение…)
- Аппалачи теория множеств: серия мастер-классов
- Йоркский университет
- Теория вычисление,
- Математика
исследования включают теорию категорий и теорию множеств
- Факультет компьютерных наук Университета Райерсона: Михаил Сутчански
(Логические языки программирования высокого уровня…)
- Аласдер
Уркхарт (заслуженный профессор философии, логики,
сложность…)
- Ванкувер (Колумбия): Университет Саймона Фрейзера, Бернаби
- Логика Группа функционального программирования
- Лаборатория логики и
Экспериментальная философия, кафедра
философии (возможно, больше не существует — старый адрес http://www.
 sfu.ca/llep/)
sfu.ca/llep/) - Центр экспериментальной и конструктивной математики
- Вычислительный
Лаборатория логики
- Ватерлоо (Онтарио)
- Математическая логика : Вычислимость Теория — теория моделей — Универсальный Алгебра
- Школа Черитона Информатика
- Алгоритмы и сложность
- Искусственный интеллект
- Формальный Методы
- Языки программирования
- Компьютер Алгебра и символьные вычисления
Мексика
Academia Mexicana de LógicaSociedad Mexicana de Inteligencia Artificial
- Национальный автономный университет Мексики,
Мехико.
- Топология и Теория множеств = топология y teoría de conjuntos
- Instituto de Investigaciones Filosóficas: Lógica
- Теоретические основы вычислительной техники и искусственного интеллекта, факультет компьютерных наук CINVESTAV-IPN, Мексика
США
Аризона
- Феникс: Темпе (Университет штата Аризона):
- Автоматизированный Группа рассуждений
Калифорния
- Калифорнийский университет в Сан-Диего
- Математика:
Джефф Реммел
— Сэмюэл Р.
 Басс
— Миа Миннес
Басс
— Миа Миннес - Компьютерный факультет Наука и техника
- Программирование Системы
- Безопасность и Криптография
- Теория
Район Лос-Анджелеса
- Калифорнийский университет в Лос-Анджелесе: Логический центр поддерживает обучение и исследования в области логики и ее приложений.
- Калтех: Александр Кехрис: Основы математики; математическая логика и теория множеств; их взаимодействие с анализом и динамическим системы.
- Калифорнийский университет в Ирвине
- Логика и основы математики (теория множеств, с акцент на форсинге, большие кардиналы, теория внутренней модели, штраф теория структур, регулярная и сингулярная кардинальная комбинаторика, и дескриптивная теория множеств.) + Пол К. Эклоф, Почетный.
- Центр Алгоритмы и теория вычислений (в основном алгоритмы и сложность)
- Исследования Группа логики и философии математики
Район Сан-Франциско
- Стэнфорд: Логика в
Стэнфорд
- Центр изучения языка и информации
- Группа логики сфокусирована
по вычислительной логике в Стэнфордском университете компьютерных наук
Отделение.

- Формальное рассуждение Группа
- Омар Де ла Круз работал над аксиомой выбора .
- (Стэндфорд
Группа теории кажется не очень близкой к логике)
- Калифорнийский университет в Беркли: Группа в Логика и методология науки — Роберт Соловей
- Менло-Парк: SRI International
- Информатика Лаборатория
- Официальный Методы и надежные системы
- Переписывание Логика и системы
- Искусственный интеллект Центр
- Представительство и рассуждения
Колорадо
- Валун: Логика и основы (Агнес Сендрей, Кит Кернс, Питер Майр; заслуженный: Дон Монах)
- Университет
из Денвера: Наташа
Добринен (теория множеств, булевы алгебры, рекурсия).
Теория…), Ник
Галатос (универсальная алгебра, алгебраическая логика…)
Коннетикут
- Университет Коннетикута, Сторрс:
- UConn Group по философской и математической логике включает математическую Члены логики и философии
- Семинар по логике в Коннектикуте
- Новый Семинар по рекурсии и определимости в Англии
- Уэслиан
Университет, Миддлтаун (с акцентом на алгебру и теорию моделей)
: Филип Х.
 Скоукрофт — Кэрол С. Вуд — Алекс
Крукман. (Заслуги: В. Вистар Комфорт
— Фред Э.Дж. Линтон
— Льюис С. Робертсон)
Скоукрофт — Кэрол С. Вуд — Алекс
Крукман. (Заслуги: В. Вистар Комфорт
— Фред Э.Дж. Линтон
— Льюис С. Робертсон)
Вашингтон, округ Колумбия
- Университет Говарда: Нил
Хиндман (теория множеств)
Делавэр (Университет Делавэра, Ньюарк)
- Математический Логические интересы
- Компьютер и информация наук
- Искусственный Интеллект
- Натуральный Языковая обработка
- Теория вычислений
Флорида
- Гейнсвилл: Логика и Теория множеств, Университет Флориды.
- Департамент компьютерных наук, Университет Майами. Д-р Джефф Сатклифф участвовал во многих конференциях и журналах .
- Бока-Ратон: математический факультет Атлантического университета Флориды: Доктор Роберт Любарски и Фред Рихман (конструктивная математика).
Джорджия (Атланта)
- Техническая школа Джорджии компьютерных наук: теория — Алгоритм и случайность Центр
- Дискретная математика и теоретическая информатика,
Университет Эмори, факультет математики и компьютерных наук.

Гавайи
- Гавайский университет в Маноа Математические исследования
: Люди логики и теории решеток,
курсы ,
Описание
Айдахо
- Набор Теоретическая группа в Государственном университете Бойсе
Иллинойс
- Урбана: Университет штата Иллинойс в Урбана-Шампейн
- Логика, Министерство Математика: теория моделей и ее приложения и в описательная теория множеств; нестандартный анализ ; аспекты теории групп со значительным связи с логикой.
- Компьютерный факультет наука
- искусственный
разведка
- Формальный Системная лаборатория
- Теория и алгоритмы
- Департамент философии
- Чикаго
- Логика в UIC (чистая математика, Иллинойсский университет в Чикаго)
- научных интересов преподавателей включают логику и теоретическая информатика — Группа теории (Чикагский университет)
- Другой Теоретические группы в районе Чикаго
- Университет Лойолы: Питер Ларс Дордал
- Аргоннская национальная лаборатория
- Теоретическая информатика
- ПроВЕСА: Проверка программы для приложений экстремального масштаба
- (автоматический вычет в Страница Argonne устарела, поскольку Уильям МакКьюн мертв)
Индиана
- Блумингтон (Университет Индианы)
- Индиана Университетская программа по чистой и прикладной логике (для студенты)
- Математические исследования
: Лоуренс С.
 Мосс.
Мосс. - Теоретическая Информатика
- Логика, Философия математики, философия языка
- Саут-Бенд: Университет Нотр-Дам
- Логика
исследовательская группа кафедры математики
- Некоторые члены
кафедры философии интересуются логикой.
Айова
- Университет штата Айова, Эймс
- Департамент математических научных интересов: логика
- Исследовательские лаборатории компьютерных наук
- Формальные методы и Исследовательская группа по проверке
- Теория
- Фэрфилд: Пол Корацца,
Университет Махариши
управления
Канзас
- Лоуренс : Набор Теория в Канзасском университете???
Мэриленд
- Мэрилендский университет в Колледж-Парке
- Компьютер Научный отдел, группа Active Logic (Active Logic, МЕтакогнитивные вычисления и разум)
- Математика
- Д.
 В.
Теория модели Кукера
В.
Теория модели Кукера - М.К.
Теория моделей Ласковского, теория множеств
Массачусетс
- Амхерст: Даниэль Дж. Веллеман в Амхерст-колледже
- Бостон:
- Акихиро Канамори в Бостонском университете, фокусируется на крупных кардиналах.
- Алгоритмы и теория
семинар, кафедра компьютерных наук Бостонского университета
- Питер А. Фейер (Массачусетский университет в Бостоне): Теория вычислимости (также известная как теория рекурсии) и теоретический компьютер Наука
- Список
логики недалеко от Бостона
- Кембридж:
- Логика в Гарварде
- Изучение
Границы неполноты
- Массачусетский технологический институт информатики и Лаборатория искусственного интеллекта
- Теория
Расчет
- Агустин Райо,
философ из Массачусетского технологического института, работающий на пересечении
философия логики и философия языка.

- Массачусетский технологический институт Mathematical Logic & Foundations (логическая группа Массачусетского технологического института прекратила свою деятельность)
- Нортгемптон: Пол Багински
и Джеймс М.
Хенле в колледже Смита.
Мичиган
- Анн-Арбор, Мичиганский университет.
- Логика и фундаменты
- Кафедра электротехники и вычислительной техники Наука
- Искусственный Разведка: Лаборатория
- Теория вычислительной техники: лаборатория
- Формальные методы и автоматические рассуждения
- Абстрактное состояние
Машины (прекращено)
- Детройт, Университет
Детройт Милосердия — Майкл
Канжар работает над теорией множеств
Миннесота
- Математический Логика Миннесотского университета.
Миссури
- Канзас-Сити: Эрик
Джонатан Холл (Характеристика моделей перестановок — аксиома
по выбору и топологии)
Небраска
- Омаха: Анджей
Рослановски, Университет Небраски (набор
Теория, Общая топология,
Абстрактная алгебра, теоретико-множественная
Аспекты реального анализа)
Невада
- Лас-Вегас: Деррик
ДюБоз и Дуглас Берк,
на математическом факультете Университета Невады.

Нью-Гэмпшир
- Ганновер : Дартмут Логик
- Специализированная исследовательская группа в области алгоритмической случайности (2007-2010).
Нью-Джерси
- Ньюарк: Университет Рутгерса
- Логика группа на кафедре математики
- Центр дискретных Математика и теоретическая информатика
- Принстон
- Эдвард
Нельсон (прошел
выезд 10 сентября 2014)
- Компьютер наука
- Программирование Языки и безопасность
- Теоретическая Информатика
- Центр
Вычислительная сложность
- Институт повышения квалификации Исследование
- Теоретическая Информатика и дискретная математика
- Универсальный
Основы математики 2012-2013
Нью-Мексико
- Альбукерке: Информатика, Университет Нью-Мексико: Дипак Капур (Роберт Верофф, заслуженный; Уильям МакКьюн умер в 2011 году)
- Лас-Крусес :
- Представление знаний, логика, и Лаборатория расширенного программирования (KLAP)
- Логика и группа фондов
Нью-Йорк
- Логические события в Нью-Йорке области, включая логику Семинар в CUNY (Городской университет Нью-Йорка), семинар по теории множеств
- Нью-Йоркский университет: Компьютер Наука
- Алгоритмы и Теория
- Формальные методы и проверка
- Машинное обучение
- Естественный язык и обработка речи
- Среди исследований
групп в Центре выпускников CUNY является одним из Logic
- Барух
Колледж: Лоуренс Кирби
(теория конечных множеств), Артур У.
 Аптер (теория множеств: большие кардиналы и форсинг).
Аптер (теория множеств: большие кардиналы и форсинг). - Новый
Йоркский городской технологический колледж: направления исследований факультета математики
- Корнельский университет, Итака
- Математическая логика
- Вычислительная техника и Информатика
- Естественный язык Корнелла Группа обработки
- Теория вычислительной техники
- Программирование Языки
- Искусственный Интеллект
- Доказательство/Уточнение программы Логический проект: основанные на логике инструменты для поддержки программирование, формальная вычислительная математика
- Хемпстед: Дэниел Сиболд в Университете Хофстра, работает над теорией вычислимых моделей с бесконечным временем.
- Рочестер
- Центр для языковых наук
- Департамент Информатика
- Искусственный Интеллект
- Теоретическая Информатика: алгоритмы и вычисления сложность и их приложения
- Скенектади, Юнион
Колледж: математические исследования
- Сиракузы Электрик
Инженерия и информатика: формальный
методы; Эндрю
С.
 -Ю. Ли
-Ю. Ли
Северная Каролина
- Шарлотта (Университет Северной Каролина): Алан Доу (теория множеств и топология)
- Роли (Университет штата Северная Каролина)
- Logic and Cognitive Science Initiative — Курсы логики
- Компьютер
Области научных исследований включают алгоритмы и теорию
Расчет.
Огайо
- Афины (Университет Огайо): Филип Эрлих
(философия математики) — Тодд Эйсворт
(теория множеств)
- Колумбус: Университет штата Огайо
- Математический факультет: люди интересуется математической логикой и основами; лекция примечания — логика семинар
- Теория и алгоритмы
- Философия: Стюарт Шапиро — Нил Теннант
- Группа чтения по логике, языку, информации и вычислениям
- Колледж Кеньон: Патрик
Ридер — Боб
Милникеля (математический анализ логики, используемый в
информатика) — Ной
Айдын (алгебраическая теория кодирования).

- Оксфорд: Математика Майами
области исследований включают теорию множеств
Пенсильвания
- Государственный колледж: математический
Логика в Университете штата Пенсильвания: Стив Симпсон и
другие — (Томас Джех,
проф. заслуженный, теория множеств)
- Филадельфия: Логика и вычислений в Пенсильванском университете: междисциплинарная исследовательская группа, состоящая из преподавателей и аспиранты факультетов вычислительной техники и Информатика, лингвистика, математика и философия — включает бакалавриат Программа по логике, информации и вычислениям
- Бенджамин С.
Пирс написал книги по программированию
- Питтсбург
- Чистая и прикладная логика, Университет Карнеги-Меллона: междисциплинарная принадлежность доктора философии. программы в 3 отделениях: Информатика, Математические науки, философия.
- Нуэль Белнап, Университет Питтсбурга
- Университет Скрэнтона : исследования Якуба по теории множеств.
 Ясински — Кен
Монахи — Кшиштоф
Плотка
Ясински — Кен
Монахи — Кшиштоф
Плотка
Южная Каролина
- Колледж Чарльстона: Ренлин Джин:
нестандартный анализ, теория множеств, теория моделей…
Теннесси
- Университет Вандербильта, Нэшвилл: математика
исследование : Универсальный
Семинар по алгебре и логике.
Техас
Юта
- Прово: Университет Бригама Янга: Искусственный Интеллект и машинное обучение
Вирджиния
- Арлингтон: Томек Бартошинский, Национальный Научный фонд
- (Харрисонбург: Элизабет Браун, Чистый Математика, Университет Джеймса Мэдисона)
- Моргантаун: Департамент Математика, Университет Западной Вирджинии: Кшиштоф Цесельский — Ежи Войцеховский
Вашингтон
Университет Вашингтона: теория вычисленийВисконсин
- Мэдисон
- Домашняя страница UW–Madison Logic Group
- Факультет компьютерных наук: Теория Компьютеры
- Милуоки: Вим Руитенбург, Университет Маркетт.

- Ошкош: Джоан Харт работает над теорией множеств и ее приложениями к общим топология, теория меры и функциональный анализ.
Вайоминг
Компьютер Наука: Применение логики и формальных методов в информатике: формальные методы и доказательство теорем…Другое
Веб-страница для логиков в ASL Азиатско-Тихоокеанского регионаАргентина
INFINIS — французско-аргентинская лаборатория. (Laboratoire Internationale Associé) исследований в области компьютерных наук, между CNRS и Парижским университетом Дидро, с одной стороны, и Consejo Nacional de Investigaciones Cientéficas y Técnicas (CONICET) и Университет Буэнос-Айреса, с другой.- Буэнос-Айрес: Instituto de Ciencias de la Computación (Facultad de Ciencias Exactas y Naturales):
- Теория вычислений
- (устаревшая страница одной группы: Logic, Language and Computability = GLyC: Grupo en Lógica, Lenguaje y Computabilidad)
- Лаборатория фундаментов и Инструменты для разработки программного обеспечения (LaFHIS)
- Кордова: Universal Algebra & Logic Research Group
Австралия
Австралазийский Ассоциация логики- Канберра: теория (алгоритмы,
Теория баз данных, логика) — программирование
языки.

- Мельбурн, Университет Монаша
- Факультет
Информационные технологии
- Джон Кроссли (почетный)
- (Математика исследования включают дискретную математику — Вычислительная математика)
- Сидней
- Департамент вычислительной техники, Университет Маккуори
- Центр Австралийской теории категорий
- Центр для передовых вычислений — алгоритмы и криптография
- Центр языков Технология
- Интеллектуальный Группа систем
- Программирование Группа языковых исследований
- Теоретическая Группа компьютерных наук, Информатика и инженерия, инженерный факультет, Университет Нового Южного Уэльса
- Слияние CSIRO Data61 с NICTA (Национальный Австралия) и CSIRO (Организация научных и промышленных исследований Содружества) Digital Productivity
- Исследовательская группа надежных систем
- Философия: Марк Коливан — Ник Смит
Бразилия
- Бразилиа: Lógica no Avião: некоммерческая организация
продвигать и распространять идеи, развитые в логике и философии.

- Кампинас
- Центр логики, эпистемологии и истории науки, Universidade Estadual де Кампинас
- бразильский Логическое общество (Sociedade Brasileira de Lógica) (философия).
- Флорианополис: центр философия и гуманитарные науки, Федеральный университет Санта-Катарины: Группа Мультидисциплинарный де Pesquisa em Lógica e Fundamentos da Ciência с Альберто Оскар Купани; NEL — Центр эпистемологии и логики
- Натал : Группа для Логика, язык, информация, теория и приложения
- Порту-Аллегре: Институт информатики UFRGS: Компьютер Основы и формальные методы
- Ресифи: Теория и логические основы вычислительной техники, Федеральный университет Пернамбуку (устарело?)
- Rio
- Группа формальных методов, Департамент информатики, PUC-Rio
- формальных методов,
искусственный интеллект и логика в информатике, Insituto
de Computação в Федеральном университете Флуминенсе.

- Сальвадор Баия: Федеральный университет Баии
- Математический институт — Исследовательская работа Группа в логике, множествах и топологии = Grupo de Pesquisa em Lógica, Conjuntos e Topologia (исследование темы) — математические Логика УФБА
- Departamento de Ciência da Computação (DCC)
- МЕФЕС — Métodos Formais em Engenharia de Software — Формальные методы в группе разработки программного обеспечения — MEFES
- ФОРМЫ — Formalismos e Aplicações Semanticas
Китай
- Пекин, Институт программного обеспечения: Джордж Бармпалиас
- Шанхай
- Математическая логика в Фудане (архив): Хао Чжаокуань — Ицзя Чен — Ян Руижи — Яо Нинюань
- Университет Нанкина: Лян Юй
Колумбия
- Богота Логическая группа (Университет Национальный де Колумбия, Университет де-лос-Андес)
- Universidad Sergio Arboleda: исследования чистой математики
Индия
Ассоциация логики в Индии
- Бангалор: Департамент Информатики и автоматизации (CSA)
- Теоретическая информатика
- Бомбей: Центр Формальный дизайн и проверка программного обеспечения
- Ченнаи: теоретическая информатика в Институте математических наук, IIT Madras и Математический институт Ченнаи
- Калькутта Логический круг
- Канпур :
- Департамент математики и статистики, Индийский технологический институт: Мохуа Банерджи: грубая теория множеств и модальная логика
- Кафедра гуманитарных и социальных наук,
Индийский технологический институт: А.
 В. Равишанкар Сарма
В. Равишанкар Сарма - Мумбаи: Школа технологий и информатики Института фундаментальных исследований Тата.
Иран
Логики в ИранИранская ассоциация логики
- Тегеран
- Институт исследований теоретической физики и математики (ИПМ)
- Комбинаторика и Компьютеры
- Математическая логика
- Группа логики в Университете Шарифа
Израиль
Логика в Израиле: устаревшая страница
- Беэр-Шева: математический
и исследовательская группа вычислительной логики, Бен-Гурион
Университет Негева
- Хайфа
- Математический факультет: Лия Эпштейн (теоретическая информатика) — Коби Петерзил
- Компьютер
Департамент науки (Технион — Израильский институт
технологии) исследования
районы
- Теория Вычислительная лаборатория (ТОЛ)
- Системы и Лаборатория разработки программного обеспечения (SSDL)
- Центр Интеллектуальные системы (СНГ и ИСЛ)
- Еврейский университет им.
 Иерусалим.
Иерусалим. - Теоретическая Информатика
- Реховот: Исследования в основах компьютерных наук
- Рамат-Ган (Бар-Илан) университет): Дорон А. Пелед (формальная верификация, семантика программирования Языки, Темпоральная логика,…), Даган Идо (Естественный Языковая обработка), Амир Лешем
- Тель-Авив
- Математика: Арнон Аврон (основы математики, философская логика) — Моти Гитик (форсирование, большие кардиналы, кардинальная арифметика, внутренние модели).
- Компьютерная школа Наука
Япония
Список семинаров RIMS по теории множеств(расположение с запада на восток)
- Мацуяма: Хироси Фудзита (департамент математики, Высшая школа естественных наук и Engineering, Университет Эхимэ) работает над дескриптивной теорией множеств
- Университет Окаямы: теория группы программирования и искусственного интеллекта
- Университет Кобе: Группа логики, статистики и информатики:
- ТОО: Язык программирования линейной логики и его система компиляции
- теория множеств: Хироши Сакаи; Сакаэ Фучино
- Макото Кикучи
- Осака, Департамент математики и информатики: Масару Када (кардинальные инварианты вещественных чисел, диаграмма Чихона, форсинг, бесконечная комбинаторика, компактификация)
- Нагоя
- Департамент
математической информатики
- Набор Нагоя Теоретический семинар (устарело)
- Регион Исикава : Номи : Исихара
Лаборатория, Школа
Информатики, Японский институт передовых технологий
Наука и техника (архив
страницы старой логической группы — Ono
лаборатория)
- Сидзуока, Департамент
математики.
 Кафедра фундаментальной математики
включает алгебру, топологию, дифференциальную геометрию и
математическая логика.
Кафедра фундаментальной математики
включает алгебру, топологию, дифференциальную геометрию и
математическая логика. - Цукуба : Информация группа математики: Акито Цубои (Математическая логика) — Масахиро Сиоя (набор теория) — Ко Сакаи (теоретическая информатика) — Кота Такеучи
- Сендай, Университет Тохоку: Ямадзаки Такэси — Казуюки Танака
(чтобы не перепутать с другим Казуюки
Танака в том же университете): логика, основы
математика и теория вычислений.
Новая Зеландия
- Окленд :
- Бакалавриат программа Logic and Computation (другая страница — информатика, философия…)
- Центр Дискретная математика и теоретическая информатика
- Гамильтон: Университет Вайкато
- Группа формальных методов
- Веллингтон: Университет Виктории
- Центр логики, Language and Computation (объединенный центр математики, информатика, философия и лингвистика)
- По математике: логика и алгебра: Род Дауни.
 (ранее: доктор Колин Бейли и Роб
Голдблатт)
(ранее: доктор Колин Бейли и Роб
Голдблатт)
Пакистан
- Языковой центр
Машиностроение
Реюньон (Франция)
- Лаборатория д’Информатик и математических наук
Россия
- Москва
- Департамент математической логики и теории алгоритмов, факультет механико-математического факультета МГУ.
- Российская академия наук
- Департамент Логика, Институт философии
- Департамент
математической логики, Математический институт им. В. А. Стеклова
- Новосибирск
- Алгебра и логика
- Соболев
Институт математики СО РАН
Академия наук включает в себя математическую логику
- Переславль
- Искусственный Центр разведывательных исследований
- Санкт-Петербург : Лаборатория
математической логики МИАН.

Сингапур
- Департамент
математика: Фрэнк Стефан (теория рекурсии…), Ян Юэ (теория рекурсии,
Модели арифметики), Дилип Рагхаван
(Математическая логика, теория множеств и общая топология)…
Южная Африка
- Ле Кап: Исследования в области компьютерных наук
- Проверка системного программного обеспечения
- Теория и приложения автоматов и грамматик
Южная Корея
Корейская ассоциация математической логики- Факультет математики, Университет Ёнсе: Бьюнхан Ким — Сан Мун Ким
Тайвань
Тони Тан (кафедра компьютерных наук и информационной инженерии, Колледж электротехники и компьютерных наук, Национальный Тайваньский университет)Украина
- Львов Алгебра и логика
Венесуэла
- Маракай: группа
de Álgebra y Lógica de la Universidad Central de Venezuela
Все еще неполный, больше ссылок будет добавлено позже.

При создании этой страницы использован весь следующие источники, что сделало их устаревшими (ссылки не были скопировано, но полностью обновлено и перестроено, и многое другое было добавлено):
- Большое спасибо Антону Сетцеру за то, что несколько лет назад он сделал самый большой список ссылок к логическим серверам по всему миру, хотя большинство его ссылки были битые.
- world.logic.at
- dmoz : исследовательские группы и центры (умирающий портал с ужасным отсутствия редакторов, так как многие ушли, в том числе и я, отталкиваясь от неправильный управленческий аппарат и абсурдные бюрократические правила)
- См. также: Набор
домашние страницы теории (меньший список был на http://www.ipc.shizuoka.ac.jp/~styorio/links.html, теперь удален)
Компьютеры булевой алгебры
Джордж Буль Викисклад Есть две основные причины, по которым математика очаровывала человечество на протяжении двух тысяч лет.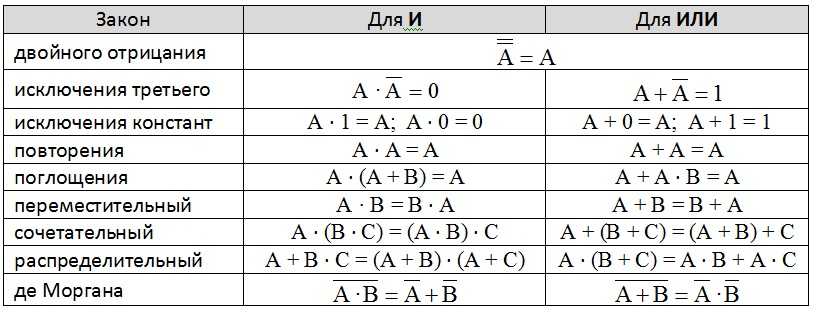 Во-первых, математика дает нам инструменты, необходимые для понимания Вселенной и построения вещей. Во-вторых, изучение самих математических объектов может быть красивым и интригующим, даже если они не имеют очевидного практического применения.
Во-первых, математика дает нам инструменты, необходимые для понимания Вселенной и построения вещей. Во-вторых, изучение самих математических объектов может быть красивым и интригующим, даже если они не имеют очевидного практического применения.
Что действительно удивительно, так это то, что иногда область математики начинается как нечто совершенно абстрактное, не имеющее непосредственного научного или инженерного применения, а затем гораздо позже может быть найдено практическое применение.
«И», «Или», «Не»
Булева алгебра — это комбинация логики и алгебры, первоначально разработанная Джорджем Булем, в честь которого назван предмет, в 1840-х и 50-х годах, а затем усовершенствованная другими логики на протяжении остальной части девятнадцатого и начала двадцатого веков.
Формальная логика касается истинности или ложности утверждений или предложений. «Барак Обама — президент Соединенных Штатов» — утверждение верное. «Google производит iPhone» — ложное утверждение.
Все становится интереснее, когда мы начинаем комбинировать простые предложения вместе. «Барак Обама — президент Соединенных Штатов, а Джо Байден — вице-президент» — это правда, поскольку оба простых утверждения, соединенные «и» в середине, верны. «Либо в Техасе проживает 300 человек, либо телевидение было изобретено Исааком Ньютоном» — ложно, поскольку два простых утверждения, соединенные «или» в середине, ложны.
Булева алгебра и другие формы абстрактной логики высказываний основаны на работе со сложными предложениями, состоящими из простых предложений, соединенных логическими связями, такими как «и», «или» и «не». Все, что имеет значение для того, чтобы сказать, является ли такое составное утверждение истинным, — это абстрактные значения истинности составных утверждений и формальные правила, основанные на том, какие логические соединители мы используем.
Например, если утверждение X истинно, а высказывание Y истинно, то составное высказывание «X и Y» также истинно. Если либо X, либо Y ложны, либо оба ложны, то «X и Y» также ложны.
Если либо X, либо Y ложны, либо оба ложны, то «X и Y» также ложны.
Буль понял, что этот тип логики, основанный на объединении символов для предложений с использованием таких соединителей, как «и», «или» и «не», имеет структуру, аналогичную нормальной алгебре и арифметике. В обычной алгебре переменные, представляющие числа, объединяются в формулы и уравнения с помощью арифметических операций сложения, вычитания, умножения и деления.
В логической алгебре Буля переменные, представляющие логические предложения, объединяются в формулы и уравнения с помощью логических операций и, или, и не. Утверждение «X и Y истинно» преобразуется в уравнение X × Y = 1. Утверждение «X или Y ложно» становится X + Y = 0,9.0007
Булева алгебра позволяет использовать те же виды алгебраических методов, которые мы используем для решения нормальных уравнений с участием чисел для установления логических отношений. Решая булевы уравнения, логики могут легче увидеть, когда одна комбинация предложений логически ведет к другой.
Сто лет спустя
Если это кажется чрезвычайно абстрактным, это так. Логика всегда находилась на грани между философией и математикой, пытаясь рассуждать о том, как мы можем рассуждать, и добираясь до фундаментальных идей о том, что такое истина и как убедиться, что мы знаем вещи. При всей своей увлекательности логика высказываний и булева алгебра изначально относились строго к области чистой математики с меньшим количеством приложений, чем такие разделы математики, как дифференциальные уравнения и исчисление, лежащие в основе нашего понимания физики.
Примечательно, что примерно через столетие после первоначальных исследований Буля математики и ученые открыли чрезвычайно мощный набор приложений для формальной логики, и теперь этот кажущийся абстрактным математический и логический инструмент лежит в основе глобальной экономики.
Викисклад
Булева алгебра — получение истинных и ложных значений, манипулирование ими в соответствии с логическими правилами и получение соответствующих истинных и ложных результатов — является фундаментальной основой современного цифрового компьютера.
Одно из первых серьезных применений булевой алгебры было получено в 1937 году в магистерской диссертации Клода Шеннона, одного из самых важных математиков и инженеров 20-го века. Шеннон понял, что переключатели в ретрансляционных сетях, таких как телефонная сеть или ранний протокомпьютер, можно легко описать, рассматривая «включенные» переключатели, имеющие логическое значение «истина», «выключенные» переключатели как имеющие логическое значение. «false» и с различными шаблонами, в которых переключатели связаны друг с другом, соответствующими логическим операциям «и», «или» и «не».
Инновация Шеннона значительно упростила проектирование коммутационных сетей: вместо того, чтобы фактически экспериментировать с самими сетевыми соединениями, методы, разработанные Булем и его последователями, обеспечили математическую основу, позволяющую создавать более эффективные схемы сети.
Связь между электрическими переключателями и булевой алгеброй идет и в другом направлении. Центральный процессор компьютера в значительной степени построен из логических вентилей: физических проявлений булевых операторов. Логические элементы принимают одно или несколько электрических логических значений: провод с высоким напряжением может представлять «истину», а провод с низким напряжением может представлять «ложь». Выход логического элемента, рассчитанный с использованием электронных свойств полупроводников, представляет собой соответствующее напряжение от желаемой логической операции.
Центральный процессор компьютера в значительной степени построен из логических вентилей: физических проявлений булевых операторов. Логические элементы принимают одно или несколько электрических логических значений: провод с высоким напряжением может представлять «истину», а провод с низким напряжением может представлять «ложь». Выход логического элемента, рассчитанный с использованием электронных свойств полупроводников, представляет собой соответствующее напряжение от желаемой логической операции.
Логический элемент «И», например, принимает два входа. Если оба входа имеют высокое напряжение (представляющее «истина»), затвор «и» также имеет выход высокого напряжения «истина», а если один или оба входа имеют низкое напряжение или ложь, затвор будет иметь низкое напряжение. вывод ложного.
Правильное соединение этих ворот позволяет выполнять компьютерные программы. Возможность выполнять логические операции с различными входными данными, по сути, позволяет процессору решать, как обрабатывать эти входные данные.
Далее, эта булева алгебра, встроенная в компьютеры, возвращается к обычной математике. Булева дихотомия истинности и ложности прекрасно подходит для представления двоичных чисел: истина соответствует 1, а ложь соответствует 0. В соответствии с этой интерпретацией можно собрать логические схемы, которые просто путем правильного комбинирования двух двоичных входных чисел с использованием и, или, и не операции, могут складывать, вычитать, умножать или делить числа.
Иногда достижения в области чистой математики спустя десятилетия или столетия могут найти удивительное применение.
Логические методы в информатике
1. Суперпозиция для логики высшего порядка без лямбда
Александр Бенткамп ; Жасмин Бланшетт ; Саймон Круанес ; Уве Вальдманн.
Введем опровержимо полные суперпозиционные исчисления для преднамеренных и экстенсиональная клаузальная $\lambda$-свободная логика высшего порядка, два формализма, которые разрешить частичное применение и прикладные переменные.Исчисления параметризованы порядком членов, который не обязательно должен быть полностью монотонным, что позволяет использовать $\lambda$-свободный лексикографический путь высшего порядка и порядки Кнута-Бендикса. Мы внедрил исчисления в Zipperposition Prover и оценил их на Тесты Isabelle/HOL и TPTP. Они кажутся многообещающими в качестве трамплина к полным, высокоэффективным автоматическим средствам доказательства теорем для полного логика высшего порядка.
2. Коалгебраическая семантика для вероятностного логического программирования
Тао Гу; Фабио Занаси.
Программирование вероятностной логики становится все более важным в искусственных интеллект и смежные области как формализм для рассуждения о неопределенности. Это обобщает логическое программирование с возможностью аннотирования предложений с помощью вероятности.В этой статье предлагается коалгебраическая семантика вероятностных логическое программирование. Программы моделируются как коалгебры для некоторого функтора F, и две семантики даны в терминах косвободных коалгебр. Во-первых, F-коалгебра дает семантику в терминах деревьев вывода. Во-вторых, по вложив F в другой тип G, как косвободную G-коалгебру, мы получаем «возможный мировая интерпретация программ, из которой можно извлечь обычную семантика распределения вероятностного логического программирования. Кроме того, мы показываем что аналогичный подход можно использовать для предоставления коалгебраической семантики взвешенное логическое программирование.
3. Полупулбэки размеченных марковских процессов
Ян Пахль; Педро Санчес Терраф.
Помеченный марковский процесс (LMP) состоит из измеримого пространства $S$ вместе с индексированным семейством марковских ядер из $S$ в себя.Эта структура имеет использовался для моделирования вероятностных вычислений в информатике, и один из основная проблема в этой области состоит в том, чтобы определить и решить, являются ли два LMP $S$ и $S’$ «вести себя так же». Есть два естественных категорических определения одинаковость поведения: $S$ и $S’$ биподобны, если существуют ЛМП $T$ и карты, сохраняющие меру, образующие диаграмму вида $ S\leftarrow T \rightarrow{S’}$; и они поведенчески эквивалентны, если существуют некоторые $ U$ и отображения, образующие двойственную диаграмму $ S\rightarrow U \leftarrow{S’}$. Эти два понятия различаются для общих измеримых пространств, но Доберкат (расширив результат Эдала) доказал, что они совпадают для аналитических борелевских пространств, показывая, что из каждой диаграммы $S\rightarrow U \leftarrow{S’}$ можно получить диаграмму биподобности, как указано выше. Кроме того, полученный квадрат отображения, сохраняющие меру, коммутативны (полупулбэк). В этой статье мы распространяем предыдущий результат на измеримые пространства $S$ изоморфно универсально измеримому подмножеству польского пространства со следом борелевской $\sigma$-алгебры, используя вариант теоремы Штрассена об общих расширения конечно аддитивных мер.
4. Прямые спектры пространств Бишопа и их пределы
Иосиф Петракис.
Мы применяем фундаментальные понятия теории множеств Бишопа (BST), неформальной теории которая дополняет теорию множеств Бишопа теорией пространств Бишопа, теоретико-функциональный подход к конструктивной топологии. В рамках BST мы разрабатываем понятия прямого семейства множеств, прямого спектра пространств Бишопа, прямой предел прямого спектра пространств Бишопа и обратного предел контравариантного прямого спектра пространств Бишопа. В расширении неформальной системы конструктивной математики Бишопа BISH с индуктивной определения с правилами счетного числа посылок, мы доказываем фундаментальное теоремы о прямом и обратном пределах спектров пространств Бишопа и принцип двойственности между ними.
5.
 Скульптуры в параллелизме
Скульптуры в параллелизмеУли Фаренберг ; Кристиан Йохансен ; Кристофер А. Троттер ; Кшиштоф Земяньский.
Мы формируем интуитивный процесс скульптуры Пратта для многомерные автоматы (HDA). Интуитивно HDA — это скульптура, если она может быть встроены в (т. е. вылеплены) из одной ячейки более высокого измерения (гиперкуб). Первый важный результат этой статьи состоит в том, что не все HDA могут быть скульптурный, представленный несколькими природными ациклическими HDA, одним из которых является знаменитый Пример «сломанной коробки» ван Глаббика. Более того, мы показываем, что даже естественное операция разворачивания совершенно не связана с лепкой, например, есть скульптуры, развертывание которых невозможно вылепить. Мы исследуем выразительность скульптур, как собственного подкласса HDA, показывая их быть эквивалентным обычным ST-структурам (событийный аналог HDA) и к (обычным) пространствам Чу над 3 (в их параллельной интерпретации, заданной Пратт).Мы считаем, что наши результаты проливают новый свет на интуицию, стоящую за лепка как метод моделирования параллельного поведения, показывающий точную достигает своей выразительности. Помимо выразительности, мы также развиваем алгоритм, чтобы решить, можно ли лепить HDA. Что еще более важно, мы показываем что скульптуры эквивалентны евклидовым кубическим комплексам (будучи геометрический аналог нашего комбинаторного определения), которые включают популярные модели PV, используемые для обнаружения взаимоблокировок. Это свидетельствует о тесной связи между геометрическими и комбинаторными моделями для параллелизма, который может быть полезен для обеих областей.
6. Алгебраическая теория языка для Эйленберга — Алгебры Мура
Ахим Блюменсат.
Мы разрабатываем теорию алгебраического языка, основанную на понятии Алгебра Эйленберга—Мура.По сравнению с предыдущими такими фреймворками основной вкладом является поддержка алгебр с бесконечным числом сортов и связь с логикой в виде так называемых «определимых алгебр».
7. Логика для точной действительной арифметики
Гельмут Швихтенберг ; Франциск Визнет.
Продолжая предыдущую работу первого автора с У. Бергером, К. Миямото и Х. Цуики показано, как алгоритм деления действительных чисел, заданных в виде поток цифр со знаком может быть извлечен из соответствующего формального доказательства. свойство быть действительным числом, представленным в виде потока, формулируется с помощью коиндуктивно определенных предикатов, а формальные доказательства включают коиндукцию. Помощник по доказательству Minlog используется для создания формальных доказательств и извлечения их вычислительное содержание как термины базовой теории, форма теории типов для конечных или бесконечных данных.Некоторые эксперименты с запуском извлеченного термина описаны после его перевода на Haskell.
8. Построение высших индуктивных типов как коэффициентов группоида
Никколо Велтри; Нильс ван дер Вейде.
В данной работе мы изучаем финитные 1-усеченные высшие индуктивные типы (ВИТ) в теория гомотопических типов. Начнем с того, что покажем, что все эти типы могут быть построенный из группоидного частного. Определим внутреннее понятие подписи для HIT, и для каждой подписи мы строим бикатегорию алгебры в 1-типах и в группоидах. Мы продолжаем доказывать начальную алгебру семантика для наших подписей. После этого покажем, что группоидный фактор индуцирует пересоединение между бикатегориями алгебр в 1-типах и в группоиды. Затем мы строим биинициальный объект в бикатегории алгебр в группоидах, что дает желаемую алгебру.Из всего этого делаем вывод, что все конечные 1-усеченные HIT могут быть построены из группоидного частного. Мы представляем несколько примеров HIT, которые можно определить, используя наше понятие подпись. В частности, мы показываем, что каждая подпись порождает HIT. соответствующей свободно порожденной алгебраической структуре над ним. Мы также начать разработку универсальной алгебры в 1-типах. Мы показываем, что бикатегория алгебр имеет ограничения PIE, то есть произведения, средства вставки и эквалайзеры, и мы доказываем вариант первой теоремы об изоморфизме для 1-типов. Окончательно, мы даем альтернативную характеристику фундаментальным группам некоторых HIT, используя нашу конструкцию HIT через группоидное частное. Все результаты формализованы над библиотекой унивалентной математики UniMath в Кок.
9. LNL-FPC: линейное/нелинейное исчисление с фиксированной точкой
Берт Линденховиус ; Майкл Мислов ; Владимир Замджиев.
Мы описываем систему типов со смешанными линейными и нелинейными рекурсивными типами называется LNL-FPC (линейное/нелинейное исчисление с фиксированной точкой). Система типов поддерживает линейную типизацию, что повышает безопасность программ, но также поддерживает нелинейную типизацию, что делает систему типов более удобно для программирования. Так же, как и в FPC, мы показываем, что LNL-FPC поддерживает рекурсия на уровне типов, которая, в свою очередь, вызывает рекурсию на уровне терминов. Мы также предоставить надежные и адекватные в вычислительном отношении категориальные модели для LNL-FPC, которые описать категориальную структуру подструктурных операций Интуиционистская линейная логика во всех нелинейных типах, включая рекурсивные те. Для этого мы опишем новый метод решения рекурсивных задач. уравнения области в декартовых категориях путем построения решений над предварительные вложения. Система типов также имеет неявное ослабление и сжатие.правила, которые мы можем смоделировать, идентифицируя каноническую структуру комоноида всех нелинейных типов. Мы также показываем, что требования нашего реферата модели разумны, строя большой класс конкретных моделей, которые нашли применение не только в классическом функциональном программировании, но и в новые парадигмы программирования, включающие линейные типы, такие как квантовые языки программирования и описания схем.
10. Игры с переключением достижимости
Джон Фернли ; Мартин Гейринг; Матиас Мних; Рахул Савани.
Изучаем задачу определения победителя игр с переключением достижимости для вариантов с нулевым, одним и двумя игроками. Переключение игр обеспечивает детерминированный аналог стохастических игр. Покажем, что случай нулевого игрока является NL-трудным, случай с одним игроком является NP-полным, а случай с двумя игроками — PSPACE-жесткий и в EXPTIME.Для случая с нулевым игроком мы также показываем P-жесткость для кратко представленной модели, сохраняющей верхнюю границу NP $\cap$ соНП. Для случаев с одним и двумя игроками наши результаты верны как в естественном, так и в явная модель и кратко представленная модель. Наши результаты показывают, что переключаемый вариант игры сложнее с точки зрения теории сложности, чем соответствующую стохастическую версию.
11. Семантика трассировки отказов для алгебры процессов с тайм-аутами
Роб ван Глаббек.
Эта статья расширяет стандартную алгебру процессов с помощью оператора тайм-аута, тем самым повышая его абсолютную выразительность, оставаясь при этом в рамках царство алгебры процессов без времени, в том смысле, что ход времени не количественно. Эквивалентность трассировки и отказов не может быть конгруэнтностью для этого оператор; их замыкание конгруэнтности характеризуется как трасса отказа эквивалентность.
12. DRAT и доказательство избыточности распространения без новых переменных
Сэм Басс ; Нил Тапен.
Мы изучаем сложность ряда систем доказательства высказываний, которые позволяют правила вывода вида: из набора дизъюнктов $\Gamma$ вывести множество предложения $\Gamma \cup \{ C \}$, где из-за некоторого синтаксического условия $\Gamma \cup \{ C \}$ выполнимо, если $\Gamma$ есть, но где $\Gamma$ нет обязательно подразумевают $C$. Эти правила вывода включают BC, RAT, SPR и PR. (соответственно сокращение от заблокированных предложений, разрешающих асимметричных тавтологий, избыточность распространения подмножества и избыточность распространения), которая возникла из-за работа в решении выполнимости (SAT). Введем новое, более общее правило SR (замещающая избыточность). Если в новом предложении $C$ разрешено включать новые переменные, то системы на основе этих правил все эквивалентны расширенному разрешению.-$ опровержения. К ним относятся […]
13. Параметрические обновления в параметрических временных автоматах
Этьен Андре; Дидье Лайм; Матиас Рампарисон.
Мы представляем новый класс параметрических автоматов с временной задержкой (PTA), где мы разрешаем часы сравнивать с параметрами в гвардейцах, как и в классических ПТА, но и с быть обновлены до параметров. Здесь мы сосредоточимся на проблеме EF-пустоты: множество оценок параметров, для которых некоторое заданное местоположение достижимо в экземпляр временного автомата пуст?». Хорошо известно, что эта проблема неразрешима для PTA, и поэтому она неразрешима для нашего расширения. Тем не менее, если мы обновим все часы каждый раз, когда мы сравниваем часы с параметром, и каждый раз, когда мы обновить часы до параметра, мы получаем синтаксический подкласс, для которого мы можем решить проблему EF-пустоты и даже выполнить точный синтез множества рациональных оценок, таких, что данное местоположение достижимо.В меру насколько нам известно, это первый нетривиальный подкласс ПТА, на самом деле даже расширен параметрическими обновлениями, для которых это возможно.
14. Частично упорядоченные автоматы и кусочная тестируемость
Томаш Масопуст ; Маркус Крётч.
Частично упорядоченные автоматы — это автоматы, в которых отношение перехода индуцирует частичный порядок по штатам. Выразительная сила частично упорядоченных автоматов тесно связана с выразительностью фрагментов первопорядковой логики на конечные слова или, что то же самое, языковые классы уровней Иерархия Штраубинга-Териана. Несколько фрагментов (уровней) интенсивно исследованы под разными именами. Например, фрагмент первого порядка формулы с одним экзистенциальным блоком кванторов в пренексной нормальной форме известен как кусочно проверяемые языки или $J$-тривиальные языки.Эти языки характеризуются конфлюэнтными частично упорядоченными DFA или полными, конфлюэнтные и частично упорядоченные NFA, детерминированные самопетлей (ptNFA для короткая). В этой статье мы изучаем сложность основных вопросов для нескольких типы частично упорядоченных автоматов на конечных словах; а именно вопросы включения, эквивалентности и ($k$-)кусочной проверяемости. Нижняя граница сложность сводится к сложности универсальности. Универсальность задача спрашивает, распознает ли система все слова в своем алфавите. За ptNFA, сложность универсальности уменьшается, если алфавит фиксирован, но он открыт, если алфавит может расти с увеличением количества состояний. Мы показываем, что определение универсальности для общих ptNFA так же сложно, как и для общих NFA. Наш доказательство является новым и нетривиальным расширением нашей недавней конструкции для частично упорядоченные НКА, детерминированные петлей, а […]
15. Разрешимость порождений символических куч с массивами
Дайсуке Кимура ; Макото Тацута.
В этой статье представлены два результата разрешимости задачи проверки правильности для следствий символических куч в логике разделения с Presburger арифметика и массивы. Первый результат для системы с массивами и кванторы существования. Доказана правильность процедуры принятия решения при условии, что размеры массивов в последующем не являются экзистенциально количественно. Это условие отличается от условия, предложенного Brotherston et al. др. в 2017 году и одно из них не влечет за собой другого. Основная идея романа перевод из следствия символических куч в формулу в Presburger арифметика. Второй результат — разрешимость системы с обоими массивами и списки. Ключевая идея состоит в том, чтобы расширить технику разворачивания коллапса, предложенную Бердин и др. в 2005 г. к массивам и арифметике, а также к двусвязным спискам.
16. Вычислимый анализ и понятия непрерывности в Coq
Флориан Стейнберг ; Лоран Тери ; Хольгер Тис.
Приведен ряд формальных доказательств теорем из области вычислимых анализ. Многие из наших результатов определяют исполняемые алгоритмы, которые работают на бесконечные входы с помощью операций с конечными приближениями и доказаны правильно в смысле вычислимого анализа. Разработка ведется в помощник по проверке доказательств Coq и в значительной степени полагается на библиотеку Incone для получения информации теоретическая преемственность. Эта библиотека разработана одним из авторов и статья может быть использована в качестве введения в библиотеку, поскольку она описывает многие из ее наиболее важные особенности в деталях. В то время как возможность иметь полную исполняемость в формальном развитии математических утверждений о действительных числах и like не является уникальной функцией библиотеки Incone, это ее оригинальная вклад состоит в том, чтобы придерживаться соглашений вычислимого анализа, чтобы обеспечить интерфейс общего назначения для алгоритмических рассуждений о непрерывных структурах.Результаты, которые обеспечивают полное вычислительное содержание, включают в себя то, что алгебраические операции и эффективный предельный оператор над вещественными числами: вычислимо, что некоторые счетно бесконечные произведения изоморфны пространствам функций, совместимость перечислительного представления подмножеств натуральные числа с абстрактным определением пространства открытых подмножеств натуральные числа, и что непрерывная реализуемость подразумевает последовательную непрерывность. Мы также формализуем доказательства невычислительных результатов, которые поддерживают правильность наших определений. Эти […]
17. Презентабельные подписи и начальная семантика
Бенедикт Аренс ; Андре Хиршовиц ; Амбруаз Лафон ; Марко Маггези.
Мы представляем устройство для определения и рассуждения о синтаксисе для типов данных, языки программирования и логические вычисления.Точнее, мы изучаем понятие «подпись» для указания синтаксических конструкций. В духе начальной семантики мы определяем «синтаксис, созданный подпись» в качестве начального объекта — если он существует — в подходящей категории моделей. В нашей структуре наличие связанного синтаксиса для подпись не гарантируется автоматически. Мы идентифицируем через понятие представление подписи, большой класс подписей, которые генерируют синтаксис. Наши (представимые) подписи включают в себя классические алгебраические подписи (т.е. сигнатуры для языков с привязкой переменных, таких как чистая лямбда исчисление) и расширить их, включив несколько других важных примеров синтаксические конструкции. Одной из ключевых особенностей наших понятий подписи, синтаксиса и представления является то, что они очень композиционны, в том смысле, что сложные примеры могут быть получается путем склеивания более простых. Более того, через Исходную Семантику подход, наша структура обеспечивает, помимо желаемой алгебры терминов, корректная замена и связанные с ней принципы индукции и рекурсии к синтаксису.
Эта статья основана на идеях предыдущей попытки Хиршовица-Маггези, который, в свою очередь, был непосредственно вдохновлен некоторыми более ранними работами Гани-Уусталу-Хамана и Маттес-Уусталу. Основные результаты, представленные в статье, проверены компьютером […]
18. Теории вещественного сложения с предикатом и без него для целых чисел
Алексис Бес; Кристиан Чоффрут.
Мы показываем, что можно разрешить вопрос о том, можно ли определить отношение вещественных в структуре $\langle \mathbb{R}, +,<, \mathbb{Z} \rangle$ можно определить в структуре $\langle \mathbb{R}, +,<, 1 \rangle$. Этот результат достигается получив топологическую характеристику $\langle \mathbb{R}, +,<, 1 \rangle$-определимые отношения в семействе $\langle \mathbb{R}, +,<, \mathbb{Z} \rangle$-определимыми соотношениями, а затем, следуя формуле Мучника подход, показывающий, что характеристику отношения $X$ можно выражается в логике $\langle \mathbb{R}, +,<,1, X \rangle$.Приведенная выше характеристика позволяет нам доказать отсутствие промежуточного структура между $\langle \mathbb{R}, +,<, \mathbb{Z} \rangle$ и $\langle \mathbb{R}, +,<, 1 \rangle$. Мы также показываем, что $\langle \mathbb{R}, +,<, \mathbb{Z} \rangle$-определимое отношение равно $\langle \mathbb{R}, +,<, 1 \rangle$-определим тогда и только тогда, когда его пересечение с каждым $\langle \mathbb{R}, +,<, 1 \rangle$-определяемая строка $\langle \mathbb{R}, +,<, 1 \rangle$-определяемый. Это дает неэффективную, но простую характеристику $\langle \mathbb{R}, +,<, 1 \rangle$-определимые отношения.
19. Моделирование интерфейса для управления качеством и ресурсами
Мартин Хендрикс ; Марк Гейлен ; Кис Гуссенс; Роб де Йонг; Тван Бастен.
Мы разрабатываем структуру моделирования интерфейса для обеспечения качества и ресурсов.управление, которое фиксирует настраиваемые рабочие точки аппаратного и программного обеспечения компонентов с точки зрения функциональности, использования и предоставления ресурсов, а также качества такие показатели, как производительность и энергопотребление. Мы основываем эти аспекты на частично упорядоченные наборы для определения уровней качества, размеров бюджета и функциональных совместимость. Это делает структуру широко применимой и доменной. независимыми (хотя мы нацелены на встроенные и киберфизические системы). Framework прокладывает путь к динамической (ре)конфигурации и многоцелевому оптимизация компонентных систем для управления качеством и ресурсами целей.
20. Звездные игры и Гидры
Йорг Эндруллис ; Ян Виллем Клоп; Рой Овербик.
Рекурсивное упорядочивание путей является установленным и важным инструментом в терминах переписывание, чтобы доказать расторжение.Мы возвращаемся к его изложению с помощью некоторых простые правила на деревьях (или соответствующие термины), снабженные «звездой» как управляющий символ, обозначающий команду уменьшить это дерево (или терм) в порядок определяется. Это приводит к звездным играм, которые очень удобны для доказывая прекращение многих задач переписывания. Например, используя уже простейшей звездной игры на конечных непомеченных деревьях, мы получаем очень прямое доказательство окончание знаменитой битвы Гидры, прямое в том смысле, что нет обычное упоминание ординалов. Мы также включаем альтернативный путь к настройке Звездные игры, используя проверенный метод Бухгольца, адаптированный ван Остромом, в результате получилась количественная версия звезды в качестве контрольного символа. Мы заключаем с рядом вопросов и будущих направлений исследований.
21. Семантика реализуемости для индуктивных формальных топологий, тезис Чёрча и аксиома выбора
Мария Эмилия Майетти ; Самуэле Маскио ; Майкл Ратьен.
Мы представляем семантику реализуемости Клини для интенсионального уровня Minimalist Foundation, для краткости mtt, дополненный индуктивно генерируемым формальные топологии, тезис Чёрча и аксиома выбора. Эта семантика является расширение того, что используется для демонстрации постоянства интенсионального уровня Минималистский фундамент с аксиомой выбора и формальным тезисом Чёрча в Предыдущая работа. Главное нововведение здесь состоит в том, что такая семантика формализована в конструктивная теория, представленная конструктивной теорией множеств Акцеля CZF, расширенная с регулярной аксиомой продолжения.
22. Предикативные теории непрерывных решеток
Тацудзи Каваи.
Введем понятие сильной полурешетки соединения близости, предикативного понятие непрерывной решетки, которая возникает как оболочка Каруби категория алгебраических решеток.Полурешётки с сильным близостью могут быть характеризуется коалгебрами низшей степени в более широкой категории посетов близости (также известных как абстрактные базисы или R-структуры). Более того, локально компактные локали можно охарактеризовать с точки зрения сильной близости джойн-полурешетки коалгебрами двойной степенной локали на категории посетов близости. Мы также даем более логичную характеристику сильного полурешеткой, называемой сильным непрерывным конечным покрытием, которое использует отношение влечения для представления базовой полурешетки соединения. Мы показываем что эта структура естественным образом соответствует понятию непрерывной решетки в предикативной бесточечной топологии. Наш результат делает предикативное и финитный аспект понятия непрерывной решетки в бесточечной топологии подробнее явный.
23. Алгебраическая кополнота и финитные функторы
Йиржи Адамек.
Представлен ряд категорий, алгебраически полных и кополный, т. е. каждый эндофунктор имеет начальную алгебру и терминальную коалгебра. Для всех финитных (и вообще всех преднепрерывных) множеств Доказано, что функторы начальной алгебры и терминальной коалгебры несут канонический частичный порядок с тем же идеальным CPO-пополнением. И они тоже оба несут каноническую ультраметрику с тем же пополнением Коши.
24. Обнаружение уязвимостей электронных паспортов с помощью биподобия
Росс Хорн ; Сьюке Мау.
Мы обнаруживаем уязвимости конфиденциальности в стандарте ICAO 9303, реализованном Электронные паспорта по всему миру. Эти уязвимые места, подтвержденные ИКАО, позволяют Владелец электронного паспорта, который недавно прошел через контрольно-пропускной пункт для повторной идентификации без открытия электронного паспорта.В этой статье объясняется, как использовалось биподобие. обнаружить эти уязвимости, использующие протокол BAC — оригинальный ИКАО 9303 стандартный протокол аутентификации электронного паспорта — и остается действителен для протокола PACE, который повышает безопасность BAC в последние стандарты ИКАО 9303. Чтобы решить такие проблемы биподобия, мы разработайте здесь цепочку методов прикладного $\pi$-исчисления, включая символическое недоподобие биподобия, называемое открытым биподобием, и модальная логика, называемая классической FM, для описания и сертификации атак. Приведены доказательства в пользу новой схемы определения таких проблемы несвязываемости, что более точно отражает возможности злоумышленник.
25. Кодирование многозначной логики в $\lambda$-исчислении
Фер-Ян де Врис.
Мы расширим известную кодировку Черча булевой логики в $\lambda$-исчисление к кодированию $3$-значной логики Маккарти в подходящее бесконечное расширение $\lambda$-исчисления, которое идентифицирует все неразрешимых на $\bot$, где $\bot$ — свежая константа.Эта кодировка уточняет к $n$-значной логике для $n\in\{4,5\}$. Такие кодировки существуют и для Черча. оригинальное $\lambda\mathbf{I}$-исчисление. В качестве мотивации мы рассматриваем Парадокс Рассела, использующий тот факт, что одна и та же кодировка позволяет нам также вычислить значения истинности бесконечных закрытых предложений в этом бесконечном параметр.
Математика для информатики: дискретная математика | Магистерская программа в области компьютерных наук
Что такое дискретная математика?Дискретная математика — это раздел математики, связанный с изучением объектов, которые могут быть представлены конечно (или счетно). Он охватывает широкий спектр тем, которые можно использовать для ответа на многие осязаемые вопросы, возникающие в повседневной жизни:
- Логика: Является ли данный аргумент логически обоснованным или он содержит ошибку?
- Теория чисел: если високосный год бывает каждые 4 года, а сенаторы США избираются каждые 6 лет, как часто выборы в Сенат проводятся в високосный год?
- Подсчет: сколько различных нарядов вы можете сделать из одежды в вашем шкафу?
- Вероятность: Каковы ваши шансы выиграть в лотерею? (Подсказка: очень, очень низкий)
- Повторения: сколько вы будете платить в течение срока действия ипотеки, если проценты начисляются ежемесячно?
- Теория графов: как быстрее всего добраться из дома на работу?
Все эти темы рассматриваются в курсе погружения в дискретную математику MPCS.
Дискретная математика обеспечивает необходимую основу практически для каждой области компьютерных наук, и, соответственно, ее приложения обширны.
На самом фундаментальном уровне все данные компьютера представлены в виде битов (нули и единицы). Компьютеры производят вычисления, изменяя эти биты в соответствии с законами Булева алгебра , которые составляют основу всех цифровых схем (которые представлены в виде графов). Языки программирования низкого уровня напрямую зависят от логических операторов, таких как , а не и или. Разработчики программного обеспечения, использующие языки высокого уровня, часто работают над оптимизацией своего кода, сводя к минимуму количество низкоуровневых операций, и даже могут работать непосредственно с битами. Программисты также используют булеву логику для управления ходом программы, то есть, какие инструкции выполняются при определенных условиях.
При программировании важно быть уверенным, что ваш код достигнет желаемых результатов. Программы можно точно описать с помощью математики, а инструменты пропозициональной логики можно использовать для рассуждений об их правильности. Этот навык имеет решающее значение для разработки и анализа алгоритмов, основной области информатики. Итеративное программирование и функциональное программирование — две основные парадигмы, основанные на принципе математической индукции для проверки циклов (for и while) и рекурсивных вызовов функций соответственно. Logic — это язык, используемый для большинства языков формальных спецификаций, и он является фундаментальным для понимания большей части литературы по верификации, основам и проектированию языков программирования. Например, языки семейства SQL — это просто реализации реляционной логики с дополнительными функциями, а многие другие предметно-ориентированные языки — это аналогичные реализации некоторых конкретных логических вычислений. Верификация программ и формальные методы получают все большее распространение в промышленности и используются в тандеме с традиционными методами тестирования, чтобы повысить уверенность в том, что программное обеспечение ведет себя так, как предполагается.
Верификация программ и формальные методы получают все большее распространение в промышленности и используются в тандеме с традиционными методами тестирования, чтобы повысить уверенность в том, что программное обеспечение ведет себя так, как предполагается.
Индукция и рекурсия являются ключевыми понятиями в понимании функциональной парадигмы программирования, которая получает все более широкое распространение в промышленности таких компаний, как Apple (Swift), Microsoft (F#), Microsoft Research (F*, Haskell), Oracle (Java 8, Javascript), Facebook (Haskell) и Amazon, использующих эту парадигму как для узкоспециализированных задач, так и для общего использования. Повторы также являются распространенным способом определения алгоритмов и структур данных, даже если конкретная реализация определяется итеративно. Более того, они составляют основу многих моделей вычислений и более теоретических областей информатики. Они также имеют основополагающее значение для проверки программного обеспечения, еще одной области информатики, которая получает все большее распространение, поскольку свойства правильности и безопасности программного обеспечения становятся все более важными в конфиденциальных приложениях.
Теория чисел имеет важные приложения для блокчейна, криптографии и компьютерной безопасности. Современные криптографические системы должны быть математически корректными, чтобы защитить данные пользователей от злоумышленников. Модульная арифметика является математической основой для хэш-функций, которые являются чрезвычайно полезными инструментами для многих приложений. Контрольные суммы, основанные на хешировании, могут подтвердить, что файлы, передаваемые через Интернет, не содержат ошибок. Структуры данных, такие как хэш-карты, основаны на модульной арифметике для эффективных операций. Теория чисел также используется в компьютерной архитектуре и операционных системах, связанных с памятью.
Метод счета используется для развития количественной интуиции. Например, их можно использовать для определения количества действительных паролей, которые могут быть сформированы из заданного набора правил, и того, сколько времени потребуется злоумышленнику, чтобы подобрать их все методом грубой силы. Принцип сортировки объясняет, почему не существует универсального алгоритма сжатия без потерь: каждый алгоритм сжатия должен делать одни файлы меньше, а другие больше. Поэтому каждый алгоритм сжатия предназначен для сжатия файлов разных типов (текст, изображения, видео и т. д.). Подсчет полезен при анализе сложности алгоритмов. В реальных приложениях существуют сложные компромиссы между несколькими доступными ресурсами. Некоторые задачи требуют быстрых алгоритмов и могут позволить использовать много места для достижения скорости, в то время как другие не имеют много места и поэтому должны жертвовать временем ради места. В более сложных ситуациях необходимо достичь оптимального уровня использования ресурсов, чтобы система не испытывала нехватки ресурсов и могла продолжать работать. Подсчет является основой для систематизированного рассмотрения таких соображений и фактически может использоваться для предоставления формальных гарантий использования ресурсов.
Принцип сортировки объясняет, почему не существует универсального алгоритма сжатия без потерь: каждый алгоритм сжатия должен делать одни файлы меньше, а другие больше. Поэтому каждый алгоритм сжатия предназначен для сжатия файлов разных типов (текст, изображения, видео и т. д.). Подсчет полезен при анализе сложности алгоритмов. В реальных приложениях существуют сложные компромиссы между несколькими доступными ресурсами. Некоторые задачи требуют быстрых алгоритмов и могут позволить использовать много места для достижения скорости, в то время как другие не имеют много места и поэтому должны жертвовать временем ради места. В более сложных ситуациях необходимо достичь оптимального уровня использования ресурсов, чтобы система не испытывала нехватки ресурсов и могла продолжать работать. Подсчет является основой для систематизированного рассмотрения таких соображений и фактически может использоваться для предоставления формальных гарантий использования ресурсов.
Вероятность повсеместно используется не только в компьютерных науках, но и в других количественных областях. Инженеры-программисты используют вероятность для оценки риска. Например, при проектировании определенной системы можно использовать вероятность для расчета вероятности того, что система испытает пиковую нагрузку, превышающую ее возможности, и выйдет из строя. Точно так же вероятность можно использовать для измерения надежности сети. Условная вероятность имеет множество применений в машинном обучении, которое используется для решения самых разных задач, от калибровки спам-фильтров до разработки более эффективных методов лечения путем сворачивания белков. Рандомизированные алгоритмы часто более эффективны на практике, а иногда являются наиболее известными алгоритмами для аппроксимации задач, которые слишком сложно вычислить точно. Вероятность также является одной из основ статистики и, следовательно, науки о данных, одной из самых горячих областей промышленности в настоящее время. Изучение вероятности в контексте информатики дает учащимся количественную интуицию, которая полезна в их карьере и повседневной жизни.
Инженеры-программисты используют вероятность для оценки риска. Например, при проектировании определенной системы можно использовать вероятность для расчета вероятности того, что система испытает пиковую нагрузку, превышающую ее возможности, и выйдет из строя. Точно так же вероятность можно использовать для измерения надежности сети. Условная вероятность имеет множество применений в машинном обучении, которое используется для решения самых разных задач, от калибровки спам-фильтров до разработки более эффективных методов лечения путем сворачивания белков. Рандомизированные алгоритмы часто более эффективны на практике, а иногда являются наиболее известными алгоритмами для аппроксимации задач, которые слишком сложно вычислить точно. Вероятность также является одной из основ статистики и, следовательно, науки о данных, одной из самых горячих областей промышленности в настоящее время. Изучение вероятности в контексте информатики дает учащимся количественную интуицию, которая полезна в их карьере и повседневной жизни.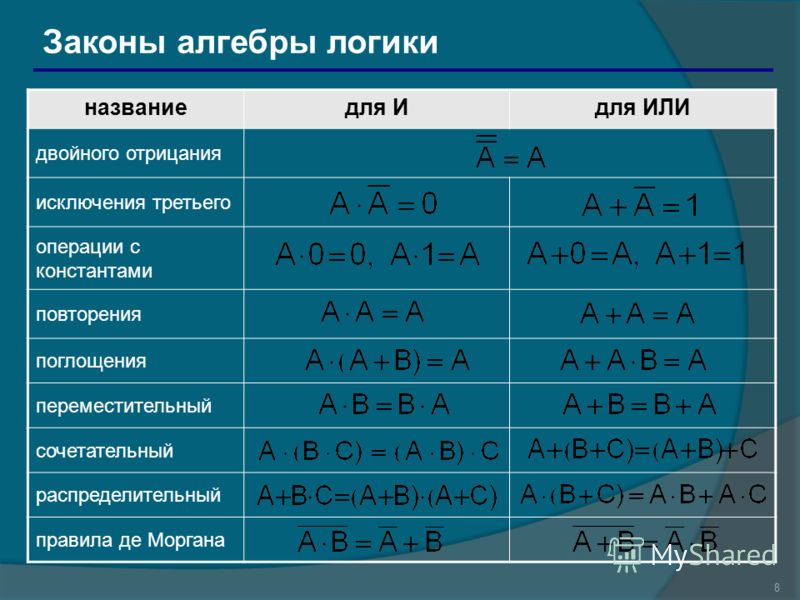
Графики — это мощные структуры данных, которые используются для моделирования отношений и ответов на вопросы об указанных данных: например, ваше навигационное приложение использует алгоритм поиска по графу, чтобы найти самый быстрый маршрут от вашего дома до вашего рабочего места. Linked-In использует граф для моделирования вашей профессиональной сети, как и ваша телекоммуникационная компания для своей сотовой сети (на самом деле сеть — это альтернативное название графа). Ученые-компьютерщики широко используют графы: для представления файловых систем, для контроля версий, а также в функциональном программировании, глубоком обучении, базах данных и многих других приложениях.
Какие преимущества дает учащимся MPCS изучение дискретной математики? Освоение дискретной математики позволяет студенту MPCS добиться успеха как в магистерской программе, так и в карьере в области разработки программного обеспечения или в аналогичной технической области.


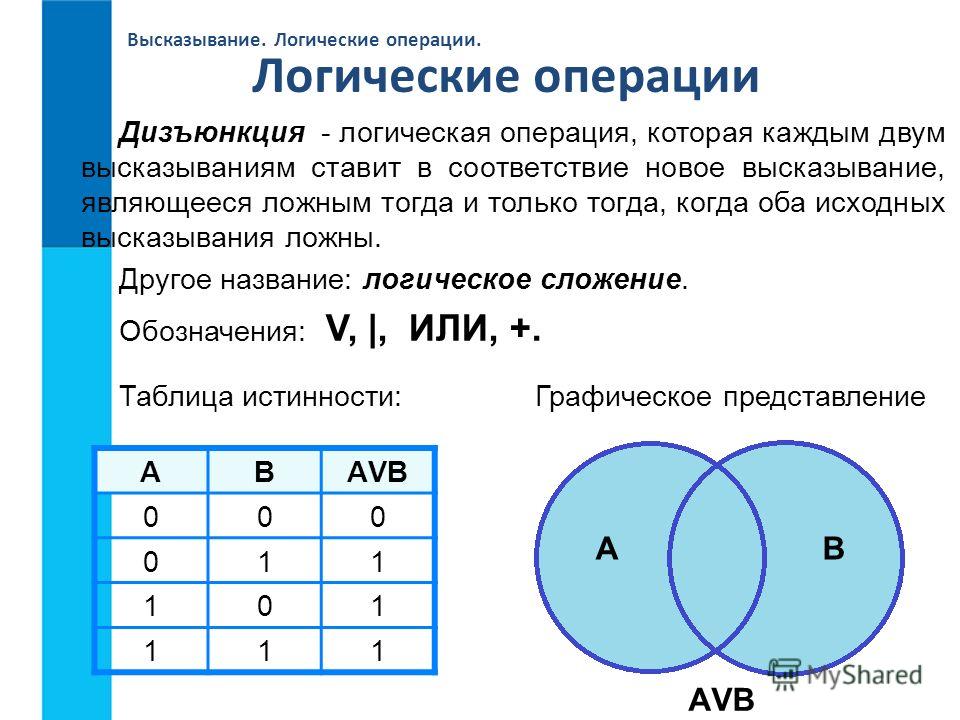 Но относительно логических операторов их приоритет станет самым высоким.
Но относительно логических операторов их приоритет станет самым высоким.

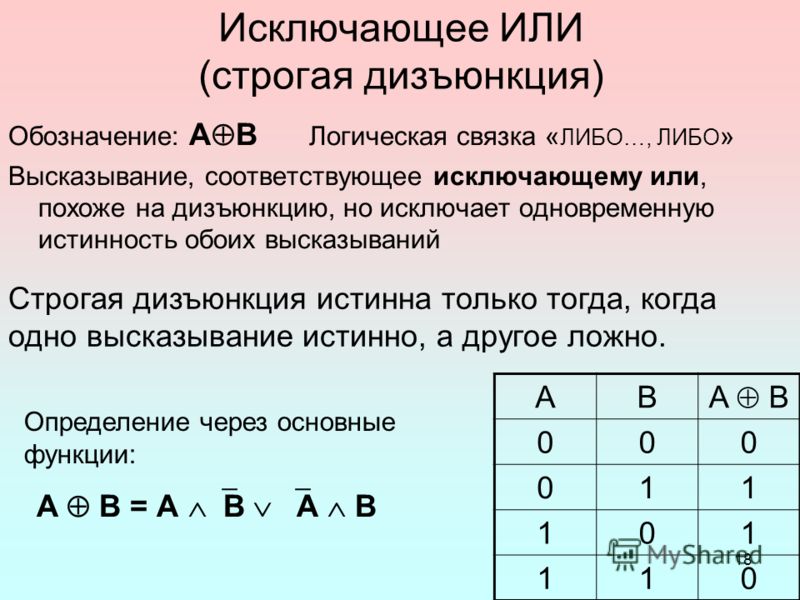 Высказывание, никакая часть которого не является высказыванием, называется элементарным (простым).
Высказывание, никакая часть которого не является высказыванием, называется элементарным (простым).

 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic.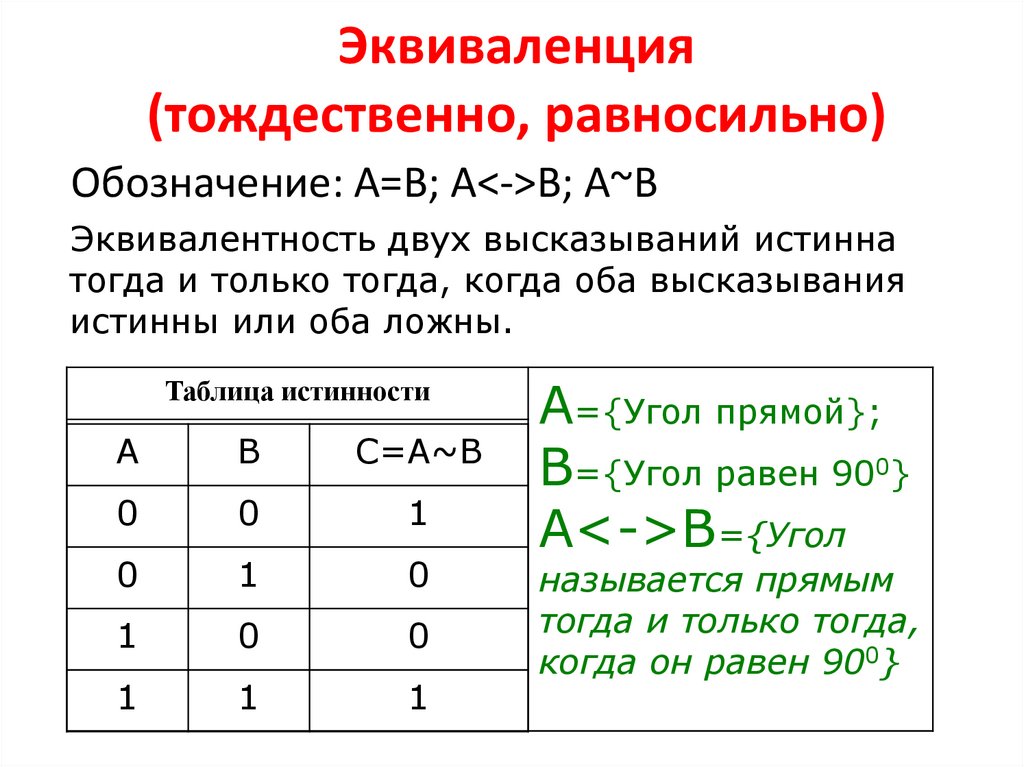

 Организует ежемесячные семинары.
Организует ежемесячные семинары.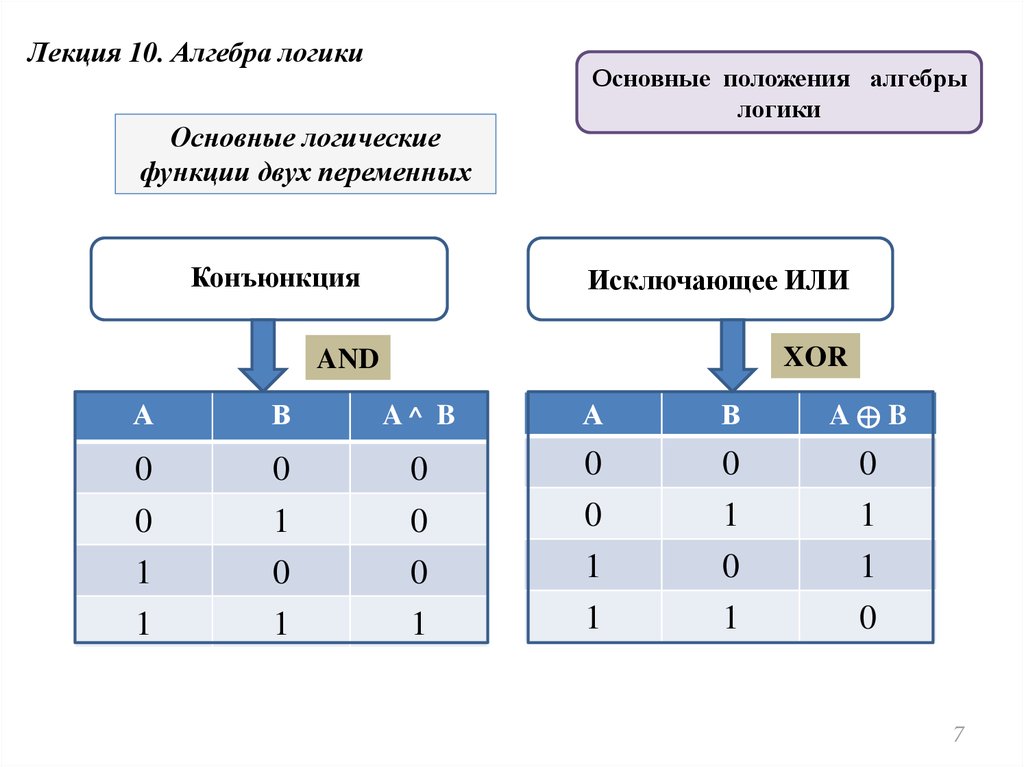 ), исследовательская деятельность (Extremal Graph
Теория и компьютерные научные открытия).
), исследовательская деятельность (Extremal Graph
Теория и компьютерные научные открытия).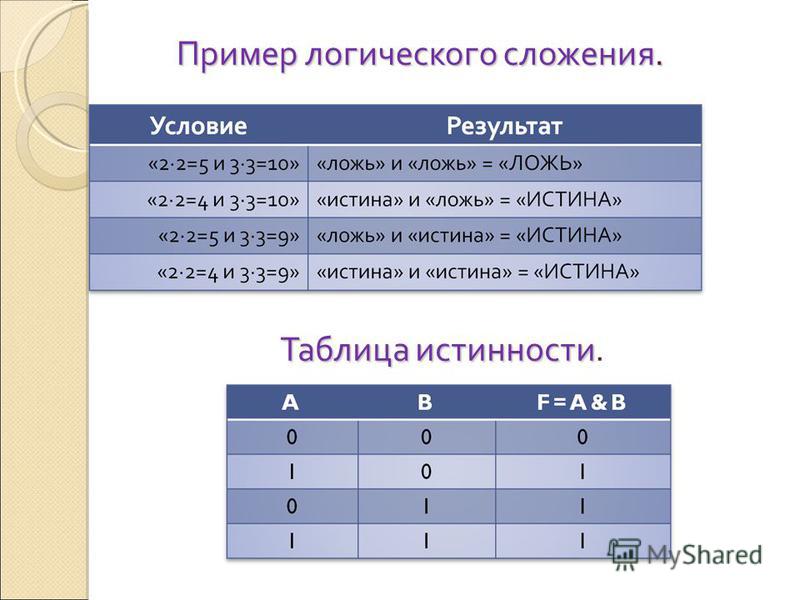


 Вклад в логику и доказательство
теория, методы проверки распределенных и
реактивные системы, вирусология и безопасность. Логика, модели для
вычисления, программирование моделей, переписывание, моделирование,
спецификация…
Вклад в логику и доказательство
теория, методы проверки распределенных и
реактивные системы, вирусология и безопасность. Логика, модели для
вычисления, программирование моделей, переписывание, моделирование,
спецификация…
 Фридриха Вильгельма)
Фридриха Вильгельма)
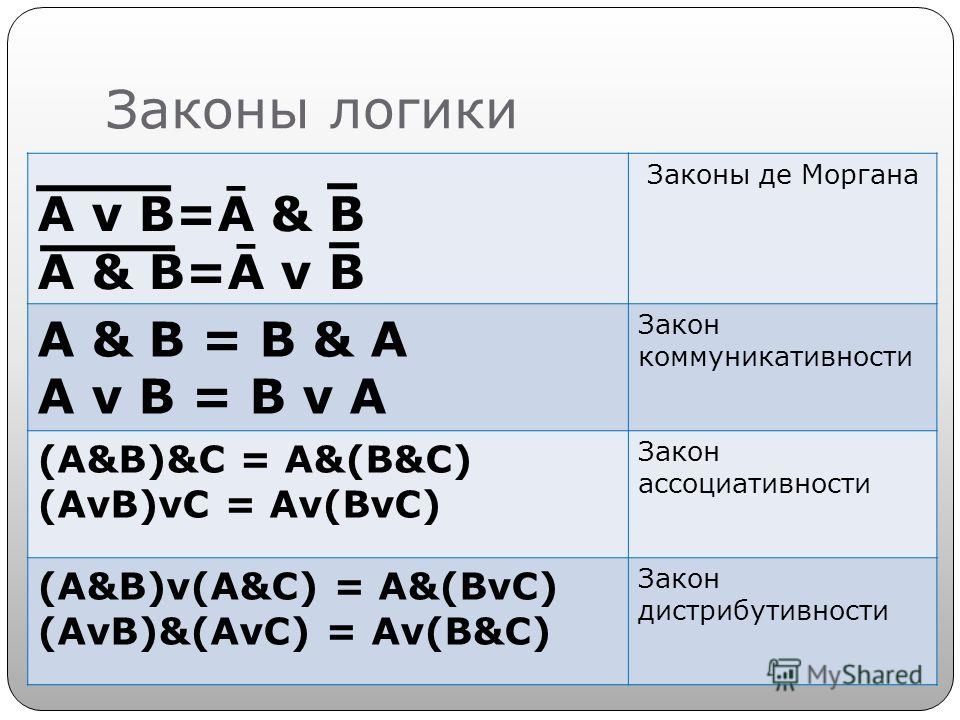
 Вайденбах (Автоматизация логики)
Вайденбах (Автоматизация логики)
 Фаэдо»
Фаэдо»

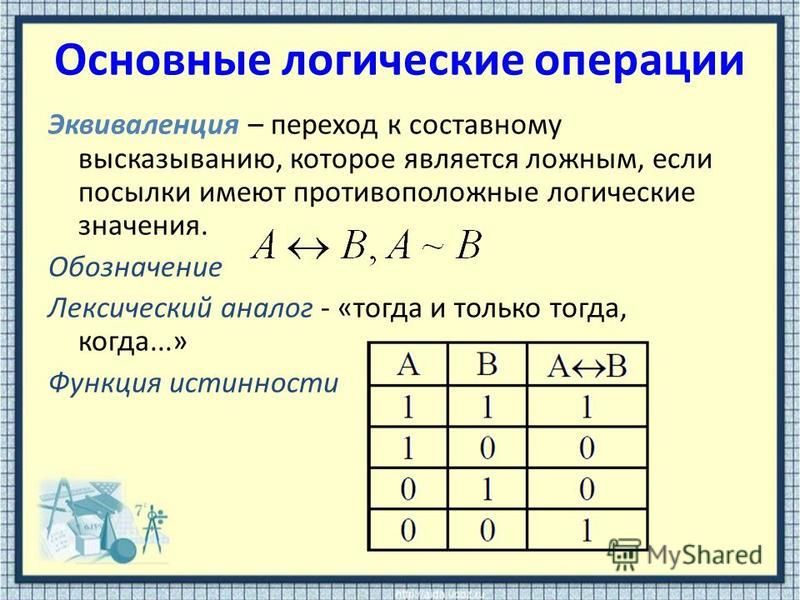

 Халбайзен работает над бесконечной комбинаторикой и теорией множеств.
в Цюрихском университете.
Халбайзен работает над бесконечной комбинаторикой и теорией множеств.
в Цюрихском университете.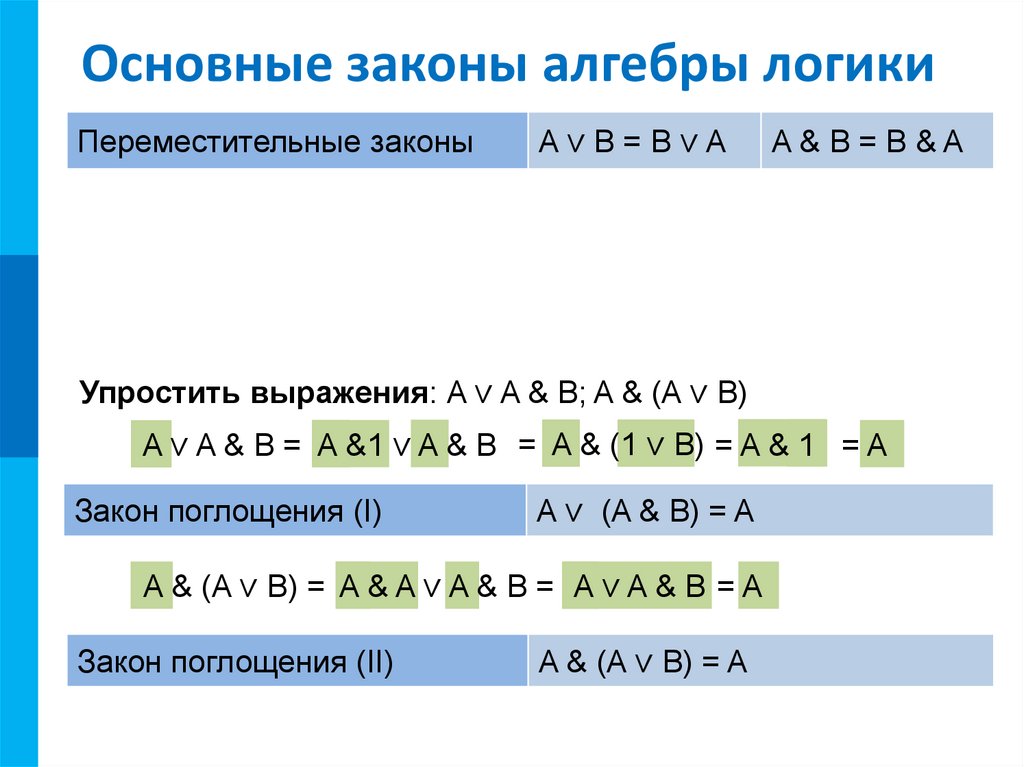
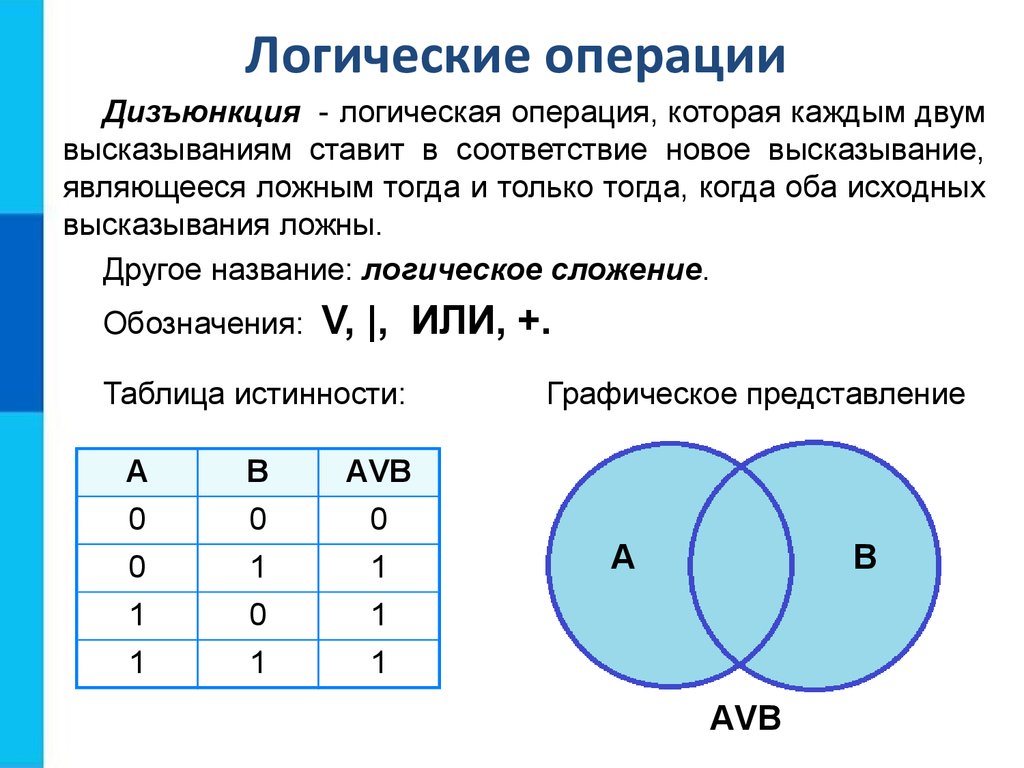 Широкий
круг интересов, от разработки новой математики
вычислительного поведения, к изучению и развитию
проектирование системы и методы проверки. Есть большая группа
посвященный автоматизации логики — Манчестер является домом
двух мировых чемпионов автоматизированных систем доказательства теорем.
Широкий
круг интересов, от разработки новой математики
вычислительного поведения, к изучению и развитию
проектирование системы и методы проверки. Есть большая группа
посвященный автоматизации логики — Манчестер является домом
двух мировых чемпионов автоматизированных систем доказательства теорем.
 Берк (Набор
теория, общая топология…)
Берк (Набор
теория, общая топология…) sfu.ca/llep/)
sfu.ca/llep/) Басс
— Миа Миннес
Басс
— Миа Миннес
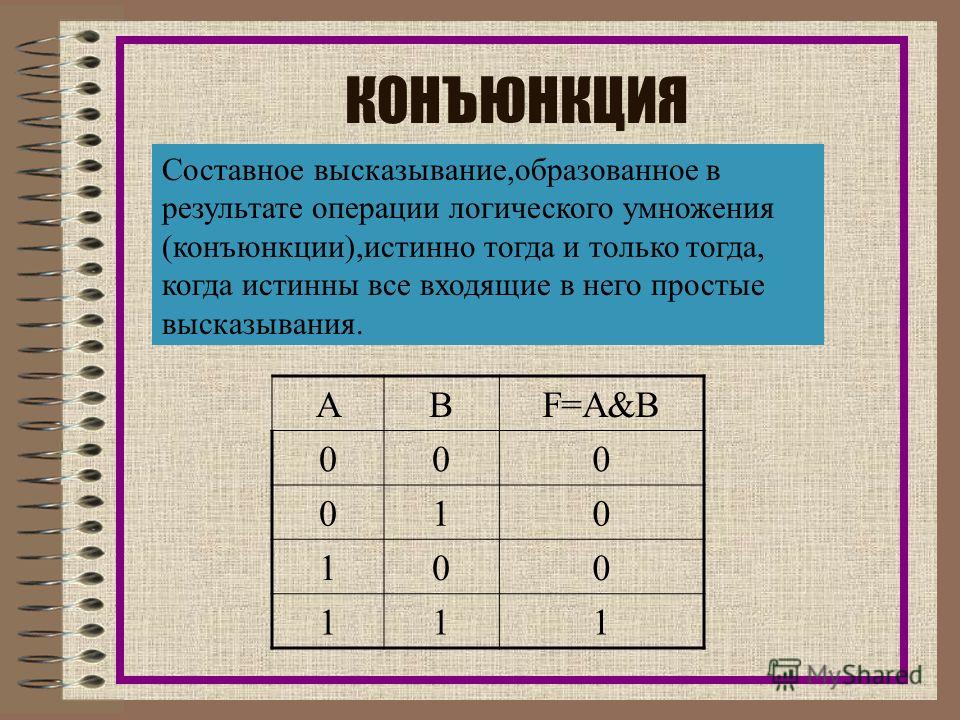 Скоукрофт — Кэрол С. Вуд — Алекс
Крукман. (Заслуги: В. Вистар Комфорт
— Фред Э.Дж. Линтон
— Льюис С. Робертсон)
Скоукрофт — Кэрол С. Вуд — Алекс
Крукман. (Заслуги: В. Вистар Комфорт
— Фред Э.Дж. Линтон
— Льюис С. Робертсон) 
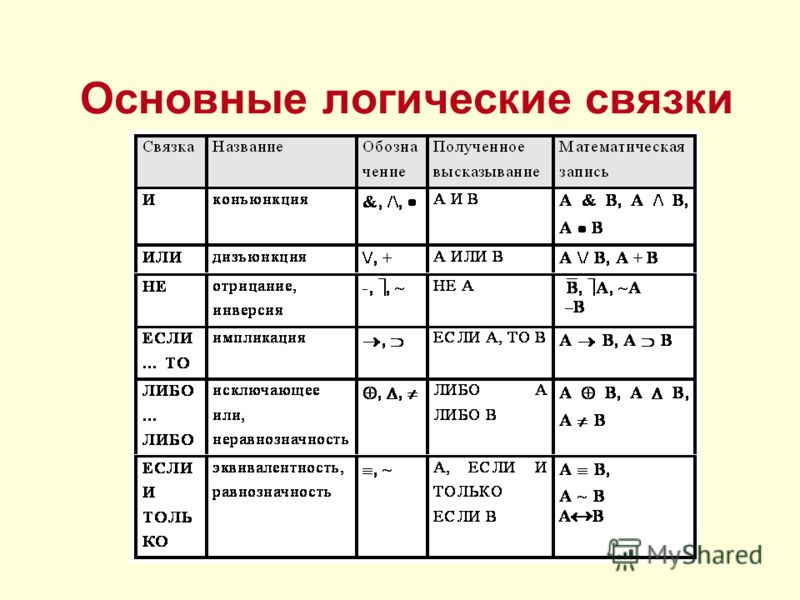 Мосс.
Мосс.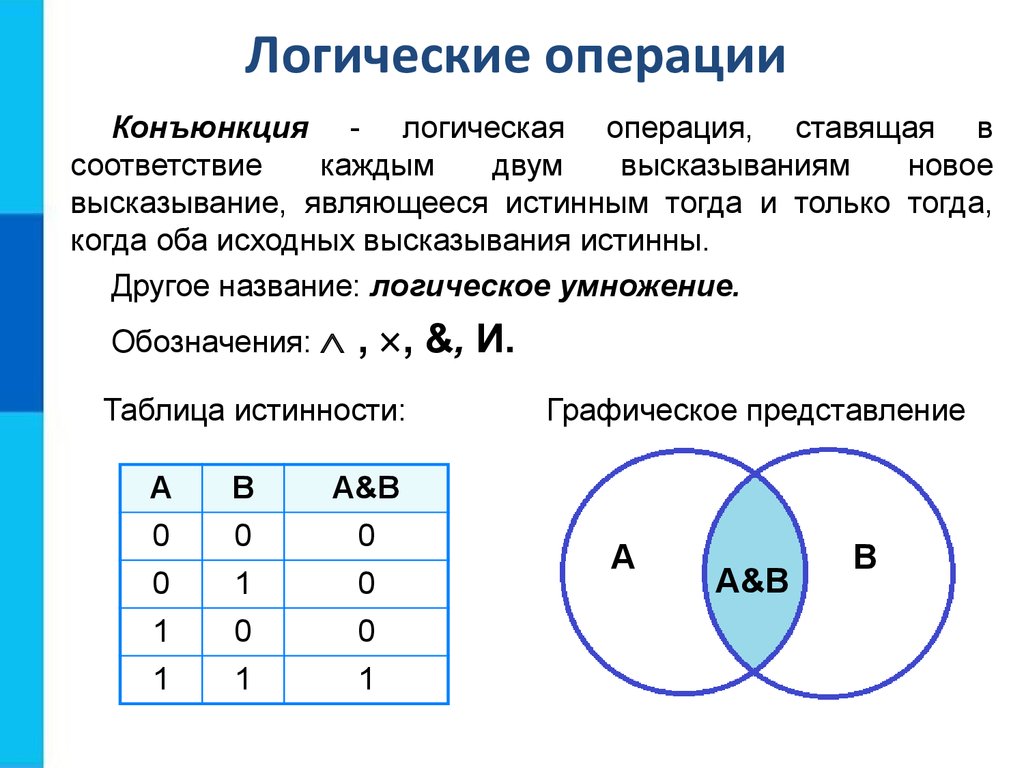 В.
Теория модели Кукера
В.
Теория модели Кукера

 Аптер (теория множеств: большие кардиналы и форсинг).
Аптер (теория множеств: большие кардиналы и форсинг). -Ю. Ли
-Ю. Ли 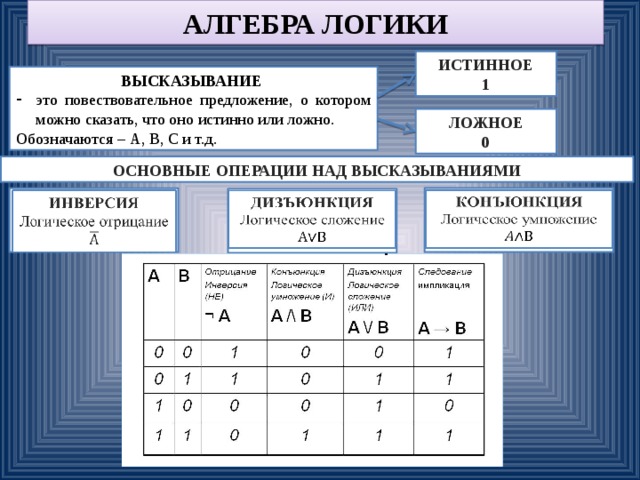
 Ясински — Кен
Монахи — Кшиштоф
Плотка
Ясински — Кен
Монахи — Кшиштоф
Плотка 
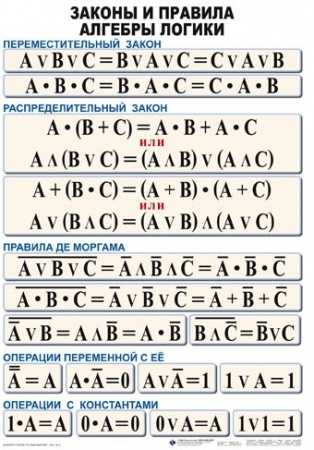
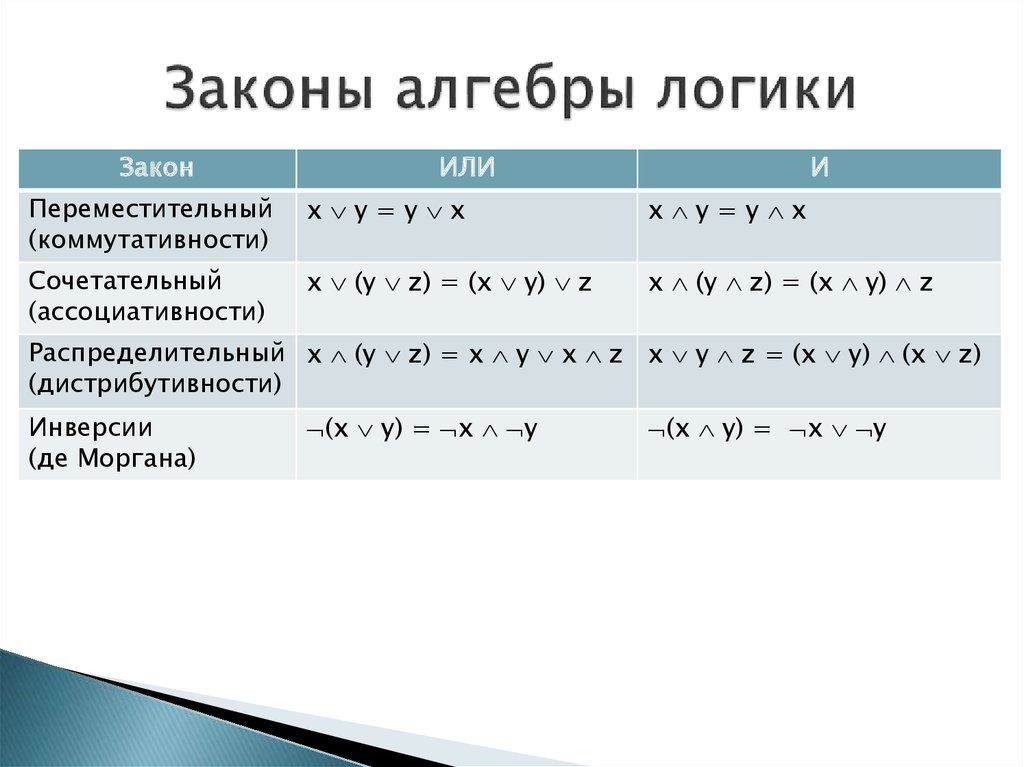

 В. Равишанкар Сарма
В. Равишанкар Сарма Иерусалим.
Иерусалим. Кафедра фундаментальной математики
включает алгебру, топологию, дифференциальную геометрию и
математическая логика.
Кафедра фундаментальной математики
включает алгебру, топологию, дифференциальную геометрию и
математическая логика. (ранее: доктор Колин Бейли и Роб
Голдблатт)
(ранее: доктор Колин Бейли и Роб
Голдблатт)
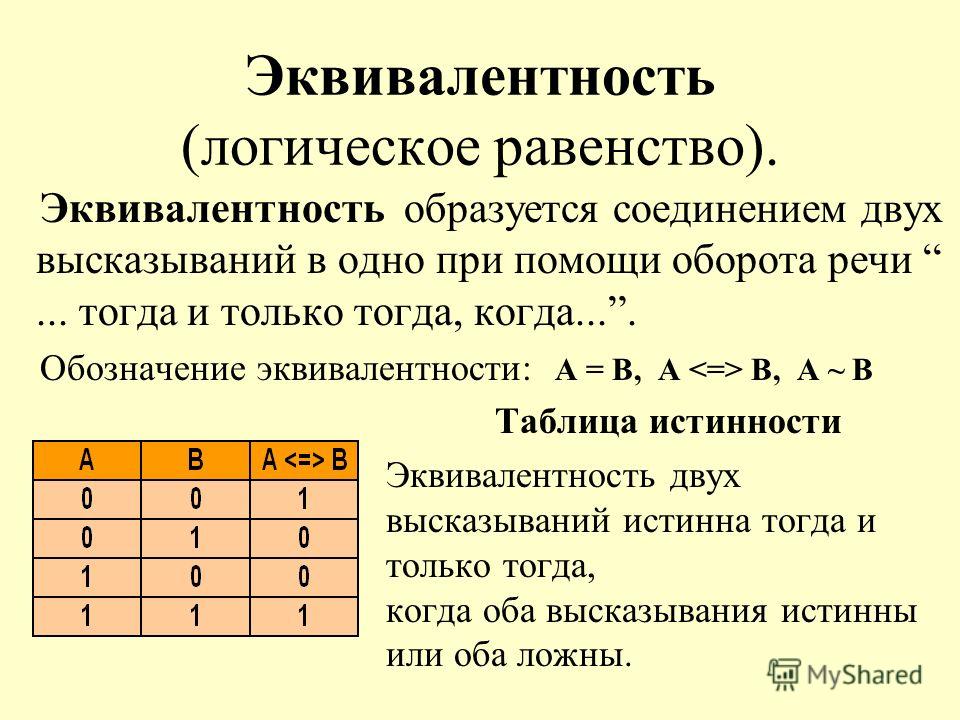 Исчисления параметризованы
порядком членов, который не обязательно должен быть полностью монотонным, что позволяет использовать
$\lambda$-свободный лексикографический путь высшего порядка и порядки Кнута-Бендикса. Мы
внедрил исчисления в Zipperposition Prover и оценил их на
Тесты Isabelle/HOL и TPTP. Они кажутся многообещающими в качестве трамплина
к полным, высокоэффективным автоматическим средствам доказательства теорем для полного
логика высшего порядка.
Исчисления параметризованы
порядком членов, который не обязательно должен быть полностью монотонным, что позволяет использовать
$\lambda$-свободный лексикографический путь высшего порядка и порядки Кнута-Бендикса. Мы
внедрил исчисления в Zipperposition Prover и оценил их на
Тесты Isabelle/HOL и TPTP. Они кажутся многообещающими в качестве трамплина
к полным, высокоэффективным автоматическим средствам доказательства теорем для полного
логика высшего порядка. В этой статье предлагается коалгебраическая семантика вероятностных
логическое программирование. Программы моделируются как коалгебры для некоторого функтора F,
и две семантики даны в терминах косвободных коалгебр. Во-первых,
F-коалгебра дает семантику в терминах деревьев вывода. Во-вторых, по
вложив F в другой тип G, как косвободную G-коалгебру, мы получаем «возможный
мировая интерпретация программ, из которой можно извлечь обычную
семантика распределения вероятностного логического программирования. Кроме того, мы показываем
что аналогичный подход можно использовать для предоставления коалгебраической семантики
взвешенное логическое программирование.
В этой статье предлагается коалгебраическая семантика вероятностных
логическое программирование. Программы моделируются как коалгебры для некоторого функтора F,
и две семантики даны в терминах косвободных коалгебр. Во-первых,
F-коалгебра дает семантику в терминах деревьев вывода. Во-вторых, по
вложив F в другой тип G, как косвободную G-коалгебру, мы получаем «возможный
мировая интерпретация программ, из которой можно извлечь обычную
семантика распределения вероятностного логического программирования. Кроме того, мы показываем
что аналогичный подход можно использовать для предоставления коалгебраической семантики
взвешенное логическое программирование. Эта структура имеет
использовался для моделирования вероятностных вычислений в информатике, и один из
основная проблема в этой области состоит в том, чтобы определить и решить, являются ли два LMP $S$ и
$S’$ «вести себя так же». Есть два естественных категорических определения
одинаковость поведения: $S$ и $S’$ биподобны, если существуют ЛМП $T$ и
карты, сохраняющие меру, образующие диаграмму вида $ S\leftarrow T
\rightarrow{S’}$; и они поведенчески эквивалентны, если существуют некоторые $ U$
и отображения, образующие двойственную диаграмму $ S\rightarrow U \leftarrow{S’}$.
Эти два понятия различаются для общих измеримых пространств, но Доберкат
(расширив результат Эдала) доказал, что они совпадают для аналитических борелевских
пространств, показывая, что из каждой диаграммы $S\rightarrow U \leftarrow{S’}$ можно
получить диаграмму биподобности, как указано выше. Кроме того, полученный квадрат
отображения, сохраняющие меру, коммутативны (полупулбэк).
В этой статье мы распространяем предыдущий результат на измеримые пространства $S$
изоморфно универсально измеримому подмножеству польского пространства со следом
борелевской $\sigma$-алгебры, используя вариант теоремы Штрассена об общих
расширения конечно аддитивных мер.
Эта структура имеет
использовался для моделирования вероятностных вычислений в информатике, и один из
основная проблема в этой области состоит в том, чтобы определить и решить, являются ли два LMP $S$ и
$S’$ «вести себя так же». Есть два естественных категорических определения
одинаковость поведения: $S$ и $S’$ биподобны, если существуют ЛМП $T$ и
карты, сохраняющие меру, образующие диаграмму вида $ S\leftarrow T
\rightarrow{S’}$; и они поведенчески эквивалентны, если существуют некоторые $ U$
и отображения, образующие двойственную диаграмму $ S\rightarrow U \leftarrow{S’}$.
Эти два понятия различаются для общих измеримых пространств, но Доберкат
(расширив результат Эдала) доказал, что они совпадают для аналитических борелевских
пространств, показывая, что из каждой диаграммы $S\rightarrow U \leftarrow{S’}$ можно
получить диаграмму биподобности, как указано выше. Кроме того, полученный квадрат
отображения, сохраняющие меру, коммутативны (полупулбэк).
В этой статье мы распространяем предыдущий результат на измеримые пространства $S$
изоморфно универсально измеримому подмножеству польского пространства со следом
борелевской $\sigma$-алгебры, используя вариант теоремы Штрассена об общих
расширения конечно аддитивных мер.
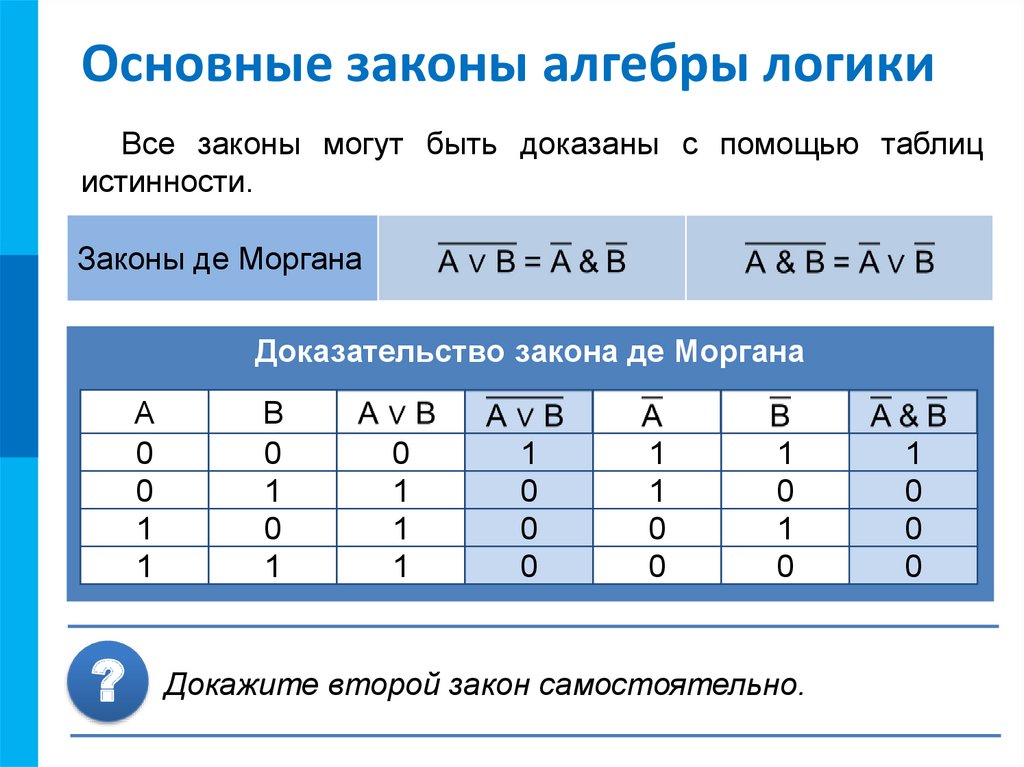 Мы считаем, что наши результаты проливают новый свет на интуицию, стоящую за
лепка как метод моделирования параллельного поведения, показывающий точную
достигает своей выразительности. Помимо выразительности, мы также развиваем
алгоритм, чтобы решить, можно ли лепить HDA. Что еще более важно, мы показываем
что скульптуры эквивалентны евклидовым кубическим комплексам (будучи
геометрический аналог нашего комбинаторного определения), которые включают
популярные модели PV, используемые для обнаружения взаимоблокировок. Это свидетельствует о тесной связи
между геометрическими и комбинаторными моделями для параллелизма, который может быть полезен
для обеих областей.
Мы считаем, что наши результаты проливают новый свет на интуицию, стоящую за
лепка как метод моделирования параллельного поведения, показывающий точную
достигает своей выразительности. Помимо выразительности, мы также развиваем
алгоритм, чтобы решить, можно ли лепить HDA. Что еще более важно, мы показываем
что скульптуры эквивалентны евклидовым кубическим комплексам (будучи
геометрический аналог нашего комбинаторного определения), которые включают
популярные модели PV, используемые для обнаружения взаимоблокировок. Это свидетельствует о тесной связи
между геометрическими и комбинаторными моделями для параллелизма, который может быть полезен
для обеих областей.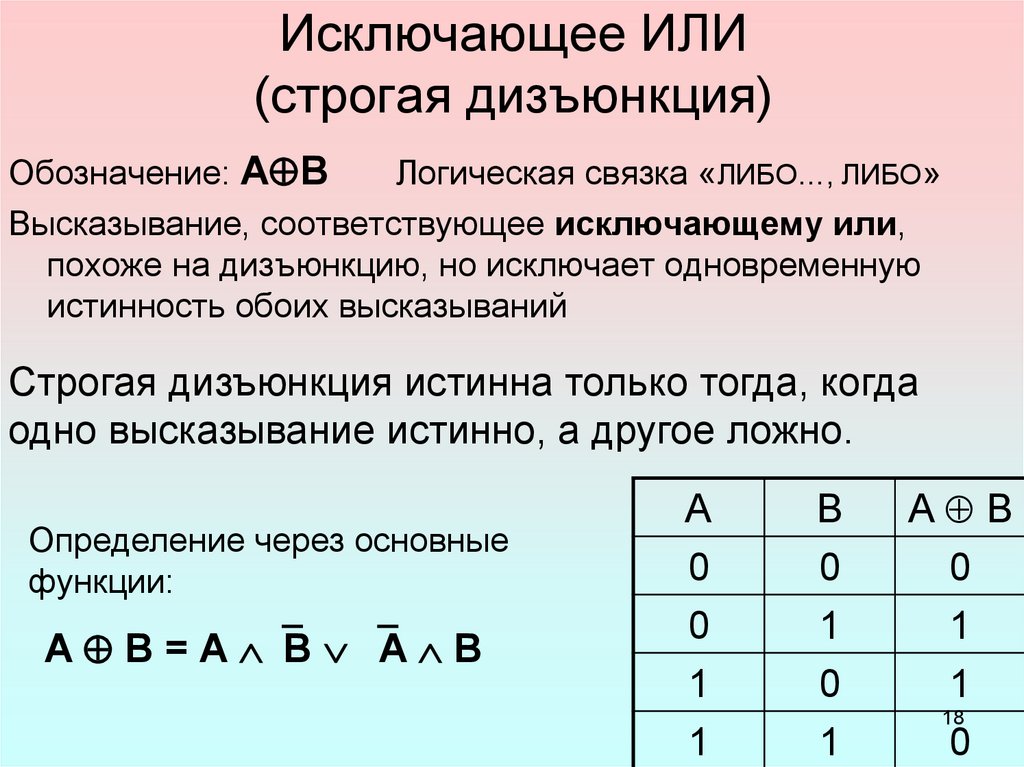 По сравнению с предыдущими такими фреймворками основной
вкладом является поддержка алгебр с бесконечным числом сортов и
связь с логикой в виде так называемых «определимых алгебр».
По сравнению с предыдущими такими фреймворками основной
вкладом является поддержка алгебр с бесконечным числом сортов и
связь с логикой в виде так называемых «определимых алгебр». Некоторые эксперименты с запуском извлеченного термина
описаны после его перевода на Haskell.
Некоторые эксперименты с запуском извлеченного термина
описаны после его перевода на Haskell.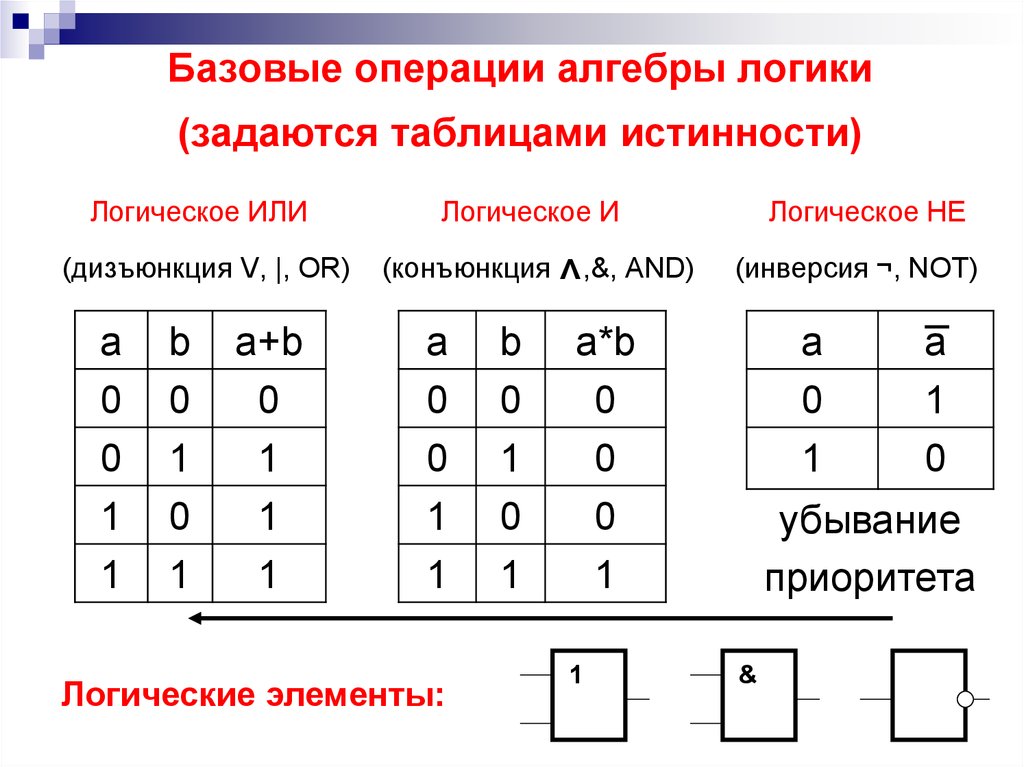 Из всего этого делаем вывод, что
все конечные 1-усеченные HIT могут быть построены из группоидного частного.
Мы представляем несколько примеров HIT, которые можно определить, используя наше понятие
подпись. В частности, мы показываем, что каждая подпись порождает HIT.
соответствующей свободно порожденной алгебраической структуре над ним. Мы также
начать разработку универсальной алгебры в 1-типах. Мы показываем, что
бикатегория алгебр имеет ограничения PIE, то есть произведения, средства вставки и эквалайзеры,
и мы доказываем вариант первой теоремы об изоморфизме для 1-типов. Окончательно,
мы даем альтернативную характеристику фундаментальным группам некоторых
HIT, используя нашу конструкцию HIT через группоидное частное. Все
результаты формализованы над библиотекой унивалентной математики UniMath в
Кок.
Из всего этого делаем вывод, что
все конечные 1-усеченные HIT могут быть построены из группоидного частного.
Мы представляем несколько примеров HIT, которые можно определить, используя наше понятие
подпись. В частности, мы показываем, что каждая подпись порождает HIT.
соответствующей свободно порожденной алгебраической структуре над ним. Мы также
начать разработку универсальной алгебры в 1-типах. Мы показываем, что
бикатегория алгебр имеет ограничения PIE, то есть произведения, средства вставки и эквалайзеры,
и мы доказываем вариант первой теоремы об изоморфизме для 1-типов. Окончательно,
мы даем альтернативную характеристику фундаментальным группам некоторых
HIT, используя нашу конструкцию HIT через группоидное частное. Все
результаты формализованы над библиотекой унивалентной математики UniMath в
Кок. правила, которые мы можем смоделировать, идентифицируя каноническую структуру комоноида
всех нелинейных типов. Мы также показываем, что требования нашего реферата
модели разумны, строя большой класс конкретных моделей, которые
нашли применение не только в классическом функциональном программировании, но и в
новые парадигмы программирования, включающие линейные типы, такие как квантовые
языки программирования и описания схем.
правила, которые мы можем смоделировать, идентифицируя каноническую структуру комоноида
всех нелинейных типов. Мы также показываем, что требования нашего реферата
модели разумны, строя большой класс конкретных моделей, которые
нашли применение не только в классическом функциональном программировании, но и в
новые парадигмы программирования, включающие линейные типы, такие как квантовые
языки программирования и описания схем. Для случая с нулевым игроком мы также показываем P-жесткость
для кратко представленной модели, сохраняющей верхнюю границу NP $\cap$
соНП. Для случаев с одним и двумя игроками наши результаты верны как в естественном, так и в
явная модель и кратко представленная модель. Наши результаты показывают, что
переключаемый вариант игры сложнее с точки зрения теории сложности, чем
соответствующую стохастическую версию.
Для случая с нулевым игроком мы также показываем P-жесткость
для кратко представленной модели, сохраняющей верхнюю границу NP $\cap$
соНП. Для случаев с одним и двумя игроками наши результаты верны как в естественном, так и в
явная модель и кратко представленная модель. Наши результаты показывают, что
переключаемый вариант игры сложнее с точки зрения теории сложности, чем
соответствующую стохастическую версию.
 -$
опровержения. К ним относятся […]
-$
опровержения. К ним относятся […] В меру
насколько нам известно, это первый нетривиальный подкласс ПТА, на самом деле даже
расширен параметрическими обновлениями, для которых это возможно.
В меру
насколько нам известно, это первый нетривиальный подкласс ПТА, на самом деле даже
расширен параметрическими обновлениями, для которых это возможно.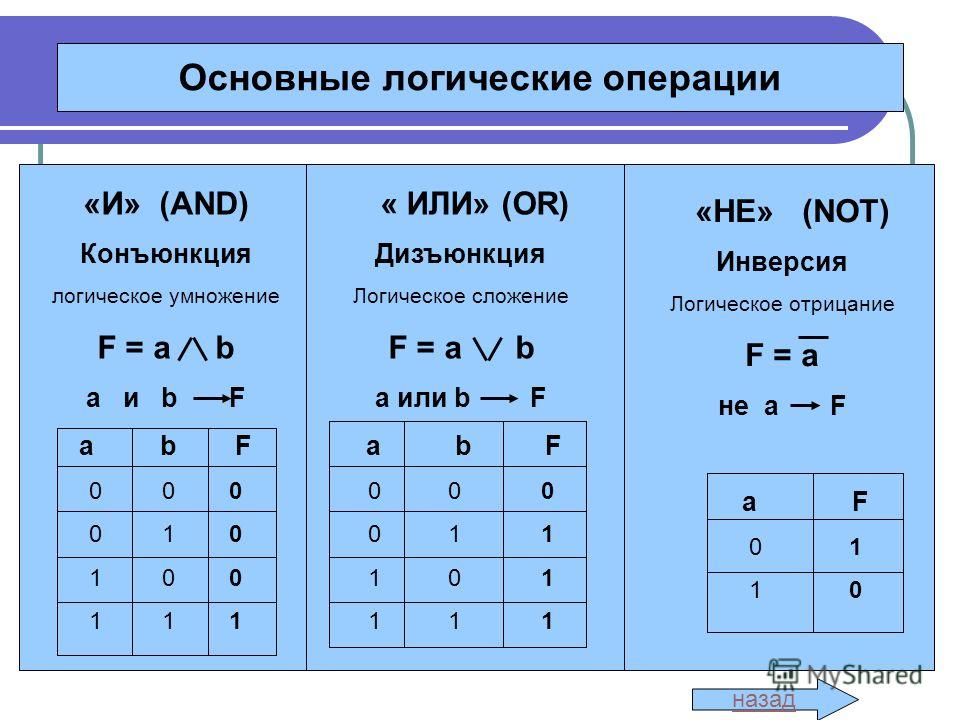 Эти
языки характеризуются конфлюэнтными частично упорядоченными DFA или полными,
конфлюэнтные и частично упорядоченные NFA, детерминированные самопетлей (ptNFA для
короткая). В этой статье мы изучаем сложность основных вопросов для нескольких
типы частично упорядоченных автоматов на конечных словах; а именно вопросы
включения, эквивалентности и ($k$-)кусочной проверяемости. Нижняя граница
сложность сводится к сложности универсальности. Универсальность
задача спрашивает, распознает ли система все слова в своем алфавите. За
ptNFA, сложность универсальности уменьшается, если алфавит фиксирован, но
он открыт, если алфавит может расти с увеличением количества состояний. Мы показываем, что
определение универсальности для общих ptNFA так же сложно, как и для общих NFA. Наш
доказательство является новым и нетривиальным расширением нашей недавней конструкции для
частично упорядоченные НКА, детерминированные петлей, а […]
Эти
языки характеризуются конфлюэнтными частично упорядоченными DFA или полными,
конфлюэнтные и частично упорядоченные NFA, детерминированные самопетлей (ptNFA для
короткая). В этой статье мы изучаем сложность основных вопросов для нескольких
типы частично упорядоченных автоматов на конечных словах; а именно вопросы
включения, эквивалентности и ($k$-)кусочной проверяемости. Нижняя граница
сложность сводится к сложности универсальности. Универсальность
задача спрашивает, распознает ли система все слова в своем алфавите. За
ptNFA, сложность универсальности уменьшается, если алфавит фиксирован, но
он открыт, если алфавит может расти с увеличением количества состояний. Мы показываем, что
определение универсальности для общих ptNFA так же сложно, как и для общих NFA. Наш
доказательство является новым и нетривиальным расширением нашей недавней конструкции для
частично упорядоченные НКА, детерминированные петлей, а […] Результаты, которые обеспечивают полное вычислительное содержание, включают в себя то, что
алгебраические операции и эффективный предельный оператор над вещественными числами:
вычислимо, что некоторые счетно бесконечные произведения изоморфны пространствам
функций, совместимость перечислительного представления подмножеств
натуральные числа с абстрактным определением пространства открытых подмножеств
натуральные числа, и что непрерывная реализуемость подразумевает последовательную
непрерывность. Мы также формализуем доказательства невычислительных результатов, которые поддерживают
правильность наших определений. Эти […]
Результаты, которые обеспечивают полное вычислительное содержание, включают в себя то, что
алгебраические операции и эффективный предельный оператор над вещественными числами:
вычислимо, что некоторые счетно бесконечные произведения изоморфны пространствам
функций, совместимость перечислительного представления подмножеств
натуральные числа с абстрактным определением пространства открытых подмножеств
натуральные числа, и что непрерывная реализуемость подразумевает последовательную
непрерывность. Мы также формализуем доказательства невычислительных результатов, которые поддерживают
правильность наших определений. Эти […]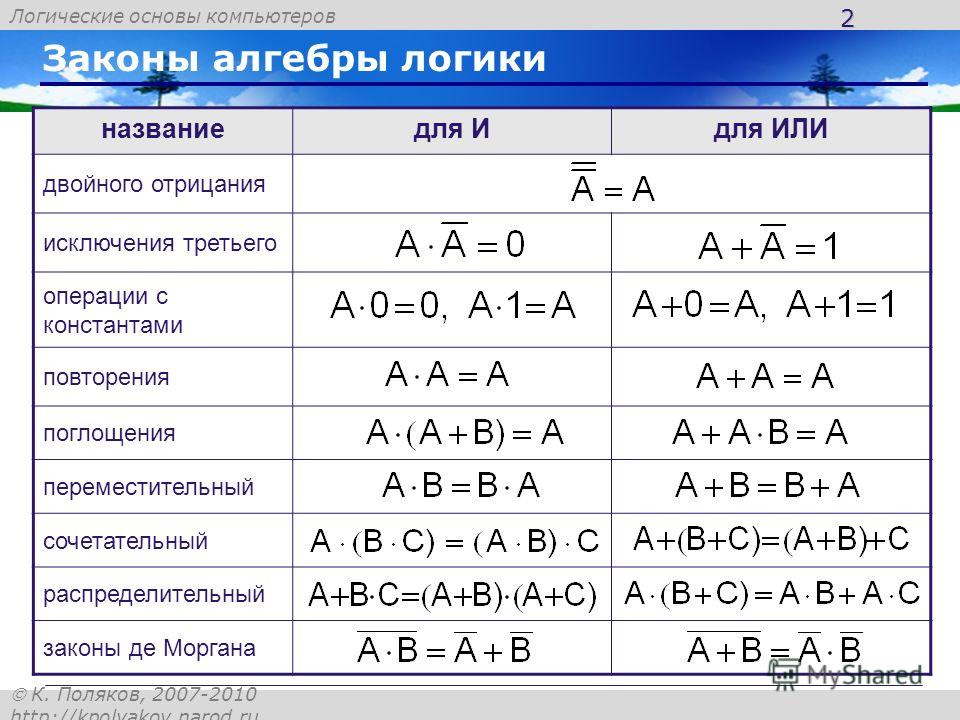 Точнее, мы изучаем понятие
«подпись» для указания синтаксических конструкций.
В духе начальной семантики мы определяем «синтаксис, созданный
подпись» в качестве начального объекта — если он существует — в подходящей категории
моделей. В нашей структуре наличие связанного синтаксиса для
подпись не гарантируется автоматически. Мы идентифицируем через понятие
представление подписи, большой класс подписей, которые генерируют
синтаксис.
Наши (представимые) подписи включают в себя классические алгебраические подписи (т.е.
сигнатуры для языков с привязкой переменных, таких как чистая лямбда
исчисление) и расширить их, включив несколько других важных примеров
синтаксические конструкции.
Одной из ключевых особенностей наших понятий подписи, синтаксиса и представления является то, что
они очень композиционны, в том смысле, что сложные примеры могут быть
получается путем склеивания более простых. Более того, через Исходную Семантику
подход, наша структура обеспечивает, помимо желаемой алгебры терминов,
корректная замена и связанные с ней принципы индукции и рекурсии
к синтаксису.
Точнее, мы изучаем понятие
«подпись» для указания синтаксических конструкций.
В духе начальной семантики мы определяем «синтаксис, созданный
подпись» в качестве начального объекта — если он существует — в подходящей категории
моделей. В нашей структуре наличие связанного синтаксиса для
подпись не гарантируется автоматически. Мы идентифицируем через понятие
представление подписи, большой класс подписей, которые генерируют
синтаксис.
Наши (представимые) подписи включают в себя классические алгебраические подписи (т.е.
сигнатуры для языков с привязкой переменных, таких как чистая лямбда
исчисление) и расширить их, включив несколько других важных примеров
синтаксические конструкции.
Одной из ключевых особенностей наших понятий подписи, синтаксиса и представления является то, что
они очень композиционны, в том смысле, что сложные примеры могут быть
получается путем склеивания более простых. Более того, через Исходную Семантику
подход, наша структура обеспечивает, помимо желаемой алгебры терминов,
корректная замена и связанные с ней принципы индукции и рекурсии
к синтаксису. Эта статья основана на идеях предыдущей попытки Хиршовица-Маггези,
который, в свою очередь, был непосредственно вдохновлен некоторыми более ранними работами
Гани-Уусталу-Хамана и Маттес-Уусталу.
Основные результаты, представленные в статье, проверены компьютером […]
Эта статья основана на идеях предыдущей попытки Хиршовица-Маггези,
который, в свою очередь, был непосредственно вдохновлен некоторыми более ранними работами
Гани-Уусталу-Хамана и Маттес-Уусталу.
Основные результаты, представленные в статье, проверены компьютером […] Приведенная выше характеристика позволяет нам доказать отсутствие промежуточного
структура между $\langle \mathbb{R}, +,<, \mathbb{Z} \rangle$ и $\langle
\mathbb{R}, +,<, 1 \rangle$. Мы также показываем, что $\langle \mathbb{R}, +,<,
\mathbb{Z} \rangle$-определимое отношение равно $\langle \mathbb{R}, +,<, 1
\rangle$-определим тогда и только тогда, когда его пересечение с каждым $\langle
\mathbb{R}, +,<, 1 \rangle$-определяемая строка $\langle \mathbb{R}, +,<, 1
\rangle$-определяемый. Это дает неэффективную, но простую характеристику
$\langle \mathbb{R}, +,<, 1 \rangle$-определимые отношения.
Приведенная выше характеристика позволяет нам доказать отсутствие промежуточного
структура между $\langle \mathbb{R}, +,<, \mathbb{Z} \rangle$ и $\langle
\mathbb{R}, +,<, 1 \rangle$. Мы также показываем, что $\langle \mathbb{R}, +,<,
\mathbb{Z} \rangle$-определимое отношение равно $\langle \mathbb{R}, +,<, 1
\rangle$-определим тогда и только тогда, когда его пересечение с каждым $\langle
\mathbb{R}, +,<, 1 \rangle$-определяемая строка $\langle \mathbb{R}, +,<, 1
\rangle$-определяемый. Это дает неэффективную, но простую характеристику
$\langle \mathbb{R}, +,<, 1 \rangle$-определимые отношения. управление, которое фиксирует настраиваемые рабочие точки аппаратного и программного обеспечения
компонентов с точки зрения функциональности, использования и предоставления ресурсов, а также качества
такие показатели, как производительность и энергопотребление. Мы основываем эти аспекты на
частично упорядоченные наборы для определения уровней качества, размеров бюджета и функциональных
совместимость. Это делает структуру широко применимой и доменной.
независимыми (хотя мы нацелены на встроенные и киберфизические системы).
Framework прокладывает путь к динамической (ре)конфигурации и многоцелевому
оптимизация компонентных систем для управления качеством и ресурсами
целей.
управление, которое фиксирует настраиваемые рабочие точки аппаратного и программного обеспечения
компонентов с точки зрения функциональности, использования и предоставления ресурсов, а также качества
такие показатели, как производительность и энергопотребление. Мы основываем эти аспекты на
частично упорядоченные наборы для определения уровней качества, размеров бюджета и функциональных
совместимость. Это делает структуру широко применимой и доменной.
независимыми (хотя мы нацелены на встроенные и киберфизические системы).
Framework прокладывает путь к динамической (ре)конфигурации и многоцелевому
оптимизация компонентных систем для управления качеством и ресурсами
целей. Мы возвращаемся к его изложению с помощью некоторых
простые правила на деревьях (или соответствующие термины), снабженные «звездой» как
управляющий символ, обозначающий команду уменьшить это дерево (или терм) в
порядок определяется. Это приводит к звездным играм, которые очень удобны для
доказывая прекращение многих задач переписывания. Например, используя уже
простейшей звездной игры на конечных непомеченных деревьях, мы получаем очень прямое доказательство
окончание знаменитой битвы Гидры, прямое в том смысле, что нет
обычное упоминание ординалов. Мы также включаем альтернативный путь к настройке
Звездные игры, используя проверенный метод Бухгольца, адаптированный ван Остромом,
в результате получилась количественная версия звезды в качестве контрольного символа. Мы заключаем
с рядом вопросов и будущих направлений исследований.
Мы возвращаемся к его изложению с помощью некоторых
простые правила на деревьях (или соответствующие термины), снабженные «звездой» как
управляющий символ, обозначающий команду уменьшить это дерево (или терм) в
порядок определяется. Это приводит к звездным играм, которые очень удобны для
доказывая прекращение многих задач переписывания. Например, используя уже
простейшей звездной игры на конечных непомеченных деревьях, мы получаем очень прямое доказательство
окончание знаменитой битвы Гидры, прямое в том смысле, что нет
обычное упоминание ординалов. Мы также включаем альтернативный путь к настройке
Звездные игры, используя проверенный метод Бухгольца, адаптированный ван Остромом,
в результате получилась количественная версия звезды в качестве контрольного символа. Мы заключаем
с рядом вопросов и будущих направлений исследований. Полурешётки с сильным близостью могут быть
характеризуется коалгебрами низшей степени в более широкой категории
посетов близости (также известных как абстрактные базисы или R-структуры). Более того,
локально компактные локали можно охарактеризовать с точки зрения сильной близости
джойн-полурешетки коалгебрами двойной степенной локали на категории
посетов близости. Мы также даем более логичную характеристику сильного
полурешеткой, называемой сильным непрерывным конечным покрытием, которое
использует отношение влечения для представления базовой полурешетки соединения. Мы показываем
что эта структура естественным образом соответствует понятию непрерывной решетки
в предикативной бесточечной топологии. Наш результат делает предикативное и
финитный аспект понятия непрерывной решетки в бесточечной топологии подробнее
явный.
Полурешётки с сильным близостью могут быть
характеризуется коалгебрами низшей степени в более широкой категории
посетов близости (также известных как абстрактные базисы или R-структуры). Более того,
локально компактные локали можно охарактеризовать с точки зрения сильной близости
джойн-полурешетки коалгебрами двойной степенной локали на категории
посетов близости. Мы также даем более логичную характеристику сильного
полурешеткой, называемой сильным непрерывным конечным покрытием, которое
использует отношение влечения для представления базовой полурешетки соединения. Мы показываем
что эта структура естественным образом соответствует понятию непрерывной решетки
в предикативной бесточечной топологии. Наш результат делает предикативное и
финитный аспект понятия непрерывной решетки в бесточечной топологии подробнее
явный. В этой статье объясняется, как использовалось биподобие.
обнаружить эти уязвимости, использующие протокол BAC —
оригинальный ИКАО 9303 стандартный протокол аутентификации электронного паспорта — и остается
действителен для протокола PACE, который повышает безопасность BAC в
последние стандарты ИКАО 9303. Чтобы решить такие проблемы биподобия, мы
разработайте здесь цепочку методов прикладного $\pi$-исчисления, включая
символическое недоподобие биподобия, называемое открытым биподобием, и
модальная логика, называемая классической FM, для описания и сертификации атак.
Приведены доказательства в пользу новой схемы определения таких
проблемы несвязываемости, что более точно отражает возможности
злоумышленник.
В этой статье объясняется, как использовалось биподобие.
обнаружить эти уязвимости, использующие протокол BAC —
оригинальный ИКАО 9303 стандартный протокол аутентификации электронного паспорта — и остается
действителен для протокола PACE, который повышает безопасность BAC в
последние стандарты ИКАО 9303. Чтобы решить такие проблемы биподобия, мы
разработайте здесь цепочку методов прикладного $\pi$-исчисления, включая
символическое недоподобие биподобия, называемое открытым биподобием, и
модальная логика, называемая классической FM, для описания и сертификации атак.
Приведены доказательства в пользу новой схемы определения таких
проблемы несвязываемости, что более точно отражает возможности
злоумышленник.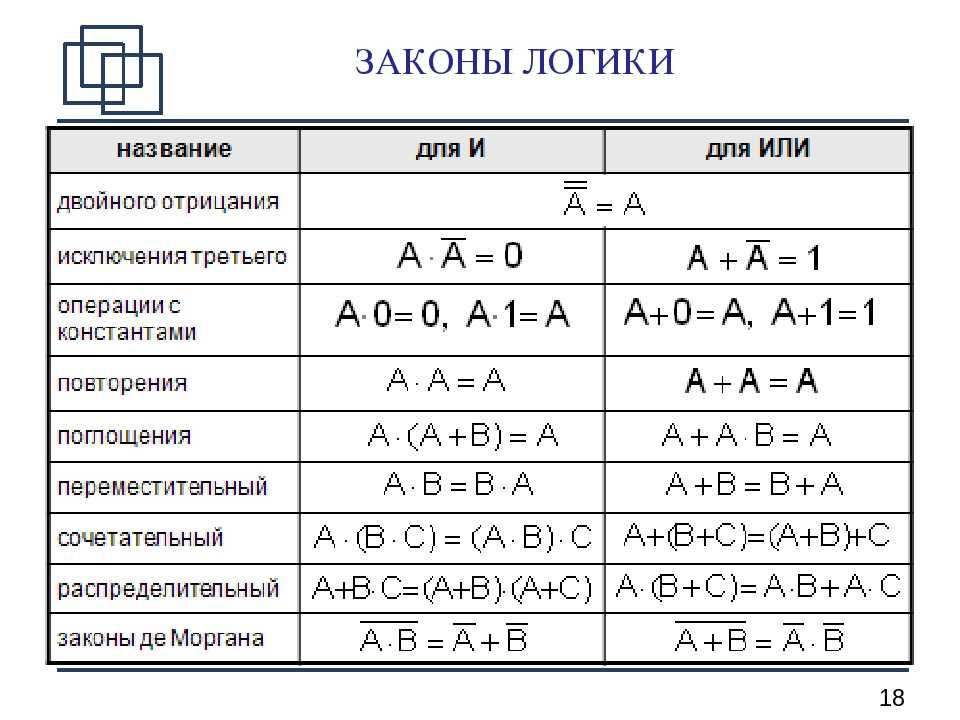 Эта кодировка уточняет
к $n$-значной логике для $n\in\{4,5\}$. Такие кодировки существуют и для Черча.
оригинальное $\lambda\mathbf{I}$-исчисление. В качестве мотивации мы рассматриваем
Парадокс Рассела, использующий тот факт, что одна и та же кодировка позволяет нам также
вычислить значения истинности бесконечных закрытых предложений в этом бесконечном
параметр.
Эта кодировка уточняет
к $n$-значной логике для $n\in\{4,5\}$. Такие кодировки существуют и для Черча.
оригинальное $\lambda\mathbf{I}$-исчисление. В качестве мотивации мы рассматриваем
Парадокс Рассела, использующий тот факт, что одна и та же кодировка позволяет нам также
вычислить значения истинности бесконечных закрытых предложений в этом бесконечном
параметр.