Вектор, модуль вектора. Коллинеарные векторы. Компланарные векторы. Координаты вектора
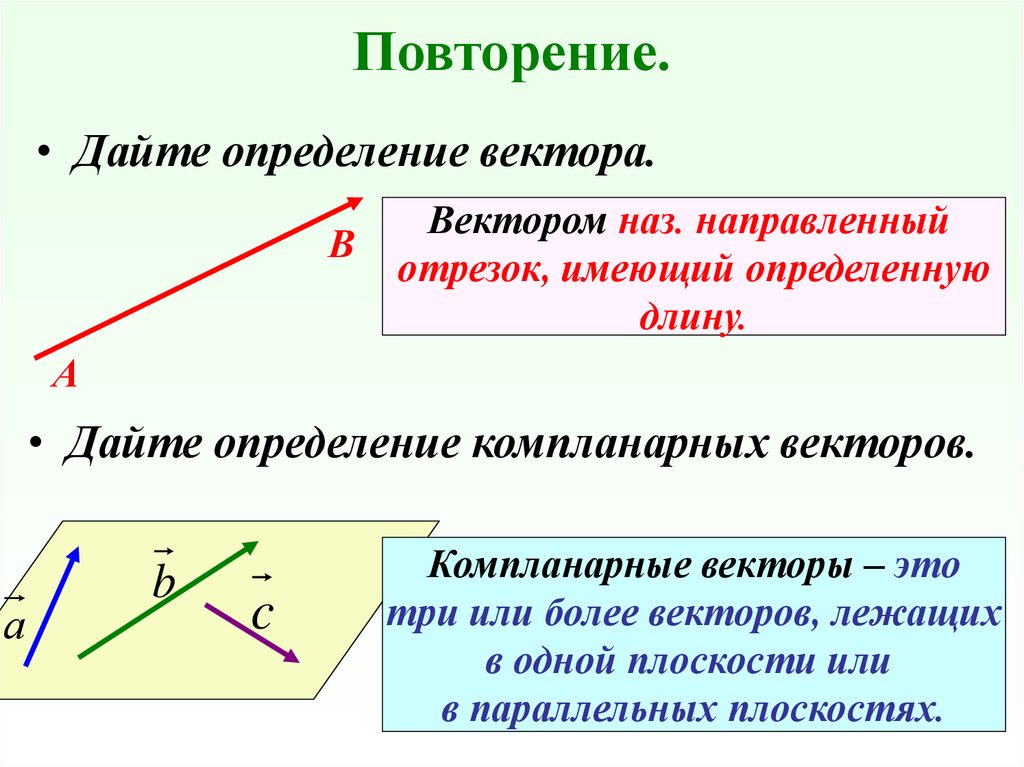
Напомним, что вектором называется направленный отрезок, то есть отрезок, имеющий длину и определённое направление. Если начало вектора находится в точке , а конец в точке , то такой вектор обозначается: . Часто векторы обозначаются и вот таким образом: .
Модулем, или длиной вектора, называется длина отрезка, который изображает вектор (, ).
Нулевым вектором называется вектор, начало и конец которого совпадают ().
Направления нулевой вектор не имеет, а его длина равна нулю ().
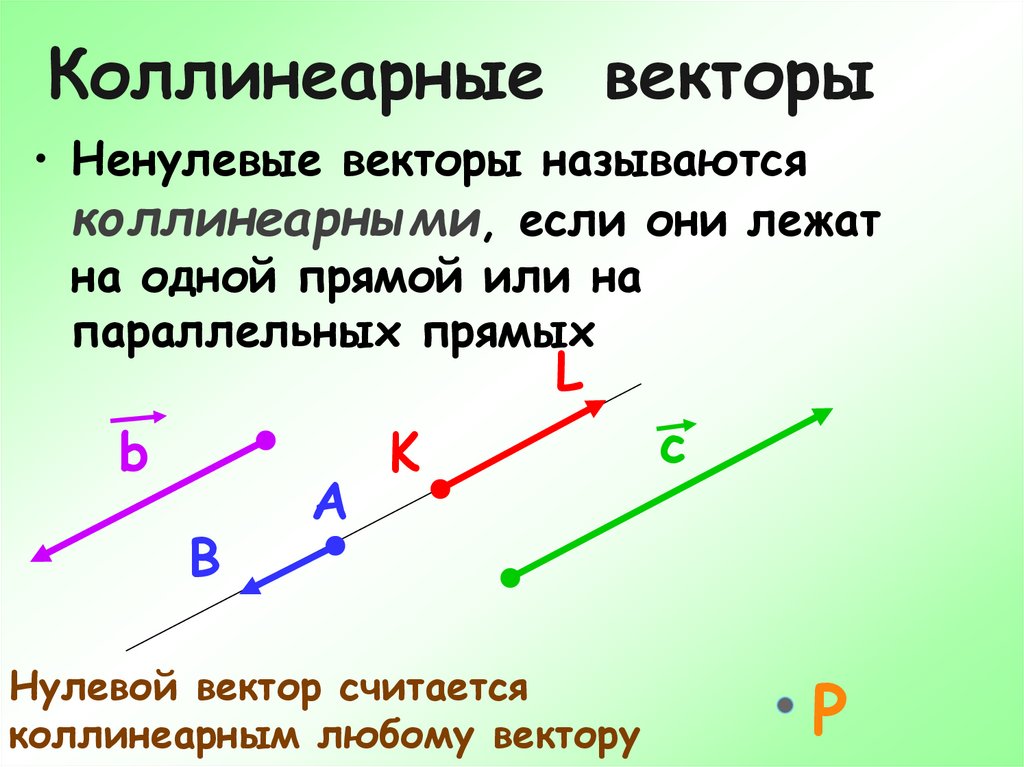
Два отличных от нуля вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. При этом два коллинеарных вектора могут быть сонаправленными () или противоположно направленными (, ).
Векторы называются равными, если они одинаково направлены и
их длины равны.
Сумму двух векторов можно найти
А также по правилу параллелограмма:
Отметим, что для любого вектора справедливо равенство .
Также напомним, что для любых векторов , и справедливы:
1. (переместительный закон).
2. (сочетательный закон).
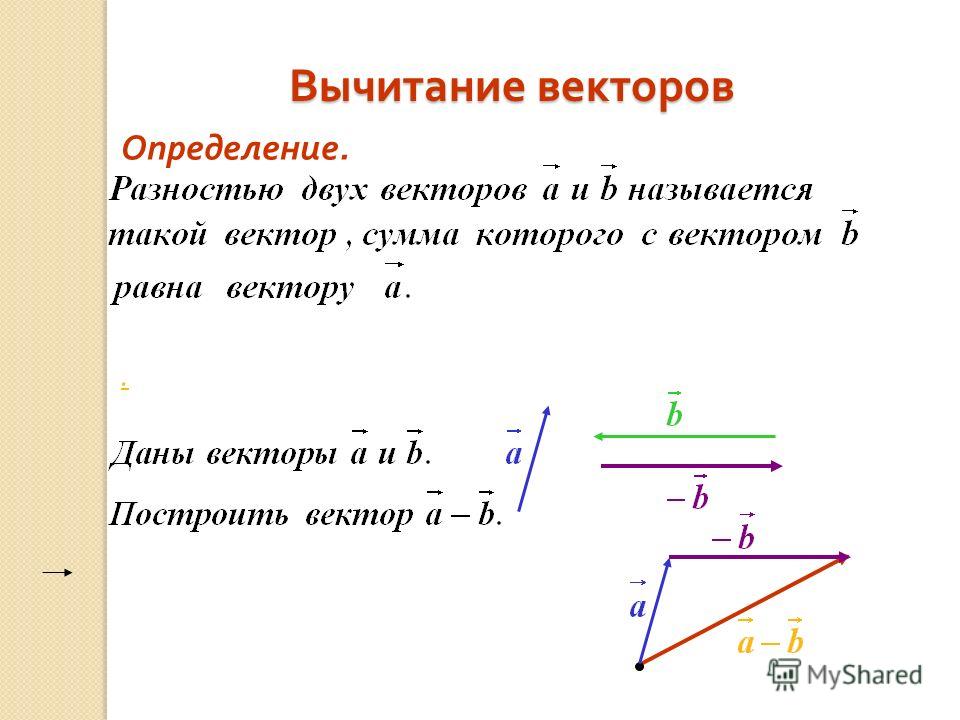
Разностью векторов и называется такой вектор, сумма которого с вектором даст вектор .
Для любых векторов и справедливо следующее равенство .
Произведением ненулевого вектора на число называется такой вектор , длина которого равна произведению .
При этом векторы и сонаправлены при и противоположно направлены при .
Основные свойства умножения вектора на число.
Для любых чисел , и любых векторов , справедливы:
1. (сочетательный закон).
2. (первый распределительный закон).
3. (второй распределительный закон).
Теорема. На плоскости любой вектор
можно разложить по двум неколлинеарным векторам, причём коэффициенты разложения
определяются единственным образом.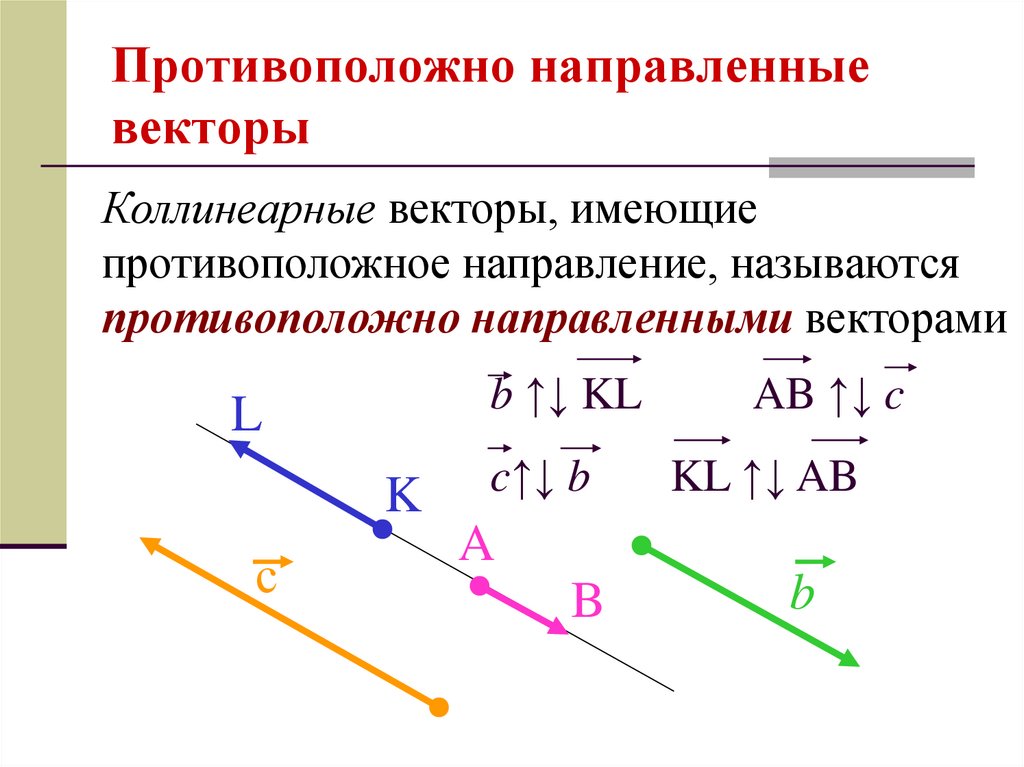
,
, – неколлинеарные векторы,
, – коэффициенты разложения.
Векторы, лежащие в параллельных плоскостях (или в одной плоскости), называются компланарными.
При этом, если вектор можно разложить по векторам и , то есть представить в виде
,
где и – некоторые числа, то векторы , и компланарны.
Для сложения трёх некомпланарных векторов можно использовать правило параллелепипеда:
Теорема. Любой вектор можно разложить по трём данным некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.
,
, , – некомпланарные векторы,
, , – коэффициенты разложения.
Коэффициенты разложения вектора по координатным векторам называются координатами вектора в данной системе координат.
, .
, .
Также напомним, что координатами вектора с началом в точке и концом в точке называются числа , .
В пространстве координатами вектора с началом в точке и концом в точке называются числа , , .
Теперь вспомним следующие правила.
Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.
, ,
вектор имеет координаты .
, ,
вектор имеет координаты .
Каждая координата разности равна разности соответствующих координат этих векторов.
, ,
вектор имеет координаты .
вектор имеет координаты .
Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
, – произвольное число,
вектор имеет координаты .
, – произвольное число,
вектор имеет координаты .
Также напомним, что длина вектора вычисляется .
В пространстве длина вектора по его координатам вычисляется аналогично.
, .
Скалярным произведением двух
векторов называется произведение их длин на косинус угла между ними.
Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
Скалярный квадрат вектора (то есть скалярное произведение вектора на себя) равен квадрату его длины.
Скалярное произведение двух векторов можно вычислить, зная координаты этих векторов. Скалярное произведение векторов и выражается следующей формулой:
.
В пространстве скалярное произведение векторов определяется аналогичным образом.
, , .
И напомним свойства скалярного произведения векторов.
Для любых векторов , , и любого числа справедливы соотношения:
1. , причём при .
2. (переместительный закон).
3. (распределительный закон).
4. (сочетательный закон).
Отметим, что распределительный закон имеет место для любого числа слагаемых.
Мы
с вами повторили основные моменты, а теперь давайте перейдём к практической
части занятия.
Задание первое. Стороны равностороннего треугольника равны . Найдите длину вектора, равного сумме векторов и .
Решение.
Задание второе. Найдите координаты вектора и его модуль, если , .
Решение.
Задание третье. Даны векторы и . Найдите координаты вектора и его модуль.
Решение.
Задание четвёртое. При каких значениях векторы и взаимно перпендикулярны?
Решение.
Задание пятое. Найдите модуль суммы и модуль разности векторов и .
Решение.
Задание шестое. Найдите косинус угла треугольника , если , и .
Решение.
Действия над векторами
Понятие вектора является одним из основных в
математике, объединяющим такие ее разделы, как
геометрия, алгебре, математический анализ.
В стереометрии изучаются векторы в пространстве. Их определение и свойства аналогичны определению и свойствам векторов на плоскости.
Цели урока:
- Образовательные: повторение теоретических сведений по теме; рассмотрение правил треугольника и параллелограмма сложения векторов в пространстве, законы сложения векторов; изучение правил сложения нескольких векторов в пространстве и его применение при нахождении векторных сумм, не прибегая к рисункам; рассмотрение правил умножения вектора на число и основные свойства этого действия, а так же их применение при решении задач.
- Развивающие: развитие памяти,
математической речи, наблюдательности, развитие
графических навыков у учащихся.

- Воспитательные: формирование культуры ученического труда.
Тип урока: урок изучения нового материала
Оборудование:
1) Учебник: Геометрия, 10-11: Учеб. для
общеобразоват. учреждений / Л.С. Атанасян, В.Ф.
Бутузов, С.Б. Кадомцев и др. – 11-е изд. – М. :
Просвещение, 2002. – 206 с. : ил.
2) раздаточный материал (Приложение
1)
3) мультимедийный проектор, Презентация
«Действия над векторами».
ХОД УРОКА
1. Организационный момент
Сообщение темы и цели урока
Учитель: Ребята, тема нашего урока
«Действия над векторами» (Слайд 1). Сегодня
мы рассмотрим правила треугольника и
параллелограмма сложения векторов в
пространстве; изучим правило сложения
нескольких векторов в пространстве и его
применение при нахождении векторных сумм, не
прибегая к рисункам; рассмотрим правила
умножения вектора на число и основные свойства
этого действия, а так же их применение при
решении задач.
2. Актуализация знаний (Устная работа)
Учащиеся отвечают на вопросы учителя. Если учащиеся затрудняются ответить, учитель помогает.
Учитель: 1вопрос. Что называется вектором в пространстве? Его обозначения.
Ученик: Отрезок, для которого указано, какой из его концов считается началом, а какой концом, называется вектором.
Учитель: 2 вопрос. Что называется длиной вектора? Ее обозначение.
Ученик: Длиной ненулевого вектора называется длина отрезка АВ.
Учитель: 3 вопрос. Какой вектор называется нулевым?
Ученик: Любая точка пространства может рассматриваться как вектор. Такой вектор называется нулевым.
Учитель: 4 вопрос.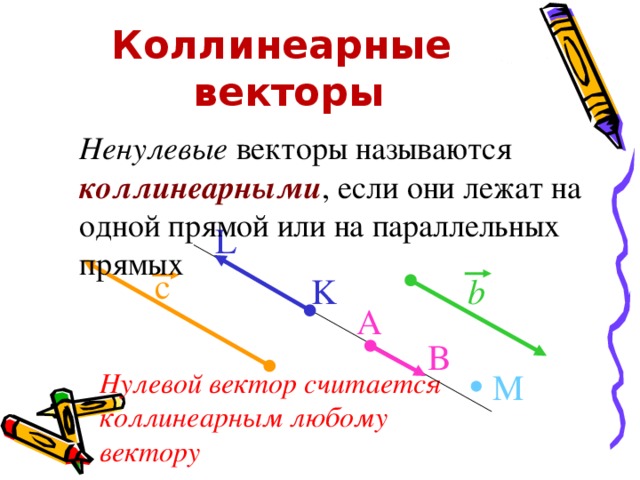 Какие
векторы называются коллинеарными?
Какие
векторы называются коллинеарными?
Ученик: Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Учитель: 5 вопрос. Какие векторы называются сонаправленными? Обозначение.
Ученик: Если два ненулевых вектора и коллинеарны и если при этом лучи АВ и СД сонаправленны, то векторы и называются сонаправленными. .
Учитель: 6 вопрос. Какие векторы называются противоположно направленными? Обозначение.
Ученик: Если два ненулевых вектора и коллинеарны
и если при этом лучи АВ и СД противоположно
направленны, то векторы и называются противоположно
направленными. .
Учитель: 7 вопрос. Каким (сонаправленным или противоположно направленным) принять нулевой вектор?
Ученик: Нулевой вектор принято считать сонаправленным с любым вектором.
3. Изучение нового материала
Задача учителя подчеркнуть, что сложение и вычитание векторов в пространстве вводится так же, как и на плоскости, и подчиняется тем же законам. Раздать опорную схему по теме и дать время для работы над конспектом в тетради.
Учитель: Введем правило сложения двух
произвольных векторов и .Отложим от какой-нибудь
точки А вектор , равный . Затем от точки В отложим
вектор ,
равный .
Вектор
называется суммой векторов и : =+ .
Это правило сложения векторов называется правилом
треугольника (Слайд 3, 4, 5).
Для любых трех точек А, В и С имеет место равенство + = .
Учащиеся делают записи в тетрадях (Слайд 6).
Учитель: Для сложения двух неколлинеарных векторов можно пользоваться также правилом параллелограмма, известным из курса планиметрии. Это правило пояснено на рисунке (Слайд 7).
Учитель: Два ненулевых вектора называются противоположными, если их длины равны и они противоположно направлены. Вектором, противоположным нулевому вектору, считается нулевой вектор. Очевидно, вектор является противоположным вектору .
Учитель: Разностью векторов и называется такой вектор,
сумма которого с вектором равна вектору (Слайд 6).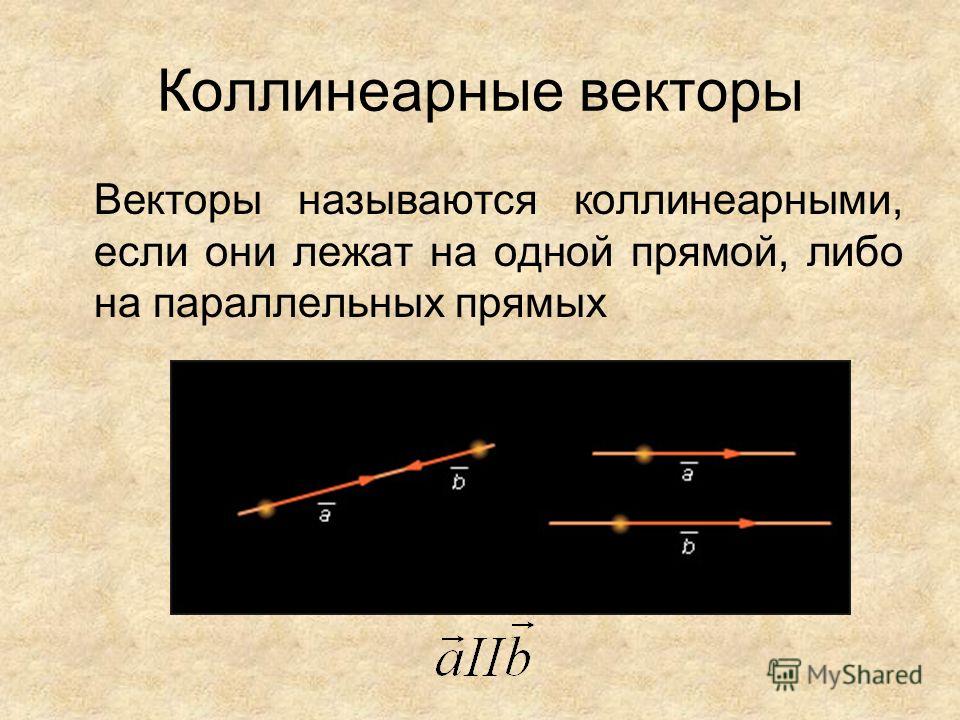
Разность
– векторов
и можно найти
по формуле –
= + (– ), где (– ) – вектор,
противоположный вектору
Учитель: Для любых трех векторов справедливы переместительный и сочетательный законы (Слайд 6).
Учитель просит учащихся записать законы в тетрадь.
Учитель: Сформулируем правило многоугольника. Сложение нескольких векторов в пространстве выполняется так же, как и на плоскости: первый вектор складывается со вторым, затем их сумма — с третьим вектором и т. д. Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются (Слайд 8).
4. Закрепление изученного материала (выполнение задач)
а) Применение знаний в стандартной ситуации
Учащиеся выполняют № 327: один учащийся у доски, учитель комментирует (Слайд 9)
№
327. На рисунке 97 изображен параллелепипед
АВСДА1В1С1Д1. Назовите вектор, начало и конец
которого является вершинами параллелепипед,
равный сумме векторов:
На рисунке 97 изображен параллелепипед
АВСДА1В1С1Д1. Назовите вектор, начало и конец
которого является вершинами параллелепипед,
равный сумме векторов:
а)
б)
в)
г)
д)
Учащиеся выполняют № 328: один учащийся у доски, учитель комментирует (Слайд 10)
№ 328 (а). Тетраэдр АВСД. Докажите, что .
Дано: АВСД – тетраэдр
Докажите, что .
Решение: ,
.
Следовательно, .
б) Самостоятельная работа обучающего характера с последующей самопроверкой (решение на обратной стороне доски) (Слайд 11)
Задача. Дан тетраэдр АВСД. Найдите сумму:
а)
б)
в)
5. Изучение нового материала
Учитель: Сформулируем правило умножения вектора на число: ; (Слайд 12)
Если , то, при ;
при .
Если , то .
Рассмотреть законы умножения вектора на число и попросить ребят изобразить схему в тетрадях. (Слайд 12)
6. Закрепление изученного материала (выполнение задач)
Учащиеся выполняют № 345: один учащийся у доски, учитель комментирует (Слайд 14)
№ 345. Точки E и F – середины сторон АВ и ВС параллелограмма АВСД, а О – точка произвольная точка пространства. Выразите вектор через вектор .
Решение:
Так как EF – средняя линия треугольника АВС,
EF|| АС и EF = 1/2 АС.
Поэтому ,
,
№ 347. Упростить выражение:
а)
7. Домашнее задание (с комментарием учителя)
§ 2 (п. 36, 37, 38), № 335, № 337 (а, б), № 347 (б). (Слайд 15)
(Слайд 15)
8. Подведение итогов урока
В конце урока желательно с помощью ребят перечислить понятия, правила, свойства, которые были рассмотрены на уроке и которые необходимо запомнить. Выставление оценок.
Учитель: Давайте подведем итоги урока.
Блиц-опрос по вопросам:
– Что называется произведением ненулевого
вектора на число?
– Что называется произведением нулевого вектора
на число?
– Свойства умножения вектора на число.
– Справедливо ли утверждение:
а) любые два противоположно направленных вектора коллинеарны;
б) любые два вектора коллинеарных противоположно направленны;
в) любые два равных вектора коллинеарны;
г) любые два сонаправленных вектора равны?
(Слайд 16)
Что такое векторное изображение и зачем оно мне? — Vivid Image, Inc.
Если вы когда-либо занимались графическим дизайном, вы, вероятно, сталкивались с термином «векторная графика» и у вас возникали подобные вопросы. Не волнуйтесь, это хорошо. Давайте начнем с основ и узнаем, «что такое векторное изображение!».
Растровая графика против векторной графики
Растровая графика (файлы jpg / png / tiff)
Большинство людей знакомы с изображениями в формате .jpg — такими, которые можно получить с помощью цифровой камеры. Если вы когда-либо увеличивали слишком близко или увеличивали слишком большое изображение .jpg, вы могли заметить, что изображение становится размытым, а цвета превращаются в маленькие квадратики или точки. Маленькие точки называются пикселями, а такое изображение называется растровой графикой. Если вам когда-либо приходилось редактировать цифровую фотографию, вы знаете, сколько времени может занимать изменение даже самой маленькой детали.
Слева: Полное изображение. Справа: изображение увеличено, чтобы показать квадратные пиксели, которые делают его растровым.
Векторная графика (файлы ai / eps / svg)
Чем отличается векторное изображение? Вы видите сотни векторных рисунков в день и, вероятно, не осознаете этого. Большинство логотипов представляют собой векторные файлы. В частности, векторная графика — это произведение искусства, состоящее из точек, линий и кривых, основанных на математических уравнениях, а не на сплошных квадратных пикселях.
Это означает, что независимо от размера или степени увеличения изображения линии, кривые и точки остаются гладкими. Художественное произведение никогда не будет иметь неровных линий или размытости.
Кроме того, цвета разделены на отдельные формы (вместо множества маленьких квадратов, образующих цветную область), что делает изменение цвета в этой графике таким же простым, как нажатие кнопки.
Почему это важно…
Изучив основы векторной графики, вы должны понять, почему это важно.
#1: Векторная графика позволяет создавать профессионально выглядящие бренды.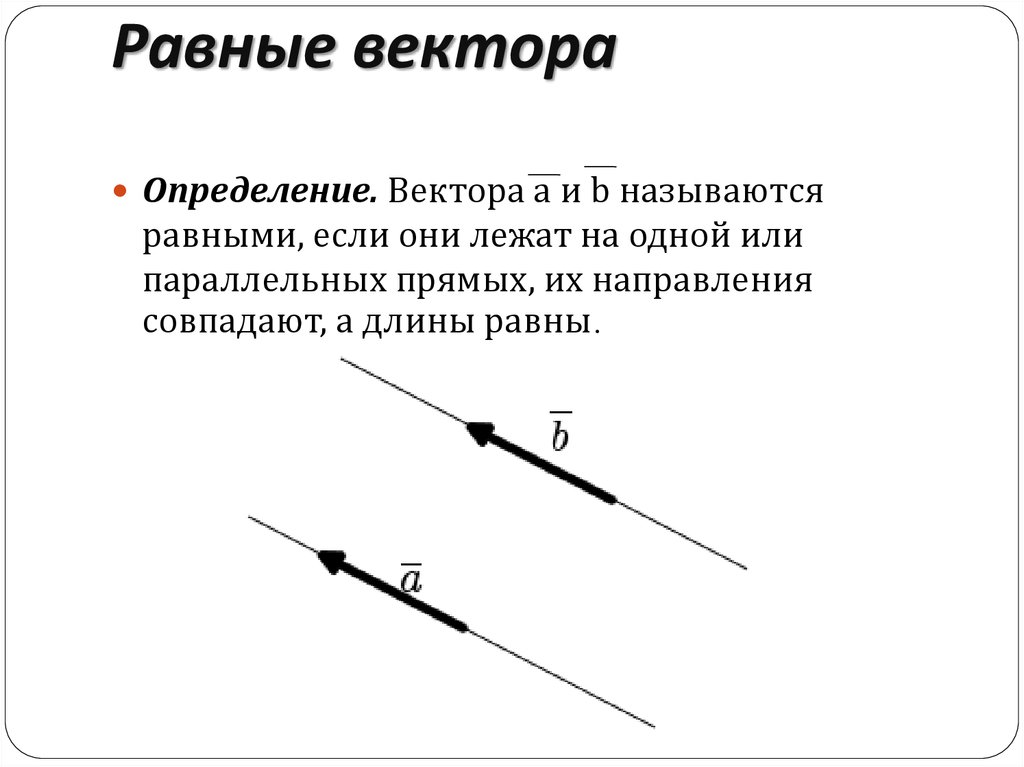 Они составляют большую часть большинства печатных или опубликованных материалов. Логотипы, например, всегда должны иметь векторный формат. Благодаря этим плавным линиям и формам получаются печатные материалы самого высокого качества с четкими, равномерными цветами и четким, четким текстом. Вы можете использовать большой векторный логотип на рекламном щите, маленький для ручек или футболку с трафаретной печатью. Иконки и другие иллюстрированные изображения также хорошо иметь в векторных файлах.
Они составляют большую часть большинства печатных или опубликованных материалов. Логотипы, например, всегда должны иметь векторный формат. Благодаря этим плавным линиям и формам получаются печатные материалы самого высокого качества с четкими, равномерными цветами и четким, четким текстом. Вы можете использовать большой векторный логотип на рекламном щите, маленький для ручек или футболку с трафаретной печатью. Иконки и другие иллюстрированные изображения также хорошо иметь в векторных файлах.
#2: Векторная графика сэкономит время вашего графического дизайнера. Это сэкономит ваши деньги и даст более качественные результаты.
#3: Векторные файлы не теряют качества. Jpg и другие файлы, основанные на пикселях, будут терять данные файла каждый раз, когда они открываются и сохраняются.
Обычный пользователь редко будет использовать векторную графику, если у вас нет программного обеспечения для ее открытия (например, продукты Adobe и QuarkXPress). Большинство людей называют векторную графику файлом .eps. Они также могут использовать расширение .ai для файлов Illustrator или .svg для веб-приложений. Хотя вы можете никогда не использовать эти файлы лично или даже не иметь программы для их открытия, очень важно НЕ удалять файлы векторных изображений. Если вы когда-нибудь планируете заняться графическим дизайном или хотите разместить свой логотип на рекламных материалах, вам будет предложено предоставить файлы векторной графики.
Большинство людей называют векторную графику файлом .eps. Они также могут использовать расширение .ai для файлов Illustrator или .svg для веб-приложений. Хотя вы можете никогда не использовать эти файлы лично или даже не иметь программы для их открытия, очень важно НЕ удалять файлы векторных изображений. Если вы когда-нибудь планируете заняться графическим дизайном или хотите разместить свой логотип на рекламных материалах, вам будет предложено предоставить файлы векторной графики.
«А что, если у меня нет векторной версии моего логотипа?»
Свяжитесь с первоначальным дизайнером вашего логотипа, чтобы узнать, была ли когда-либо создана векторная версия вашего логотипа, и запросите ее копию. Если нет доступной векторной версии, часто их можно воссоздать из растровой графики, в зависимости от ее сложности и качества. Важно иметь комплект фирменного стиля для вашей организации, который, среди прочего, содержит эту версию вашего логотипа.
«Всегда ли мне нужен векторный файл, если я выполняю проектные работы?»
Не всегда. Есть способы использовать другие форматы файлов, но тип выполняемой вами работы в конечном итоге определит, понадобятся ли вам векторные файлы или нет.
Есть способы использовать другие форматы файлов, но тип выполняемой вами работы в конечном итоге определит, понадобятся ли вам векторные файлы или нет.
В конечном счете, если вы занимаетесь дизайном, обязательно поговорите со своим дизайнером о форматах ваших файлов, чтобы вы могли собрать соответствующие файлы или создать их, если они недоступны.
Нужна дополнительная помощь?
Рубрики: Дизайн С тегами: типы произведений искусства, графика, растровые изображения, векторное изображение, что такое векторное изображение
Что такое векторная графика | CorelDRAW
Что такое векторная графика | CorelDRAWCorelDRAW
Развивайте свои навыки художника и дизайнера с помощью руководства CorelDRAW по векторному дизайну. Изучите основы векторной графики и дизайна и почувствуйте себя способным справиться с любой задачей, которая встретится вам на пути.
Содержание В этой первой главе мы разбираем определение векторной графики, что такое векторы, почему дизайнеры должны их использовать, что вы можете сделать с их помощью и многое другое.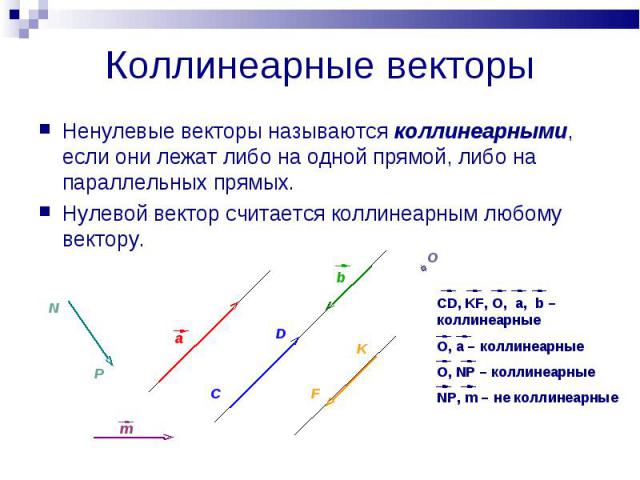 Прорабатывая каждую главу этой серии, вы узнаете об истории векторного искусства, его роли в поп-культуре и бизнесе, карьере художника векторной графики и многом другом.
Прорабатывая каждую главу этой серии, вы узнаете об истории векторного искусства, его роли в поп-культуре и бизнесе, карьере художника векторной графики и многом другом.
Используя элементы дизайна, определенные с помощью последовательности математических операторов или команд, пользователи могут создавать потрясающую двух- или трехмерную векторную графику. Эти линии, точки, кривые и формы в этой графике, называемые векторами, позволяют дизайнерам создавать изображения, которые можно масштабировать практически в любом месте и любого размера без потери качества.
Несмотря на то, что они в основном используются в цифровом пространстве, векторы присутствуют во всем мире вокруг нас — когда вы видите обертку автобуса или логотип компании на стене здания, это векторные рисунки. Если вы ищете дизайн с четкими краями и чистым внешним видом, программное обеспечение для векторной графики позволит вам создать эти потрясающие произведения искусства.
Векторная иллюстрация является ценным дизайнерским навыком для цифровых дизайнеров, поскольку она позволяет им бесконечно изменять размеры дизайна без ущерба для качества. Мы обсудим это и углубимся в то, что такое векторная графика, почему вы должны ее использовать, что вы можете сделать и кто использует эти дизайны в этом руководстве.
Мы обсудим это и углубимся в то, что такое векторная графика, почему вы должны ее использовать, что вы можете сделать и кто использует эти дизайны в этом руководстве.
Что такое векторная графика?
Проще говоря, векторная графика определяется математикой и считается полной противоположностью растровых изображений. Другими словами, растровые изображения хранят данные в виде карты пикселей, а векторы представляют собой набор математически определенных линий и форм. Если бы вы увеличили масштаб вектора, это не повлияло бы на его четкость. Независимо от того, насколько сильно вы увеличиваете или уменьшаете масштаб, вы всегда будете видеть четкие края — вот чем эта графика отличается от растровых изображений. Вы увидите пиксели, если увеличите растровое изображение, тогда как вектор можно масштабировать бесконечно.
Вы можете найти примеры векторных рисунков на повседневных вещах, например, на обложке для автобусов, или на крупномасштабных печатных материалах, таких как рекламные щиты.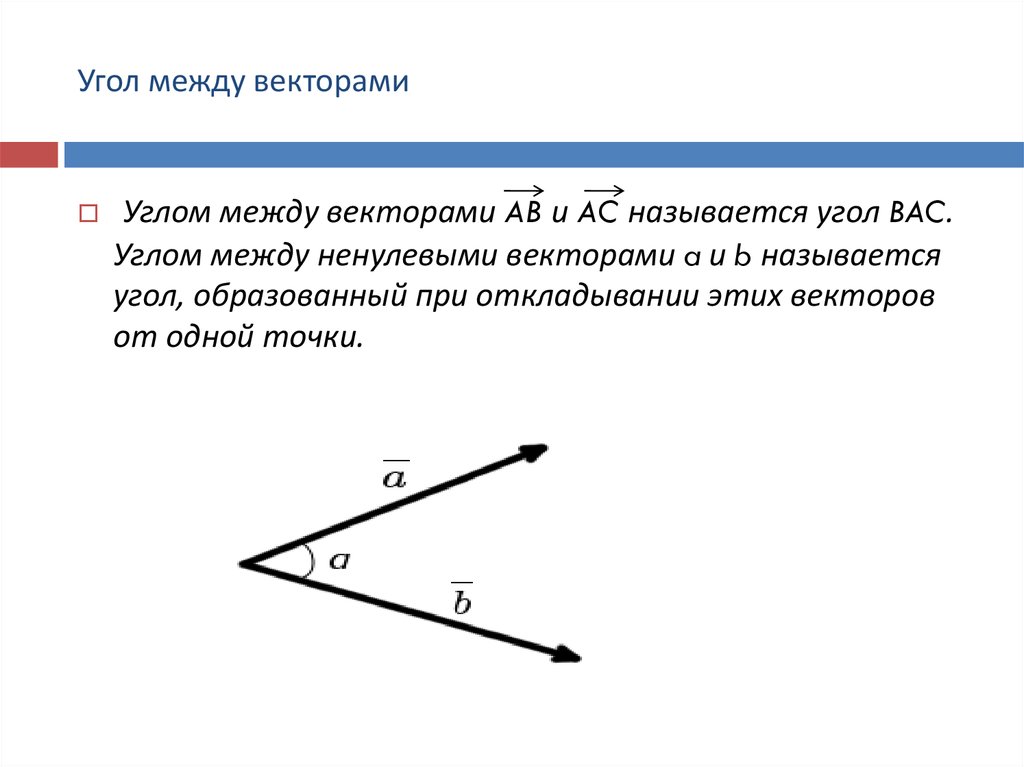 Подумайте об этом так: если вы смотрите на плоский дизайн, скорее всего, это векторный дизайн. Имейте в виду, однако, что если вы видите что-то фотореалистичное, это растровое изображение.
Подумайте об этом так: если вы смотрите на плоский дизайн, скорее всего, это векторный дизайн. Имейте в виду, однако, что если вы видите что-то фотореалистичное, это растровое изображение.
Если вам нужно что-то вроде логотипа, иконки или плоской иллюстрации, идеально подойдет векторная графика. Основная причина в том, что это небольшие файлы, несмотря на их бесконечную масштабируемость. С векторной графикой также намного проще манипулировать, если вам нужно создать новую форму, соединить две точки или настроить кривую.
Зачем использовать векторы при создании искусства?
Векторный рисунок — это технический термин, обозначающий использование математических алгоритмов для создания простых иллюстраций с использованием геометрических фигур, линий и кривых. Эти математические конструкции используют геометрию и хранятся в виде набора формул, а не пикселей, как в фотографии.
Векторная графика отображается в различных форматах. Вы можете увидеть расширения файлов, показывающие . eps или .svg или .ai или .pdf. Каждый имеет различное использование.
eps или .svg или .ai или .pdf. Каждый имеет различное использование.
- CDR: Эти файлы векторной графики хранятся в виде цифровых изображений, закодированных и сжатых, чтобы пользователи могли открывать и редактировать их с помощью CorelDRAW.
- EPS (Encapsulated Postscript): Это изображение состоит из растровых и векторных данных, при этом векторную информацию можно редактировать с помощью графического программного обеспечения. Этот формат файла является стандартным требованием для высококачественной и профессиональной печати изображений.
- SVG (масштабируемая векторная графика): Изображения на основе XML отображают двухмерную графику, которая позволяет искать, индексировать, создавать сценарии и сжимать эти файлы изображений.
- AI (файл Adobe Illustrator Artwork): Собственные векторные файлы, созданные системами Adobe.
 Вы найдете его в печатных СМИ и логотипах. Хотя они похожи на файлы EPS, их синтаксис компактен и ограничен.
Вы найдете его в печатных СМИ и логотипах. Хотя они похожи на файлы EPS, их синтаксис компактен и ограничен. - PDF (Portable Document Format): Создавайте файлы с помощью программного обеспечения для работы с векторными изображениями, чтобы обмениваться такими документами, как брошюры, листовки и другие ресурсы, дизайн которых не должен изменяться.
С векторной графикой объекты могут казаться более глубокими, чем просто плоское изображение. Например, двумерное изображение, такое как круг, треугольник, квадрат, прямоугольник или пятиугольник, может стать трехмерным цилиндром, пирамидой, кубом или призмой с помощью программного обеспечения для векторной графики.
Что можно сделать с векторной графикой?
Профессиональные и непрофессиональные дизайнеры и иллюстраторы всех жанров используют векторную графику разными способами для создания яркой и четкой графики, которую можно использовать где угодно — например:
- Веб-дизайн и UX (дизайн взаимодействия с пользователем): Благодаря масштабируемости векторной графики это идеальный творческий инструмент для веб-дизайна.
 Одно изображение может отображаться на разных устройствах разного размера без искажений и потери качества.
Одно изображение может отображаться на разных устройствах разного размера без искажений и потери качества. - Логотипы: Вы можете создать логотип, используя простые формы, которые можно увеличивать до бесконечности, и ваш дизайн никогда не потеряет качества. Логотипы должны быть качественными и согласованными, а гибкость векторной графики позволяет использовать их практически в любом мыслимом приложении.
- Рекламные щиты, плакаты и флаеры: Векторные изображения поют на рекламных щитах, плакатах и флаерах, потому что они такие чистые, ясные, последовательные и четкие, независимо от того, насколько они большие или маленькие.
- Одежда: Векторные изображения необходимы для процессов вышивки и сублимации, используемых при изготовлении одежды на заказ, чтобы оборудование могло следовать четким и четким линиям. А если вы хотите создать дизайн футболок, одеял, керамики или других нестандартных подарков, компании, занимающиеся печатью по запросу, предпочитают векторную графику.

Вы можете узнать больше о том, что можно создать с помощью векторной графики, прочитав эту главу из нашей серии: Что можно сделать с помощью векторной графики?
Итак, что за люди создают и используют векторную графику?
Появление «плоского дизайна» в период с 2010 по 2020 год послужило катализатором для тех, кто создает и использует векторную графику. Раньше бренды предпочитали дизайны с тенями, тиснением или высокой детализацией. Затем в течение этого десятилетия произошел сдвиг в сторону более чистого и четкого дизайна. Вместо дизайнов с большим количеством «шума», таких как текстуры и декоративные элементы, бренды хотели видеть минималистичный, чистый и четкий дизайн.
Цифровые художники в основном используют векторную графику для улучшения цифровых презентаций, инфографики, мобильных приложений и веб-сайтов. Вы также найдете эту графику в рекламных и маркетинговых материалах и других материалах бренда.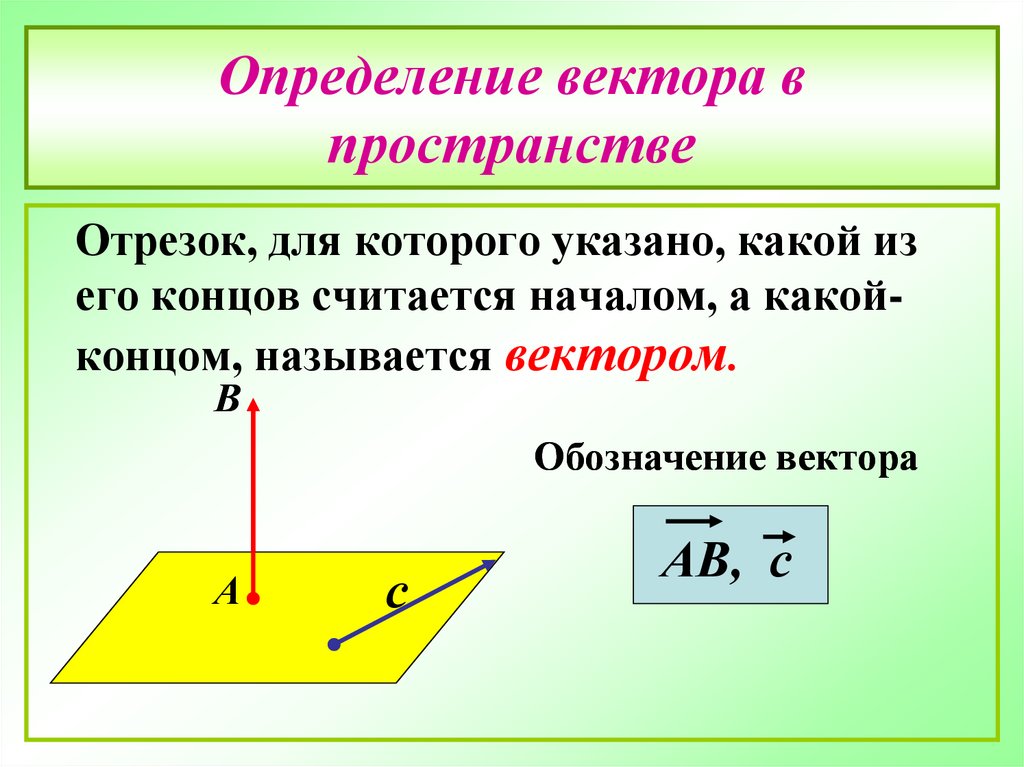 Другие примеры того, кто создает и использует векторную графику, включают:
Другие примеры того, кто создает и использует векторную графику, включают:
- Веб-дизайнеры/UX-дизайнеры: Эти дизайнеры предпочитают векторную графику, потому что она отлично выглядит на любом устройстве. Масштабируемость этой графики делает ее отзывчивой, поэтому даже если вы смотрите на нее на портативном устройстве или большом мониторе, изображения будут четкими. В качестве дополнительной ценности векторная графика поддерживает прозрачность, экспоненциально расширяя возможности веб-дизайнера.
- Полиграфия: Графические дизайнеры используют векторную графику в полиграфии, потому что она обеспечивает более качественный и четкий дизайн, чем растровые изображения. Например, если дизайнер хочет печатать на одежде, четкость и качество изображения не ухудшаются.
- Иллюстраторы: Эти профессионалы используют программное обеспечение для работы с векторной графикой для создания результатов, аналогичных тому, как если бы они не использовали цифровые инструменты — четкие линии, органичные изображения и реалистичные рисунки.
 Например, если им нужно создать изображение с использованием цвета, освещения и затенения, они могут добиться этого с помощью векторной графики.
Например, если им нужно создать изображение с использованием цвета, освещения и затенения, они могут добиться этого с помощью векторной графики. - CAD/Engineers: CAD — это инструмент для трехмерного картографирования, использующий ту же логику, что и программное обеспечение для векторного проектирования. Например, если вы хотите сделать куб, вы будете использовать те же принципы проектирования, в соответствии с которыми вы наносите на карту определенные точки и соединяете их линиями, и это та же самая геометрия, которую вы использовали бы для создания вектора. Когда инженерам нужно сопоставить сложные изображения, они могут использовать эту математику для создания этих проектов. Например, если они проектируют склон холма с круто выглядящим склоном, это все векторы и крошечные полигоны.
Помимо того, что векторное искусство используется в бизнесе, упомянутом выше, вы также найдете векторное искусство в популярной культуре, включая комиксы, анимацию, видеоигры, моду и татуировки.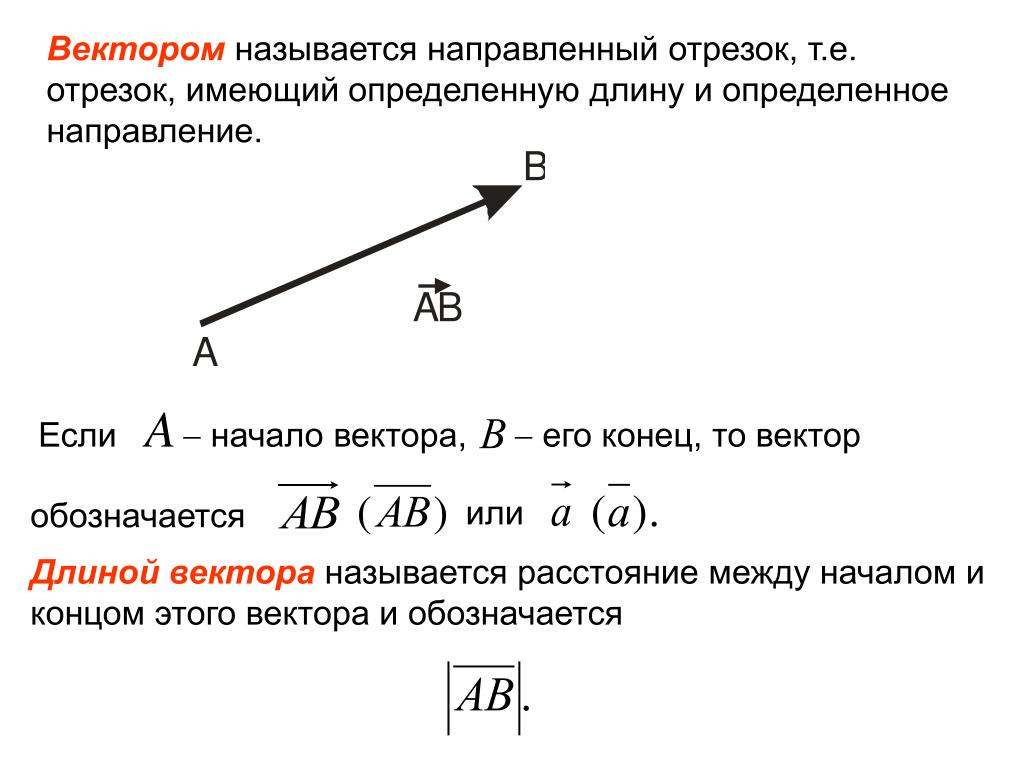
Как долго мы используем векторы?
Мы можем проследить векторную графику до 1950-х годов на первых компьютерах, потому что они занимали меньше места, чем растровые или растровые изображения. В первые дни эта графика была идеальной, потому что она представляла собой простые дисплеи, не требующие значительного объема памяти. Поскольку у ранних компьютерных систем было гораздо меньше памяти, векторные дисплеи были лучшим выбором.
В 1963 году ученый из Массачусетского технологического института Айван Сазерленд создал программу под названием Sketchpad. Это была первая реализация редактирования цифровых изображений, и теперь она считается началом программ САПР и компьютерной графики. Sketchpad организовал геометрические данные или то, что мы сейчас называем графическим интерфейсом, что в конечном итоге привело к CorelDRAW и подобным редакторам изображений.
В 1970-х годах индустрия видеоигр ожила. Раньше игры были текстовыми, но векторная графика изменила правила игры, что привело к использованию лучших консолей и, в конечном счете, домашних компьютеров с более мощными процессорами.
Раньше считалось, что компьютеры для обработки данных предназначены для бизнеса, но 1980-е изменили это, принося персональные компьютеры в дома. Их раннее внедрение графики среди пользователей домашних компьютеров позволило пользователям играть в игры, вводить данные, рассчитывать бюджеты и создавать дизайны. Это был важный шаг, поскольку пользователи перешли от печати к цифре.
У нас есть более подробная хронология векторной графики в этой главе нашей серии: «Векторная графика в истории».
Заключительные мысли: что такое векторная графика?
Из всех преимуществ использования векторной графики на первом месте стоит масштабируемость. Поскольку они основаны на математике, это ставит векторную графику на передний план дизайнерских активов в цифровом мире. Профессиональные художники и художники-любители могут использовать эти изображения для создания впечатляющих работ, четких и с чистыми линиями, независимо от того, какое устройство они используют. Функциональность CorelDRAW позволяет цифровым художникам создавать мощные файлы изображений независимо от их размера и приложения.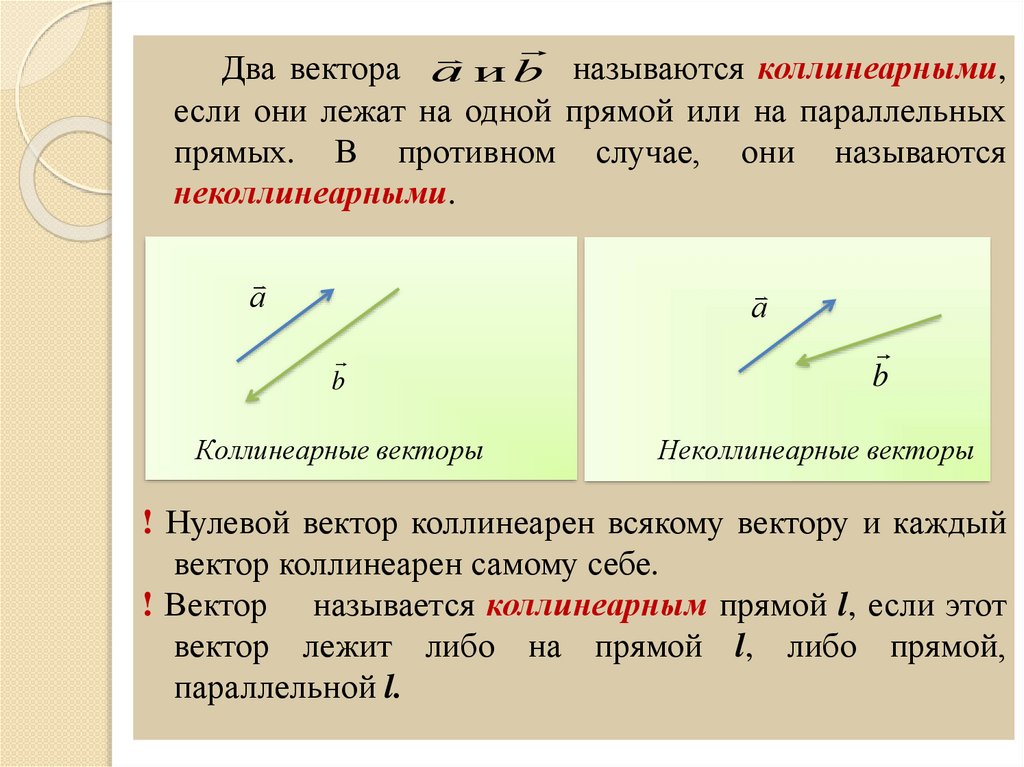



 Вы найдете его в печатных СМИ и логотипах. Хотя они похожи на файлы EPS, их синтаксис компактен и ограничен.
Вы найдете его в печатных СМИ и логотипах. Хотя они похожи на файлы EPS, их синтаксис компактен и ограничен. Одно изображение может отображаться на разных устройствах разного размера без искажений и потери качества.
Одно изображение может отображаться на разных устройствах разного размера без искажений и потери качества.
 Например, если им нужно создать изображение с использованием цвета, освещения и затенения, они могут добиться этого с помощью векторной графики.
Например, если им нужно создать изображение с использованием цвета, освещения и затенения, они могут добиться этого с помощью векторной графики.