Динамика твердого тела. Основное уравнение динамики вращательного движения. Момент инерции. Вращение твердого тела вокруг неподвижной оси. Плоское движение твердого тела
Тема 12 Динамика твердого тела
1 Основное уравнение динамики вращательного движения
2 Момент инерции
3 Вращение твердого тела вокруг неподвижной оси
4 Плоское движение твердого тела
Основные понятия по теме
К основным видам движения твердого тела относятся:
— поступательное движение твердого тела;
— вращение твердого тела вокруг неподвижной оси;
— плоское движение твердого тела;
— вращение твердого тела вокруг неподвижной точки;
— свободное движение твердого тела.
Из перечисленных видов движения четыре последних типа связаны с вращательным движением. При описании этих видов движения используется уравнение моментов
, (12.1)
которое
принято называть основным уравнением динамики вращательного движения.
Так же как и основное уравнение динамики основное уравнение динамики
вращательного движения (12.1) можно записать в другом виде
, (12.2)
где угловое ускорение тела.
Величина , входящая в уравнение (12.2), является аналогом массы при вращательном движении твердого тела. Ее называют момент инерции. Момент инерции материальной точки равен
, (12.3)
где масса материальной точки, расстояние от материальной точки до оси вращения. Для системы материальных точек и твердого тела моменты инерции соответственно равны
; (12.4)
. (12.5)
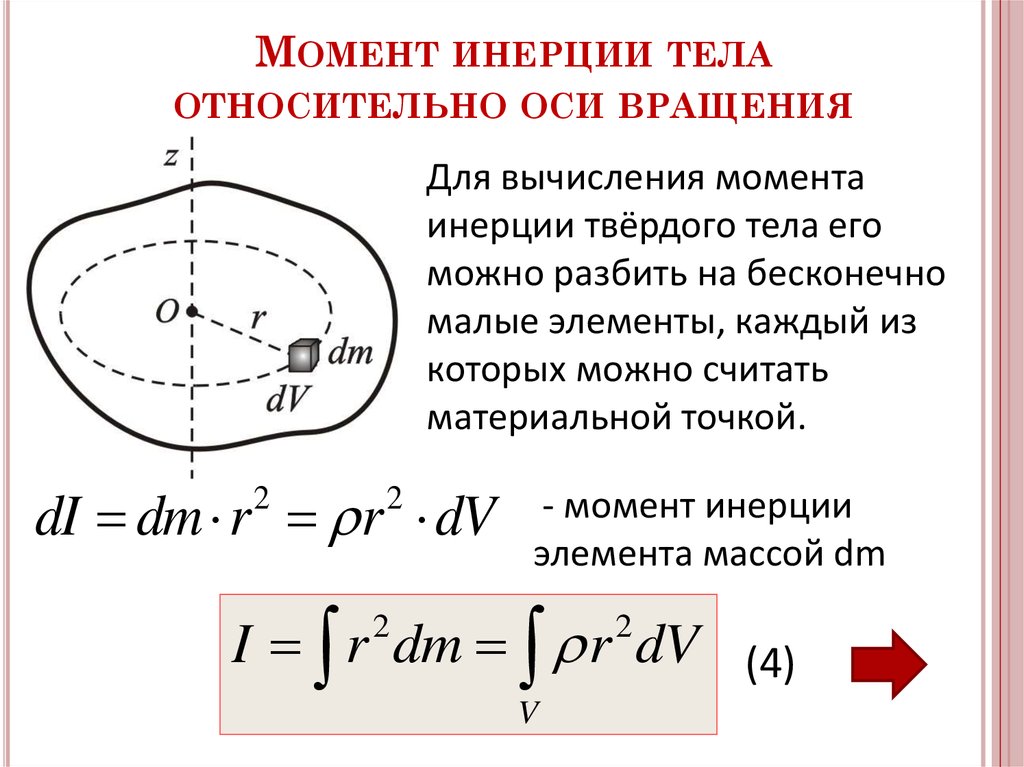
В выражении (12.5) интегрирование ведется по объему тела.
Момент инерции зависит от положения оси вращения и
распределения масс относительно этой оси. Приведем выражения для моментов
инерции некоторых тел относительно оси вращения,.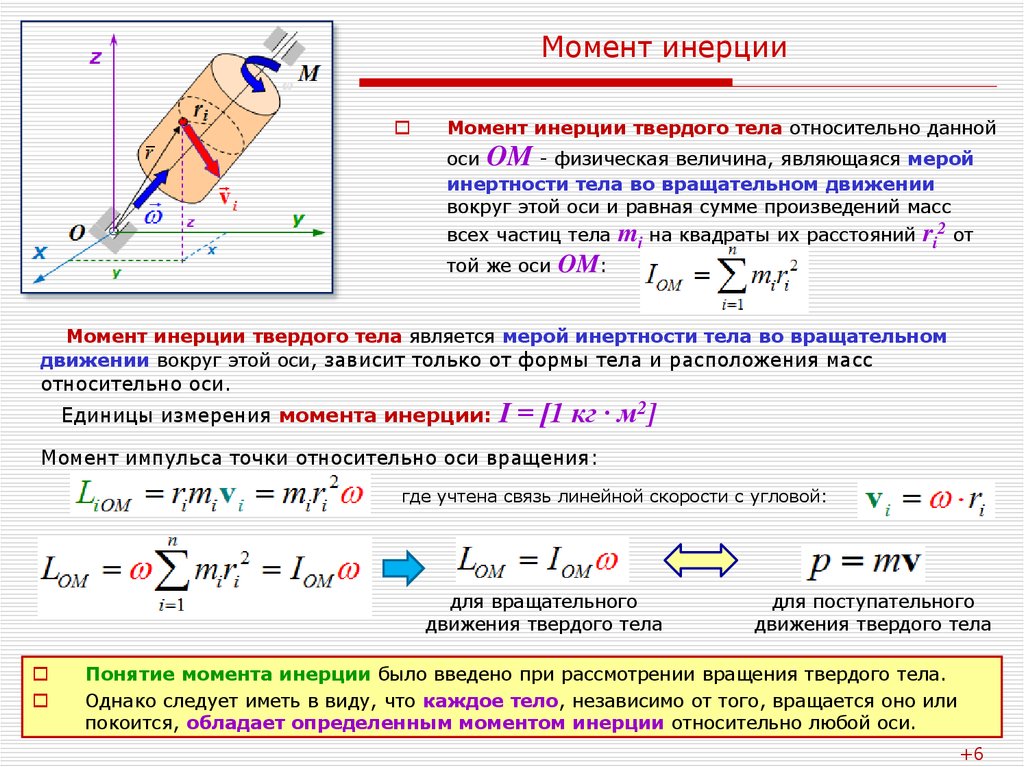
положение которой указывается
в скобках.
Сплошной цилиндр или диск радиуса R(ось симметрии)
. (12.6)
Полый тонкостенный цилиндр радиуса R или обруч (ось симметрии)
. (12.7)
Однородный тонкий стержень длиной
. (12.8)
Шар радиуса R (ось проходит через центр шара)
. (12.9)
Если известен момент инерции тела относительно оси, проходящей через его центр масс С, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера:
момент инерции тела J относительно произвольной оси Z равен сумме момента инерции тела относительно параллельной оси, проходящей через центр масс С тела, и произведения массы
Вращающееся тело, как и тело движущееся поступательно, обладает энергией движения.
Кинетическая энергия твердого тела вращающегося вокруг неподвижной оси Z с угловой скоростью
. (12.10)
Кинетическая энергия тела совершающего плоское движение равна
, (12.11)
где скорость центра масс тела, угловая скорость тела, момент инерции тела относительно собственной оси.
Вопросы для самоконтроля
1 Назовите виды движения твердого тела.
2 Что понимают под плоским движением твердого тела? Приведите примеры такого движения. Почему этот вид движения называют плоское движение?
3 Чем отличаются траектории точки твердого тела вращающегося вокруг неподвижной оси и вокруг неподвижной точки О?
4 Дайте определение момента инерции материальной точки, системы материальных точек, твердого тела. Что характеризует момент инерции? От каких факторов он зависит?
5 Объясните смысл утверждения «момент инерции это
аддитивная величина».
6 Сформулируйте теорему Штейнера.
7 Что понимаю под тензором моментов инерции? Чем обусловлено необходимость введения такого понятия? Какие моменты инерции называются осевыми?, центробежными?
8 Запишите основное уравнение динамики вращательного движения в различных формах. Установите аналогию записанных выражений с уравнениями динамики поступательного движения.
9 Опишите последовательность действий при решении основной задачи динамики твердого тела.
10 Запишите выражения для энергии твердого тела вращающегося вокруг неподвижной оси, вокруг неподвижной точки. Напишите аналогичное выражение для тела, совершающего плоское движение.
Примеры решения задач
1 В схеме, показанной на рисунке 12.1, определить ускорение груза массы m. Масса
Решение. Силы, действующие на груз и блок, показаны на рисунке 12.1. Запишем второй закон Ньютона для груза m
.
(1)
Для блока, который участвует в поступательном и вращательном движениях, необходимо записать второй закон Ньютона и основное уравнение динамики вращательного движения
; (2)
. (3)
В уравнении (3) через обозначен момент, соответствующий силе относительно точки О лежащей на оси блока.
В проекциях на оси системы координат XYZ система векторных уравнений () принимает вид
; (4)
; (5)
(6)
и содержит шесть неизвестных: , , , , , .
Для решения системы уравнений () учтем, что, согласно третьему закону Ньютона . Кроме того, для точки A, участвующей в поступательном движении груза m и вращательном движении блока, и точки В, участвующей в поступательном и вращательном движениях блока, можем записать
и .
Учитывая приведенные выше соотношения, вместо системы уравнений ()имеем
; (7)
; (8)
протоколы / мех / №20
Задание 2. Определение ускорения свободного падения без учета момента инерции блока.
.
. 3. Окончательный результат записать в виде:
Контрольные вопросы
| ДГТУ кафедра «Физика» Лабораторная работа №20 Определение ускорения свободного падения на машине Атвуда ____________________ Ф.И.О. студента Проверил преподаватель каф. «Физика» ____________________ Ф. Ростов-на-Дону 201 г. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Цель работы: Оборудование: машина Атвуда, набор грузиков, электронный секундомер. Порядок выполнения Задание 1. Определение ускорения свободного падения с учетом момента инерции блока.
а) ; б) абсолютные погрешности каждого измерения ; в) квадраты . Таблица 1
, , , | Таблица 2 Таблица 3
5. . 6. Рассчитать относительную и абсолютную погрешности, результаты занести в таблицу 3. ; . 7.Сравнить результат экспериментального определения с . |
И.О.
преподавателя
1:
2:
Определить
ускорение свободного падения по
формуле:Соседние файлы в папке мех
- #
19.05.2015156.67 Кб5~WRL1048.tmp
- #
19.05.201579.36 Кб5~WRL3434.tmp
- #
19.05.2015151.04 Кб5фронт.doc
- #
19.05.2015157.18 Кб5№10а.doc
- #
19.05.2015150.02 Кб5№13.doc
- #
19.05.2015123.9 Кб5№20.doc
- #
19.05.2015124.93 Кб5№21.doc
- #
19.
05.2015134.14 Кб5№3.doc - #
19.05.201573.22 Кб5№5.doc
- #
19.05.201583.97 Кб5№8.doc
05.2015134.14 Кб5№3.docФакторы, от которых зависит момент инерции
Момент инерции в физике есть мера объема вращательной инерции тела, т. е. сопротивления тела, показывающего скорость его вращения относительно оси, изменяемой крутящим моментом.
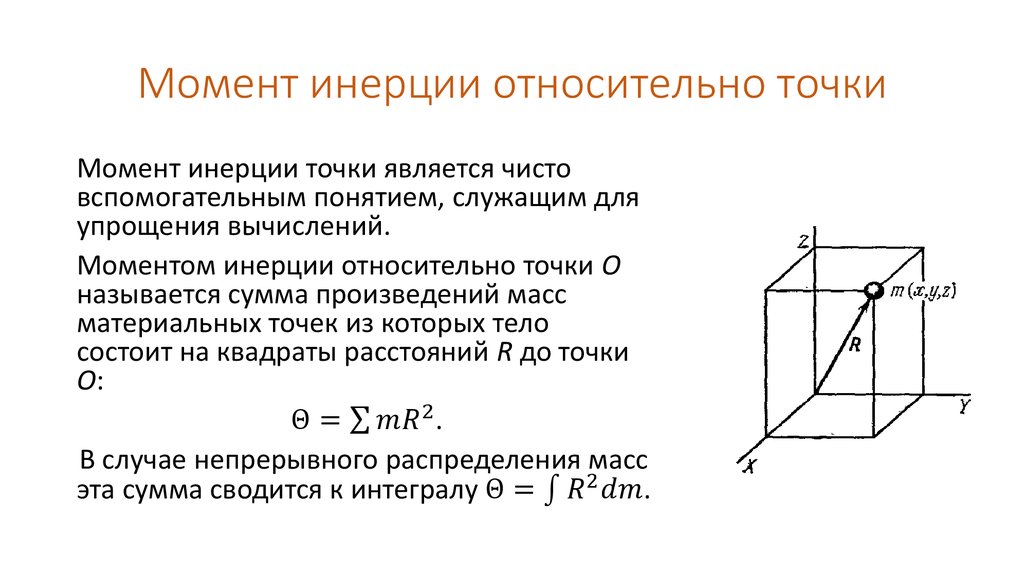
Ось может быть внутренней или внешней, наклонной или прямой. Момент инерции (I) всегда указывается относительно этой оси. Он определяется как результат сложения всех произведений, полученных при умножении каждой частицы в теле на квадрат ее расстояния от оси.
Моментом инерции называется вращательная инерция, вращательный аналог веса прямого движения. Оно возникает из-за способности вращающегося тела сопротивляться изменению его вращательного движения. Это свойство также связано с плотностью материала, из которого состоит корпус.
Для данной точки момент инерции всего в несколько раз превышает квадрат расстояния, перпендикулярного оси вращения, I = mr2.
Примеры момента инерции
Представьте, что вы сидите в движущемся автобусе. Когда через некоторое время он останавливается, ваша верхняя часть тела движется вперед, а нижняя часть тела не двигается. Это из-за инерции. Ваша нижняя часть тела подключена к шине, но верхняя часть тела не связана с шиной напрямую. Поэтому, когда автобус останавливается, ваша нижняя часть тела останавливается вместе с автобусом, но верхняя часть тела продолжает двигаться вперед. То есть сопротивляется изменениям своего положения.
Точно так же ваше тело отбрасывается назад, когда вы садитесь в движущийся поезд. Это потому, что перед посадкой в поезд вы были расслаблены. Как только вы садитесь в движущийся поезд, ваша нижняя часть тела встречается с поездом, но верхняя часть тела все еще находится в состоянии покоя. Поэтому он оттесняется назад, то есть сопротивляется изменению своего положения.
Факторы, от которых зависит момент инерции
Масса тела
Масса оценивает количество вещества в теле. Это также свойство, благодаря которому тело сопротивляется ускорению или изменению своей скорости, когда к нему прикладывается внешняя сила, действующая как инерция. Базовой единицей массы в системе СИ является килограмм (кг). Когда тело имеет большую массу, внешней силе труднее изменить состояние его движения. Точно так же, когда тело имеет большую массу или когда плотность материала, из которого сделано тело, высока, его момент инерции высок. Следовательно, для изменения вращения тела требуется более высокий крутящий момент.
Момент инерции зависит от оси вращения. Ось вращения тела зависит от размера и формы тела. По мере изменения размера и формы меняется и ось вращения тела. Это вызывает изменение момента инерции тела.
Чтобы измерить, как вес твердого вращающегося тела распределяется относительно оси вращения, мы определяем новый параметр, известный как радиус вращения. Это связано с моментом инерции и общей массой тела. Когда масса на одной стороне тяжелее, ось вращения тела ближе к ней, и момент инерции требует более высокого крутящего момента на этой стороне, чтобы изменить движение.
Это размещение тела на оси и его ориентация. Если есть изменение направления оси, направление крутящего момента также должно измениться, чтобы вызвать изменение вращения тела. Точно так же изменение точки, в которой ось вращения проходит через тело, то есть изменение его положения, изменило бы и момент инерции тела.
Формула момента инерции
Момент инерции равен I = mr2.
Где,
m = Сумма произведения массы.
r = Расстояние от оси вращения.
Промежуточная единица инерции является составной единицей измерения.
В международной системе единиц (СИ) масса измеряется в килограммах, а расстояние в метрах. Следовательно, размерность момента инерции равна килограмм-метрам в квадрате.
Момент инерции любой формы тела, которую можно определить по математической формуле, обычно рассчитывается с помощью интегрального исчисления. Момент инерции диска можно измерить, разрезав его на число неподвижных колец, найдя их количество, умножив массу на их расстояния от точки отсчета и сложив эти произведения. Процесс слияния выполняется автоматически; ответ: I = (mR2) / 2,
Вращающиеся тела можно разделить на следующие категории:
Момент инерции системы частиц
Для системы различных точечных частиц, вращающихся вокруг фиксированной оси, момент инерции может быть задан как I = ∑jmjrj2, где mj — масса каждой точечной частицы, rj — расстояние этих частиц от оси. Из-за члена r2 время инерции увеличивается, поскольку квадрат расстояния до оси вращения не изменяется.
Момент инерции является вращательным аналогом веса при прямолинейном движении.
Момент инерции твердого тела
Когда мы говорим о твердом теле, мы предполагаем, что все частицы в твердом теле распределены равномерно. Если бы мы выбрали два поперечных сечения твердого тела наугад так, что оба сечения имеют одинаковую площадь, то мы имели бы одинаковое количество частиц в обоих поперечных сечениях. Будем также считать, что плотность материала тела фиксирована и не колеблется.
Таким образом, можно сказать, что момент инерции твердого тела можно описать через момент инерции системы частиц, с той лишь разницей, что формула I=∫r2dm,. То же самое верно даже для твердых тел странной формы.
Заключение
Момент инерции — это название, данное вращательной инерции, вращательный аналог веса прямого движения. Оно возникает из отношения вращения вращательного движения. Входное время должно быть указано относительно выбранной оси вращения.
С точки зрения точки, момент инерции всего в несколько раз превышает квадрат перпендикулярного расстояния к оси вращения, I = mr2. Это отношение «точка-точка» становится основой всех других времен инерции, поскольку из набора точек можно построить что угодно.
Момент инерции определяется выражением I = mr2.
Промежуточная единица инерции является составной единицей измерения. В международной системе единиц (СИ) масса измеряется в килограммах, а расстояние в метрах. Следовательно, размерность момента инерции равна килограмм-метрам в квадрате.
Назовите фактор, от которого зависит момент инерции тела. В этом вопросе несколько правильных вариантов ответа. МассаБ. ForceC. Расстояние от оси вращения D. Плотность
Дата последнего обновления: 07 марта 2023 г. 92 + …$ . Затем используйте уравнения, чтобы уточнить, как момент инерции зависит от массы и расстояния от оси вращения.
Полный пошаговый ответ:
Момент инерции — Его также называют массовым моментом инерции или вращательной инерцией тела.
Момент инерции представляет собой сумму произведений массы каждой частицы на квадрат расстояния каждой частицы от оси вращения. Момент инерции основан на понятии центра масс. Центр масс — это воображаемая точка тела, в которой можно считать, что вся масса тела собрана. 92 + …$
Из приведенного выше уравнения мы узнаем некоторые важные моменты. Проще говоря, момент инерции тела зависит от распределения массы тела и расстояния от оси вращения.
Момент инерции тела прямо пропорционален его массе и расстоянию частиц тела от оси вращения.
Следовательно, момент инерции зависит от массы и расстояния от оси вращения, а сила и плотность не влияют на момент инерции тела.
Следовательно, варианты A и C являются правильными вариантами.
Примечание: Понятие центра масс очень важно для расчета момента инерции. Понятие центра масс очень интересно. Мы знаем, что для расчета электростатической и гравитационной сил, действующих на тело, мы также рассматриваем их как точечный заряд и точечную массу соответственно.
По существу, мы считаем, что все заряды и масса сосредоточены в центре. Помните, что этот заряд или масса всегда считается находящейся внутри тела, но в случае с центром масс он также может быть расположен вне тела, например – Центр масс Банана.
Недавно обновленные страницы
Большинство эубактериальных антибиотиков получены из биологии Rhizobium класса 12 Neet_ug
Биоинсектициды для саламин были извлечены из Class 12 Biology Neet_ug
, которые из следующих утверждений, касающихся Baculoviressires. муниципальные канализационные трубы не должны быть непосредственно 12 класса биологии NEET_UG
Очистка сточных вод осуществляется микробами A B Удобрения 12 класса биологии NEET_UG
Иммобилизация ферментов — это конверсия активного фермента класса 12 биологии NEET_UG
Большинство эубактериальных антибиотиков получают из биологии класса 12 Rhizobium NEET_UG
Саламиновые биоинсектициды были извлечены из биологии класса 12 NEET_UG
, следуя заявлениям относительно вируса Ba.
