Вопреки распространённому заблуждению, двоичная система счисления была придумана не инженерами-конструкторами ЭВМ, а математиками и философами задолго до появления компьютеров, ещё в 17 веке. Великий немецкий учёный Лейбниц считал: Впервые двоичная система появилась в 1605 году в работах Томаса Хэрриота (он изобрёл знаки > и ). Позже двоичная система была забыта, и только в 1936-1938 гг. американский инженер и математик Клод Шеннон нашёл замечательные применения двоичной системы при конструировании электронных схем. Двоичная система удобна для компьютера, но неудобна для человека — числа получаются очень длинными и их трудно записывать и запоминать. Она используется, как правило, для «внутренних нужд» компьютера. Двоичная система счисления позволяет достаточно просто организовать числа, и для того, чтобы представить число в ЭВМ, достаточно иметь устройство, которое обладает только двумя устойчивыми состояниями, одно из которых соответствует логической «1», а другое — «0». Таких элементов достаточно много: намагниченный или не намагниченный сердечник, открытый или закрытый транзистор и др. 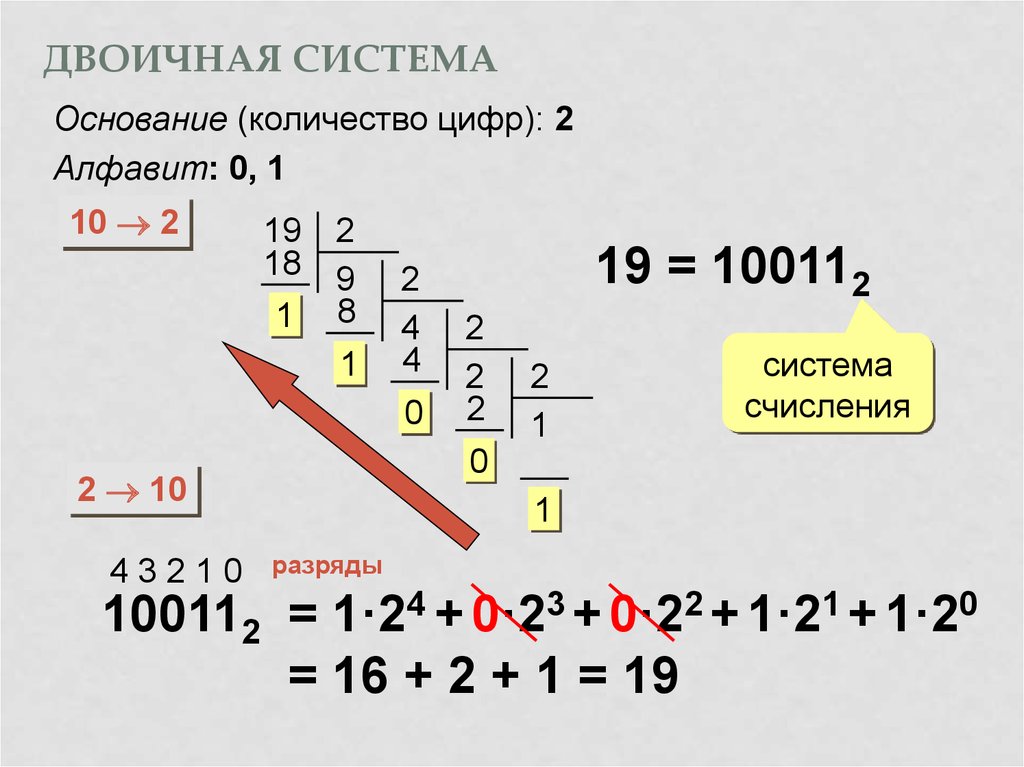 Другим важным достоинством двоичной системы является простота вычислений. Рассмотрим, как выполняются арифметические действия в двоичной системе. Для этого проведём анализ таблиц сложения и умножения в двоичной системе. Примеры сложения двоичных чисел: Примеры умножения двоичных чисел: Следует обратить внимание на аналогию в правилах выполнения арифметических действий в двоичной и десятичной системах счисления: например, если при сложении двух двоичных чисел сумма цифр окажется больше единицы, то возникает перенос в старший разряд. Вычитание двоичных чисел осуществляется следующим образом: Вычитаемое число преобразуется в дополнительный код. Например, если надо вычесть из числа 10110 число 01000, то вычитаемое 01000 преобразуется в дополнительный код так: в числе вместо 0 пишется 1, а вместо 1 пишется 0, следовательно, получим из вычитаемого число 10111.  И вычитаемое, и уменьшаемое состоят из 5 разрядов, а результат суммы — число 6-разрядное. Старший разряд суммы отнимается от числа и складывается с результатом: Такой приём часто используется в практике вычислений. Например, в десятичной системе числа можно вычесть так. Допустим требуется найти разность 842-623. Представим число 623 в дополнительный вид, отняв его от 1000. Получим число 377. Затем найдём сумму: 842+377=1219. Отбросим перенос в старший разряд и получим число 219. Мы нашли решение этого примера. Деление двоичных чисел выполняется аналогично делению десятичных чисел. Вычитание и умножение в процессе деления необходимо выполнять рассмотренными ранее способами. Важнейшее преимущество двоичной арифметики заключается в том, что она позволяет все арифметические действия свести к одному — сложению, а это значительно упрощает устройство процессора ЭВМ. Отметим недостаток, характерный для двоичной системы счисления — значительный рост числа разрядов при увеличении числа. 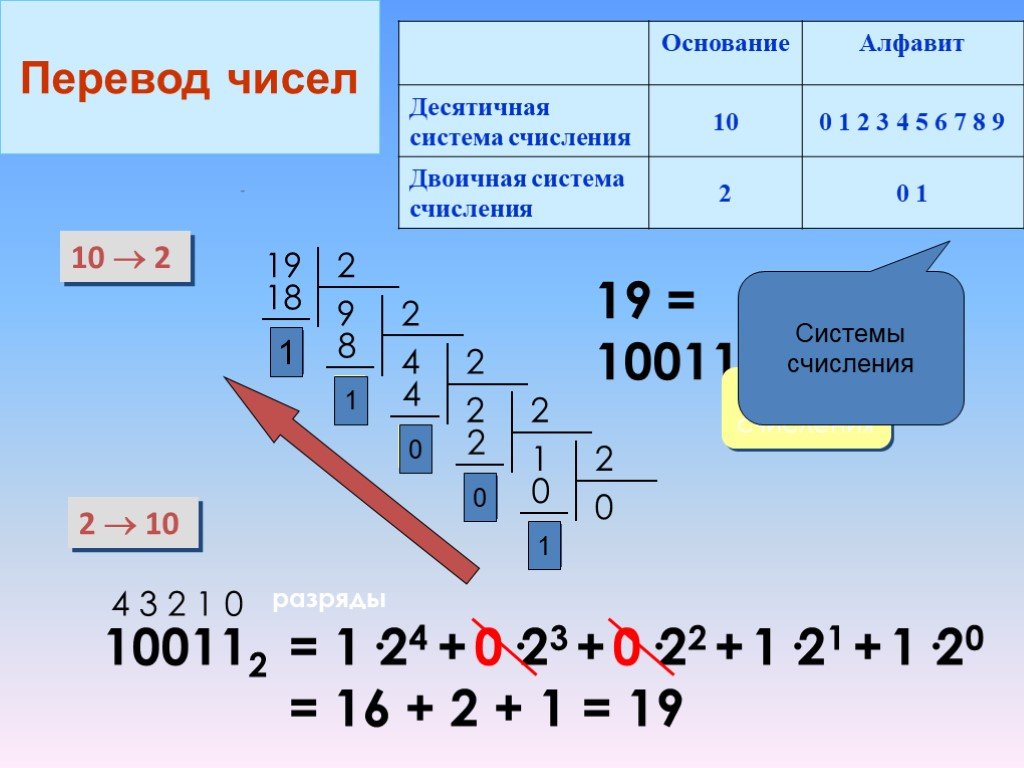 Но все достоинства этой системы делают такой недостаток не столь существенным. |
| ||
Двоичная система счисления и точный перевод чисел: таблица, примеры десятичной, восьмеричной и других систем
Самой короткой системой счисления является двоичная. Она полностью основана на позиционной форме записи числа. Основной характеристикой считается принцип удвоения цифры при выполнении перехода от определённой позиции к последующей.
Из одной системы счисления в другую можно осуществить перевод как при помощи специальной программы, так и вручную….
Содержание
Историческое признание
Появление двоичной СС в истории связано с учёным математиком В.Г. Лейбницем. Именно он впервые заговорил о правилах выполнения операций с числовыми значениями данного рода. Но первоначально этот принцип остался невостребованным. Мировое признание и применение алгоритм получил на заре возникновения вычислительных машин.
Удобство и несложность выполнения операций привели к необходимости более детального изучения данного подраздела арифметики, который стал незаменимым при развитии компьютерной технологии с программным обеспечением. Впервые такие механизмы появились на немецком и французском рынках.
Внимание! Конкретную точку над превосходством двоичной системы по отношению десятичной, именно в данной отрасли, было поставлено в 1946 году и обосновано в статье А.
Бекса, Х. Гольдстайна и Дж.Фон Неймана. Перевод числа из десятичной системы счисления в двоичную.
Особенности двоичной арифметики
Вся двоичная СС основана на применении только двух символов, которые очень точно совпадают с особенностями цифровой схемы. Каждый из символов отвечает за определённое действие, которое зачастую подразумевает два состояния:
- наличие отверстия или его отсутствие, к примеру, перфокарты или перфоленты,
- на магнитных носителях отвечает за состояние намагничивания или размагничивания,
- по уровню сигнала, высокий или низкий.
В науке, в которой применяется СС, введена определённая терминология, суть ее состоит в следующем:
- Бит – двоичный разряд, который состоит из двух составляющих, несущих в себе определённый смысл. Размещённый слева, определяется как старший и является приоритетным, а справа – младшим, являющийся менее весомым.
- Байт – это единица, которая состоит из восьми битов.
Многие модули воспринимают и обрабатывают информацию порциями или словами. Каждое слово имеет разный вес и может состоять из 8-ми, 16-ти или 32-х битов.
Это интересно! Свойства натуральных логарифмов: график, основание, функции, предел, формулы и область определения
Правила переводов из одной системы в другую
Одним из важнейших факторов арифметики машин является перевод из одной СС в другую. Поэтому обратим внимание на основные алгоритмы выполнения процесса, который покажет, как перевести число в двоичную систему.
Переводим десятичную систему в двоичную
Первоначально обратимся к вопросу, как осуществить перевод системы из десятичной в двоичную систему счисления. Для этого существует правило перевода из десятичных чисел в двоичный код, которое подразумевает математические действия.
Необходимо число, записанное в десятичном виде разделить на 2.
Деление выполнять до тех пор, пока в частном не останется единица. Если необходима двоичная система счисления перевод осуществляется так:
186:2=93 (ост. 0)
93:2=46 (ост. 1)
46:2=23 (ост. 0)
23:2=11 (ост. 1)
11:2=5 (ост. 1)
5:2=2 (ост.1)
2:2=1
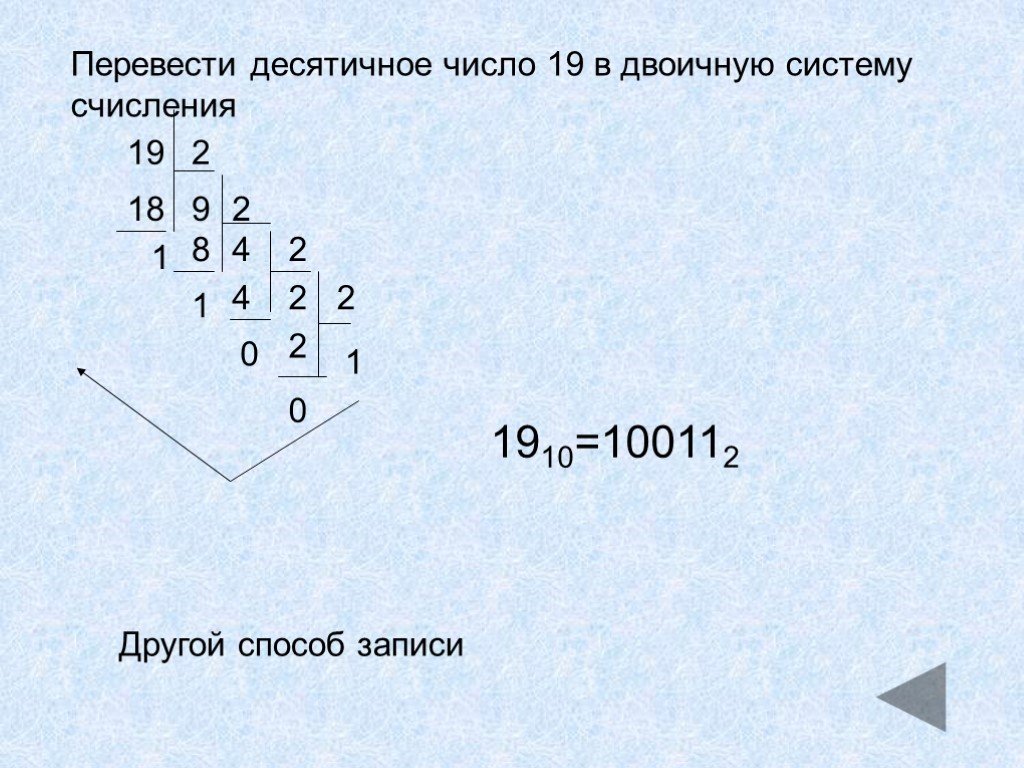
После того, как процесс деления закончен, то единицу в частном и все остатки записываем последовательно в обратном делению порядке. То есть, 18610=1111010. Правило перевода десятичных чисел в СС надо соблюдать всегда.
Перевод числа из десятичной системы в двоичную.
Это интересно! Изучение основных правил умножения: как из неправильной дроби сделать правильную
Перевод из десятичной СС в восьмеричную
Аналогичный процесс проводится при переводе из десятичной СС в восьмеричную. Его ещё называют «правилом замещения». Если в предыдущем примере деление данных осуществлялось на 2, то здесь необходимо делить на 8.
Алгоритм перевода числа X10 в восьмеричную состоит из следующих шагов:
- Число X10 начинают делить на 8. Полученное частное берём для следующего деления, а остаток записывается, как бит младшего порядка.
- Продолжаем деление до тех пор, пока не получим в результат частного равного нулю или остаток, который по своему значению меньше восьми. При этом все остатки записываем, как младшие порядки бита.
К примеру, необходимо перевести число 160110 в восьмеричное.
1601:8=200 (ост. 1)
200:8=25 (ост. 0)
25:8=3 (ост.1)
Итак, получим: 161010=31018.
Перевод из десятичной системы в восьмеричную.
Это интересно! Как определить определенные интегралы от нуля, константы и с доказательством
Записываем десятичное число шестнадцатеричным
Перевод из десятичной в шестнадцатиричную СС осуществляется аналогично с использованием системы замещения.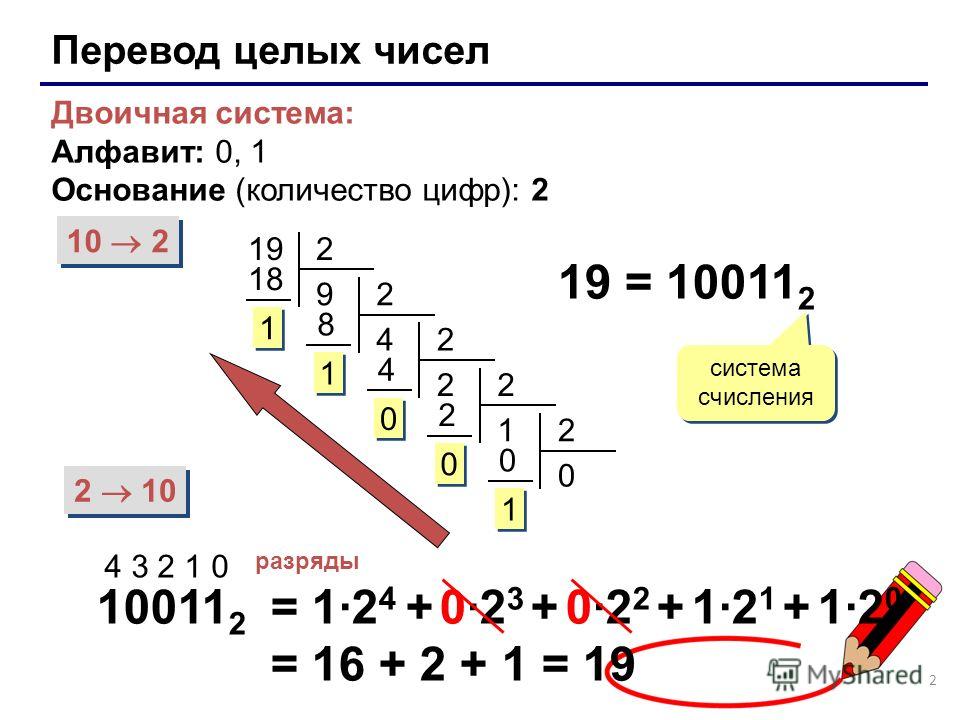
Но кроме цифр применяют ещё и буквы латинского алфавита A, B, C, D, E, F. Где A обозначает остаток 10, а F остаток 15. Десятичное число делят на 16. К примеру, переводим 10710 в шестнадцатеричную:
107:16=6 (ост. 11 – заменяем В)
6 – меньше, чем шестнадцать. Деление прекращаем и записываем 10710=6В16.
Переходим из другой системы в двоичную
Следующий вопрос, как преобразовать из восьмеричной в двоичную запись числа. Перевод чисел из любой системы в двоичную выполняется достаточно просто. Помощником в этом деле выступает таблица для систем счисления.
Важно! Сам принцип основывается на замене набора цифр одной системы на числа другой. Пример перевода 247388=1010011101122
Аналогичный ответ имеет вопрос, как перевести из шестнадцатиричной в двоичную. Необходимо преобразовать каждый символ числа А16 в набор символов двоичного числа. Выполнить это можно посредством представленной таблицы.
| Шестнадцатеричная | Двоичная |
| 0000 | |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
К примеру, число А2316=1010000100112.
Это интересно! Изучение точного предмета: натуральные числа — это какие числа, примеры и свойства
Перевод чисел в восьмеричную и шестнадцатеричную систему счисления и обратно
Перевод между двоичной, восьмеричной, и шестнадцатеричной системой счисления
youtube.com/embed/fBkxxegb8eg» frameborder=»0″ allowfullscreen=»allowfullscreen»> Итог
Кроме всех перечисленных систем, существует и четвертичная система, основанием которой является цифра 4. Записывается она посредством четырёх символов 0, 1, 2, 3. К примеру 1010=224, а 1510=334.
Двоичная система счисленияЭто интересно! Что такое экстремумы функции: критические точки максимума и минимума
и история Индии
Культура и история, образование, наука и техника
арпитакармакар030615
Двоичные числа, система счисления, десятичные коды, компьютеры и технологии, двоичные коды, теория информации, цифровые логические вентили — эти вещи взаимосвязаны друг с другом. Двоичные числа мы обычно узнаем об этой системе счисления в нашем младшем классе компьютерного класса, и мы использовали для решения таких двоичных задач, как преобразование десятичного числа в двоичное число.
давайте узнаем, что такое двоичная система счисления двоичное число
Теперь, если мы поищем историю теории двоичной системы счисления или двоичного кода, мы увидим, что современная двоичная система счисления, являющаяся основой для двоичного кода, была изобретена
Полное название переводится на английский язык как «Объяснение двоичной арифметики». он был первым изобретателем двоичной системы в мире. Ачарья Пингала автор Чандахшастра (Пингала-сустра) или Чандхи относится к одной из шести Веданг или разделов ведических исследований Чандахшастра л дословно переводится как наука о метрах на санскрите. Пингала использовала двоичные числа в виде коротких и длинных слогов, что делало его похожим на азбуку Морзе, здесь двоичные числа увеличивались вправо, а не влево, как в современной двоичной системе, в этой книге число начиналось с 1, а не с 0. Пингала использовала лагху (легкий) и гуру (тяжелый), а не 0 и 1 описанные слоги (четыре коротких слога — двоичное «0000» — это первый образец), То, что двоичный код был изобретен в Индии, неудивительно. Не так давно ученые обнаружили очень интригующий древний индийский текст, известный как манускрипт Бахшали , который переписывает историю числа ноль и математики.
Оценить:
Нравится:
Нравится Загрузка…
древний векПодход к обучению коммуникативному языкукомпьютерное изучение языковИнформационно-коммуникационные технологииматематикаНаука и технологии- 1 633 544 Читатели
Введите свой адрес электронной почты, чтобы вступить в Клуб ученых и исследователей
Адрес электронной почты:
Присоединяйтесь к 79 102 другим подписчикам
ijr@ijrjournal.
com
Указатель журнала Copernicus
Мы рады сообщить, что наш Международный исследовательский журнал был проиндексирован в базе данных Index Copernicus за качественные публикации, сделанные за последние несколько лет.
Надеемся увидеть сотрудничество наших уважаемых авторов, ученых-исследователей, профессоров и других академиков и в будущем.
IJR Journal — это междисциплинарный, влиятельный и индексируемый журнал для научных публикаций. IJR — это ежемесячный журнал для научных публикаций.
Двоичные числа: введение
Двоичные числа: введениеДвоичная система счисления, используемая для кодирования информации с помощью нулей и единиц, лежит в основе каждого цифрового компьютера.
Что такое двоичный код?
Двоичная система счисления — это система счисления с основанием 2, в которой используются только две цифры (0 и 1).
Это система, используемая в основе каждого цифрового компьютера, позволяющая им кодировать информацию, выполнять арифметические операции и выполнять логические процессы управления.
Использование двух цифр вместо, скажем, привычных десяти цифр, используемых в десятичных системах (от 0 до 9) позволяет легко реализовать аппаратное обеспечение с помощью простых состояний схемы «включено» или «выключено» или логических вентилей. Это основа всех цифровых систем.
Понимание двоичных чисел
Чтобы понять двоичные значения, представьте, что каждая цифра (или «бит») двоичной записи представляет собой возрастающую степень числа 2, где крайняя правая цифра представляет 2 0 , следующая представляет 2 1 , затем 2 2 и так далее.
Для каждого бита 1 или 0 означает, соответствует ли значение возрастающей степени двух суммированию общего числа.
| 2 нет | 2 3 | 2 2 | 2 1 | 2 0 |
| Десятичный | 8 | 4 | 2 | 1 |
1. Увеличение степени двойки, представленное десятичным результатом.В качестве наглядного примера на рис. 2 показано преобразование двоичного значения 1100 в десятичное значение 12. Синие числа представляют двоичное представление, красные числа представляют возрастающую степень числа 2, а зеленые числа представляют десятичные значения.
Рисунок 2. Двоичное представление в десятичное: представление 12.Двоичные значения часто представляются с разной длиной «бит» или размером «слов». В приведенном выше примере значение представлено в 4 битах, называемых «полубайтами». Это означает, что может быть представлено значение от 0 до 15. 8-битные значения, называемые «байтами», могут представлять значения от 0 до 255. На рис. 3 показано 4-битное двоичное представление для каждого десятичного значения от 0 до 15.
| Десятичное число | Двоичный |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
