Как найти векторное произведение векторов
ФОРМУЛА
Чтобы найти векторное произведение \(\ [\overline{a}, \overline{b}] \) двух векторов, заданных их координатами \(\ \overline{a}=\left(a_{x} ; a_{y} ; a_{z}\right) \quad{и}\quad \overline{b}=\left(b_{x} ; b_{y} ; b_{z}\right) \)соответственно, необходимо вычислить следующий определитель
\(\ [\overline{a}, \overline{b}]=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {a_{x}} & {a_{y}} & {a_{z}} \\ {b_{x}} & {b_{y}} & {b_{z}}\end{array}\right| \)
Как правило, такой определитель вычисляется путем разложения первой строки. Также обратите внимание, что результатом векторного произведения является вектор.
ПРИМЕРЫ РАСЧЕТА ВЕКТОРНОЙ ПРОДУКЦИИ ВЕКТОРОВ
ПРИМЕР
\(\ [\overline{a}, b]=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {a_{x}} & {a_{y}} & {a_{z}} \\ {b_{x}} & {b_{y}} & {b_{z}}\end{array}\right| \)
Подставляя координаты указанных векторов, получаем:
\(\ [\overline{a}, \overline{b}]=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {1} & {0} & {0} \\ {0} & {1} & {0}\end{array}\right| \)
Разобьем определитель по первой строке:
\(\ [\overline{a}, \overline{b}]=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {1} & {0} & {0} \\ {0} & {1} & {0}\end{array}\right|= \)
\(\ =\overline{i} \cdot \left| \begin{array}{ll}{0} & {0} \\ {1} & {0}\end{array}\right|-\overline{j} \cdot \left| \begin{array}{cc}{1} & {0} \\ {0} & {0}\end{array}\right|+\overline{k} \cdot \left| \begin{array}{cc}{1} & {0} \\ {0} & {1}\end{array}\right|= \)
\(\ =0 \cdot \overline{i}-0 \cdot \overline{j}+1 \cdot \overline{k} \)
Первые два определителя равны нулю, так как они содержат нулевой столбец, а третий определитель вычисляется как определитель второго порядка: мы берем произведение вторичных элементов из произведения элементов главной диагонали.
Итак, координаты искомого вектора равны коэффициентам ортов, то есть
\(\ [\overline{a}, \overline{b}]=(0 ; 0 ; 1) \)
ПРИМЕР
\(\ [\overline{a}, \overline{b}]=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {a_{x}} & {a_{y}} & {a_{z}} \\ {b_{x}} & {b_{y}} & {b_{z}}\end{array}\right| \)
Подставляя координаты указанных векторов, получаем:
\(\ [\overline{a}, \overline{b}]=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {5} & {3} & {-4} \\ {6} & {7} & {-8}\end{array}\right|= \)
Разобьем полученный определитель по первой строке:
\(\ =\vec{i} \cdot \left| \begin{array}{cc}{3} & {-4} \\ {7} & {-8}\end{array}\right|-\overline{j} \cdot \left| \begin{array}{cc}{5} & {-4} \\ {6} & {-8}\end{array}\right|+\overline{k} \cdot \left| \begin{array}{cc}{5} & {3} \\ {6} & {7}\end{array}\right|= \)
\(\ =[3 \cdot(-8)-7 \cdot(-4)] \cdot \overline{i}-[5 \cdot(-8)-6 \cdot(-4)] \cdot \overline{j}+ \)
\(\ +[5 \cdot 7-6 \cdot 3] \cdot \overline{k}=(-24+28) \overline{i}-(-40+24) \overline{j}+(35-18) \overline{k}= \)
\(\ =4 \cdot \overline{i}+16 \cdot \overline{j}+17 \cdot \overline{k} \)
Тогда
\(\ [\overline{a}, \overline{b}]=(4 ; 16 ; 17) \)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Как найти скалярное произведение векторов Как найти угол между векторами Как найти координаты вектора Как найти длину вектора
Узнать цену работы
Узнай цену
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
Как найти векторное произведение?
Векторное произведение векторов , заданных в
ортонормированном базисе , выражается
формулой:
В верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем их в строгом порядке – сначала координаты
вектора «вэ», затем координаты вектора «дубль-вэ».
Данный определитель всегда раскрываем по первой строке, что
продемонстрировано выше. Что получается в результате раскрытия определителя?
Задача 51
Найти векторное произведение векторов и его длину.
Решение: Задача состоит из двух частей: во-первых, необходимо найти само векторное произведение (вектор), а во-вторых – его длину.
1) Найдём векторное произведение:
В результате получен вектор или .
Выполним проверку: по определению, вектор должен быть ортогонален векторам . Ортогональность векторов, как мы помним, проверяется с
помощью скалярного произведения:
– если получилось хотя бы одно число, отличное от нуля, ищите ошибку в раскрытии определителя.
2) Вычислим длину векторного произведения. Используем простейшую формулу для вычисления длины вектора:
Ответ:
Аналогичный пример для самостоятельного решения:
Задача 52
Даны векторы . Найти и вычислить .
Будьте внимательны!
Задача 53
Даны вершины треугольника . Найти его площадь.
Решение: Алгоритм решения, думаю, многие уже представляют. Сначала найдём векторы:
Затем векторное произведение:
Вычислим его длину:
Формулы площадей параллелограмма и треугольника, само собой, остаются те же:
Ответ:
В рассмотренной задаче было не обязательно выбирать стороны ,
существует ещё два варианта.
Решение допустимо провести через векторы либо . Желающие могут
проверить, что во всех трёх случаях получится один и тот же ответ. …Почему именно эти стороны? Мысленно представьте или изобразите на черновике
этот треугольник.
Еще одна важная особенность состоит в том, что в задачах на нахождение площади фигуры порядок векторов не имеет значения. Действительно, если находить , то получим противоположно направленный вектор , но формула вычисления длины вектора всё равно «съест» эти минусы. Заметьте, что такую перестановку нельзя делать в Задачах 51-52, поскольку там требовалось найти вполне конкретный вектор.
Задача 54
Вычислить площадь параллелограмма, построенного на векторах , если
Самостоятельно. Решение и ответ в конце книги.
И в заключение параграфа обещанная задача:
Задача 55
Проверить, будут ли коллинеарны следующие векторы пространства:
а)
б)
Решение: проверка основана на упомянутом ранее факте: если векторы коллинеарны, то их векторное произведение равно нулевому вектору: .
а) Найдём векторное произведение:
Таким образом, векторы не коллинеарны.
б) Найдём векторное произведение:
Значит,
Ответ: а) не коллинеарны, б)
Вот, пожалуй, и все основные сведения о векторном произведении векторов.
1.10.1. Смешанное произведение векторов
1.9.2. Свойства векторного произведения
| Оглавление |
Автор: Aлeксaндр Eмeлин
Как рассчитать перекрестный продукт в Python
Предположим, что у нас есть вектор A с элементами (A 1 , A 2 , A 3 ) и вектор B с элементами (B 1 , B 2 , B 3 9000), мы можем вычислить перекрестное произведение этих двух векторов как:
перекрестное произведение = [(A 2 *B 3 ) – (A 3 *B 2 ), (A 34 *B 9 1
) – (А 1 *В 3 ), (А 1 *B 2 ) – (A 2 *B 1 )]
Например, предположим, что у нас есть следующие векторы:
- Вектор A: (1, 2, 3)
- Вектор B: (4, 5, 6)
Мы можем вычислить перекрестное произведение этих векторов как: В 1 ) – (А 1 *В 3 ), (А 1 *В 2 ) – (А 2 *В 1 )]
Вы можете использовать один из следующих двух методов для вычисления перекрестного произведения двух векторов в Python:
Метод 1: используйте функцию cross() из NumPy
import numpy as np #рассчитать векторное произведение векторов A и B np.cross(A, B)
cross(A, B)
Способ 2: определение собственной функции
# определить функцию для вычисления векторного произведения
определение cross_prod (а, б):
результат = [а[1]*b[2] - а[2]*b[1],
а[2]*б[0] - а[0]*б[2],
а[0]*б[1] - а[1]*б[0]]
вернуть результат
#рассчитать перекрестный продукт
cross_prod(A, B) В следующих примерах показано, как использовать каждый метод на практике.
Пример 1. Использование функции cross() из NumPyВ следующем коде показано, как использовать функцию cross() из NumPy для вычисления векторного произведения двух векторов:
импортировать numpy как np #определить векторы А = np.массив ([1, 2, 3]) B = np.массив ([4, 5, 6]) #рассчитать векторное произведение векторов A и B np.cross(A, B) [-3, 6, -3]
Перекрестное произведение получается (-3, 6, -3) .
Это соответствует перекрестному произведению, которое мы вычислили ранее вручную.
Пример 2. Определение собственной функцииВ следующем коде показано, как определить собственную функцию для вычисления векторного произведения двух векторов:
#define функция для вычисления перекрестного произведения
определение cross_prod (а, б):
результат = [а[1]*b[2] - а[2]*b[1],
а[2]*б[0] - а[0]*б[2],
а[0]*б[1] - а[1]*б[0]]
вернуть результат
#определить векторы
А = np.массив ([1, 2, 3])
B = np.массив ([4, 5, 6])
#рассчитать перекрестный продукт
cross_prod (А, Б)
[-3, 6, -3]
Перекрестное произведение получается (-3, 6, -3) .
Это соответствует перекрестному произведению, которое мы вычислили в предыдущем примере.
Дополнительные ресурсыВ следующих руководствах объясняется, как выполнять другие распространенные задачи в Python:
Как рассчитать скалярное произведение с помощью NumPy
Как нормализовать матрицу NumPy
Как добавить строку в матрицу в NumPy
Просмотреть все сообщения Zach
Нахождение векторного произведения двух векторов — Криста Кинг Математика
Построение формулы векторного произведения двух векторов
Получение векторного произведения двух векторов
???a\langle a_1,a_2,a_3\rangle???
???b\langle b_1,b_2,b_3\rangle???
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
создадим матрицу вида
???\begin{vmatrix}\bold i&\bold j&\bold k\\a_1&a_2&a_3\\b_1&b_2&b_3\end{vmatrix}???
Как всегда, мы будем использовать матрицу знаков
???\begin{vmatrix}+&-&+\\-&+&-\\+&-&+\end{vmatrix}???
, чтобы определить знаки для нашей верхней строки. Мы расширим матрицу до
???\begin{vmatrix}\bold i&\bold j&\bold k\\a_1&a_2&a_3\\b_1&b_2&b_3\end{vmatrix}=\bold i\begin{vmatrix}a_2&a_3\\b_2&b_3 \end{vmatrix}-\bold j\begin{vmatrix}a_1&a_3\\b_1&b_3\end{vmatrix}+\bold k\begin{vmatrix}a_1&a_2\\b_1&b_2\end{vmatrix}???
???=\жирный i(a_2b_3-a_3b_2)-\жирный j(a_1b_3-a_3b_1)+\жирный k(a_1b_2-a_2b_1)???
и потом взять коэффициенты на ???i???, ???j??? и ???к??? чтобы сформировать вектор векторного произведения ???c\langle{c_1},c_2,c_3\rangle???, где
???c_1=a_2b_3-a_3b_2???
???c_2=a_1b_3-a_3b_1???
???c_3=a_1b_2-a_2b_1???
Если вы помните формулу для
???\bold i(a_2b_3-a_3b_2)-\bold j(a_1b_3-a_3b_1)+\bold k(a_1b_2-a_2b_1)???
, то вы можете пропустить матрицы и сразу перейти к этому шагу.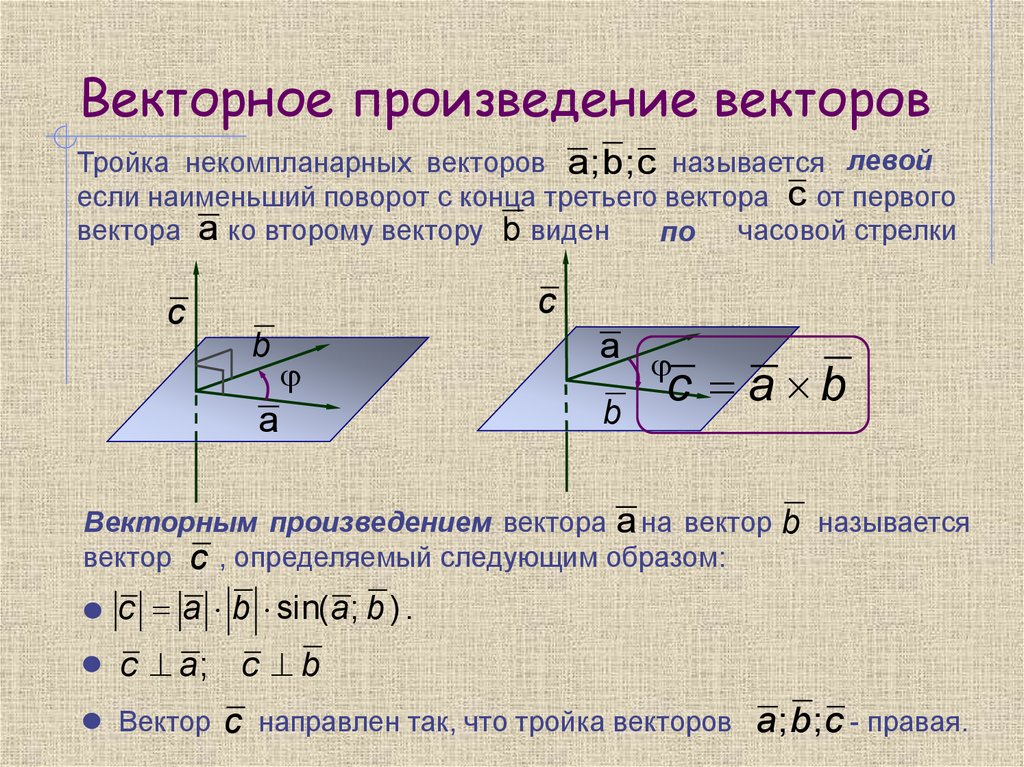
Если нет, просто используйте матричный подход.
Как найти векторное произведение двух векторов
Пройти курс
Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого. 🙂
Использование матрицы 3×3 для нахождения векторного произведения двух векторов
Пример
Найдите векторное произведение векторов.
???a\langle2,-4,1\rangle???
???b\langle-2,5,7\rangle???
Для этого примера предположим, что мы не можем вспомнить формулу для
???\bold i(a_2b_3-a_3b_2)-\bold j(a_1b_3-a_3b_1)+\bold k(a_1b_2- а_2б_1)???
и используйте матрицу.
Если вы помните формулу
, тогда вы можете пропустить матрицы и сразу перейти к этому шагу. Если нет, просто используйте матричный подход.
Подстановка значений из заданных векторов в наше ???3\times3??? матрица, получаем
???\overrightarrow{a}\times\overrightarrow{b}=\begin{vmatrix}\bold i & \bold j & \bold k \\ 2 & -4& 1 \\ -2& 5 & 7\end {vmatrix}???
???\overrightarrow{a}\times\overrightarrow{b}=\bold i\begin{vmatrix}-4 & 1 \\ 5 & 7\end{vmatrix}-\bold j\begin{vmatrix}2 & 1 \\ -2 & 7\end{vmatrix}+\bold k\begin{vmatrix}2 & -4 \\ -2 & 5\end{vmatrix}???
???\overrightarrow{a}\times\overrightarrow{b}=\bold i\left[(-4)(7)-(1)(5)\right]-\bold j\left[(2 )(7)-(1)(-2)\вправо]+\жирный k\влево[(2)(5)-(-4)(-2)\вправо]???
???\overrightarrow{a}\times\overrightarrow{b}=\bold i(-28-5)-\bold j(14+2)+\bold k(10-8)???
???\overrightarrow{a}\times\overrightarrow{b}=-33\жирный i-16\жирный j+2\жирный k???
???\overrightarrow{a}\times\overrightarrow{b}=\langle-33,-16,2\rangle???
Это векторное произведение векторов ???a??? и ???б???.
