Коды двоичных чисел
- Виды кодов отрицательных чисел
- Прямой код двоичного числа
- Обратный код двоичного числа
- Дополнительный код двоичного числа
В принципы работы вычислительных машин заложен принцип двоичного кодирования: все данные представлены в виде закодированных некоторым образом двоичных чисел. коды двоичных чисел необходимы для того, чтобы производить над данными логические и арифметические операции.
В статье «Системы счисления» мы рассматривали только положительные числа. При записи двоичных чисел со знаком в их формате необходимо предусмотреть два поля: поле, определяющее знак числа, и поле, характеризующее модуль числа. Под знак числа отводится специальный знаковый бит (двоичный разряд). Остальные разряды определяют модуль числа. Знаковый разряд приписывается слева от модуля числа, причём знаку «+» соответствует нулевое значение знакового бита, а знаку «-» — единичное.
В истории развития компьютеров использовались три основных варианта представления знаковых чисел:
- прямой код или знак и величина;
- обратный код или код с дополнением до единицы;
- дополнительный код или код с дополнением до двух.
Во всех трёх кодах положительные числа выглядят одинаково. Различия в форме записи отрицательных чисел в обратном и дополнительном кодах касаются только способа представления модуля числа, а способ кодирования и место расположения знакового бита остаются неизменными.
В системе представления в прямом коде число состоит из кода знака и модуля числа, причём обе эти части обрабатываются по отдельности.
Примеры прямого кода для правильных дробей:
Примеры прямого кода для целых чисел:
Представление чисел в прямом коде имеет существенный недостаток — формальное суммирование чисел с различающимися знаками даёт неверный результат. Пример — сложение двух чисел и . В прямом коде эти числа имеют вид: и . Очевидно, что результат должен быть равен -2, что в прямом коде может быть записано как 1.010. В то же время при непосредственном сложении получаем
,
то есть значение, существенно отличающееся от ожидаемого.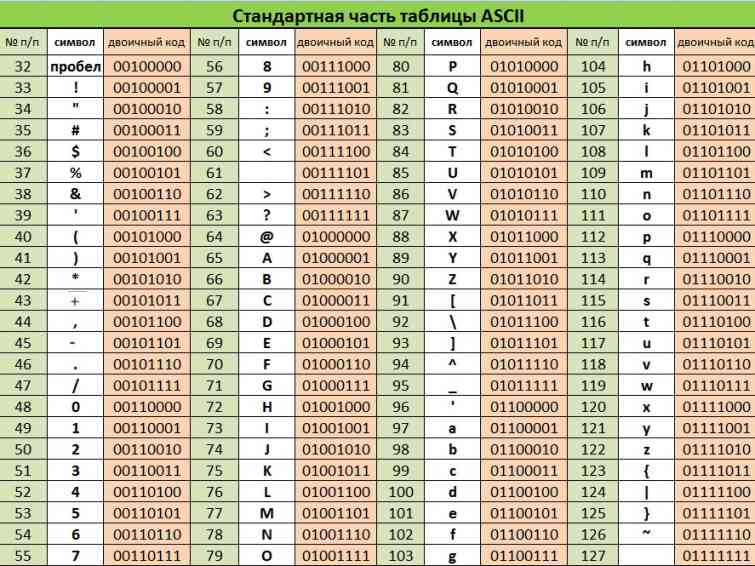
Процедура для корректного сложения чисел в прямом коде всё же существует, но она очень громоздка. Прямой код имеет ещё один недостаток — нуль имеет два различных представления, а именно и , что математически не имеет смысла.
По причине отмеченных недостатков в вычислительных машинах используется не прямой код, а обратный и дополнительный коды.
В этих системах кодирования чисел место расположения знакового разряда и способ кодирования остаются теми же, что и в прямом кодировании. Однако знаковый разряд уже не рассматривается как обособленный, а считается неотъемлемой частью числа аналогично разрядам модуля числа и совместно с ними.
Для отрицательных двоичных чисел процедура получения обратного кода следующая: в знаковой разряд записывается единица, а в цифровых разрядах прямого кода единицы заменяются нулями, а нули единицами.
Примеры обратного кода для правильных дробей:
.
Примеры обратного кода для целых чисел:
.
Как нетрудно заметить, положительные числа в прямом и обратном кодах выглядят одинаково.
Дополнительный код отрицательного двоичного числа формируется по следующему правилу: в цифровых разрядах прямого кода единицы заменить нулями, а нули — единицами, после чего к младшему разряду прибавить единицу.
Для примера рассмотрим число X, которое в прямом коде имеет вид:
.
Тогда обратный код можно записать как
.
Для получения дополнительного кода прибавим 1 к младшему разряду обратного кода:
.
Примеры дополнительного кода для правильных дробей:
.
Примеры дополнительного кода для целых чисел:
.
Положительные числа в дополнительном коде записываются так же, как и в прямом. При представлении чисел в дополнительном коде есть только одна форма записи нуля: 0.0…00, причём ноль считается положительным числом, так как его знаковый бит равен 0.
В большинстве вычислительных машин отрицательные числа представлены в дополнительном коде.
Сложение и вычитание чисел в обратном и дополнительном кодах
Вычитание производится как сложение чисел, одно из которых с отрицательным знаком.
При выполнении алгебраического сложения знаковый разряд и цифры модуля рассматриваются как
единое целое и обрабатываются совместно. Перенос из старшего (знакового) разряда в обратном и дополнительном кодах
учитывается по-разному.
В случае обратного кода единица переноса из знакового разряда прибавляется
к младшему разряду суммы. При использовании дополнительного кода единица переноса из знакового разряда отбрасывается.
Пример 1. Сложить числа и
При использовании обратного кода получим:
При использовании дополнительного кода получим:
Если знаковый разряд результата равен нулю, это означает, что получено положительное число, которое выглядит так же, как и в прямом коде. Единица в знаковом разряде означает, что результат отрицательный и его запись соответствует представлению в том коде, в котором производилась операция.
К началу страницы
НОУ ИНТУИТ | Лекция | Двоичные числа и двоичная арифметика
Аннотация: Рассматривается двоичная система счисления как частный случай позиционной системы и основные правила двоичной арифметики.
Ключевые слова: вес, целое число, запись, аналогия, выражение, логический, основание, связь, восьмеричная система счисления, обратный код, дополнительный код, прямой, система счисления, сложение, вычитание
Принцип представления чисел в позиционных системах счисления
intuit.ru/2010/edi»>Позиционной называется система счисления, в которой вес разряда числа определяется его позицией в записи числа [1].Вспомним нашу привычную десятичную систему счисления, в которой мы с детства производим все расчеты. Уже в начальной школе мы привыкли к терминам «единицы», «десятки», «сотни», «тысячи», «десятые», «сотые», «тысячные» и не задумываемся над тем, что они означают вес разряда, выраженный в виде числа, равного , где — целое число. Например, число 125, 46 можно представить в виде суммы:
сотни десятки единицы десятые доли сотые доли
Аналогично любое число в десятичной системе счисления можно представить в виде подобной суммы:
(
11. 1) |
где — количество знаков в целой части числа, — количество знаков в дробной части числа, — вес -го разряда, — весовой коэффициент для -го разряда числа. Количество возможных вариантов значения коэффициента в десятичной системе счисления равно , поскольку для записи чисел в ней используются десять знаков — арабские цифры «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9». Число является основанием системы счисления. Исторически сложилось, что десятичная система получила наибольшее распространение, хотя по этому принципу можно сделать аналогичную запись в любой другой системе счисления c любым другим основанием. В табл. 11.1 прослежива ется аналогия между позиционными системами счисления.
Основание системы счисления — это число, равное количеству знаков, которые используются в этой системе для записи чисел.
intuit.ru/2010/edi»>Для числа в системе счисления с основанием выражение (11.1) преобразуется к виду:| ( 11.2) |
| Название системы счисления | Основание системы счисления | Знаки, использующиеся для записи чисел |
|---|---|---|
| Двоичная | 2 | 0, 1 |
| Троичная | 3 | 0, 1, 2 |
| Четверичная | 4 | 0, 1, 2, 3 |
| … | … | … |
| Восьмеричная | 8 | 0, 1, 2, 3, 4, 5, 6, 7 |
| … | … | … |
| Десятичная | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| … | … | … |
| Шестнадцатеричная | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
| … | … | … |
intuit.ru/2010/edi»>С началом развития цифровой вычислительной техники большой интерес стала вызывать двоичная система, поскольку вычислительная машина любого поколения и любой степени сложности — это совокупность логических схем. Работа элементов этих схем основана на ключевом режиме работы транзистора, в котором он может быть только в двух состояниях, принимаемых за логический 0 и логическую 1.Запись двоичного числа, как будет показано ниже, как правило, довольно длинна и громоздка, поэтому для более короткой записи двоичных чисел применяются восьмеричные и шестнадцатеричные числа. Выбор именно этих систем обусловлен тем, что их основания равны целой степени числа 2. Основание восьмеричной системы , а основание шеснадцатиричной системы — это . Для записи шестнадцатеричных чисел арабских цифр не хватает, поэтому используются первые шесть заглавных букв латинского алфавита.
Итак, далее мы подробно рассмотрим именно эти позиционные системы — двоичную, восьмеричную, шестнадцатеричную и их связь с привычной нам десятичной системой счисления.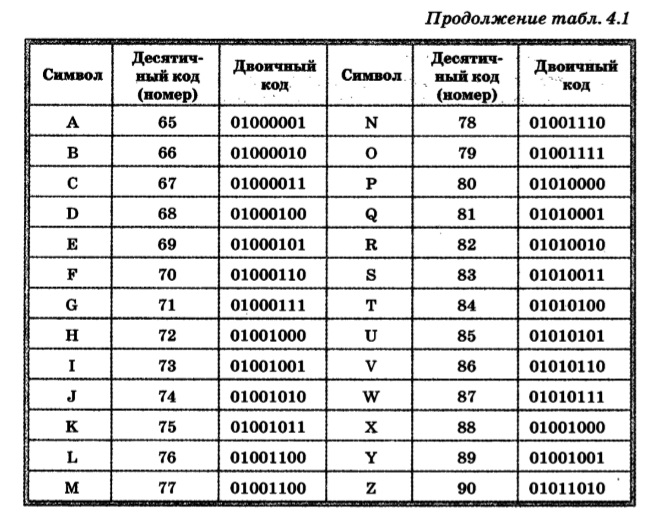
Приведем примеры записи чисел в указанных системах и найдем их десятичные эквиваленты по формуле (11.2).
Для двоичного числа:
Здесь и далее будем придерживаться следующего правила: числа в двоичной, восьмеричной и шестнадцатеричной системах записываются с указанием основания, десятичные — без этой записи.
Для восьмеричного числа:
Для шестнадцатеричного числа:
Округление относится к дробной части числа, целая часть переводится точно. Особенностью перевода из шестнадцатеричного кода в десятичный код является то, что в качестве коэффициента используется десятичный эквивалент шестнадцатеричного знака в соответствии с таблицей 11.2. Для нашего примера вместо знака » » в расчетную формулу (11.2) подставляется десятичное число .
Из рассмотренных примеров видно, что общая формула (11.2) может использоваться для перевода числа из системы счисления с любым основанием в десятичную.
Перевод чисел из одной системы счисления в другую
Перевод из десятичной системы в любую другую. Перевод целых чисел
Целое десятичное число нужно поделить на основание новой системы счисления. Остаток от этого деления является самым младшим разрядом в новой записи числа. Результат деления вновь делится на основание. Остаток от этого деления будет следующим разрядом в новой записи числа, результат деления вновь делится на основание и т.д. до тех пор, пока в результате деления получится число, меньшее по величине, чем основание новой системы. Остаток этого последнего деления будет предпоследним разрядом в новой записи числа, а результат этого последнего деления — самым старшим разрядом в новой записи числа.
intuit.ru/2010/edi»>Проверка перевода осуществляется по формуле (11.2), так, как это показано ниже на примерах.Пример. Перевести десятичное число 125 в двоичную, восьмеричную и шестнадцатеричную системы счисления. Проверить результаты по формуле (П11.2).
| a) | б) | в) |
Проверка:
- в двоичном коде: ;
- в восьмеричном коде ;
- в шестнадцатеричном коде — .
В рассмотренном примере при переводе вместо коэффициента используется его десятичный эквивалент в соответствии с таблицей 11.
2.
Перевод из двоичной системы в шестнадцатеричную (восьмеричную)
Как уже было сказано выше, шестнадцатеричный и восьмеричный коды используются для более компактной и удобной записи двоичных чисел. Так, программирование в машинных кодах осуществляется в большинстве случаев в шестнадцатеричном коде. Правила перевода для шестнадцатеричной и восьмеричной системы структурно одинаковы, отличия для восьмеричной системы отображаются в скобках.
Двоичная запись числа делится на группы по четыре ( три ) двоичных знака влево и вправо от запятой, отделяющей целые и дробные части Неполные крайние группы (если они есть) дополняются нулями до четырех ( трех ) знаков. Каждая группа заменяется одним шестнадцатеричным ( восьмеричным ) знаком в соответствии с кодом группы (табл. 11.2).
| Двоичная группа | Шестнадцатеричный знак | Десятичный эквивалент | Двоичная группа | Восьмеричный знак |
|---|---|---|---|---|
| 0000 | 0 | 0 | 000 | 0 |
| 0001 | 1 | 1 | 001 | 1 |
| 0010 | 2 | 2 | 010 | 2 |
| 0011 | 3 | 3 | 011 | 3 |
| 0100 | 4 | 4 | 100 | 4 |
| 0101 | 5 | 5 | 101 | 5 |
| 0110 | 6 | 6 | 110 | 6 |
| 0111 | 7 | 7 | 111 | 7 |
| 1000 | 8 | 8 | ||
| 1001 | 9 | 9 | ||
| 1010 | A | 10 | ||
| 1011 | B | 11 | ||
| 1100 | C | 12 | ||
| 1101 | D | 13 | ||
| 1110 | E | 14 | ||
| 1111 | F | 15 |
2.
Соответствие двоичных групп, шестнадцатеричных и восьмеричных знаков
intuit.ru/2010/edi»>Примеры:- перевод в шестнадцатеричную систему:
- перевод в восьмеричную систему:
Перевод из шестнадцатеричной (восьмеричной) системы в двоичную
Обычно программы в машинных кодах записаны в шестнадцатеричной системе счисления, реже — в восьмеричной. При необходимости отдельные числа такой программы записываются в двоичном коде, например, при рассмотрении форматов регистров, кодов операции команд и т.п. В этом случае нужен обратный перевод из шестнадцатеричной (восьмеричной) системы счисления в двоичную по следующему правилу.
Каждая цифра (без всяких сокращений!) шестнадцатеричного ( восьмеричного ) числа заменяется одной двоичной группой из четырех ( трех ) двоичных знаков (табл. 11.2).
Примеры:
- для восьмеричного числа: .
intuit.ru/2010/edi»>для шестнадцатеричного числа: ;Как показано в примерах, крайние нули слева и справа при желании можно не писать, но такое сокращение делается уже после перевода в двоичную систему.
Бесплатный учебник по двоичным кодам — Code Conquest
Двоичный код — это система представления чисел, букв, команд, изображений и звуков. Удивительно, но для этого он использует только два типа информации — 1 и 0. Строки из 1 и 0, составляющие двоичный код, могут показаться случайными, но, конечно же, это не так.
Двоичный код лежит в основе всего, что происходит внутри компьютера, и все же это то, что не рассматривается в большинстве руководств по программированию.
Вот объяснение основ двоичного кода. В конце у вас должно быть общее представление о том, что означают все эти 1 и 0.
Двоичные числа
Двоичная система счисления — это система с основанием два, что означает, что в ней используются две различные цифры — 0 и 1.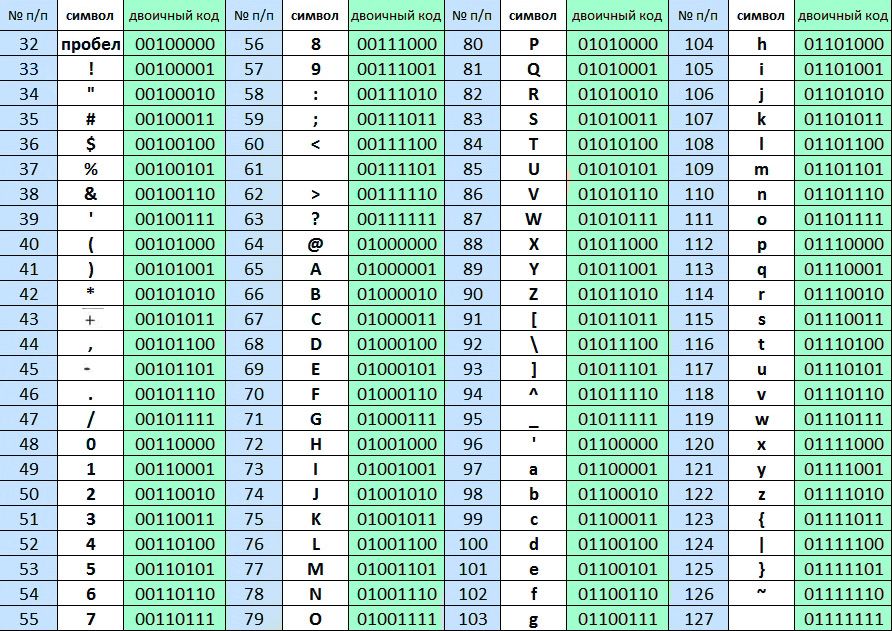
Десятичная система счисления, с которой мы все знакомы, — это система с основанием десять, что означает, что в ней используются десять различных цифр. цифры – 0 и 1, а также 2, 3, 4, 5, 6, 7, 8 и 9.
При счете в десятичной системе, когда все десять цифр исчерпаны, следующее число представляется как «10». В двоичной системе все точно так же. После 0 и 1 идет 10. На самом деле, вот первые 15 чисел, выраженные в двоичном виде:
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111.Как видите, в двоичной системе счет ведется в логическом порядке, и всякий раз, когда достигается число, состоящее исключительно из единиц, добавляется дополнительная цифра. Это точно то же самое, что происходит в десятичной системе, когда достигается число, полностью состоящее из девяток.
Как видите, существует 16 различных чисел, которые могут быть представлены 4 или менее цифрами (от 1 до 15, а также 0). Это можно рассчитать, потому что 16 = 2 4 .
Однако двоичные числа в вычислительном контексте всегда представлены 8 цифрами или менее — 8 двоичных цифр составляют один байт. Общее количество различных чисел, которые могут быть представлены 8 цифрами, равно 2 8 = 256. От 1 до 255, а также от 0,
Таким образом, 255 в двоичном виде равно 11111111.
Шестнадцатеричная система
Шестнадцатеричная система, или шестнадцатеричная система, тесно связанная с двоичной системой. Вот почему.
Чтобы представить число 255 в двоичном формате, требуется 8 цифр. Это много, учитывая, что в десятичной системе для представления числа 255 требуется всего 3 цифры. Однако шестнадцатеричная система делает еще один шаг вперед и позволяет представить число 255 только двумя цифрами.
Это потому, что шестнадцатеричная система с основанием шестнадцать, и 16 2 = 256. Другими словами, наибольшее число, которое может быть представлено двумя цифрами в шестнадцатеричном формате, равно 255. Другими словами, любое 8-значное двоичное число байт может быть представлен как двузначный шестнадцатеричный байт.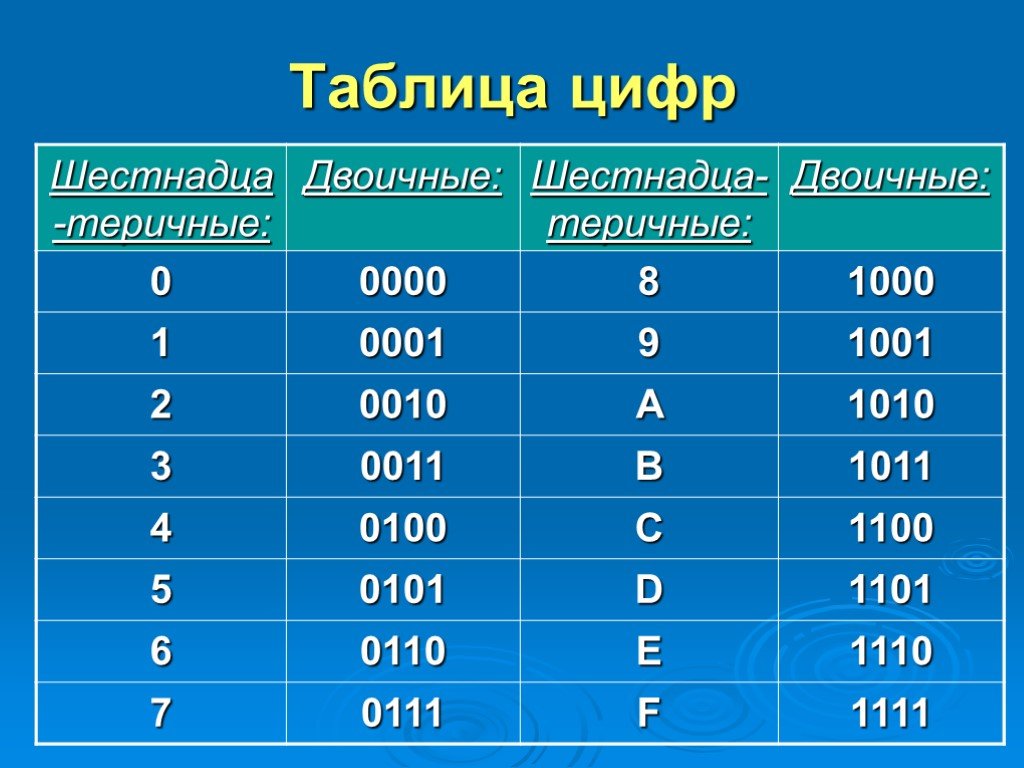
Это отлично подходит как для компьютеров, так и для людей. Для компьютеров это экономит место, а для людей улучшает читаемость.
Если вам интересно, 16 «цифр», используемых в шестнадцатеричной системе, — это числа от 0 до 9.а затем буквы от A до F. F — шестнадцатеричный код числа 15, а FF — шестнадцатеричный код числа 255.
| Десятичное число | Двоичный | Шестнадцатеричный |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | А |
| 11 | 1011 | Б |
| 12 | 1100 | С |
| 13 | 1101 | Д |
| 14 | 1110 | Е |
| 15 | 1111 | Ф |
| 16 | 10000 | 10 |
Двоичные буквы
Двоичный код, представляющий числа, довольно однообразен — есть только один способ сделать это.
Однако существует несколько способов представления букв и символов в двоичном коде. Эти методы называются кодировками.
Например, кодировка ASCII присваивает уникальные двоичные байты 128 различным символам. Это позволяет кодировать любую строку текста. Это строка «Hello World», кодируемая в ASCII:
01001000 01100101 01101100 01101100 01101111 00100000 01010111 01101111 01110010 01101100 01100100
Каждая бата представляет собой букву (за исключением того, что представляет пространство между словами). Пробелы между байтами нужны только для того, чтобы сделать двоичный файл более читабельным для нас. Компьютеры их не читают.
Другие применения двоичного кода
Помимо чисел и букв, двоичный код может представлять команды, изображения и звуки, но это выходит за рамки данного руководства. Удивительно, как всего две цифры могут так много сделать.
Раскрытие существенной связи : Некоторые ссылки в посте выше являются «партнерскими ссылками».
Это означает, что если вы нажмете на ссылку и купите товар, я получу партнерскую комиссию. Несмотря на это, я рекомендую только те продукты или услуги, которыми пользуюсь лично и считаю, что они принесут пользу моим читателям.
Двоичные коды
FutureLearn использует куки-файлы для повышения удобства пользования веб-сайтом. Все файлы cookie, кроме строго необходимых, в настоящее время отключены для этого браузера. Включите JavaScript, чтобы применить настройки файлов cookie для всех необязательных файлов cookie. Вы можете ознакомиться с политикой FutureLearn в отношении файлов cookie здесь.
В этой статье объясняются двоичные коды
© Институт научного образования Дэвидсона, образовательное подразделение Института науки Вейцмана
В наше время, когда произошла «цифровая революция», возникла потребность в новой системе кодирования, которая подходила бы для компьютеров и других электрических устройств.
-цифровые устройства. Была выбрана двоичная система, в которой все числа закодированы только цифрами 0 и 1. Двоичные символы очень важны в компьютерном мире. Цифры 0 и 1 называются битами. Они переводятся в потоки электрического тока — бит 1 символизирует факт наличия потока, а бит 0 символизирует отсутствие потока внутри компьютера. Последовательность этих электрических символов является «языком» компьютера, и, используя его, компьютер может выполнять инструкции, которые мы ему даем.
Двоичная система счисления
Сегодня мы записываем числа как «строки», состоящие из цифр 1,2,3,4,5,6,7,8,9,0. Каждая цифра принимает различные числовые значения в зависимости от ее положения. В числе 101, например, числовое значение 1 в левой части равно 100, а числовое значение 1 в правой части равно 1. С математической точки зрения используемая нами позиционная десятичная запись определяет значение числа в соответствии со степенями десяти. . Цифры, записанные в колонке единиц, самая правая цифра, сохраняют свое числовое значение, потому что они умножаются на 1, что равно десяти в степени нуля (10 0 ).
Числовое значение цифр в следующем столбце слева, столбце «десятки», представляет собой цифру, умноженную на десять в степени один (10 1 ), т. е. 10 и так далее. Итак, числовое значение строки цифр: 973 на самом деле:
9 х 10 2 + 7 х 10 1 + 3 х 10 0 = 9 х 100 + 7 х 10 + 3 х 1 = 973 .
В двоичной системе расположение цифр определяет их значение в соответствии со степенью двойки. Двоичная система представляет собой систему с основанием 2, в которой используются только цифры 0 и 1. Эти цифры умножаются на 2 0 =1 когда в крайнем правом столбце, на 2 1 =2, когда в следующем столбце слева, на 2 2 =4, когда в следующем столбце слева и так далее .
Вот двоичная таблица для первых 32 чисел:
| Десятичный | Двоичный |
|---|---|
| 0 | 00000 |
| 1 | 00001 |
| 2 | 00010 |
| 3 | 00011 |
| 4 | 00100 |
| 5 | 00101 |
| 6 | 00110 |
| 7 | 00111 |
| 8 | 01000 |
| 9 | 01001 |
| 10 | 01010 |
| 11 | 01011 |
| 12 | 01100 |
| 13 | 01101 |
| 14 | 01110 |
| 15 | 01111 |
| 16 | 10000 |
| 17 | 10001 |
| 18 | 10010 |
| 19 | 10011 |
| 20 | 10100 |
| 21 | 10101 |
| 22 | 10110 |
| 23 | 10111 |
| 24 | 11000 |
| 25 | 11001 |
| 26 | 11010 |
| 27 | 11011 |
| 28 | 11100 |
| 29 | 11101 |
| 30 | 11110 |
| 31 | 11111 |
Преобразование двоичного кода в десятичный и наоборот
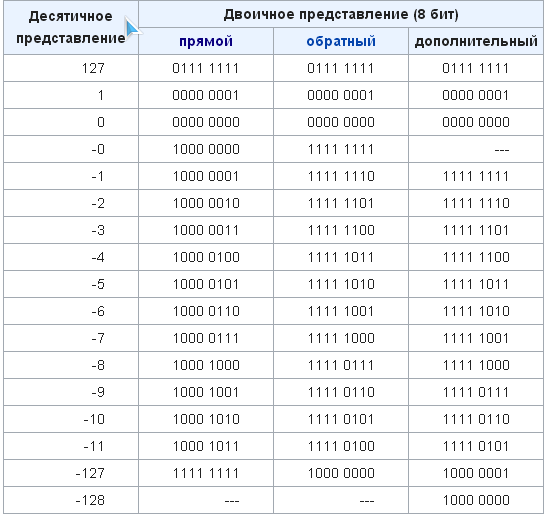
Чтобы перевести двоичное число в десятичное, умножьте крайнюю правую цифру на 1 (2 0 ), вторую цифру слева на 2 (2 1 ), третью цифру слева на 4 (2 2 ), четвертая цифра на 8 (2 3 ) и так далее.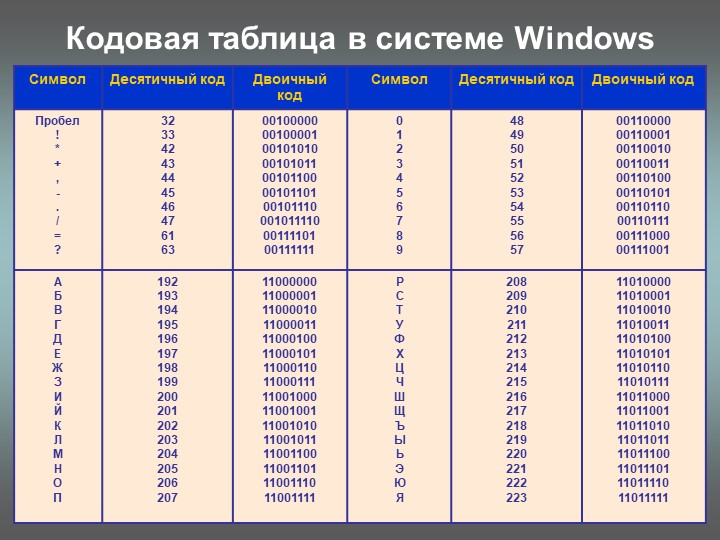
Пример: двоичное число 1011 является десятичным числом 11:
1 x 2 3 + 0 x 2 2 + 1 x 2 1 + 1 x 2 0 = 1 x 8 + 0 x 4 + 1 х 2 + 1 х 1 = 11
Существует несколько способов преобразования десятичного числа в двоичное. Самый простой способ — найти ближайшую степень двойки, написать 1 в соответствующей позиции и вычесть из исходного числа. Продолжайте делать это, пока не достигнете нуля. Пример: число 36 в двоичном виде: 100100: Ближайшая степень числа 2 к 36 равна 32, что равно 2 9.0017 5 , поэтому мы знаем, что двоичное число будет состоять из 6 цифр с 1 в шестом столбце справа: 1——.
36 – 32 = 4, что равно 2 2 , поэтому следующий бит «1» будет располагаться в третьем столбце справа: 1001–.
4 – 4 = 0, значит мы закончили и остальные биты равны нулю: 100100.
© Институт научного образования Дэвидсона, образовательное подразделение Научного института Вейцмана
Эта статья из бесплатного онлайн
Математические головоломки: криптарифмы, символы и секретные коды
Создано
Присоединяйся сейчас
Наша цель — изменить доступ к образованию.
