Моменты инерции ⚡ Моменты инерции простейших фигур
Дата публикации:
02 Фев 2022г
Автор:
Александр Заболотный
Меня часто спрашивают: «…а что такое моменты инерции в сопротивлении материалов и зачем они вообще?» Об этом в сегодняшней теме
Моменты инерции сечения из простых фигур
Начнем с моментов инерции простых фигур и на их примере выясним для сложных фигур и составных сечений из стандартных профилей.
Начать объяснение о том, что такое моменты инерции нужно с того, что спросить, а что такое площадь?
Обычная площадь квартиры, огорода сечения стержня? Зачем она и почему?
Так вот площадь это характеристика которую придумали и вывели для разных фигур, чтобы была возможность сравнивать земельные наделы. Не всегда они были прямоугольные или квадратные. А сравнить кто сколько получил в надел было нужно. Вот и вывели такую закономерность для прямоугольника, что если перемножить стороны — получим величину, которую можно будет сравнить с перемноженной высотой на основание деленное пополам для треугольника или для круга Пи умножить на эр в квадрате )). Т.е. площади простых фигур
Т.е. площади простых фигур
Что касается моментов инерции в сопротивлении материалов, то тут они появились, когда стало понятно, что есть какая то геометрически измеримая величина для разных форм сечения, которая позволит сравнить сопротивляемость этих сечений изгибу.
Момент инерции это мера сопротивляемости сечения балки изгибу. Чем больше момент инерции тем труднее балку изогнуть. Это очень упрощенное определение, но отображающее суть момента инерции.
Проще говоря бревно, которое выполняет роль балки и изгибается может иметь форму прямоугольника, квадрата или круга, а нам нужно сравнить их сопротивляемость изгибу. Вот для этих целей выводили формулу напряжений и оказалось, что в числителе оказался изгибающий момент, а в знаменателе момент инерции:
Деформированное и не деформированное состояния балки при расчете на изгибна балке изображены главные центральные оси z yпрогибы для таких балок будут разными относительно осей z и y, т.к. моменты инерции будут разные.
Вывод моментов инерции для простых фигур
Так вот ниже я приведу видео уроки, плейлист, в котором один за одним выведены моменты инерции для простых фигур, а именно для прямоугольника, треугольника и круга. А затем приводится стандартный расчет моментов инерции для более сложной фигуры, которая состоит из нескольких простых. Всегда сложную фигуру можно разбить на несколько простых. Исходя из этого расчет и ведется.
В чем измеряется момент инерции плоской фигуры
Моменты инерции измеряются в единицах длины в 4 степени, т.е. см⁴ или м⁴. Чаще всего используется см⁴, т.к. такие единицы измерения приведены в сортаменте прокатной стали.
Что такое момент инерции вообще
Момент инерции, это величина, которая показывает сопротивляемость сечения изгибу. На примере линейки хорошо понятно что изгиб в одной плоскости и изгиб в другой плоскости будут сильно отличаться, хотя площадь сечения не меняется. Вот это и было выведено в формуле для напряжений и для прогибов. Что величина, которая сопротивляется изгибающему моменту есть интеграл до координаты центра тяжести площадки в квадрате на площадь элементарной площадки.
Вот это и было выведено в формуле для напряжений и для прогибов. Что величина, которая сопротивляется изгибающему моменту есть интеграл до координаты центра тяжести площадки в квадрате на площадь элементарной площадки.
Что такое центральные оси
Центральными осями называют оси, которые проходят через центр тяжести сечения
Что такое главные оси
Главные оси располагаются в сечении таким образом, что центробежный момент относительно них равен нулю. Т.е. это максимальный и минимальный осевые моменты инерции
Главные центральные оси, что это такое
Оси, которые проходят через центр тяжести сечения и центробежный момент инерции относительно них равен нулю. При этом данные осевые моменты инерции являются экстремальными, т.е. имеют максимальное и минимальное значение. Именно относительно этих осей ведут расчет и к ним приводят нагрузки. Т.е. если какое нибудь внешнее усилие проходит в стороне от главных центральных осей. Это усилие переносят соблюдая правила переноса к главным центральным осям. Только после этого рассматривают действие сил и находят внутренние усилия относительно главных центральных осей инерции.
Т.е. если какое нибудь внешнее усилие проходит в стороне от главных центральных осей. Это усилие переносят соблюдая правила переноса к главным центральным осям. Только после этого рассматривают действие сил и находят внутренние усилия относительно главных центральных осей инерции.
Что такое центробежный момент инерции
При вычислении моментов инерции осевых, при переходе от одних осей к другим появляется центробежный момент инерции, как составляющая пары осевых моментов инерции. И только для главных осей центробежные моменты инерции равны нулю. Именно эти оси мы и отыскиваем в наших расчетах. Поэтому мы ищем величину центробежного момента инерции для не главных осей и из свойства, что главные центральные оси это такие оси, относительно которых центробежный момент инерции равен нулю, находим положение главных центральных осей.
Моменты инерции для прямоугольника
моменты инерции для прямоугольника для главных центральных осей равны, формуламоменты инерции для прямоугольника для осей проходящих через основные размеры равны, формулаМоменты инерции для треугольника
youtube.com/embed/_pixohVoc-4″ frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Моменты инерции треугольника относительно произвольых осейМоменты инерции треугольника относительно центральных осей
Примеры расчетов моментов инерции для сечений
Ниже приводятся примеры расчетов моментов инерции относительно главных центральных осей, объяснение, что такое центробежный момент инерции и почему оси называются главными центральными для примеров:
- простейшие фигуры — прямоугольник, треугольник
- составные сечения из простейших треугольника и прямоугольника
- составные из прокатных профилей
Пример расчета моментов инерции относительно главных центральных осей для простейших фигур
Подробно объясняется как найти центробежный момент инерции, как найти осевые моменты инерции, как относительно центральных и как относительно главных осей для простых фигур.
Пример расчета моментов инерции для сечения состоящего из прямоугольника и треугольника
Сечения балок может быть составным, т.е. таким, которое складывается из нескольких фигур. В примере, в видеоуроке ниже рассказыватся как найти моменты инерции относительно главных центральных осей для такого сечения балки
Расчет моментов инерции сечения составного из стандартных прокатных профилей
В видеоуроке ниже разбирается порядок расчета моментов инерции относительно главных центральных осей для сечения составленого из трех прокатных профилей уголков
|
Random converter |
Конвертер момента инерцииКонвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления.  Исходная величина килограмм кв. метркилограмм кв. сантиметркилограмм кв. миллиметрграмм кв. сантиметрграмм кв. миллиметркилограмм-сила метр кв. секундаунция кв. дюймунция-сила дюйм кв. секундафунт кв. футфунт-сила фут кв. секундафунт кв. дюймфунт-сила дюйм кв. секундаслаг кв. фут Преобразованная величина килограмм кв. метркилограмм кв. сантиметркилограмм кв. Угловая скоростьЗнаете ли вы, что у спутников есть «загробная жизнь» и что их отправляют на орбиту захоронения по окончании эксплуатации? Подробнее… Маховик сделан так, чтобы его высокий момент инерции оказывал сопротивление изменениям в скорости его вращения. Это позволяет хранить в нем энергию, которая накапливается в нем в результате вращения. Общие сведения В спорте Высокой момент инерции Низкий момент инерции Общие сведенияМомент инерции — это свойство тела противостоять изменению скорости вращения. Чем момент инерции выше — тем больше это противостояние. Момент инерции часто сравнивают с понятием массы для прямолинейного движения, так как масса определяет, насколько тело сопротивляется такому движению. Распределение массы по объему тела не влияет на прямолинейное движение, но имеет большое значение при вращении, так как от него зависит момент инерции. В центробежном регуляторе скорость вращения двигателя контролируется с помощью момента инерции: с достижением определенной скорости количество топлива, подаваемого в двигатель, уменьшается. Двигатель вращает два шара в верней части устройства, и, при увеличении скорости они расходятся, увеличивая момент инерции всего устройства. Когда момент инерции достигает определенной величины, это устройство ограничивает поступление топлива. Определить момент инерции для тел простой геометрической формы и с постоянной плотностью можно, используя общепринятые формулы. Для тел более сложных форм используют математический анализ. В зависимости от того, как вес распределен внутри тел, два тела с одинаковой массой могут иметь разный момент инерции. Например, момент инерции I для однородного шара, с одинаковой по всему объему плотностью, находят по формуле: I = 2mr²/5 Тут m — это масса шара, а r — его радиус. Если взять два шара одинаковой массы, с радиусом первого вдвое больше радиуса второго, то момент инерции большего шара будет в 2²=4 раза больше первого. I = mr²/3 в случае, если цилиндр вращается вокруг его основания. Момент инерции будет равен: I = mr²/12 если цилиндр вращается вокруг оси, проходящей через его центр по длине. При таком вращении цилиндр становится похожим на пропеллер. Вторую формулу легко получить из первой: радиус от центра вращения до наиболее удаленной точки равен половине длины цилиндра, но так как этот радиус возведен в квадрат, то 1/2 L (или r) становится 1/4 L² (или r²). В любом случае, глядя на эти формулы, легко заметить, что форма тела и даже просто смещение центра вращения существенно влияют на момент инерции. В спортеЧасто, уменьшив или увеличив момент инерции, можно улучшить показатели в спорте. Высокий момент инерции поддерживает постоянную скорость вращения или помогает сохранить равновесие, даже если скорость равна нулю. Если скорость равна нулю, то человек или предмет просто не вращается. Малый момент инерции, наоборот, позволяет легко изменить скорость вращения. То есть, уменьшение момента инерции уменьшает количество энергии, необходимой для того, чтобы увеличить или уменьшить скорость вращения. Момент инерции настолько важен в спорте, что некоторые исследователи считают, что для упражнений, в которых используется несколько снарядов или спортивного инвентаря одинакового веса, но разных конфигураций, следует подбирать снаряды и инвентарь с близким моментом инерции. Это практикуется, например, в гольфе: некоторые считают, что если использовать клюшки с одинаковым моментом инерции, то это поможет спортсмену улучшить свинг, то есть основной удар по мячу. Высокой момент инерцииСерфингист вытянул руки, чтобы увеличить момент инерции и тем самым улучшить равновесие на доске. Оаху, Гавайи. В некоторых случаях, необходимо чтобы вращательное движение продолжалось и не останавливалось, несмотря на то, что силы, действующие на тело, противостоят этому движению. К примеру, гимнастам, танцорам, ныряльщикам или фигуристам, которые крутятся или переворачиваются на льду или в воздухе, необходимо продолжать это движение в течение определенного времени. Для этого они могут увеличить момент инерции, увеличив вес тела. Вместо массы можно также увеличить радиус от центра вращения до точки, наиболее от него удаленной. Для этого можно вытянуть руки или ноги в стороны от туловища, или взять в руки длинный шест. Спортсмену, например ныряльщику, может понадобиться увеличить момент инерции перед тем, как он входит в воду. Когда он крутится в воздухе и принимает правильное направление, он распрямляется, чтобы остановить вращение, и в то же время увеличить радиус и, соответственно, момент инерции. Таким образом, его нулевую скорость вращения труднее изменить, и спортсмен входит в воду под правильным углом. Вес распределен по длинной штанге, чтобы улучшить равновесие и обеспечить безопасность спортсмена. Несмотря на это, лучше всего заниматься тяжелой атлетикой с товарищем, который в случае необходимости может подстраховать. Как мы только что увидели, чем выше момент инерции — тем легче поддерживать постоянную скорость вращения, даже если она равна нулю, то есть тело находится в состоянии покоя. Это бывает нужно как для того, чтобы поддержать вращение, как и для поддержания равновесия в отсутствии вращения. Например, чтобы не упасть, акробаты, которые ходят по канату, часто держат в руках длинный шест, увеличивая тем самым радиус от центра вращения до самой отдаленной от него точки. Момент инерции часто используют и в тяжелой атлетике. Вес дисков распределяется по штанге, чтобы обеспечить безопасность во время упражнений по поднятию штанги. У гирь очень высокий момент инерции. Упражняться с ними нужно очень осторожно, так как легко потерять над ними контроль. Гири желательно двигать плавно, и держать их как можно дальше от тела, чтобы не получить травму в результате случайного удара гирей. Для обеспечения безопасности во время тренировок с гирями обычно смещают центр вращения как можно дальше от центра гири. Чаще всего новый центр вращения — на теле спортсмена, например в районе плеча. То есть, обычно гирю не вращают с помощью кисти руки или вокруг локтевого сустава. Ее, наоборот, качают из стороны в сторону или вверх и вниз вокруг туловища, иначе работа с ней опасна. Низкий момент инерцииФигуристка прижимает руки к туловищу, чтобы увеличить момент инерции. При этом ее скорость вращения увеличивается. В спорте нередко бывает нужно увеличить или уменьшить скорость вращения, используя как можно меньше энергии. В некоторых случаях важен общий момент инерции тела спортсмена. В этой ситуации спортсмены прижимают руки и ноги к туловищу, чтобы уменьшить момент инерции во время вращения. Это позволяет им ускорить движение и вращаться быстрее. Такой прием используют в фигурном катании, нырянии, гимнастике и в танцах. Чтобы испытать на себе этот эффект не обязательно заниматься одним из этих видов спорта, достаточно просто сесть в офисное кресло, раскрутить сидение, выставив руки и ноги, а потом прижать руки и ноги к корпусу. При этом скорость вращения увеличится. Момент инерции очень важен во время вращения спортивного инвентаря. Чем ниже момент инерции инвентаря, тем быстрее можно его вращать. Это дает спортсменам дополнительное время, чтобы следить за противниками, и часто это помогает сделать более точный размах или удар. В других видах спорта вращается не все тело спортсмена, а только его часть, например рука битой или клюшкой для гольфа. Следует помнить, что при одинаковой скорости вращения биты, та, у которой более высокий момент инерции передаст при ударе большую скорость мячу, хоть и вращать эту биту нужно с затратой большего количества энергии. На клюшках для гольфа и теннисных ракетках обычно указана информация об их моменте инерции, а на бейсбольных битах ее чаще всего не пишут. Почему это так — неизвестно, хотя вероятно это связано с маркетингом в спорте. В любом случае, если информации о моменте инерции спортивного снаряда нет, то стоит перед покупкой хорошо испробовать этот снаряд, и сравнить с несколькими другими, чтобы определить, подходит ли он вам для ваших целей. Литература Автор статьи: Kateryna Yuri Вас могут заинтересовать и другие конвертеры из группы «Механика»:Плоский угол Конвертер угловой скорости и частоты вращения Конвертер ускорения Конвертер углового ускорения Конвертер площади Конвертер плотности Конвертер энергии и работы Конвертер силы Конвертер длины и расстояния Конвертер массы Конвертер момента силы Конвертер давления, механического напряжения, модуля Юнга Конвертер удельного объема Конвертер вращающего момента Конвертер объема и единиц измерения в кулинарных рецептах Конвертер мер объема сыпучих продуктов и продуктов питания Конвертер линейной скорости Компактный калькулятор Полный калькулятор Определения единиц Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. |
Момент инерции: площадь или масса?
Момент инерции является важным параметром при расчете и выборе линейной системы. Но очень важно знать, какой тип инерции — плоский момент инерции или массовый момент инерции — задан и как он влияет на производительность системы.
Плоский момент инерции
Плоский момент инерции (также называемый вторым моментом площади или моментом инерции площади) определяет, как точки площади распределяются относительно произвольной плоскости и, следовательно, ее сопротивление изгибу. Терминология варьируется, а иногда и частично совпадает, для плоского момента и массового момента инерции. Если непонятно, какой тип момента указан, просто посмотрите на единицы термина. Плоский момент инерции выражается как длина в четвертой степени (фут 4 , м 4 ).
I = ∫∫ x 2 D A
I = Планарный момент INERTIA
X = Расстояние до ссылки.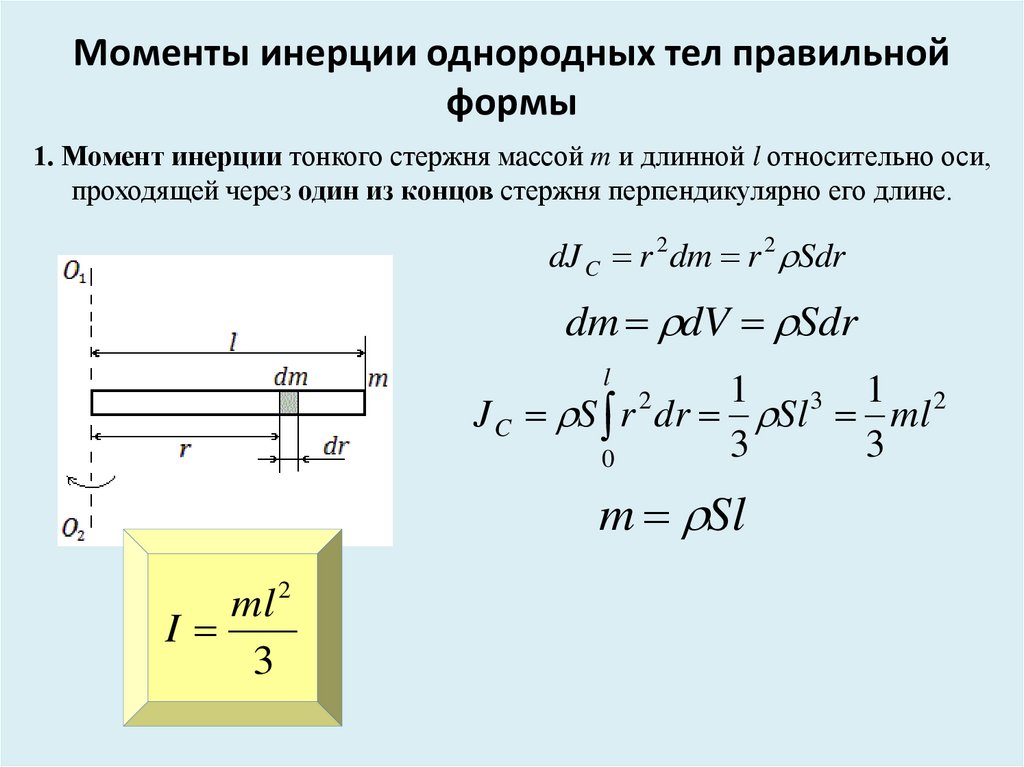 площадь
площадь
Второй момент площади может быть плоским или полярным. Полярный момент инерции описывает сопротивление объекта крутящему моменту или кручению. Уравнение такое же, как и у плоского момента инерции, но базовым расстоянием становится расстояние до оси, а не до плоскости.
I = ∫∫ r 2 D A
I = Полярный момент инерции
R = расстояние до Axis
9002 R = расстояние. площади
Плоский момент инерции поперечного сечения балки является важным фактором при расчете прогиба балки, а также используется для расчета напряжения, вызванного моментом на балке. В линейных системах модели отклонения балки используются для определения отклонения консольных осей в многоосевых системах. Неподдерживаемые валы также анализируются с использованием расчетов прогиба балки.
Консольный луч с концентрированной нагрузкой на свободном конце
P = нагрузка
L = длина луча (расстояние до нагрузки)
E = модуль эластичности
I = Planarar момент инерции
Момент инерции массы
Момент инерции массы (также называемый вторым моментом массы, угловой массой или моментом инерции вращения) определяет крутящий момент, необходимый для получения желаемого углового ускорения относительно оси вращения, и зависит от распределение массы объекта (т. е. его формы) вокруг оси. Оно имеет такое же отношение к угловому ускорению, как масса к линейному ускорению. Массовый момент инерции, как и плоский момент, обычно обозначается буквой «I», но, в отличие от плоского момента, единицами для массового момента инерции являются квадрат массы-расстояния (фунт-фут 2 , кгм 2 ).
е. его формы) вокруг оси. Оно имеет такое же отношение к угловому ускорению, как масса к линейному ускорению. Массовый момент инерции, как и плоский момент, обычно обозначается буквой «I», но, в отличие от плоского момента, единицами для массового момента инерции являются квадрат массы-расстояния (фунт-фут 2 , кгм 2 ).
Массовый момент уравнения инерции для точечной массы составляет просто:
I = MR 2
I = массовый момент инерции
M = точка масса 9001
M = точка 9001
M = точка 9000 9001
M = точка 9000
расстояние до оси вращения
Для твердого тела момент инерции массы рассчитывается путем интегрирования момента массы каждого элемента массы тела:
I = ∫ r 2 D M
I = Масса -момент инерции
D M = элемент массы
R = Расстояние до аксис из ряд
R = расстояние до Axis of Rettation
R = расстояние. , наиболее важное использование момента инерции масс, вероятно, связано с выбором двигателя, где соотношение между инерцией нагрузки и инерцией двигателя является критическим фактором производительности.
, наиболее важное использование момента инерции масс, вероятно, связано с выбором двигателя, где соотношение между инерцией нагрузки и инерцией двигателя является критическим фактором производительности.
Источник изображения: wikipedia.org
Советы по линейному движению
Рубрики: Советы по линейному движению, управление движением • управление двигателем
Момент инерции — Physics Stack Exchange
Во-первых, следует помнить, что момент сопротивление тела вращению. Это вращательный аналог массы в F=ma. Больший момент требует большей силы для достижения той же скорости вращения. Момент инерции массы, м 92.
Возьмите пластиковую линейку для тетрадей с отверстиями, предназначенную для хранения в папке на кольцах. Вставьте карандаш в центральное отверстие и вращайте его, как пропеллер вертолета (горизонтальная плоскость). Он имеет момент инерции стержня, вращающегося вокруг своего центра масс. Теперь поместите карандаш в отверстие рядом с концом линейки и вращайте его. На моей линейке ось вращения находится на расстоянии 5,5 дюймов (14 см) от центра масс. Момент инерции разный. На самом деле оно больше, как вы можете почувствовать по большей силе, необходимой для вращения линейки. Повторите опыт на разных расстояниях, и вы обнаружите, что момент инерции больше на больших расстояниях от центра масс.
Теперь поместите карандаш в отверстие рядом с концом линейки и вращайте его. На моей линейке ось вращения находится на расстоянии 5,5 дюймов (14 см) от центра масс. Момент инерции разный. На самом деле оно больше, как вы можете почувствовать по большей силе, необходимой для вращения линейки. Повторите опыт на разных расстояниях, и вы обнаружите, что момент инерции больше на больших расстояниях от центра масс.
Что происходит? Вращающаяся линейка на самом деле представляет собой серию частиц, вращающихся на разных расстояниях от оси вращения (с разными радиусами). Каждая частица имеет момент инерции, зависящий от ее массы и радиуса. Для упрощения будем считать, что все частицы одинаковы и имеют одинаковую массу. Частицы, близкие к оси, имеют меньшие радиусы и меньшие моменты инерции, тогда как частицы с большими радиусами имеют большие моменты.
Момент инерции линейки представляет собой сумму всех этих отдельных моментов. Мы могли бы разделить линейку на тысячу частиц и вычислить момент, складывая отдельные моменты вместе. Мы могли бы разделить его на миллион частей и получить лучший результат. Миллиард будет еще лучше. Непрерывная сумма даст нам точное значение, что мы и делаем, когда выполняем интегрирование в исчислении. Интеграл — это непрерывная сумма, поэтому знак интеграла выглядит как вытянутая буква S? 92/100 и т. д.
Мы могли бы разделить его на миллион частей и получить лучший результат. Миллиард будет еще лучше. Непрерывная сумма даст нам точное значение, что мы и делаем, когда выполняем интегрирование в исчислении. Интеграл — это непрерывная сумма, поэтому знак интеграла выглядит как вытянутая буква S? 92/100 и т. д.
Так при чем здесь центр масс? Центр масс тела является точкой равновесия. Вы можете подвесить тело за его центр масс, и оно будет находиться в равновесии, т. е. не будет вращаться под действием силы тяжести. Поскольку линейка однородна, она балансирует в своем физическом центре, 6 дюймов. Это центр масс. Это точка, вокруг которой тело имеет вращательное равновесие, это красивые слова, означающие, что линейка будет балансировать в этой точке. Кроме того, линейка будет вращаться вокруг центра масс, если ее бросить. Более того, это центр масс вращающегося снаряда, движущегося по параболической траектории. Мы обращаемся с телом так, как будто вся его масса сосредоточена в центре масс.
Время эксперимента
1) Вырежьте кусок толстого картона какой-нибудь необычной формы. Привяжите несколько скрепок к короткой веревке. Проткните картон булавкой рядом с любым краем, затем привяжите к булавке нить. Держите булавку и позвольте веревке и картону висеть под ней. Возьмите ручку или карандаш и обведите линию нити на картоне. Повторите весь процесс еще два раза с двух разных точек на картоне. Три линии должны пересекаться в одной точке, центре масс.
2) Отметьте эту точку большой черной точкой. Нарисуйте вокруг него несколько концентрических кругов, монеты отлично справляются со своей задачей. Держите картон в любой точке так, чтобы плоская сторона была вертикальной, и подбрасывайте его вверх, как подбрасывая фрисби на ребро вертикально. Убедитесь, что он вращается. Вы должны увидеть, как картон вращается вокруг центра масс.



 миллиметрграмм кв. сантиметрграмм кв. миллиметркилограмм-сила метр кв. секундаунция кв. дюймунция-сила дюйм кв. секундафунт кв. футфунт-сила фут кв. секундафунт кв. дюймфунт-сила дюйм кв. секундаслаг кв. фут
миллиметрграмм кв. сантиметрграмм кв. миллиметркилограмм-сила метр кв. секундаунция кв. дюймунция-сила дюйм кв. секундафунт кв. футфунт-сила фут кв. секундафунт кв. дюймфунт-сила дюйм кв. секундаслаг кв. фут
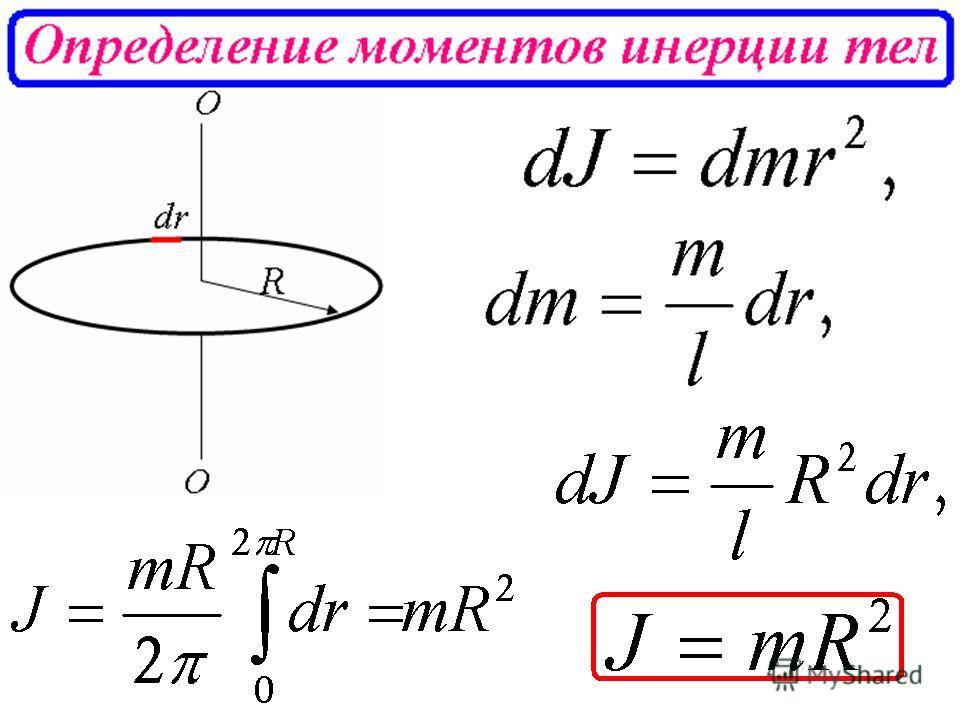 В этой формуле радиус — это расстояние от центра вращения до наиболее удаленной от этого центра точки на теле, для которого измеряется момент инерции. Если взять цилиндр с массой m, которая равна массе одного из шаров выше, и с расстоянием L от центра вращения до самой удаленной точки, так что эта величина равна радиусу этого шара, то момент инерции цилиндра I будет равен:
В этой формуле радиус — это расстояние от центра вращения до наиболее удаленной от этого центра точки на теле, для которого измеряется момент инерции. Если взять цилиндр с массой m, которая равна массе одного из шаров выше, и с расстоянием L от центра вращения до самой удаленной точки, так что эта величина равна радиусу этого шара, то момент инерции цилиндра I будет равен: Момент инерции играет важную роль в спорте и в механике, и его регулируют, изменяя массу или форму предметов и даже тела спортсмена.
Момент инерции играет важную роль в спорте и в механике, и его регулируют, изменяя массу или форму предметов и даже тела спортсмена. В других видах спорта спортсмены иногда, наоборот, выбирают инвентарь с разным моментом инерции, в зависимости от того, какого эффекта они хотят добиться, например как быстро им необходимо ударить мяч клюшкой, или битой. Некоторые используют спортивный инвентарь с высоким моментом инерции, чтобы увеличить силу и выносливость мышц, не добавляя веса к снаряду. Так, например, момент инерции бейсбольной биты влияет на то, какую скорость она придаст мячу.
В других видах спорта спортсмены иногда, наоборот, выбирают инвентарь с разным моментом инерции, в зависимости от того, какого эффекта они хотят добиться, например как быстро им необходимо ударить мяч клюшкой, или битой. Некоторые используют спортивный инвентарь с высоким моментом инерции, чтобы увеличить силу и выносливость мышц, не добавляя веса к снаряду. Так, например, момент инерции бейсбольной биты влияет на то, какую скорость она придаст мячу. Можно добиться этого, держа во время вращения грузы, которые потом отпускают или отбрасывают, когда такой большой момент инерции уже не нужен. Это не всегда целесообразно и может быть даже опасно, если груз отлетит не в ту сторону и нанесет повреждения или травмы. Два человека могут также взяться за руки во время вращения, соединив свой вес, а потом отпустить друг друга, когда им не нужно больше крутиться. Этот прием нередко используется в фигурном катании.
Можно добиться этого, держа во время вращения грузы, которые потом отпускают или отбрасывают, когда такой большой момент инерции уже не нужен. Это не всегда целесообразно и может быть даже опасно, если груз отлетит не в ту сторону и нанесет повреждения или травмы. Два человека могут также взяться за руки во время вращения, соединив свой вес, а потом отпустить друг друга, когда им не нужно больше крутиться. Этот прием нередко используется в фигурном катании. Такой прием используют также танцоры, гимнасты и фигуристы в время танцев и упражнений, чтобы после вращения в воздухе аккуратно приземлиться.
Такой прием используют также танцоры, гимнасты и фигуристы в время танцев и упражнений, чтобы после вращения в воздухе аккуратно приземлиться. Если вместо штанги поднимать предмет меньшего размера, но одинакового со штангой веса, например мешок с песком или гирю, то даже совсем небольшое смещение угла подъема может быть опасным. Если спортсмен толкает гирю вверх, но под углом, то она может начать вращаться вокруг своей оси. Большой вес и маленький радиус гири означает, что, по сравнению со штангой того же веса, ее намного легче начать вращать. Поэтому если она начнет вращаться вокруг своей оси, ее очень трудно остановить. Спортсмену легко потерять контроль над гирей и уронить ее. Это особенно опасно, если спортсмен поднимает гирю над головой стоя, или над грудью лежа. Даже если гиря не упадет, спортсмен может повредить кисти рук, пытаясь предотвратить вращение и падение. То же самое может произойти при упражнениях с особо тяжелой штангой, поэтому крепление дисков у штанг, предназначенных для упражнений с очень большим весом — подвижно. Диски прокручиваются вокруг своей оси во время подъема штанги, а сама штанга остается неподвижной.
Если вместо штанги поднимать предмет меньшего размера, но одинакового со штангой веса, например мешок с песком или гирю, то даже совсем небольшое смещение угла подъема может быть опасным. Если спортсмен толкает гирю вверх, но под углом, то она может начать вращаться вокруг своей оси. Большой вес и маленький радиус гири означает, что, по сравнению со штангой того же веса, ее намного легче начать вращать. Поэтому если она начнет вращаться вокруг своей оси, ее очень трудно остановить. Спортсмену легко потерять контроль над гирей и уронить ее. Это особенно опасно, если спортсмен поднимает гирю над головой стоя, или над грудью лежа. Даже если гиря не упадет, спортсмен может повредить кисти рук, пытаясь предотвратить вращение и падение. То же самое может произойти при упражнениях с особо тяжелой штангой, поэтому крепление дисков у штанг, предназначенных для упражнений с очень большим весом — подвижно. Диски прокручиваются вокруг своей оси во время подъема штанги, а сама штанга остается неподвижной. Штанги, предназначенные для Олимпийских игр, которые так и называются, олимпийскими штангами, имеют именно такую конструкцию.
Штанги, предназначенные для Олимпийских игр, которые так и называются, олимпийскими штангами, имеют именно такую конструкцию. Для этого спортсмены выбирают снаряды и инвентарь с малым моментом инерции, или уменьшают момент инерции своего тела.
Для этого спортсмены выбирают снаряды и инвентарь с малым моментом инерции, или уменьшают момент инерции своего тела. В этом случае вес распределен по бите или клюшке так, чтобы увеличить момент инерции. Это важно также для мечей, как настоящих, так и деревянных мечей для тренировок в восточных единоборствах, да и для любых других снарядов, которые спортсмены крутят или вращают, включая мячи для боулинга. Момент инерции влияет также на то, каким тяжелым кажется инвентарь во время его использования и насколько много затрачивается энергии на изменение его скорости вращения. Чем меньше момент инерции — тем обычно легче кажется инвентарь, и тем быстрее его можно вращать. Это позволяет спортсмену больше времени наблюдать за противником перед тем, как начать движение. Иногда это дополнительное время дает преимущество в спортивных играх, так как спортсмен может быстрее реагировать на движения противника. За эти дополнительные секунды становится проще предсказать траекторию движения противника, или мяча, например в теннисе и бейсболе, и сделать более точный удар.
В этом случае вес распределен по бите или клюшке так, чтобы увеличить момент инерции. Это важно также для мечей, как настоящих, так и деревянных мечей для тренировок в восточных единоборствах, да и для любых других снарядов, которые спортсмены крутят или вращают, включая мячи для боулинга. Момент инерции влияет также на то, каким тяжелым кажется инвентарь во время его использования и насколько много затрачивается энергии на изменение его скорости вращения. Чем меньше момент инерции — тем обычно легче кажется инвентарь, и тем быстрее его можно вращать. Это позволяет спортсмену больше времени наблюдать за противником перед тем, как начать движение. Иногда это дополнительное время дает преимущество в спортивных играх, так как спортсмен может быстрее реагировать на движения противника. За эти дополнительные секунды становится проще предсказать траекторию движения противника, или мяча, например в теннисе и бейсболе, и сделать более точный удар. Поэтому снаряд с низким моментом инерции не обязательно лучше — в некоторых случаях спортсмены, наоборот, отдают предпочтение снарядам с высоким моментом инерции. Такие снаряды развивают мышцы, что помогает, в свою очередь, ускорить реакцию.
Поэтому снаряд с низким моментом инерции не обязательно лучше — в некоторых случаях спортсмены, наоборот, отдают предпочтение снарядам с высоким моментом инерции. Такие снаряды развивают мышцы, что помогает, в свою очередь, ускорить реакцию. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.
Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения. », то есть «…умножить на десять в степени…». Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах.
», то есть «…умножить на десять в степени…». Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах. com на YouTube
com на YouTube