Гибридизация орбиталей — Википедия

Модель молекулы метана, образованной sp³-гибридными орбиталями углерода и s-орбиталями водорода

Гибридизация орбиталей — гипотетический процесс смешения разных (s, p, d, f) орбиталей центрального атома многоатомной молекулы с возникновением одинаковых орбиталей, эквивалентных по своим характеристикам.

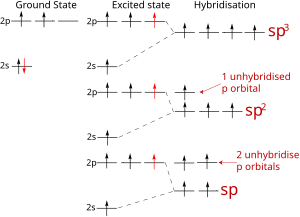Схема гибридизации атомных орбиталей атома углерода

Концепция гибридизации валентных атомных орбиталей была предложена американским химиком Лайнусом Полингом в 1931 г. для ответа на вопрос, почему при наличии у центрального атома разных (s, p, d) валентных орбиталей, образованные им связи в многоатомных молекулах с одинаковыми лигандами оказываются эквивалентными по своим энергетическим и пространственным характеристикам.

Представления о гибридизации занимают центральное место в методе валентных связей. Сама гибридизация не является реальным физическим процессом, а только удобной моделью, позволяющей объяснить электронное строение молекул, в частности гипотетические видоизменения атомных орбиталей при образовании ковалентной химической связи, в частности, выравнивание длин химических связей и валентных углов в молекуле.

Концепция гибридизации с успехом была применена для качественного описания простых молекул, но позднее была расширена и для более сложных. В отличие от теории молекулярных орбиталей не является строго количественной, например, она не в состоянии предсказать фотоэлектронные спектры даже таких простых молекул, как вода. В настоящее время используется в основном в методических целях и в синтетической органической химии.

В 1954 году Нобелевский комитет удостоил Л.Полинга премии по химии «За изучение природы химической связи и его применение к объяснению строения сложных молекул». Но сам Л.Полинг не был удовлетворён введением σ,π — описания для двойной и тройной связи и сопряжённых систем.

В 1958 году на симпозиуме, посвящённом памяти Кекуле, Л. Полинг развил теорию изогнутой химической связи, учитывающую кулоновское отталкивание электронов. По этой теории двойная связь описывалась как комбинация двух изогнутых химических связей, а тройная связь как комбинация трёх изогнутых химических связей.^[1]

Этот принцип нашёл отражение в теории отталкивания электронных пар Гиллеспи — Найхолма, первое и наиболее важное правило которое формулировалось следующим образом:

«Электронные пары принимают такое расположение на валентной оболочке атома, при котором они максимально удалены друг от друга, т.е электронные пары ведут себя так, как если бы они взаимно отталкивались»^[2].

Второе правило состояло в том, что «все электронные пары, входящие в валентную электронную оболочку, считаются расположенными на одинаковом расстоянии от ядра».^[2]

sp-гибридизация[править | править код]

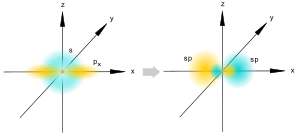sp-гибридизация

Происходит при смешивании одной s- и одной p-орбиталей. Образуются две равноценные sp-атомные орбитали, расположенные линейно под углом 180 градусов и направленные в разные стороны от ядра центрального атома. Две оставшиеся негибридные p-орбитали располагаются во взаимно перпендикулярных плоскостях и участвуют в образовании π-связей.

sp²-гибридизация[править | править код]

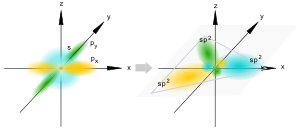sp²-гибридизация

Происходит при смешивании одной s- и двух p-орбиталей. Образуются три гибридные орбитали с осями, расположенными в одной плоскости и направленными к вершинам треугольника под углом 120 градусов. Негибридная p-атомная орбиталь перпендикулярна плоскости и, как правило, участвует в образовании π-связей

sp³-гибридизация[править | править код]

sp³-гибридизация

Происходит при смешивании одной s- и трех p-орбиталей, образуя четыре равноценные по форме и энергии sp³-гибридные орбитали.

Оси sp³-гибридных орбиталей направлены к вершинам тетраэдра, тогда как ядро центрального атома расположено в центре описанной сферы этого тетраэдра. Угол между любыми двумя осями приближённо равен 109°28′^[3], что соответствует наименьшей энергии отталкивания электронов. Также sp³-орбитали могут образовывать четыре σ-связи с другими атомами или заполняться неподеленными парами электронов. Такое состояние характерно для атомов углерода в насыщенных углеводородах и соответственно в алкильных радикалах и их производных.

Представление о гибридизации атомных орбиталей лежит в основе теории отталкивания электронных пар Гиллеспи-Найхолма. Каждому типу гибридизации соответствует строго определённая пространственная ориентация гибридных орбиталей центрального атома, что позволяет её использовать как основу стереохимических представлений в неорганической химии.

В таблице приведены примеры соответствия наиболее распространённых типов гибридизации и геометрической структуры молекул в предположении, что все гибридные орбитали участвуют в образовании химических связей (отсутствуют неподелённые электронные пары)

[4].

Тип гибридизации	Число гибридных орбиталей	Геометрия	Структура	Примеры
sp	2	Линейная		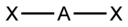BeF2, CO2, NO2+
sp2	3	Треугольная		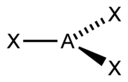BF3, NO3—, CO32-
sp3, d3s	4	Тетраэдрическая		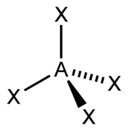CH4, ClO4—, SO42-, NH4+
dsp2	4	Плоскоквадратная		[Ni(CN)4,](2-) [PdCl4]2-
sp3d	5	тригонально-бипирамидальная		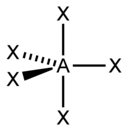PCl5, AsF5
sp3d2, d2sp3	6	Октаэдрическая		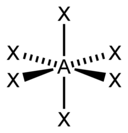SF6, Fe(CN)63-, CoF63-

1. ↑ Под редакцией Р. Х. Фрейдлиной. Теоретическая органическая химия. — пер. с англ. канд. хим. наук Ю.Г.Бунделем. — М.: Издательство иностранной литературы, 1963. — Т. 1. — С. 11. — 365 с.
2. ↑ ^{1 2} Гиллеспи Р. Геометрия молекул / Пер. с англ. Е. З. Засорина и В. С. Мастрюкова, под ред. Ю. А. Пентина. — М.: Мир, 1975. — С. 18-19. — 278 с.
3. ↑ Теоретически этот угол в правильном тетраэдре равен arccos(-1/3)≈109°28′.
4. ↑ Здесь A — центральный атом, X — гибридные связывающие орбитали

• Полинг Л. Природа химической связи / Пер. с англ. М. Е. Дяткиной. Под ред. проф. Я. К. Сыркина. — М.; Л.: Госхимиздат, 1947. — 440 с.
• Полинг Л. Общая химия. Пер. с англ. — М.: Мир, 1974. — 846 с.
• Минкин В. И., Симкин Б. Я., Миняев Р. М. Теория строения молекул. — Ростов-на-Дону: Феникс, 1997. — С. 397-406. — ISBN 5-222-00106-7.
• Гиллеспи Р. Геометрия молекул / Пер. с англ. Е. З. Засорина и В. С. Мастрюкова, под ред. Ю. А. Пентина. — М.: Мир, 1975. — 278 с.

Изометрическая проекция — Википедия

Стол в прямоугольной изометрической проекции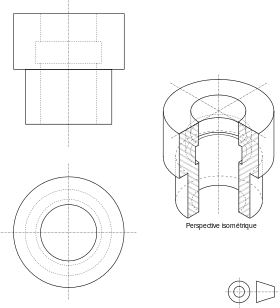

Изометри́ческая прое́кция (др.-греч. ἴσος «равный» + μετρέω «измеряю») — это разновидность аксонометрической проекции, при которой в отображении трёхмерного объекта на плоскость коэффициент искажения (отношение длины спроецированного на плоскость отрезка, параллельного координатной оси, к действительной длине отрезка) по всем трём осям один и тот же. Слово «изометрическая» в названии проекции пришло из греческого языка и означает «равный размер», отражая тот факт, что в этой проекции масштабы по всем осям равны. В других видах проекций это не так.

Изометрическая проекция используется в машиностроительном черчении и САПР для построения наглядного изображения детали на чертеже, а также в компьютерных играх для трёхмерных объектов и панорам.

Необходимо отметить, что параллельные проекции, разновидностью которых являются аксонометрические и, в том числе, изометрические проекции, делятся также на ортогональные (перпендикулярные), с направлением проекции перпендикулярным к плоскости проекции, и косоугольные, с углом между направлением и плоскостью, отличным от прямого. По советским стандартам (см. ниже) аксонометрические проекции могут быть и ортогональными, и косоугольными^[1]. В результате, по западным стандартам изометрическая проекция определяется более узко и, помимо равенства масштабов по осям, включает условие равенства 120° углов между проекциями любой пары осей. Во избежание путаницы далее, если не указано иное, под изометрической проекцией будет подразумеваться только прямоугольная изометрическая проекция.

• 

  …прямоугольной

• 

  …косоугольной фронтальной

• 

  …косоугольной горизонтальной

Прямоугольная (ортогональная) изометрическая проекция[править | править код]

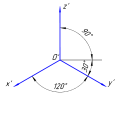
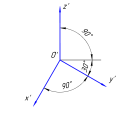
В прямоугольной изометрической проекции аксонометрические оси образуют между собой углы в 120°, ось Z’ направлена вертикально. Коэффициенты искажения (kx,ky,kz{\displaystyle k_{x},k_{y},k_{z}}) имеют числовое значение 23≈0,82{\displaystyle {\sqrt {\frac {2}{3}}}\approx 0{,}82}. Как правило, для упрощения построений изометрическую проекцию выполняют без искажений по осям, то есть коэффициент искажения принимают равным 1, в этом случае получают увеличение линейных размеров в 10,82≈1,22{\displaystyle {\frac {1}{0{,}82}}\approx 1{,}22} раза.

Приближённо аксонометрические оси прямоугольной проекции можно построить, если принять tg 30°=4/7 (0,577 и 0,571 соотв.).

Косоугольная фронтальная изометрическая проекция[править | править код]

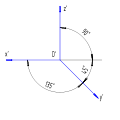
Ось Z’ направлена вертикально, угол между осью X’ и Z’ равен 90°, ось Y’ с углом наклона 135° (допускается 120° и 150°) от оси Z’.

Фронтальная изометрическая проекция выполняется по осям X’, Y’ и Z’ без искажения.

Кривые, параллельные фронтальной плоскости, проецируются без искажений.

Косоугольная горизонтальная изометрическая проекция[править | править код]

Ось Z’ направлена вертикально, между осью Z’ и осью Y’ угол наклона равен 120° (допускается 135° и 150°), при этом сохраняется угол между осями X’ и Y’ равным 90°.

Горизонтальную изометрическую проекцию выполняют без искажения по осям X’, Y’ и Z’.

Кривые, параллельные горизонтальной плоскости^[2] проецируются без искажений.

Стоит отметить, что, поскольку ортогональный трёхгранник невозможно повернуть так, чтобы два его ребра были бы видны взаимно-перпендикулярными, и третье ребро при этом не проецировалась бы в точку, все проекции, в которых видны все три оси.

Изометрический вид объекта можно получить, выбрав направление обзора таким образом, чтобы углы между проекцией осей x, y, и z были одинаковы и равны 120°. К примеру, если взять куб, это можно выполнить направив взгляд на одну из граней куба, после чего повернув куб на ±45° вокруг вертикальной оси и на ±arcsin (tan 30°) ≈ 35,264° вокруг горизонтальной оси. Обратите внимание: на иллюстрации изометрической проекции куба контур проекции образует правильный шестиугольник — все рёбра равной длины и все грани равной площади.

Подобным же образом изометрический вид может быть получен, к примеру, в редакторе трёхмерных сцен: начав с камерой, выровненной параллельно полу и координатным осям, её нужно повернуть вниз на ≈35.264° вокруг горизонтальной оси и на ±45° вокруг вертикальной оси.

Другой путь визуализации изометрической проекции заключается в рассмотрении вида кубической комнаты с верхнего угла с направлением взгляда в противолежащий нижний угол. Ось x здесь направлена диагонально вниз и вправо, ось y — диагонально вниз и влево, ось z — прямо вверх. Глубина также отражается высотой картинки. Линии, нарисованные вдоль осей, имеют угол 120° между собой.

Имеется 8 различных вариантов получения изометрической проекции в зависимости от того, в какой октант смотрит наблюдатель. Изометрическое преобразование точки ax,y,z{\displaystyle a_{x,y,z}} в трёхмерном пространстве в точку bx,y{\displaystyle b_{x,y}} на плоскости при взгляде в первый октант может быть математически описано с помощью матриц поворота следующим образом. Вначале, как объяснено в разделе Визуализация, выполняется поворот вокруг горизонтальной оси (здесь x) на α = arcsin (tan 30°) ≈ 35,264° и вокруг вертикальной оси (здесь y) на β = 45°:

[cxcycz]=[1000cos⁡αsin⁡α0−sin⁡αcos⁡α][cos⁡β0−sin⁡β010sin⁡β0cos⁡β][axayaz]=16[30−31212−22][axayaz]{\displaystyle {\begin{bmatrix}\mathbf {c} _{x}\\\mathbf {c} _{y}\\\mathbf {c} _{z}\\\end{bmatrix}}={\begin{bmatrix}1&0&0\\0&{\cos \alpha }&{\sin \alpha }\\0&{-\sin \alpha }&{\cos \alpha }\\\end{bmatrix}}{\begin{bmatrix}{\cos \beta }&0&{-\sin \beta }\\0&1&0\\{\sin \beta }&0&{\cos \beta }\\\end{bmatrix}}{\begin{bmatrix}\mathbf {a} _{x}\\\mathbf {a} _{y}\\\mathbf {a} _{z}\\\end{bmatrix}}={\frac {1}{\sqrt {6}}}{\begin{bmatrix}{\sqrt {3}}&0&-{\sqrt {3}}\\1&2&1\\{\sqrt {2}}&-{\sqrt {2}}&{\sqrt {2}}\\\end{bmatrix}}{\begin{bmatrix}\mathbf {a} _{x}\\\mathbf {a} _{y}\\\mathbf {a} _{z}\\\end{bmatrix}}}

Затем применяется ортогональная проекция на плоскость x-y:

[bxby0]=[100010000][cxcycz]{\displaystyle {\begin{bmatrix}\mathbf {b} _{x}\\\mathbf {b} _{y}\\0\\\end{bmatrix}}={\begin{bmatrix}1&0&0\\0&1&0\\0&0&0\\\end{bmatrix}}{\begin{bmatrix}\mathbf {c} _{x}\\\mathbf {c} _{y}\\\mathbf {c} _{z}\\\end{bmatrix}}}

Другие семь возможных видов получаются поворотом к противостоящим сторонам и/или инверсией направления взгляда.^[3]

Ограничения аксонометрической проекции[править | править код]

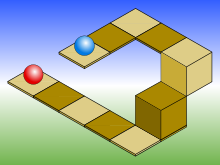Изометрический рисунок с голубым шаром на два уровня выше красного

Как и в других видах параллельных проекций, объекты в аксонометрической проекции не выглядят больше или меньше при приближении или удалении от наблюдателя. Это полезно в архитектурных чертежах и удобно в спрайто-ориентированных компьютерных играх, но, в отличие от перспективной (центральной) проекции, приводит к ощущению искривления, поскольку человеческий глаз или фотография работают иначе.

Это также легко приводит к ситуациям, когда глубину и высоту невозможно оценить, как показано на иллюстрации справа. В этом изометрическом рисунке голубой шар на два уровня выше красного, но это нельзя увидеть, если смотреть только на левую половину картинки. Если выступ, на котором находится голубой шар, расширить на один квадрат, то он окажется точно рядом с квадратом, на котором находится красный шар, создавая оптическую иллюзию, будто оба шара на одном уровне.

Дополнительная проблема, специфичная для изометрической проекции — сложность определения, какая сторона объекта наблюдается. При отсутствии теней и для объектов, которые относительно перпендикулярны и соразмерны, сложно определить, какая сторона является верхней, нижней или боковой. Это происходит из-за приблизительно равных по размеру и площади проекций такого объекта.

Большинство современных компьютерных игр избегают этого за счёт отказа от аксонометрической проекции в пользу перспективного трёхмерного рендеринга. Однако эксплуатация проекционных иллюзий популярна в оптическом искусстве — таком, как работы из серии «невозможной архитектуры» Эшера. Водопад (1961) — хороший пример, в котором строение в основном изометрическое, в то время как блеклый фон использует перспективную проекцию. Другое преимущество заключается в том, что в черчении даже новички легко могут строить углы в 60° с помощью только циркуля и линейки.

Изометрическая проекция в компьютерных играх и пиксельной графике[править | править код]

Рисунок телевизора в почти-изометрической пиксельной графике. У пиксельного узора видна пропорция 2:1

В области компьютерных игр и пиксельной графики аксонометрическая проекция была весьма популярна в силу лёгкости, с которой двухмерные спрайты и плиточная графика могли быть использованы для представления трёхмерной игровой среды — поскольку во время перемещения по игровому полю объекты не меняют размер, компьютеру не требуется масштабировать спрайты или выполнять вычисления, необходимые для моделирования зрительной перспективы. Это позволяло старым 8-битным и 16-битным игровым системам (и, позднее, портативным игровым системам) легко отображать большие трёхмерные пространства. И хотя неразбериха с глубиной (см. выше) иногда могла быть проблемой, хороший дизайн игры способен её смягчить. С приходом более мощных графических систем аксонометрическая проекция стала терять свои позиции.

Проекция в компьютерных играх обычно несколько отличается от «истинной» изометрической в силу ограничений растровой графики — линии по осям x и y не имели бы аккуратного пиксельного узора, если бы рисовались под углом в 30° к горизонтали. Хотя современные компьютеры могут устранять эту проблему с помощью сглаживания, ранее компьютерная графика не поддерживала достаточную цветовую палитру или не располагала достаточной мощностью процессоров для его выполнения. Вместо этого использовалась пропорция пиксельного узора 2:1 для рисования осевых линий x и y, в результате чего эти оси располагались под углом arctg 0,5 ≈ 26,565° к горизонтали. (Игровые системы с неквадратными пикселями могли, однако, приводить к другим углам, включая полностью изометрические^[4]). Поскольку здесь из трёх углов между осями (116,565°, 116,565°, 126,87°) равны только два, такой вид проекции более точно характеризуется как вариация диметрической проекции. Однако большинство представителей сообществ компьютерных игр и растровой графики продолжает называть эту проекцию «изометрической перспективой». Также, часто используются термины «вид 3/4 (англ.)» и «2.5D».

Термин применялся и к играм, не использующим пропорцию 2:1, общую для многих компьютерных игр. Fallout^[5] и SimCity 4^[6], в которых используется триметрическая проекция, были отнесены к «изометрическим». Игры с косоугольной проекцией, такие как The Legend of Zelda: A Link to the Past^[7] и Ultima Online^[8], а также игры с перспективной проекцией с видом «с воздуха» (англ.)русск., такие как The Age of Decadence (англ.)^[9] и Silent Storm^[10], также иногда относят к изометрическим или «псевдо-изометрическим».

Кадр из игры «echochrome»

Интересный пример использования особенностей изометрической проекции наблюдается в игре echochrome (яп. 無限回廊 муген кайро:). Слоган игры — «В этом мире то, что ты видишь, становится реальностью». Смысл игры заключается в том, что иллюзия, возникающая при взгляде на изометрически построенный трёхмерный уровень с определённой точки, перестаёт быть иллюзией. Например, если посмотреть на уровень таким образом, чтобы площадки, находящиеся на разной высоте, выглядели так, будто они находятся на одной и той же высоте (см. изображение с синим и красным шарами из предыдущего раздела), игрой они будут расцениваться как находящиеся на одной высоте, и человек (игрок) сможет запросто «перешагнуть» с одной площадки на другую. Затем, если повернуть карту уровня и посмотреть на конструкцию так, чтобы было отчётливо видно разницу в высоте, можно понять, что в действительности человек «перешагнул» на другую высоту, пользуясь тем, что изометрическая иллюзия на какой-то момент стала реальностью. На приведённом в качестве иллюстрации кадре из игры положение площадки, находящейся вверху лестницы, можно представить двояко: в одном случае она находится на одной высоте с площадкой, на которой находится игрок (можно перешагнуть), а в другом случае — под ней (можно спрыгнуть через чёрное отверстие). Оба случая будут одновременно являться правдой. Очевидно, этот эффект достигается отсутствием перспективы в изометрии.

История изометрических компьютерных игр[править | править код]

Q*bert (1982), одна из первых игр с изометрической графикой

Первыми играми, использующими изометрическую проекцию, были аркадные игры начала 1980-х: так, Q*bert^[11] и Zaxxon^[12] выпущены в 1982 году. Q*bert показывает статичную пирамиду, нарисованную в изометрической перспективе, по которой должен прыгать управляемый игроком персонаж. Zaxxon предлагает прокручиваемые изометрические уровни, над которыми летает управляемый игроком самолётик. Год спустя, в 1983 году, была выпущена аркадная игра Congo Bongo (англ.)^[13], работавшая на тех же игровых автоматах, что и Zaxxon. В этой игре персонаж перемещается по большим изометрическим уровням, включающим трёхмерные подъёмы и спуски. То же самое предлагается и в аркадной игре Marble Madness (1984).

С выходом Ant Attack (англ.) (1983) для ZX Spectrum изометрические игры перестали быть изюминкой только аркадных игровых автоматов и пришли также и в домашние компьютеры. Журнал CRASH присудил этой игре 100 % в категории «графика» за новую «трёхмерную» технологию.^[14] Год спустя для ZX была выпущена игра Knight Lore, которая расценивается как революционное произведение^[15], определившее последующий жанр изометрических квестовых игр^[16]. На домашних компьютерах было отмечено столько изометрических игр-последователей Knight Lore, что эта игра стала считаться вторым наиболее клонируемым образцом программного обеспечения после текстового редактора WordStar (англ.).^[17] Среди клонов большой успех имела игра Head Over Heels (1987)^[18]. Однако, изометрическая проекция не ограничивалась только аркадами и квестовыми играми — например, стратегическая игра Populous (1989) также использовала изометрическую перспективу.

На протяжении 1990-х некоторые очень успешные игры вроде Civilization II и Diablo использовали фиксированную изометрическую перспективу. С приходом 3D ускорителей на персональные компьютеры и игровые консоли игры с трёхмерной перспективой в основном переключились на полноценную трёхмерность вместо изометрической перспективы. Это можно видеть в преемницах вышеназванных игр — начиная с Civilization IV в этой серии используется полная трёхмерность. Diablo II, как и ранее, использует фиксированную перспективу, но опционально применяет перспективное масштабирование спрайтов на расстоянии, получая псевдо-трёхмерную перспективу.^[19]

1. ↑ ^{1 2} По ГОСТ 2.317-69 — Единая система конструкторской документации. Аксонометрические проекции.
2. ↑ Здесь горизонтальной называется плоскость, перпендикулярная оси Z (которая является прообразом оси Z’).
3. ↑ Ingrid Carlbom, Joseph Paciorek. Planar Geometric Projections and Viewing Transformations // ACM Computing Surveys (CSUR) : журнал. — ACM, декабрь 1978. — Т. 10, № 4. — С. 465—502. — ISSN 0360-0300. — DOI:10.1145/356744.356750.
4. ↑ Так, в распространённом разрешении CGA/VGA 320×200 этот угол равняется arctg 0,6 ≈ 30,96°.
5. ↑ Jeff Green. GameSpot Preview: Arcanum (англ.) (недоступная ссылка). GameSpot (29 февраля 2000). Дата обращения 29 сентября 2008. Архивировано 31 августа 2000 года.
6. ↑ Steve Butts. SimCity 4: Rush Hour Preview (англ.). IGN (9 сентября 2003). Дата обращения 29 сентября 2008. Архивировано 19 февраля 2012 года.
7. ↑ GDC 2004: The History of Zelda (англ.). IGN (25 марта 2004). Дата обращения 29 сентября 2008. Архивировано 19 февраля 2012 года.
8. ↑ Dave Greely, Ben Sawyer. Has Origin Created the First True Online Game World? (англ.). Gamasutra (19 августа 1997). Дата обращения 29 сентября 2008. Архивировано 19 февраля 2012 года.
9. ↑ Age of Decadence (англ.). Iron Tower Studios. Дата обращения 29 сентября 2008. Архивировано 19 февраля 2012 года.
10. ↑ Steve O’Hagan. PC Previews: Silent Storm (англ.). GamesRadar—CVG (7 августа 2003). Дата обращения 29 сентября 2008. Архивировано 19 февраля 2012 года.
11. ↑ Q*bert (англ.) на сайте Killer List of Videogames
12. ↑ Zaxxon (англ.) на сайте Killer List of Videogames
13. ↑ Congo Bongo (англ.) на сайте Killer List of Videogames
14. ↑ Soft Solid 3D Ant Attack // CRASH : журнал. — февраль 1984. — № 1.
15. ↑ Ultimate Play The Game — Company Lookback // Retro Micro Games Action — The Best of gamesTM (англ.) Retro. — Highbury Entertainment, 2006. — Т. 1. — С. 25.
16. ↑ Steven Collins. Game Graphics During the 8-bit Computer Era // ACM SIGGRAPH. Computer Graphics. — май 1998. — Т. 32, № 2. Архивировано 9 сентября 2012 года.
17. ↑ Krikke J. Axonometry: a matter of perspective // IEEE. Computer Graphics and Applications. — июль-август 2000. — Т. 20, № 4. — С. 7—11. — DOI:10.1109/38.851742.
18. ↑ Looking for an old angle // CRASH : журнал. — апрель 1988. — № 51.
19. ↑ Diablo II Nears Completion As Blizzard Prepares For Final Phase Of Beta Testing (неопр.) (недоступная ссылка). Market Wire (май 2000). Дата обращения 29 сентября 2008. Архивировано 10 июля 2012 года.

• Introduction to 3 Dimensional graphics (англ.) (недоступная ссылка). Blueprint project. IDER group, Manufactuing Systems Engineering Centre, University of Hertfordshire. — Пояснения и учебник по рисованию в изометрической перспективе из Хертфорширдского университета. Дата обращения 29 сентября 2008. Архивировано 28 октября 2000 года.
• Herbert Glarner. Isometric Projection (англ.) (19 марта 2007). Дата обращения 29 сентября 2008. Архивировано 19 февраля 2012 года.
• PixelDam (англ.). — A collaborative pixelart community. Дата обращения 29 сентября 2008. Архивировано 19 февраля 2012 года.
• Tom Gersic. Rendering Isometric Tiles in Blender 3D (англ.). — Учебник с примерами по созданию изометрических плиток в программе Blender 3D. Дата обращения 29 сентября 2008. Архивировано 19 февраля 2012 года.

• Богданов В. Н., Малежик И. Ф., Верхола А. П. и др. Справочное руководство по черчению. — М.: Машиностроение, 1989. — С. 864. — ISBN 5-217-00403-7.
• Фролов С. А. Начертательная геометрия. — 2-е изд., перераб. и доп. — М.: Машиностроение, 1983. — С. 240.

Наклон оси вращения — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 февраля 2019; проверки требуют 3 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 февраля 2019; проверки требуют 3 правки.

Накло́н о́си враще́ния — угол отклонения оси вращения небесного тела от перпендикуляра к плоскости его орбиты. Другими словами — угол между плоскостями экватора небесного тела и его орбиты.

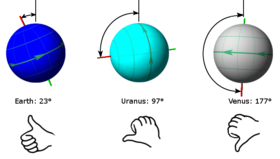Применение правила буравчика для определения положительного полюса планеты.
Если пальцы правой руки согнуты в направлении вращения, то большой палец укажет положительный полюс (выделен красной линией). Тогда наклон оси будет определён как угол между направлением этого полюса и перпендикуляром к плоскости орбиты. Для Земли, Урана и Венеры эти углы составят около 23°, 97° и 177° соответственно

Международный астрономический союз установил два стандартных метода определения угла наклона.

Согласно первому из них за точку отсчета принимается северный полюс планеты. Он определяется как полюс, который лежит с той же стороны плоскости Лапласа, что и Северный полюс Земли^[1]. Согласно этому методу Венера имеет угол наклона 3° и вращается ретроградно.

Второй метод использует правило буравчика (правило правой руки) для определения положительного полюса, принимаемого за точку отсчета^[2]. В этом случае Венера наклонена на 177° (расположена «вверх ногами»).

• Наклон оси вращения Земли около 23.44°. Наблюдатель с расположен на Солнце. Разрыв в круговых стрелках — ближе к наблюдателю, чем остальная часть стрелки.

Наклон оси вращения Земли является основной причиной сезонных климатических изменений (смены времен года).

Наклон оси вращения важнейших небесных тел[править | править код]

Тело	Наклон оси (°)
Солнце	7,15-7,25
Меркурий	~0,01
Венера	177,3
Земля	23°26′14″
Луна	1,5424
Марс	25,19
Юпитер	3,13
Сатурн	26,73
Уран	97,77
Нептун	28,32
Плутон	119,61
Церера	~4
Паллада	~84

1. ↑ Explanatory Supplement 1992, p. 384
2. ↑ Seidelmann, P. Kenneth; Archinal, B. A.; a’Hearn, M. F.; Conrad, A.; Consolmagno, G. J.; Hestroffer, D.; Hilton, J. L.; Krasinsky, G. A.; Neumann, G.; Oberst, J.; Stooke, P.; Tedesco, E. F.; Tholen, D. J.; Thomas, P. C.; Williams, I. P. Report of the IAU/IAG Working Group on cartographic coordinates and rotational elements: 2006 (англ.) // Celestial Mechanics and Dynamical Astronomy : journal. — 2007. — Vol. 98, no. 3. — P. 155—180. — DOI:10.1007/s10569-007-9072-y.

Углы между связями и гибридизация

    Угол между связями (валентный угол) является свойством двух связей одного общего атома и должен рассматриваться как свойство этого атома Согласно теории гибридизации Полинга — Слейтера валентный угол определяется характером гибридных орбиталей для вр -гибридных он равен 109,5°, вр -гибридных — 120°, вр-гибридных— 180° И наоборот, по величине валентного угла можно судить [c.76]
    В молекуле этилена валентные электроны углерода находятся а состоянии хр -гибридизации. Угол между связями Н—С—С равен 121,5°, а не 120°. Объясните причину. [c.34]

    В молекуле воды угол между связями О—Н равен не 90°, как можно было ожидать., исходя из угла между осями двух р-орбиталей атома кислорода, а приближается к тетраэдрическому (109,5 ) и составляет 104,5°. Вероятно, это можно объяснить sp -гибридизацией (см. гл. Ill, 4) четырех атомных орбиталей кислорода. [c.90]

    Плоское строение молекулы и угол между связями 120 позволяют в методе ЛМО считать, что в локализованных а-связях атом углерода участвует гибридными хр -орбиталями. Каждый атом углерода участвует своими тремя электронами в трех таких о-связях двух С—Н и одной С—С. Еще одну связь С—С образуют не участвующие в гибридизации р -электроны, по одному от каждого атома. Так как р -орбитали направлены перпендикулярно плоскости молекулы, их перекрыванием образуется я-орбиталь, электронная плотность которой располагается над и под плоскостью молекулы. Таким образом, связь С=С оказывается двойной симметричной о л -связью. Разделяя связь между углеродными атомами в этилене на о- и л-связь и принимая энергию разрыва о-связи равной Е (С—С) = 347 кДж/моль. можно приписать л-связи в этилене энергию 250 кДж/моль. Таким образом, л-связь (С—С) в этилене менее прочна, чем а-связь, и легче разрывается, чем объясняется склонность этилена к реакции присоединения. [c.107]

    В молекулах Н2О и ЫНз угол между связями не равен 90°, а близок к тетраэдрическому (109°). Какой вид гибридизации атомных орбиталей у атомов кислорода и азота Представьте графически структуру молекул Н2О и ЫНз. [c.32]

    Укажите тип гибридизации электронов 5е в молекуле НгЗе, если угол между связями равен 90°. [c.231]

    Напряженность молекулы циклопропана объясняется главным образом ненормальными углами между С—С-связями — взаимным отталкиванием электронных облаков этих связей. В результате этого связи (т. е. максимумы перекрывания электронных облаков) не находятся на прямых, соединяющих центры атомов углерода, а располагаются на некотором расстоянии — вне треугольника молекулы (рис. 57). Несмотря на то что при подобном искажении электронного облака перекрывание становится менее полным, такое расположение свяаей оказывается энергетически более выгодным. Таким образом, по современным представлениям с-связи в циклопропане отличаются от обычных а-связей и их гибридизация отличается от обычной sp -гибридизации. Они носят название банановых связей (бананообразное электронное облако искаженной ст-связи) и, по существу, занимают промежуточное положение между обычными о- и я-связями. Это отражается на многих свойствах циклопропана, особенно на его способности к сопряжению с кратными связями (см. далее). Угол между связями в циклопропане 106°, вместо 60° по классическим представлениям, угол Н—С—Н примерно 120°. Благодаря такому строению циклопропан склонен к реакциям электрофильного присоединения и в этом отношении напоминает соединения с двойными связями (хотя значительно пассивнее последних). [c.539]

    Угол между связями в молекуле воды равен 104,5°. В молекуле NHa (рис. 17) этот угол еще больше (107,3°), т. е. ближе к тетраэдрическому (109°28 ). Чем это можно объяснить Ведь у атома кислорода в образовании химической связи участвуют два неспаренных р-электрона, а у атома азота — три неспаренных / -электрона, облака которых гантелеобразны. А как вам уже известно, гантелеобразные облака р-электронов располагаются в пространстве взаимно перпендикулярно. Поэтому угол между ними должен быть 90°, а не 104,5° или 107,3°. Задумываясь над этим вопросом, ученые пришли к выводу, что при образовании молекул воды и аммиака, так же как и при образовании молекул метана, характерна гибридизация орбиталей по типу sp . [c.78]

    Благодаря малому размеру ион водорода внедряется в электронные оболочки молекулы воды, связывается с молекулой воды очень прочной связью и изменяет угол между связями Н—О—Н, возможно, даже изменяя тип гибридизации электронных орбиталей кислорода. Ионы же щелочных металлов не могут проникать в электронные оболочки молекулы воды, связь их с молекулой воды значительно слабее, а значение угла [c.123]

    Летучесть этих соединений свидетельствует о ковалентном характере связей и отсутствии дипольного момента. Так как в любом валентном состоянии у атома инертного газа действуют электроны разных типов, т. е. имеет место гибридизация связей, то образующиеся молекулы фторидов должны иметь довольно симметричное строение. Молекула ХеРа имеет линейное строение оставшиеся у атома ксенона 3 пары электронов располагаются по углам равностороннего треугольника, находящегося в экваториальной плоскости к линиям связи Хе—Р. Тетрафторид имеет форму квадрата, над центром которого вверху и внизу находится по одной паре электронов угол между связями 90° (рис. 138). Что касается гексафторида ксенона, то он представляется в виде искаженного октаэдра, на одной из плоскостей которого имеется пара электронов. [c.638]

    Укажите тип гибридизации электронов в молекуле СН4, если угол между связями равен 109°. [c.231]

    ИОНОВ. Часто наблюдаются отклонения валентных углов от предсказываемых теорией, что может быть вызвано еще более сложной гибридизацией или электростатическим взаимодействием атомов и орбиталей. Так, в молекуле Н2О угол между связями равен 104°, что объясняется или р -негибридизированными электронами атома кислорода (теоретический угол 90°) и взаимным отталкиванием перекрывающихся с ними s-орбиталей двух атомов водорода или же 5рЗ-гибридизацией электронов атома кислорода. Уменьшение угла до 105° по сравнению с теоретическим (109°) объясняется отталкивающим действием двух заполненных пйрами электронов орбиталей атома кислорода. [c.230]

    ВАЛЕНТНЫЕ УГЛЫ. До сих нор мы рассматривали только свойства связей. Угол между связями (валентный угол) фактически является свойством двух связей, пршшдлежащих общему атому, и должен рассматриваться как свойство этого атома. Действительно, по величине валентного угла можно судить о состоянни гибридизации атома. [c.59]

    В молекуле этилена орбитали атомов углерода находятся в состоянии р -гибридизации. Угол между связями И—С—С равен 121,5°, а не 120°. Объясните причину такого отличия. [c.43]

    В структуре молекулы воды угол между связями О—Н равен 104,5°, т.е. близок к тетраэдрическому. Объясняется это тем, что атом кислорода также под

угол между кристаллографическими осями — это… Что такое угол между кристаллографическими осями?



угол между кристаллографическими осями

n

geol. Achsenwinkel

Универсальный русско-немецкий словарь. Академик.ру. 2011.

• угол между кривошипами коленчатого вала
• угол между кромкой и продольной осью

Смотреть что такое «угол между кристаллографическими осями» в других словарях:

• бета — 1. Приставка, обозначающая один из двух или нескольких тесно связанных между собой минералов. 2. В двуосных кристаллах – промежуточный показатель преломления. 3. Угол между кристаллографическими осями А и С. [Англо русский геммологический… …   Справочник технического переводчика

• Астеризм (минералогия) — У этого термина существуют и другие значения, см. Астеризм. Астеризм в кабошоне сапфира Астеризм (в минералогии)  оптический эффект в кристаллах некоторых минералов, обработанных с образованием сферической или другой выпуклой криволинейной… …   Википедия

• КРИСТАЛЛЫ И КРИСТАЛЛОГРАФИЯ — Кристаллом (от греч. krystallos прозрачный лед ) вначале называли прозрачный кварц (горный хрусталь), встречавшийся в Альпах. Горный хрусталь принимали за лед, затвердевший от холода до такой степени, что он уже не плавится. Первоначально главную …   Энциклопедия Кольера

• Кристаллографическая точечная группа симметрии — Кристаллографическая точечная группа симметрии  это точечная группа симметрии, которая описывает макросимметрию кристалла. Поскольку в кристаллах допустимы оси (поворотные и несобственного вращения) только 1, 2, 3, 4 и 6 порядков, из всего… …   Википедия

• КОНСТАНТЫ КРИСТАЛЛА ГЕОМЕТРИЧЕСКИЕ — углы между кристаллографическими координатными осями (α, β, γ) θ отношение отрезков, отсекаемых единичной гранью на координатных осях a: b : с (α угол между второй и третьей, β угол между первой и третьей, γ… …   Геологическая энциклопедия

• Магнетизм —     Классическая электродинамика …   Википедия

Угловой коэффициент — Википедия

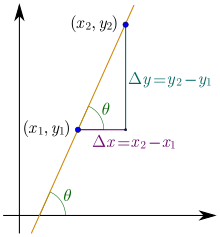Угловой коэффициент: k=ΔyΔx=tgθ{\displaystyle k={\frac {\Delta y}{\Delta x}}=\mathrm {tg} \,\theta }

Угловой коэффициент прямой — коэффициент k{\displaystyle k} в уравнении y=kx+b{\displaystyle y=kx+b} прямой на координатной плоскости, численно равен тангенсу угла (составляющего наименьший поворот от оси Ox к оси Оу) между положительным направлением оси абсцисс и данной прямой.^[1]

Тангенс угла может рассчитываться как отношение противолежащего катета к прилежащему. k всегда равен ΔyΔx{\displaystyle {\frac {\Delta y}{\Delta x}}}, то есть производной уравнения прямой по x.

Угловой коэффициент не существует (иногда формально говорят «обращается в бесконечность») для прямых, параллельных оси Oy.

При положительных значениях углового коэффициента k и нулевом значении коэффициента сдвига b прямая будет лежать в первом и третьем квадрантах (в которых x и y одновременно положительны и отрицательны). При этом большим значениям углового коэффициента k будет соответствовать более крутая прямая, а меньшим — более пологая.

Прямые y=k1x+b1{\displaystyle y=k_{1}x+b_{1}} и y=k2x+b2{\displaystyle y=k_{2}x+b_{2}} перпендикулярны, если k1k2=−1{\displaystyle k_{1}k_{2}=-1}, а параллельны при k1=k2{\displaystyle k_{1}=k_{2}}.

1. ↑ Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.

Угол между прямыми

Определение угла между прямыми

Две прямые называются пересекающимися, если они имеют единственную общую точку. Эта точка называется точкой пересечения прямых. Прямые разбиваются точкой пересечения на лучи, которые образуют четыре неразвернутых угла, среди которых две пары вертикальных углов и четыре пары смежных углов. Если известен размер одного из углов, образованных пересекающимися прямыми, то легко определить размер остальных углов. Если один из углов прямой, то все остальные тоже прямые, а прямые перпендикулярны.

Определение Угол между прямыми — размер наименьшего из углов, образованных этими прямыми.

Угол между прямыми на плоскости

Угол между прямыми заданными уравнениями с угловым коэффициентом

Если две прямые заданы уравнениями с угловым коэффициентом

y = k₁x + b₁,
y = k₂x + b₂,

то угол между ними можно найти, используя формулу:

tg γ = k₁ — k₂1 + k₁·k₂

Если знаменатель равен нулю (1 + k₁·k₂ = 0), то прямые перпендикулярны.

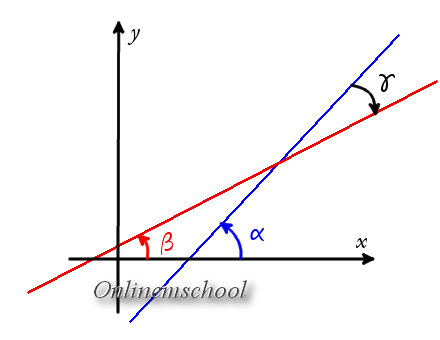Доказательство. Если прямые заданы уравнениями с угловыми коэффициентами, то легко найти углы между этими прямыми и осью OX

tg α = k₁
tg β = k₂

Соответственно легко найти угол между прямыми

γ = α — β

tg γ = tg (α — β) = tg α — tg β1 + tg α ·tg β = k₁ — k₂1 + k₁·k₂

Угол между прямыми через направляющие векторы этих прямых

Если a — направляющий вектор первой прямой и b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

cos φ = |a · b||a| · |b|

Если уравнение прямой задано параметрически

x = l t + ay = m t + b

то вектор направляющей имеет вид {l; m}

Если уравнение прямой задано как

A x + B y + C = 0

то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = -CB значит точка на прямой имеет координаты K(0, -CB), при y = 0 => x = -CA значит точка на прямой имеет координаты M(-CA, 0). Вектор направляющей KM = {-CA; CB}.

Если дано каноническое уравнение прямой

x — x₀l = y — y₀m

то вектор направляющей имеет вид {l; m}

Если задано уравнение прямой с угловым коэффициентом

y = kx + b

то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b). Вектор направляющей KM = {1; k}

Угол между прямыми через векторы нормалей этих прямых

Если a — вектор нормали первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

cos φ = |a · b||a| · |b|

Если уравнение прямой задано как

A x + B y + C = 0

то вектор нормали имеет вид {A; B}

Если задано уравнение прямой с угловым коэффициентом

y = kx + b

то вектор нормали имеет вид {1; -k}

Угол между прямыми через направляющий вектор и вектор нормали этих прямых

Если a — направляющий вектор первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

sin φ = |a · b||a| · |b|

Примеры задач на вычисления угла между прямыми на плоскости

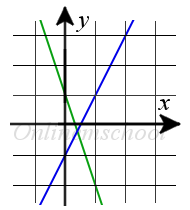Пример 1. Найти угол между прямыми y = 2x — 1 и y = -3x + 1.

Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:

tg γ = k₁ — k₂1 + k₁·k₂ = 2 — (-3)1 + 2·(-3) = 5-5 = 1

Ответ. γ = 45°

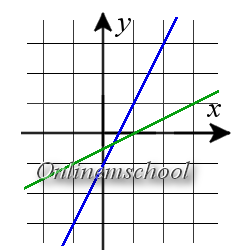Пример 2. Найти угол между прямыми y = 2x — 1 и x = 2t + 1y = t.

Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.

Для первой прямой направляющий вектор {1; 2}, для второй прямой направляющий вектор {2; 1}

cos φ = |1 · 2 + 2 · 1|1² + 2² · 2² + 1² = 45 · 5 = 0.8

Ответ. φ ≈ 36.87°

Пример 3 Найти угол между прямыми 2x + 3y = 0 и x — 23 = y4.

Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.

Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.

2x + 3y = 0 => y = -23x   (k₁ = -23)

x — 23 = y4 => y = 43x — 83   (k₂ = 43)

tg γ = k₁ — k₂1 + k₁·k₂ = -23 — 431 + (-23)·43 = -631 — 89 = 18

Ответ. γ ≈ 86.82°

Угол между прямыми в пространстве

Если a — направляющий вектор первой прямой, а b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

cos φ = |a · b||a| · |b|

Если дано каноническое уравнение прямой

x — x₀l = y — y₀m = z — z₀n

то направляющий вектор имеет вид {l; m; n}

Если уравнение прямой задано параметрически

x = l t + ay = m t + bz = n t + c

то направляющий вектор имеет вид {l; m; n}

Пример 4. Найти угол между прямыми x = 2t + 1y = tz = -t — 1 и x = t + 2y = -2t + 1z = 1.

Решение: Так как прямые заданы параметрически, то {2; 1; -1} — направляющий вектор первой прямой, {1; -2; 0} направляющий вектор второй прямой.

cos φ = |2 · 1 + 1 · (-2) + (-1) · 0|2² + 1² + (-1)² · 1² + (-2)² + 0² = 06 · 5 = 0

Ответ. φ = 90°

Пример 5 Найти угол между прямыми x — 23 = y4 = z — 35 и -x — 22 = 1 — 3y = 3z — 52.

Решение: Для решения этой задачи найдем направляющие векторы этих прямых.

Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор {3; 4; 5}.

Преобразуем второе уравнение к каноническому вид.

-x — 22 = x — 2-2

1 — 3y = 1 + y-1/3 = y — 1/3-1/3

3z — 52 = z — 5/32/3

Получено уравнение второй прямой в канонической форме

x — 2-2 = y — 1/3-1/3 = z — 5/32/3

{-2; -13; 23} — направляющий вектор второй прямой.

cos φ = 3·(-2) + 4·(-13) + 5·233² + 4² + 5² · (-2)² + (-13)² + (23)² = -6 — 43 + 1039 + 16 + 25 · 4 + 19 + 49 = -450 · 41/9 = 12582 = 682205

Ответ. φ ≈ 74.63°