Момент инерции цилиндра сплошного и полого относительно разных осей. Пример задачи :: SYL.ru
Как известно, масса в динамике поступательного движения играет важную роль, определяя инерционные свойства движущихся тел. В динамике вращения вместо массы пользуются моментом инерции. Рассмотрим в статье, что это за величина и как определяется момент инерции цилиндра относительно оси.
Что такое момент инерции?
Эту величину обычно обозначают буквой I. Для материальной точки математическая формула момента инерции записывается так:
I = m*r2.
Где r — расстояние до оси вращения от точки массой m. Из формулы понятно, что единицей измерения величины являются килограммы на квадратный метр (кг*м2).
Если тело имеет сложную форму и его объемная плотность является переменной, тогда для определения I следует использовать такое интегральное выражение:
I = ∫m(r2*dm) = ∫V(r2*ρ*dV).
Где dm — это элементарная масса, находящаяся от оси вращения на расстоянии r.
Таким образом, момент инерции определяет распределение материи в теле сложной формы относительно конкретной оси вращения системы.
Сплошной цилиндр и главная ось

Момент инерции сплошного цилиндра может быть вычислен вокруг абсолютно любой оси с использованием интегрального выражения, записанного в предыдущем пункте. Здесь рассмотрим ситуацию, когда цилиндр массой M, радиусом R и высотой L вращается вокруг главной оси. Последняя представляет собой прямую, параллельную генератрисе фигуры и проходящую через центры ее круглых оснований.
Не будем вдаваться в подробности математических вычислений по интегральной формуле, а приведем сразу конечное выражение:
I1 = 1/2*M*R2.
Мы видим, что чем больше масса цилиндра и его радиус, тем больше момент инерции I1. В то же время эта величина никак не зависит от высоты фигуры L, то есть момент инерции тонкого диска можно вычислить также по этой формуле.
Отметим, что если всю массу цилиндра собрать в одну материальную точку, находящуюся от оси вращения на расстоянии радиуса R, то для нее момент инерции окажется в два раза больше, чем для сплошного цилиндра.
Однородный цилиндр и перпендикулярная генератрисе ось
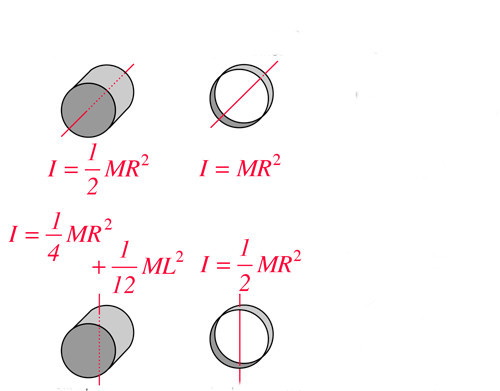
Теперь возьмем однородный цилиндр из примера выше и перевернем его на бок. Начнем вращать объект вокруг оси, которая проходит также через центр его масс, но уже перпендикулярна генератрисе (главной оси). Чему будет равен момент инерции цилиндра однородного в данном случае?
Как и в примере выше, здесь также ограничимся приведением соответствующего выражения. Оно будет иметь следующий вид:
I2 = 1/4*M*R2 + 1/12*M*L2.
Момент инерции I2 имеет более сложную зависимость от параметров цилиндра, чем I1, поскольку он определяется не только массой и радиусом, но и высотой фигуры. Заметим, что два слагаемых этой формулы представляют собой два крайних случая:
- Если цилиндр слишком маленькую высоту имеет, то мы получаем диск, который, вращаясь вокруг оси, проходящей через его диаметр, будет иметь момент 1/4*M*R2.
- Если радиус цилиндра стремится к нулю, то рассматриваемый объект превратится в стержень, и его момент инерции станет равным 1/12*M*L2.
Полый цилиндр
Выше мы рассмотрели, как рассчитывать момент инерции цилиндра вращающегося и однородного. Теперь предположим, что высота цилиндра и его масса остались теми же самыми, однако он стал полым, то есть, имеет два радиуса: внешний R1 и внутренний R2.
Применение все той же интегральной формулы позволяет получить выражение для момента инерции цилиндра полого, который вращается вокруг своей главной оси. Соответствующая формула выглядит так:
I3 = 1/2*M*(R12+R22).
Это выражение позволяет сделать важный вывод: при одинаковых массах полого и сплошного цилиндров первый обладает большим моментом инерции. Связан этот факт с тем, что большая часть массы полого цилиндра находится дальше от оси вращения, а как видно из формул, от радиуса изучаемая величина растет квадратично.

Где используются знания величин I для цилиндров?
Пожалуй, основной областью применения изложенной выше теории является автомобильная промышленность. В частности, коленчатый вал автомобиля снабжен тяжелым сплошным маховиком, имеющим цилиндрическую форму. Необходим маховик для того, чтобы обеспечить максимальную плавность вращения коленчатого вала, что отражается на плавности автомобильного хода. Маховик гасит любые большие угловые ускорения как во время разгона транспортного средства, так при его торможении.

Из формулы выше для момента инерции I1 понятно, что для увеличения этой величины выгоднее увеличить радиус, чем массу цилиндра (маховика). Так, удвоение массы приведет лишь к удвоению момента инерции. Однако если увеличить в два раза радиус, то I1 возрастет аж в 4 раза, что обеспечит более эффективное использование маховика.
Пример решения задачи
Прежде чем решать задачу, скажем несколько слов о динамике вращения. Как и в динамике поступательного движения, в ней существует формула, подобная второму закону Ньютона. Эта формула называется уравнением моментов. Записывается она так:
dL/dt = M.
Где L — момент импульса, M — момент внешних сил. Чаще всего это уравнение записывают в следующем виде:
M = I*α.
Здесь α — ускорение угловое. Из этого выражения видна аналогия со вторым ньютоновским законом.
Теперь перейдем к решению задачи. Известно, что сила в 100 Н действует по касательной к цилиндрической поверхности перпендикулярно главной оси вращения сплошного цилиндра на расстоянии 20 см. Масса цилиндра равна 10 кг, а его радиус составляет 20 см. Необходимо определить угловую скорость ω цилиндра через 5 секунд после начала действия силы.
Угловая скорость рассчитывается по формуле для равноускоренного движения:
ω = α*t.
Выражая ускорение из уравнения моментов и подставляя его в выражение, получим:
ω = M*t/I.
Момент силы вычисляется так:
M = F*d.
Где по условию задачи d = R. Подставляя это выражение и выражение для I сплошного цилиндра, получим конечную рабочую формулу:
ω = 2*F*t/(m*R).
Осталось сюда подставить все величины в единицах СИ и записать ответ: ω = 500 рад/с, что равно приблизительно 80 оборотам в секунду.
Момент инерции цилиндра сплошного и полого: разное положение осей вращения
Знание момента инерции тела позволяет воспользоваться законом сохранения момента импульса либо выражением для описания кругового движения с угловым ускорением. В данной статье рассмотрим, как находить для цилиндра момент инерции при различном положении осей вращения.
Момент инерции: математическое определение
Осевой момент инерции вводится в физику благодаря изучению законов вращательного движения тел. Для точки материальной с массой m, вращающейся на расстоянии r от оси, момент инерции будет равен:
I = m*r2
В общем же случае для тела, которое имеет произвольное распределение вещества в пространстве (любую геометрическую форму), величину I можно вычислить так:
I = ∫r2dm
По сути, это выражение является обобщением предыдущего. В нем производится суммирование (интегрирование) моментов от каждой элементарной частицы dm, дистанция до оси от которой равна r.
Если говорить о физическом значении рассматриваемой величины I, то она показывает, насколько «сильно» система сопротивляется воздействию внешнего момента силы, который пытается ее раскрутить или, наоборот, остановить.
Момент инерции цилиндра относительно оси, его основаниям перпендикулярной
Из приведенной выше формулы можно понять, что величина I является характеристикой всей вращающейся системы, то есть она зависит как от формы тела и распределения в нем массы, так и от относительного положения оси.
В данном пункте рассмотрим простой случай: определить необходимо момент инерции для сплошного цилиндра, ось вращения которого перпендикулярна его основаниям и проходит через гравитационный центр фигуры.
Для решения проблемы применим интегральную формулу для I. В процессе операции интегрирования мысленно разобьем цилиндр на тонкие колечки толщиной dr. Каждое колечко будет иметь объем: dV = 2*pi*r*dr*h, здесь h — высота фигуры. Учитывая, что dm = ρ*dV, где ρ — плотность цилиндра, получаем:
I = ∫r2dm = ρ*∫r2dV = 2*pi*ρ*h*∫r3dr
Этот интеграл необходимо вычислить для пределов от 0 до R, где R — радиус фигуры. Тогда получим:
I = 2*pi*ρ*h*∫R0r3dr = 2*pi*ρ*h/4*(r4)∣R0 = pi*ρ*h*R4/2
Воспользовавшись формулой для массы цилиндра через его объем и плотность, приходим к конечному выражению:
I = m*R2/2, где m = pi*ρ*h*R2
Мы получили формулу инерции момента цилиндра однородного. Она показывает, что величина I для этой фигуры в 2 раза меньше, чем для материальной точки аналогичной массы, которая вращается на расстоянии радиуса цилиндра от оси.
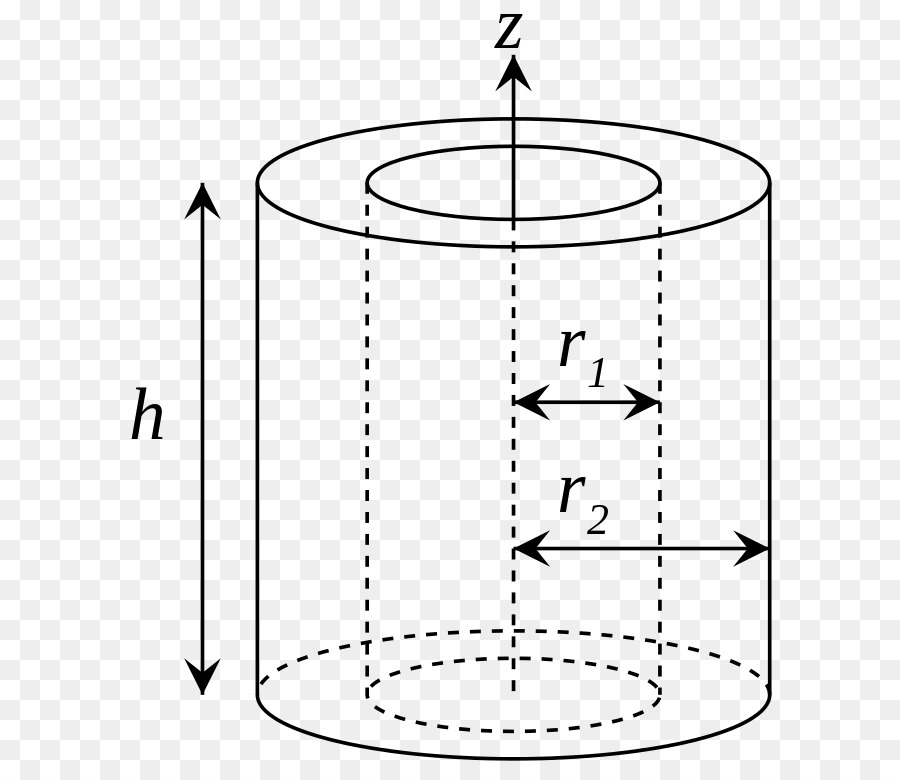
Момент инерции полого цилиндра
Теперь оставим ось на том же месте и найдем значение I для цилиндра с пустотой внутри (втулка, труба). Такую фигуру описывают двумя радиусами: внешним R1 и внутренним R2. В этом случае для интегрирования применяется абсолютно тот же подход, что и для сплошного цилиндра, только пределы теперь изменяются от R2 до R1. Имеем:
I = 2*pi*ρ*h/4*(r4)∣R1R2 = pi*ρ*h*R4/2∣R1R2 = pi*ρ*h/2*(R14-R24)
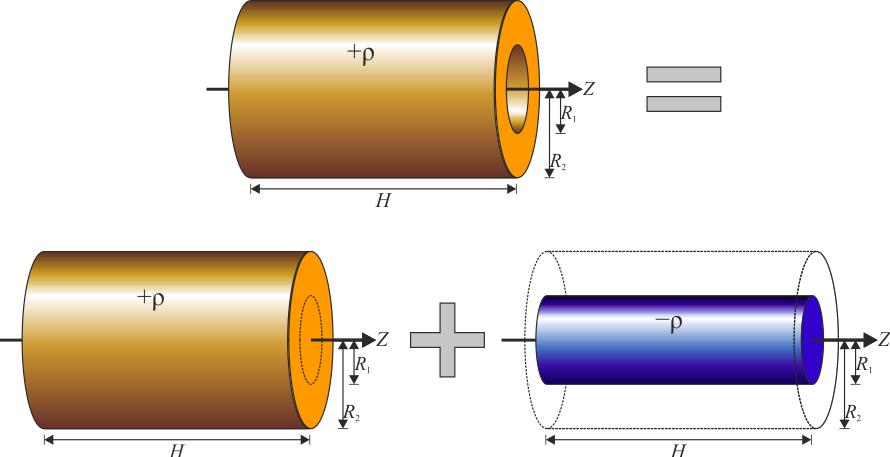
Для дальнейшего упрощения этой формулы воспользуемся разложением на множители выражения в скобках, получим:
I = pi*ρ*h*(R12-R22)*(R12+R22)/2
Часть этого выражения вместе с первыми скобками является массой полого цилиндра, поэтому получаем конечную формулу:
I = m*(R12+R22)/2
Отсюда видно, что момент инерции полого цилиндра больше этого значения для сплошного цилиндра аналогичной массы и такого же внешнего радиуса на величину m*R22/2. Этот результат не вызывает удивления, поскольку в полом цилиндре центр масс находится от оси вращения дальше, чем в сплошном.

Величина I для цилиндра, ось вращения которого проходит параллельно плоскостям его основания
В такой системе ось вращения проходит также через центр массы цилиндра, но теперь он лежит как бы на боку (на цилиндрической поверхности, см. рис. ниже).
Расчет для момента инерции цилиндра для такой ситуации является непростой задачей, поскольку требует наличия дополнительных знаний для ее решения. Тем не менее приведем необходимые математические выкладки, чтобы читатели имели более полное представление о проведении интегрирования при вычислении I.
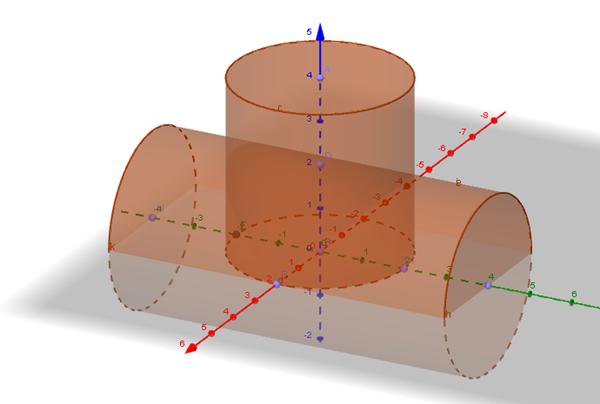
Начинаем решать задачу. Разбиваем сплошной цилиндр на отдельные диски бесконечно малой толщины. Чтобы узнать, каким моментом инерции обладает этот диск относительно оси, которая проходит через него и параллельна его основаниям, необходимо выполнить отдельное интегрирование. Оно дает следующий результат:
Ii = R2*dm/4
Чтобы найти, величину Ii для этого диска относительно уже новой оси, которая рассматривается в задаче, необходимо воспользоваться теоремой Штейнера. Получим:
Ii = R2*dm/4 + L2*dm, здесь L — расстояние от оси до тонкого диска.
Зная, что dm = pi*R2*dL*ρ, подставляем в интегральную формулу для I и проводим интегрирование по пределам (-L0/2; +L0/2), имеем:
I = ∫mIi = ∫m(R2*dm/4 + L2*dm) = pi*R2*ρ*∫L0/2-L0/2(R2*dL/4 + L2*dL)
Решение этого интеграла приводит к конечной формуле:
I = m*(R2/4 + L02/12)
Пример решения задачи
Решим интересную задачу на нахождение осевого момента инерции цилиндра. Пусть он лежит на цилиндрической поверхности, а ось вращения расположена параллельно его основанию и проходит через конец фигуры.
Эта ситуация полностью аналогична рассмотренной в предыдущем пункте, только ось пересекает не гравитационный центр цилиндра, а конец этой фигуры. Тем не менее для решения проблемы можно воспользоваться результатом предыдущего пункта статьи. Применим вышеупомянутую теорему Штейнера, получим:
I = m*R2/4 + m*L02/12 + m*(L0/2)2 = m*R2/4 + m*L02/3
Заметим, что если R<<L0, тогда первым слагаемым можно пренебречь, и формула сводится к равенству:
I = m*L02/3
Этот момент инерции соответствует стержню с осью вращения на его конце.
Глава 4
Механика твердого тела
§ 16. Момент инерции
При изучении вращения твердого тела пользуются понятием момента инерции. Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:
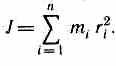
В случае непрерывного распределения масс эта сумма сводится к интегралу
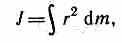
где интегрирование производится по всему объему тела. Величина r в этом случае есть функция положения точки с координатами
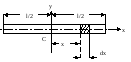
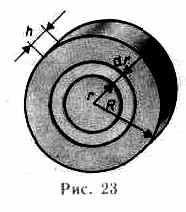
В качестве примера найдем момент инерции однородного сплошного цилиндра высотой Л и радиусом R относительно его геометрической оси (рис.23). Разобьем
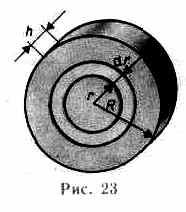
32
цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним — r+dr. Момент инерции каждого полого цилиндра dJ = r2dm (так как dr<<r, то считаем, что расстояние всех точек цилиндра от оси равно r), где dm — масса всего элементарного цилиндра; его объем
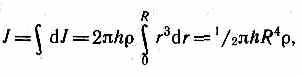
но так как R’2h — объем цилиндра, то его масса m = R2h, а момент инерции
J = 1/2R2.
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела
Таблица 1
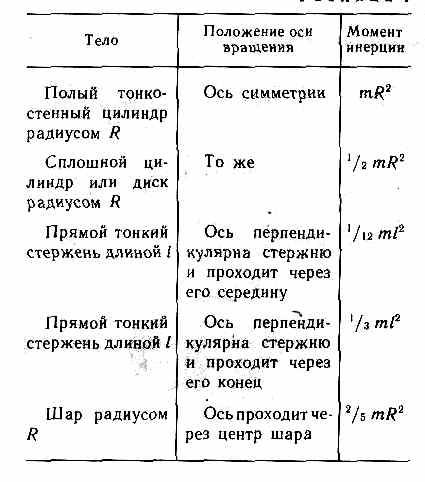
В заключение приведем значения моментов инерции (табл. 1) для некоторых тел (тела считаются однородными, т — масса тела).
§ 17. Кинетическая энергия вращения
= v1/r1= v2/r2 = … = vn/rn. (17.1)
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:
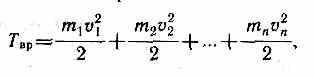

33
или
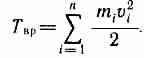
Используя выражение (17.1), получим
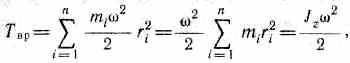
где Jz — момент инерции тела относительно оси 2. Таким образом, кинетическая энергия вращающегося тела
Tвр = Jz2/2. (17.2)
Из сравнения формулы (17.2) с выражением (12.1) для кинетической энергии тела, движущегося поступательно (T= mv2/2), следует, что момент инерции вращательного движения — мера инертности тела.
В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:
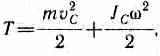
где m — масса катящегося тела; vc — скорость центра масс тела; J с — момент инерции тела относительно оси, проходящей через его центр масс; — угловая скорость тела.
10. Момент инерции относительно параллельных осей (теорема Гюйгенса

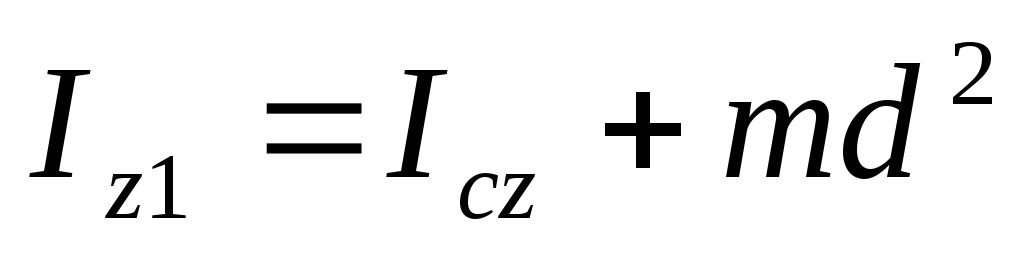 — теорема Гюйгенса
– Штейна.
— теорема Гюйгенса
– Штейна.
11. Осевые моменты инерции однородных тел: стержень, полый и сплошной цилиндры, шар.
— момент инерции тонкого прямого стержня постоянного сечения
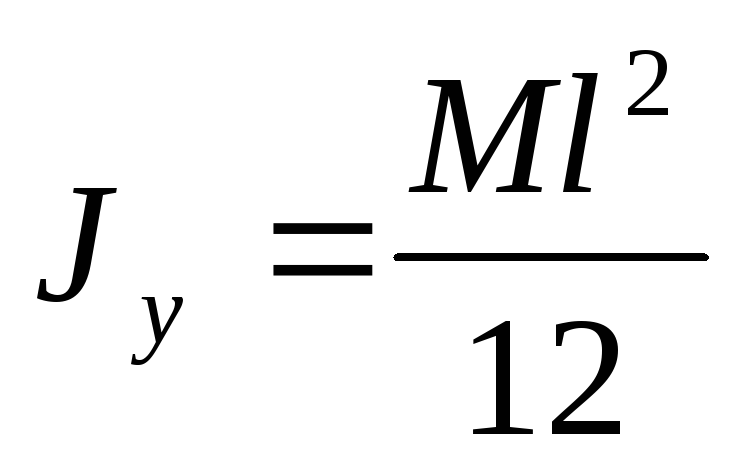
 Момент инерции
однородного прямого тонкого стержня
относительно его центральной оси
симметрии равен 1/12 произведения массы
стержня на квадрат его длины.
Момент инерции
однородного прямого тонкого стержня
относительно его центральной оси
симметрии равен 1/12 произведения массы
стержня на квадрат его длины.— момент инерции сплошного
круглого цилиндра.
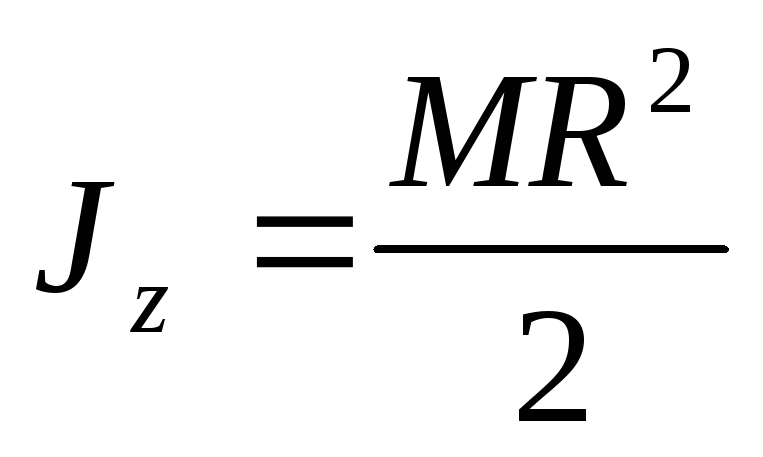
М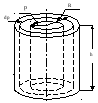 омент
инерции однородного сплошного круглого
цилиндра относительно его оси вращения
равен половине произведения массы
цилиндра на квадрат его радиуса.
омент
инерции однородного сплошного круглого
цилиндра относительно его оси вращения
равен половине произведения массы
цилиндра на квадрат его радиуса.
— момент инерции полого круглого цилиндра.
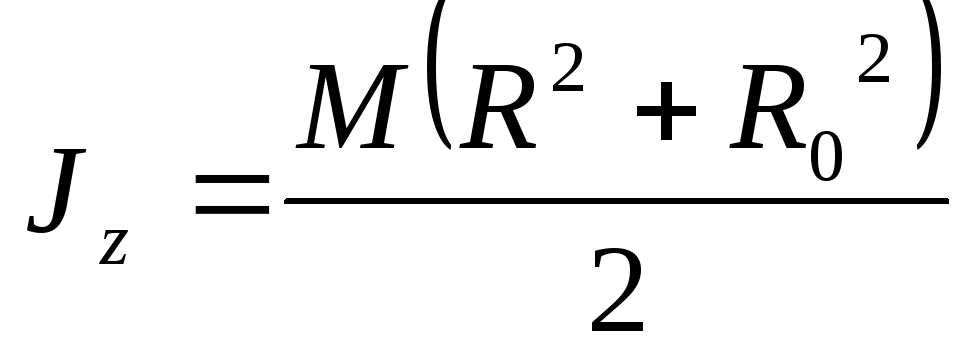
p
Момент инерции однородного полого круглого цилиндра относительно его оси вращения равен половине произведения массы цилиндра на сумму квадратов его наружного и внутреннего радиусов.
12. Динамическое уравнение вращения твердого тела вокруг неподвижной оси.
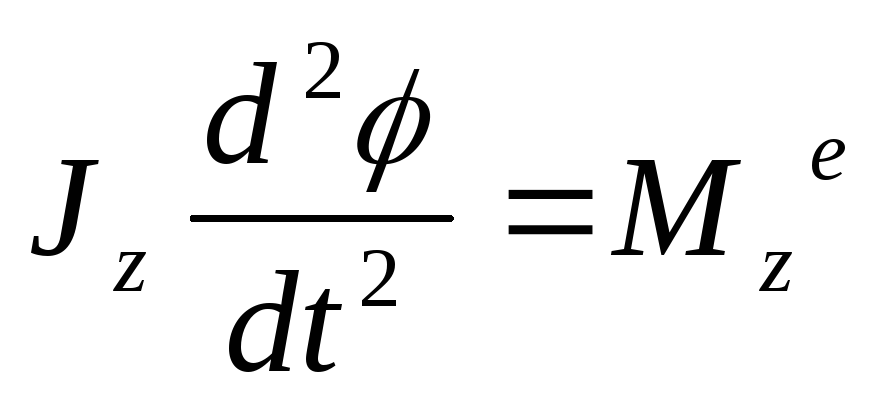 (1), где
(1), где 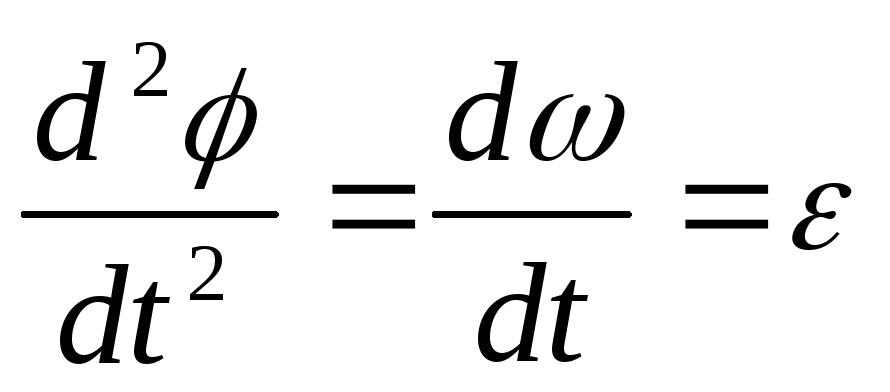
Произведение момента инерции тела относительно его оси вращения на угловое ускорение тела равно главному моменту всех приложенных к телу внешних сил относительно той же оси.
Уравнение (1) называется динамическим уравнением вращательного движения твердого тела.
13. Теорема об изменении кинетической энергии материальной системы.
Изменение кинетической энергии механической системы на некотором перемещении равно сумме работ внешних и внутренних сил, действующих на материальные точки системы на этом перемещении.
 ,
где Т – кинетическая энергия в конечный
момент времени
,
где Т – кинетическая энергия в конечный
момент времени
Т0 — кинетическая энергия в начальный момент времени
∑Аiе +∑Аij – сумма работ внешних и внутренних сил
Условие: необходимо начальное и конечное положения.
14. Кинетическая энергия материальной системы. Теорема Кенига.
Механическая система – совокупность тел, связанных между собой различными связями.
Положения и движение
каждого из тел взаимно обусловлено.
Кинетическая энергия механической
системы определяется как арифметическая
сумма кинетических энергий i-го
тела, входящего в систему. 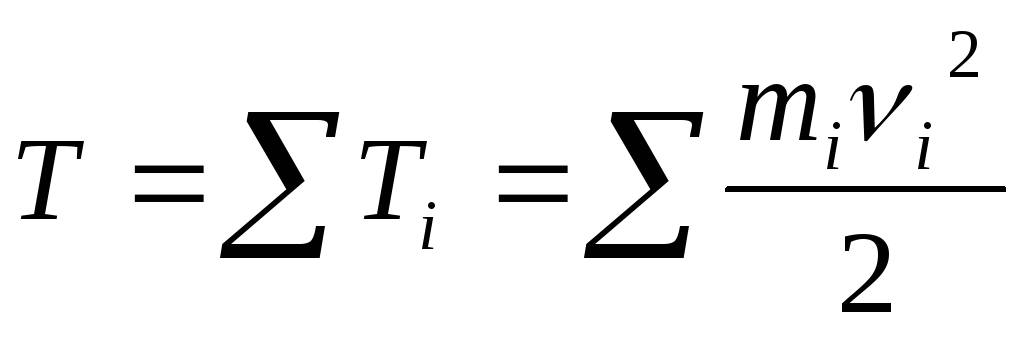
Теорема Кенига:
Кинетическая энергия механической системы равна сумме кинетической энергии центра масс системы, масса которого равна массе всей системы, и кинетической энергии этой системы в ее относительном движении относительно центра масс.
15. Кинетическая энергия твердого тела при разных видах его движения.
Кинетическая энергия тела определяется в зависимости от того – какое движение совершается.
1)поступательное
движение 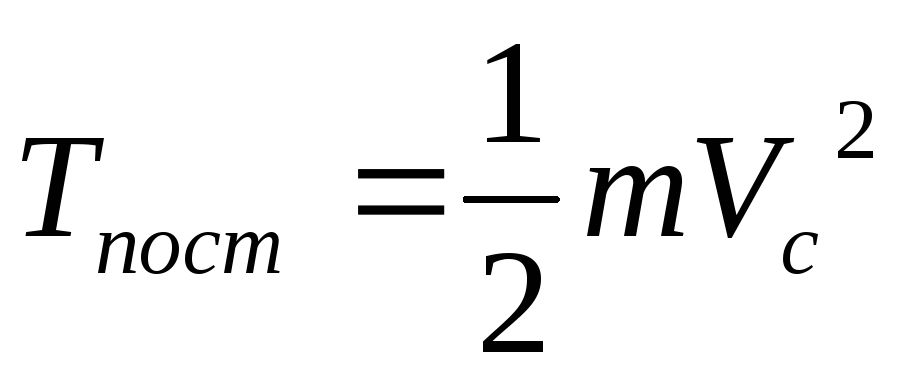
2)вращательное
движение 
3)плоскопараллельное
движение 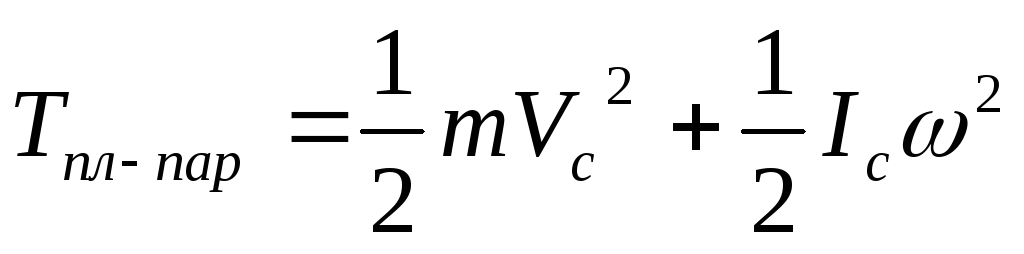
16. Динамическое плоскопараллельное движение твердого тела.

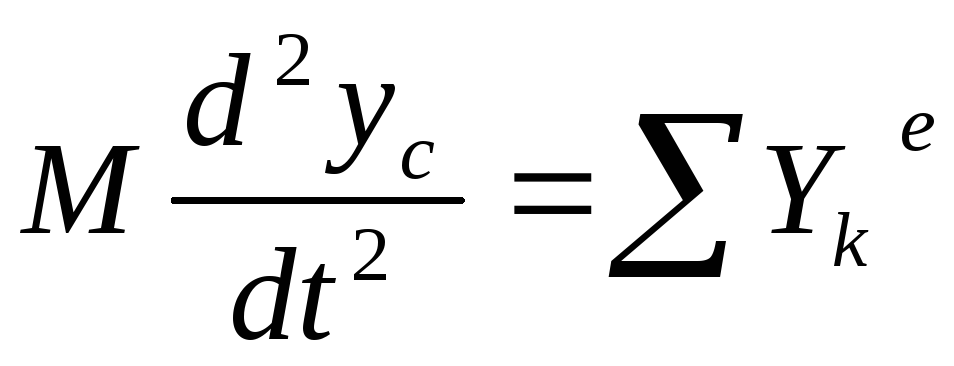
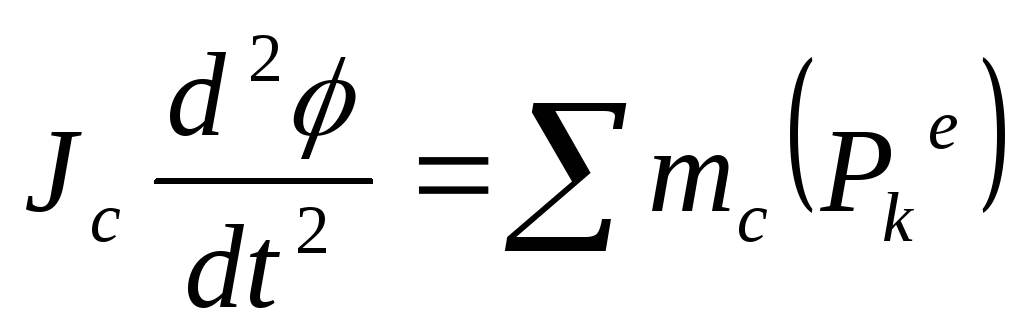
17. Принцип Даламбера для материальной точки.
Геометрическая
сумма всех приложенных к точке сил и
силы инерции этой точки равны нулю.  ,
где
,
где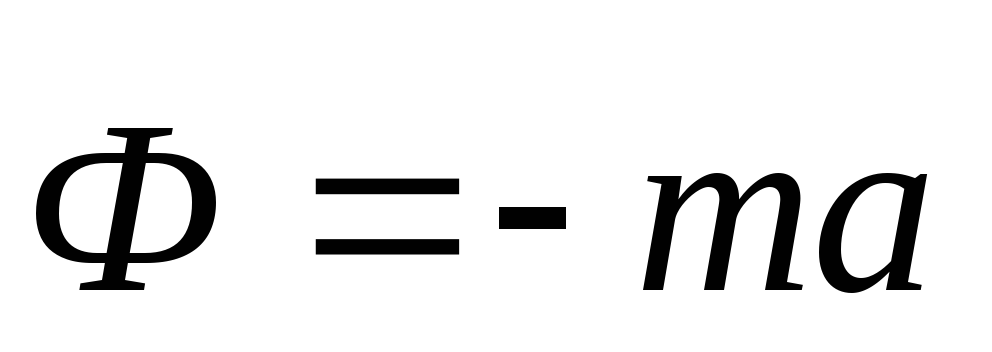
18. Принцип Даламбера для материальной системы.
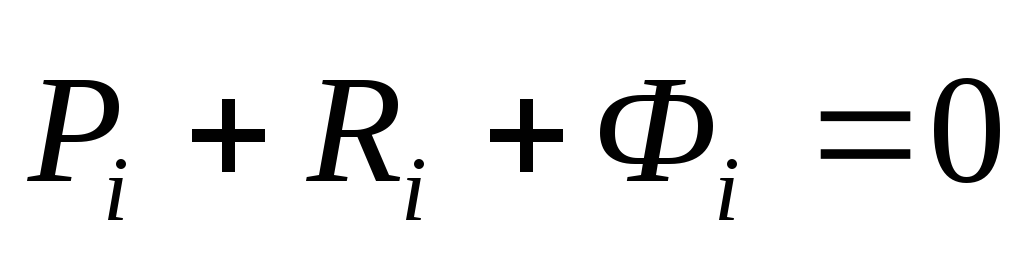 (i=1,2,…,n),
где
(i=1,2,…,n),
где 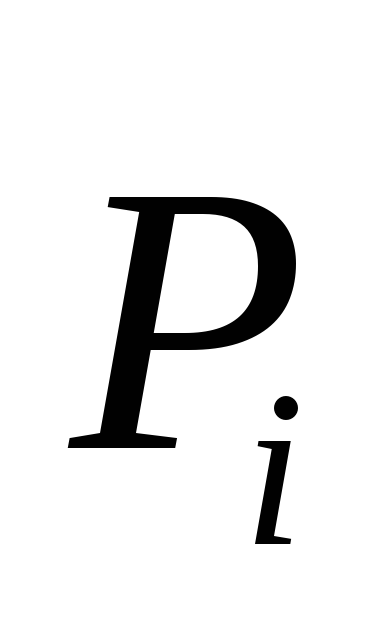 -равнодействующая
задаваемых сил, приложенных к точке;
-равнодействующая
задаваемых сил, приложенных к точке;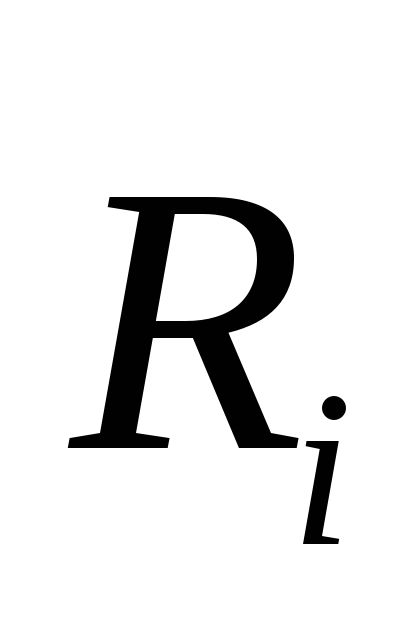 -равнодействующая
реакций связей, приложенных к этой
точке;
-равнодействующая
реакций связей, приложенных к этой
точке;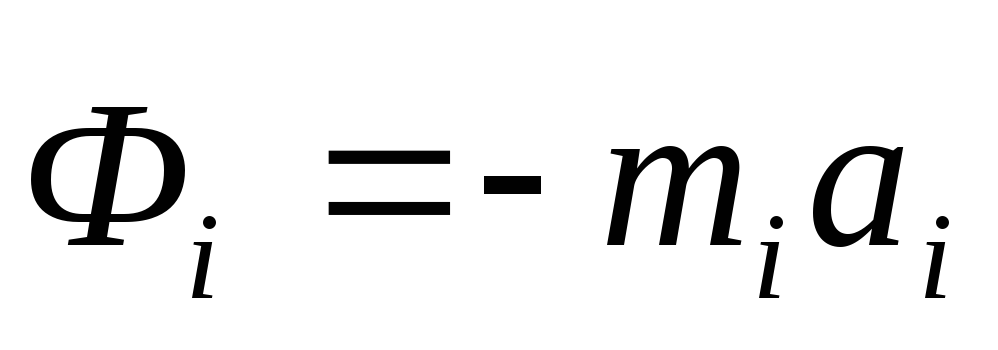 -сила
инерции материальной точки.
-сила
инерции материальной точки.
Уравнение показывает, что в любой момент времени геометрическая сумма равнодействующей задаваемых сил, равнодействующей реакции связей и силы инерции для каждой материальной точки несвободной механической системы равна нулю.
19. Главный вектор и главный момент сил инерции абсолютно твердого тела.
— поступательное движение
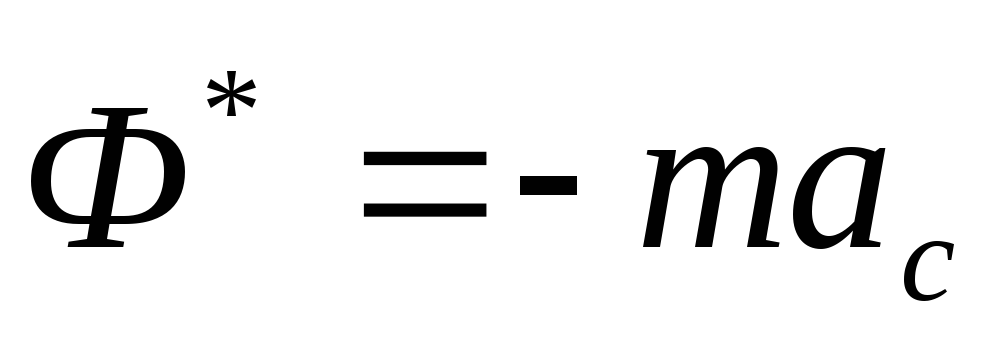 — главный вектор,
— главный вектор, 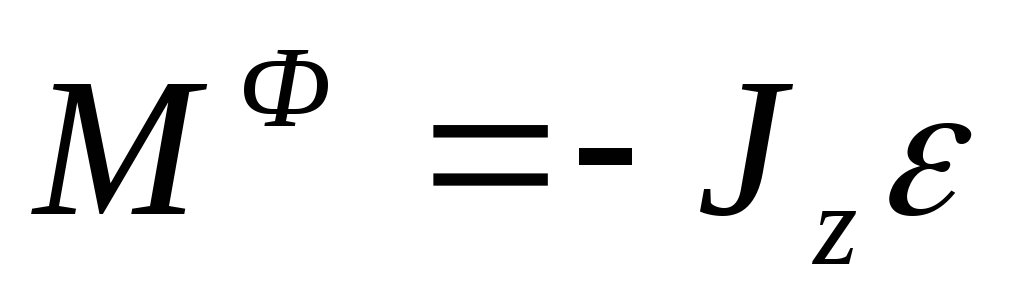 — главный момент, гдеJz – момент инерции тела относительно оси
вращения, ε – алгебраическая величина
углового ускорения тела.
— главный момент, гдеJz – момент инерции тела относительно оси
вращения, ε – алгебраическая величина
углового ускорения тела.
20. Механические связи, удерживающие и неудерживающие связи, стационарные и нестационарные, головные и неголовные.
Связи – тела, ограничивающие свободу перемещения другого тела.
OA=l
– гибкая нить 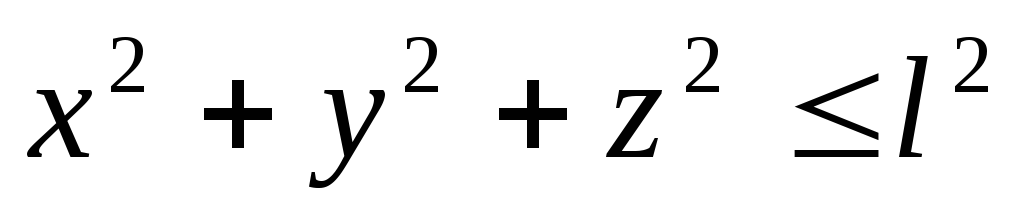 — уравнение жесткой связи
— уравнение жесткой связи
К лассификация
связей:
лассификация
связей:
1)головные – связи, уравнения которых не содержат
дифференциалы координат.
2)неголовные – связи, уравнения которых содержат
дифференциалы координат.
— стационарные (уравнения которых не содержат
параметр t.)
— нестационарные (уравнения которых содержат
параметр t.)
— удерживающие (уравнение определяется
равенством).
— неудерживающие (уравнение определяется неравенством).
Глава 4 Механика твердого тела § 16. Момент инерции
При изучении вращения твердых тел будем пользоваться понятием момента инерции. Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная суммепроизведений масс л материальных точек системы на квадраты их расстояний до рассматриваемой оси:
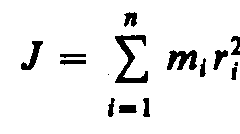
В случае непрерывного распределения масс эта сумма сводится к интегралу
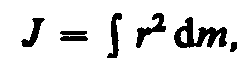
где интегрирование производится по всему объему тела. Величина rв этом случае есть функция положения точки с координатамих, у, z.
В качестве примера найдем момент инерции однородного сплошного цилиндра высотой hи радиусомRотносительно его геометрической оси (рис. 23). Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщиныdrс внутренним радиусомrи внешнимr+dr. Момент инерции каждого полого цилиндраdJ=r2dm(так какdr<<r,то считаем, что расстояние всех точек цилиндра от оси равноr), гдеdm —масса всего элементарного цилиндра; его объем 2rhdr.Если—плотность материала, тоdm=2rhdrи dJ=2hrзdr.Тогда момент инерции сплошного цилиндра
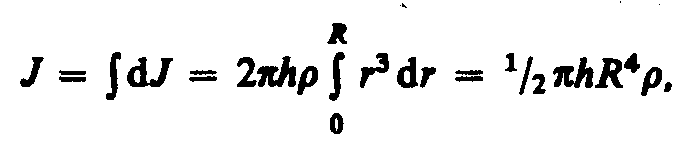
но так как R2h —объем цилиндра, то его массаm=R2h,а момент инерции
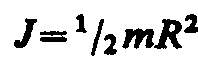
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера:момент инерции телаJотносительно произвольной оси равен моменту его инерцииJcотносительно параллельной оси, проходящей через центр массСтела, сложенному с произведением массыттела на квадрат расстоянияамежду осями:
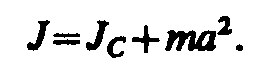 (16.1)
(16.1)
В заключение приведем значения моментов инерции (табл. 1) для некоторых тел (тела считаются однородными, т —масса тела).
Таблица 1


§ 17. Кинетическая энергия вращения
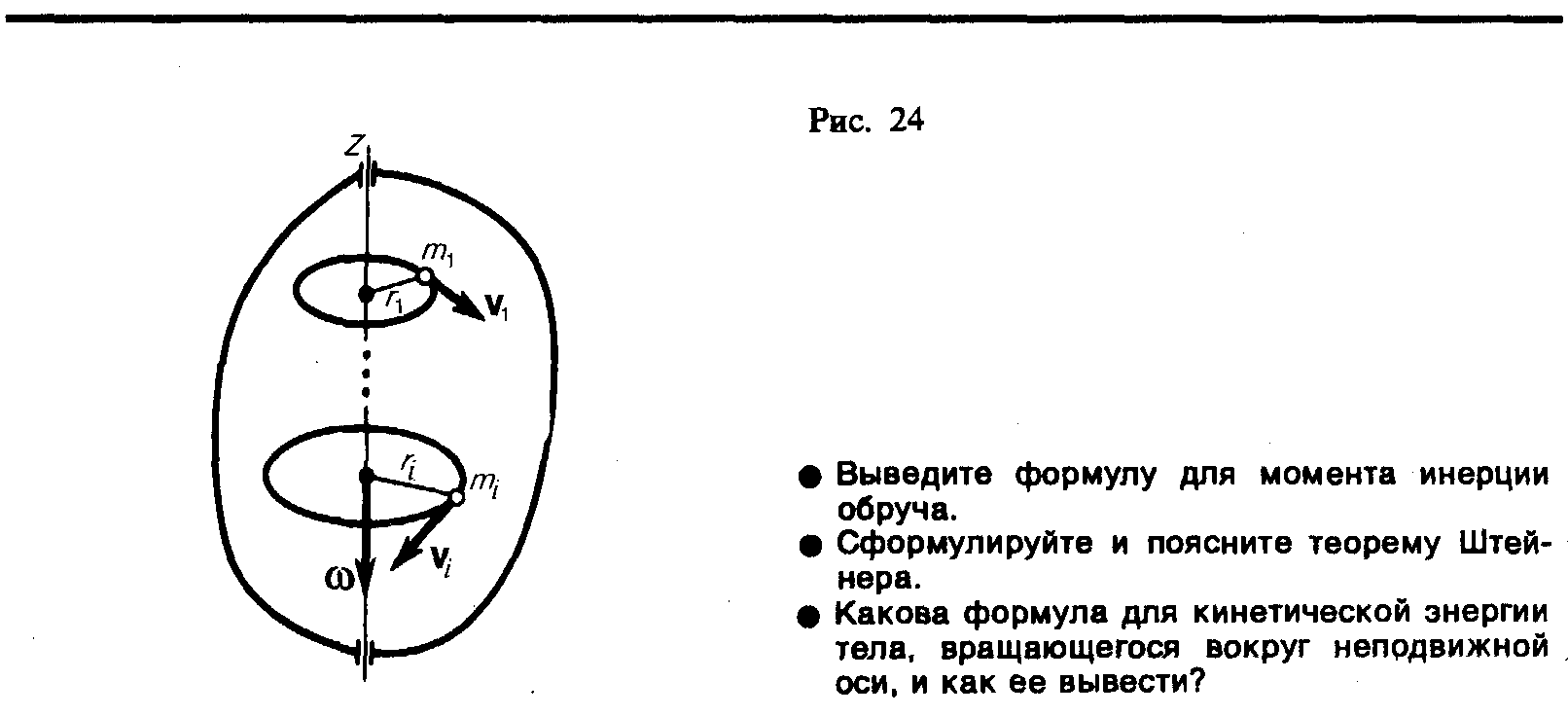
Рассмотрим абсолютно твердое тело (см. § 1), вращающееся около неподвижной оси z, проходящей через него (рис. 24). Мысленно разобьем это тело на маленькие объемы с элементарными массамит1, т2 ,…, тn ,находящиеся на расстоянииr1,r2,…,rnот оси.
При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами miопишут окружности различных радиусовri, и имеют различные линейные скоростиvi.Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:
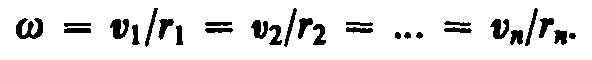 (17.1)
(17.1)
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:
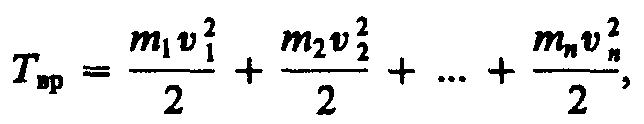
или

Используя выражение (17.1), получаем
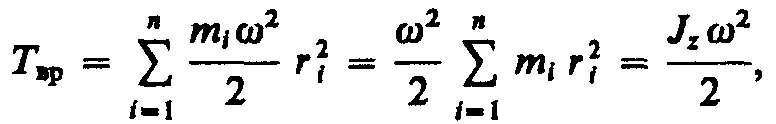
где Jz —момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела
 (17.2)
(17.2)
Из сравнения формулы (17.2) с выражением (12.1) для кинетической энергии тела движущегося поступательно (T=mv2/2),следует, что момент инерции —мера инертности телапри вращательном движении. Формула (17.2) справедлива для тела вращающегося вокруг неподвижной оси.
В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:
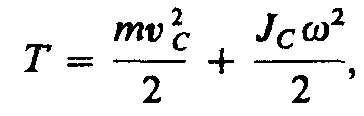
где m— масса катящегося тела;vc —скорость центра масс тела;Jc —момент инерции тела относительно оси, проходящей через его центр масс;— угловая скорость тела.
Глава 4
Механика твердого тела
§ 16. Момент инерции
При изучении вращения твердого тела пользуются понятием момента инерции. Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:
В случае непрерывного распределения масс эта сумма сводится к интегралу

где интегрирование производится по всему объему тела. Величина r в этом случае есть функция положения точки с координатами х, у, z.
В качестве примера найдем момент инерции однородного сплошного цилиндра высотой Л и радиусом R относительно его геометрической оси (рис.23). Разобьем
32
цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним — r+dr. Момент инерции каждого полого цилиндра dJ = r2dm (так как dr<<r, то считаем, что расстояние всех точек цилиндра от оси равно r), где dm — масса всего элементарного цилиндра; его объем 2rhdr. Если — плотность материала, то dm=•2rhdr и dJ = 2r3dr. Тогда момент инерции сплошного цилиндра
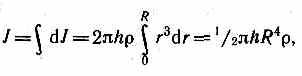
но так как R’2h — объем цилиндра, то его масса m = R2h, а момент инерции
J = 1/2R2.
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно любой оси вращения равен моменту его инерции Jc относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями: J = Jc + ma2. (16.1)
Таблица 1

В заключение приведем значения моментов инерции (табл. 1) для некоторых тел (тела считаются однородными, т — масса тела).
§ 17. Кинетическая энергия вращения
Рассмотрим абсолютно твердое тело (см. § 1), вращающееся около неподвижной оси z, проходящей через него (рис. 24). Мысленно разобьем это тело на маленькие объемы с элементарными массами m1, m2, …, mn, находящиеся на расстоянии r1, r2, …, rn от оси вращения. При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами mi, опишут окружности различных радиусов ri и имеют различные линейные скорости vi. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова:
= v1/r1= v2/r2 = … = vn/rn. (17.1)
Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов:
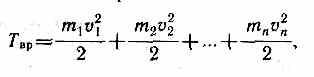
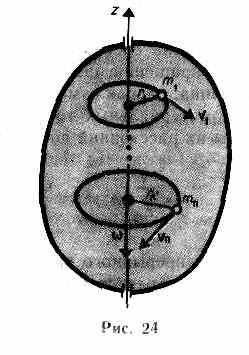
33
или
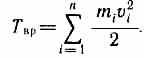
Используя выражение (17.1), получим
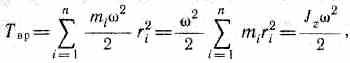
где Jz — момент инерции тела относительно оси 2. Таким образом, кинетическая энергия вращающегося тела
Tвр = Jz2/2. (17.2)
Из сравнения формулы (17.2) с выражением (12.1) для кинетической энергии тела, движущегося поступательно (T= mv2/2), следует, что момент инерции вращательного движения — мера инертности тела. Формула (17.2) справедлива для тела, вращающегося вокруг неподвижной оси.
В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения:
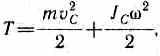
где m — масса катящегося тела; vc — скорость центра масс тела; J с — момент инерции тела относительно оси, проходящей через его центр масс; — угловая скорость тела.
9. Понятие о моменте инерции тела. Радиус инерции.
Моментом инерции твердого тела относительно какой – либо осиz (осевым моментом инерции) называется скалярная величина, равная сумме, составленной из произведений массы mk каждой точки тела на квадрат ее расстояния rk до данной оси.
Момент инерции бесконечно тонкого кольца (материальной окружности) относительно его оси вращения равен произведению его массы на квадрат радиуса:
Момент инерции тела относительно оси представить в виде произведения массы тела на квадрат длины некоторого отрезка , называемого радиусом инерции тела относительно соответствующей оси:
Под радиусом инерции тела относительно какой – либо оси можно понимать радиус такого бесконечно тонкого кольца, в котором нужно сосредоточить всю массу М тела, чтобы получить момент инерции кольца, равный моменту инерции тела относительно этой оси.
10. Момент инерции относительно параллельных осей (теорема Гюйгенса — Штейна).
Момент инерции тела относительно какой – либо оси равен моменту инерции этого тела относительно центральной оси, параллельной данной оси, сложенному с произведением массы тела на квадрат расстояния между этими осями.
— теорема Гюйгенса – Штейна.
11. Осевые моменты инерции однородных тел: стержень, полый и сплошной цилиндры, шар.
— момент инерции тонкого прямого стержня постоянного сечения
Момент инерции однородного прямого тонкого стержня относительно его центральной оси симметрии равен 1/12 произведения массы стержня на квадрат его длины.
— момент инерции сплошного
круглого цилиндра.
Момент инерции однородного сплошного круглого цилиндра относительно его оси вращения равен половине произведения массы цилиндра на квадрат его радиуса.
— момент инерции полого круглого цилиндра.
Момент инерции однородного полого круглого цилиндра относительно его оси вращения равен половине произведения массы цилиндра на сумму квадратов его наружного и внутреннего радиусов.
12. Динамическое уравнение вращения твердого тела вокруг неподвижной оси.
(1), где
Произведение момента инерции тела относительно его оси вращения на угловое ускорение тела равно главному моменту всех приложенных к телу внешних сил относительно той же оси.
Уравнение (1) называется динамическим уравнением вращательного движения твердого тела.
13. Теорема об изменении кинетической энергии материальной системы.
Изменение кинетической энергии механической системы на некотором перемещении равно сумме работ внешних и внутренних сил, действующих на материальные точки системы на этом перемещении.
, где Т – кинетическая энергия в конечный момент времени
Т0 — кинетическая энергия в начальный момент времени
∑Аiе +∑Аij – сумма работ внешних и внутренних сил
Условие: необходимо начальное и конечное положения.
14. Кинетическая энергия материальной системы. Теорема Кенига.
Механическая система – совокупность тел, связанных между собой различными связями.
Положения и движение каждого из тел взаимно обусловлено. Кинетическая энергия механической системы определяется как арифметическая сумма кинетических энергий i-го тела, входящего в систему.
Теорема Кенига:
Кинетическая энергия механической системы равна сумме кинетической энергии центра масс системы, масса которого равна массе всей системы, и кинетической энергии этой системы в ее относительном движении относительно центра масс.

