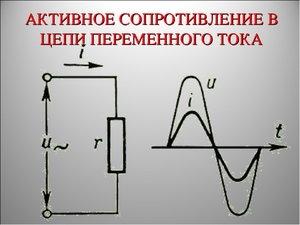
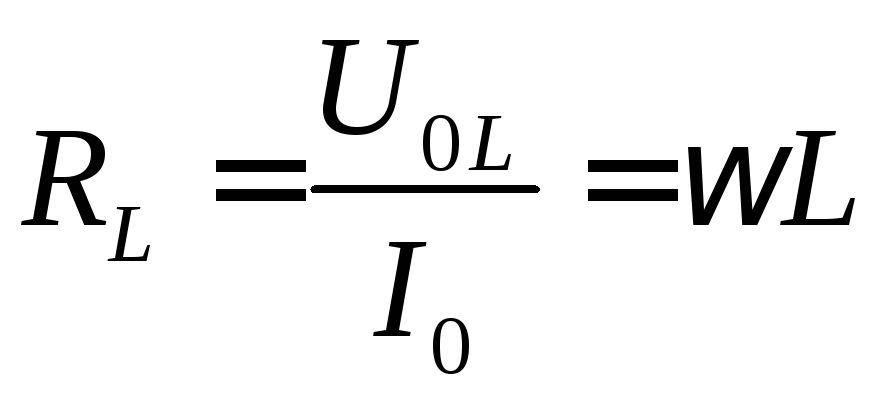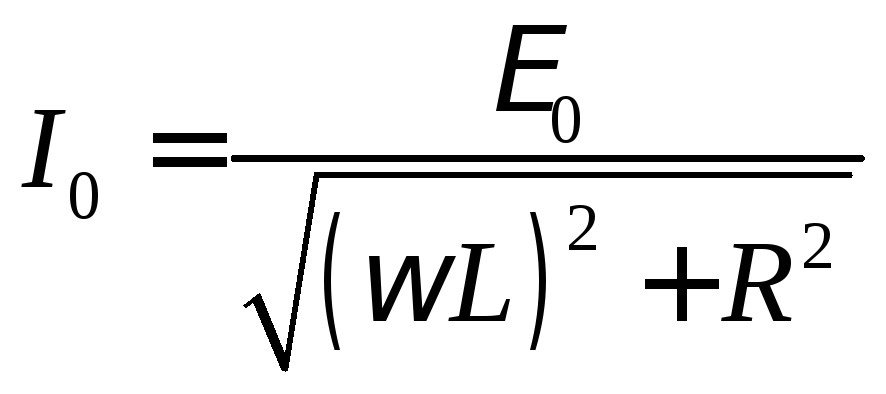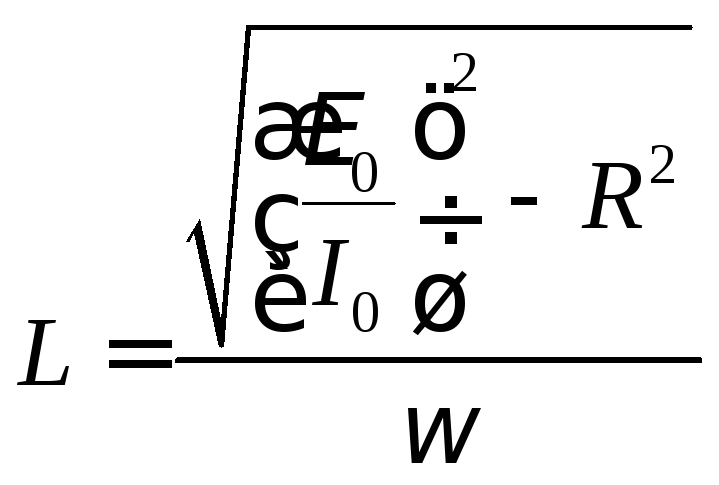6.2 Активное сопротивление в цепи переменного тока
Рассмотрим сначала частный случай, когда генератор переменного тока замкнут на внешнюю цепь, имеющую сопротивление R и настолько малые индуктивность и емкость, что ими можно пренебречь. Сопротивление резистора называется активным, так как оно обуславливает необратимый переход электрической энергии во внутреннюю энергию проводника, который при этом нагревается. Положим, что в цепи идет переменный ток
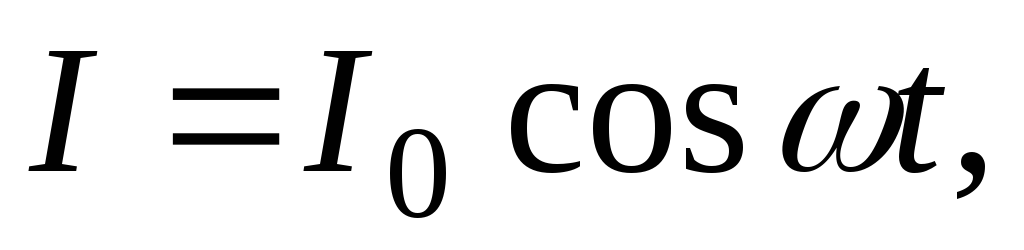 (6.2)
(6.2)
и найдем, по какому закону изменяется напряжение между концами внешней цепи (рисунок 6.1).
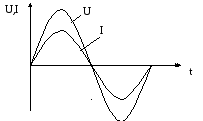
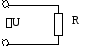
Рисунок 6.1 Рисунок 6.2
Применяя закон Ома, имеем
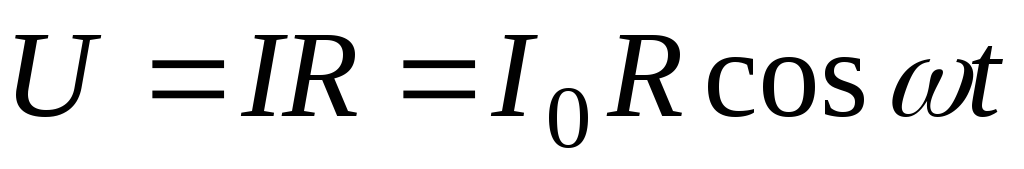 . (6.3)
. (6.3)
Таким образом,
напряжение на концах участка цепи
изменяется также по гармоническому
закону, причем разность фаз между
колебаниями тока и напряжения равна
нулю. Это означает, что напряжение и ток
одновременно достигают максимальных
значений, одновременно обращаются в
нуль и т. д. (рисунок 6.2). Максимальное
значение напряжения 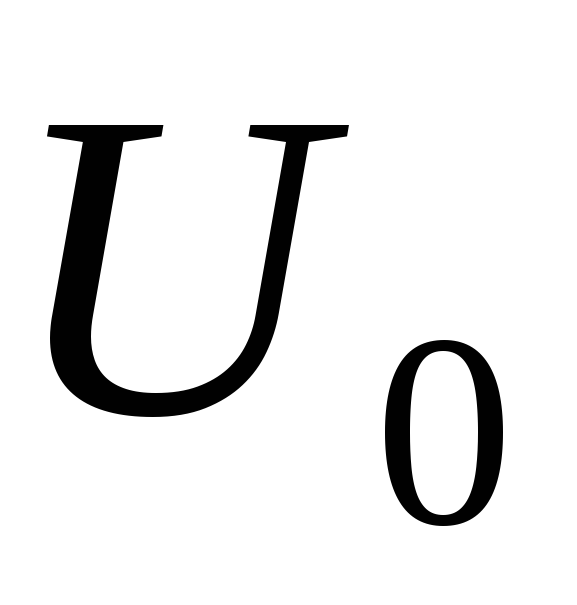
 участка цепи
участка цепи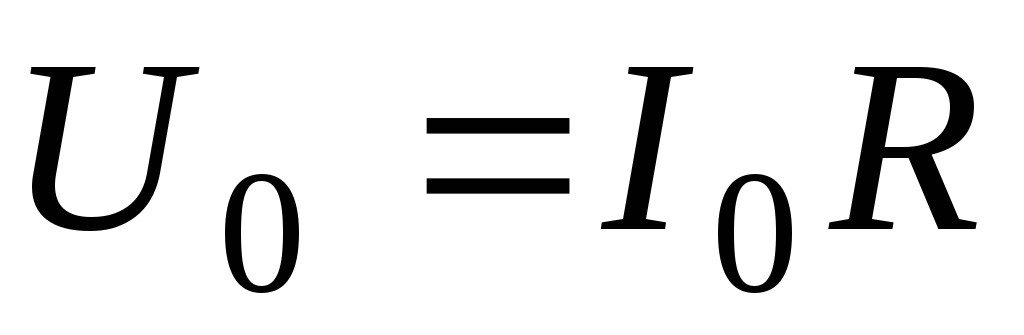 .
.Гармонически изменяющиеся величины можно наглядно изображать при помощи векторных диаграмм.
Выберем ось
диаграммы таким образом, чтобы вектор,
изображающий колебания тока, был
направлен вдоль этой оси. В дальнейшем
мы будем называть его осью
токов. Вектор,
изображающий колебания напряжения,
будет направлен вдоль оси токов (рисунок
6.3). Поскольку разность фаз между током
и напряжением равна нулю, то длина этого
вектора равна амплитуде напряжения 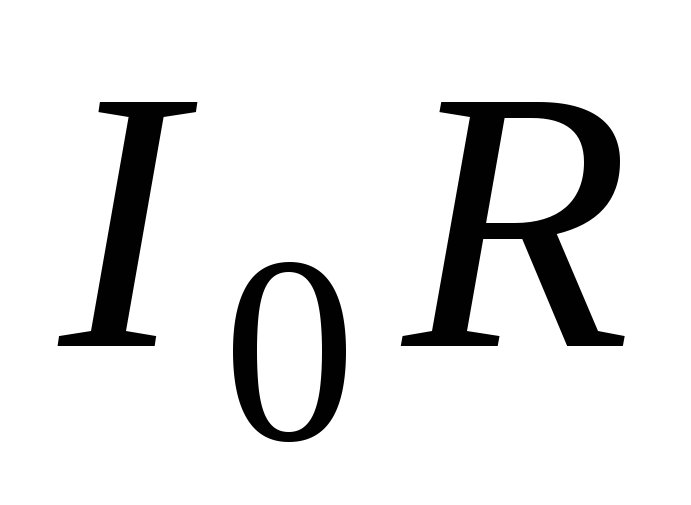

Рисунок 6.3
6.3 Емкость в цепи переменного тока
Положим теперь,
что участок цепи содержит конденсатор
емкости  ,
причем сопротивлением и индуктивностью
можно пренебречь. Выясним, по какому
закону будет изменяться напряжение на
концах участка цепи в этом случае.
Полагаем, что сила тока изменяется по
закону
,
причем сопротивлением и индуктивностью
можно пренебречь. Выясним, по какому
закону будет изменяться напряжение на
концах участка цепи в этом случае.
Полагаем, что сила тока изменяется по
закону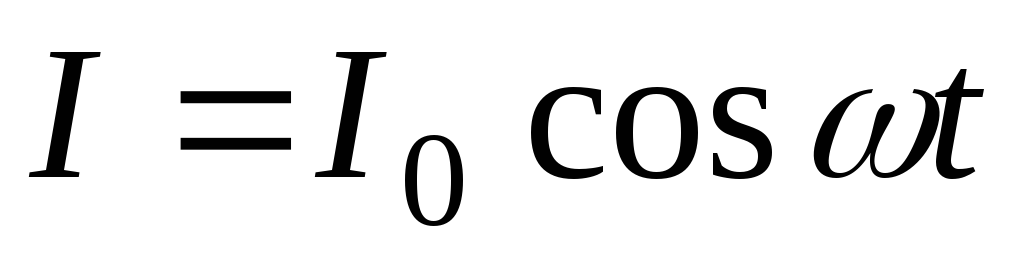
Напряжение на конденсаторе равно
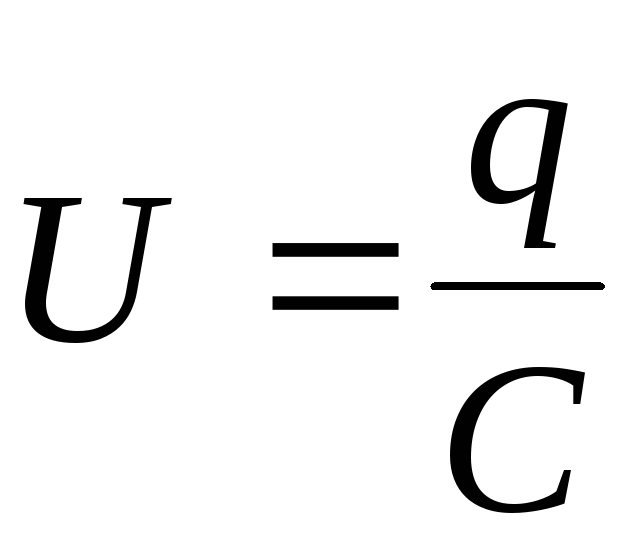 . (6.4)
. (6.4)
Ток можно записать
через величину заряда 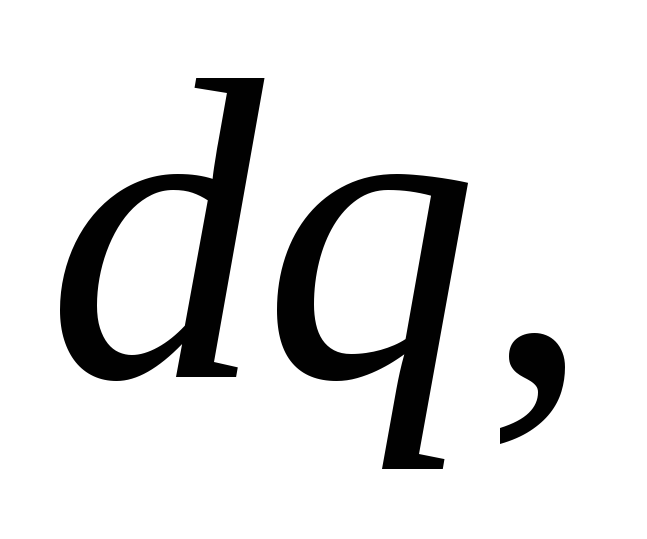 протекающего через сечение проводника
и увеличивающего заряд конденсатора
за промежуток времени
протекающего через сечение проводника
и увеличивающего заряд конденсатора
за промежуток времени
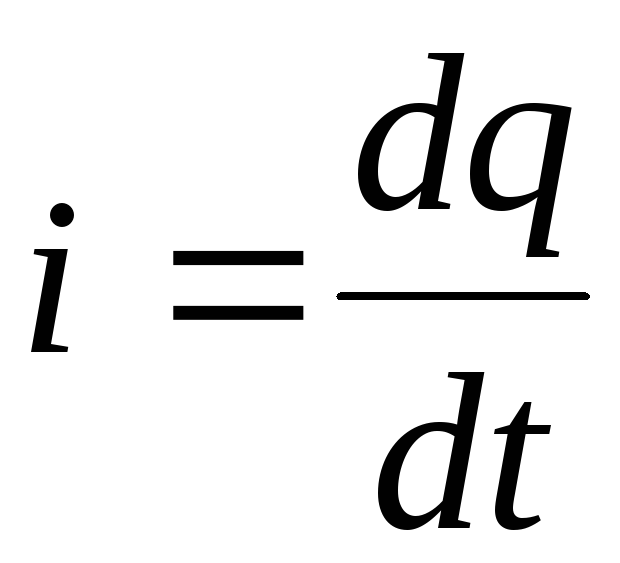
Тогда заряд конденсатора можно найти интегрированием
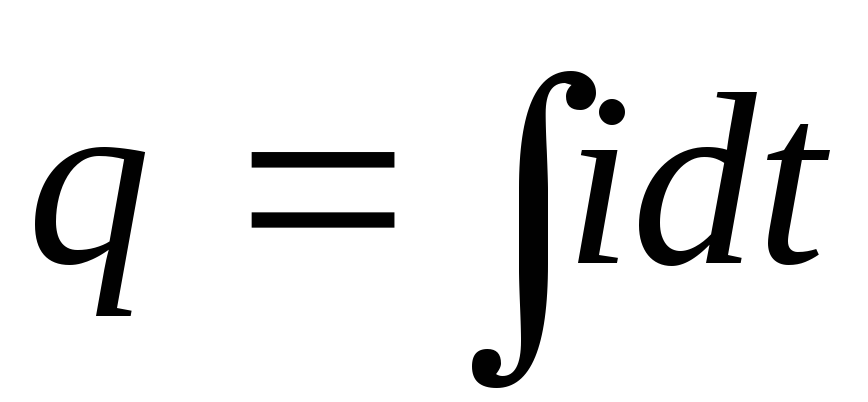 . (6.6)
. (6.6)
Поскольку сила тока в цепи изменяется по закону
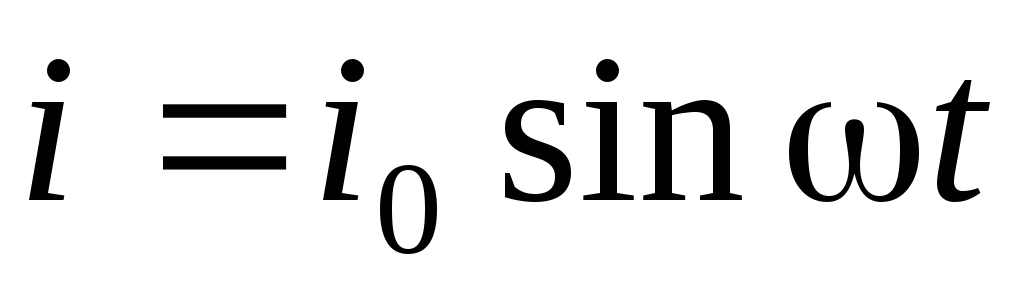 , (6.7)
, (6.7)
то заряд равен
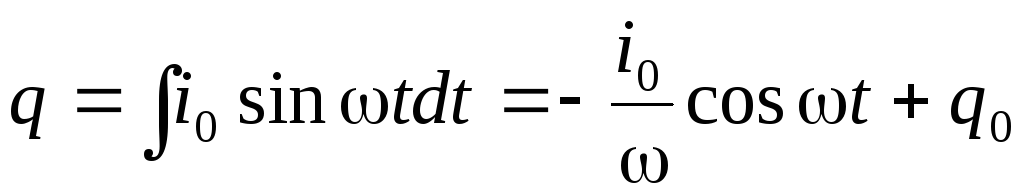 . (6.8)
. (6.8)
Постоянная
интегрирования 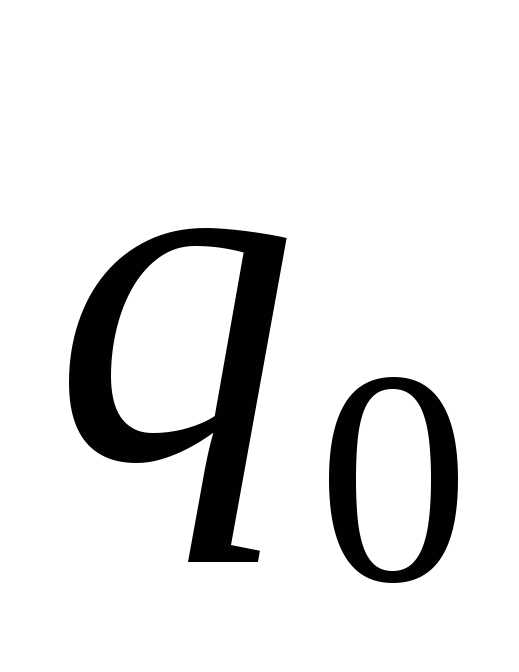
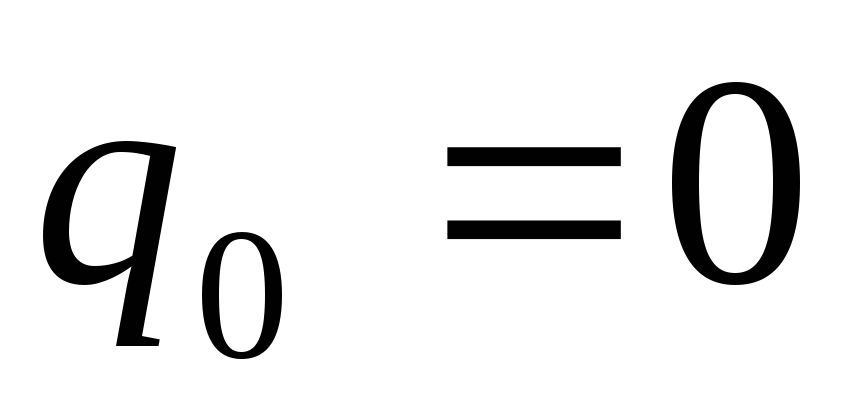 .
Следовательно, с учетом формулы (6.4)
можно записать для напряжения
.
Следовательно, с учетом формулы (6.4)
можно записать для напряжения 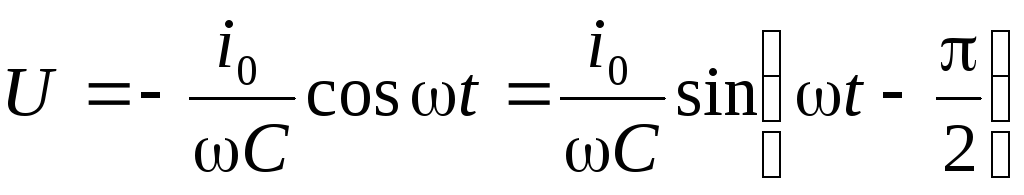
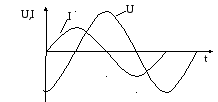 (6.9)
(6.9)
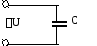
Рисунок 6.4 Рисунок 6.5
Сравнение выражений
(6.7) и (6.9) показывает, что при гармонических
колебаниях тока в цепи напряжение на
конденсаторе изменяется также по
гармоническому закону, однако колебания
напряжения на конденсаторе отстают по
фазе от колебаний тока на 
Изменение тока и напряжения во времени изображено графически на рисунке 6.5.
Полученный результат
имеет простой физический смысл. Напряжение
на конденсаторе в какой – либо момент
времени определяется существующим
зарядом конденсатора. Но этот заряд был
образован током, протекавшим предварительно
в более ранней стадии колебаний. Поэтому
колебания напряжения, как и колебания
заряда, запаздывают относительно
колебаний тока. Так, например, когда в
момент времени 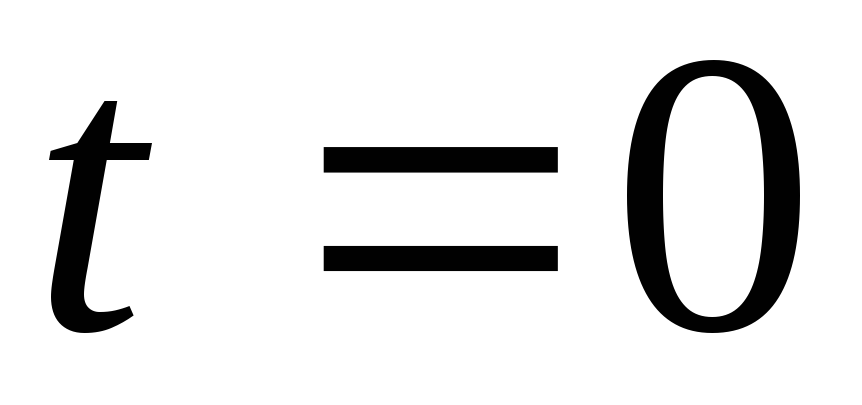
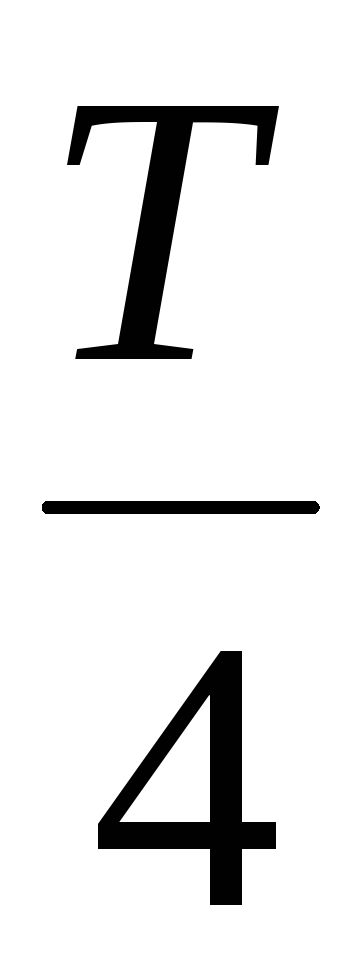 ,
проходил ток положительного направления.
Однако, когда заряд конденсатора (а
значит, и напряжение) станет равным
нулю, сила тока уже не будет равна нулю
(рисунок 6.5)–она принимает максимальное
значение.
,
проходил ток положительного направления.
Однако, когда заряд конденсатора (а
значит, и напряжение) станет равным
нулю, сила тока уже не будет равна нулю
(рисунок 6.5)–она принимает максимальное
значение.Формула (6.9) показывает, что амплитуда напряжения на конденсаторе равна
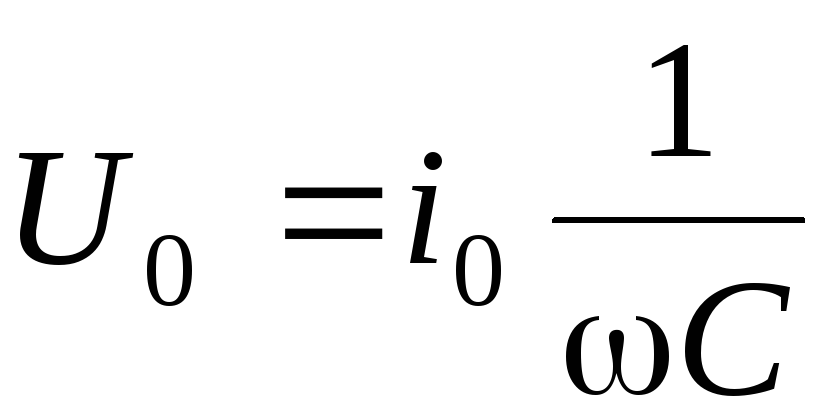 . (6.10)
. (6.10)
Сравнивая это
выражение с законом Ома для участка
цепи постоянного тока 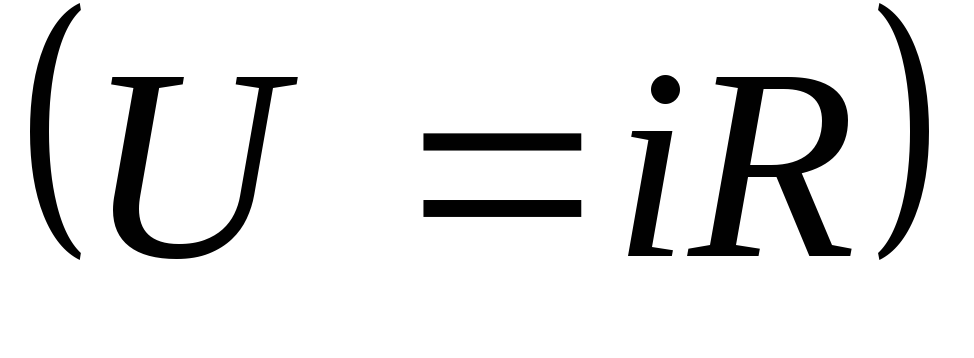 ,
мы видим, что величина
,
мы видим, что величина
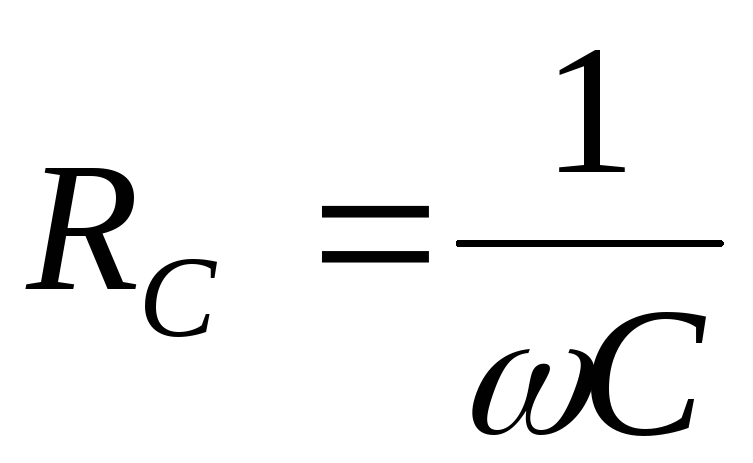
зависящая от
емкости конденсатора  ,
играет роль сопротивления участка цепи.
Поэтому она получила названиекажушегося
сопротивления емкости или емкостным сопротивлением. Емкостное
сопротивление равно отношению амплитуды
напряжения на емкости к амплитуде силы
тока в цепи. В Международной системе
единиц СИ емкостное сопротивление
выражается в омах.
,
играет роль сопротивления участка цепи.
Поэтому она получила названиекажушегося
сопротивления емкости или емкостным сопротивлением. Емкостное
сопротивление равно отношению амплитуды
напряжения на емкости к амплитуде силы
тока в цепи. В Международной системе
единиц СИ емкостное сопротивление
выражается в омах. 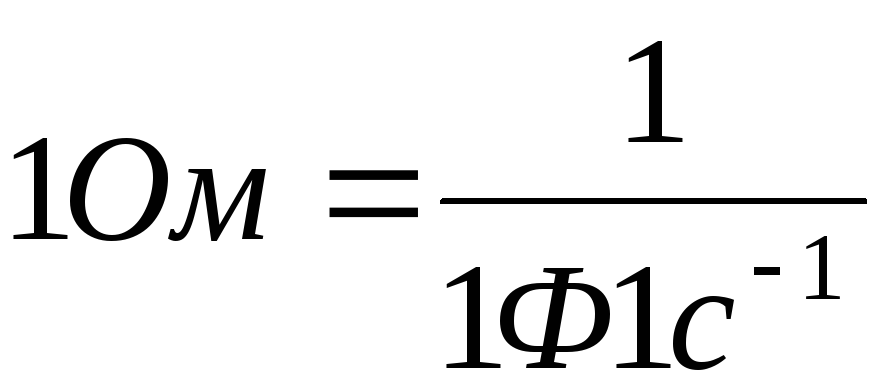 .
Емкостное сопротивление равно величине,
обратной произведению электрической
емкости ( в
.
Емкостное сопротивление равно величине,
обратной произведению электрической
емкости ( в
 (в
(в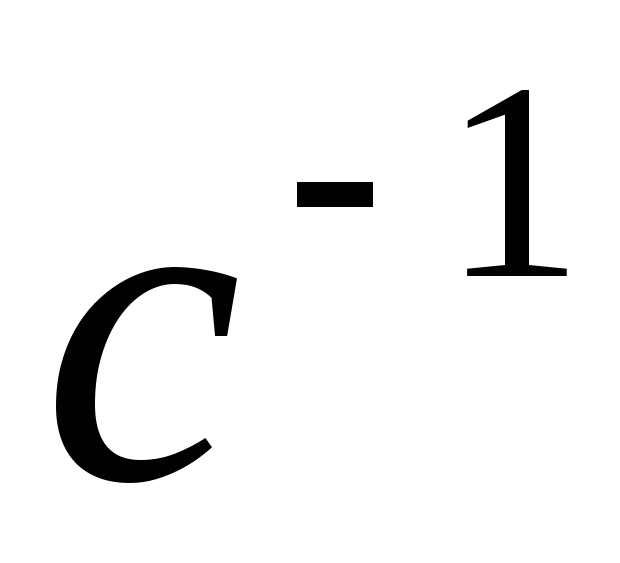 ).
). П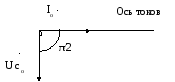 олученные
результаты можно представить в виде
векторной диаграммы (рисунок 6.6). Здесь
вектор, изображающий колебания напряжения,
уже не совпадает с осью токов. Он повернут
в отрицательном направлении (по часовой
стрелке) на угол
олученные
результаты можно представить в виде
векторной диаграммы (рисунок 6.6). Здесь
вектор, изображающий колебания напряжения,
уже не совпадает с осью токов. Он повернут
в отрицательном направлении (по часовой
стрелке) на угол .
Модуль этого вектора равен амплитуде
напряжения
.
Модуль этого вектора равен амплитуде
напряжения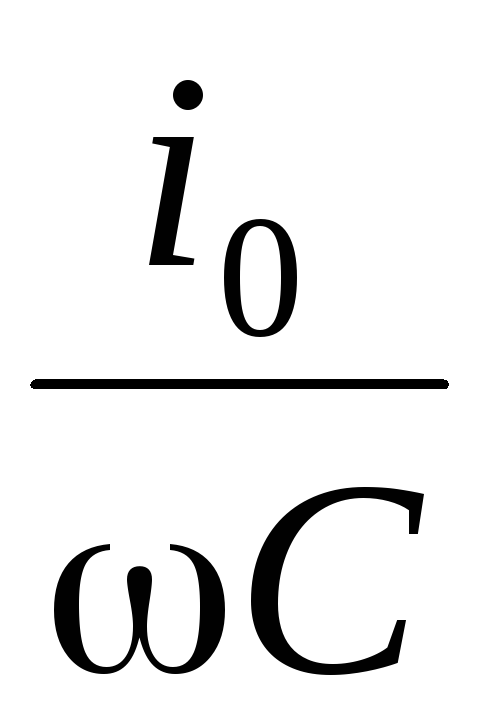
Рисунок 6.6
Из формулы (6.11)
видно, что сопротивление емкости 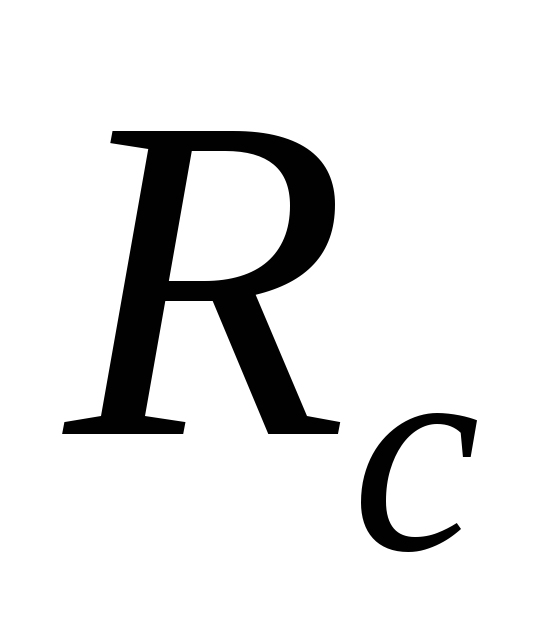 зависит также от частоты
зависит также от частоты .
Поэтому при очень высоких частотах даже
малые емкости могут представлять совсем
небольшое сопротивление для переменного
тока.
.
Поэтому при очень высоких частотах даже
малые емкости могут представлять совсем
небольшое сопротивление для переменного
тока.
Что такое активное сопротивление переменного тока?

Активное и реактивное сопротивление — сопротивлением в электротехнике называется величина, которая характеризует противодействие части цепи электрическому току. Это сопротивление образовано путем изменения электрической энергии в другие типы энергии. В сетях переменного тока имеется необратимое изменение энергии и передача энергии между участниками электрической цепи.
При необратимом изменении электроэнергии компонента цепи в другие типы энергии, сопротивление элемента является активным. При осуществлении обменного процесса электроэнергией между компонентом цепи и источником, то сопротивление реактивное.
В электрической плите электроэнергия необратимо преобразуется в тепло, вследствие этого электроплита имеет активное сопротивление, так же как и элементы, преобразующие электричество в свет, механическое движение и т.д.
В индуктивной обмотке переменный ток образует магнитное поле. Под воздействием переменного тока в обмотке образуется ЭДС самоиндукции, которая направлена навстречу току при его увеличении, и по ходу тока при его уменьшении. Поэтому, ЭДС оказывает противоположное действие изменению тока, создавая индуктивное сопротивление катушки.
С помощью ЭДС самоиндукции осуществляется возвращение энергии магнитного поля обмотки в электрическую цепь.
В итоге обмотка индуктивности и источник питания производят обмен энергией. Это можно сравнить с маятником, который при колебаниях преобразует потенциальную и кинетическую энергию. Отсюда следует, что сопротивление индуктивной катушки имеет реактивное сопротивление.
Самоиндукция не образуется в цепи постоянного тока, и индуктивное сопротивление отсутствует. В цепи емкости и источника переменного тока изменяется заряд, значит между емкостью и источником тока протекает переменный ток. При полном заряде конденсатора его энергия наибольшая.
В цепи напряжение емкости создает противодействие течению тока своим сопротивлением, и называется реактивным. Между конденсатором и источником происходит обмен энергией.
После полной зарядки емкости постоянным током напряжение его поля выравнивает напряжение источника, поэтому ток равен нулю.
Конденсаторикатушкав цепи переменного тока работают некоторое время в качестве потребителя энергии, когда накапливают заряд. И также работают в качестве генератора при возвращении энергии обратно в цепь.
Если сказать простыми словами, то активное и реактивное сопротивление – это противодействие току снижения напряжения на элементе схемы. Величина снижения напряжения на активном сопротивлении имеет всегда встречное направление, а на реактивной составляющей – попутно току или навстречу, создавая сопротивление изменению тока.
Настоящие элементы цепи на практике имеют все три вида сопротивления сразу. Но иногда можно пренебречь некоторыми из них ввиду незначительных величин. Например, емкость имеет только емкостное сопротивление (при пренебрежении потерь энергии), лампы освещения имеют только активное (омическое) сопротивление, а обмотки трансформатора и электромотора – индуктивное и активное.
Содержание
- 1 Активное сопротивление
- 2 Реактивное сопротивление
- 3 Тип сопротивления, определяющий соотношение напряжения и тока на емкостной и индуктивной нагрузке, не обусловленное количеством израсходованной электроэнергии, называется реактивным сопротивлением. Оно имеет место только при переменном токе, и может иметь отрицательное и положительное значение, в зависимости от направления сдвига фаз тока и напряжения. При отставании тока от напряжения величина реактивной составляющей сопротивления имеет положительное значение, а если отстает напряжение от тока, то реактивное сопротивление имеет знак минус.
- 4 Активное и реактивное сопротивление, свойства и разновидности
- 5 Треугольник сопротивлений
- 6 Если изобразить это выражение в виде графика, то получится треугольник сопротивлений. Он образуется, если рассчитать последовательную цепь всех трех видов сопротивлений. По этому треугольному графику можно увидеть, что катеты представляют собой активное и реактивное сопротивление, а гипотенуза является полным сопротивлением.
- 7 Похожие темы:
- 8 Активное сопротивление
- 9 Реактивное сопротивление
- 10 Конденсатор обладает реактивным сопротивлением благодаря своей ёмкости. Его сопротивление с увеличением частоты тока уменьшается, что позволяет его активно использовать в электронике в качестве шунта переменной составляющей тока. Сопротивление конденсатора можно рассчитать по формуле
- 11 Треугольник сопротивлений
Активное сопротивление
В цепи действия напряжения и тока, создает противодействие, снижения напряжения на активном сопротивлении. Падение напряжения, созданное током и оказывающее противодействие ему, равно активному сопротивлению.
При протекании тока по компонентам с активным сопротивлением, снижение мощности становится необратимым. Можно рассмотреть резистор, на котором выделяется тепло.Выделенное тепло не превращается обратно в электроэнергию.
Активное сопротивление, также может иметь линия передачи электроэнергии, соединительные кабели, проводники, катушки трансформаторов, обмотки электромотора и т. д.Отличительным признаком элементов цепи, которые обладают только активной составляющей сопротивления, является совпадение напряжения и тока по фазе. Это сопротивление вычисляется по формуле:R = U/I, где R– сопротивление элемента,U– напряжение на нем, I– сила тока, протекающего через элемент цепи.На активное сопротивление влияют свойства и параметры проводника: температура, поперечное сечение, материал, длина.
Реактивное сопротивление
Тип сопротивления, определяющий соотношение напряжения и тока на емкостной и индуктивной нагрузке, не обусловленное количеством израсходованной электроэнергии, называется реактивным сопротивлением. Оно имеет место только при переменном токе, и может иметь отрицательное и положительное значение, в зависимости от направления сдвига фаз тока и напряжения. При отставании тока от напряжения величина реактивной составляющей сопротивления имеет положительное значение, а если отстает напряжение от тока, то реактивное сопротивление имеет знак минус.
Активное и реактивное сопротивление, свойства и разновидности
Рассмотрим два вида этого сопротивления: емкостное и индуктивное.
Для трансформаторов, соленоидов, обмоток генераторов и моторов характерно индуктивное сопротивление. Емкостный вид сопротивления имеют конденсаторы. Чтобы определить соотношение напряжения и тока, нужно знать значение обоих видов сопротивления, которое оказывает проводник.
Реактивное сопротивление образуется при помощи снижения реактивной мощности, затраченной на образование магнитного поля в цепи. Снижение реактивной мощности создается путем подключения к трансформатору прибора с активным сопротивлением.
Конденсатор, подключенный в цепь, успевает накопить только ограниченную часть заряда перед изменением полярности напряжения на противоположный. Поэтому ток не снижается до нуля, так как при постоянном токе. Чем ниже частота тока, тем меньше заряда накопит конденсатор, и будет меньше создавать противодействие току, что образует реактивное сопротивление.
Иногда цепь имеет реактивные компоненты, но в результате реактивная составляющая равна нулю. Это подразумевает равенство фазного напряжения и тока. В случае отличия от нуля реактивного сопротивления, между током и напряжением образуется разность фаз.
Катушка имеет индуктивное сопротивлением в схеме цепи переменного тока.
В идеальном виде ее активное сопротивление не учитывают. Индуктивное сопротивление образуется с помощью ЭДС самоиндукции. При повышении частоты тока возрастает и индуктивное сопротивление.
На индуктивное сопротивление катушки оказывает влияние индуктивность обмотки и частота в сети.
Конденсатор образует реактивное сопротивление из-за наличия емкости. При возрастании частоты в сети его емкостное противодействие (сопротивление) снижается. Это дает возможность активно его применять в электронной промышленности в виде шунта с изменяемой величиной.
Треугольник сопротивлений
Схема цепи, подключенной к переменному току, имеет полное сопротивление, которое можно определить в виде суммы квадратов реактивного и активного сопротивлений.
Если изобразить это выражение в виде графика, то получится треугольник сопротивлений. Он образуется, если рассчитать последовательную цепь всех трех видов сопротивлений.
По этому треугольному графику можно увидеть, что катеты представляют собой активное и реактивное сопротивление, а гипотенуза является полным сопротивлением.
Похожие темы:
[ads-pc-1]Ток и напряжение.
При включении в цепь переменного тока активного сопротивления R (рис. 175, а) напряжение и источника создает в цепи ток i. Если напряжение и изменяется по синусоидальному закону u = Uтsin ?t, то ток i также изменяется синусоидально:
i = Iтsin ?t
При этом
Iт= Uт/ R
Таким образом, ток и напряжение изменяются по одному и тому же закону; они одновременно достигают своих максимальных значений и одновременно проходят через нуль (рис.
175,б). Следовательно,при включении в цепь переменного тока активного сопротивления ток и напряжение совпадают по фазе (рис. 175, в).
Если обе части равенства Iт= Uт/ Rразделить на ?2, то получим выражение закона Ома для рассматриваемой цепи для действующих значений напряжения и тока:
I = U / R
Следовательно, для цепи переменного тока, содержащей только активное сопротивление, этот закон имеет такую же математическую форму, как и для цепи постоянного тока.
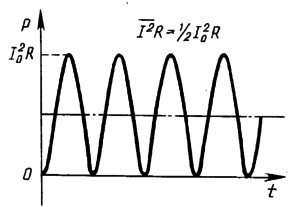
Электрическая мощность.Электрическая мощность р в цепи с активным сопротивлением в любой момент времени равна произведению мгновенных значений силы тока i и напряжения и. Следовательно, мгновенная мощность р не является постоянной величиной, как при постоянном токе, а изменяется по кривой (см.
рис. 175,б). Эту кривую можно также получить графически, перемножая ординаты кривых силы тока i и напряжения и при различных углах ?t.
Изменение мощности происходит с двойной частотой ?t по отношению к изменению тока и напряжения, т. е. один период изменения мощности соответствует половине периода изменения тока и напряжения.
Все значения мощности являются положительными. Физически положительное значение мощности означает, что энергия передается от источника электрической энергии к приемнику. Максимальное значение мощности при ?t = 90° и ?t = 270°
Pmax= UтIт= 2UI
Рис. 175. Схема включения в цепь переменного тока активного сопротивления (а), кривые тока i, напряжения и, мощности р (б) и векторная диаграмма (в)
Практически об энергии W, создаваемой электрическим током, судят не по максимальной мощности, а по средней мощности Рср= Р, так как эта энергия может быть выражена как произведение среднего значения мощности Р на время протекания тока:
W = Pt.
Кривая мгновенной мощности симметрична относительно линии АБ, которая соответствует среднему значению мощности Р. Поэтому
P = Pmax/ 2 = UI
Используя формулу (67) закона Ома, активную мощность можно выразить также в виде P = I2R или P=U2/R.
В электротехнике среднюю мощность, потребляемую активным сопротивлением, обычно называют активной мощностью, или просто мощностью, и обозначают буквой Р.
Поверхностный эффект. Следует отметить, что активное сопротивление проводников в цепи переменного тока всегда больше их сопротивления в цепи постоянного тока.
Переменный ток i не протекает равномерно по всему поперечному сечению проводника, как постоянный ток i, а вытесняется на его поверхность (рис. 176, а). Поэтому полезное сечение проводника как бы уменьшается и сопротивление его при переменном токе возрастает.
Это явление носит название поверхностного эффекта. Неравномерное распределение переменного тока по поперечному сечению проводника объясняется действием э. д.
с. самоиндукции, индуцированной в проводнике магнитным полем, которое создается проходящим по проводнику током I. Это магнитное поле действует не только в пространстве, окружающем проводник (внешний поток Ф2), но и внутри самого проводника (внутренний поток Ф2) (рис.
176,б). Поэтому слои проводника, расположенные ближе к его центру, будут охватываться большим магнитным потоком, чем слои, расположенные ближе к его поверхности, и э. д.
с. самоиндукции, индуцированная во внутренних слоях, будет большей, чем во внешних. Поскольку э.
д. с. самоиндукции препятствует изменению
Рис. 176. Схема протекания постоянного I и переменного i токов по проводнику (а) и возникновение поверхностного эффекта (б)
Рис. 177. Схема термообработки деталей токами высокой частоты: 1 — высокочастотный индуктор; 2 — закаливаемая деталь; 3 — разогретый слой
тока, последний будет стремиться пройти там, где э. д.
с. самоиндукции имеет наименьшее значение, т. е.
пройдет преимущественно по поверхностным слоям проводника. В результате этого плотность тока У в поверхностных слоях будет больше, чем во внутренних. Чем больше частота тока, тем больше э.
д. с. самоиндукции индуцируется во внутренних слоях проводника и тем в большей степени ток вытесняется на поверхность.
При частоте 50 Гц увеличение сопротивления медных и алюминиевых проводников при малом их диаметре практически ничтожно, и сопротивление таких проводников в цепях переменного и постоянного тока можно считать одинаковым. Но для медных и алюминиевых проводников диаметром свыше 10 мм, а для стальных проводников при еще меньших диаметрах необходимо при расчетах учитывать влияние поверхностного эффекта на их активное сопротивление.
При токах высокой частоты, принятых в радиотехнике, телевидении и различных высокочастотных установках, с целью лучшего использования металла проводников их обычно изготовляют полыми.
На свойстве переменного тока высокой частоты протекать, главным образом, по поверхности проводников основаны различные методы высокочастотной закалки и термообработки.
Например, при высокочастотной термообработке деталей вихревыми токами (рис. 177) эти токи индуцируются в основном в поверхностном слое металла. Они быстро разогревают поверхностные слои обрабатываемой детали, раньше, чем ее внутренняя часть успеет заметно нагреться за счет теплопроводности металла.
[ads-pc-2]
В электрической цепи переменного токасуществует два вида сопротивлений:активноеи реактивное. Это является существенным отличием от цепей постоянного тока.
Активное сопротивление
При прохождении тока через элементы, имеющие активное сопротивление, потери выделяющейся мощности необратимы. Примером может служить резистор, выделяющееся на нем тепло, обратно в электрическую энергию не превращается. Кроме резистора активным сопротивлением может обладать линии электропередач, соединительные провода, обмотки трансформатора или электродвигателя.
Отличительной чертой элементов имеющих чисто активное сопротивление – это совпадение по фазе тока и напряжения, поэтому вычислить его можно по формуле
Активное сопротивление зависит от физических параметров проводника, таких как материал, площадь сечения, длина, температура.
Реактивное сопротивление
При прохождении переменного тока через реактивные элементы возникает реактивноесопротивление. Оно обусловлено в первую очередь ёмкостями и индуктивностями.
Индуктивностью в цепи переменного тока обладает катушка индуктивности, причём в идеальном случае, активным сопротивлением её обмотки пренебрегают. Реактивное сопротивление катушки переменному току создаётся благодаря её ЭДС самоиндукции. Причем с ростом частоты тока, сопротивление также растёт.
Реактивное сопротивление катушки зависит от частоты тока и индуктивности катушки
Конденсатор обладает реактивным сопротивлением благодаря своей ёмкости. Его сопротивление с увеличением частоты тока уменьшается, что позволяет его активно использовать в электронике в качестве шунта переменной составляющей тока.
Сопротивление конденсатора можно рассчитать по формуле
Треугольник сопротивлений
Цепи переменного тока обладают полным сопротивлением. Полное сопротивление цепи определяется как сумма квадратов активного и реактивного сопротивлений
Графическим изображением этого выражения служит треугольник сопротивлений, который можно получить в результате расчёта последовательной RLC-цепи. Выглядит он следующим образом:На треугольнике видно, что катетами являются активное и реактивное сопротивление, а полной сопротивление гипотенуза.Величина и начальная фаза переменного тока, создаваемого переменным напряжением, зависят не только от величины сопротивлений, образующих электрическую цепь, но и от индуктивности и емкости этой цепи.Активное сопротивление в цепи переменного тока.Строго говоря, любая электрическая цепь обладает, кроме сопротивления, также индуктивностью и емкостью. Если по проводнику проходит ток, то вокруг него возбуждается магнитное поле, т.
е. имеют место явления индуктивности. Ток возникает под действием электрического поля на заряды, следовательно, проводник должен обладать емкостью, так как в диэлектрической среде вокруг него возникает поток смещения.Однако в ряде случаев относительная роль двух из трех параметров R, L, С в электрической цепи практически незначительна.
Это позволяет рассматривать подобную цепь как обладающую только сопротивлением, или только индуктивностью, или только емкостью.Мы рассмотрим поочередно условия в трех таких простейших цепях переменного тока.В цепи, содержащей только сопротивление г, синусоидальное напряжени u = Um sin ?t источника электроэнергии создает ток:i = u : r = (Um: r ) sin ?tТак как сопротивление r от времени не зависит, то в этой цепи ток совпадает по фазе с напряжением (рис. 1) и изменяется также синусоидально:i = Imsin ?tздесь:Im= Um: rРисунок 1 Кривые мгновенных значений напряжения и тока в цепи,содержащей только сопротивление r.Разделив последнее выражение на , получим формулу закона Омадля действующих значений напряжения и тока:I = U : rКак видно из формулы, этот закон для цепей переменного тока, содержащих только сопротивление r, имеет такой же вид, как и закон Ома для цепи постоянного тока.В цепи переменного тока сопротивление r называется активным сопротивлением. Это сопротивление, в котором электроэнергия преобразуется в другую форму (в теплоту и др.).Оно может существенно отличаться от сопротивления rпри постоянном токе.
Сопротивление для постоянного тока называют омическим, чтобы отличить его от активного сопротивления для переменного тока.Различие между активным и омическим сопротивлениями обуславливается рядом причин. Одна из них – поверхностный эффект, частичное вытеснение переменного тока в поверхностные слои проводника.Чем больше частота переменного тока, тем это вытеснение значительнее. Из-за поверхностного эффекта сопротивлениеrоказывается уже существенно большим, чем вычисленное по формуле:r = ?
(l : S)Поверхностный эффект создается тем, что переменное магнитное поле индуктирует во внешних слоях проводника меньшую ЭДС самоиндукции, чем во внутренней его части.Особенно сильно поверхностный эффект увеличивает активное сопротивление стальных проводов. На активное сопротивление медных и алюминиевых проводов при промышленной частоте поверхностный эффект существенно влияет только при больших сечениях проводов (свыше 25 кв. мм).Кроме поверхностного эффекта, большое увеличение активного сопротивления электрической цепи могут вызывать потери энергии в переменном электромагнитном поле цепи от гистерезиса и вихревых токов.Поделитесь полезной статьей:
Источники:
- electrosam.ru
- electrono.ru
- electroandi.ru
- fazaa.ru
Цепь переменного тока с активным сопротивлением
Когда в электрическую цепь переменного тока подключается активное сопротивление R, то под воздействием разницы потенциалов источника в цепи начинает течь ток I. В тех случаях, когда изменение напряжения происходит по синусоидальному закону, который выражается, как u = Um sin ωt, то изменение тока i также идет по синусоиде:
Активное сопротивление
i = Im sin ωt
При этом
Так что получается, что изменение напряжения и тока происходят по одинаковым законам. При этом через нулевое значение они проходят одновременно и своих максимальных значений также достигают одновременно. Из этого следует, что когда в электрическую цепь переменного тока подключается активное сопротивление R, то напряжение и ток совпадают по фазе.
Мощность, ток, напряжение
Если взять равенство Im = Um / R и каждую из его частей разделить на √2, то в итоге получится ни что иное, как закон Ома, применимый для той цепи, которая рассматривается:
I = U/R.
Таким образом, получается, что это основополагающий закон для той цепи, которая имеет в своем составе только активное сопротивление, с точки зрения математики имеет такую же форму, что и для цепи тока постоянного.
Электрическая мощность
Такой показатель, как электрическая мощность P для цепи, имеющей в своем составе активное сопротивление, равняется произведению мгновенного значения напряжения U на мгновенное значение силы тока i в любой момент времени. Из этого следует, что в цепях переменного тока, в отличие от цепей тока постоянного, мгновенная мощность P – величина непостоянная, а ее изменение происходит по кривой. Для того чтобы получить ее графическое представление, необходимо ординаты кривых напряжения U и силы тока i перемножить при разных углах ωt. Мощность изменяется по отношению к изменению тока с двойной частотой ωt. Это означает, что половине периода изменения напряжения и тока соответствует один период изменения мощности. Следует заметить, что абсолютно все значения, которые может принимать мощность, являются положительными величинами. С точки зрения физики это означает, что от источника к приемнику передается энергия. Своих максимальных значений мощность достигает тогда, когда ωt = 270° и ωt = 90°.
В практическом отношении о той энергии W, которую создает электрический ток, принято судить по средней мощности, выражаемой формулой Рср = Р, а не по мощности максимальной. Ее можно определить, перемножив на время протекания тока среднее значение мощности W = Pt.
Относительно линии АБ, соответствующей среднему значению мощности P, кривая мгновенной мощности симметрична. По этой причине
P = Pmax / 2 = UI
Если использовать закон Ома, то можно выразить активную мощность в следующем виде:
P = I2R или P = U2/R.
Специалисты в области электротехники ту среднюю мощность, которую потребляет активное сопротивление, чаще всего именуют или просто мощностью, или активной мощностью, а для ее обозначения используется буква P.
Поверхностный эффект
Необходимо особо отметить такую особенность проводников, включенных в сеть переменного тока: их активное сопротивление во всех случаях оказывается больше, чем если бы они были включены в сеть тока постоянного. Причина этого состоит в том, что переменный ток не протекает равномерно распределяясь по всему поперечному сечению проводника, как ведёт себя постоянный ток, а выводится на его поверхность. Таким образом, получается, что при включении проводника в цепь переменного тока его полезное сечение оказывается значительно меньшим, чем при включении в цепь тока постоянного. Именно поэтому его сопротивление возрастает. В физике и электротехнике это явление называется поверхностным эффектом.
То, что переменный ток распределяется по сечению проводника неравномерно, объясняется действием электродвижущей силы самоиндукции. Она индуцируется в проводнике тем магнитным полем, которое создается током, проходящим по нему. Необходимо заметить, что действие этого магнитного поля распространяется не только на окружающее проводник пространство, но и на внутреннюю его часть. По этой простой причине те слои проводника, которые располагаются ближе к его центру, находятся под воздействием большего магнитного потока, чем те слои, что располагаются ближе к его поверхности. Соответственно, электродвижущая сила самоиндукции, которая возникает во внутренних слоях, существенно больше, чем та, что образуется в слоях внешних.
Электродвижущая сила самоиндукции является существенным препятствием для изменения тока, и поэтому он будет следовать преимущественно по поверхностным слоям проводника. Необходимо также отметить, что сопротивление активных проводников в цепях переменного тока существенно зависит от частоты: чем она больше, тем выше ЭДС самоиндукции, и поэтому ток в большей степени подвергается вытеснению на поверхность.
§50. Активное сопротивление в цепи переменного тока
Ток и напряжение. При включении в цепь переменного тока активного сопротивления R (рис. 175, а) напряжение и источника создает в цепи ток i. Если напряжение и изменяется по синусоидальному закону u = Uт sin ?t, то ток i также изменяется синусоидально:
i = Iт sin ?t
При этом
Iт = Uт / R
Таким образом, ток и напряжение изменяются по одному и тому же закону; они одновременно достигают своих максимальных значений и одновременно проходят через нуль (рис. 175,б). Следовательно, при включении в цепь переменного тока активного сопротивления ток и напряжение совпадают по фазе (рис. 175, в).

Если обе части равенства Iт = Uт / R разделить на ?2, то получим выражение закона Ома для рассматриваемой цепи для действующих значений напряжения и тока:
I = U / R
Следовательно, для цепи переменного тока, содержащей только активное сопротивление, этот закон имеет такую же математическую форму, как и для цепи постоянного тока.
Электрическая мощность. Электрическая мощность р в цепи с активным сопротивлением в любой момент времени равна произведению мгновенных значений силы тока i и напряжения и. Следовательно, мгновенная мощность р не является постоянной величиной, как при постоянном токе, а изменяется по кривой (см. рис. 175,б). Эту кривую можно также получить графически, перемножая ординаты кривых силы тока i и напряжения и при различных углах ?t. Изменение мощности происходит с двойной частотой ?t по отношению к изменению тока и напряжения, т. е. один период изменения мощности соответствует половине периода изменения тока и напряжения. Все значения мощности являются положительными. Физически положительное значение мощности означает, что энергия передается от источника электрической энергии к приемнику. Максимальное значение мощности при ?t = 90° и ?t = 270°
Pmax = UтIт = 2UI
Рис. 175. Схема включения в цепь переменного тока активного сопротивления (а), кривые тока i, напряжения и, мощности р (б) и векторная диаграмма (в)
Практически об энергии W, создаваемой электрическим током, судят не по максимальной мощности, а по средней мощности Рср = Р, так как эта энергия может быть выражена как произведение среднего значения мощности Р на время протекания тока:
W = Pt.
Кривая мгновенной мощности симметрична относительно линии АБ, которая соответствует среднему значению мощности Р. Поэтому
P = Pmax / 2 = UI
Используя формулу (67) закона Ома, активную мощность можно выразить также в виде P = I2R или P=U2/R.
В электротехнике среднюю мощность, потребляемую активным сопротивлением, обычно называют активной мощностью, или просто мощностью, и обозначают буквой Р.
Поверхностный эффект. Следует отметить, что активное сопротивление проводников в цепи переменного тока всегда больше их сопротивления в цепи постоянного тока. Переменный ток i не протекает равномерно по всему поперечному сечению проводника, как постоянный ток i, а вытесняется на его поверхность (рис. 176, а). Поэтому полезное сечение проводника как бы уменьшается и сопротивление его при переменном токе возрастает. Это явление носит название поверхностного эффекта. Неравномерное распределение переменного тока по поперечному сечению проводника объясняется действием э. д. с. самоиндукции, индуцированной в проводнике магнитным полем, которое создается проходящим по проводнику током I. Это магнитное поле действует не только в пространстве, окружающем проводник (внешний поток Ф2), но и внутри самого проводника (внутренний поток Ф2) (рис. 176,б). Поэтому слои проводника, расположенные ближе к его центру, будут охватываться большим магнитным потоком, чем слои, расположенные ближе к его поверхности, и э. д. с. самоиндукции, индуцированная во внутренних слоях, будет большей, чем во внешних. Поскольку э. д. с. самоиндукции препятствует изменению
Рис. 176. Схема протекания постоянного I и переменного i токов по проводнику (а) и возникновение поверхностного эффекта (б)
Рис. 177. Схема термообработки деталей токами высокой частоты: 1 — высокочастотный индуктор; 2 — закаливаемая деталь; 3 — разогретый слой
тока, последний будет стремиться пройти там, где э. д. с. самоиндукции имеет наименьшее значение, т. е. пройдет преимущественно по поверхностным слоям проводника. В результате этого плотность тока У в поверхностных слоях будет больше, чем во внутренних. Чем больше частота тока, тем больше э. д. с. самоиндукции индуцируется во внутренних слоях проводника и тем в большей степени ток вытесняется на поверхность.
При частоте 50 Гц увеличение сопротивления медных и алюминиевых проводников при малом их диаметре практически ничтожно, и сопротивление таких проводников в цепях переменного и постоянного тока можно считать одинаковым. Но для медных и алюминиевых проводников диаметром свыше 10 мм, а для стальных проводников при еще меньших диаметрах необходимо при расчетах учитывать влияние поверхностного эффекта на их активное сопротивление.
При токах высокой частоты, принятых в радиотехнике, телевидении и различных высокочастотных установках, с целью лучшего использования металла проводников их обычно изготовляют полыми.
На свойстве переменного тока высокой частоты протекать, главным образом, по поверхности проводников основаны различные методы высокочастотной закалки и термообработки. Например, при высокочастотной термообработке деталей вихревыми токами (рис. 177) эти токи индуцируются в основном в поверхностном слое металла. Они быстро разогревают поверхностные слои обрабатываемой детали, раньше, чем ее внутренняя часть успеет заметно нагреться за счет теплопроводности металла.

основные сведения, формулы и зависимости для цепи переменного тока
 Для проектирования электронных устройств следует рассчитывать различные параметры, одним из которых является электропроводимость или сопротивление проводника. Для цепей, питающихся постоянным током, вычислить его несложно. Но в цепях переменного тока (ПТ) существуют совсем другие соотношения. Для расчета активного сопротивления необходимо ознакомиться с основными формулами, а также альтернативными способами его вычисления.
Для проектирования электронных устройств следует рассчитывать различные параметры, одним из которых является электропроводимость или сопротивление проводника. Для цепей, питающихся постоянным током, вычислить его несложно. Но в цепях переменного тока (ПТ) существуют совсем другие соотношения. Для расчета активного сопротивления необходимо ознакомиться с основными формулами, а также альтернативными способами его вычисления.
Основные сведения об электропроводимости
Каждое вещество проводит ток по-разному. Все зависит от электронной конфигурации, которую можно получить из таблицы Д. И. Менделеева. Электронная конфигурация показывает основной параметр, от которого зависит величина сопротивления R, — количество свободных электронов (Nсэ). Вещество состоит из атомов, которые образуют кристаллическую решетку (КР). Не все электроны прочно удерживаются ядром.
Классификация веществ
В веществах присутствует несколько электронов (Э), которые имеют очень слабую силу взаимодействия с ядром. Кроме того, в металлах, кроме обыкновенных Э, есть определенное Nсэ. При приложении незначительной сторонней энергии происходит отрыв электронов от ядер атомов, и это приводит к образованию ионов. Металл остается незаряженным, так как отрицательный заряд всех Э равен положительному заряду элементарных частиц (ЭЧ), входящих в состав ядер. Ядро состоит из нуклонов, а именно:
- протонов — положительно заряженных ЭЧ;
- нейтронов — нейтральные ЭЦ.
Свободные Э движутся хаотично, однако среди них есть такие, которые летят близко к поверхности металла, и они не могут вылететь из вещества, так как их удерживает сила притяжения ионов и ядер. Исходя из Nсэ, можно разделить любое вещество на 3 группы по проводимости:
- Проводники.
- Полупроводники.
- Диэлектрики.
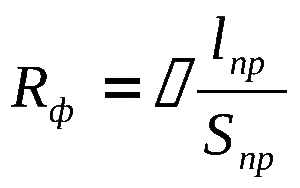 К проводникам (П) относятся вещества, обладающие большим Nсэ. К ним относятся металлы, электролитические растворы и ионизированные газы. В металлах свободными носителями заряда (СНЗ) являются свободные Э, в электролитах и ионизированных газах — ионы, под действием электрического поля движение СНЗ становится упорядоченным, в результате которого образуется электрический ток (ЭТ).
К проводникам (П) относятся вещества, обладающие большим Nсэ. К ним относятся металлы, электролитические растворы и ионизированные газы. В металлах свободными носителями заряда (СНЗ) являются свободные Э, в электролитах и ионизированных газах — ионы, под действием электрического поля движение СНЗ становится упорядоченным, в результате которого образуется электрический ток (ЭТ).
В полупроводниках Nсэ зависит от различных внешних факторов, при действии которых происходит освобождение некоторых Э от действия силы притяжения ядра — силы Кулона при взаимодействии 2 и более частиц. Место, которое покинул Э, называется дыркой. Движение дырок и Э является противоположным, и при этом возникает ЭТ. К веществам полупроводникового типа относятся следующие: кремний (Si), германий (Ge), селен (Se) и т. д.
К группе диэлектриков или изоляторов относятся вещества, которые вообще не обладают СНЗ, а следовательно, они не проводят электрический ток вообще. При некоторых условиях диэлектрик может стать отличным от П тока, например, если будет покрыт каплями электропроводящей жидкости. Этот момент является очень важным для избежания выхода аппаратуры из строя или поражения ЭТ. При протекании по П ЭТ оказывает тепловое действие на него. Это свойство обусловлено тем, что Э взаимодействуют с узлами КР, и кинетическая энергия Э превращается в тепловую.
В результате происходит снижение скорости Э, а затем ее полное восстановление при воздействии электромагнитного поля. Этот процесс повторяется большое количество раз и называется электрическим сопротивлением, которое обозначается для цепей постоянного тока R, а для цепей переменного тока (ПТ) существует полное сопротивление — Z. Измеряется R и Z в Ом.
Зависимость от различных параметров
R является величиной, зависящей от многих факторов. Эти факторы можно разделить на группы:
- Физические свойства: длина, площадь поперечного сечения (S) и деформация.
- Внешняя среда: температура.
- Электрические: I, U, e (электродвижущая сила — ЭДС).
R рассчитывается по закону Ома: I = U / R. Формулировка этого закона следующая: I, протекающий на участке цепи, прямо пропорционален U и обратно пропорционален R выбранного участка.
Формулировка для всей цепи: I, протекающий по всей цепи, прямо пропорционален ЭДС и обратно пропорционален R всего участка с учетом внутреннего сопротивления источника питания (ИП). Формула имеет вид: I = e / (R + Rип). Из соотношений для полной и участка цепи можно получить R:
- R = U / I.
- R = (e / I) — Rип.
 Тип вещества определяется коэффициентом удельного сопротивления p, который берется из справочника. Однако следует учесть, что в справочнике приведено его значение при температуре +20 градусов. Кроме того, существует и удельная проводимость, которая обратно пропорциональна p. Она обозначается σ и равна: p = 1 / σ.
Тип вещества определяется коэффициентом удельного сопротивления p, который берется из справочника. Однако следует учесть, что в справочнике приведено его значение при температуре +20 градусов. Кроме того, существует и удельная проводимость, которая обратно пропорциональна p. Она обозначается σ и равна: p = 1 / σ.

При меньшей величине S Э протекают через П и взаимодействия с КР учащаются, что иллюстрирует зависимость R от S. Для вычисления S необходимо воспользоваться справочной литературой или интернетом. Если учесть, что проводник является плоскостью, то необходимо разрезать его при помощи другой плоскости (стереометрия).
При разрезе получается плоская фигура в виде квадрата, окружности, эллипса, прямоугольника или треугольника. Затем необходимо вычислить S этой фигуры. Если П состоит из определенного количества жил, то нужно измерить S одной жилы, а затем умножить на количество жил.
R зависит прямо пропорционально от длины П (L): чем больше длина, тем больше взаимодействий совершает Э при движении. Исходя из всех зависимостей можно выразить R формулами:
- R = p * L / S.
- R = L / (σ * S).
Эти соотношения справедливы при температуре +20 градусов, но для проведения точных расчетов этого недостаточно. Некоторые сверхчувствительные элементы могут работать некорректно из-за низких значений I.
Значение p зависит от t и выражается следующим соотношением: p = p20 * [1 + a * (t — 20)]. В этом соотношении присутствуют следующие величины:
- p — удельное сопротивление, полученное при вычислении.
- p20 — величина удельного сопротивления, взятого из справочной литературы при температуре (температура +20 градусов по Цельсию).
- Температурный коэффициент a, который берется из справочной литературы. Для металлов он всегда больше 1, а для электролитических растворов — меньше.
- Температура П при конкретных условиях эксплуатации, температурная шкала по Цельсию — t.
Кроме того, p зависит еще и от уровня деформации КР. Деформация бывает упругой и пластической. При упругой происходит увеличение p, а при пластической — уменьшение. Это связано с условиями деформаций, а также со степенью затрудненности движения Э. Конечная формула при учете основных факторов примет следующий вид: R = p20 * [1 + a * (t — 20)] * L / S.
Соотношения для переменного тока
 Для того чтобы разобраться в некоторых терминах, например, какое сопротивление называется активным, и что оно из себя представляет, необходимо применить формулу полного сопротивления: sqr (Z) = sqr® +sqr (Xc-Xl). Сопротивление переменного тока является полным и состоит из активного R, индуктивного (Хl) и емкостного (Xc).
Для того чтобы разобраться в некоторых терминах, например, какое сопротивление называется активным, и что оно из себя представляет, необходимо применить формулу полного сопротивления: sqr (Z) = sqr® +sqr (Xc-Xl). Сопротивление переменного тока является полным и состоит из активного R, индуктивного (Хl) и емкостного (Xc).
Формула сопротивления
Сопротивление называется активным, если на участке или в полной цепи нет индуктивности или емкости. Для расчета необходимо измерить амплитудные значения тока и напряжения. Для этих целей применяются вольтметр и амперметр для переменного тока и напряжения. Однако минусом таких измерений является получение не амплитудных, а действующих значений. Амплитудные значения высчитываются по формулам:
- Для U: Um = 1,4142 * Ud.
- Для I: Im = 1,4142 * Id.
Исходя из этих соотношений формула активного сопротивления вычисляется по формуле: R = Um / Im. Активное сопротивление зависит еще и от Um и Im.
Простые способы измерения
 Не всегда требуются точные расчеты R, и для этих целей применяется прибор, называющиеся омметром. С ростом научного прогресса на рынке появились комбинированные приборы — мультиметры. Они имеют много функций, но основной из них является измерение значений I, R и U. Существуют также и специализированные приборы для измерения больших значений R, которые называются мегаомметрами. Мегаомметр применяется для измерения R уровня изоляции между жилами кабеля.
Не всегда требуются точные расчеты R, и для этих целей применяется прибор, называющиеся омметром. С ростом научного прогресса на рынке появились комбинированные приборы — мультиметры. Они имеют много функций, но основной из них является измерение значений I, R и U. Существуют также и специализированные приборы для измерения больших значений R, которые называются мегаомметрами. Мегаомметр применяется для измерения R уровня изоляции между жилами кабеля.
Омметр применяется и для поиска неисправностей в электроцепях, а также позволяет определить радиодеталь на предмет исправности. Для измерения значений R, а также для выявления неисправностей, необходимо соблюдать правила электробезопасности и обесточить участок цепи. Нужно разрядить и конденсаторы, так как их заряд может вывести из строя прибор, который находится в режиме измерения R.
Таким образом, активным сопротивлением в цепи переменного тока является любая нагрузка, не являющаяся емкостной или индуктивной, и зависящей от температуры, вида деформации, типа вещества, Um, Im, длины и S проводника.
2. Индуктивность, емкость и активное сопротивление в цепи переменного тока
Р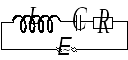 ассмотрим
контур, который включает в себя
индуктивность
ассмотрим
контур, который включает в себя
индуктивность 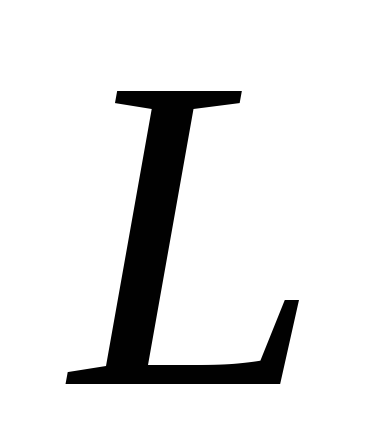 ,
емкость
,
емкость  и активное сопротивление
и активное сопротивление  .
Пусть в этот контур включен источник
ЭДС, который изменяется по гармоничному
закону (синуса или косинуса) с амплитудой
.
Пусть в этот контур включен источник
ЭДС, который изменяется по гармоничному
закону (синуса или косинуса) с амплитудой 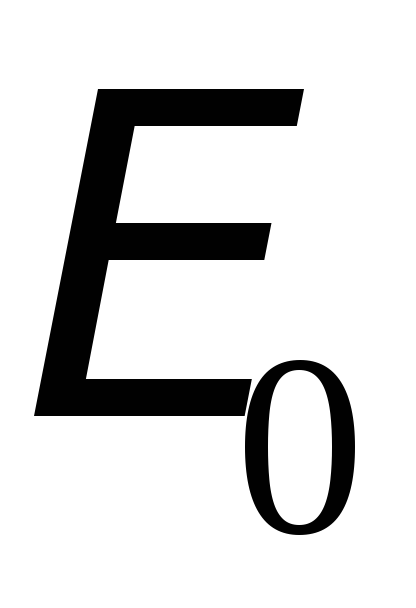 и циклической частотой
и циклической частотой 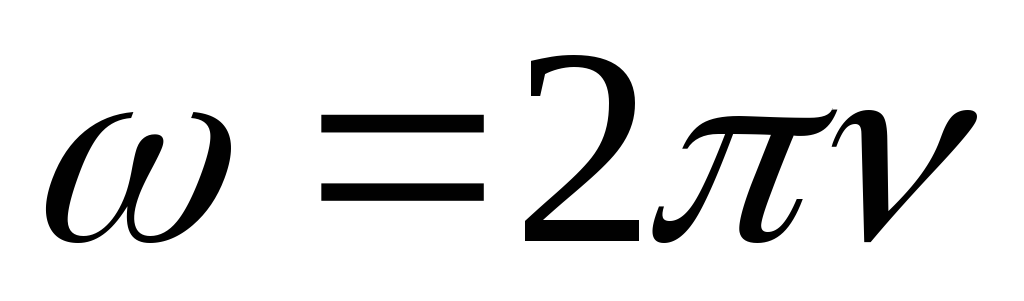 ,
где
,
где 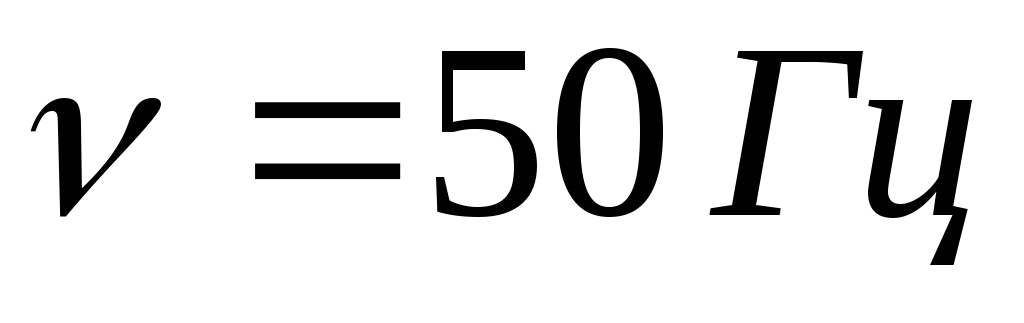 – линейная частота. Выясним, как влияют
– линейная частота. Выясним, как влияют 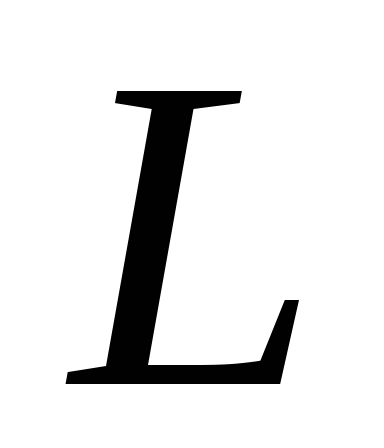 ,
,  и
и  отдельно и вместе на ток в этом цепи и
какие падения напряжения будут на этих элементах. Ток на всех
элементах цепи будет одинаковым (ток
неразрывный). Пусть он меняется по закону
синуса
отдельно и вместе на ток в этом цепи и
какие падения напряжения будут на этих элементах. Ток на всех
элементах цепи будет одинаковым (ток
неразрывный). Пусть он меняется по закону
синуса
| (1) |
где 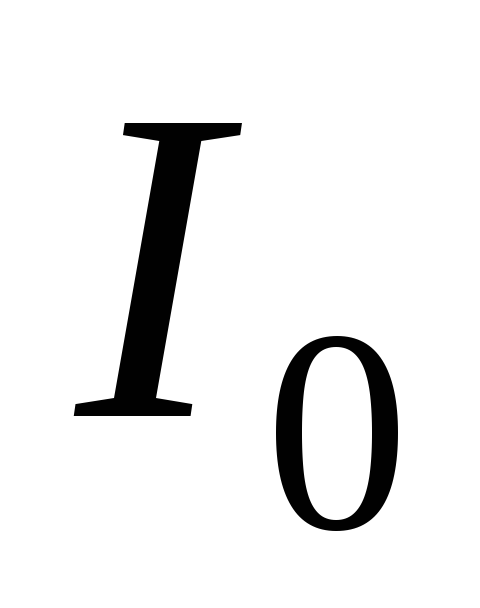 – амплитудное значение силы тока (пока
еще неизвестное).
– амплитудное значение силы тока (пока
еще неизвестное).
2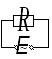 .1.Активное
сопротивление в цепи переменного тока
.1.Активное
сопротивление в цепи переменного тока
Рассмотрим электрическую цепь, которая состоит только из источника переменного тока и активного сопротивления R. Падение напряжения на активном сопротивлении определяется из закона Ома и выражения (1)
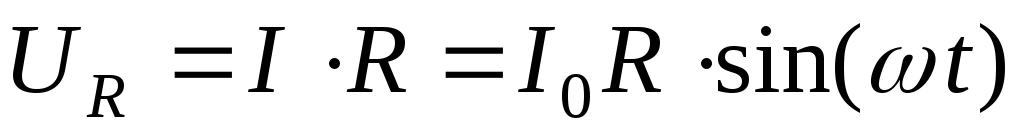
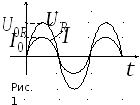 .
(2)
.
(2)
Величина 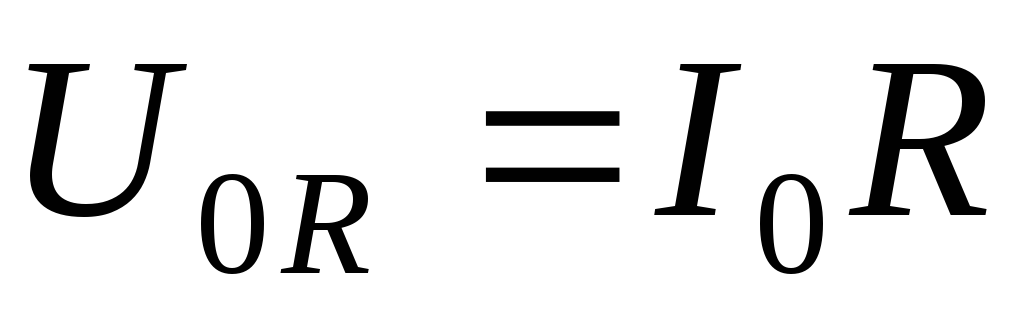 будет представлять собой амплитудное
значение напряжения на активном
сопротивлении. Сравнивая выражения (1)
и (2) видим, что колебания напряжения и
тока на активном сопротивлении происходит
с одинаковой фазой (по закону синуса,
рис.1). Заметим, что в цепи с активным
сопротивлением происходит необратимый
процесс преобразования электрической
энергии в тепловую.
будет представлять собой амплитудное
значение напряжения на активном
сопротивлении. Сравнивая выражения (1)
и (2) видим, что колебания напряжения и
тока на активном сопротивлении происходит
с одинаковой фазой (по закону синуса,
рис.1). Заметим, что в цепи с активным
сопротивлением происходит необратимый
процесс преобразования электрической
энергии в тепловую.
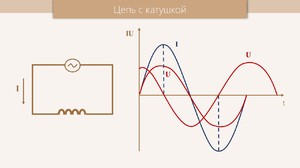
2.2.Индуктивность в цепи переменного тока
 Если
катушка индуктивности
Если
катушка индуктивности 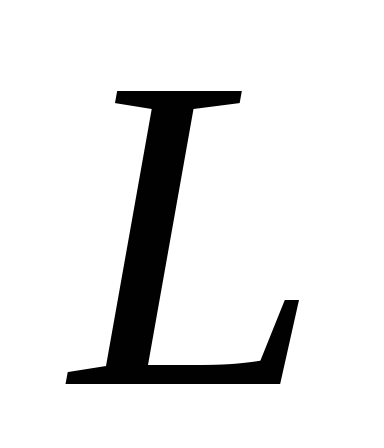 находится в контуре с переменным током,
то в ней все время будет возникать ЭДС
самоиндукции, которая противодействует
внешний переменной ЭДС. Вследствие
этого катушка будет создавать сопротивление
(дополнительное к активному) переменному
току, который называют индуктивным
сопротивлением. Найдем это сопротивление.
находится в контуре с переменным током,
то в ней все время будет возникать ЭДС
самоиндукции, которая противодействует
внешний переменной ЭДС. Вследствие
этого катушка будет создавать сопротивление
(дополнительное к активному) переменному
току, который называют индуктивным
сопротивлением. Найдем это сопротивление.
Пусть
активное сопротивление катушки очень
мало ( ).
Тогда на индуктивности создается падение
напряжения
).
Тогда на индуктивности создается падение
напряжения 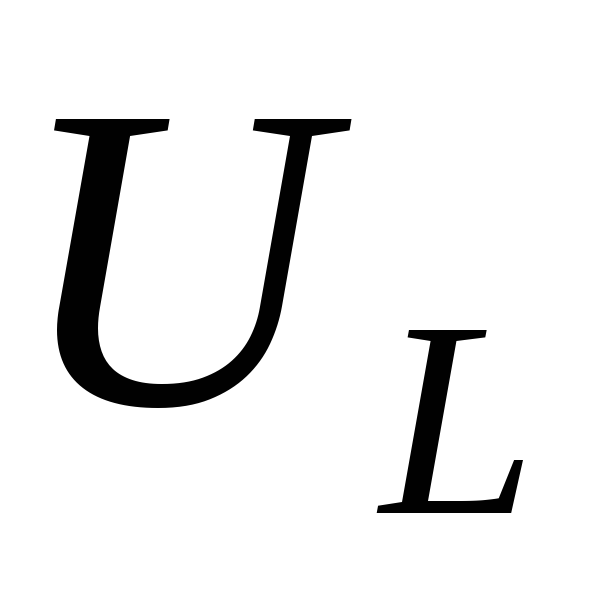 ,
которое равняется минус ЭДС самоиндукции
(ЭДС самоиндукции противодействует
внешнему напряжению),
,
которое равняется минус ЭДС самоиндукции
(ЭДС самоиндукции противодействует
внешнему напряжению), 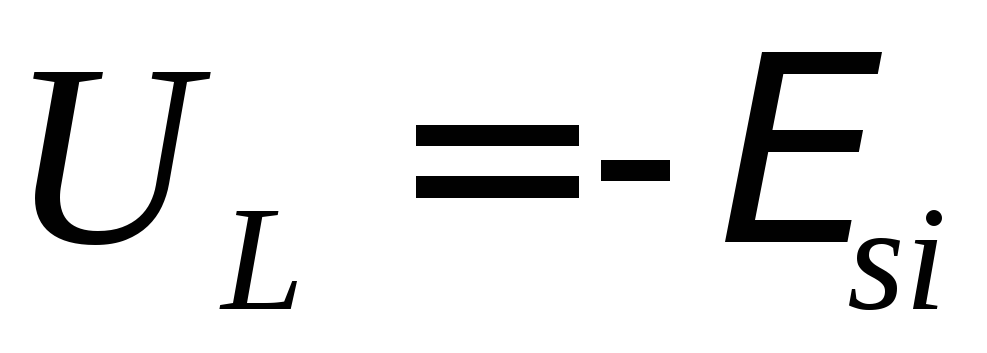 .
Подставив выражение для силы тока (1) в
выражение для ЭДС самоиндукции (11*),
получим значение напряжения на
индуктивности
.
Подставив выражение для силы тока (1) в
выражение для ЭДС самоиндукции (11*),
получим значение напряжения на
индуктивности 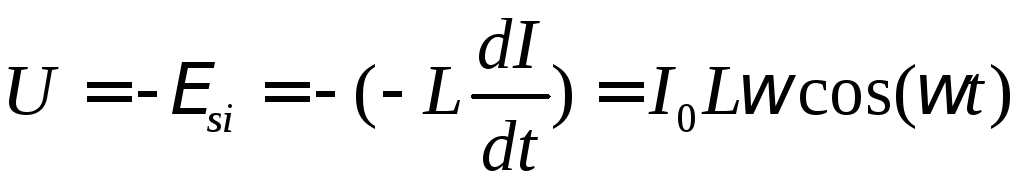 ,
или учитывая, что
,
или учитывая, что 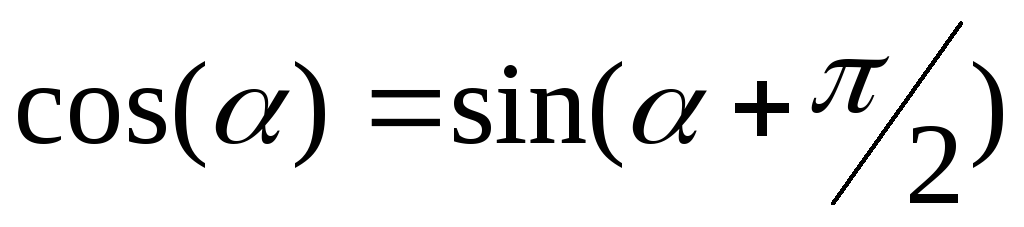
| (3) |
Величина 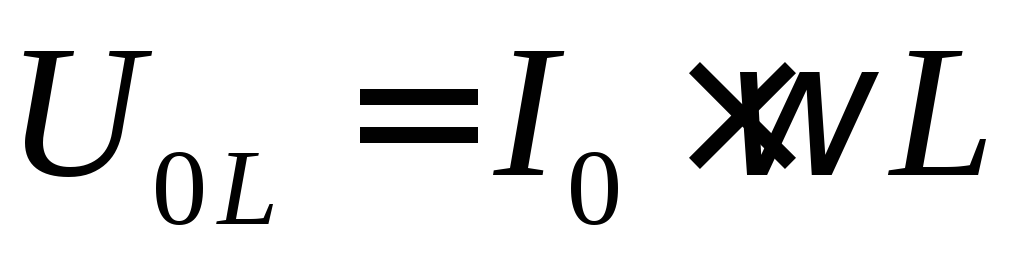 является амплитудным значением напряжения
на индуктивности, а отношение
является амплитудным значением напряжения
на индуктивности, а отношение
| (4) |
называют индуктивным
сопротивлением. Анализируя это выражение, можно сделать
вывод, что катушка
индуктивности хорошо пропускает
постоянный ток (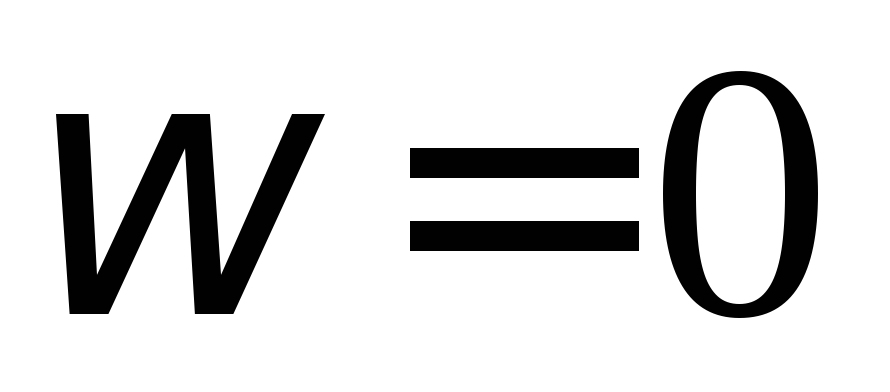 )
и хуже пропускает переменный ток (
)
и хуже пропускает переменный ток (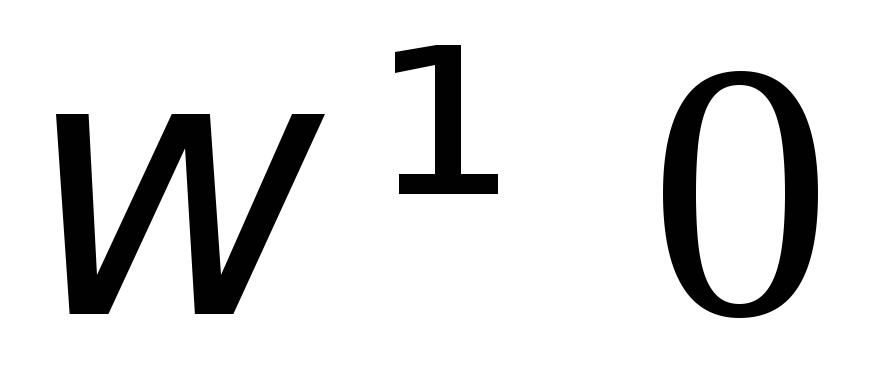 ).
В отличие от активного сопротивления,
индуктивное сопротивление не вызывает
выделение джоулева тепла.
).
В отличие от активного сопротивления,
индуктивное сопротивление не вызывает
выделение джоулева тепла.
И з
сравнения выражений для тока (1) и
напряжения (3) на индуктивности вытекает,
что колебания напряжения на катушке
опережают колебания тока на
з
сравнения выражений для тока (1) и
напряжения (3) на индуктивности вытекает,
что колебания напряжения на катушке
опережают колебания тока на 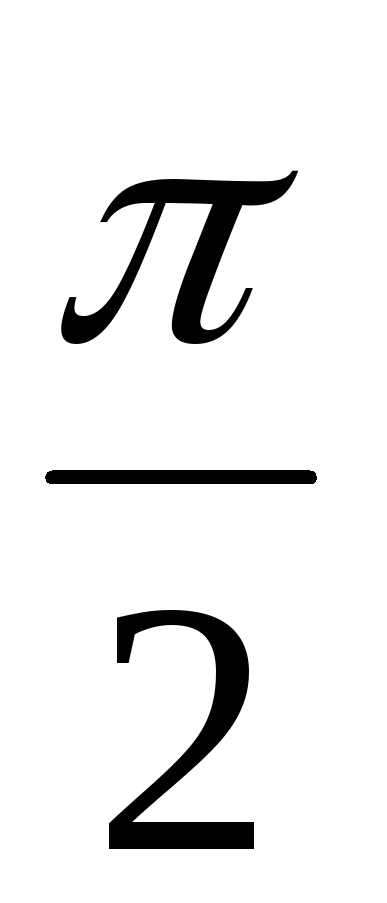 (рис. 2). Это означает, что на катушке
сначала возникает напряжение – ЭДС
самоиндукции, а уже потом начинает
возрастать ток (мгновенному росту тока
мешает ЭДС самоиндукции, которая
противодействует
первичной переменной ЭДС).
Когда ток достигает максимального
значения – напряжение на катушке
минимально (производная в максимуме
равна нулю), И наоборот, когда напряжение
максимально – ток равняется нулю.
(рис. 2). Это означает, что на катушке
сначала возникает напряжение – ЭДС
самоиндукции, а уже потом начинает
возрастать ток (мгновенному росту тока
мешает ЭДС самоиндукции, которая
противодействует
первичной переменной ЭДС).
Когда ток достигает максимального
значения – напряжение на катушке
минимально (производная в максимуме
равна нулю), И наоборот, когда напряжение
максимально – ток равняется нулю.
2.3.Емкость в цепи переменного тока
Р ассмотрим
электрическую цепь, которая состоит
только из источника переменного тока
и конденсатора
ассмотрим
электрическую цепь, которая состоит
только из источника переменного тока
и конденсатора  .
Как
известно, конденсатор (две металлические
пластины, между которыми – диэлектрик)
вообще не пропускает постоянный ток
(ток будет протекать только до тех пор,
пока конденсатор заряжается, а потом
исчезает). Но если на конденсатор подавать
переменное напряжение, он все время
будет перезаряжаться, то есть через
конденсатор может идти переменный ток
.
Как
известно, конденсатор (две металлические
пластины, между которыми – диэлектрик)
вообще не пропускает постоянный ток
(ток будет протекать только до тех пор,
пока конденсатор заряжается, а потом
исчезает). Но если на конденсатор подавать
переменное напряжение, он все время
будет перезаряжаться, то есть через
конденсатор может идти переменный ток 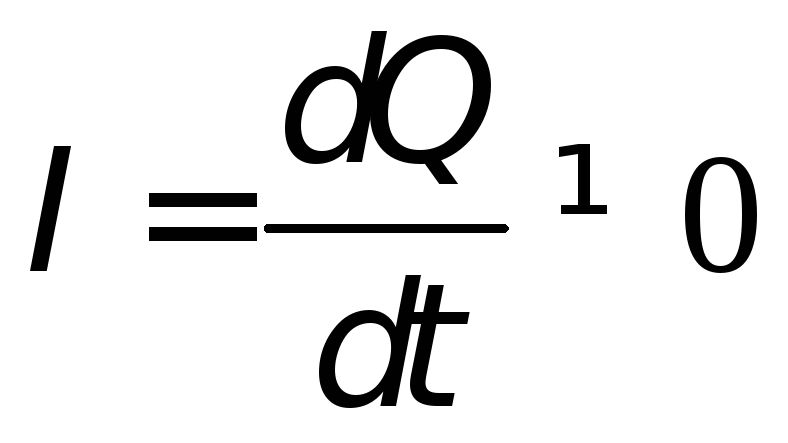 .
Чем больше частота переменного тока и
емкость конденсатора, тем лучше он
пропускает ток, тем меньшим будет его емкостное
сопротивление.
Найдем это сопротивление, то есть
сопротивление, которое создает конденсатор
переменному току.
.
Чем больше частота переменного тока и
емкость конденсатора, тем лучше он
пропускает ток, тем меньшим будет его емкостное
сопротивление.
Найдем это сопротивление, то есть
сопротивление, которое создает конденсатор
переменному току.
Пусть
через конденсатор течет ток, который
меняется по закону (1) 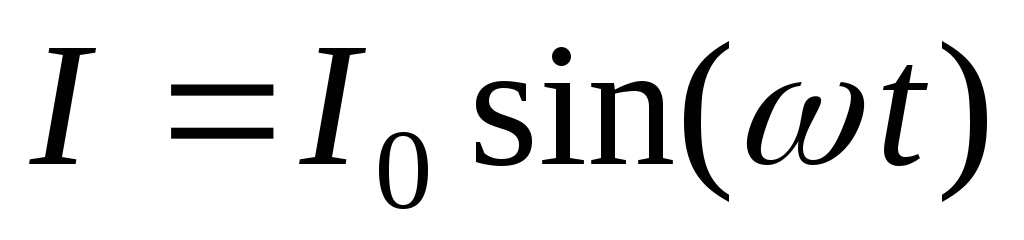 .
Из определения силы тока (1*)
.
Из определения силы тока (1*) 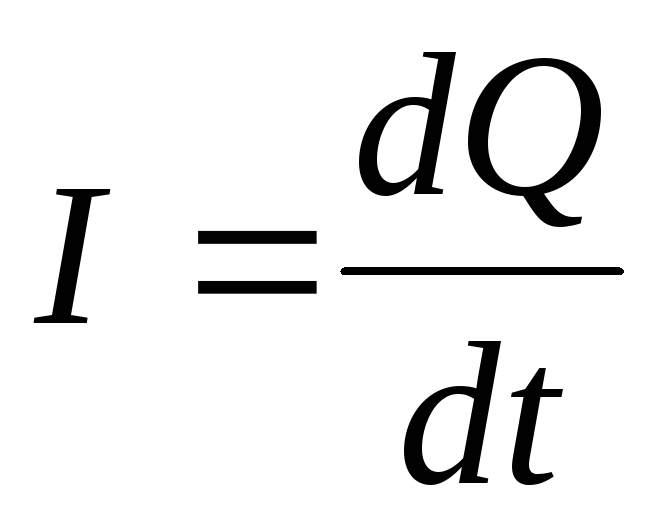 ,
можно найти заряд
,
можно найти заряд  на обкладках конденсатора:
на обкладках конденсатора: 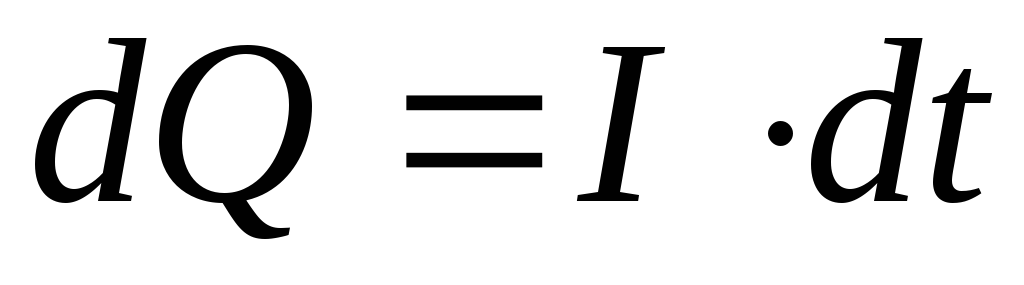 ,
,  .
Учитывая,
что
.
Учитывая,
что 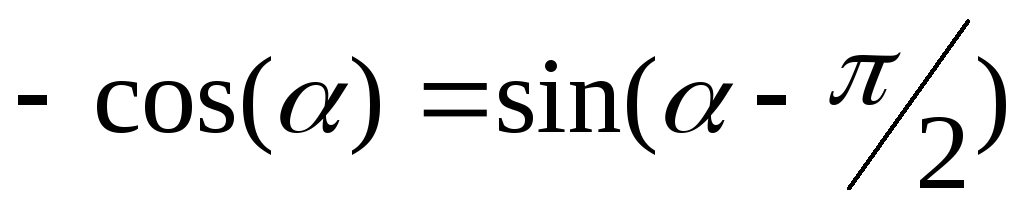 ,
получаем
,
получаем 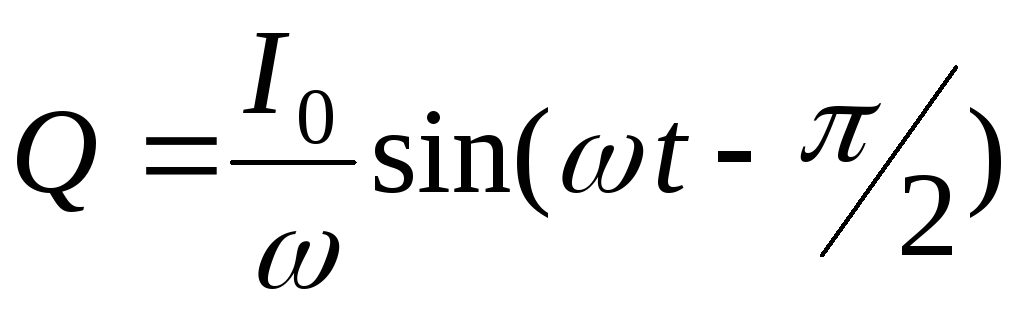 .
Из определения электроемкости конденсатора
(7)
.
Из определения электроемкости конденсатора
(7) 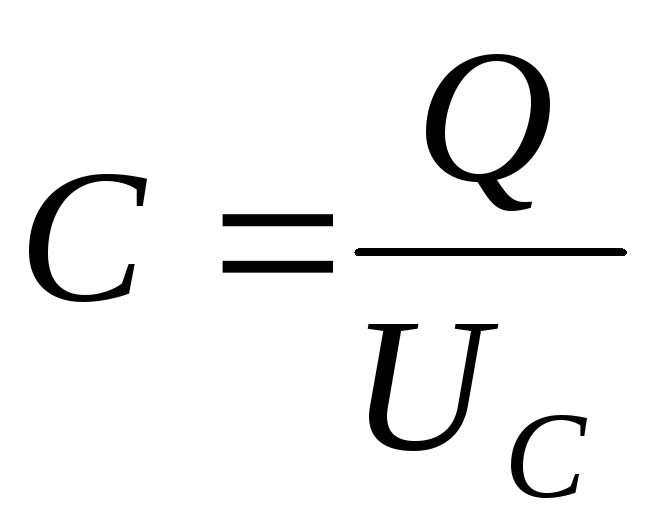 ,
вытекает, что напряжение на его обкладках
будет
,
вытекает, что напряжение на его обкладках
будет
| (5) |
Величина 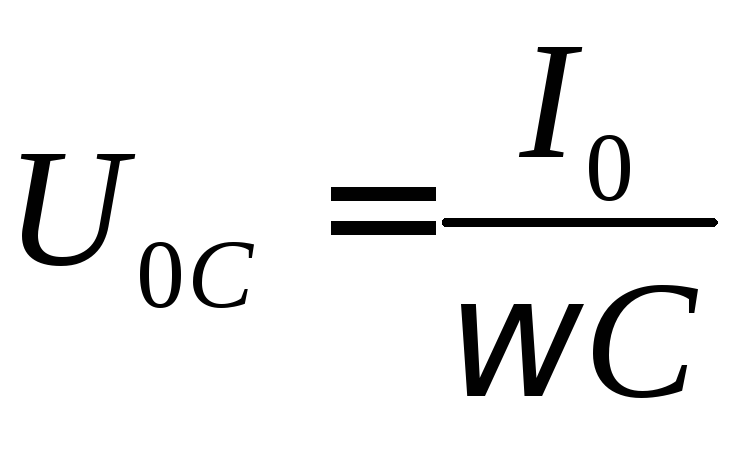 является амплитудным значением напряжения
на емкости, а отношение
является амплитудным значением напряжения
на емкости, а отношение
| (6) |
называют емкостным сопротивлением. На емкостном сопротивлении, как и на индуктивном, джоулево тепло не выделяется. Анализируя это выражение, можно сделать вывод, что конденсатор хорошо пропускает переменный ток высокой частоты и хуже пропускает ток малой частоты.
И з
сравнения выражений для тока (1) и
напряжения (5) на конденсаторе вытекает,
что колебания напряжения на конденсаторе
отстают от колебаний тока на
з
сравнения выражений для тока (1) и
напряжения (5) на конденсаторе вытекает,
что колебания напряжения на конденсаторе
отстают от колебаний тока на 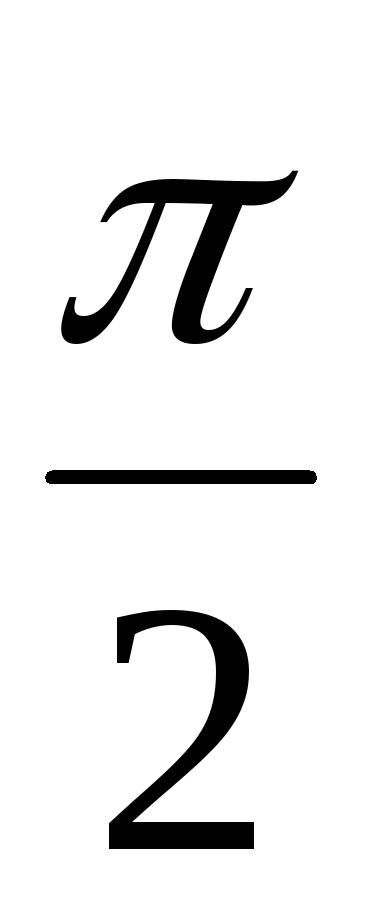 (рис. 3). То есть сначала через конденсатор
протекает ток (конденсатор заряжается),
а уже потом на нем возникает напряжение.
Когда ток достигает максимального
значения – напряжение на конденсаторе
равняется нулю, и наоборот, когда
напряжение максимальное – ток равняется
нулю.
(рис. 3). То есть сначала через конденсатор
протекает ток (конденсатор заряжается),
а уже потом на нем возникает напряжение.
Когда ток достигает максимального
значения – напряжение на конденсаторе
равняется нулю, и наоборот, когда
напряжение максимальное – ток равняется
нулю.
1.3.1. Активное сопротивление в цепи переменного тока
Р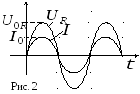 ассмотрим
электрическую цепь, состоящую только
из источника переменного тока и активного
сопротивления R.
Падение напряжения на активном
сопротивлении определяется из закона
Ома и выражения (1):
ассмотрим
электрическую цепь, состоящую только
из источника переменного тока и активного
сопротивления R.
Падение напряжения на активном
сопротивлении определяется из закона
Ома и выражения (1):
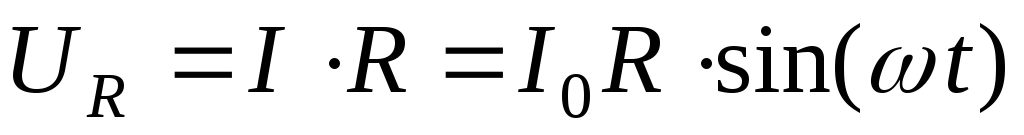 . (2)
. (2)
Величина 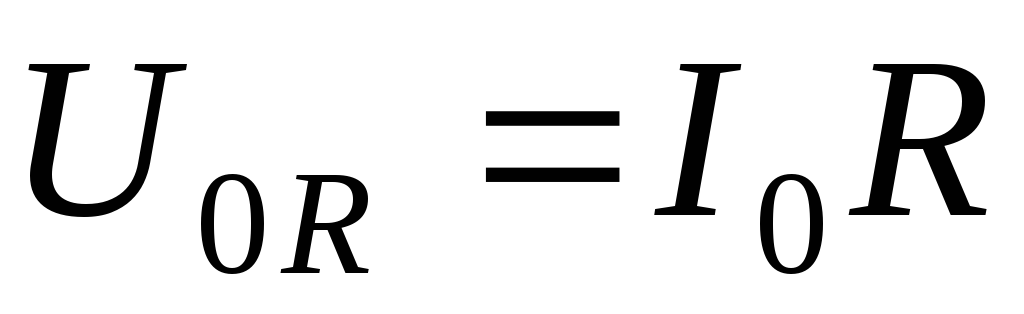 будет представлять собой амплитудное
значение напряжения на активном
сопротивлении. Сравнивая выражения (1)
и (2) видим, что колебания напряжения и
тока на активном сопротивлении происходит
в одинаковой фазе (по закону синуса,
рис.2). Заметим, что в цепи с активным
сопротивлением происходит необратимый
процесс преобразования электрической
энергии в тепловую.
будет представлять собой амплитудное
значение напряжения на активном
сопротивлении. Сравнивая выражения (1)
и (2) видим, что колебания напряжения и
тока на активном сопротивлении происходит
в одинаковой фазе (по закону синуса,
рис.2). Заметим, что в цепи с активным
сопротивлением происходит необратимый
процесс преобразования электрической
энергии в тепловую.
1.3.2. Индуктивность в цепи переменного тока
 Если
катушка индуктивности
Если
катушка индуктивности 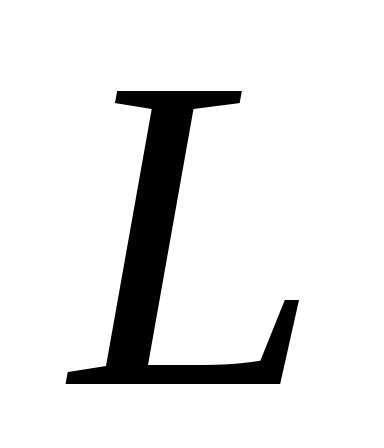 находится в контуре с переменным током,
то в ней все время будет возникать ЭДС
самоиндукции, которая противодействует
внешний переменной ЭДС. Вследствие
этого катушка будет создавать сопротивление
(дополнительное к активному) переменному
току, который называют индуктивным
сопротивлением. Найдем это сопротивление.
находится в контуре с переменным током,
то в ней все время будет возникать ЭДС
самоиндукции, которая противодействует
внешний переменной ЭДС. Вследствие
этого катушка будет создавать сопротивление
(дополнительное к активному) переменному
току, который называют индуктивным
сопротивлением. Найдем это сопротивление.
Пусть
активное сопротивление катушки очень
мало ( ).
Тогда на индуктивности создается падение
напряжения
).
Тогда на индуктивности создается падение
напряжения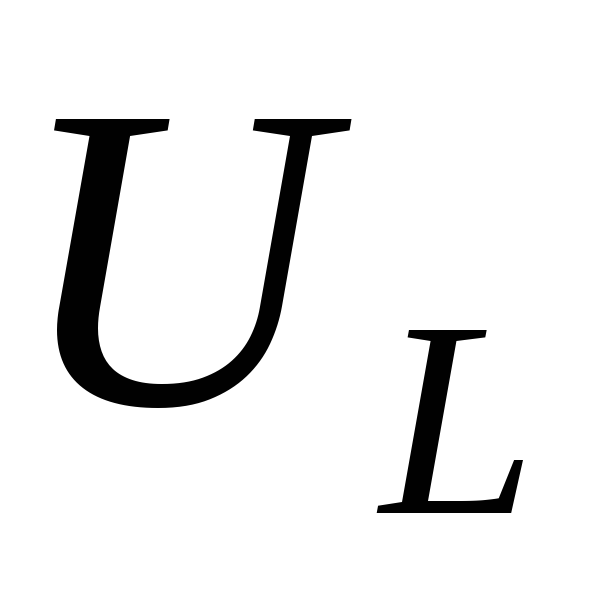 ,
которое равняется минус ЭДС самоиндукции
(ЭДС самоиндукции противодействует
внешнему напряжению),
,
которое равняется минус ЭДС самоиндукции
(ЭДС самоиндукции противодействует
внешнему напряжению),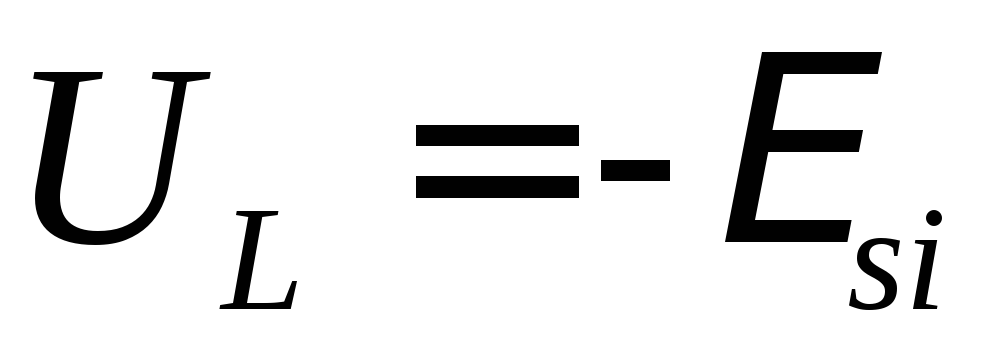 .
Подставив выражение для силы тока (1) в
выражение для ЭДС самоиндукции (11*),
получим значение напряжения на
индуктивности
.
Подставив выражение для силы тока (1) в
выражение для ЭДС самоиндукции (11*),
получим значение напряжения на
индуктивности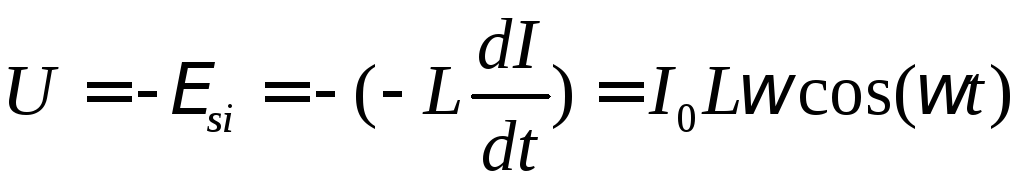 ,
или учитывая, что
,
или учитывая, что 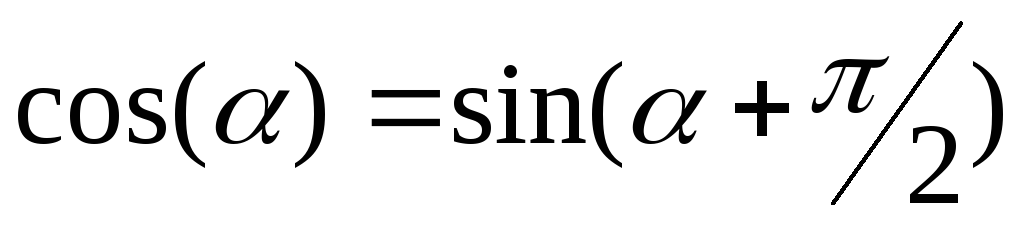
| (3) |
Величина 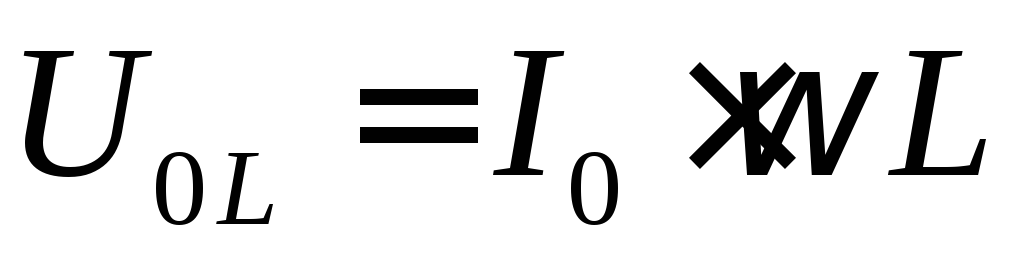 является амплитудным значением напряжения
на индуктивности, а отношение
является амплитудным значением напряжения
на индуктивности, а отношение
| (4) |
называют индуктивным
сопротивлением. Анализируя это выражение, можно сделать
вывод, что катушка
индуктивности хорошо пропускает
постоянный ток (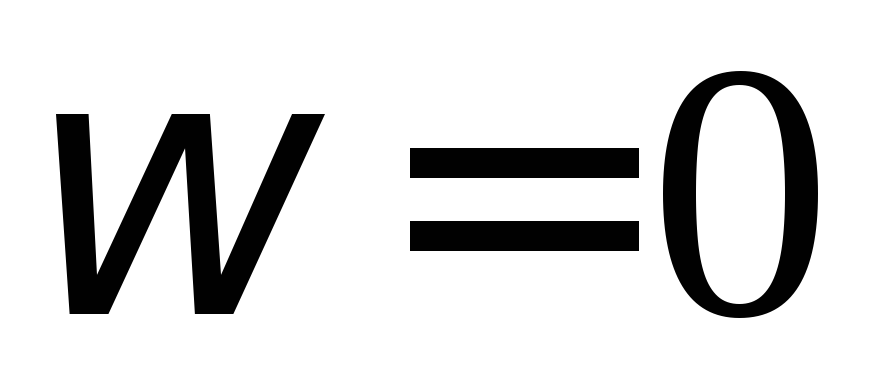 )
и хуже пропускает переменный ток (
)
и хуже пропускает переменный ток (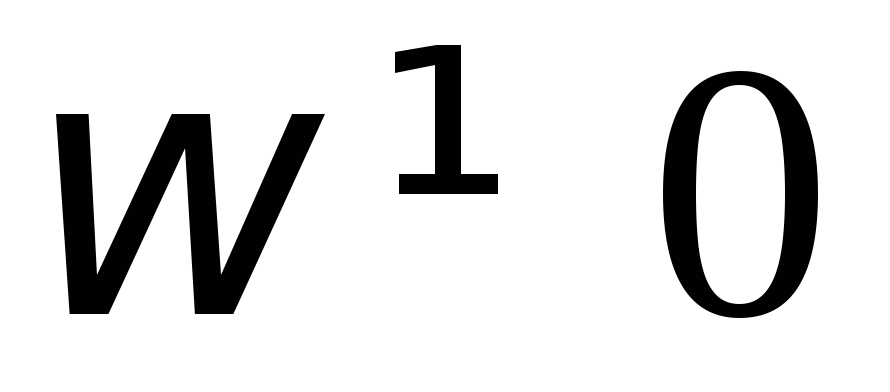 ).
В отличие от активного сопротивления,
индуктивное сопротивление не вызывает
выделение джоулева тепла.
).
В отличие от активного сопротивления,
индуктивное сопротивление не вызывает
выделение джоулева тепла.
И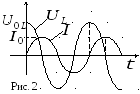 з
сравнения выражений для тока (1) и
напряжения (3) на индуктивности вытекает,
что колебания напряжения на катушке
опережают колебания тока на
з
сравнения выражений для тока (1) и
напряжения (3) на индуктивности вытекает,
что колебания напряжения на катушке
опережают колебания тока на 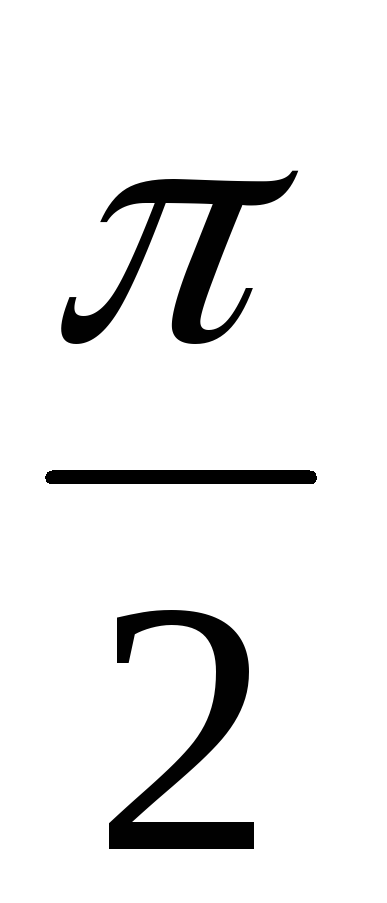 (рис. 2). Это означает, что на катушке
сначала возникает напряжение – ЭДС
самоиндукции, а уже потом начинает
возрастать ток (мгновенному росту тока
мешает ЭДС самоиндукции, которая
противодействует
первичной переменной ЭДС).
Когда ток достигает максимального
значения – напряжение на катушке
минимально (производная в максимуме
равна нулю), И наоборот, когда напряжение
максимально – ток равняется нулю.
(рис. 2). Это означает, что на катушке
сначала возникает напряжение – ЭДС
самоиндукции, а уже потом начинает
возрастать ток (мгновенному росту тока
мешает ЭДС самоиндукции, которая
противодействует
первичной переменной ЭДС).
Когда ток достигает максимального
значения – напряжение на катушке
минимально (производная в максимуме
равна нулю), И наоборот, когда напряжение
максимально – ток равняется нулю.
1.3.3. L и r в цепи переменного тока
Р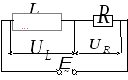 ассмотрим
теперь последовательное соединение
активного сопротивления и индуктивности
в цепи переменного тока. Сила тока в
данной цепи на всех участках одинакова
и меняется по закону (1). В этом законе
(
ассмотрим
теперь последовательное соединение
активного сопротивления и индуктивности
в цепи переменного тока. Сила тока в
данной цепи на всех участках одинакова
и меняется по закону (1). В этом законе
(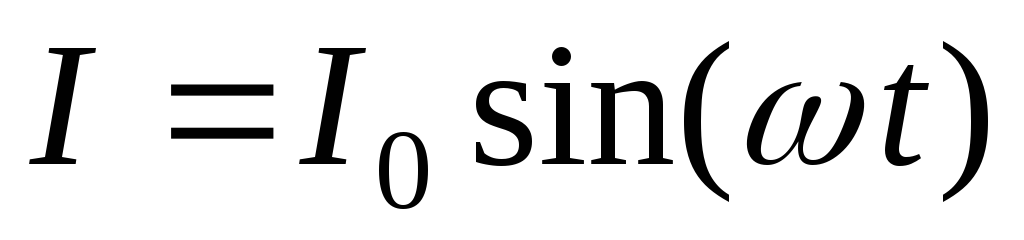 )
необходимо найти амплитудное значение
силы тока
)
необходимо найти амплитудное значение
силы тока 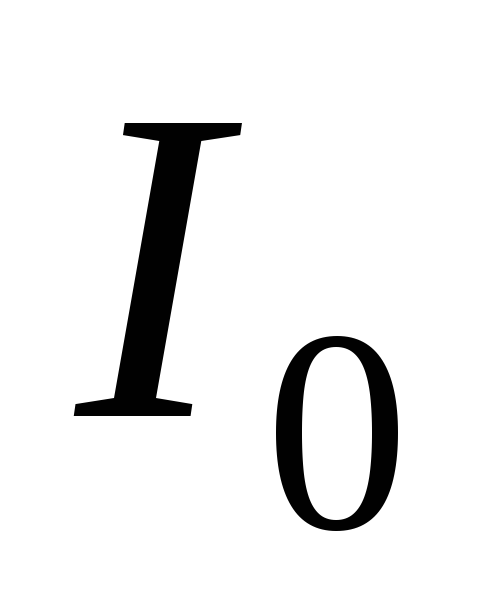 .
Также необходимо найти суммарное падение
напряжения на последовательно соединенных
сопротивлении и индуктивности. Сложность
этой задачи заключается в том, что фаза
колебаний напряжения на
.
Также необходимо найти суммарное падение
напряжения на последовательно соединенных
сопротивлении и индуктивности. Сложность
этой задачи заключается в том, что фаза
колебаний напряжения на и
и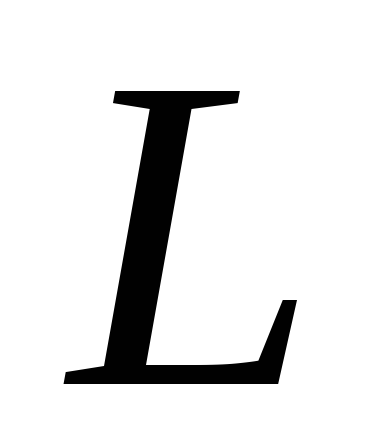 будет разной. Таким образом, необходимо
сложить колебания с одинаковыми
частотами, но разными фазами. Для этого
воспользуемся известным из теории
колебаний методом векторного сложения
амплитуд.
будет разной. Таким образом, необходимо
сложить колебания с одинаковыми
частотами, но разными фазами. Для этого
воспользуемся известным из теории
колебаний методом векторного сложения
амплитуд.
Напряжения на отдельных участках цепи с учетом их фаз показаны на векторной диаграмме, рис. 4. Объясним этот рисунок.
Пусть
амплитудное значение тока 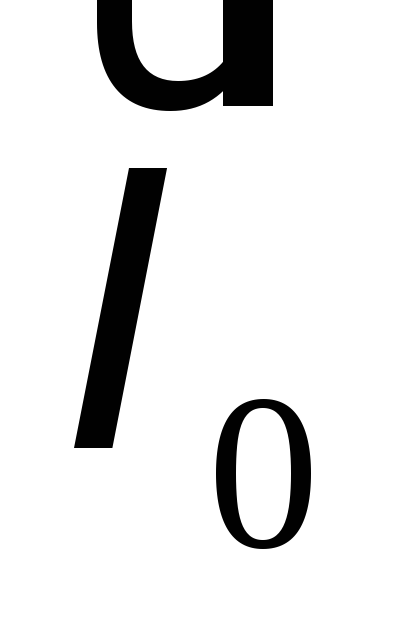 отложено вдоль горизонтальной оси.
отложено вдоль горизонтальной оси.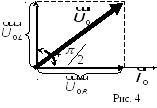 Колебания
напряжения на индуктивности
Колебания
напряжения на индуктивности будет опережать колебания тока на
будет опережать колебания тока на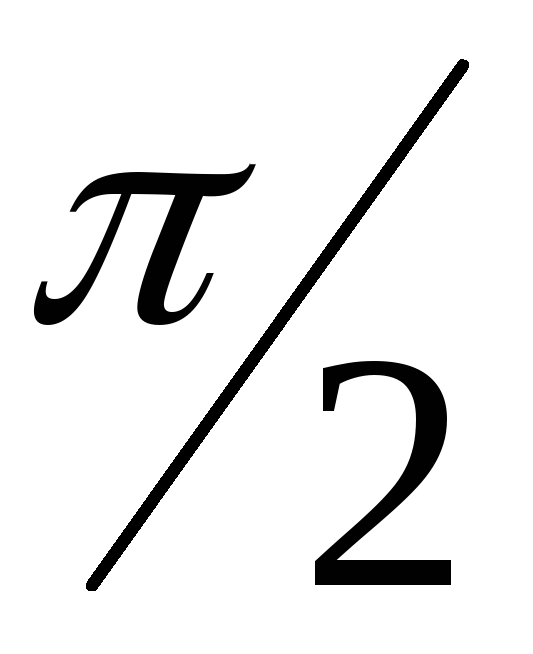 (или на 900).
Тогда вектор
(или на 900).
Тогда вектор 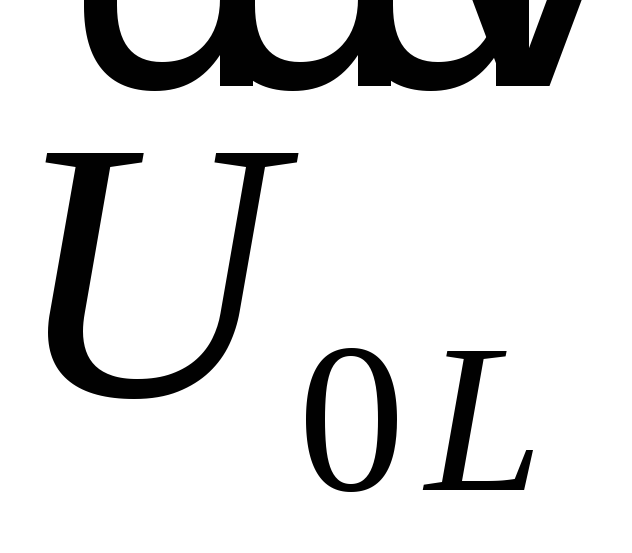 ,
который соответствует амплитудному
значению напряжения на индуктивности,
будет перпендикулярным вектору
,
который соответствует амплитудному
значению напряжения на индуктивности,
будет перпендикулярным вектору и направленным вверх.
и направленным вверх.
Колебания
напряжения на активном сопротивлении 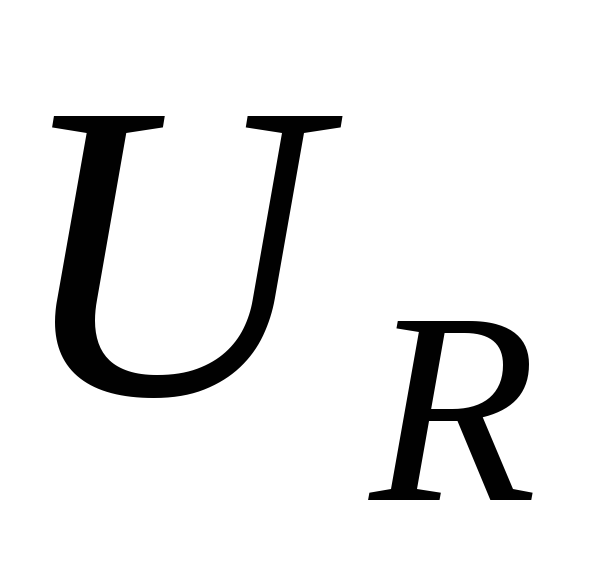 будут происходить в одинаковой фазе с
током. Тогда вектор
будут происходить в одинаковой фазе с
током. Тогда вектор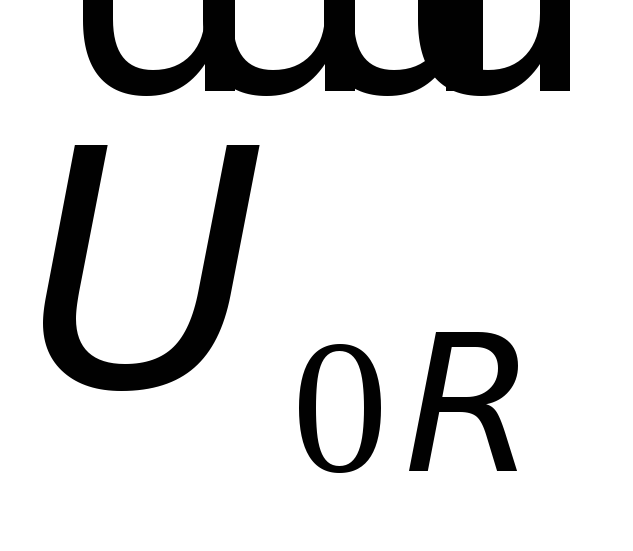 ,
соответствующий амплитудному значению
напряжения на активном сопротивлении,
будет направлен по правую сторону,
параллельно направлению
,
соответствующий амплитудному значению
напряжения на активном сопротивлении,
будет направлен по правую сторону,
параллельно направлению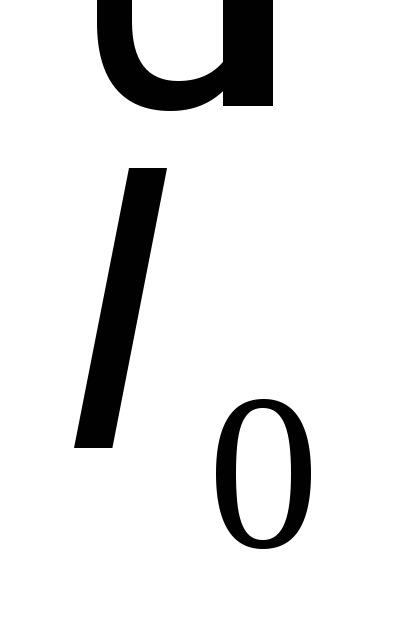 .
.
Амплитуда
суммарного напряжения 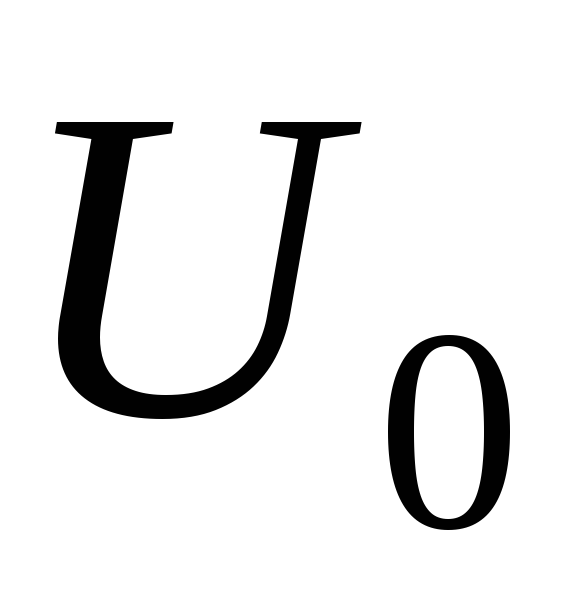 равняется векторной сумме напряжений
на отдельных участках:
равняется векторной сумме напряжений
на отдельных участках: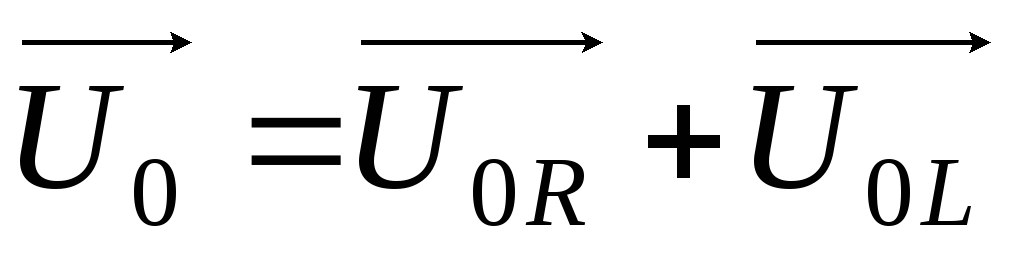 .
Длину вектора
.
Длину вектора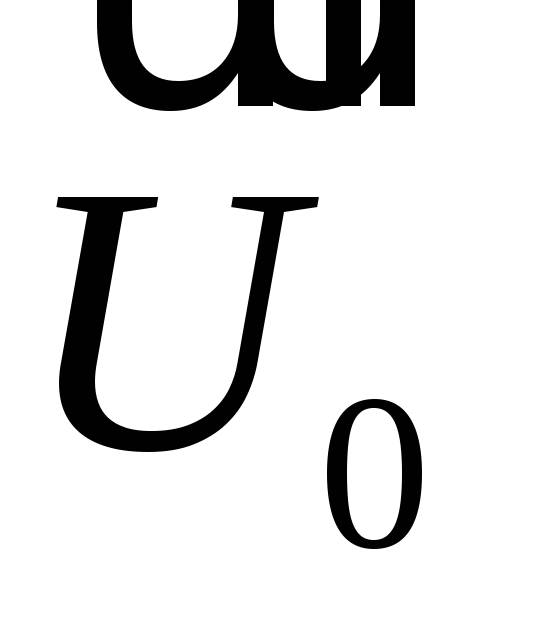 можно найти по теореме Пифагора:
можно найти по теореме Пифагора: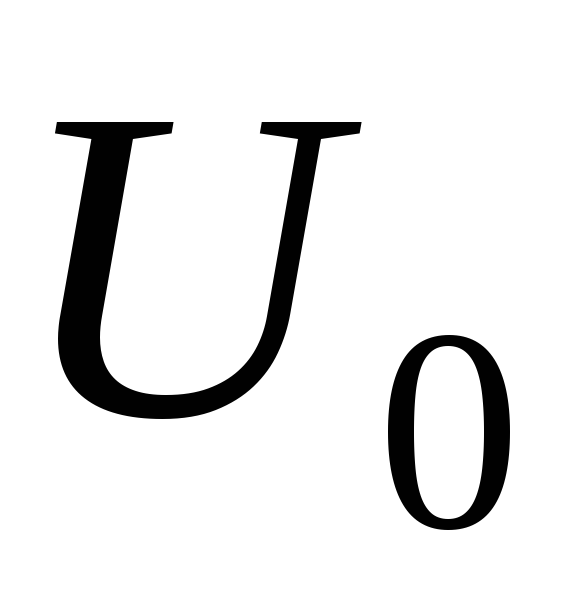 будет гипотенузой треугольника с
катетами
будет гипотенузой треугольника с
катетами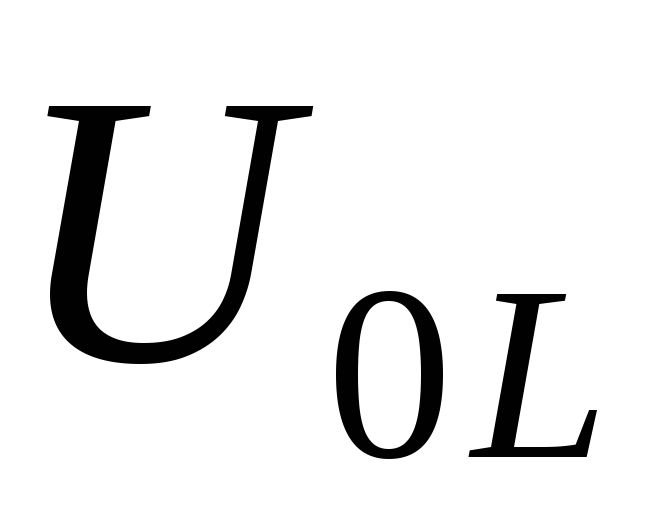 и
и 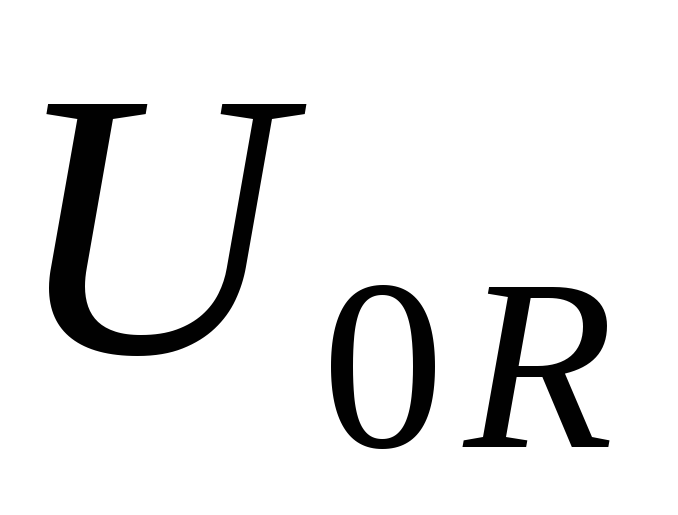 .
Она равняется
.
Она равняется 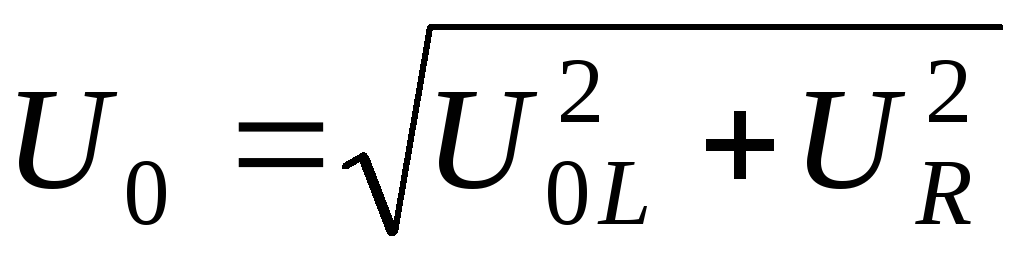 ,или, учитывая
соотношение (4) и
,или, учитывая
соотношение (4) и  ,
можно записать
,
можно записать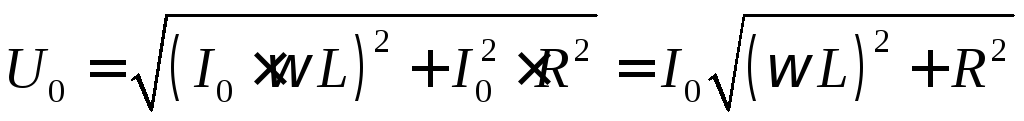 .
По второму правилу Кирхгофа сумма
амплитуд напряжений на отдельных
элементах цепи должна равняться амплитуде
внешней ЭДС:
.
По второму правилу Кирхгофа сумма
амплитуд напряжений на отдельных
элементах цепи должна равняться амплитуде
внешней ЭДС: 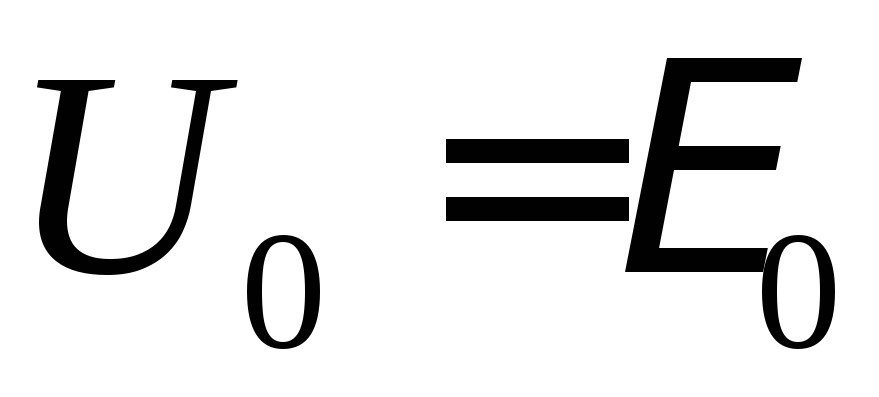 .
Тогда можно записать
.
Тогда можно записать
| (5) |
Выражение (5) представляет собой закон Ома для последовательной цепи переменного тока, состоящей из активного сопротивления и индуктивности. Из этого выражения можно найти индуктивность катушки:
| (6) |


 ,.
,.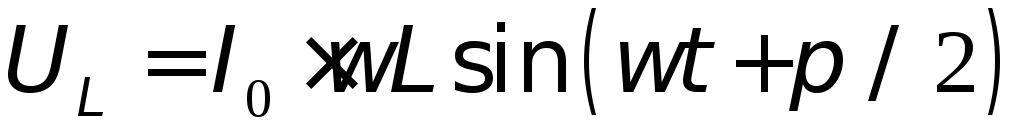 .
.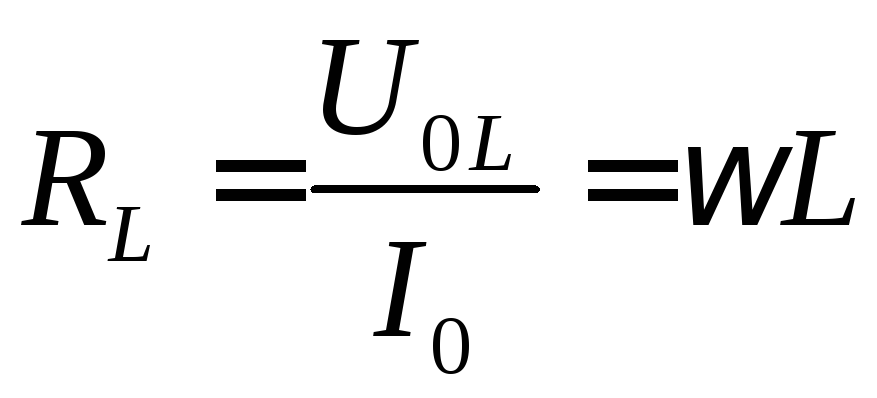
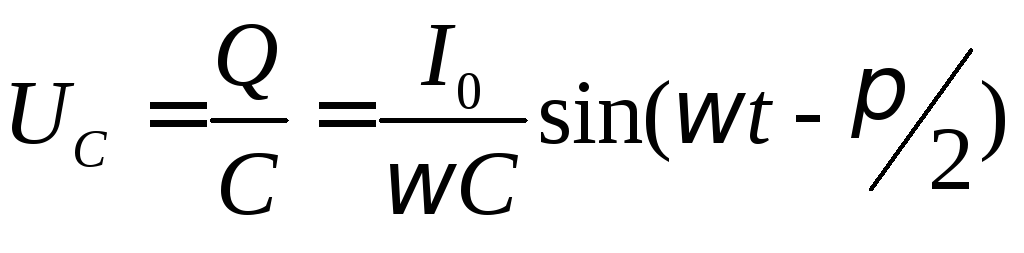 .
.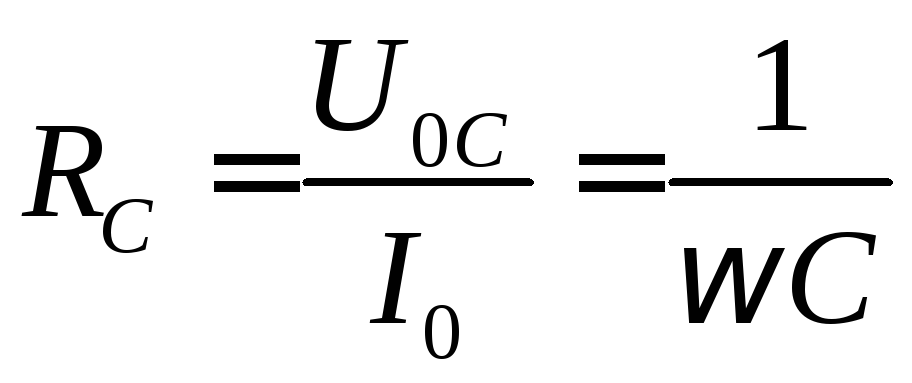
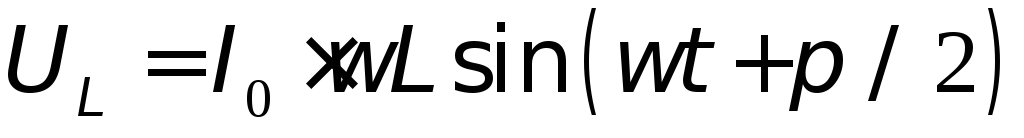 .
.