Системы счисления — презентация онлайн
1. Системы счисления
2. Литература
Острейковский В.А. Информатика: Учеб.для вузов .-М. : Высш. шк.,2000
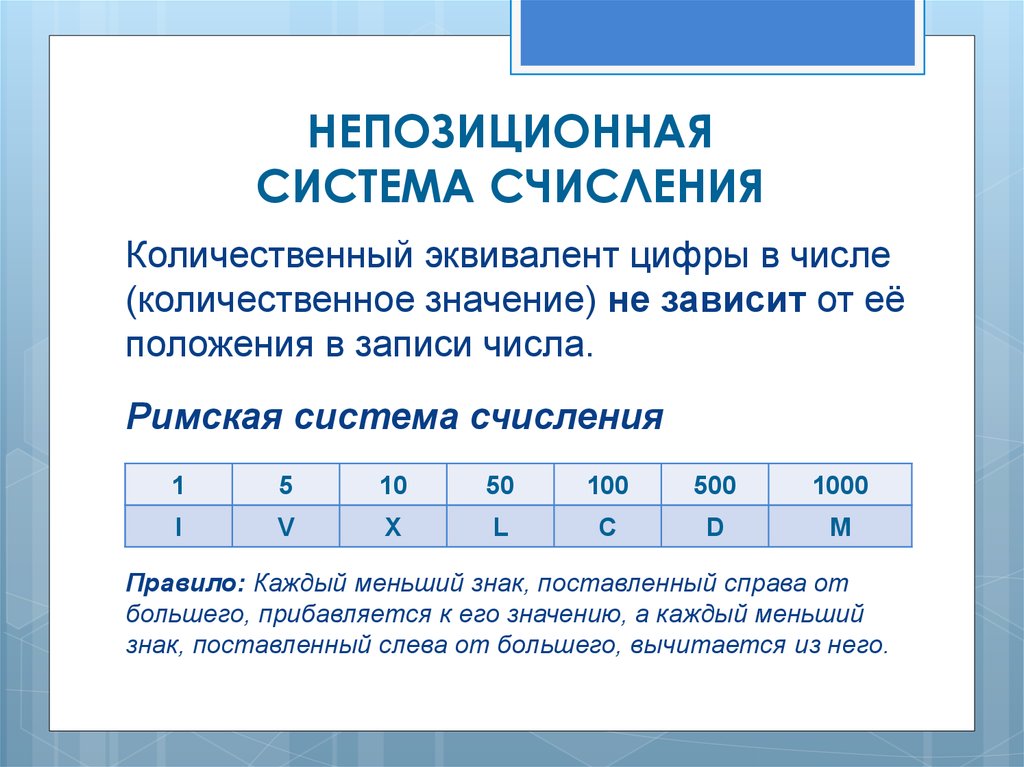
3. Система счисления
Система счисления — это метод записичисел с помощью набора специальных
знаков, которые называются цифрами.
Множество цифр, используемых в системе
счисления, называется алфавитом.
Системы счисления бывают позиционными
и непозиционными.
Непозиционные системы счисления
Вес цифры (т.е. тот вклад, который она
вносит в значение числа) не зависит от ее
позиции в записи числа.
Пример. Римская система счисления:
в числе ХХХII (тридцать два) вес цифры Х
в любой позиции равен десяти, вес цифры
I в любой позиции равен единице и т.д.
5. Позиционные системы счисления
В позиционных системах счислениязначимость (вес) каждой цифры числа
зависит от позиции, которую она занимает
в числе.
Пример: в числе 757,7 первая семерка
означает 7 сотен, вторая – 7 единиц, а
третья – 7 десятых долей единицы.

6. Позиционные системы счисления
Сама запись числа 757,7 означаетсокращенную запись выражения
700+50+7+0,7 = 7•102+5•101+7•100+7•10-1= 757,7
Любая позиционная система счисления
характеризуется своим основанием.
7. Позиционные системы счисления
За основание системы счисления можнопринять любое натуральное число — 2, 3, 4
и т.д.
Следовательно, возможно бесчисленное
множество позиционных систем: двоичная,
троичная, четверичная и т.д.
8. Алфавит позиционной системы счисления
Для записи чисел в позиционной системе соснованием q нужен алфавит из q цифр.
Таким образом, основание позиционной
системы счисления — это количество цифр в
её алфавите.
Обычно при q < 10 используют q первых
арабских цифр, а при n > 10 к десяти арабским
цифрам добавляют латинские буквы.
9. Алфавит позиционной системы счисления
Примеры алфавитов нескольких систем:Если требуется указать основание системы, к
которой относится число, то основание
приписывается нижним индексом к этому
числу.
 Пример:
Пример:1011012, 36718, 3B8F16.
10. Позиционные системы счисления
Запись чисел в каждой из систем счисления соснованием q означает сокращенную запись
многочлена:
an-1qn-1 + an-2qn-2 +…+ a1q1 + a0q0 + a-1q-1 +…+ a-mq-m,
Здесь:
ai – цифры системы счисления;
n и m – число целых и дробных разрядов,
соответственно.
11. Позиционные системы счисления
Примеры:Это и есть способ перевода числа из
системы счисления с основанием q в 10-ю
систему счисления.
12. Перевод числа из системы счисления с основанием q в 10-ю систему счисления
Пример.Дано действительное число 101,012.
Записать его в десятичной системе
счисления.
Решение.
101,012 = 1•22 + 0•21 + 1•20 + 0•2-1 + 1•2-2 = 4 +
0 + 1 + 0 + 0,25 = 5,2510
13. Перевод числа из системы счисления с основанием q в 10-ю систему счисления
Пример: перевести число из 16-ой системысчисления в 10-ю.
Решение:
14. Задачи
Перевести данные числа в 10-ю систему счисления:А) 10000012
Б) 1000011111,01012
В) 1216,048
Г) 29А,516
15.
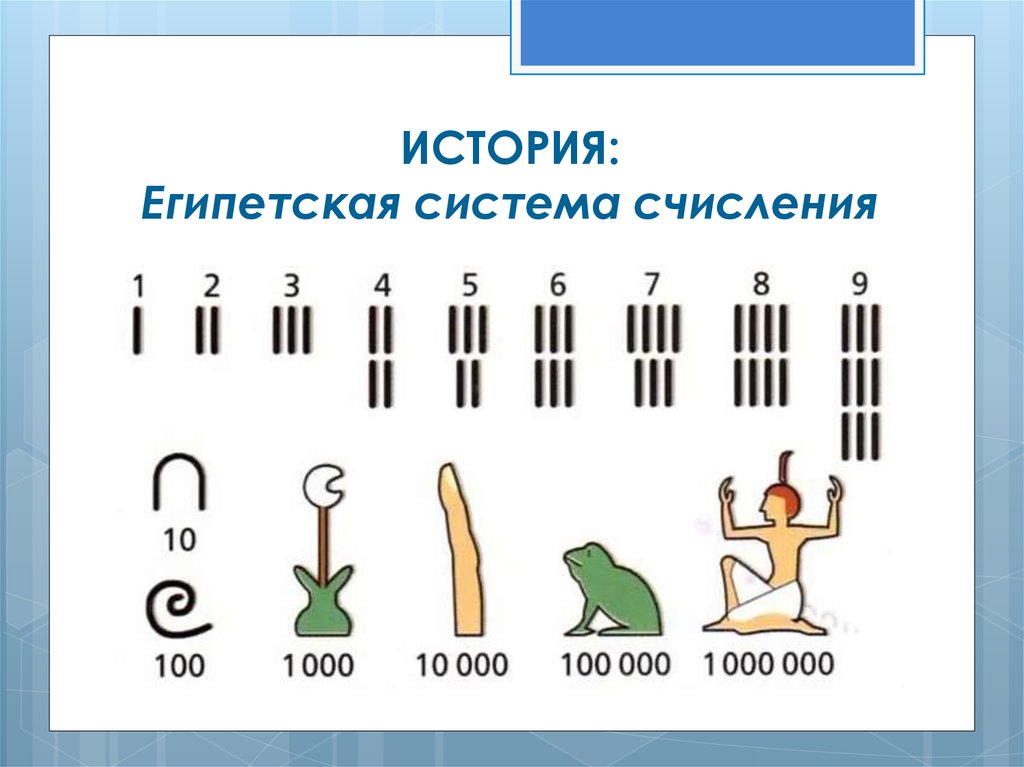 ЗадачиПример. Определить наименьшие основания
ЗадачиПример. Определить наименьшие основанияпозиционных систем счисления, при которых
56X = 63Y.
Решение. Запишем числа в виде многочленов:
56x = 5∙x1 + 6 ∙x0 и 63Y = 6∙y1 + 3 ∙y0
Получаем равенство: 5x + 6 = 6y + 3
Преобразуем равенство: x = (6y — 3)/5
При этом имеем еще 2 ограничения:
Х > 6 и Y > 6.
Теперь нужно найти значения X и Y,
удовлетворяющие всем трем условиям.
16. Пример
Перебирая значения Y>6 по возрастанию,подбираем такое при котором X должно
быть целое:
Y=7: x = (6 ∙ 7 — 3)/5 = 39 / 5 – не целое
Y=8: x = (6 ∙ 8 — 3)/5 = 45 / 5 = 9
Ответ: Y = 8, X = 9.
17. Порождение чисел в позиционных системах счисления
В системе счисления цифры упорядочены в соответствии сих значениями: 1 > 0, 2 > 1 и т.д.
Порождаются числа в позиционных системах счисления с
помощью правила продвижения цифры.
Продвижение цифры – это замена её на следующую по
величине.
Продвинуть цифру 1 значит заменить её на 2, продвинуть
цифру 2 значит заменить её на 3 и т.
 д.
д.Продвинуть старшую цифру (например, 9 в 10-ой системе)
значит заменить её на 0.
В двоичной системе, использующей только две цифры – 0 и
1, продвижение 0 означает замену его на 1, а
продвижение 1 – замену её на 0.
18. Порождение чисел в позиционных системах счисления
Целые числа в любой системе счисленияпорождаются с помощью Правила счета:
Для образования целого числа, следующего за
любым данным целым числом, нужно
продвинуть самую правую цифру числа;
если какая-либо цифра после продвижения
стала нулем, то нужно продвинуть цифру,
стоящую слева от неё.
19. Порождение чисел в позиционных системах счисления
Пример. Применяя правило счета, записатьпервые десять целых чисел в 2-ой, 3-ой, 5ой, 8-ой системах счисления.
Решение.
2-я: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;
3-я: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;
5-я: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;
8-я: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.
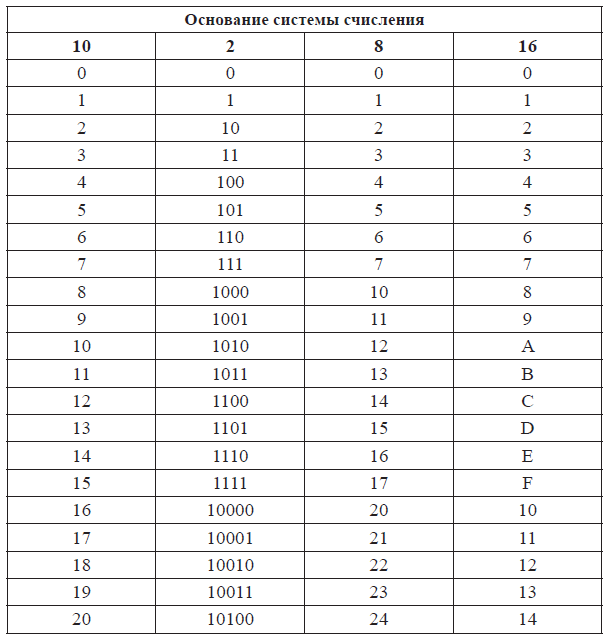
20. Перевод целых десятичных чисел в систему счисления с основанием q
При переводе целого десятичного числа Х всистему с основанием q данное число
нужно последовательно делить на q до тех
пор, пока не будет получен остаток < q.
Число в системе с основанием q
записывается как последовательность
остатков от деления, записанных в
обратном порядке, начиная с последнего.
21. Перевод целых десятичных чисел в систему счисления с основанием q
Пример. Перевести число 7510 из 10-й в 2-ю с.с.Решение.
1 001 0112
22. Задача
Перевести число 3710 в 2-ю.Решение.
Ответ: 3710 = 1001012 .
23. Перевод целых десятичных чисел в систему счисления с основанием q
Пример. Перевести число 31510 в 8-ю и 16-ю с.с.Решение.
8-я с.с.
16-я с.с.
Ответ:
31510 = 4738 = 13B16
Примечание. 1110 – это B16.
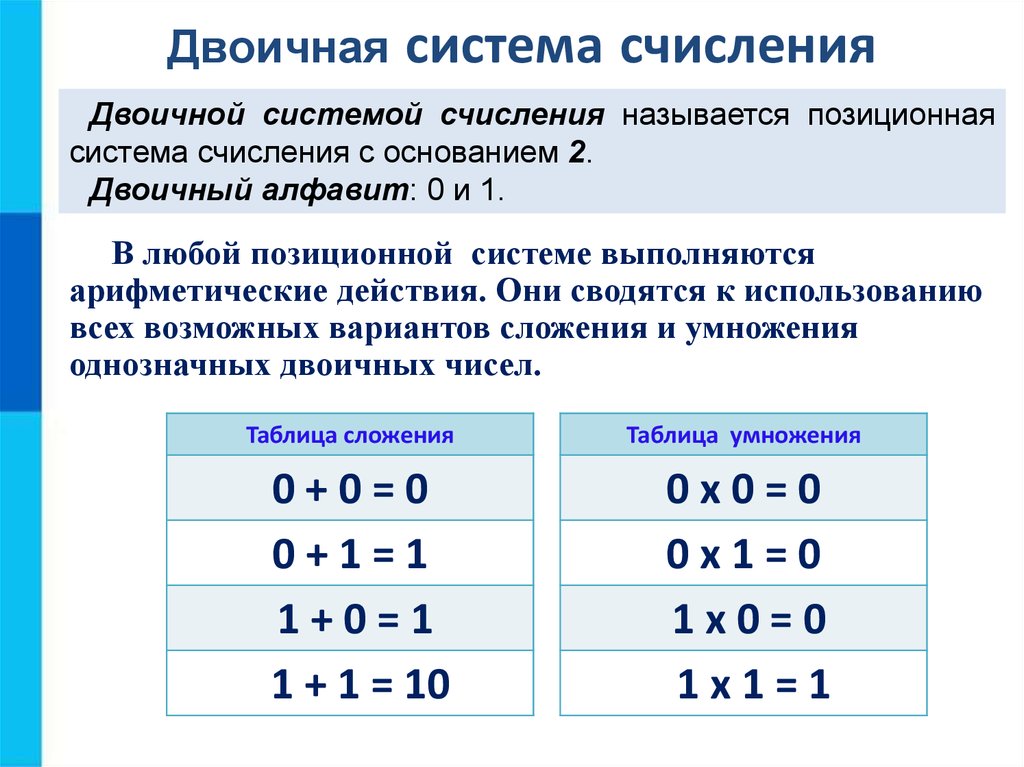
24. Задача
Перевести число 7510 в восьмеричную ишестнадцатеричную:
72
3 8
1
1
1138
Ответ: 7510 = 1138 = 4B16.
64
11
4
4(11)8 = 4В16
25. Перевод правильной десятичной дроби в систему счисления с основанием q
1. Дробь умножается на q.2. Результат умножения разделяется на 2 части целая часть произведения записывается в
результат, а дробная снова умножается.
3. Умножение производится, пока дробная часть
произведения не станет равной нулю (дробь
переводится точно), или не выявится период или
не будет достигнута заданная точность (например,
до 5 знаков после запятой).
26. Перевод правильной десятичной дроби в систему счисления с основанием q
Пример. Перевести десятичную дробь 0,1875 в 2-ю, 8-ю и 16-ю c.с.Решение.
2-я
8-я
16-я
0,1875
×
2
0,3750
×
2
0,750
× 2
1,50
× 2
1,00
0,1875
×
8
0,5000
× 2
4,0
0,1875
×
16
11350
1 875
3,0000
Результат: 0,316
Результат: 0,148
Результат: 0,00112
Здесь в левом столбце находится целая часть чисел, а в
правом — дробная.
 Умножается только дробная.
Умножается только дробная.Ответ: 0,187510 = 0,00112 = 0,148 = 0,316
27. Задача
Пример: Перевести число 0,3510 в 2-ю с.с.Решение.
0, 35
×
2
0, 70
× 2
1, 4
× 2
0, 8
× 2
1, 6
× 2
1, 2
× 4
0, 8
× 2
1, 6 и т.д
Результат: 0,3510 = 0,0101101…2 = 0,01(011)2
28. Задача
Пример: Перевести число 0,3510 в 8-ю с.с.Решение.
0, 35
×
8
2, 80
× 8
6, 4
× 8
3, 2
× 8
1, 6
× 2
1, 2
× 4
0, 8
× 8
6, 4 и т.д.
Результат: 0,3510 = 0,2631106…8 = = 0,2(63110)8
29. Задача
Пример: Перевести число 0,3510 в 2-ю, 8-ю и 16-ю.Решение.
0, 35
× 16
5, 60
×16
9, 6
× 16
9, 6 и т.д.
Результат: 0,3510 = 0,5(9)16
30. Перевод смешанных десятичной чисел в систему счисления с основанием q
Перевод смешанных чисел, содержащих целуюи дробную части:
1. Переводится целая часть по алгоритму
перевода целых чисел.
2. Переводится дробная часть по алгоритму
перевода правильной десятичной дроби .
3. В итоговой записи числа в новой системе
счисления целая часть отделяется от
дробной запятой (точкой).
31. Задачи
1. Перевести число 20,37510 в 2-ю, 8-ю и 16-ю.Ответ: 20,37510 =10100,0112 = 24,38 = 14,316
2. Перевести число 44,289062510 в 2-ю, 8-ю и
16-ю.
Ответ: 44,289062510 = 101100,01001012 = 54,2218 =
2С,4А16
32. Схема быстрого перевода между системами счисления, основания которых – это степени одного числа
Пример таких оснований — 2, 4, 8, 16.Перевод осуществляется через систему счисления,
основание которой равно возводимому степень
числу. Для примера – это двоичная с.с.
Перевод 8-х чисел в 2-ю с.с.: каждую 8-ю цифру
заменяем эквивалентной ей двоичной триадой тройкой цифр (23 = 8).
Перевод 16-х чисел в 2-ю с.с.: каждую 16-ю цифру
заменяем эквивалентной ей двоичной тетрадой
— четверкой цифр (24 = 16).
33.
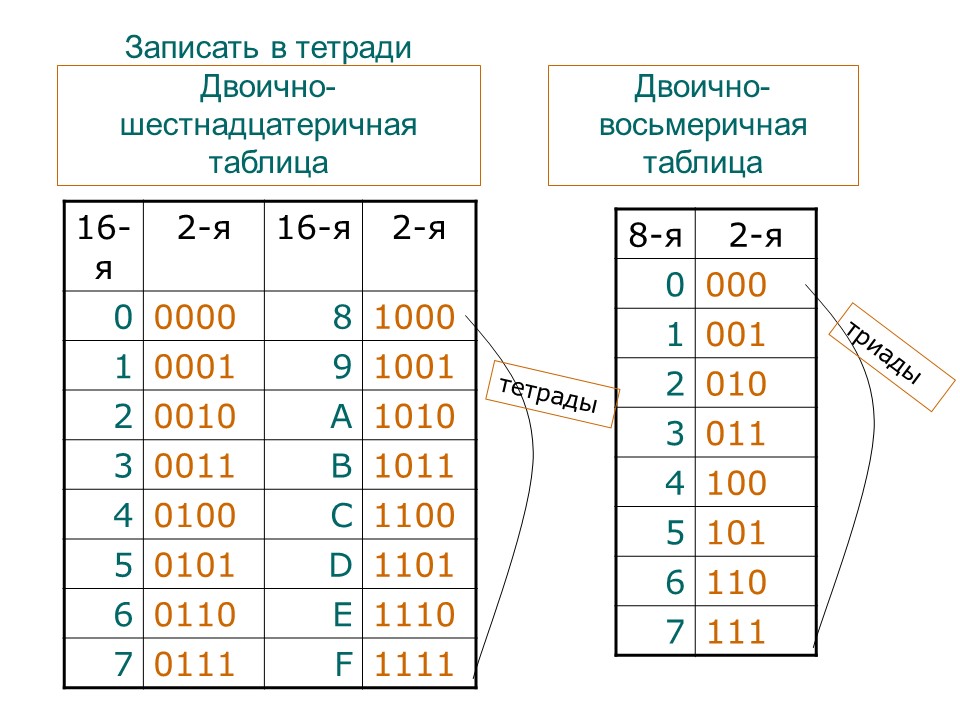
 Схема быстрого перевода между системами счисления, основания которых – это степени одного числаТаблицы перевода:
Схема быстрого перевода между системами счисления, основания которых – это степени одного числаТаблицы перевода:10 — я
0
1
2
3
2–я
00
01
10
11
4–я
0
1
2
3
10 — я
0
1
2
3
4
5
6
7
2–я
000
001
010
011
100
101
110
111
8–я
0
1
2
3
4
5
6
7
10 — я
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2–я
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
16 – я
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
34. Схема быстрого перевода между системами счисления, основания которых – это степени одного числа
Пример: Число 1111010101,112 перевести в 16-ю с.с.Решение:
35. Задачи
Перевести число 10101001,101112 :А) в 8-ю
Б) в 16-ю
36.
 Арифметические операции в системе счисления с основанием qПравила выполнения сложения, вычитания,
Арифметические операции в системе счисления с основанием qПравила выполнения сложения, вычитания,умножения и деления те же, что и в
десятичной системе счисления —сложение,
вычитание и умножение выполняются
столбиком, а деление углом.
Эти правила применимы и ко всем другим
позиционным системам счисления
37. Двоичная система счисления: сложение
Таблица сложения:Пример: Сложить число 11112 и 1102
перенос
38. Задача
Сложить два числа:Решение.
39. Восьмеричная система счисления: сложение
Пример. 75368 + 4728Решение. 7 5 3 68
+
4 7 28
7 9(10)8
-8
7 9(11)0
-8
7(10)3 0
-8
8 2 30
-8
1 0 2 3 08 Ответ: 75368 + 4728 = 102308
40. 16-я система счисления: сложение
Пример. 7B3E16 + 7AD16Решение. Сначала заменим буквы числами
7B3E16 + 7AD16 = 7(11)3(14)16+ 7(10)(13)16
7 (11) 3 (14)16
+ 7 (10) (13)16
7 (18) (13) (27)
— 16
7 (18) (14) (11)
— 16
8 2 (14) (11)
Заменим числа на буквы :
8 2 E
B 16
Ответ: 7B3E16 + 7AD16 = 82EB16
41.
 Задачи1.
Задачи1.Решение:
Ответ: 311,28
2. A8D,816 + 93B,C16
Ответ: 13C9,416
42. Двоичная система счисления: вычитание
Выполнить действие:Решение:
Ответ:
= 10001101,12
43. Задача
1100000011,0112 — 101010111,1(2)Решение:
—
Ответ: 110101011,1112
44. 8-я система счисления: вычитание
Выполнить действие:Решение:
Ответ:
= 215,48
45. Задача
1510,28 – 1230,548Решение:
—
Ответ: 257,448
46. 16-я система счисления: вычитание
Выполнить действие:Решение:
(12) 9 , 4
3 (11),(12)
8 (13), 8
Ответ:
= 8D,816
47. Задача
Вычислить: 27D,D816 – 191,216Решение:
1 — заём
—
2 7 (13),(13) 8
1 9 1 , 2
(14)(12),(11) 8
Ответ: 27D,D816 – 191,216 = EC,B816
48. 2-я система счисления: умножение
При умножении в двоичной системе счислениявыполняется по правилам умножения в столбик.
Пример: 1001112 10001112
Решение:
Ответ: 1001112 10001112 = 1010110100012
49.
 ЗадачаВыполнить умножение:
ЗадачаВыполнить умножение:Ответ: 11100112 ● 1100112 = 10110111010012
50. 8-я система счисления: умножение
Пример. Вычислить 1638 × 638Умножаем на разряды 2-го
Решение. × 2 6 38
сомножителя, пока не учитывая
5 38
перенос.
Теперь, начиная с младших,
6 (18) 9
+
последовательно корректируем
10 (30) (15)
разряды, значение которых > 7:
10 (36) (34) 1
9 : 8 = частное 1 и остаток 1
10 (40) 2 1 Частное – это перенос, остаток –
это цифра разряда.
(15) 0 2 1
34 : 8 = частное 4 и остаток 2
40 : 8 = частное 5 и остаток 0
Заменяем двухразрядные числа на буквы:
Ответ: 1638 × 638 = F0218
51. Задача
Выполнить умножение:Ответ: = 133518
52. 16-я система счисления: умножение
Пример. Вычислить 61A16 40D16Решение. Заменяем буквы числами и перемножаем:
6 1 (10)16 Умножаем на разряды 2-го
× 4 0 (13) сомножителя, пока не учитывая
16
перенос.
(78)(13)(130)
Начиная с младших,
+
(24) 4 (40)
корректируем разряды,
значение которых > 15:
(24) 4(118)(13)(130)
130 : 16 = частное 8 и остаток 2
(24) 4(118)(21) 2
21 : 16 = частое 1 и остаток 5
(24) 4(119) 5 2
119 : 16 = частое 7 и остаток 7
24 : 16 = частое 1 и остаток 8
(24)(11) 7 5 2
Заменяем числа > 9 на буквы.

1 8 (11) 7 5 2
Ответ: 61A16 40D16 = 18B75216
53. Задача
Выполнить умножение: 173C16 4FA16Ответ: = 73A09816
16 в 16 ричной системе счисления. Перевод чисел из одной системы счисления в другую онлайн
Теперь предстоит совсем легкая прогулка, связанная с шестнадцатеричной системой счисления. В этом случае, надеемся, вы подозреваете и, видимо, справедливо, что у нас должно теперь быть 16 различных цифр.
Но, как мы знаем, традиционных («арабских») цифр всего десять. А требуется шестнадцать. Получается, что не хватает шести знаков.
Замечание
Таким образом, возникает чисто дизайнерская задача по теме «Знаки» — придумать недостающие символы для цифр .
Значит, в свое время специалистам необходимо было придумать какие-нибудь новые знаки. Но когда-то, в начале компьютерной эры, особого выбора в знаках не было. Программисты располагали только знаками цифр и букв. Поэтому они пошли по элементарному пути: взяли первые буквы латинского алфавита в качестве цифр, тем более что исторически это не первый случай (мы уже упоминали, что первоначально вместо цифр многие народы использовали буквы).
Замечание
Надеемся, что всем понятно, почему в этом случае нельзя использовать, например, числа «10», «11», «12» и т. д.? Потому что, если мы говорим о шестнадцатеричной системе счисления, то должно быть шестнадцать цифр , а не чисел .
И десятичное число «10» стали обозначать латинской буквой «А» (точнее, «цифрой А»). Соответственно, дальше идут цифры «В», «С», «D», «Е» и «Р.
Поскольку мы намеревались построить шестнадцатеричную систему, то, начиная с нуля, здесь как раз и получится 16 цифр. Например, цифра «D» — это десятичное число «13», а цифра «F» — это десятичное число «15».
Когда к шестнадцатеричному числу «F» прибавляем единицу, то, поскольку эти цифры у нас кончились, в этом разряде ставим «О», а в следующий разряд переносим единицу, поэтому получается, что десятичное число «16» будет представлено в шестнадцатеричной системе счисления числом «10», т. е. получается «шестнадцатеричная десятка». Соединим десятичные и шестнадцатеричные числа в единую таблицу (табл.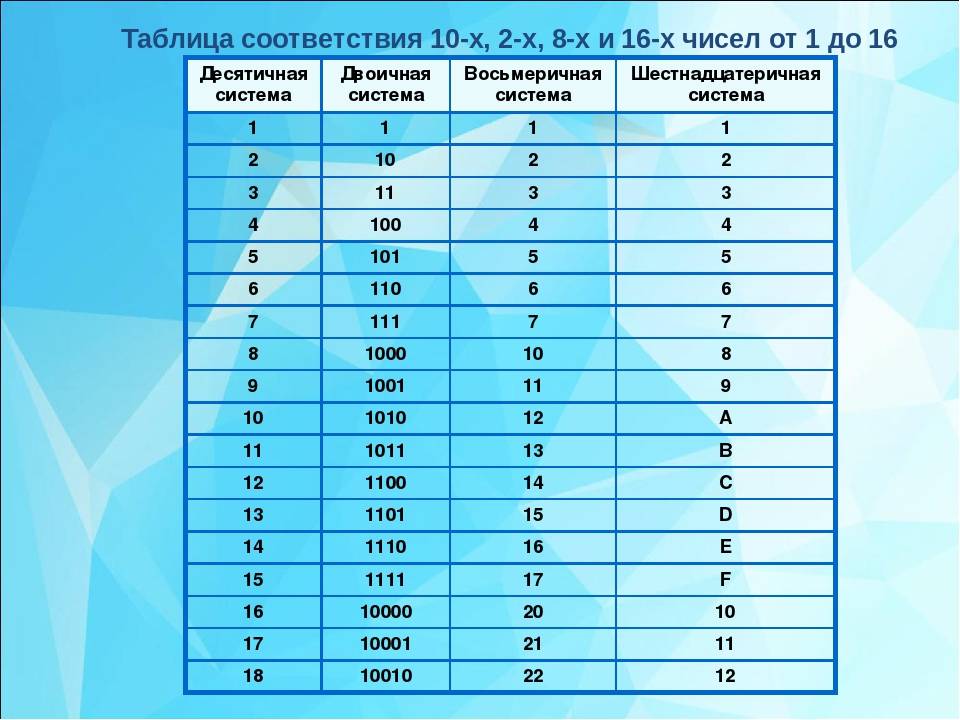
Таблица 4.5 . Соответствие десятичных и шестнадцатеричных чисел.
| Десятичное число | Шестнадцатеричное число | Десятичное число | Шестнадцатеричное число |
|---|---|---|---|
| 0-9 | 0-9 | 1D | |
| 10 | А | 30 | 1Е |
| 11 | В | 31 | 1F |
| 12 | С | 32-41 | 20-29 |
| 13 | D | 42-47 | 2A-2F |
| 14 | Е | 48-255 | 30-FF |
| 15 | F | 256 | 100 |
| 16 | 10 | 512 | 200 |
| 17-25 | 11-19 | 1024 | 400 |
| 26 | 1А | 1280 | 500 |
| 27 | 1В | 4096 | 1000 |
| 28 | 1C |
Шестнадцатеричная система используется, чтобы более компактно записывать двоичную информацию. В самом деле, «шестнадцатеричная тысяча», состоящая из четырех разрядов, в двоичном виде занимает тринадцать разрядов (1000 16 = 1000000000000 2).
В самом деле, «шестнадцатеричная тысяча», состоящая из четырех разрядов, в двоичном виде занимает тринадцать разрядов (1000 16 = 1000000000000 2).
При обсуждении систем счисления неоднократно фигурировали «десятки», «сотни» и «тысячи», поэтому необходимо обратить внимание на так называемые «круглые» числа.
| Десятичная система | 16-ричная система | Десятичная система | 16-ричная система |
|---|---|---|---|
| 0 | 0 (0000) | 10 | A (1010) |
| 1 | 1(0001) | 11 | B (1011) |
| 2 | 2 (0010) | 12 | C (1100) |
| 3 | 3 (0011) | 13 | D (1101) |
| 4 | 4 (0100) | 14 | E (1110) |
| 5 | 5 (0101) | 15 | |
| 6 | 6 (0110) | 16 | 10 (00010000) |
| 7 | 7 (0111) | 17 | 11 (00010001) |
| 8 | 8 (1000) | 18 | 12 (00010010) |
| 9 | 19 | 13 (00010011) |
Для перевода 16-ричного числа в десятичное необходимо умножить значение
младшего (нулевого) разряда на единицу,
значение
следующего (первого) разряда на 16, второго разряда на 256 (16 2) и т.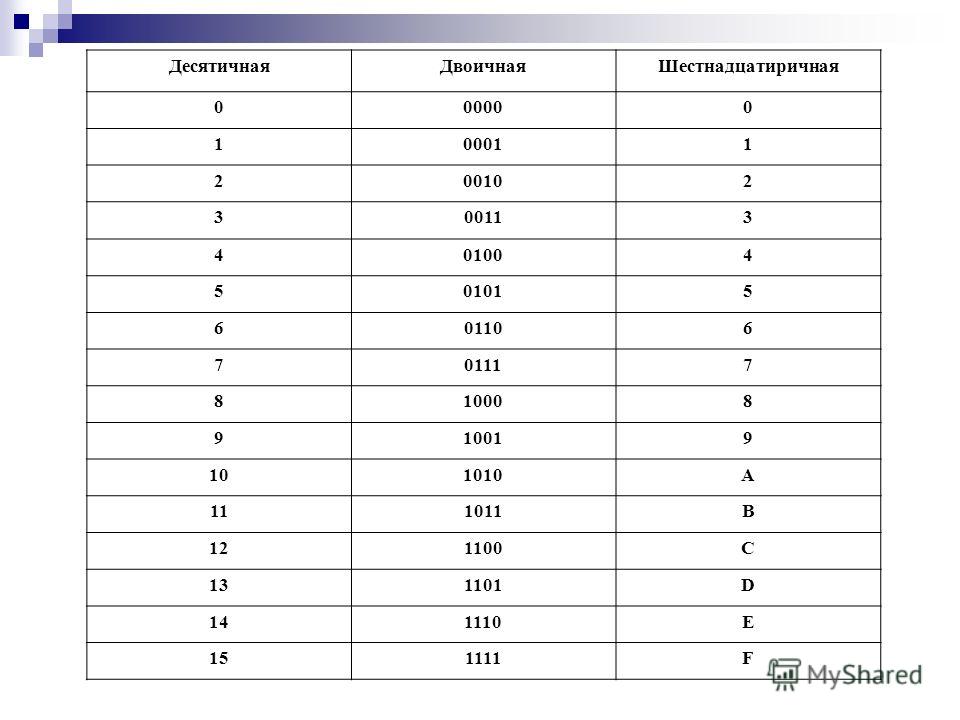 д., а затем сложить все произведения.
Например, возьмем число A17F
:
д., а затем сложить все произведения.
Например, возьмем число A17F
:
A17F=F*16 0 + 7*16 1 + 1*16 2 + A*16 3 = 15*1 + 7*16+1*256+10*4096=41343
| 8-ричная система | Десятичная система | 8-ричная система | |
|---|---|---|---|
| 0 | 0 (000) | 10 | 12 (001010) |
| 1 | 1(001) | 11 | 13 (001011) |
| 2 | 2 (010) | 14 (001100) | |
| 3 | 3 (011) | 13 | 15 (001101) |
| 4 | 4 (100) | 14 | 16 (001110) |
| 5 | 5 (101) | 15 | 17 (001111) |
| 6 | 16 | 20 (010000) | |
| 7 | 7 (111) | 17 | 21 (010001) |
| 8 | 10 (001000) | 18 | 22 (010010) |
| 9 | 11 (001001) | 19 | 23 (010011) |
Но каждому специалисту по
цифровой аппаратуре (разработчику, оператору, ремонтнику, программисту и т.
Значительно реже, чем 16-ричное, используется восьмеричное кодирование , которое строится по такому же принципу, что и 16-ричное, но двоичные разряды разбиваются на группы по три разряда. Каждая группа (разряд кода) затем обозначается одним символом. Каждый разряд 8-ричного кода может принимать восемь значений: 0, 1, 2, 3, 4, 5, 6, 7 (табл. 2.5) .
Помимо рассмотренных кодов, существует также и так называемое двоично-десятичное представление
чисел.
Как и в 16-ричном коде, в двоично-десятичном коде каждому разряду кода соответствует четыре двоичных
разряда, однако каждая группа
из четырех двоичных разрядов может принимать не шестнадцать, а только
десять значений, кодируемых символами 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. То есть одному десятичному
разряду соответствует четыре двоичных. В результате получается, что написание чисел в двоично-десятичном коде
ничем не отличается от написания в обычном десятичном коде (табл.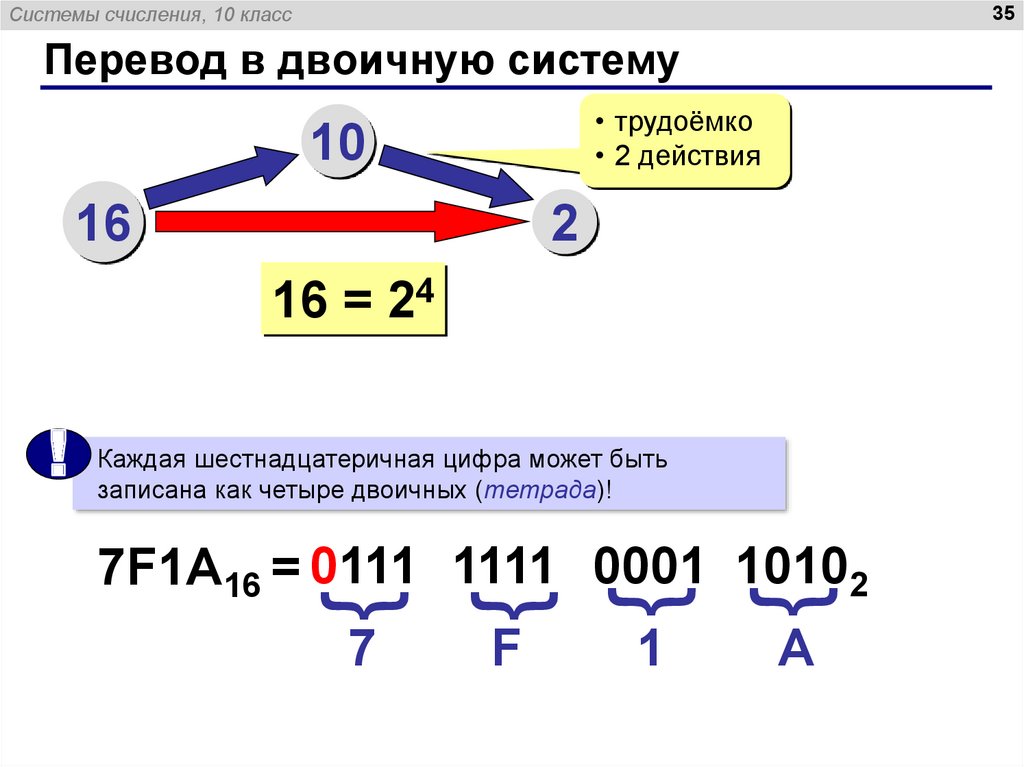 2.6) , но в реальности это всего лишь
специальный двоичный код, каждый разряд которого может принимать только два значения: 0 и 1.
Двоично-десятичный код иногда очень удобен для организации десятичных цифровых индикаторов и табло.
2.6) , но в реальности это всего лишь
специальный двоичный код, каждый разряд которого может принимать только два значения: 0 и 1.
Двоично-десятичный код иногда очень удобен для организации десятичных цифровых индикаторов и табло.
| Десятичная система | Двоично-десятичная система | Десятичная система | Двоично-десятичная система |
|---|---|---|---|
| 0 | 0 (0000) | 10 | 10 (00010000) |
| 1 | 1(0001) | 11 | 11 (00010001) |
| 2 | 2 (0010) | 12 | 12 (00010010) |
| 3 | 3 (0011) | 13 | 13 (00010011) |
| 4 | 4 (0100) | 14 | 14 (00010100) |
| 5 | 5 (0101) | 15 | 15 (00010101) |
| 6 | 6 (0110) | 16 | 16 (00010110) |
| 7 | 7 (0111) | 17 | 17 (00010111) |
| 8 | 8 (1000) | 18 | 18 (00011000) |
| 9 | 9 (1001) | 19 | 19 (00011001) |
В двоичном коде над числами можно проделывать любые арифметические операции
: сложение
, вычитание
, умножение
, деление
.
Рассмотрим, например, сложение двух 4-разрядных двоичных чисел. Пусть надо сложить число 0111 (десятичное 7) и 1011 (десятичное 11). Сложение этих чисел не сложнее, чем в десятичном представлении:
При сложении 0 и 0 получаем 0, при сложении 1 и 0 получаем 1, при сложении 1 и 1 получаем 0 и перенос в следующий разряд 1. Результат — 10010 (десятичное 18). При сложении любых двух n-разрядных двоичных чисел может получиться n-разрядное или (n+1) -разрядное число.
Точно так же производится вычитание . Пусть из числа 10010 (18) надо вычесть число 0111 (7). Записываем числа с выравниванием по младшему разряду и вычитаем точно так же, как в случае десятичной системы:
При вычитании 0 из 0 получаем 0, при вычитании 0 из 1 получаем 1, при вычитании 1 из 1 получаем 0, при вычитании 1 из 0 получаем 1 и заем 1 в следующем разряде. Результат — 1011 (десятичное 11).
При вычитании возможно получение отрицательных чисел, поэтому необходимо использовать двоичное представление
отрицательных чисел.
Для одновременного представления как двоичных положительных, так и двоичных отрицательных чисел чаще всего используется так называемый дополнительный код . Отрицательные числа в этом коде выражаются таким числом, которое, будучи сложено с положительным числом такой же величины, даст в результате нуль. Для того чтобы получить отрицательное число, надо поменять все биты такого же положительного числа на противоположные (0 на 1, 1 на 0) и прибавить к результату 1. Например, запишем число –5. Число 5 в двоичном коде выглядит 0101. Заменяем биты на противоположные: 1010 и прибавляем единицу: 1011. Суммируем результат с исходным числом: 1011 + 0101 = 0000 (перенос в пятый разряд игнорируем).
по модулю 2 два двоичных числа 0111 и 1011:
Среди других побитовых операций над двоичными числами можно отметить функцию И и функцию ИЛИ. Функция
И дает в результате единицу только тогда, когда в соответствующих битах двух исходных чисел обе единицы,
в противном случае результат -0. Функция
ИЛИ дает в результате единицу тогда, когда хотя бы один из
соответствующих битов исходных чисел равен 1, в противном случае результат 0.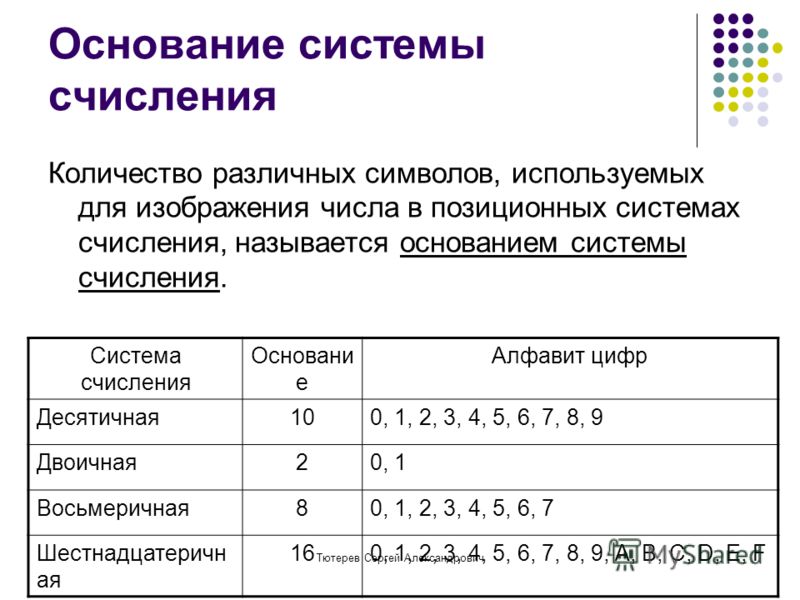
Для написания программ на Ассемблере, необходимо разобраться с шестнадцатеричной системой счисления. Ничего сложного в ней нет. Мы используем в жизни десятичную систему. Уверен, что вы все ее знаете, поэтому я постараюсь объяснить шестнадцатеричную систему, проводя аналогию с десятичной.
Итак, в десятичной системе если мы к какому-нибудь числу справа добавим нуль, то это число увеличится в 10 раз. Например: 1 х 10 = 10; 10 х 10 = 100; 100 х 10 = 1000 и т.д. В этой системе мы используем цифры от 0 до 9, т.е. десять разных цифр (собственно, поэтому она и называется десятичная).
В шестнадцатеричной системе мы используем, соответственно, шестнадцать «цифр». Я специально написал слово «цифр» в кавычках, т.к. в ней используются не только цифры. Да и в самом деле как так? Объясняю: от 0 до 9 мы считаем так же, как и в десятичной, а вот дальше будет так: A, B, C, D, E, F. Число F, как не трудно посчитать, будет равно 15 в десятичной системе (см. табл. 1).
Десятичное число | Шестнадцатеричное число |
Таблица 1. Десятичная и шестнадцатеричная системы.
Десятичная и шестнадцатеричная системы.
Т.о., если мы к какому-нибудь числу в шестнадцатеричной системе добавим справа нуль, то это число увеличится в 16 раз.
Пример 1: 1 х 16 = 10; 10 х 16 = 100; 100 х 16 = 1000 и т.д.
Вы смогли отличить в Примере 1 шестнадцатеричные числа от десятичных? А из этого ряда: 10, 12, 45, 64, 12, 8, 19? Это могут быть как шестнадцатеричные, так и десятичные. Для того, чтобы не было путаницы, и компьютер смог бы однозначно отличить одни числа от других, в Ассемблере принято после шестнадцатеричного числа ставить символ h или H (H это сокращение от англ. hexadecimal (шестнадцатеричное). Для краткости его иногда называют просто Hex ) . А после десятичного ничего не ставить. Т.к. числа от 0 до 9 в обоих системах имеют одинаковые значения, то числа, записанные как 5 и 5h одно и тоже.
Т.о. Пример 1 (см.
выше) правильнее будет записать
так: 1 х 16 = 10h; 10h x 16 = 100h; 100h x 16 = 1000h. Либо так: 1h x 10h = 10h; 10h x 10h = 100h; 100h x 10h =
1000h.
Либо так: 1h x 10h = 10h; 10h x 10h = 100h; 100h x 10h =
1000h.
Для чего нужна шестнадцатеричная система, мы рассмотрим в последующих выпусках. А в данный момент для нашего примера программы, который будет рассмотрен ниже, нам необходимо знать о существовании шестнадцатеричных чисел.
Итак, подведем итог. Шестнадцатеричная система счисления состоит из 10 цифр (от 0 до 9) и 6 букв латинского алфавита (A, B, C, D, E, F). Если к какому-нибудь числу в шестнадцатеричной системе добавим справа нуль, то это число увеличится в 16 раз. Очень важно уяснить данную тему , так как мы будем постоянно использовать ее при написании программ.
Теперь немного о том, как я буду строить примеры на Ассемблере. Не совсем удобно приводить их в HTML-формате, поэтому сперва будет сам код программы с пронумерованными строчками, а сразу же после него объяснения и примечания.
Примерно так:
| строк | Код программы |
| (1) | mov ah,9 |
Объяснения:
В строке (1) мы
делаем то-то, а в строке (15) то-то.
Огромная просьба: НЕ копируйте программы со страницы в буфер, а затем не вставляйте их в Блокнот (или еще куда-нибудь)! Перепечатывайте их вручную в текстовом редакторе. Если есть принтер, то выделите программу, распечатайте выделенный фрагмент, а затем перебейте в редактор с бумаги. Все примеры нужно набирать самостоятельно! Это ускорит запоминание операторов.
И еще. Строчные и ПРОПИСНЫЕ буквы в Ассемблере не различаются. Записи вида:
Ассемблером воспринимаются одинаково. Можно, конечно, заставить Ассемблер различать строчные и ПРОПИСНЫЕ символы, но мы пока этого делать не будем. Для удобства чтения программы лучше всего операторы печатать строчными буквами, а названия подпрограмм и меток начинать с прописной. Но это как кому будет удобно.
Итак, переходим к нашей первой программе:
(1) CSEG segment
(2) org 100h
(4) Begin:
(6) mov ah,9
(7) mov dx,offset Message
(8) int 21h
(10) int 20h
(11)
(12) Message db «Hello, world!$»
(13) CSEG ends
(14) end Begin
Для того, чтобы
объяснить все операторы данного
примера, нам потребуется несколько
выпусков. Поэтому описание
некоторых команд мы просто опустим
на данном этапе. Просто считайте,
что так должно быть. В самое
ближайшее время мы рассмотрим эти
операторы подробно. Итак, строки с
номерами (1), (2) и (13) вы просто
игнорируете.
Поэтому описание
некоторых команд мы просто опустим
на данном этапе. Просто считайте,
что так должно быть. В самое
ближайшее время мы рассмотрим эти
операторы подробно. Итак, строки с
номерами (1), (2) и (13) вы просто
игнорируете.
Строки (3), (5), (9) и (11) остаются пустыми. Это делается для наглядности. Ассемблер их будет просто опускать.
Теперь перейдем к рассмотрению остальных операторов. Со строки (4) начинается код программы. Это метка, указывающая Ассемблеру на начало кода. В строке (14) стоят операторы end Begin ( Begin англ. начало; end конец). Это конец программы. Вообще вместо слова Begin можно было бы использовать что-нибудь другое. Например, Start:. В таком случае, нам пришлось бы и завершать программу End Start (14).
Строки (6) (8) выводят на экран сообщение Hello, world!. Здесь придется вкратце рассказать о регистрах процессора (более подробно эту тему мы рассмотрим в следующем выпуске).
Регистр
процессора это специально
отведенная память для хранения
какого-нибудь числа.
Например:
Если мы хотим сложить два числа, то в математике запишем так:
A, B и C это своего рода регистры (если говорить о компьютере), в которых могут хранится некоторые данные. А=5 можно прочитать как: Присваиваем А число 5 .
Для присвоения регистру какого-нибудь значения, в Ассемблере существует оператор mov (от англ. move загрузить). Строку (6) следует читать так: Загружаем в регистр AH число 9 (проще говоря, присваиваем AH число 9). Ниже рассмотрим зачем это надо.
В строке (7) загружаем в регистр DX адрес сообщения для вывода (в данном примере это будет строка Hello, world!$ ).
Прерывания будут подробно рассматриваться в последующих выпусках. Здесь я скажу несколько слов.
Прерывание MS-DOS это своего рода подпрограмма (часть MS-DOS) , которая находится постоянно в памяти и может вызываться в любое время из любой программы.
Рассмотрим вышесказанное на примере (мелким шрифтом выделим примечания ):
Программа сложения двух чисел
НачалоПрограммы
A=5 в переменную A заносим значение 5
B=8 в переменную B значение 8
ВызовПодпрограммы Сложение
теперь С равно 13
A=10 тоже самое, только другие числа
B=25
ВызовПодпрограммы Сложение
теперь С равно 35
КонецПрограммы
Подпрограмма Сложение
C=A+B
ВозвратИзПодпрограммы возвращаемся в то место, откуда вызывали
КонецПодпрограммы
В данном примере
мы дважды вызвали подпрограмму Сложение ,
которая сложила два числа,
переданные ей в переменных
A и
B. Результат помещается в переменную
С. Когда вызывается подпрограмма,
компьютер запоминает с какого
места она была вызвана, а затем,
когда закончила работу
подпрограмма, компьютер
возвращается в то место, откуда она
вызывалась. Т.о. можно вызывать
подпрограммы неопределенное
количество раз с любого места.
Результат помещается в переменную
С. Когда вызывается подпрограмма,
компьютер запоминает с какого
места она была вызвана, а затем,
когда закончила работу
подпрограмма, компьютер
возвращается в то место, откуда она
вызывалась. Т.о. можно вызывать
подпрограммы неопределенное
количество раз с любого места.
При выполнении
строки (8) программы на Ассемблере
мы вызываем подпрограмму (в данном
случае это называется прерывание),
которая выводит на экран строку.
Для этого мы, собственно, и помещаем
необходимые значения в регистры.
Всю необходимую работу (вывод
строки, перемещение курсора) берет
на себя подпрограмма. Эту строку
можно прочитать так: вызываем
двадцать первое прерывание ( int от англ.
interrupt прерывание). Обратите
внимание, что после числа 21 стоит
буква
h. Это, как
мы уже знаем, шестнадцатеричное
число (33 в десятичной системе).
Конечно, нам ничего не мешает
заменить строку
int 21h на
int 33. Программа будет
работать корректно. Просто в
Ассемблере принято указывать номер
прерывания в шестнадцатеричной
системе.
В строке (10) мы, как вы уже догадались, вызываем прерывание 20 h. Для вызова данного прерывания не нужно указывать какие-либо значения в регистрах. Оно выполняет только одну задачу: выход из программы (выход в DOS). В результате выполнения прерывания 20h, программа вернется туда, откуда ее запускали (загружали, вызывали). Например, в Norton Commander или DOS Navigator.
Строка (12) содержит сообщение для вывода. Первое слово ( message сообщение) название сообщения. Оно может быть любым (например, mess или string и пр.). Обратите внимание на строку (7), в которой мы загружаем в регистр DX адрес нашего сообщения.
Можно создать еще одну строку, которую назовем Mess2. Затем, начиная со строки (9) вставим следующие команды:
(10) mov dx,offset Mess2
(13) Message db «Hello, world!$»
(14) Mess2 db «Это Я! $»
и ассемблировать нашу программу заново. Надеюсь, что вы догадались, что произойдет
Обратите внимание
на последний символ в строках
Message
и
Mess2 — $. Он указывает на конец
строки. Если мы его уберем, то 21
h прерывание продолжит
вывод до тех пор, пока не встретится
где-нибудь в памяти символ
$. На экране мы увидим
мусор
.
Он указывает на конец
строки. Если мы его уберем, то 21
h прерывание продолжит
вывод до тех пор, пока не встретится
где-нибудь в памяти символ
$. На экране мы увидим
мусор
.
Если у вас есть отладчик, то можно посмотреть как будет работать наша программа.
Целю настоящего выпуска не было разобраться подробно с каждым оператором . Это невозможно, т.к. у вас еще недостаточно знаний. Я полагаю, что уже через 3-4 выпуска вы поймете принцип и структуру программы на Ассемблере. Может быть, вам показался язык Ассемблера чрезвычайно сложным, но это, поверьте, с первого взгляда.
Шестнадцатеричная система счисления. аша первая программа.
Для написания программ на Ассемблере, необходимо разобраться с шестнадцатеричной системой счисления. Ничего сложного в ней нет. Мы используем в жизни десятичную систему. Уверен, что вы все ее знаете, поэтому я постараюсь объяснить шестнадцатеричную систему, проводя аналогию с десятичной.
Итак, в десятичной
системе если мы к какому-нибудь
числу справа добавим нуль, то это
число увеличится в 10 раз. Например: 1
х 10 = 10; 10 х 10 = 100; 100 х 10 = 1000 и т.д. В
этой системе мы используем цифры от
0 до 9, т.е. десять разных цифр
(собственно, поэтому она и
называется десятичная).
Например: 1
х 10 = 10; 10 х 10 = 100; 100 х 10 = 1000 и т.д. В
этой системе мы используем цифры от
0 до 9, т.е. десять разных цифр
(собственно, поэтому она и
называется десятичная).
В шестнадцатеричной системе мы используем, соответственно, шестнадцать «цифр». Я специально написал слово «цифр» в кавычках, т.к. в ней используются не только цифры. Да и в самом деле как так? Объясняю: от 0 до 9 мы считаем так же, как и в десятичной, а вот дальше будет так: A, B, C, D, E, F. Число F, как не трудно посчитать, будет равно 15 в десятичной системе (см. табл. 1).
Десятичное число | Шестнадцатеричное число |
Таблица 1. Десятичная и шестнадцатеричная системы.
Т.о., если мы к какому-нибудь числу в шестнадцатеричной системе добавим справа нуль, то это число увеличится в 16 раз.
Пример 1: 1 х 16 = 10; 10 х 16 = 100; 100 х 16 = 1000 и т.д.
Вы смогли отличить в Примере 1 шестнадцатеричные числа от десятичных? А из этого ряда: 10, 12, 45, 64, 12, 8, 19? Это могут быть как шестнадцатеричные, так и десятичные. Для того, чтобы не было путаницы, и компьютер смог бы однозначно отличить одни числа от других, в Ассемблере принято после шестнадцатеричного числа ставить символ h или H (H это сокращение от англ. hexadecimal (шестнадцатеричное). Для краткости его иногда называют просто Hex ) . А после десятичного ничего не ставить. Т.к. числа от 0 до 9 в обоих системах имеют одинаковые значения, то числа, записанные как 5 и 5h одно и тоже.
Т.о. Пример 1 (см.
выше) правильнее будет записать
так: 1 х 16 = 10h; 10h x 16 = 100h; 100h x 16 = 1000h.
Либо так: 1h x 10h = 10h; 10h x 10h = 100h; 100h x 10h =
1000h.
Для чего нужна шестнадцатеричная система, мы рассмотрим в последующих выпусках. А в данный момент для нашего примера программы, который будет рассмотрен ниже, нам необходимо знать о существовании шестнадцатеричных чисел.
Итак, подведем итог. Шестнадцатеричная система счисления состоит из 10 цифр (от 0 до 9) и 6 букв латинского алфавита (A, B, C, D, E, F). Если к какому-нибудь числу в шестнадцатеричной системе добавим справа нуль, то это число увеличится в 16 раз. Очень важно уяснить данную тему , так как мы будем постоянно использовать ее при написании программ.
Теперь немного о том, как я буду строить примеры на Ассемблере. Не совсем удобно приводить их в HTML-формате, поэтому сперва будет сам код программы с пронумерованными строчками, а сразу же после него объяснения и примечания.
Примерно так:
| строк | Код программы |
| (1) | mov ah,9 |
Объяснения:
В строке (1) мы
делаем то-то, а в строке (15) то-то.
Огромная просьба: НЕ копируйте программы со страницы в буфер, а затем не вставляйте их в Блокнот (или еще куда-нибудь)! Перепечатывайте их вручную в текстовом редакторе. Если есть принтер, то выделите программу, распечатайте выделенный фрагмент, а затем перебейте в редактор с бумаги. Все примеры нужно набирать самостоятельно! Это ускорит запоминание операторов.
И еще. Строчные и ПРОПИСНЫЕ буквы в Ассемблере не различаются. Записи вида:
Ассемблером воспринимаются одинаково. Можно, конечно, заставить Ассемблер различать строчные и ПРОПИСНЫЕ символы, но мы пока этого делать не будем. Для удобства чтения программы лучше всего операторы печатать строчными буквами, а названия подпрограмм и меток начинать с прописной. Но это как кому будет удобно.
Итак, переходим к нашей первой программе:
(1) CSEG segment
(2) org 100h
(4) Begin:
(6) mov ah,9
(7) mov dx,offset Message
(8) int 21h
(10) int 20h
(11)
(12) Message db «Hello, world!$»
(13) CSEG ends
(14) end Begin
Для того, чтобы
объяснить все операторы данного
примера, нам потребуется несколько
выпусков. Поэтому описание
некоторых команд мы просто опустим
на данном этапе. Просто считайте,
что так должно быть. В самое
ближайшее время мы рассмотрим эти
операторы подробно. Итак, строки с
номерами (1), (2) и (13) вы просто
игнорируете.
Поэтому описание
некоторых команд мы просто опустим
на данном этапе. Просто считайте,
что так должно быть. В самое
ближайшее время мы рассмотрим эти
операторы подробно. Итак, строки с
номерами (1), (2) и (13) вы просто
игнорируете.
Строки (3), (5), (9) и (11) остаются пустыми. Это делается для наглядности. Ассемблер их будет просто опускать.
Теперь перейдем к рассмотрению остальных операторов. Со строки (4) начинается код программы. Это метка, указывающая Ассемблеру на начало кода. В строке (14) стоят операторы end Begin ( Begin англ. начало; end конец). Это конец программы. Вообще вместо слова Begin можно было бы использовать что-нибудь другое. Например, Start:. В таком случае, нам пришлось бы и завершать программу End Start (14).
Строки (6) (8) выводят на экран сообщение Hello, world!. Здесь придется вкратце рассказать о регистрах процессора (более подробно эту тему мы рассмотрим в следующем выпуске).
Регистр
процессора это специально
отведенная память для хранения
какого-нибудь числа.
Например:
Если мы хотим сложить два числа, то в математике запишем так:
A, B и C это своего рода регистры (если говорить о компьютере), в которых могут хранится некоторые данные. А=5 можно прочитать как: Присваиваем А число 5 .
Для присвоения регистру какого-нибудь значения, в Ассемблере существует оператор mov (от англ. move загрузить). Строку (6) следует читать так: Загружаем в регистр AH число 9 (проще говоря, присваиваем AH число 9). Ниже рассмотрим зачем это надо.
В строке (7) загружаем в регистр DX адрес сообщения для вывода (в данном примере это будет строка Hello, world!$ ).
Прерывания будут подробно рассматриваться в последующих выпусках. Здесь я скажу несколько слов.
Прерывание MS-DOS это своего рода подпрограмма (часть MS-DOS) , которая находится постоянно в памяти и может вызываться в любое время из любой программы.
Рассмотрим вышесказанное на примере (мелким шрифтом выделим примечания ):
Программа сложения двух чисел
НачалоПрограммы
A=5 в переменную A заносим значение 5
B=8 в переменную B значение 8
ВызовПодпрограммы Сложение
теперь С равно 13
A=10 тоже самое, только другие числа
B=25
ВызовПодпрограммы Сложение
теперь С равно 35
КонецПрограммы
Подпрограмма Сложение
C=A+B
ВозвратИзПодпрограммы возвращаемся в то место, откуда вызывали
КонецПодпрограммы
В данном примере
мы дважды вызвали подпрограмму Сложение ,
которая сложила два числа,
переданные ей в переменных
A и
B. Результат помещается в переменную
С. Когда вызывается подпрограмма,
компьютер запоминает с какого
места она была вызвана, а затем,
когда закончила работу
подпрограмма, компьютер
возвращается в то место, откуда она
вызывалась. Т.о. можно вызывать
подпрограммы неопределенное
количество раз с любого места.
Результат помещается в переменную
С. Когда вызывается подпрограмма,
компьютер запоминает с какого
места она была вызвана, а затем,
когда закончила работу
подпрограмма, компьютер
возвращается в то место, откуда она
вызывалась. Т.о. можно вызывать
подпрограммы неопределенное
количество раз с любого места.
При выполнении
строки (8) программы на Ассемблере
мы вызываем подпрограмму (в данном
случае это называется прерывание),
которая выводит на экран строку.
Для этого мы, собственно, и помещаем
необходимые значения в регистры.
Всю необходимую работу (вывод
строки, перемещение курсора) берет
на себя подпрограмма. Эту строку
можно прочитать так: вызываем
двадцать первое прерывание ( int от англ.
interrupt прерывание). Обратите
внимание, что после числа 21 стоит
буква
h. Это, как
мы уже знаем, шестнадцатеричное
число (33 в десятичной системе).
Конечно, нам ничего не мешает
заменить строку
int 21h на
int 33. Программа будет
работать корректно. Просто в
Ассемблере принято указывать номер
прерывания в шестнадцатеричной
системе.
В строке (10) мы, как вы уже догадались, вызываем прерывание 20 h. Для вызова данного прерывания не нужно указывать какие-либо значения в регистрах. Оно выполняет только одну задачу: выход из программы (выход в DOS). В результате выполнения прерывания 20h, программа вернется туда, откуда ее запускали (загружали, вызывали). Например, в Norton Commander или DOS Navigator.
Строка (12) содержит сообщение для вывода. Первое слово ( message сообщение) название сообщения. Оно может быть любым (например, mess или string и пр.). Обратите внимание на строку (7), в которой мы загружаем в регистр DX адрес нашего сообщения.
Можно создать еще одну строку, которую назовем Mess2. Затем, начиная со строки (9) вставим следующие команды:
(10) mov dx,offset Mess2
(13) Message db «Hello, world!$»
(14) Mess2 db «Это Я! $»
и ассемблировать нашу программу заново. Надеюсь, что вы догадались, что произойдет
Обратите внимание
на последний символ в строках
Message
и
Mess2 — $. Он указывает на конец
строки. Если мы его уберем, то 21
h прерывание продолжит
вывод до тех пор, пока не встретится
где-нибудь в памяти символ
$. На экране мы увидим
мусор
.
Он указывает на конец
строки. Если мы его уберем, то 21
h прерывание продолжит
вывод до тех пор, пока не встретится
где-нибудь в памяти символ
$. На экране мы увидим
мусор
.
Если у вас есть отладчик, то можно посмотреть как будет работать наша программа.
Целю настоящего выпуска не было разобраться подробно с каждым оператором . Это невозможно, т.к. у вас еще недостаточно знаний. Я полагаю, что уже через 3-4 выпуска вы поймете принцип и структуру программы на Ассемблере. Может быть, вам показался язык Ассемблера чрезвычайно сложным, но это, поверьте, с первого взгляда.
Шестнадцатеричная система счисления (также — шестнадцатеричный код) является позиционной системой счисления с целочисленным основанием 16. Иногда в литературе также используется термин hex (произносится «хекс», сокращение от англ. hexadecimal). Цифрами данной системы счисления принято использовать арабские цифры 0—9, а также первые символы латинского алфавита A—F. Буквы соответствуют следующим десятичным значениями:
- * A —10;
- * B —11;
- * C —12;
- * D —13;
- * E — 14;
- * F — 15.

Таким образом, десять арабских цифр вкупе с шестью латинскими буквами и составляют шестнадцать цифр системы.
Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн .
Применение . Шестнадцатеричный код широко применяется в низкоуровневом программировании, а также в различных компьютерных справочных документах. Популярность системы обоснована архитектурными решениями современных компьютеров: в них в качестве минимальной единицы информации установлен байт (состоящий из восьми бит) — а значение байта удобно записывать с помощью двух шестнадцатеричных цифр. Значение байта может ранжироваться с #00 до #FF (от 0 до 255 в десятичной записи) — другими словами, используя шестнадцатеричный код , можно записать любое состояние байта, при этом не остаётся «лишних» не используемых в записи цифр.
В кодировке Юникод для записи номера символа используется четыре шестнадцатеричных цифры.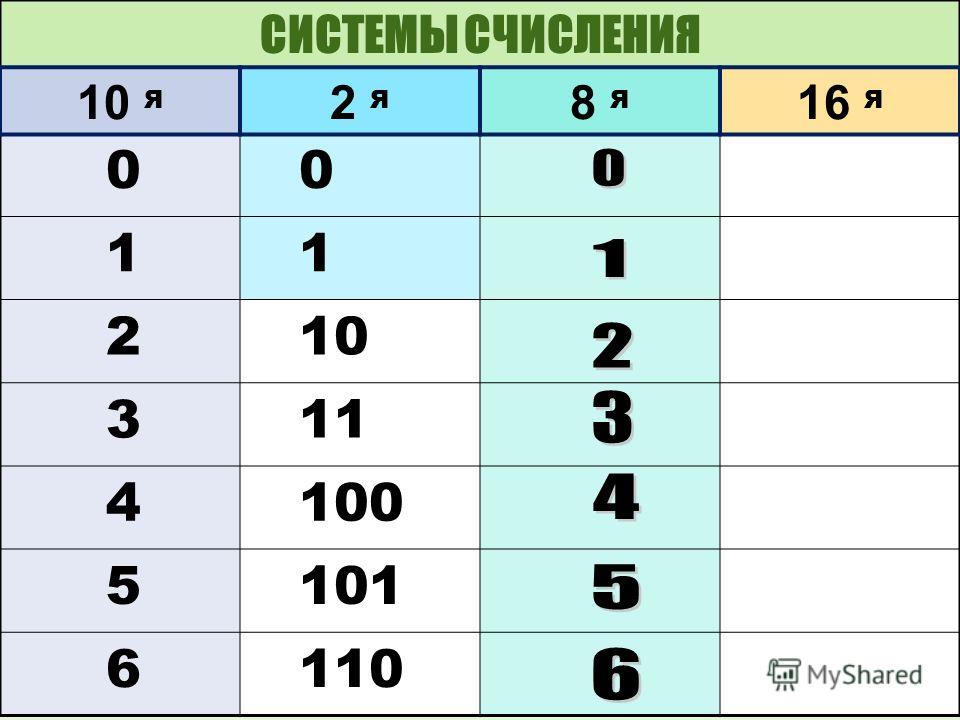 Запись цвета стандарта RGB (Red, Green, Blue — красный, зелёный, синий) также часто использует шестнадцатеричный код (например, #FF0000 — запись ярко-красного цвета).
Запись цвета стандарта RGB (Red, Green, Blue — красный, зелёный, синий) также часто использует шестнадцатеричный код (например, #FF0000 — запись ярко-красного цвета).
Способ записи шестнадцатеричного кода.
Математический способ записи . В математической записи основание системы записывают в десятичном виде в нижнем индексе справа от числа. Десятичную запись числа 3032 можно записать как 3032 10 , в шестнадцатеричной системе данное число будет иметь запись BD8 16 .
В синтаксисе языков программирования . Синтаксис различных языков программирования по-разному устанавливает формат записи числа, использующего шестнадцатеричный код :
* В синтаксисе некоторых разновидностей языка ассемблера используется латинская буква «h», которая ставится справа от числа, например: 20Dh. Если число начинается с латинской буквы, то перед ним ставится ноль, например: 0A0Bh. Это сделано для того, чтобы отличать от констант значения, использующие шестнадцатеричный код ;
* В прочих разновидностях ассемблера, а также в Pascal (и его разновидностях, таких как Delphi) и некоторых диалектах Basic, применяют префикс «$»: $A15;
* В языке разметки HTML, а также в каскадных файлах CSS, для указания цвета в формате RGB с шестнадцатеричной системой записи, используется префикс «#»: #00DC00.
Как перевести шестнадцатеричный код в другую систему?
Перевод из шестнадцатеричной системы в десятичную. Для совершения операции перевода из шестнадцатеричной системы в десятичную, требуется представить исходное число как сумму произведений цифр в разрядах шестнадцатеричного числа на степень основания.
Двоичная СС | шестнадцатеричная СС |
Например, требуется выполнить перевод шестнадцатеричного числа A14: в нём три цифры. Используя правило, запишем его в виде суммы степеней с основанием 16:
Используя правило, запишем его в виде суммы степеней с основанием 16:
A14 16 = 10.16 2 + 1.16 1 + 4.16 0 = 10.256 + 1.16 + 4.1 = 2560 + 16 + 4 = 2580 10
Перевод чисел из двоичной в шестнадцатеричную систему и наоборот.
Для перевода используется таблица тетрад. Чтобы выполнить перевод числа из двоичной в десятичную систему, необходимо произвести разбиение его на отдельные тетрады справа налево, после чего, используя таблицу, выполнить замену каждой тетрады на соответствующую шестнадцатеричную цифру. При этом, если количество цифр не кратно четырём, то необходимо добавить соответствующее количество нулей справа от числа, для того, чтобы общее число двоичных цифр стало кратно четырём.
Таблица тетрад для перевода.
Для перевода из шестнадцатеричной системы в двоичную, необходимо выполнить обратную операцию: выполнить замену каждой цифры на тетраду из таблицы.
Двоичная СС | Восьмеричная СС |
Пример перевода из шестнадцатеричной системы в двоичную : A5E 16 = 1010 0101 1110 = 101001011110 2
Пример перевода из двоичной системы в шестнадцатеричную : 111100111 2 = 0001 1110 0111 = 1E7 16
В этом примере количество цифр в исходном двоичном числе не было равным четырём (9), поэтому были добавлены незначащие нули — общее число цифр стало 12.
Автоматический перевод . Быстрый перевод из шестнадцатеричной системы счисления в одну из трёх популярных систем (двоичную, восьмеричную и десятичную), как и обратный перевод, можно выполнить, используя стандартный калькулятор из комплекта поставки ОС Windows. Откройте калькулятор, выберите в меню Вид -> Программист. В данном режиме можно устанавливать систему счисления, используемую в данный момент (см. меню слева: Hex, Dec, Oct, Bin). При этом изменение текущей системы счисления автоматически производит перевод.
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие… Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья. Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного… Интересное: Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом… Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего… Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 16 из 16 Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F (буквы латинского алфавита заменяю недостающие цифры системы счисления и соответствуют числам 10, 11, 12, 13, 14, 15). Основание S = 16 Базис – степени числа 16: 160, 161, 162, 163, …или 1, 16, 256, 4096, … Представим любое 16-ричное число через его цифры и веса разрядов: A5D16 = D×160 + 5×161 + A×162 = 13×1 + 5×16 + 10×256 = 265310 Этим же способом любое 16-ричное число переводится в десятичную систему счисления. Обратный перевод – из десятичной в 16-ричную систему счисления – осуществляется последовательным деление десятичного числа на основание 16-ричной системы счисления 16 и считыванием остатков от деления справа налево: 2653/16 = 165 остаток 13, то есть D 165/16 = 10 остаток 5 10/16 = 0 остаток 10, то есть A, получаем A5D16.
Особый случай перевода – двоично-шестнадцатеричный Для перевода двоичного числа в 16-ричное необходимо: 1. 100110001012 = 0100 1100 01012 2. каждую четверку цифр представить числом в 16-ричной системе счисления: 0100 1100 01012 = 4C516 4 12=C 5 Для перевода 16-ричного числа в двоичное необходимо каждую цифру 16-ричного числа представить ее четырехразрядным двоичным эквивалентом: A5D16 = 1010 0101 11012 A 5 D Для быстрого перевода чисел из одной системы счисления в другую полезно запомнить следующую таблицу соответствия:
Арифметические операции в двоичной системе счисления Таблица сложения двоичной системы счисления состоит из четырех строк: 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10 (ноль в младшем разряде и единица переноса в старшем)
Сложим два двоичных числа: Переносы 10110110012 + 1110110112 ————- 100101101002 Вычтем одно двоичное число из другого, притом в старшем разряде при необходимости занимаем две единицы младшего: 10111110012 — 1110110112 ————- 1000111102
Результат вычитания можно проверить обратным сложением: 1000111102 + 1110110112 ————- 10111110012
Арифметические операции в восьмеричной системе счисления
Они выполняются по знакомым нам правилам вычислений в десятичной системе счисления, за исключением того, что старшая цифра не 9, а 7: Перенос 5638 + 528 —— 6358
Рассмотрим образование следующей суммы: 68 + 58 — 138 Добавляем к первому слагаемому недостающее число до 8 – основания системы счисления. При вычитании чисел из старшего разряда при необходимости занимаем восемь единиц младшего: 5238 — 528 —— 4518
Арифметические операции в 16-ричной системе счисления Они выполняются по знакомым нам правилам вычислений в десятичной системе счисления, за исключением того, что старшая цифра не 9, а F (15): Перенос 9DA16 + 8216 —— A5C16
Рассмотрим образование следующей суммы: D16 + 816 — 1516 Добавляем к первому слагаемому (D=13) недостающее число до 16 – основания системы счисления. При вычитании чисел из старшего разряда при необходимости занимаем шестнадцать единиц младшего: A5C16 — 8216 —— 9DA16
Приложение 3 Ошибки при компиляции
Ошибки времени выполнения а) Ошибки системы MS-DOS
б)Ошибки ввода-вывода При включенной директиве {$I-} номер ошибки ввода-вывода возвращается функцией IOResult
в)Критические ошибки
г)Фатальные ошибки
⇐ Предыдущая78910111213141516 Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого. Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… |
Преобразование с решенными примерами и часто задаваемыми вопросами
Шестнадцатеричная система счисления с основанием 16. В результате в этой системе используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 и 15. Шестнадцатеричная система счисления является одним из типов техники представления чисел. Это также иногда произносится как «гекс». В 1859 году Нистром предложил шестнадцатеричную (с основанием 16) систему обозначений, арифметику и метрологию, названную тональной системой.
В этой статье мы изучим, что такое шестнадцатеричная система счисления, кто ее отец, сколько цифр в ней используется, таблица преобразования, шестнадцатеричное в двоичное, восьмеричное и десятичное преобразование, решенные примеры, использование и преимущества шестнадцатеричной системы счисления и часто задаваемых вопросов.
Тем временем читайте о преобразовании десятичных чисел в двоичные здесь.
Шестнадцатеричная система счисления
В «шестнадцатеричной» или «шестнадцатеричной» системе счисления используется система с основанием 16, и она является распространенным выбором для кодирования больших двоичных значений из-за ее компактного формата и простоты понимания по сравнению с длинными двоичными строками из 1 и 0 с. Шестнадцатеричная нумерация использует 16 (шестнадцать) отдельных цифр, используя сочетание чисел от 0 до 15, потому что это система с основанием 16. Другими словами, на выбор предлагается 16 различных числовых символов.
База шестнадцатеричной системы счисления
Шестнадцатеричная система счисления — это название системы счисления с основанием 16.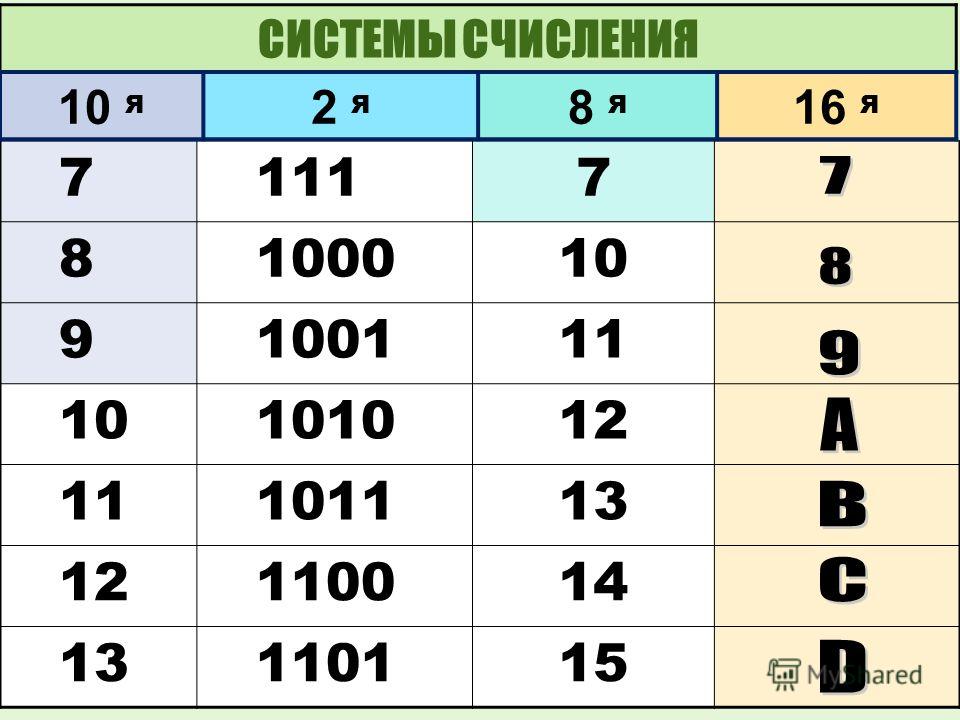 В результате в этой системе используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 и 15. Это означает, что двузначные десятичные числа 10, 11, 12, 13, 14 и 15 должны быть представлены одной цифрой, чтобы существовать в этой системе счисления.
В результате в этой системе используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 и 15. Это означает, что двузначные десятичные числа 10, 11, 12, 13, 14 и 15 должны быть представлены одной цифрой, чтобы существовать в этой системе счисления.
Представление шестнадцатеричного числа
Шестнадцатеричная система счисления представляет собой разновидность числового представления, в котором базовое число равно 16. Это означает, что существует только 16 возможных значений цифр: 0, 1, 2, 3, 4, 5, 6 , 7, 8, 9, A, B, C, D, E, F. Где A, B, C, D, E и F представляют десятичные значения 10, 11, 12, 13, 14 и 15 в отдельных битах. Значение любой цифры может быть представлено всего четырьмя битами. Для представления значения любой цифры требуется всего 4 бита. Шестнадцатеричные числа обозначаются добавлением либо префикса 0x, либо суффикса h.
Позиция каждой цифры имеет вес в 16-й степени. Каждое место в шестнадцатеричной системе в 16 раз значительнее предыдущего, поэтому числовое значение шестнадцатеричного числа вычисляется путем умножения каждой цифры на значение позиции, в которой стоит цифра, с последующим сложением произведений. В результате это взвешенная (или позиционная) система счисления.
В результате это взвешенная (или позиционная) система счисления.
Каждое шестнадцатеричное число может быть представлено только 4 битами, причем каждая группа битов имеет отличное значение от 0000 (для 0) до 1111 (для F = 15 = 8+4+2+1).
Таблица шестнадцатеричной системы счисления
Эквивалент двоичного числа шестнадцатеричного числа приведен ниже.
| HEX Digit | Двоирный | HEX Digit | БАЙНАЛЬНЫЙ |
| 1 | |||
1 0035| 0 | 8 | 1000 | |
| 0 | 1 | 9 | 1001 |
| 2 | 10 | A = 10 | 1010 |
| 3 | 11 | B = 11 | 1011 |
| 4 | 100 | C = 12 | 1100 |
| 5 | 101 | D = 13 | 1101 |
| 6 | 110 | E = 14 | 1110 |
| 7 | 111 | F = 15 | 1111 |
Digit , шестнадцатеричный использует 16 символов, где символы «0»–»9″ (или альтернативно «a»–«f») представляют значения от 0 до 9, а «A»–«F» (или альтернативно «a»–» f”), представляющие значения от 10 до 15.
Преобразование шестнадцатеричной системы счисления
Четыре распространенных типа систем счисления:
- Десятичная система счисления: Основание 10.
- Двоичная система счисления: Основание 2.
- Восьмеричная система счисления: Основание 8.
- Шестнадцатеричная система счисления: Основание 16
На экзаменах часто требуется преобразовать одну форму системы в другую форму. Давайте посмотрим, как мы можем преобразовать шестнадцатеричную систему счисления в двоичную, шестнадцатеричную и восьмеричную.
Преобразование шестнадцатеричной системы в двоичную 9{n-1}\), начиная с цифры на n-м месте. После того, как вы умножили термины, сложите их вместе. Десятичное число, эквивалентное указанному шестнадцатеричному числу, является результатом. Теперь это десятичное число необходимо преобразовать в двоичное. Разделите десятичное число на 2. Обратите внимание на напоминание. Повторяйте предыдущие две процедуры для частного, пока оно не станет равным нулю.
 Обратный порядок остатков. Результатом является требуемое двоичное число.
Обратный порядок остатков. Результатом является требуемое двоичное число.Решенный пример
Преобразование шестнадцатеричной системы счисления в десятичную
При преобразовании шестнадцатеричной системы счисления в десятичную учитываются основные числа каждой из систем счисления. Шестнадцатеричная система счисления использует как цифры, так и символы, причем символы используются для представления двузначных цифр. Всего имеется 16 обозначений: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 и 10-15 представлены A, B, C, D, E и F соответственно. Десять обозначений представлены как 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.{п-1}\). После того, как вы умножили термины, сложите их вместе. Сопоставимая десятичная форма является результирующей. 8 делится на десятичное число. Скиньте остальную информацию. С частным повторяйте два предыдущих шага, пока частное не станет равным нулю. Обратный порядок остатков. Полученное число соответствует желаемому результату.
Пример решения
Использование шестнадцатеричной системы счисления
Использование и применение шестнадцатеричной системы счисления:
- В компьютерном программировании и микропроцессорах широко используется шестнадцатеричная система счисления. Описания цветов на веб-страницах также выполняются с использованием шестнадцатеричного числа. Каждый из трех основных цветов (красный, зеленый и синий) представлен двумя шестнадцатеричными цифрами, что дает 255 возможных значений и в общей сложности более 16 миллионов цветов. Каждый байт описывается в памяти с использованием шестнадцатеричной системы счисления.
- Программисты часто используют шестнадцатеричную схему счисления для упрощения двоичной системы счисления. Между числами 2 и 16 существует линейная зависимость, поскольку 16 равно 24. Это соответствует четырем двоичным цифрам для каждой шестнадцатеричной цифры. Чтобы сократить двоичный код и упростить его понимание, компьютеры используют двоичные системы счисления, тогда как люди используют шестнадцатеричные системы счисления.

- Адреса управления доступом к среде (MAC) также представлены шестнадцатеричными числами. MAC-адреса представляют собой шестнадцатеричные числа с 12 цифрами. ММ:ММ:ММ:СС:СС:СС или ММММ-ММСС-СССС являются используемыми форматами. Первые шесть цифр MAC-адреса — это идентификатор производителя адаптера, а последние шесть цифр — серийный номер адаптера.
- Сообщения об ошибках также отображаются с использованием шестнадцатеричных чисел. Шестнадцатеричный код используется для указания адреса памяти ошибки. Это помогает программистам находить и исправлять ошибки.
Узнайте о свойствах рациональных чисел здесь.
Преимущества шестнадцатеричной системы счисления
Преимущества шестнадцатеричной системы счисления заключаются в следующем:
- Преимущество шестнадцатеричных чисел заключается в том, что для хранения большего количества чисел требуется меньше памяти; например, 256 чисел могут храниться в виде двух цифр, но десятичные числа могут хранить только 100 чисел в виде двух цифр.

- Адреса памяти компьютера также представлены в этой системе счисления. Преобразование из шестнадцатеричной системы в двоичную и наоборот очень просто, поскольку для представления каждой цифры в двоичной системе требуется всего четыре бита.
- Ввод и вывод легче управлять в шестнадцатеричном формате. В области науки о данных, искусственного интеллекта и машинного обучения есть множество преимуществ.
- Он облегчает жизнь, позволяя группировать двоичные числа, что облегчает их чтение, запись и понимание. Это более удобно для человека, так как люди привыкли группировать числа и объекты вместе для простоты понимания. Кроме того, запись меньшим количеством цифр снижает вероятность ошибки.
Недостатки шестнадцатеричной системы счисления
Недостатки шестнадцатеричной системы счисления заключаются в следующем:
Она облегчает жизнь, позволяя группировать двоичные числа, что облегчает их чтение, запись и понимание. Это более удобно для человека, так как люди привыкли группировать числа и объекты вместе для простоты понимания. Кроме того, запись меньшим количеством цифр снижает вероятность ошибки.
Кроме того, запись меньшим количеством цифр снижает вероятность ошибки.
Также читайте об отношениях и функциях здесь. 90[/latex] 1 13
Шаг 2: Сложите разрядность каждой цифры.
4096×1 + 256×10 + 16×7 + 1×13
4096 + 2560 + 112 + 13 = 6781
Итак, 1a7d в шестнадцатеричном формате равно 6781.
_{16}\) = \((6781)_{10}\)
Пример : Вычислить: \((BA 3)_{16}\) + \((5 D E)_{16} \)
Решение:
Шестнадцатеричное сложение:
Таблица для шестнадцатеричного сложения выглядит следующим образом:
Сложение шестнадцатеричных чисел можно легко осуществить с помощью приведенной выше таблицы.
Заметим из таблицы, что
3 + E = 11 (11 перенос)
A + D = 17 (B A 3)
17 + 1 (перенос) = 18 (5 D E)
B + 5 = 10
10 + 1 (перенос) = 11 (1 1 8 1)
Следовательно, требуемая сумма равна 1181 в шестнадцатеричном формате.
Решенный пример : Преобразование \(100100010101111_{2}\) в шестнадцатеричное число.
Чтобы преобразовать двоичное число в шестнадцатеричное, просто разделите его на группы из четырех цифр (начиная справа и добавив ведущие нули, если цифры заканчиваются), а затем интерпретируйте эти группы из четырех цифр как шестнадцатеричные значения, указанные выше. . Установив это, мы имеем
\(100100010101111_{2}=0100 1000 1010 1111\)
\(0100=4, 1000=8, 1010=A, 1111=F\)
\(1001000010101}181010111810101} )
Чтобы преобразовать двоичное число в восьмеричное, мы можем просто разбить его на группы по три цифры, а затем выполнить те же действия, что и при преобразовании двоичного числа в шестнадцатеричное. Возьмем то же двоичное число и преобразуем его в восьмеричное:
\(100100010101111_{2}=100 100 010 101 111\)
100=4
010=2
101=5
111=7
\(100100010101111_{2}=44257_{8}\)
Обратный процесс еще проще. Допустим, мы хотим преобразовать \(FC7_{16}\) в двоичный формат. Мы можем прочитать двоичные значения для каждой цифры шестнадцатеричного целого числа из таблицы:
Допустим, мы хотим преобразовать \(FC7_{16}\) в двоичный формат. Мы можем прочитать двоичные значения для каждой цифры шестнадцатеричного целого числа из таблицы:
\(F_{16} = 1111_{2}$ $C_{16} = 1100_{2}$ $7_{16} = 0111_{2 }\)
\(FC7_{16}=111111000111_{2}\)
Процесс преобразования восьмеричного числа в двоичную форму точно такой же.
Надеюсь, что эта статья о шестнадцатеричной системе счисления была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Часто задаваемые вопросы о шестнадцатеричной системе счисления
В.1 Сколько цифр используется в шестнадцатеричной системе счисления?
Ответ 1 Шестнадцатеричная система счисления представляет собой вид числового представления, в котором основанием числа является 16. Это указывает на то, что существует только 16 возможных значений цифр: 0, 1, 2, 3, 4, 5 , 6, 7, 8, 9, A, B, C, D, E, F. Где A, B, C, D, E и F представляют десятичные значения 10, 11, 12, 13, 14 и 15 в отдельных битах. Значение любой цифры может быть представлено всего четырьмя битами. Для представления значения любой цифры требуется всего 4 бита. Каждая позиция цифры имеет вес в 16-й степени. Каждое место в шестнадцатеричной системе в 16 раз значительнее предыдущего, поэтому числовое значение шестнадцатеричного числа вычисляется путем умножения каждой цифры на значение позиции, в которой стоит цифра, с последующим сложением произведений. В результате это взвешенная (или позиционная) система счисления.
Значение любой цифры может быть представлено всего четырьмя битами. Для представления значения любой цифры требуется всего 4 бита. Каждая позиция цифры имеет вес в 16-й степени. Каждое место в шестнадцатеричной системе в 16 раз значительнее предыдущего, поэтому числовое значение шестнадцатеричного числа вычисляется путем умножения каждой цифры на значение позиции, в которой стоит цифра, с последующим сложением произведений. В результате это взвешенная (или позиционная) система счисления.
Q.2 Что такое шестнадцатеричная система счисления на примере?
Ответ 2 Шестнадцатеричная система представлена с основанием 16. Это означает, что в шестнадцатеричной системе 16 шестнадцатеричных чисел. Шестнадцатеричная (иногда известная как основание 16 или просто шестнадцатеричная) система счисления представляет собой позиционную систему счисления, используемую в математике и вычислительной технике. Шестнадцатеричное используется в кодировке передачи Base 16, которая делит каждый байт открытого текста на два 4-битных значения и две шестнадцатеричные цифры.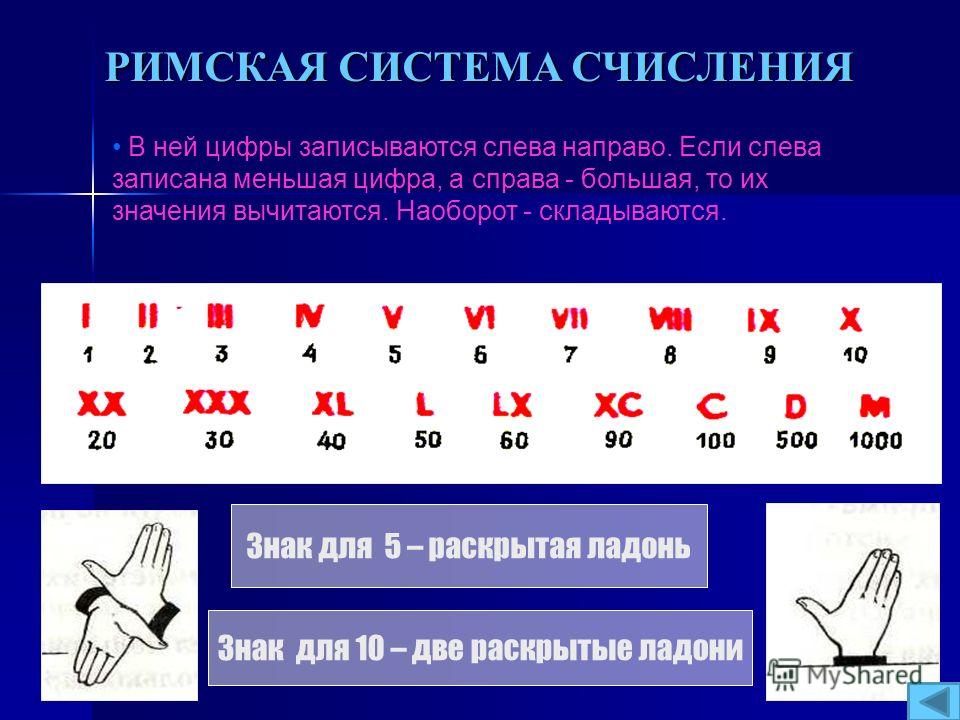 Шестнадцатеричные числа обычно используются разработчиками программного обеспечения и проектировщиками систем, поскольку они обеспечивают удобное для человека представление данных в двоичном коде. Каждая шестнадцатеричная цифра, обычно известная как полубайт, представляет собой четыре бита (двоичные цифры) (или полубайт).
Шестнадцатеричные числа обычно используются разработчиками программного обеспечения и проектировщиками систем, поскольку они обеспечивают удобное для человека представление данных в двоичном коде. Каждая шестнадцатеричная цифра, обычно известная как полубайт, представляет собой четыре бита (двоичные цифры) (или полубайт).
Q.3 Какие существуют 4 типа системы счисления?
Ответ 3 Четыре распространенных типа систем счисления: Десятичная система счисления: имеет основание 10. Десятичная система счисления также известна как система счисления с основанием 10, поскольку в ней используются десять цифр от 0 до 9. Десятичная система счисления — это та, которую мы часто используем в нашей повседневной жизни. Двоичная система счисления: имеет основание 2. Двоичная система счисления или система с основанием 2 составляют только две цифры, равные 0 и 1. Компьютеры манипулируют и хранят все свои данные, включая числа, слова, фильмы, изображения и музыку, используя двоичная система счисления. Восьмеричная система счисления: имеет основание 8. Восьмеричная система счисления представлена с основанием 8, то есть она использует цифры от 0 до 7, то есть 0, 1, 2, 3, 4, 5, 6 и 7 для представления числа. Термин восьмеричный используется для описания чисел с восьмизначным основанием. Шестнадцатеричная система счисления: имеет основание 16. Шестнадцатеричная система представлена с основанием 16. Это означает, что в шестнадцатеричной системе 16 шестнадцатеричных чисел. Шестнадцатеричная (иногда известная как основание 16 или просто шестнадцатеричная) система счисления представляет собой позиционную систему счисления, используемую в математике и вычислительной технике.
Восьмеричная система счисления: имеет основание 8. Восьмеричная система счисления представлена с основанием 8, то есть она использует цифры от 0 до 7, то есть 0, 1, 2, 3, 4, 5, 6 и 7 для представления числа. Термин восьмеричный используется для описания чисел с восьмизначным основанием. Шестнадцатеричная система счисления: имеет основание 16. Шестнадцатеричная система представлена с основанием 16. Это означает, что в шестнадцатеричной системе 16 шестнадцатеричных чисел. Шестнадцатеричная (иногда известная как основание 16 или просто шестнадцатеричная) система счисления представляет собой позиционную систему счисления, используемую в математике и вычислительной технике.
В.4 Что такое двоичные числа?
Ответ 4 Двоичная система счисления или система с основанием 2 состоит только из двух цифр, равных 0 и 1. Компьютеры обрабатывают и хранят все свои данные, включая числа, слова, фильмы, изображения и музыку, используя двоичную систему счисления.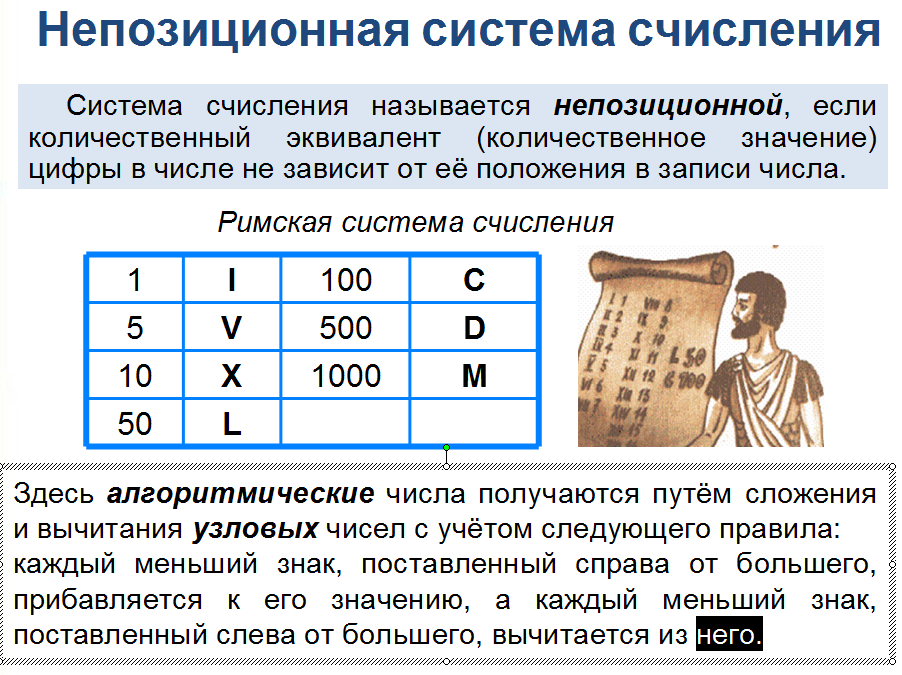 Поскольку числа «2» в этой системе не существует, 1 + 1 = 10. Джордж Буль, британский математик, в 1854 году написал основополагающую работу, описывающую алгебраическую систему логики, основанную на бинарной системе, которая стала известна как булева алгебра. Его логическое исчисление сыграет ключевую роль в развитии цифровых электрических схем.
Поскольку числа «2» в этой системе не существует, 1 + 1 = 10. Джордж Буль, британский математик, в 1854 году написал основополагающую работу, описывающую алгебраическую систему логики, основанную на бинарной системе, которая стала известна как булева алгебра. Его логическое исчисление сыграет ключевую роль в развитии цифровых электрических схем.
В.5 Что такое десятичные числа?
Ответ 5 Десятичная система счисления также известна как система счисления с основанием 10, поскольку в ней используются десять цифр от 0 до 9. Десятичная система счисления — это та система, которую мы часто используем в нашей повседневной жизни. жизнь. В десятичной системе счисления прогрессивная позиция находится слева от десятичной точки, представленной единицами, десятками, сотнями, тысячами и так далее. Каждая позиция описывает определенную мощность основания (10). Например, десятичное число 1245 состоит из цифры 5 в позиции единиц, 4 в позиции десятков, 2 в позиции сотен и 1 в позиции тысяч.
В.6 Что такое шестнадцатеричные числа?
Ответ 6 Шестнадцатеричная система представлена с основанием 16. Это означает, что в шестнадцатеричной системе 16 шестнадцатеричных чисел. Шестнадцатеричная (иногда известная как основание 16 или просто шестнадцатеричная) система счисления представляет собой позиционную систему счисления, используемую в математике и вычислительной технике. Шестнадцатеричное используется в кодировке передачи Base16, которая делит каждый байт открытого текста на два 4-битных значения и две шестнадцатеричные цифры. Шестнадцатеричные числа обычно используются разработчиками программного обеспечения и проектировщиками систем, поскольку они обеспечивают удобное для человека представление данных в двоичном коде. Каждая шестнадцатеричная цифра, обычно известная как полубайт, представляет собой четыре бита (двоичные цифры) (или полубайт).
Скачать публикацию в формате PDF| Свойства целых чисел: закрытие обучения, коммутативный, ассоциативный, распределительный, решаем Формула себестоимости: изучите C.P. Формула прибыли и убытка с примерами |
| Свойства натуральных чисел, объясненные с решенными примерами |
| Длинное деление, исследование с использованием символа, шагов, полиномиального деления и решенных примеров |
Основания счисления: введение и двоичные числа bases на самом деле довольно прост, но поначалу мысли, лежащие в его основе, могут показаться немного запутанными. И хотя тема различных систем счисления может показаться вам несколько бессмысленной, появление компьютеров и компьютерной графики увеличило потребность в знании того, как работать с различными (недесятичными) системами счисления, особенно с двоичными системами (единицы и нули) и шестнадцатеричные системы (числа от нуля до девяти, за которыми следуют буквы от A до F).
Содержание продолжается ниже
MathHelp.
 com
comВ нашей обычной десятичной системе у нас есть цифры для чисел от нуля до девяти. У нас нет однозначного числа «десять». (Римляне так и сделали, в их иероглифе «X».) Да, мы пишем «10», но это означает «1 десяток и 0 единиц». Это две цифры; у нас нет ни одной одиночной цифры, обозначающей «десять».
Вместо этого, когда нам нужно сосчитать на единицу больше девяти, мы обнуляем столбец единиц и добавляем единицу к столбцу десятков. Когда мы становимся слишком большими в столбце десятков — когда нам нужно на единицу больше, чем девять десятков и девять единиц («99″), мы обнуляем столбцы десятков и единиц и прибавляем единицу к столбцу десяти умножить на десять, или сотням. Следующий столбец — это столбец десять умножить на десять, или тысяч. и так далее, причем каждый больший столбец в десять раз больше предыдущего. Мы помещаем цифры в каждый столбец, говоря нам, сколько копий этой степени десяти нам нужно. другие системы счисления не связаны с тем, что вы занимаетесь счислением с основанием десять с детства.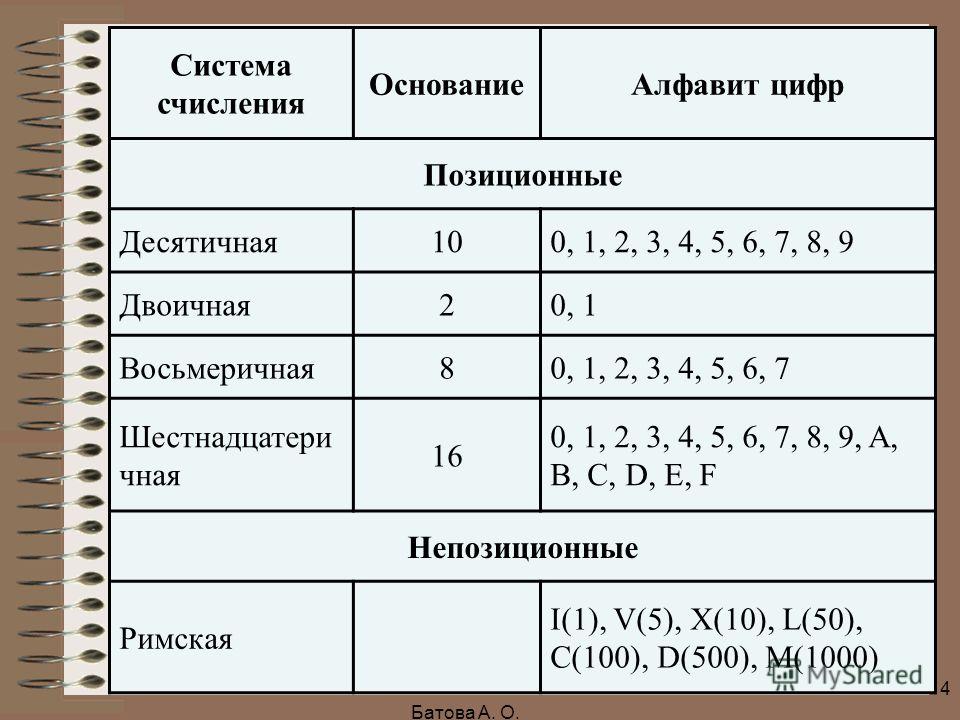 И (почти) каждая цивилизация использовала математику с основанием десять, вероятно, по той простой причине, что у нас десять пальцев. Если бы вместо этого мы жили в мультипликационный мир, где у нас было бы только четыре пальца на каждой руке (считайте их в следующий раз, когда вы смотрите телевизор или читаете комиксы), тогда «естественной» базовой системой, вероятно, была бы восьмеричная система счисления.
И (почти) каждая цивилизация использовала математику с основанием десять, вероятно, по той простой причине, что у нас десять пальцев. Если бы вместо этого мы жили в мультипликационный мир, где у нас было бы только четыре пальца на каждой руке (считайте их в следующий раз, когда вы смотрите телевизор или читаете комиксы), тогда «естественной» базовой системой, вероятно, была бы восьмеричная система счисления.
Двоичный
Давайте посмотрим на числа с основанием два или двоичные. Как бы вы написали, например, 12 10 («двенадцать, основание десять») в виде двоичного числа? Вам нужно будет преобразовать в столбцы с основанием два, аналог столбцов с основанием десять. В базе десять у вас есть столбцы или «места» для 10 0 = 1, 10 1 = 10, 10 2 = 100, 10 3 = 1000 и так далее. Точно так же в базе два у вас есть столбцы или «места» для 2 0 = 1, 2 1 = 2, 2 2 = 4, 2 3 = 8, 2 4 = 16 и так далее.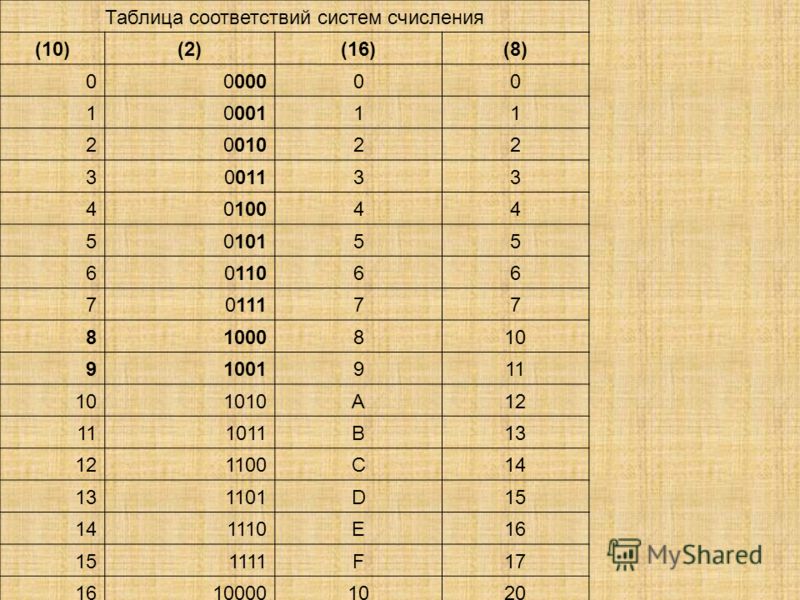
Первый столбец в математике с основанием два — это столбец единиц. Но только «0» или «1» могут быть в столбце единиц. Когда вы дойдете до «два», вы обнаружите, что нет ни одной одиночной цифры, обозначающей «два» в математике с основанием два. Вместо этого вы помещаете «1» в столбец «двойки» и «0» в столбец «единицы», указывая на «1 два и 0 единиц». Базовая десятка «два» (2 10 ) записывается в двоичном виде как 10 2 .
«Три» по основанию два на самом деле «1 два и 1 один», поэтому оно записывается как 11 2 . «Четыре» на самом деле дважды два, поэтому мы обнуляем столбец двоек и столбец единиц и ставим «1» в столбец четверок; 4 10 записывается в двоичной форме как 100 2 . Вот список первых нескольких чисел:
Преобразование между двоичными и десятичными числами довольно просто, если вы помните, что каждая цифра в двоичном числе представляет собой степень двойки.
Я перечислю цифры по порядку, как они появляются в номере, который мне дали. Затем в другом ряду я буду считать эти цифры СПРАВА, начиная с нуля:
Затем в другом ряду я буду считать эти цифры СПРАВА, начиная с нуля:
Первая строка выше (обозначенная как «цифры») содержит цифры двоичного числа; вторая строка (обозначенная как «нумерация») содержит степень числа 2 (основание), соответствующую каждой цифре. Я буду использовать этот список для преобразования каждой цифры в степень двойки, которую она представляет:
1×2 8 + 0×2 7 + 1×2 6 + 1×2 5 + 0× 2 4 + 0×2 3 + 1×2 2 + 0×2 1 + 1×2 0
= 1×256 + 0×128 + 1×364 + 1×364 + 0×16 + 0×8 + 1×4 + 0×2 + 1×1
= 256 + 64 + 32 + 4 + 1
= 357
Тогда 101100101 2 преобразуется в 357 10 .
Преобразование десятичных чисел в двоичные почти так же просто: просто разделите на 2.
Чтобы выполнить это преобразование, мне нужно несколько раз делить на 2, отслеживая остатки по ходу дела. Смотрите ниже:
Приведенный выше рисунок анимирован на «живой» веб-странице.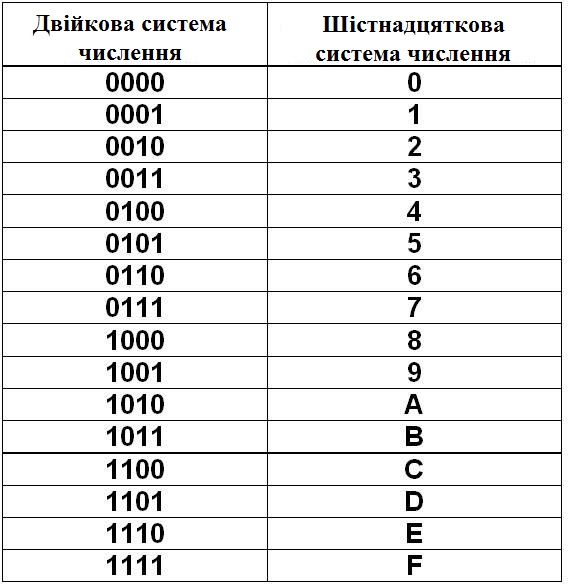
Как видите, после многократного деления на 2 я получил следующие остатки:
Эти остатки говорят мне, что такое двоичное число. Я читал числа снаружи деления, начиная сверху с конечного значения и его остатка, и двигался по правой стороне последовательного деления вниз. Затем:
357 10 преобразуется в 101100101 2 .
Этот метод преобразования подходит для преобразования в любую недесятичную систему счисления. Только не забудьте включить эту первую цифру вверху, перед списком остатков. Если вам интересно, объяснение того, почему этот метод работает, доступно здесь.
Вы можете преобразовать десятичную систему счисления в любую другую. Когда вы будете изучать эту тему в классе, вы, вероятно, будете преобразовывать числа в различные другие системы счисления, поэтому давайте рассмотрим еще несколько примеров…
URL: https://www.purplemath.com/modules/numbbase .htm
Страница 2 Страница 3
ДЕСЯТИЧНАЯ функция
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel для Mac 2011 Больше.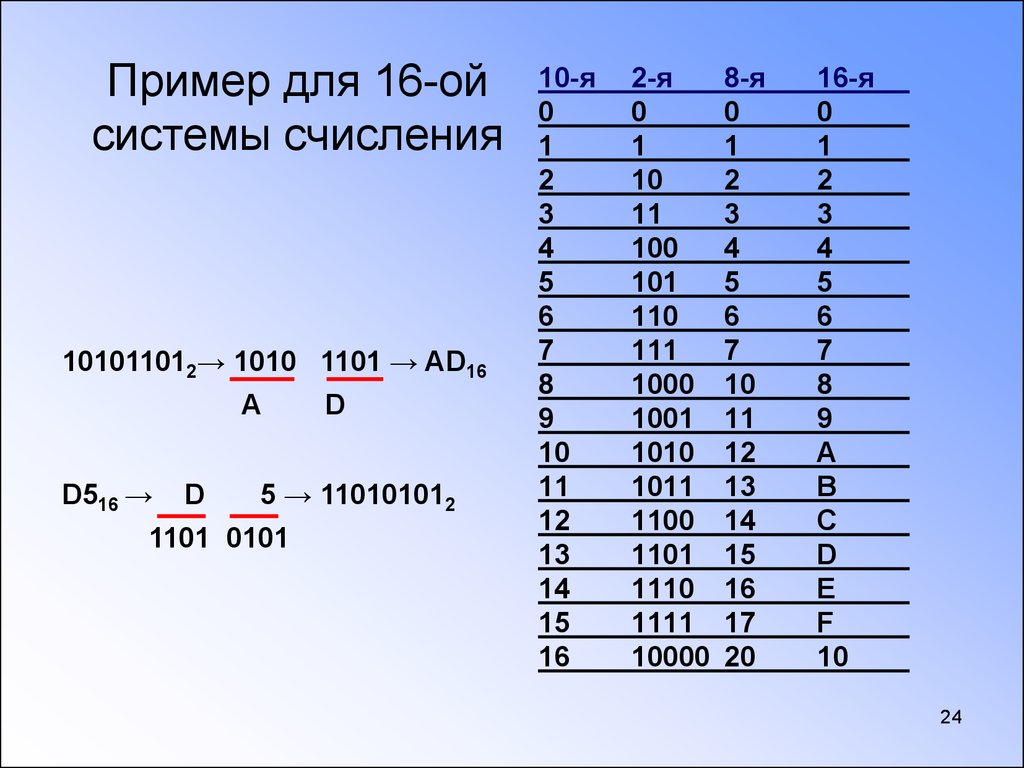 ..Меньше
..Меньше
В этой статье описаны синтаксис формулы и использование DECIMAL . функция в Microsoft Excel.
Описание
Преобразует текстовое представление числа в заданной системе счисления в десятичное число.
Синтаксис
ДЕСЯТИЧНОЕ(текст, основание)
Синтаксис функции DECIMAL имеет следующие аргументы.
Замечания
Длина строки Text должна быть меньше или равна 255 символам.
Аргумент «Текст» может быть любой комбинацией буквенно-цифровых символов, допустимой для системы счисления, без учета регистра.
53, может привести к потере точности.Основание должно быть больше или равно 2 (двоичное или по основанию 2) и меньше или равно 36 (по основанию 36).
В системе счисления больше 10 используйте числовые значения 0–9 и буквы A–Z по мере необходимости. Например, основание 16 (шестнадцатеричное) использует 0-9 и A-F, а основание 36 использует 0-9 и A-Z.Если какой-либо из аргументов выходит за пределы ограничений, функция DECIMAL может вернуть ошибку #NUM! или #ЗНАЧ! значение ошибки.
Пример
Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового рабочего листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите клавишу ВВОД.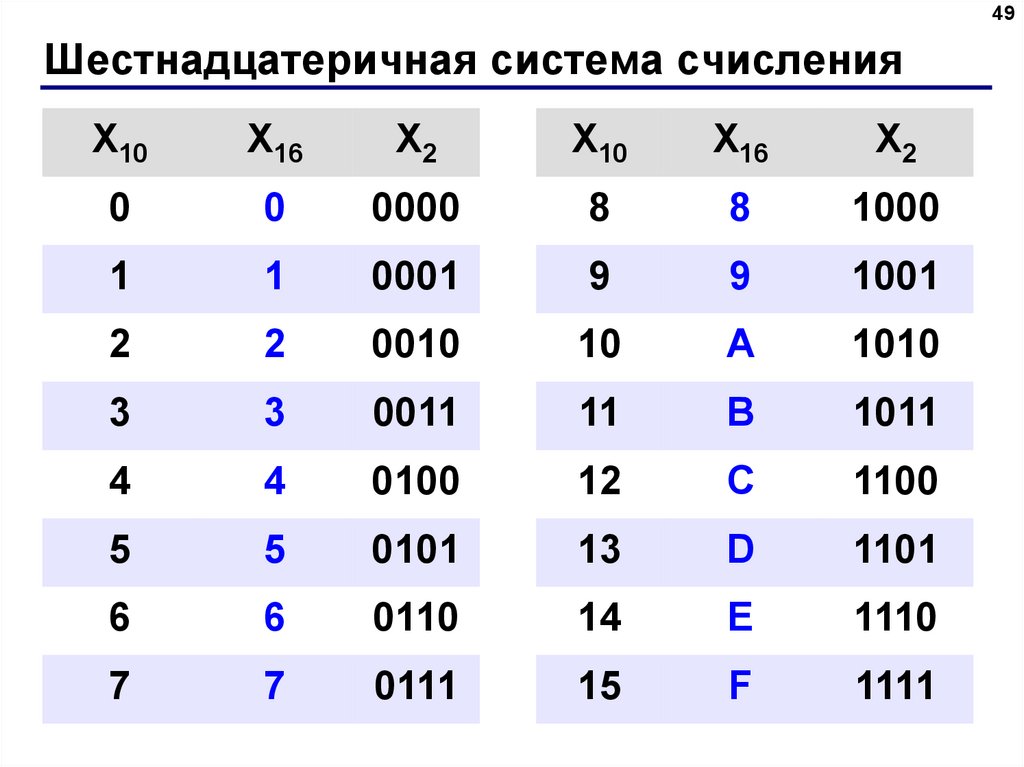 При необходимости вы можете настроить ширину столбцов, чтобы увидеть все данные.
При необходимости вы можете настроить ширину столбцов, чтобы увидеть все данные.
Формула | Описание | Результат | Как это работает |
‘= ДЕСЯТИЧНОЕ («FF», 16) | Преобразует шестнадцатеричное (с основанием 16) значение FF в его эквивалентное десятичное (с основанием 10) значение (255). | = ДЕСЯТИЧНОЕ («FF», 16) | «F» находится в позиции 15 в системе счисления с основанием 16. |
Функция HEX2DEC в ячейке C3 проверяет этот результат. | =HEX2DEC(«ff») 90)) | ||
‘= ДЕСЯТИЧНОЕ (111,2) | Преобразует двоичное (с основанием 2) значение 111 в его эквивалентное десятичное (с основанием 10) значение (7). | = ДЕСЯТИЧНОЕ (111,2) | «1» находится в позиции 1 в системе счисления с основанием 2. В приведенной ниже формуле показано, как оно преобразуется в десятичную форму: . |
Функция BIN2DEC в ячейке C6 проверяет этот результат. | =БИН2ДЕК(111) | 90)) | |
‘= ДЕСЯТИЧНОЕ («зап», 36) | Преобразует значение «zap» по основанию 36 в его эквивалентное десятичное значение (45745). | = ДЕСЯТИЧНОЕ («зап», 36) | «z» находится в позиции 35, «a» — в позиции 10, а «p» — в позиции 25. В приведенной ниже формуле показано, как оно преобразуется в десятичное число. |


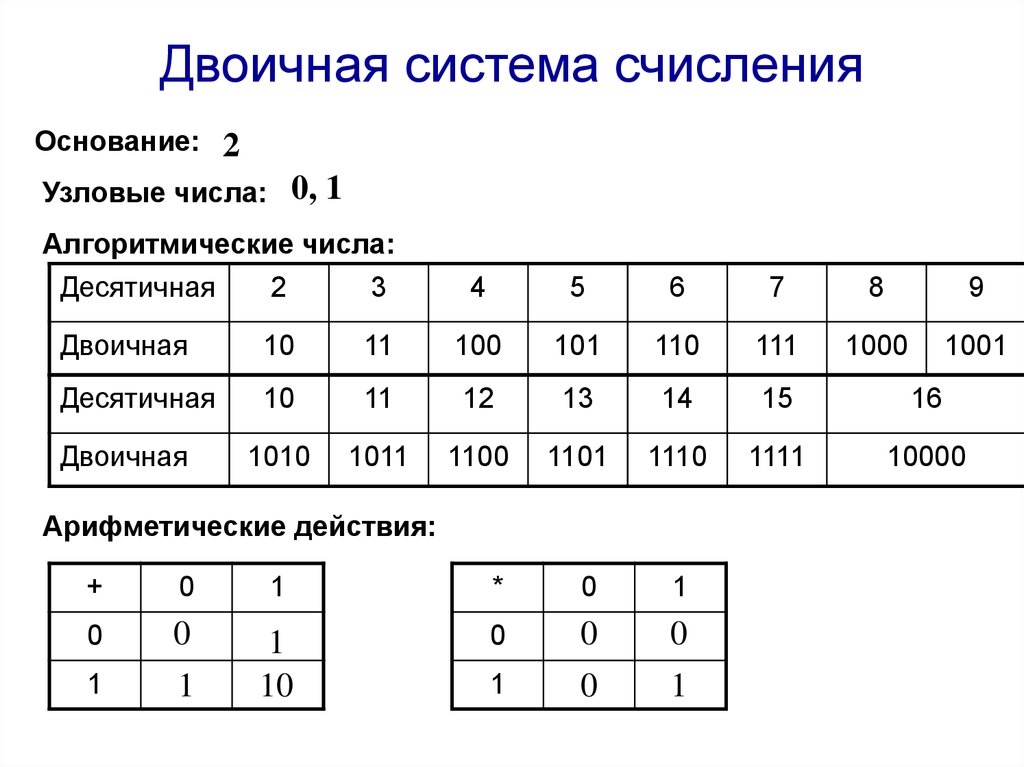
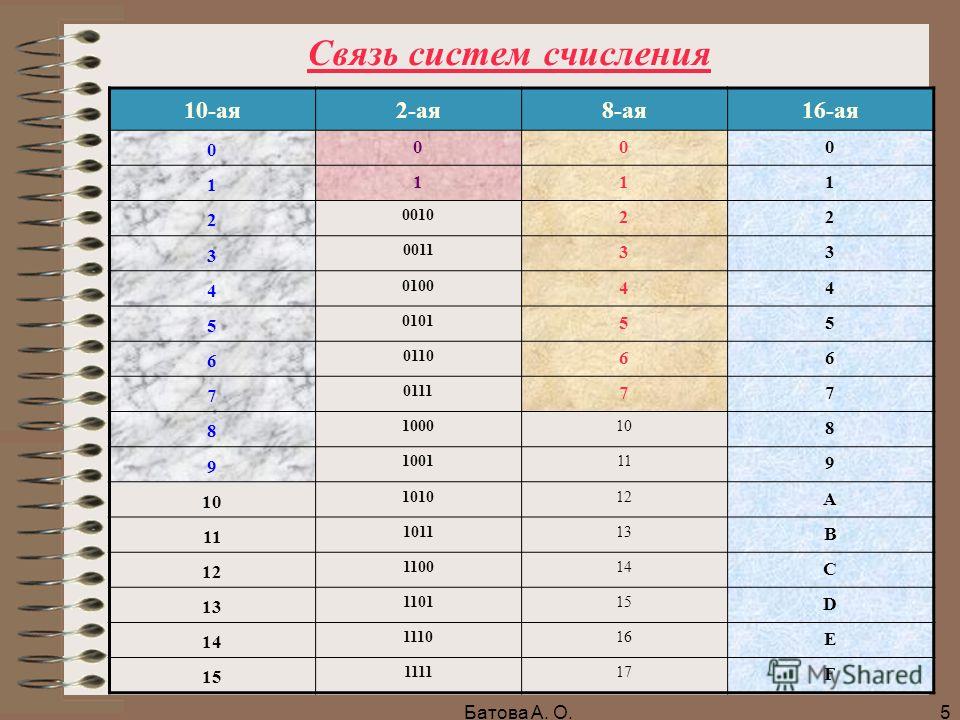 ..
..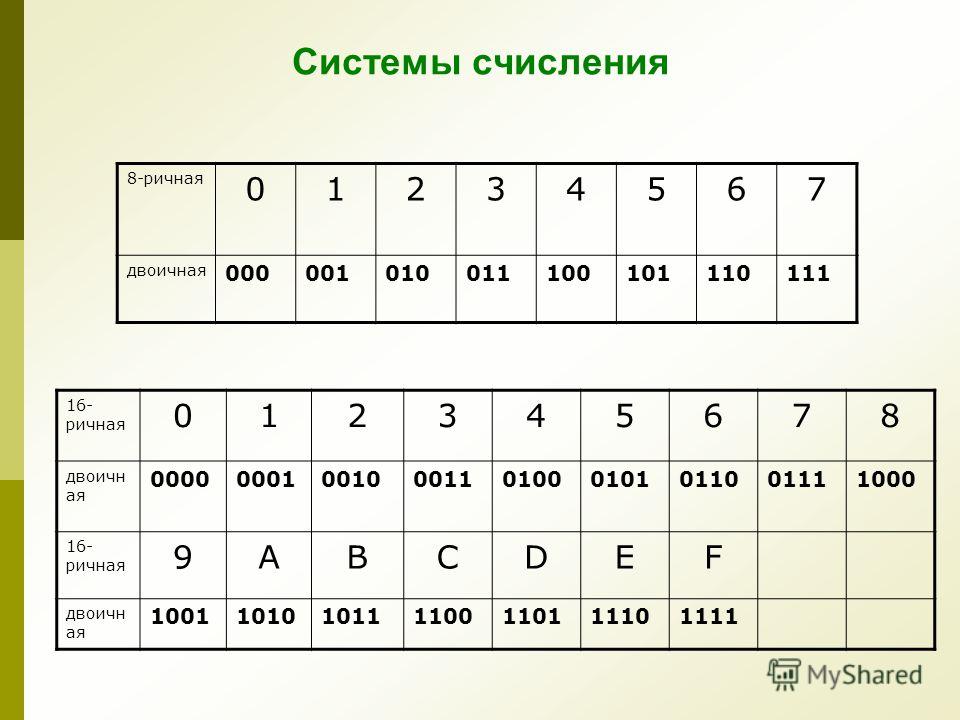
 разбить двоичное число справа налево по четыре цифры (недостающие слева дополнить нулями):
разбить двоичное число справа налево по четыре цифры (недостающие слева дополнить нулями):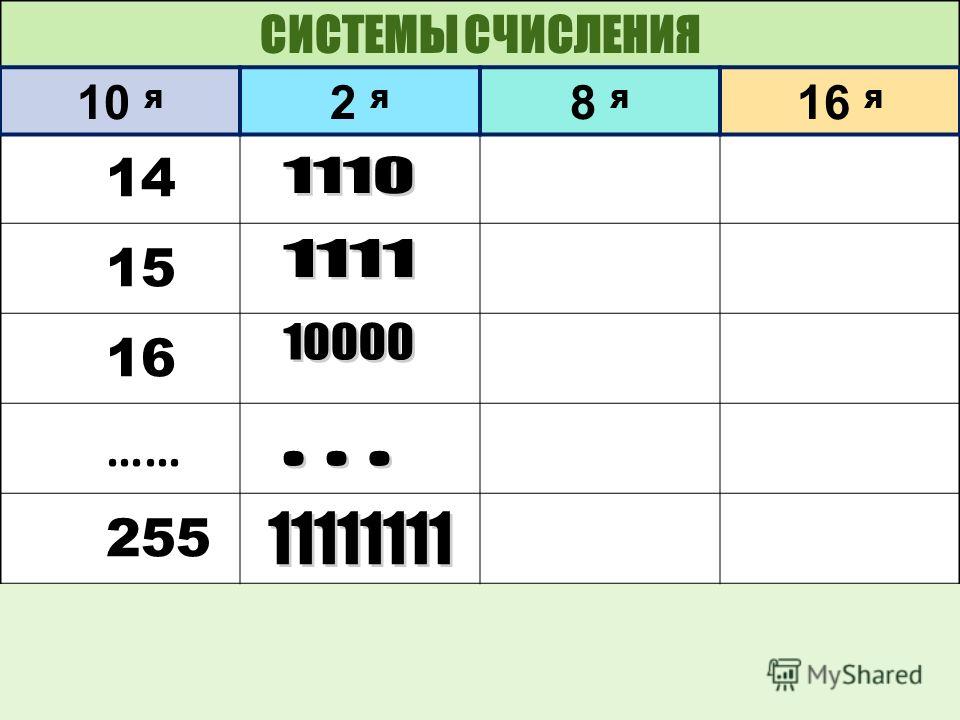 Это число 2, которое мы берем из второго слагаемого. Во втором слагаемом остается 3, которое и записывается в этот разряд, а единица переноса уходит в старший разряд суммы.
Это число 2, которое мы берем из второго слагаемого. Во втором слагаемом остается 3, которое и записывается в этот разряд, а единица переноса уходит в старший разряд суммы. Это число 3, которое мы берем из второго слагаемого. Во втором слагаемом остается 5, которое и записывается в этот разряд, а единица переноса уходит в старший разряд суммы.
Это число 3, которое мы берем из второго слагаемого. Во втором слагаемом остается 5, которое и записывается в этот разряд, а единица переноса уходит в старший разряд суммы. Идентификатор не был описан
Идентификатор не был описан
 Имя файла неверно или указывает на несуществующий путь
Имя файла неверно или указывает на несуществующий путь
 Базовый тип множества должен представлять собой отрезок порядкового типа с границами 0…255 или перечисляемый тип с не более чем 256 значениями
Базовый тип множества должен представлять собой отрезок порядкового типа с границами 0…255 или перечисляемый тип с не более чем 256 значениями
 Действительный, строковый, структурный и указательный типы в данном случае недопустимы
Действительный, строковый, структурный и указательный типы в данном случае недопустимы
 В интерфейсном разделе два модуля не могут ссылаться друг на друга
В интерфейсном разделе два модуля не могут ссылаться друг на друга
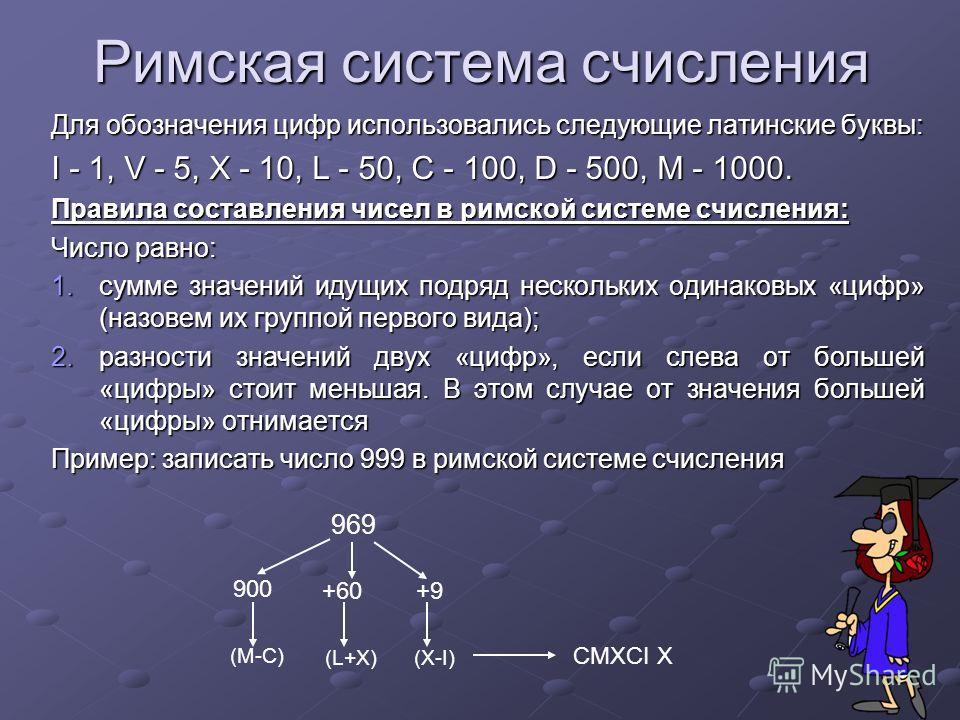 ’ expected
’ expected
 Файл не может быть открыт или создан
Файл не может быть открыт или создан
 Файловой переменной не поставлено в соответствие имя файла
Файловой переменной не поставлено в соответствие имя файла
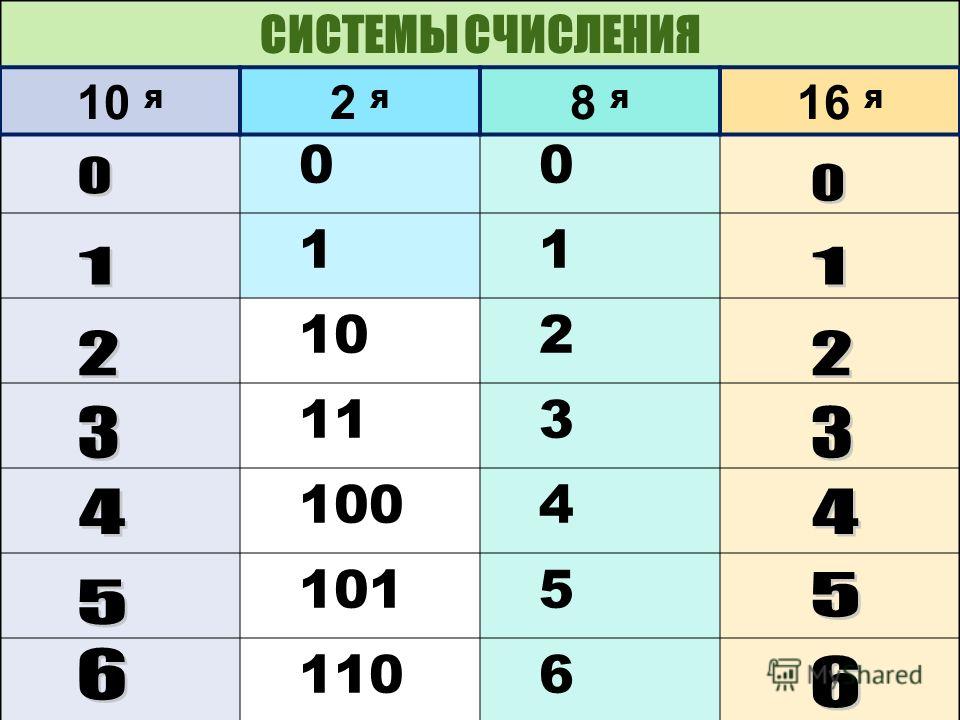 ..
..

 com
com Поскольку все системы счисления начинаются с 0, 16-й символ в шестнадцатеричном формате будет на 15-й позиции. В приведенной ниже формуле показано, как оно преобразуется в десятичную форму:
Поскольку все системы счисления начинаются с 0, 16-й символ в шестнадцатеричном формате будет на 15-й позиции. В приведенной ниже формуле показано, как оно преобразуется в десятичную форму: