Диэлектрическая проницаемость вакуума
Эта статья об электрической постоянной. Для аналогичной магнитной постоянной см. Вакуумная проницаемость. Для порядкового числа ε0, видеть Числа Эпсилона (математика).
В физическая постоянная ε0 (произносится как «эпсилон ноль» или «эпсилон ноль»), обычно называемый диэлектрическая проницаемость вакуума, диэлектрическая проницаемость свободного пространства или же электрическая постоянная или распределенная емкость вакуума, — идеальная (базовая) физическая константа, которая является значением абсолютная диэлектрическая проницаемость из классический вакуум. Его CODATA ценность
- ε0 = 8.8541878128(13)×10−12 F⋅m−1 (фарады на метр ), с относительной неопределенностью 1.5×10−10.[1]
| Значение ε0 | Единица измерения | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8.8541878128(13)×10−12 | F ⋅м−1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
55. {2} }}} {2} }}}Значение постоянной дроби, 1/4πε0{ displaystyle 1/4 pi varepsilon _ {0}}, составляет примерно 9 × 109 Нм2⋅C−2, q1 и q2 обвинения, и р расстояние между их центрами. Так же, ε0 появляется в Уравнения Максвелла, которые описывают свойства электрический и магнитные поля и электромагнитное излучение, и соотнесите их с их источниками. Содержание
ЦенитьЗначение ε0 является определенный по формуле[3]
куда c определенное значение для скорость света в классический вакуум в Единицы СИ,[4] и μ0 это параметр, который международные организации по стандартизации называют «магнитная постоянная «(обычно называется проницаемостью вакуума или проницаемостью свободного пространства). Историческое происхождение электрической постоянной ε0, и его значение более подробно описаны ниже. Новое определение единиц СИОсновная статья: 2019 новое определение базовых единиц СИ В ампер было переопределено путем определения элементарный заряд как точное количество кулонов по состоянию на 20 мая 2019 г.,[9] в результате чего электрическая диэлектрическая проницаемость вакуума больше не имеет точно определенного значения в единицах СИ. Величина заряда электрона стала численно определенной величиной, а не измеренной, что сделало μ0 измеренное количество. Как следствие, ε0 не совсем. Как и прежде, он определяется уравнением ε0 = 1/(μ0c2), и, таким образом, определяется значением μ0, то магнитная вакуумная проницаемость что в свою очередь определяется экспериментально определенным безразмерным постоянная тонкой структуры α:
с е будучи элементарный заряд, час будучи Постоянная Планка, и c будучи скорость света в вакуум, каждый с точно определенными значениями. ТерминологияИсторически параметр ε0 был известен под разными именами. Термины «диэлектрическая проницаемость вакуума» или ее варианты, такие как «диэлектрическая проницаемость в вакууме / в вакууме»,[11][12] «диэлектрическая проницаемость пустого пространства»,[13] или «диэлектрическая проницаемость свободное место «[14] широко распространены. Организации по стандартизации во всем мире теперь используют термин «электрическая постоянная» как единый термин для этой величины,[7] и официальные документы по стандартам приняли этот термин (хотя они продолжают перечислять старые термины как синонимы).[15][16] В новой системе СИ диэлектрическая проницаемость вакуума больше не будет постоянной, а будет измеряемой величиной, связанной с (измеренным) безразмерным постоянная тонкой структуры. Другим историческим синонимом была «диэлектрическая проницаемость вакуума», поскольку «диэлектрическая постоянная» иногда использовалась в прошлом для обозначения абсолютной диэлектрической проницаемости.[17][18] Однако в современном использовании термин «диэлектрическая проницаемость» обычно относится исключительно к относительная диэлектрическая проницаемость ε/ε0 и даже это использование считается «устаревшим» некоторыми органами по стандартизации в пользу относительная статическая диэлектрическая проницаемость.[16][19] Следовательно, термин «диэлектрическая проницаемость вакуума» для электрической постоянной ε0 считается устаревшим большинством современных авторов, хотя время от времени можно найти примеры продолжающегося использования. Что касается обозначений, то константу можно обозначать либо ε0{ displaystyle varepsilon _ {0} ,} или же ϵ0{ displaystyle epsilon _ {0} ,}, используя любой из общих глифы для письма эпсилон. Созданная таким образом система уравнений известна как рационализированная система уравнений метр – килограмм – секунда (rmks) или система уравнений «метр – килограмм – секунда – ампер (mksa)». Это система, используемая для определения единиц СИ.[21]Новое количество q получил название «рмкс электрический заряд», или (в настоящее время) просто «электрический заряд». Ясно, что количество qs использованный в старой системе cgs esu связан с новым количеством q к
Определение стоимостиε0Теперь добавляется требование о том, чтобы сила измерялась в ньютонах, расстояние в метрах, а заряд измерялся в практической единице инженеров, кулонах, которые определяются как заряд, накопленный, когда ток в 1 ампер протекает на одного человека. второй. Это показывает, что параметр ε0 следует выделить блок C2⋅N−1⋅m−2 (или эквивалентные единицы — на практике «фарады на метр»). Чтобы установить числовое значение ε0, используется тот факт, что если использовать рационализированные формы закона Кулона и Закон силы Ампера (и другие идеи) для развития Уравнения Максвелла, то обнаруживается, что указанная выше связь существует между ε0, μ0 и c0. В принципе, у каждого есть выбор: сделать кулон или ампер фундаментальной единицей электричества и магнетизма. В международном масштабе было принято решение использовать ампер. Это означает, что значение ε0 определяется значениями c0 и μ0, как указано выше. Для краткого объяснения того, как ценность μ0 решено, см. статью о μ0. Разрешимость реальных медиаУсловно электрическая постоянная ε0 появляется в отношениях, определяющих электрическое поле смещения D с точки зрения электрическое поле E и классическая электротехника плотность поляризации п среды. Диэлектрическая постоянная различных материалов | PHYWENach oben Информация
Обслуживание
Компания
Please note * Prices subject to VAT. We only supply companies, institutions and educational facilities. No sales to private individuals. Please note: To comply with EU regulation 1272/2008 CLP, PHYWE does not sell any chemicals to the general public. We only accept orders from resellers, professional users and research, study and educational institutions. Пожалуйста, введите имя, под которым должна быть сохранена Ваша корзина. Название корзины Эпсилон 0 в чем измеряетсяДиэлектрическая проницаемость: что это такое, формула, таблицаВ этой статье мы расскажем о самых важных вещах, связанных с диэлектрической проницаемостью. Среди прочего, вы узнаете о важных ролях, которые он играет, и о типичных значениях. Простое объяснениеВ повседневной жизни вы сталкиваетесь с различными веществами, такими как металлы, вода или кислород. Диэлектрическая проницаемость (диэлектрическая постоянная или абсолютная диэлектрическая проницаемость) ε описывает способность материала к поляризации электрическими полями и определяется следующим образом: ε = εr * ε0. Здесь εr – относительная проницаемость, а ε0 – электрическая постоянная (или диэлектрическая проницаемость вакуума). Если понимать значение термина “проницаемость” буквально, то это мера того, насколько сильно материя “пропускает” электрическое поле. Поэтому проницаемость можно рассматривать как меру того, насколько материя может быть поляризована. Диэлектрическая проницаемость вакуумаОсобую роль играет диэлектрическая проницаемость вакуума (также называемая проницаемостью вакуума). В этом разделе мы расскажем вам о значении и единицах измерения проницаемости вакуума, о том, как она связана с другими константами, и о ее значении в контексте других важных законов. Числовое значение и единица измеренияДиэлектрическая проницаемость вакуума ε0 имеет значение 8,85418781762039 * 10 -12 или 8.85 * 10 -12 , что более практично для расчетов. Единицей измерения константы является [ Ф·м −1 ] или если выражать через основные единицы СИ [ м −3 ·кг −1 ·с 4 ·А 2 ]. Взаимосвязь с другими константамиСуществует замечательная связь между электрической постоянно ε0, магнитной постоянно μ0 и скоростью света в вакууме с0. То есть верно следующее соотношение: c0 2 = 1 / ε0 * μ0 . До 2019 года это уравнение точно определяло значение постоянной электрического поля. Однако в ходе пересмотра ситуация изменилась, и с 20 мая 2019 года как электрическая постоянная, так и магнитная постоянная имеют определенную погрешность измерения. Это уравнение было первым указанием на то, что свет может быть электромагнитной волной. Закон Кулона и электрический потенциалПомимо связи со скоростью света, электрическая постоянная фигурирует в других важных законах электродинамики. К ним относятся, например:
В частности, закон Кулона является основой электростатики, поэтому константа электрического поля также имеет большое значение. Диэлектрическая проницаемость: общий случайВ этом разделе мы рассмотрим общий случай. Мы объясним физический смысл абсолютной диэлектрической проницаемости с помощью электроизоляционных материалов и объясним, что такое относительная диэлектрическая проницаемость. Диэлектрическая проницаемость диэлектриковВ электроизолирующих материалах (диэлектриках) электрические заряды связаны с атомами или молекулами. Поэтому они могут лишь немного перемещаться внутри атомов или молекул. Электрическое поле может изменить распределение заряда в диэлектрике двумя важными способами: деформацией и вращением. ПоляризацияВ зависимости от того, состоит ли материал из полярных или неполярных молекул, реакция на внешнее электрическое поле различна. С неполярной молекулой происходит растягивание (деформация), при котором поле индуцирует дипольный момент в каждой молекуле материала. Все эти дипольные моменты направлены в ту же сторону, что и электрическое поле. В полярной молекуле, с другой стороны, происходит вращение, так что и здесь все дипольные моменты направлены в сторону электрического поля. В целом внешнее электрическое поле вызывает образование в материале большого количества диполей, все из которых ориентированы в том же направлении, что и внешнее поле. Таким образом, материал поляризуется. Поляризация P описывает, сколько дипольных моментов приходится на единицу объема материала. Диэлектрическая проницаемость диэлектриков Таким образом, поляризация диэлектрика вызывается электрическим полем. P = ε0 * χ * E , где Здесь ε0 – электрическая постоянная, а χ – электрическая поляризуемость. Электрическое поле E в этом уравнении является полным полем. Поэтому причиной этого могут быть частично свободные заряды и частично сама поляризация.. Свободные заряды – это все те носители заряда, которые не являются результатом поляризации. Таким образом, это полное электрическое поле очень трудно рассчитать, поскольку мы обычно не имеем информации о распределении поляризационных зарядов.
Электрическая индукцияЧтобы иметь возможность рассчитать электрическое поле даже в присутствии диэлектрика, вводится электрическая индукция D. В линейной среде: D = ε0 * E + P = ε0 * E + ε0 * χe * E = ε0 * ( 1 + χe ) * E и поэтому D также пропорциональна E . Если вы объедините константы вместе ε = ε0 * ( 1 + χe ), то получится: D = ε * E . Постоянная ε и называется диэлектрической проницаемостью. Относительная диэлектрическая проницаемостьВеличина: εr = 1 + χe = ε / ε0 называется относительной проницаемостью (также относительной диэлектрической проницаемостью). При постоянной электрической индукции относительная проницаемость, таким образом, определяет, насколько сильно ослабляется электрическое поле. Чем больше относительная проницаемость, тем больше ослабляется электрическое поле и, следовательно, уменьшается общая напряженность электрического поля. Термин относительная проницаемость может привести к неправильному пониманию того, что относительная проницаемость для данного материала является константой. На самом деле, относительная проницаемость зависит от многих факторов. Среди них:
Для некоторых материалов относительная проницаемость дополнительно зависит от направления. Следовательно, в случае таких материалов это не просто число, а часто тензор второго порядка. Особенно наглядную иллюстрацию влияния диэлектриков с разной относительной проницаемостью можно получить, поместив диэлектрик между двумя пластинами конденсатора. Если измерить электрическое напряжение на конденсаторе до и после введения диэлектрика, то можно обнаружить, что напряжение на конденсаторе уменьшается ровно на величину εr относительной диэлектрической проницаемости. Это следует непосредственно из уравнения: E = U / d для величины электрического поля между пластинами конденсатора, расположенными на расстоянии d друг от друга. Это также иллюстрирует, почему εr называется относительной проницаемостью. Напряжение на конденсаторе уменьшается на коэффициент εr за счет введения диэлектрика, по сравнению со случаем, когда между пластинами только вакуум. Относительные диэлектрические проницаемости отдельных материаловНаконец, мы приводим таблицу с типичными значениями относительной диэлектрической проницаемости (относительной диэлектрической проницаемости) различных материалов.
Таблица 1. В предыдущем разделе мы упоминали, что относительная проницаемость зависит, помимо прочего, от температуры и частоты. Поэтому важно знать и температуру, и частоту, если вы хотите получить значение из таблицы. Например, относительная проницаемость воды при температуре 20°C и частоте 0 ГГц равна 80. Если температура 0°C, а частота та же, относительная проницаемость воды равна 88. Медь, с другой стороны, имеет относительную проницаемость 5,6. Это означает, что вода как среда уменьшит напряжение на конденсаторе в 80 раз, в то время как медь уменьшит его только в 5,6 раз. Электрическая постояннаягде m 0 – магнитная постоянная. В отличие от диэлектрич. проницаемости e, зависящей от типа вещества, темп-ры, давления и др. параметров, Э. п. e 0 зависит только от выбора системы единиц. Напр., в гауссовой СГС системе единиц Физическая энциклопедия. В 5-ти томах. Смотреть что такое «ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ» в других словарях:ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — коэффициент пропорциональности ?о в законе Кулона определяющем (в единицах СИ) силу взаимодействия F двух находящихся на расстоянии r точечных электрических зарядов q1 и q2; ?о = (?оc2) 1 Ф/м = 8,854187817.10 12 Ф/м, где ?о магнитная постоянная.… … Большой Энциклопедический словарь электрическая постоянная — Коэффициент, применяемый при записи ряда соотношений в СИ, равный величине, обратной произведению магнитной постоянной на квадрат скорости света в пустоте. Примечание — Электрическая постоянная приблизительно равна 8,85419 • 10 12 Ф/м … Справочник технического переводчика ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — (см.) … Большая политехническая энциклопедия электрическая постоянная — электрическая постоянная; отрасл. диэлектрическая проницаемость пустоты Скалярная величина, характеризующая электрическое поле в пустоте, равная отношению суммарного электрического заряда, заключенного внутри некоторой замкнутой поверхности, к… … Политехнический терминологический толковый словарь Электрическая постоянная — 14. электрическая постоянная — коэффициент пропорциональности ε0 в законе Кулона , определяющем (в единицах СИ) силу взаимодействия F двух находящихся на расстоянии r точечных электрических зарядов q1 и q2; ε0 = (μ0c2) 1Ф/м = 8,854187817·10 12Ф/м, где μ0 магнитная постоянная … Энциклопедический словарь Электрическая постоянная — (ранее также носила название диэлектрической постоянной) физическая константа, скалярная величина, определяющая напряжённость электрического поля в вакууме; входящая в выражения некоторых законов электромагнетизма, в том числе закона Кулона … Википедия электрическая постоянная — elektrinė konstanta statusas T sritis automatika atitikmenys: angl. электрическая постоянная — elektrinė konstanta statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. electric constant; permittivity of vacuum vok. absolute Dielektrizitätskonstante, f;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas электрическая постоянная — elektrinė konstanta statusas T sritis fizika atitikmenys: angl. permittivity constant; permittivity of free space; permittivity of vacuum vok. Dielektrizitätskonstante, f; elektrische Feldkonstante, f; Verschiebungskonstante, f rus. абсолютная… … Fizikos terminų žodynas Чему равна электрическая постоянная? |
| Метод измерения | Ключевые точки |
| Коаксиальный зонд | Широкополосный, удобный, неразрушающий. Лучше всего подходит для MUT с потерями; жидкости и полутвердые вещества |
| Линия передачи | Широкополосный. Лучше всего подходит для MUT с потерями и низкими потерями; обрабатываемые твердые тела |
| Свободное место | Широкополосный; Бесконтактный. Лучше всего подходит для плоских листов, порошков, высоких температур |
| Резонатор | Одночастотный; Точный. Лучше всего подходит для MUT с низкими потерями; маленькие образцы Лучше всего подходит для MUT с низкими потерями; маленькие образцы |
| Параллельная пластина | Точно. Лучше всего подходит для низких частот; тонкие, плоские листы |
| Измерение индуктивности | Точное, простое измерение, требуется тороидальная конструкция сердечника |
Применение и материалы
Электроника
Диэлектрик с низким k имеет низкую диэлектрическую проницаемость или низкую способность поляризоваться и удерживать заряд. Из-за этого их можно использовать для изоляции проводников, несущих сигнал, друг от друга, поэтому они бесценны для очень плотных многослойных интегральных схем для защиты от снижения производительности.
Диэлектрик с высоким коэффициентом k обладает высокой диэлектрической проницаемостью и может легко поляризоваться. Вот почему они предпочтительны для конденсаторов для хранения электрического заряда и для ячеек памяти для хранения цифровых данных.
Погода
Можно отслеживать изменения относительной диэлектрической проницаемости воздуха, которые дают представление о влажности и температуре.
Аналитическая химия
Информация о диэлектрической проницаемости важна в хроматографии, поскольку разные растворители могут иметь сильно различающиеся поляризуемости.
Информационные технологии
Диэлектрическая проницаемость оптических волокон тщательно контролируется путем введения примесей для изменения их показателя преломления и, следовательно, режима передачи света (данных).
Таблица 2. Значения диэлектрической проницаемости обычных материалов [3]
| Материал | Относительная диэлектрическая проницаемость | Материал | Относительная диэлектрическая проницаемость |
| Вакуум | 1 | Слюда | 4 |
| Воздух | 1 | Пенополистирол | 1,03 |
| Титанат бария | 100 | Тефлон | 2. 1 1 |
| Стекло | 5-10 | Фарфор | 4-8 |
| Кевлар | 3-4,5 | Кварц | 5 |
| Титанат свинца | 200 | Резина | 2 |
| Целлулоид | 4 | Резина, силикон | 3,2 |
| Цемент | 2 | Полипропилен | 2,25 – 2,5 |
| Алмаз | 5,87 | Кремний | 11,8 |
| Бумага | 3 – 3,5 | Ниобат калия | 700 |
| Оргстекло | 2,6 – 3,5 | Ниобат танталата калия, при 20°C | 6000 |
Будущие материалы и применение
Информация о диэлектрической проницаемости на сегодняшний день наиболее широко используется при выборе и создании лучших диэлектрических материалов для использования в микроэлектромеханических системах (МЭМС). Мир электроники постоянно стремится создавать более быстрые схемы в меньших размерах. Изучение диэлектрической проницаемости находит дальнейшее применение в медицине (с развитием микросердечных клапанов), автоматизации (с более быстрым временем реакции на срабатывание подушки безопасности), системах защиты (на основе объемной сегнетоэлектрической технологии), исследовании космоса (с чрезвычайно чувствительными приводами для телескопов) и многие другие приложения в высокотехнологичных гаджетах.
Мир электроники постоянно стремится создавать более быстрые схемы в меньших размерах. Изучение диэлектрической проницаемости находит дальнейшее применение в медицине (с развитием микросердечных клапанов), автоматизации (с более быстрым временем реакции на срабатывание подушки безопасности), системах защиты (на основе объемной сегнетоэлектрической технологии), исследовании космоса (с чрезвычайно чувствительными приводами для телескопов) и многие другие приложения в высокотехнологичных гаджетах.
Источники
[1] https://www.iiserkol.ac.in/~ph424/ExptManuals/DielectricConstant.pdf
[2] https://www.keysight.com/hk/en/assets/7018 -01284/application-notes/5989-2589.pdf
[3] https://www.degruyter.com/downloadpdf/books/9783110455403/9783110455403-007/9783110455403-007.pdf
Институт фундаментальных измерений ™
с описанием постоянной Кулона
с использованием только единиц Планка
2018 CODATA
MQ
8. 9875517923(14) 10 9 Н·м 2 C -2
9875517923(14) 10 9 Н·м 2 C -2
8.98755179227(44) 10 9 Н·м 2 C -2
———————————————————————————— ——— просмотр препринта
Входные данные
- θ si , составляет 3,26239 радиан или кг м/с (импульс) или не имеет единиц вообще в зависимости от выбранной системы отсчета. Это новая константа современной теории, которая присутствует почти в каждом уравнении модели. Его можно измерить макроскопически, учитывая определенные состояния Белла, необходимые для квантовой запутанности рентгеновских лучей, таких как те, которые были выполнены Шварцем и Харрисом.
- l f , m f и t f фактически являются планковскими единицами длины, массы и времени, но не совсем одинаковыми.
 В MQ мы признаем их основными единицами.
В MQ мы признаем их основными единицами.
- c – скорость света, которую также можно записать в виде c= n L l f /n T t f = 299 792 458 м/с, так что 4 n
1 8 n T =1 физически значимо.
- Q L является дробной частью счета l f при более точном расчете.
- n Lr описывает отсчет l f представитель положения наблюдаемой относительно системы координат центра масс.
- Δ f — метрический дифференциал ; описывает числовую разницу в расстоянии между дискретной и недискретной системами отсчета.

- Q L n Lr , также известный как Дифференциал информативности описывает сокращение длины, связанное с дискретной мерой.
- ɛ 0 электрическая постоянная
- μ 0 — магнитная постоянная
- e это элементарный заряд
- х — приведенная постоянная Планка, 1,054571817 10 -34 м 2 кг с -1 . При учете дифференциала информативности по верхней границе счета этот термин не выделяется курсивом (т. е. ħ=1,0545349844(45) -34 м 2 кг с -1 ).
- α f -1 является основной формой обратной постоянной тонкой структуры, определенной относительно Целевого Кадра.

- α p -1 – планковская форма обратной постоянной тонкой структуры, определяемой относительно системы измерений.
- α c -1 — это классическая форма обратной постоянной тонкой структуры, принятая коллаборацией CODATA. Этот термин учитывает сокращение длины, связанное с дискретной мерой.
- γ — это набор терминов, описывающих геометрию между целевой и измерительной рамками.
- k e — постоянная Кулона.
Расчеты
Экспериментальная поддержка
[3] NIST: CODATA Рекомендуемые значения фундаментальных физических констант: 2018 г. (май 2019 г.), https://physics. nist.gov/cuu/pdf/wall_2018.pdf, doi:10.1103/RevModPhys.93.025010.
nist.gov/cuu/pdf/wall_2018.pdf, doi:10.1103/RevModPhys.93.025010.
Обсуждение
Мы обнаружили, что постоянная Кулона является продолжением электрической постоянной. По сравнению с обратной величиной электрической постоянной мы берем ее произведение с корреляцией материи/волны, исключая это измерение, и получаем постоянную Кулона. Эффект подобен делению длины на время и умножению на массу, чтобы перейти от описания скорости света к описанию планковского импульса. Таким же образом в каждом примере определяется граница измерения относительно расположения измерений.
С другой стороны, значение константы Кулона как физически значимого дескриптора вместе с дескрипторами компонентов является скорее вопросом удобства, чем физической значимости. Мы быстро пройдемся по вычислениям, отсылая читателя к статьям о системах отсчета, дифференциале информативности , постоянной тонкой структуры и электрической постоянной, чтобы распутать большее значение тех составных членов, которые составляют постоянную Кулона. Мы также воздержимся от типичных длинных объяснений того, как определяются эти классические понятия, исходя из понимания того, что содержание вспомогательных статей доступно при необходимости.
Мы также воздержимся от типичных длинных объяснений того, как определяются эти классические понятия, исходя из понимания того, что содержание вспомогательных статей доступно при необходимости.
Таким образом, там, где есть три физически значимых системы отсчета – эталонная, измерительная и целевая – мы берем разницу между измерительной и целевой рамкой для разрешения метрического дифференциала .
Нам также потребуется учитывать сокращение длины, связанное с дискретной мерой, описываемое дифференциалом информативности . Эффект представляет собой свойство меры, чувствительное к расстоянию, описанное в нескольких опубликованных статьях [1-6]. Хотя эта разница в счете является результатом теоремы Пифагора, счет n L of l f , связанные с излучением черного тела, должны быть решены заранее. Мы распознаем этот счет как разграничение черного тела .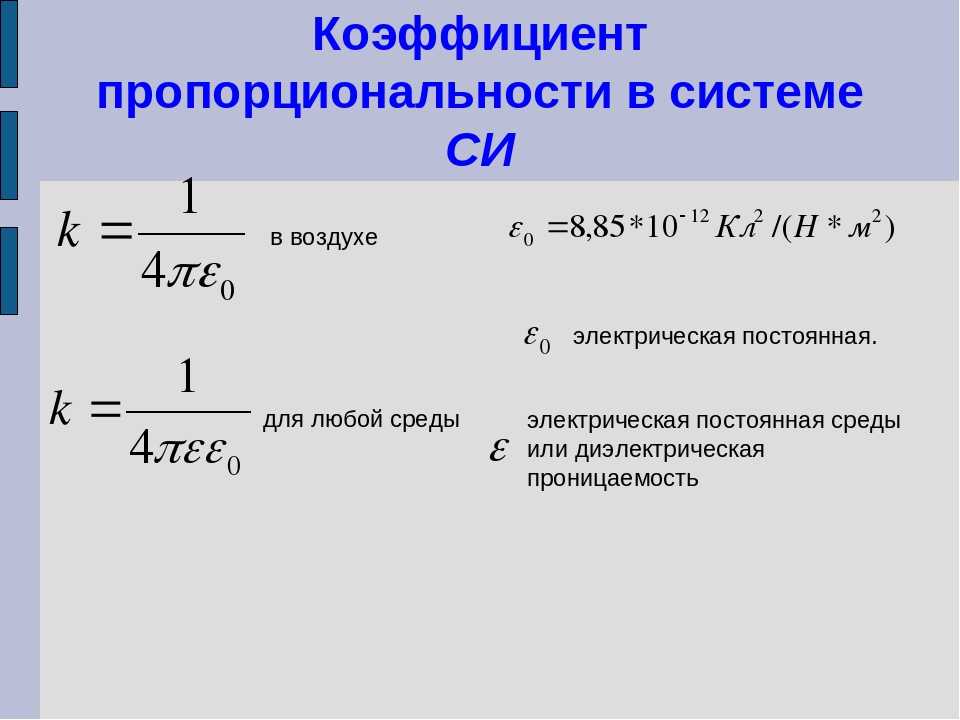
С помощью этих двух эффектов мы разрешаем дискретное выражение для обратной постоянной тонкой структуры. Мы начнем, как отмечалось ранее, с его фундаментальной формы, а затем применим метрический дифференциал , за которым следует дифференциал информативности 9.0010, чтобы разрешить выражение и значение того, что мы называем его классической формой, также описанной в макроскопической форме с любой публикацией CODATA.
Частично разрешенная форма электрической постоянной может быть затем разрешена с помощью этих выражений.
И это можно применить к типичному описанию постоянной Кулона.
И, наконец, нам потребуется дискретное описание элементарного заряда. Элементарный заряд — очень сложное явление, так как не существует известного решения как функции θ si , определенной относительно недискретной системы отсчета, ее фундаментальной формы.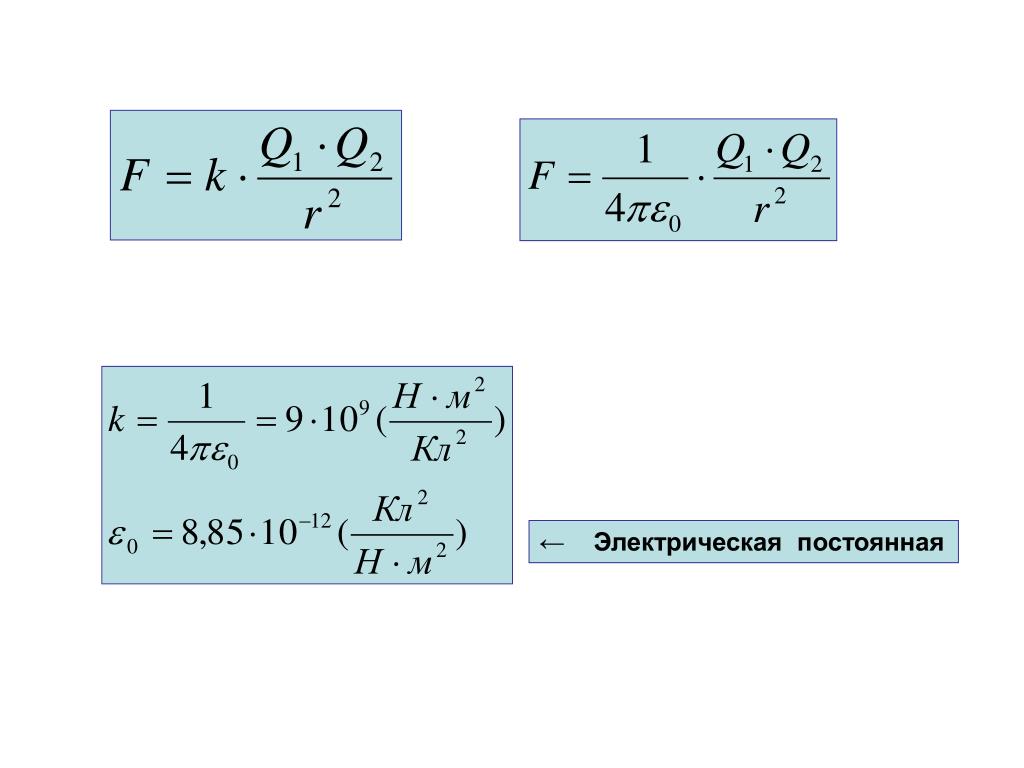


 {- 1}} (или же А2⋅s4⋅кг−1⋅м−3 в Базовые единицы СИ, или же C2⋅N−1⋅м−2 или же C ⋅V−1⋅м−1 с использованием других когерентных единиц СИ).[7][8]
{- 1}} (или же А2⋅s4⋅кг−1⋅м−3 в Базовые единицы СИ, или же C2⋅N−1⋅м−2 или же C ⋅V−1⋅м−1 с использованием других когерентных единиц СИ).[7][8]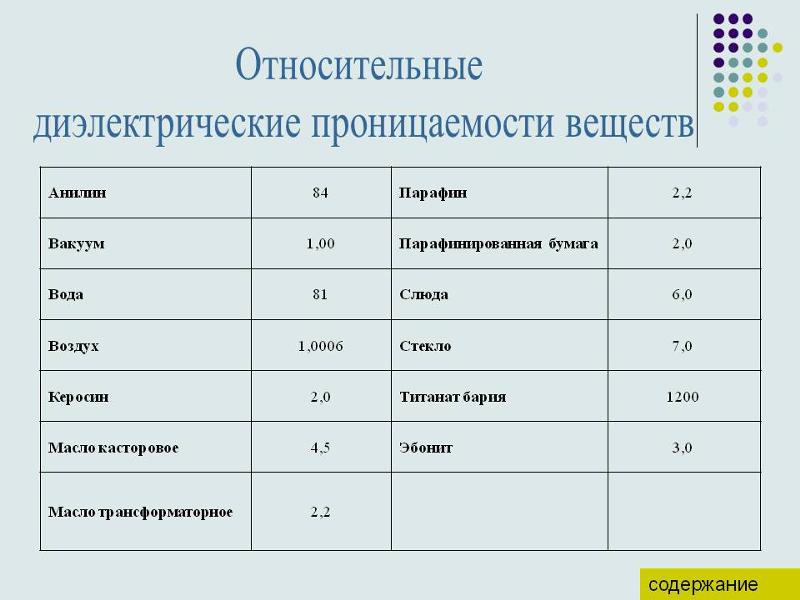 Относительная неопределенность значения ε0 поэтому такой же, как и для безразмерного постоянная тонкой структуры, а именно 1.5×10−10.[10]
Относительная неопределенность значения ε0 поэтому такой же, как и для безразмерного постоянная тонкой структуры, а именно 1.5×10−10.[10]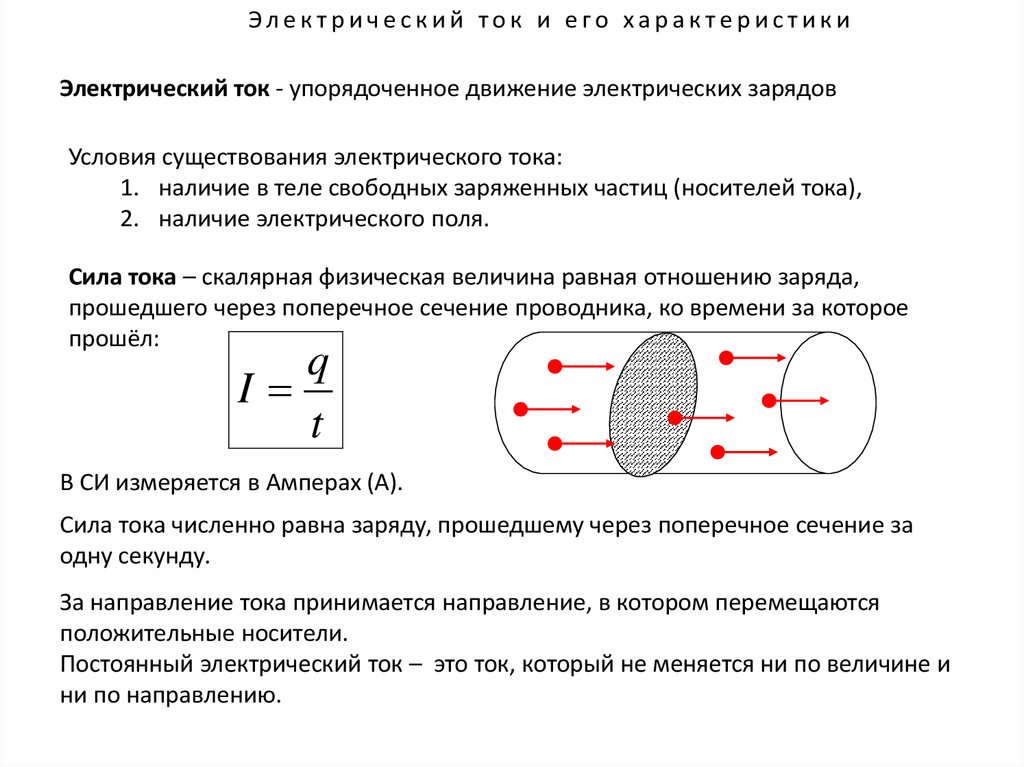
 {2}}}.}
{2}}}.}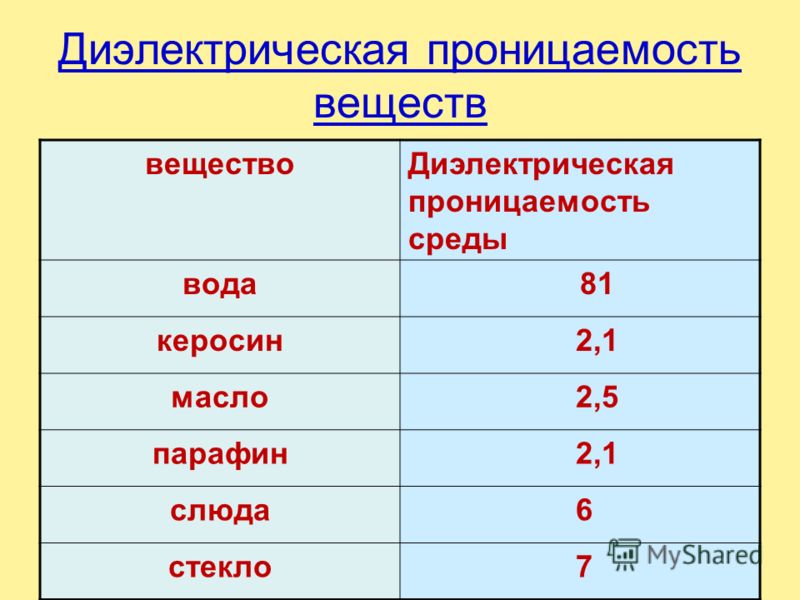
 Jenö Sólyom (2008). «Уравнение 16.1.50». Основы физики твердого тела: Электронные свойства. Springer. п. 17. ISBN 978-3-540-85315-2.
Jenö Sólyom (2008). «Уравнение 16.1.50». Основы физики твердого тела: Электронные свойства. Springer. п. 17. ISBN 978-3-540-85315-2.
 Каждое из этих веществ по-разному реагирует на электрические поля.
Каждое из этих веществ по-разному реагирует на электрические поля.

 Даже если отдельные электрические заряды могут двигаться незначительно, совокупность всех движений определяет поведение электроизоляционного материала.
Даже если отдельные электрические заряды могут двигаться незначительно, совокупность всех движений определяет поведение электроизоляционного материала. Возникающие направленные дипольные моменты, в свою очередь, создают электрическое поле, противодействующее внешнему полю. Таким образом, это противоположное поле ослабляет внешнее поле. В целом, связь между поляризацией и внешним электрическим полем сложная. Для многих веществ, так называемых линейных диэлектриков, поляризация пропорциональна полю. Применяется следующее соотношение:
Возникающие направленные дипольные моменты, в свою очередь, создают электрическое поле, противодействующее внешнему полю. Таким образом, это противоположное поле ослабляет внешнее поле. В целом, связь между поляризацией и внешним электрическим полем сложная. Для многих веществ, так называемых линейных диэлектриков, поляризация пропорциональна полю. Применяется следующее соотношение: д. (от одних факторов более сильно, от других слабее, конечно же и в зависимости от диапазона изменений каждого), и называемый (электрической) поляризуемостью (а чаще, по крайней мере для того случая, когда он выражается скаляром — диэлектрической восприимчивостью) данной среды.
д. (от одних факторов более сильно, от других слабее, конечно же и в зависимости от диапазона изменений каждого), и называемый (электрической) поляризуемостью (а чаще, по крайней мере для того случая, когда он выражается скаляром — диэлектрической восприимчивостью) данной среды. С его помощью полное электрическое поле в присутствии диэлектрика определяется следующим образом: E = D / ε = D / εr * ε0 .
С его помощью полное электрическое поле в присутствии диэлектрика определяется следующим образом: E = D / ε = D / εr * ε0 .
 Следует отметить, что в таких таблицах обычно указывается относительная проницаемость, а не сама абсолютная диэлектрическая проницаемость. Поэтому, если вы ищете таблицу для определения абсолютной диэлектрической проницаемости определенного материала, вы должны помнить, что приведенное там значение не является непосредственно той проницаемостью, которую вы ищете. Однако для заданного значения относительной проницаемости можно вычислить соответствующую абсолютную диэлектрическую проницаемость без особых дополнительных усилий. То есть нужно применять следующую уже известную нам формулу: ε = εr * ε0.
Следует отметить, что в таких таблицах обычно указывается относительная проницаемость, а не сама абсолютная диэлектрическая проницаемость. Поэтому, если вы ищете таблицу для определения абсолютной диэлектрической проницаемости определенного материала, вы должны помнить, что приведенное там значение не является непосредственно той проницаемостью, которую вы ищете. Однако для заданного значения относительной проницаемости можно вычислить соответствующую абсолютную диэлектрическую проницаемость без особых дополнительных усилий. То есть нужно применять следующую уже известную нам формулу: ε = εr * ε0. Относительная диэлектрическая проницаемость выбранных веществ
Относительная диэлектрическая проницаемость выбранных веществ — М.: Советская энциклопедия . Главный редактор А. М. Прохоров . 1988 .
— М.: Советская энциклопедия . Главный редактор А. М. Прохоров . 1988 . Электрическая постоянная Постоянная, равная в системе СИ величине, обратной произведению магнитной постоянной на квадрат скорости света в пустоте. П .р и м е ч а н и е. Электрическая постоянная приблизительно равна 8,35*4 • 10 12 Ф/м Источник … Словарь-справочник терминов нормативно-технической документации
Электрическая постоянная Постоянная, равная в системе СИ величине, обратной произведению магнитной постоянной на квадрат скорости света в пустоте. П .р и м е ч а н и е. Электрическая постоянная приблизительно равна 8,35*4 • 10 12 Ф/м Источник … Словарь-справочник терминов нормативно-технической документации electric constant; permittivity constant; permittivity of free space; permittivity of vacuum vok. dielektrische konstante, f; Dielektrizitätskonstante, f; elektrische… … Automatikos terminų žodynas
electric constant; permittivity constant; permittivity of free space; permittivity of vacuum vok. dielektrische konstante, f; Dielektrizitätskonstante, f; elektrische… … Automatikos terminų žodynas
 Так k e должны иметь единицы Н м² / C².
Так k e должны иметь единицы Н м² / C².
 Мы сказали, что такое кулоны, но как насчет ньютонов и метров? Ньютон определяется в терминах килограмма, метра и секунды, и определения всех этих единиц также изменились.
Мы сказали, что такое кулоны, но как насчет ньютонов и метров? Ньютон определяется в терминах килограмма, метра и секунды, и определения всех этих единиц также изменились.
 Но почему полные названия единиц измерения «кулон» и «ампер» не пишутся с заглавной буквы? Потому что полные названия единиц СИ , а не с большой буквы. Кроме Цельсия. C’est comme ça parce que c’est comme ça .
Но почему полные названия единиц измерения «кулон» и «ампер» не пишутся с заглавной буквы? Потому что полные названия единиц СИ , а не с большой буквы. Кроме Цельсия. C’est comme ça parce que c’est comme ça .
 Диэлектрический материал улучшает накопительную емкость конденсатора, компенсируя заряды на электродах, которые в нормальных условиях добавлялись бы к внешнему полю. Диэлектрическая проницаемость может быть выражена отношением емкости конденсатора с диэлектрическим материалом к емкости без диэлектрического материала.
Диэлектрический материал улучшает накопительную емкость конденсатора, компенсируя заряды на электродах, которые в нормальных условиях добавлялись бы к внешнему полю. Диэлектрическая проницаемость может быть выражена отношением емкости конденсатора с диэлектрическим материалом к емкости без диэлектрического материала. .
.

 В MQ мы признаем их основными единицами.
В MQ мы признаем их основными единицами.
