Уравнение по 2 закону кирхгофа

Два закона Кирхгофа вкупе с законом Ома составляют тройку законов, при помощи которых можно найти характеристики электрической цепи хоть какой трудности. Законы Кирхгофа мы будем инспектировать на примерах простых электрических схем, собрать которые не составит никакого труда. Для этого пригодится несколько резисторов, пара источников питания, в качестве которых подходят гальванические элементы (батарейки) и мультиметр.

1-ый закон Кирхгофа

1-ый закон Кирхгофа гласит, что сумма токов в любом узле электрической цепи равна нулю. Существует и другая, подобная по смыслу формулировка: сумма значений токов, входящих в узел, равна сумме значений токов, выходящих из узла.

Давайте разберем произнесенное более тщательно. Узлом именуют место соединения 3-х и поболее проводников.

Ток, который втекает в узел, обозначается стрелкой, направленной в сторону узла, а выходящий из узла ток – стрелкой, направленной в сторону от узла.

Согласно первому закону Кирхгофа

Условно присвоили символ «+» всем входящим токам, а «-» ‑ все выходящим. Хотя это не принципно.

1 закон Кирхгофа согласуется с законом сохранения энергии, так как электрические заряды не могут скапливаться в узлах, потому, поступающие к узлу заряды покидают его.

Убедиться в справедливости 1-го закона Кирхгофа нам поможет обычная схема, состоящая из источника питания, напряжением 3 В (две последовательно соединенные батарейки по 1,5 В), три резистора различного номинала: 1 кОм, 2 кОм, 3,2 кОм (можно использовать резисторы всех других номиналов). Токи будем определять мультиметром в местах, обозначенных амперметром.

Если сложить показания 3-х амперметров с учетом символов, то, согласно первому закону Кирхгофа, мы должны получить ноль:

Либо показания первого амперметра А1 будет приравниваться сумме показаний второго А2 и третьего А3 амперметров.

2-ой закон Кирхгофа

2-ой закон Кирхгофа воспринимается начинающими радиолюбителями еще труднее, ежели 1-ый. Но на данный момент вы удостоверьтесь, что он довольно прост и понятен, если разъяснять его нормальными словами, а не заумными определениями.

Упрощенно 2 закон Кирхгофа гласит: сумма ЭДС в замкнутом контуре равна сумме падений напряжений

ΣE = ΣIR

Самый обычный случай данного закона разберем на примере батарейки 1,5 В и 1-го резистора.

Так как резистор всего один и одна батарейка, то ЭДС батарейки 1,5 В будет равна падению напряжения на резисторе.

Если мы возьмем два резистора одинакового номинала и подключим к батарейке, то 1,5 В распределятся поровну на резисторах, другими словами по 0,75 В.

Если возьмем три резистора опять одинакового номинала, к примеру по 1 кОм, то падение напряжения на них будет по 0,5 В.

Формулой это будет записано следующим образом:

Разглядим условно более непростой пример. Добавим в последнюю схему очередной источник питания E2, напряжением 4,5 В.

Направьте внимание, что оба источника соединены последовательно и согласно, другими словами плюс одной батарейки соединяется с минусом другой батарейки либо напротив. При таком методе соединения гальванических частей их электродвижущие силы складываются: E1 + E2 = 1,5 + 4,5 = 6 В, а падение напряжения на каждом сопротивлении составляет по 2 В. Формулой это описывается так:

И последний отличительный вариант, который мы разглядим в данной статье, подразумевает последовательное встречное соединение гальванических частей. При таком соединении источников питания из большей ЭДС отнимается значение наименьшей ЭДС. Поэтому к резисторам R1…R3 будет приложена разница E1 – E2, другими словами 4,5 – 1,5 = 3 В, – по одному вольту на каждый резистор.

2-ой закон Кирхгофа работает не зависимо от количества источников питания и нагрузок, также независимо от места их расположения в контуре схемы. Полезно будет собрать рассмотренные схемы и выполнить надлежащие измерения при помощи мультиметра.

Законы Кирхгофа действуют как для неизменного, так и для переменного тока.

При решении задач на законы Кирхгофа лучше придерживаться определенного метода: 1. найти число неведомых токов – столько уравнений должно быть в системе ; 2. найти количество узлов – уравнений по первому закону тогда необходимо составить на одно меньше; 3. проложить контуры и записать для них уравнения по второму закону. Кто желает разобраться конкретно – есть видео .

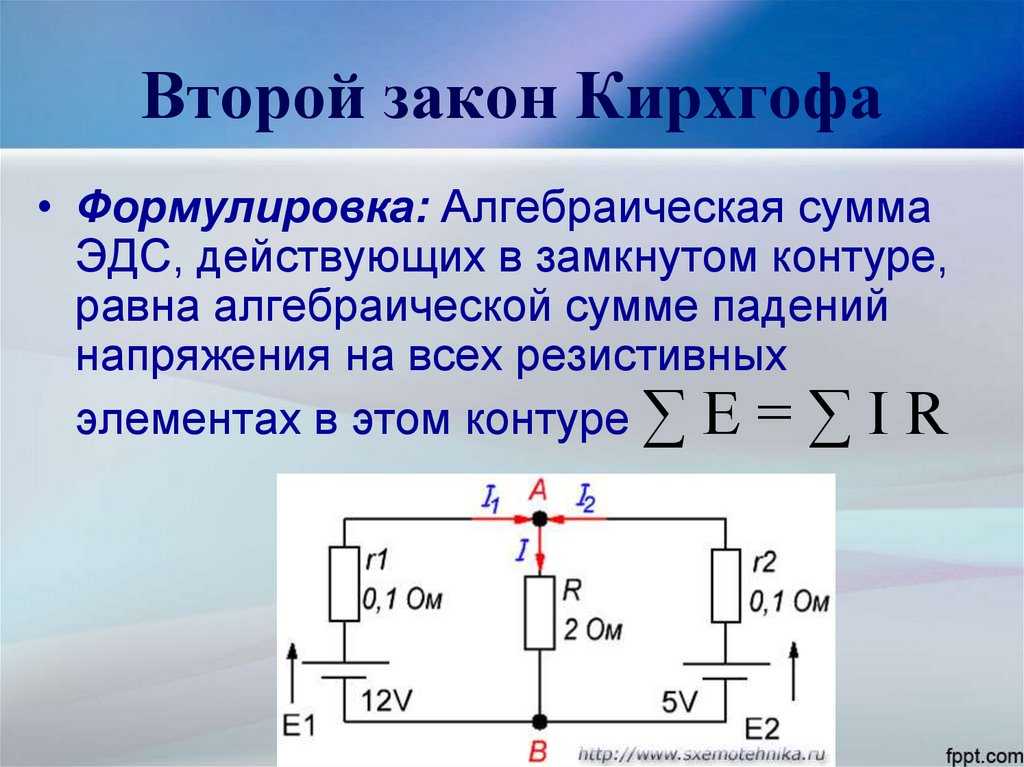
Задачка 1. Два элемента с В и В соединены по схеме, показанной на рисунке . Сопротивление Ом. Внутреннее сопротивление частей идиентично Ом. Найти силу тока, идущего через сопротивление .

Обозначим токи в ветвях произвольно. По первому закону Кирхгофа сумма токов, сходящихся в узле, равна 0:

Будем обходить верхний контур против часовой стрелки. По второму закону Кирхгофа сумма падений напряжений в контуре равна сумме ЭДС:

Будем обходить 2-ой контур по часовой стрелке:

Неведомых токов – три, мы составили три уравнения. Этого довольно, дабы отыскать токи:

Выразим из второго уравнения, а – из третьего:

Подставим эти выражения в 1-ое уравнение:

Тогда токи и

Ответ: A, A, A.
Задачка 2. Отыскать силу тока на всех участках цепи‚ если В, В‚ В, Ом‚ Ом‚ Ом‚ Ом‚ Ом, Ом.

Обозначаем токи в ветвях произвольно, избираем направления обходов контуров и сами контуры. Составляем систему уравнений. Поначалу составим уравнение по первому закону Кирхгофа – у нас два узла, потому уравнение будет одно.

Потом, обходя контуры, составим два уравнения по второму закону: их необходимо составить два, так как неведомых токов в цепи три.

Решаем систему и находим ответ (я решала при помощи он-лайн калькулятора): , , .

Ответ: , , .

Задачка 3. В схеме, показанной на рисунке, отыскать силу тока через гальванометр, если В, кОм; В, кОм. Сопротивлением гальванометра пренебречь.

Нам непонятно сопротивление гальванометра, запишем для напряжения на нем два уравнения:

Заметим, что, если , то равенство будет выполнено. Таким макаром, ток через гальванометр не течет.

Ответ: .

Задачка 4. В цепи В‚ В, Ом, Ом. Отыскать рассредотачивание токов в цепи. Внутреннее сопротивление источников тока не учесть.

Обозначаем токи в ветвях произвольно, избираем направления обходов контуров и сами контуры. Составляем систему уравнений. Поначалу составим уравнение по первому закону Кирхгофа – у нас три узла, потому уравнений будет два. Потом, обходя контуры, составим три уравнения по второму закону: их необходимо составить конкретно три, так как неведомых токов в цепи 6.

Решаем систему и находим ответ (я решала при помощи он-лайн калькулятора): , , , , , .

Ответ: , , , , , .
Задачка 5. Какую силу тока покажет амперметр в схеме, изображенной на рисунке? Сопротивлением амперметра пренебречь.

Обозначим токи в цепи произвольно. Обозначим направления обхода контуров. Запишем систему уравнений: составим три уравнения по первому закону (на одно меньше, чем количество узлов) и три уравнения по второму закону, так как неведомых токов 6 и система должна состоять из 6 уравнений.

Дабы пользоваться калькулятором, я задала Ом и В. В конечном итоге вышло: , , , , , .

Минусы свидетельствуют о обратном направлении тока в этой ветки тому, что мы нарисовали.

Закон Кирхгофа

Содержание статьи

1. Дифференциальная форма закона Кирхгофа

2. Интегральная форма закона Кирхгофа

Закон Кирхгофа связывает между собой параметры, связанные с тепловым излучением тел. Такие как монохроматический коэффициент поглощения (поглощательная способность) ($A_{\nu ,T}$) и спектральная плотность энергетической светимости тела ($E_{\nu ,T}$). Напомню, что коэффициент $A_{\nu ,T}\ $ определяется как:

где $dW_{pad}$- элемент энергии, который падает на единичную площадку поверхности в единицу времени, $dW_{pogl}$ — элемент энергии, поглощаемый единичной площадкой поверхности в единицу времени.

Выражение, определяющее величину $E_{\nu ,T}$ имеет вид:

где $dW$- энергия теплового излучения единицы площади поверхности тела, в единицу времени при частоте, которая находится в интервале от $\nu $ до $\nu $+d$\nu $.

Дифференциальная форма закона Кирхгофа

Между вышеназванными величинами для любого непрозрачного тела существует соотношение, которое называют законом Кирхгофа. В дифференциальной форме он имеет следующий вид:

\[\frac{E_{\nu ,T}}{A_{\nu ,T}}={\varepsilon }_{\nu ,T\ }\left(3\right),\]

где ${\varepsilon }_{\nu ,T\ }$— излучательная способность абсолютно черного тела. Уравнение (3) показывает, что для любой температуры и частоты отношение излучательной способности тела к его поглощательной способности одинаково для любых тел и равно излучательной способности черного тела. ${\varepsilon }_{\nu ,T\ }={\varepsilon }_{\nu ,T\ }(\nu ,T)$ — функция частоты и температуры ее еще называют функцией Киргхофа.

Из закона Кирхгофа следует, что если в данном интервале частот $A_{\nu ,T}=0$, то есть тело не поглощает излучение, то $E_{\nu ,T}=0$, то есть тело в этом же интервале частом не может и излучать. Чем больше тело излучает, на какой — то определенной частоте, тем больше поглощает на той же частоте.

{\infty }_0{{\varepsilon }_{\nu ,T}d\nu \ }}\ \left(9\right).\]

Степень черноты зависит от температуры, материала и состояния поверхности тела.

Поглощающая способность тел может изменяться в пределах $0{

Закону Кирхгофа подчиняется только тепловое излучение. Если излучение не подчиняется закону Кирхгофа, то оно не является тепловым.

Пример 1

Задание: Две пластины изолированы от внешней среды. Одна из пластин — абсолютно черное тело. Получите закон Кирхгофа, рассмотрев равновесное тепловое излучение.

Решение:

Итак, даны две пластины (1 и 2), пусть пластина (1) является абсолютно черным телом. Из определения коэффициента поглощение ($A_{\nu ,T}$), запишем:

\[dW_{pogl}=A_{\nu ,T}dW_{pad\ }\left(1.1\right).\]

Так как пластины находятся в состоянии равновесия, то запишем следующее:

\[dW_{pad\ }=dW_{izl\ \ }\left(1.2\right).\]

На пластину (2) падает $dW_{pad\left(2\right)}$ энергии, так как пластины находятся в состоянии равновесия, то вторая пластина получает энергии столько, сколько излучает первая пластина, запишем это:

\[dW_{pad\left(2\right)}=dW_{izl\left(1\right)\ }={\varepsilon }_{\nu ,T\ }d\nu \ \left(1.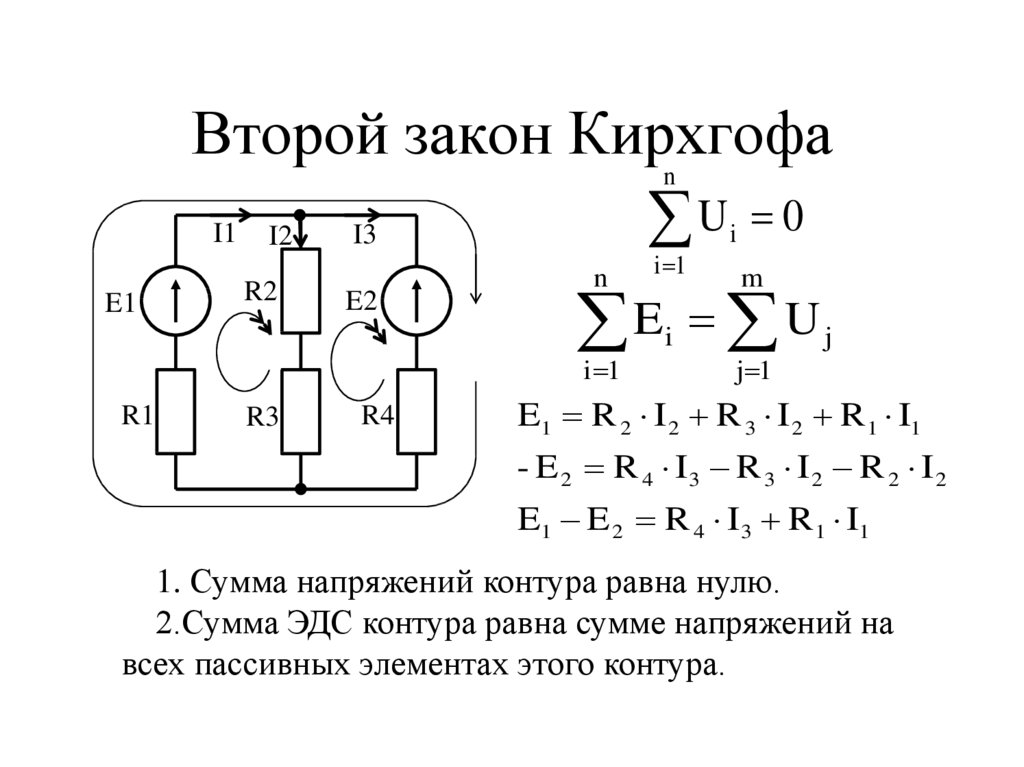

3\right),\]

где ${\varepsilon }_{\nu ,T\ }$— излучательная способность пластины 1 (абсолютно черного тела). Пластина (2) поглощает падающую на нее энергию, запишем:

\[dW_{pogl(2)}=A_{\nu ,T}dW_{pad\left(2\right)}\left(1.4\right).\]

Но мы уже установили в (1.3) чему равно $dW_{pad\left(2\right)}$, подставим в (1.4), получим:

\[dW_{pogl\left(2\right)}=A_{\nu ,T}{\varepsilon }_{\nu ,T\ }d\nu \ \ \left(1.5\right).\]

Но пластина (2) не только поглощает энергию, но и излучает, причем $dW_{izl\left(2\right)\ }$ равно:

\[dW_{izl\left(2\right)\ }=E_{\nu ,T\ }d\nu \left(1.6\right).\]

Причем пластина излучает столько же энергии, сколько ее поглощает, то есть:

\[dW_{pogl\left(2\right)}=dW_{izl\left(2\right)\ }\to A_{\nu ,T}{\varepsilon }_{\nu ,T\ }d\nu \ =E_{\nu ,T\ }d\nu (1.7)\]

Получаем из (1.7), что

\[\frac{E_{\nu ,T\ }}{A_{\nu ,T}}={\varepsilon }_{\nu ,T\ . }\]

Ответ: итак, мы показали, что отношение энергетической светимости любого тела к поглощательной способности этого же тела равно излучательной способности абсолютно черного тела при одинаковых температурах.

Пример 2

Задание: Закон Кирхгофа выполняется для монохроматического излучения. Запишите его используя интенсивность излучения $I_{\lambda }$.

Решение:

Запишем закон Кирхгофа в форме, которую уже рассматривали:

\[\frac{E_{\nu ,T}}{A_{\nu ,T}}={\varepsilon }_{\nu ,T\ }\left(2.1\right)\]

Для того, чтобы перейти к интенсивности монохроматического света закон Кирхгофа удобнее записать через излучательную способность тела, он примет вид:

\[\frac{E_{\lambda ,T}}{A_{\lambda ,T}}=\frac{I_{\lambda ,T}}{A_{\lambda ,T}}{=\varepsilon }_{\lambda ,T}=i_{\lambda ,T}\left(2.2\right)\]

$i_{\lambda ,T}$ — интенсивность излучения абсолютно черного тела, $E_{\lambda ,T}=\frac{с}{{\lambda }^2}E_{\nu ,T}$.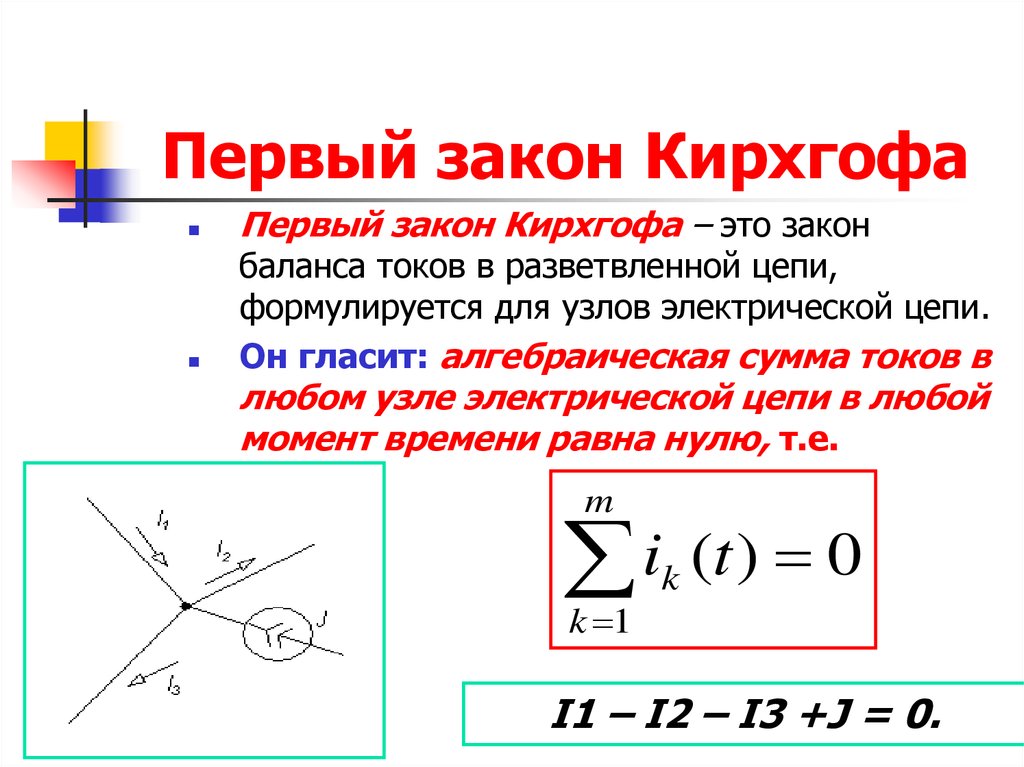

Ответ: закон Кирхгофа в требуемом виде запишется как: $\frac{E_{\lambda ,T}}{A_{\lambda ,T}}=\frac{I_{\lambda ,T}}{A_{\lambda ,T}}{=\varepsilon }_{\lambda ,T}=i_{\lambda ,T}$.

Сообщество экспертов Автор24

Автор этой статьи Дата последнего обновления статьи: 27.11.2021

Ток в замкнутой цепи закон кирхгофа

Формулировка правил

Каждое правило Кирхгофа обладает универсальными свойствами. Как первое, так и второе, хоть и не относятся к фундаментальным законам, но твёрдо обоснованы.

Определения

Прежде, чем рассматривать простые принципы и смысл решения СУ (систем уравнений), нужно определиться с применяемыми формулировками. В типологии цепей пользуются следующими понятиями:

• ветвь;
• узел;
• контур.

Всё это – элементы электрической цепи (ЭЦ).

Элементы ЭЦ

Часть электроцепи, через которую проходит электричество одной и той же величины, называется ветвью. Место, в котором соединяются три и более ветви, именуют узлом. Обычно на схемах узлы обозначаются крупными точками. Контуром называется путь, по которому протекает электрический ток, проходя через несколько участков ЭЦ, включающих в себя узлы и ветви.

Важно! Ток (I), выходя из одной точки контура и единожды проходя по разветвлениям и узлам, должен обязательно вернуться в начало. Контур – это замкнутая цепь

Узлы и ветви, подлежащие изучаемому в определённый момент контуру, могут входить в состав других контуров: являться общими для нескольких замкнутых ЭЦ одновременно.

Первое правило

Первая закономерность Кирхгофа звучит так: «Сумма всех токов в узлах ЭЦ равна нулю». Если придать направление токам, текущим сквозь пересечения проводников, имеющих общий контакт (узел), то можно промаркировать стрелками, указывающими на узел, втекающие токи. Стрелками, имеющими направленность от узла, удобно отмечать вытекающие токи:

I1 + I2 – I3 – I4 – I5 = 0

Изображение направления движения электричества

Условно считая, что входящие I имеют плюсовой знак, а выходящие – минусовой, можно перефразировать утверждение.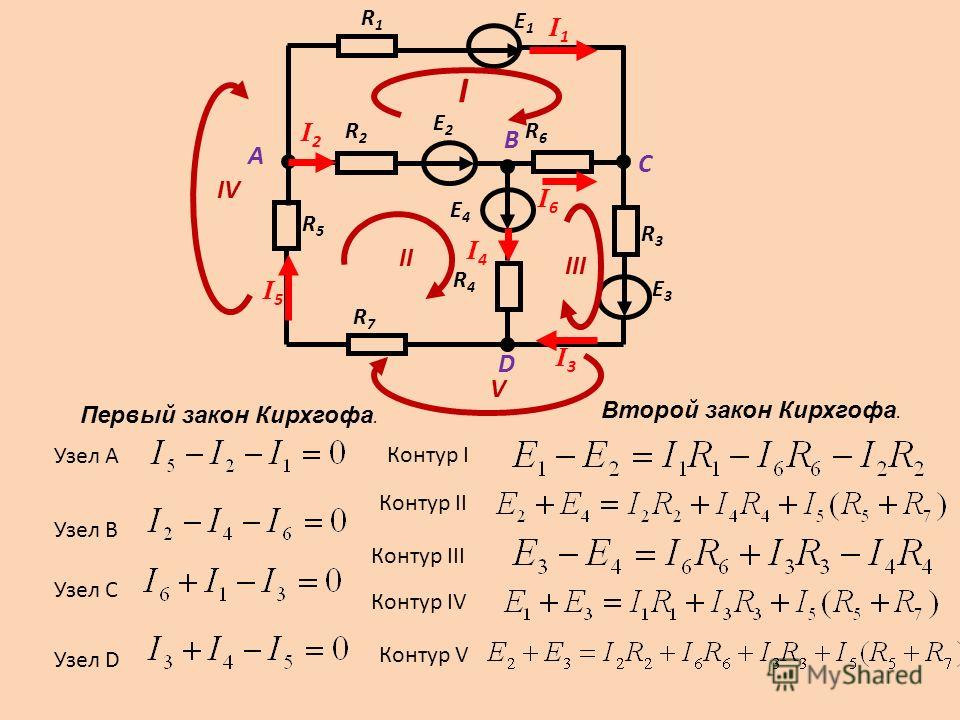 Согласно закону сохранения заряда, алгебраические суммы входящих в узел и выходящих из него I по значению равны.

Первый закон

Убедиться в истинности первого правила можно, собрав смешанную схему включения резисторов, в качестве нагрузки, для источника питания U = 3 В.

Включенные в ветви амперметры позволяют визуально зафиксировать значения токов, входящих и выходящих из первого узла. Их алгебраическая сумма (учитывая знаки) будет равна нулю.

Схема цепи с установкой амперметров

Второе правило

Его называют правилом напряжений, оно утверждает, что сумма всех E (ЭДС), входящих в контур, равняется сумме падений напряжений на резистивных элементах, при условии, что контур замкнутый:

ΣE = ΣI*R.

Например, для цепи с элементом питания и резистором напряжение на резисторе U = I*R будет равно ЭДС батарейки. По второму определению Кирхгофа выражение будет иметь вид:

E = I*R.

Схема с одной ЭДС и одним резистором

По аналогии, если количество резисторов увеличить, то падение напряжения на них распределится так, что в сумме они сравняются со значением ЭДС источника питания:

E = I*R1 + I*R2 + I*R.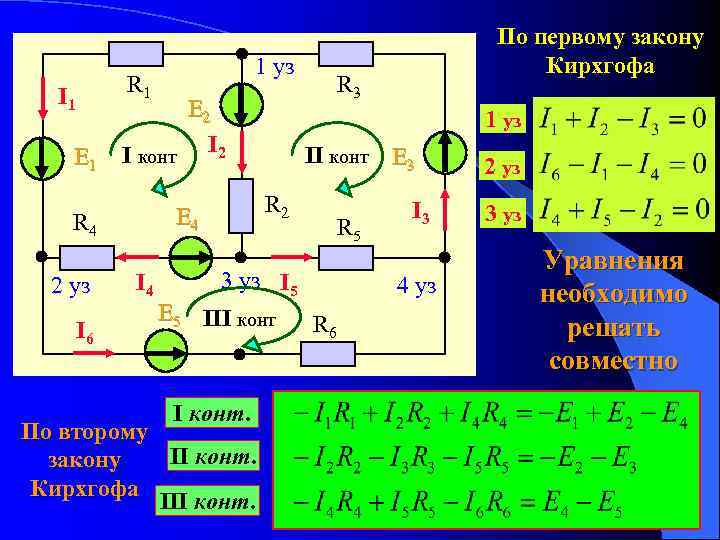

Включение одной ЭДС и трёх резисторов одного номинала

Объяснение было бы не полным, если не рассмотреть схему с несколькими ЭДС, входящими в контур. В этом случае выражать равенство следует следующим образом:

E1 + E2 = I*R1 + I*R2 + I*R3.

К сведению. При подключении нескольких источников в один контур необходимо соблюдать полярность, выполняя последовательное соединение плюса одного источника с минусом другого, таким образом, значения ЭДС будут суммироваться.

Включение двух источников в контур

История

Пополнил ряды немецких ученых Кирхгоф в девятнадцатом столетии, когда в стране, находившаяся на пороге революции индустриальной, требовались новейших технологии. Ученые занимались поиском решений, которые могли бы ускорить развитие промышленности.

Активно занимались исследованиями в области электричества, поскольку понимали, что в будущем оно будет широко использоваться. Проблема состояла на тот момент не в том, как составлять электрические цепи из возможных элементов, а в проведении математических вычислений. Тут и появились законы, сформулированные физиком. Они очень помогли.

К узлу подходят 2 провода, а отходит один. Значение тока, текущего от узла, такое же, как сумма его, протекающего по двум остальным проводникам, т.е. идущим к нему. Правило Кирхгофа объясняет, что, при ином раскладе, накапливался бы заряд, но такого не бывает. Все знают, что всякую сложную цепь легко разделить на отдельные участки.

Но, при этом непросто определить путь, по которому он проходит. Тем более, что на различных участках сопротивления не одинаковы, поэтому и распределение энергии не будет равномерным.

В соответствие со Вторым правилом Кирхгофа, энергия электронов на каждом из замкнутых участков электрической цепи равняется нулю – нулю равняется всегда в таком контуре суммарное значение напряжений. Если бы нарушилось данное правило, энергия электронов при прохождении определенных участков, уменьшалась бы или увеличивалась. Но, этого не наблюдается.

Применение

Рекомендуем:

• Частотный преобразователь для однофазного электродвигателя
• Электродвигатели асинхронные трехфазные, их достоинства, технические характеристики, виды, особенности
• Сила тока в цепи: как ее определить?

Формула Первого закона такова:

Для схемы, приведенной ниже, справедливо:

I1 — I2 + I3 — I4 + I5 = 0

Плюсовые — это токи, идущие к точке, а те, что выходят из нее «-».

Записывается это так:

• k — количество ЭДС источников;
• m – ветви замкнутого контура;
• Ii,Ri – их сопротивление i-й и ток.

В данной схеме: Е1 — Е2 + Е3 = I1R1 — I2R2 + I3R3 — I4R4.

• ЭДС принимается «+» при совпадении ее направления с выбранным направлением обхода.
• При совпадении направления тока и обхода на резисторе, с плюсом будет также напряжение.

Основы электротехники и электроники: Курс лекций , страница 3

При свертке параллельных ветвей эквивалентное сопротивление всегда меньше наименьшего из сворачиваемых.

Если параллельно соединены n

одинаковых сопротивлений (Рис. 3.3 ), эквивалентное сопротивление вn раз меньше сопротивления любой из ветвей.

Если на участке цепи параллельно соединены лишь два элемента (Рис. 3.4

), выражение (3.2) упрощается. В этом случае эквивалентное сопротивление можно определить как отношение произведения двух сопротивлений к их сумме:

4. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

К основным законам электрических цепей относятся закон Ома и законы Кирхгофа.

Закон Ома

Если в ветви не содержится ЭДС, к ней применим уже известный закон Ома для пассивного участка цепи (1.1). Его можно сформулировать и следующим образом. Ток в ветви, не содержащей ЭДС, равен падению напряжения в ветви, деленному на сопротивление ветви (Рис. 4.1

):

Закон Ома для ветви, содержащей ЭДС, позволяет найти ток этой ветви по известной разности потенциалов на концах ветви. Ток в ветви, содержащей ЭДС, равен дроби, знаменатель которой – это сопротивление ветви. В числителе дроби – напряжение на концах ветви плюс алгебраическая сумма ЭДС, заключенных между концами ветви. С плюсом берутся напряжения и ЭДС, направление которых совпадает с направлением тока, с минусом – противоположные.

Другие работы

Кирхгоф массу времени посвятил разным отраслям науки. К примеру, нашёл ошибку в постановке граничных условий для решения дифференциальных уравнений по колебаниям мембран, представленных на суд публики в 1811 году Софи Жермен.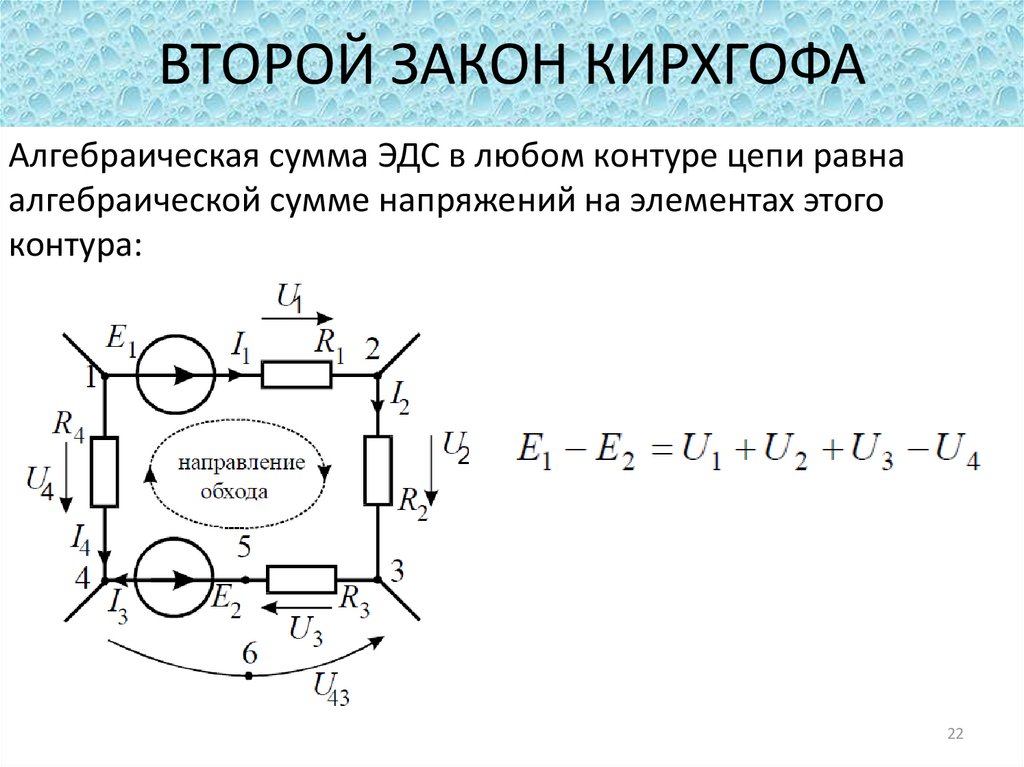 Не нужно думать, что словосочетание закон Кирхгофа узко ограничено двумя правилами, причём одно прямо приводит к сформулированному ранее закону Ома.

Учёный Г.Кирхгоф

Учёный представлен для получения звания члена-корреспондента Берлинской Академии наук в отделении математики, корреспондента Петербургской Академии наук. Если в первом случае заявители в основном указывали на дар в решении задач механики, наши соотечественники (Ленц и Якоби) немало отметили заслуги Кирхгофа в спектральном анализе.

Учёный преподавал, обладал феноменальной памятью, назубок читал длинные лекции без отступлений от формального текста. Чувство скрупулёзности помогало безукоризненно собирать материалы, и лишь недостаток технической оснастки помешал, вероятно, сделать новые открытия. К примеру, учёный отмечал, что одна из линий спектра кальция совпадает с железом, но не сумел достоверно сказать, кажущееся ли совпадение. Теперь известно, что длины волн отличаются на 5-6 ангстремов, но тогда на глаз сказать оказалось невозможно с полной уверенностью.

Алгебраическая сумма разностей потенциалов

Закон напряжения по Густаву Кирхгофу – второй закон этого автора, используемый для анализа электрической цепи. Второй закон Кирхгофа гласит, что для последовательной замкнутой цепи алгебраическая сумма всех напряжений в круге любой замкнутой цепи равна нулю. Претензия связана с тем, что петля петли представляет собой замкнутый токопроводящий путь, где потери энергии исключены. Другими словами, алгебраическая сумма разностей потенциалов замкнутого контура теоретически равна нулю:

V = 0

Примечание. Термин «алгебраическая сумма» означает учет полярностей и знаков источников ЭДС, а также падения напряжения в цепи. Эта концепция закона Кирхгофа, известного как «сохранение энергии», как движение по контуру или замкнутому контуру, подтверждает логику возврата к началу цепи и к исходному потенциалу без потери напряжения во всей цепи.

Итак, вывод следует: при применении второго закона Кирхгофа к определенному элементу электрической цепи важно обращать особое внимание на алгебраические признаки падений напряжения на элементах (источниках ЭДС), иначе расчеты обернутся ошибкой

Одиночный контурный элемент — резистор

В качестве простого примера с резистором предположим, что ток течет в том же направлении, что и поток положительного заряда. В этом случае ток протекает через резистор от точки A к точке B. Действительно, от положительной клеммы к отрицательной. Следовательно, поскольку движение положительного заряда отмечается в направлении, аналогичном направлению протекания тока, на резистивном элементе будет зафиксировано падение потенциала, что приведет к падению отрицательного потенциала на резисторе (- I * R).

Если ток, протекающий из точки B в точку A, течет в направлении, противоположном потоку положительного заряда, вы заметите увеличение потенциала через резистивный элемент, поскольку происходит переход от отрицательного потенциала к положительному потенциалу, что дает падение напряжения. (+ I * R). Следовательно, чтобы правильно применить закон Кирхгофа к электрической цепи, необходимо точно определить направление полярности. Очевидно, знак падения напряжения на резисторе зависит от направления тока, протекающего через резистор.

Направление протекания тока в замкнутом контуре можно определять по или против часовой стрелки, и любой вариант допустим на выбор. Если выбранное направление отличается от фактического направления тока, соблюдение закона Кирхгофа будет правильным и действительным, но приведет к результату, когда алгебраический расчет имеет знак минус. Чтобы лучше понять эту концепцию, логично рассмотреть еще один пример с петлевой петлей на соответствие второму закону Кирхгофа.

Одиночный контур электрической цепи

Второй закон Кирхгофа гласит, что алгебраическая сумма разностей потенциалов каждого замкнутого контура равна нулю. Демонстрационная схема действия Второго закона Кирхгофа для замкнутой цепи с двумя резисторами и источником ЭДС. Если принять условие, что два резистора R1 и R2 соединены последовательно, оба элемента являются частью одной цепи. В результате через каждый из резисторов протекает одинаковый ток.

Таким образом, падение напряжения на резисторе R1 = I * R1 и падение напряжения на резисторе R2 = I * R2 дают напряжение согласно второму закону Кирхгофа:

V = I * Rs

где: Rs = R1 + R2.

Очевидно, что применение второго закона Кирхгофа к одиночному замкнутому контуру дает формулу для эквивалента или импеданса для последовательной цепи. Допускается расширить эту формулу для нахождения значений капель потенциала по контурной окружности:

I = V / Rs

Vr1 = V * (R1 / R1 + R2)

Vr2 = V * (R2 / R1 + R2)

Есть три резистора с номинальным сопротивлением 10, 20, 30 Ом соответственно. Все три резистивных элемента соединены последовательно с батареей на 12 вольт.

Необходимо рассчитать:

• полное сопротивление,
• ток цепи,
• ток через каждый резистор,
• падение напряжения на каждом резисторе.

Рассчитываем полное сопротивление:

Ro = R1 + R2 + R3 = 10 Ом + 20 Ом + 30 Ом = 60 Ом

Ток цепи:

I = V / Ro = 12/60 = 0,2 А (200 мА)

Ток через каждый резистор:

I * R1 = I * R2 = I * R3 = 0,2 А (200 мА)

Потенциальное падение на каждом из резисторов:

VR1 = I * R1 = 0,2 * 10 = 2 В

VR2 = I * R2 = 0,2 * 20 = 4 В

VR3 = I * R3 = 0,2 * 30 = 6 В

Таким образом, действует Второй закон Кирхгофа, поскольку отдельные падения напряжения, обнаруживаемые по окружности замкнутого контура, в конечном итоге являются суммой напряжений.

Законы Кирхгофа для расчёта электрических цепей

При расчёте электрических цепей, в том числе для целей моделирования, широко применяются законы Кирхгофа, позволяющие полностью определить режим её работы.

Воспользуйтесь программой онлайн-расчёта электрических цепей.

Прежде чем перейти к самим законам Кирхгофа, дадим определение ветвей и узлов электрической цепи.

Ветвью электрической цепи называется такой её участок, который состоит только из последовательно включённых источников ЭДС и сопротивлений, вдоль которого протекает один и тот же ток. Узлом электрической цепи называется место (точка) соединения трёх и более ветвей. При обходе по соединённым в узлах ветвям можно получить замкнутый контур электрической цепи. Каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел в рассматриваемом контуре встречается не более одного раза .

Первый закон Кирхгофа

Первый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов в узле равна нулю:

∑i = 0,

или в комплексной форме

∑I = 0.

Второй закон Кирхгофа

Второй закон Кирхгофа применяется к контурам электрической цепи и формулируется следующим образом: в любом замкнутом контуре алгебраическая сумма напряжений на сопротивлениях, входящих в этот контур, равна алгебраической сумме ЭДС:

∑Z ∙ I = ∑E.

Количество уравнений, составляемых для электрической цепи по первому закону Кирхгофа, равно Nу – 1, где Nу – число узлов. Количество уравнений, составляемой для электрической цепи по второму закону Кирхгофа, равно Nв – Nу + 1, где Nв – число ветвей. Количество составляемых уравнений по второму закону Кирхгофа легко определить по виду схемы: для этого достаточно посчитать число «окошек» схемы, но с одним уточнением: следует помнить, что контур с источником тока не рассматривается.

Опишем методику составления уравнений по законам Кирхгофа. Рассмотрим её на примере электрической цепи, представленной на рис. 1.

Рис. 1. Рассматриваемая электрическая цепь

Для начала необходимо задать произвольно направления токов в ветвях и задать направления обхода контуров (рис. 2).

Рис. 2. Задание направления токов и направления обхода контуров для электрической цепи

Количество уравнений, составляемых по первому закону Кирхгофа, в данном случае равно 5 – 1 = 4. Количество уравнений, составляемых по второму закону Кирхгофа, равно 3, хотя «окошек» в данном случае 4. Но напомним, что «окошко», содержащее источник тока J1, не рассматривается.

Составим уравнения по первому закону Кирхгофа. Для этого «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» — со знаком «-». Отсюда для узла «1 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:

I1 – I2 – I3 = 0;

для узла «2 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:

—I1 – I4 + I6 = 0;

для узла «3 у.»:

I2 + I4 + I5 – I7 = 0;

для узла «4 у.»:

I3 – I5 – J1 = 0

Уравнение для узла «5 у.» можно не составлять.

Составим уравнения по второму закону Кирхгофа. В этих уравнениях положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура. Для контура «1 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:

ZC1 ∙ I1 + R2 ∙ I2 – ZL1 ∙ I4 = E1;

для контура «2 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:

-R2 ∙ I2 + R4 ∙ I3 + ZC2 ∙ I5 = E2;

для контура «3 к.»:

ZL1 ∙ I4 + (ZL2 + R1) ∙ I6 + R3 ∙ I7 = E3,

где ZC = — 1/(ωC), ZL = ωL.

Таким образом, для того, чтобы найти искомые токи, необходимо решить следующую систему уравнений:

В данном случае это система из 7 уравнений с 7 неизвестными. Для решения данной системы уравнений удобно пользоваться Matlab. Для этого представим эту систему уравнений в матричной форме:

Для решения данной системы уравнений воспользуемся следующим скриптом Matlab:

>> syms R1 R2 R3 R4 Zc1 Zc2 Zl1 Zl2 J1 E1 E2 E3; >> A = ; >> b = ; >> I = A\b

В результате получим вектор-столбец I токов из семи элементов, состоящий из искомых токов, записанный в общем виде. Видим, что программный комплекс Matlab позволяет существенно упростить решение сложных систем уравнений, составленных по законам Кирхгофа.

Список использованной литературы

1. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.

Рекомендуемые записи

• Метод контурных токов для расчёта электрических цепей При расчёте электрических цепей, помимо законов Кирхгофа, часто применяют метод контурных токов. Метод контурных токов…
• Метод фазных координат: пример расчёта матрицы передачи Расчёт матриц передачи многополюсников различной формы осуществляется достаточно просто. Матрицы передачи — это математическое описание рассматриваемой…

Первый закон Кирхгофа для тока

Также известный под другими именами, такими как Закон Кирхгофа для тока, это закон сохранения заряда. В нем просто говорится, что в любой точке или соединении в электрической цепи общая величина тока, поступающего в это соединение, равна общей величине тока, который покидает это соединение.

Предположим, что есть электрическая цепь, которая имеет точку, обозначенную на рисунке 1, показанном ниже.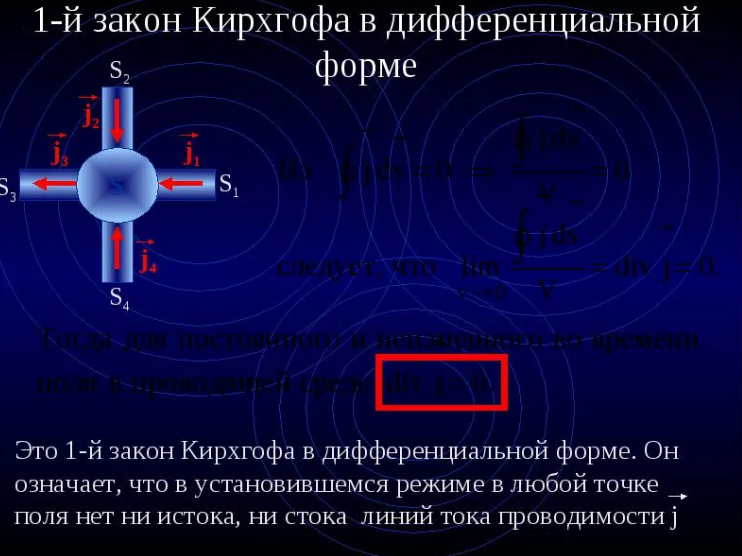 Точка соединения действует как точка встречи для четырех проводников, каждый из которых проводит ток в направлении, указанном черными наконечниками стрел. Согласно закону Кирхгофа общая сумма тока, входящего в соединение, должна быть равна току, выходящему из него. Это может быть математически представлено следующим образом

Ia = Ib + Ic + Id

Где I — ток в каждом из проводников a, b, c и d соответственно.

В этой точке также следует отметить, что конденсатор представляет собой устройство, которое используется для накопления заряда в виде электростатической силы в диэлектрическом материале, окруженном пластинами проводника с обеих сторон. Есть некоторые исключения из первого правила Кирхгофа, если конденсатор присутствовал в каком-либо из узлов, но лучше не вдаваться в такие детали на этом базовом уровне. Следовательно, для всех практических целей в других ситуациях применяется закон Кирхгофа.

Первый закон Кирхгофа — применение

Чтобы продемонстрировать, как правильно применять первый закон Кирхгофа, мы будем использовать простой пример.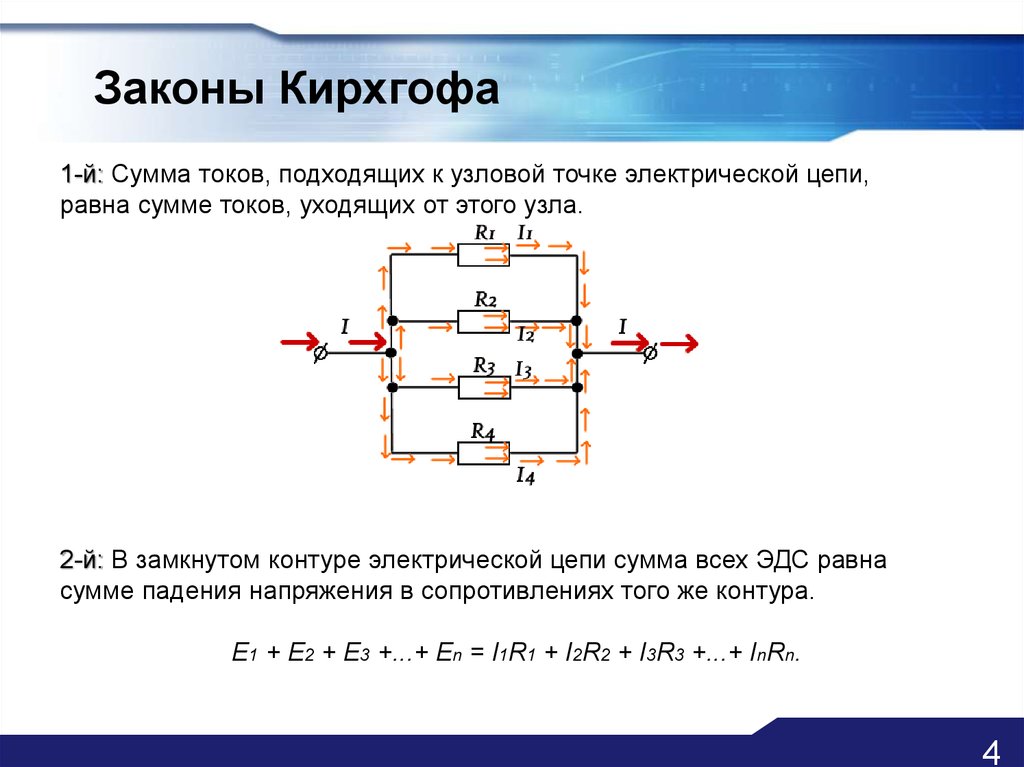 На рисунке ниже показана электрическая цепь, состоящая из превосходного источника электродвижущей силы и двух резисторов с сопротивлениями R₁ и R₂.

Ток интенсивности I, исходящий из источника ЭДС, имеет то же значение в левой ветви (BAD), ток I 1 — в средней ветви (BD), а ток I 2 — в правой ветви (BCD)

Сосредоточим внимание на узле B: электрический заряд поступает в этот узел от источника ЭДС вместе с током I и течет с токами I 1 и I 2 , протекающими через резисторы R 1 и R 2соответственно, Общий заряд в узле B не изменяется, поэтому в соответствии с первым законом Кирхгофа сумма токов, протекающих в этот узел, должна быть равна сумме токов, протекающих из этого узла, которые мы можем записать так:. Точно такое же выражение, как и выше для узла B, получаем узел D

В узел D влияют токи I 1 и I 2 , и ток протекает с интенсивностью I, являющейся суммой этих двух токов:

Точно такое же выражение, как и выше для узла B, получаем узел D. В узел D влияют токи I ₁ и I ₂ , и ток протекает с интенсивностью I, являющейся суммой этих двух токов:

чтобы вычислить, сколько стоят значения этих токов, мы будем использовать второй закон Кирхгофа.

Законы Киргофа для электрических цепей

1. Первый закон Киргофа гласит, что алгебраическая сумма токов в узле цепи равна нулю. Исходящие токи берутся при вычислениях с отрицательным знаком, входящие – с положительным. Хотя в русскоязычной литературе говорится, что допустимо наоборот. Суть неизменна.
2. Второй закон Киргофа формулируется для замкнутых контуров. Утверждает, что сумма падений напряжений при обходе по кругу равна всем встречающимся на пути ЭДС. Причём контуры любой цепи нужно обходить в едином направлении: по или против часовой стрелки.

Первое уравнение не нуждается в пояснении. Порой сложно понять, в каком направлении течёт ток, с отрицательным или положительным знаком требуется подставить в формулу. Рекомендуется помнить: количество уравнений на единицу меньше, нежели узлов. Если присутствуют сомнения по точке, допустимо исключить её из рассмотрения. В прочих ситуациях анализируется знак разницы потенциалов на концах проблемного участка. Для этого складываются или вычитаются действующие здесь источники питания (в задачках по физике – батарейки).

По общепринятым нормам более длинная черта в графическом обозначении аккумулятора считается положительным полюсом. Ток вытекает отсюда по правилам, принятым в физике, хотя на практике все происходит наоборот – движение образовано отрицательно заряженными электронами. Если ЭДС действуют на участке в разных направлениях, они вычитаются, а направление тока задаётся наибольшей.

Что касается второго закона, знак вхождения в формулу падения напряжения на установленном участке определяется направлением протекания тока. ЭДС берутся с противоположным знаком, либо стоят по другую сторону равенства. Как указано выше, ячейки нужно обходить в одном направлении. Не смущайтесь, что в формулах над напряжением и током стоит точка. Это знак комплексного числа.

Обратите внимание – дана упрощённая запись второго закона. Здесь все ЭДС берутся с обратным реально присутствующему на рисунке знаком

Известна иная форма записи, где падения напряжения отделены от ЭДС знаком равенства. Тогда знаки менять не нужно. Последняя форма записи даётся в школьном курсе физики и приведена на рисунке чуть ниже общей.

Правило Кирхгофа

Закон Кирхгофа для термодинамики

Кирхгоф показал, что соотношение излучательной и поглощательной способности твёрдого тела не зависит от вещества, но считается функцией частоты и температуры при термодинамическом равновесии. Особенно интересной абстракцией в этом плане стало абсолютно-чёрное тело. Это объект, поглощающий падающее на него излучение. Для него формула, представленная на рисунке упрощается. Излучающая способность абсолютно-чёрного тела описывает функцию формулы для прочих тел. Эта ипостась имеет максимум, определяемый законом смещения Вина и амплитуды, определяемую первым законом Вина (частным случаем считается формула Планка).

Отношение излучательной и поглощательной способности любого тела находится по формулам для любых температур и частот. При помощи спектрометра возможно оценить испускаемые волны. Это позволяют теоретически предсказать поглощательную способность любого предмета. На практике подобные исследования приводят к созданию объектов типа самолёт-невидимка, с трудом видимый локаторами.

Из закона сохранения энергии следует, что полное излучение равняется поглощению в термодинамическом равновесии. Значит, по всему спектру их соотношение равняется единице. До признания закона Кирхгофа уже установлено, что – чем лучше тело поглощает энергию, тем оно больше излучает

Обратите внимание, спектральные плотности поглощения и излучения имеют разную форму. В этом и заключается гениальное прозрение Кирхгофа

Взаимодействие определяется законом Вина и на графике выглядит подобно горе с вершиной, смещённой влево относительно центра фигуры.

Это позволяет понять, где находится максимум излучения (на макушке). Во всех участках графика, где линия находится ниже единицы, тело преимущественно поглощает энергию. Благодаря законам возможно предсказать температуру звёзд, к примеру, по цвету, а каждый кузнец знает, что деталь в горне дошла до кондиции лишь по характерному оттенку свечения. Это практические проявления законов Вина и Кирхгофа.

Вторым интересным наблюдением становится температура. Из графиков плотности излучения видно, чем показатель больше, тем активнее идёт излучение. В частности, звезды не поглощают энергию за малым исключением, но преимущественно излучают. У холодных планет преобладает противоположный процесс. Тело излучает, если его температура выше окружающей среды. В остальных ситуациях преобладает поглощение энергии.

Аналогия закона Кирхгофа

Формулировка правил

Определения

Для формулировки правил Кирхгофа вводятся понятия узел

,ветвь иконтур электрической цепи. Ветвью называют участок электрической цепи с одним и тем же током, например, на рис. отрезок, обозначенный R1, I1 есть ветвь. Узлом называют точку соединения трех и более ветвей (на рис. обозначены жирными точками). Контур — замкнутый путь, проходящий через несколько ветвей и узлов разветвлённой электрической цепи. Терминзамкнутый путь означает, что, начав с некоторого узла цепи иоднократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел.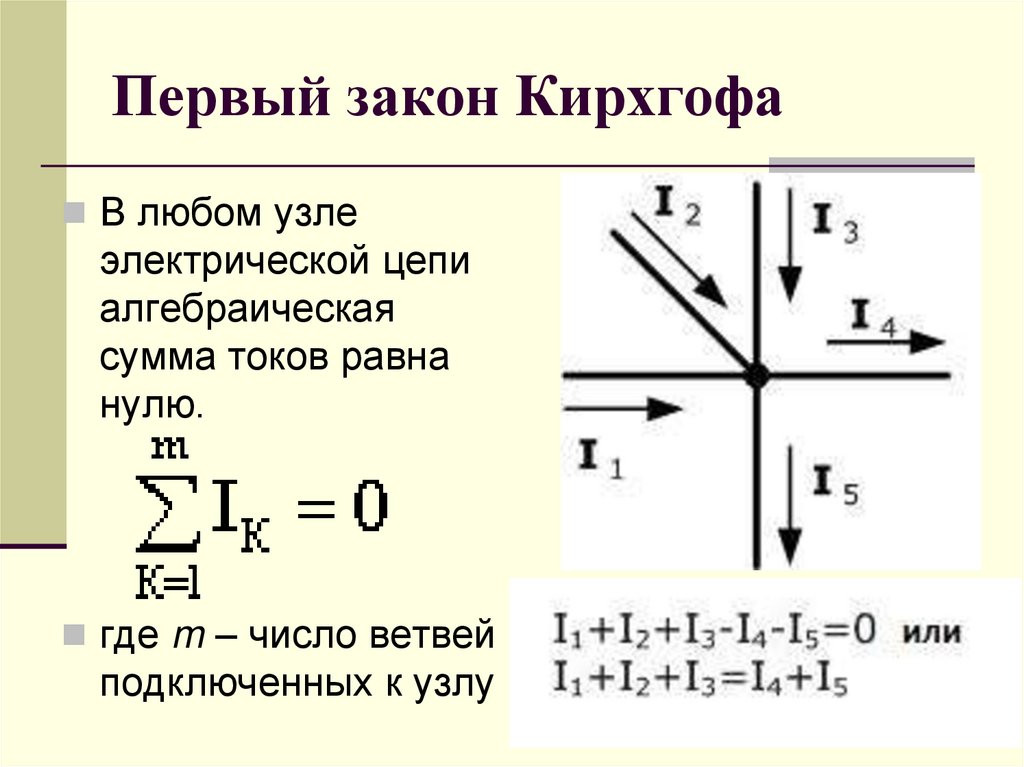 {m}u_{C\,k}.}

Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.

Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).

Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.

Закон Кирхгофа для теплового излучения

Данный закон имеет другое название «третий закон». Сперва для лучшего понимания введем понятие теплового излучения. Принято называть тепловым излучение электромагнитное излучение, возникающее благодаря чужеродной энергии вращательного и колебательного движения атомов, молекул. Данное явление можно обнаружить абсолютно у всех тел, имеющих температуру не равняющуюся нулю или меньше. Основной количественной характеристикой теплового излучения выступает энергетическая светимость. Она должна быть вычислена одной из первых или же указана в условиях. Рассчитать её самостоятельно весьма проблематично. Её значение не постоянное, оно может меняться в зависимости от определенных характеристик: оказывает влияние температура окружающей среды, а также уровень нагретости тела. Имеет значение и длина, чем длиннее — тем значение меньше.

Формула выглядит таким образом:

R = E/(S·t), [Дж/(м2с)] = [Вт/м2]

Ещё одной характеристикой остаётся спектральная плотность энергетической светимости.

Важно ввести ещё одно понятие: коэффициент поглощения – это отношение поглощенной телом энергии к падающей энергии. Только теперь перейдем непосредственно к выделенному закону

Первое, что нужно сказать, что тепловое излучение является равновесной величиной. Это указывает на то, что сколько энергии будет излучаться телом, столько и им же и поглотится. При расчётах данное заявление имеет существенное значение. Можно сразу приравнивать оба значение. Таким образом, для трёх тел, которые находятся в замкнутой полости, формула примет вид:

Закон для теплового излучения

Раннее указанная формула будет верной даже тогда, когда какое-либо тело из указанных будет АЧ:

Закон звучит данным образом: отношение спектральной плотности энергетической светимости тела к его монохроматическому коэффициенту поглощения (при определенной температуре и для определенной длины волны) не зависит от природы тела и равно для всех тел спектральной плотности энергетической светимости при тех же самых температуре и длине волны.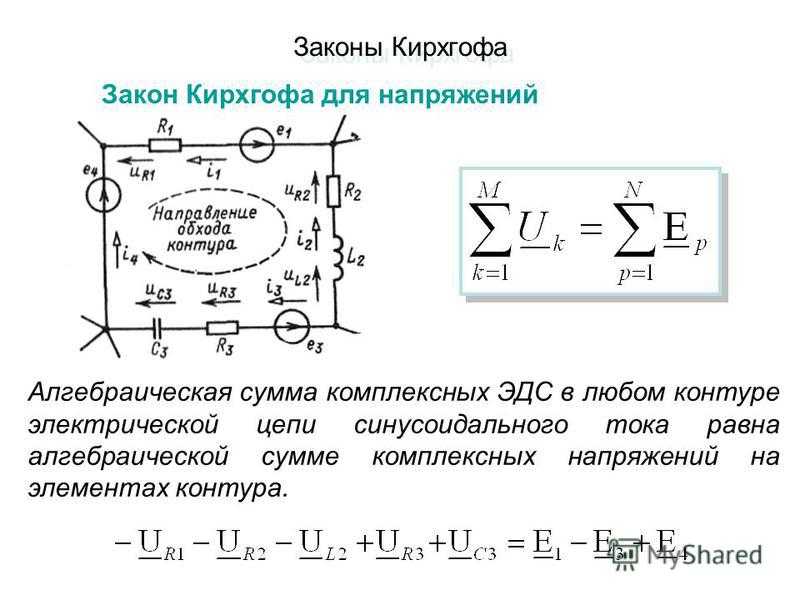

Закон Ома для участка цепи

С камушками в трубе все понятно, но не только же от них зависит сила, с которой поток воды идет по трубе — от насоса, которым мы эту воду качаем, тоже зависит. Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.

Например, источником может быть гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. В результате этих реакций выделяется энергия, которая потом передается электрической цепи.

У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения, по сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «−».

У нас уже есть две величины, от которых зависит электрический ток в цепи — напряжение и сопротивление. Кажется, пора объединять их в закон.

Сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.

Математически его можно описать вот так:

Закон Ома для участка цепи I = U/R I — сила тока U — напряжение R — сопротивление

Напряжение измеряется в Вольтах и показывает разницу между двумя точками цепи: от этой разницы зависит, насколько сильно будет течь ток — чем больше разница, тем выше напряжение и ток будет течь сильнее.

Сила тока измеряется в амперах, а подробнее о ней вы можете прочитать в нашей статье.

Давайте решим несколько задач на закон Ома для участка цепи.

Задача раз

Найти силу тока в лампочке накаливания торшера, если его включили в сеть напряжением 220 В, а сопротивление нити накаливания равно 880 Ом.

Решение:

Возьмем закон Ома для участка цепи:

I = U/R

Подставим значения:

I = 220/880 = 0,25 А

Ответ: сила тока, проходящего через лампочку, равна 0,25 А

Давайте усложним задачу. И найдем силу тока, зная все параметры для вычисления сопротивления и напряжение.

Задача два

Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а длина нити накаливания равна 0,5 м, площадь поперечного сечения 0,01 мм2, а удельное сопротивление нити равно 1,05 Ом · мм2/м.

Решение:

Сначала найдем сопротивление проводника.

R = ρ · l/S

Площадь дана в мм2, а удельное сопротивления тоже содержит мм2 в размерности.

Это значит, что все величины уже даны в СИ и перевод не требуется:

R = 1,05 · 0,5/0,01 = 52,5 Ом

Теперь возьмем закон Ома для участка цепи:

I = U/R

Подставим значения:

I = 220/52,5 ≃ 4,2 А

Ответ: сила тока, проходящего через лампочку, приблизительно равна 4,2 А

А теперь совсем усложним! Определим материал, из которого изготовлена нить накаливания.

Задача три

Из какого материала изготовлена нить накаливания лампочки, если настольная лампа включена в сеть напряжением 220 В, длина нити равна 0,5 м, площадь ее поперечного сечения равна 0,01 мм2, а сила тока в цепи — 8,8 А

Решение:

Возьмем закон Ома для участка цепи и выразим из него сопротивление:

I = U/R

R = U/I

Подставим значения и найдем сопротивление нити:

R = 220/8,8 = 25 Ом

Теперь возьмем формулу сопротивления и выразим из нее удельное сопротивление материала:

R = ρ · l/S

ρ = RS/l

Подставим значения и получим:

ρ = 25 · 0,01/0,5 = 0,5 Ом · мм2/м

Обратимся к таблице удельных сопротивлений материалов, чтобы выяснить, из какого материала сделана эта нить накаливания.

Ответ: нить накаливания сделана из константана.

Составление уравнений

При расчете электрической цепи при помощи правил Кирхгофа составляются уравнения токов. Количество уравнений находится в прямой зависимости от числа узлов в цепи. Они используются для описания физических явлений и в промышленном секторе: при изготовлении жидкостных трубопроводов и электрических насосов.

При составлении уравнения нужно руководствоваться следующим алгоритмом:

1. Выбрать направление потоков заряженных частиц на ветвях, обозначенных на электрической схеме.
2. Отобрать напряжения с одинаковым направлением обхода закрытого контура.
3. Выбрать контуры с разными ветвями и узлами для применения второго правила.

Многие физики сталкиваются с трудностями при составлении линейных уравнений для гальванической цепи, расположенной в сложных непланарных графах — математических объектах с минорами, полученными при помощи стягивания 1 ребра. В этом случае для расчета электрической цепи необходимо составить систему уравнений, где совмещены выражения как для первого, так и для второго законов Кирхгофа.

Для проверки правильности составления линейных используется потенциальная диаграмма, представляющая собой графическое изображение. Она строится для контура гальванической цепи. Если точки начала и конца диаграммы обладают идентичными потенциалами, независимыми от направления движения тока, то уравнение составлено верно.

Закон Кирхгофа о напряжении — справочник Digilent

Понимание контуров в цепи

Закон тока Кирхгофа и закон напряжения Кирхгофа являются основой для анализа схем с сосредоточенными параметрами. Эти законы вместе с вольтамперными характеристиками элементов цепи в системе дают нам возможность производить систематический анализ любой электрической сети. В этом разделе представлен закон напряжения Кирхгофа.

KVL зависит от концепции цикла. Петля — это любой замкнутый путь в цепи, который не встречается ни с одним узлом более одного раза. По сути, чтобы создать петлю, начните с любого узла в цепи и проследите путь по цепи, пока не вернетесь к исходному узлу. Понятие цикла, вероятно, проще всего объяснить с помощью нескольких простых примеров, которые мы привели ниже.

Пример 1:

• Закон напряжения Кирхгофа (обычно сокращенно KVL) гласит:

• Альтернативная формулировка этого закона:

  • Сумма повышений напряжения на замкнутом контуре должна равняться сумме падений напряжения на контуре.

• Или даже:

  • При обходе контура вы должны вернуться к тому же напряжению, с которого начали.

---

Примечание

Полярность напряжения в петле основана на предполагаемой полярности разности напряжений в петле. Пока предполагаемые направления напряжений одинаковы от петли к петле, окончательный результат анализа будет отражать фактических полярностей напряжения в цепи.

---

Пример 2:

На рисунке ниже предполагаемая полярность напряжений В ₁ , В ₂ , V ₃ , V ₄ , V ₅ и V ₆ , как показано. В схеме возможны три петли: a-b-e-d-a, a-b-c-e-d-a и b-c-e-b. Мы применим KVL к каждому из этих циклов.

Наше соглашение о знаках для применения знаков к полярностям напряжения в наших уравнениях КВЛ будет следующим: при обходе контура, если положительный вывод разности напряжений встречается перед отрицательным выводом, разность напряжений будет интерпретироваться как положительный в уравнении КВЛ. Если отрицательная клемма встречается первой, разница напряжений будет интерпретироваться как минус в уравнении KVL. Мы используем это соглашение о знаках для удобства; для правильного применения КВЛ это не требуется, лишь бы знаки разности напряжения трактовались последовательно.

Применение KVL к циклу a-b-e-d-a и использование нашего соглашения о знаках, как указано выше, приводит к следующему результату:

$${V_1} — {V_4} — {V_6} — {V_3} = 0$$

Начальная точка цикла и направление, в котором мы зацикливаемся, произвольны; мы могли бы эквивалентно написать то же уравнение цикла, что и цикл d-e-b-a-d , и в этом случае наше уравнение стало бы таким:

$${V_6} + {V_4} — {V_1} + {V_3} = 0$$

Это уравнение идентично предыдущему уравнению, с той лишь разницей, что знаки всех переменных изменились и переменные стоят в уравнении в другом порядке. Теперь мы применяем KVL к циклу b-c-e-b, что приводит к:

$$- {V_2} + {V_5} + {V_4} = 0$$

Наконец, применение КВЛ к контуру a-b-c-e-d-a обеспечивает:

$${V_1} — {V_2} + {V_5} — {V_6} — {V_3} = 0$$

---

Важный момент

Закон напряжения Кирхгофа гласит, что сумма разностей напряжений вокруг любого замкнутого контура в цепи должна быть равна нулю. Петля в цепи — это любой путь, который заканчивается в той же точке, в которой он начинается.

---

Проверьте свои знания

1. Какое напряжение V в цепи ниже?
2. Какое напряжение V в цепи ниже?
3. Какое напряжение V в цепи ниже? (Подсказка: это вопрос с подвохом.)
4. Какие напряжения В ₁ , В ₂ и В ₃ в цепи ниже?

Ответы

1. Цикл по часовой стрелке, начиная с левого нижнего угла, дает:

$$- 3В — В + 7В = 0$$

Итак, V = 4 В. (Обратите внимание, что при зацикливании мы принимаем разность напряжений как положительную, если сначала встречаемся с клеммой «+», и как отрицательную, если сначала встречаем клемму «-».

2. Цикл по часовой стрелке, начиная с левого нижнего угла, дает:

$$+ 9В — 2В + В = 0$$

Итак, V = -7В. (Обратите внимание, что при зацикливании мы принимаем разность напряжений как положительную, если сначала встречаемся с клеммой «+», и как отрицательную, если сначала встречаем клемму «-».

3. Нет значения напряжения, удовлетворяющего этой схеме. Если вы примените KVL вокруг самого левого цикла, вы получите $3V + 1V — V = 0$, поэтому $V = 4V$. KVL вокруг самого правого цикла приводит к $V + 7V = 0$, поэтому $V = — 7V$. Две петли дают противоречивые результаты!

Корень проблемы в том, что данные напряжения несовместимы с законом напряжения Кирхгофа. Если мы применим KVL вокруг самого внешнего цикла, мы получим:

$$3В + 1В + 7В = 0$$

Что строго неверно.

4. Этот ответ подробно описан в нескольких различных ситуациях в цепи:

• Нахождение V ₁ : КВЛ вокруг петли, показанной ниже, дает: ${V_1} + 1V + 7V — 3V = 0$, поэтому ${V_1} = — 5V$

• Нахождение V ₂ : KVL вокруг петли, показанной ниже, дает: ${V_2} + 7V = 0$, поэтому ${V_2} = — 7V$

• Нахождение V ₃ : KVL вокруг петли, показанной ниже, дает: ${V_3} — V3 = 0$, поэтому ${V_3} = 3V$

---

Важный момент

Вы можете проверить свои результаты, применяя КВЛ вокруг других петель в схеме. Например, цикл слева внизу дает: $3V{\rm{ + }}{V_2} + 7V — {V_3} = 0$. Подстановка значений V ₂ и V ₃ , определенных выше, дает $3V + \left( { — 7V} \right) + 7V — {\rm{3}}V = 0$, что верно!

Аналогично, цикл слева внизу дает ${V_1} + 1V — {V_2} — 3V = 0$. Подстановка значений для V 9Определенные выше 0053 1 и V ₂ дают $\left( { — 5V} \right) + {V_1} — \left( { — 7V} \right) — 3V = 0$, что тоже верно!

Для большей практики попробуйте пройтись по всему внешнему циклу в качестве еще одной проверки.

учиться, основы, схемы, квл, Кирхгоф-напряжение-закон

электричество | Определение, факты и типы

электрическая сила между двумя зарядами

См. все СМИ

Ключевые люди:

Томас Эдисон Рукс Эвелин Белл Кромптон Эдвард Уэстон Чарльз Фрэнсис Браш Флиминг Дженкин

Похожие темы:

биоэлектричество термоэлектричество электрический потенциал электролиз электрофорез

Просмотреть весь связанный контент →

Резюме

Прочтите краткий обзор этой темы

электричество , явление, связанное с неподвижными или движущимися электрическими зарядами. Электрический заряд является фундаментальным свойством материи и переносится элементарными частицами. В электричестве задействованной частицей является электрон, несущий заряд, условно обозначаемый как отрицательный. Таким образом, различные проявления электричества являются результатом накопления или движения множества электронов.

Электростатика — это изучение электромагнитных явлений, происходящих при отсутствии движущихся зарядов, т. е. после установления статического равновесия. Заряды быстро достигают своего положения равновесия, потому что электрическая сила чрезвычайно велика. Математические методы электростатики позволяют рассчитывать распределения электрического поля и электрического потенциала по известной конфигурации зарядов, проводников и изоляторов. И наоборот, по набору проводников с известными потенциалами можно рассчитать электрические поля в областях между проводниками и определить распределение заряда на поверхности проводников. Электрическую энергию набора зарядов в состоянии покоя можно рассматривать с точки зрения работы, необходимой для сборки зарядов; в качестве альтернативы можно также считать, что энергия находится в электрическом поле, создаваемом этим набором зарядов. Наконец, энергию можно хранить в конденсаторе; энергия, необходимая для зарядки такого устройства, запасается в нем в виде электростатической энергии электрического поля.

Изучите, что происходит с электронами двух нейтральных тел, потертых друг о друга в сухой среде

Просмотреть все видео к этой статье

Статическое электричество — это известное электрическое явление, при котором заряженные частицы переходят от одного тела к другому. Например, если два предмета потереть друг о друга, особенно если эти предметы являются изоляторами, а окружающий воздух сухой, предметы приобретают равные и противоположные заряды, и между ними возникает сила притяжения. Объект, потерявший электроны, становится положительно заряженным, а другой — отрицательно заряженным. Сила — это просто притяжение между зарядами противоположного знака. Свойства этой силы были описаны выше; они включены в математическое соотношение, известное как закон Кулона. Электрическая сила на заряде

Q ₁ при этих условиях за счет заряда Q ₂ на расстоянии r дается законом Кулона,

Жирные буквы в уравнении указывают на векторный характер силы, а единичный вектор r̂ — это вектор размера 1, который указывает от заряда Q ₂ до заряда Q ₁ . Константа пропорциональности k равна 10 ⁻⁷ c ² , где c — скорость света в вакууме; k имеет числовое значение 8,99 × 10

9 ньютонов-квадратный метр на кулон в квадрате (Нм ² /C ² ). На рисунке 1 показано усилие на Q ₁ из-за Q ₂ . Числовой пример поможет проиллюстрировать эту силу. Оба Q ₁ и Q ₂ выбраны произвольно как положительные заряды, каждый с величиной 10 ⁻⁶ кулона. Заряд Q ₁ расположен по координатам x , y , z со значениями 0.03, 0, 0 соответственно, а Q 2 ₂ имеет координаты все. координаты даны в метрах. Таким образом, расстояние между Q ₁ и Q ₂ составляет 0,05 метра.

Тест «Британника»

Тест «Вооружение, энергетика и энергосистемы»

Какой английский инженер и изобретатель построил и запатентовал первую паровую машину? Кто разработал первый процесс недорогого производства стали? Проверьте свои знания. Пройди тест.

Величина силы F на заряде Q ₁ , рассчитанная по уравнению (1), составляет 3,6 ньютона; его направление показано на рис. 1. Сила, действующая на Q ₂ из-за Q ₁ , равна − F , которая также имеет величину 3,6 ньютона; однако его направление противоположно направлению F . Сила F может быть выражена через ее составляющие вдоль x и y , так как вектор силы лежит в плоскости x y . Это делается с помощью элементарной тригонометрии из геометрии рисунка 1, а результаты показаны на рисунке 2. Таким образом, в ньютонах. Закон Кулона математически описывает свойства электрического взаимодействия между покоящимися зарядами. Если бы заряды имели противоположные знаки, сила была бы притягивающей; притяжение будет указано в уравнении (1) отрицательным коэффициентом единичного вектора руб. Таким образом, электрическая сила, действующая на Q ₁ , будет иметь направление, противоположное единичному вектору r̂ , и будет направлена ​​от Q ₁ к 4 4, Q . В декартовых координатах это привело бы к изменению знаков обеих составляющих силы x и y в уравнении (2).

Как можно понять эту электрическую силу на Q ₁ ? Принципиально сила обусловлена ​​наличием электрического поля в положении Q ₁ . Поле обусловлено вторым зарядом Q ₂ и имеет величину, пропорциональную размеру Q ₂ . При взаимодействии с этим полем первый заряд, находящийся на некотором расстоянии, либо притягивается, либо отталкивается от второго заряда в зависимости от знака первого заряда.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Закон напряжения Кирхгофа — Цепи постоянного тока

Цепи постоянного тока

В 1847 г. Г. Р. Кирхгоф расширил использование закона Ома, разработав простой понятие о напряжениях, содержащихся в контуре последовательной цепи. Закон напряжения Кирхгофа гласит:

Алгебраическая сумма напряжений на любом замкнутом пути в цепи равна до нуля.

Закон напряжения Кирхгофа можно записать в виде уравнения, как показано ниже:

где В ₁ , В ₂ и т. д. — напряжения вокруг любой замкнутой цепи.

Используя закон Кирхгофа, можно решить схемные задачи, которые быть трудным, а часто и невозможным, зная только закон Ома. Когда При правильном применении закона Кирхгофа можно составить уравнение для замкнутой петля и неизвестные значения цепи могут быть рассчитаны.

Полярность напряжения

Чтобы применить закон напряжения Кирхгофа, значение полярности напряжения должны быть поняты.

В схеме, показанной на рисунке ниже, показано, что ток течет в направление против часовой стрелки. Обратите внимание, что конец резистора R ₁ , в который течет ток, маркируется положительным (+). Конец R ₁ , на котором отмечен текущий лист отрицательный (-). Эти обозначения полярности используются, чтобы показать, что конец R ₁ , в который течет ток, находится на более высоком положительном потенциала, чем конец резистора, с которого уходит ток. Точка А более положительна, чем точка Б.

Полярность напряжения.

Точка С, имеющая тот же потенциал, что и точка В, считается положительной. Этот означает указать, что точка C более положительна, чем точка D. Сказать, что точка положительный (или отрицательный) без указания полярности на основе не имеет смысла. В работе с законом Кирхгофа положительные и отрицательная полярность назначается в направлении протекания тока.

Полярность напряжения также может быть обозначена стрелкой, указывающей от положительная (+) точка в отрицательную (-) точка (красная стрелка на рисунке выше). В случае резисторов стрелка напряжения имеет того же направления, что и ток. Часто это более практичное указание полярностей.

Применение закона напряжения Кирхгофа

Закон напряжения Кирхгофа применяется к цепи следующим образом:

Предположим направление тока в цепи. (Правильное направление желательно, но не обязательно.)

Используя предполагаемое направление тока, назначьте полярность напряжения для всех резисторы, через которые протекает ток.

Соблюдайте полярность всех источников, включенных в цепь.

Начиная с любой точки цепи, обведите цепь (петлю) в выбранном направлении (по часовой стрелке или против часовой стрелки), записывая сумму и полярность напряжения последовательно на каждом компоненте. Полярность используется знак перед предполагаемый ток прошел через составная часть. Остановиться, когда будет достигнута точка, в которой была начата трассировка.
Когда стрелки используются для указания полярности напряжения, полярность (знак) напряжения можно получить с помощью следующего Правило: Если стрелка имеет то же направление, что и кривая, знак напряжения в уравнение положительное (+). Напротив, если стрелка имеет противоположное направлении знак отрицательный (-).

Поместите эти напряжения с их полярностями в уравнение и решить для нужного количества.

Пример :
Три резистора подключены к источнику 50 В (см. рисунок ниже). Каково будет напряжение на третьем резисторе, если напряжение упадет на первые два резистора на 25 вольт и на 15 вольт?

Определение неизвестного напряжения в последовательной цепи.

Решение :
Сначала предполагается направление тока (как показано). Используя этот ток, маркировка полярности («+» и «-» знаки и/или стрелки) размещены на каждом конце каждого резистора, а также на клеммах источника. Начиная с точки А, обведите цепь в направлении протекания тока, записывая напряжение и полярность каждого компонента. Начиная с точки А и используя компоненты из схемы:

Подставляем значения из схемы:

Неизвестное напряжение ( В _x ) равно 10 В.

Используя ту же идею, что и выше, вы можете решить задачу, в которой ток является неизвестной величиной.

Пример :
Цепь с источником напряжения 60 вольт содержит три резистора 5 Ом, 10 Ом и 15 Ом. Найдите ток в цепи.

Правильное направление предполагаемого тока.

Решение: Нарисуйте и обозначьте схему (рисунок выше). Установить направление тока и назначить полярность. Далее, начиная с любой точки — точки В этом примере будет использоваться A — запишите уравнение контура.

Основное уравнение:

Поскольку V = I × R , заменой:

Объединение подобных терминов:

Вычисление I :

Поскольку ток, полученный в приведенных выше расчетах, составляет положительные 2 ампера, предполагаемое направление тока было правильным. Чтобы показать, что произойдет, если предполагается неправильное направление тока, проблема будет решаться, как и раньше, но с противоположным направлением тока.