Схема ИЛИ | Техника и Программы

Логической схемой ИЛИ называется схема с одним выхо­дом и любым числом входов, когда выходной сигнал образует­ся в результате .воздействия входного сигнала иа один или не­сколько входов схемы. На рис. 8.2, а показана типичная схема (вентиль) ИЛИ, выполненная на диодах. На схеме изображе­ны три входа, хотя можно использовать только два входа или же добавить другие входы. Такой вентиль ИЛИ не нуждается в источнике питания, поскольку для обеспечения проводимости диодов подаются входные сигналы соответствующей поляр­ности.

Когда к входу A прикладывается положительное (по отно­шению к земле) напряжение или импульс, диод Д] становится проводящим. Возникающий при этом ток создает на резисторе падение напряжения, представляющее выходной сигнал. Таким образом, при подаче импульса на вход А возникает выходной-импульс. Такой же результат получается при подаче импульса на вход В или С. Если импульсы напряжения; одинаковой высоты приложены к двум или трем входам одновременно, выход­ной сигнал практически не отличается от рассмотренного. Та­ким образом, один и тот же выходной сигнал образуется при воздействии сигнала на вход Л, ИЛИ на вход

В, ИЛИ на вход С, ИЛИ на два, ИЛИ на все три входа. Вместо использования положительного сигнала (импульса), соответствующего логиче­ской единице, или логическому высказыванию ИСТИНА, мо­жет использоваться импульс отрицательной полярности. В этом случае диоды, показанные на рис. 8.2, а, должны быть включе­ны в обратном направлении. (Если для представления логиче­ской 1 выбраны положительные сигналы, то сигналы отрица­тельной полярности, а также состояние отсутствия сигнала представляются 0. Аналогично этому использование логической 1 для отрицательных сигналов означает соответствие 0 положи­тельных сигналов, а также состояния отсутствия сигнала.)

Рис. 8.2. Схемы ИЛИ и их условные обозначения.

На рис. 8.2,6 показана схема ИЛИ, реализованная на тран­зисторах, включенных с объединенным эмиттером. Для увеличе­ния числа входов можно использовать три или более транзисто­ра. На оба коллектора подается положительное напряжение, создающее обратное смещение коллекторных переходов. При отсутствии входных сигналов транзисторы практически заперты и выходной сигнал отсутствует. Однако, когда к входу А при­кладывается импульс положительной полярности, транзистор Т₁ отпирается. Возникает ток эмиттера, который протекает через резистор в цепи эмиттера и создает на этом резисторе падение напряжения, являющееся выходным сигналом. Аналогично им­пульс положительной полярности на входе

В также приводит к появлению выходного сигнала, поскольку в этом случае от­пирается транзистор Т₂. Как и в случае схемы, показанной на рис. 8.2, а, при одновременном воздействии сигналов на оба входа также возникает выходной сигнал, что соответствует ло­гической функции ИЛИ.

На рис. 8.2,в — д показаны условные обозначения схемы ИЛИ с различным числом входов (2, 3 и 5) [В отечественной научно-технической литературе используются другие обозначения схемы ИЛИ. —

Прим. ред.]. Булева алгебра, упомянутая в разд. 8.1, является разделом математики; она описывает поведение переключающих логических схем и в сим­волическом виде выражает соотношения между состояниями таких схем. В булевой алгебре знак + используется для обозна­чения функции ИЛИ — логического сложения. Поэтому выра­жение А + В в действительности обозначает А ИЛИ В, а вовсе не указывает на арифметическое сложение. Можно производить логическое сложение нескольких величин, например А + В + + С + D [Чтобы отличать логическую схему от арифметической, используется спе­циальный символ логического сложения V- Тогда приведенное здесь выраже­ние будет выглядеть следующим образом: A\/B\/C\/D. — Прим. ред.].

Как отмечалось выше, логическим состояниям ИСТИНА (И) и ЛОЖЬ (Л) соответствуют два значения логической величины. Логическая сумма двух логических величин может принимать значения, указанные в табл. 8.1 — 8.3.

Таблица 8.1

0 + 0 = 0

A + 0 = 1

0 + B = 1

A + B = 1

Таблица 8.2

Л + Л = Л

И + Л = И

Л + И = Л

И + И = И

Таблица 8.3

0 + 0 = 0

1 + 0 = 1

0 + 1 =1

1 + 1 = 1

При большем числе логических слагаемых возможны соот­ношения:

0+0 + 0 = 0; 0 + 1+0=1 и т. д.

❶ Что такое логическая схема «или» 🚩 Математика

В основу компьютерной системы вычислений положена двоичная логика. Это значит, что для проведения всех возможных математических расчетов используются только два числа – 1 и 0. Человеку такая система вычислений покажется очень неудобной, но для машины она является наиболее оптимальной, так как позволяет преобразовать самые сложные вычисления к операциям с нулем и единицей. Что, в свою очередь, позволяет добиться высокого быстродействия системы.

В соответствии с двоичной системой счисления, используют всего две логические переменные – 1 и 0. Базовыми логическими элементами являются схемы «И», «ИЛИ», «НЕ», каждая из которых выполняет одну функцию.

Базовый логический элемент «И» реализует конъюнкцию (логическое умножение) и работает следующим образом. Логический элемент микросхемы имеет три вывода: два на входе и один на выходе. Логическая единица (то есть напряжение) появляется на выходе только в том случае, если напряжение будет подано сразу на оба входа – на первый и на второй. То есть если на обоих входах 1, то и на выходе 1. Если на входах 0, на выходе 0. Если на одном (любом) входе 0, на другом 1, на выходе будет 0. Таким образом, логическая единица появляется на выходе только в одном случае из четырех.

Логический элемент «ИЛИ» реализует дизъюнкцию (логическое сложение) и отличается от предыдущего только логикой. Логическая единица появляется на выходе в том случае, если логическая 1 будет подана на один из двух входов. То есть на один или на другой. Во всех других вариантах на выходе будет логический ноль, то есть отсутствие выходного напряжения на соответствующем выводе микросхемы.

Очень важным является логический элемент «НЕ», реализующий инверсию (отрицание). В нем всего два вывода – один на входе и один на выходе. Логика работы очень проста: если на входе 0, на выходе 1. Если на вход подается 1, на выходе появляется 0.

Три описанных выше основных логических элемента могут образовывать более сложные комбинации – например, «ИЛИ-НЕ», когда сигнал на выходе инвертируется, «И-НЕ» — здесь тоже присутствует инвертирование сигнала. Наличие разнообразных логических элементов позволило разработчикам компьютеров «научить» их выполнять необходимые математические вычисления.

Логические элементы компьютера

Основные логические элементы реализуют 3 основные логические операции:

• логическое умножение;
• логическое сложение;
• инверсию (отрицание).

Устройства компьютера, которые выполняют обработку и хранение информации, могут быть собраны из базовых логических элементов, у которых $2$ входа и $1$ выход. К логическим устройствам компьютера относятся группы переключателей, триггеры, сумматоры.

Связь между алгеброй логики и компьютерной техникой также лежит в двоичной системе счисления, которая используется в ЭВМ. Поэтому в устройствах ПК можно хранить и обрабатывать как числа, так и значения логических переменных.

Определение 1

Логический элемент компьютера – это часть электронной схемы, которая выполняет элементарную логическую функцию.

Переключательные схемы

В ЭВМ используются электрические схемы, которые состоят из большого количества переключателей. Переключатель, находясь в замкнутом состоянии ток пропускает, в разомкнутом – не пропускает. Работа таких схем удобно описывается при помощи алгебры логики. В зависимости от состояния переключателя можно регулировать получение или неполучение сигналов на выходах.

Вентили

Среди логических элементов компьютеров выделяют электронные схемы И, ИЛИ, НЕ, И–НЕ, ИЛИ–НЕ и другие (их называют вентили).

Эти схемы позволяют реализовать любую логическую функцию, которая описывает работу устройств ПК. Обычно вентили имеют $2–8$ входов и $1$ или $2$ выхода.

Для представления двух логических состояний ($1$ и $0$) в вентилях, входные и выходные сигналы имеют разные уровни напряжения. Например, $+3 \ B$ (вольт) для состояния $«1»$ и $0 \ B$ для состояния $«0»$.

У каждого логического элемента есть условное обозначение, выражающее его логическую функцию, но не указывающее на электронную схему, которая в нем реализована. Такой подход реализован для упрощения записи и понимания сложных логических схем.

Работа логических элементов описывается таблицами истинности.

Рисунок 1.

Триггер

Триггеры и сумматоры состоят из вентилей.

Триггер – важнейшая структурная единица оперативной памяти ПК и внутренних регистров процессора.

Определение 2

Триггер – логическая схема, которая способна хранить $1$ бит информации ($1$ или $0$). Строится на $2$-х элементах ИЛИ–НЕ или на $2$-х элементах И–НЕ.

Рисунок 2.

Самый распространённый тип триггера – $RS$-триггер (Reset/Set), который имеет $2$ входа $S$ и $R$ и два выхода $Q$ и $\bar{Q}$. На каждый из входов $S$ и $R$ могут подаваться входные сигналы в виде кратковременных импульсов (рис.3): есть импульс – $1$, нет импульса – $0$.

Рисунок 3. Кратковременный импульс

Сумматор

Сумматоры широко применяются в арифметико-логических устройствах процессора и отвечают за суммирование двоичных разрядов.

Определение 3

Сумматор – логическая схема, которая способна суммировать 2 одноразрядных двоичных числа с переносом из предыдущего разряда.

Рисунок 4.

Сумматор может находить применение и в других устройствах машины.

Для суммирования двоичных слов длиной от двух бит можно использовать последовательное соединение многоразрядных сумматоров, причём для двух соседних сумматоров выход переноса одного сумматора является входом для другого.

Пример реализации логической схемы

Рисунок 5.

Алгоритм реализации:

1. Определим количество переменных данного выражения, значит столько входов будет иметь схема. В данном случае это входы $A, B, C$.

2. С помощью базовых логических элементов реализуются основные операции в порядке их следования:

   I – инверсия переменных $A, B, C$ реализуется логическим элементом «НЕ»;

   II – логическое умножение реализуется логическим элементом «И»;

   III – логическое сложение реализуется логическим элементом «ИЛИ».

На выходе каждого элемента прописывается логическое выражение, которое реализуется данным элементом, что позволяет осуществить обратную задачу, т.е. по готовой схеме составить логическое выражение, которое реализует данная схема.

❶ Что такое логическая схема «и-не» 🚩 3 и не 🚩 Естественные науки

Имея в распоряжении элементы «и», «или», «не» и комбинируя их, можно сделать цифровое устройство произвольной сложности. Электронная часть любого ЭВМ состоит из этих базовых логических элементов и их различных комбинаций. Данные элементы работают с бинарными числами 1 и 0, что реализуется в схеме в виде подачи напряжения (1) и его отсутствия (0) на входах (контактах) элементов.

Логический элемент «и» реализует конъюнкцию, то есть выполняет операцию логического умножения. Сам он называется конъюнктором. Единица на выходе устройства будет только тогда, когда все входные потоки положительны. Если же хотя бы на одном из входов стоит ноль, можно сразу сказать, что на выходе получится ноль, не рассматривая остальные контакты. Поэтому в результирующем столбце таблицы истинности для конъюнктора с двумя входами три нуля и одна единица. Причем единица — результат логического умножения при наличии на всех входах единицы (наличие напряжения на контактах).

Элемент инвертор обращает входное значение на противоположное и подает его на выход: ноль превратится в единицу, единица станет нулем. Изолированный инвертор сам по себе способен обработать только одну входную величину. Его таблица истинности проста, и ее значимая часть представлена квадратной матрицей размерности два.

В логической схеме «и-не» выполняется сначала умножение, затем отрицание. Для правильной работы устройства необходимо как минимум два входных потока, но возможно и больше. Конъюнктор обозначается прямоугольником со знаком «&» внутри, инвертор – прямоугольником с белым кружком в точке выхода. Комбинированное устройство «и-не» включает обе эти детали. Обычно выходы элементов изображают на правой боковой стороне, а входы — на левой. Таблица истинности данной логической схемы для двух входов инверсна конъюнктору, т.е. имеет три результирующих единицы и один ноль.

Чтобы не тратить время на прохождение пошагового алгоритма, можно сразу заключить правило о работе схемы «и-не». Если хотя бы один из входов нулевой, на выходе будет единица. И только при всех положительных контактах (наличие напряжения) на выходе устройства получится ноль.

логическая схема и или — с русского на английский

логическая схема — вентиль «ИЛИ» — Схема, дающая выход, когда совпадает несколько входных импульсов [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN OR gate …   Справочник технического переводчика

логическая схема И-ИЛИ — loginis IR ARBA grandynas statusas T sritis radioelektronika atitikmenys: angl. AND OR circuit vok. logische UND ODER Schaltung, f rus. логическая схема И ИЛИ, f pranc. circuit ET OU, m …   Radioelektronikos terminų žodynas

Логическая схема (модель данных) — Логическая схема модель данных специфической области вопросов, выраженная в понятиях технологии управления данными. Не будучи продуктом исключительно теории управления базами данных, она оперирует терминами и понятиями или реляционных таблиц и… …   Википедия

логическая схема ИЛИ-НЕ — loginis ARBA NE grandynas statusas T sritis radioelektronika atitikmenys: angl. NOR circuit; NOT OR circuit vok. logische NOR Schaltung, f; logische ODER NICHT Schaltung, f rus. логическая схема ИЛИ НЕ, f pranc. circuit OU NON, m …   Radioelektronikos terminų žodynas

логическая схема ИЛИ — loginis ARBA grandynas statusas T sritis radioelektronika atitikmenys: angl. OR circuit vok. logische ODER Schaltung, f; OR Schaltung, f rus. логическая схема ИЛИ, f pranc. circuit OU, m …   Radioelektronikos terminų žodynas

ЛОГИЧЕСКАЯ СХЕМА АЛГОРИТМА — одна из основных форм записи алгоритма деятельности оператора, использующая символьные обозначения, позволяющие комплексно описать трудовой процесс и его психофизиологические особенности. В качестве составляющих алгоритма используются оперативные …   Энциклопедический словарь по психологии и педагогике

Схема — Схема: графический документ [1]; изложение, изображение, представление чего либо в самых общих чертах, упрощённо (например, схема доклада)[2]; электронное устройство, содержащее множество компонентов (интегральная схема). Графический документ… …   Википедия

Схема снежинки — образуется из схемы звезды, в случае нормализации таблиц измерений последней. Схема снежинки получила свое название за свою форму, в виде которой отображается логическая схема таблиц в многомерной базе данных. Так же как и в …   Википедия

ЛОГИЧЕСКАЯ СЕМАНТИКА — раздел металогики, в к ром изучаются интерпретации логических исчислений. Осн. понятия Л. с. можно разделить на 2 группы: (1) понятия, применение к рых к выражениям логич. исчисления существенно зависит от выбора интерпретации (см. также Модель)… …   Философская энциклопедия

Схема функциональной целостности — (СФЦ) это логически универсальное графическое средство структурного представления исследуемых свойств системных объектов. Описание аппарата схем функциональной целостности было впервые опубликовано Можаевым А.С. в 1982 году [1]. По построению… …   Википедия

Логическая дизъюнкция — Дизъюнкция  логическая операция, по своему применению максимально приближенная к союзу «или» в смысле «или то, или это, или оба сразу». Синонимы: логическое «ИЛИ», включающее «ИЛИ», логическое сложение, иногда просто «ИЛИ». Это бинарная инфиксная …   Википедия

Логическое ИЛИ — это… Что такое Логическое ИЛИ?

Дизъю́нкция — логическая операция, по своему применению максимально приближенная к союзу «или» в смысле «или то, или это, или оба сразу». Синонимы: логи́ческое «ИЛИ», включа́ющее «ИЛИ», логи́ческое сложе́ние, иногда просто «ИЛИ».

Это бинарная инфиксная операция, то есть, она имеет два операнда и стоит между ними. Чаще всего встречаются следующие варианты записи: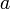
|| | .

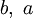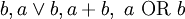Булева алгебра

В булевой алгебре дизъюнкция — это функция двух переменных (они же — операнды операции). Переменные Правило: результат равен , если оба операнда равны 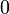; во всех остальных случаях результат равен .

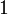Многозначная логика

В многозначной логике операция дизъюнкции может определяться другими способами. Чаще всего применяется схема: , где . Возможны и другие варианты. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндов .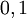

Классическая логика

В классическом исчислении высказываний свойства дизъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства дизъюнкции. Один из самых распространенных вариантов включает 3 аксиомы для дизъюнкции: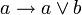

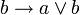
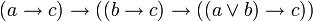
С помощью этих аксиом можно доказать другие формулы, содержащие операцию дизъюнкции. Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.

Программирование

В компьютерных языках используется два основных варианта дизъюнкции: логическое «ИЛИ» и побитовое «ИЛИ». Например, в языках C/C++ логическое «ИЛИ» обозначается символом «||», а побитовое — символом «|».

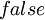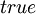Логическое «ИЛИ» применяется в операторах условного перехода или в аналогичных случаях, когда требуется получение результата или . Например:

if (a || b) 
{
    /* какие-то действия */
};

Результат будет равен 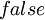, если оба операнда равны 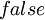или 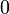. В любом другом случае результат будет равен .

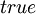При этом применяется стандартное соглашение: если значение левого операнда равно 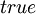, то значение правого операнда не вычисляется (вместо 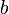может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приемом в некоторых случаях. Например, если левый операнд проверяет необходимость вычисления правого операнда:

if (a == NULL || a->x == 0) 
{
    /* какие-то действия */
};

В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдет разыменования нулевого указателя.

Побитовое «ИЛИ» выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,

если
a =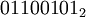
b =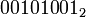
то
a ИЛИ b =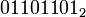

Связь с естественным языком

Часто указывают на сходство между дизъюнкцией и союзом «или» в естественном языке, когда он употребляется в смысле «или то, или то, или оба сразу». В юридических документах часто пишут: «и/или», подразумевая «или то, или то, или оба сразу». Составное утверждение «A и/или B» считается ложным, когда ложны оба утверждения A и B, в противном случае составное утверждение истинно. Это в точности соответствует определению дизъюнкции в булевой алгебре, если «истину» обозначать как 1, а «ложь» как 0.

Неоднозначность естественного языка заключается в том, что союз «или» используется в двух значениях: то для обозначения дизъюнкции, то для другой операции — исключающего «ИЛИ».

См. также

Wikimedia Foundation. 2010.