Особенности схем подключения к тиристорному регулятору

Наиболее часто на практике используется четыре схемы подключения нагрузок к тиристорному регулятору: звезда, треугольник, звезда с рабочей нейтралью и разомкнутый треугольник.

Схемы подключения звезда и треугольник приведены на рисунке 1.

Рисунок 1 Подключение нагрузки к трехфазному тиристорному регулятору по схемам звезда и треугольник

Основное достоинство этих двух схем – простота и минимальное количество силового провода, за счет чего они и получили наиболее широкое распространение. При соединении нагрузки звездой максимальное напряжение на нагрузочном сопротивлении равно фазному напряжению Uф, а при соединении треугольником – линейному Uл. Соответственно, звездой соединяют нагрузку, рассчитанную на напряжение 220 В, а треугольником – 380 В.

Кривая тока, протекающего по фазному проводу изображена на рисунке 2.

Рисунок 2 Кривая тока в фазах при соединении звездой или треугольником, активная нагрузка

Однако у простоты схемы есть обратная сторона медали – напряжения на нагрузочных сопротивлениях распределяются поровну только при условии строго равенства фазных напряжения (Uа = Ub = Uс) и равенства сопротивлений нагрузок (Ra = Rb = Rc или Rab = Rbc = Rca). Как правило, на практике это условие почти никогда не выполняется и возникает небаланс напряжений: на разных сопротивления нагрузки при полностью включенных тиристорах устанавливаются неравные напряжения, например, на одном сопротивлении 210 В, на другом 215 В, на третьем 230 В.

В большинстве своем эти небалансы невелики: разброс по напряжению невелик и составляет не больше 4-8%, что вполне допустимо. Но иногда при неудачном соотношении параметров – сильном «перекосе» фаз с одновременно неравными сопротивлениями нагрузки — напряжения могут распределиться с большим разбросом, например 190, 220 и 250 В. Это ведет к неравномерному износу ТЭНов и преждевременному выгоранию одного из них.

Довольно часто бывает, что в одной из фаз постоянно выгорает ТЭН неизвестно от чего. Обычно это является следствием выше описанного явления.

   В схемах подключения звезда с рабочей нейтралью и разомкнутый треугольник (рисунок 3) это явление проявляется гораздо меньшей степени.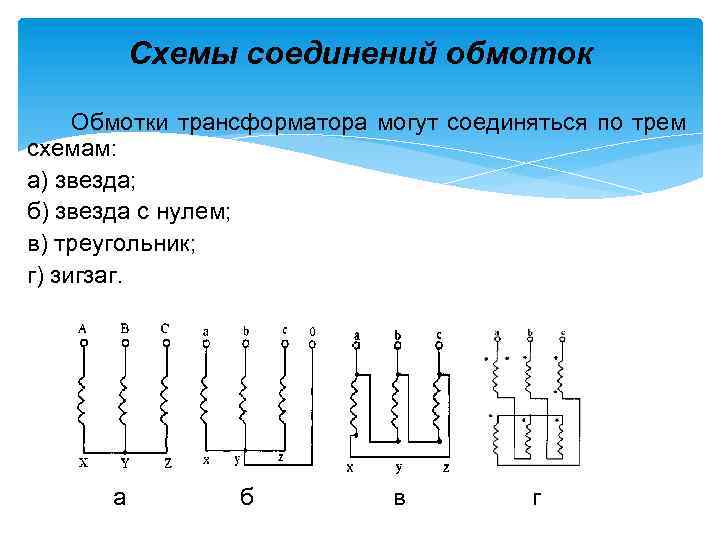

Рисунок 3 Подключение нагрузок по схемам звезда с рабочей нейтралью и разомкнутый треугольник

При подключении нагрузки по схеме звезда с нулем максимальное напряжение на нагрузочном сопротивлении равно фазному напряжению сети, при этом ток каждой фазы определяется лишь напряжением фазы и сопротивлением нагрузочного резистора, включенного в эту фазу, и не зависит напряжений других фаз и от сопротивлений остальных нагрузочных сопротивлений, то есть Ia = Ua / Ra, Ib = Ub / Rb, Ic = Uc / Rc.

Другое важное свойство схемы – возможность выравнивания токов, напряжений и мощностей на нагрузочных сопротивлениях в случае «перекоса» фаз питающей сети. Например, тиристорный регулятор ТРМ-С может автоматически корректировать напряжение на нагрузке таким образом, чтобы на каждом сопротивлении нагрузки выделялась равная мощность. Это способствует продлению срока службы ТЭНов, а также энергосбережению – за счет устранения перекосов по фазам достигается дополнительная экономия электроэнергии 1-3%.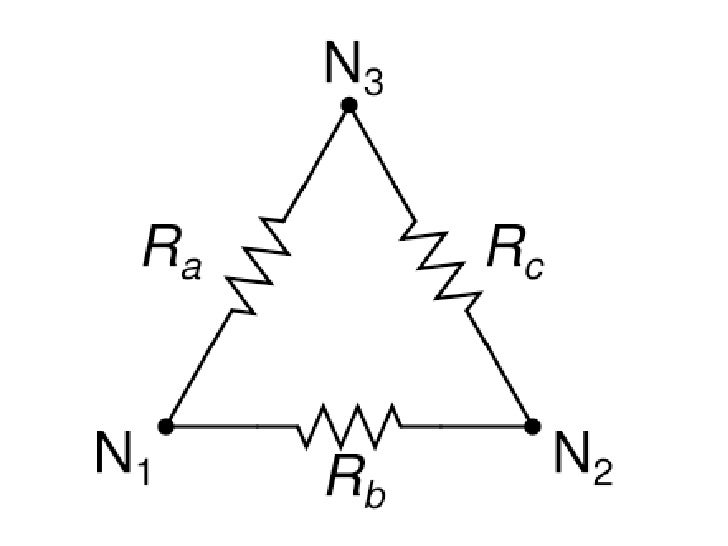

Еще один плюс этой схемы – это меньший уровень излучаемых электромагнитных помех.

Все выше сказанное также верно и для схемы разомкнутого треугольника, с той лишь разницей, что максимальное напряжение на нагрузочных сопротивлениях равно линейному, а ток нагрузки определяется линейным напряжением Iab = Uab / Rab, Ibc = Ubc / Rbc, Ica = Uca / Rca.

Недостатков у схемы звезда с нейтралью два. Первый – это необходимость подключения нулевого провода, что на практике иногда бывает затруднительно. Например, у нагревательного аппарата может быть сделано три вывода для подключения фазных проводов, а общая точка звезды – внутри аппарата и недоступна для подключения. В этом случае реализовать подключение по схемы звезды с нейтралью невозможно.

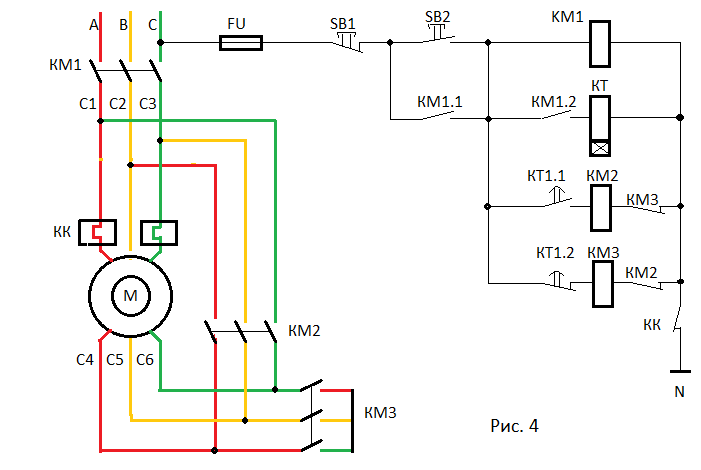
Второй недостаток – это протекание тока через нейтраль при фазо-импульсном управлении даже при полностью равных сопротивлениях нагрузки и фазных напряжениях, что проиллюстрировано на рисунке 4: в верхней его части изображены кривые токов, протекающие по фазам А, В и С, а внизу – ток в нулевом проводе.

Рисунок 4 Протекание тока через нулевой проводник

При этом величина тока в нулевом проводе может быть в 1,5-2 раза больше чем ток в фазах. Это приводит к необходимости прокладки нулевого проводника увеличенным сечением, что, разумеется, увеличивает и стоимость кабельных линий. Незнание или недооценка же этого явления приводит к постепенному выходу из строя нейтрального провода.

Это иногда вызывает удивление: казалось бы, напряжения фаз равные, сопротивления фаз равные, откуда ток в нуле?! Но объясняется это явление просто. Дело в том, что при фазо-импульсном управлении тиристорами форма тока становится не синусоидальной и поэтому не происходит полной компенсации токов в нулевом проводе, как при питании трехфазной нагрузки синусоидальным током.

Отсюда вывод – чтобы ток в нулевом проводе был минимальный необходимо использовать управление пропуском периодов. В этом случае токи фаз будут синусоидальны, а значит ток в нейтрали будет определятся лишь небалансом напряжений фаз и сопротивлений.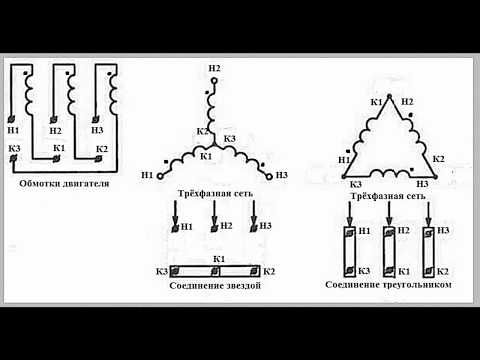 Практически, это приводит к тому, что ток в нуле становится не больше 10% от тока фазы.

Напоследок, рассмотрим схему соединения разомкнутый треугольник. У схемы есть замечательное свойство – тиристоры при таком соединении коммутируют не фазные токи, а линейные, которые меньше в 1,73 раза. Например, если ток фазы составляет 650 А, то токи в линейных проводах составляют Iл = 650 / 1,73 = 380 А. По сравнению со схемой соединения обычным треугольником, это дает возможность приобретать тиристорный регулятор на меньший номинальный ток, который соответственно дешевле и меньше в габаритах. Это показано на рисунке 5. В верхней части рисунка нагрузка соединена треугольником, при этом через тиристоры протекают токи 650 А, а значит необходимо приобретение тиристорного регулятора номинальным током не менее 700-800 А. А в нижней части нагрузка соединена разомкнутым треугольником, при этом по фазам протекает такой же ток 650 А, но поскольку тиристоры коммутируют ток 380 А, то достаточно иметь тиристорный регулятор с номинальным током 400-500 А, что в 1,5-2 раза дешевле.

Рисунок 5 Сравнение схем треугольник и разомкнутый треугольник

Жаль, но несмотря на такое преимущество, эта схема не получила большого распространения. Почему? Первое, как и для звезды с нейтралью, для реализации такой схемы подключения должны быть доступны оба конца выводов нагрузок, что опять же не всегда возможно. Например, у трансформатора, первичная обмотка которого соединена треугольником чаще всего выведена только три конца, а вторые три спрятаны внутри. Второе – это увеличенная стоимость кабельного хозяйства – посмотрите внимательно на рисунок 5: при соединении разомкнутым треугольником требуется дополнительный силовой кабель ( «обратный» кабель от нагрузки). Учитывая высокую стоимость кабелей, можно сказать, что такая схема целессобразно лишь при небольшой длине кабельных линий до 20-30 метров при прокладке медным кабелем и до 50-70 метров при прокладке алюминиевым. При большой длине экономия, полученная от приобретения более дешевого регулятора обнуляется за счет более высокой стоимости кабельного хозяйства.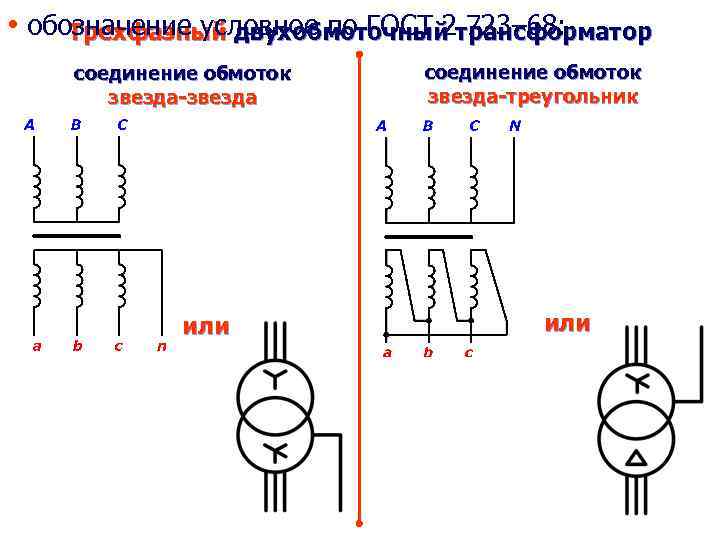

виды подключения, особенности и отличия

Асинхронные электрические двигатели в настоящее время используются очень активно. У них есть определенные преимущества, благодаря которым они и стали так популярны. Для подключения к электрической сети мощных двигателей используются схемы «звезда», «треугольник». Электродвигатели, работающие на таких схемах, обладают своими достоинствами и недостатками. Сами же они отличаются надежностью в эксплуатации, возможностью получить большой крутящий момент, а также высоким показателем производительности.

Подключение двигателя

Как показывает практика, существует две оптимальных схемы — «звезда», «треугольник». Электродвигатели подключаются по одной из них. Возможно также преобразование «звезды» в «треугольник», к примеру.

Среди достоинств асинхронных двигателей выделяются следующие:

• возможность переключения обмоток во время работы;
• восстановление обмотки электрического двигателя;
• невысокая стоимость прибора по отношению к другим;
• наличие высокой стойкости к механическим повреждениям.

Основная особенность, характеризующая все асинхронные электрические двигатели, — это простота конструкции. Однако при всех своих преимуществах, есть и некоторые недостатки, возникающие во время работы:

1. Отсутствует возможность контролировать частоту вращения ротора, не теряя при этом мощности.
2. При увеличении нагрузки уменьшается крутящий момент.
3. Высокие показатели пусковых токов.

Описание подключений

Схемы «звезда» и «треугольник» для электродвигателя имеют определенные различия в подключении. «Звезда» означает, что концы статорной обмотки оборудования собираются в одной точке. При этом напряжение сети в 380 В будет подаваться на начало каждой из обмоток. Обычно на всех схемах подключения такой способ обозначается как Y.

В случае использования схемы подключения «треугольник» статорные обмотки электродвигателя соединяются последовательно. То есть, конец первой обмотки соединяется с началом второй, она, в свою очередь, — с третьей. Последняя будет замыкать цепь, соединяясь с началом первой.

Отличия схем подключения

Схемы «звезда» и «треугольник» у электродвигателя — это единственные способы их подключения. Они отличаются между собой, обеспечивая разные режимы работы. Так, к примеру, подключение при помощи схемы Y обеспечивает более мягкую работу, если сравнивать с двигателями, соединенными в «треугольник». Данная разница играет ключевую роль при выборе мощности электрического устройства.

Более мощные двигатели эксплуатируются только на «треугольнике». Схема подключения электродвигателя «звезда-треугольник» отлично подходит для тех случаев, когда необходимо обеспечить плавный пуск. А в нужный момент переключиться между обмотками для получения максимальной мощности.

Здесь важно добавить: подключение Y гарантирует мягкую работу, но при этом двигатель не сможет набрать свою паспортную мощность.

С другой стороны, схема соединения электродвигателя «треугольник-звезда-звезда» обеспечит большую мощность, но вместе с этим значительно возрастет и значение пускового тока для оборудования.

Именно разница в мощности между подключением Y и треугольником является основным показателем. Электродвигатель со схемой звезды будет обладать мощностью примерно в 1,5 раза ниже, чем через треугольник, однако такое подключение поможет снизить значение пускового тока. Все соединения, которые имеют в своем составе два способа подключения, являются комбинированными. Обычно они применяются лишь в тех случаях, когда необходимо запустить в работу электрический двигатель с большой паспортной мощностью.

Схема пуска «звезда-треугольник» для электродвигателя отличается еще одним преимуществом. Включение осуществляется по схеме Y, что снижает значение пускового тока. Когда во время работы устройство набирает достаточные обороты, происходит переход на схему треугольника для достижения максимальной мощности.

Комбинированные подключения

Схема переключения «звезда-треугольник» электродвигателя достаточно часто применяется в случаях, когда нужно запустить двигатель с минимальным пусковым током.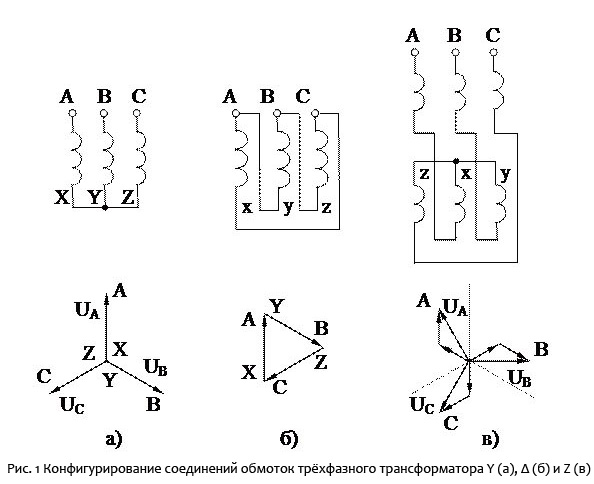 Но при этом всю работу осуществлять нужно на соединении «треугольник». Для создания такого переключения используются специальные контакторы на три фазы. Для обеспечения автоматического переключения между схемами необходимо выполнить два условия. Во-первых, обеспечить блокировку контактов от одновременного включения. Во-вторых, все работы обязательно должны выполняться с задержкой по времени.

Второй пункт необходим, чтобы со 100% вероятностью произошло полное отключение «звезды» перед включением «треугольника». Если этого не сделать, то во время переключения между фазами будет происходить короткое замыкание. Для выполнения нужных условий используется реле времени с задержкой от 50 до 100 миллисекунд.

Осуществление задержки времени

При использовании комбинированного метода подключения «звезда-треугольник» наличие реле времени для задержки переключения необходимо. Специалисты чаще всего выбирают один из трех способов:

1. Первый вариант осуществляется при помощи нормально-разомкнутого контакта реле времени. В таком случае РВ будет отключать схему подключения треугольником во время пуска, а за переключение будет отвечать токовое реле РТ.
2. Второй вариант предполагает применение современного реле времени с задержкой переключения от 6 до 10 секунд.
3. Третий способ — это управление контакторами электродвигателя автоматическими приборами или вручную.

Рассмотрение способа переключения

Использование классического варианта с применением реле времени для комбинированных схем «звезда-треугольник» ранее считалось наиболее оптимальным. У него имелся лишь один недостаток, который иногда становился достаточно существенным, — габариты самого РВ. Такие типы приспособления гарантировали задержку времени переключения при помощи намагничивания сердечника. Однако на обратный процесс требовалось время.

В настоящее время такие РВ и прочие приборы были вытеснены современными приборами — частотными преобразователями. Переключение схемы электродвигателя со схемой «звезда-треугольник» при помощи ПЧ обладает большими преимуществами. Сюда относят более стабильную работу, низкие пусковые токи.

Это оборудование имеет встроенный микропроцессор, отвечающий за изменение частоты. Если рассматривать суть ПЧ для электродвигателя, то его принцип работы следующий: преобразователь вырабатывает нужную частоту переменного тока. На сегодняшний день в промышленности используются специальные или универсальные модели ПЧ для подключения асинхронных двигателей.

Специальные модели разрабатываются и используются лишь с определенными типами двигателей. Универсальные могут применяться в комплекте с любыми устройствами.

Недостатки схемы

Несмотря на то что классическая схема подключения проста и надежна, она имеет свои определенные недостатки.

Во-первых, очень важно точно определить нагрузку на вал электродвигателя. В противном случае он будет слишком долго набирать обороты, что, в свою очередь, исключит возможность быстрого переключения на схему треугольника при помощи токового реле. В этом режиме нежелательно долго эксплуатировать электрическое устройство.

Во-вторых, при такой схеме подключения возможен перегрев обмоток, из-за чего специалисты рекомендуют установить в схему дополнительное тепловое реле.

В-третьих, при использовании современных временных реле необходимо точно соблюдать паспортную нагрузку на вал электрического двигателя.

Заключение

При использовании подключения схемы «звезда-треугольник» очень важно правильно рассчитать нагрузку на вал электродвигателя. Еще один неприятный факт кроется в том, что в момент переключения с Y на треугольник, когда двигатель еще не набрал нужных оборотов, происходит самоиндукция. В этот момент в сети появляется повышенное напряжение. Это грозит выходом из строя других приборов и устройств, подключенных к этой же сети.

Летний Треугольник: Указатель сезона

Летний Треугольник, восходящий на востоке июньскими вечерами. Диаграмма через Челинн Кэмпион.

Летнее время — время Летнего Треугольника

Лето здесь, в Северном полушарии. Дни длинные. Солнце находится на своей высоте в полуденном небе. И летнее небо тоже с нами. Следите за знаменитым Летним треугольником, который теперь поднимается в восточном небе в эти поздние июньские и июльские вечера.

Летний треугольник — это не созвездие. Это астеризм или заметный узор из звезд. Этот узор состоит из трех ярких звезд в трех отдельных созвездиях — Денеб в созвездии Лебедя Лебедя, Веги в созвездии Лиры Арфы и Альтаира в созвездии Орла Орла.

Научитесь распознавать астеризм Летнего Треугольника прямо сейчас, и вы сможете наблюдать за ним все лето, пока он смещается выше на восток, а затем, наконец, появляется высоко над головой в небе поздним северным летом и ранней северной осенью.

Летний треугольник. Изображение Джимми Уэстлейка/Steamboat Pilot & Today.

Как найти Летний Треугольник

Когда в июне или июле наступает ночь, посмотрите на восток в поисках сверкающей сине-белой звезды. Это будет Вега в Лире. Вега, правящая на вершине знаменитого Летнего треугольника, также является самой яркой из трех звезд Летнего треугольника, которые достаточно ярки, чтобы их можно было увидеть из многих залитых светом городов.

Посмотрите в правый нижний угол Веги, чтобы найти вторую по яркости звезду Летнего Треугольника. Это Альтаир, самая яркая звезда в созвездии Орла Орла. Линейка (12 дюймов, 30 см), которую держат на расстоянии вытянутой руки, заполняет промежуток между этими двумя звездами.

Посмотрите в нижний левый угол Веги и найдите еще одну яркую звезду: Денеб, самую яркую в созвездии Лебедя и третью по яркости в Летнем Треугольнике. Вытянутая рука на расстоянии вытянутой руки примерно равна расстоянию от Веги до Денеба.

Трудно передать огромные размеры Летнего Треугольника. Но вы это увидите. Эти три яркие звезды — Вега, Денеб и Альтаир — станут фаворитами лета.

Увеличить. | Летний треугольник состоит из 3 ярких звезд — Веги, Денеба и Альтаира — в 3 разных созвездиях. Изображение от нашей подруги Сьюзен Гис Дженсен в Одессе, штат Вашингтон.

Летний треугольник как дорожная карта к Млечному Пути

Если вам посчастливится оказаться под темным звездным небом в безлунную ночь, вы увидите огромную полосу звезд, проходящих между Вегой и Альтаиром Летнего треугольника.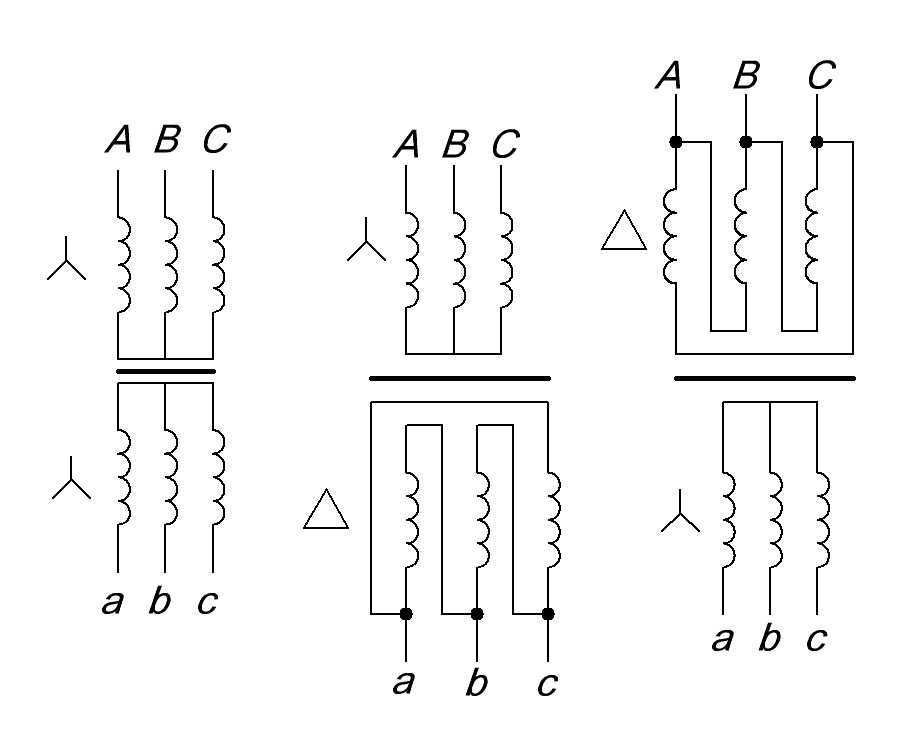 Звезда Денеб качается посреди этой реки звезд, которая дугой течет по темному летнему небу. Эта небесная река, конечно же, вид сбоку на нашу собственную галактику Млечный Путь. Хотя каждая звезда, которую вы видите невооруженным глазом, является членом Млечного Пути, в это время года мы можем ясно видеть плоский диск галактики, где собирается большинство звезд. К августу и сентябрю у нас будет хороший вид на центр галактики.

Как только вы освоите Летний треугольник, вы всегда сможете найти Млечный Путь в ясную темную ночь. Как насчет того, чтобы максимально использовать темную летнюю ночь, чтобы исследовать эту полосу звезд, этот залитый звездами бульвар с его небесными прелестями? Используйте бинокль, чтобы увидеть паутинную красоту призрачных туманностей и усыпанных драгоценностями звездных скоплений вдоль звездного следа.

Скотт Макнейл из творческой мастерской Exit Pupil сделал эту фотографию Летнего треугольника, созвездия Геркулеса, яркого Млечного Пути и ярко-красной звезды Антарес, и это лишь некоторые из видимых объектов.

Сезонный календарь природы

Летний треугольник служит звездным календарем, отмечая времена года. Когда звезды Летнего Треугольника освещают восточные сумерки в середине-конце июня, это верный признак смены времен года, весны, уступающей место лету. Однако, когда Летний Треугольник находится высоко на юге в сумерках и ранним вечером, изменение положения Летнего Треугольника указывает на то, что лето перешло в осень.

Великий Разлом Млечного Пути проходит через созвездие Кассиопеи и Летний Треугольник.

Несколько слов о астеризмах

Как мы упоминали выше, астеризмы не являются созвездиями; они просто узоры на куполе неба. Созвездия вообще пришли к нам из глубокой древности. В 1930-х годах Международный астрономический союз официально обозначил границы 88 созвездий, которые мы знаем сегодня.

Между тем, вы можете придумать и назвать свои собственные астеризмы, почти так же, как вы можете распознавать формы в пушистых облаках в летний день.

Некоторые астеризмы настолько очевидны, что их узнают во всем мире. «Летний треугольник» — один из них.

Летний треугольник и вершина пирамиды Лувра от друга EarthSky на Facebook VegaStar Carpentier в Париже. Спасибо, ВегаСтар!

Итог: июньскими и июльскими вечерами вы найдете Летний треугольник на востоке с наступлением темноты. Он поднимается высоко над головой после полуночи и садится на западе на рассвете.

Дебора Берд

Просмотр статей

Об авторе:

Дебора Берд создала серию радиопрограмм EarthSky в 1991 году и основала EarthSky.org в 1994 году. Сегодня она является главным редактором этого веб-сайта. Она получила множество наград от вещательного и научного сообществ, в том числе астероид под названием 3505 Берд в ее честь. Научный коммуникатор и педагог с 19 лет.76, Берд верит в науку как в силу добра в мире и жизненно важный инструмент для 21-го века. «Быть ​​редактором EarthSky — это все равно, что организовывать большую глобальную вечеринку для крутых любителей природы», — говорит она.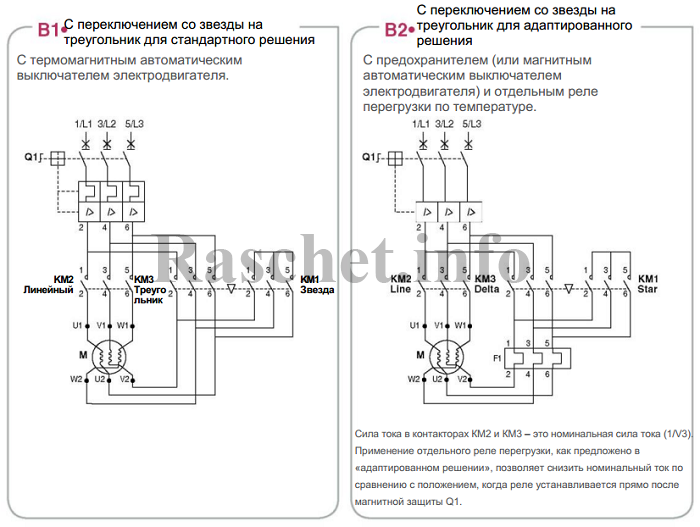

Геометрия звезд

Геометрия звезд

MartianCraft

• Услуги
• Команда
• Карьера
• Блог

 

Звезда — широко известный символ, используемый для рейтингов. Если вы создаете пользовательский интерфейс для рейтинга в приложении, скорее всего, вы где-то будете использовать звездочку. Есть много разных способов получить звезду на экране в вашем приложении, но лучший способ — нарисовать ее с нуля в коде. Это не только дает вам полную гибкость с точки зрения размера и разрешения экрана, а также возможность создавать удивительные эффекты с помощью основной анимации, но также позволяет вам полный ботаник в геометрии . Вы можете указать на подобные статьи в следующий раз, когда кто-то осмелится спросить, почему вы изучаете все это в школе, потому что «вы никогда не будете использовать это в реальной жизни».

Круги

Начните с классической пятиконечной звезды.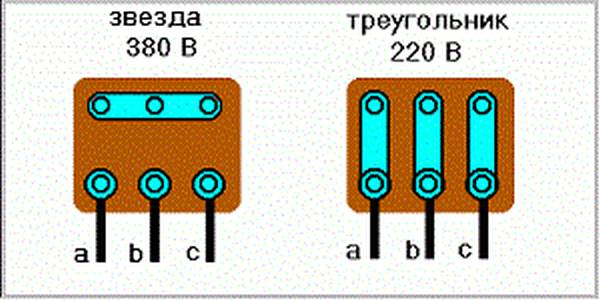

Звезда помещается внутри круга. Острие звезды идет прямо вверх. В полном круге 2 𝛑 радиана, поэтому каждая другая точка попадает в круг на 2 𝛑 / 5 радиан раунда от предыдущего:

Чтобы вычислить координаты каждой точки по краю круга, я могу использовать Метод UIBezierPath addArc . Меня не интересуют сами дуги, но currentPoint пути, когда вы добавляете каждую дугу, будут представлять интерес. Это расширение на UIBezierPath дает мне то, что мне нужно:

расширение UIBezierPath {
    статический пусть двенадцатиоклок: CGFloat = .pi * 1,5
    класс func pointsOnCircle(
        центр: CGPoint,
        радиус: CGFloat,
        очки: инт,
        startAngle: CGFloat = двенадцатиоклок) ->
  [CGPoint] {
        пусть pointOffsetAngle = ((.pi * 2.0) / CGFloat (точки))
        вар начальный угол = начальный угол
        вар конечный угол = начальный угол
        пусть путь = UIBezierPath()
        path.move (к: .  zero)
        var CirclePoints = [CGPoint]()
        за _ в 1...баллах {
            path.addArc (withCenter: центр, радиус: радиус, startAngle: startAngle, endAngle: endAngle, по часовой стрелке: true)
            CirclePoints.append (путь.currentPoint)
            начальный угол = конечный угол
            endAngle += pointOffsetAngle
        }
        вернуть кругОчки
    }
}
 

Как только я наберу очки, я могу нарисовать звезду, соединив точки на круге, как показано здесь, начиная с 1 и до 5, а затем возвращаясь к 1:

Рисование такой звезды не дает нужного результата. Это нормально, если все, что я хочу сделать, это заполнить путь, но если я хочу иметь пустые или частично заполненные звезды (например, для представления среднего рейтинга в 3,6 звезды), тогда этот путь не будет работать. В середине весь этот беспорядок, который я не хочу видеть. Как я могу рассчитать, где будут эти внутренние точки? Пришло время разобраться с тригонометрией.

Треугольники

Тригонометрия состоит из прямоугольных треугольников, и на первый взгляд на диаграмме их нет. Но это только потому, что я не нарисовал на нем достаточно лишних линий. Я могу сделать пятиугольник большего размера, соединив все внешние точки звезды, и я могу провести линию из центра круга, которая проходит через внутреннюю точку. Это дает мне что-то вроде этого:

Оранжевая область представляет собой прямоугольный треугольник! Тем не менее, я недостаточно знаю об этом. Для описания прямоугольного треугольника мне нужно хотя бы два числа из:

• Длины сторон
• Неправильные углы

В настоящее время я могу вычислить только длину одной стороны — стороны, которая проходит на полпути вдоль края этого большого пятиугольника. Я могу сделать это, используя это расширение на CGPoint для расчета средних точек и расстояний. Дистанционный метод использует теорему Пифагора, так что

вы чертовски правы, он используется в реальной жизни! :

расширение CGPoint {
    расстояние функции (до: CGPoint) -> CGFloat {
        пусть deltaX = Double (to. x - self.x)
        пусть deltaY = Double (to.y - self.y)
        пусть расстояние = sqrt((deltaX * deltaX) + (deltaY * deltaY))
        вернуть CGFloat(расстояние)
    }
    func midPoint(to: CGPoint) -> CGPoint {
        пусть deltaX = to.x - self.x
        пусть deltaY = to.y - self.y
        return self.applying(CGAffineTransform(translationX: deltaX * 0,5, y: deltaY * 0,5))
    }
}
 

Что я хочу сделать, так это выяснить, где должны быть внутренние точки звезды, чтобы я мог рисовать прямо к ним, а не полагаться на пересекающиеся линии. Для этого мне нужно узнать расстояние от центра круга до внутренней точки звезды. Внутренняя точка выделена синим цветом на диаграмме выше.

Пентагоны

В центре пятиконечной звезды находится пятиугольник. Это не совпадение. В центре шестиконечной звезды вы найдете шестиугольник и так далее. Вот геометрический факт, который вы, возможно, забыли со школы (я точно забыл): внутренние углы правильного многоугольника, например пятиугольника, можно найти по следующей формуле: ((n — 2) * 𝛑) / n , где n — количество сторон.

Вот внутренние углы пятиугольника:

Таким образом, каждый из отмеченных углов равен 3𝛑 / 5 . Почему меня это волнует? Присмотритесь к внутренней точке, где виден пятиугольник:

.

Рассмотрим окружность над внутренней точкой. Синяя часть круга соответствует внутреннему углу пятиугольника. Внизу справа это 𝛑 — это значение, потому что именно столько радиан содержится в половине круга. Эти значения отражаются в верхней половине круга, поэтому желтая часть круга совпадает с внутренним углом пятиугольника. Верхний правый желтый участок — это интересующий меня угол — край треугольника проходит через него, и, поскольку край заканчивается в средней точке линии между двумя внешними точками, я знаю, что край пересекает этот желтый угол пополам — так что теперь у меня есть один из внутренних углов моего треугольника! Этой информации мне достаточно, чтобы рассчитать все, что мне нужно знать.

Термины, используемые при описании прямоугольного треугольника:

• Гипотенуза — ребро треугольника, противоположное прямому углу
• 𝜃 (тета) — интересующий вас непрямой угол
• Противоположный — край треугольника напротив 𝜃
• Смежный — ребро треугольника рядом с 𝜃

Как было сказано ранее, мне нужны любые две из этих частей информации. У меня есть 𝜃, который составляет половину внутреннего угла пятиугольника, или (3𝛑 / 5) / 2 (упрощено до 0,3𝛑 , если хотите) и у меня есть длина стороны напротив . Меня интересует длина соседней стороны .

На этой диаграмме показаны различные части треугольника:

Есть три формулы тригонометрии, которые вам, возможно, приходилось учить в школе. Тот, который включает противоположные и смежные стороны, таков:

Желто-коричневый 𝜃 = напротив / рядом

Мне нужно поставить две вещи, которые я знаю, на одну сторону, чтобы я мог вычислить вещь, которую я не знаю, а это значит, что формулу нужно изменить так:

рядом = напротив / желтовато-коричневый 𝜃

Это дает мне расстояние от внутренней точки до средней точки двух внешних точек. На самом деле мне важно расстояние от центра круга до внутренней точки, но его легко рассчитать с помощью моего расширения CGPoint .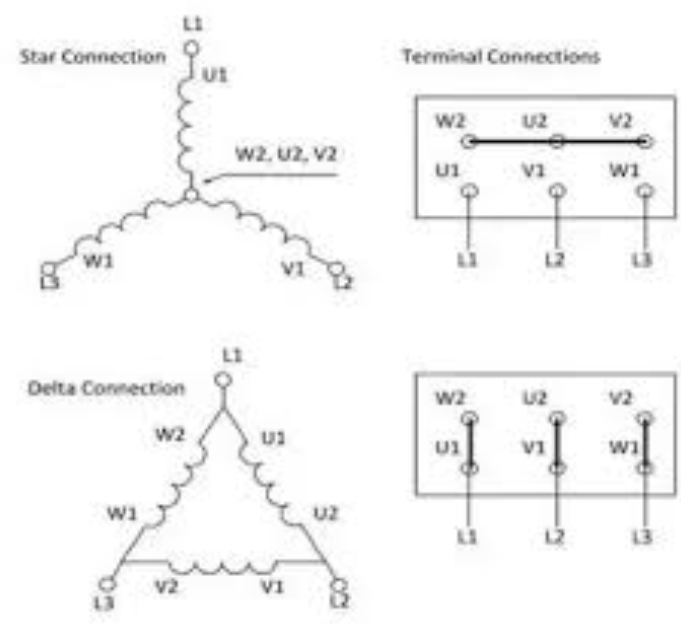

Теперь у меня есть радиус другого, меньшего круга, у которого есть все внутренние точки по окружности. Это означает, что я могу снова использовать свой метод

pointsOnCircle , передав новый радиус и другой начальный угол (на полпути между первыми двумя внешними точками). Вот внутренний круг:

Объединение двух массивов точек в один путь дает мне идеальную звезду без грязных внутренних линий. ★★★★★ для геометрии!

Код

Это расширение дает новый инициализатор для UIBezierPath , который возвращает звезду с заданным количеством точек внутри заданного прямоугольника. Это зависит от других расширений ранее в статье:

расширение UIBezierPath {
    удобство инициализации (starIn rect: CGRect, points: Int = 5) {
        предварительное условие (точки > = 3, «Неверное количество баллов»)
        // Константы, описывающие звезду
        пусть центр = CGPoint (x: rect.midX, y: rect.midY)
        пусть радиус = rect. size.width * 0,5
        пусть externalPoints = UIBezierPath.pointsOnCircle (центр: центр, радиус: радиус, точки: точки)
        // Этот расчет вычисляет расстояние от линии между первыми двумя внешними
        // точки и первая внутренняя точка
        // Внутренний угол правильного многоугольника в центре звезды
        пусть внутренний угол: CGFloat = (CGFloat (точки - 2) * .pi) / CGFloat (точки)
        // Середина линии между двумя внешними точками
        пусть midPoint = externalPoints[0].midPoint(to: externalPoints[1])
        // Длина этой строки
        пусть opp = externalPoints[0].distance(to: midPoint)
        пусть тета = внутренний угол * 0,5
        пусть DistanceIn = opp / tan (тета)
        // Это даст нам радиус внутреннего круга
        пусть внутреннийРадиус: CGFloat
        точки переключения {
        случай 3, 4: innerRadius = center.distance(to: midPoint) * 0,5
        по умолчанию: innerRadius = center.distance(to: midPoint) - DistanceIn
        }
        // Теперь мы можем повторить трюк с дугами окружностей, чтобы получить точки на внутренней окружности.  Начальный угол необходимо отрегулировать, так как он будет не в верхней части круга, а на полпути между двумя внешними точками.
        пусть innerPointOffset = (.pi * 2,0 / CGFloat (точки)) * 0,5
        пусть innerPoints = UIBezierPath.pointsOnCircle (центр: центр, радиус: innerRadius, точки: точки, startAngle: UIBezierPath.twelveOClock + innerPointOffset)
        // Наконец, используем два набора точек для создания пути
        самостоятельная инициализация()
        self.move (к: externalPoints [0])
        для (внешнего, внутреннего) в zip (outerPoints, innerPoints) {
            self.addLine (к: внешнему)
            self.addLine (к: внутренний)
        }
        self.close ()
        // Центрируем звезду по вертикали в переданном прямоугольнике
        пусть starBounds = self.bounds
        пусть heightAdjustment = (rect.height - starBounds.height) * 0,5
        self.apply(CGAffineTransform(translationX: 0, y: heightAdjustment))
    }
}
 

Одним из способов использования этого кода было бы нарисовать изображение звезды — вот способ нарисовать частично закрашенную звезду:

расширение UIImage {
    class func star (размер: CGSize, цвет: UIColor, точки: Int = 5, заполнено: CGFloat = 1. 0) -> UIImage {
        let renderer = UIGraphicsImageRenderer (размер: размер)
        пусть изображение = renderer.image { rendererContext в
            пусть границы = rendererContext.format.bounds
            пусть starPath = UIBezierPath (starIn: bounds.insetBy (dx: 2, dy: 2), точки: точки)
            звездный путь.lineWidth = 4
            цвет.setStroke()
            starPath.stroke()
            starPath.addClip()
            var fillRect = границы
            fillRect.size.width *= заполнено
            цвет.setFill()
            UIRectFill(fillRect)
        }
        вернуть изображение
    }
}
UIImage.star (из: CGSize (ширина: 200, высота: 200), цвет: .orange, точки: 5, заполнено: 0,6)
 

Дает вам:

Звездообразный путь более гибкий и обеспечивает лучшую производительность при использовании вместе с CAShapeLayer . Эта реализация оставлена ​​в качестве упражнения для читателя.

Заключение

Наличие геометрических форм в виде путей Безье дает вам полную гибкость для дизайна пользовательского интерфейса и упрощает изменение размера, стиля и цвета.