Построение логических схем. Определение сигнала на выходе логической схемы по заданным значениям сигналов на всех входах этой схемы Правила построения логических схем

Пример решение логических задач средствами алгебры логики

Логические схемы

Логическая схема – это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также из входов и выходов, на которые подаётся и с которых снимается электрический сигнал.

Каждый переключатель имеет только два состояния: замкнутое и разомкнутое . Переключателю Х поставим в соответствие логическую переменную х, которая принимает значение 1 в том и только в том случае, когда переключатель Х замкнут и схема проводит ток; если же переключатель разомкнут, то х равен нулю.

Две схемы называются равносильными , если через одну из них проходит ток тогда и только тогда, когда он проходит через другую (при одном и том же входном сигнале).

Из двух равносильных схем более простой считается та схема, функция проводимости которой содержит меньшее число логических операций или переключателей.

При рассмотрении переключательных схем возникают две основные задачи: синтез и анализ схемы.

СИНТЕЗ СХЕМЫ по заданным условиям ее работы сводится к следующим трём этапам:

1. составлению функции проводимости по таблице истинности, отражающей эти условия;
2. упрощению этой функции;
3. построению соответствующей схемы.

АНАЛИЗ СХЕМЫ сводится к:

1. определению значений её функции проводимости при всех возможных наборах входящих в эту функцию переменных.
2. получению упрощённой формулы.

Задача : Составить таблицу истинности для данной формулы: (x ~ z) | ((x y) ~ (y z)).

Решение

: В таблицу истинности данной формулы полезно включить таблицы истинности промежуточных функций:

xyz	x ~ z	x y	y z	(x y) ~ (y z)	(x~ z)|((x y) ~ (yz)

Методические указания для выполнения практического задания №2.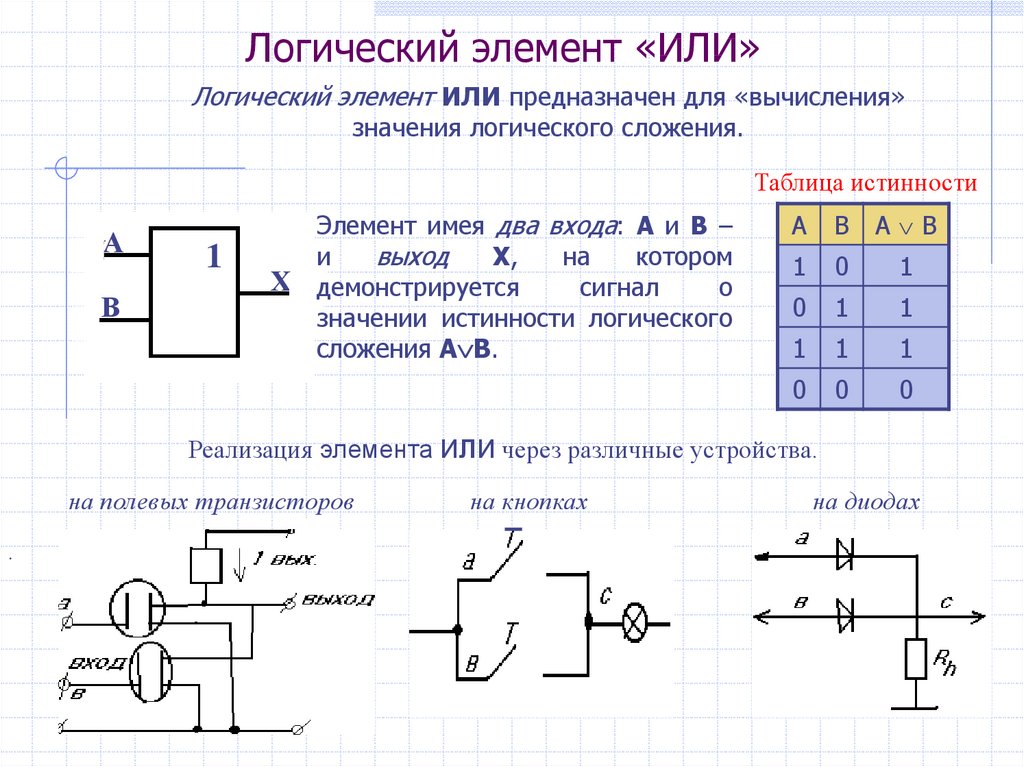 «Алгебра логики». Построение таблиц истинности.

Цель работы : Ознакомиться с основными арифметическими операциями, базовыми логическими элементами (И, И-НЕ, ИЛИ, ИЛИ-НЕ, исключающее ИЛИ) и изучить методы построения на их основе таблиц истинности.

Задание:

1. В приложении 2 выбрать вариант задания и составить таблицу истинности

.

2. Выполнить задание, используя пример решение логических задач средствами алгебры логики.

Задача :

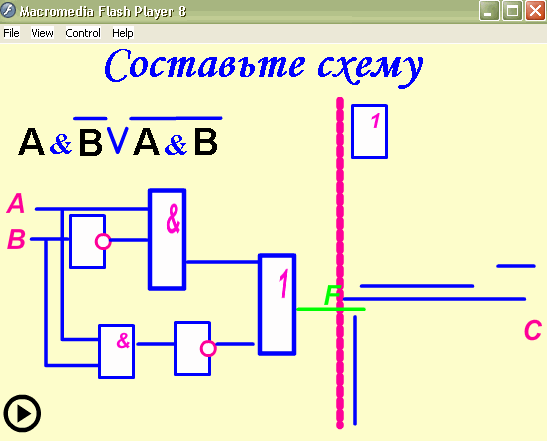
Построить логическую схему по заданному булевому выражению:

F =`BA + B`A + C`B.

Решение:

Как правило, построение и расчет любой схемы осуществляется начиная с ее выхода.

Первый этап : выполняется логическое сложение, логическую операцию ИЛИ, считая входными переменными функции`B A, B`A и C`B:

Второй этап : к входам элемента ИЛИ подключаются логические элементы И, входными переменными которых являются уже A, B, C и их инверсии:

Третий этап : для получения инверсий`A и`B на соответствующих входах ставят инверторы:

Данное построение основано на следующей особенности, – поскольку значениями логических функций могут быть только нули и единицы, то любые логические функции могут быть представлены как аргументы других более сложных функций. Таким образом, построение логической схемы осуществляется с выхода ко входу.

Методические указания для выполнения практического задания №3. «Алгебра логики». Построение логических схем

Цель работы : Ознакомиться с основными арифметическими операциями, базовыми логическими элементами (И, И-НЕ, ИЛИ, ИЛИ-НЕ, исключающее ИЛИ) и изучить методы построения на их основе простейших логических схем.

Задание:

1. В приложении 2 выбрать вариант задания и построить логическую схему .

2. Выполнить задание, используя пример построения логических схем.

3. Оформить работу в тетради для практических работ.

4. Результат работы предъявить преподавателю.

5. Защитить выполненную работу у преподавателя.

Приложение 2. Таблица вариантов заданий

Составить таблицу истинности и логическую схему для данных операций
Вариант	Операции

4. Индивидуальное задание. Модуль 1. «Построение логических схем по заданным булевым выражениям»

Задания к ИДЗ:

1. В приложении 3 выбрать вариант индивидуального задания.
2. Выполнить задание, пользуясь теоретическими сведениями
3. Проверить логическую схему у тьютора.
4. Оформить ИДЗ в формате А4, титульный лист по образцу Приложение 4.
5. Результат работы предъявить преподавателю.
6. Защитить выполненную работу у преподавателя.

Приложение 3. Таблица вариантов индивидуального задания

Варианты	Составить таблицу истинности и логическую схему по формулам

Приложение 4. Титульный лист ИДЗ

Почему необходимо уметь строить логические схемы?

Дело в том, что из вентилей составляют более сложные схемы, которые позволяют выполнить арифметические операции и хранить информацию. Причем схему, выполняющую определенные функции, можно построить из различных по сочетанию и количеству вентилей. Поэтому значение формального представления логической схемы чрезвычайно велико. Оно необходимо для того, чтобы разработчик имел возможность выбрать наиболее подходящий ему вариант построения схемы из вентилей. Процесс разработки общей логической схемы устройства (в том числе и компьютера в целом) таким образом становится иерархическим, причем на каждом следующем уровне в качестве «кирпичиков» используются логические схемы, созданные на предыдущем этапе.

Алгебра логики дала в руки конструкторам мощное средство разработки, анализа и совершенствования логических схем. В самом деле, гораздо проще, быстрее и дешевле изучать свойства и доказывать правильность работы схемы с помощью выражающей ее формулы, чем создавать реальное техническое устройство.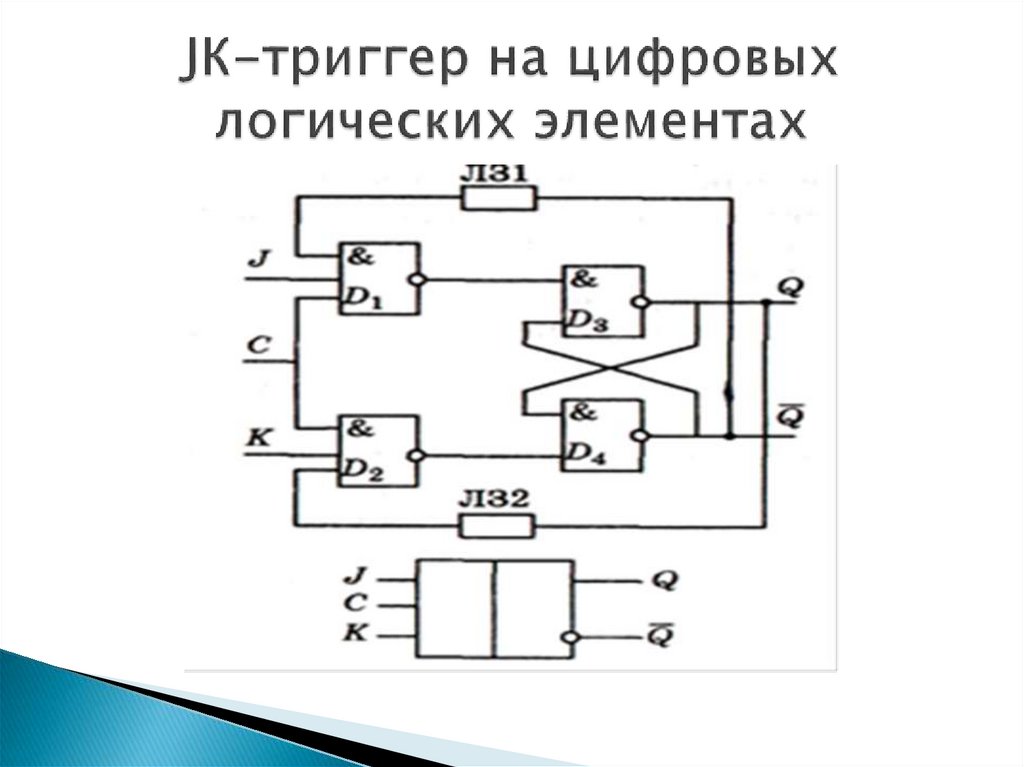

Именно в этом состоит смысл любого математического моделирования.

Логические схемы необходимо строить из минимально возможного количества элементов, что в свою очередь, обеспечивает большую скорость работы и увеличивает надежность устройства.

Алгоритм построения логических схем :

1) Определить число логических переменных.

2) Определить количество базовых логических операций и их порядок.

3) Изобразить для каждой логической операции соответствующий ей вентиль.

4) Соединить вентили в порядке выполнения логических операций.

Пример 10 Составить логическую схему для логического выражения: F =¬ X v Y & X . 1) Две переменные – X и Y . 2) Две логические операции: 1 3 2 ¬ X v Y & X . 3) Строим схему, соединяя вентили в порядке выполнения логических операций: Пример 11 Постройте логическую схему, соответствующую логическому выражению F = X & Y v¬ (Y v X ). Вычислить значения выражения для X =1, Y =0. 1) Переменных две: X и Y . 2) Логических операций четыре: конъюнкция, две дизъюнкции и отрицание. Определяем порядок выполнения операций: 1 4 3 2 X & Y v ¬ (Y v X ). 3) Схему строим слева направо в соответствии с порядком выполнения логических операций: 4) Вычислим значение выражения: F =1&0 v¬ (0 v 1)=0.

Упражнение 15

Постройте логическую схему, соответствующую логическому выражению, и найдите значение логического выражения:

1) F=A v B& ¬ C, если A=1, B=1, C=1 .

2) F = ¬ (A v B&C), если A=0, B=1, C=1 .

Разделы: Информатика

Цели:

1. Образовательные

• Основные логические операции.
• Построение таблиц истинности сложных высказываний.
• Логические схемы и логические выражения.

2. Развивающие

• Развитие исследовательской и познавательной деятельности.
• Лаконично, полно и содержательно отвечать и делать обобщающие выводы.

3. Воспитательные

• Формирование аккуратности при работе с компьютером.
• Понимание связей между другими учащимися, культурой поведения.

Тип урока: комбинированный

Методы организации учебной деятельности:

• фронтальная
• индивидуальная
• ученик-компьютер

Программно-дидактическое обеспечение: ПК, презентация, задание для практической работы, раздаточный материал, Electronics Workbench (EWB512), PowerPoint.

ХОД УРОКА

I. Организационный момент.

II. Актуализация ранее изученного материала и проверка домашнего задания.

Задания для выполнения в тетради и у доски.

№1. Составьте таблицы истинности для следующих логических выражений:

№3. Нарисовать на доске логические элементы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ.

III. Новый материал.

Над возможностями применения логики в технике ученые и инженеры задумывались уже давно.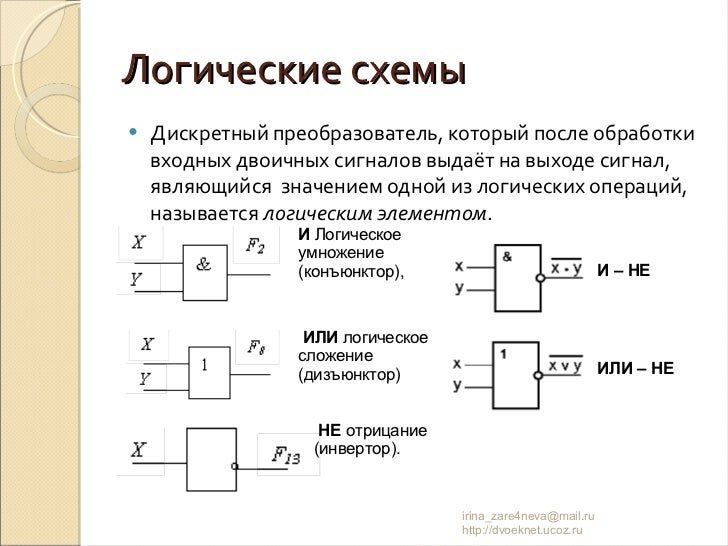 Например, голландский физик Пауль Эренфест (1880 — 1933), еще в 1910 году писал: «…Пусть имеется проект схемы проводов автоматической телефонной станции. Надо определить:

1) будет ли она правильно функционировать при любой комбинации, могущей встретиться в ходе деятельности станции;
2) не содержит ли она излишних усложнений.

Каждая такая комбинация является посылкой, каждый маленький коммутатор есть логическое «или-или», воплощенное в эбоните и латуни; все вместе — система чисто качественных… «посылок», ничего не оставляющая желать в отношении сложности и запутанности… правда ли, что, несмотря на существование алгебры логики, своего рода «алгебра распределительных схем» должна считаться утопией?».

Созданная позднее М.А. Гавриловым (1903 — 1979) теория релейно-контактных схем показала, что это вовсе не утопия.

Посмотрим на микросхему. На первый взгляд ничего того, что нас бы удивило, мы не видим!
Но если рассматривать ее при сильном увеличении, она поразит нас своей стройной архитектурой.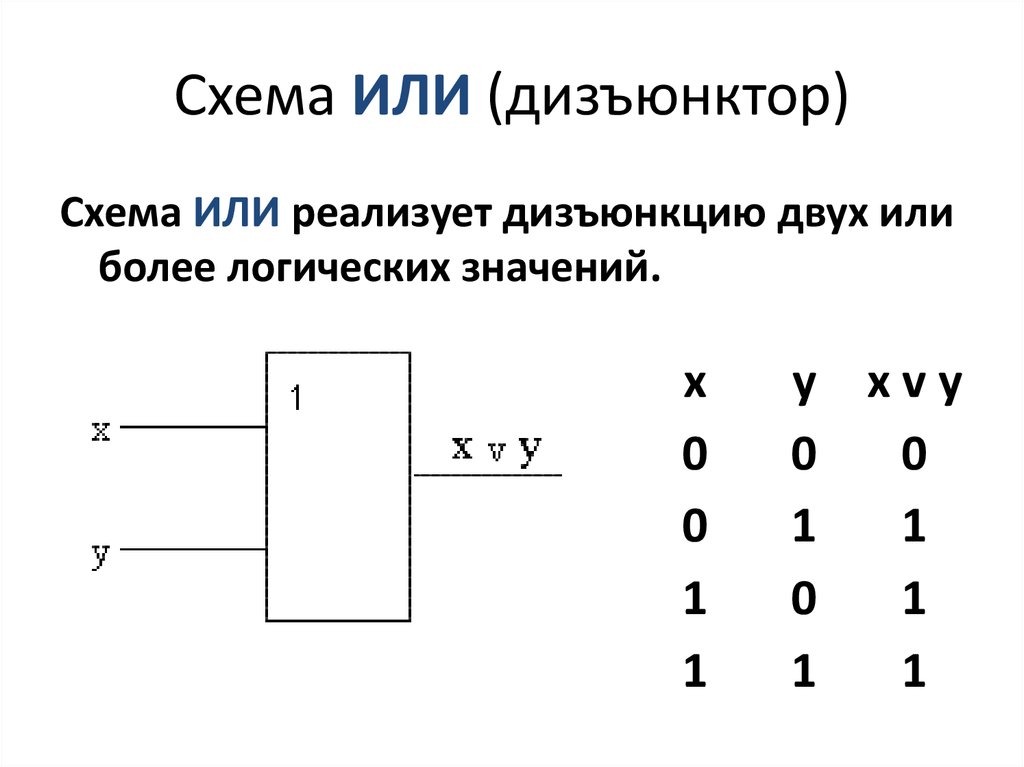 Чтобы понять, как она работает, вспомним, что компьютер работает на электричестве, то есть любая информация представлена в компьютере в виде электрических импульсов.

Почему необходимо уметь строить логические схемы?

Дело в том, что из вентилей составляют более сложные схемы, которые позволяют выполнять арифметические операции и хранить информацию. Причем схему, выполняющую определенные функции, можно построить из различных по сочетанию и количеству вентилей. Поэтому значение формального представления логической схемы чрезвычайно велико. Оно необходимо для того, чтобы разработчик имел возможность выбрать наиболее подходящий ему вариант построения схемы из вентилей. Процесс разработки общей логической схемы устройства (в том числе и компьютера в целом), становится иерархическим, причем на каждом следующем уровне в качестве «кирпичиков» используются логические схемы, созданные на предыдущем этапе.
Алгебра логики дала в руки конструкторам мощное средство разработки, анализа и совершенствования логических схем. В самом деле, гораздо проще, быстрее и дешевле изучать свойства и доказывать правильность работы схемы с помощью выражающей ее формулы, чем создавать реальное техническое устройство. Именно в этом состоит смысл любого математического моделирования.

Логические схемы необходимо строить из минимально возможного количества элементов, что в свою очередь, обеспечивает большую скорость работы и увеличивает надежность устройства.

Правило построения логических схем:

1) Определить число логических переменных.
2) Определить количество базовых логических операций и их порядок.
3) Изобразить для каждой логической операции соответствующий ей вентиль и соединить вентили в порядке выполнения логических операций.

Рассмотрение двух примеров перехода от выражения к схеме. (Презентация)

Рассмотрение двух примеров перехода от схемы к выражению. (Презентация)

Чаще в жизни возникает ситуация, когда известен результат и для его реализации необходимо построить устройство.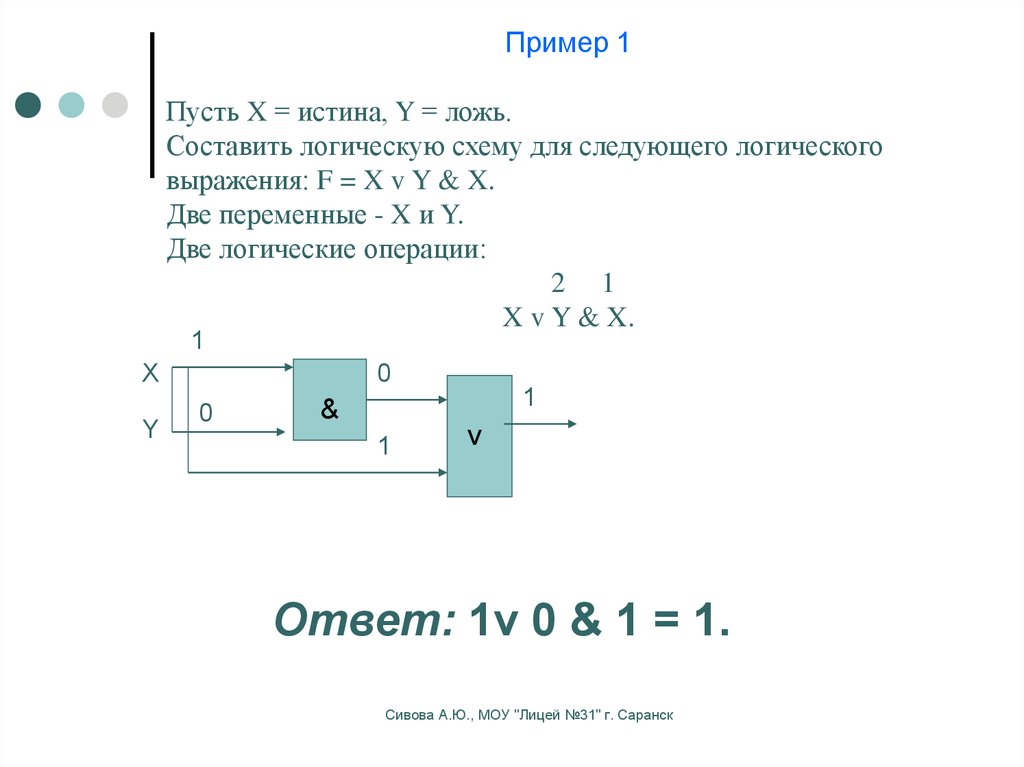

Рассмотрим следующую задачу: (Презентация)

Задача 1. В двухэтажном доме лестница освещается одной лампой Х. На первом этаже установлен один выключатель А, на втором этаже — выключатель В. Если включают А, то лампа загорается. При поднятии на второй этаж и включении В лампа гаснет. Если кто-то выходит и нажмет В, то лампа включается, при спуске на первый этаж и нажатии А лампа должна погаснуть.

Алгоритм решения:

• Составить таблицу истинности.
• Определить логическую функцию.
• Построить логическую схему.

A	B	X
0	0	0
1	0	1
1	1	0
0	1	1
0	0	0

Чтобы создать логическую функцию по таблице истинности, надо записывать значения выходной переменной.

Между строками таблицы будет стоять знак логического сложения, а между столбцами — знак логического умножения .

IV. Закрепление изученного материала.

Работа у доски и в тетради по карточкам.

№1. По логическому выражению построить логическую схему:

№2. По логической схеме составьте логическое выражение:

V. Компьютерный практикум.

Практическая работа с использованием электронной лаборатории Electronics Workbench (EWB512).

Вариант 1

1. Упростите логическое выражение

2. Проверьте свою работу, используя программу Electronics Workbench:

Запишите исходное выражение в Logic Converter;
— Составьте таблицу истинности
— Упростите выражение используя
— Постройте упрощенную логическую схему .

3. Проверьте правильность выполненных упрощений.

VI. Домашнее задание:

а) упростите логическое выражение, постройте логическую схему и таблицу истинности
б) по таблице истинности (00001011) составьте выражение, упростите его, нарисуйте схему.

Конспект урока
«Построение логических схем с помощью базовых логических элементов»

10 класс

Тип урока: лекция, самостоятельная работа.

Оборудование: проектор, карточки с заданиями.

Формы работы: коллективная, индивидуальная.

Продолжительность урока: 45 мин.

Цели урока:

Образовательные:

научиться строить логические схемы для логических функций с помощью основных базовых логических элементов;

научиться выписывать соответствующую логическую функцию из логической схемы.

Воспитательные:

привитие навыков самостоятельности в работе, воспитание аккуратности, дисциплинированности.

Развивающие:

развитие внимания, мышления, памяти учащихся.

Ход урока:

1. Организационный момент (1 мин).
2. Проверка пройденного материала (5 мин).

Фронтальный опрос.

Перечислите основные логические операции.

Что такое логическое умножение?

Что такое логическое сложение?

Что такое инверсия?

Что такое таблица истинности?

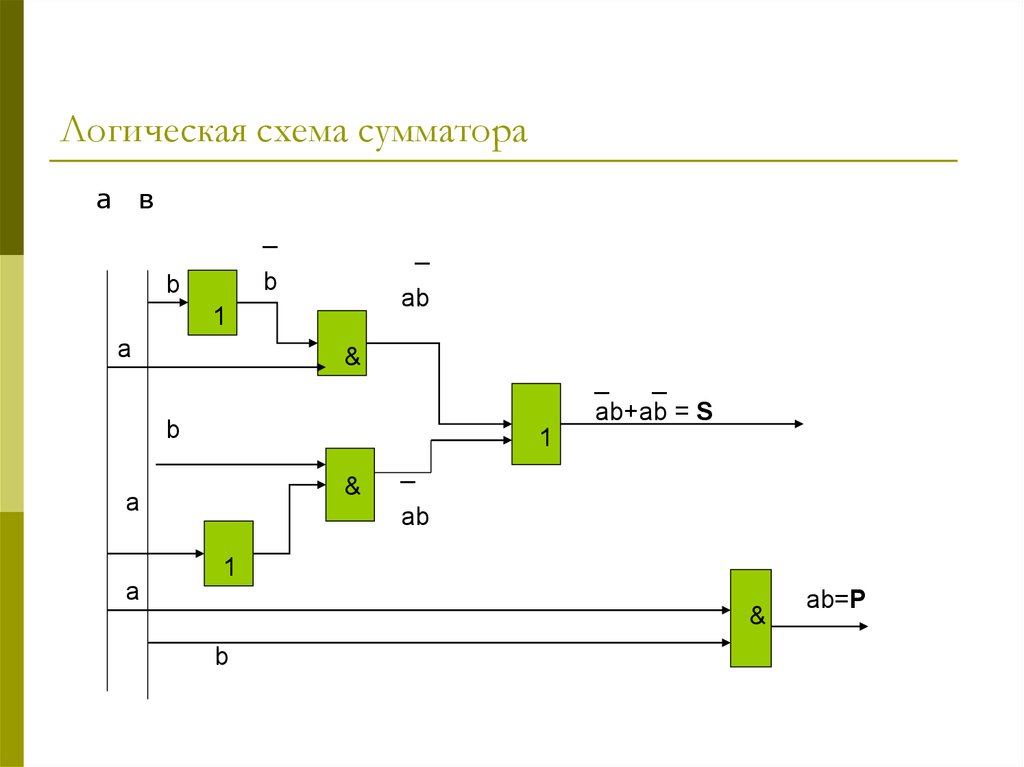
Что такое сумматор?

Что такое полусумматор?

3. Изучение нового материала (20 мин).

Дискретный преобразователь, который после обработки входных двоичных сигналов выдает на выходе сигнал, являющийся значением одной из логических операций, называется логическим элементом.
Поскольку любая логическая операция может быть представлена в виде комбинаций трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов, как из «кирпичиков».
Логические элементы компьютера оперируют сигналами, представляющими собой электрические импульсы. Есть импульс – логический смысл сигнала – 1, нет импульса – 0. На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции.
Преобразование сигнала логическим элементом задается таблицей состояния, которая фактически является таблицей истинности, соответствующей логической функции.
На доске приведены условные обозначения (схемы) базовых логических элементов, реализующих логическое умножение (конъюнктор), логическое сложение (дизъюнктор) и отрицание (инвертор).

Логический элемент «И»:

Логический элемент «ИЛИ»:

Логический элемент «НЕ»:

Устройства компьютера (сумматоры в процессоре, ячейки памяти в оперативной памяти и др.) строятся на основе базовых логических элементов.

Пример 1. построить логическую схему.

Наше построение схемы, мы начнем с логической операции, которая должна выполнятся последней. В нашем случае такой операцией является логическое сложение, следовательно, на выходе логической схемы должен быть дизъюнктор. На него сигналы будут подаваться с двух конъюнкторов, на которые в свою очередь подаются один входной сигнал нормальный и один инвертированный (с инверторов).

Пример 2. Выписать из логической схемы соответствующую ей логическую формулу:

Решение:

4. Закрепление нового материала (15 мин).

Для закрепления материала учащимся раздаются карточки на два варианта для самостоятельной работы.

Вариант 1.

Решение:

Решение:

Вариант 2.

1. По заданной логической функции построить логическую схему и таблицу истинности.
Решение:

2. Выписать из логической схемы соответствующую ей логическую формулу:

Решение:

5. Постановка домашнего задания. (3 мин).

По заданной логической функции построить логическую схему и таблицу истинности.

6. Подведение итогов урока. (1 мин).

Проанализировать, дать оценку успешности достижения цели и наметить перспективу на будущее. Оценка работы класса и отдельных учащихся, аргументация выставления отметок, замечания по уроку.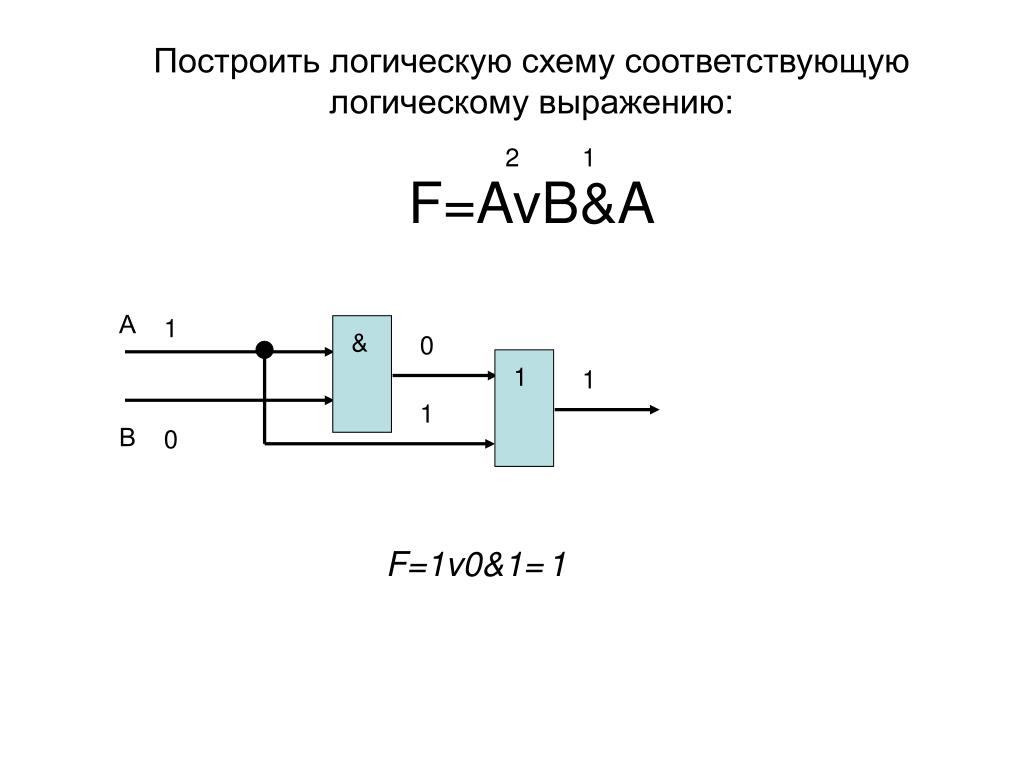

Литература, эор:

Информатика и информационные технологии. Учебник для 10-11 классов, Н. Д. Угринович – 2007г.;

Практикум по информатике и информационным технологиям. Учебное пособие для общеобразовательных учреждений, Н. Д. Угринович, Л. Л. Босова, Н. И. Михайлова – 2007г.

Познакомимся с ними поочередно.

Построение логической схемы по заданной логической функции.

Задача:

Дана логическая функция:

Составить логическую схему для неё.

Решение:

Расставим порядок выполнения логических операций, руководствуясь правилами:

1. отрицание
2. умножение
3. сложение

Не забываем про приоритет скобок.
Получаем:

Строим схему по указанному порядку.

Запись логической функции по заданной логической схеме.

Задача:

Дана логическая схема:

Составить логическую функцию по ней.

Решение:

Рассматриваем схему с конца и записываем соответствующие логические операции, учитывая, что в записываемой функции три операнда А, В, С

Можно сначала подписать на схеме промежуточные функции, получаемые на выходе каждого блока, а потом сцепить их логическими операциями.

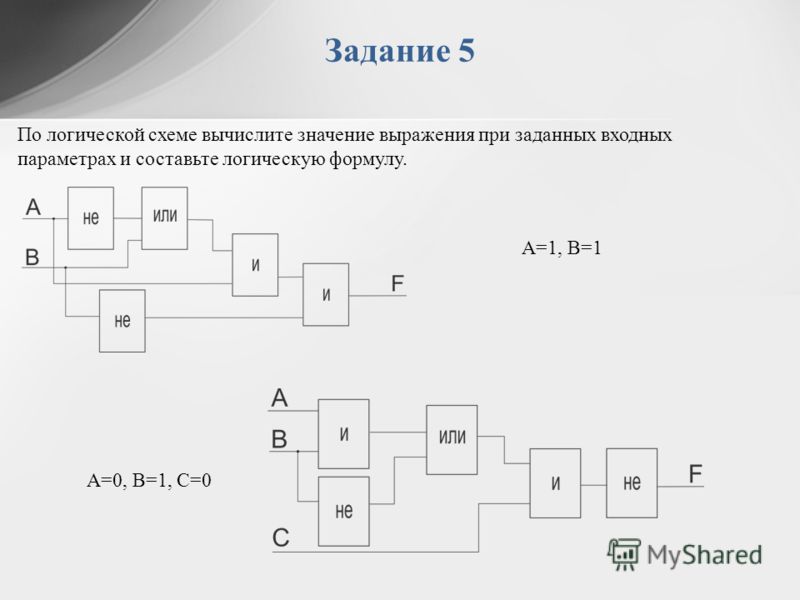
Определение сигнала на выходе логической схемы по заданным значениям сигналов на всех входах этой схемы.

Задача:

Дана логическая схема и значения сигналов на всех входах:

Определить значение функции F на выходе схемы.

Решение:

Пользуясь таблицами истинности для соответствующих логических элементов схемы, расставляем значения сигналов на выходах и соответственно на входах каждого логического элемента пока не доберёмся до конца схемы. Получаем:

Ответ:

Значение функции F на выходе схемы = 1.

Построение таблицы истинности для заданной логической схемы.

Задача:

Дана логическая схема:

Построить для неё таблицу истинности.

Решение:

Проверяем количество входов на схеме. Количество комбинаций сигналов на 2 входах равно 4, для 3 входов равно 8, для 4 входов равно 16 и т. д. Составляем таблицу истинности, в которой первые столбцы — это входы схемы, обозначенные буквами, следущие столбцы — функции, полученные на выходах каждого элемента схемы, а строки — отражают разные комбинации сигналов на входах. Количество строк совпадает с количеством комбинаций сигналов. Пользуясь таблицами истинности для соответствующих логических элементов схемы, расставляем значения сигналов на выходах каждого логического элемента, т. е. по каждому столбцу пока не доберёмся до конца схемы. Получаем:

Ответ:

25. Логические функции. Построение логических схем.

    Правильность построения логической схемы можно проверить, сравнив результат работы логических преобразователей логической схемы со значением соответствующей логической функции, записанным в таблице истинности для каждого набора значений логических аргументов. Например, результатом работы логической схемы для значений логических аргументов A=1, B=0 будет значение F(A, B) = 0. На рисунке ниже представлена проверка логической схемы с этими значениями:

    Сравнив значение, полученное на выходе логической схемы, со значением логической функции для соответствующих логических аргументов (см. Таблица №1), можно убедиться, что для этих значений логических аргументов логическая схема работает верно. 

    Логические преобразователи могут быть строены по-разному. Различают механические, пневматические, гидравлические, электрические, электронные и другие логические преобразователи. Так, например, в качестве логического преобразователя «НЕ» может использоваться электрическое реле с замкнутыми контактами. При отсутствии тока на обмотке реле (логический ноль) ток течет через замкнутые контакты (логическая единица). И наоборот, когда на обмотку реле подается ток (логическая единица), реле срабатывает, размыкает соединение и течение тока через контакты прекращается (логический ноль). 

    Примером логического преобразователя «И» является обычная елочная гирлянда. Она горит (логическая единица) только тогда, когда исправны все последовательно соединенные в гирлянде лампочки (логические единицы). Выход из строя хотя бы одной лампы (логический ноль) приводит к тому, что гаснет вся гирлянда (логический ноль). В то же время люстру, состоящую из нескольких ламп, соединенных параллельно, можно рассматривать в качестве примера электрического логического преобразователя «ИЛИ». Такой светильник не может освещать помещение (логический ноль) только тогда, когда неисправны все без исключения лампы (логические нули).  

    Работа современных компьютеров основана на использовании электронных логических преобразователей. Объединение миллионов таких электронных компонентов позволяет создавать микропроцессор, микросхемы оперативной памяти и другие устройства. 

    Таким образом, действия над информацией можно описать с помощью логических выражений и логических функций. Выполнение входящих в их состав логических операций можно осуществить с помощью основных логических преобразователей. Правильное соединение этих элементов в логические схемы позволяет создать устройства, выполняющие достаточно сложные действия над информацией, а значит, и дающие возможность автоматизировать информационные процессы.

Практические задания.

Кроссворд по теме «Логические функции. Построение логических схем». (Онлайн — версия)

В разделе «Файлы» доступна версия для скачивания.

Тест по теме «Логические функции. Построение логических схем»

Логические схемы (Интерактивное задание)
Сопоставь логические схемы и соответствующие им логические функции.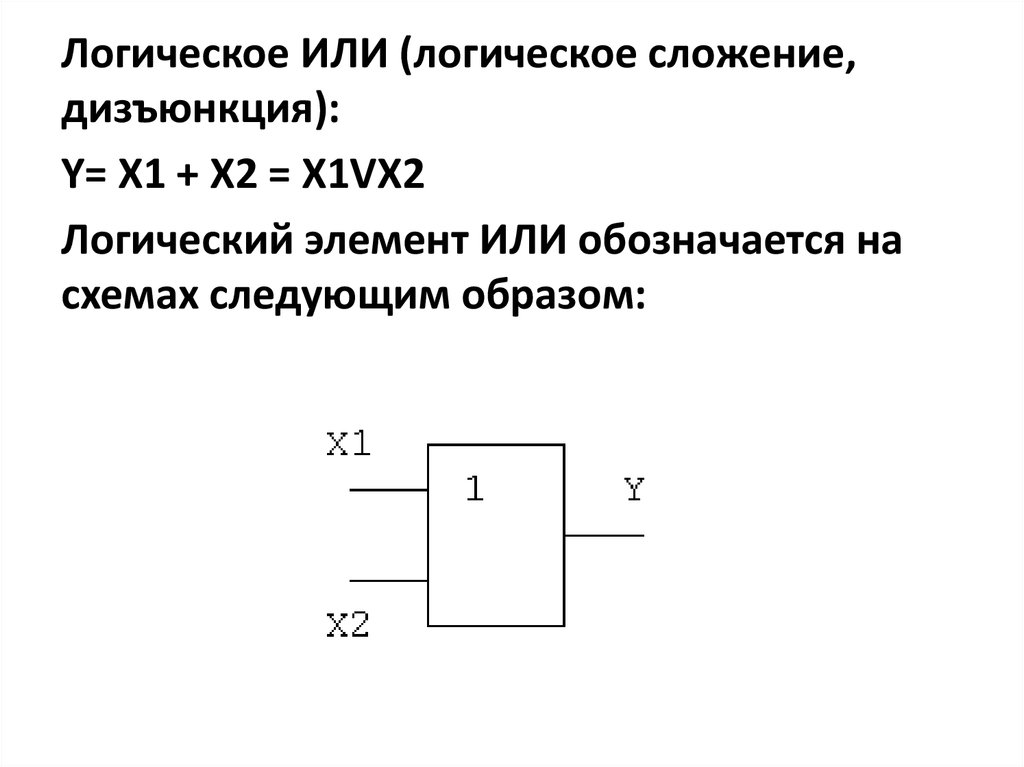

Видео с вопросами: Использование таблиц истинности для поиска выходных данных логических схем

Стенограмма видео

На схеме показана логическая схема состоящая из нескольких логических элементов. В таблице показан результат для некоторых различных возможных комбинаций входных данных.

Итак, у нас есть принципиальная схема показывая нам три логических элемента, объединенных вместе, чтобы сформировать логическую схему. И здесь у нас есть таблица, показывающая некоторые возможные комбинации значений для входов A, B, C и D и значение для вывод в каждом случае.

Теперь первый вопрос задает нам каково значение 𝑝 в таблице?

Итак, если мы посмотрим в таблицу, мы можно увидеть, что он не полностью заполнен нулями и единицами. Фактически, для некоторых строк вывод значения были помечены как 𝑝, 𝑞, 𝑟 и 𝑠. И первый вопрос задает нам чтобы найти значение 𝑝. Итак, чтобы сделать это, первое, что нужно мы собираемся сделать, это идентифицировать логические вентили, которые мы находим в этой логике. схема. Мы видим, что их три разные логические элементы, но два из них идентичны. Этот логический элемент имеет тот же символ как этот логический вентиль. Теперь мы можем вспомнить, исходя из их символы, что эти логические вентили на самом деле являются вентилями ИЛИ, а другие логические вентили, вот этот — вентиль И. И теперь, когда мы определили это, стоит вспомнить таблицы истинности для вентилей ИЛИ и И. Итак, вот таблица истинности для ИЛИ ворота. А вот таблица истинности для И ворота. Стоит отметить, что мы использовали 𝛼 и 𝛽 в обоих случаях для представления входных данных и 𝛺 для представления выходных данных эти ворота.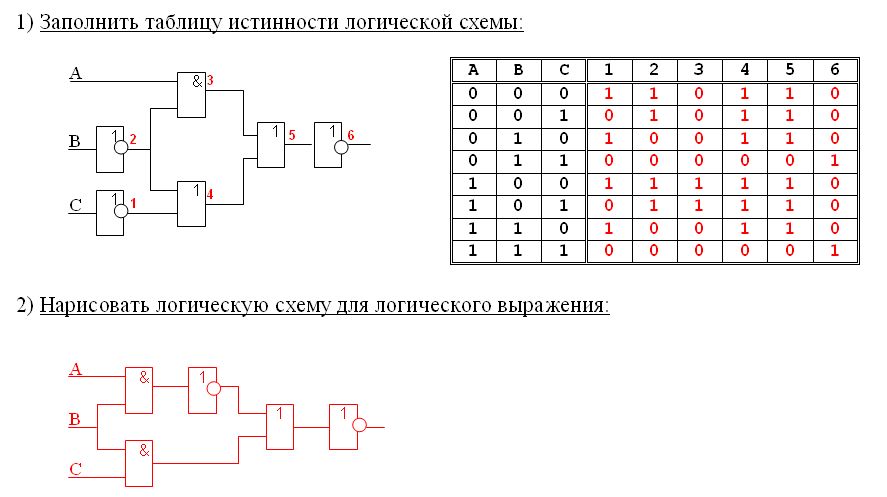 Чтобы мы не путались с эти входы и этот выход, которые уже были обозначены на нашей диаграмме.

Теперь мы можем видеть, что для ИЛИ ворота, выход устанавливается в единицу, если либо вход 𝛼, либо вход 𝛽 установлен в единицу. И для вентиля И выход устанавливается в единицу только в том случае, если и вход 𝛼, и ввод 𝛽 установлены в единицу. Теперь, возвращаясь к нашей логике принципиальной схемы, мы можем видеть, что выход первого элемента ИЛИ становится одним из входы в логический элемент И. И то же самое верно для вывода вторых ворот ИЛИ. Он становится вторым входом в И ворота. Так что, возможно, стоит продлить наша таблица истинности здесь немного. В частности, возможно, стоит вызывая выход первого логического положения ИЛИ E и выход второго ИЛИ положение ворот F. И E, и F затем становятся входы логического элемента И. И, возможно, стоит отслеживать что с ними происходит, хотя бы на промежуточных стадиях добавлением двух лишних столбцы нашей таблицы истинности. Мы можем удалить их, как только мы заполнил таблицу истинности. Но пока будет полезно иметь их там.

Таким образом, если мы пытаясь вычислить значение 𝑝, то это соответствует тому, когда вход A установлен на ноль, B устанавливается равным нулю, C устанавливается равным нулю и D устанавливается равным нулю. Итак, начнем с расстановки нулей рядом с входом A, B, C и D. Затем мы видим, что входы A и B являются входами в первый вентиль ИЛИ. Таким образом, мы можем решить, что выход того ИЛИ ворот будет. Другими словами, то, что E собирается сделать использовать таблицу истинности для вентиля ИЛИ.

Мы видим, что когда оба входа вентиль ИЛИ устанавливается в ноль, тогда выход также устанавливается в ноль. И поэтому мы можем видеть, что выход первого элемента ИЛИ, то есть E, будет равен нулю. И тогда мы можем сделать то же самое для входов C и D. Это входы для второго ИЛИ ворота. И поскольку оба они установлены на ноль, мы можем видеть, что выход вентиля ИЛИ, то есть F, будет равен нулю, поскольку хорошо. Но тогда то, что у нас происходит, что E и F становятся входами логического элемента AND. А так как в данном конкретном случае оба они установлены на ноль, мы можем видеть, что когда оба входа логического элемента И установлен в ноль, выход логического элемента И также равен нулю. И, следовательно, мы можем сказать, что выход всей логической схемы сам обнуляется. Но тогда это выходное значение соответствует 𝑝. И вот в этот момент мы прикинули вышел ответ на первый вопрос. Значение 𝑝 в таблице равно нуль. Итак, ответив на это, мы можем перейти к следующему вопросу.

Каково значение 𝑞 в стол?

Теперь мы видим, что 𝑞 — это выходное значение, которое соответствует, когда вход A равен нулю, вход B равен нулю, вход C равен ноль, а вход D равен единице. Итак, давайте поставим значения ноль, ноль, ноль и единица рядом с входами A, B, C и D соответственно. Тогда мы видим, что входные данные для первый вентиль ИЛИ устанавливается в ноль. Итак, глядя на правду о наших воротах ИЛИ В таблице мы видим, что когда оба входа равны нулю, выход также равен нулю. Иными словами, в этом конкретном случае значение E равно нулю. И тогда мы можем видеть, что входы C и D равны нулю и единице соответственно. Итак, мы видим, что когда первый вход установлен на ноль, а второй вход установлен на единицу для вентиля ИЛИ, выход вентиля ИЛИ равен единице.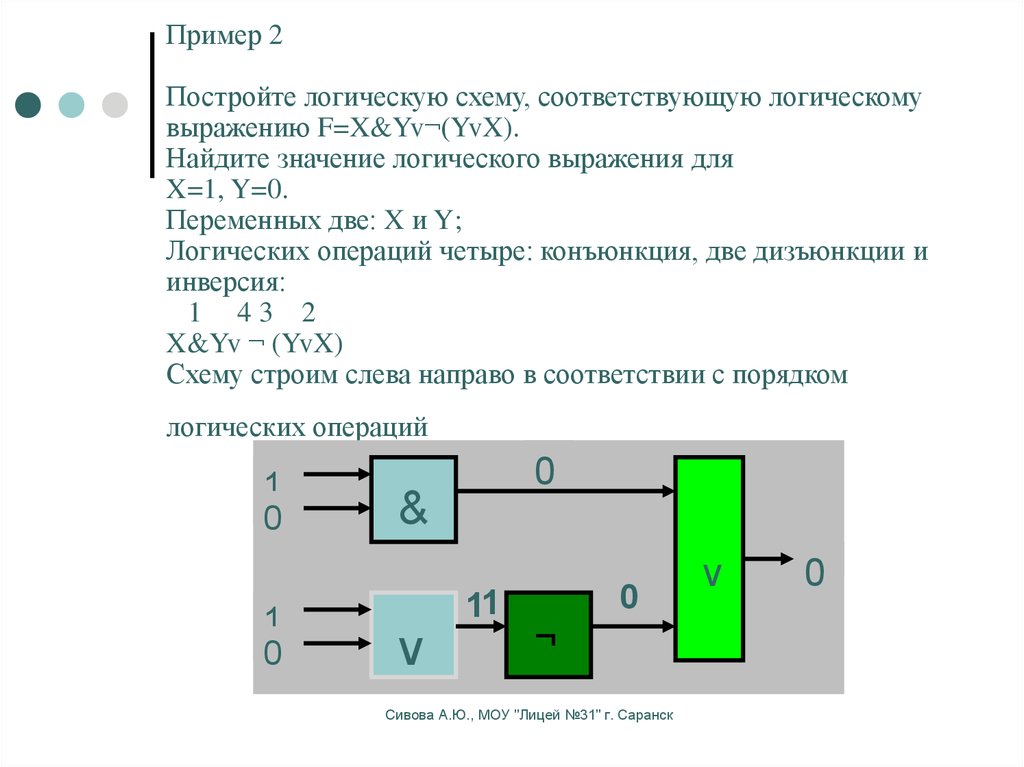 Итак, в этом случае значение F это один. Итак, что у нас сейчас происходит, значение Е равно нулю. И значение F равно единице. И они становятся входными данными к воротам И. И поэтому, когда первый вход в Логический элемент И установлен в ноль, а второй вход установлен в единицу, выход И ворота нулевые. И вот в этот момент мы нашли значение 𝑞 в нашей таблице. Значение 𝑞 равно нулю.

Тогда переходим к следующему вопросу, этот спрашивает нас, каково значение 𝑟 в таблице?

Теперь 𝑟 соответствует входу A равен нулю, вход B равен нулю, вход C равен единице, а вход D равен единице. И поэтому, если мы установим эти значения рядом на входы A, B, C и D соответственно, мы видим, что ввод двух нулей приводит вывод нуля для вентиля ИЛИ. Таким образом, значение E равно нулю, тогда как a набор из двух единиц в качестве входов в вентиль ИЛИ приводит к выходу из одной. Таким образом, значение F равно единице. Но это мы уже видели если первый вход логического элемента И равен нулю, а второй установлен в единицу, то выход логического элемента И будет равен нулю. Итак, наше значение 𝑟 равно нулю. Итак, мы нашли ответ на этот вопрос.

Переходим к нашему последнему вопросу. тогда каково значение 𝑠 в таблице?

Теперь мы видим, что 𝑠 соответствует на входной набор из нуля, единицы, единицы и нуля. Поэтому запишите их рядом с входы A, B, C и D, мы видим, что когда первый вход равен нулю, а второй вход один для вентиля ИЛИ, выход один. Итак, мы видим, что значение E это один. Во-вторых, мы можем видеть для нижней Элемент ИЛИ, если первый вход равен единице, а второй вход равен нулю, то выход равен тоже один. Итак, наше значение F равно единице. И так сейчас происходит то, что два входа логического элемента И, E и F, установлены в единицу.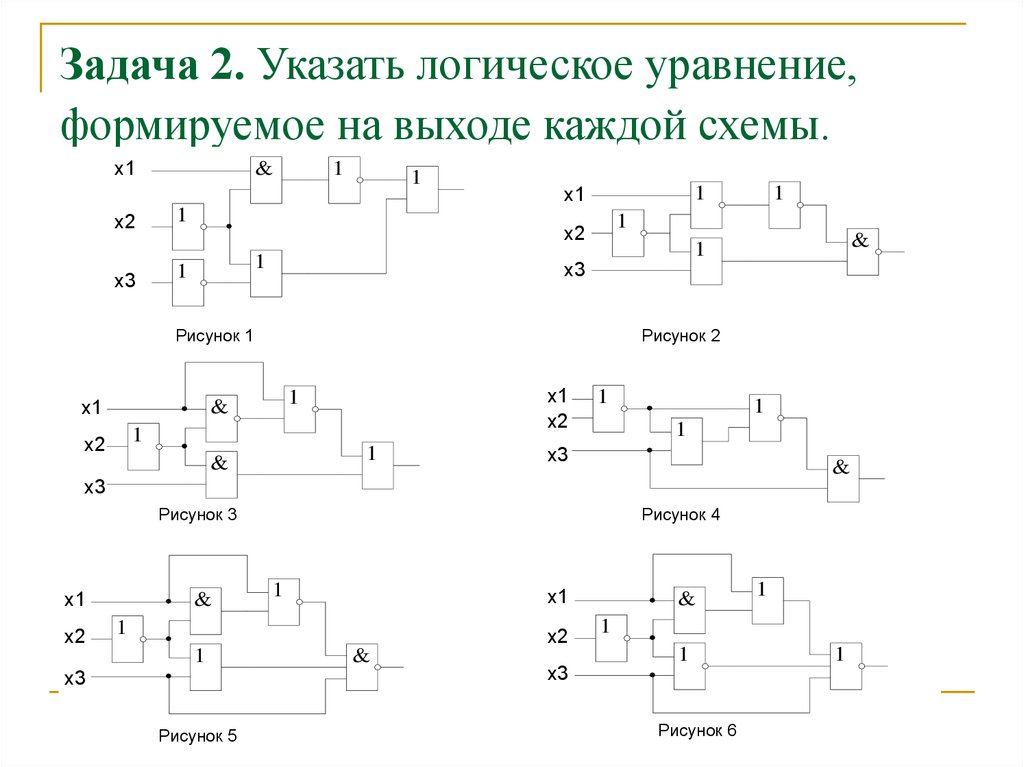 И мы можем видеть, что когда оба входы установлены на единицу для логического элемента И, выход также равен единице. Таким образом, на данный момент мы нашли значение 𝑠 в нашей таблице. Итак, теперь, когда мы все посчитали необходимые значения, мы можем избавиться от столбцов для E и F. И мы можем вспомнить, что 𝑝 было равно нулю, 𝑞 было нулем, 𝑟 было нулем, а 𝑠 было единицей.

CuriouSTEM — Логические ворота — Что это такое?

6-8 классы Технологии

30 сент.

Автор Rema Shivakumar, CuriouSTEM Staff

Как мы видели в предыдущей статье о двоичной системе счисления, компьютеры используют двоичные данные для своей работы. Компьютерам нужен способ манипулировать входными данными, поступающими в виде нулей и единиц, для выполнения различных операций и получения двоичного вывода.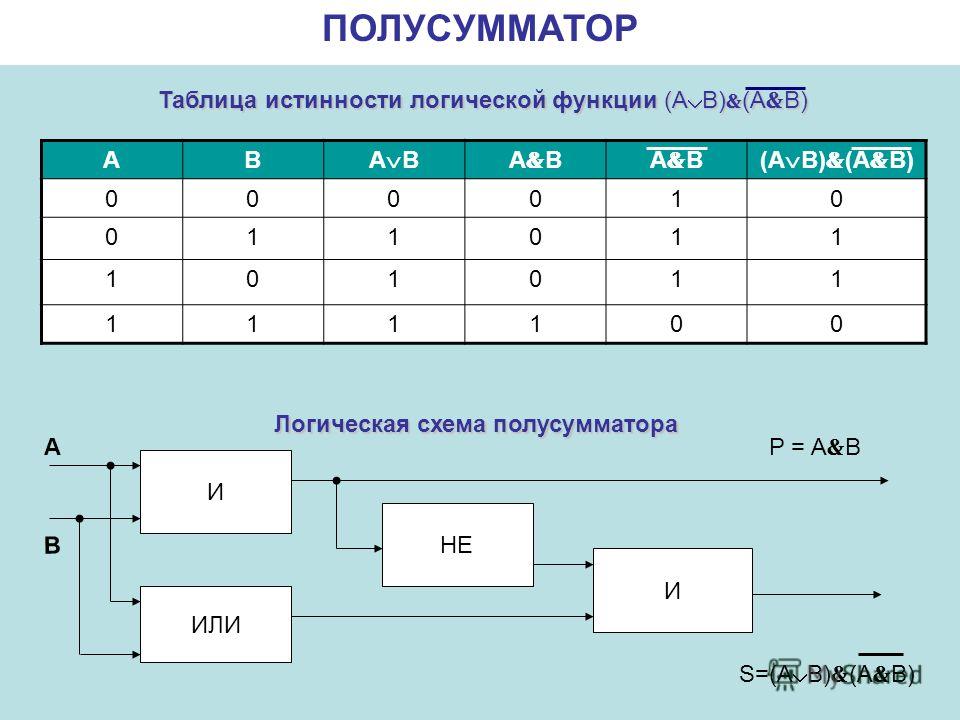 Здесь на помощь приходят логические вентили. Логические вентили — это устройства, подобные транзисторам, которые можно использовать для реализации логических функций. Булевы функции обозначают логические операции, в которых есть несколько двоичных входов и один выход. Таким образом, логические элементы являются, по сути, строительными блоками цифровых систем.

Логические элементы работают по принципу, согласно которому цифровые схемы работают с двумя логическими/двоичными значениями 0 и 1. Когда двоичные входы входят в логический элемент, выход принимает значение 0 или 1 после выполнения некоторых логических операций (подключенных в вентиле). ). Логические элементы построены с использованием диодов или транзисторов, которые действуют как переключатели. Логические элементы могут быть соединены между собой несколькими способами для представления любой булевой функции и, следовательно, любого алгоритма или сложной операции. Эти вентили используются во множестве цифровых схем, таких как регистры, компьютерная память, арифметико-логические устройства (ALU), микропроцессоры и т.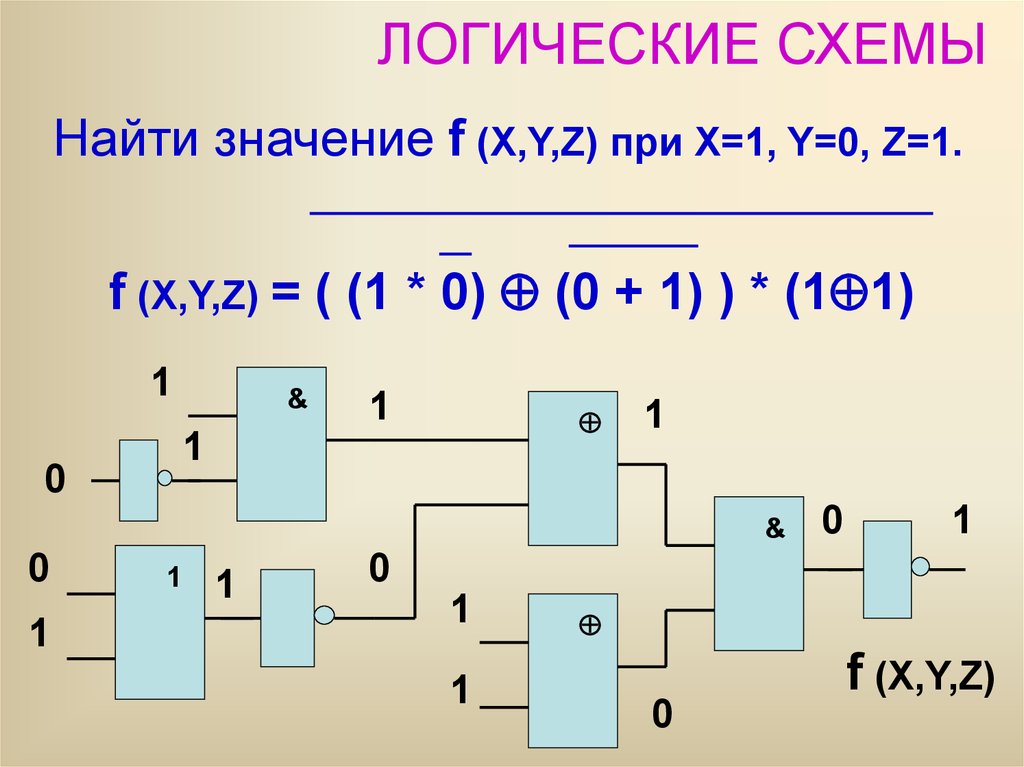 д.

Существует семь типов логических вентилей. Входы и выходы вентилей представлены значениями 0 и 1 или True(T) и False(F). Мы можем представить функцию, выполняемую логическим вентилем, в виде логического выражения или таблицы истинности. Таблицы истинности представляют различные комбинации входов и соответствующих выходов для любого заданного логического элемента. Давайте рассмотрим различные типы логических элементов с двумя входами:

1) Элемент И: Элемент И имеет два входа (A и B) и один выход (Q). Значение Q равно 1(T) только тогда, когда и A, и B равны 1(T).
Логическое выражение: Q = A.B
Q = A AND B

2) Элемент ИЛИ: Элемент ИЛИ имеет два входа (A и B) и один выход (Q). Значение Q принимает значение 1(T), если либо A, либо B, либо оба равны 1(T).
Логическое выражение: Q = A+B
Q = A ИЛИ B

3) Элемент NOT: Элемент NOT имеет один вход (A) и один выход (Q). Значение Q является отрицательным значением ввода. Следовательно, если A есть 1(T), Q есть 0(F) и наоборот.
Логическое выражение: Q = НЕ A

4) Элемент И-НЕ: Элемент И-НЕ имеет два входа (А и В) и один выход (Q). Значение Q является отрицательным выходом логического элемента И. Следовательно, этот вентиль возвращает 1(T), когда любой из входов равен 0(F).
Логическое выражение: Q = НЕ(A.B)
Q = НЕ(A AND B)
5) Логический элемент ИЛИ: Логический элемент ИЛИ-ИЛИ имеет два входа (A и B) и один выход (Q). Значение Q является инвертированным выходом вентиля ИЛИ. Следовательно, этот вентиль возвращает 0 (F), когда любой из входов равен 1 (T).
Логическое выражение: Q = НЕ(А+В)
Q = НЕ(А ИЛИ В)

6) Схема XOR: Схема XOR обозначает схему Исключающее ИЛИ. Этот вентиль имеет два входа (A и B) и один выход Q. Выход Q равен 1(T), если либо A, либо B истинно, но Q равен 0(F), когда оба они равны 1(T).
Логическое выражение: Q = (A И НЕ B) ИЛИ (НЕ A И B)
Q = A⊕B

7) Схема XNOR: Схема XNOR обозначает исключающую схему NOR. Этот вентиль имеет два входа (A и B) и один выход Q.