Добавление постоянной составляющей сигнала на выход генератора функций
24 Марта 2018
Максим Писковацков,
руководитель направления измерительного оборудования общего назначения
[email protected]
Подача постоянной составляющей на выход генератора функций необходима при различных испытаниях радиоэлектронной аппаратуры. Результирующий сигнал, подаваемый на испытуемое устройство, представляет собой известную форму волны, наложенную на напряжение постоянного тока. Например, для проверки устойчивости схем к шуму, который может возникнуть на реальных рабочих напряжениях, можно использовать синусоидальную волну, добавленную поверх напряжения смещения. При испытании усилителя смещение транзистора можно производить с помощью постоянного напряжения, переменная составляющая которого располагалась бы поверх этого напряжения. Даже повторяющуюся серию униполярных импульсов, используемую для управления затвором полярного транзистора в DC/DC-преобразователях, принято рассматривать как импульсную последовательность с постоянным смещением.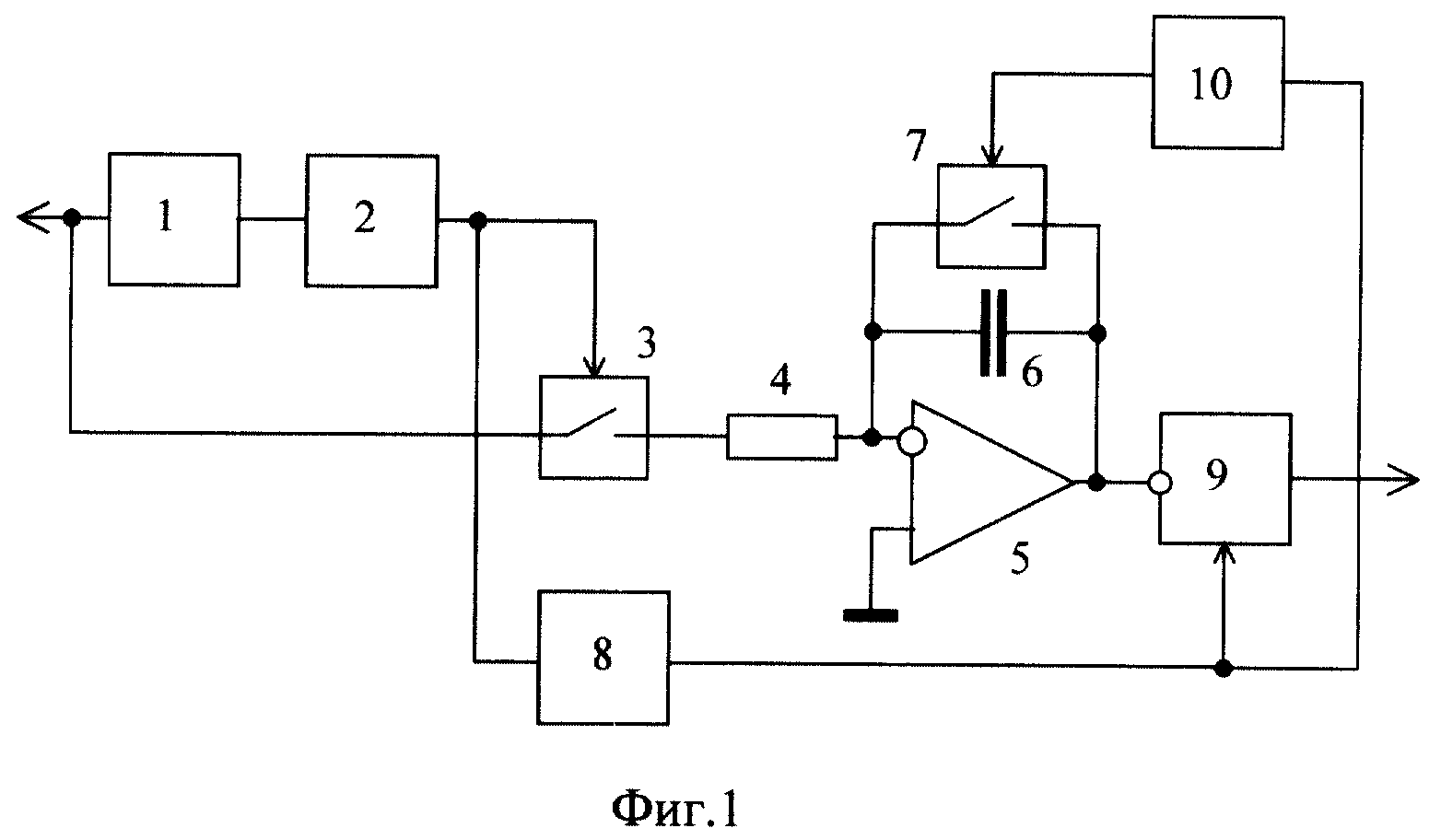
Существуют разные методы генерации форм сигнала, наложенных поверх напряжения постоянного тока. Генератор функций может создавать форму волны со смещением постоянного тока. В случае необходимости подачи более высокого смещения можно использовать источник питания (ИП) постоянного напряжения, последовательно подключенный к генератору функций. Если требуется более высокая сила тока, можно использовать управляемый генератором функций ИП постоянного тока с клеммами внешнего аналогового программирования. Также возможно применение трансформатора тока, управляемого генератором функций, для формирования сигнала переменного тока на выходе ИП постоянного тока. Наконец, некоторые ИП могут создавать формы переменного тока на собственных выходах постоянного тока.
Для справки:
Разработка преобразователя DC/DC
Инженерам, работающим над созданием преобразователя DC/DC, в ходе эксперимента требуется частота переключения и управление уровнем затвора полевого транзистора.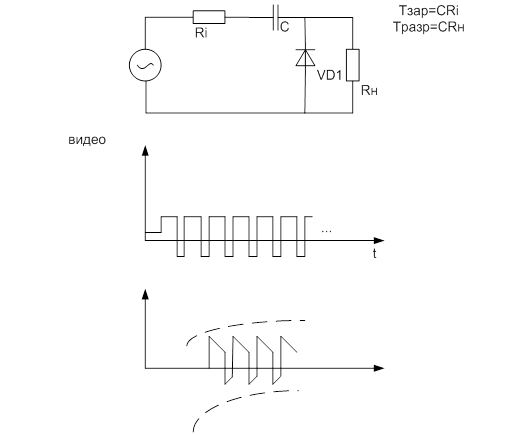 Для экспериментирования с управляющими сигналами схемы управления затвором полевого транзистора необходимо создание различных сигналов возбуждения, состоящих из импульсов и смещения постоянного напряжения. Используя встроенные органы управления генератора функций/сигналов произвольной формы Keysight 33522B, инженерам удалось создать требуемые формы сигнала с постоянной составляющей и возможностью изменения частоты, ширины и времени нарастания импульса.
Для экспериментирования с управляющими сигналами схемы управления затвором полевого транзистора необходимо создание различных сигналов возбуждения, состоящих из импульсов и смещения постоянного напряжения. Используя встроенные органы управления генератора функций/сигналов произвольной формы Keysight 33522B, инженерам удалось создать требуемые формы сигнала с постоянной составляющей и возможностью изменения частоты, ширины и времени нарастания импульса.
Метод использования только одного генератора функций
Большинство генераторов функций способны вносить поверх заданной формы сигнала постоянную составляющую (рис. 1). Однако из-за размещенных внутри аттенюаторов некоторые генераторы функций при установке малых значений амплитуды формы сигнала не способны выдать полный диапазон выходного напряжения постоянного тока. У последних моделей генераторов функций Keysight Technologies, Inc. данное ограничение отсутствует. Например, генератор функций/сигналов произвольной формы Keysight 33522B может генерировать форму сигнала с постоянной составляющей в диапазоне от –5 до +5 В на нагрузке 50 Ом (от –10 до +10 В при разомкнутой цепи).
Рис. 1. Сгенерированный DC+AC-сигнал с использованием только одного генератора функций
Для справки:
Большинство генераторов функций оснащены выходными каналами с 50-Ом нагрузкой, что, по сути, является резистором с номиналом 50 Ом, который последовательно соединен с выходом внутри генератора функций. Такая схема позволяет минимизировать отражение сигнала при подключении коаксиального кабеля с характерным значением импеданса и конечной нагрузкой в 50 Ом.
VOUT = 2VSET [RL / (50+RL)] (рис. 2)
Рис. 2. Влияние на выходное напряжение выходного 50-Ом импеданса функционального генератора
Метод использования источника питания, управляемого генератором функций
В этом способе для получения сигнала с большим смещением по постоянному току требуется ИП с внешним входом аналогового программирования. Напряжение, подаваемое на этот вход, усиливается ИП и производит пропорциональное напряжение на его выходных клеммах. Таким образом, можно подключить выход функционального генератора ко входу аналогового программирования и модулировать выходное напряжение ИП сигналом функционального генератора (рис. 3). Этот метод обеспечивает наибольшую гибкость установки напряжения смещения и величины тока для необходимой пользователю нагрузки (определяются техническими характеристиками источника питания). Тем не менее, характеристики большинства ИП постоянного тока накладывают существенные ограничения по полосе пропускания. В то время как генераторы функций могут производить формы волн в диапазоне МГц, выход большинства ИП постоянного тока имеет пропускную способность всего в несколько кГц. Таким образом, при использовании данного метода полученный сигнал с добавленной постоянной составляющей на выходе ИП будет иметь полосу пропускания всего в несколько килогерц.
Напряжение, подаваемое на этот вход, усиливается ИП и производит пропорциональное напряжение на его выходных клеммах. Таким образом, можно подключить выход функционального генератора ко входу аналогового программирования и модулировать выходное напряжение ИП сигналом функционального генератора (рис. 3). Этот метод обеспечивает наибольшую гибкость установки напряжения смещения и величины тока для необходимой пользователю нагрузки (определяются техническими характеристиками источника питания). Тем не менее, характеристики большинства ИП постоянного тока накладывают существенные ограничения по полосе пропускания. В то время как генераторы функций могут производить формы волн в диапазоне МГц, выход большинства ИП постоянного тока имеет пропускную способность всего в несколько кГц. Таким образом, при использовании данного метода полученный сигнал с добавленной постоянной составляющей на выходе ИП будет иметь полосу пропускания всего в несколько килогерц.
Рис. 3. Сигнал DC+AC, полученный с помощью генератора функций, приводит в действие вход аналогового программирования источника питания постоянного тока
Метод использования трансформатора тока, управляемого генератором функций
Для извлечения всех преимуществ полного выходного напряжения и тока ИП в сочетании с более широкой полосой пропускания сигнала генератора функций, можно подключить трансформатор тока, управляемый генератором функций, последовательно с выходом ИП. При этом необходимо выбрать трансформатор тока, способный поддерживать необходимую пропускную способность. Также следует убедиться, что трансформатор способен поддерживать максимальный постоянный ток, который будет протекать по нему к необходимой пользователю нагрузке. Схема подключения показана на рис. 4.
При этом необходимо выбрать трансформатор тока, способный поддерживать необходимую пропускную способность. Также следует убедиться, что трансформатор способен поддерживать максимальный постоянный ток, который будет протекать по нему к необходимой пользователю нагрузке. Схема подключения показана на рис. 4.
Рис. 4. DC+AC-сигнал, полученный с помощью источника питания постоянного тока, подключенного последовательно через трансформатор тока и управляемого функциональным генератором
Метод использования генератора функции, подключенного последовательно с источником питания
При необходимости создания сигнала с постоянной составляющей, напряжение смещения которого превышает значение, задаваемое на генераторе функций, можно использовать последовательное соединение ИП постоянного тока с генератором функций (рис. 5). При использовании данного метода, наряду с гибкостью установки уровня постоянного тока, обеспечиваемого источником питания, сохраняются возможности полной пропускной способности генератора функций.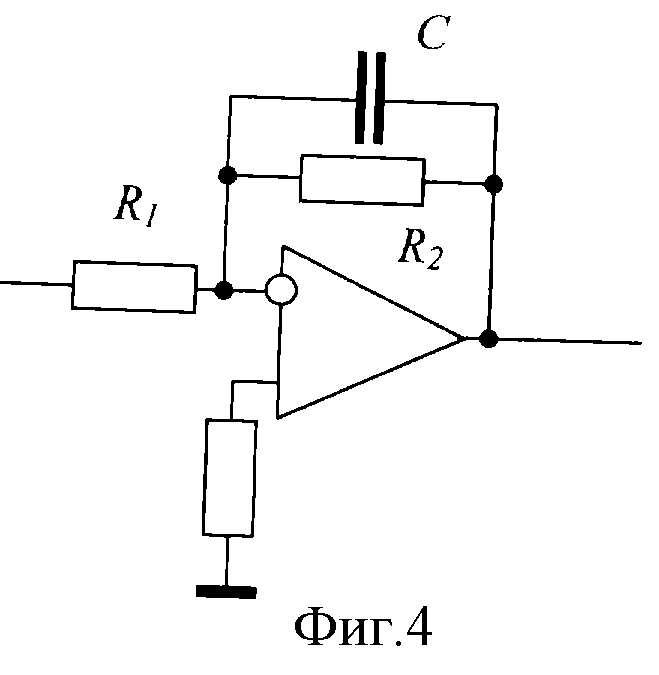
Кроме того, большинство генераторов функций имеют выходной импеданс номиналом 50 Ом, т.е. любой ток нагрузки будет протекать через это сопротивление, которое, в свою очередь, будет формировать делитель напряжения с импедансом нагрузки. Поэтому следует обязательно отрегулировать соответствующее выходное напряжение источника постоянного тока.
Рис. 5. DC+AC-сигнал, полученный с помощью последовательного соединения функционального генератора с источником питания постоянного тока
Для справки:
Генераторы функций произвольной формы Keysight 33210A (серии 33500B и 33600A) позволяют вводить значение для ожидаемого сопротивления нагрузки (Rl) в диапазоне от 1 Ом до 10 кОм или бесконечно. При изменении данного параметра генератор функций автоматически отрегулирует внутреннее производимое напряжение для учета делителя напряжения, образованного 50-Ом резистором и таким сопротивлением нагрузки, при котором значение Vout равно установленной величине напряжения. Такая настройка применяется к части переменного тока выходного сигнала функционального генератора и обеспечивает смещение постоянного тока.
Такая настройка применяется к части переменного тока выходного сигнала функционального генератора и обеспечивает смещение постоянного тока.
Метод использования источника питания со встроенным генератором сигналов
Если необходимо обеспечить напряжение или ток со значениями, превышающими максимальные значения на генераторе функций, а требования к частоте невелики (до нескольких килогерц), стоит задуматься об использовании ИП со встроенным генератором сигналов. Анализатор мощности Keysight N6705A DC способен производить произвольные формы сигналов поверх своих выходных напряжений постоянного тока без необходимости использования какого-либо внешнего оборудования (например, генератора функций или трансформатора тока). Поскольку такая возможность полностью интегрирована в продукт, это самый удобный способ для получения сигналов данного типа. Однако, поскольку в действительности выходы являются ИП постоянного тока, пропускная способность также будет ограничена величиной в несколько килогерц.
Вывод
Потребность в добавлении постоянной составляющей на выход функционального генератора возникает при различных испытаниях. Существует несколько способов решения этой задачи, и каждый метод имеет свои преимущества и недостатки, влияющие на выходное напряжение, ток, пропускную способность и простоту реализации. Генераторы функций Keysight предоставляют возможность задавать смещение постоянного тока по всему диапазону выходного напряжения даже с малым значением амплитуды сигнала. Окончательный выбор метода будет зависеть от конкретных потребностей пользователя, имеющегося оборудование и время.
Постоянная составляющая — сигнал — Большая Энциклопедия Нефти и Газа, статья, страница 1
Постоянная составляющая — сигнал
Cтраница 1
Постоянная составляющая сигнала измеряется вольтметром постоянного тока V, показания которого используются для настройки компенсационного устройства К — Переменная составляющая продетектированного сигнала несет информацию о дефектах. [2]
[2]
Постоянная составляющая сигнала выделяется однородным КИХ-фильтром ( ОКИХ), т.е. формируется выходной сигнал / ОКИХ-фильтра. [3]
Постоянная составляющая продетектнрованного сигнала используется для автоматической регулировки усиления. Для стабилизации температуры и режимов транзисторов введен резистор R10, обеспечивающий постоянство коэффициента усиления. Получаемое при этом обратное смещение на диод компенсируется дополнительным напряжением противоположной полярности, которое создается на резисторе R10 за счет тока эмиттера транзистора ТЗ. Это позволяет обеспечить надежную работу АРУ и всего тракта усиления ПЧ без ухудшения чувствительности приемника, так как диод Д1, имея нулевое смещение, начинает работать уже при самых малых сигналах. [4]
Постоянная составляющая сигнала ПЧ с низкочастотного фильтра R17 С19 подается на вход усилителя АРУ. [5]
[5]
В качестве напряжения АРУ используется постоянная составляющая сигнала на регуляторе громкости R2, сопротивление которой уменьшается при увеличении уровня выходного сигнала детектора. Подается напряжение АРУ на базы всех четырех транзисторов УПЧ через фильтры RiaC и RtsCta. Применение эмиттерно-го повторителя на выходе детектора увеличивает коэффициент передачи последнего и уменьшает вносимые им нелинейные искажения, так как детектор работает на высокоомную нагрузку. [6]
Для качественного воспроизведения цветного изображения постоянная составляющая сигнала яркости должна почти без потерь передаваться в яркостном канале или быть восстановлена на его выходе. Поэтому яркостный канал выполняется либо по схеме усилителя постоянного тока, либо с восстановлением постоянной составляющей. [7]
Видеодетектор связан с усилителем гальванически, благодаря чему постоянная составляющая сигналов изображения проходит на видеоусилитель. [8]
[8]
В сеточной цапи одного из них ( обычно оконечного) восстанавливается постоянная составляющая сигнала, несущая информацию о средней яркости изображения. Этот каскад должен работать в режиме УПТ, а остальные являются широкополосными видеоусилителями, имеющими цепи коррекции и охваченными ООС. [9]
В сеточной цепи одного из них ( обычно оконечного) восстанавливается постоянная составляющая сигнала, несущая информацию о средней яркости изображения. Этот каскад должен работать в режиме УПТ, а остальные являются широкополосными видеоусилителями, имеющими цепи коррекции и охваченными ООС. Для уменьшения искажений гари работе оконечного каскада модулятора на комплексное сопротивление промежутка сетка — катод модулируемого генератора оконечный каскад собирается по схеме либо катодного повторителя, либо каскада с параллельным регулированием. На выходе его включаются цепи нейтрализации паразитной емкости источника смещения.
[10]
На выходе его включаются цепи нейтрализации паразитной емкости источника смещения.
[10]
На рис, 29 представлена вторая схема активной матрицы сиг налов основных цветов, в которой постоянная составляющая сигналов яркости и цветности передается без искажений. [12]
Конденсатор С1; которого не было в схеме простейшего супергетеродина, нужен для того, чтобы постоянная составляющая сигнала АРУ не замыкалась на общий минус питания цепей приемника через контурные катушки. [13]
Поскольку трудно сконструировать многокаскадный усилитель с такой полосой пропускания, то применяют усилители с полосой от нескольких десятков герц и выше, а постоянная составляющая сигнала, теряемая вследствие отсутствия части полосы от нуля до нескольких герц, восстанавливается в выходном каскаде усилителя. [14]
Оценка дисперсии [ см.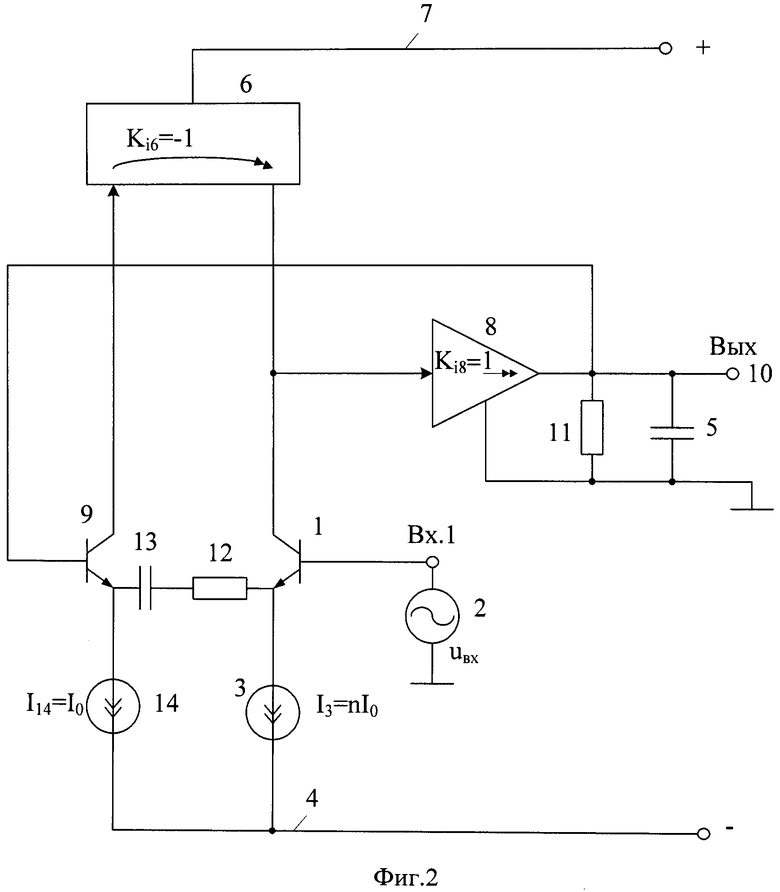 формулу ( 10 — 6) J может быть измерена также электронным вольтметром среднеквадратического значения, но с закрытым входом; с помощью разделительного конденсатора исключается постоянная составляющая сигнала и измеряется только переменная. Динамический диапазон используемого вольтметра должен быть значительным, так как в случайных сигналах возможны большие отношения пикового значения к среднеквадратическому.
[15]
формулу ( 10 — 6) J может быть измерена также электронным вольтметром среднеквадратического значения, но с закрытым входом; с помощью разделительного конденсатора исключается постоянная составляющая сигнала и измеряется только переменная. Динамический диапазон используемого вольтметра должен быть значительным, так как в случайных сигналах возможны большие отношения пикового значения к среднеквадратическому.
[15]
Страницы: 1 2 3 4
FM и PM демодулятор
Содержание
Обнаружили ошибку? Выделите ее мышью и нажмитеВведение
Ранее мы рассмотрели
сигналы с фазовой и частотной модуляцией PM и FM,
в данной статье мы разберем вопросы
выделения из
полосового радиосигнала
информационной составляющей при угловой модуляции. Предполагается, что читатель знаком с принципом работы
квадратурного гетеродина
Предполагается, что читатель знаком с принципом работы
квадратурного гетеродина
Выделение фазы комплексной огибающей радиосигнала. Структуре фазового демодулятора
Пусть имеется входной полосовой сигнал с фазовой модуляцией:
| (1) |
где — амплитуда входного сигнала, — несущая частота сигнала, — девиация фазы PM сигнала (индекс фазовой модуляции) и — модулирующий сигнал, который необходимо выделить из . Предполагается, что модулирующий сигнал по модулю не превосходит единицу.
Выделим при помощи квадратурного гетеродина огибающую фазы сигнала , как это показано на рисунке 1.
Рисунок 1: Выделение комплексной огибающей при помощи квадратурного гетеродина
После умножения исходного сигнала на квадратурные компоненты получим:
| (2) |
На выходе ФНЧ компоненты на удвоенной частоте будут отфильтрованы и останется:
| (3) |
Из выражения (3) можно выразить:
| (4) |
Таким образом, мы смогли
продемодулировать PM сигнал и выделить
исходный модулирующий сигнал
. При этом необходимо обратить внимание на следующие моменты. Во
первых, приведенные выражения подразумевают когерентный прием PM
сигнала, т.е. отсутствие частотного и фазового рассогласования
несущей частоты и частоты квадратурного гетеродина, и во вторых
предполагается, что арктангенс вычисляется в пределах
радиан
(функция арктангенс 2). Если же условие когерентного приема не
обеспечивается, то имеются частотное рассогласование
и случайный фазовый сдвиг
принятого PM сигнала относительно начальной
фазы гетеродина. Таким образом, можно (2) переписать в виде:
При этом необходимо обратить внимание на следующие моменты. Во
первых, приведенные выражения подразумевают когерентный прием PM
сигнала, т.е. отсутствие частотного и фазового рассогласования
несущей частоты и частоты квадратурного гетеродина, и во вторых
предполагается, что арктангенс вычисляется в пределах
радиан
(функция арктангенс 2). Если же условие когерентного приема не
обеспечивается, то имеются частотное рассогласование
и случайный фазовый сдвиг
принятого PM сигнала относительно начальной
фазы гетеродина. Таким образом, можно (2) переписать в виде:
| (5) |
Соответственно на выходе ФНЧ получим:
| (6) |
Тогда
| (7) |
Таким образом,
некогерентный прием приводит к тому, что к демодулированному сигналу
добавляется линейная составляющая пропорциональная частотной
расстройке плюс случайная начальная фаза. При этом начинает
проявляться второй эффект, который заключается в периодичности
арктангенса. Если линейное слагаемое
превысит по модулю
,
то в силу периодичности арктангенса на выходе будет «пила»
как это показано на рисунке 2. Для устранения периодичности применяют
функции раскрытия арктангенса (unwrap –
функции ).
При этом начинает
проявляться второй эффект, который заключается в периодичности
арктангенса. Если линейное слагаемое
превысит по модулю
,
то в силу периодичности арктангенса на выходе будет «пила»
как это показано на рисунке 2. Для устранения периодичности применяют
функции раскрытия арктангенса (unwrap –
функции ).
Рисунок2: Эффект периодичности арктангенса
Таким образом, для приема
PM сигнала требуется когерентная обработка,
в противном случае возможны искажения демодулированного сигнала. На
практике, аналоговая PM модуляция не
получила широкого распространения ввиду указанных недостатков. Однако
цифровая фазовая модуляция, когда модулирующий сигнал —
цифровой, нашла огромное применение. При цифровой фазовой модуляции
модулирующий сигнал представляет собой прямоугольные импульсы и фаза
меняется скачкообразно и получается фазовая манипуляция (phase
shift key PSK), но о ней подробно в следующих разделах. Мы же
вернемся к частотной модуляции.
Мы же
вернемся к частотной модуляции.
Струтурная схема FM демодулятора
При частотной FM модуляции исходный модулирующий сигнал интегрируется:
| (8) |
где — девиация частоты FM сигнала. Тогда в соответствии с (7) при некогерентном приеме огибающая фазы FM сигнала равна:
| (9) |
Продифференцировав огибающую фазы получим мгновенную частоту:
| (10) |
Обратите внимание, после
взятия производной частотное рассогласование влияет лишь на
постоянную составляющую демодулированного сигнала, которая как
правило не несет информации и может быть устранена при помощи фильтра
верхних частот.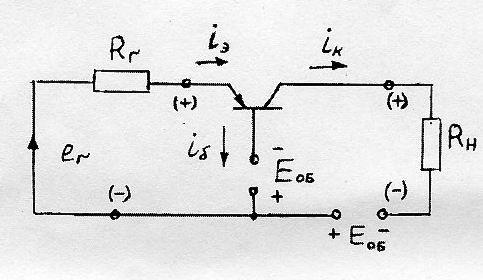 Однако перед дифференцированием остался арктангенс с
«нежелательной периодичностью». Давайте от него
избавимся, рассчитав производную арктангенса в выражении (10) как
производную сложной функции:
Однако перед дифференцированием остался арктангенс с
«нежелательной периодичностью». Давайте от него
избавимся, рассчитав производную арктангенса в выражении (10) как
производную сложной функции:
| (11) |
Структурная схема FM демодулятора соответствующего выражению (11) представлена на рисунке 3.
Рисунок3: Структурная схема FM демодулятора
Необходимо сделать
замечание. Деление в выражении (11) на квадрат амплитудной огибающей
приводит к устранению влияния паразитной амплитудной модуляции,
возникающей при прохождении сигнала через избирательные цепи
приемника. При цифровой реализации демодулятора вычисление
производной можно заменить расчетом конечных разностей первого
(«текущий минус предыдущий») или второго порядка
(центральная разность «следующий минус предыдущий») .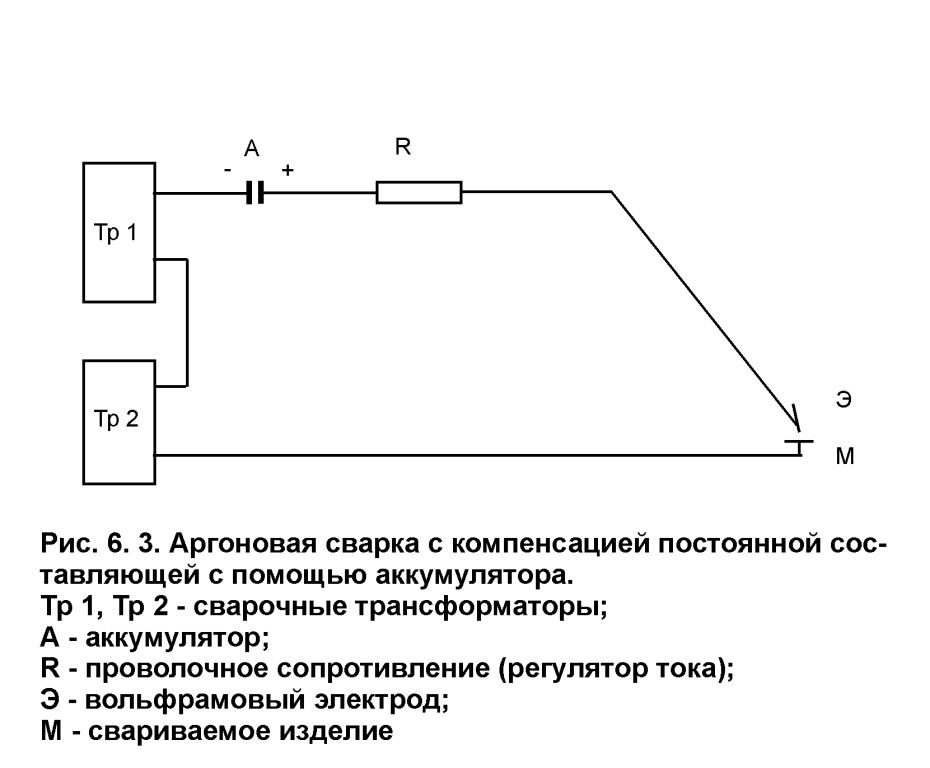
Пример работы PM и FM демодуляторов
Пусть исходный сигнал представляет собой сигнал вида:
| (12) |
Нормированный исходный модулирующий сигнал показан на рисунке 4. Исходным модулирующим сигналом производилась частотная и фазовая модуляция сигнала на несущей частоте 25 кГц с девиацией частоты при FM модуляции равной 2 кГц и девиации фазы PM равной 7.
|
Рисунок4: Осциллограмма исходного нормированного модулирующего сигнала |
Рисунок 5: Выход фазового демодулятора без раскрытия периодичности арктангенса |
|
Рисунок 6: Выход PM и FM демодуляторов с нормировкой и раскрытием арктангенса с точной настройкой частоты гетеродина |
Рисунок 7: Выход PM и FM демодуляторов с нормировкой и раскрытием арктангенса с расстройкой частоты гетеродина |
На рисунке 5 показан выход
фазового детектора при демодуляции PM сигнала. Видно, что на выходе арктангенса явные перегрузки по фазе, вызванные
периодичностью по фазе. Раскрытие периодичности арктангенса, с
соответствующими нормировками PM и FM
демодуляторов при точной настройке частоты гетеродина на
несущую частоту FM и PM
сигнала показаны на рисунке 6. Хорошо видно, что при точной
настройке частоты гетеродина сигнал на выходе FM
демодулятора полностью повторяет исходный модулирующий сигнал,
а на выходе PM демодулятора смещен на
постоянную составляющую пропорционально случайной начальной фазе.
Сигнал на выходе PM и FM
демодуляторов при частотной расстройке гетеродина
соответственно 100 (в случае PM сигнала) и
500 Гц (для FM сигнала) показаны на рисунке
7. Можно заметить, что частотная расстройка при FM
сигнале смещает только постоянную составляющую на выходе FM
демодулятора, в то время как на выходе PM
демодулятора добавляется линейное слагаемое с коэффициентом
пропорциональности зависящим от частотной расстройки гетеродина.
Видно, что на выходе арктангенса явные перегрузки по фазе, вызванные
периодичностью по фазе. Раскрытие периодичности арктангенса, с
соответствующими нормировками PM и FM
демодуляторов при точной настройке частоты гетеродина на
несущую частоту FM и PM
сигнала показаны на рисунке 6. Хорошо видно, что при точной
настройке частоты гетеродина сигнал на выходе FM
демодулятора полностью повторяет исходный модулирующий сигнал,
а на выходе PM демодулятора смещен на
постоянную составляющую пропорционально случайной начальной фазе.
Сигнал на выходе PM и FM
демодуляторов при частотной расстройке гетеродина
соответственно 100 (в случае PM сигнала) и
500 Гц (для FM сигнала) показаны на рисунке
7. Можно заметить, что частотная расстройка при FM
сигнале смещает только постоянную составляющую на выходе FM
демодулятора, в то время как на выходе PM
демодулятора добавляется линейное слагаемое с коэффициентом
пропорциональности зависящим от частотной расстройки гетеродина.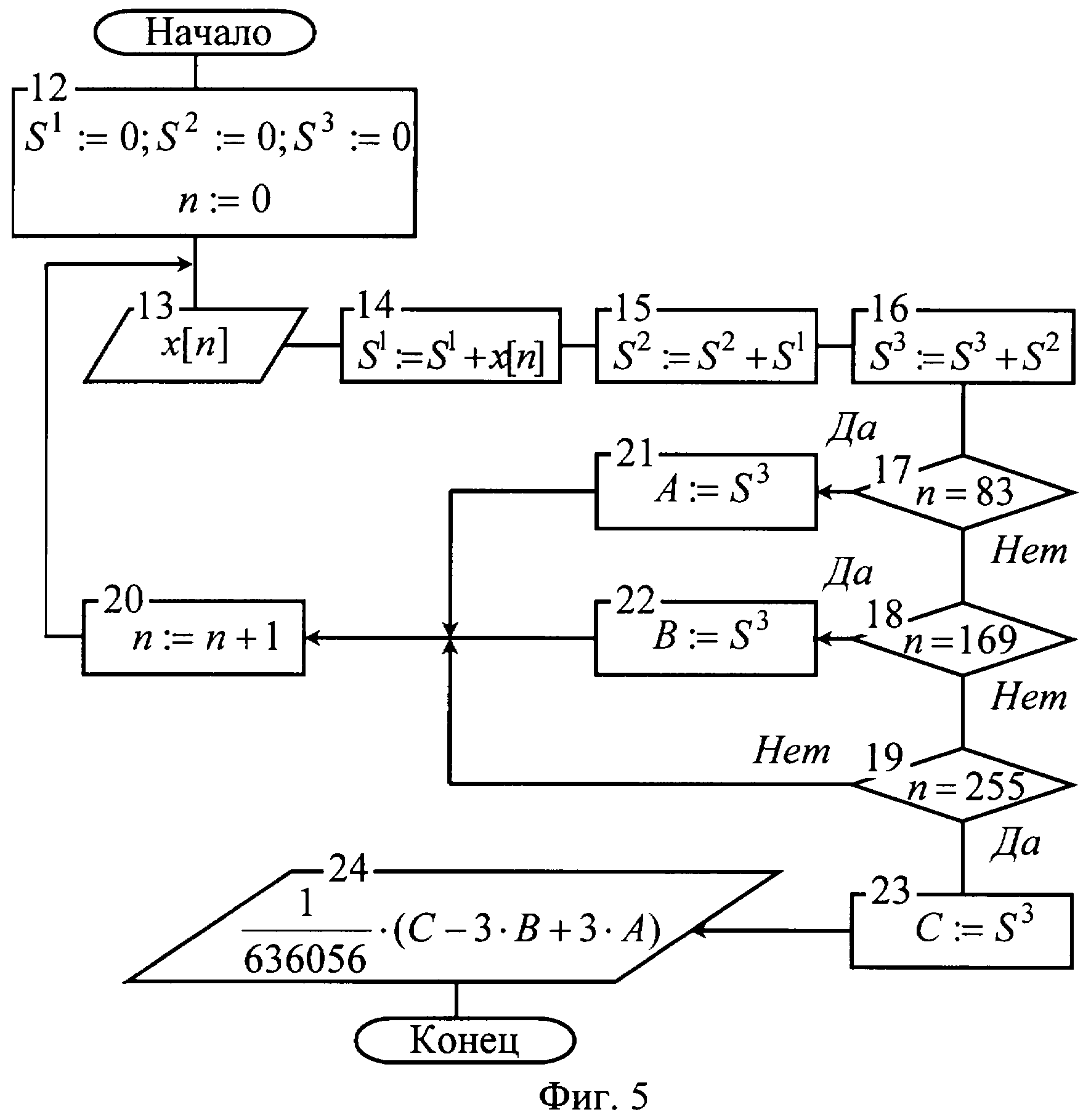
Раскрытие периодичности арктангенса
Давайте теперь рассмотрим вопрос раскрытия периодичности арктангенса. Для этого применяют unwrap -алгоритмы, которых существует несколько вариантов. Первый вариант заключается в обнаружении скачков фазы на выходе арктангенса близких к радиан. Принцип работы данного алгоритма показан на рисунке 8.
Рисунок8: Раскрытие периодичности арктангенса (unwrap)
при обнаружении скачков по фазе равных (или близких) к радиан, которые показаны на верхнем графике рисунка 8 красным, формируется сигнал (средний график рисунка 8) по следующему правилу. Если скачок фазы произошел вниз, то к добавляется , если вверх, то вычитается . Сигнал с раскрытой фазой равен ( нижний график рисунка 8 ) :
| (13) |
Сложность данного
алгоритма заключается в том, что скачки по фазе как правило меньше
из-за шумов и из-за дискретизации сигнала. В этом случае есть
вероятность пропустить скачок по фазе и сформировать неправильный
сигнал
.
В этом случае есть
вероятность пропустить скачок по фазе и сформировать неправильный
сигнал
.
Второй вариант раскрытия периодичности арктангенса заключается в следующем. PM сигнал демодулируют при помощи FM демодулятора в соответствии с (11) при помощи структуры приведенной на рисунке 3. В результате получают мгновенную частоту , равную производной от фазы . После этого интегрируют и восстанавливают фазу без использования арктангенса ( см. рисунок 9 ) .
Рисунок 9: Раскрытие периодичности арктангенса при использовании FM демодулятора
Данный способ не приемлем в случае цифровой модуляции, так как частотный демодулятор не сохраняет информации о начальной фазе, кроме того в результате интегрирования к сигналу на выходе добавляется случайная постоянная интегрирования.
Еще один, пожалуй, самый
лучший способ раскрытия периодичности арктангенса, который нашел
широкое распространение в цифровых системах с фазовой манипуляцией -
это недопускание набега фазы больше
(т.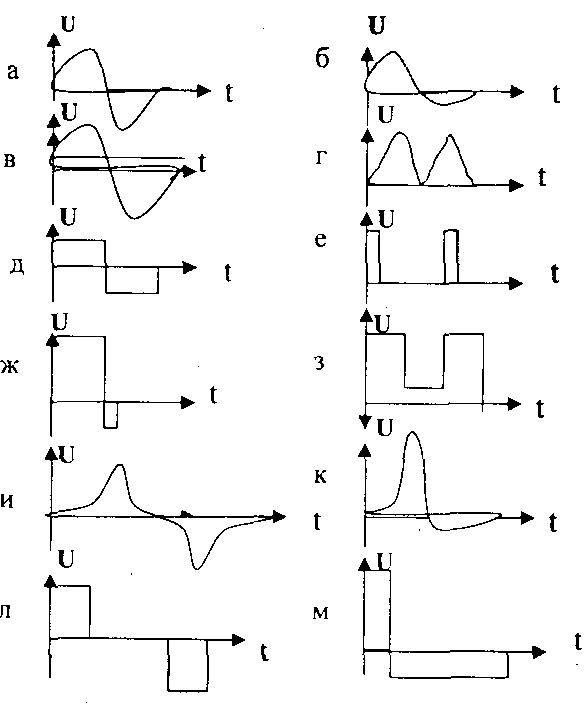 е. недопускание периодичности арктангенса) за счет использования
следящих контуров фазовой автоподстройки частоты, подробно рассмотренных в данной статье.
е. недопускание периодичности арктангенса) за счет использования
следящих контуров фазовой автоподстройки частоты, подробно рассмотренных в данной статье.
Выводы
Таким образом, мы рассмотрели вопросы построения PM и FM демодуляторов. Показали, что для PM сигнала частотная расстройка гетеродина приводит к линейному слагаемому на выходе PM демодулятора, а в случае FM сигнала при частотной расстройке меняется лишь постоянная составляющая на выходе демодулятора. Приведены unwrap алгоритмы раскрытия периодичности арктангенса.
Информация была полезна? Поделитесь с друзьями!Мой мир
Вконтакте
Одноклассники
Список литературы
[1] Баскаков, С.И. Радиотехнические цепи и сигналы. Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4
[2]
Гоноровский И.С.
Радиотехнические цепи и сигналы
Москва, Советское радио, 1977, 608 c.
[3] Сергиенко А.Б. Цифровая обработка сигналов СПб, Питер, 2002.
Последнее изменение страницы: 07.02.2021 (14:13:28)
Страница создана Latex to HTML translator ver. 5.20.11.14
Метод цифровой обработки сигналов синусно-косинусного инкрементального датчика положения для исключения влияния постоянной составляющей этих сигналов Текст научной статьи по специальности «Электротехника, электронная техника, информационные технологии»
УДК 621.372.542.3
Метод цифровой обработки сигналов синусно-косинусного инкрементального датчика положения для исключения влияния
V V 1
постоянной составляющей этих сигналов’
А.С. Анучин, В.С. Подзорова, В.И. Кульманов, Д.М. Шпак ФГБОУВО «Национальный исследовательский университет «МЭИ»», г.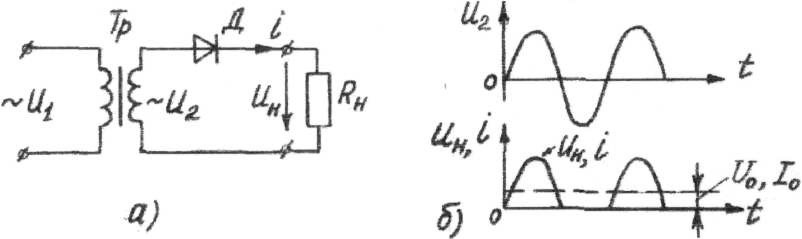 Москва, Российская Федерация
Москва, Российская Федерация
E-mail: [email protected]
Авторское резюме
Состояние вопроса: В настоящее время синусно-косинусные инкрементальные датчики положения ротора находят применение в высокоскоростных электроприводах. Постоянная составляющая сигналов таких датчиков может существенно снижать точность оценки скорости. Обычно данная проблема решается применением фильтров верхних частот 0. Из-за дифференцирования по времени данные фильтры имеют проблемы с работой на малых скоростях. В связи с этим необходим метод устранения влияния постоянной составляющей в системе оценки скорости, не имеющий данного недостатка. Требуемые показатели системы оценки скорости: полоса пропускания измерителя скорости должна быть не менее 4 кГц; точность -±25 об/мин в диапазоне от 0 до 30000 об/мин.
Материалы и методы: Использованы результаты моделирования и экспериментальных исследований электропривода с синусно-косинусным инкрементальным датчиком положения, показывающие влияние постоянной составляющей во входных сигналах на точность оценки скорости на основе ФАПЧ (PLL).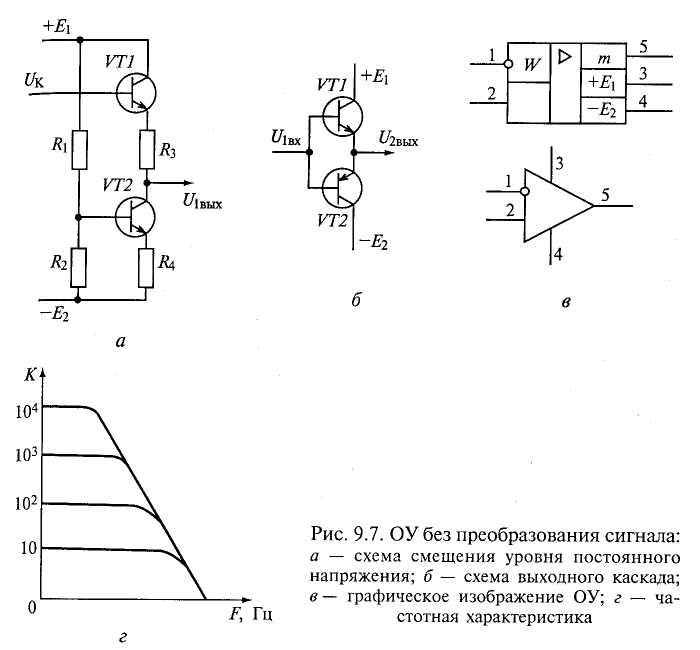 Для устранения влияния постоянной составляющей использованы методы цифровой обработки сигналов. Результаты: Предложена реализация цифрового фильтра верхних частот, в которой дифференцирование по времени заменяется дифференцированием по углу. Результаты моделирования и экспериментов показывают корректность работы такого фильтра в широком диапазоне рабочих скоростей привода, включая нулевую скорость (останов).
Для устранения влияния постоянной составляющей использованы методы цифровой обработки сигналов. Результаты: Предложена реализация цифрового фильтра верхних частот, в которой дифференцирование по времени заменяется дифференцированием по углу. Результаты моделирования и экспериментов показывают корректность работы такого фильтра в широком диапазоне рабочих скоростей привода, включая нулевую скорость (останов).
Выводы: Установлено, что предложенный метод подавления постоянной составляющей сигналов может применяться для повышения точности системы оценки скорости с синусно-косинусными инкрементальными датчиками положения. Погрешность расчета скорости укладывается в допустимые пределы ±25 об/мин.
Ключевые слова: регулируемый электропривод, автоматическая настройка, управление приводами, управление движением, станочные приводы, датчики положения, обработка сигналов.
Method of digital processing of sine/cosine incremental encoder signals for eliminating the effect of the dc component of these signals
A.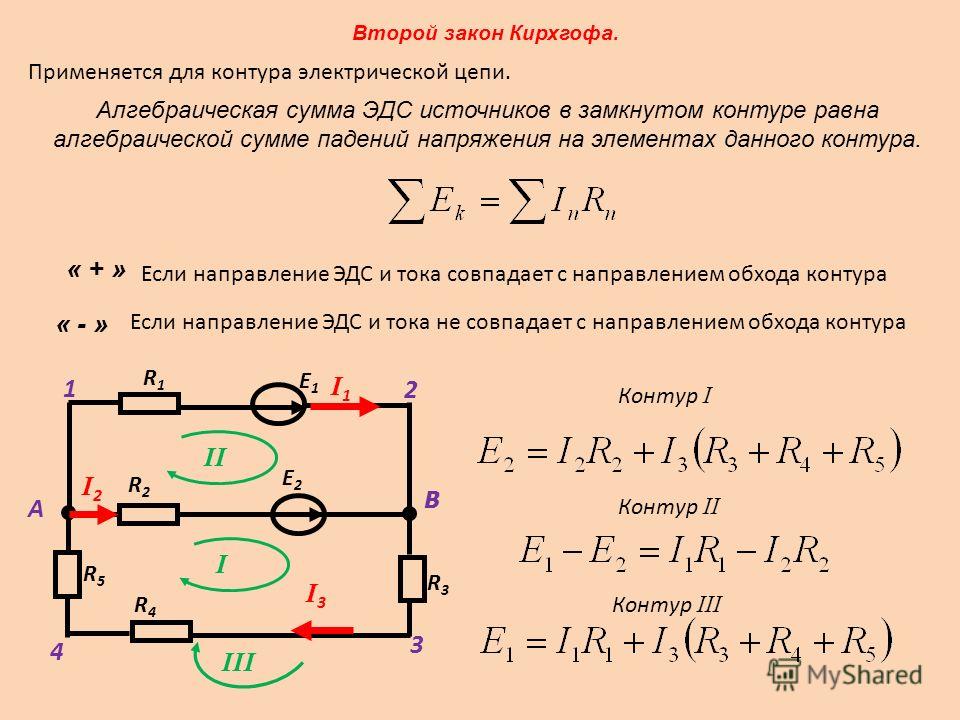 S. Anuchin, V.S. Podzorova, V.I. Kulmanov, D.M. Shpak National Research University «Moscow Power Engineering Institute», Moscow, Russian Federation
S. Anuchin, V.S. Podzorova, V.I. Kulmanov, D.M. Shpak National Research University «Moscow Power Engineering Institute», Moscow, Russian Federation
E-mail: [email protected]
Abstract
Background: Sine/cosine incremental encoders are used currently in high-speed electric drives. The signal DC component of such encoders can significantly reduce the accuracy of speed estimation. Usually this problem is solved by applying high-pass filters 0. Due to time differentiation, these filters have problems in operation at low speeds. A method without this drawback should be developed to eliminate the effect of the DC component on the speed estimation system. The required speed estimation system performance parameters are: the speed estimator bandwidth of at least 4 kHz; the accuracy of ± 25 rpm in the range from 0 to 30000 rpm. Materials and methods: We used the results of simulation and experimental studies of the electric drive with a sine/cosine incremental encoder, showing the effect of the constant component of the input signals on the PLL-based speed estimation system accuracy.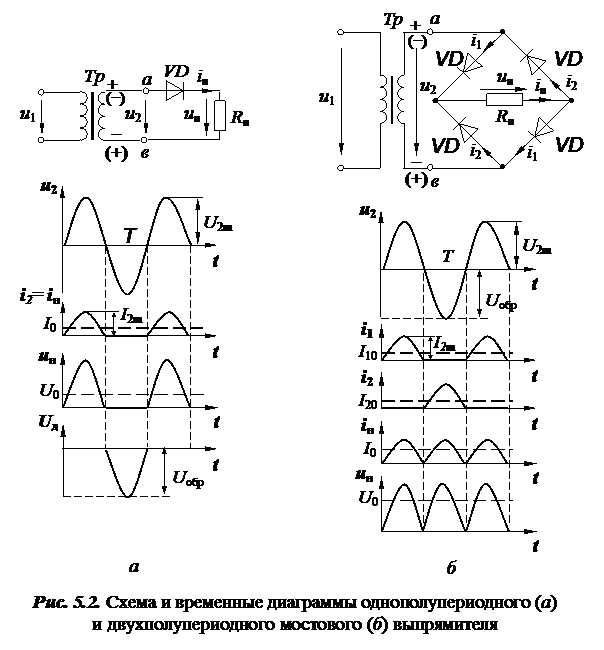 To eliminate the effect of the DC component, we used methods of digital signal processing.
To eliminate the effect of the DC component, we used methods of digital signal processing.
Results: We propose implementation of a digital high-pass filter in the angle domain instead of the time domain. The results of the simulation and experiments show the correctness of such filter operation in a wide range of drive operating speeds, including zero speed (stop).
Conclusions: It has been determined that the proposed method of signal DC component suppression can be used to improve the accuracy of a speed estimation system with sine/cosine incremental encoders. The accuracy of speed calculation is within the permissible limits of ± 25 rpm.
Key words: controlled electric drive, auto-tuning, drive control, motion control, machine tool drives, encoders, signal processing.
DOI: 10.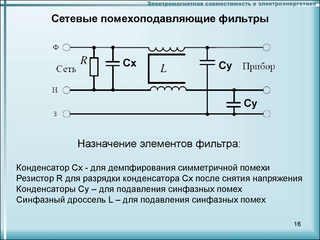 17588/2072-2672.2017.6.033-039
17588/2072-2672.2017.6.033-039
1 Исследование проводилось при поддержке гранта Российского научного фонда (проект № 16-19-10618).
Введение. Синусно-косинусные инкрементальные датчики положения ротора (ДПР) используются в различных типах электроприводов. Такие ДПР имеют меньшее количество импульсов на оборот, по сравнению с инкрементальными ДПР с прямоугольными выходными сигналами, но аналоговые синусные и косинусные сигналы могут быть использованы для увеличения разрешения и получения углового положения внутри одного импульса. Эти ДПР нашли применение в высокоскоростных приводах шпинделей благодаря простоте своей конструкции и высокой точности. Внешний вид установленного датчика представлен на рис. 1.
Рис. 1. Синусно-косинусный инкрементальный энкодер, установленный на валу двигателя
Шестерня с зубьями помещается на вал двигателя, а считывающая головка размещается на его корпусе. В ней используется постоянный магнит для возбуждения и магниторезистивные датчики для получения квадратурных сигналов синуса и косинуса.
В ней используется постоянный магнит для возбуждения и магниторезистивные датчики для получения квадратурных сигналов синуса и косинуса.
На высоких скоростях частота сигналов увеличивается, их можно преобразовать к ТТЬуровню и использовать для оценки положения и скорости с помощью квадратурного декодера (ОБР) микроконтроллера 00. Но для низких скоростей (до 3000 об/мин) частота сигнала снижается, поэтому полоса пропускания алгоритма оценки скорости оказывается недостаточной. В этом случае для оценки скорости должны использоваться синусные и косинусные сигналы.
Одним из простейших методов оценки скорости для квадратурных сигналов синусоидальной формы является метод на основе фазовой автоподстройки частоты (ФАПЧ) (в англоязычной литературе РЩ 0, 0. Структурная схема этого метода представлена на рис. 2. В РИ содержится оценка скорости и углового положения. Сигналы с датчика преобразуются с помощью АЦП микроконтроллера. РИ проверяет правильность оценки скорости и угла, сравни-
РИ проверяет правильность оценки скорости и угла, сравни-
вая расчетный и измеренный углы. Углы можно сравнить путем вычитания расчетного угла из измеренного. Но для получения измеренного угла из синусоидальных и косинусных сигналов должна быть рассчитана функция а1ап2 (арктангенс угла между осью х и линией, проходящей через начало координат и точку, заданную координатами х,у).
Рис. 2. Модуль оценки скорости на основе PLL
Эта функция достаточно сложна даже для современных микроконтроллеров, и для экономии вычислительных ресурсов лучше получить синус и косинус расчетного угла и выполнить умножение данных с датчика и расчетных как комплексных чисел. Мнимая часть произведения одного числа с комплексно сопряженным другого числа приблизительно пропорциональна ошибке в значении угла между оценкой и данными энкодера. Эта погрешность используется как вход ПИ-регулятора, который производит расчет значения скорости.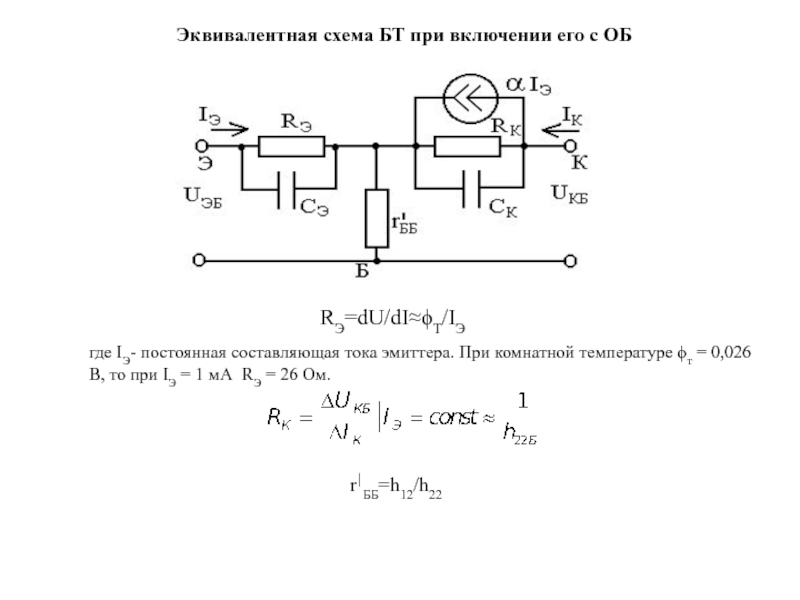 Его выход является оценкой скорости с высоким уровнем шума, но его интегральная составляющая содержит отфильтрованный сигнал скорости, подходящий для использования в качестве обратной связи. Использование ПИ-регулятора в обратной связи позволяет добиться широкой полосы пропускания модуля оценки скорости и подавления шумов АЦП во входных сигналах.
Его выход является оценкой скорости с высоким уровнем шума, но его интегральная составляющая содержит отфильтрованный сигнал скорости, подходящий для использования в качестве обратной связи. Использование ПИ-регулятора в обратной связи позволяет добиться широкой полосы пропускания модуля оценки скорости и подавления шумов АЦП во входных сигналах.
Шумы АЦП могут быть сглажены без существенного влияния на полосу пропускания. Помимо этого, сигналы аЦп зачастую имеют постоянную составляющую. Она невелика, но приводит к смещению годографа сигналов синуса и косинуса. Это вызывает периодические пульсации измеренного угла, которые имеют гораздо меньшую частоту, чем шум АЦП, по причине чего не могут быть отфильтрованы без уменьшения полосы пропускания модуля оценки скорости.
Постоянное смещение можно настроить вручную, когда на вход АЦП микроконтроллера подается нулевой сигнал. Но во время настройки необходимо отключать датчик положения.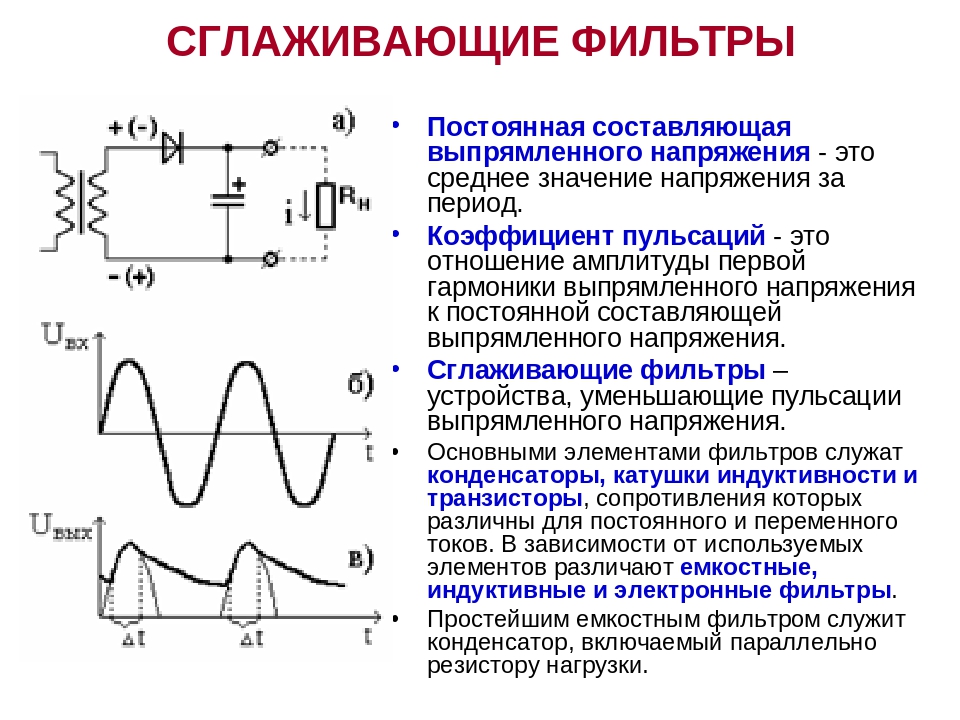 Кроме того, этот метод
Кроме того, этот метод
не применим, если сам энкодер имеет постоянную составляющую в своих сигналах.
Другой способ — использовать цифровой фильтр верхних частот для устранения постоянной составляющей сигнала. Проблема этого метода заключается в том, что он должен быть отключен, когда привод остановлен. В противном случае фильтр «обнулит» неизменные во времени сигналы как постоянную составляющую и это приведет к неправильной оценке скорости при запуске двигателя. Даже на высоких скоростях проблема фильтра верхних частот будет возникать из-за эффектов дискретизации, потому что, если измерения производятся только в нескольких точках на периоде сигнала, их вычисленная постоянная составляющая может отличаться от фактической.
Для решения проблемы постоянной составляющей во входных сигналах было предложено реализовать фильтр верхних частот не во временной области, а в угловой (дифференцирование по времени заменить дифференцированием по углу).
Методы исследования. Проблема шумов и постоянных составляющих в АЦП и датчике. Испытательный стенд включает в себя асинхронный двигатель и синусно-косинусный энкодер с 128 импульсами на один оборот. На низких скоростях оценка скорости выполняется с использованием метода на основе PLL. На высоких скоростях используется модуль квадратурного декодера (QEP) микроконтроллера.
Есть два вида ошибок, которые влияют на метод оценки скорости PLL. Это шумы АЦП и смещение сигнала. Уровень шума АЦП обычно зависит от качества входных цепей и их устойчивости к помехам от воздействия коммутаций инвертора. Обычно этот шум может быть представлен как случайный «дребезг» двух младших двоичных разрядов данных АЦП. В случае низкой устойчивости к помехам от инвертора эта ошибка может стать систематической, если время переключения соответствует окну выборки АЦП. В этом случае требуется
улучшение помехоустойчивости. Модуль на основе PLL обеспечивает две оценки скорости: на выходе ПИ-регулятора (справа от сумматора) и на выходе интегральной составляющей ПИ-регулятора (слева от сумматора). В выходе интегральной составляющей шумы АЦП отфильтрованы. Параметры регулятора — его пропорциональный и интегральный коэффициенты — должны быть подобраны для достижения максимально возможной полосы пропускания с подавлением шумов АЦП.
Модуль на основе PLL обеспечивает две оценки скорости: на выходе ПИ-регулятора (справа от сумматора) и на выходе интегральной составляющей ПИ-регулятора (слева от сумматора). В выходе интегральной составляющей шумы АЦП отфильтрованы. Параметры регулятора — его пропорциональный и интегральный коэффициенты — должны быть подобраны для достижения максимально возможной полосы пропускания с подавлением шумов АЦП.
Смещение сигналов от датчика складывается из двух смещений различной природы. Первое — смещение АЦП, а второе -смещение самого датчика. В идеальном случае сигнал от датчика не должен иметь постоянной составляющей, но, если используется недорогой датчик, это смещение может достигать 20 % от амплитуды сигнала. Подобный худший случай показан на рис. 3. Синусоидальный сигнал датчика имеет постоянную составляющую около 0,2 В. Наличие такого значительного смещения в сигнале приводит к отклонению расчетной скорости, которое достигает ±195 об/мин от фактической скорости привода, равной 445 об/мин.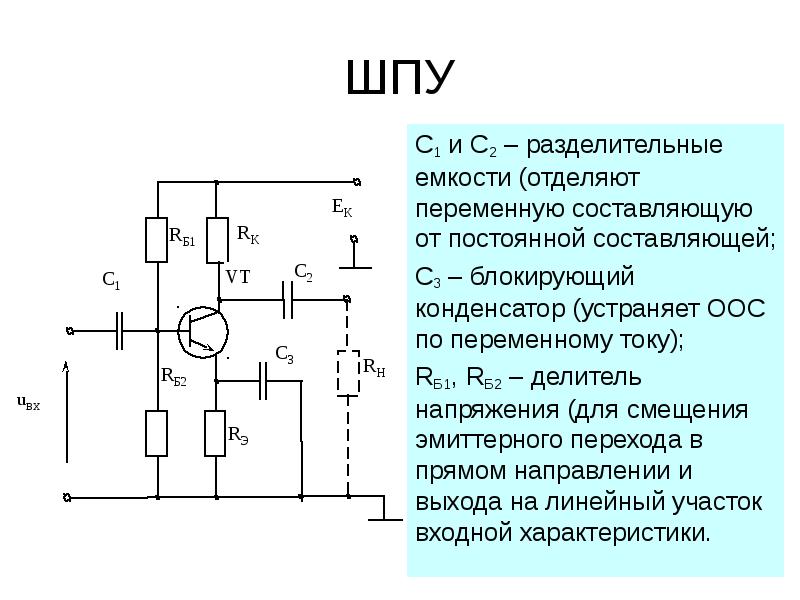
Обычно предлагается использовать фильтр верхних частот для удаления постоянной составляющей сигналов:
П (р) = — Р
Р + -.
1 «
‘Ф
(1)
Проблема этого метода проявляется при работе на малых и высоких скоростях. Если привод остановлен, то входной сигнал для фильтра является постоянным и он начинает обрабатывать его, как если бы он был постоянной составляющей переменного сигнала. С другой стороны, во время работы на высоких скоростях уменьшается количество выборок в течение одного периода синусного и косинусного сигналов. В этом случае может появиться субгармоническая составляющая, влияющая на работу фильтра.
Y\Ш V «Л \ /
\л У/ \ / \/ X / V/
21 Tsamp 63 Tsamp 106 Tsamp 148 Tsamp 191 Tsamp
Value time
Speed(515F,08) Encoder SIN(4010,0E] Encoder CO S (4010,11)
Cursorl 147 Tsamp 640 rpm
-0,38672 V ■0,78516 V
Cursor2 160 Tsamp 251 rpm
1,1875 V 0,16406 V
1-2 -13 Tsamp 388 rpm
-1,5742 V -0,84822 V
Рис. 3. Оценка скорости на основе PLL с собственной постоянной составляющей в сигналах датчика положения
3. Оценка скорости на основе PLL с собственной постоянной составляющей в сигналах датчика положения
Фильтр в угловой области. Чтобы избежать проблем с работой на нулевой и высокой скоростях, было предложено реализовать фильтр верхних частот в угловой области вместо временной области (метод переменного периода выборки 0). Таким образом, оператор дифференцирования по времени р = ММ заменяется оператором 5 = М60 дифференцирования по углу. Реализация фильтра в угловой области может быть определена как
у (0) _ 5
М (5 ) =
X (0)
5 + —
1
(2)
ф
где ©ф — угловая постоянная фильтра (аналогично постоянной времени во временной области).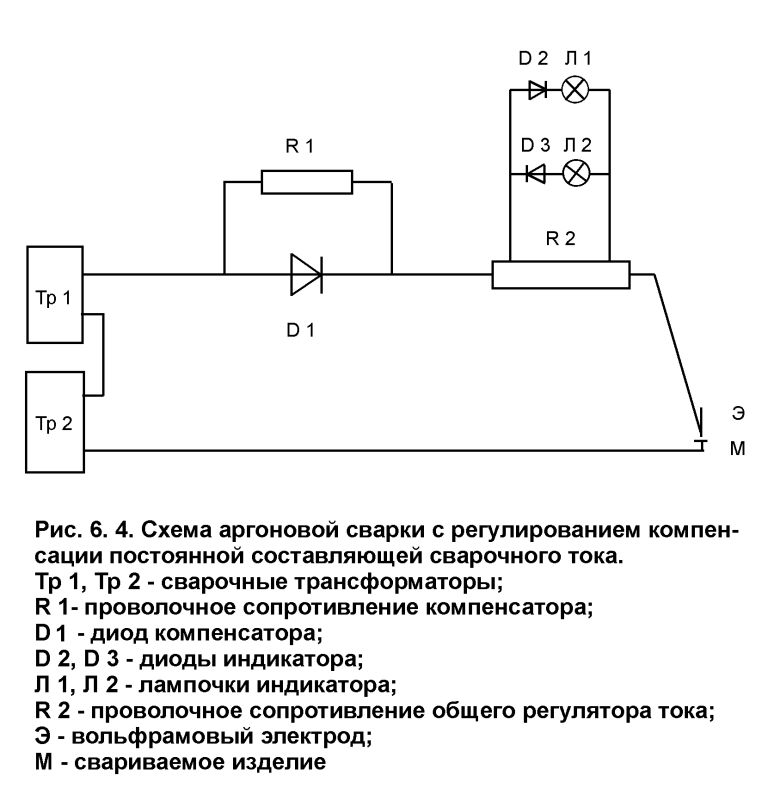
Уравнение для численного расчета оператора фильтра (2) может быть получено следующим образом:
— У (0) +—У (0) = —х (0), (3)
сЮ ©ф с/0
а для дискретного угла:
У [К ]-У [К -1 ] +_1 у [К] = х [К ]- х [К -1 ] (4)
А© ©ф 1 * А©
что дает
У [к] =
©ф + А©
(У [К -1] + х[К]- х [К -1]). (5)
Полученное уравнение содержит переменный шаг интегрирования А©, который изменяется с изменением скорости./19244.gif) , (6)
, (6)
где Юрасч — расчетная скорость, взятая с выхода интегральной составляющей PLL; Л — период дискретизации АЦП.
Для правильного вычисления (5) должно быть определено минимальное значение шага интегрирования, которое лимитировано форматом вычислений.
Результаты исследования. Моделирование предложенного решения. Моделирование проводилось для изменения скорости двигателя с 5000 об/мин до нуля и обратно до 5000 об/мин. На рис. 4-6 показан процесс оценки скорости с различными настройками фильтра верхних частот во временной области. Первый эксперимент (рис. 4) производится при максимальной частоте среза. Низкочастотные сигналы подавляются, и они близки к нулю, когда привод остановлен. Но поскольку эти сигналы полностью подавлены, расчетная скорость не равна нулю. Это происходит потому, что комплексное умножение в PLL возвращает ноль и не изменяет интегральную составляющую оценки скорости.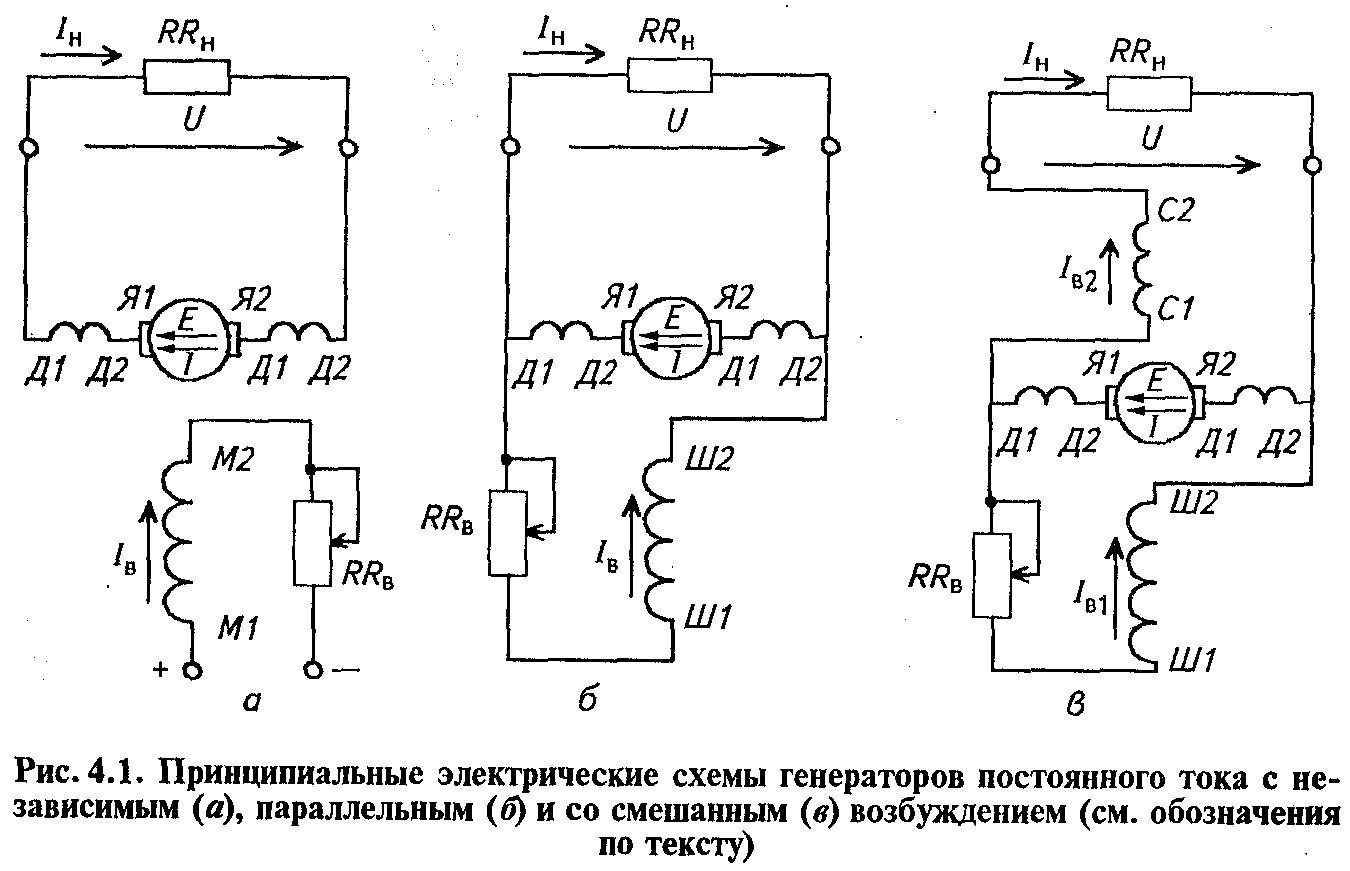 При запуске двигателя оценка скорости неточна из-за переходных процессов в фильтре.
При запуске двигателя оценка скорости неточна из-за переходных процессов в фильтре.
При уменьшении частоты среза качество оценки на низкой скорости увеличивается, но для этого конкретного случая в нуле расчетная скорость очень мала и отрицательна (рис. 5). При запуске двигателя видны небольшие колебания в переходном процессе расчетной скорости.
6000
-2000
-1
Время, с
Рис. 4. Оценка скорости с фильтром верхних частот во временной области с максимальной частотой среза
3
Ю о
6000
5000
4000
3000
2000
1000
-1000
-2000
1,5
го ср а) чд о
О
0,5
Время, с
Рис.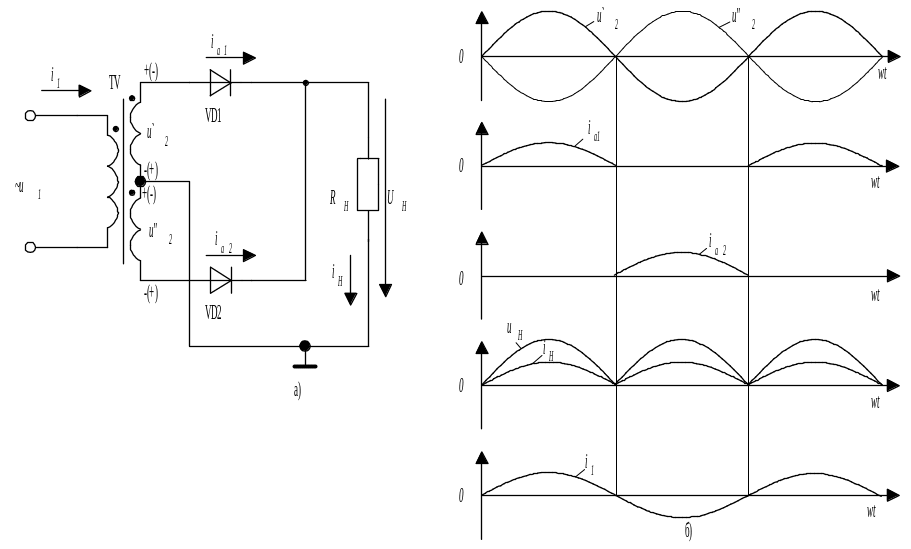 5. Оценка скорости с фильтром верхних частот во временной области со средней частотой среза
5. Оценка скорости с фильтром верхних частот во временной области со средней частотой среза
Последний опыт с наименьшей частотой среза показывает наилучшее отслеживание нулевой скорости, но при запуске привода происходят сильные колебания в сигнале расчетной скорости (рис. 6).
Предлагаемый фильтр в угловой области показывает наилучшие результаты (рис. 7). Отфильтрованные сигналы быстро
6000
5000
4000
3000
теряют постоянную составляющую, их амплитуды не изменяются с изменением скорости и остаются постоянными, когда привод остановлен. Во время запуска некоторые незначительные колебания в расчетной скорости видны, но переходный процесс лучше, чем для стандартного фильтра во временной области.
3
ю о
2000
1000
-1000
-2000
Время, с
Рис. 6. Оценка скорости с фильтром верхних частот во временной области с минимальной частотой среза
3
5
0
1
0
ю о
6000
5000
4000
3000
2000
1000
-1000
-2000
Время, с
Рис.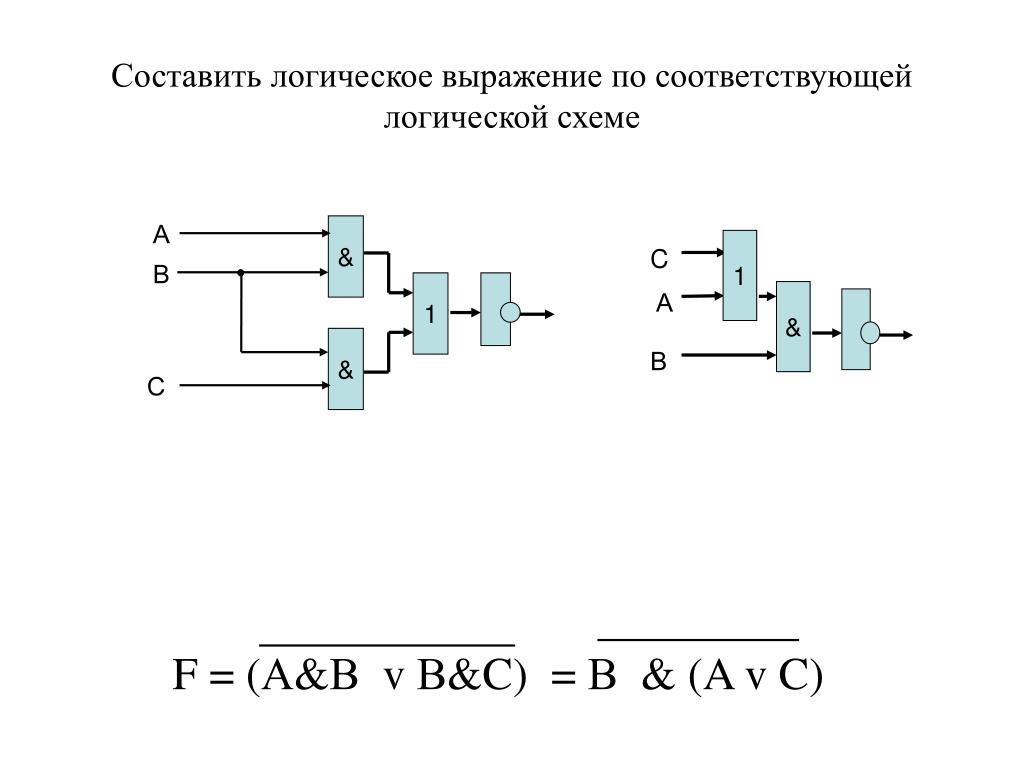 7. Оценка скорости с предложенным фильтром верхних частот в угловой области
7. Оценка скорости с предложенным фильтром верхних частот в угловой области
Результаты экспериментов. Рассматриваемый метод фильтрации реализован на микроконтроллере TMS320F28335. Он работает в качестве одного из модулей программного обеспечения векторной системы управления асинхронным двигателем с ориентацией по потоку. На рис. 8 показана работа модуля оценки скорости с включенным алгоритмом фильтрации. По сравнению с осциллограммой на рис. 3, отклонение скорости в течение одного периода сигналов синуса и косинуса значительно снижается и укладывается в допустимую погрешность ±25 об/мин. Девиация в скорости объясняется некоторой несинусоидальностью входных сигналов.
\ /\ /Л/, \\ Г, \/Л
/Ч/ 1; \ У/ \у /\У,
21 Tsamp 63 Tsamp 10 > Tsamp 149 Tsamp 191 Tsamp
SpeedlSI 5F.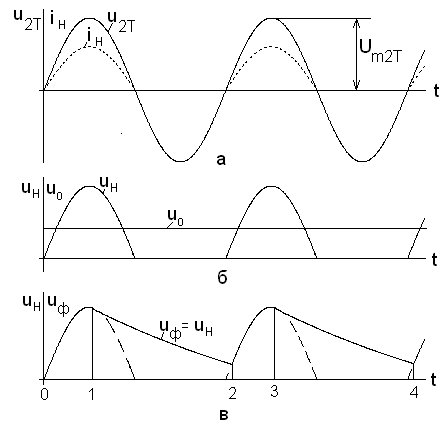 08] Encoder SIN[4010.0E] Encoder C05[4010.11]
08] Encoder SIN[4010.0E] Encoder C05[4010.11]
Cursoil 103 Tsamp 504 rpm
■0,65025 V
СигзогЗ 117 Tsamp 462 rpm
3.90234 V 0.44141V
1-3 ■14 Tsamp 42 rpm
■1.6172 V ■1.0977 V
Рис. 8. Оценка скорости с фильтром в угловой области для данных сигнала энкодера
Выводы. Предложенная реализация фильтра для сигналов с переменной частотой показывает хорошие результаты на разных скоростях, включая нулевую. Этот метод может использоваться не только для
фильтрации сигналов энкодера, но и для различных задач, таких как фильтрация ошибки чистого интегрирования в некоторых наблюдателях потока рассеяния для бездатчиковых систем управления.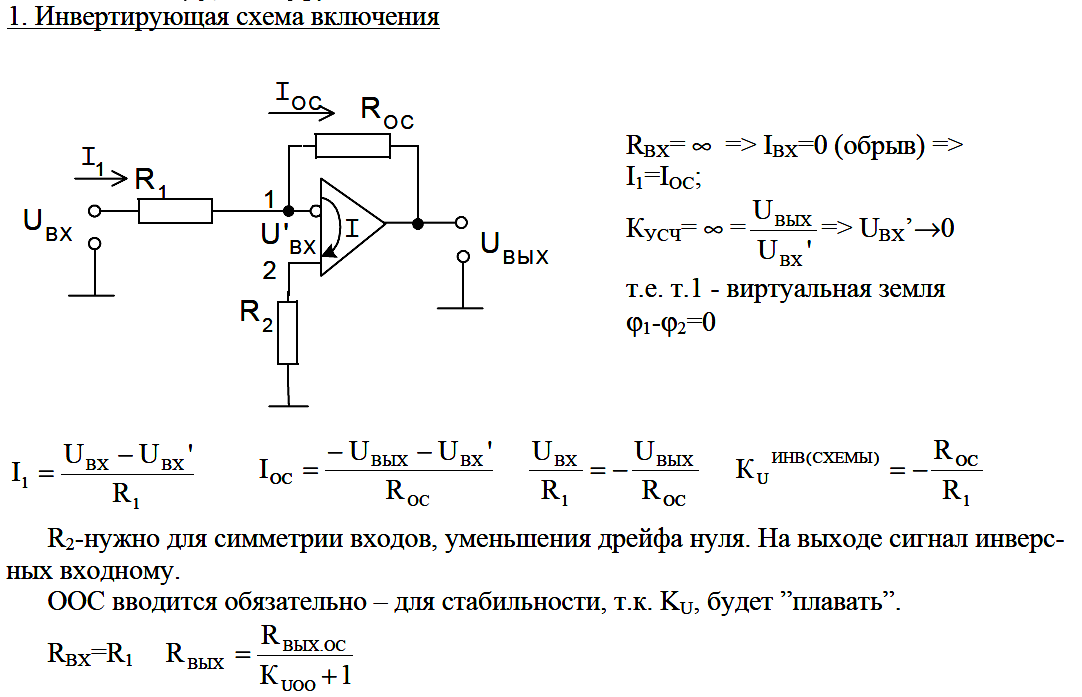 В будущем планируется реализовать нормализацию сигнала вместе с фильтрацией постоянной составляющей.
В будущем планируется реализовать нормализацию сигнала вместе с фильтрацией постоянной составляющей.
Список литературы
1. Peter Vas. Sensorless Vector and Direct Torque Control / Oxford University Press. — Oxford , 1998. — 760 с.
2. Ilmiawan A.F., Wijanarko D., Arofat A.H., Hindersyah H., Purwadi A. An easy speed measurement for incremental rotary encoder using multi stage moving average method // Proceedings of International Conference on Electrical Engineering and Computer Science (ICEECS). — 2014. — С. 363-368. doi: 10.1109/ICEECS.2014.7045279.
3. Petrella R., Tursini M., Peretti L., Zigliotto M. Speed measurement algorithms for low-resolution incremental encoder equipped drives: a comparative analysis // Proceedings of International Conference on Electrical Machines and Power Electronics (ACEMP). -2007. — С. 780-787. doi: 10.1109/ACEMP.2007.4510607.
-2007. — С. 780-787. doi: 10.1109/ACEMP.2007.4510607.
4. Negrea C. Alin, Imecs M., Incze I. lov, Pop A., Szabo C. Error compensation methods in speed identification using incremental encoder // Proceedings of International Conference and Exposition on Electrical and Power Engineering (EPE). — 2012. — С. 441-445. doi: 10.1109/ICEPE.2012.6463857.
5. Negrea C. Alin, Incze I. Iov, Imecs M., Pop A.V., Szabo C. An improved speed identification method using incremental encoder in electric drives // Proceedings of IEEE International Conference on Automation Quality and Testing Robotics (AQTR), 2012. -2012. — С. 536-540. doi: 10.1109/AQTR.2012.6237769.
6. El-Murr G., Giaouris D., Finch J.W. UNIVERSAL PLL STRATEGY FOR SENSORLESS SPEED AND POSITION ESTIMATION OF PMSM // Proceedings of IEEE Region 10 and the Third international
3
0
Conference on Industrial and Information Systems, 2008. -2008. — C. 1-6. doi: 10.1109/ICIINFS.2008.4798473.
-2008. — C. 1-6. doi: 10.1109/ICIINFS.2008.4798473.
7. Dong Yeob Han, Yongsoo Cho, Kyo-Beum Lee. Simple Rotor Position Estimation for Sensorless Control of IPMSM using PLL based on EEMF // Proceedings of IEEE Transportation Electrification Conference and Expo, Asia-
Pacific (ITEC). — 2016. — C. 656-660. doi: 10.1109/ITEC-AP.2016.7513034.
8. German A. Ramos, Ramon Costa-Castello, Josep M. Olm. Digital Repetitive Control under Varying Frequency Conditions // Springer Heidelberg New York Dordrecht London. — 2013. — T. 446. — 157 c.
Анучин Алексей Сергеевич,
ФГБОУВО «Национальный исследовательский университет «МЭИ»»,
кандидат технических наук, доцент, зав. кафедрой автоматизированного электропривода,
адрес: г. Москва, ул. Красноказарменная, д. 13, кор. Е, второй этаж,
Москва, ул. Красноказарменная, д. 13, кор. Е, второй этаж,
телефоны: +7(495)362-74-25, +7(495)362-70-21,
e-mail: [email protected]
Anuchin Aleksei Sergeyevich,
National Research University «Moscow Power Engineering Institute»,
Candidate of Engineering Sciences (PhD), Associate Professor, Head of the Automatic Electric Drive Department, address: Moscow, Krasnokazarmennaya St., No. 13, Building E, 2nd floor, tel. +7(495)362-74-25, +7(495)362-70-21, e-mail: [email protected]
Подзорова Валентина Сергеевна,
ФГБОУВО «Национальный исследовательский университет «МЭИ»», студентка кафедры автоматизированного электропривода, адрес: г. Москва, ул. Красноказарменная, д. 13, кор. Е, второй этаж, телефоны: +7(495)362-74-25, +7(495)362-70-21, e-mail: [email protected]. Podzorova Valentina Sergeyevna,
Москва, ул. Красноказарменная, д. 13, кор. Е, второй этаж, телефоны: +7(495)362-74-25, +7(495)362-70-21, e-mail: [email protected]. Podzorova Valentina Sergeyevna,
National Research University «Moscow Power Engineering Institute»,
Student of the Automatic Electric Drive Department,
address: Moscow, Krasnokazarmennaya St., No. 13, Building E, 2nd floor,
tel. +7(495)362-74-25, +7(495)362-70-21,
e-mail: [email protected]
Кульманов Василий Игоревич,
ФГБОУВО «Национальный исследовательский университет «МЭИ»»,
инженер кафедры автоматизированного электропривода,
адрес: г. Москва, ул. Красноказарменная, д. 13, кор. Е, второй этаж,
Москва, ул. Красноказарменная, д. 13, кор. Е, второй этаж,
телефоны: +7(495)362-74-25, +7(495)362-70-21,
e-mail: [email protected]
Kulmanov Vasily Igorevich,
National Research University «Moscow Power Engineering Institute»,
Engineer of the Automatic Electric Drive Department,
address: Moscow, Krasnokazarmennaya St., No. 13, Building E, 2nd floor,
tel. +7(495)362-74-25, +7(495)362-70-21,
e-mail: [email protected]
Шпак Дмитрий Михайлович,
ФГБОУВО «Национальный исследовательский университет «МЭИ»»,
инженер кафедры автоматизированного электропривода,
адрес: г. Москва, ул. Красноказарменная, д. 13, кор. Е, второй этаж,
Москва, ул. Красноказарменная, д. 13, кор. Е, второй этаж,
телефоны: +7(495)362-74-25, +7(495)362-70-21,
e-mail: [email protected]
Shpak Dmitry Mikhailovich,
National Research University «Moscow Power Engineering Institute»,
Engineer of the Automatic Electric Drive Department,
address: Moscow, Krasnokazarmennaya St., No. 13, Building E, 2nd floor,
tel. +7(495)362-74-25, +7(495)362-70-21,
e-mail: [email protected]
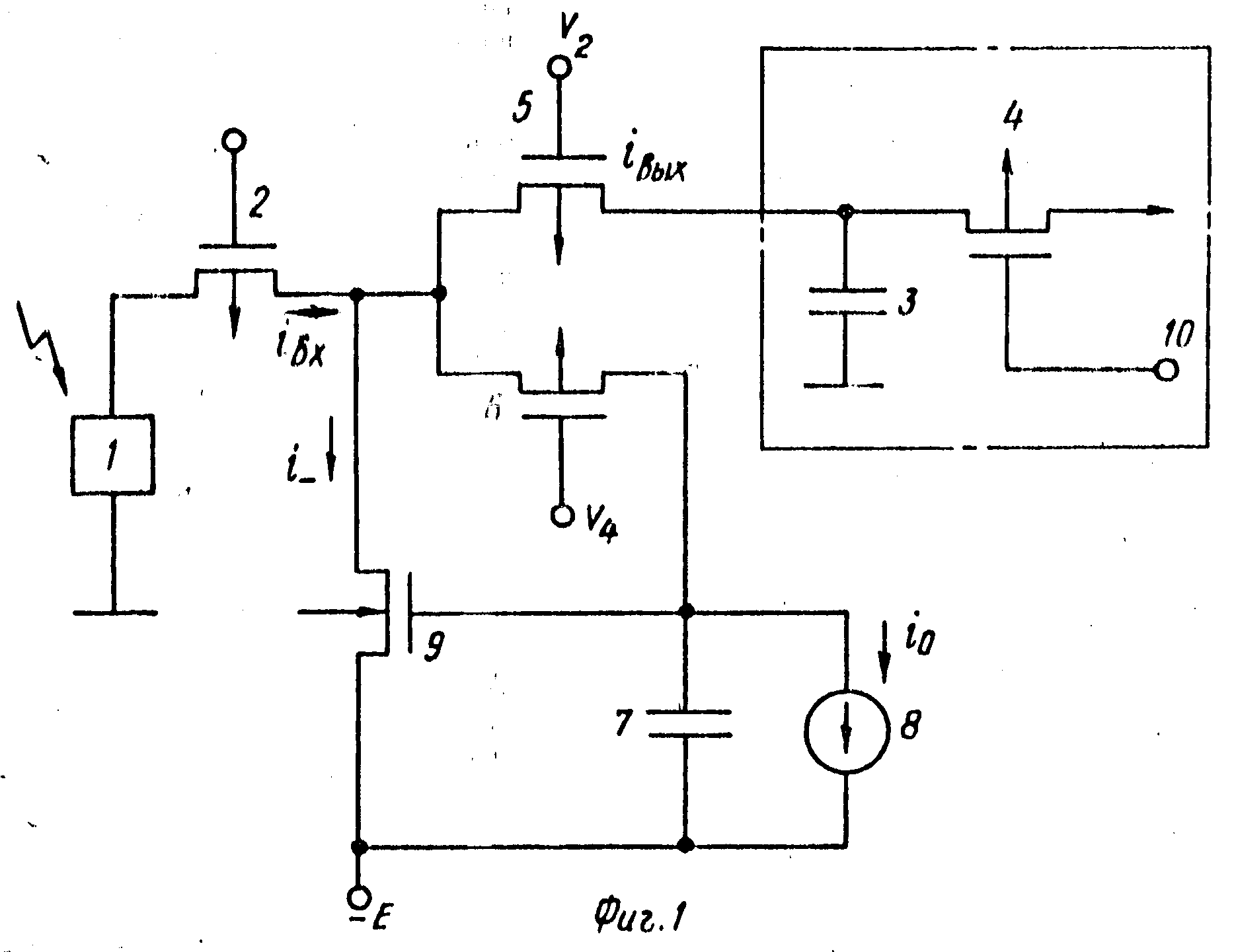
2.5 Способы обработки сигналов фотоприемников Измеряемое однолучевым измерительным преобразователем напряжение пропорционально отношению переменной составляющей выходного напряжения фотоприемника к его постоянной составляющей. Формирование этого отношения может быть реализовано различными способами.Первый способ формирования отношения заключается в выделении с помощью фильтров верхних и нижних частот переменной и постоянной составляющих выходного напряжения усилителя фототока и последующего деления мгновенного значения переменного напряжения на постоянное напряжение. Использование аналоговых схем для такого деления напряжений не позволяет обеспечить высокую точность, а преобразование составляющих выходного напряжения фотоприемника в цифровые значения и деление этих значений в цифровой форме, усложняет преобразователь и ограничивает его полосу пропускания частотой дискретизации аналого-цифровых преобразователей.  Второй способ формирования отношения заключается в выделении с помощью фильтра нижних частот постоянной составляющей выходного напряжения усилителя фототока, и изменении его коэффициента передачи так, чтобы постоянная составляющая всегда была равна некоторому опорному напряжению U0. В этом случае составляющие выходного напряжения усилителя фототока Для реализации этого способа необходимо автоматически изменять коэффициент передачи усилителя фототока. Использование аналоговых схем приводит к появлению нелинейной зависимости коэффициента передачи от величины сигнала, а цифровые схемы усложняют преобразователь. Третий способ формирования отношения заключается в выделении с помощью фильтра нижних частот постоянной составляющей выходного напряжения усилителя фототока, и изменении интенсивности источника света так, чтобы постоянная составляющая всегда была равна некоторому опорному напряжению U0. Это наиболее простой способ, при его реализации необходимо изменять только ток источника света, а параметры фотоприемника и усилителя фототока остаются неизменными. 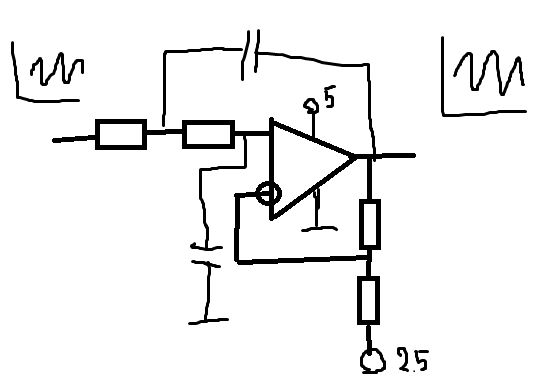 Измеряемое двухлучевым измерительным преобразователем напряжение пропорционально отношению разности выходных напряжений фотоприемников к сумме этих напряжений. Формирование этого отношения может быть реализовано, аналогично способам однолучевых измерительных преобразователей. Однако в двухлучевых преобразователя необходимо выполнение равенства коэффициентов преобразования фотоприемников, которое может быть обеспечено только изменение коэффициента передачи усилителей фототока. Невыполнение этого равенства приводит к появлению постоянной составляющей в разности напряжений фотоприемников, что не желательно. Для выравнивания коэффициентов преобразования фотоприемников необходимо выделить с помощью фильтров нижних частот постоянные составляющие выходного напряжения каждого усилителя фототока, и изменить его коэффициент передачи так, чтобы постоянная составляющая каждого усилителя всегда была равна некоторому опорному напряжению U0. Преимуществом двухлучевых измерительных преобразователей является удвоенный коэффициент преобразования. 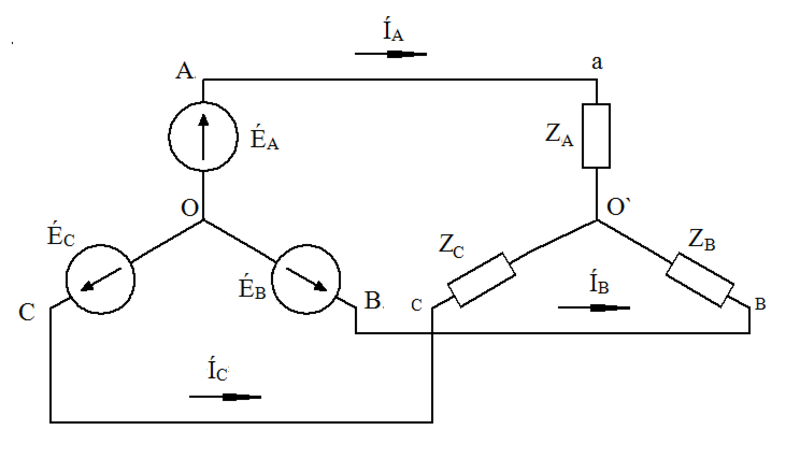 |
Нелинейное усиление и умножение частоты: схемы, режимы
Нелинейная схема усиления (умножения) частоты
Задача усиления колебаний в общем виде формулируется следующим образом. На вход некоторого преобразователя поступает сигнал S1(t). На выходе необходимо получить сигнал S2(t) = kS1(t — τ) при k > 1, который повторяет форму входного сигнала, но усиливается за счет энергии местного источника. Время запаздывания τ при этом не должно искажать форму сигнала.
Рис. 3.8. Нелинейная схема усиления (умножения) частоты
Рассмотрим в качестве примера схему резонансного усилителя на транзисторе, контур на выходе которого настроен на частоту входного сигнала (рис. 3.8). На вход усилителя подается сигнал (Формула). Для вольт-амперной характеристики используем кусочно-линейную аппроксимацию.
Усиление колебаний в линейном режиме
Обратимся сначала к линейному усилению. Угол отсечки в этом случае θ = 180°.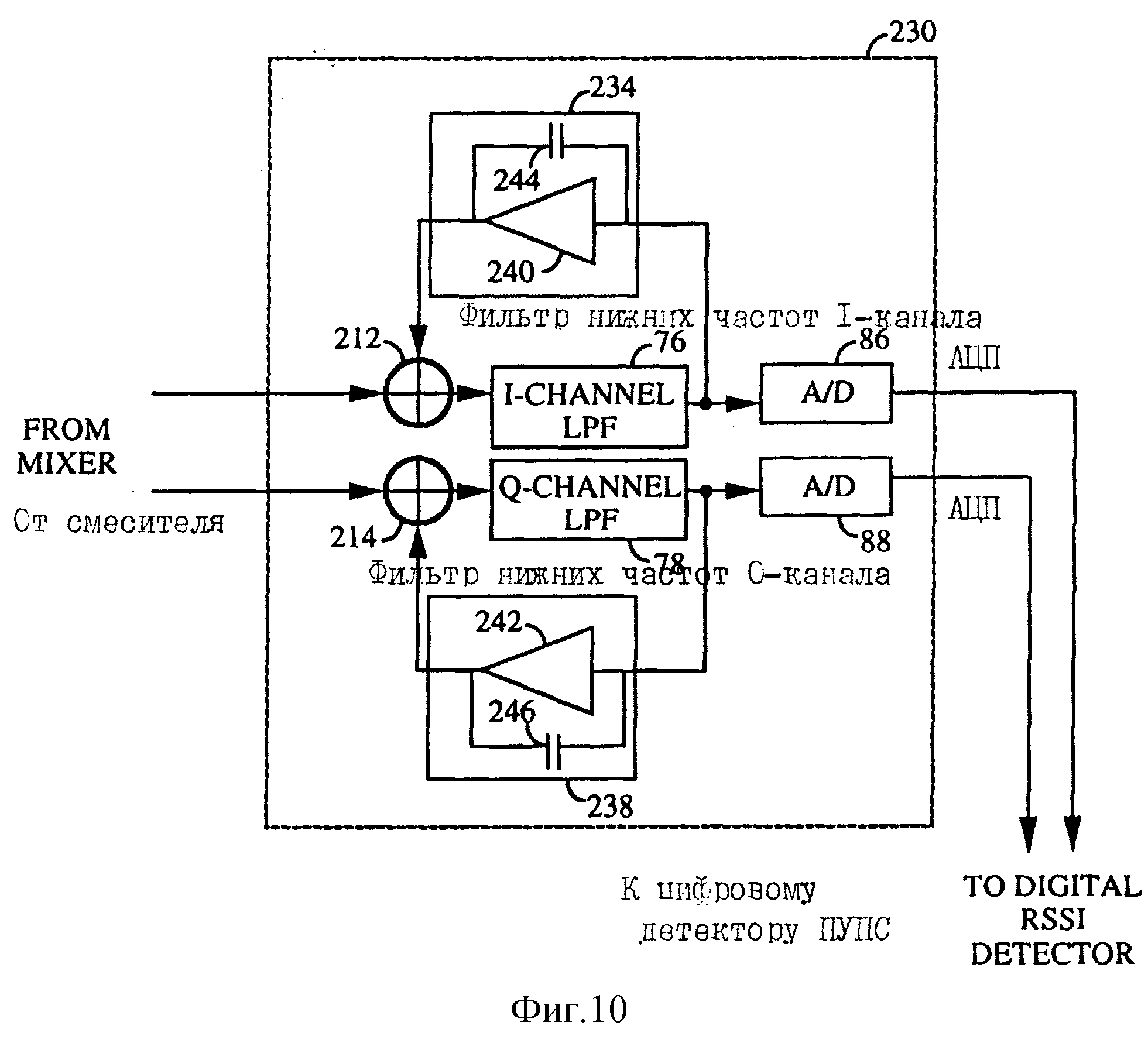 Рис. 3.9 соответствует этому режиму работы усилителя, так как входной сигнал не выходит за пределы линейного участка характеристики (Формула). Поэтому ток на выходе усилителя изменяется по тому же закону, что и входной сигнал. Выходной ток содержит постоянную составляющую (Формула) и переменную составляющую с амплитудой (Формула) и частотой ω.
Рис. 3.9 соответствует этому режиму работы усилителя, так как входной сигнал не выходит за пределы линейного участка характеристики (Формула). Поэтому ток на выходе усилителя изменяется по тому же закону, что и входной сигнал. Выходной ток содержит постоянную составляющую (Формула) и переменную составляющую с амплитудой (Формула) и частотой ω.
Рис. 3.9. Усиление колебаний в линейном режиме
В линейном режиме всегда, а амплитуда напряжения в контуре на выходе усилителя Uk не может быть больше напряжения источника энергии Ek, т. е. Uk ≤ Ек. Если принять, a Uk = Ек, то в самом благоприятном случае коэффициент полезного действия не превысит значения η = 0,5.
Усиление колебаний в нелинейном режиме
Рассмотрим теперь нелинейный режим работы усилителя, который иллюстрирует рис. 3.10. В данном случае угол отсечки θ < 180°, отношение (Формула). Например, при θ = 60° отношение (из справочных таблиц или графиков). Тогда при Uk = Ек коэффициент полезного действия η ≈ 0,8 … 0,9. Угол отсечки менее 60° нежелателен, поскольку при этом существенно уменьшается γ1, а следовательно, и полезная мощность Р1.
Угол отсечки менее 60° нежелателен, поскольку при этом существенно уменьшается γ1, а следовательно, и полезная мощность Р1.
Из сказанного можно сделать следующий вывод: в нелинейных режимах усиления можно получить гораздо большие значения КПД, чем в линейных. Правда, при этом возникают нелинейные искажения сигнала, связанные с появлением дополнительных гармонических составляющих.
Рис. 3.10. Усиление колебаний в нелинейном режиме
Рассмотрим теперь умножение частоты. Под умножением частоты принято понимать формирование на выходе устройства колебания, частота которого в целое число раз больше частоты входного сигнала. Если на входе действует сигнал (Формула), то на выходе должна быть частота колебания. Принципиальным фактом здесь является наличие нелинейного преобразователя, поскольку умножение частоты связано с появлением новых спектральных составляющих, которых не было на входе. Реализовать умножитель частоты применением только линейных элементов невозможно.
Пусть нелинейный преобразователь аппроксимирован многочленом n-й степени и на его вход подается гармоническое колебание.
После разложения данного соотношения по методу формул кратных дуг нетрудно увидеть, что выходной сигнал содержит вторую, третью и другие гармоники. Поэтому необходимую гармонику можно выделить с помощью фильтра, включаемого на выходе нелинейного преобразователя.
В качестве нелинейного преобразователя при умножении частоты можно использовать рассмотренный ранее нелинейный усилитель, только теперь в качестве нагрузки следует взять колебательный контур, настроенный на частоту n-й гармоники. На вход такого умножителя частоты подается колебание большой амплитуды, что приводит к нелинейным эффектам и позволяет использовать при расчете кусочно-линейную аппроксимацию и метод угла отсечки.
Ранее было показано, что амплитуда n-й гармоники. Если значение задано, то коэффициент будет максимален при оптимальном угле отсечки θ, который выбирается из справочных таблиц или графиков.
Причем максимум коэффициента имеет место, если θопт ≈ 120°/n. Так, для удвоения частоты оптимальный угол отсечки должен быть равен 60°, а для утроения — θ ≈ 40°.
Расчеты коэффициентов показывают, что они быстро уменьшаются с ростом номера гармоник, а следовательно, уменьшаются и амплитуды гармоник. Поэтому данную схему применяют только для умножения частоты в небольшое число раз, т.е. в 2 — 3 раза.
Для умножения частоты в большее число раз следует преобразовать гармоническое колебание в периодическую последовательность прямоугольных импульсов. Известно, что в спектральном составе таких импульсов имеются колебания всех частот, кратных частоте их следования. Поэтому требуемая гармоника далее выделяется с помощью узкополосного фильтра.
Выпрямители
4.3. Выпрямители
Из курса физики Вам
известно, что выпрямитель представляет собой прибор, преобразующий
переменный по величине и направлению ток в ток одного направления. Выпрямители
относятся к вторичным источникам электропитания.
Выпрямители
относятся к вторичным источникам электропитания.
Простейший выпрямитель переменного тока состоит из трансформатора и полупроводникового диода (рис. 4.11 а). Для простоты будем считать трансформатор и диод идеальными, то есть у трансформатора активное сопротивление обмоток равно нулю, прямое сопротивление диода также равно нулю, а обратное сопротивление диода равно бесконечности (обратным током можно пренебречь).
На вход выпрямителя со
вторичной обмотки трансформатора подается синусоидальное напряжение (рис. 4.11 б). В первый полупериод, когда на верхней (по схеме) точке обмотки
положительный потенциал относительно нижней точки, диод открыт и через
нагрузочный резистор протекает ток. Во второй полупериод (полярность напряжения
указана в скобках) диод закрыт и ток в резисторе отсутствует. Таким образом,
выходное напряжение (оно снимается с нагрузочного резистора) имеет форму
половинок синусоиды (рис. 4.11в). Оно называется пульсирующим.
Рассмотренный выпрямитель называется однополупериодным, поскольку в нем используются только половины каждого из периодов сетевого напряжения. Схема однополупериодного выпрямителя в практике применяется очень редко, поскольку получается большой коэффициент пульсаций выпрямленного напряжения (по сравнению с двухполупериодным выпрямителем при одинаковых сопротивлениях нагрузки).
В практике применяются двухполупериодные выпрямители. Они бывают мостовыми и с выводом от средней точки вторичной обмотки трансформатора. В двухполупериодных выпрямителях используются оба полупериода напряжения сети, поэтому они являются более эффективными, чем однополупериодные.
Рассмотрим работу двухполупериодного выпрямителя
с двумя диодами и выводом от средней точки вторичной обмотки трансформатора
(рис. 4.12а). Его можно рассматривать как совокупность двух
однополупериодных выпрямителей, к которым подсоединен один и тот же резистор
нагрузки.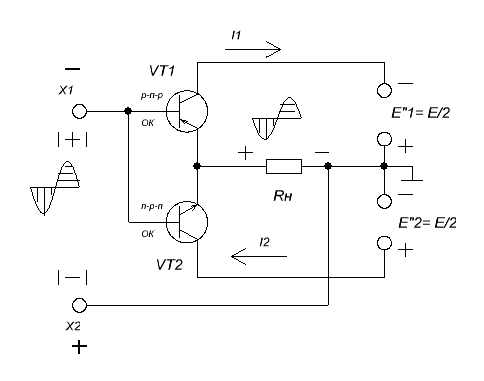
Пусть в первый полупериод на верхней (по схеме) точке обмотки трансформатора оказался положительный потенциал относительно нижней точки и, соответственно, относительно средней точки. Тогда ток будет протекать от верхней точки обмотки через диод VD1 к выводу “+”, через резистор нагрузки к выводу “-” и средней точке обмотки. Во второй полупериод на нижней (по схеме) точке обмотки окажется положительный потенциал относительно средней и верхней точки. Ток в этом случае будет протекать от нижней точки обмотки через диод VD2 к выводу “+”, через резистор нагрузки к выводу “-” и средней точке вторичной обмотки трансформатора. Таким образом, ток через резистор все время протекает в одном направлении и на выходе получается форма напряжения, изображенная на рисунке 4.12 в.
Недостатком рассмотренного выпрямителя является
то, что в каждый из полупериодов напряжение снимается только с половины
вторичной обмотки трансформатора. Более экономичным является двухполупериодный
выпрямитель, собранный на четырех диодах (рис. 4.13 а). Эта схема
называется мостовой, поскольку в ней применен диодный мост. К одной из
диагоналей моста присоединяют вторичную обмотку трансформатора, а к другой —
нагрузочный резистор. Иногда на схемах диодный мост изображают с помощью одного
диода (рис. 4.13 б).
4.13 а). Эта схема
называется мостовой, поскольку в ней применен диодный мост. К одной из
диагоналей моста присоединяют вторичную обмотку трансформатора, а к другой —
нагрузочный резистор. Иногда на схемах диодный мост изображают с помощью одного
диода (рис. 4.13 б).
В положительный полупериод сетевого напряжения (сверху по схеме на обмотке “+”, снизу “-”) ток протекает от верхней точки обмотки через диод VD2 к клемме “+”, через резистор нагрузки к клемме “-”, через диод VD4 к
нижней точке обмотки. В отрицательный полупериод сетевого напряжения (полярность показана в скобках) ток протекает от нижней точки обмотки через диод VD3 к клемме “+”, через резистор нагрузки к клемме “-”, через диод VD1 к верхней точке обмотки. Таким образом, каждая пара диодов работает поочередно и оба полупериода ток через резистор нагрузки имеет одно и то же направление.
Для питания операционных усилителей необходимо
иметь два источника питания разной полярности, имеющих общую точку. На рисунке 4.13в показана схема выпрямителя, обеспечивающего двухполупериодное
выпрямление каждого из напряжений на резисторах
RН1,
RН2
На рисунке 4.13в показана схема выпрямителя, обеспечивающего двухполупериодное
выпрямление каждого из напряжений на резисторах
RН1,
RН2
Выпрямленное напряжение, получаемое на выходе всех рассмотренных типов выпрямителей, является пульсирующим; в нем можно выделить постоянную и переменную составляющие. Постоянная составляющая выпрямленного напряжения — это среднее значение напряжения за период. Коэффициент пульсаций — это отношение амплитуды первой гармоники выпрямленного напряжения к постоянной составляющей выпрямленного напряжения. Для нормальной работы большинства электронных устройств необходимо, чтобы пульсации напряжения были как можно меньше. Поэтому на выходе выпрямителей достаточно часто устанавливают сглаживающие фильтры, уменьшающие пульсации выпрямленного напряжения.
Основными элементами фильтров служат
конденсаторы, катушки индуктивности и транзисторы, сопротивления которых
различны для постоянного и переменного токов.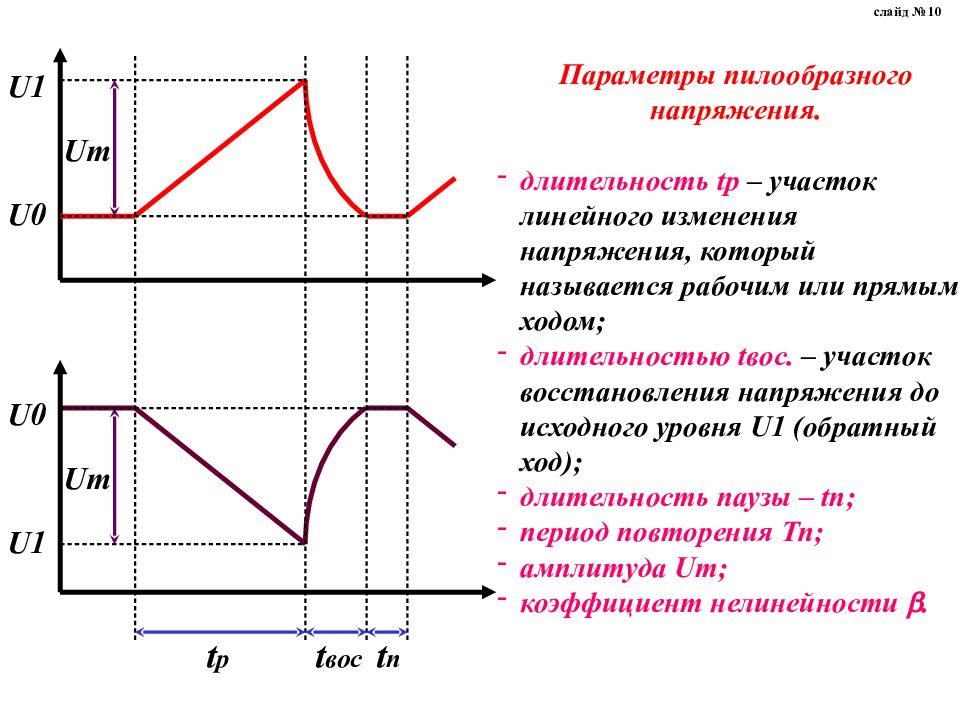 В зависимости от используемых
элементов различают емкостные, индуктивные и электронные фильтры.
В зависимости от используемых
элементов различают емкостные, индуктивные и электронные фильтры.
Простейшим емкостным фильтром служит
конденсатор, включаемый параллельно резистору нагрузки. Рассмотрим, как
изменится выходное напряжение при использовании такого фильтра в
однополупериодном выпрямителе (рис. 4.14а). В интервал времени
Dt
положительного полупериода сетевого напряжения конденсатор через открытый диод
заряжается в полярности, указанной на схеме. Когда напряжение на вторичной
обмотке трансформатора становится меньше напряжения, до которого зарядился
конденсатор, он начинает разряжаться через нагрузочный резистор. Причем
направление разрядного тока совпадает с направлением тока, протекающего в
резисторе через открытый диод. В следующий положительный полупериод конденсатор
через открытый диод снова заряжается и процессы разрядки повторяются. Тем самым
заполняются паузы в токе, протекающем через резистор, и пульсации выпрямленного
напряжения сглаживаются (рис.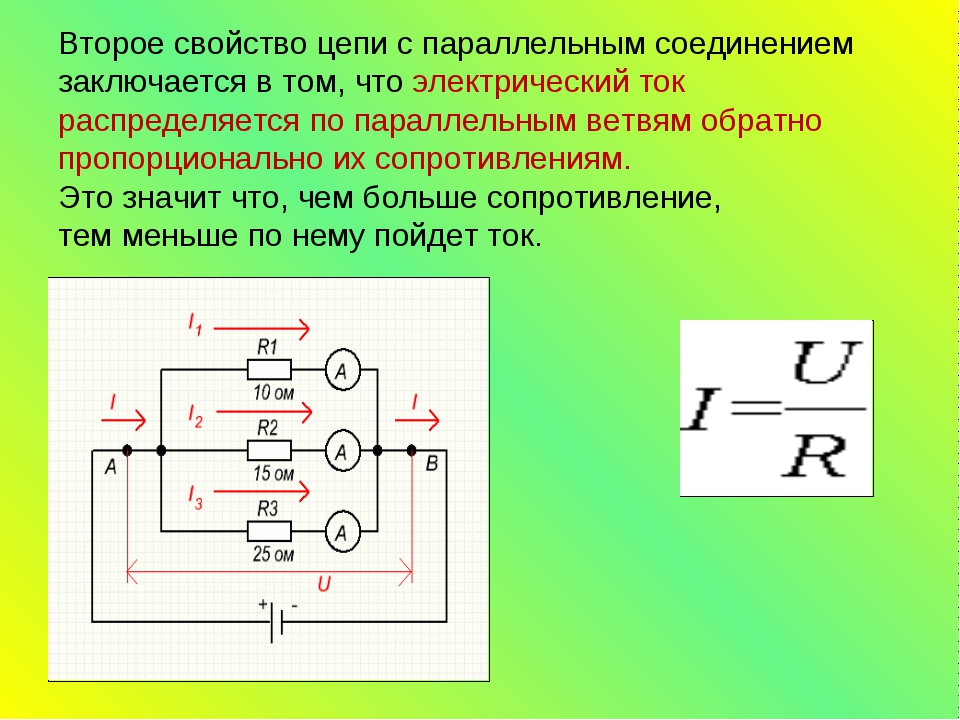 4.14 в).
4.14 в).
В выпрямителях применяются
емкостно — индуктивные, емкостно — резистивные и электронные фильтры. Простейшие
варианты схем таких фильтров приведены на рисунках 4.15 а, б, в соответственно. Емкостно-резистивные фильтры в настоящее время применяются очень
редко и при очень небольших токах нагрузки. Для фильтрации выпрямленного
напряжения достаточно часто используются электронные фильтры. В качестве примера
на рисунке 4.16 приведена схема электронного фильтра, примененного в
экономичном импульсном стабилизаторе напряжения [42]. Ток базы транзистора VT2
протекает по цепи: плюс источника, резистор
R2,
переход баз-эмиттер транзистора, резистор нагрузки, минус источника. Ток базы
транзистора
VT1
протекает по цепи: плюс источника питания, переход эмиттер-база транзистора VT1,
выводы коллектор-эмиттер транзистора
VT2,
резистор нагрузки, минус источника питания. Напряжение на конденсаторе С2 изменяется в основном за счет изменения силы тока базы транзистора
VT2,
а ток базы этого транзистора существенно меньше тока нагрузки (транзисторы
должны иметь большой коэффициент усиления по току).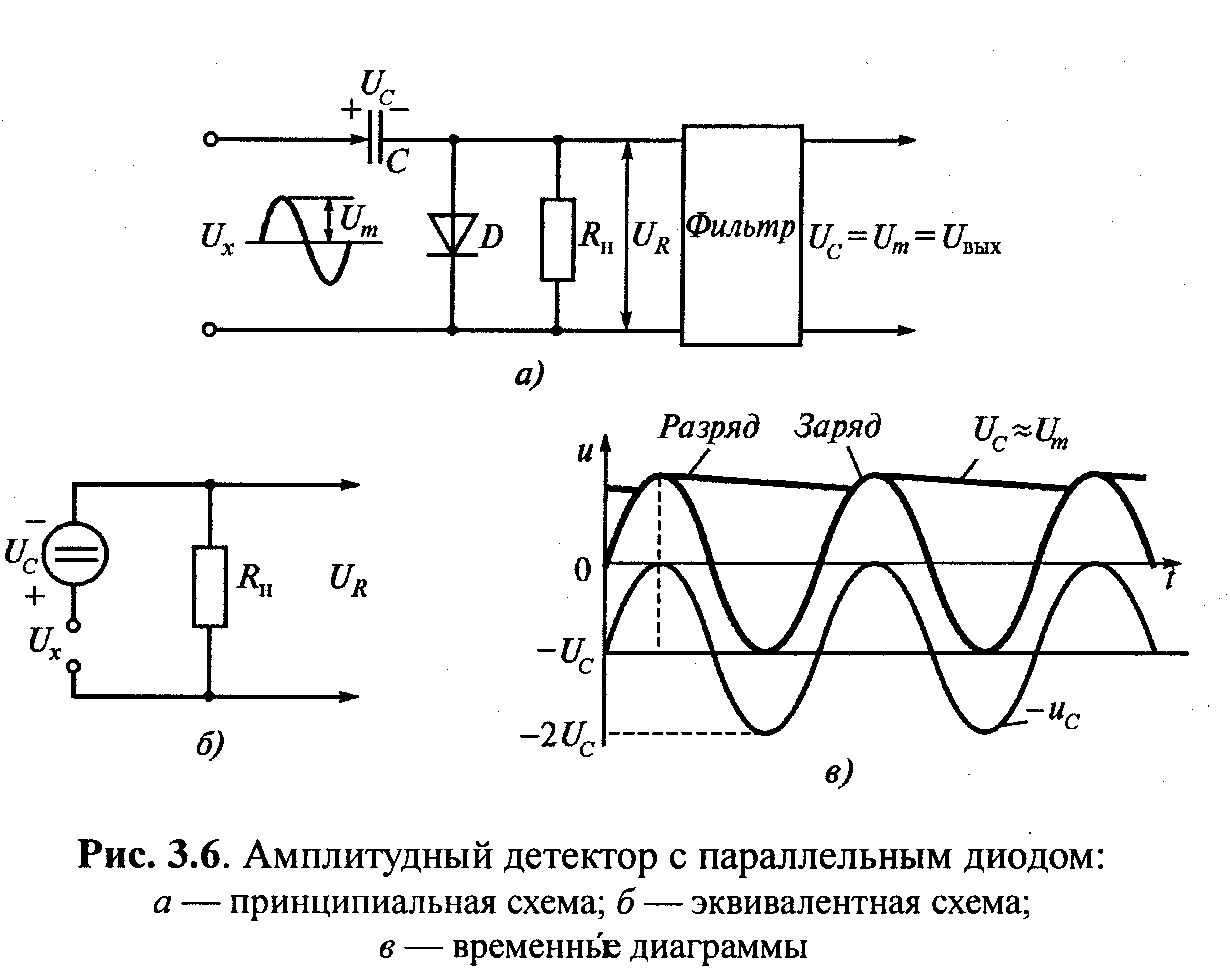
Для получения высоких напряжений обычно используют схемы умножения напряжения. На рисунке 4.17а приведена схема умножителя напряжения. Умножители напряжения позволяют получить большое значение выпрямленного напряжения при не очень больших обратных напряжениях, приложенных к диодам. Выпрямители по схеме умножения напряжения используют для питания электронно-лучевых трубок осциллографов и телевизоров.
Если в распоряжении пользователя нет
полупроводниковых диодов с необходимым обратным напряжением, то диоды можно
включать последовательно для повышения допустимого обратного напряжения. Чтобы
диоды не вышли из строя из-за разброса их обратных сопротивлений параллельно
каждому диоду подключают резисторы сопротивлением 30-100 кОм (рис. 4.17 б).
Сопротивление резисторов должно быть одинаковым и меньше наименьшего из обратных
сопротивлений диодов. Тогда к каждому из диодов будут приложены примерно
одинаковые обратные напряжения.
Если нужно получить прямой ток, больший предельного тока одного диода, используют параллельное соединение диодов (рис. 4.17в). Чтобы диоды не вышли из строя из-за разброса прямых токов (даже у однотипных диодов разброс может составлять десятки процентов) последовательно с диодами включают уравнительные резисторы сопротивлением десятые доли ома или единицы ом. Сопротивления резисторов подбирают экспериментально, чтобы токи через диоды были одинаковыми.
Учебное пособие по физике: Требования схемы
Предположим, вам дали небольшую лампочку, электрохимический элемент и оголенный медный провод, и вас попросили найти четыре различных расположения трех элементов, которые приведут к образованию электрической цепи, которая зажгла бы лампочку. Какие четыре расположения могут привести к успешному зажиганию лампочки? И что еще более важно, что общего у каждой из четырех схем, что привело бы нас к пониманию двух требований к электрической цепи? Само по себе упражнение является стоящим занятием, и если оно не выполнялось раньше, следует попробовать его, прежде чем читать дальше. Как и во многих лабораторных занятиях, в фактическом участии в работе есть сила, которую нельзя заменить простым чтением о ней. Когда это упражнение выполняется в классе физики, есть множество наблюдений, которые можно сделать, наблюдая за классом, полным студентов, стремящихся найти четыре схемы. Часто используются следующие меры, которые не приводят к включению лампочки.
Как и во многих лабораторных занятиях, в фактическом участии в работе есть сила, которую нельзя заменить простым чтением о ней. Когда это упражнение выполняется в классе физики, есть множество наблюдений, которые можно сделать, наблюдая за классом, полным студентов, стремящихся найти четыре схемы. Часто используются следующие меры, которые не приводят к включению лампочки.
После нескольких минут попыток, нескольких здоровых смешков и периодических восклицаний о том, насколько сильно нагревается провод, нескольким ученикам удается зажечь лампочку.В отличие от вышеупомянутых попыток, первая успешная попытка характеризуется созданием полной проводящей петли от положительной клеммы к отрицательной клемме, при этом как батарея, так и лампочка являются частью петли. Как показано на схеме справа, основание лампочки подключается к положительному выводу элемента, а провод проходит от ребристых сторон лампы до отрицательного вывода элемента. Создается полная проводящая петля, в которую входит лампочка. Существует цепь, и заряд течет по всему проводящему пути, зажигая при этом лампочку. Сравните расположение элемента, лампы и провода справа с неудачным расположением, показанным выше. При попытке A провод не возвращается к отрицательному выводу ячейки. В попытке B провод действительно образует петлю, но не возвращается к отрицательному выводу ячейки. В попытке C нет полного цикла. Попытка D похожа на попытку B тем, что есть петля, но не от положительной клеммы к отрицательной.А при попытке E возникает петля, и она идет от положительной клеммы к отрицательной; это цепь, но лампочка в нее не входит. ВНИМАНИЕ: При попытке E ваши пальцы нагреваются, когда вы держите оголенный провод, и заряд начинает течь с высокой скоростью между положительной и отрицательной клеммами.
Существует цепь, и заряд течет по всему проводящему пути, зажигая при этом лампочку. Сравните расположение элемента, лампы и провода справа с неудачным расположением, показанным выше. При попытке A провод не возвращается к отрицательному выводу ячейки. В попытке B провод действительно образует петлю, но не возвращается к отрицательному выводу ячейки. В попытке C нет полного цикла. Попытка D похожа на попытку B тем, что есть петля, но не от положительной клеммы к отрицательной.А при попытке E возникает петля, и она идет от положительной клеммы к отрицательной; это цепь, но лампочка в нее не входит. ВНИМАНИЕ: При попытке E ваши пальцы нагреваются, когда вы держите оголенный провод, и заряд начинает течь с высокой скоростью между положительной и отрицательной клеммами.
Как только одна группа студентов успешно зажигает лампочку, многие другие лабораторные группы быстро следуют ее примеру.Но тогда возникает вопрос, какими еще способами можно расположить элемент, лампочку и оголенный провод, чтобы зажечь лампочку. Часто короткий урок анатомии лампочки побуждает лабораторные группы быстро найти одну или несколько оставшихся схем.
Часто короткий урок анатомии лампочки побуждает лабораторные группы быстро найти одну или несколько оставшихся схем.
Лампочка — это относительно простое устройство, состоящее из нити накала, опирающейся на два провода или как-то прикрепленных к ним. Провода и нить накала — это проводящие материалы, которые позволяют заряду проходить через них.Один провод подключается к ребристым сторонам лампочек. Другой провод подключается к нижнему цоколю лампочки. Ребристый край и нижнее основание разделены изоляционным материалом, который предотвращает прямой поток заряда между нижним основанием и ребристым краем. Единственный путь, по которому заряд может пройти от ребристого края к нижнему основанию или наоборот, — это путь, который включает провода и нить накала. Заряд может входить в ребристый край, проходить через нить и выходить из нижнего основания; или он может войти в нижнее основание, пройти через нить и выйти из ребристого края.Таким образом, есть две возможные точки входа и две соответствующие точки выхода.
Успешный способ зажечь лампочку, как показано выше, заключался в размещении нижнего основания лампы на положительной клемме и соединении ребристого края с отрицательной клеммой с помощью провода. Любой заряд, который попадает в лампочку в нижнем основании, выходит из лампы в том месте, где провод соприкасается с ребристым краем. Тем не менее, нижнее основание не обязательно должно быть той частью лампы, которая касается положительной клеммы.Лампа загорится так же легко, если ребристый край поместить поверх положительной клеммы, а нижнее основание соединить с отрицательной клеммой с помощью провода. Последние две компоновки, которые приводят к включению лампочки, включают размещение лампы на отрицательном выводе ячейки, либо путем соприкосновения с ребристым краем, либо с нижним основанием. Затем провод должен соединить другую часть лампы с положительной клеммой элемента.
Требование замкнутого проводящего пути Есть два требования, которые должны быть выполнены, чтобы установить электрическую цепь. Первое наглядно продемонстрировано вышеупомянутой деятельностью. Должен быть замкнутый проводящий путь, который простирается от положительной клеммы к отрицательной. Недостаточно просто наличия замкнутого проводящего контура; Сама петля должна проходить от положительного вывода к отрицательному выводу электрохимической ячейки. Электрический контур похож на водяной контур в аквапарке. Поток заряда по проводам аналогичен потоку воды по трубам и горкам в аквапарке.Если труба закупоривается или ломается так, что вода не может пройти полный путь через контур , то поток воды скоро прекратится. В электрической цепи все соединения должны быть выполнены из проводящих материалов, способных нести заряд. По мере продолжения эксперимента с ячейкой, лампочкой и проводом некоторые студенты исследуют способность различных материалов нести заряд, вставляя их в свои цепи. Металлические материалы являются проводниками и могут быть вставлены в цепь, чтобы успешно зажечь лампочку.С другой стороны, бумага и пластмассы обычно являются изоляторами, и их вставка в цепь будет препятствовать прохождению заряда до такой степени, что ток пропадет и лампочка больше не загорится.
Первое наглядно продемонстрировано вышеупомянутой деятельностью. Должен быть замкнутый проводящий путь, который простирается от положительной клеммы к отрицательной. Недостаточно просто наличия замкнутого проводящего контура; Сама петля должна проходить от положительного вывода к отрицательному выводу электрохимической ячейки. Электрический контур похож на водяной контур в аквапарке. Поток заряда по проводам аналогичен потоку воды по трубам и горкам в аквапарке.Если труба закупоривается или ломается так, что вода не может пройти полный путь через контур , то поток воды скоро прекратится. В электрической цепи все соединения должны быть выполнены из проводящих материалов, способных нести заряд. По мере продолжения эксперимента с ячейкой, лампочкой и проводом некоторые студенты исследуют способность различных материалов нести заряд, вставляя их в свои цепи. Металлические материалы являются проводниками и могут быть вставлены в цепь, чтобы успешно зажечь лампочку.С другой стороны, бумага и пластмассы обычно являются изоляторами, и их вставка в цепь будет препятствовать прохождению заряда до такой степени, что ток пропадет и лампочка больше не загорится. Должен быть замкнутый проводящий контур от положительного к отрицательному выводу, чтобы установить цепь и иметь ток.
Должен быть замкнутый проводящий контур от положительного к отрицательному выводу, чтобы установить цепь и иметь ток.
С пониманием этого первого требования к электрической цепи становится ясно, что происходит, когда лампа накаливания в настольной лампе или торшере перестает работать.Со временем нить накаливания лампочки становится слабой и хрупкой, часто может сломаться или просто ослабнуть. Когда это происходит, цепь разомкнута, замкнутая проводящая петля больше не существует. Без замкнутого проводящего контура не может быть ни цепи, ни потока заряда, ни горящей лампочки. В следующий раз, когда вы обнаружите сломанную лампочку в лампе, осторожно извлеките ее и осмотрите нить. Часто встряхивание снятой лампы вызывает дребезжание; нить накала, вероятно, упала с опорных стоек, на которые она обычно опирается, на дно стеклянного шара.При встряхивании вы услышите стук нити, ударяющейся о стеклянный шар.
Потребность в энергоснабжении Второе требование к электрической цепи, которое является общим для каждой из успешных попыток, продемонстрированных выше, заключается в том, что на двух концах схемы должна быть разность электрических потенциалов.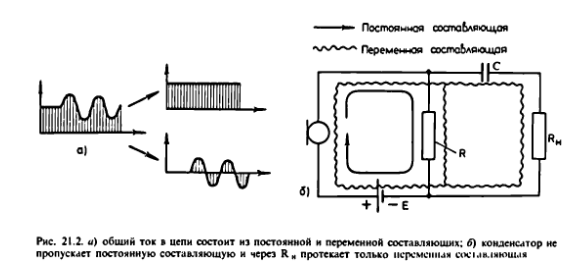 Чаще всего это устанавливается при использовании электрохимической ячейки, набора ячеек (т.е.е., аккумулятор) или какой-либо другой источник энергии. Существенно, что существует некоторый источник энергии, способный увеличивать электрическую потенциальную энергию заряда, когда он перемещается от терминала с низкой энергией к терминалу с высокой энергией. Как обсуждалось в Уроке 1, для перемещения положительного тестового заряда против электрического поля требуется энергия. Применительно к электрическим цепям движение положительного тестового заряда через элемент от вывода с низким энергопотреблением к выводу с высоким энергопотреблением является движением против электрического поля.Это движение заряда требует, чтобы над ним была проделана работа, чтобы поднять его вверх к терминалу с более высокой энергией. Электрохимический элемент выполняет полезную роль в обеспечении энергии для работы с зарядом, чтобы накачать его, или переместить его через элемент от отрицательного вывода к положительному.
Чаще всего это устанавливается при использовании электрохимической ячейки, набора ячеек (т.е.е., аккумулятор) или какой-либо другой источник энергии. Существенно, что существует некоторый источник энергии, способный увеличивать электрическую потенциальную энергию заряда, когда он перемещается от терминала с низкой энергией к терминалу с высокой энергией. Как обсуждалось в Уроке 1, для перемещения положительного тестового заряда против электрического поля требуется энергия. Применительно к электрическим цепям движение положительного тестового заряда через элемент от вывода с низким энергопотреблением к выводу с высоким энергопотреблением является движением против электрического поля.Это движение заряда требует, чтобы над ним была проделана работа, чтобы поднять его вверх к терминалу с более высокой энергией. Электрохимический элемент выполняет полезную роль в обеспечении энергии для работы с зарядом, чтобы накачать его, или переместить его через элемент от отрицательного вывода к положительному. Таким образом, ячейка устанавливает разность электрических потенциалов на двух концах электрической цепи. (Концепция разности электрических потенциалов и ее применение к электрическим цепям подробно обсуждались в Уроке 1.)
Таким образом, ячейка устанавливает разность электрических потенциалов на двух концах электрической цепи. (Концепция разности электрических потенциалов и ее применение к электрическим цепям подробно обсуждались в Уроке 1.)
В бытовых электрических цепях энергия подается местной коммунальной компанией, которая отвечает за обеспечение того, чтобы пластины hot и нейтральные в монтажной коробке вашего дома всегда имели разность электрических потенциалов около 110 вольт. 120 Вольт (в США). В типичной лабораторной деятельности электрохимический элемент или группа элементов (то есть батарея) используется для установления разности электрических потенциалов на двух концах внешней цепи около 1.5 Вольт (одна ячейка) или 4,5 Вольт (три ячейки в упаковке). Часто проводят аналогии между электрической цепью и водяным контуром в аквапарке или поездкой на американских горках в парке развлечений. Во всех трех случаях что-то движется по полному циклу, то есть по цепи. И во всех трех случаях важно, чтобы схема включала участок, в котором энергия подводится к воде, каботажному кораблю или заряду, чтобы переместить его на вверх по против его естественного направления движения от низкопотенциальной энергии к низкоэнергетическому.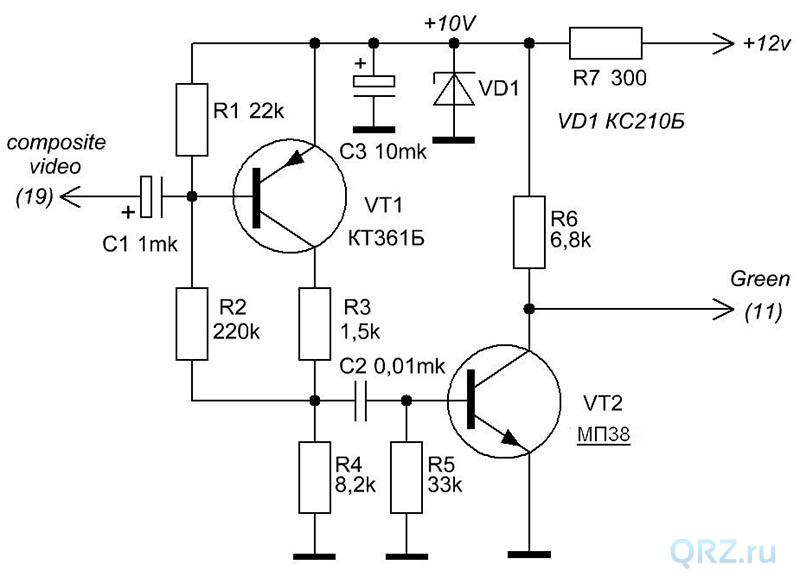 высокая потенциальная энергия.В аквапарке есть водяной насос, который перекачивает воду с уровня земли на вершину горки. У аттракционов «американские горки» есть цепь с приводом от двигателя, которая переносит поезд каботажных вагонов от уровня земли до вершины первого падения. А электрическая цепь имеет электрохимический элемент, батарею (группу ячеек) или какой-либо другой источник энергии, который перемещает заряд с уровня земли (отрицательный вывод) на положительный вывод. Путем постоянной подачи энергии для перемещения заряда от клеммы с низкой энергией и низким потенциалом к клемме с высокой энергией и высоким потенциалом можно поддерживать непрерывный поток заряда.
высокая потенциальная энергия.В аквапарке есть водяной насос, который перекачивает воду с уровня земли на вершину горки. У аттракционов «американские горки» есть цепь с приводом от двигателя, которая переносит поезд каботажных вагонов от уровня земли до вершины первого падения. А электрическая цепь имеет электрохимический элемент, батарею (группу ячеек) или какой-либо другой источник энергии, который перемещает заряд с уровня земли (отрицательный вывод) на положительный вывод. Путем постоянной подачи энергии для перемещения заряда от клеммы с низкой энергией и низким потенциалом к клемме с высокой энергией и высоким потенциалом можно поддерживать непрерывный поток заряда.
Устанавливая эту разницу в электрическом потенциале, заряд может течь вниз по внешней цепи. Это движение заряда естественно и не требует энергии. Подобно движению воды в аквапарке или американским горкам в парке развлечений, движение под уклон является естественным и происходит без потребности в энергии из внешнего источника. Разница в потенциалах — будь то гравитационный или электрический потенциал — заставляет воду, каботажную машину и заряд двигаться.Эта разность потенциалов требует ввода энергии от внешнего источника. В случае электрической цепи одним из двух требований для создания электрической цепи является источник энергии.
В заключение, есть два требования, которые должны быть выполнены, чтобы установить электрическую цепь. Требования:
- Должен быть источник энергии, способный выполнять работу на заряде, чтобы переместить его из места с низким энергопотреблением в место с высоким энергопотреблением и, таким образом, установить разность электрических потенциалов на двух концах внешней цепи.
- Во внешней цепи должен быть замкнутый проводящий контур, который простирается от положительной клеммы с высоким потенциалом к отрицательной клемме с низким потенциалом.
1. Если электрическую схему можно сравнить с водным контуром в аквапарке, то …
… батарея будет аналогична ____.… положительный полюс аккумуляторной батареи будет аналогичен ____.
… ток аналогичен ____.
… заряд будет аналогичен ____.
… разность электрических потенциалов аналогична ____.
Выбор:
A. давление воды
млрд. Галлонов воды, стекающей по горке в минуту
С.вода
D. нижняя часть салазок
E. водяной насос
F. верх горки
2. Используйте свое понимание требований к электрической цепи, чтобы определить, будет ли проходить заряд через следующие устройства ячеек, лампочек, проводов и переключателей.Если нет расхода заряда то объясните почему нет.
| а. | б. |
| Поток заряда: да или нет? Пояснение: | Поток заряда: да или нет? Пояснение: |
| c. | d. |
| Поток заряда: да или нет? Пояснение: | Поток заряда: да или нет? Пояснение: |
3.На схеме справа показана лампочка, подключенная к автомобильному аккумулятору 12 В. Показаны клеммы + и -.
а. Когда + заряд проходит через батарею от D к A, он ________ (получает, теряет) потенциальную энергию и ________ (получает, теряет) электрический потенциал. Точка максимальной энергии в батарее — это клемма ______ (+, -).г. Когда + заряд движется по внешней цепи от A к D, он ________ (получает, теряет) потенциальную энергию и ________ (получает, теряет) электрический потенциал.Точка максимальной энергии во внешней цепи находится ближе всего к клемме ______ (+, -).
г. Используйте знаки>, <и = для сравнения электрического потенциала (В) в четырех точках цепи.
V A V B V C V D
4. В фильме « Tango and Cash » Курт Рассел и Сильвестр Сталлоне сбегают из тюрьмы, спрыгнув с вершины высокой стены по воздуху на высоковольтную линию электропередачи.Перед прыжком Сталлоне возражает против этой идеи, говоря Расселу: «Мы собираемся поджариться». Рассел отвечает: «Вы ведь не учились в школе физики. Пока вы касаетесь только одного провода и ваши ноги не касаются земли, вас не ударит током». Это правильное утверждение?
Страница не найдена | MIT
Перейти к содержанию ↓- Образование
- Исследовать
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О Массачусетском технологическом институте
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О Массачусетском технологическом институте
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов
Предложения или отзывы?
10.5 RC Circuits — University Physics Volume 2
Учебные цели
К концу раздела вы сможете:- Опишите процесс зарядки конденсатора
- Опишите процесс разрядки конденсатора
- Перечислите некоторые применения RC-цепей
При использовании камеры со вспышкой зарядка конденсатора, питающего вспышку, занимает несколько секунд. Световая вспышка разряжает конденсатор за крошечные доли секунды. Почему зарядка занимает больше времени, чем разрядка? Этот вопрос и несколько других явлений, связанных с зарядкой и разрядкой конденсаторов, обсуждаются в этом модуле.
Цепи с сопротивлением и емкостью
Цепь RC — это цепь, содержащая сопротивление и емкость. Как показано в разделе «Емкость», конденсатор — это электрический компонент, который накапливает электрический заряд, накапливая энергию в электрическом поле.
На рис. 10.38 (a) показана простая схема RC , в которой используется источник постоянного напряжения εε, резистор R , конденсатор C и двухпозиционный переключатель. Схема позволяет конденсатору заряжаться или разряжаться в зависимости от положения переключателя.Когда переключатель перемещается в положение A, , конденсатор заряжается, в результате чего возникает цепь в части (b). Когда переключатель перемещается в положение B , конденсатор разряжается через резистор.
Рисунок 10.38 (a) Схема RC с двухполюсным переключателем, который можно использовать для зарядки и разрядки конденсатора. (b) Когда переключатель перемещается в положение A , схема сводится к простому последовательному соединению источника напряжения, резистора, конденсатора и переключателя.(c) Когда переключатель перемещается в положение B , схема сводится к простому последовательному соединению резистора, конденсатора и переключателя. Источник напряжения снимается с цепи.
Зарядка конденсатора
Мы можем использовать правило петли Кирхгофа, чтобы понять заряд конденсатора. Это приводит к уравнению ε − VR − Vc = 0. ε − VR − Vc = 0. Это уравнение можно использовать для моделирования заряда как функции времени при зарядке конденсатора. Емкость определяется как C = q / V, C = q / V, поэтому напряжение на конденсаторе равно VC = qCVC = qC.Согласно закону Ома падение потенциала на резисторе VR = IRVR = IR, а ток определяется как I = dq / dt.I = dq / dt.
ε − VR − Vc = 0, ε − IR − qC = 0, ε − Rdqdt − qC = 0. ε − VR − Vc = 0, ε − IR − qC = 0, ε − Rdqdt − qC = 0.Это дифференциальное уравнение можно проинтегрировать, чтобы найти уравнение для заряда конденсатора как функции времени.
ε − Rdqdt − qC = 0, dqdt = εC − qRC, ∫0qdqεC − q = 1RC∫0tdt.ε − Rdqdt − qC = 0, dqdt = εC − qRC, ∫0qdqεC − q = 1RC∫0tdt.Пусть u = εC − qu = εC − q, тогда du = −dq.du = −dq. Результат
−∫0qduu = 1RC∫0tdt, ln (εC − qεC) = — 1RCt, εC − qεC = e − tRC.−∫0qduu = 1RC∫0tdt, ln (εC − qεC) = — 1RCt, εC − qεC = e − tRC.В результате упрощения получается уравнение для заряда зарядного конденсатора как функции времени:
q (t) = Cε (1 − e − tRC) = Q (1 − e − tτ). q (t) = Cε (1 − e − tRC) = Q (1 − e − tτ).10,8
График зависимости заряда конденсатора от времени показан на Рисунке 10.39 (а). Во-первых, обратите внимание, что по мере приближения времени к бесконечности экспонента стремится к нулю, поэтому заряд приближается к максимальному заряду Q = CεQ = Cε и имеет единицы кулонов. Единицы измерения RC — секунды, единицы времени.Эта величина известна как постоянная времени:
.В момент времени t = τ = RCt = τ = RC заряд равен 1 − e − 1 = 1−0,368 = 0,6321 − e − 1 = 1−0,368 = 0,632 от максимального заряда Q = CεQ = Cε. Обратите внимание, что изменение скорости заряда во времени представляет собой наклон в точке графика зависимости заряда от времени. Наклон графика большой в момент времени t = 0,0st = 0,0 с и приближается к нулю с увеличением времени.
По мере увеличения заряда конденсатора ток через резистор уменьшается, как показано на Рисунке 10.39 (b). Ток через резистор можно найти, взяв производную заряда по времени.
I (t) = dqdt = ddt [Cε (1 − e − tRC)], I (t) = Cε (1RC) e − tRC = εRe − tRC = Ioe − tRC, I (t) = dqdt = ddt [Cε (1 − e − tRC)], I (t) = Cε (1RC) e − tRC = εRe − tRC = Ioe − tRC, I (t) = I0e − t / τ. I (t) = I0e − t / τ.10,10
В момент времени t = 0,00 с, t = 0,00 с ток через резистор равен I0 = εRI0 = εR. Когда время приближается к бесконечности, ток приближается к нулю. В момент времени t = τt = τ ток через резистор равен I (t = τ) = I0e − 1 = 0,368I0.I (t = τ) = I0e − 1 = 0,368I0.
Рис. 10.39 (a) Заряд конденсатора в зависимости от времени, когда конденсатор заряжается.(б) Ток через резистор в зависимости от времени. (c) Разность напряжений на конденсаторе. (d) Разность напряжений на резисторе.
На рисунках 10.39 (c) и 10.39 (d) показаны разности напряжений на конденсаторе и резисторе соответственно. По мере увеличения заряда конденсатора ток уменьшается, как и разница напряжений на резисторе VR (t) = (I0R) e − t / τ = εe − t / τ. VR (t) = (I0R) e − t / τ = εe − t / τ. Разность напряжений на конденсаторе увеличивается как VC (t) = ε (1-e-t / τ).VC (t) = ε (1 − e − t / τ).
Разряд конденсатора
Когда переключатель на рис. 10.38 (a) перемещается в положение B , схема сокращается до схемы в части (c), и заряженному конденсатору позволяют разрядиться через резистор. График зависимости заряда конденсатора от времени показан на Рисунке 10.40 (а). Использование правила петли Кирхгофа для анализа цепи при разряде конденсатора приводит к уравнению -VR-Vc = 0-VR-Vc = 0, которое упрощается до IR + qC = 0IR + qC = 0.Используя определение тока dqdtR = −qCdqdtR = −qC и интегрируя уравнение контура, получаем уравнение для заряда конденсатора как функции времени:
q (t) = Qe − t / τ.q (t) = Qe − t / τ.10,11
Здесь Q — начальный заряд конденсатора, а τ = RCτ = RC — постоянная времени цепи. Как показано на графике, заряд экспоненциально уменьшается от начального заряда, приближаясь к нулю, когда время приближается к бесконечности.
Ток как функцию времени можно найти, взяв производную заряда по времени:
I (t) = — QRCe − t / τ.I (t) = — QRCe − t / τ.10,12
Отрицательный знак показывает, что ток течет в направлении, противоположном току, наблюдаемому при зарядке конденсатора. На рис. 10.40 (b) показан пример графика зависимости заряда от времени и тока от времени. График зависимости разности напряжений на конденсаторе и разницы напряжений на резисторе от времени показан в частях (c) и (d) рисунка. Обратите внимание, что величины заряда, тока и напряжения экспоненциально уменьшаются, приближаясь к нулю с увеличением времени.
Рис. 10.40 (a) Заряд конденсатора в зависимости от времени по мере разряда конденсатора. (б) Ток через резистор в зависимости от времени. (c) Разность напряжений на конденсаторе. (d) Разность напряжений на резисторе.
Теперь мы можем объяснить, почему упомянутой в начале этого раздела фотовспышке требуется гораздо больше времени для зарядки, чем для разрядки: сопротивление во время зарядки значительно больше, чем во время разрядки. Внутреннее сопротивление батареи составляет большую часть сопротивления во время зарядки.По мере старения аккумулятора возрастающее внутреннее сопротивление делает процесс зарядки еще медленнее.
Пример 10.8
Осциллятор релаксации
Одним из применений схемы RC является релаксационный генератор, как показано ниже. Релаксационный генератор состоит из источника напряжения, резистора, конденсатора и неоновой лампы. Неоновая лампа действует как разомкнутая цепь (бесконечное сопротивление), пока разность потенциалов на неоновой лампе не достигнет определенного напряжения.При таком напряжении лампа действует как короткое замыкание (нулевое сопротивление), и конденсатор разряжается через неоновую лампу и производит свет. В показанном релаксационном генераторе источник напряжения заряжает конденсатор до тех пор, пока напряжение на конденсаторе не станет 80 В. Когда это происходит, неон в лампе выходит из строя и позволяет конденсатору разряжаться через лампу, создавая яркую вспышку. После того, как конденсатор полностью разрядится через неоновую лампу, он снова начинает заряжаться, и процесс повторяется.Если предположить, что время, необходимое конденсатору для разряда, ничтожно мало, каков временной интервал между вспышками?Стратегия
Период времени можно найти, рассматривая уравнение VC (t) = ε (1 − e − t / τ), VC (t) = ε (1 − e − t / τ), где τ = (R + r) C .τ = (R + r) C.Решение
Неоновая лампа мигает, когда напряжение на конденсаторе достигает 80 В. Постоянная времени RC равна τ = (R + r) C = (101 Ом) (50 × 10−3F) = 5,05 с. Τ = (R + r) C = (101 Ом) (50 × 10−3F) = 5,05 с. Мы можем решить уравнение напряжения для времени, за которое конденсатор достигает 80 В: VC (t) = ε (1 − e − t / τ), e − t / τ = 1 − VC (t) ε, ln (e − t / τ) = ln (1 − VC (t) ε), t = −τln (1 − VC (t) ε) = — 5.05s · ln (1−80V100V) = 8.13s.VC (t) = ε (1 − e − t / τ), e − t / τ = 1 − VC (t) ε, ln (e − t / τ) = ln (1 − VC (t) ε), t = −τln (1 − VC (t) ε) = — 5,05 с · ln (1−80V100V) = 8,13 с.Значение
Одним из применений генератора релаксации является управление световыми индикаторами, которые мигают с частотой, определяемой значениями для R и C . В этом примере неоновая лампа будет мигать каждые 8,13 секунды, частота f = 1T = 18,13 с = 0,123 Гц. F = 1T = 18,13 с = 0,123 Гц. Осциллятор релаксации имеет много других практических применений. Он часто используется в электронных схемах, где неоновая лампа заменяется транзистором или устройством, известным как туннельный диод.Описание транзистора и туннельного диода выходит за рамки этой главы, но вы можете рассматривать их как переключатели, управляемые напряжением. Обычно это разомкнутые переключатели, но при подаче правильного напряжения переключатель замыкается и проводит ток. «Выключатель» можно использовать для включения другой цепи, включения света или запуска небольшого двигателя. Осциллятор релаксации может быть использован для того, чтобы заставить мигать поворотники вашего автомобиля или ваш мобильный телефон вибрировать.Цепи RC находят множество применений.Их можно эффективно использовать в качестве таймеров для таких приложений, как стеклоочистители прерывистого действия, кардиостимуляторы и стробоскопы. В некоторых моделях стеклоочистителей прерывистого действия используется переменный резистор для регулировки интервала между движениями стеклоочистителя. Увеличение сопротивления увеличивает постоянную времени RC , что увеличивает время между срабатываниями дворников.
Еще одно приложение — кардиостимулятор. Частота сердечных сокращений обычно контролируется электрическими сигналами, которые заставляют сердечные мышцы сокращаться и перекачивать кровь.Когда сердечный ритм ненормален (сердцебиение слишком высокое или слишком низкое), для исправления этого нарушения можно использовать кардиостимуляторы. У кардиостимуляторов есть датчики, которые обнаруживают движение тела и дыхание, чтобы увеличить частоту сердечных сокращений во время физических нагрузок, таким образом удовлетворяя повышенную потребность в крови и кислороде, а схема синхронизации RC может использоваться для контроля времени между сигналами напряжения, подаваемыми на сердце.
Забегая вперед к изучению цепей переменного тока (цепей переменного тока), напряжения переменного тока изменяются как синусоидальные функции с определенными частотами.Ученые часто регистрируют периодические изменения напряжения или электрических сигналов. Эти сигналы напряжения могут исходить от музыки, записанной с помощью микрофона, или от атмосферных данных, собранных радаром. Иногда эти сигналы могут содержать нежелательные частоты, известные как «шум». Фильтры RC могут использоваться для фильтрации нежелательных частот.
В области изучения электроники популярное устройство, известное как таймер 555, выдает синхронизированные импульсы напряжения. Время между импульсами контролируется схемой RC .Это лишь некоторые из бесчисленных применений схем RC .
Пример 10.9
Стеклоочистители с прерывистым режимом работы
Осциллятор релаксации используется для управления парой дворников. Релаксационный генератор состоит из конденсатора емкостью 10,00 мФ и переменного резистора 10,00 кОм и 10,00 кОм, известного как реостат. Ручка, подключенная к переменному резистору, позволяет регулировать сопротивление от 0,00 Ом до 10,00 кОм. Выход конденсатора используется для управления переключателем, управляемым напряжением.Переключатель обычно разомкнут, но когда выходное напряжение достигает 10,00 В, переключатель замыкается, запитывая электродвигатель и разряжая конденсатор. Двигатель заставляет дворники один раз подметать лобовое стекло, и конденсатор снова начинает заряжаться. На какое сопротивление нужно настроить реостат, чтобы время работы щеток стеклоочистителя составляло 10,00 секунд?Стратегия
Сопротивление учитывает уравнение Vout (t) = V (1 − e − t / τ), Vout (t) = V (1 − e − t / τ), где τ = RC.τ = RC. Приведены емкость, выходное напряжение и напряжение батареи.Нам нужно решить это уравнение для сопротивления.Решение
Выходное напряжение будет 10,00 В, а напряжение батареи 12,00 В. Емкость задана как 10,00 мФ. Решение для сопротивления дает Vout (t) = V (1 − e − t / τ), e − t / RC = 1 − Vout (t) V, ln (e − t / RC) = ln (1 − Vout (t) V), −tRC = ln (1 − Vout (t) V), R = −tCln (1 − VC (t) V) = — 10,00 с10 × 10−3Fln (1−10V12V) = 558,11 Ом. Vout (t) = V (1 − e − t / τ), e − t / RC = 1 − Vout (t) V, ln (e − t / RC) = ln (1 − Vout (t) V), — tRC = ln (1 −Vout (t) V), R = −tCln (1 − VC (t) V) = — 10,00 с10 × 10−3Fln (1−10V12V) = 558,11 Ом.Значение
Увеличение сопротивления увеличивает задержку между срабатываниями дворников.Когда сопротивление равно нулю, дворники работают постоянно. При максимальном сопротивлении период работы дворников составляет: t = −RCln (1 − Vout (t) V) = — (10 × 10−3F) (10 × 103Ω) ln (1−10V12V) = 179,18s = 2,98 мин. t = −RCln (1 − Vout (t ) V) = — (10 × 10−3F) (10 × 103Ω) ln (1−10V12V) = 179,18 с = 2,98 мин.Схема RC имеет тысячи применений и очень важна для изучения. Его можно не только использовать для измерения времени в цепях, но и для фильтрации нежелательных частот в цепи и в источниках питания, например в вашем компьютере, чтобы преобразовать переменное напряжение в постоянное.
Простые эквиваленты схемы для элемента постоянной фазы
Abstract
Элемент постоянной фазы (CPE) — это емкостной элемент с независимой от частоты отрицательной фазой между током и напряжением, которая интерполируется между конденсатором и резистором. Он широко используется для моделирования сложности физики, например, в области биоимпеданса и электрохимии. Существует также аналогичный элемент с положительным фазовым углом, и как емкостные, так и индуктивные CPE являются членами семейства элементов дробной схемы или дробления.Физический смысл CPE понятен лишь частично, и многие считают его идеализированным схемным элементом. Цель здесь состоит в том, чтобы предоставить альтернативные эквивалентные схемы, которые могут привести к лучшей интерпретации разрыва. И емкостные, и индуктивные CPE могут быть интерпретированы во временной области, где импульсные и ступенчатые характеристики являются временными степенными законами. Здесь мы показываем, что импульсные характеристики по току емкостного CPE такие же, как и у простой изменяющейся во времени последовательной RL-цепи, где значение индуктивности линейно увеличивается со временем.Точно так же характеристика напряжения индуктивного CPE соответствует характеристике простой параллельной RC-цепи, где емкость конденсатора линейно увеличивается со временем. Для независимой проверки мы используем программу моделирования схем Micro-Cap, которая может обрабатывать изменяющиеся во времени схемы. Моделирование точно соответствует ожидаемому отклику от предложенных эквивалентов с погрешностью 0,1%. Реализация с изменяющимися во времени компонентами коррелирует с известными изменяющимися во времени свойствами в приложениях и может привести к лучшему пониманию связи между CPE и приложениями.
Образец цитирования: Holm S, Holm T, Martinsen ØG (2021) Эквиваленты простых схем для элемента постоянной фазы. PLoS ONE 16 (3): e0248786. https://doi.org/10.1371/journal.pone.0248786
Редактор: Мухаммад Зубайр, Университет информационных технологий, ПАКИСТАН
Поступила: 13.01.2021; Принята к печати: 5 марта 2021 г .; Опубликован: 26 марта 2021 г.
Авторские права: © 2021 Holm et al.Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии указания автора и источника.
Доступность данных: В статье не используются данные измерений. Настройка моделирования находится в файлах вспомогательной информации.
Финансирование: Авторы не получали специального финансирования на эту работу.
Конкурирующие интересы: Авторы заявили, что никаких конкурирующих интересов не существует.
Введение
Элемент постоянной фазы (CPE) — это емкостной импеданс с фазовым углом в диапазоне 〈- π /2, 0〉, который не зависит от частоты. Впервые он был введен Коулом в связи с электрическим импедансом суспензий сфер [1] и клеточных мембран [2]. Йоншер заметил, что эта модель применима для большого диапазона диэлектриков, назвав ее «универсальным» диэлектрическим откликом. Он также связал это с временным степенным переходом закона Кюри-фон-Швайдлера [3], который впервые наблюдался для реальных конденсаторов более века назад.Далее Вестерлунд заметил, что функция отклика может быть выражена нецелым числом, дробной производной [4] и эффективной изменяющейся во времени емкостью со степенным изменением во времени. CPE удовлетворяет взаимности, как и обычные конденсаторы, то есть возбуждение и результирующий отклик можно менять местами [5]. В [6] также было обнаружено, что CPE, который по сути является линейным, может быть смоделирован как емкость, зависящая от напряжения, которая превращает его в нелинейную схему.
Элемент постоянной фазы применяется для моделирования экспериментальных данных для сложных систем, и здесь, в частности, будут выделены поля биоимпеданса и электрохимического импеданса.В первом поле CPE является общей моделью ткани [7, гл. 9.2.5] вместе с соответствующей моделью импеданса Коула [8, гл. 5.8]. Часто это интерпретируется как распределение постоянных времени из-за статистического распределения размеров ячеек.
В электрохимии поведение CPE также обычно наблюдается экспериментально и интерпретируется как статистическое распределение постоянных времени, обусловленное, например, ориентацией кристаллов, шероховатостью поверхности и распределением сопротивления в оксидном слое на поверхности [9, гл.8], [10, гл. 13] и [11]. Хотя существует несколько физических объяснений поведения CPE, такое поведение наблюдается даже в идеализированных экспериментах с графитовыми электродами [12], и подгонка эквивалентной схемы с использованием элементов CPE часто используется без предварительного обоснования. Затем модель CPE часто используется с резисторами, включенными последовательно и параллельно. То же самое и с тканевым биоимпедансом [13], а также с моделированием суперконденсаторов [14].
Интерпретация CPE с точки зрения статистического распределения размеров ячеек в поле биоимпеданса и статистического распределения постоянных времени в электрохимии приведет к приближению CPE с ограниченной полосой частот, как показано в [8, гл.7.2]. Эта модель множественной релаксации CPE также может быть преобразована в сетевую модель. Простейшим примером является модель кабеля с сосредоточенными параметрами, в которой проводимость увеличивается пропорционально квадратному корню из частоты для низких частот, то есть описывается производной половинного порядка. В [8, гл. 7.4], это обобщается на любой порядок для механических моделей либо в лестничной топологии, либо в самоподобном дереве. Подобные топологии могут быть разработаны и для электрических моделей, напоминая топоэлектрические схемы из [15].
Здесь мы демонстрируем новую интерпретацию поведения CPE в терминах простых схем с изменяющимися во времени значениями компонентов. Обычный емкостный CPE с отрицательным фазовым углом будет иметь такой же отклик по току на импульс входного напряжения, что и резистор, включенный последовательно с катушкой индуктивности, который линейно увеличивается со временем. Индуктивный CPE с положительным фазовым углом будет иметь такой же отклик по напряжению, как резистор, подключенный параллельно линейно возрастающему конденсатору. Эти модели вдохновлены аналогичными моделями линейной вязкоупругости [16, 17], где они могут моделировать вязкость из-за скачкообразного движения между зернами в водонасыщенных осадках [18].
Работа начинается с определения CPE и связывает его частотные и временные характеристики с описанием дробной производной. Затем предложенные линейно изменяющиеся во времени схемы анализируются аналитически и находятся как точные, так и приближенные решения. Результаты подтверждены моделированием откликов изменяющихся во времени схем в Micro-Cap 12.
Модели разрушения
Устройство разрыва представляет собой элемент с импедансом, где -1 < α <1 [19, 20].Его еще называют элементом постоянной фазы, особенно если он емкостной. Здесь мы делаем различие между обычным емкостным CPE и менее распространенным индуктивным CPE. Тильда используется для обозначения преобразования Фурье.
Емкостный элемент постоянной фазы
Емкостной элемент с постоянной фазой имеет импеданс, равный [4, 6]: (1) где ω, — угловая частота, и — преобразования Фурье напряжения и тока соответственно, C α — параметр CPE в F s α −1 и α — порядок.Импеданс имеет отрицательный фазовый угол — απ /2, который изменяется от 0 до — π /2. Значение α = 1 дает обычный конденсатор, a = 0 — резистор, а a = 0,5 соответствует элементу Варбурга, используемому для моделирования процессов диффузии. Модель CPE соответствует эквивалентной комплексной относительной диэлектрической проницаемости (2) где d и A — эквивалентное расстояние между пластинами и площадь пластин конденсатора соответственно, а ε 0 — диэлектрическая проницаемость вакуума.
Обратное преобразование Фурье (1) представляет собой свертку входного напряжения с текущей импульсной характеристикой, которая здесь является временным степенным законом во времени t , [8, App. A.3]: (3) Текущая ступенчатая характеристика является интегралом импульсной характеристики, а также степенной функцией: (4) Это закон Кюри-фон-Швайдлера [3, 4]. Оба ответа имеют начальную особенность, которая указывает на то, что модель CPE — это упрощенная и идеализированная модель реального явления. Фактически можно показать, что CPE является приближением к более реалистичной диэлектрической модели Коула-Коула [21], а также к моделям Коула-Дэвидсона и Хавриляка-Негами.
Степенный закон в частотной области — это один из способов определения дробной производной, и это широкое определение применяется к нескольким типам операторов, включая операторы Капуто и Римана-Лиувилля. Следовательно, CPE из (1) эквивалентен дробному конденсатору [4, 8, гл. 5.8]: (5) Дробный оператор является инвариантным во времени оператором, и в [22] показано, что дробная модель является линейной, имеет временную память и моделирует медленные динамические электростатические процессы. Соответствующая ступенчатая характеристика (4) соответствует практическим конденсаторам, используемым в электронных схемах, со значениями дробного порядка, очень близкими к 1, и приведены примеры с α от 0.От 9821 до 0,999952 в зависимости от типа конденсатора. Подгонка лучше, чем то, что достигается с помощью стандартных эквивалентных схем, которые имеют последовательный резистор для учета сопротивления пластин и соединителей конденсатора и / или резистор, включенный параллельно, для учета утечки в изоляции. Следует отметить, что в этой работе дробным является модель среды, то есть комплексная диэлектрическая проницаемость (2) или эквивалентная емкость (1) и (5). Это контрастирует с [23], где есть дробно-мерное пространство.
Индуктивный элемент постоянной фазы
Индуктивный элемент с постоянной фазой, у которого полное сопротивление имеет положительный фазовый угол απ /2, можно описать как (6) где L α в единицах H s α −1 и α = 1 дает обычную индуктивность. Напряжение является дробной производной тока: (7)
Схема реализации элемента постоянной фазы
Мы моделируем CPE, используя изменяющиеся во времени катушки индуктивности и конденсаторы.Это примеры линейных схем, которые не подчиняются временной инвариантности, которые не обязательно существуют как физические устройства, хотя некоторые устройства могут их приближать. В теории цепей обычное определение состоит в том, что магнитный поток Φ ( t ) — это произведение индуктивности и тока, дающее следующие вольт-амперные характеристики: (8) где L ( t ) — изменяющаяся во времени индуктивность. В изменяющемся во времени конденсаторе ток будет иметь аналогичную связь с зарядом. Иногда вместо этого предполагается более простое отношение, которое включает только первый член: (9) Эта неоднозначность отражена в том, как изменяющиеся во времени катушки индуктивности и конденсаторы реализованы в имитаторах схем.Micro-Cap от Spectrum Software реализует оба условия (8). С другой стороны, OrCAD PSpice реализует более простой вариант (9), но в [24] это рассматривается как проблема. Simulink ® от Mathworks, Inc. дает пользователю выбор между ними. Здесь изначально будут использоваться оба члена (8), но окажется, что, поскольку изменение индуктивности или емкости линейно со временем в предлагаемых моделях, пропуск последнего члена не изменит существенно конечный результат.
В области линейной вязкоупругости, которая послужила вдохновением для этой статьи, предполагается простое соотношение, эквивалентное (9) [25]: (10) где σ — напряжение, ε — деформация и η ( t ) — кажущаяся изменяющаяся во времени вязкость, используемая в [16–18].Следовательно, результаты не могут быть напрямую перенесены из одного поля в другое.
Емкостный элемент постоянной фазы
Схема на рис. 1a), где L ( t ) = L 0 + θt ′ — это индуктивность, которая линейно увеличивается со временем, а θ имеет единицу H / s = Ω. Здесь также используется вторая временная переменная t ′, что является обычным для систем с изменяющимся временем. Время входного импульса t и время начала изменения индуктивности t ‘в такой схеме, как правило, не зависят друг от друга.Однако мы предположим, что переменная катушка индуктивности начинает изменяться в тот момент, когда подается входной импульс, так что t ′ = t . Тогда соотношение напряжения и тока будет следующим: (11) Очевидно, что единственный эффект включения второго члена в (8) в определение изменяющейся во времени индуктивности состоит в том, что θ вносит вклад в эффективное сопротивление.
Рис. 1. Эквиваленты емкостных и индуктивных CPE.
Эквивалентная схема для емкостного элемента с постоянной фазой (a) и индуктивного элемента с постоянной фазой (b).Индуктивность и емкость соответственно линейно увеличиваются со временем.
https://doi.org/10.1371/journal.pone.0248786.g001
При подаче импульса напряжения в качестве входа в момент времени t = 0 ток в течение положительного времени после появления импульса будет следующим: (12) Следуя [16, Прил. 1] интегрирование (12) дает (13) где K — постоянная, определяемая начальными условиями.
Точное CPE.
Сначала предположим, что начальное значение индуктивности L 0 равно нулю.Взяв экспоненту из предыдущего уравнения, получаем: (14) Константу пропорциональности в общем случае найти невозможно. Однако это можно определить, рассмотрев практический случай, связанный со следующим моделированием в Micro-Cap. Если входной импульс реализуется путем возбуждения одной выборки длительностью t s , интеграл импульса, равный единице, требует напряжения 1/ t s . В этом случае начальным условием является то, что i ( t s ) = 1 / ( Rt s ).Таким образом, окончательный результат будет (15) При положительном значении R , θ эта простая схема на удивление имеет точно такую же импульсную характеристику, что и CPE (3), за исключением знака, для всех положительных значений времени. Знак может быть изменен с учетом отрицательного сопротивления, т.е. R <0, возможно также отрицательной индуктивности, θ <0.
Приблизительное CPE.
Поскольку может быть трудно представить практическую схему, изменяющуюся во времени, где значение компонента начинается с нулевого значения, теперь допустим L 0 ≠ 0.Тогда решение: (16) Если предположить, что t ≫ τ , так что второй член в скобках доминирует, это (17) Этот результат также имеет ту же функциональную форму, что и (3), и поэтому эта изменяющаяся во времени схема приближается к CPE. Чтобы знак также был правильным, может потребоваться, чтобы одно или несколько значений параметра были отрицательными.
Индуктивный элемент постоянной фазы
Схема на рис. 1b) параллельна схеме на рис. 1а) в том смысле, что напряжение и ток обмениваются ролями, в результате чего возникает зависимость тока от напряжения, подобная (11): (18) где изменяющаяся во времени составляющая теперь представляет собой конденсатор, а θ имеет единицу F / s = S.Следовательно, когда C 0 = 0, ответ будет аналогичен ответу (15) и будет: (19) Кроме того, он будет иметь ответ напряжения на импульс тока, который будет иметь ту же форму, что и (17), когда C 0 > 0: (20)
Проверка моделированием
Micro-Cap версии 12 [26] — универсальный инструмент для моделирования сложных схем. Он используется для нормализованного случая с положительными значениями составляющих, R = 1, L = 1 + t /0.9, и, таким образом, θ = α = 0,9, а длина импульса t с = 1 мс, как показано на рис. 2. Симулятор Micro-Cap 12 теперь доступен бесплатно, а его принципиальная схема и схема файл можно найти в файлах S1 и S2.
Рис 2. Независимая проверка.
Micro-Cap 12 моделирование отклика тока на импульс напряжения для схемы (11), показанной на рис. 1a) с R = 1, L = 1 + t /0.9, т.е. τ = α = 0,9 (красные, белые квадраты), R = 1, L = t / 0,9, т.е. α = 0,9 (зеленый, сплошной) по сравнению с обычным RL-контур с откликом e — t / τ / R , τ = L / R , L = 1, R = 1 (синие, закрашенные квадраты) . Длительность импульса т с = 1 мс.
https: // doi.org / 10.1371 / journal.pone.0248786.g002
Следует отметить, что входом для моделирования является изменяющаяся во времени схема, показанная на рис. 1a), как указано в (11). Следовательно, его согласие с решениями (14) и (16) является независимым подтверждением их справедливости. На этом рисунке, а также на двух следующих, также проводится сравнение с неизменяющейся во времени схемой с R = 1, L = 1 с экспоненциальным откликом.
Уравнения (15), (16) и (17) были затем реализованы в Matlab и нанесены на логарифмическую сетку.Случай для α = 0,9 показан на рис. 3. Расхождение между расчетами в Matlab и моделированием Micro-Cap составляет максимум порядка 0,1%. Случай для R = 1, L = 1 + 0,5 t и, таким образом, θ = α = 0,5, соответствующий элементу Варбурга, показан на рис. 4.
Рис. 4. График аналитически найденного отклика.
Отклик по току на импульс напряжения для схемы на рис. 1а) для α = 0.5 (элемент Варбурга), вычисленный в Matlab из (15) (зеленая сплошная линия), (16) (красная пунктирная линия) и (17) (черная пунктирная линия) по сравнению со стандартной RL-схемой (синяя , пунктир).
https://doi.org/10.1371/journal.pone.0248786.g004
Точное выражение и приближение CPE аналогичны для времени выше 4-5 секунд, когда τ = 0,9, как показано на рис. 3. В в случае τ = 0,5, рис. 4, это происходит через несколько секунд. Это соответствует ожиданиям теории, поскольку приближение (17) справедливо, когда t >> τ .
Обсуждение
Моделирование емкостных и индуктивных элементов с постоянной фазой с изменяющимися во времени цепями не критически зависит от того, какое определение отношения тока к напряжению для зависимой от времени индуктивности предполагается. Второй член (8) добавляет к R только θ . Таким образом, (14) и (16) имеют в показателях степени ( R + θ ) / θ , а не R / θ . Таким образом, функциональная форма окончательного результата не зависит от определения, но она изменит показатель степени на 1.
Результаты (15) и (17) демонстрируют, что изменяющаяся во времени схема на рис. 1a) имеет такой же отклик по току на импульс входного напряжения, что и емкостной CPE. Следует отметить, что из-за отсутствия временной инвариантности в схеме это не означает, что верно обратное, т.е. что реакция напряжения на импульс входного тока такая же, как для CPE. Кроме того, переходная характеристика отличается, поскольку простая интеграция импульсной характеристики не дает переходной характеристики в системе с изменяющейся во времени системой.Это ограничения модели.
Есть несколько примеров зависящих от времени электрических параметров в биологических материалах, оправдывающих моделирование CPE с изменяющейся во времени схемой. Одним из кандидатов является мемристанс, проявляемый, например, кожей человека [27, 28]. Сопротивление изменяется в зависимости от общего количества заряда, прошедшего через материал, и когда электрический ток меняется на противоположное, сопротивление изменяется в противоположном направлении. Хотя изменение вызвано зарядом, при подаче периодического сигнала переменного тока оно будет проявляться как резистор, зависящий от времени.Сообщалось об аналогичных механизмах для емкости и индуктивности, названных memcapacitance и meminductance [29], а неопубликованные результаты нашей группы указывают на то, что некоторые биоматериалы также обладают мем-емкостными свойствами. Кроме того, измерения биоимпеданса часто содержат элементы нелинейных свойств, как правило, при использовании небольших электродов, когда плотность тока в некоторых объемах может превышать линейный диапазон [30, 31].
Другой пример системы, которая сбрасывается при каждом изменении полярности, — это зарядка двойного слоя в электрохимической системе из-за наложенного сигнала.В каждый период приложенный сигнал приводит к перемещению ионов в растворе к поверхности электрода или от нее. Во время зарядки ионы движутся к электроду и придают электростатическое сопротивление последующему перемещению ионов. Точно так же во время разряда ионы удаляются от электрода и оказывают сопротивление процессу разряда, которое изменяется со временем.
Эти свойства открывают возможность нахождения эквивалента переходной реакции в установившемся состоянии. Один из способов — позволить второй временной переменной t ‘сбрасываться при каждом переходе через нуль.В этом случае будет легче обосновать приближенное соотношение Фурье между импульсной характеристикой и передаточной функцией.
Часто целью является преобразование неидеального элемента CPE в эквивалентный конденсатор, яркими примерами которых являются уравнение Бруга [32], модель оксидного слоя [33] и подходы [34–36]. Интерпретация часто ограничивается конкретными системами, где уравнение Бруга применяется наиболее широко. Хотя здесь и ограничены входным импульсом напряжения, представленные схемы эквивалентности могут способствовать пониманию общего поведения CPE и, следовательно, установлению более надежных методов интерпретации.
Представленные здесь изменяющиеся во времени модели также могут указывать на метод реализации CPE в практической схеме. Катушка индуктивности может быть реализована с гиратором, реализованным с одним или несколькими операционными усилителями. Эффективная индуктивность будет пропорциональна произведению конденсатора и резистора, и, в частности, последний может быть легче изменить во времени, чем индуктор. Этот метод требует дальнейшей проверки, поскольку в практических гираторах существуют ограничения по диапазону частот [37].Также могут быть ограничения при обработке переходных процессов.
Наконец, следует отметить, что точное решение (15), где L 0 = 0, применимо и к вязкой модели из [16, 18]. В этих статьях обсуждается только приближенная модель (17), но установив постоянную часть изменяющейся во времени вязкости равной нулю, η 0 = 0, в уравнениях (6) и (8) из [16 ] точное решение можно найти даже для вязкой модели.
Заключение
Мы показали, что емкостный элемент с постоянной фазой (CPE) имеет точно такую же импульсную характеристику по току, что и резистор, включенный последовательно, с линейно увеличивающейся индуктивностью.Точно так же индуктивный CPE имеет импульсную характеристику напряжения, аналогичную характеристике резистора, включенного параллельно, с линейно увеличивающейся емкостью. Сходство демонстрируется при условии, что обе временные переменные в изменяющейся во времени схеме отслеживают друг друга.
Программа моделирования схем Micro-Cap 12, которая обрабатывает такие изменяющиеся во времени схемы, используется для независимого подтверждения того, что импульсные характеристики соответствуют временному степенному закону, предсказанному теорией. Реализация с изменяющимися во времени компонентами коррелирует с известными изменяющимися во времени свойствами в приложениях, но это свойство необходимо будет исследовать и более твердо установить в будущей работе.
Благодарности
Авторы хотели бы поблагодарить доктора Викаша Панди за полезные обсуждения ступенчатой и импульсной реакции.
Ссылки
- 1. Коул К.С. Электрическое сопротивление подвесов шаров. J Gen Physiol. 1928; 12 (1): 29.
- 2. Коул К.С. Проницаемость и непроницаемость клеточных мембран для ионов. В: Симпозиумы Колд-Спринг-Харбор по количественной биологии. т. 8. Лабораторный пресс Колд-Спринг-Харбор; 1940 г.п. 110–122.
- 3. Jonscher AK. «Универсальный» диэлектрический отклик. Природа. 1977 г., 267 (5613): 673–679.
- 4. Вестерлунд С. У мертвой материи есть память! Phys Scr. 1991; 43 (2): 174.
- 5. Аллагуи А., Элвакил А.С., Фриборн Т.Дж. Взаимность суперконденсатора и реакция на линейные изменения тока и напряжения. Electrochim Acta. 2017; 258: 1081–1085.
- 6. Fouda ME, Allagui A, Elwakil AS, Das S, Psychalinos C, Radwan AG. Нелинейная зависимость заряда от напряжения в элементе постоянной фазы.AEU-Int. Электронный журнал C. 2020; 117: 153104.
- 7. Grimnes S, Martinsen ØG. Основы биоимпеданса и биоэлектричества, 3-е изд. Академическая пресса; 2015.
- 8. Холм С. Волны со степенным затуханием. Швейцария: Springer и ASA Press; 2019.
- 9. Ласиа А. Электрохимическая импедансная спектроскопия и ее приложения. Springer; 2002.
- 10. Оразем М.Е., Триболлет Б. Электрохимическая импедансная спектроскопия. Wiley; 2008 г.
- 11. Хиршорн Б., Оразем М.Э., Триболлет Б., Вивье В., Фратёр I, Мусиани М. Поведение элементов постоянной фазы, вызванное распределением удельного сопротивления в пленках: I. Теория. J Electrochem. 2010; 157 (12): C452.
- 12. Шарма Т., Холм Т., Диас-Реал Дж., Мерида В. Экспериментальная проверка теории импеданса пор: просверленные графитовые электроды с постепенно более сложным распределением пор по размерам. Electrochim Acta. 2019; 317: 528–541.
- 13. Martinsen ØG, Grimnes S, Sveen O.Диэлектрические свойства некоторых ороговевших тканей. Часть 1. Роговой слой и ноготь на месте. Med Biol Eng Comput. 1997. 35 (3): 172–176.
- 14. Zhang L, Hu X, Wang Z, Sun F, Dorrell DG. Обзор моделирования, оценки и приложений суперконденсаторов: взгляд на контроль / управление. Обновите Sust Energ Rev.2018; 81: 1868–1878.
- 15. Ли Ч., Имхоф С., Бергер С., Байер Ф, Брем Дж., Моленкамп Л. В. и др. Топоэлектрические схемы. Comm Phys. 2018; 1 (1): 1–9.
- 16.Панди В., Холм С. Связывание дробной производной и закона ползучести Ломница с неньютоновской изменяющейся во времени вязкостью. Phys Rev E. 2016; 94: 032606–1–6. pmid: 27739858
- 17. Ян Х, Цай В., Лян И, Холм С. Новое представление изменяющейся во времени вязкости с помощью степенного закона и сравнительного исследования. Int J Non-Lin Mech. 2020; 119: 103372–1–10.
- 18. Букингем MJ. Распространение волн, релаксация напряжений и сдвиг от зерна к зерну в насыщенных, рыхлых морских отложениях.J Acoust Soc Am. 2000. 108 (6): 2796–2815.
- 19. Radwan AG, Elwakil AS. Выражение для отклика напряжения возбуждаемого током устройства разрушения на основе тригонометрических тождеств дробного порядка. Int J Circ Theor App. 2012. 40 (5): 533–538.
- 20. Абделуахаб М.С., Лози Р., Чуа Л. Memfractance: математическая парадигма для схемных элементов с памятью. Int J Bifurcat Chaos. 2014; 24 (09): 1430023.
- 21. Холм С. Характеристика диэлектрической модели Коула-Коула во временной области.J Electr Bioimp. 2020; 11 (1): 101–105.
- 22. Вестерлунд С., Экстам Л. Теория конденсаторов. IEEE Trans Dielectr Electr Ins. 1994; 1 (5): 826–839.
- 23. Зубайр М., Могол М.Дж., Накви К.А. Электромагнитные поля и волны в дробно-мерном пространстве. Springer Science & Business Media; 2012.
- 24. Биолек Д., Колка З., Биолкова В. Моделирование изменяющихся во времени компонентов хранения в PSpice. В: Proc. Электронные устройства и системы IMAPS CS Международная конференция EDS.т. 2007. Citeseer; 2007. с. 39–44.
- 25. Chhabra RP. 1. Неньютоновские жидкости: Введение. В кн .: Реология сложных жидкостей. Нью-Йорк, Нью-Йорк: Springer Нью-Йорк; 2010. с. 3–34.
- 26. Программное обеспечение Spectrum, Micro-Cap 12 ;. http://www.spectrum-soft.com/.
- 27. Йонсен Г.К., Люткен К.А., Мартинсен О.Г., Гримнес С. Мемристивная модель электроосмоса в коже. Phys Rev E. 2011; 83 (3): 031916.
- 28. Пабст О., Мартинсен О. Г., Чуа Л.Нелинейные электрические свойства человеческой кожи делают ее обычным мемристором. Научный доклад 2018; 8 (1): 1–9.
- 29. Ди Вентра М, Першин Ю.В., Чуа ЛО. Элементы схем с памятью: мемристоры, мемконденсаторы, меминдукторы. Proc IEEE. 2009. 97 (10): 1717–1724.
- 30. Ямамото Т., Ямамото Ю. Нелинейные электрические свойства кожи в низкочастотном диапазоне. Med Biol Eng Comput. 1981; 19 (3): 302.
- 31. Kalvøy H, Frich L, Grimnes S, Martinsen ØG, Hol PK, Stubhaug A.Распознавание тканей на основе импеданса для направления иглы. Physiol Meas. 2009; 30 (2): 129.
- 32. Brug G, Van Den Eeden A, Sluyters-Rehbach M, Sluyters J. Анализ импедансов электродов, усложненных наличием элемента с постоянной фазой. Ж Электроанал. 1984. 176 (1-2): 275–295.
- 33. Хиршорн Б., Оразем М.Э., Триболлет Б., Вивье В., Фратур И., Мусиани М. Определение эффективной емкости и толщины пленки по параметрам элемента с постоянной фазой.Electrochim Acta. 2010. 55 (21): 6218–6227.
- 34. Hsu C, Mansfeld F. Относительно преобразования параметра Y0 элемента постоянной фазы в емкость. Коррозия. 2001. 57 (9): 747–748.
- 35. Аллагуи А., Фриборн Т.Дж., Элвакил А.С., Чистый Б.Дж. Переоценка характеристик двухслойных электрических конденсаторов по данным заряда / разряда постоянным током и циклической вольтамперометрии. Научный доклад 2016; 6 (1): 1–8.
- 36. Гарби О., Тран М.Т., Триболлет Б., Турмин М., Вивье В.Возвращаясь к анализу циклической вольтамперометрии и спектроскопии электрохимического импеданса для измерения емкости. Electrochim Acta. 2020; п. 136109.
- 37. Гринейх EW, Деланский JF. Элементы управляемой схемы (гл. 14). В: Чен В.К., редактор. Справочник по схемам и фильтрам. CRC Press; 2018.
Причина отказа от мемристора как основного элемента схемы
Периодическая таблица основных пассивных элементов
Периодическая таблица на рис.2 имеет строки и столбцы сетки, помеченные буквами верхнего регистра вдоль левого и верхнего краев. Мы будем обращаться к сетке по ее метке (строка, столбец). Фактическая электрическая переменная, которая применяется к каждой строке или столбцу, отображается вдоль правого и нижнего края. На горизонтальной оси каждый столбец справа представляет собой производную по времени от столбца слева. Например, ось x для (A, Y) — это \ (\ dot {\ varnothing} \), которая является производной от ϕ , оси x для (A, Z). Точно так же по оси Y ось Y каждой более высокой строки является производной от строки под ней.
Рисунок 2Периодическая таблица основных пассивных элементов в области заряд-напряжение.
Существующие основные элементы удовлетворяют следующим правилам. Мы ожидаем такой же податливости от пизастора.
- (я)
Правило 1. Только один фундаментальный элемент может занимать позицию в периодической таблице.
- (ii)
Правило 2: переходное событие не считается удовлетворяющим конститутивным отношениям.
Правило 1 основывается на периодической таблице химических элементов, в которой элементы упорядочены по атомному номеру. Периодическая таблица электрических элементов организует свои элементы на основе производной заряда n -й , которая связывает феноменологическую константу с напряжением, возникающим на устройстве.
Правило 2 выводится из определения существующих основных элементов, а именно C , R и L . {- 1 } \ точка {q} = \ точка {\ nu} \).Аналогично в столбце X мы замечаем, что (C, X) — это \ (r \, \ ddot {q} = \ dot {\ nu} \), что является определением малого сигнала резистора, эквивалентным \ (r = \ гидроразрыва {d \ nu} {di} \). Осмотр показывает, что каждый из известных фундаментальных элементов движется по диагоналям в нашей периодической таблице, что приводит к представлению производной n th в терминах заряда и напряжения.
Толстый вертикальный разделитель между столбцами Z и Y подтверждает идею о том, что фундаментальные элементы не проникают в столбец Z.{2}} \), где U — еще не открытая феноменологическая константа. Однако позже мы продемонстрируем, что оккупант (D, Y) будет активным, следовательно, ни пассивным, ни основным.
Прежде чем обсуждать столбец Z, давайте рассмотрим основное уравнение, которое связывает напряжение с магнитным потоком; а именно закон Фарадея. Закон Фарадея гласит, что отрицательная величина скорости изменения магнитного потока (\ ({\ varnothing} _ {B} \)) будет равна электрическому потенциалу (∈), развиваемому в элементе, таком как индуктор.
$$ {\ epsilon} = — \, \ frac {d {\ varnothing} _ {B}} {dt} $$
(1)
Предположим, что экспериментатор вызывает изменение магнитного потока. Отрицательный знак означает, что результирующее напряжение будет в таком направлении, чтобы генерировать ток, магнитное поле которого будет пытаться противодействовать принудительно индуцированному изменению потока. Уравнение предназначено для использования в ситуации, когда поток действительно является магнитным потоком. Однако мы замечаем, что мы можем интегрировать левую часть уравнения (1), чтобы получить \ (\ varphi = — \, \ int {\ epsilon} \, dt \), не настаивая на магнитном поле.Мы использовали ϕ без индекса для обозначения вычисленного потока, а не реального магнитного потока. Хотя этот подход является математически правильным, он может привести к неправильному использованию термина «поток». Постулат 1971 года колеблется из-за использования как ϕ (временной интеграл напряжения), так и слов потокосцепление (используемых в нем семь раз), предполагая, что первоначально постулированная концепция мемристора действительно зависела от существования магнитного потока 5 .Учитывая, что у нас уже есть плоскость заряда-напряжения для проверки, давайте приспособимся к определению \ (\ varphi = — \, \ int {\ epsilon} \, dt \) и проигнорируем потребность в магнитном потоке.
Это перемещает наше обсуждение в столбец Z на рис. 2. Все элементы в столбце Z генерируют поток \ (\ varphi = \ int \ nu \, dt \). Здесь \ (\ nu \ Equiv {\ epsilon} \) и представляет собой напряжение (электрический потенциал). Отсутствующий отрицательный знак (в отношении магнитного контекста) служит только для определения направления напряжения, и его отсутствие не приводит к потере точности при обсуждении.{-1} \ int q \, dt \) и быть правильным. Однако это поставило бы нас в бессмысленный слот ниже (A, Z). В этой системе с пассивными элементами конденсатор не попал в столбец Z, потому что заряд на конденсаторе не может быть осмысленно преобразован в интеграл напряжения. Этот пример с конденсатором показывает, как создать периодическую таблицу с бесконечной сеткой.
Обращая наше внимание на слот (A, Z), обобщенное определяющее уравнение: \ (U \, q = \ varnothing \). Мы временно ввели феноменологическую константу U , чтобы заменить то, что мы можем обнаружить.Простая перестановка дает \ (U = \ frac {\ varnothing} {q} \). Мы можем переписать это на основе его формы производной по времени, где точка над точкой представляет производную по времени.
$$ U = \ frac {\ dot {\ varnothing}} {\ dot {q}} = \ frac {d \ varphi} {dq} = \ frac {\ nu} {i} $$
(2)
Уравнение (2) определяет резистор, делая U в (A, Z) равным R , как показано на рис. 2. Prodromakis et al . среди прочего используйте промежуточное выражение \ ((\ frac {\ frac {d \ varnothing} {dt}} {\ frac {dq} {dt}}) \), содержащее ссылку на заряд, чтобы предположить, что U = M = M ( q ( t )) 6 .Здесь есть два неудобных момента.
- (я)
Хотя вывод не является ошибочным, он нарушает правило 1, потому что простой резистор также будет подходящим образом занимать слот (A, Z).
- (ii)
Любая феноменологическая константа, выведенная из зависимых от времени промежуточных уравнений, является незначительной и нарушает Правило 2.
Сравнение с таблицей фундаментальных элементов Струкова
На рисунке 3 сравнивается периодическая таблица фундаментальных элементов, опубликованная Струковым и др. . в Hewlett Packard (HP) с предложением в этой статье 7 . Мы видим, что поворот на девяносто градусов влево на сетке (A, Z) — (B, Y) на рис. 3 (b) определенно делает ее похожей на диаграмму Струкова. В исходной таблице фундаментальных элементов есть ошибка 7,8,9 .Выражение в рамке на положительной оси x, dq = idt , конфликтует с положительной осью x, одновременно помеченной как q . Алгебраическая обработка сформированного выражения дает \ (\ frac {dq} {dt} = i \); подразумевая, что ток равен заряду метки вдоль положительной оси x. Это может быть типографская ошибка и не наблюдается влияния на какие-либо выводы, поскольку выражение всегда игнорируется. Nalawade и др. . исправили это, но сумели неправильно пометить ось потока 10 .Кватинский и др. . просто оставьте пустые рамки 11 . Кумар правильно обозначил оси диаграммы в обзоре 12 .
Рисунок 3Схема основных пассивных элементов в области заряда-напряжения. ( a ) Интерпретация Струкова приписывается Чуа. ( b ) В нашем представлении диаграмма Струкова представлена в виде подмножества, заключенного в синий пунктирный прямоугольник.
При параллельном сравнении на рис. 3 мы видим, что нижняя часть диаграммы Струкова соответствует нашему столбцу Z на рис.3 (б). Жители столбца Z не являются фундаментальными, потому что их отношения определяются математическим интегрированием, требующим начальных условий. Даже если мы впустили такие элементы в основную складку, то место, предложенное для мемристора, уже занято резистором.
Плоскость заряд-напряжение иногда называют областью заряд-поток, которая точно такая же, как на рис. 2, включая запрещенный столбец Z. Резистор памяти 2008 года с его феноменологической постоянной M не находит место в плоскости заряда-напряжения по двум причинам.
- (я)
Слот (A, Z) уже занят резистором. Правило 1 запрещает второго жильца.
- (ii)
Мемристор с \ (M (q (t)) = \ frac {\ varnothing} {q} \) может быть оценен только интегрированием, нарушая Правило 2, требуя временного окна для интеграла.
Теоретико-схемотехническая периодическая таблица пассивных элементов
Движущийся заряд генерирует магнитное поле. Закон Ампера можно использовать для вывода, что провод с током будет создавать силовые линии магнитного поля, перпендикулярные проводу, в направлении, предлагаемом правилом правой руки. Это означает, что рис. 1 (b) и (c) имеют магнитные вклады, отмеченные пунктирными изогнутыми стрелками. Это побуждает нас расширить периодическую таблицу фундаментальных элементов в магнитную плоскость.
Рисунок 4 — это расширенная версия рисунка 2, с плоскостью заряда-напряжения справа от пунктирной синей центральной иглы и плоскостью потока заряда (магнитной) слева от пунктирной синей центральной линии. Поток на магнитной стороне — это истинный магнитный поток, представленный как ϕ B . Заряд и его производные расположены по оси y. Столбцы помечены шляпками на магнитной стороне; указатели строк являются общими для обоих доменов. Обсуждение будет касаться слотов в стиле (строка, столбец).Для всех устройств в столбцах Z и \ (\ hat {{\ rm {Z}}} \) необходимо указать начальные условия в их производных формах от Y и \ (\ hat {{\ rm {Y}}}} \). Слева от центра каждый столбец ведет к производной n -й истинного магнитного потока. Справа каждый столбец аналогичным образом ведет к производной n th вычисленного потока, определяемой как интеграл напряжения от времени. Фундаментальные элементы выделены светло-зелеными прямоугольниками, которые представляют их конститутивные отношения. Начнем обсуждение с известных кандидатов.
Рисунок 4Периодическая таблица основных элементов в областях заряд-поток (магнитный) и заряд-напряжение.
Конденсатор из плоскости заряд-напряжение не проявляется на магнитной стороне, потому что для стационарных зарядов нет магнетизма. Это автоматически удаляет все магнитные диагонали с емкостью C , например \ (({\ rm {A}}, \ hat {{\ rm {Y}}}) \), \ (({\ rm {B}} , \ hat {{\ rm {X}}}) \), \ (({\ rm {C}}, \ hat {{\ rm {W}}}) \) и т.д., показанные в красных пунктирных прямоугольниках.
Что касается катушек индуктивности, мы сразу же замечаем, что катушка индуктивности существует в слоте \ (({\ rm {C}}, \ hat {{\ rm {Y}}}) \), как и должно быть. Индуктор переходит в паз \ (({\ rm {B}}, \ hat {{\ rm {Z}}}) \), переходит в электрическую область в точке (B, Z) и далее в прорезь (C, Y ). Катушка индуктивности может жить в обеих плоскостях. Катушка индуктивности генерирует напряжение, пропорциональное скорости изменения тока.
Катушка индуктивности также создает истинное магнитное поле вокруг катушек для условий переменного тока в \ (({\ rm {C}}, \ hat {{\ rm {Y}}}) \).
$$ — {\ dot {\ varphi}} _ {B} = L \, \ ddot {q} $$
(4)
В условиях постоянного тока индуктор удовлетворяет следующему соотношению в \ (({\ rm {B}}, \ hat {{\ rm {Z}}}) \) и (B, Z).
$$ — {\ varphi} _ {B} = L \, i = \ varnothing $$
(5)
Мы понимаем, что \ (({\ rm {B}}, \ hat {{\ rm {Z}}}) \) — это односторонняя связь, когда постоянный ток может создавать постоянное магнитное поле, но не наоборот.Аналогично \ (L \, i = \ varnothing \) в (B, Z) требует интегрирования. Следовательно, уравнение (5) не является определяющим соотношением для индуктора. Уравнение (4) из паза \ (({\ rm {C}}, \ hat {{\ rm {Y}}}) \) или уравнение (3) из (C, Y) является истинным определяющим соотношением для индуктора потому что только он описывает способность индуктора соединять магнитные и электрические домены 2,3 .
Предположим теперь, что исходный постулат о магнитном мемристоре верен. Это будет означать, что устройство должно занимать слот \ (({\ rm {A}}, \ hat {{\ rm {Z}}}) \) на основе определяющего отношения \ (M = — \, \ frac {{ \ varnothing} _ {B}} {q} \) с правильным знаком и нижним индексом.На данный момент у нас недостаточно данных, чтобы опровергнуть это существование. Из множества фундаментальных элементов мы знаем, что действующий элемент в \ (({\ rm {A}}, \ hat {{\ rm {Z}}}) \) также должен жить в \ (({\ rm {B }}, \ hat {{\ rm {Y}}}) \). Управляющее уравнение для слота \ (({\ rm {B}}, \ hat {{\ rm {Y}}}) \): \ (U \, \ dot {q} = — \, {\ dot {\ varphi}} _ {B} \). Это правило требует, чтобы было какое-то устройство с феноменологической постоянной U , которое будет создавать магнитное поле, которое изменяется с постоянной скоростью, когда через него проходит постоянный ток (\ (\ dot {q} \)).Рассмотрим мемристор HP 2008 года (или Chua 1971 года) для этого слота. Подача постоянного тока в мемристор вызовет изменение напряжения на устройстве \ ((\ dot {v}) \) при изменении его сопротивления. Однако постоянный ток стимула будет создавать только постоянное магнитное поле, а не \ (- {\ dot {\ varphi}} _ {B} \). Следовательно, устройство HP 2008 года (и устройство Чуа 1971 года) не может занимать \ (({\ rm {B}}, \ hat {{\ rm {Y}}}) \), кроме тривиального условия \ (- {\ dot {\ varnothing}} _ {B} = 0 \). Резистор также удовлетворяет этому тривиальному условию.Попробуем вывести правило наблюдаемого \ (\ dot {\ nu} \) из основных законов. Дифференциация закона Фарадея по времени дает \ (\ frac {d} {dt} {\ epsilon} = — \, \ frac {d} {dt} (\ frac {d {\ varphi} _ {B}} {dt}) \), то есть \ (\ dot {\ nu} = — \, {\ ddot {\ varphi}} _ {B} \). Мы видим \ (- {\ ddot {\ varphi}} _ {B} \) в слоте \ (({\ rm {C}}, \ hat {{\ rm {X}}}) \). Для этого требуется, чтобы устройство генерировало скорость магнитного потока, когда через него проходит ток, то есть \ (r \ frac {di} {dt} = — \, {\ ddot {\ varphi}} _ {B} = \ frac {dv} {dt} \). Другими словами, подача тока в устройство должна привести к изменению напряжения \ (\ dot {\ nu} \); что будет происходить на устройствах HP 2008 года и Chua 1971 года.Однако изменение напряжения является нетривиальным только на мгновение и будет оцениваться как ноль, как только завершится переход от низкого сопротивления к высокому (или наоборот); что делает это временным событием и нарушает Правило 2. Следовательно, нет места в \ (({\ rm {C}}, \ hat {{\ rm {X}}}) \) для мемристора 2008 (или 1971). Следовательно, если \ (({\ rm {C}}, \ hat {{\ rm {X}}}) \) и \ (({\ rm {B}}, \ hat {{\ rm {Y}) }}) \) лишены мемристоров, то \ (({\ rm {A}}, \ hat {{\ rm {Z}}}) \) также запрещены для мемристоров. Кроме того, в \ (({\ rm {A}}, \ hat {{\ rm {Z}}}) \) нет действующего возможного, потому что стационарные электрические заряды не могут создавать магнитное поле.Таким образом, мы покрасили все исключенные квадраты периодической таблицы в красный цвет, исключив устройство HP 2008 года (и 1971 года) из магнитной плоскости. Предположение, что q в \ (({\ rm {A}}, \ hat {{\ rm {Z}}}) \) является интегралом тока, а не буквальным стационарным зарядом, помещает нас в область абстракции -путем интеграции. Тогда мемристор — это абстрактное устройство, реагирующее на абстрактный электрический заряд. В любом случае резистор уже удовлетворяет условиям \ (({\ rm {A}}, \ hat {{\ rm {Z}}}) \) даже в этой области абстракции.
Может ли постулат 1971 года быть вероятным где-нибудь на магнитной стороне? Расположение основных элементов предполагает, что ничто иное, как резистор, не может занимать траекторию \ (({\ rm {A}}, \ hat {{\ rm {Z}}}) \), \ (({\ rm {B}}, \ hat {{\ rm {Y}}}) \), \ (({\ rm {C}}, \ hat {{\ rm {X}}}) \), \ (({ \ rm {D}}, \ hat {{\ rm {W}}}) \) и т. д., предложенных для мемристора. Таким образом, мемристор в любом проявлении исключен из магнитной и электрической стороны периодической таблицы в соответствии с Правилом 1 и / или Правилом 2.
Общая оппозиция концепции мемристора
Vongehr et al .указать на проблемы со смешиванием ϕ B и ϕ 13 . Для них отсутствие магнетизма в модели HP 2008 года является ее основным дисквалифицирующим фактором, и они полагают, что если мемристор без магнетизма действителен, то мы также обнаружили индуктор, который работает без магнетизма. Ди Вентра и Першин интерпретируют мем-устройства как ответные функции. Они предлагают возможность получения вольт-амперных кривых, которые не пересекают начало координат 14 .Это не согласуется с определением Чуа, в котором говорится, что если его защемить, это мемристор 15 . Чуа очень четко заявляет: «В этой статье любой черный ящик с двумя клеммами называется мемристором тогда и только тогда, когда он демонстрирует сжатую петлю гистерезиса для всех биполярных периодических сигналов входного тока (соответственно, сигналов входного напряжения). ), что приводит к периодической характеристике напряжения (соответственно, тока) той же частоты в плоскости напряжение-ток ( v — i ) » 15 .Сундквист и др. . изучите мемристор с термодинамическими соображениями и сделайте вывод, что уравнения мемристора физически неполны по отношению к пассивности или активности 16,17 . Они возражают против утверждения, что существующий претендент на мемристор является пассивным устройством, поскольку он нарушает второй закон термодинамики в бесконечно большом количестве случаев, в то время как никакой положительный пример не может быть идентифицирован из-за нефизического характера фундаментального определения мемристора Чуа.Аналогичные критические замечания по поводу нарушения принципа Ландауэра, отсутствия магнитного потока, изменения определений и т. Д. Представлены Jeltsema 18 . Общий знаменатель возражений сводится к отсутствию магнетизма и вероятной необходимости присутствия активных элементов.
Линейно-нелинейные дебаты
Представление о том, что мемристор, постулированный в 1971 году, может каким-то образом существовать как нелинейная, но фундаментальная сущность, можно развеять, просмотрев основополагающую статью Чуа.Раздел III статьи Чуа утверждает, что, когда кривая мемристора ϕ — q представляет собой прямую линию, мемристор сокращается до линейного резистора , не зависящего от времени, ; в значительной степени соответствует нашим выводам в предыдущих разделах 5 .
Теперь рассмотрим нелинейный случай. Чуа заявляет, что «… только мемристоры, характеризующиеся монотонно возрастающей кривой ϕ — q , могут существовать в виде устройства без внутренних источников питания». Нелинейная кривая ϕ — q всегда будет иметь положительный, хотя и переменный наклон.Однако отношение ϕ к q все еще имеет единицы ом, без фазового сдвига , что делает его нелинейным резистором. Простые pn-диоды или транзисторы, показанные в таблице 1, могут имитировать нелинейные резисторы. В контексте трех известных фундаментальных устройств Tour et al . заявляют, что «Поведение каждого из этих элементов описывается простой линейной зависимостью…», четко подтверждая, что линейность является центральным элементом фундаментальности 8 .Нелинейные резисторы не являются фундаментальными, потому что их можно моделировать сборкой кусочно-линейных компонентов.
Отчет Ди Вентра и др. . а общие знания моделирования показывают, что только активный элемент может создавать отрицательное дифференциальное сопротивление (NDR), которое видно на вольт-амперных кривых мемристора 14 . NDR исключает возможность нелинейного пассивного диода моделировать мемристор, оставляя активные схемы в качестве единственного варианта для моделирования мемристоров.
Рассмотрим мемристор в свете выражения Струкова для феноменологической константы \ (M (q (t)) = \ frac {\ varnothing} {q} \). Когда M ( q ( t )) является положительной константой и \ (\ frac {d} {dq} M (q (t)) = 0 \), тогда устройство является линейным устройством времени — инвариантный резистор , который является уже известным фундаментальным элементом R . Все остальные случаи как минимум нелинейны и исключены из фундаментальных. В силу нелинейности и игнорирования любого критерия активности мемристор должен занимать (C, X) на рис.4.
Предположение, что элемент схемы может быть фундаментальным пассивом в силу нелинейности, ошибочно. Если бы это было правдой, то резистор малых сигналов r в (C, X), который мог бы представлять пассивный диод, также был бы фундаментальным элементом. Даже если отныне мы решим признать нелинейные пассивные устройства фундаментальными в некотором «расширенном пространстве проектирования», как было предложено Уильямсом и др. ., (i) мемристор не может занимать (A, Z) или \ (({\ rm {A }}, \ hat {{\ rm {Z}}}) \), потому что эти слоты заняты линейным резистором и (ii) мемристор не может занимать (C, X), потому что в вольт-амперной области устройство демонстрирует гистерезис — активное явление, тем самым полностью исключив его из любой таблицы фундаментальных пассивных элементов 5,7,19 .Слот \ (({\ rm {C}}, \ hat {{\ rm {X}}) \) был отклонен в предыдущем обсуждении.
Расширение области действия периодической таблицы
Имея в нашем распоряжении хорошо разработанную таблицу понятий в таблице 1, периодическую таблицу и два кратких правила, мы хорошо подготовлены и склонны рассматривать другие формы устройств, такие как устройства с контролируемым потоком. индуктор, конденсатор с контролируемым зарядом и т.д. поток.Любая катушка индуктивности будет создавать напряжение на клеммах устройства с определяющим соотношением \ (L \ frac {di} {dt} = \ nu \) в (C, Y). Замените i в основном уравнении после обобщения всех величин, чтобы они зависели от потока. Получаем \ (L ({\ varnothing} _ {B}) \ frac {d \, f ({\ varnothing} _ {B})} {dt} = \ nu ({\ varnothing} _ {B}) \ ), поэтому \ (L ({\ varnothing} _ {B}) = \ frac {\ nu ({\ varnothing} _ {B})} {\ dot {f} ({\ varnothing} _ {B})} \). Устройство является фундаментальным, если L (∅ B ) является положительной константой и \ (\ frac {d} {d {\ varnothing} _ {B}} L ({\ varnothing} _ {B}) \) тождественно равен нулю.{2}} i \).
В качестве другого примера рассмотрим устройство с ν = г ( q ). Все конденсаторы реагируют на заряд и вырабатывают напряжение в соответствии с Cν = q . Переформатируя определяющее отношение, чтобы оно соответствовало нашему тесту, мы получаем C ( q ) g ( q ) = q . Транспонирование, \ (C (q) = \ frac {q} {g (q)} \). Устройство является фундаментальным, если C ( q ) является положительной константой и \ (\ frac {d} {dq} C (q) \) тождественно равен нулю.{-1} \ frac {d} {dt} q \).
Оглядываясь назад, мы замечаем, что столбец X содержит небольшое сигнальное представление фундаментальных элементов, точно так же, как только столбец Y содержит определяющие отношения фундаментальных элементов.
Что такое мемристор Чуа или HP?
Если мемристор не является фундаментальным, мы стремимся понять, что это такое. Первое свидетельство — оригинальная модель от HP. Так выглядит потенциометр из двух резисторов и ползунка 7 . Ползунок должен перемещаться в зависимости от времени, чтобы устройство переходило между состояниями с низким и высоким сопротивлением.Несмотря на множество недостатков модели HP, она отражает суть мемристора — двухполюсное последовательное соединение резисторов с низким сопротивлением R LO и высоким сопротивлением R HI , демонстрируя NDR. Хотя Ди Вентра и др. . утверждают, что отрицательное сопротивление может происходить только от активного элемента, сообщество мемристоров не сразу приравнивает NDR к наличию активного элемента 14 .Благодаря грамотному использованию оконных функций, произвольно вводимых в уравнения, HP скрывает присутствие активных элементов в своей мемристорной модели. В конце концов, потенциометру нет гистерезиса.
Оригинальное исследование в области символьного моделирования выявило два импеданса, которые скручивают в комплексной плоскости 20,21 . Этот подход предлагает логистическую функцию как решение уравнения Бюргерса с переменным коэффициентом. Модель Бюргерса показывает мемристор как сумму реального и отрицательного импеданса; где сумма реактивных компонентов всегда равна нулю.Комплексные резисторы имеют вид \ ({R} _ {1} = \ pm \, a \ mp j \, b \) и \ ({R} _ {2} = \ mp \, c \ pm j \, b \), где положительный член из числа a , c всегда больше. Следовательно, композитное сопротивление всегда положительное. Модель однозначно выявляет наличие недоминантного отрицательного сопротивления. Отрицательный импеданс можно связать с ударной волной, которую Tang et al . вывели 22 . Отрицательное сопротивление не видно внешнему наблюдателю, кроме как во время перехода, и необходимо для представления гистерезиса, зависящего от потока, который является ключом к функциональности мемристора.Без гистерезиса вольт-амперные кривые мемристора не могут иметь лепестков. Вольт-амперная кривая со сжатым гистерезисом является отличительной чертой мемристора 15 . Символьная модель Абрахама генерирует традиционные вольт-амперные кривые и демонстрирует разумное соответствие эмпирическим данным о времени переключения 21 . Также было продемонстрировано, что указанная модель демонстрирует правильную температурную зависимость от эмпирических данных 20 .
Миграция вакансий в мемристоре похожа на пузырьки в стекле по аналогии Вильямса или, скорее, на поведение устройств с токами, ограниченными пространственным зарядом, где постоянная времени тепловой релаксации пространственного заряда велика 19 .Полученная граница между областями низкой и высокой концентрации вакансий в мемристоре имитирует ползунок реостата, разделяет устройство на два (последовательно) резистора и реализует (активный) гистерезис. Гистерезис признан многими авторами, включая Чуа, Вильямса, Струкова и Биолек 5,7,15,19,23 . Гистерезис может быть реализован в схеме с операционным усилителем, триггером Шмитта или элементами управления напряжением / током, все из которых являются активными.
На веб-сайте Мемристорного центра Чуа утверждается, что Corinto et al .построили мемристорную модель с однопортовыми пассивными компонентами 24,25 . Это невозможно, если мемристор является фундаментальным элементом. В другой рецензируемой публикации, связанной со схемой, предполагаемый пассивный резистор заменяется диодом Чуа; который является локально активным устройством 26 . Локальная активность подразумевает отрицательное сопротивление 27 . Для моделирования мемристора всегда требовались активные элементы, потому что он неявно активен 5,28,29 .
На рис.5 мы моделируем мемристор в виде двух резисторов, выбираемых с помощью двухполюсного двухпозиционного переключателя U3, управляемого генератором гистерезиса U2. Клеммы устройства: a и b . Модель VTEAM имеет положительный и отрицательный порог, который может быть произведен U2 30 . Интегратор U1 вычисляет поток. Генератор гистерезиса U2 — неизбежный активный компонент.
Рисунок 5Модель схемы мемристора с гистерезисом на основе потока. ( a ) Гистерезис необходим для правильного выбора низкого или высокого сопротивления при заданном пороге магнитного потока.{-1} \ nu \, t \). Однако для умножения требуются активные элементы, поэтому пассивные устройства никогда не занимают (D, Y). Поэтому набор основных элементов строго ограничен C , R и L вдоль ([A, B, C], Y) на рис. 4.
Мы суммируем наши результаты в таблице 2, где мы перечисляем каждый фундаментальный элемент и его определяющие отношения в электрической и магнитной плоскостях. Переменная ν представляет напряжение (В), а ϕ B представляет истинный магнитный поток в Вебере (Wb).Возвращаясь к рис. 4, мы видим, что в электрической области напряжение — это измеряемая величина, которая генерируется на выводах основных элементов в столбце Y. В силу симметрии скорость изменения магнитного потока \ (- {\ dot {\ varphi}} _ {B} \) — единственная измеримая величина, которая должна помочь найти фундаментальный элемент в магнитной области в столбце \ (\ hat {{\ rm {Y}}} \).
Таблица 2 Таблица определяющих соотношений для основных элементов.В новом бюллетене представлены устройства Circuit Setter Plus с калиброванными балансировочными клапанами
Мортон-Гроув, Иллинойс — 29 апреля 2005 г.
Bell & Gossett® опубликовала новый бюллетень, описывающий конструкцию и рабочие характеристики калиброванных балансировочных клапанов Circuit Setter Plus®.В литературе описаны преимущества метода системной балансировки и показано, как Circuit Setter Plus обеспечивает оптимальный и точный поток в системе с минимальной рабочей мощностью.
В бюллетене (A-508K) представлены подробные характеристики клапана и поясняются типичные применения клапанов для балансировки и измерения уровней расхода и управления отсечкой.
Конкретные преимущества и компоненты устройства Circuit Setter Plus, упомянутые в литературе, включают:
- Восстановление напора скорости
- Устройство для расчета балансировочного клапана
- Расходомер с регулируемой диафрагмой
- Пропорциональные весы
- Система принудительной отсечки
- Остановка памяти
- Клапаны считывания
- Дренажное соединение
В бюллетень также включены диаграммы продуктов, на которых показаны размеры моделей NPT и Sweat, а также моделей с фланцами и канавками.Кроме того, для каждой конструкции клапана дается подробное описание конструкции клапана.
Изображение с высоким разрешением доступно для загрузки по адресу: http://www.bellgossett.com/WhatsNew/images/Bulletin-A-508K-cover.jpg
Загрузка изображения:
Если у вас возникли проблемы с загрузкой этого изображения, попробуйте ПРАВО щелкнуть ссылку на изображение выше и выбрать «Сохранить объект (ссылку) как…». Затем вы можете указать, где на вашем компьютере вы хотите сохранить изображение.
Bell & Gossett, подразделение ITT Industries, является ведущим производителем центробежных насосов, специальных гидравлических устройств, теплообменников, оборудования для обработки конденсата и комплексных систем для перекачки с переменной и постоянной скоростью, теплопередачи и повышения давления.
За дополнительной информацией обращайтесь в Bell & Gossett, 8200 N. Austin Avenue, Morton Grove, IL 60053; телефон 847 / 966-3700; факс 847 / 966-9052. Или посетите веб-сайт Bell & Gossett по адресу www.bellgossett.com
.резисторов последовательно и параллельно
Резисторы серии
Общее сопротивление в цепи с последовательно включенными резисторами равно сумме отдельных сопротивлений.
Цели обучения
Рассчитайте общее сопротивление в цепи с последовательно включенными резисторами
Основные выводы
Ключевые моменты
- Один и тот же ток последовательно проходит через каждый резистор.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.
- Общее сопротивление в последовательной цепи равно сумме отдельных сопротивлений: [латекс] \ text {RN} (\ text {series}) = \ text {R} _1 + \ text {R} _2 + \ text {R} _3 +… + \ text {R} _ \ text {N} [/ latex].
Ключевые термины
- серия : ряд элементов, которые следуют одно за другим или связаны друг за другом.
- сопротивление : Противодействие прохождению электрического тока через этот элемент.
Обзор
В большинстве схем имеется более одного компонента, называемого резистором, который ограничивает поток заряда в цепи. Мера этого предела для потока заряда называется сопротивлением. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.
Цепи серии : Краткое введение в анализ последовательных и последовательных цепей, включая закон Кирхгофа по току (KCL) и закон Кирхгофа по напряжению (KVL).
Резисторы серии
Резисторы включены последовательно всякий раз, когда заряд или ток должны проходить через компоненты последовательно.
Резисторы в серии : Эти четыре резистора подключены последовательно, потому что, если бы ток подавался на один конец, он бы протекал через каждый резистор последовательно до конца.
показывает резисторы, последовательно подключенные к источнику напряжения. Общее сопротивление в цепи равно сумме отдельных сопротивлений, поскольку ток должен последовательно проходить через каждый резистор.
Резисторы, подключенные последовательно. : Три резистора, подключенные последовательно к батарее (слева), и эквивалентное одиночное или последовательное сопротивление (справа).
Использование закона Ома для расчета изменений напряжения в резисторах серии
Согласно закону Ома падение напряжения V на резисторе при протекании через него тока рассчитывается по формуле V = IR, где I — ток в амперах (A), а R — сопротивление в омах (Ω). .
Таким образом, падение напряжения на R 1 равно V 1 = IR 1 , на R 2 равно V 2 = IR 2 , а на R 3 равно V 3 = IR 3 .Сумма напряжений будет равна: V = V 1 + V 2 + V 3 , исходя из сохранения энергии и заряда. Если подставить значения отдельных напряжений, получим:
[латекс] \ text {V} = \ text {IR} _1 + \ text {IR} _2 + \ text {IR} _3 [/ latex]
или
[латекс] \ text {V} = \ text {I} (\ text {R} _1 + \ text {R} _2 + \ text {R} _3) [/ латекс]
Это означает, что полное сопротивление в серии равно сумме отдельных сопротивлений. Следовательно, для каждой цепи с Н количество резисторов, включенных последовательно:
[латекс] \ text {RN} (\ text {series}) = \ text {R} _1 + \ text {R} _2 + \ text {R} _3 +… + \ text {R} _ \ text {N }.[/ латекс]
Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.
Поскольку напряжение и сопротивление имеют обратную зависимость, отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его. Об этом свидетельствует пример, когда две лампочки соединены в последовательную цепь с аккумулятором. В простой схеме, состоящей из одной батареи 1,5 В и одной лампочки, падение напряжения на лампе будет равно 1.5V через него. Однако, если бы две лампочки были соединены последовательно с одной и той же батареей, на каждой из них было бы падение напряжения 1,5 В / 2 или 0,75 В. Это будет очевидно по яркости света: каждая из двух последовательно соединенных лампочек будет в два раза слабее, чем одиночная лампочка. Следовательно, резисторы, соединенные последовательно, потребляют такое же количество энергии, как и один резистор, но эта энергия распределяется между резисторами в зависимости от их сопротивлений.
Параллельные резисторы
Общее сопротивление в параллельной цепи равно сумме обратных сопротивлений каждого отдельного сопротивления.
Цели обучения
Рассчитайте общее сопротивление в цепи с резисторами, включенными параллельно
Основные выводы
Ключевые моменты
- Общее сопротивление в параллельной цепи меньше наименьшего из отдельных сопротивлений.
- Каждый резистор, включенный параллельно, имеет то же напряжение, что и приложенный к нему источник (напряжение в параллельной цепи постоянно).
- Не каждый параллельный резистор получает полный ток; они делят его (ток зависит от номинала каждого резистора и общего количества резисторов в цепи).
Ключевые термины
- сопротивление : Противодействие прохождению электрического тока через этот элемент.
- параллельно : Расположение электрических компонентов, при котором ток течет по двум или более путям.
Обзор
Резисторы в цепи могут быть включены последовательно или параллельно. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.
Parallel Circuits : Краткий обзор анализа параллельных цепей с использованием таблиц VIRP для школьников-физиков.
Параллельные резисторы
Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения путем соединения проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника.
Параллельное соединение резисторов : Параллельное соединение резисторов.
Каждый резистор потребляет такой же ток, как если бы он был единственным резистором, подключенным к источнику напряжения. Это верно для схем в доме или квартире. Каждая розетка, подключенная к устройству («резистор»), может работать независимо, и ток не должен проходить через каждое устройство последовательно.
ЗаконОм и параллельные резисторы
Каждый резистор в цепи имеет полное напряжение. Согласно закону Ома токи, протекающие через отдельные резисторы, равны [латекс] \ text {I} _1 = \ frac {\ text {V}} {\ text {R} _1} [/ latex], [latex] \ text {I} _2 = \ frac {\ text {V}} {\ text {R} _2} [/ latex] и [latex] \ text {I} _3 = \ frac {\ text {V}} {\ text {R} _3} [/ латекс].Сохранение заряда подразумевает, что полный ток является суммой этих токов:
Параллельные резисторы : три резистора, подключенных параллельно батарее, и эквивалентное одиночное или параллельное сопротивление.
[латекс] \ text {I} = \ text {I} _1 + \ text {I} _2 + \ text {I} _3. [/ Latex]
Подстановка выражений для отдельных токов дает:
[латекс] \ text {I} = \ frac {\ text {V}} {\ text {R} _1} + \ frac {\ text {V}} {\ text {R} _2} + \ frac {\ текст {V}} {\ text {R} _3} [/ latex]
или
[латекс] \ text {I} = \ text {V} (\ frac {1} {\ text {R} _1} + \ frac {1} {\ text {R} _2} + \ frac {1} { \ text {R} _3}) [/ latex]
Это означает, что полное сопротивление в параллельной цепи равно сумме обратных сопротивлений каждого отдельного сопротивления.Таким образом, для каждой схемы с числом [latex] \ text {n} [/ latex] или резисторов, подключенных параллельно,
[латекс] \ text {R} _ {\ text {n} \; (\ text {parallel})} = \ frac {1} {\ text {R} _1} + \ frac {1} {\ text { R} _2} + \ frac {1} {\ text {R} _3}… + \ frac {1} {\ text {R} _ \ text {n}}. [/ Latex]
Это соотношение приводит к общему сопротивлению, которое меньше наименьшего из отдельных сопротивлений. Когда резисторы соединены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.
Каждый резистор, включенный параллельно, имеет такое же полное напряжение источника, как на него, но делит общий ток между ними. Примером может служить соединение двух лампочек в параллельную цепь с аккумулятором на 1,5 В. В последовательной цепи две лампочки будут вдвое менее тусклыми при подключении к одному источнику батареи. Однако, если бы две лампочки были подключены параллельно, они были бы столь же яркими, как если бы они были подключены к батарее по отдельности. Поскольку к обеим лампочкам подается одинаковое полное напряжение, батарея также разряжается быстрее, поскольку она по существу обеспечивает полную энергию для обеих лампочек.В последовательной цепи батарея будет работать столько же, сколько и с одной лампочкой, только тогда яркость будет разделена между лампочками.
Комбинированные схемы
Комбинированная цепь может быть разбита на аналогичные части, работающие последовательно или параллельно.
Цели обучения
Описать расположение резисторов в комбинированной схеме и его практическое значение
Основные выводы
Ключевые моменты
- Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного.
- Различные части комбинированной схемы могут быть идентифицированы как последовательные или параллельные, уменьшены до их эквивалентов, а затем уменьшены до тех пор, пока не останется единственное сопротивление.
- Сопротивление в проводах снижает ток и мощность, подаваемые на резистор. Если сопротивление в проводах относительно велико, как в изношенном (или очень длинном) удлинительном шнуре, то эти потери могут быть значительными и влиять на выходную мощность в устройствах.
Ключевые термины
- серия : ряд элементов, которые следуют одно за другим или связаны друг за другом.
- параллельно : Расположение электрических компонентов, при котором ток течет по двум или более путям.
- Комбинированная схема : электрическая цепь, содержащая несколько резисторов, которые соединены как последовательным, так и параллельным соединением.
Комбинированные схемы
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного. Это часто встречается, особенно если учитывать сопротивление проводов.В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинированная цепь может быть разбита на аналогичные части, которые являются последовательными или параллельными, как показано на схеме. На рисунке общее сопротивление может быть вычислено путем соединения трех резисторов друг с другом последовательно или параллельно. R 1 и R 2 соединены параллельно по отношению друг к другу, поэтому мы знаем, что для этого подмножества сопротивление, обратное сопротивлению, будет равно:
Сеть резисторов : В этой комбинированной схеме цепь может быть разбита на последовательный компонент и параллельный компонент.
Комбинированные схемы : Два параллельных резистора, соединенные последовательно с одним резистором.
[латекс] \ frac {1} {\ text {R} _1} + \ frac {1} {\ text {R} _2} [/ latex] или [латекс] \ frac {\ text {R} _1 \ text {R} _2} {\ text {R} _1 + \ text {R} _2} [/ latex]
R 3 соединен последовательно с как R 1 , так и R 2 , поэтому сопротивление будет рассчитываться как:
[латекс] \ text {R} = \ frac {\ text {R} _1 \ text {R} _2} {\ text {R} _1 + \ text {R} _2} + \ text {R} _3 [/ latex ]
Сложные комбинированные схемы
Для более сложных комбинированных схем различные части могут быть идентифицированы как последовательные или параллельные, уменьшены до их эквивалентов, а затем уменьшены до тех пор, пока не останется единственное сопротивление, как показано на.На этом рисунке комбинация из семи резисторов была идентифицирована как включенные последовательно или параллельно. На исходном изображении две обведенные кружком секции показывают резисторы, включенные параллельно.
Сокращение комбинированной схемы : Эта комбинация из семи резисторов имеет как последовательные, так и параллельные части. Каждое из них идентифицируется и приводится к эквивалентному сопротивлению, а затем уменьшается до тех пор, пока не будет достигнуто одно эквивалентное сопротивление.
Уменьшение этих параллельных резисторов до одного значения R позволяет нам визуализировать схему в более упрощенном виде.На верхнем правом изображении мы видим, что обведенная кружком часть содержит два последовательно соединенных резистора. Мы можем дополнительно уменьшить это до другого значения R, добавив их. Следующий шаг показывает, что два обведенных резистора включены параллельно. Уменьшение тех бликов, что последние два соединены последовательно и, таким образом, могут быть уменьшены до одного значения сопротивления для всей цепи.
Одним из практических следствий комбинированной схемы является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.Комбинированная цепь может быть преобразована в последовательную цепь на основе понимания эквивалентного сопротивления параллельных ветвей комбинированной цепи. Последовательная цепь может использоваться для определения общего сопротивления цепи. По сути, сопротивление провода является последовательным с резистором. Таким образом, увеличивается общее сопротивление и уменьшается ток. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение ИК-излучения в проводах также может быть значительным.
Зарядка аккумулятора: последовательные и параллельные ЭДС
При последовательном включении источников напряжения их ЭДС и внутренние сопротивления складываются; параллельно они остаются прежними.
Цели обучения
Сравнить сопротивления и электродвижущие силы для источников напряжения, подключенных с одинаковой и противоположной полярностью, последовательно и параллельно
Основные выводы
Ключевые моменты
- ЭДС, соединенные последовательно с одинаковой полярностью, являются аддитивными и приводят к более высокой общей ЭДС.
- Две ЭДС, соединенные последовательно с противоположной полярностью, имеют общую ЭДС, равную разнице между ними, и могут использоваться для зарядки источника с более низким напряжением.
- Два источника напряжения с идентичными ЭДС, соединенные параллельно, имеют чистую ЭДС, эквивалентную одному источнику ЭДС, однако чистое внутреннее сопротивление меньше и, следовательно, дает более высокий ток.
Ключевые термины
- параллельно : расположение электрических компонентов, при котором ток течет по двум или более путям.
- электродвижущая сила : (ЭДС) — напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.
- серия : ряд элементов, которые следуют одно за другим или связаны друг за другом.
Когда используется более одного источника напряжения, они могут быть подключены последовательно или параллельно, аналогично резисторам в цепи.Когда источники напряжения включены последовательно в одном направлении, их внутренние сопротивления складываются, а их электродвижущая сила или ЭДС складываются алгебраически. Эти типы источников напряжения распространены в фонариках, игрушках и других приборах. Обычно ячейки включены последовательно, чтобы обеспечить большую суммарную ЭДС.
Фонарик и лампочка : Последовательное соединение двух источников напряжения в одном направлении. Эта схема представляет собой фонарик с двумя последовательно включенными ячейками (источниками напряжения) и одной лампочкой (сопротивление нагрузки).
Батарея представляет собой соединение нескольких гальванических элементов. Однако недостатком такого последовательного соединения ячеек является то, что их внутреннее сопротивление увеличивается. Иногда это может быть проблематично. Например, если вы поместите в машину две батареи на 6 В вместо обычной батареи на 12 В, вы должны добавить как ЭДС, так и внутреннее сопротивление каждой батареи. Таким образом, у вас будет такая же ЭДС 12 В, хотя внутреннее сопротивление тогда будет удвоено, что вызовет у вас проблемы, когда вы захотите запустить двигатель.
Но, если ячейки противостоят друг другу — например, когда одна вставляется в прибор задом наперед, — общая ЭДС меньше, так как это алгебраическая сумма отдельных ЭДС. Когда он перевернут, он создает ЭДС, которая противодействует другой, и приводит к разнице между двумя источниками напряжения.
Зарядное устройство : представляет собой два источника напряжения, соединенных последовательно с противоположными ЭДС. Ток течет в направлении большей ЭДС и ограничивается суммой внутренних сопротивлений.(Обратите внимание, что каждая ЭДС представлена на рисунке буквой E.) Зарядное устройство, подключенное к аккумулятору, является примером такого подключения. Зарядное устройство должно иметь большую ЭДС, чем батарея, чтобы через него протекал обратный ток.
Когда два источника напряжения с одинаковыми ЭДС соединены параллельно и также подключены к сопротивлению нагрузки, общая ЭДС равна индивидуальным ЭДС. Но общее внутреннее сопротивление уменьшается, поскольку внутренние сопротивления параллельны. Таким образом, параллельное соединение может производить больший ток.
Две идентичные ЭДС : Два источника напряжения с одинаковыми ЭДС (каждый помечен буквой E), подключенные параллельно, создают одинаковую ЭДС, но имеют меньшее общее внутреннее сопротивление, чем отдельные источники. Параллельные комбинации часто используются для подачи большего тока.
ЭДС и напряжение на клеммах
Выходное напряжение или напряжение на клеммах источника напряжения, такого как аккумулятор, зависит от его электродвижущей силы и внутреннего сопротивления.
Цели обучения
Выразите взаимосвязь между электродвижущей силой и напряжением на клеммах в форме уравнения
Основные выводы
Ключевые моменты
- Электродвижущая сила (ЭДС) — это разность потенциалов источника при отсутствии тока.
- Напряжение на клеммах — это выходное напряжение устройства, измеренное на его клеммах.
- Напряжение на клеммах рассчитывается по формуле V = ЭДС — Ir.
Ключевые термины
- электродвижущая сила : (ЭДС) — напряжение, генерируемое батареей или магнитной силой в соответствии с законом Фарадея. Она измеряется в вольтах, а не в ньютонах, и поэтому на самом деле не является силой.
- напряжение на клеммах : Выходное напряжение устройства, измеренное на его клеммах.
- разность потенциалов : разница в потенциальной энергии между двумя точками в электрическом поле; разница в заряде между двумя точками в электрической цепи; Напряжение.
Когда вы забываете выключить автомобильные фары, они постепенно тускнеют по мере разрядки аккумулятора. Почему они просто не мигают, когда батарея разряжена? Их постепенное затемнение означает, что выходное напряжение батареи уменьшается по мере разряда батареи. Причина снижения выходного напряжения для разряженных или перегруженных батарей заключается в том, что все источники напряжения состоят из двух основных частей — источника электрической энергии и внутреннего сопротивления.
Электродвижущая сила
Все источники напряжения создают разность потенциалов и могут подавать ток, если подключены к сопротивлению. В небольшом масштабе разность потенциалов создает электрическое поле, которое воздействует на заряды, вызывая ток. Мы называем эту разность потенциалов электродвижущей силой (сокращенно ЭДС). ЭДС — это вообще не сила; это особый тип разности потенциалов источника при отсутствии тока. Единицы измерения ЭДС — вольты.
Электродвижущая сила напрямую связана с источником разности потенциалов, например, с конкретной комбинацией химических веществ в батарее.Однако при протекании тока ЭДС отличается от выходного напряжения устройства. Напряжение на выводах батареи, например, меньше, чем ЭДС, когда батарея подает ток, и оно падает дальше, когда батарея разряжается или разряжается. Однако, если выходное напряжение устройства можно измерить без потребления тока, то выходное напряжение будет равно ЭДС (даже для сильно разряженной батареи).
Напряжение на клеммах
представляет схематическое изображение источника напряжения.Выходное напряжение устройства измеряется на его выводах и называется напряжением на выводах В, . Напряжение на клеммах определяется уравнением:
Схематическое изображение источника напряжения : Любой источник напряжения (в данном случае углеродно-цинковый сухой элемент) имеет ЭДС, связанную с источником разности потенциалов, и внутреннее сопротивление r, связанное с его конструкцией. (Обратите внимание, что сценарий E означает ЭДС.) Также показаны выходные клеммы, на которых измеряется напряжение на клеммах V.Поскольку V = ЭДС-Ir, напряжение на клеммах равно ЭДС, только если ток не течет.
[латекс] \ text {V} = \ text {emf} — \ text {Ir} [/ latex],
где r — внутреннее сопротивление, а I — ток, протекающий во время измерения.
I является положительным, если ток течет от положительного вывода. Чем больше ток, тем меньше напряжение на клеммах. Точно так же верно, что чем больше внутреннее сопротивление, тем меньше напряжение на клеммах.


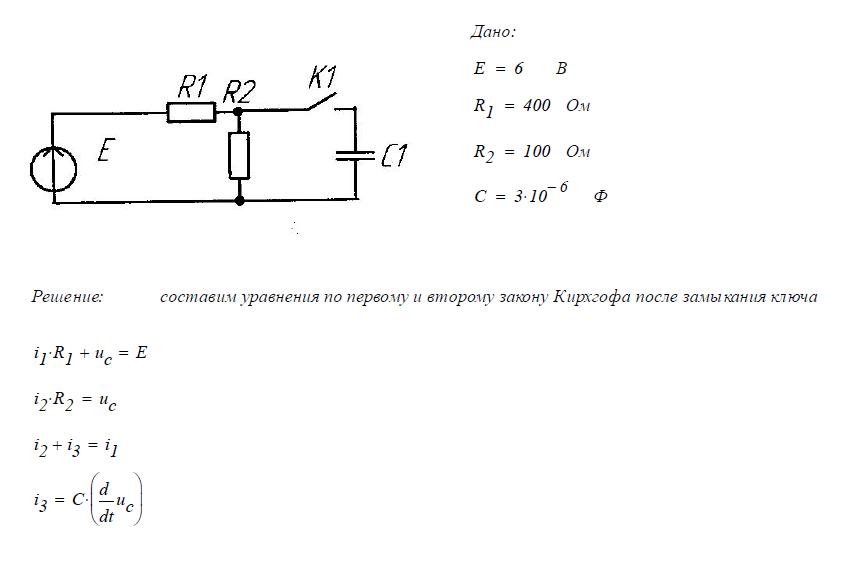 Причем максимум коэффициента имеет место, если θопт ≈ 120°/n. Так, для удвоения частоты оптимальный угол отсечки должен быть равен 60°, а для утроения — θ ≈ 40°.
Причем максимум коэффициента имеет место, если θопт ≈ 120°/n. Так, для удвоения частоты оптимальный угол отсечки должен быть равен 60°, а для утроения — θ ≈ 40°.