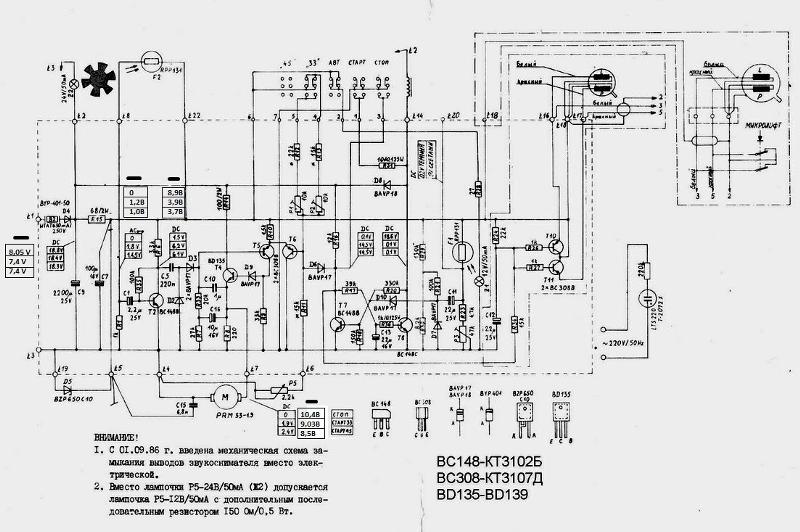
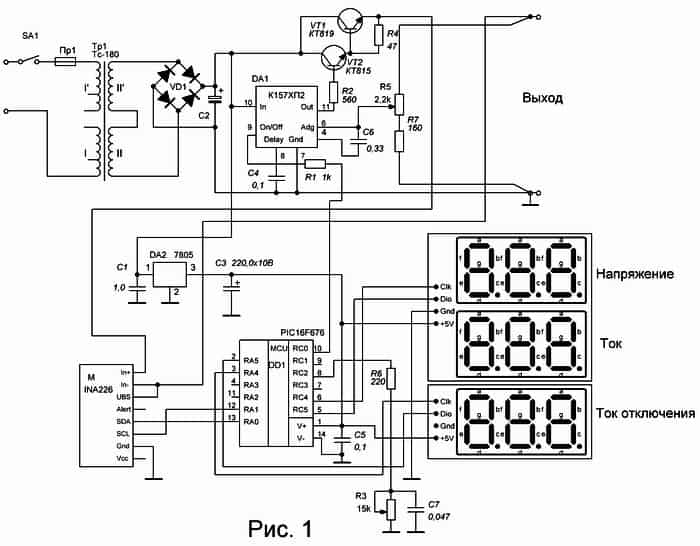
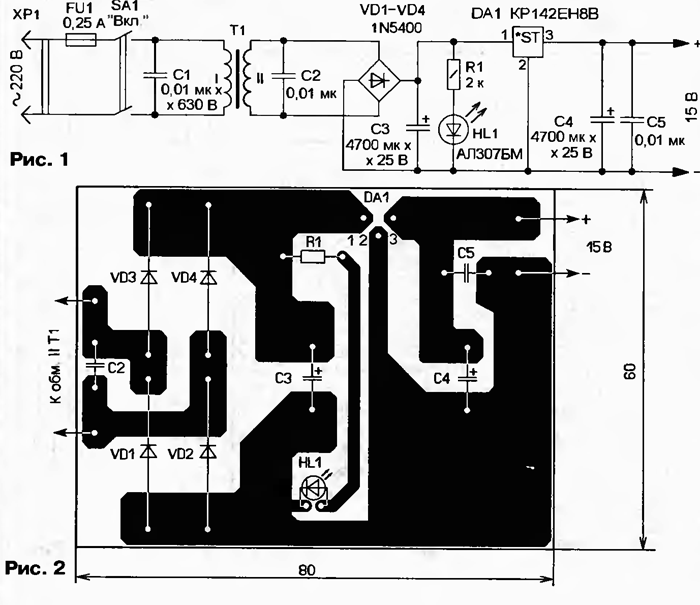
Стабилизатор вега 9 схема

При колебаниях напряжения в сети стабилизатор автоматически поддерживает необходимое напряжение питания телевизора, при этом не надо контролировать величину напряжения. Стабилизаторы включают в сеть переменного тока напряжением или В. При этом стабилизированное напряжение в обоих случаях одинаково и равно В. Для питания приборов или аппаратов с электродвигателями компрессионные холодильники, стиральные машины и т. Стабилизаторы напряжения выпускаются с линейным сопротивлением в виде выделенного ненасыщенного дросселя, а также с магнитным шунтом.

Поиск данных по Вашему запросу:

Стабилизатор вега 9 схема

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

• Ремонт стабилизаторов напряжения сети «Ресанта». Электрические схемы стабилизаторов напряжения
• Ремонт стабилизаторов напряжения сети «Ресанта». Электрические схемы стабилизаторов напряжения
• Стабилизатор напряжения однофазный Ortea VEGA 7 — 15/5-20 7 кВА
• Стабилизатор напряжения
• Стабилизатор напряжения Vega 5-15/20
• Стабилизаторы напряжения
• Лучшие схемы
• Стабилизатор напряжения Штиль R9000-3

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Деньги с мусора №2 — Стабилизатор напряжения, сдали на металл

Ремонт стабилизаторов напряжения сети «Ресанта».

Электрические схемы стабилизаторов напряжения

В цепи регулятора напряжения установлен автомат защиты от перегрузок и коротких замыканий. Стабилизаторы серии Vega выдерживают десятикратную перегрузку и обеспечивают полную номинальную мощность. На передней части корпуса располагается цифровой вольтметр, на котором отображается параметры напряжения и информация о работе стабилизатора.

Стабилизатор реагирует на изменения напряжения моментально. Стабилизаторы ORTEA оснащены встроенной молниезащитой — благодаря ей, высоковольтные разряды не причинят ущерба электроприборам.

Для этой цели используются разрядники тока молнии и ограничители импульсных перенапряжений. Это устройства защиты от импульсных перенапряжений I и II класса отводящие импульсы с большой энергией.

Данная характеристика определяет максимальную мощность нагрузки на стабилизатор. Для электрических схем с переменным током принято различать несколько понятий мощности. Это реактивная мощность для нагрузки, в которую входят реактивные элементы — конденсаторы и индуктивности и активная мощность для нагрузки, которая содержит резистивные элементы.

При выборе стабилизатора необходимо учитывать, что его выходная мощность должна быть больше мощности, потребляемой нагрузкой. В зависимости от типа нагрузки это может быть либо полная, либо активная мощность.

Если в нагрузку входят мощные электродвигатели, крупная бытовая техника, электроника, то при выборе стабилизатора рекомендуется ориентироваться на его полную мощность. Диапазон входного напряжения является одним из важнейших параметров стабилизатора. Чем шире диапазон, тем более универсальным является стабилизатор, но вместе с этим повышаются сложность устройства, габариты и цена. Работать эффективно при сверхнизком напряжении В могут только самые дорогие стабилизаторы.

Рабочим напряжением считают то напряжение, при котором устройство может функционировать постоянно и без перегрузок. Точность стабилизации, или погрешность работы, является важной характеристикой стабилизатора и непосредственно влияет на класс устройства и его цену. Эта величина измеряется в процентах и показывает максимально возможное отклонение напряжения на выходе.

Чем ближе это значение к нулю, тем лучше. Купленную в нашей компании продукцию можно забрать самовывозом или заказать доставку по России, Белоруссии, Казахстану. На нашем складе постоянно поддерживается более наименований товаров в наличии. Это гарантирует оперативную отгрузку товара и актуальную информацию о наличии и стоимости на нашем сайте.

Любые формы оплаты — картой, в кредит , Яденьги, по счету для организаций при заказе в интернет магазине. Про оферту Все права защищены. Копирование материалов сайта запрещено и карается законом об авторских правах. Вся информация, представленная на сайте, может содержать неточности в описании товаров и орфографические ошибки, а так же не является полной и исчерпывающей.

Перед оформлением заказа рекомендуем уточнить у наших специалистов интересующие Вас характеристики выбранных товаров. Вся представленная на сайте информация, касающаяся технических характеристик, наличия на складе, комплектаций, монтажа оборудования, а также стоимости продукции и сервисного обслуживания, носит информационный характер и ни при каких условиях не является публичной офертой, определяемой положениями Статьи 2 Гражданского кодекса Российской Федерации.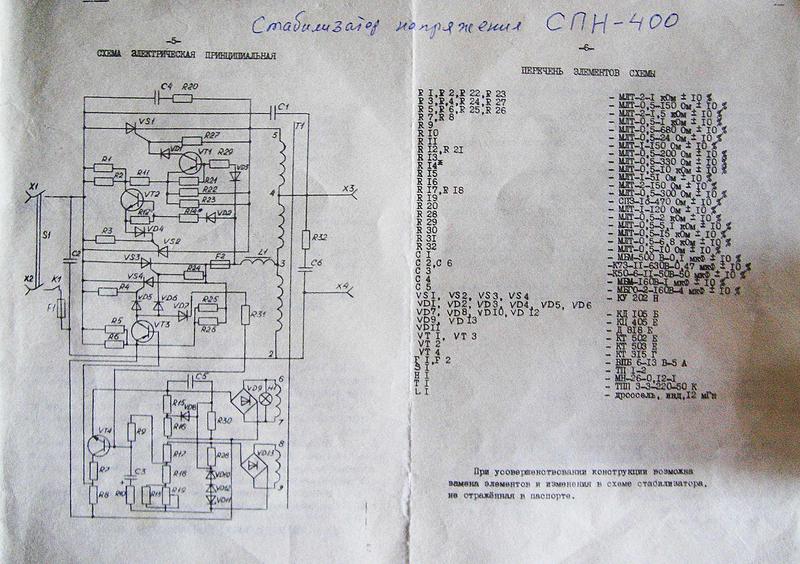

Ваш город. Резервное и автономное электроснабжение для вашего загородного дома. Продажа, установка и обслуживание солнечных электростанций для частных домов. Проектирование, монтаж и сервисное обслуживание котельных в коттеджах.

Звоните нам бесплатно. Перезвонить Ваше имя. Удобное время -. Каталог товаров. Каталог товаров Производство Реалсолар. Сетевые солнечные электростанции. Автономные солнечные электростанции Акции! Солнечное отопление и горячее водоснабжение дома. Оформить заказ.

Ваш личный Кабинет. Заказы Список сравнения Отложенные товары Отслеживание заказа. Отслеживание заказа. Войти Регистрация E-mail. Пароль Забыли пароль? Создать учетную запись. Наведите на картинку для увеличения. Написать отзыв. Доступность: Нет на складе, предзаказ. Цена в бонусах: бонусов. Начислим : бонусов. Технические характеристики. Мощность, кВА. Бесплатный расчет системы автономного или резервного электроснабжения Заказать расчет.

Расчет доставки. Варианты оплаты. VEGA работает в широком диапазоне напряжений, оснащена революционным токосъемным механизмом, обеспечивающим максимальную скорость срабатывания и точность регулировки.

VEGA оснащена защитой от высокого напряжения, выдерживает десятикратные перегрузки и работает при отрицательных температурах. Отложить Сравнить. Описание Характеристики Документация Вопрос-ответ. На этот элемент итальянская компания дает пожизненную гарантию.

Встроенная молниезащита Стабилизаторы ORTEA оснащены встроенной молниезащитой — благодаря ей, высоковольтные разряды не причинят ущерба электроприборам. Технические характеристики стабилизатора Макс. Мощность, кВА Данная характеристика определяет максимальную мощность нагрузки на стабилизатор. Рабочий диапазон входного напряжения Диапазон входного напряжения является одним из важнейших параметров стабилизатора. Модель: Vega. Вес, кг: Сообщения не найдены Добавить вопрос.

Популярные разделы. Наши работы Солнечные батареи Солнечные электростанции Резервное электроснабжение Стабилизаторы напряжения Инверторы Генераторы. Как оплатить? Доставка Бонусные баллы Монтаж оборудования Контакты Возврат. ООО «Реалсолар» г. Санкт-Петербург, Октябрьская наб. Все права защищены.

Ремонт стабилизаторов напряжения сети «Ресанта». Электрические схемы стабилизаторов напряжения

Стабилизаторы напряжения: обслуживание, продажа со склада, самые низкие цены в городе Санкт-Петербурге. Наши сотрудники имеют опыт работы в этой среде более 10 лет. Главный наш девиз — не продать Вам стабилизатор напряжения, а помочь с выбором, что бы проблемы с напряжением более Вас не беспокоили. Что делать, когда в доме не кипятит чайник? Как быть, если перестает стирать стиральная машина?

[СКАЧАТЬ] Электрическая схема стабилизатора райдер PDF бесплатно или читать онлайн на планшете и Стабилизатор напряжения Вега

Стабилизатор напряжения однофазный Ortea VEGA 7 — 15/5-20 7 кВА

Пришел ко мне в гости мой старый знакомый, умный вроде бы дядька и как-то вскользь упомянул, что купил к своему телевизору крутой стабилизатор напряжения. Однако уже через каких-то 15 минут спора, его уверенность несколько поугасла. Вообще, удивительно, насколько сильно мы подвержены влиянию маркетинговых уловок.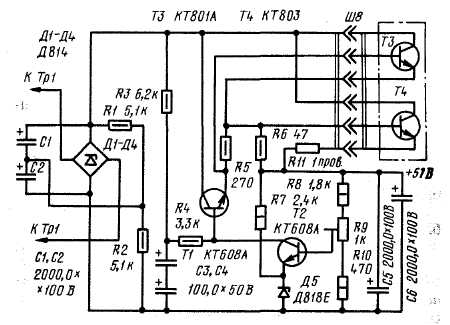 Даже, казалось бы, умные люди, с развитым критичным мышлением, с легкостью ведутся на различные рекламные трюки и слащавые заверения продаванов. В случае же со стабилизаторами, думаю, сыграли воспоминания из далекого прошлого — из старого доброго Советского Союза. Содержание: Старые ламповые телевизоры Современные телевизоры и стабилизаторы Короткое замыкание и выгорание пикселей Слишком низкое и чересчур высокое напряжение в розетке Сетевые фильтры Источники бесперебойного питания Выводы. Ящик, как правило, был горячим и обязательно тяжелым.

Стабилизатор напряжения

Стабилизаторы напряжения серии N-Power серии Vega 0. На передней панели управления стабилизатора установлен индикатор наличия входного напряжения. Старшие модели серии Vega оснащены звуковой сигнализацией выходной перегрузки устройства. В силовой цепи стабилизаторов серии Vega установлены термомагнитные размыкатели или плавкие предохранители. Имя обязательное.

Регистрация Вход. Ответы Mail.

Стабилизатор напряжения Vega 5-15/20

Стабилизатор напряжения Вега На В, Вт. В рабочем состоянии. Внутри катушки меди три кг. Выходная мощность стабилизатора: мин.

Стабилизаторы напряжения

Всем известно, что существуют государственные стандарты, по которым производятся товары и предоставляются услуги. Не обошли стороной ГОСТы и такую услугу, как подача напряжения в жилые дома и на промышленные объекты. И если говорить об однофазном напряжении, где номинал равен В, то перепад его варьируется в пределах вольта. То есть, это норма, которая закреплена стандартами. Но не все бытовые приборы могут корректно работать при минимальном или максимальном напряжении из данного диапазона, так что хотите вы того или нет, а многие обыватели стали устанавливать стабилизаторы напряжения. Итак, начнем с перепадов напряжения, а именно, по каким причинам оно происходит.

Купить стабилизатор напряжения ortea vega ( кВт) в Сб: — 13 . Схема управления стабилизатора напряжения для дома и офиса.

Лучшие схемы

Стабилизатор вега 9 схема

Безупречный трехфазный стабилизатор, собранный в едином корпусе, обладающий новейшим графическим дисплеем для вывода информации о состоянии сети. Защита от перенапряжения. Плавная и точная регулировка напряжения. Безупречный стабилизатор.

Стабилизатор напряжения Штиль R9000-3

Voltage regulator — электромеханическое [1] или электрическое электронное устройство, имеющее вход и выход по напряжению , предназначенное для поддержания выходного напряжения в узких пределах, при существенном изменении входного напряжения и выходного тока нагрузки. Источник стабилизированного питания англ. Power conditioner — оборудование, применяемое для преобразования электрической энергии в форму, пригодную для последующего использования. По типу выходного напряжения стабилизаторы делятся на стабилизаторы постоянного напряжения и переменного напряжения.

Главная iXBT. Последние темы.

Искать в успешных завершенных Продать! Иваново, доставка: Россия Стоимость доставки: Набережные Челны, доставка: Россия и мир Экономная доставка: Стабилизатор напряжения Восток — 2. Данилов, доставка: Россия и мир Экономная доставка:

Подписка на рассылку «схема минусового напряжения в стабилизаторе il» Рассылка выходит раз в сутки и содержит список программ из App Store для iPhone перешедших в категорию бесплатные за последние 24 часа.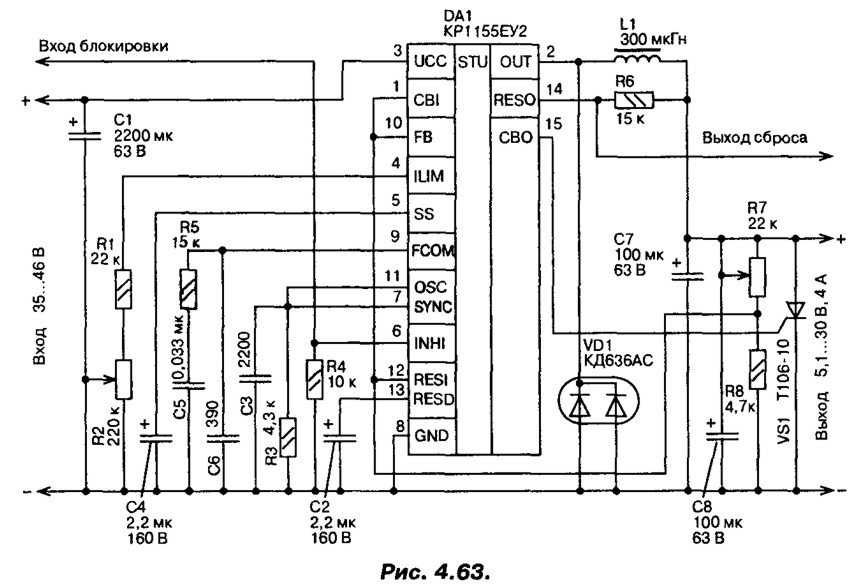

Чтобы оставить комментарий Вы должны быть зарегистрированны на сайте. О сайте.

Ortea Vega 9 -15 / 45 three-phase

Особенности:
• Качественный, надежный стабилизатор, произведенный по европейским стандартам.
• Плавное регулирование выходного напряжения и высокая точность – важное преимущество перед ступенчатыми стабилизаторами напряжения.
• Перегрузочная способность 200% в течение 2 мин.
• Оснащен автоматическим транзитом, имеет аварийный звуковой сигнал.
• Температурный режим от -25 до +45 С.

  
Благодаря использованию в регуляторе уникальных графитовых
роликов и отслеживанию напряжения 2000 раз в секунду.
Стабилизатор реагирует на изменения напряжения моментально.

Стабилизаторы ORTEA оснащены встроенной
молниезащитой – благодаря ей, высоковольтные
разряды не причинят ущерба электроприборам
Для этой цели используются разрядники тока молнии и ограничители
импульсных перенапряжений. Это устройства защиты от импульсных
перенапряжений I и II класса отводящие импульсы с большой энергией.

В стабилизаторах встроена интеллектуальная
система защиты от перенапряжения
французской компании Schneider Electric.

Стабилизаторы оснащены интеллектуальной защитой,
срабатывающей автоматически, призванной оберегать
любое оборудование от внезапных скачков напряжения.

Использование морозостойких компонентов и уникальной
технологии вакуумной пропитки трансформаторов позволяет
всем стабилизаторам работать при -25°С.

Стабилизаторы ORTEA собираются в Италии из лучших комплектующих,
существующих на рынке. Традиции европейского качества позволяют
добиться исключительной надёжности.

В комплекте вepтикaльный cтeллaж c  уcтaнoвлeнным тpexфaзным бaйпacoм пpeднaзнaчaeтcя для мoнтaжa нa нeй cтaбилизaтopoв (в cocтaвe тpexфaзнoгo) c oбщeй мoщнocтью дo 30000 ВА .  Стeллaж и блoк бaйпac изгoтoвлeн из мeтaллa c диэлeктpичecким пoкpытиeм. Рaбoчий peжим тeмпepaтуp — oт +5 дo +40 °С, пpи влaжнocти нe бoлee 80 %.

Уcтaнoвкa блoкa бaйпaca  пoзвoляeт пуcтить нaпpяжeниe в oбxoд cтaбилизaтopa в cлучae пpoвeдeния peглaмeнтныx paбoт, пpи peмoнтe oбopудoвaния, пpoвeдeнии элeктpocвapoчныx paбoт нa линии нaгpузки, либo пpи oтcутcтвии нeoбxoдимocти cтaбилизaции.   Кoмплeктующими для бaйпaca являютcя:

1.    Автoмaтичecкий выключaтeль cepии бaйпac, пoзвoляющий пepeключaть нa пoтpeбитeля либo линию co вxoдa, либo c выxoдa cтaбилизaтopa.
2.    Автoмaтичecкий выключaтeль пoзвoляющий пpи нeoбxoдимocти пoлнocтью oбecтoчить cтaбилизaтop.
3.    Щитoк cepии IP31 для мoнтaжa нa cтeну cxeмы бaйпaca.
4.    Пepeмычки, кoлoдки, нaкoнeчники для кoммутaции cxeмы.
5.    Пpoвoд ПВ-3 (ГОСТ) 6мм2.

Количество фаз

Три

Мощность, ВА

9000

Мощность, кВт

8.1

Тип стабилизатора

трехфазный

Гарантия

2 года

Диапазон входных напряжений (рабочий), В

121-253

Диапазон входных напряжений (предельный), В

97-278

Процент отклонения выходного напряжения

0. 5

Металл обмотки трансформатора

медь

Термозащита

есть

Выходное напряжение, В

220-230-240 В ;380 – 400 – 415 (выбирается)

Байпас

Есть

Системы защиты

Встроенная молниезащита. Защита от перенапряжения: «Безопасный старт» — обеспечивается контактором на выходе + SPD II

Способ размещения

Напольный / Настенный

Рабочий диапазон выходного напряжения, В

380

Диапазон температуры окружающей среды,°С

от -25 до +45

Дисплей

Цифровой мультиметр на выходе

Срок службы

10 лет.

Класс защиты

IP21

КПД не менее, %

98

Масса, кг

133

Относительная влажность, %

95

Разъёмы

клеммная колодка

Климатическое исполнение

В помещении

Перегрузочная способность

200% в течение 2-х минут

Входная частота, Гц

50 / 60

Охлаждение

естественное

Форма выходного сигнала

чистый синус

Габариты, мм

400х700х1510

Дополнительная информация

Допустимое изменение нагрузки: До 100%

Дополнительно

Быстродействие, мс/В 8

Дополнительно

электромеханический тип работы, по обмотке трансформатора перемещается контактор

Дополнительно

стабилизатор можно монтировать на стене / Гармонические искажения: Не вносятся / Iвх (max), А 24 по 1 фазе / Iвых (nominal), А 13 по 1 фазе

Страна происхождения

Италия

Стабилизатор напряжения ORTEA VEGA 1500-15 мощностью 15 кВА Екатеринбург

ORTEA VEGA 1500-15

Данная модель снята с производства

Новая модель: ОРТЕА ВЕГА 15 (15-15/10-20)

Однофазный электродинамический стабилизатор напряжения Ortea серии Vega модель 1500-15 / 1000-20, мощностью 15 кВА, Имеет два способа подключения.

More details

Описание

Механическая часть

• В стабилизаторах напряжения ORTEA (ОРТЕА) вместо графитовой щетки применен уникальный графитовый ролик, что заметно увеличивает срок службы.
• Надёжный электродинамический (модернизированный электромеханический) принцип регулирования, благодаря чему достигается невероятная плавность и быстрота, точность.
• Имеющийся запас дает возможность выдерживать значительные перегрузки

Электрическая часть

• Стабилизаторы напряжения ORTEA (ОРТЕА) отслеживают напряжение 2 000 раз/сек.
• Стабилизаторы ORTEA оснащены встроенной молниезащитой – благодаря ей, высоковольтные разряды не причинят ущерба электроприборам. Для этой цели используются разрядники тока молнии и ограничители импульсных перенапряжений. Это устройства защиты от импульсных перенапряжений I и II класса отводящие импульсы с большой энергией.
• В стабилизаторах встроена интеллектуальная система защиты от перенапряжения.  Стабилизаторы оснащены интеллектуальной защитой, срабатывающей автоматически, призванной оберегать любое оборудование от внезапных скачков напряжения французской компании Schneider Electric.
• Цифровая индикация параметров сети на дисплеях Lovato Electric
• Интеллектуальной защитой нагрузки.
• На плате установлен термостат для контроля внутренней температуры и выработки сигнала аварии в случае перегрева.
• Автоматический выключатель с тепловым и магнитным расцепителями служит для защиты от перегрузок и коротких замыканий и находится в цепи регулятора напряжения. 
• Предохранители служат для защиты вспомогательных цепей. 
• Заменяемые плавкие предохранители служат для защиты платы управления.  
• Выходной автоматический выключатель для защиты от перегрузки и короткого замыкания (только для стабилизаторов до VEGA 500-15).
• Вольтодобавочный трансформатор (начиная с модели VEGA 500-15)

Подключение

• Стабилизаторы напряжения ORTEA (ОРТЕА) имеют возможность подключения по двум диапазонам:

Мощность 15 кВА, диапазон входного напряжения ±15%;

Мощность 10 кВА, диапазон входного напряжения ±20%

Исполнение

• В стабилизаторах напряжения ORTEA (ОРТЕА) серии VEGA производятся в корпусах напольного исполнения, одновременно имеющих крепление для настенного вывешивания.

Соответствие

• Стабилизаторы напряжения ORTEA (ОРТЕА) удовлетворяют европейским требованиям в соответствии с Нормативами CE для низковольтного оборудования 2006/95/EEC и Нормативами по электромагнитной совместимости 2004/EEC

Сборка

• Стабилизаторы напряжения ORTEA (ОРТЕА) собираются в Италии.

Принцип работы

• В стабилизаторах напряжения ORTEA (ОРТЕА) схема управления сравнивает значение выходного напряжения с заданным значением: если процент разности напряжения превышает требуемое значение, схема управления приводит в действие редукторный двигатель регулятора. В результате этого происходит изменение положения роликов регулятора, отбираемого с них напряжения и, следовательно, напряжения, подаваемого на первичную обмотку вольтодобавочного трансформатора. Напряжение на вторичной обмотке находится в фазе или в противофазе по отношению к напряжению сети и, таким образом, суммируется с последним или вычитается из него для компенсации изменений напряжения.

Назначение

• Стабилизаторы напряжения ORTEA (ОРТЕА) предназначены для стабилизации переменного напряжения, подающегося на бытовые и промышленные потребители нагрузки.

Технические характеристики

Производитель	Италия (IT)
Сборка	Италия (IT)
Исполнение	Напольное/Настенное
Количество фаз	1
Мощность, кВА	15
Мощность, Вт	14 300
Мощность (в зависимости от варианта подключения), кВА	15 \ 10
Падение мощности, при отрицательном отклонении вх. напряжения	Нет
Тип регулирования	Электродинамический
Допустимое изменение нагрузки, %	0-100
Перегрузочная способность, %	200 в течении 2 минут
Диапазон входного напряжения, В	187-253
Диапазон входного напряжения (в зависимости от варианта подключения), В	187-253 \ 176-264
Устанавливаемое выходное напряжение, В	220 \ 230 \ 240
Точность выходного напряжения, %	±0,5
Максимальный ток на входе, А	76
Максимальный ток на входе (в зависимости от варианта подключения), А	76 \ 54
Ток на выходе, А	65
Ток на выходе (в зависимости от варианта подключения), А	65 \ 43
Частота, Гц	50 \ 60 ±5%
Быстродействие	16 мс\В
Быстродействие (в зависимости от варианта подключения)	16 \ 12 мс\В
Коэффициент искажений, %	Не вносит
КПД, %	98
Тип охлаждения	Естественное
Диапазон рабочей температуру, °C	-25. …+45
Диапазон температуры хранения, °C	-25….+60
Относительная влажность, %	95
Цвет корпуса	RAL 7035
Защита	IP 21
Установка	Внутри помещения
Габаритные размеры (ШхГхВ), мм	300х570х280
Вес, кг	55

Отзывы

16 товаров в этой категории:

Загрузить

Вега-9

1. Файлы
2. Руководства по эксплуатации и ремонту

Руководства по эксплуатации и ремонту

• Автосигнализации

• Аудиосистемы

• Бытовая техника

• Видеосистемы

• Компьютеры и комплектующие

• Кондиционеры

• Научно-исследовательское и лабораторное оборудование

• Принтеры и копировальная аппаратура

• Руководства пользователя ПО

• Телевизоры

• Телефоны и факсы

• Фотоаппаратура

• формат djvu
• размер 242,51 КБ
• добавлен 25 января 2017 г.

Похожие разделы

1. Академическая и специальная литература
2. Автоматизация
3. Руководства, инструкции, правила, положения

1. Академическая и специальная литература
2. Военные дисциплины
3. Оружие и военная техника
4. Артиллерийское вооружение
5. Руководства по эксплуатации ракетно-артиллерийского вооружения

1. Академическая и специальная литература
2. Пищевая промышленность
3. Машины и оборудование пищевых производств
4. Оборудование предприятий общественного питания

1. Академическая и специальная литература
2. Промышленное и гражданское строительство
3. Строительные машины и оборудование
4. Руководства по эксплуатации, обслуживанию и ремонту

1. Академическая и специальная литература
2. Топливно-энергетический комплекс
3. Нормативно-техническая документация (НТД)

1. Академическая и специальная литература
2. Топливно-энергетический комплекс
3. Релейная защита и автоматизация ЭС
4. Руководства и инструкции по РЗА

1. Академическая и специальная литература
2. Топливно-энергетический комплекс
3. Релейная защита и автоматизация ЭС
4. Руководящие указания по релейной защите

1. Академическая и специальная литература
2. Топливно-энергетический комплекс
3. Справочники по оборудованию

1. Академическая и специальная литература
2. Транспорт
3. Авиационные двигатели
4. Руководства, инструкции, правила, положения

1. Академическая и специальная литература
2. Транспорт
3. Автомобильная и тракторная техника
4. Руководства по эксплуатации и ремонту

1. Прикладная литература
2. Досуг
3. Радиолюбителям

Старое железо СССР.

Часть 3 / Хабр

Старое жедезо СССР. Часть 3.

15ИЭ0013, он же Фрязинский дисплей.

Место , время, автор все те же. Ленинград, Петродворец, ЛГУ ФизФак. НИИ Физики. 1980е.В нашу лабораторию завезли 15ИЭ0013, он же Фрязинский дисплей, несколько штук. Распаковали, включили, хорошая вещь, работает. Ретроспективно понимаю, что 15ИЭ был чемпионом. Ну все штампы, которые принято говорить. Прорывная разработка, наголову выше аналогов, решения, опередившие время, на уровне мировых образцов итд.

Отступление о терминах. Терминал, дисплей, монитор это разные устройства. Интуитивно понятно, но  строгие определения дать трудно. Если начну, будет драка, попробуйте сами. Часто эти термины смешивают, употребляют как синонимы. И я буду так же, прошу не судить строго.  Вот, например, VT-52 назван довольно точно, Видео Терминал.  (Самый первый, классический терминал был телетайп. Чудо теслапанка, последовательный код на электромеханике. Пароль “В ЧАЩАХ ЮГА ЖИЛ БЫ ЦИТРУС?” Отзыв “ДА, НО ФАЛЬШИВЫЙ ЭКЗЕМПЛЯР!0123456789”) Но мы отвлеклись.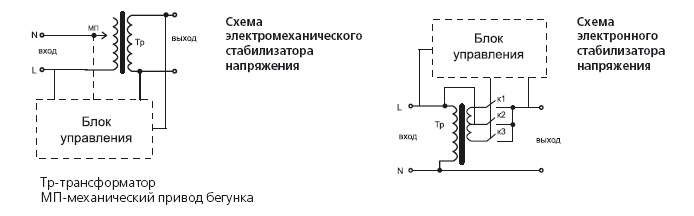

Что собой представлял типичный дисплей того времени. Сравним с современным монитором для персонального компьютера. Главное принципиальное отличие в том, что если монитор отсоединить от компьютера – системного блока, то изображение на мониторе пропадет. А если отсоединить дисплей от ЭВМ, изображение останется. Дисплей подключен к ЭВМ через медленный интерфейс и поэтому должен  хранить картинку в себе.

Свойства дисплея, что он должен делать и из каких частей состоит. Дисплей символьный, цифры, буквы и немного знаков. Символ может находится в знакоместе. 80 символов в строке, 24 (25) строк. 2000 символов на экране. Символы чаще всего формируются растровым способом, 5х7 точек это совсем грубо, только заглавные буквы, 7х9 получше, уже буквы большие и маленькие и аккуратные. Видел еще экзотический дисплей на ЕС, символ формируется векторно, внутри знакоместа своя развертка, отклоняющая луч в пределах знакоместа. Символы  рисовались кривенькие, да еще с переменной яркостью луча, как бы рукописные.

Чтобы изображение показывать, дисплей имеет оперативную память и знакогенератор. Ну раз уж мы видим целую страницу, естественно иметь возможность содержимое редактировать. Появляется курсор – указатель знакоместа, команды управления им, а также команды сдвига всего экрана – скроллинг по горизонтали и по вертикали. Стандартом команд по факту был VT-52, образец для подражания от DEC. Исполнение этого набора – возможность пользоваться программным обеспечением, позаимствованным у DEC.

Почти единственный способ визуализации на то время – кинескоп. Растр, строчная и кадровая развертки. Необходимость высокого напряжения для кинескопа, 15-20 киловольт, чтобы придать электронам эгергию, достаточную для засвечивания люминофора.

Все разработчики дисплеев действовали в одинаковой логике. Берем кинескоп. Без него никак. Для кинескопа уже есть вся схемотехника, это  телевизор. Копируем, немного улучшим там и тут, укладываемся в требования ТЗ. На троечку, удовлетворительно но не идеально.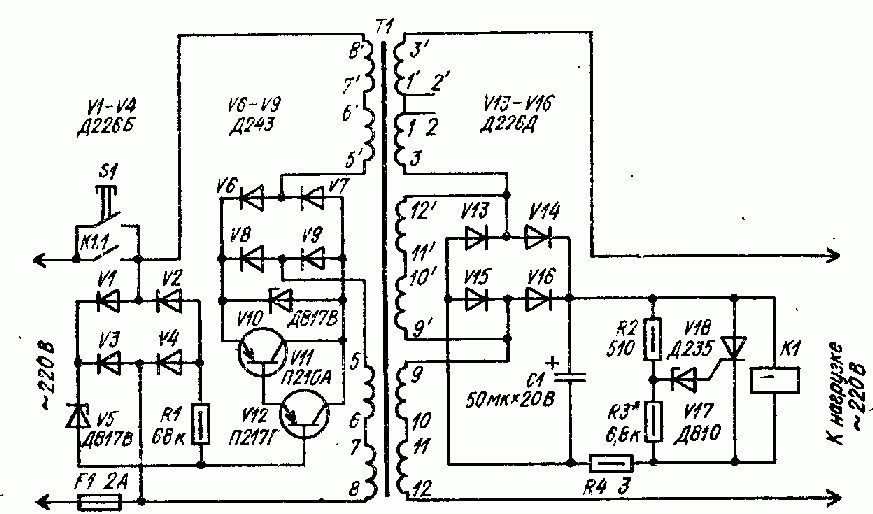 Потому, что бытовой телевизор предназначен для отображения пятен яркости, а дисплей должен рисовать картинку, всю состоящую из мелких четких деталей. Телевизор смотрят с расстояния в метры, а дисплей прямо перед глазами.

Типичное конструктивное исполнение дисплея тех времен– большой железный ящик. Часто моноблок, клавиатура жестко привинчена перед экраном. Кинескоп с небольшим наклоном, “чтобы удобно смотреть”. Кожух заходит вперед на экран, отсекая засветку с боков и сверху. Вот и все.

В принципе, народ был счастлив и такому. Поищите, был обзор дисплея РИН-609. Я его немного пользовал, работать можно. В подтверждение критики “телевизорного” подхода. В документации на РИН было чудесное предупреждение. “Количество одновременно выводимых символов Ш и Щ не должно превышать 80% площади экрана”. Смысл в том, что не хватало тока луча кинескопа. Прочитав такое, удержаться было невозможно. Все зажимали клавишу Щ и ждали, что будет. Ничего ужасного не происходило, так что ограничение было ,видимо, на ресурс. Если долго, днями, держать полный экран Щ, то поплохеет.

Разработчики 15ИЭ не пошли по проторенному пути. Они просто сделали наилучший дисплей, HI-END на тот момент.

Чем отличался 15ИЭ. Он состоял из 3 блоков. Отдельная клавиатура. Отдельный блок “системный”. Отдельный блок индикации на подставке. Рассмотрим подробнее.

Блок индикации. Форма усеченная призма, По бокам ручки-маховички, зажимающие положение по наклону. Подставка с фетровой подошвой позволяет поворачивать экран как удобно, крутить по горизонтали, наклонять по вертикали. Кинескоп специальный, не телевизионный. Длинный, с маленьким углом отклонения луча, лучше геометрия и фокусировка. Вместо “телевизорного” блока строчной развертки с одновременным получением высокого напряжения 2  канала, отдельно  строчная развертка и отдельно формирование высокого напряжения. В каждом свой стабилизатор питания. Как результат,  изображение на экране не плывет совсем. Фокусировка луча электростатическая и электромагнитная. След луча на экране это точка с четким краем, стабильной яркости и размера по всему полю.  Регулировки яркости и фокуса выведены на переднюю панель. Цвет луча зеленый.

Клавиатура неубиваемая. Принцип действия емкостной. Немного громоздкая схема, на каждую клавишу свой транзистор – усилитель.  

Системный блок. Очень похож конструктивно на Электронику -60. Выполнен на таких же разъемах РППМ288, видимо у МЭП их было. В корзине стопка плат. Плата ОЗУ на 565РУ1. Плата знакогенератора. Плата ПЗУ микрокоманд.  Плата логики, микрокомандное управление, специализированная ЭВМ на “чипсете” 155 серии, логическое устройство вроде бы 155ИП3, 4 битное АЛУ, их 2, байтовый компьютер. Не помню точно,  еще были платы синхроимпульсов и интерфейсов. Блок питания надежный и скучный, трансформатор и отдельные каналы 5 вольт и напряжения для блока индикации, не ломался.  В комплекте ЗИП была плата-удлинитель, вроде даже 2, ремонтируемую плату можно было высунуть наружу из корзины.

Специально отдельно подчеркну достоинства.

Великолепная эргономика. Оператору не нужно подстраиваться под дисплей, можно дисплей подстроить под оператора. Моноблок так не подвигаешь и наклона экрана там нет.

Яркая,четкая, совершенно не утомляющая глаза картинка. Отдельное спасибо от многих тысяч пользователей, программистов, инженеров, студентов и школьников

Удобная тактильная клавиатура. Раздолбать ее было тяжело. Клавиатуры других дисплеев герконные или  контактные были гораздо хуже, неоднократно чинил-перепаивал кнопки.

Мгновенное, не замечаемое глазом исполнение команд. Скроллинг по вертикали, по горизонтали – пожалуйста. Результат грамотного проектирования, применения микрокомандного управления. В сравнении с дисплеем ВТА-200, где скроллинг по одной из координат вызывал у наблюдателя просто морскую болезнь, мутило и тошнило. Скроллинг в ВТА осуществлялся программно, с переписью содержимого всего экрана, картинка шла волной.

Ну и технологичность изготовления. Электроника  на печатных платах, на стандартной элементной базе. Доступно для производства среднеквалифицированному персоналу. Сравните с РИН-609, с его чудовищным шифратором на тысяче диодов, с развесистым внутренним монтажом. Как результат, 15ИЭ можно было сделать много, их и сделали довольно много. Позже в ЛЭТИ видел учебный класс, где на рабочих местах стояли сдвоенные индикаторы от 15ИЭ, символьный и  графический один над другим.

Были и недостатки.

Дисплей был тяжелым. Нет, ОЧЕНЬ тяжелым. Корпуса блоков были сделаны из алюминиевого сплава, толстое литье, возможно с фрезеровкой. Спасало только, что для перемещения на другое место дисплей можно было разобрать на 3 части. Так и делали.

Кабели, соединяющие блоки, были отвратительны. Толстые, жесткие и короткие, в белой ПВХ трубке, длина только-только. Разъемы на вид ненадежные, но как-то держались. Один комплект мы даже переделали, сделали подлиннее. Как же стало удобно.

Ну и недостаток, который не был недостатком. Интерфейс дисплея был последовательный . Некоторый аналог СОМа, электрически не напряжением, а током 20 миллиампер, с оптронными развязками. У Электроники-60 последовательного интерфейса не было. Проблема потом решилась, в номенклатуре микросхем ДВК последовательный интерфейс был, но это было уже потом.  Можно сделать последовательный интерфейс на 155 серии, малой-средней интеграции. Так и  сделано в MERA-60, польской версии Электроника-60. У нас же сделали иначе. В наборе 580 была К580ИК51, готовый последовательный интерфейс. Для работы ее нужно было запрограммировать, байт скорость и байт тип посылки, длина, стопбит, четность. Есть выражение “да тут нечего делать, как два байта переслать” Вот и нужно было переслать два байта. Задачу решил, говорят,  студент ЛЭТИ. Его творение называлось DLV. Схема содержала стандартный интерфейс Q-шины для работы с Электроникой-60, К580ИК51 и автомат программирования, счетчик, дешифратор, мультиплексоры, записывающие в К580ИК51  2 байта перемычек.  Автомат запускался сигналом шины RESET. К580ИК51 производилась в двух вариантах корпусов, курамика 48 ножек и пластик DIP, были печатные платы под тот и другой корпус.

Мне тогда удалось добыть немного этих плат, 5-8.. А дальше сочинение”как я провел лето”. Лето, все разъехались, у меня каникулы. Подъем, жарится сковородка картошки. Половина – завтрак. Потом паяем.  Жало паяльника “копыто”, флюс-канифоль на спирте.  Примерно 30 корпусов, еще резисторы-конденсаторы, перемычки. Обед, снова паяем. День на плату. Через неделю в руках пачка интерфейсов. Каждому дисплею по интерфейсу. Укомплектовал свою лабораторию, раздал соседям. Еще один шаг к светлому будущему.

ВЕГА 9 | НЕПАРАЛЛЕЛЬНЫЙ

ВЕГА 9 | НЕПАРАЛЛЕЛЬНЫЙ

google-site-verification = M-cPfZQSZ1sWPTs_G4KhDuCcXTgdHga1DSUhVNbmOrA

Поиск

НЕПАРАЛЛЕЛЬНЫЙ

Артикул:

ЛМ774657

СКП:

843673101052

MPN:

3242-090

Наличие:

В наличии

В настоящее время: 159,95 долларов США

Часто покупают вместе:

• Описание

Описание

Vega — это универсальная обувь с загнутым вниз краем, которая не жертвует комфортом ради производительности. V-образная застежка на липучке обеспечивает идеальную посадку, быструю регулировку и простоту включения/выключения. Полная резиновая подошва RS и промежуточная подошва средней жесткости обеспечивают идеальный баланс трения, чувствительности и жесткости, а окрашенная резина в области носка обеспечивает дополнительное трение при зацепах без ущерба для комфорта в области носка.

Посмотреть всеЗакрыть

• сопутствующие товары
• Клиенты также просмотрели

Сопутствующие товары

В корзину

Быстрый просмотр

ВЕГА 4.5

НЕПАРАЛЛЕЛЬНЫЙ

Сейчас: 159,95 $

Vega — это универсальная обувь с загнутым вниз краем, которая не жертвует комфортом ради производительности. V-образная застежка на липучке обеспечивает идеальную посадку, быструю регулировку и простоту включения/выключения…

Артикул:

ЛМ774648

Наличие:

В наличии

В корзину

Быстрый просмотр

ВЕГА 8

НЕПАРАЛЛЕЛЬНЫЙ

Сейчас: 159,95 $

Vega — это универсальная обувь с загнутым вниз краем, которая не жертвует комфортом ради производительности. V-образная застежка на липучке обеспечивает идеальную посадку, быструю регулировку и простоту включения/выключения…

Артикул:

ЛМ774655

Наличие:

В наличии

В корзину

Быстрый просмотр

ВЕГА 8.

5

НЕПАРАЛЛЕЛЬНЫЙ

Сейчас: 159,95 $

Vega — это универсальная обувь с загнутым вниз краем, которая не жертвует комфортом ради производительности. V-образная застежка на липучке обеспечивает идеальную посадку, быструю регулировку и простоту включения/выключения…

Артикул:

ЛМ774656

Наличие:

В наличии

В корзину

Быстрый просмотр

ВЕГА 9.5

НЕПАРАЛЛЕЛЬНЫЙ

Сейчас: 159,95 $

Vega — это универсальная обувь с загнутым вниз краем, которая не жертвует комфортом ради производительности. V-образная застежка на липучке обеспечивает идеальную посадку, быструю регулировку и простоту включения/выключения. ..

Артикул:

ЛМ774658

Наличие:

В наличии

В корзину

Быстрый просмотр

ВЕГА 13

НЕПАРАЛЛЕЛЬНЫЙ

Сейчас: 159,95 $

Vega — это универсальная обувь с загнутым вниз краем, которая не жертвует комфортом ради производительности. V-образная застежка на липучке обеспечивает идеальную посадку, быструю регулировку и простоту включения/выключения…

Артикул:

ЛМ774665

Наличие:

В наличии

Клиенты также просмотрели

В корзину

Быстрый просмотр

КУЛА ТКАНЬ МЕРЦАЮЩАЯ ПАЛАТКА

ТКАНЬ KULA

Сейчас: $19,99

Kula Cloth™ — первая в своем роде тканевая салфетка многоразового использования с антимикробным покрытием! В условиях дикой природы очень важно соблюдать правила гигиены. \nТрадиционно мы…

Артикул:

ЛМ8

Наличие:

В наличии

В корзину

Быстрый просмотр

Champro Youth Rebel Basketball Jersey Темно-синий Золотой Белый Большой

Чампро

Сейчас: 6,95 $

Баскетбольная майка Champro Rebel Basketball изготовлена ​​из легкой ткани интерлок, состоящей из 100% полиэстера. Он имеет контрастные вставки и окантовку в профессиональных цветовых решениях, скошенные, из собственного материала…

Артикул:

МО1119253

В корзину

Быстрый просмотр

Trimax TRZ6AL-RP Razor 6in Aluminium Adjustable Titch-Dual Ball

Тримакс

Сейчас: $188,95

TRZ6AL-RP — это 6-дюймовая сцепка со штифтом и зажимом, изготовленная из сверхпрочного, на 100% полированного цельного алюминия. Шаровое крепление легко регулируется вверх или вниз с шагом в 1 дюйм. Обеспечивает до 6…

Артикул:

МО4010228

В корзину

Быстрый просмотр

SPELEO II — 9MM X 200′ БЕЛЫЙ

Эдельвейс

Сейчас: 144,99 $

Легкая, малорастяжимая веревка от Edelweiss. Отличная веревка для жонглирования и больших приключений. Прочность на разрыв 19 кН и удлинение 3,6% при весе 80 кг.

Артикул:

ЛМ443376

Наличие:

18.11.2021

Квантовое преимущество унитарных схем Клиффорда с входами в магическом состоянии

• Список журналов
• Proc Math Phys Eng Sci
• PMC6545052

Proc Math Phys Eng Sci. 2019 май; 475(2225): 20180427.

Опубликовано в сети 15 мая 2019 г. doi: 10.1098/rspa.2018.0427

Информация об авторе Примечания к статье Информация об авторских правах и лицензии Отказ от ответственности схемы с входами исключительно в магическом состоянии (схемы CM), дополненные классическими эффективными вычислениями. Мы показываем, что схемы CM сложно классически моделировать с точностью до мультипликативной ошибки (в предположении, что полиномиальная иерархия не коллапсирует), а также до аддитивной ошибки при правдоподобных предположениях о стойкости в среднем случае. В отличие от других подобных известных классов, применим широкий спектр возможных гипотез. Попутно мы даем расширение теоремы Готтсмана-Книлла, которое применимо к универсальным вычислениям, показывая, что для схем Клиффорда с совместными входами стабилизатора и нестабилизатора часть стабилизатора может быть исключена в пользу классического моделирования, оставив схему Клиффорда. только на нестабилизирующей части. Наконец, мы обсудим преимущества реализации схем CM.

Ключевые слова: квантовые вычисления, квантовая теория информации

Фундаментальная цель квантовой теории сложности состоит в том, чтобы доказать, что квантовые компьютеры не могут быть эффективно смоделированы классическими компьютерами. Подход к доказательству этого был предложен Bremner et al.  [1], показывающий, что если бы определенный класс квантовых схем, так называемые схемы IQP, можно было бы эффективно классически смоделировать с точностью до мультипликативной ошибки, то полиномиальная иерархия (PH) рухнула бы. Однако с физической точки зрения более естественно рассматривать классические модели с аддитивным или л ₁ ошибка. В этом ключе Ааронсон и Архипов [2] показали, что при условии справедливости двух правдоподобных гипотез теории сложности квантовый процесс выборки бозонов не может быть эффективно смоделирован с точностью до аддитивной ошибки, если только не происходит PH-коллапс.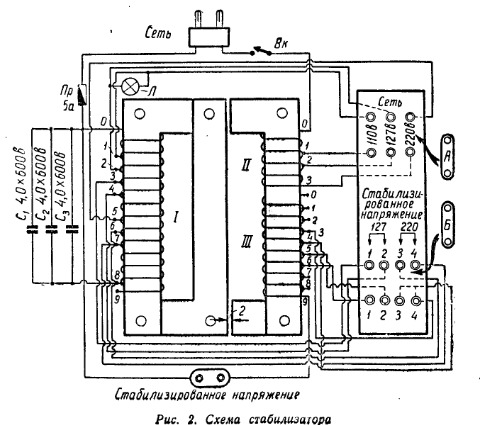 Гипотезы называются гипотезой об антиконцентрации и гипотезой о средней твердости. Бремнер и др. . [3] показали аналогичный результат для контуров IQP, и, кроме того, они смогли доказать гипотезу об антиконцентрации в их контексте. С тех пор аналогичные результаты были получены для различных классов [4–8].

В этой статье мы представляем подкласс квантовых вычислений, который мы называем CM, вдохновленный моделью PBC (вычисления на основе Паули) Bravyi et al . [9], и установить ряд его свойств. Класс CM включает квантовые схемы унитарных вентилей Клиффорда с фиксированным входом | A 〉 ^{⊗ t} (для t линий кубитов), где |A⟩=(1/2)(|0⟩+eiπ/4|1⟩) и с выходом, заданным окончательным измерением некоторого числа кубитов в вычислительной базе. Для вычислительных приложений мы также разрешим классическое вычисление полиномиального времени для помощи до и после запуска схемы Клиффорда, в частности, для определения структуры CM-процесса Cw для каждой вычислительной входной битовой строки в .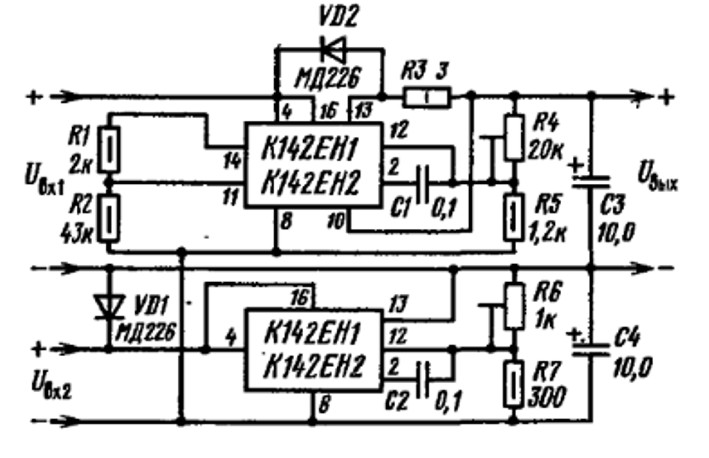 Если бы вентили Клиффорда могли адаптивно зависеть от дальнейших промежуточных измерений (здесь это не разрешено), последняя модель была бы универсальной для квантовых вычислений, но наша модель оказывается слабее, чем универсальная. Наш основной результат состоит в том, чтобы показать, что, тем не менее, этот класс трудно классически моделировать с точностью до аддитивной ошибки, учитывая любую из множества гипотез о стойкости в среднем случае.

Этот результат был показан в недавних работах [4,8] (и наши результаты развивались независимо одновременно), но только для одной конкретной гипотезы твердости. Кроме того, обе статьи доказывают гипотезу об антиконцентрации, используя тот факт, что случайные схемы Клиффорда образуют к — конструкция подходит для к . Идея использования k -планов для доказательства антиконцентрационных гипотез исследована в [10]. В данной работе мы используем другой подход. Мы показываем, что этот класс, хотя и вряд ли будет универсальным, достаточен для эмуляции сложности других классов вычислений, уже известных обладающих желаемыми свойствами, тем самым устанавливая сложность моделирования CM с точностью до аддитивной ошибки при любом из ряда унаследованных сложностей.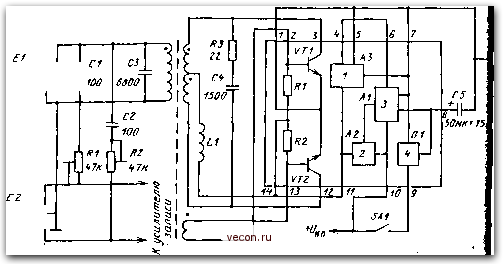 предположения.

Попутно мы также устанавливаем обобщенную форму теоремы Готтсмана-Книлла , а именно . что любое адаптивное вычисление Клиффорда (теперь позволяющее промежуточные измерения) с входными данными σ ⊗ ρ , где σ — состояние стабилизатора, может быть смоделировано адаптивной схемой Клиффорда только на ρ с помощью полиномиального времени. классическая обработка. Этот результат представляет собой перевод модели PBC обратно в модель схемы, но сам по себе представляет значительный концептуальный интерес, применимый также к универсальным квантовым вычислениям. Стандартная теорема Готтсмана–Книлла [11] получается в том случае, когда весь вход является состоянием стабилизатора, и тогда моделирование можно провести полностью классически. Таким образом, для универсальных квантовых вычислений, представленных в модели адаптивных схем Клиффорда с входными данными магического состояния [12], мы можем обменять часть квантовой обработки на классическую обработку, сжимая требования к квантовому пространству, то есть количество необходимых кубитов.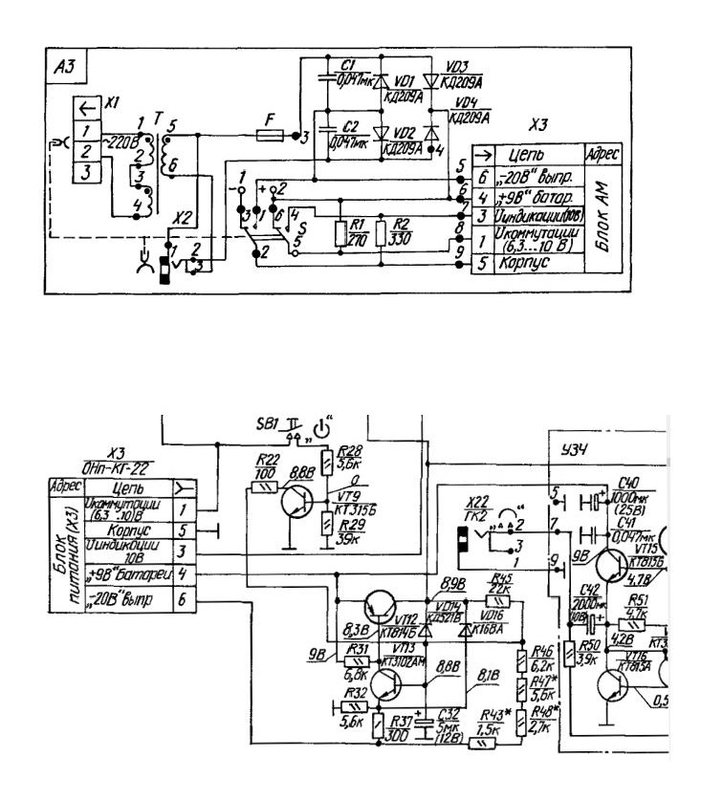

Наконец, мы рассмотрим возможность экспериментальной реализации CM-схем. Это становится все более актуальной темой в связи с ожидаемой неизбежной доступностью небольших квантовых компьютеров, которые могут позволить физическую реализацию квантовых алгоритмов, которые вряд ли можно смоделировать даже на лучших классических компьютерах [13]. Мы показываем, что схемы CM обладают несколькими свойствами, которые могут сделать их выгодными для предполагаемой экспериментальной реализации в ближайшем будущем. Мы показываем, что в модели вычислений на основе измерений (MBQC) при стандартном состоянии графа любая схема CM может быть реализована без адаптаций и, следовательно, может быть реализована на глубине MBQC один. Мы также показываем, что CM имеет хорошие свойства, когда он сделан отказоустойчивым как в модели схемы, так и в модели MBQC: хотя должны выполняться измерения синдрома, нет необходимости применять соответствующие операторы коррекции. Кроме того, в MBQC при заданном начальном состоянии, которое может быть создано в автономном режиме с высокой точностью, CM может быть отказоустойчиво реализован с одним дополнительным временным шагом.

X , Y и Z будут обозначать стандартные 1-кубитные операции Паули, а Pn будет обозначать n -кубитную группу Паули (генерируемую тензорными произведениями 1-кубитных операций Паули). Z i будет обозначать операцию Паули, имеющую Z в строке i th и I во всех остальных строках. Измерения Паули для P∈Pn будут иметь результат ±1. Это относится к Z i тоже измерения, имеющие выходы ±1, а не битовые значения 0 и 1. Мы будем явно указывать, когда последние используются в качестве выходных меток. A Pauli measurement P is said to be dependent on Pauli measurements Q 1 , …,  Q K if P  = ±  Q a 1 1 … Q a K K для некоторых a 1 , …,  a K ∈{0, 1}.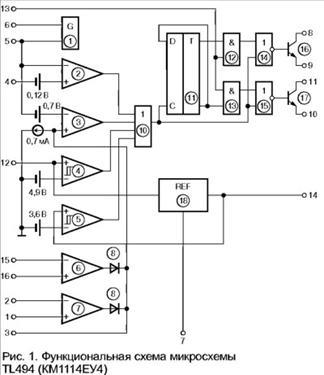 |A⟩ будет обозначать 1-кубитное магическое состояние |A⟩=(1/2)(|0⟩+eiπ/4|1⟩).

Стабилизаторная группа S — это коммутирующая подгруппа группы Pn, не содержащая −I . Чистое состояние из n кубитов |ψ⟩ является чистым стабилизирующим состоянием, если оно стабилизируется каждым элементом группы стабилизаторов S (т.е. S|ψ⟩=|ψ⟩ для всех S∈S), которая имеет n независимых образующих (так что |ψ⟩ однозначно фиксируется S). В общем, n состояние кубита ρ является состоянием смешанного стабилизатора, если оно имеет вид

ρ=12n−s∏I+Si2.

2.1

где S ₁ , …,  S _s с s  ≤  n являются независимыми генераторами группы стабилизаторов S, и все они также могут быть стабилизированы элементами группы стабилизаторов S. как состояние, полученное путем измерения максимально смешанного состояния с (коммутирующими) измерениями S ₁ , …,  S _s и последующий выбор каждого по результату +1.

Всегда предполагается, что унитарные схемы Клиффорда заданы как схемы некоторого выбранного набора одно- и двухкубитных вентилей Клиффорда, достаточных для любой операции Клиффорда, например вентиль Адамара H , управляемый вентиль NOT CX и фазовый вентиль S  = diag(1  i ). Мы также рассмотрим схемы с промежуточными измерениями Z и, возможно, с адаптивным выбором более поздних вентилей, как формализовано в следующем определении.

Мы будем использовать гейт не Clifford T , определенный как T  = diag(1  e ^{iπ /4} ). Хорошо известно, что вентиль T может быть реализован с помощью так называемого гаджета T [11], использующего дополнительную вспомогательную линию кубитов (обозначенную a ) в состоянии | A 〉 и адаптивные операции Клиффорда: чтобы применить T к кубитной линии k в цепи, мы сначала применяем CX _ka с вспомогательным кубитом в качестве целевого кубита, а затем измеряем вспомогательный кубит в Z базис, дающий результат +1 или -1 (всегда с равной вероятностью).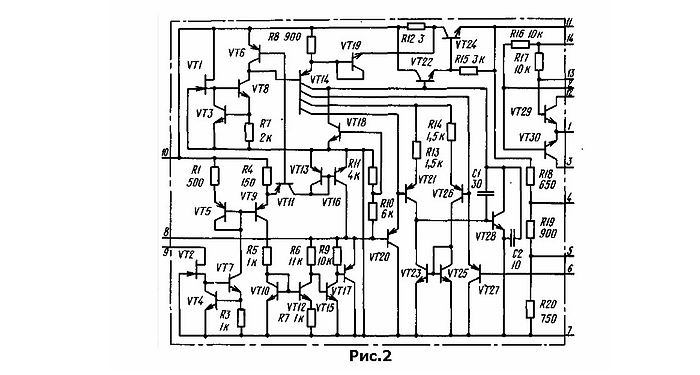 Наконец, к исходной строке кубита применяется поправка S , если результат равен -1. Вспомогательный кубит больше никогда не используется и может быть отброшен. Конечным результатом в каждом случае является применение T к строке k до общей фазы. Также будет полезно отметить, что мы можем реализовать вентиль T ^† , используя аналогичный гаджет: мы выполняем процесс T -gadget, как указано выше, но для окончательной адаптивной коррекции мы вместо этого применяем S ³ исправление, если результат +1.

Операции Клиффорда с вентилями T универсальны для квантовых вычислений. С помощью гаджета T мы видим, что любая (универсально общая) схема, состоящая из вентилей Клиффорда и числа t из T вентилей, может быть переписана как адаптивная схема, состоящая только из вентилей Клиффорда (и промежуточных Z базовых измерений). ) с добавлением t дополнительных линий вспомогательных кубитов, инициализированных в состоянии | А 〉 ^{⊗ т} .

Наконец, мы определим понятие слабого моделирования одного квантового процесса другим, которое мы будем использовать в этой работе.

(Точнее, в приведенных выше определениях границы поли( n ) относятся к ситуации, в которой мы рассматриваем однородное семейство схем, зависящее от ассоциированного параметра n∈N, что будет понятно из контекста, когда необходимо.)

Мы начнем с установления расширенной формы теоремы Готтсмана-Книлла, которая будет использоваться позже при разработке CM-схем.

Стандартная форма теоремы Готтсмана-Нилла утверждает, что любая адаптивная схема Клиффорда со стабилизатором состояния на входе может быть классически эффективно слабо смоделирована [14,15]. Как отмечалось выше, универсальные квантовые вычисления могут быть выполнены с использованием адаптивных схем Клиффорда, которые включают дополнительные (нестабилизирующие) вспомогательные входы состояния |A⟩, что мотивирует рассмотрение схем Клиффорда на таких более общих входных данных. В нашем расширении теоремы Готтсмана – Книлла мы рассматриваем адаптивные схемы Клиффорда, но теперь допускаем, чтобы вход имел нестабилизирующую часть. Мы показываем, что он может быть слабо смоделирован гибридным классически-квантовым процессом, квантовая часть которого (полученная эффективной классической редукцией из описания исходной схемы) представляет собой адаптивную схему Клиффорда, действующую теперь только на нестабилизирующую часть исходной схемы. ввода, тем самым переводя часть исходного вычисления со стабилизатором на вход в эффективное классическое вычисление. В особом случае, когда начальный вход является полностью стабилизирующим состоянием, мы восстанавливаем стандартную теорему Готтсмана-Книлла, поскольку тогда наш гибридный процесс не имеет остаточной квантовой части. Формально это формулируется следующим образом.

Доказательство расширенной теоремы Готтсмана–Книлла будет дано в §3b ниже. Он основан на так называемой модели вычислений на основе Паули (PBC), представленной Bravyi et al . [9]. Перед доказательством теоремы 3.1 мы в §3a дадим описание (слегка обобщенной версии) формализма PBC и его основных особенностей, которые мы будем использовать.

В этой статье будет использована расширенная теорема Готтсмана–Нилла, чтобы показать, что некоторые квантовые схемы могут быть смоделированы с помощью КМ-схем (см. §4). Однако мы ожидаем, что теорема будет представлять самостоятельный интерес, например, для соображений компиляции квантовых схем с как можно меньшим числом кубитов. Действительно, начиная с схемной модели квантовых вычислений, мы можем представить любую схему как схему вентилей Клиффорда и T , а затем использовать T -гаджеты для реализации вентилей T , в результате чего получается адаптивная схема Клиффорда. Такая реализация схемы позволяет исправлять ошибки с помощью стабилизирующих кодов [11], но также увеличивает количество кубитов. Учитывая высокую практическую стоимость добавления дополнительных кубитов, естественно стремиться минимизировать их количество в ближайших устройствах. Расширенная теорема Готтсмана-Книлла дает способ удалить все кубиты, изначально находившиеся в стабилизирующем состоянии, а также любые вспомогательные стабилизаторы. Результирующая схема также является адаптивной схемой Клиффорда, имеющей теперь не более т измерения. Это обобщено в .

Открыть в отдельном окне

Расширенная теорема Готтсмана–Нилла (теорема 3.1) позволяет нам взять универсальную квантовую схему, выраженную в виде схемы Клиффорда с T -устройствами, и сжать ее, используя только классическое полиномиальное время. Это сжатие удаляет все компоненты входного состояния, которые являются стабилизаторами, и результирующая схема представляет собой адаптивную схему Клиффорда с количеством измерений (промежуточных и конечных), не превышающим количество строк в сжатой схеме.

В [16,17] развито другое расширение теоремы Готтесмана–Книлла. Показано, что схема на n кубитных линиях с входом стабилизатора и t T вентили могут быть классически смоделированы во времени экспоненциально в t и полиномиально в n .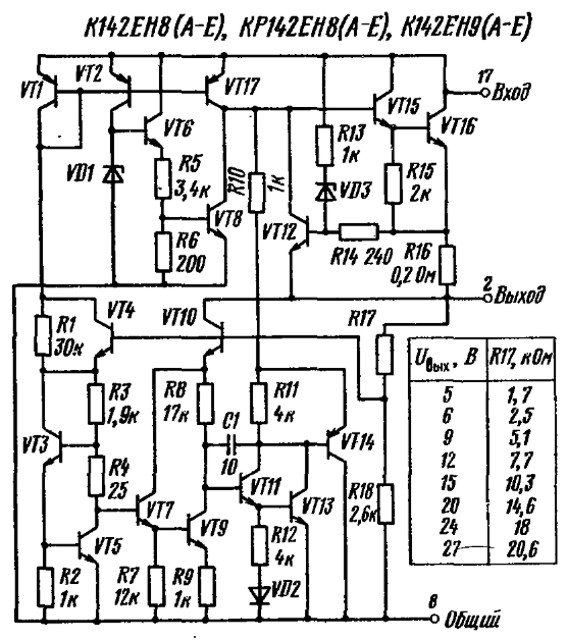 Это сводится к исходной теореме Готтсмана-Книлла, когда t  =  0. Наша расширенная теорема Готтсмана-Книлла дает альтернативное доказательство этого факта: с помощью теоремы 3.1 любое такое вычисление (после замены T вентилей с помощью T -гаджетов) могут быть сжаты до квантовых вычислений на t кубитах, и это может быть и затем классически смоделировано экспоненциально во времени в t .

(a) Модель вычислений, основанная на Паули

Мы приводим доказательство полностью (следуя методу из [9] и расширяя последний для пунктов (ii) и (iii) выше), разделив его на помеченные части. Начнем с двух опорных лемм.

Мы также будем использовать следующий факт, который легко проверяется.

(b) Доказательство расширенной теоремы Готтсмана–Книлла

Схема PBC с общим входным состоянием ρ аналогична адаптивной схеме Клиффорда, хотя и без унитарных шагов вентиля, за исключением того, что измерения являются общими измерениями Паули, а не просто элементарные Z измерения. Соответственно наша расширенная теорема Готтсмана–Книлла 3.1 получается как перевод теоремы 3.3 в стандартную схемную форму.

Мы вводим класс квантовых процессов, который мы называем «Магия Клиффорда», пишется CM.

Наша мотивация для введения и изучения цепей CM двояка. Первая причина, обсуждаемая в §4a, связывает процессы CM с известными результатами классического моделирования. В частности, мы показываем, что класс CM-схем эквивалентен классу квантовых схем, которые, вероятно, обладают сверхклассической мощностью, но при этом слабее, чем BQP. Наша вторая мотивация, обсуждавшаяся в §4b, заключается в том, что схемы CM являются многообещающими кандидатами для экспериментальной проверки квантового преимущества. В отличие от других предложений квантового превосходства, небольшое количество исправлений ошибок может быть легко включено со скромными накладными расходами. Кроме того, добавление адаптивных измерений к процессам CM делает класс универсальным, а также обеспечивает экономию количества необходимых кубитов, как описано ранее в . Таким образом, схемы CM можно рассматривать как практичную ступеньку на пути к реализации универсальных квантовых вычислений.

(a) Связь между схемами Клиффорда и известными результатами классического моделирования

Рассмотрим схемы вида, показанного на . Схемы слева содержат унитарные вентили Клиффорда с входом |0⟩⊗n|A⟩⊗poly(n) и одной измеряемой линией на выходе. Такие схемы известны как классически моделируемые [15]. С другой стороны, если разрешены промежуточные измерения Z вместе с адаптациями, схемы могут выполнять T -гаджеты, что делает их универсальными для вычислений BQP, как показано справа.

Открыть в отдельном окне

Схемы слева имеют магические состояния, а также входы стабилизатора. Однако, если применяется унитарная схема Клиффорда и измеряется только одна линия, она поддается классическому моделированию ( a ). С другой стороны, если включены промежуточные измерения Z и схема может адаптивно зависеть от результатов измерений, тогда схема может выполнять любые вычисления BQP ( b ).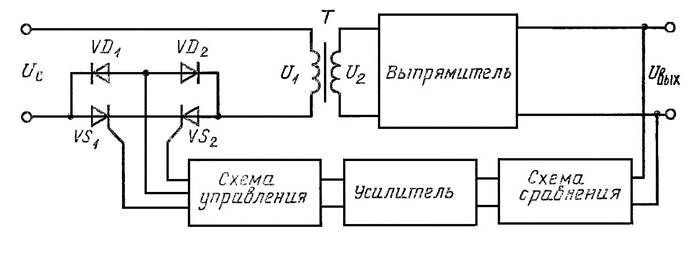

Теперь рассмотрим семейство всех схем Клиффорда с входом |0⟩⊗n|A⟩⊗poly(n) и одной измеряемой линией для конечного выхода, допускающей промежуточные измерения. Обозначим через MI совокупность полученных промежуточных результатов измерений. Тогда мы можем рассмотреть использование MI одним из следующих трех способов:

• (A) Отказ от МИ, и ни в коем случае не использовать его (ни для вывода, ни для адаптаций).

• (B) Сохранение MI как части выходных данных (но не используемых в других целях).

• (C) Использование МИ по мере их появления для последующей адаптации в ходе процесса, а также предоставление МИ как части результата.

Схемы вида (C) могут выполнять любые вычисления BQP, но схемы вида (A) можно моделировать классически [15]. Случай (B) не предполагает полной мощности BQP. Но кроме того, используя методы [15, ср. особенно теоремы 6 и 7 в нем] и при правдоподобных предположениях о сложности) случай (B) также не поддается точному классическому моделированию (ни в сильном, ни в слабом смысле). В этой работе (см. § 5) мы покажем, что, кроме того, он также не поддается классическому моделированию с точностью до мультипликативной или аддитивной ошибки (при правдоподобных предположениях).

Случай (B) явно занимает промежуточное положение между (A) и (C). Действительно, (C) допускает дополнительные возможности адаптации по сравнению с (B), и по сравнению с (A), сохранение MI в (B) дает больше информации о конечном состоянии, которое в (A) было бы назначено как вероятностная смесь всех пост- -состояния измерения, возникающие из всех возможных значений результата для Ми.

Класс цепей CM явно является подмножеством класса цепей в случае (B) , а именно . те, у которых нет части |0⟩ на входе, и все измерения выполняются только в конце. Однако подмножество CM фактически эквивалентно полному классу в (B): каждая схема в последнем может быть слабо смоделирована схемой CM, как следует из применения расширенной теоремы Готтсмана – Книлла. Поскольку промежуточные измерения в случае (B) не являются адаптивными, теорема 3. 1(ii) говорит нам, что результирующая сжатая схема является CM-схемой.

В этом смысле вычислительная мощность класса CM-схем напрямую связана с мощностью сохранения промежуточных измерений в схеме Клиффорда. В § 5 мы доказываем, что схемы КМ не могут быть классически смоделированы (с точностью до мультипликативной или аддитивной ошибки) при правдоподобных предположениях, показывая, что простое сохранение промежуточных результатов измерений, как описано выше, можно рассматривать как своего рода «квантовый ресурс», повышающий классически моделируемый случай (A) к сверхклассической вычислительной мощности в (B).

(b) Экспериментальные преимущества схем Клиффорда

Схемы CM предлагают несколько преимуществ для отказоустойчивой реализации и для реализации в модели MBQC, частично унаследованных от таких преимуществ для схем Клиффорда.

(i) Отказоустойчивость цепей Клиффорда.

В схемной модели отказоустойчивость часто достигается путем замены вентилей T гаджетами T , при этом дистилляция магического состояния используется для создания высокой точности | A 〉 находится в автономном режиме [12]. Однако, поскольку гаджеты T включают в себя адаптацию, схема не может быть полностью создана заранее, и вместо этого часть схемы должна быть создана в режиме реального времени. Это потенциально увеличивает требуемое время когерентности. CM не требуют такого рода адаптации, даже если они сделаны отказоустойчивыми с помощью кода стабилизатора.

Может показаться, что измерения синдрома и связанные с ними корректирующие операции вносят дополнительную адаптацию в схему, но на самом деле этого можно избежать. Действительно, эти поправки являются операциями Паули, и их всегда можно заменить унитарными измерениями Клиффорда и измерениями синдрома (Паули), поскольку измерения Паули в лучшем случае меняют знак при сопряжении с поправками Паули. Тогда поправки Паули могут быть учтены после завершения квантовых вычислений посредством простой классической обработки результатов измерения.

Еще одно преимущество CM-схем, являющихся схемами Клиффорда, заключается в том, что любая такая схема на t кубитных линиях может быть выражена как схема глубины, ограниченная O ( t ² / log t ) [16 ], опять же обеспечивая потенциальные преимущества для более короткого времени когерентности в реализации.

(ii) Цепи Клиффорда в модели MBQC.

В дальнейшем мы будем предполагать следующую стандартную форму MBQC (см., например, [20]). Начальное состояние ресурса — это стандартное состояние кластера. 9Операции 0271 CZ в цепях реализуются путем использования CZ , которые использовались при построении состояния кластера. 1-кубитные измерения, применяемые к состоянию кластера, представляют собой либо Z измерений, либо M ( α ) измерений в базисе {| ±  _α 〉}, где |±α⟩=1/2(|0⟩±e−iα|1⟩). Последние обеспечивают реализацию 1-кубитных вентилей J ( α ) =  H (|0〉〈0| +  e ^Iα | 1 сотрудника 1 |), появляясь как x ^S J ( α ), где S = 0,0271 и и 2777777777777272777777777777777777777777777777777777777777777777777777777712771. и . — связанный оператор побочного продукта. Шиберы J ( α ) вместе с CZ составляют универсальный комплект.

В модели MBQC есть несколько других схем квантового превосходства с малой глубиной [6,22,23]. Однако нашу схему также можно сделать отказоустойчивой на малой глубине следующим образом.

Теперь мы устанавливаем нижние границы сложности классического моделирования цепей CM, допуская либо мультипликативные, либо аддитивные ошибки при моделировании. Сценарий аддитивной ошибки обычно считается разумной моделью того, что можно физически реализовать на практике.

Распределение q ( x ) является ϵ -аддитивной аппроксимацией распределения p ( x ), если

∑x|p(x)−q(x)|≤ϵ.

5.1

Число Y является ϵ -мультипликативной аппроксимацией числа X , если | X  −  Y | ≤  ϵX . Распределение Q ( x ) представляет собой ϵ -Мюльтипиличное приближение A P ( x ), если для каждого x , Q (). ) —) —) —) —) —). мультипликативное приближение p ( x ). Таким образом, очевидно, что ϵ -мультипликативная аппроксимация распределений подразумевает ϵ — аддитивное приближение.

(a) Сложность классического моделирования схем Клиффорда с мультипликативной ошибкой

Хотя (однородные семейства) CM-схемы сами по себе вряд ли будут универсальными для квантовых вычислений, мы сначала установим, что CM-схемы с поствыделением достаточны в качестве квантового ресурса для поствыборки. универсальное квантовое вычисление. Используя аргументы из [1], этого достаточно, чтобы установить, что класс не может быть классически смоделирован с мультипликативной ошибкой, не вызывая коллапса PH.

(b) Исходные данные для случая аддитивной ошибки

Прежде чем рассматривать моделирование цепей CM до аддитивной ошибки, мы сначала наметим общую структуру и аргумент (следуя [2,3], но с некоторым обобщением контекста для наших более поздних целей), что использовался в литературе (например, в [2-4,7,24,25]), чтобы аргументировать сложность классического моделирования, с точностью до аддитивной ошибки, различных классов квантовых вычислительных процессов.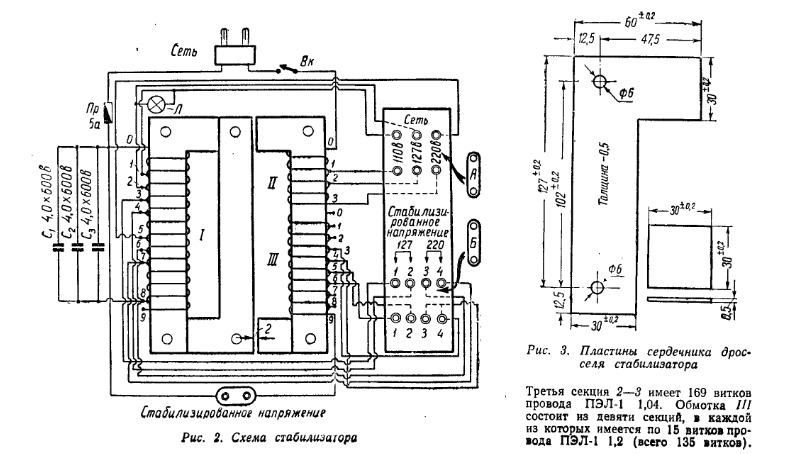

Рассмотрим заданный класс C={Cθ:θ∈Θ} квантовых схем, параметризованных θ ∈ Θ , причем для каждой схемы также указано состояние входа. В общем случае мы будем обозначать количество линий кубитов C _θ через n . Пусть вывод будет назначен по измерению всех линий N и пусть P _θ ( x ) с x ∈ B _{272727272727272727272727272727272727272727272727272727272. 72727272727272727272727272727272. 7272727272727272727272727272727272727272727272. θ .}

Introduce the following computational (sampling) task TC associated with the class C: for any given θ , return ( θ ,  y ) where y ∈ B _n has been sampled согласно выходному распределению p _θ of C _θ . Нас будет интересовать сложность моделирования этой задачи (и некоторых приближенных вариантов) в зависимости от н .

Под ϵ -аддитивным моделированием ошибок задачи TC мы подразумеваем процесс, который при заданных θ возвращает ( θ ,  y ′ ), q _θ на B _n , что является ϵ -аддитивной аппроксимацией распределения p 6 1

Альтернативная задача (которую ни классический, ни квантовый компьютер вряд ли смогут эффективно решить) состоит в том, чтобы вычислить значение для p _θ ( x ) для данных θ и x , с точностью до (соответствующим образом заданной) мультипликативной ошибки. Действительно, для соответствующих классов, которые изучаются в литературе, можно показать, что вычисление таких аппроксимаций в худшем случае является #P трудным. Эта задача имеет вычислительное значение, поскольку для правильно выбранных классов С значения вероятности могут использоваться для представления величин, представляющих независимый физический или математический интерес.

Наша цель состоит в том, чтобы обосновать классическую сложность моделирования задачи выборки TC с точностью до аддитивного приближения. Для этого нам потребуется предположить, что оценка значения p _θ ( x ) с точностью до (подходящей) мультипликативной аппроксимации остается #P трудной не только в худшем случае, но и в среднем -случайная установка следующего вида.

Для каждого класса С и количества линий м ввести комплект

D={(θ,x):Cθ имеет m строк и x∈Bm}.

Для каждого m у нас есть заданная вероятностная мера π на множестве θ , которые встречаются в D, и пусть ν обозначает равномерную вероятностную меру на B _m . Тогда π  ×  ν является мерой произведения на D. Наконец, классу C мы связываем две константы: размер меры 0 <  f  < 1 и допуск на ошибку η .

Введем следующую гипотезу, которую мы будем называть Hardness(C,π).

Обратите внимание, что если π также является равномерной мерой, то подмножества F (для каждого м ) также будут иметь дробный размер f . Но для неоднородных π будут подмножества меры f , которые имеют меньший дробный размер, чем f , и утверждение их твердости #P является более сильной гипотезой. Использование неравномерных распределений также существенно влияет на свойство антиконцентрации, описанное ниже.

Например, в [3] классы схем IQP C , и гипотезы 2 и 3 из [3] могут быть выражены, как указано выше, где π — равномерное распределение, f  = 1/24 и η  = 1/4 +  o ( ). В [26] авторы также рассматривают те же классы схем IQP, но используют неравномерное π . Это приводит к другой гипотезе о средней твердости случая, отличной от тех, что появляются в [3].

Приведенные ниже аргументы будут использовать несколько классов сложности, которые мы опишем здесь в общих чертах таким образом, чтобы было достаточно, чтобы выразить сложность аргумента моделирования. Более полные описания см., например, в [27]. БПП ^NP — это класс задач принятия решений, которые могут быть решены с помощью рандомизированных классических вычислений за полиномиальное время с использованием оракула для любой задачи в NP. FBPP ^NP аналогичен, за исключением того, что выходные данные могут быть битовыми строками, а не одним битом. BPP ^NP находится на третьем уровне башни классов сложности, известной как полиномиальная иерархия PH. P ^#P — класс задач принятия решений, решаемых за классическое полиномиальное время при наличии доступа к оракулу для любой задачи #P; и известно (теорема Тоды), что PH⊆P ^#P .

Теперь предположим, что задача выборки TC может быть решена с точностью до аддитивной ошибки с помощью классического алгоритма A с полиномиальным временем. Первый шаг — показать, что эта возможность выборки подразумевает существование алгоритма FBPP ^NP , который с использованием A , может оценить p _θ ( x ) с точностью до аддитивной ошибки для каждого θ и постоянной доли вариантов x . После этого результат антиконцентрации будет использоваться для преобразования аддитивной ошибки в мультипликативную, по крайней мере, для достаточного числа случаев ( θ ,  x ). Последним шагом является вызов гипотезы средней сложности для C: если наше определение мультипликативной аппроксимации (вычислимое в FBPP ^NP ) #P hard, то P ^#P ⊆P ^{FBPP NP}  = BPP ^НП . Последний класс находится на третьем уровне PH, а затем по теореме Тоды PH схлопнется до третьего уровня. Однако такой коллапс широко рассматривается как крайне неправдоподобный (аналогичный коллапсу NP в P), что обеспечивает правдоподобие того, что предполагаемый классический алгоритм полиномиального времени A для решения TC с точностью до аддитивной ошибки не может существовать (если принять гипотезу о средней твердости ).

Эта лемма легко доказывается, следуя рассуждениям доказательства леммы 4 из [3] с небольшими изменениями в обозначениях.

Чтобы получить мультипликативную ошибку из этой аддитивной, нам потребуется свойство антиконцентрации следующего вида.

В литературе свойство этой формы доказано для некоторых классов C (например, в [3,4,7,26]) и предполагается, что оно выполняется для других (например, в [2]). Доказательства свойства обычно включают применение неравенства Пэли–Зигмунда к вероятностной мере π  ×  ν .

Предположим теперь, что свойство антиконцентрации выполняется для C. Тогда, выбирая δ в лемме 5.3 равным β /2, мы гарантируем перекрытие Ξ⊂D вероятностной меры по крайней мере β /2, на котором свойство антиконцентрации p _θ ( x )/ α ≥1/2 ⁿ и оценка аддитивного приближения уравнения (5.2) выполняются.

Затем подставляя p _θ ( x )/ α для 1/2 ⁿ в уравнении (5.2) оценка приближения становится

pθ(x)poly(n)+(1+o(1))⋅2ϵαβpθ(x),

давая мультипликативную аппроксимацию границы размера (2 ϵ / αβ ) +  o (1) для p _θ θ ( x ) для подмножества 1 .

Наконец, собрав все вышесказанное, приходим к следующему выводу.

Например, в [3] имеем ϵ  = 1/192, а свойство антиконцентрации показано при однородных π , α  = 1/2 и β  1= 1. Таким образом, чтобы получить коллапс PH, нам нужно, чтобы гипотеза средней твердости была верной с допуском ошибки 1/24.

(c) Сложность классического моделирования схем Клиффорда с аддитивной ошибкой

Теперь мы покажем, что схемы CM не могут быть классически эффективно смоделированы с аддитивной ошибкой, если только PH не коллапсирует, учитывая предположения о стойкости в среднем случае. В то время как ранее [4, 8] было показано, что схемы CM обладают этим свойством для одной конкретной гипотезы о среднем случае, здесь мы показываем, что на самом деле применимо большое количество таких гипотез, так что если любая из них доказана, это влечет за собой сложность моделирования схемы CM. Кроме того, в предыдущей работе этот результат твердости для CM был показан с учетом того факта, что ворота Клиффорда образуют 2-дизайн [28] и что 2-дизайн антиконцентрата [5,10], чтобы обеспечить необходимое свойство антиконцентрации. Здесь мы следуем совершенно другому методу, вместо этого используя способность CM-схем (через теорему 3.1) моделировать любую неадаптивную схему. Это позволяет схемам CM моделировать несколько других классов схем (не обязательно 2-схемы) и наследовать их гипотезу о средней стойкости в качестве основы для устойчивости моделирования схемы CM с точностью до аддитивной ошибки.

Рассмотрим любой класс унитарных цепей C={Cθ:θ∈Θ} и ассоциированную меру π на Θ , для которых выполняется подходящее свойство антиконцентрации и чье классическое моделирование с точностью до аддитивной ошибки подразумевало бы коллапс PH, если мы предполагаем Твердость (C, π). Предположим, что эти схемы были выражены как схемы элементов из универсального набора основных элементов Клиффорда с T и T ^† . Мы можем использовать любой выбор такого представления. Теперь рассмотрим расширенный класс ТТ, полученный путем взятия каждой схемы по C _θ и заменив каждые T и T ^† ворота на T или T ^{† 2 в комбинации из 90. Если C _θ имеет t T и T † Гейтс, тогда это приведет к 2 T Цепи в CT, и они могут быть помечены на ( θ , 1 τ ) ( θ , 1 τ ) ( θ , 1 τ )), где θ , 1 τ )) ( θ , 1 τ )). -битная строка, указывающая выбор из Т и Т † . Соответственно пишем CT={Cθ,τ:θ∈Θ, τ∈Bt}.}

CT — это именно тот класс схем, который мы получим, если реализуем схемы Cθ с использованием гаджетов T для каждого логического элемента T и T ^† , но опустим все адаптивные коррекции S логического элемента, которые обычно указываются по T — результаты измерений гаджета. Обозначим эту неадаптивную схему через U _θ с выходами ( x , τ ), где τ ∈ B _T — это строка из измерения GADGET и x ARISES от вывода из 9027 CEROMES и x ARISES из вывода 9027 -CEREMENT и x ARISES от 9027 -C. Каждая из 2 ^t возможностей для τ произойдет с равной вероятностью. Обратите внимание, что схемы U _θ являются унитарными схемами Клиффорда (имеющими только окончательные измерения Z ). Действительно, измерение в пределах любого (как правило, промежуточного) T — гаджет теперь можно переместить в конец цепи, так как на эту линию больше не действуют, а результат измерения не используется ни в каких адаптациях. Поскольку эти схемы являются унитарными схемами Клиффорда, их можно смоделировать с помощью CM-схем, используя теорему 3.1 (ii). Обозначим связанную схему CM (со входным состоянием |A⟩⊗t) как V _θ . Наконец, пусть p _θ ( x ), p _{θ , τ} ( x ) and u _θ ( x ,  τ ) (with x ∈ B _n , τ ∈ B _t ) denote the output probabilities for the circuits C _θ , C _{θ , τ} and U _θ , respectively.

Обратите внимание, что для каждого θ there is a τ ₀  =  τ ₀ ( θ ) for which p _{θ , τ 0} ( x ) =  p _θ ( x ), , а именно . τ ₀ просто указывает варианты T и T ^† , которые фактически встречаются в C _θ . Кроме того, поскольку каждые τ возникают на выходе U _θ with equal probability 1/2 ^t , the relationship between C _{θ , τ} and U _θ gives (via conditional probabilities) :

pθ,τ(x)=uθ(x,τ) 2t.

5,3

Наконец, в дополнение к распределению π на θ , пусть ν и ν ′ обозначают равномерное распределение на x и τ соответственно. Пусть Проблема _{π × ν × ν ′} ( θ , x , τ ). π  ×  ν  ×  ν ′, and similarly for prob _{π × ν ′} ( θ ,  τ ), prob _π ( θ ) etc.

Мы покажем, что для некоторых классов цепей C, уже доказанных, что они обладают свойством аддитивной устойчивости моделирования из теоремы 5.4 (с учетом соответствующей гипотезы Hardness(C,π)), что CT не содержит новых схем, которых еще не было. в C. Таким образом, метки ( θ ,  τ ) будут обозначать схемы C с обычно высокой избыточностью, и мы пишем CT = C в этой ситуации. Поскольку такие схемы могут быть смоделированы схемами CM, классическое моделирование цепей CM с точностью до аддитивной ошибки может затем подразумевать коллапс PH в соответствии с гипотезой Hardness (C, π) класса C, как будет формализовано в теореме ниже.

Предположим теперь, что C=CT. Тогда для каждого ( θ ,  τ ) существует θ~=θ~(θ,τ) с C _{θ , τ} является Cθ~ поэтому

pθ,τ(x)=pθ~(x).

Нам также потребуется следующее θ -выборочное отношение: C _θ цепей, многократно встречающихся в CT, встречаются в CT с той же вероятностью (относительно распределения π  ×  ν ) в C (относительно распределения π ):

∑(θ,τ):θ~(θ,τ)=θ0probπ×ν′(θ,τ)=probπ(θ0).

5.4

Примеры классов цепей в литературе, для которых выполняется подходящее свойство антиконцентрации, C=CT и θ — уравнение отношения выборки (5.4) выполняется, включая следующее.

Цепи CM, имитирующие любой из этих трех классов, наследуют твердость исходных цепей. Если для любого из них показана средняя твердость, то это означает, что то же самое верно и для цепей CM, и, следовательно, CM не может быть эффективно смоделирован классически с точностью до аддитивной ошибки. Этот результат является естественным следствием расширенной теоремы Готтсмана-Книлла, которая показывает, как схемы CM могут моделировать другие типы квантовых вычислений.

Для других классов цепей мы обычно имеем C≠CT, т. е. CT содержит цепи, которых еще не было в C. Однако, если CT также обладает подходящим свойством антиконцентрации, то с точностью до предположения о твердости в среднем случае PH будет разрушается, если цепи ТТ могут быть классически смоделированы с аддитивной ошибкой. Обратите внимание, что если C имеет результат жесткости в наихудшем случае (как это обычно бывает для рассматриваемых классов), то то же самое имеет и CT, поскольку его схемы всегда образуют надмножество C. Это свидетельствует в пользу аналогичной гипотезы о среднем случае для CT. Следовательно, в случае, когда CT также антиконцентрирует, его также, вероятно, будет трудно смоделировать классически. Для любого C схемы в CT всегда могут быть смоделированы схемами CM (в смысле выше, используемом в теореме 5. 5, с равномерным распределением по τ , как указано выше), и мы получаем следующий результат.

Одним из примеров схем, для которых C⊊CT и CT также являются антиконцентраторами, является класс сопряженных схем Клиффорда , введенный в [4]. Здесь мы имеем схемы вида V ^{⊗ n †} UV ^{⊗ n} , где V — любая фиксированная 1-кубитная схема U получить класс за каждый выбор V ), и π — равномерное распределение. Представление V в виде вентилей Clifford+T+T ^† обычно содержит вентили T и T ^† , и когда они переназначаются во всех комбинациях в 72 72 708 ⊂ 8 , результатом уже не обязательно будет вентиль вида W ^{⊗ n} , т. е. вентили, применяемые на разных линиях, в общем случае будут разными, и n -кубитный вентиль на одном конце также не обязательно будет инверсия того, что на другом конце. Следовательно, C⊊CT. Однако этот новый класс цепей действительно антиконцентрирован. Это следует из оригинального доказательства антиконцентрации в [4, лемма 4.3 там], которое все еще применимо для произвольных n — кубитовые вентили, заменяющие V ^{⊗ n} и V ^{⊗ n †} на концах.

Мы ожидаем, что будут другие классы, к которым может быть применена теорема 5.6, обеспечивающая дальнейшие соответствующие предположения о средней твердости, которых достаточно, чтобы классически моделировать схемы CM было трудно с точностью до аддитивной ошибки. Это связано с тем, что обычная стратегия доказательства того, что класс цепей антиконцентрируется, состоит в том, чтобы показать, что это ϵ -аппроксимировать 2-схемы, а затем использовать результат [5,10], что такие 2-схемы обладают свойством антиконцентрации. В этом ключе следующая гипотеза, если она верна, была бы полезным результатом.

Класс схемы CT зависит от выбора представления схемы в C в терминах Клиффорда + T + T ^† вентилей. Если бы гипотеза 5.7 была верна только для одного выбора такого представления для (C,π), который является ϵ -приближенным 2 планом, то выводы теоремы 5.6 будут применимы.

Благодарим М. Бремнера и А. Монтанаро за полезные обсуждения и разъяснения. Мы благодарим Рюхея Мори и анонимного рецензента за то, что они указали нам на подход (b) в теореме 5.1. Мы признательны Мему Фоксу за предложенную терминологию.

Эта статья не содержит никаких дополнительных данных.

Все авторы в совместной работе внесли существенный вклад в концепцию и подготовку этой работы. Все авторы дали окончательное согласие на публикацию.

Мы заявляем, что у нас нет конкурирующих интересов.

Мы признательны за поддержку QuantERA ERA-NET Cofund в области квантовых технологий, реализованной в рамках программы Европейского Союза Horizon 2020 (проект QuantAlgo) и управляемой посредством гранта EPSRC №. ЕР/R043957/1. МОЙ. поддерживается австралийской программой стипендий Кембриджа Брэгга, а SS — программой стипендий Leverhulme Early Career Fellowship.

1. Бремнер М.Дж., Йожа Р., Шеперд Д.Дж. 2011. Классическое моделирование коммутирующих квантовых вычислений предполагает коллапс полиномиальной иерархии. проц. Р. Соц. А 467, 459–472. ( 10.1098/rspa.2010.0301) [CrossRef] [Google Scholar]

2. Ааронсон С., Архипов А. 2011. Вычислительная сложность линейной оптики. В проц. 43-го ежегодного симпозиума ACM по теории вычислений — STOC ’11 , с. 333. Нью-Йорк, штат Нью-Йорк, США: ACM Press.

3. Бремнер М.Дж., Монтанаро А., Шеперд Д.Дж. 2016. Средняя сложность по сравнению с приближенным моделированием коммутирующих квантовых вычислений. физ. Преподобный Летт. 117, 080501 ( 10.1103/PhysRevLett.117.080501) [PubMed] [CrossRef] [Google Scholar]

4. Bouland A, Fitzsimons JF, Koh DE. 2017 Квантовое преимущество сопряженных схем Клиффорда. (http://arxiv.org/abs/1709.01805.)

5. Манн Р.Л., Бремнер М.Дж. 2017 О сложности случайных квантовых вычислений и многочлене Джонса. (http://arxiv.org/abs/1711.00686. )

6. Миллер Дж., Сандерс С., Мияке А. 2017. Квантовое превосходство в вычислениях на основе измерений с постоянным временем: унифицированная архитектура для выборки и проверки. физ. Преп. А 96, 062320 ( 10.1103/PhysRevA.96.062320) [CrossRef] [Google Scholar]

7. Моримае Т. 2017. Сложность классической выборки модели с одним чистым кубитом с постоянной общей ошибкой вариационного расстояния. физ. Преп. А 96, 040302 (10.1103/PhysRevA.96.040302) [CrossRef] [Google Scholar]

8. Pashayan H, Bartlett SD, Gross D. 2017 От оценки квантовых вероятностей к моделированию квантовых цепей. (http://arxiv.org/abs/1712.02806. )

9. Бравый С., Смит Г., Смолин Ю.А. 2016. Торговля классическими и квантовыми вычислительными ресурсами. физ. Версия X 6, 021043 ( 10.1103/physrevx.6.021043) [CrossRef] [Google Scholar]

10. Ханглейтер Д., Бермехо-Вега Дж., Шварц М., Эйзерт Дж. 2015 Теоремы против концентрации для схем, показывающих квантовое ускорение. (http://arxiv.org/abs/1706. 03786.)

11. Нильсен М., Чуанг И. 2010. Квантовые вычисления и квантовая информация, 10-е изд. Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar]

12. Бравый С, Китаев А. 2004. Универсальное квантовое вычисление с идеальными вентилями Клиффорда и зашумленными помощниками. физ. Преп. А 71, 022316 ( 10.1103/PhysRevA.71.022316) [CrossRef] [Google Scholar]

13. Харроу А.В., Монтанаро А. 2017. Квантовое вычислительное превосходство. Природа 549, 203–209. ( 10.1038/nature23458) [PubMed] [CrossRef] [Google Scholar]

14. Готтесман Д. 2008 Гейзенберговское представление квантовых компьютеров. (http://arxiv.org/abs/quant-ph/9807006.)

15. Джожа Р., Ван ден Нест М. 2013. Классическая сложность моделирования расширенной схемы Клиффорда. Квантовая инф. вычисл. 14, 9–10. (https://arxiv.org/abs/1305.6190) [Google Scholar]

16. Ааронсон С., Готтесман Д. 2004. Улучшено моделирование цепей стабилизатора. физ. Преп. А 70, 052328 ( 10. 1103/PhysRevA.70.052328) [CrossRef] [Google Scholar]

17. Бравый С., Госсет Д. 2016. Улучшенное классическое моделирование квантовых схем, в которых преобладают вентили Клиффорда. физ. Преподобный Летт. 116, 250501 ( 10.1103/PhysRevLett.116.250501) [PubMed] [CrossRef] [Google Scholar]

18. Preskill J. 2018. Конспект лекций по физике 219/информатике 219 Квантовые вычисления. Пасадена, Калифорния: Калифорнийский технологический институт. [Google Scholar]

19. Йодер Т.Дж. 2012. Обобщение формализма стабилизатора для моделирования произвольных квантовых схем. См. http://www.scottaaronson.com/showcase2/report/ted-yoder.pdf.

20. Данос В., Кашефи Э., Панангаден П. 2007. Измерительный исчисление. Дж. АКМ 54, 8 (10.1145/1219092) [CrossRef] [Google Scholar]

21. Рауссендорф, Роберт и Браун, Даниэль Э., Бригель, Ханс Дж. 2003. Квантовые вычисления на основе измерений состояний кластеров. физ. Преп. А 68, 022312 (10.1103/PhysRevA.68.022312) [CrossRef] [Google Scholar]

22. Gao X, Wang S-T, Duan L-M. 2017. Квантовое превосходство для моделирования трансляционно-инвариантной модели спина Изинга. физ. Преподобный Летт. 118, 040502. [PubMed] [Google Scholar]

23. Ханглейтер Д., Бермехо-Вега Дж., Шварц М., Эйзерт Дж. 2018. Теоремы антиконцентрации для схем, демонстрирующих квантовое ускорение. квант 2, 65. [Google Scholar]

24. Буланд А., Фефферман Б., Нирхе К., Вазирани У. 2018 Квантовое превосходство и сложность выборки случайных цепей. (http://arxiv.org/abs/1803.04402.)

25. Фефферман Б., Уманс К. 2015 О мощности квантовой выборки Фурье. (http://arxiv.org/abs/1507.05592.)

26. Бремнер М.Дж., Монтанаро Р., Шеперд Д.Дж. 2016 Достижение квантового превосходства с помощью разреженных и шумных коммутирующих квантовых вычислений. (http://arxiv.org/abs/1610.01808.)

27. Арора С., Барак Б. 2009. Вычислительная сложность: современный подход. Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar]

28. Данкерт С., Клив Р., Эмерсон Дж., Ливайн Э. 2009. Точные и приближенные унитарные 2-планы и их применение для оценки точности. физ. Преп. А 80, 012304 (10.1103/PhysRevA.80.012304) [CrossRef] [Google Scholar]

29. Бойшо С., Исаков С.В., Смелянский В.Н., Баббуш Р., Дин Н., Цзян З., Бремнер М.Дж., Мартинис Дж.М., Невен Х. 2016 Характеристика квантового превосходства в ближайших устройствах. (http://arxiv.org/abs/1608.00263.)

---

Статьи из сборников. Математические, физические и инженерные науки предоставлены здесь с разрешения The Royal Society

---

[PDF] Схемы нормализаторов и теорема Готтесмана-Книлла для бесконечномерных систем

• title={Схемы нормализаторов и теорема Готтсмана-Книлла для бесконечномерных систем}, автор={Хуан Бермехо-Вега и Седрик Йен-Ю Лин и Маартен Ван ден Нест}, журнал={Квантовая инф. вычисл.}, год = {2016}, объем = {16}, страницы = {361-422} }
  • J. Bermejo-Vega, Cedric Yen-Yu Lin, M.V.D. Nest
  • Опубликовано 10 сентября 2014 г.
  • Mathematics
  • Quantum Inf. вычисл.

  $\textit{Схемы-нормализаторы}$ [1,2] — обобщенные схемы Клиффорда, действующие на произвольные конечномерные системы $\mathcal{H}_{d_1}\otimes … \otimes \mathcal{H} _{d_n}$ со стандартным базисом, помеченным элементами конечной абелевой группы $G=\mathbb{Z}_{d_1}\times… \times \mathbb{Z}_{d_n}$. Вентиляторы нормализатора реализуют операции, связанные с группой $G$, и могут быть трех типов: квантовые преобразования Фурье, вентили группового автоморфизма и квадратичные фазовые вентили. В этой работе мы… 

  View PDF on arXiv

  The computational power of normalizer circuits over black-box groups

  • J. Bermejo-Vega, Cedric Yen-Yu Lin, M. V. D. Nest

  • Computer Science, Mathematics

    ArXiv

  • 2014

  В этой работе представлена ​​точная связь между схемами Клиффорда, алгоритмом факторизации Шора и несколькими другими известными квантовыми алгоритмами с экспоненциальным квантовым ускорением для решения абелевых задач со скрытыми подгруппами, а также обнаружено, что схемы нормализаторов достаточно эффективны для факторизации и решения классически трудных задач. проблемы в настройке черного ящика.

  О топологических квантовых вычислениях с представлениями групп классов отображений

  Доказано, что для абелевых энионов все элементы из этих представлений групп классов отображений являются вентилями-нормализаторами, что позволяет использовать это кодирование для топологических квантовых вычислений с использованием квантовых представлений групп классов отображений. эффективно моделируется на классическом компьютере.

  Непрерывные симметрии и приближенная квантовая коррекция ошибок

  • П. Фаист, Сепер Незами, Дж. Прескилл

  • Информатика

    Physical Review X

  • 2020

  Этот подход позволяет понять, как эволюция времени в балке соответствует эволюции времени на границе, не нарушая теоремы Истина-Нилла, а пятироторный код может складываться для формирования ковариантного голографического кода.

  Схемы нормализаторов и квантовые вычисления

  • J. Bermejo-Vega

  • Физика, информатика

    ArXiv

  • 2016

  Эффективный формализм для моделирования семейств квантовых схем, которые не являются универсальными, но содержат важные квантовые элементы, такие как QFT или CNOT, разработан и используется для разработки новых алгоритмов, обеспечивающих квантовое ускорение.

  Abelian Hypergroups and Quantum Computation

  • J. Bermejo-Vega, K. Zatloukal

  • Mathematics

    ArXiv

  • 2015

  A stabilizer formalism using abelian hypergroups and an associated classical simulation theorem is developed and a new , разработан гипергрупповой алгоритм для HNSP на нильпотентных группах.

  Модели многих тел для топологической квантовой информации

  • Кортни Г. Брелл

  • Физика

  • 2014

  Мы разрабатываем и исследуем несколько квантовых спиновых моделей многих тел, используемых для обработки и хранения топологической квантовой информации. Эти модели делятся на две грубые категории: те, которые…

  Контекстуальность как ресурс для моделей квантовых вычислений с кубитами.

  • Дж. Бермеджо-Вега, Николас Дельфосс, Д. Браун, К. Окей, Р. Рауссендорф

  • Физика

    Физические обзорные письма

  • 2017

  Эта работа устанавливает контекстуальность магических состояний как необходимый ресурс для большого класса схем квантовых вычислений на кубитах для квантовых вычислений на основе измерений.

  Надежное кодирование кубита в молекуле

  • Виктор В. Альберт, Дж. Кови, Дж. Прескилл

  • Физика

    Physical Review X

  • 2020
  8 90 кодов, исправляющих квантовые ошибки конечномерное кодовое пространство в бесконечномерном гильбертовом пространстве состояний вращательных состояний твердого тела. Эти коды, которые защищают…

  Обобщенные кластерные состояния, основанные на конечных группах

  • Кортни Г. Брелл

  • Математика

  • 2015

  Мы определяем обобщенные кластерные состояния на основе конечных групповых алгебр обобщения квантово-торического кода до квантово-торического обобщения кода двойные модели. Для этого мы показываем общий…

  ПОКАЗЫВАЕМ 1-10 ИЗ 109 ССЫЛОК

  СОРТИРОВАТЬ ПОРелевантность Наиболее влиятельные документыНедавность

  Улучшенное моделирование цепей стабилизатора

  • S. Aaronson, D. Gottesman

  • Информатика

    ArXiv

  • 2004

  и фазовые вентили могут быть эффективно смоделированы на классическом компьютере, усовершенствованы в нескольких направлениях.

  Вычислительная мощность схем нормализатора над группами черного ящика

  • Дж. Бермеджо-Вега, Седрик Йен-Ю Лин, М. В. Д. Нест

  • Информатика, математика

    ArXiv

  • 2014

  В этой работе представлена ​​точная связь между схемами Клиффорда, алгоритмом факторинга Шора и несколькими другими известными квантовыми алгоритмами с экспоненциальным квантовым ускорением для решения абелевых задач со скрытыми подгруппами, и обнаруживает, что схемы нормализаторов достаточно мощны, чтобы факторизовать и решать классически сложные задачи в условиях черного ящика.

  Классическое моделирование схем нормализатора абелевой группы с промежуточными измерениями

  Эта работа показывает, что схемы нормализаторов, дополненные промежуточными измерениями, также могут быть эффективно смоделированы классическим способом, даже когда вычисления проходят адаптивно, и дает обобщение теоремы Готтесмана-Книлла для квантовых схем, описываемых произвольными конечными абелевыми группами.

  Эффективное классическое моделирование квантовых преобразований Фурье и схем нормализаторов над абелевыми группами

  • М. В. Д. Нест

  • Информатика, математика

    Квантовая инф. вычисл.

  • 2013

  В этой статье доказывается, что все схемы нормализаторов имеют полиномиальное время классического моделирования, и обобщается теорема Готтсмана-Книлла, которая доказывает, что схемы Клиффорда для d-уровневых кудитов возникают как схемы нормализаторов над группой Zdm.

  Формализм линеаризованного стабилизатора для систем конечной размерности

  Получено простое доказательство того, что моделирование схем стабилизатора на n кудитах, включающее любое постоянное число раундов измерений, является полным для класса сложности coModdL и может быть смоделировано за O(log( n)2)-глубинные схемы для любой константы d ≥ 2,

  Метод Эпсилон-сети для оптимизации сепарабельных состояний

  • Яоюнь Ши, Сяоди Ву

  • Информатика, Математика

    Теор. вычисл. науч.

  • 2015

  Классическое моделирование квантовых вычислений, теорема Готтесмана-Книлла и немного больше

  Показано, как каждую схему Клиффорда можно свести к эквивалентной явно моделируемой схеме (нормальная форма), которая обеспечивает простую доказательство теоремы Готтсмана-Книлла без использования стабилизаторов.

  Классическое моделирование квантовых вычислений, теорема Готтесмана-Книлла и несколько более отправная точка.

  Мы показываем, как каждую схему Клиффорда можно свести к эквивалентной, очевидно моделируемой…

  Квантовые вычисления: алгоритмы и коррекция ошибок

  • Китаев А.

  • Информатика

  • 1997

  В книге обсуждаются классические модели вычислений, квантовый формализм, симплекто-классические случаи и исправление ошибок в вычислительном процессе: общие принципы.

  Проверка сдвиговой эквивалентности полиномов с помощью детерминированных, вероятностных и квантовых машин

  • Д. Григорьев

  • Математика

    Теор. вычисл. науч.

  • 1997

  От оценки квантовых вероятностей к моделированию квантовых схем – Quantum

  Изучение классической моделируемости квантовых схем открывает многообещающий путь к пониманию вычислительной мощности квантовых систем. Можно ли эффективно смоделировать класс квантовых цепей с помощью вероятностного классического компьютера или же его трудно смоделировать, в значительной степени зависит от точного понятия «классического моделирования» и, в частности, от требуемой точности. Мы утверждаем, что понятие классического моделирования, которое мы называем EPSILON-симуляцией (или $\epsilon$-симуляцией для краткости), отражает суть обладания «эквивалентной вычислительной мощностью» моделируемой квантовой системы: это статистически невозможно. отличить агента, имеющего доступ к $\epsilon$-симулятору, от агента, обладающего симулируемой квантовой системой. Мы связываем $\epsilon$-моделирование с различными альтернативными понятиями моделирования, преимущественно фокусируясь на симуляторе, который мы называем $\textit{poly-box}$. Полибокс выводит аддитивные оценки вероятностей и маргиналов Борна с точностью $1/poly$. Это понятие моделирования получило известность благодаря ряду недавних результатов моделирования. Принимая некоторые правдоподобные предположения теории вычислений, мы показываем, что $\epsilon$-моделирование строго сильнее, чем поли-бокс, показывая, что схемы IQP и схемы Клиффорда с инъекцией магического состояния в безусловном состоянии трудно $\epsilon$-симулировать, но они все же допускают полибокс. Напротив, мы также показываем, что эти два понятия эквивалентны при дополнительном предположении о разреженности выходного распределения ($\textit{poly-sparsity}$).

  @article{Pashayan2020fromestimationof, дои = {10.22331/q-2020-01-13-223}, URL = {https://doi.org/10.22331/q-2020-01-13-223}, title = {От оценки квантовых вероятностей до моделирования квантовых схем}, автор = {Пашаян, Хакоп и Бартлетт, Стивен Д. и Гросс, Дэвид}, журнал = {{квант}}, иссн = {2521-327X}, издатель = {{Verein zur F{\»{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, громкость = {4}, страницы = {223}, месяц = ​​янв, год = {2020} }

  [1] Р. П. Фейнман, Моделирование физики с помощью компьютеров, Int. Дж. Теор. Phys., 21, 467–488 (1982).
  https://​/doi.org/​10.1007/​BF02650179

  [2] Ааронсон С., Готтесман Д. Улучшенное моделирование схем стабилизаторов // Физ. Ред. А, 70, 052328 (2004).
  https://​/​doi.org/​10. 1103/​PhysRevA.70.052328

  [3] Л. Г. Валиант, «Квантовые схемы, которые можно классически моделировать за полиномиальное время», SIAM Journal on Computing, 31, 1229– 1254 (2002).
  https://​/​doi.org/​10.1137/​S0097539700377025

  [4] Терхал Б.М., Ди Винченцо Д.П. Классическое моделирование квантовых цепей с невзаимодействующими фермионами // Физ. Ред. А 65, 032325 (2002).
  https://​/doi.org/​10.1103/​PhysRevA.65.032325

  [5] Бартлетт С.Д., Сандерс Б.С., Браунштейн С.Л., Немото К. Эффективное классическое моделирование квантовых информационных процессов с непрерывной переменной. «Физ. Преподобный Летт. 88, 097904 (2002).
  https://​/doi.org/​10.1103/​PhysRevLett.88.097904

  [6] Л. Гурвиц, «О сложности смешанных дискриминантов и родственных проблемах», в: Jedrzejowicz J., Szepietowski A. (редакторы) Математические основы информатики 2005. MFCS 2005. Конспект лекций по информатике, том 3618. Springer, Берлин, Гейдельберг (2005).
  https://​/doi. org/​10.1007/​11549345_39

  [7] Ааронсон С., Архипов А. Вычислительная сложность линейной оптики // Материалы сорок третьего ежегодного симпозиума ACM. по теории вычислений, 333–342, ACM (2011).
  https://doi.org/10.1145/1993636.1993682

  [8] M.J. Bremner, R. Jozsa, and D.J. Shepherd, «Классическое моделирование коммутирующих квантовых вычислений подразумевает коллапс полиномиальной иерархии», Proc. . Р. Соц. А 467, (2010).
  https://​/​doi.org/​10.1098/​rspa.2010.0301

  [9] M.J. Bremner, A. Montanaro, and D.J. Shepherd, «Средняя сложность в сравнении с приближенным моделированием коммутирующих квантовых вычислений», Phys. Преподобный Летт. 117, 080501 (2016).
  https://​/​doi.org/​10.1103/​PhysRevLett.117.080501

  [10] X. Gao, S.-T. Ван и Л.-М. Дуан, «Квантовое превосходство для моделирования трансляционно-инвариантной модели спина Изинга», Phys. Преподобный Летт. 118, 040502 (2017).
  https://​/​doi.org/​10.1103/​PhysRevLett.118.040502

  [11] J. Bermejo-Vega, D. Hangleiter, M. Schwarz, R. Raussendorf, and J. Eisert, «Архитектуры для квантового моделирования, демонстрирующие квантовое ускорение», Phys. Ред. X 8, 021010 (2018).
  https://​/doi.org/​10.1103/​PhysRevX.8.021010

  [12] Б. Фефферман и К. Уманс, «Мощь квантовой выборки Фурье», препринт arXiv arXiv:1507.05592, (2015 г.) ).
  arXiv:1507.05592

  [13] T. Morimae, K. Fujii, and J. F. Fitzsimons, «Трудность классического моделирования модели с одним чистым кубитом», Phys. Преподобный Летт. 112, 130502 (2014).
  https://​/doi.org/​10.1103/​PhysRevLett.112.130502

  [14] T. Morimae, K. Fujii, and H. Nishimura, Power of one nonclean qubit, Phys. Ред. А 95, 042336 (2017).
  https://​/​doi.org/​10.1103/​PhysRevA.95.042336

  [15] Бойшо С., Исаков С.В., Смелянский В.Н., Баббуш Р., Дин Н., Цзян З., Бремнер М.Дж., Мартинис Дж.М. и Х. Невен, «Характеризуя квантовое превосходство в ближайших устройствах», Nature Phys. 14, 595-600 (2018).
  https://​/​doi. org/​10.1038/​s41567-018-0124-x

  [16] A. Bouland, JF Fitzsimons, and D.E. Koh, «Классификация сложности сопряженных цепей Клиффорда», на 33-й конференции по вычислительной сложности (CCC 2018) (RA Servedio, ed.), vol. 102 of Leibniz International Proceedings in Informatics (LIPIcs), (Dagstuhl, Germany), стр. 21:1–21:25, Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik, 2018.
  https://​/​doi.org/​ 10.4230/​LIPIcs.CCC.2018.21

  [17] Д. Дж. Брод, «Эффективное классическое моделирование схем спаривания с обобщенными входами и измерениями,» Phys. Версия А 93, 062332 (2016).
  https://​/doi.org/​10.1103/​PhysRevA.93.062332

  [18] Р. Джожа и А. Мияке, «Спичгейты и классическое моделирование квантовых схем», Proc. Р. Соц. А 464, 3089–3106 (2008).
  https://​doi.org/​10.1098/​rspa.2008.0189

  [19] Вейч В., Ферри К., Гросс Д., Эмерсон Дж. Отрицательная квазивероятность как ресурс для квантовые вычисления», New J. Phys. 14, 113011 (2012).
  https://​/​doi. org/​10.1088/​1367-2630/​14/​11/​113011

  [20] В. Вейч, Н. Вибе, К. Ферри и Дж. Эмерсон, «Эффективная схема моделирования для класса экспериментов по квантовой оптике с неотрицательным представлением Вигнера», New J. Phys. 15, 013037 (2013).
  https://​/​doi.org/​10.1088/​1367-2630/​15/​1/​013037

  [21] А. Мари и Дж. Эйзерт, «Положительные функции Вигнера отображают классическое моделирование квантовых вычислительная эффективность,» Phys. Преподобный Летт. 109, 230503 (2012).
  https://​/​doi.org/​10.1103/​PhysRevLett.109.230503

  [22] С. Брави и Д. Госсет, «Улучшенное классическое моделирование квантовых схем, в которых доминируют вентили Клиффорда», Phys. Преподобный Летт. 116, 250501 (2016).
  https://​/​doi.org/​10.1103/​PhysRevLett.116.250501

  [23] Р.С. Беннинк, Э.М. Феррагут, Т.С. Хамбл, Дж.А. Ласка, Дж.Дж. Квантовые схемы, близкие к Клиффорду, Phys. Ред. А 95, 062337 (2017).
  https://​/doi.org/​10.1103/​PhysRevA.95.062337

  [24] M. J. Bremner, A. Montanaro, and D.J. Shepherd, «Достижение квантового превосходства с помощью разреженных и шумных коммутирующих квантовых вычислений», Quantum 1, 8 (2017).
  https://​/doi.org/​10.22331/​q-2017-04-25-8

  [25] М. Ошманец и Д. Дж. Брод, «Классическое моделирование фотонной линейной оптики с потерянными частицами», New J. Phys. 20, 0

  (2018).
  https://​/​doi.org/​10.1088/​1367-2630/​aadfa8

  [26] М. Ховард и Э. Кэмпбелл, Применение теории ресурсов для магических состояний к отказоустойчивым квантовым вычислениям , »Физ. Преподобный Летт. 118, 0 (2017).
  https://​/doi.org/​10.1103/​PhysRevLett.118.0

  [27] Пашаян Х., Уоллман Дж.Дж., Бартлетт С.Д. Оценка вероятности исхода квантовых схем с использованием квазивероятностей // Физ. Преподобный Летт. 115, 070501 (2015).
  https://​/doi.org/​10.1103/​PhysRevLett.115.070501

  [28] М. Ван Ден Нест, «Эффективное классическое моделирование квантовых преобразований Фурье и схем нормализаторов над абелевыми группами», препринт arXiv arXiv :1201. 4867, 2012.
  arXiv:1201.4867

  [29] Дж. Бермеджо-Вега и М. Ван Ден Нест, «Классическое моделирование схем нормализатора абелевой группы с промежуточными измерениями», Quantum Info. вычисл. 14, 181–216 (2014).

  [30] М. Шварц и М. Ван Ден Нест, «Моделирование квантовых схем с разреженными выходными распределениями», препринт arXiv arXiv: 1310.674

  .
  arXiv:1310.6749

  [31] Брави С., Смит Г., Смолин Дж. А. Торговля классическими и квантовыми вычислительными ресурсами // Физ. Ред. X, 6, 021043 (2016).
  https://doi.org/10.1103/PhysRevX.6.021043

  [32] K. Temme, S. Bravyi, and JM Gambetta, « Уменьшение ошибок для квантовых схем малой глубины » Phys. Преподобный Летт. 119, 180509 (2017).
  https://​/doi.org/​10.1103/​PhysRevLett.119.180509

  [33] М. Ван Ден Нест, «Классическое моделирование квантовых вычислений, теорема Готтесмана-Книлла и немного больше,» Quantum Информация. вычисл. 10, 258–271 (2010).

  [34] Р. Джожа и Н. Линден, «О роли запутанности в ускорении квантовых вычислений», Proc. Р. Соц. А 459, 2011–2032 (2003).
  https://​/doi.org/​10.1098/​rspa.2002.1097

  [35] Б. М. Терхал и Д. П. Ди Винченцо, «Адаптивные квантовые вычисления, квантовые схемы с постоянной глубиной и игры Артура-Мерлина», Quantum Info. вычисл. 4, 134–145 (2004).

  [36] T. Morimae, «Трудность классической выборки модели с одним чистым кубитом с постоянной общей ошибкой расстояния вариации», Phys. Версия А 96, 040302 (2017).
  https://​/doi.org/​10.1103/​PhysRevA.96.040302

  [37] С. Ааронсон, Эквивалентность выборки и поиска, Теория вычислительных систем, 55, 281–298 (2014). ).
  https://​/doi.org/​10.1007/​s00224-013-9527-3

  [38] М. Ван Ден Нест, «Моделирование квантовых компьютеров вероятностными методами», Quantum Info. вычисл. 11, 784–812 (2011).

  [39] Д. Шеперд, «Бинарные матроиды и квантовые распределения вероятностей», препринт arXiv arXiv:1005.1744, (2010).
  arXiv:1005.1744

  [40] С. Бравый, А. Китаев, Универсальные квантовые вычисления с идеальными клифордовыми вентилями и шумовыми вспомогательными функциями, Phys. Ред. А 71, 022316 (2005 г.).
  https://​/doi.org/​10.1103/​PhysRevA.71.022316

  [41] Р. Джожа и М. Ван Ден Нест, «Классическая сложность моделирования расширенных схем Клиффорда», Quantum Info. вычисл. 14, 633–648 (2014).

  [42] Л. А. Голдберг и Х. Го, «Сложность аппроксимации комплекснозначных статистических сумм Изинга и Тутте», вычисл. сложный. 26, 765–833 (2017).
  https://​/doi.org/​10.1007/​s00037-017-0162-2

  [43] Г. Куперберг, «Насколько сложно аппроксимировать полином Джонса?», Теория вычислений, 11, 183–219 (2015).
  https://​/doi.org/​10.4086/​toc.2015.v011a006

  [44] K. Fujii и T. Morimae, «Коммутирующие квантовые схемы и сложность статистических сумм Изинга», New J. физ. 19, 033003 (2017).
  https://​/​doi.org/​10.1088/​1367-2630/​aa5fdb

  [45] D. Stahlke, «Квантовая интерференция как ресурс для квантового ускорения», Phys. Версия А 90, 022302 (2014).
  https://​/doi.org/​10.1103/​PhysRevA.90.022302

  [46] Д. Шеперд и М. Дж. Бремнер, «Временно неструктурированные квантовые вычисления», Proc. Р. Соц. А 465, 1413–1439 (2009).
  https://​/doi.org/​10.1098/​rspa.2008.0443

  [47] Д. Дж. Шеперд, «Квантовая сложность: ограничения алгоритмов и архитектур», препринт arXiv arXiv: 1005.1425 (2010).
  arXiv:1005.1425

  [48] Д. Вертиган, Велосипедная размерность и особые точки многочлена Тутте, J. Combin. Теория Сер. Б 74, 378–396 (1998).
  https://​/​doi.org/​10.1006/​jctb.1998.1860

  [49] Р. Реннер и С. Вольф, «Гладкая энтропия Реньи и приложения», на Международном симпозиуме по теории информации, 2004 г. ISIT 2004. Proceedings., стр. 233 (2004).
  https://​/doi.org/​10.1109/​ISIT.2004.1365269

  [50] Л. Стокмейер, «Сложность приближенного подсчета», в материалах пятнадцатого ежегодного симпозиума ACM по теории вычислений, стр. 118–126, ACM, (1983).
  https://​/​doi.org/​10.1145/​800061.808740

  [51] С. Тода, «PP так же сложна, как полиномиальная иерархия времени», SIAM Journal on Computing 20, 865–877 (1991).
  https://​/doi.org/​10.1137/​0220053

  [52] С. Ааронсон и Т. Ханс, «Обобщение и дерандомизация алгоритма приближения Гурвица для перманента», Quantum Info. вычисл. 14, 541–559 (2014).

  [1] Улисс Шабо, Дамиан Маркхэм и Адель Сохби, «Квантовое машинное обучение с адаптивной линейной оптикой», Quantum 5, 496 (2021).

  [2] Войцех Рога и Масахиро Такеока, «Классическое моделирование выборки бозонов с разреженным выходом», Scientific Reports 10 1, 14739(2020).

  [3] Тяньи Пэн, Арам В. Харроу, Марис Озолс и Сяоди Ву, «Моделирование больших квантовых схем на маленьком квантовом компьютере», Physical Review Letters 125 15, 150504 (2020).

  [4] Джеймс Р. Седдон, Бартош Регула, Хакоп Пашаян, Инкай Оуян и Эрл Т. Кэмпбелл, «Количественная оценка квантового ускорения: улучшенное классическое моделирование на основе более жестких магических монотонов», PRX Quantum 2 1, 010345 (2021).

  [5] Михал Ошманец, Ниннат Дангниам, Мауро Э.С. Моралес и Золтан Зимборас, «Выборка фермионов: надежная схема преимущества квантовых вычислений с использованием фермионной линейной оптики и магических входных состояний», PRX Quantum 3 2, 020328 (2022).

  [6] Улисс Шабо, Джулия Феррини, Фредерик Гроссанс и Дамиан Маркхэм, «Классическое моделирование гауссовских квантовых схем с негауссовыми входными состояниями», Physical Review Research 3 3, 033018 (2021).

  [7] Хакоп Пашаян, Оливер Рирдон-Смит, Камил Корзеква и Стивен Д. Бартлетт, «Быстрая оценка вероятностей результатов для квантовых схем», PRX Quantum 3 2, 020361 (2022).

  [8] Филип Б. Мацеевски, Золтан Зимборас и Михал Ошманец, «Уменьшение шума считывания в квантовых устройствах ближнего действия с помощью классической постобработки на основе детекторной томографии», Quantum 4, 257 (2020).

  [9] Леонардо Ново, Хуани Бермехо-Вега и Рауль Гарсия-Патрон, «Квантовое преимущество измерений энергии квантовых систем многих тел», Quantum 5, 465 (2021).

  [10] Рунчжоу Тао, Юнонг Ши, Цзянан Яо, Джон Хуэй, Фредерик Т. Чонг и Ронгуй Гу, Материалы 42-й Международной конференции ACM SIGPLAN по разработке и реализации языков программирования 48 (2021) ISBN: 9781450383912.

  [11] Анжела Каранджай, Джоэл Дж. Уоллман и Стивен Д. Бартлетт, «Контекстуальность ограничивает эффективность классического моделирования квантовых процессов», arXiv: 1802.07744.

  [12] Михал Ошманец и Дэниел Дж. Брод, «Классическое моделирование фотонной линейной оптики с потерянными частицами», New Journal of Physics 20 9, 0

  (2018).

  [13] Джеймс Р. Седдон и Эрл Т. Кэмпбелл, «Количественная оценка магии для операций с несколькими кубитами», Труды Лондонского королевского общества, серия A 475 2227, 201

• (2019).

  [14] Митхуна Йоганатан, Ричард Джожа и Сергей Стрельчук, «Квантовое преимущество унитарных схем Клиффорда с входами в магическом состоянии», Труды Лондонского королевского общества, серия A 475 2225, 20180427 (2019).

  [15] Патрик Ралл, Дэниел Лян, Джереми Кук и Уильям Кречмер, «Моделирование квантовых схем кубитов с помощью распространения Паули», Physical Review A 99 6, 062337 (2019).

  [16] Пирс Лиллистон и Джозеф Эмерсон, «Контекстуальная $\psi$-эпистемическая модель формализма стабилизатора $n$-кубитов», arXiv:1904. 04268.

  [17] Патрик Ралл, «Моделирование квантовых схем путем перетасовки Паулиса», arXiv:1804.05404.

  Приведенные выше цитаты взяты из службы цитирования Crossref (последнее успешное обновление 2022-10-02 07:02:54) и SAO/NASA ADS (последнее успешное обновление 2022-10-02 07:02:55). Список может быть неполным, поскольку не все издатели предоставляют подходящие и полные данные о цитировании.

  Эта статья опубликована в Quantum под лицензией Creative Commons Attribution 4.0 International (CC BY 4.0). Авторские права остаются за первоначальными правообладателями, такими как авторы или их учреждения.

  Процессоры Цена в Бангладеш | Процессоры Star Tech

  Цена в Бангладеш | Звездный Техник

  корзина для покупок

  Тележка

  0

  library_add

  Сравнить

  0

  Сравнить продукты

  закрыть

  ВАША КОРЗИНА

  закрыть

  закрыть

  Ценовой диапазон

  Доступность

  В наличии Предварительный заказ Скоро

  Бренд

  Интел AMD

  Разъем

  Интел LGA1150 Интел LGA1151 Интел LGA2011 Интел LGA2066 Интел LGA1200 Интел LGA1700 АМД АМ4 АМД АМ5 АМД ТР4

  Количество ядер

  2 4 6 8 10 12 16 24 32 64

  Количество потоков

  4 6 8 12 16 20 24 32 64 128

  Тактовая частота

  До 2,4 ГГц от 2,5 ГГц до 3,4 ГГц от 3,5 ГГц до 3,90 ГГц от 4,00 ГГц до 5,0 ГГц Выше 5,1 ГГц

  Кэш

  До 1 МБ от 2 МБ до 6 МБ от 8 МБ до 12 МБ от 14 МБ до 30 МБ 32 МБ и выше

  Процессор

  Показать:

  2024487590

  Сортировать по:

  Цена по умолчанию (Низкая > Высокая) Цена (Высокая > Низкая)

  Процессор Intel Core i3-2120 2-го поколения (лоток)

  • Тактовая частота: 3,30 ГГц
  • Кэш: 3 МБ Intel Smart Cache
  • Сердечников: 2, потоков: 4
  • Розетка: FCLGA1155

  3000৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Процессор Intel Pentium Gold G6405 Coffee Lake

  • Поддерживаемый сокет FCLGA1200
  • Скорость 4,10 ГГц, 2 ядра и 4 потока
  • Интеллектуальная кэш-память Intel 4M
  • Intel UHD Graphics 610

  6 700৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Процессор Intel Pentium Gold G7400 Alder Lake

  • Базовая тактовая частота: 3,70 ГГц
  • Кэш: 6 МБ Intel Smart Cache, разъем: LGA 1700
  • Ядра ЦП: 2, потоки ЦП: 4
  • Intel UHD Graphics 710

  7 500৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Процессор Intel Core i3 10105F 10-го поколения

  • Поддерживаемый сокет FCLGA1200
  • Скорость 3. 70 до 4,40 ГГц
  • Ядер — 4 и потоков — 8
  • Кэш-память 6 МБ

  8 300৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Процессор Intel Core i3 10-го поколения 10100F

  • Поддерживаемый сокет FCLGA1200
  • Скорость 3,60 до 4,30 ГГц
  • Ядер — 4 и потоков — 8
  • Интеллектуальная кэш-память Intel 6 МБ

  8 700৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Процессор AMD Ryzen 3 4100

  • Тактовая частота: 3,8 ГГц; До 4,0 ГГц
  • Кэш L1: 256 КБ; Кэш L2: 2 МБ; Кэш L3: 4 МБ
  • 4 ядра и 8 потоков
  • Сокет процессора: AM4

  10 500৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Процессор Intel Core i3 10-го поколения 10100

  • Поддерживаемый сокет FCLGA1200
  • Скорость 3,60 до 4,30 ГГц
  • Ядер — 4 и потоков — 8
  • Кэш-память 6 МБ

  12 000৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Intel Core i3 10105 Процессор Comet Lake 10-го поколения

  • Поддерживаемый сокет FCLGA1200
  • Скорость от 3,70 ГГц до 4,40 ГГц
  • Ядер — 4 и потоков — 8, кэш-память 6 МБ
  • Intel UHD Graphics 630

  12 500৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Процессор AMD RYZEN 5 3500

  • Частота: от 3,6 ГГц до 4,1 ГГц
  • Кэш (L2+L3): 16 МБ
  • Ядра-6 и потоки-6
  • Скорость памяти: 3200 МГц

  12 500৳

  корзина покупок Купить сейчас library_add Добавить для сравнения

  Процессор Intel Core i3-12100F 12-го поколения Alder Lake

  • Тактовая частота: 3,30 ГГц До 4,30 ГГц
  • Кэш: 12 МБ, разъем: LGA 1700
  • Ядер ЦП: 4, потоков ЦП: 8
  • Максимальный объем памяти: 128 ГБ

  12 500৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Процессор AMD Ryzen 5 4500

  • Тактовая частота: 3,6 ГГц; До 4,1 ГГц
  • Кэш L1: 384 КБ; Кэш L2: 3 МБ; Кэш L3: 8 МБ
  • 6 ядер и 12 потоков
  • Сокет процессора: AM4

  13 500৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Процессор Intel Core i5-10400F 10-го поколения

  • Тактовая частота: от 2,90 до 4,30 ГГц
  • Ядра-6 и потоки-12
  • 12 МБ SmartCache
  • Типы памяти: DDR4-2666

  14 200৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Процессор AMD Ryzen 3 PRO 4350G

  • Четырехъядерный процессор 3,8 ГГц / 4,0 ГГц
  • Сокет AMD AM4
  • 4 МБ кэш-памяти L3
  • Видеокарта Radeon Vega 6

  14 800৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Процессор AMD Ryzen 5 1600X

  • Частота: от 3,6 ГГц до 4,0 ГГц
  • Кэш L1: 576 КБ, Кэш L2: 3 МБ, Кэш L3: 16 МБ
  • Сердечников: 6, потоков: 12
  • До 2667 МГц DDR4

  15 000৳

  shopping_cart Купить сейчас library_add Добавить к сравнению

  Процессор AMD Ryzen 5 5500

  • Скорость: 3,6 ГГц; До 4,2 ГГц
  • Кэш L2: 3 МБ, Кэш L3: 16 МБ
  • Сердечников: 6, потоков: 12
  • До 3200 МГц DDR4

  15 000৳

  shopping_cart Купить сейчас библиотека_добавить Добавить к сравнению

  Процессор Intel Core i5-9400 9-го поколения

  • Тактовая частота: 4,10 ГГц
  • Ядра-6 и потоки-6
  • 9 МБ SmartCache
  • Intel UHD Graphics 630

  15 300৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Процессор Intel Core i5-9500 9-го поколения (лоток)

  • Тактовая частота: от 3,00 до 4,40 ГГц
  • Ядра-6 и потоки-6
  • Смарт-кэш 9 МБ
  • Intel UHD Graphics 630

  16 500৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  CPU Обозначает центральный процессор. Его также называют центральным основным процессором или просто процессором. По сути, это электронная схема, которая действует как мозг системы. Центральный процессор управляет другими компонентами системы для выполнения команд пользователя. Процессоры доступны в компьютерах, телефонах, телевизорах и других интеллектуальных электронных устройствах. Процессор подключен к ПК через материнскую плату. Форма, дизайн и реализация ЦП со временем менялись, но их основная работа остается почти неизменной. В настоящее время на рынке представлены два основных бренда процессоров Intel и AMD.

  Самый последний прайс-лист на процессор в BD 2022

  Выберите процессор для настольного ПК от Intel или AMD

  «Intel 4004» был первым коммерчески представленным микропроцессором на рынке в 1970 году, а наиболее широко используемой моделью был «Intel 8080», выпущенный в 1974 г., которая произвела революционные изменения почти во всех сегментах обработки. В условиях конкуренции производители мейнфреймов и мини-компьютеров запустили проприетарные программы разработки ИС для обновления своей архитектуры и разработали набор инструкций, несовместимый со своим старым оборудованием и программным обеспечением. ЦП стал синонимом микропроцессоров, поскольку он широко популярен среди персональных компьютеров. Ранее многочисленные небольшие интегральные схемы (ИС), используемые на одной или нескольких печатных платах, с другой стороны, микропроцессор представил небольшие ЦП с гораздо меньшим количеством ИС, которые можно было объединить в одну микросхему обработки. Однако размер, конструкция и общая форма процессоров сильно изменились с 19 века.50, но основная форма и функция остались неизменными.

  Процессор Intel

  Intel означает «Интегрированная электроника». Intel Corporation — американская транснациональная корпорация и технологическая компания со штаб-квартирой в Санта-Кларе, Калифорния, в Силиконовой долине. Основанная Робертом Нойсом, она является разработчиком самого первого 32-разрядного процессора x86 под названием Intel 8086. У Intel есть много серий процессоров, таких как Core, Pentium или Celeron. С наборами уникальных черт; Intel выпускает новое поколение почти каждый год. Наиболее распространенный процессор Intel — это серия Core. ЦП серии Core состоят из Core i3, Core i5, Core i7 и высокопроизводительного Core i9.. В настоящее время 4-е поколение является самым старым из доступных. Процессоры Intel до процессоров поколения 11h имеют 4 отдельных ядра. Самое последнее 12-е поколение процессоров Core было выпущено с двумя наборами ядер, называемыми E-Cores и P Cores. Intel не изменила старую 4-ядерную архитектуру в пользу производительности и энергоэффективности. Эти процессоры имеют совершенно новую гибридную архитектуру, а также некоторые черты, совершенно новые для индустрии программного обеспечения. размером от 14 до 10 нм; Процессоры Intel серии Core имеют лучшую производительность на ватт, низкое энергопотребление и высокую скорость отклика, что делает их идеальными для повышения производительности, развлечений и управления работой. Технология Turbo Boost и интегрированная HD-графика еще больше повышают производительность. У Intel есть и другие процессоры, подходящие для бюджетных диапазонов от низкого до высокого. Для игр и создания контента у Intel есть высокопроизводительные процессоры HEDT. Для нижнего бюджетного диапазона у них есть процессоры, такие как Celeron, Atom и Pentium. Процессоры Intel поддерживают новейшие высокоскоростные оперативные памяти DDR3, DDR4. Новейшие процессоры 12-го поколения поддерживают оперативную память DDR5. ЦП Intel интегрирован для Wi-Fi 802.11ax и высокоскоростных портов USB и Thunderbolt.

  Процессоры AMD

  AMD расшифровывается как Advanced Micro Devices. Это американская транснациональная полупроводниковая компания, базирующаяся в Санта-Кларе, Калифорния. Его основали Джерри Сандерс, Джек Гиффорд и Джон Кэри. Он начал поставлять 32-битные процессоры x86 в качестве второго исходного производителя и стал конкурентом со своим первым процессором Am386. AMD известна серией процессоров Ryzen как самой первой потребительской реализации новой микроархитектуры Zen, представленной еще в 2017 году. В 2018 году была выпущена первая партия 12-нм процессоров AMD Ryzen второго поколения. Последний чипсет AMD Ryzen Processor с уклоном в 7 нм был выпущен в 2019 году.. Сначала процессоры AMD были конкурентом процессоров Intel начального уровня. После появления серии AMD Ryzen это самый большой конкурент Intel. Они известны как самые бюджетные процессоры. Помимо Райзена; У AMD есть несколько других серий процессоров. Линейка процессоров AMD Ryzen включает процессоры Ryzen 3, Ryzen 5, Ryzen 7 и Ryzen 9. Хотя модели процессоров AMD Ryzen обычно включают серии Ryzen 3 3200G, 2200G, 1200; Ryzen 5 3400G, 3500, 3500X, 3600, 3600X, 2400G, 2600, 2600X; Ryzen 7 3800X, 3700X, 3800X, 2700, 2700X и Ryzen 93900X 3950X. Серия процессоров Ryzen Threadripper состоит из процессоров 1900X, 1920X, 2970WX и 2990WX. AMD также владеет другой серией под названием Epyc. Обычно они совместимы с оперативной памятью DDR3 и DDR4 DIMM. Новейшее 5-е поколение процессоров AMD Ryzen 3, Ryzen 5, Ryzen7 и Ryzen9 будет поддерживать новейшую высокоскоростную оперативную память DDR5.

  Покупайте в лучшем магазине процессоров в Бангладеш

  Star Tech — крупнейший розничный и интернет-магазин компьютеров, ноутбуков и компьютерных компонентов в Бангладеш. Посетите любой магазин Star tech или наш веб-сайт, чтобы получить желаемый ПК с предпочитаемым процессором по самой низкой цене. У нас есть филиалы в таких крупных городах, как Дакка, Читтагонг, Рангпур, Газипур и Кхулна.

  Цена материнской платы

  в Бангладеш в 2022 году Цена материнской платы

  в Бангладеш в 2022 году | Звездный Техник

  корзина для покупок

  Тележка

  0

  library_add

  Сравнить

  0

  Сравнить продукты

  закрыть

  ВАША КОРЗИНА

  закрыть

  закрыть

  Ценовой диапазон

  Доступность

  В наличии Предварительный заказ Скоро

  Тип процессора

  Интел AMD

  Бренд

  ASRock Асус Гигабайт MSI NZXT

  Фромфактор

  АТХ Расширенный ATX МикроАТХ Мини-ITX

  Тип оперативной памяти

  DDR3 DDR4 DDR5

  Особые возможности

  CrossFireX Wi-Fi СЛИ м. 2

  Материнская плата

  Показать:

  2024487590

  Сортировать по:

  Цена по умолчанию (Низкая > Высокая) Цена (Высокая > Низкая)

  Материнская плата MSI A320M-A Pro AMD Micro-ATX

  • Поддерживает AMD Ryzen 1-го, 2-го и 3-го поколения с графикой Radeon Vega Graphics
  • Поддержка оперативной памяти DDR4 с частотой до 3200 (OC) МГц
  • Core Boost: поддержка большего количества ядер
  • Усиление DDR4, усиление звука

  6 100৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  MSI A520M PRO-VH Материнская плата AMD AM4 Micro-ATX (Китай)

  • Поддерживает процессоры Ryzen серий 5000 и 3000 и Ryzen 4000 G-серии
  • Поддерживает DDR4, до 4600(OC) МГц
  • Ускорение ядра и Ускорение DDR4
  • 2 унции утолщенной медной печатной платы

  6 500৳

  корзина покупок Купить сейчас library_add Добавить для сравнения

  Материнская плата Gigabyte B450M S2H AMD AM4 Micro ATX

  • Поддержка процессоров AMD Ryzen серии 5000
  • Чипсет: AMD B450
  • Память: 2 x DDR4, макс. 32 ГБ
  • 3 слота PCI Express

  6 600৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Скидка 200৳ на онлайн-заказ

  Скидка 200৳ при онлайн-заказе

  Материнская плата Asrock h410M-HDV DDR4 8-го поколения

  • Поддержка процессоров 8-го поколения (Socket 1151)
  • Поддерживает DDR4 2666
  • 1 PCIe 3.0 x16, 1 PCIe 2.0 x1

  6 800৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Скидка 200৳ при онлайн-заказе

  Материнская плата ASRock A320M-HDV R4.0 AMD

  • 2 модуля DIMM, поддержка DDR4 3200+(OC)
  • 1 PCIe 3. 0 x16, 1 PCIe 2.0 x1
  • Графический выход: HDMI, DVI-D, D-Sub
  • 4 SATA3, 1 Ultra M.2 (PCIe Gen3 x4 и SATA3)

  7 200৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Скидка 200৳ при онлайн-заказе

  Материнская плата Gigabyte GA-H61M-S DDR3 Micro ATX

  • Процессоры Intel i7 / i5 / i3 / Pentium / Celeron
  • Поддержка сокета LGA1155
  • Набор микросхем Intel H61 Express
  • Встроенная графика

  7 600৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Скидка 100৳ при онлайн-заказе

  Материнская плата Gigabyte GA-H61M-DS2

  • Чипсет Intel® H61 Express
  • Поддерживает процессоры Intel 22-нм 3-го поколения и процессоры 2-го поколения
  • 2 x 1,5 В DDR3 DIMM
  • 1 слот PCI Express x16

  7 600৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Материнская плата Gigabyte GA-H81M-S2PH Micro ATX

  • Поддерживает процессоры Intel Core 4-го поколения
  • ГИГАБАЙТ UEFI DualBIOS
  • Все твердотельные конденсаторы
  • ЛВС с высокой защитой от электростатического разряда

  7 850৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Материнская плата Gigabyte GA-H81M-DS2 Micro ATX

  • ЦП: процессоры Intel 4-го поколения
  • Набор микросхем: Intel H81 Express
  • 2 x 1,5 В DDR3
  • 3 слота PCI Express

  7 900৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Скидка 500৳ при онлайн-заказе

  Материнская плата ASRock H81M-VG4 R4.

  0 4-го поколения Micro ATX
  • Поддержка процессоров Intel Core 4-го поколения (Socket 1150)
  • Поддерживает двухканальную память DDR3 1600
  • 1 PCIe 2.0 x16, 1 PCIe 2.0 x1
  • Графический выход: D-Sub

  8000৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Материнская плата ASUS h210M-K

  • Чипсет- Intel h210
  • Intel Socket 1151 для процессоров Core 7-го/6-го поколения
  • 2 модуля DIMM, макс. 32 ГБ, DDR4 2133
  • 1 разъем PCIe 3.0/2.0 x16

  8 200৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Скидка 200৳ на онлайн-заказ

  Материнская плата Asus H81M-K 4-го поколения

  • Intel Socket 1150 для процессоров Core i7/i5/i3/Pentium/Celeron 4-го поколения
  • 2 модуля DIMM, макс. 16 ГБ, DDR3 без ECC, небуферизованная память
  • Новый UEFI BIOS и USB 3.0 Boost (поддержка UASP)
  • AI Suite 3 — универсальный доступ к инновационным функциям ASUS

  8 300৳

  корзина покупок Купить сейчас library_add Добавить для сравнения

  Материнская плата MSI PRO h510M-B 10-го поколения Micro-ATX

  • Поддержка процессоров Intel Core, Pentium Gold и Celeron 10-го поколения для сокета LGA 1200
  • Поддерживает память DDR4, до 2933 (макс.) МГц
  • Core Boost, DDR4 Boost, Turbo M.2
  • 4 порта SATA 6 Гбит/с, 1 слот M.2

  8 800৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Материнская плата GIGABYTE GA-h210M S2PV DDR4 6-го поколения

  • Поддержка процессоров Intel Core 7-го и 6-го поколения
  • Двухканальная память DDR4, 2 модуля DIMM
  • 8-канальный HD-аудио с высококачественными аудиоконденсаторами
  • GbE LAN с программным обеспечением cFosSpeed ​​Internet Accelerator

  8 800৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Материнская плата Gigabyte GA-h210M S2PH-DDR4

  • Поддержка процессоров Intel® Core™ 6-го поколения
  • Двухканальная память DDR4, 2 модуля DIMM
  • 8-канальный HD-аудио с высококачественными аудиоконденсаторами
  • Шумоизоляция со светодиодной подсветкой

  8 900৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Скидка 100৳ при онлайн-заказе

  Материнская плата MSI H510M PRO-E Intel 10-го и 11-го поколений Mirco-ATX

  • Поддержка процессоров 10-го поколения, 11-го поколения Core, Pentium Gold и Celeron для сокета LGA 1200
  • Поддерживает память DDR4, до 3200 (макс. ) МГц
  • С премиальной компоновкой и цифровым дизайном питания
  • Молниеносная скорость: PCIe 4.0

  9 500৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Скидка 200৳ на онлайн-заказ

  Материнская плата MSI H510M-A PRO Intel 10-го и 11-го поколений Mirco-ATX

  • Поддержка процессоров Intel Core 10-го и 11-го поколений, Pentium Gold и Celeron
  • Память DDR4, до 3200 (макс.) МГц
  • Turbo M.2: работает PCIe 4.0
  • Разъем LGA 1200

  9 200৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Материнская плата Gigabyte B460M DS3H 10-го поколения Micro ATX

  • Разъем Intel LGA1200 для процессоров 10-го поколения
  • Память Intel Optane готова
  • Высококачественные аудиоконденсаторы
  • GIGABYTE Exclusive 8118 Игровая локальная сеть

  9 300৳

  shopping_cart Купить сейчас library_add Добавить для сравнения

  Материнская плата — это печатная плата или печатная плата, образующая каркас ПК. На нем размещаются такие компоненты, как процессор или центральный процессор, графический процессор или графический процессор, модуль памяти или ОЗУ, а также хранилище. Материнская плата Обеспечивает связь между всеми этими различными компонентами и содержит некоторые жизненно важные подсистемы, такие как точки ввода-вывода, контроллеры памяти, интерфейсные разъемы и т. д. В старых материнских платах использовались печатные платы в каркасе для плат, а корпус был соединен с компонентами задней панелью с набором взаимосвязанных физических разъемов. После изобретения микропроцессоров материнские платы резко изменились. Хотя в то время ЦП, память и периферийные устройства использовали отдельные печатные платы. В конце 19С 80-х по 90-е годы материнские платы стали экономичным вариантом для большого количества периферийных устройств из-за использования одиночных микросхем с низкоскоростными периферийными устройствами. Материнские платы были сделаны с последовательными и параллельными портами, включая аудио, видео, память и сетевые функции. Сегодня большинство современных устройств, таких как смартфоны, планшеты, ноутбуки и настольные компьютеры, используют эти компактные материнские платы для сборки всего вместе.

  Популярные бренды материнских плат

  Независимо от того, выбрали ли вы процессор Intel или AMD для своего настольного ПК, важно выбрать хорошую материнскую плату от известного бренда. Это важно, потому что когда человек собирает собственный настольный ПК для игр или работает с материнской платой любого известного бренда, это окажет значительное влияние на производительность вашей системы. Вы можете выбрать любую материнскую плату от популярных брендов, таких как Asrock, ASUS, Gigabyte, MSI и NZXT. Все эти популярные бренды предлагают широкий выбор материнских плат для использования в ПК любого типа, от базового рабочего ПК до игровых настольных ПК и даже настольных ПК с высокой производительностью.

  Материнская плата для процессора Intel

  Если вам нужна материнская плата для желаемого процессора Intel, существует множество вариантов на выбор. Разные процессоры Intel поддерживают разные сокеты и наборы микросхем. Процессоры Intel 4-го и 5-го поколений поддерживают процессорные разъемы LGA 1155 и LGA 1150, а также наборы микросхем H81, B85, Q85, Q87, H87 и Z87. Все 14-нм процессоры Intel от процессоров Skylake 6-го поколения до процессоров Coffe lake Refresh 9-го поколения поддерживают процессорные разъемы LGA 1151 и линейку наборов микросхем h210, B150, Q150, h270, Q170 и Z170. Все эти чипсеты, кроме Z170s, нельзя разогнать без GPU.

  Новейшие процессоры Intel 12-го поколения поддерживают процессорные разъемы LGA 1200 для материнских плат Intel серии 400. Они поддерживают новейшие модули оперативной памяти DDR5 и такие технологии, как HEVC, HDR и 10-битное кодирование VP9, ​​а также высокоскоростные порты USB 3.0 и слоты оперативной памяти DDR4.

  Материнская плата для процессора AMD

  Процессоры AMD используют сокет типа PGA. Наиболее распространенные сокеты процессоров AMD называются сокетами AM4, сокетами TRX4 и сокетами sWRX8. Новейшие процессоры AMD имеют обратную совместимость со старыми сокетами AM2 и FM2 Plus. Тип сокета AM4 совместим с большинством процессоров AMD, APU Athlon начального уровня и новейшими процессорами Ryzen. Сокет TR4X используется высокопроизводительной серией процессоров Ryzen Threadripper. Они могут содержать высокопроизводительные многоядерные процессоры с большим объемом кэш-памяти и большим количеством линий PCI-E, что делает их идеальными для игровых ПК. Третий тип сокета процессора AMD — sWRX8, используемый серией процессоров Ryzen Threadripper PRO. Это сверхмощные высокопроизводительные процессоры с энергоэффективными ядрами, оперативной памятью ECC и линиями PCIe.

  Факторы, которые необходимо учитывать перед выбором материнской платы

  Независимо от того, выбираете ли вы материнскую плату для ПК с процессорами Intel или AMD, необходимо учитывать некоторые общие факторы. Материнские платы могут быть установлены в корпусах Small Tower, Mid-Tower или Full Tower, будь то плата ATX, Micro-ATX, Mini-ATX или iATX.