Категория: Приемники КВ-Приемник рассчитан на прием CW/SSB радиостанций в диапазонах 20 и 80 метров. Его отличительная особенность в том, что переключение диапазонов происходит только во входных контурах. При этом используется один общий приемный тракт, частота гетеродина которого перестраивается в пределах 8,5-9,35 МГц независимо от выбранного диапазона. При том что промежуточная частота 5 МГц, получается что при приеме диапазона 80 метров частота гетеродина выше входной на значение ПЧ, а при приеме в диапазоне 20 метров, — соответственно ниже. Поэтому, в обоих диапазонах работает один и тот же тракт ВЧ-ПЧ, а выбор диапазона зависит от настройки входного фильтра. Сигнал от антенны поступает на два LC-полосовых фильтра, которые при выборе диапазона переключаются переключателем S1. Далее сигнал выделенного диапазона поступает на преобразователь частоты, выполненный на микросхеме А1. Все остальные узлы микросхемы (кроме преобразователя частоты и гетеродина) в схеме не задействованы. Конечно, здесь было бы уместнее применить микросхему типа SA602, но микросхемы данного типа значительно меньше распространены, чем МС3361 (или МС3359, которая так же подходит для данной схемы). Поэтому из соображений доступности и цены (МС3361 дешевле SA602) была предпринята такая расточительность (большая часть схемы МС3361 здесь не используется). Генератор плавного диапазона выполнен так же на А1. В нем используются элементы схемы гетеродина МС3361. Настройка в пределах 8,5-9,35 MHz осуществляется варикапом VD1, на который поступает управляющее напряжение с потенциометра R4. Контур ГПД выполнен на индуктивности L7. Эта единственная в схеме подстраиваемая индуктивность. Все остальные катушки — высокочастотные дроссели промышленного изготовления. На выходе преобразователя находится четырехзвенный кварцевый фильтр Q1-Q4 состоящий из резонаторов на 5 MHz. Фильтр выделяет ПЧ равную 5 MHz. С выхода кварцевого фильтра сигнал ПЧ поступает на демодулятор, выполненный на А2. Здесь так же используется микросхема МС3361, у которой задействован только преобразователь частоты и гетеродин. Практически, преобразователь частоты работает как демодулятор, а гетеродин как генератор опорной частоты. Величина опорной частоты установлена кварцевым резонатором Q5. Включенная последовательно ему индуктивность L8 немного смещает частоту опоргого генератора в строну от 5 MHz, что необходимо для работы демодулятора. Продукты демодуляции выделяются на 3-м выводе А2. Конденсатор С34 представляет собой простейший ФНЧ, подавляющий высокочастотную составляющую. Далее низкочастотный сигнал поступает на усилитель на ОУ А4. Затем следует регулятор громкости R11 и усилитель мощности ЗЧ на микросхеме А5. Катушка L7 намотана на каркасе с ферритовым сердечником, от контура модуля цветности телевизора 3-УСЦТ. |
| Поделитесь с друзьями ссылкой на схему: |
Схема
Схема Прокрутка
фото
Схема ТРЦ
Как добраться
10:00 — 22:00
Программа
лояльности
Подарочная
карта
- Главная
- Схема ТРЦ
Туалет
Комната матери
и ребенка
Гардероб
Входы и выходы
Выход из парковки
Банкоматы
Девелопер
с мировым именем
AFI Development — международная многопрофильная девелоперская компания полного цикла с 20-летним опытом работы на российском рынке.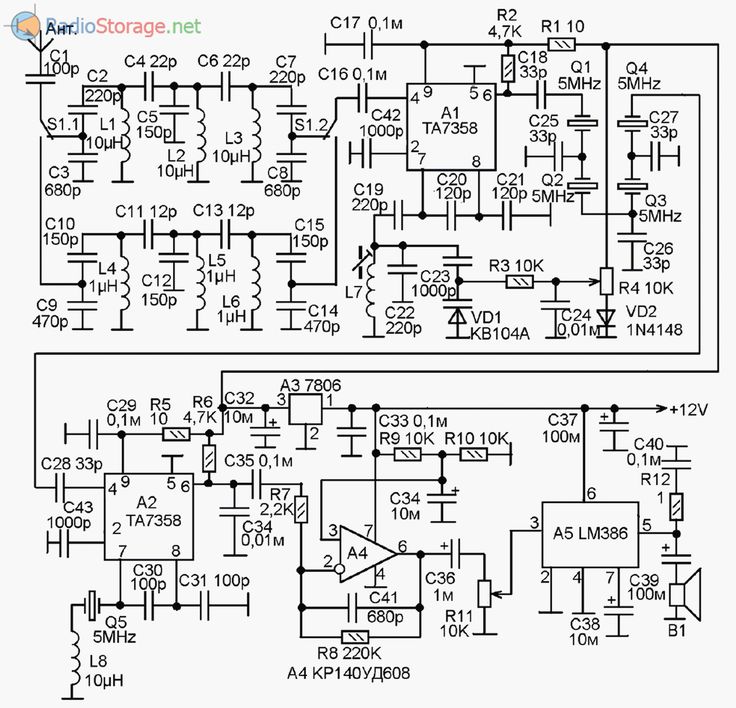
Системообразующее предприятие строительной отрасли России.
Диверсифицированный портфель AFI Development включает:
— более 1,2 млн кв. м реализованных объектов
— более 1,5 млн кв. м объектов в стадии реализации
AFI Development — международная многопрофильная девелоперская компания полного цикла с 20-летним опытом работы на российском рынке.
Системообразующее предприятие строительной отрасли России.
Диверсифицированный портфель AFI Development включает:
— более 1,2 млн кв. м реализованных объектов
— более 1,5 млн кв. м объектов в стадии реализации
Системообразующее предприятие строительной отрасли России.
Диверсифицированный портфель AFI Development включает:
— более 1,2 млн кв. м реализованных объектов
м реализованных объектов
— более 1,5 млн кв. м объектов в стадии реализации
AFI Development — международная многопрофильная девелоперская компания полного цикла с 20-летним опытом работы на российском рынке.
Системообразующее предприятие строительной отрасли России.
— более 1,2 млн кв. м реализованных объектов
— более 1,5 млн кв. м объектов в стадии реализацииПодробнее
Жилая недвижимость бизнес
и комфорт класса в Москве и области
ДЛЯ ЖИЗНИ
Офисные помещения
А+ класса в центре Москвы
Для бизнеса
Отели и санатории
в нескольких регионах России
Для отдыха
Более 450 магазинов и кафе
в центре Москва-Сити
Для Досуга
Сообщение отправлено
Спасибо, ваше сообщение отправлено. В ближайшее время с вами свяжутся наши менеджеры для уточнения всех деталей
Закрыть
Сообщение отправляется
Спасибо, ваше сообщение отправляется, подождите немного.
Закрыть
Simply Scheme: Введение в информатику, глава 4: Определение собственных процедур
Схема Simple: Введение в информатику 2/e Copyright (C) 1999 MIT
Глава 4
|
До сих пор мы использовали процедуры, которые Scheme уже знает, когда вы
начать работать с ним.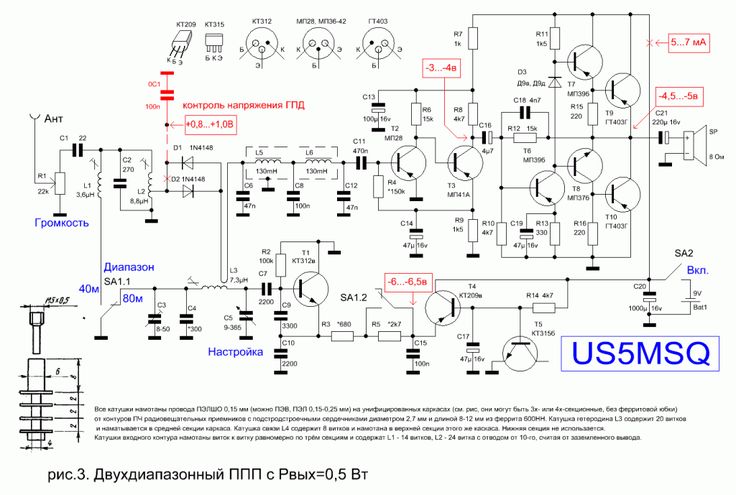
Как определить процедуру
Программа Scheme состоит из одной или нескольких процедур. Процедура описание процесса, с помощью которого компьютер может обработать некоторый результат что мы хотим. Вот как определить процедуру, которая возвращает квадрат его аргумент:
(определить (квадрат x) (* х х))
(значение, возвращаемое , определить , может отличаться в зависимости от
версия схемы, которую вы используете. Многие версии возвращают имя
процедура, которую вы определяете, но другие возвращают что-то еще. Это не
важно, потому что когда вы используете определить вас не интересует
возвращаемое значение, а скорее в том, что Scheme запоминает новое
определение для дальнейшего использования.)
Это определение процедуры под названием квадрат . Площадь принимает один аргумент, число, и возвращает квадрат этого числа.
Как только вы определили в квадрате , вы можете использовать его точно так же, как вы
использовать примитивные процедуры:
> (квадрат 7) 49 > (+ 10 (квадрат 2)) 14 > (квадрат (квадрат 3)) 81
Это определение процедуры состоит из четырех частей. Первым является слово
Первым является слово определить
(квадрат х) выглядит как как (квадрат 7) . Четвертая часть определения — body: выражение, значение которого обеспечивает возвращаемое функцией значение.Специальные формы
Определение является специальной формой , является исключением из
правило оценки, о котором мы говорили.[1] Обычно выражение представляет собой вызов процедуры, поэтому
общее правило состоит в том, что Scheme сначала вычисляет все подвыражения, а
затем применяет результирующую процедуру к результирующим значениям аргументов.
Особенность специальных форм состоит в том, что Схема не оценивает все
подвыражения. Наоборот, каждая особая форма имеет свою особую
правило оценивания. Например, когда мы определили
Наоборот, каждая особая форма имеет свою особую
правило оценивания. Например, когда мы определили квадратных , нет
оценивалась часть определения: не квадрат , не х , а
не (* х х) . Не имеет смысла вычислять (квадрат x) .
потому что вы не можете вызвать процедуру квадратов до того, как определите ее!
Можно было бы описать специальные формы, используя следующую модель:
«Некоторые процедуры хотят, чтобы их аргументы не оценивались, и Scheme распознает
их. После воздержания от оценки определить аргументы , для
например, Scheme вызывает процедуру определения с теми неоцененными
аргументы.» Но на самом деле разработчики Scheme решили подумать об этом
иначе. Вся специальная форма, начинающаяся с , определяет , это просто
совершенно разные вещи, чем вызов процедуры. В схеме есть
нет процедуры с именем определить . На самом деле определяют, это не имя
вообще ни о чем:
> + #<ПЕРВИЧНАЯ ПРОЦЕДУРА +> > определить ОШИБКА - НЕДЕЙСТВИТЕЛЬНЫЙ КОНТЕКСТ ДЛЯ KEYWORD DEFINE
Тем не менее, в этой книге, если только это не очень важно сделать
различия, мы будем говорить так, как если бы существовала процедура, называемая , определить . Например, мы поговорим о «
Например, мы поговорим о « определить аргументы » и «значение
возвращаемый , определить » и «вызов , определить «.
Функции и процедуры
На протяжении большей части этой книги наши процедуры будут описывать процессы, которые
вычислить функций. Функция представляет собой связь между некоторыми значениями
вы уже знаете, и новое значение, которое вы хотите узнать. Например,
9Функция 0070 квадрат принимает число, например 8, в качестве входного значения и
возвращает другое число, в данном случае 64, в качестве выходного значения. Функция во множественном числе принимает существительное, например «компьютер», и возвращает другое.
слово, «компьютеры» в этом примере. Технический термин для функции
входное значение является его аргументом . Функция может принимать более одного
аргумент; например, функция остатка принимает два аргумента,
например 12 и 5. Он возвращает одно значение, остаток от деления первого
аргумент вторым (в данном случае 2).
Ранее мы говорили, что процедура — это «описание процесса, посредством которого компьютер может получить некоторый результат, который нам нужен». Что мы подразумеваем под процессом ? Рассмотрим эти два определения:
г ( x )=3( x +4)
(определить (ф х) (+ (* 3 х) 12)) (определить (г х) (* 3 (+ х 4)))
, и мы бы сказали, что f и g — это две процедуры, которые
представляют одну и ту же функцию.
В реальной жизни функции не всегда представлены процедурами. Мы могли бы представить функцию таблицей , показывающей все ее возможные значения, как это:
| Алабама | Монтгомери |
| Аляска | Джуно |
| Аризона | Феникс |
| Арканзас | Литл-Рок |
| Калифорния | Сакраменто |
| … | … |

Мы скажем «процедура f », когда хотим обсудить операции
мы говорим Схеме выполнить. Мы скажем, что «функция, представленная f «, когда наше внимание сосредоточено на возвращаемом значении, а не
на механизме. (Но мы часто будем сокращать эту длинную вторую фразу
с «функция f «, если контекст не является особенно
сбивает с толку.)[2]
Имена аргументов и значения аргументов
— Длинный, — сказал Рыцарь, — но очень, очень красивый. Все, кто слышит, как я ее пою — либо слезы вызывают в душе глаза, иначе…
«Или что еще?» сказала Алиса, потому что Рыцарь сделал внезапную паузу.
«А иначе, знаешь ли. Песня называется « Глаза пикши». ’ ”
«О, это название песни, не так ли?» Алиса сказала, пытаясь почувствовать интересно.
— Нет, ты не понимаешь, — сказал Рыцарь с легким раздражением. «Так называется номер . Имя на самом деле « Старик».
Пожилой мужчина. &rsquo ”
«Тогда я должен был сказать: «Вот как называется песня »?» Алиса поправила себя.
«Нет, не надо; это совсем другое! Песня называется &lsquo способов и средств &rsquo: но это только то, что называется, ты знать!»
«Ну, тогда что такое песня?» — сказала Алиса, которая к этому времени совершенно сбит с толку.
«Я уже подходил к этому», сказал Рыцарь. «Песня на самом деле « А-сидит на воротах »: и мелодия — мое собственное изобретение».
Льюис Кэрролл, Зазеркалье и что Алиса найдена там
Обратите внимание, что когда мы определили процедуру квадрат , мы дали имя, x , за его аргумент. Напротив, когда мы вызвали в квадрате мы предоставили значение для аргумента (например, 7 ).
Слово x является «заполнителем» в определении, которое означает
любое значение, которое вы используете при вызове процедуры.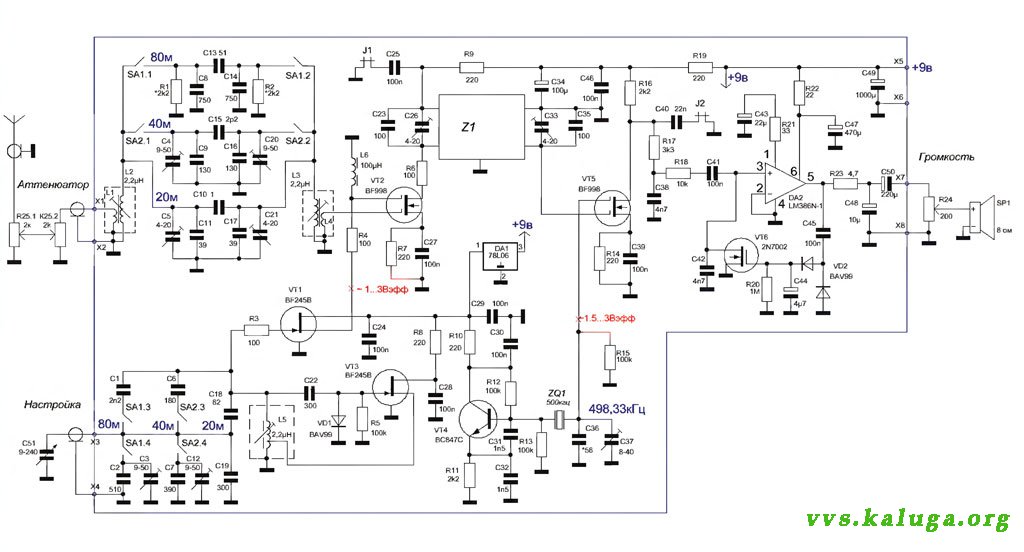 Таким образом, вы можете прочитать
определение
Таким образом, вы можете прочитать
определение в квадрате : «Для того, чтобы в квадрате число,
умножьте это число на это число. » Имя x занимает место конкретного числа, которое вы имеете в виду.
Убедитесь, что вы понимаете разницу между определением процедуры и
называя это. Процедура представляет собой общую технику, которую можно применять
ко многим конкретным случаям. Мы не хотим встраивать какой-либо конкретный случай в
определение процедуры; мы хотим, чтобы определение выражало общую природу
техника. Вам бы не понадобилась процедура, которая знает только, как принимать
квадрат 7. Но когда вы на самом деле используете в квадрате , у вас есть
чтобы быть точным в отношении того, какое число вы возводите в квадрат.
Имя для имени аргумента (фух!) — это формальный параметр. В нашем примере квадратных , x является формальным параметром. (Вы можете услышать, как люди говорят либо «формальный»,
в одиночку или только «параметр», когда им лень. )
технический термин для фактического значения аргумента — фактический аргумент . В таком случае
)
технический термин для фактического значения аргумента — фактический аргумент . В таком случае
(квадрат (+ 5 9))
вы можете захотеть отличить выражение фактического аргумента (+ 5 9) от фактического значения аргумента 14. В большинстве случаев это совершенно ясно
что вы имеете в виду, и вы просто говорите «аргумент» для всех этих вещей, но
прямо сейчас, когда вы изучаете эти идеи, важно уметь говорить
точнее.
Процедура в квадрате принимает один аргумент. Если процедура требует больше
чем один аргумент, то возникает вопрос, какой фактический аргумент идет с
какой формальный параметр? Ответ заключается в том, что они идут в том порядке, в котором
вы пишете их, как это:
(определить (f a b) (+ (*3 а) б)) > (ф 5 8) 23 > (ф 8 5) 29
Процедура как обобщение
Какое среднее значение между 17 и 25? Чтобы ответить на этот вопрос, вы можете добавить
два числа, получается 42, и делим это на два, получая 21. Вы можете спросить
Схема, чтобы сделать это для вас:
Вы можете спросить
Схема, чтобы сделать это для вас:
> (/ (+ 17 25) 2) 21
Какое среднее значение между 14 и 68?
> (/ (+ 14 68) 2) 41
Как только вы поймете технику, вы сможете ответить на любой такой вопрос, ввод выражения вида
(/ (+ ______ ______ ) 2)
к Схеме.
Но если вы собираетесь столкнуться с такими проблемами, следующий очевидный Шаг заключается в том, чтобы обобщить методику, определив процедуру:
(определить (среднее а б) (/ (+ а б) 2))
С этим определением вы можете подумать о следующей проблеме, которую приходит с точки зрения самой проблемы, а не с точки зрения шаги, необходимые для ее решения:
> (в среднем 27 4) 15,5
Это пример того, что мы имели в виду, когда определяли
«абстракция» как замечание паттерна и присвоение ему имени.
Это не так уж отличается от именования таких шаблонов на английском языке;
когда кто-то придумал название «средний», это было, наверное, после
заметив, что часто было полезно найти значение на полпути между
два других значения.
Этот процесс именования важнее, чем кажется, потому что как только мы имя для какой-либо идеи, мы можем использовать эту идею, не думая о ее частях. Например, предположим, что вы хотите узнать не только среднее значение некоторого числа, но и мера того, сгруппированы ли числа близко друг к другу среднему или широко распространенному. Статистики разработали «стандартное отклонение» как мера этого второго свойства. Вы бы скорее не надо думать об этой загадочной формуле:
но вы были бы рады использовать процедуру стандартное отклонение которые вы нашли в сборнике статистических программ.
В конце концов, нет закона природы, согласно которому компьютеры автоматически знают
как добавить или вычесть. Вы можете себе представить, что вам нужно поручить Схеме
вычислить сумму двух больших чисел цифра за цифрой, как вы это делали в
Начальная школа. Но вместо этого кто-то «научил» ваш компьютер тому, как
добавьте, прежде чем доберетесь до него, дав этой технике имя + чтобы вы
может запросить сумму двух чисел, не задумываясь о необходимых шагах. Изобретая
Изобретая среднее или стандартное отклонение , мы расширяем
репертуар вычислений, которые вы можете запросить, не беспокоясь о себе
с деталями.
Компонуемость
Мы предложили, чтобы определяемая вами процедура, такая как среднее ,
по сути аналогичен встроенному в Scheme, например + .
В частности, правила построения выражений одинаковы независимо от того,
строительные блоки — это примитивные процедуры или определенные процедуры.
> (среднее (+ 10 8) (* 3 5)) 16,5 > (в среднем (в среднем 2 3) (в среднем 4 5)) 3,5 > (кв.м. (в среднем 143 145)) 12
Любое возвращаемое значение может использоваться как самоцель, так как возвращаемое значение
значение из sqrt использовалось в последнем из этих примеров, или оно может
передать аргумент другой процедуре в качестве возвращаемого значения из * использовалось в первом из этих примеров.
Эти небольшие примеры могут показаться произвольными, но одна и та же идея композиции
функций, является основой для всего программирования Scheme.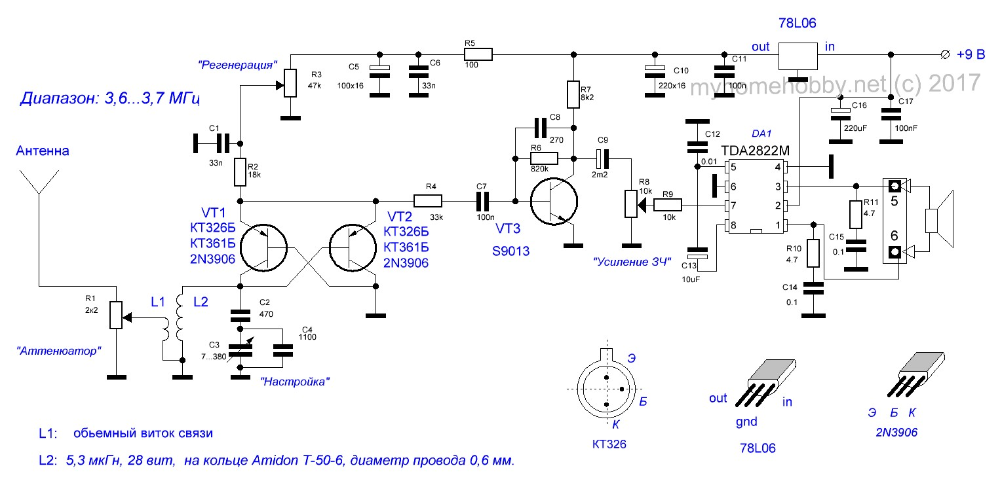 Например,
сложная формула, которую мы дали для стандартного отклонения, требует вычисления
квадраты нескольких чисел. Итак, если бы мы написали 9Процедура 0076 стандартного отклонения вызовет
Например,
сложная формула, которую мы дали для стандартного отклонения, требует вычисления
квадраты нескольких чисел. Итак, если бы мы написали 9Процедура 0076 стандартного отклонения вызовет квадратов .
Сменная модель
Мы уделили большое внимание деталям формальных параметров и фактических аргументы, но мы немного махнули рукой[3] на вопрос о том, как процедура на самом деле вычисляет значение, когда вы ее вызываете.
Мы объясним, что происходит, когда вы вызываете пользовательскую процедуру. Каждое объяснение — это история. Ни одна история не говорит всей правды, потому что всегда упускаются какие-то детали. А модель это история, которая содержит достаточно подробностей, чтобы помочь вам понять, что он пытается объяснить но не настолько подробно, чтобы за деревьями не было видно леса.
Сегодняшний рассказ о замене модели . Когда
вызывается процедура, цель состоит в том, чтобы выполнить вычисление, описанное в
его тело. Проблема в том, что тело написано в терминах формального
параметры, в то время как вычисления должны использовать фактические значения аргументов. Так
Схеме нужен способ связать фактические значения аргументов с формальными.
параметры. Это делается путем создания новой копии тела процедуры,
в котором он заменяет значения аргумента для каждого появления
формальные параметры, а затем вычисление полученного выражения. Так что если
вы определили
Проблема в том, что тело написано в терминах формального
параметры, в то время как вычисления должны использовать фактические значения аргументов. Так
Схеме нужен способ связать фактические значения аргументов с формальными.
параметры. Это делается путем создания новой копии тела процедуры,
в котором он заменяет значения аргумента для каждого появления
формальные параметры, а затем вычисление полученного выражения. Так что если
вы определили квадрат с
(определить (квадрат x) (* х х))
, тогда тело квадрата равно (* x x) . Когда ты хочешь
знать квадрат конкретного числа, как в (квадрат 5) , Схема
заменяет 5 на x везде в теле квадрата и оценивает
выражение. Другими словами, схема принимает
(* х х)
затем делает замену, получая
(* 5 5)
, а затем вычисляет это выражение, получая 25.
Если вы просто наберете (* x x) в Scheme, вы получите сообщение об ошибке
жаловаться, что x ничего не значит. Только после замены
становится ли это осмысленным выражением.
Только после замены
становится ли это осмысленным выражением.
Кстати, когда мы говорим о «замещении тела», мы не имеем в виду что определение процедуры изменено каким-либо необратимым образом. Тело процедура не меняется; происходит, как мы говорили ранее, схема создает новое выражение, похожее на тело, за исключением замены.[4]
Есть людишки, которые специализируются на квадрате , как и там
это маленькие люди, специализирующиеся на + и *. Разница в том,
что маленькие человечки, выполняющие примитивные процедуры, могут выполнять работу «по-своему».
голова», все сразу. Маленькие люди, выполняющие пользовательские процедуры
должны пройти через этот бизнес замены, о котором мы говорим здесь.
Затем они нанимают других маленьких людей, чтобы они помогли оценить получившееся выражение,
точно так же, как Алонзо нанимает людей, чтобы они помогали ему оценивать выражения, которые вы вводите
непосредственно в Схему.
Допустим, Сэм, маленький человек, который специализируется на квадратных , был
попросили вычислить (квадрат 6) .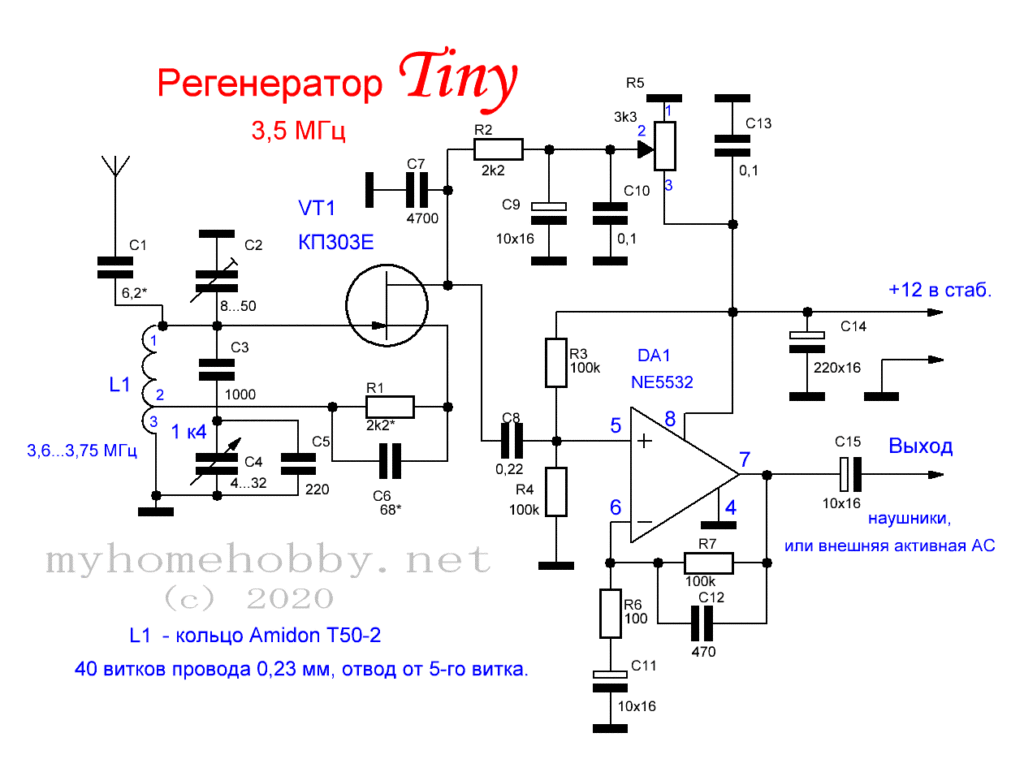 Сэм производит замену и
осталось с выражением
Сэм производит замену и
осталось с выражением (* 6 6) для оценки. Затем Сэм нанимает Тессу,
специалист по умножению, чтобы вычислить это новое выражение. Тесса говорит Сэму
что ее ответ равен 36, и, поскольку умножение — это вся проблема
решить, это тоже ответ Сэма.
Вот еще пример:
(определить (гипотенуза a b) (квадрат (+ (квадрат а) (квадрат б)))) > (гипотенуза 5 12)
Предположим, что Алонзо нанимает Гарри для вычисления этого выражения.
Сначала Гарри должен подставить фактические значения аргументов (5 и 12) в
тело гипотенуза :
(кв. (+ (кв. 5) (кв. 12)))
Теперь он оценивает это выражение так же, как его оценивал бы Алонзо.
если вы набрали его в приглашении Scheme. То есть Гарри нанимает четырех маленьких
человек: один sqrt эксперт, один + эксперт, и два квадратных эксперты.[5] В частности, некоторые небольшие
человек должен вычислить (квадрат 5) , подставив 5 вместо x в
тело квадрат , как в предыдущем примере. Точно так же мы
замените 12 на
Точно так же мы
замените 12 на x , чтобы вычислить (квадрат 12) :
(гипотенуза 5 12) ; подставить в тело ГИПОТЕНУЗЫ
(квадрат (+ (квадрат 5) (квадрат 12))) ; заменяет (КВАДРАТ 5)
(* 5 5)
25
(квадрат (+ 25 (квадрат 12))) ; заменяет (КВАДРАТ 12)
(* 12 12)
144
(кв.(+ 25 144))
(+ 25 144) ; объединить результаты, как и раньше
169(кв. 169)
13
Не забывайте, в пьянящем порыве узнать о подмене модели, то, что вы уже знали из ранее: каждая часть этого вычисления сделал маленький человек, а какой-то другой маленький человек ждет результат. Другими словами, модель подстановки говорит нам, как составная процедура выполняется, но не меняет нашу картину способ, которым вызовы процедур состоят из более крупных выражения.
Ловушки
Не забывайте, что функция может иметь только одно возвращаемое значение. Например, вот программа, которая должна возвращать сумму квадраты его двух аргументов:
(определить (сумма квадратов x y) ;; неправильно! (квадрат х) (квадрат у))
Проблема в том, что тело этой процедуры имеет два выражения,
вместо одного. Как оказалось, Scheme просто игнорирует значение
первое выражение в подобных случаях и возвращает значение последнего.
То, что хочет программист, это суммирует этих двух значений, поэтому
процедура должна сказать
Как оказалось, Scheme просто игнорирует значение
первое выражение в подобных случаях и возвращает значение последнего.
То, что хочет программист, это суммирует этих двух значений, поэтому
процедура должна сказать
(определить (сумма квадратов x y)
(+ (квадрат х)
(квадрат у)))
Еще одна ловушка связана с тем, что считается, что вызов процедуры изменяет значение параметра. Вот ошибочная программа, которая должна вычислять функция, описываемая f ( x )=3 x +10:
(определить (f x) ;; неправильно! (* х 3) (+ х 10))
Опять же, первое выражение не действует, и Scheme просто вернуть значение x +10.[6]
Очень распространенная ошибка в Scheme связана с выбором имени процедура как параметр. Это не очень часто встречается с процедуры, подобные описанным в этой главе, домены и диапазоны которых оба числа, но это будет более вероятно позже. Если у тебя есть программа такая:
(определить (квадрат x) (* х х)) (определить (квадрат площади) ;; неправильно! (квадратный квадрат))
, то у вас возникнут проблемы при вызове процедуры, т.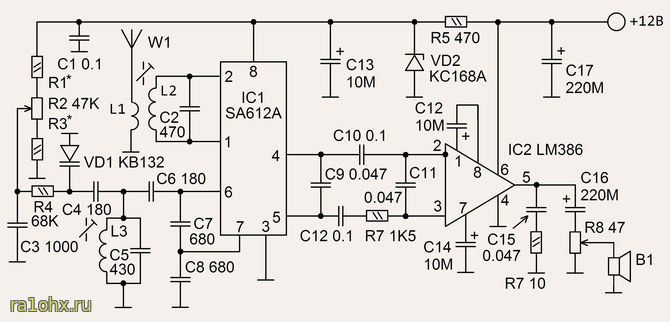 к.
например, говоря
к.
например, говоря (область 8) . площадь маленький человек будет
замените 8 на квадрат везде в определении процедуры,
оставляя вам выражение (8 8) для оценки. Это выражение
означало бы применить процедуру 8 к аргументу 8 , но 8 не является процедурой, поэтому выдается сообщение об ошибке.
Не проблема, если формальным параметром является имя процедуры, которая
вы не используете внутри тела. Проблема возникает, когда вы пытаетесь использовать
одно и то же имя, например, квадрат с двумя значениями в рамках одной процедуры.
Но специальные формы являются исключением; вы никогда не можете использовать имя специального
форму в качестве параметра.
Аналогичная проблема с конфликтами имен возникает, если вы пытаетесь
использовать ключевое слово (имя специальной формы, например, определить ) как
какое-либо другое имя — либо формальный параметр, либо имя
процедура, которую вы определяете. Мы перечисляем это отдельно, потому что
результат, скорее всего, будет другим. Вместо того, чтобы получить неправильное значение
заменены, как указано выше, вы, вероятно, увидите специальное сообщение об ошибке
по линии «неправильное использование ключевого слова».
Мы перечисляем это отдельно, потому что
результат, скорее всего, будет другим. Вместо того, чтобы получить неправильное значение
заменены, как указано выше, вы, вероятно, увидите специальное сообщение об ошибке
по линии «неправильное использование ключевого слова».
Формальные параметры должны быть словами. Некоторые пытаются писать процедуры, которые имеют составные выражения в качестве формальных параметров, например:
(определить (f (+ 3 x) y) ;; неправильно! (* х у))
Помните, что работа определения процедуры заключается только в укажите имя для аргумента. Фактический аргумент не является закреплены до тех пор, пока вы не вызовете процедуру. Люди, которые пишут такие программы, как тот, что выше, пытается заставить определение процедуры выполнять часть работы вызова процедуры.
Сверлильные упражнения
4.1 Рассмотрите эту процедуру:
(определить (хо-гум х у) (+ х (* 2 года)))
Показать замену, которая происходит при оценке
(гом 8 12)
4. 2 С учетом следующей процедуры:
2 С учетом следующей процедуры:
(определить (зевок х) (+ 3 (* х 2)))
список всех маленьких людей, которые участвуют в оценке
(зевок (/ 8 2))
(Назовите их имена, их специальности, их аргументы, кто их нанимает и что они делают со своими ответами.)
4.3 Вот несколько определений процедур. Для каждого из них опишите функцию в English, покажите пример вызова и покажите результат этого вызова.
(определить (f x y) (- y x))
(определить (тождество х) х)
(определить (три х) 3)
(определить (семь) 7)
(определить (магическое n)
(- (/ (+ (+ (*3 н)
13)
(- п 1))
4)
3))
Реальные упражнения
4.4 Каждое из следующих определений процедур содержит какую-либо ошибку. Скажите, что не так и почему, и исправьте это:
(определить (сфера-объем r) (* (/ 4 3) 3.141592654) (* р р р)) (определить (следующий х) (х + 1)) (определить (квадрат) (* х х)) (определить (треугольник-площадь треугольника) (* 0,5 высоты основания)) (определить (сумма квадратов (квадрат x) (квадрат y)) (+ (квадрат x) (квадрат y)))
4,5 Напишите процедуру преобразования температуры из градусов Фаренгейта в градусы Цельсия и
другой, чтобы преобразовать в другом направлении.  Две формулы F = 9 ⁄ 5 C +32 и C = 5 ⁄ 9 —
Две формулы F = 9 ⁄ 5 C +32 и C = 5 ⁄ 9 —
4.6 Определить процедуру четвертой , которая вычисляет четвертую степень своего
аргумент. Сделайте это двумя способами, сначала используя функцию умножения,
а затем с использованием в квадрате , а не (напрямую) с использованием умножения.
4.7 Напишите процедуру, которая вычисляет абсолютное значение своего аргумента с помощью нахождение квадратного корня из квадрата аргумента.
4.8 «Научная нотация» — это способ представления очень маленьких или очень больших
числа, комбинируя число среднего размера со степенью 10. Например,
5×10 7 представляет число 50000000, а 3,26×10 -9 представляет 0,00000000326 в экспоненциальном представлении. Написать процедуру
Написать процедуру научный , который принимает два аргумента, число и показатель степени 10,
и возвращает соответствующее значение:
> (научный 7 3) 7000 > (научный 42 -5) 0,00042
Некоторые версии Схемы представляют дроби в форме a / b , и
некоторые используют научную запись, поэтому вы можете увидеть 21/50000 или 4.2E-4 .
в результате последнего примера вместо 0,00042 , но это
такое же значение.
(Более сложная проблема для хотшотов: можете ли вы написать процедуры, которые идут в другое направление? Так что у вас будет
> (научный коэффициент 7000) 7 > (научный показатель 7000) 3
Вы можете найти примитивные процедуры журнал и этаж полезно.)
4.9 Определить процедуру скидки , которая принимает два аргумента:
начальная цена и процентная скидка. Он должен вернуть новую цену:
> (скидка 10 5) 9.50 > (скидка 29,90 50) 14,95
4.10 Напишите процедуру для расчета чаевых, которые следует оставлять в ресторане. Это
должен принимать общий счет в качестве аргумента и возвращать сумму
кончик. Он должен дать чаевые на 15%, но он должен уметь округлять, чтобы
общая сумма денег, которую вы оставляете (чаевые плюс первоначальный счет), представляет собой целое число
долларов. (Используйте потолок процедура округления.)
> (наконечник 19.98) 3.02 > (совет 29.23) 4,77 > (совет 7.54) 1,46
[1] Технически весь выражение
(define (квадрат x) &hellip) — это специальная форма; слово , определяющее само , называется ключевым словом . Но на самом деле лиспийцы
почти всегда забывают об этом различии и говорят: « определяет как
особая форма», так же, как мы сделали здесь. Слово «форма» — архаичное
синоним слова «выражение», поэтому «особая форма» просто означает «особая форма».
выражение».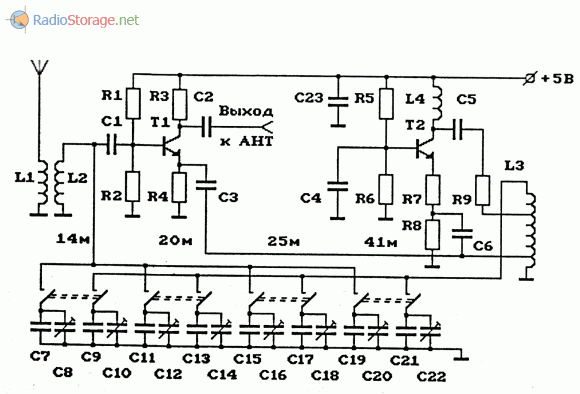
[2] Кроме того, иногда мы будем использовать термины «домен» и «диапазон», когда мы говорим о процедурах, хотя технически только функции имеют домены и диапазоны.
[3] Знаешь, это когда вы машете руками в воздухе вместо того, чтобы объяснить, что вы иметь в виду.
[4] Вы можете подумать, что это скорее неэффективный способ делать что-то — все это копирование и замена перед тем, как вы на самом деле может вычислить что угодно. Возможно, вы боитесь, что ваша Схема в результате программы будут работать очень медленно. Не волнуйся. Это реально происходит по-разному, но эффект тот же, за исключением скорость.
[5] Пока мы не начали определять наши собственные процедуры в этом
глава, все маленькие люди были наняты Алонзо, потому что все
выражения вводились непосредственно в приглашение схемы. Теперь выражения могут
исходить из органов процедур, и таким людям нужно было
вычисления этих выражений наняты маленьким человеком, который вычисляет
та процедура. Заметьте также, что каждый маленький человек отчитывается перед . другой маленький человек, не обязательно тот, кто нанял ее. В
этом случае, если Гарри наймет Шари за
другой маленький человек, не обязательно тот, кто нанял ее. В
этом случае, если Гарри наймет Шари за sqrt , Пол для + и Тонкий
и Сидней за два квадратных с, то Слим отчитывается перед Полом, а не перед
Гарри. Только Шари подчиняется непосредственно Гарри.
[6] Это особенно проблематично для людей
кто раньше программировал на таких языках, как Pascal или BASIC, где вы говорите что-то
как « X = X * 3 » все время.
(обратно к оглавлению)
ЗАДНЯЯ резьба главы СЛЕДУЮЩАЯ
Брайан Харви, [email protected] Схема— Как сделать квадрат в РАКЕТКЕ
спросил
Изменено 4 месяца назад
Просмотрено 14 тысяч раз
Вот мой код:
(определить (квадраты 1-й)
(пусть петля ([1-й 1-й] [акк 0])
(если (ноль? 1-й)
согласно
(петля (ост. 1ст) (*(первый 1ст) (первый 1ст) приб)))))
1ст) (*(первый 1ст) (первый 1ст) приб)))))
Мой тест:
(тест (сумма квадратов '(1 2 3)) => 14 )
и это не удалось.
Вход функции — это список чисел, например [1 2 3], и мне нужно возвести каждое число в квадрат и просуммировать их все вместе, выход — число. Тест вернет #t, если был введен правильный ответ.
- схема
- ракетка
2
Это очень похоже на ваш предыдущий вопрос, но с изюминкой: здесь мы добавить вместо умножения. И каждый элемент возводится в квадрат перед его добавлением:
(define (sum-squares lst)
(если (пусто? lst)
0
(+ (* (первый лст) (первый лст))
(сумма-квадраты (остальные lst)))))
Как и прежде, процедуру можно записать с использованием хвостовой рекурсии:
(определить (сумма-квадраты lst)
(let loop ([lst lst] [acc 0])
(если (пусто? lst)
согласно
(петля (ост. лст) (+ (* (первый лст) (первый лст)) согл)))))
лст) (+ (* (первый лст) (первый лст)) согл)))))
Вы должны понимать, что оба решения имеют одинаковую структуру, какие изменения:
- Мы используем
+, чтобы объединить ответы вместо* - Мы возводим в квадрат текущий элемент
(первый первый)перед его добавлением - Базовый вариант для добавления списка:
0(было1для умножения)
В качестве последнего комментария: в реальном приложении вы не должны использовать явную рекурсию, вместо этого мы будем использовать процедуры более высокого порядка для составления нашего решения:
(определить (квадрат x) (* х х)) (определить (сумма-квадраты lst) (применить + (квадрат карты lst)))
Или даже короче, как однострочный (но полезно иметь процедуру квадратов , поэтому я предпочитаю предыдущее решение):
(define (sum-squares lst) (применить + (карта (лямбда (х) (* х х)) лст)))
Конечно, любое из приведенных выше решений работает так, как ожидалось:
(сумма-квадраты '()) => 0 (сумма квадратов '(1 2 3)) => 14
3
Более функциональным способом было бы объединение простых функций ( сумма и квадрат ) с функциями высокого порядка ( карта ):
(определить (квадрат x) (* x x)) (определить (сумма lst) (foldl + 0 lst)) (определить (сумма-квадраты lst) (сумма (карта квадрат lst)))
Мне нравится ответ Бенеша, он просто немного изменил его, чтобы вам не приходилось дважды просматривать список. (Однократное сгибание по сравнению с картой и сгибанием)
(Однократное сгибание по сравнению с картой и сгибанием)
(определить (квадрат x) (* x x)) (определить (квадрат-y-и-добавить-x x y) (+ x (квадрат y))) (определить (сумма-квадраты lst) (сложить квадрат-y-and-addto-x 0 lst))
Или вы можете просто определить map-reduce
(define (map-reduce map-f reduce-f nil-value lst)
(если (пусто? lst)
нулевое значение
(карта-уменьшить карту-f уменьшить-f (уменьшить-f нулевое значение (карта-f (автомобиль первый))))))
(определить (сумма-квадраты lst) (карта-уменьшить квадрат + 0 lst))
1
ракетка@> (определить (f xs) (foldl (лямбда (x b) (+ (* x x) b)) 0 xs)) ракетка@> (f '(1 2 3)) 14
Без использования петель или ламд, cond можно использовать для решения этой проблемы следующим образом (printf добавлен только для того, чтобы мои упражнения отличались друг от друга. Это упражнение из SICP: упражнение 1.3):
;; Принимает три числа и возвращает сумму квадратов двух больших чисел.



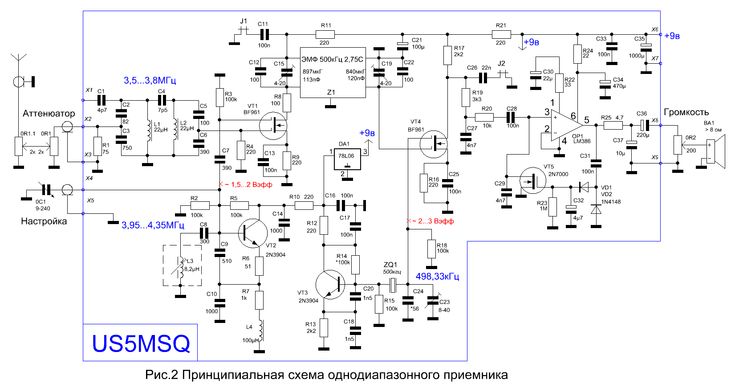 Она содержит 8,5 витков провода ПЭВ-0,12. Все остальные катушки данного приемника — готовые высокочастотные дроссели.
Она содержит 8,5 витков провода ПЭВ-0,12. Все остальные катушки данного приемника — готовые высокочастотные дроссели.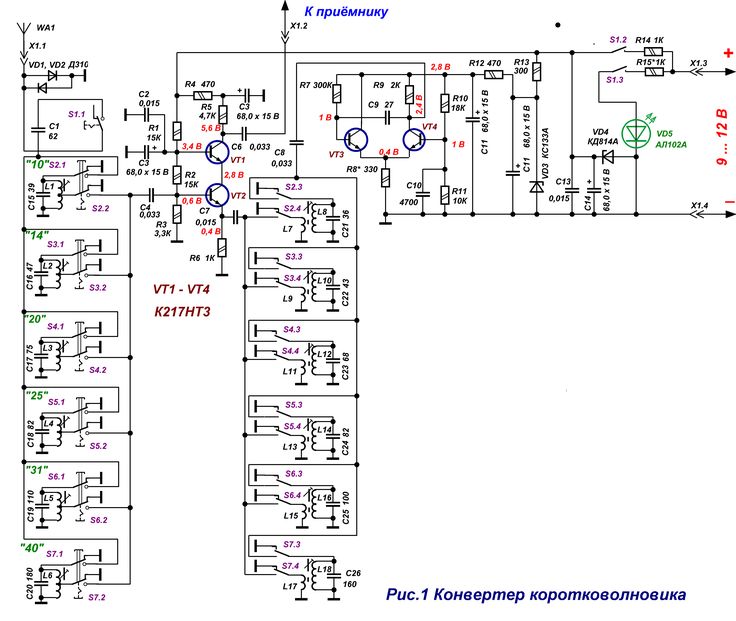 Пожилой мужчина. &rsquo ”
Пожилой мужчина. &rsquo ”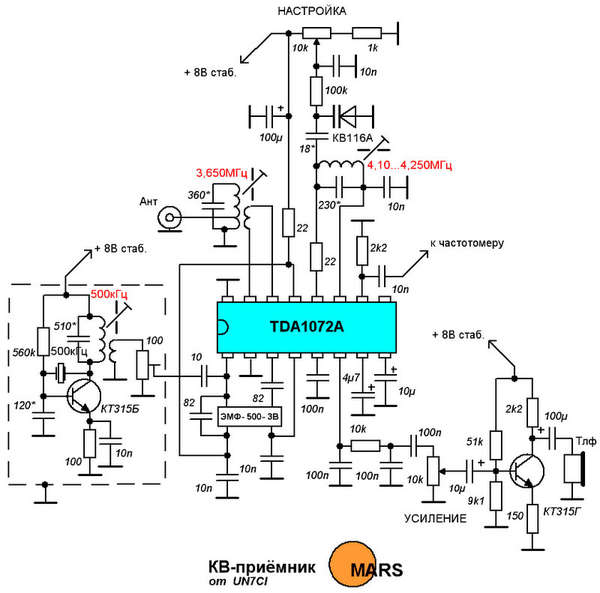 50
> (скидка 29,90 50)
14,95
50
> (скидка 29,90 50)
14,95
 1ст) (*(первый 1ст) (первый 1ст) приб)))))
1ст) (*(первый 1ст) (первый 1ст) приб)))))
 лст) (+ (* (первый лст) (первый лст)) согл)))))
лст) (+ (* (первый лст) (первый лст)) согл)))))