Резистор
16 декабря 2022 — Admin
Главная / Теория
Резистор — один из самых простых электронных компонентов. Вместе с тем, без резисторов не обходится практически ни одна схема. Казалось бы, что важного он делает — только сопротивляется току, и больше ничего? Но не всё так просто. В этой статье собраны все базовые знания о резисторах, необходимые электронщику.
Содержание статьи:
- Общие сведения о резисторах
- Закон Ома
- Как измерить сопротивление
- Параллельное и последовательное соединение резисторов
- Применение: делители напряжения и тока
- Рассеиваемая мощность
- Устройство резистора
- Паразитные характеристики
- Переменные и подстроечные резисторы
- Другие типы резисторов
Общие сведения
Резистор, или сопротивление, относятся к пассивным компонентам электрических цепей. Пассивный — значит, не привносящий в цепь дополнительную энергию. В отличие от, например, транзистора — который способен усиливать слабый сигнал, добавляя к нему энергию от более мощного источника питания.
В отличие от, например, транзистора — который способен усиливать слабый сигнал, добавляя к нему энергию от более мощного источника питания.
Резистор оказывает сопротивление идущему через него току. В качестве механической аналогии можно представить трубу с водой. Резистор — сужение на этой трубе, замедляющее поток. Из-за сужения по трубе будет проходить меньше воды в единицу времени.
Сужение в трубе, замедляющее поток
Резистор обозначается на схеме вытянутым прямоугольником, с двумя выводами. Обычно каждому резистору присваивается буква R с порядковым номером. Иногда в зарубежной литературе можно встретить обозначение ломаной линией.
Два варианта обозначения резистора на схемах
Резистор и закон Ома
Главная характеристика резистора — его сопротивление. Оно измеряется в Омах. А ток, проходящий через резистор, зависит от приложенного напряжения. Перечисленные величины связаны законом Ома. При этом в случае идеального резистора ток линейно зависит от напряжения, то есть резистор обладает линейной вольт-амперной характеристикой:
Вольт-амперные характеристики двух резисторов и закон Ома
Как измерить сопротивление резистора
В лаборатории радиолюбителя для измерения сопротивлений должен быть омметр. Обычно, эта функция входит в состав комбинированных приборов, мультиметров. Между тем, принцип измерения сопротивления основан всё на том же законе Ома: омметр прикладывает к тестируемому резистору небольшое напряжение и замеряет ток, после чего вычисляет сопротивление.
Обычно, эта функция входит в состав комбинированных приборов, мультиметров. Между тем, принцип измерения сопротивления основан всё на том же законе Ома: омметр прикладывает к тестируемому резистору небольшое напряжение и замеряет ток, после чего вычисляет сопротивление.
Измерение сопротивления с помощью мультиметра. В данном примере взят резистор 20 кОм.
Кстати, об этом нужно помнить, тыкая омметром в схемы: на схему попадает небольшое напряжение, которое для чувствительных деталей может оказаться фатальным.
Параллельное и последовательное соединение резисторов
Резисторы нужны в схеме, чтобы упрявлять токами и напряжениями. Но сначала нужно разобраться, как они взаимодействуют между собой и с другими элементами схемы.
Если соединить несколько резисторов последовательно, через каждый из них будет течь одинаковый ток. Это логично: сколько зарядов вошло в цепь, столько же должно выйти на другом конце, закон сохранения заряда. А вот напряжение (потенциал) распределяется по-разному.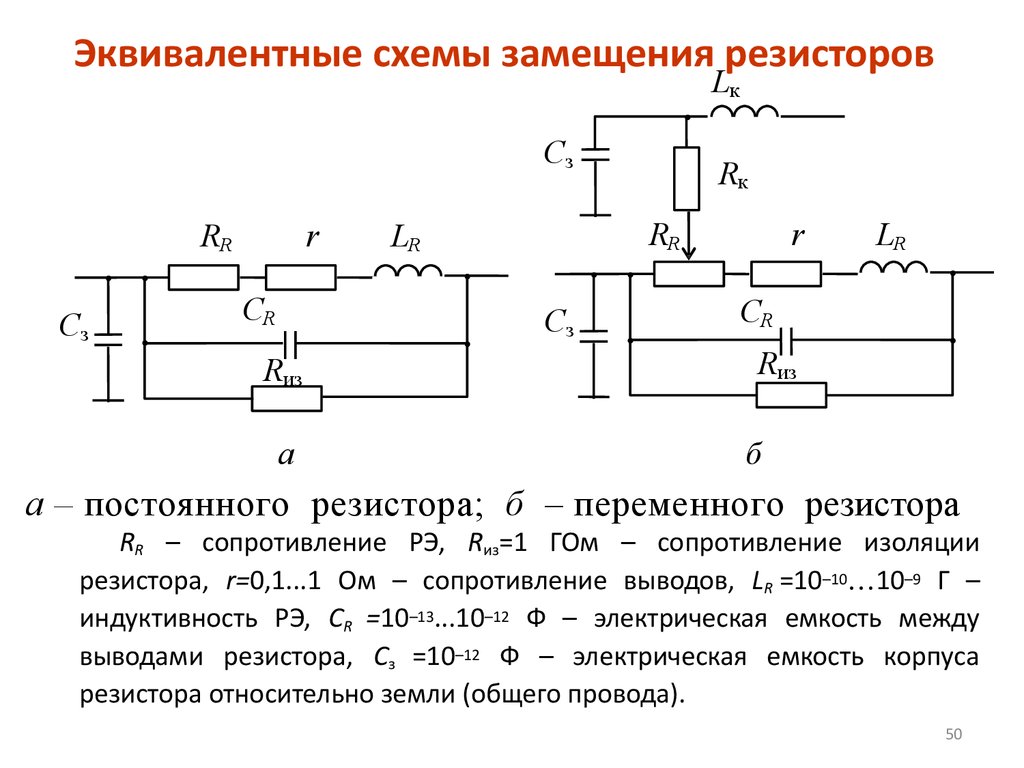 Чем выше сопротивление резистора, тем больше на нём падение напряжения — нужно большее усилие, чтобы протолкнуть через большое сопротивление заряды.
Чем выше сопротивление резистора, тем больше на нём падение напряжения — нужно большее усилие, чтобы протолкнуть через большое сопротивление заряды.
При этом, если просуммировать потенциал на всех резисторах, сумма будет равна напряжению, приложенному к концам цепи. Отсюда выводится формула суммарного сопротивления цепочки из последовательных резисторов: оно равно сумме сопротивлений всех резисторов.
Последовательное соединение резисторов
При параллельном соединении резисторов картина иная. Здесь фиксировано напряжение — оно одинаковое на каждом резисторе. А вот ток будет разный — он потечёт туда, где ему легче пройти. Опять же, применяя несложные рассуждения и используя закон Ома, выводится формула общего сопротивления параллельно соединённых резисторов.
Параллельное соединение резисторов
Более сложные, смешанные соединения резисторов разбиваются на небольшие блоки, и так последовательно, от меньших к большим блокам считается общее сопротивление:
Сложное соединение резисторов.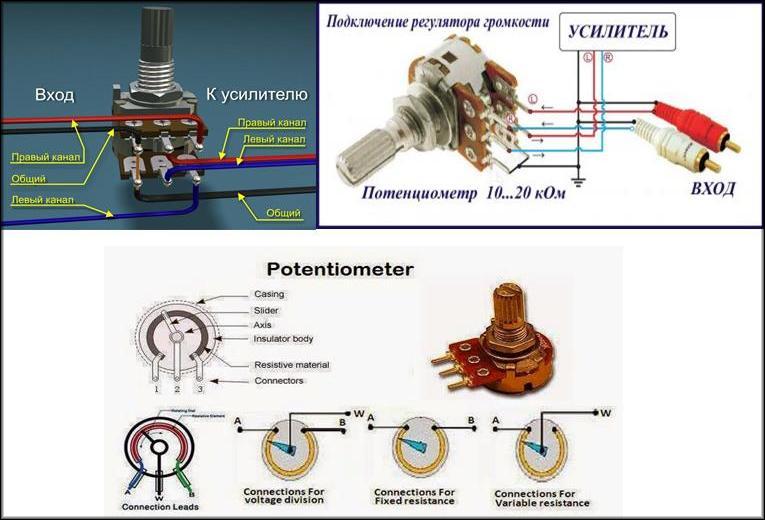 Сначала считаем блок R1,R2 (параллельные), потом к этому блоку добавляем последовательно R3, наконец, считаем параллельно R1,R2,R3 и R4. Если каждое сопротивление по 10 Ом, общее сопротивление получается 6 Ом.
Сначала считаем блок R1,R2 (параллельные), потом к этому блоку добавляем последовательно R3, наконец, считаем параллельно R1,R2,R3 и R4. Если каждое сопротивление по 10 Ом, общее сопротивление получается 6 Ом.
Нужно добавить, что иногда разбить на блоки невозможно. В этом случаи применяются более сложный метод расчёта — правила Кирхгофа.
Применение резисторов в схемах
Итак, как же с помощью резисторов управляют напряжениями и токами? Допустим, стоит задача ограничить напряжение на нагрузке. Под «нагрузкой» здесь может пониматься любой элемент или узел схемы, на котором мы хотим получить заданное напряжение или заданный ток. Это могут быть и лампочка, и светодиод, и следующий каскад усилителя и т. д.
Самое простое — поставить последовательно с нагрузкой гасящий резистор. Как мы обсуждали выше, в этом случае напряжение распределится между элементами в соответствии с сопротивлением каждого. То есть, получается делитель напряжения.
Схема делителя напряжения, когда нагрузка является элементом делителя.
А что делать, если сопротивление нагрузки очень велико или не постоянно? В этом случае ставят два последовательных резистора, образующих плечи делителя. А нагрузка снимает напряжение с одного из них. Подчеркну, что всегда нужно помнить про сопротивление нагрузки. Оно должно быть достаточно большим, чтобы им можно было пренебречь при расчёте делителя.
Схема делителя напряжения, когда нагрузка подключена параллельно нижнему плечу делителя
Если последовательное соединение резисторов является делителем напряжения, нетрудно догадаться, что паралелльное соединение — делитель тока. На рисунке приведён способ ограничить ток через нагрузку — поставить параллельно ей резистор, так называемый шунт. Который будет отвевлять на себя часть тока, обратно пропорциональную его сопротивлению.
Схема делителя тока
Мощность резистора
Резистор сопротивляется проходящему току. Значит, он отбирает у тока часть энергии. И куда она девается? Переходит в тепло.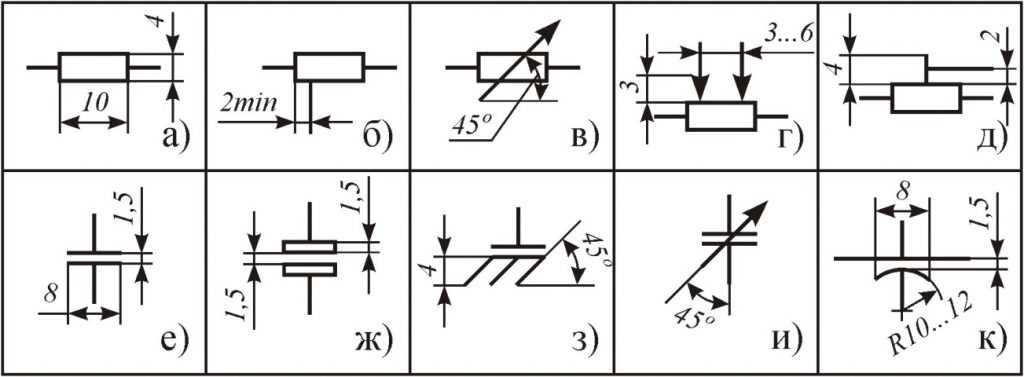 Мощность, рассеиваемая на резисторе, считается по формуле P = U*I. Поскольку U, I и R связаны законом Ома, можно записать несколько вариантов этой формулы, выражая мощность через U и R, или через R и I. Кстати, на сайте есть онлайн-калькулятор мощности и закона Ома.
Мощность, рассеиваемая на резисторе, считается по формуле P = U*I. Поскольку U, I и R связаны законом Ома, можно записать несколько вариантов этой формулы, выражая мощность через U и R, или через R и I. Кстати, на сайте есть онлайн-калькулятор мощности и закона Ома.
Так вот, если ток через резистор слишком велик, из-за большой рассеиваемой мощности резистор перегреется и выйдет из строя, в буквальном смысле, сгорит. В этом случае нужно взять резистор такого же номинала, но рассчитанный на бОльшую мощность рассеивания. Более мощные резисторы и физически большего размера, чтобы увеличить площадь рассеивания тепловой энергии.
Там, где это важно (где ожидаются сравнительно большие токи), на схемах указывают, на какую мощность должен быть рассчитан резистор, с помощью следующих обозначений:
Допустимая мощность рассеивания резистора
Устройство резисторов
Из школьного курса физики мы знаем, что сопротивление проводника определяется его удельным сопротивлением, длинной и сечением.
Формула сопротивления проводника
В начале статьи приводилась механическая аналогия резистора, как сужения трубы. Это работает и в элекрике: если уменьшить сечение проводника, его сопротивление увеличится.
Поэтому, резисторы делают из тонкой проволоки, из тонких плёнок разных металлов и сплавов, из композитных материалов. При этом, чтобы увеличить эффективную длину, в резистивном слое нарезают различного вида спирали и канавки:
Очень условно показано устройство резистора. Слева: на поверхности цилиндрической основы резистора слой токопроводящего материала, в котором нарезаны канавки для увеличения сопротивления. Справа: плёночный вариант.
Паразитные характеристики
Но, такой подход, кроме плюсов, даёт ещё и некоторые минусы. Дело в том, что реальный резистор, в отличие от идеального, обладает не только сопротивлением, но и некоторой индуктивностью и ёмкостью. То есть схема реального резистора выглядит примерно так:
Схема замещения резистора
Ёмкость и индуктивность — паразитные характеристики резистора, они искажают его функции в схеме.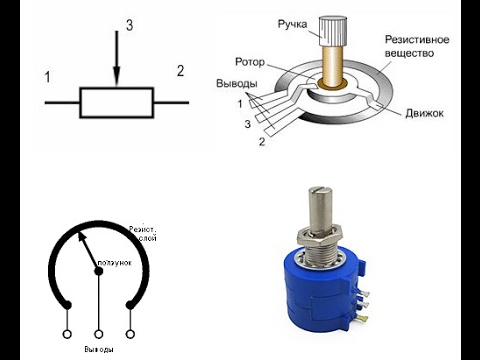 И само по себе устройство резистора может являться причиной этих паразитных свойств. Спиральные канавки в резистивном слое — чем не витки катушки индуктивности? А между близко расположенными участками проводящего слоя возникает ёмкость.
И само по себе устройство резистора может являться причиной этих паразитных свойств. Спиральные канавки в резистивном слое — чем не витки катушки индуктивности? А между близко расположенными участками проводящего слоя возникает ёмкость.
Хотя эти индуктивность и ёмкость небольшие по величине, но в некоторых ситуациях (например, на высоких частотах) способны вносить заметные искажения.
Поэтому, при изготовлении резисторов применяют различные ухищрения, чтобы снизить паразитные характеристики. Например, нарезают канавки хитрым рисунком. Впрочем, эта тема уже выходит за рамки данной статьи.
Переменные и подстроечные резисторы
Иногда в схеме необходимы резисторы с переменным сопротивлением. Они являются элементами настройки и управления.
Различают переменные резисторы (обычно их ручку выводят на панель управления) и подстроечные (которые регулируются отвёрткой на плате и к которым нет доступа, пока не разобрать корпус устройства). Вот как они выглядят:
Переменные и подстроечные резисторы
У них три вывода.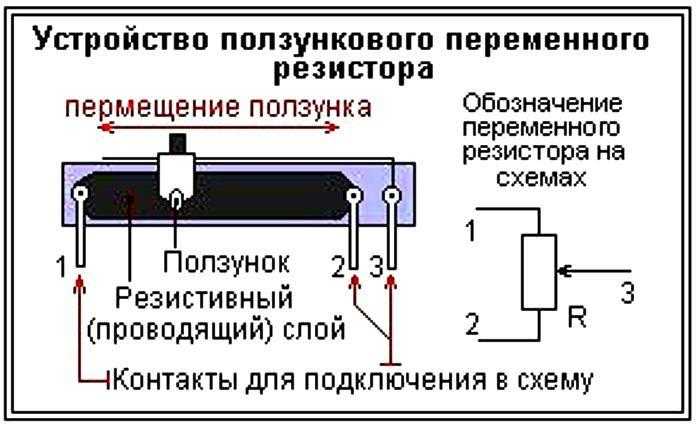 Между двумя крайними постоянное сопротивление. А средний «скользит» между ними. Таким образом, получается готовый делитель напряжения, с регулируемым сопротивлением плечей.
Между двумя крайними постоянное сопротивление. А средний «скользит» между ними. Таким образом, получается готовый делитель напряжения, с регулируемым сопротивлением плечей.
Если средний вывод соединить с одним из крайних — получится реостат, резистор с переменным сопротивлением.
Другие типы резисторов
В заключение остаётся упомянуть некоторые специфичные типы резисторов. Например, теримистор. Его сопротивление зависит от температуры, и этот тип резисторов широко используется в электронных термометрах и схемах контроля температуры.
Или, фоторезистор. Его сопротивление зависит от освещённости.
Варисторы — уменьшают своё сопротивление при росте приложенного напряжения. Могут использоваться в схемах защиты и стабилизаторах.
Поделиться в соцсетях:
Энергетическое образование
5. Термометры сопротивления
Термопары генерируют напряжение при нагревании и возникающий ток позволяет проводить измерения температуры. Термометры сопротивления наоборот представляют собой электрические температурные датчики, которые используют изменения сопротивления, которое противодействует протеканию тока. В английском языке термометр сопротивления обозначается тремя буквами «RTD».
Термометры сопротивления наоборот представляют собой электрические температурные датчики, которые используют изменения сопротивления, которое противодействует протеканию тока. В английском языке термометр сопротивления обозначается тремя буквами «RTD».
На следующем рисунке дано схематичное изображение стандартного термометра сопротивления. Основным электрическим компонентом термометра сопротивления является резистор, который часто представляет собой провод, обмотанный вокруг керамического изолятора в виде стержня. Резистор и является температурным чувствительным элементом термометра сопротивления. Для защиты чувствительного элемента от физического воздействия и изоляции электрической цепи от технологической жидкости во избежании короткого замыкания резистор обычно заключается в корпус из нержавеющей стали. Два провода подсоединяются к электрической цепи внутри корпуса посредством герметичного уплотнения.
Части термометра сопротивления.Термометры (RTD) могут использоваться для измерения температуры электрическим путем, так как существует прямо пропорциональная зависимость между изменениями сопротивления и изменением температуры.
Другими словами при повышении температуры величина сопротивления возрастает прямо пропорционально, а при понижении температуры сопротивление пропорционально уменьшается. Подобный принцип используется в термометрах сопротивления, так как сопротивление термометра уменьшается или увеличивается пропорционально температуре процесса, который он измеряет. Любое изменение сопротивления может быть зарегистрировано и преобразовано в температурные показания с помощью таблицы, или отображено на шкале, которая откалибрована в единицах измерения температуры.
Как и термопара или любой другой температурный датчик термометр сопротивления (RTD) функционален при измерении температуре только, если он подсоединен к электрической цепи. Обычно с термометрами сопротивления применяются мостовые схемы, так как такие схемы позволяют добиться высокой точности. На следующем рисунке изображена типичная мостовая схема и батарея, которая служит в качестве источника питания. Цепи термометров сопротивления должны иметь внешний источник питания, так как они не способны генерировать напряжение сами.
Мостовая схема состоит из пяти резисторов (Р1, R2, R3, R4, R5) и пяти точек соединения (А,В,С,0).
Предположим, что каждый резистор в мостовой схеме обладает одинаковым сопротивлением. Так как ток протекает от минуса к плюсу в данном контуре, то протекание начинается с минусовой клеммы батареи и ток достигает точки А. В точке А ток расщепляется на равные части: одна половина протекает через сопротивление R1 в точку В, а другая половина протекает через R2 к точке С. Так как сопротивление всех резисторов одинаковое, то между точками В и С нет разницы в величине напряжения, поэтому ток через R5 не протекает.
Когда ток через средний резистор не протекает, то мост, как говорится «уравновешен». В данном примере ток протекает от точки В, через R3 в точку D. Ток также протекает от точки С через R4 в точку D. Ток от точки D возвращается на положительную клемму батареи, завершая цепь.
Протекание тока через уравновешенный мост.
Мостовая схема, изображенная следующей схеме похожа на предыдущую схему за исключением того, что резистор R3 заменен термометром сопротивления. В данной конфигурации ток по-прежнему протекает от минусовой клеммы батареи на точки В и С. Однако, если сопротивление термометра сопротивления (RTD) отличается по величине от сопротивления резистора R4, то между точками В и С появится напряжение. Это означает, что мост неуравновешен и ток будет протекать через резистор R5.
Мостовая схема с термометром сопротивления.Ток, протекающий через мост, может быть измерен, если мы заменим R5 измерительным прибором, который и будет определять температуру, измеряя ток. Так схема обеспечивает высокую точность, то она часто используется вместе с термометрами сопротивления для измерения температуры.
Мостовая схема с термометром сопротивления и измерительным прибором.Когда для измерения температуры используются термометры сопротивления RTD, то они включаются в схему, подобно той, что показана на предидещем рисунке.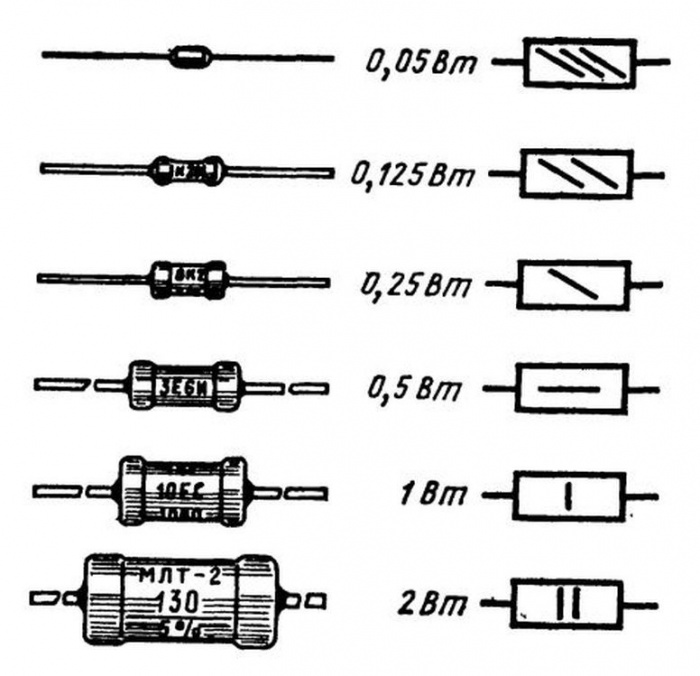 Во многих случаях термометры сопротивления расположены на удалении от остальных элементов цепи, так как они подвержены воздействию температуры технологического процесса. По мере того, как температура вокруг термометра меняется, то пропорционально меняется величина сопротивления термометра. Когда сопротивление термометра меняется, то мост становится неуравновешенным и определенный ток протекает через измерительный прибор. Этот ток пропорционален изменениям температуры. Температура процесса затем может быть определена по показаниям шкалы прибора. В некоторых случаях шкалы окалиброваны на показания величины сопротивления, а не температуры. В таких случаях надо воспользоваться переводной таблицей для перевода ом в градусы.
Во многих случаях термометры сопротивления расположены на удалении от остальных элементов цепи, так как они подвержены воздействию температуры технологического процесса. По мере того, как температура вокруг термометра меняется, то пропорционально меняется величина сопротивления термометра. Когда сопротивление термометра меняется, то мост становится неуравновешенным и определенный ток протекает через измерительный прибор. Этот ток пропорционален изменениям температуры. Температура процесса затем может быть определена по показаниям шкалы прибора. В некоторых случаях шкалы окалиброваны на показания величины сопротивления, а не температуры. В таких случаях надо воспользоваться переводной таблицей для перевода ом в градусы.
Термистор это чувствительный к изменениям температуры элемент, изготовленный из полупроводникового материала. Он ведет себя как резистор, чувствительный к изменениям температуры. Термин «термистор» это сокращение от термочувствительного резистора. Полупроводниковый материал это материал, который проводит электрический ток лучше чем диэлектрик, но не так хорошо как проводник.
Подобно термометрам сопротивления термисторы используют изменения величины сопротивления в качестве основы измерений. Однако сопротивление термистора обратно пропорционально изменениям температуры, а не прямо пропорционально. По мере увеличения температуры вокруг термистора, его сопротивление понижается, а по мере понижения температуры его сопротивление увеличивается.
Так как и термометры и термисторы реагируют на изменения температуры пропорциональным изменением сопротивления, то они оба часто используются в мостовых схемах. На следующем рисунке показана мостовая схема с термистором. В данной конфигурации резисторы R1, R2 и R4 имеют одинаковые значения сопротивления.
Мостовая схема с термистором.В данной цепи изменение температуры и обратно пропорциональная зависимость между температурой и сопротивлением термистора будет определять направление протекания тока. Иначе цепь будет функционировать таким же образом как в случае с термометром сопротивления. По мере изменения температуры термистора, изменяется его сопротивление и мост становится неуравновешенным. Теперь через прибор будет протекать ток, который можно будет измерить. Измеряемый ток можно преобразовать в единицы измерения температуры с помощью переводной таблицы, или откалибровав соответствующим образом шкалу.
Теперь через прибор будет протекать ток, который можно будет измерить. Измеряемый ток можно преобразовать в единицы измерения температуры с помощью переводной таблицы, или откалибровав соответствующим образом шкалу.
Ввиду своего сходства термисторы и термометры сопротивления часто применяются для измерения температур в сходном диапазоне. Однако необходимо знать разницу между термисторами и термометрами сопротивления. Термисторы реагируют на изменения темературы обратно пропорционально, а термометры сопротивления прямо пропорционально.
Как ведет себя резистор в цепи переменного тока
- Калькуляторы
- Задачи проектирования
Войти
Добро пожаловать! Войдите в свою учетную запись
ваше имя пользователя
ваш пароль
Забыли пароль?
Создать учетную запись
Политика конфиденциальности
Зарегистрироваться
Добро пожаловать!Зарегистрируйте аккаунт
ваш адрес электронной почты
ваше имя пользователя
Пароль будет отправлен вам по электронной почте.
Политика конфиденциальности
Восстановление пароля
Восстановить пароль
ваш адрес электронной почты
Поиск
Изменено:
Статьи категории
Цепь, содержащая только резистор в цепи переменного тока, известна как чисто резистивная цепь переменного тока. Существование индуктивности и емкости не существует в цепи чистого сопротивления. Переменный ток и напряжение движутся как вперед, так и назад, как по направлению к цепи. В результате переменный ток, а также напряжение имеют синусоидальную форму волны или называются синусоидальной формой волны.
В чисто резистивной цепи мощность рассеивается через резисторы, а фаза напряжения и тока остается неизменной, т. е. и напряжение, и ток достигают своего максимального значения одновременно. Резистор — это пассивное устройство, которое не производит и не потребляет энергию. Он преобразует электрическую энергию в тепловую.
В цепи переменного тока отношение напряжения к току зависит от частоты питания, фазового угла и разности фаз. В резистивной цепи переменного тока значение сопротивления резистора в цепи переменного тока, безусловно, будет одинаковым, независимо от частоты источника питания.
Напряжение переменного тока, приложенное в цепи, будет представлено уравнением:
Тогда мгновенное значение тока, протекающего через резистор в цепи переменного тока, будет таким, как показано на следующем рисунке:
Значение тока будет максимум, когда ωt = 90 градусов или sinωt = 1
. Подставив значение sinωt в приведенное выше уравнение, мы получим:
Фазовый угол и форма сигнала сопротивления
Формула 1 и уравнение 3 показывают, что между приложенное напряжение, а также ток, протекающий через цепь чистого сопротивления, т. Е. Фазовый угол между напряжением и током равен нулю. Следовательно, в цепи переменного тока, включающей чистое сопротивление, ток остается в фазе с напряжением, показанным на рисунке ниже.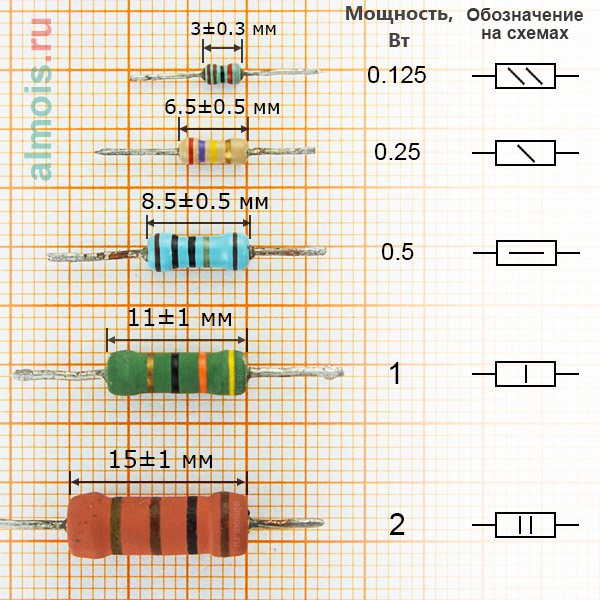
Мощность, рассеиваемая резистором в цепи переменного тока
Три цвета: красный, синий и розовый, отображаемые на кривой мощности или осциллограмме, указывают на кривую для тока, напряжения и мощности. Из диаграммы индикатора видно, что ток и напряжение находятся в фазе друг с другом, что указывает на то, что значения тока и напряжения достигают своего пика в одно и то же время, а кривая мощности всегда положительна для всех значений тока, а также напряжения. .
Как и в силовой цепи постоянного тока, произведение напряжения на ток называется мощностью в цепи, точно так же мощность в цепи переменного тока точно такая же, с той лишь разницей, что в цепи переменного тока непосредственная учитывается значение напряжения и тока. Мгновенная мощность в полностью резистивной цепи определяется уравнением, показанным ниже
Мгновенная мощность, p = vi
Средняя мощность, потребляемая в цепи за весь цикл, определяется по следующему уравнению:
Для клапана cosωt равен нулю выше значение мощности будет дано преобразованным уравнением:
Где,
- P – средняя мощность
- В действ.
 – Среднеквадратичное значение напряжения питания
– Среднеквадратичное значение напряжения питания - I действующее значение – Среднеквадратичное значение тока
Таким образом, мощность в чисто резистивной цепи определяется как:
P=VI
Напряжение и ток в чисто резистивной цепи находятся в фазе друг с другом без различия фаз с фазовым углом no. Переменная величина достигает пикового значения в интервале той же самой длительности, в которой одновременно возникают возрастающее и падающее напряжение, а также ток.
Михал
Инженер электроники и телекоммуникаций с дипломом магистра электроэнергетики. Светодизайнер опытный инженер. В настоящее время работает в сфере IT.
Английский
Закон о резисторных цепях и сопротивлении
Ключевые термины
- Резистор
- Идеальный проводник
- Сопротивление
- Закон Ома
- Падение напряжения
- Рассеиваемая мощность
Цели
- Определение сопротивления и роли резисторов в электрических цепях
- Используйте закон Ома, чтобы связать напряжение, ток и сопротивление
- Определите, сколько тепла выделяется в резисторе по отношению к его напряжению и току
Размещение проводника (например, провода) на клеммах батареи (тип источника питания) быстро истощает накопленную энергию.
Обратите внимание: не пытайтесь воспроизвести схемы, иллюстрации или инструкции в этой статье в реальных условиях. Это может привести к поражению электрическим током, травме или смерти. Эти примеры приведены только для теоретического обсуждения, а не для фактического/физического использования.
Идеальные проводники
Однако прежде чем мы обсудим резисторы, мы должны сначала сделать оговорку относительно проводников (проводов), которые мы используем в наших моделях цепей. В частности, будем считать, что их идеальные проводники: они никоим образом не сопротивляются и не препятствуют потоку заряда. Следовательно, мы можем логически заключить, что напряжение в любой точке непрерывного проводника относительно земли одинаково, независимо от его формы или длины. По соглашению и для простоты мы обычно будем говорить, что заземление равно 0 В (так же, как мы могли бы сказать, что физическая земля вокруг нас измеряется как 0 метров). Таким образом, в случае показанной ниже батареи на 1,5 В везде на верхнем проводе напряжение 1,5 В относительно земли, а на нижнем проводе везде 0 В.
Следовательно, мы можем логически заключить, что напряжение в любой точке непрерывного проводника относительно земли одинаково, независимо от его формы или длины. По соглашению и для простоты мы обычно будем говорить, что заземление равно 0 В (так же, как мы могли бы сказать, что физическая земля вокруг нас измеряется как 0 метров). Таким образом, в случае показанной ниже батареи на 1,5 В везде на верхнем проводе напряжение 1,5 В относительно земли, а на нижнем проводе везде 0 В.
Цепи резисторов
Простая цепь резисторов просто включает подключение резистора к клеммам источника питания. Символ цепи для резистора показан ниже.
Ниже приведена простая схема резистора.
Теперь давайте попытаемся понять, что происходит в цепи резистора по сравнению с гравитацией. Вспомните, что заряд, перемещаемый электрической силой, очень похож на движение массы гравитационной силой.
А что, если ввести слой воды или какой-либо другой жидкости, через которую должна провалиться масса? Эта жидкость замедлит мяч по сравнению с его (относительно) беспрепятственным падением в воздухе (или, что еще лучше, его совершенно беспрепятственным падением в вакууме). Когда мяч падает через этот слой жидкости, часть его гравитационной потенциальной энергии преобразуется в тепловую энергию. (Это же явление вызывает горение и свечение метеоров, которые с большой скоростью врезаются в атмосферу Земли.)
Когда мяч падает через этот слой жидкости, часть его гравитационной потенциальной энергии преобразуется в тепловую энергию. (Это же явление вызывает горение и свечение метеоров, которые с большой скоростью врезаются в атмосферу Земли.)
Поскольку часть гравитационной потенциальной энергии преобразуется в тепло посредством трения («трение» — например, когда вы потираете руки друг о друга, они становятся теплее), мяч не достигает земли с той же энергией, что и движение, которое оно имело бы в отсутствие жидкого слоя.
Схема резистора почти полностью аналогична этой ситуации. Вместо вакуума и жидкости у нас есть проводник и резистор. В (идеальном) проводнике заряд течет свободно, и его движение беспрепятственно. Однако в резисторе поток заряда затруднен, что приводит к выделению тепла, когда заряженные частицы (электроны) «врезаются» в атомы, заставляя их замедляться. В результате часть потенциальной электрической энергии преобразуется в тепло.
Закон Ома
Хотите узнать больше? Почему бы не пройти онлайн-курс по электронике?
Степень, в которой резистор препятствует потоку заряда, называется параметром сопротивление, , который часто выражается как R. Вспомните, что мы говорили, что более высокое напряжение обычно создает более высокий ток в цепи. И наоборот, более высокое сопротивление обычно снижает величину тока в цепи больше, чем более низкое сопротивление. Таким образом, мы можем определить сопротивление цепи как отношение напряжения к току в этом резисторе. Записав это математически, где ток выражается как
Вспомните, что мы говорили, что более высокое напряжение обычно создает более высокий ток в цепи. И наоборот, более высокое сопротивление обычно снижает величину тока в цепи больше, чем более низкое сопротивление. Таким образом, мы можем определить сопротивление цепи как отношение напряжения к току в этом резисторе. Записав это математически, где ток выражается как
Немного переформулировав это уравнение, мы получим знакомую форму закона Ома.
Единицами сопротивления являются омы (записывается как ?). Один ом равен одному джоулю-секунде на квадратный кулон (не спрашивайте, что это значит!).
Теперь вернемся к нашей цепи резисторов. Мы отметили, что напряжение постоянно на каждом проводе (который мы моделируем как идеальные проводники — в действительности провода имеют некоторое сопротивление, но для наших целей оно незначительно).
Поскольку заряд теряет потенциальную энергию при прохождении через резистор, напряжение на этом резисторе называется падением напряжения.
Практическая задача : Какой ток протекает через резистор R в цепи ниже?
Решение : Нам нужно использовать закон Ома для расчета тока ( I ), используя информацию, представленную на принципиальной схеме.
Во-первых, мы знаем, что напряжение источника питания ( В ) равно 10 вольт, а сопротивление резистора ( R ) равно 5 Ом. Ниже приведена форма закона Ома, которую мы должны использовать.
Подстановка чисел и вычисление результатов дает ответ.
Сила тока в цепи составляет 2 ампера.
Рассеиваемая мощность
Напомним из приведенного выше обсуждения, что когда заряд проходит через резистор, он теряет потенциальную энергию в виде тепла. Таким образом, когда вы подключаете лампочку накаливания к источнику питания (либо приспособлению, такому как лампа, либо батарейки в фонарике), нить накаливания в лампочке (не что иное, как проволочный резистор) нагревается до тех пор, пока не начнет светиться, создавая свет. Как оказалось, количество потенциальной энергии, преобразованной в тепло, также называемое рассеиваемой мощностью , является просто произведением напряжения ( В ) и ток ( I ) «в» резисторе. Назовем это рассеивание мощности P .
Таким образом, когда вы подключаете лампочку накаливания к источнику питания (либо приспособлению, такому как лампа, либо батарейки в фонарике), нить накаливания в лампочке (не что иное, как проволочный резистор) нагревается до тех пор, пока не начнет светиться, создавая свет. Как оказалось, количество потенциальной энергии, преобразованной в тепло, также называемое рассеиваемой мощностью , является просто произведением напряжения ( В ) и ток ( I ) «в» резисторе. Назовем это рассеивание мощности P .
Если мы проанализируем единицы измерения, мы обнаружим, что рассеиваемая мощность выражается в джоулях в секунду, которые мы также называем ваттами. Так, например, 100-ваттная лампочка преобразует 100 джоулей потенциальной энергии в секунду в тепло, заставляя нить накаливания в лампочке светиться и освещать ее окрестности. В качестве альтернативы, выполнив некоторые алгебраические манипуляции с этим выражением в сочетании с законом Ома, мощность также эквивалентна произведению сопротивления на квадрат тока.
Для наших целей оба этих уравнения являются законными средствами расчета мощности, рассеиваемой резистором R. на розетке есть напряжение 120В. Если вы подключите к этой розетке лампочку мощностью 30 Вт, какой ток будет течь по цепи?
Решение : Эта задача требует, чтобы мы сначала построили схему цепи, а затем использовали наши знания об электронике, чтобы найти ток, протекающий в лампочке (или цепи). Давайте смоделируем электрическую розетку, используя наш символ источника питания. Поскольку лампочка — это не что иное, как резистор, мы будем использовать наш символ резистора.
Обратите внимание, что резистор расположен в схеме немного иначе, чем в наших предыдущих примерах. Это не имеет никакого физического значения, потому что напряжения на проводах (которые мы называем идеальными проводниками) везде одинаковы. Таким образом, падение напряжения на резисторе по-прежнему составляет 120В.
Теперь воспользуемся уравнением мощности для расчета тока через лампочку мощностью 30 Вт.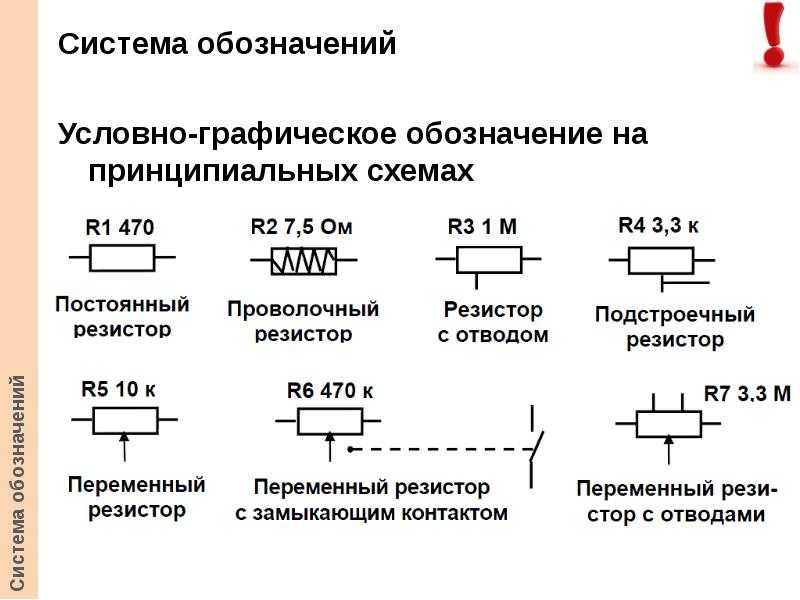


 – Среднеквадратичное значение напряжения питания
– Среднеквадратичное значение напряжения питания