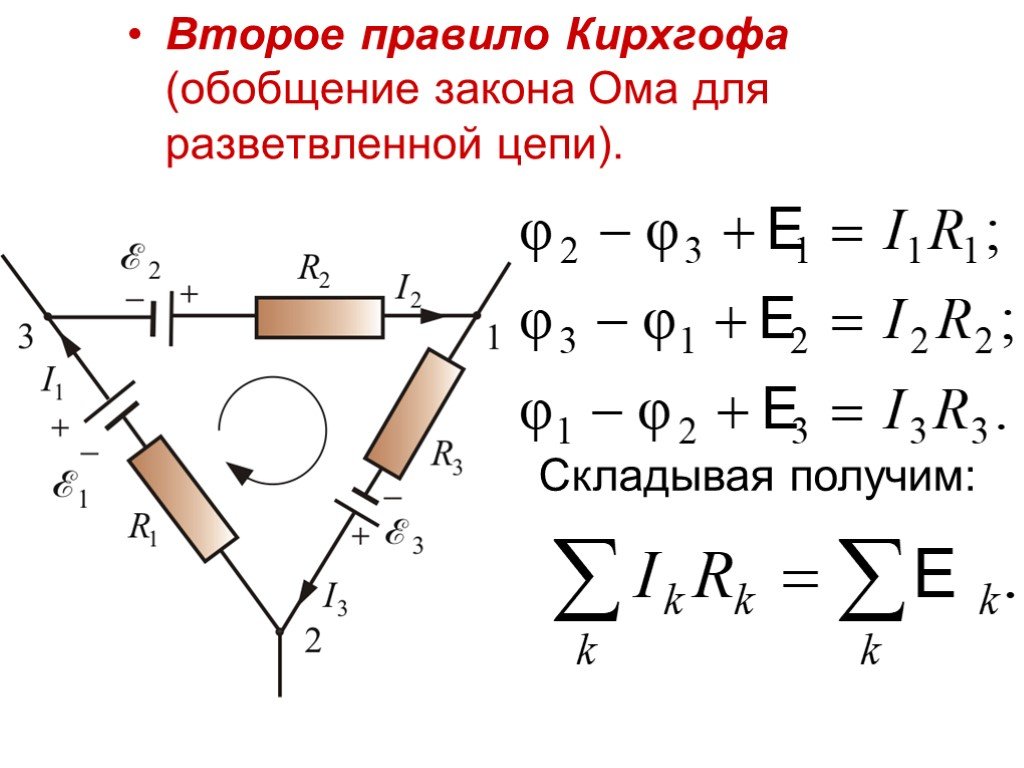
Второе правило кирхгофа: § 18. Правила Кирхгофа — ЗФТШ, МФТИ — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Второе правило Кирхгофа, теория и примеры

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Физика Второе правило Кирхгофа

Второе правило Кирхгофа – это один из приемов, который применяют для упрощения расчетов параметров сложных разветвленных цепей постоянного тока. Электрические цепи постоянного тока могут иметь в своем составе большое число сопротивлений, источников тока, множество замкнутых контуров и узлов. Параметры цепи постоянного тока любой сложности можно вычислить, если применять законы Ома и законы сохранения заряда. Правила Кирхгофа являются следствиями вышеназванных законов, с их помощью можно значительно упростить процедуру написания уравнений, связывающих силы тока, сопротивления и электродвижущие силы (ЭДС) для рассматриваемой цепи.

Первое правило Кирхгофа называют правилом узлов. Оно предназначено для написания уравнения для токов, которые сходятся в узле цепи.

Второе правило Кирхгофа относится к замкнутым контурам, которые выделяют в разветвленной цепи. Это правило еще называют правилом контуров.

Формулировка второго правила Кирхгофа

Суммы произведений алгебраических величин сил тока на внешние и внутренние сопротивления всех участков замкнутого контура равны алгебраической сумме величин сторонних электродвижущих сил (ЭДС) (), которые входят в рассматриваемый контур. В виде формулы второй закон Кирхгофа записывают как:

Величины называют падениями напряжения. До применения второго закона Кирхгофа выбирают положительное направление обхода контура. Это направление берется произвольно, либо по часовой стрелке, либо против нее. Если направление обхода совпадает с направлением течения тока в рассматриваемом элементе контура, то падение напряжения в формулу второго правила для данного контура входит со знаком плюс. ЭДС считают положительной, если при движении по контуру (в избранном направлении) первым встречается отрицательный полюс источника. Более правильно было бы сказать, что ЭДС считают положительной, если работа сторонних сил по перемещению единичного положительного заряда на рассматриваемом участке цепи в заданном направлении обхода контура является положительной величиной.

Второе правило Кирхгофа — это следствие закона Ома.

Количество независимых уравнений, получаемых при использовании правил Кирхгофа

Применяя второе правило Кирхгофа можно получить независимые уравнения для тех контуров цепи, которые не получены наложением уже рассмотренных контуров. Число независимых контуров () равно:

где – число ветвей в цепи; – количество узлов.

Количество независимых уравнений, которые дадут первое и второе правила Кирхгофа равно ():

Вывод: количество независимых уравнений, полученных с использованием обоих правил Кирхгофа равно числу разных токов в рассматриваемой цепи.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

2. 6. Правила Кирхгофа для разветвленных цепей.

До сих пор нами рассматривались простейшие электрические цепи, состоящие из одного замкнутого неразветвленного контура. На всех его участках силы тока одинаковы. Расчет I, R,  в такой цепи выполняется с помощью законов Ома.

Рис.2.2.Разветвленная электрическая цепь.

Более сложной является разветвленная электрическая цепь, состоящая из нескольких замкнутых контуров, имеющих общие участки. В каждом контуре может быть несколько источников тока. Силы тока на отдельных участках замкнутого контура могут быть различными по величине и направлению (рис.2.2). В 1847 г. Г.Кирхгоф сформулировал два правила, значительно упрощающих расчет разветвленных цепей.

Первое правило Кирхгофа: алгебраическая сумма сил токов в узле равна нулю: . Узел — точка цепи, в которой сходятся не менее трех проводников. В электрической цепи на рис.2.2 имеются два узла А и В. Ток, входящий в узел, считается положительным, выходящий — отрицательным. Например, для узла А первое правило Кирхгофа следует записать .

Первое правило выражает закон сохранения электрического заряда, так как ни в одной точке цепи они не могут возникать или исчезать.

Второе правило Кирхгофа относится к любому замкнутому контуру, выделенному в разветвленной цепи:

алгебраическая сумма произведений токов на сопротивления, включая и внутренние, на всех участках замкнутого контура равна алгебраической сумме электродвижущих сил, встречающихся в этом контуре .Контур ‑ это замкнутый участок схемы, по которому можно пройти и вернуться в исходную точку. Второе правило Кирхгофа получается из закона Ома, записанного для всех участков от узла до узла (ветвей) разветвленной схемы.

В электрической цепи на рис.2.2 имеются три контура: AMNBA, CABDC, CMNDC. При этом, токи I_i в ветвях контура, совпадающие с произвольно выбранным направлением обхода контура, считаются положительными, а направленные навстречу обхода — отрицательными. Э.д.с., проходимые от «+» к «-» считаются положительными и наоборот. В рассматриваемой электрической цепи (рис.2.2) выберем обход контуров по часовой стрелке и запишем для них уравнения по II правилу Кирхгофа: для AMNBА ; для CABDС ; для CMNDС . В данном примере внутренними сопротивлениями источников тока пренебрегаем. Первое и второе правила Кирхгофа позволяют составить систему линейных алгебраических уравнений, которые связывают параметры (I, R, ) и позволяют, зная одни, найти другие.

Простые электрические цепи имеют очень большое практическое применение. В повседневной жизни полезно знать, как подключить динамики или проигрыватель к стереосистеме, как подсоединить сигнализацию для охраны или автомобильный кассетный п

Рис. 2.3. а) Последовательное соединение сопротивлений; б) Параллельное соединение сопротивлений.

роигрыватель, как зарядить аккумуляторы или осветить новогоднюю елку.

Большинство электрических цепей содержит комбинацию последовательно или параллельно подключенных резисторов (резистор — это элемент цепи, обладающий только сопротивлением). Полное сопротивление участка цепи определяется отношением падения напряжения на нем к величине силы тока . При последовательном соединении (рис.2.3 а) через все резисторы течет один и тот же ток. При параллельном соединении (рис.2.3 б) полный ток равен сумме токов, текущих в отдельных резисторах.

При последовательном соединении падение напряжения на участке АВ равно , т.е. сумме падений напряжения на трех резисторах. Разделим обе части равенства наI и получим , т.е.. Таким образом,полное сопротивление участка цепи, состоящего из последовательно соединенных резисторов, равно их алгебраической сумме.

При параллельном соединении (рис..2.3 б) мы имеем . Разделим обе части равенства наU, где U — падение напряжения на участке цепи АВ, причем , и получим. Из этого равенства следует.Величина обратная полному сопротивлению параллельно соединенных резисторов равна алгебраической сумме величин их обратных сопротивлений .

В электрическую цепь может быть включено регулируемое (изменяющееся с помощью специального движка), сопротивление, которое называется реостатом. По назначению реостаты делятся на пусковые, служащие для ограничения силы тока во время пуска двигателей, и регулирующие — для регулировки силы тока в цепи (постепенное снижение освещенности в театральных залах), регулировки скорости вращения электродвигателей и т.д. Реостат может быть использован в качестве так называемого

датчика перемещения. В автоматических регуляторах уровня жидкости в резервуарах применяется поплавково-реостатный датчик. Специальный поплавок крепится к движку реостата.

Изменение уровня жидкости сдвигает поплавок, изменяет сопротивление реостата, и следовательно, силы тока в цепи, величина которого дает информацию об уровне.

Второе правило Кирхгофа (правило напряжения или правило петли)

Оно утверждает, что в замкнутой цепи алгебраическая сумма произведений тока и сопротивления каждой части цепи равна полной ЭДС, включенной в цепь.

Второе правило Кирхгофа (Напряжение правило или правило цикла)

В нем говорится, что в замкнутая цепь алгебраическая сумма произведений тока и сопротивления каждой части цепи равна полной ЭДС, включенной в цепь. Это правило следует из закона сохранения энергии для изолированной системы (Энергия, подводимая источниками ЭДС, равна сумме энергии подается на все резисторы). Произведение тока и сопротивления принимается как положительна, если соблюдается направление тока. Предположим, если направление тока противоположно направлению петли, то произведение ток и напряжение на резисторе отрицательны.

Он показан на рис. 2.24. (а) и (б). ЭДС считается положительной, если исходить из отрицательной к положительному выводу клетки. Он показан на рис. 2.24 (в) и (г).

Правило напряжения Кирхгофа должен применяться только тогда, когда все токи в цепи достигают устойчивого состояния состояние (ток в различных ветвях постоянен).

ПРИМЕР 2.21

Следующий рисунок показывает сложную сеть проводников, которую можно разделить на два замкнутых петли, такие как ACE и ABC. Примените правило напряжения Кирхгофа.

Solution

Таким образом, применяя второй закон Кирхгофа к замкнутому контуру EACE

I ₁ R ₁ 900 38 + I ₂ R ₂ + I ₃ R ₃ = ξ

и для замкнутого контура ABCA

I ₄ Р ₄ + I ₅ R ₅ — I ₂ R ₂ = 0

ПРИМЕР 2. 22

Вычислить ток, протекающий через резистор 1 Ом в следующей цепи.

Решение

Мы можем обозначим ток, который течет от батареи 9 В, как I ₁, и он разделяется в я ₂ и я ₁ – я ₂ в стыке по текущему правилу Кирхгофа (KCR). Это показано ниже.
Теперь рассмотрим цикл EFCBE и применим КВР, получим
1I ₂ + 3I ₁ + 2I ₁ = 9
5I ₁ + I + I ₂ = 9 (1)
Применив КВР к контуру EADFE, получим
3 (Я ₁ – I ₂ ) – 1I ₂ = 6
3I ₁ – 4I ₂ = 6 (2)
Решение уравнения (1) и (2), получаем
I ₁ = 1,83 А и I ₂ = -0,13 А
It подразумевает, что ток в резисторе 1 Ом течет от F к E. Задачи, 12-й Физика: Текущее электричество
Учебный материал, Лекционные заметки, Задание, Справочник, Объяснение описания Wiki, краткая информация
12-я физика: ток Электричество: второе правило Кирхгофа (правило напряжения или правило петли) | Объяснение, формулы, решенные примеры задач
21.
3: Правила Кирхгофа — Физика LibreTexts
Последнее обновление
Сохранить как PDF
Идентификатор страницы
2690
OpenStax
OpenStax
Цели обучения
К концу этого раздела вы сможете:
Анализировать сложную схему, используя правила Кирхгофа, используя соглашения для определения правильных знаков различных термов.
Многие сложные схемы, такие как показанная на рисунке \(\PageIndex{1}\), не могут быть проанализированы с помощью последовательно-параллельных методов, разработанных в разделе Резисторы, включенные последовательно и параллельно, и Электродвижущая сила: напряжение на клеммах. Однако есть два правила анализа цепей, которые можно использовать для анализа любой схемы, простой или сложной. Эти правила являются частными случаями законов сохранения заряда и сохранения энергии. Эти правила известны как правила Кирхгофа в честь их изобретателя Густава Кирхгофа (1824–1887).
Рисунок \(\PageIndex{1}\): Эта схема не может быть сведена к комбинации последовательного и параллельного соединений. Для его анализа можно использовать правила Кирхгофа, специальные приложения законов сохранения заряда и энергии. (Примечание: буква E на рисунке обозначает электродвижущую силу, ЭДС.)
Определение: Правила Кирхгофа
Первое правило Кирхгофа — правило соединения: Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения. перекресток.
Второе правило Кирхгофа — правило петли: Алгебраическая сумма изменений потенциала вокруг любого замкнутого контура (петли) должна быть равна нулю.
Теперь будут даны объяснения двух правил, за которыми следуют советы по решению проблем для применения правил Кирхгофа и рабочий пример, который их использует.
Первое правило Кирхгофа (правило соединения)
Первое правило Кирхгофа (правило соединения) представляет собой применение закона сохранения заряда к соединению; это показано на рисунке \(\PageIndex{2}\). Ток — это поток заряда, а заряд сохраняется; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу. Первое правило Кирхгофа требует, чтобы \(I_1 = I_2 + I_3\) (рис. \(\PageIndex{2}\)). Подобные уравнения могут и будут использоваться для анализа схем и решения схемных задач.
Рисунок \(\PageIndex{2}\): Правило соединения. На диаграмме показан пример первого правила Кирхгофа, в котором сумма токов, поступающих в соединение, равна сумме токов, выходящих из соединения. В этом случае ток, входящий в переход, разделяется и выходит в виде двух токов, так что \(I_1 = I_2 + I_3\). Здесь \(I_1\) должно быть 11 А, так как \(I_2\) равно 7 А, а \(I_3\) равно 4А.
Второе правило Кирхгофа (правило цикла)
Второе правило Кирхгофа (правило цикла) является применением закона сохранения энергии. Правило петли сформулировано в терминах потенциала, а не потенциальной энергии, но они связаны, поскольку \(PE_{elec} = qV\). Напомним, что ЭДС — это разность потенциалов источника при отсутствии тока. В замкнутом контуре любая энергия, поставляемая ЭДС, должна быть переведена в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в контур или из него. На рисунке \(\PageIndex{3}\) показаны изменения потенциала в простой последовательной цепи.
Второе правило Кирхгофа требует \(ЭДС — Ir — IR_1 — IR_2 = 0\). В перестановке это \(ЭДС = Ir + IR_1 + IR_2\), что означает, что ЭДС равна сумме падений \(IR\) (напряжения) в контуре.
Рисунок \(\PageIndex{3}\): Правило цикла. Пример второго правила Кирхгофа, согласно которому сумма изменений потенциала вокруг замкнутого контура должна быть равна нулю. (a) В этой стандартной схеме простой последовательной цепи ЭДС подает 18 В, которое сводится к нулю сопротивлениями, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки, для всего 18 В. (b) Этот вид в перспективе представляет потенциал как что-то вроде американских горок, где потенциал повышается за счет ЭДС и снижается за счет сопротивления. (Обратите внимание, что буква E означает ЭДС.)
Применение правил Кирхгофа
Применяя правила Кирхгофа, мы получаем уравнения, позволяющие находить неизвестные в цепях. Неизвестными могут быть токи, ЭДС или сопротивления. Каждый раз, когда применяется правило, создается уравнение. Если независимых уравнений столько же, сколько неизвестных, то задача решаема. При применении правил Кирхгофа вы должны принять два решения. Эти решения определяют знаки различных величин в уравнениях, которые вы получаете, применяя правила.
Применяя первое правило Кирхгофа, правило соединения, вы должны обозначить ток в каждой ветви и решить, в каком направлении он течет. Например, на рисунке, рисунке и рисунке токи помечены \(I_1, \, I_2, \, I_3\) и \(I\), а стрелки указывают их направления. Здесь нет никакого риска, потому что, если вы выберете неправильное направление, ток будет правильной величины, но отрицательным.
Применяя второе правило Кирхгофа, правило петли, вы должны определить замкнутую петлю и решить, в каком направлении ее обойти, по часовой или против часовой стрелки. Например, на рисунке петля была пройдена в том же направлении, что и ток (по часовой стрелке). Опять же, нет никакого риска; Обход цепи в противоположном направлении меняет знак каждого члена в уравнении, что похоже на умножение обеих частей уравнения на -1.
Рисунок \(\PageIndex{4}\) и следующие пункты помогут правильно расставить знаки плюс или минус при применении правила цикла. Обратите внимание, что резисторы и ЭДС пересекаются при переходе от a к b. Во многих схемах будет необходимо построить более одного контура. При обходе каждого цикла необходимо соблюдать последовательность знака изменения потенциала (пример \(\PageIndex{1}\)).
Рисунок \(\PageIndex{4}\): Каждый из этих резисторов и источников напряжения проходит от a до b. Возможные изменения показаны под каждым элементом и пояснены в тексте. (Обратите внимание, что буква E означает ЭДС.)
Когда резистор перемещается в том же направлении, что и ток, изменение потенциала равно \(-IR\). (См. рисунок.)
Когда резистор перемещается в направлении, противоположном току, изменение потенциала равно \(+IR\). (См. рисунок.)
Когда ЭДС перемещается от — к + (в том же направлении, что и положительный заряд), изменение потенциала равно +ЭДС. (См. рисунок.)
Когда ЭДС перемещается от + к — (противоположно направлению движения положительного заряда), изменение потенциала равно -ЭДС. (См. рис.)
Пример \(\PageIndex{1}\): расчет тока: с использованием правил Кирхгофа
Найдите токи, протекающие в цепи на рисунке \(\PageIndex{5}\).
Рисунок, но указаны сопротивления и ЭДС. (Каждая ЭДС обозначена буквой E.) Токи в каждой ветви помечены и предполагается, что они движутся в показанных направлениях. В этом примере для нахождения токов используются правила Кирхгофа.
Стратегия
Эта схема настолько сложна, что токи нельзя найти с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. Токи были помечены \(I_1, \, I_2,\) и \(I_3\)
на рисунке, и были сделаны предположения об их направлениях. Места на схеме обозначены буквами от a до h. В решении мы будем применять правила соединения и петли, ища три независимых уравнения, которые позволят нам найти три неизвестных тока.
Решение
Начнем с применения первого правила Кирхгофа или правила соединения в точке а. Это дает
\[I_1 = I_2 + I_3,\]
, так как \(I_1\) впадает в соединение, а \(I\) и \(I_3\) вытекают. Применение правила соединения в точке e дает точно такое же уравнение, так что никакой новой информации не получается. Это одно уравнение с тремя неизвестными — нужны три независимых уравнения, поэтому необходимо применить правило цикла.
Теперь рассмотрим цикл abcdea. Переходя от a к b, мы пересекаем \(R_2\) в том же (предполагаемом) направлении тока \(I_2\), поэтому изменение потенциала равно \(-I_2R_2\). Затем, переходя от b к c, мы переходим от — к +, так что изменение потенциала равно \(+ЭДС_1\). Перемещение внутреннего сопротивления \(r_1\) от c к d дает \(-I_2r_1\). Завершение цикла путем перехода от d к a снова пересекает резистор в том же направлении, что и его ток, что дает изменение потенциала \(-I_1R_1\).
Правило цикла гласит, что сумма изменений потенциала равна нулю. Таким образом,
\[-I_2R_2 + эдс_1 -I_2r_1 — I_1R_1 = -I_2(R_2 + r_1) + эдс_1 — I_1R_1 = 0.\]
Обратите внимание, что знаки меняются местами по сравнению с другим циклом, потому что элементы проходятся в противоположное направление. С введенными значениями это становится \[+6I_1 + 2I_3 -45 = 0.\] Этих трех уравнений достаточно, чтобы решить для трех неизвестных токов. Сначала решите второе уравнение для \(I_2\).
\[I_2 = 6 — 2I_1.\]
Теперь решите третье уравнение для \(I_3\):
\[I_3 = 22,5 — 3I_1.\]
Подстановка этих двух новых уравнений в первое позволяет нам найти значение для
\[I_1 = I_2 + I_3 = (6 — 2I_1) + (22,5 — 3I_1) = 28,5 — 5I_1.\]
Объединение членов дает
\[6I_1 = 28,5, \, и\]\[I_1 = 4,75 \, A. \ ]
Подстановка этого значения вместо \(I\) обратно в четвертое уравнение дает
\[I_2 = 6 — 2I_1 = 6 — 9,50\]\[I_2 = -3,50 \, A\]
Знак минус означает, что \(I_2\) течет в направлении, противоположном предполагаемому на рисунке .
Наконец, подстановка значения \(I_1\) в пятое уравнение дает
\[I_3 = 22,5 — 3I_1 = 22,5 — 14,25\]\[I_3 = 8,25 \, A.\]
Обсуждение 90 003
Просто для проверки отметим, что действительно \(I_1 = I_2 + I_3\). Результаты также можно проверить, введя все значения в уравнение для цикла abcdefgha.
Стратегии решения проблем по правилам Кирхгофа
Убедитесь, что имеется четкая принципиальная схема, на которой вы можете отметить все известные и неизвестные сопротивления, ЭДС и токи. Если ток неизвестен, вы должны присвоить ему направление. Это необходимо для определения признаков потенциальных изменений. Если вы зададите направление неправильно, то обнаружится, что ток имеет отрицательное значение — никакого вреда не будет.
Примените правило соединения к любому соединению в цепи. Каждый раз, когда применяется правило соединения, вы должны получать уравнение с током, которого не было в предыдущем приложении — если нет, то уравнение избыточно.
Примените правило цикла к такому количеству циклов, которое необходимо для поиска неизвестных в задаче. (Независимых уравнений должно быть столько же, сколько и неизвестных.) Чтобы применить правило цикла, вы должны выбрать направление обхода цикла. Затем тщательно и последовательно определите знаки потенциальных изменений для каждого элемента, используя четыре маркированных пункта, рассмотренных выше в сочетании с рисунком.
Решите уравнения для неизвестных. Это может включать в себя множество алгебраических шагов, требующих тщательной проверки и перепроверки.
Проверьте, разумны ли и последовательны ли ответы. Числа должны быть правильного порядка, ни чрезмерно большими, ни исчезающе малыми. Признаки должны быть разумными — например, отсутствие сопротивления не должно быть отрицательным. Убедитесь, что полученные значения удовлетворяют различным уравнениям, полученным в результате применения правил. Например, токи должны удовлетворять правилу соединения.
Материал в этом разделе теоретически верен. Мы должны быть в состоянии проверить это, произведя измерения тока и напряжения. На самом деле, некоторые из устройств, используемых для таких измерений, являются прямым применением принципов, рассмотренных до сих пор, и рассматриваются в следующих модулях. Как мы увидим, отсюда вытекает очень простой, даже глубокий факт: проведение измерения изменяет измеряемую величину.
Упражнение \(\PageIndex{1}\)
Можно ли применять правила Кирхгофа к простым последовательным и параллельным схемам, или они ограничены для использования в более сложных схемах, которые не являются комбинацией последовательной и параллельной?
Ответить
Правила Кирхгофа можно применить к любой схеме, поскольку они являются приложениями к схемам двух законов сохранения. Законы сохранения являются наиболее широко применимыми принципами в физике. Обычно математически проще использовать правила для последовательной и параллельной схемы в более простых схемах, поэтому мы подчеркиваем правила Кирхгофа для использования в более сложных ситуациях. Но правила последовательностей и параллелей можно вывести из правил Кирхгофа. Кроме того, правила Кирхгофа могут быть распространены на устройства, отличные от резисторов и ЭДС, такие как конденсаторы, и являются одним из основных устройств анализа в анализе цепей.
Резюме
Правила Кирхгофа можно использовать для анализа любой схемы, простой или сложной.
Первое правило Кирхгофа — правило соединения: сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения.
Второе правило Кирхгофа — правило петли: алгебраическая сумма изменений потенциала вокруг любого замкнутого контура (петли) должна быть равна нулю.
Два правила основаны соответственно на законах сохранения заряда и энергии.
При расчете потенциала и тока по правилам Кирхгофа необходимо соблюдать ряд правил для определения правильных знаков различных членов.
Простые ряды и параллельные правила являются частными случаями правил Кирхгофа.
Глоссарий
Правила Кирхгофа
набор из двух правил, основанных на сохранении заряда и энергии, управляющих током и изменениями потенциала в электрической цепи
соединительная линейка
первое правило Кирхгофа, применяющее закон сохранения заряда к соединению; ток — это поток заряда; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу; можно указать правило \(I_1 = I+2 + I_3\)
правило петли
Второе правило Кирхгофа, которое гласит, что в замкнутом контуре любая энергия, поставляемая ЭДС, должна быть переведена в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в контур или из него.