Простейшие одноклеточные животные и их признаки (Таблица)
К подцарству Одноклеточных, или Простейших, относят животных, тело которых состоит из одной клетки. Размеры простейших в среднем 0,1—0,5 мм. Бывают особи ещё меньшей величины — около 0,01 мм. Встречаются и довольно крупные организмы, длиной в несколько миллиметров и даже сантиметров.
Обитают простейшие одноклеточные животные преимущественно в жидкой среде — в морской и пресной воде, влажной почве, в других организмах. Внешне они весьма разнообразны. Одни напоминают бесформенные студенистые комочки (например, амёбы), другие имеют геометрически правильную форму (например, лучевики).
Простейшие насчитывает около 30 тысяч видов.
Строение инфузории туфельки и амебы
Строение эвглены зеленой
Таблица признаки простейших одноклеточных животных
|
Признаки простейших одноклеточных |
Амеба обыкновенная (Класс Корненожки) |
Эвглена зеленая (класс Жгутиконосцы) |
Инфузория туфелька (класс Инфузории) |
|
Строение |
Состоит из цитоплазмы, ядра, сократительной вакуоли, ложноножки, пищеварительной вакуоли (см. |
Состоит из оболочки, ядра, жгутика, глазок, сократительной вакуоли, питательных веществ, хлоропласты (см. рис.) |
Состоит из мембраны, малого и большого ядра, сократительной и пищеварительной вакуоли, рот, порошица, реснички (см. рис.) |
|
Движение |
«Перетекание» с помощью ложноножек |
Передвижение с помощью жгутика |
Передвижение с помощью ресничек |
|
Питание |
Кормом могут быть бактерии, микроскопические водоросли. Амёба захватывает пищу, вытягивая ложноножки на любом участке тела. Они обволакивают добычу и вместе с небольшим количеством воды погружают её в цитоплазму. Так образуется пищеварительная вакуоль — фагоцитоз, захват капель жидкости — пиноцитоз. Из пищеварительной вакуоли растворимые продукты пищеварения поступают в цитоплазму, а непереваренные остатки выводятся из организма в любой части клетки. |
Автотрофное (фотосинтез) или гетеротрофное (фагоцитоз и пиноцитоз) |
Питаются различными микроорганизмами, преимущественно бактериями. Движением ресничек, расположенных вдоль ротового углубления, загоняют в него добычу. Вместе с водой она попадает в клеточный рот, затем в глотку. Образуется пищеварительная вакуоль, непереваренные остатки выбрасываются через порошицу. |
|
Размножение |
Амеба размножается делением. При этом ядро делится надвое. Образовавшиеся новые ядра расходятся в стороны, и между ними появляется поперечная перетяжка, разделяющая амёбу на две дочерние клетки, которые живут самостоятельно. Через некоторое время молодые амёбы также начинают делиться. Для размножения благоприятна температура воды около +20 °С. |
Размножение организмов данного вида эвглен бесполое — делением клетки пополам, в отличие от инфузории-туфельки, для которой характерен еще и половой процесс. |
Инфузории размножаются бесполым путём — поперечным делением, как амёбы. Первым делится надвое малое ядро, затем большое. Одновременно появляется поперечная перетяжка. Она со временем разделяет инфузорию на две молодые (дочерние) клетки. Они растут и при хорошем питании и оптимальной температуре уже на следующие сутки становятся взрослыми и снова могут делиться. Для инфузорий характерен и половой процесс в форме конъюгации (слияние двух клеток и обмен генетической информацией) |
_______________
Источник информации: Биология в таблицах и схемах./ Издание 2е, — СПб.: 2004.
Простейшие схемы подключения светодиодов в 220 вольт без драйвера (самое простое питание светодиода от сети напряжением 220В)
Потому что нужно грамотно решить сразу две задачи:
- Ограничить прямой ток через светодиод, чтобы он не сгорел.
- Обеспечить защиту светодиода от пробоя обратным током.
Если проигнорировать любой из этих пунктов, светодиод моментально накроется медным тазом.
В самом простейшем случае ограничить ток через светодиод можно резистором и/или конденсатором. А предотвратить пробой от обратного напряжения можно с помощью обычного диода или еще одного светодиода.
Поэтому самая простая схема подключения светодиода к 220В состоит всего из нескольких элементов:
Защитный диод может быть практически любым, т.к. его обратное напряжение никогда не будет превышать прямого напряжения на светодиоде, а ток ограничен резистором.
Сопротивление и мощность ограничительного (балластного) резистора зависит от рабочего тока светодиода и рассчитывается по закону Ома:
R = (Uвх — ULED) / I
А мощность рассеивания резистора рассчитывается так:
P = (U
где Uвх = 220 В,
ULED — прямое (рабочее) напряжение светодиода. Обычно оно лежит в пределах 1.5-3.5 В. Для одного-двух светодиодов им можно пренебречь и, соответственно, упростить формулу до R=Uвх/I,
I — ток светодиода. Для обычных индикаторных светодиодов ток будет 5-20 мА.
Пример расчета балластного резистора
Допустим, нам нужно получить средний ток через светодиод = 20 мА, следовательно, резистор должен быть:
R = 220В/0.020А = 11000 Ом (берем два резистора: 10 + 1 кОм)
P = (220В)2/11000 = 4.4 Вт (берём с запасом: 5 Вт)
Необходимое сопротивление резистора можно взять из таблицы ниже.
Таблица 1. Зависимость тока светодиода от сопротивления балластного резистора.
| Сопротивление резистора, кОм | Амплитудное значение тока через светодиод, мА | Средний ток светодиода, мА | Средний ток резистора, мА | Мощность резистора, Вт |
|---|---|---|---|---|
| 43 | 7.2 | 2.5 | 5 | 1.1 |
| 24 | 13 | 4.5 | 9 | 2 |
| 22 | 14 | 5 | 10 | 2.2 |
| 12 | 26 | 9 | 4 | |
| 10 | 31 | 11 | 22 | 4.8 |
| 7.5 | 41 | 15 | 29 | 6.5 |
| 4.3 | 72 | 25 | 51 | 11.3 |
| 2.2 | 141 | 50 | 100 | 22 |
Другие варианты подключения
В предыдущих схемах защитный диод был включен встречно-параллельно, однако его можно разместить и так:
Это вторая схема включения светодиодов на 220 вольт без драйвера. В этой схеме ток через резистор будет в 2 раза меньше, чем в первом варианте. А, следовательно, на нем будет выделяться в 4 раза меньше мощности. Это несомненный плюс.
Но есть и минус: к защитному диоду прикладывается полное (амплитудное) напряжение сети, поэтому любой диод здесь не прокатит. Придется подобрать что-нибудь с обратным напряжением 400 В и выше. Но в наши дни это вообще не проблема. Отлично подойдет, например, вездесущий диод на 1000 вольт — 1N4007 (КД258).
Не смотря на распространенное заблуждение, в отрицательные полупериоды сетевого напряжения, светодиод все-таки будет находиться в состоянии электрического пробоя. Но благодаря тому, что сопротивление обратносмещенного p-n-перехода защитного диода очень велико, ток пробоя будет недостаточен для вывода светодиода из строя.
Внимание! Все простейшие схемы подключения светодиодов в 220 вольт имеют непосредственную гальваническую связь с сетью, поэтому прикосновение к ЛЮБОЙ точке схемы — ЧРЕЗВЫЧАЙНО ОПАСНО!
Для уменьшения величины тока прикосновения нужно располовинить резистор на две части, чтобы получилось как показано на картинках:
Благодаря такому решению, даже поменяв местами фазу и ноль, ток через человека на «землю» (при случайном прикосновении) никак не сможет превысить 220/12000=0.018А. А это уже не так опасно.
Как быть с пульсациями?
В обеих схемах светодиод будет светиться только в положительный полупериод сетевого напряжения. То есть он будет мерцать с частой 50 Гц или 50 раз в секунду, причём размах пульсаций будет равен 100% (10 мс горит, 10 мс не горит и так далее). Это будет заметно глазу.
К тому же, при подсветке мерцающими светодиодами каких-либо движущихся объектов, например, лопастей вентилятора, колес велосипеда и т.п., неизбежно будет возникать стробоскопический эффект. В некоторых случаях данный эффект может быть неприемлем или даже опасен. Например, при работе за станком может показаться, что фреза неподвижна, а на самом деле она вращается с бешенной скоростью и только и ждет, чтобы вы сунули туда пальцы.
Чтобы сделать пульсации менее заметными, можно удвоить частоту включения светодиода с помощью двухполупериодного выпрямителя (диодного моста):
Обратите внимание, что по сравнению со схемой #2 при том же самом сопротивлении резисторов, мы получили в два раза больший средний ток. И, соответственно, в четыре раза большую мощность рассеивания резисторов.
К диодному мосту при этом не предъявляется каких-либо особых требований, главное, чтобы диоды, из которых он состоит, выдерживали половину рабочего тока светодиода. Обратное напряжение на каждом из диодов будет совсем ничтожным.
Еще, как вариант, можно организовать встречно-параллельное включение двух светодиодов. Тогда один из них будет гореть во время положительной полуволны, а второй — во время отрицательной.
Фишка в том, что при таком включении максимальное обратное напряжение на каждом из светодиодов будет равно прямому напряжению другого светодиода (несколько вольт максимум), поэтому каждый из светодиодов будет надежно защищен от пробоя.
Светодиоды следует разместить как можно ближе друг к другу. В идеале — попытаться найти сдвоенный светодиод, где оба кристалла размещены в одном корпусе и у каждого свои выводы (хотя я таких ни разу не видел).
Вообще говоря, для светодиодов, выполняющих индикаторную функцию, величина пульсаций не очень-то и важна. Для них самое главное — это максимально заметная разница между включенным и выключенным состоянием (индикация вкл/выкл, воспроизведение/запись, заряд/разряд, норма/авария и т.п.)
А вот при создании светильников, всегда нужно стараться свести пульсации к минимуму. И не столько из-за опасностей стробоскопического эффекта, сколько из-за их вредного влияния на организм.
Какие пульсации считаются допустимыми?
Все зависит от частоты: чем она ниже, тем заметнее пульсации. На частотах выше 300 Гц пульсации становятся совершенно невидимыми и вообще никак не нормируются, то есть даже 100%-ные считаются нормой.
Не смотря на то, что пульсации освещенности на частотах 60-80 Гц и выше визуально не воспринимаются, тем не менее, они способны вызывать повышенную усталость глаз, общую утомляемость, тревожность, снижение производительности зрительной работы и даже головные боли.
Для предотвращения вышеперечисленных последствий, международный стандарт IEEE 1789-2015 рекомендует максимальный уровень пульсаций яркости для частоты 100 Гц — 8% (гарантированно безопасный уровень — 3%). Для частоты 50 Гц — это будут 1.25% и 0.5% соответственно. Но это для перфекционистов.
На самом деле, для того, чтобы пульсации яркости светодиода перестали хоть как-то досаждать, достаточно, чтобы они не превышали 15-20%. Именно таков уровень мерцания ламп накаливания средней мощности, а ведь на них никто и никогда не жаловался. Да и наш российский СНиП 23-05-95 допускает мерцание света в 20% (и только для особо кропотливых и ответственных работ требование повышено до 10%).
В соответствии с ГОСТ 33393-2015 «Здания и сооружения. Методы измерения коэффициента пульсации освещенности» для оценки величины пульсаций вводится специальный показатель — коэффициент пульсаций (Кп).
Коэфф. пульсаций в общем рассчитывается по сложной формуле с применением интегральной функции, но для гармонических колебаний формула упрощается до следующей:
Кп = (Еmax — Emin) / (Emax + Emin) ⋅ 100%,
где Емах — максимальное значение освещенности (амплитудное), а Емин — минимальное.
Мы будем использовать эту формулу для расчета емкости сглаживающего конденсатора.
Очень точно определить пульсации любого источника света можно при помощи солнечной панели и осциллографа:
Как уменьшить пульсации?
Посмотрим, как включить светодиод в сеть 220 вольт, чтобы снизить пульсации. Для этого проще всего подпаять параллельно светодиоду накопительный (сглаживающий) конденсатор:
Из-за нелинейного сопротивления светодиодов, расчет емкости этого конденсатора является довольно нетривиальной задачей.
Однако, эту задачу можно упростить, если сделать несколько допущений. Во-первых, представить светодиод в виде эквивалентного постоянного резистора:
А во-вторых, сделать вид, что яркость светодиода (а, следовательно, и освещенность) имеет линейную зависимость от тока.
Давайте попробуем приблизительно рассчитать емкость конденсатора на конкретном примере.
Расчет емкости сглаживающего конденсатора
Допустим, мы хотим получить коэфф. пульсаций 2.5% при токе через светодиод 20 мА. И пусть в нашем распоряжении оказался светодиод, на котором при токе в 20 мА падает 2 В. Частота сети, как обычно, 50 Гц.
Так как мы решили, что яркость линейно зависит от тока через светодиод, а сам светодиод мы представили в виде простого резистора, то освещенность в формуле расчета коэффициента пульсаций можем спокойно заменить на напряжение на конденсаторе:
Кп = (Umax — Umin) / (Umax + Umin) ⋅ 100%
Подставляем исходные данные и вычисляем Umin:
2.5% = (2В — Umin) / (2В + Umin) ⋅ 100% => Umin = 1.9В
Период колебаний напряжения в сети равен 0.02 с (1/50).
Таким образом, осциллограмма напряжения на конденсаторе (а значит и на нашем упрощенном светодиоде) будет выглядеть примерно вот так:
Вспоминаем тригонометрию и считаем время заряда конденсатора (для простоты не будем учитывать сопротивление балластного резистора):
tзар = arccos(Umin/Umax) / 2πf = arccos(1.9/2) / (2⋅3.1415⋅50) = 0.0010108 с
Весь остальной остаток периода кондер будет разряжаться. Причем, период в данном случае нужно сократить в два раза, т.к. у нас используется двухполупериодный выпрямитель:
tразр = Т — tзар = 0.02/2 — 0.0010108 = 0.008989 с
Осталось вычислить емкость:
C = ILED⋅ dt/dU = 0.02 ⋅ 0.008989/(2-1.9) = 0.0018 Ф (или 1800 мкФ)
На практике вряд ли кто-то будет ставить такой большой кондер ради одного маленького светодиодика. Хотя, если стоит задача получить пульсации в 10%, то нужно всего 440 мкФ.
Повышаем КПД
Обратили внимание, насколько большая мощность выделяется на гасящем резисторе? Мощность, которая тратится впустую. Нельзя ли ее как-нибудь уменьшить?
Оказывается, еще как можно! Достаточно вместо активного сопротивления (резистора) взять реактивное (конденсатор или дроссель).
Дроссель мы, пожалуй, сразу откинем из-за его громоздкости и возможных проблем с ЭДС самоиндукции. А насчет конденсаторов можно подумать.
Как известно, конденсатор любой емкости обладает бесконечным сопротивлением для постоянного тока. А вот сопротивление переменному току рассчитывается по этой формуле:
Rc = 1 / 2πfC
то есть, чем больше емкость C и чем выше частота тока f — тем ниже сопротивление.
Прелесть в том, что на реактивном сопротивлении и мощность тоже реактивная, то есть ненастоящая. Она как бы есть, но ее как бы и нет. На самом деле эта мощность не совершает никакой работы, а просто возвращается назад к источнику питания (в розетку). Бытовые счетчики ее не учитывают, поэтому платить за нее не придется. Да, она создает дополнительную нагрузку на сеть, но вас, как конечного потребителя, это вряд ли сильно обеспокоит =)
Таким образом, наша схема питания светодиодов от 220В своими руками приобретает следующий вид:
Но! Именно в таком виде ее лучше не использовать, так как в этой схеме светодиод уязвим для импульсных помех.
Включение или выключение распложенных на одной с вами линии мощной индуктивной нагрузки (двигатель кондиционера, компрессор холодильника, сварочный аппарат и т.п.) приводит к появлению в сети очень коротких выбросов напряжения. Конденсатор С1 представляет для них практически нулевое сопротивление, следовательно мощный импульс направится прямиком к С2 и VD5.
К сожалению, электролитические конденсаторы, из-за своей большой паразитной индуктивности, плохо справляются с ВЧ-помехами, поэтому большая часть энергии импульса пойдет через p-n-переход светодиода.
Еще один опасный момент возникает в случае включения схемы в момент пучности напряжения в сети (т.е. в тот самый момент, когда напряжение в розетке находится на пике своего значения). Т.к. С1 в этот момент полностью разряжен, то возникает слишком большой бросок тока через светодиод.
Все это со временем это приводит к прогрессирующей деградации кристалла и падению яркости свечения.
Во избежание таких печальных последствий, схему нужно дополнить небольшим гасящим резистором на 47-100 Ом и мощностью 1 Вт. Кроме того, резистор R1 будет выступать в роли предохранителя на случай пробоя конденсатора С1.
Получается, что схема включения светодиода в сеть 220 вольт должна быть такой:
И остается еще один маленький нюанс: если выдернуть эту схему из розетки, то на конденсаторе С1 останется какой-то заряд. Остаточное напряжение будет зависеть от того, в какой момент была разорвана цепь питания и в отдельных случаях может превышать 300 вольт.
А так как конденсатору некуда разряжаться, кроме как через свое внутреннее сопротивление, то заряд может сохраняться очень долго (сутки и более). И все это время кондер будет ждать вас или вашего ребенка, через которого можно будет как следует разрядиться. Причем, для того, чтобы получить удар током, не нужно лезть в недра схемы, достаточно просто прикоснуться к обоим контактам штепсельной вилки.
Чтобы помочь кондеру избавиться от ненужного заряда, подключим параллельно ему любой высокоомный резистор (например, на 1 МОм). Этот резистор не будет оказывать никакого влияния на расчетный режим работы схемы. Он даже греться не будет.
Таким образом, законченная схема подключения светодиода к сети 220В (с учетом всех нюансов и доработок) будет выглядеть так:
Значение емкости конденсатора C1 для получения нужного тока через светодиод можно сразу взять из Таблицы 2, а можно рассчитать самостоятельно.
Вот здесь можно посмотреть, как еще сильнее усовершенствовать данную схему, добавив в нее стабилизатор тока на одном транзисторе и стабилитроне. Это существенно понизит пульсации и продлит срок службы светодиодов.Расчет гасящего конденсатора для светодиода
Не буду приводить утомляющие математические выкладки, дам сразу готовую формулу емкости (в Фарадах):
C = I / (2πf√(U2вх — U2LED)) [Ф],
где I — ток через светодиод, f — частота тока (50 Гц), Uвх — действующее значение напряжения сети (220В), ULED — напряжение на светодиоде.
Если расчет ведется для небольшого числа последовательно включенных светодиодов, то выражение √(U2вх — U2LED) приблизительно равно Uвх, следовательно формулу можно упростить:
C ≈ 3183 ⋅ ILED / Uвх [мкФ]
а, раз уж мы делаем расчеты под Uвх = 220 вольт, то:
C ≈ 15 ⋅ ILED [мкФ]
Таким образом, при включении светодиода на напряжение 220 В, на каждые 100 мА тока потребуется примерно 1.5 мкФ (1500 нФ) емкости.
Кто не в ладах с математикой, заранее посчитанные значения можно взять из таблицы ниже.
Таблица 2. Зависимость тока через светодиоды от емкости балластного конденсатора.
| C1 | 15 nF | 68 nF | 100 nF | 150 nF | 330 nF | 680 nF | 1000 nF |
|---|---|---|---|---|---|---|---|
| ILED | 1 mA | 4.5 mA | 6.7 mA | 10 mA | 22 mA | 45 mA | 67 mA |
Немного о самих конденсаторах
В качестве гасящих рекомендуется применять помехоподавляющие конденсаторы класса Y1, Y2, X1 или X2 на напряжение не менее 250 В. Они имеют прямоугольный корпус с многочисленными обозначениями сертификатов на нем. Выглядят так:
Если вкратце, то:
- X1 – используются в промышленных устройствах, подключаемых к трехфазной сети. Эти конденсаторы гарантированно выдерживают всплеск напряжения в 4 кВ;
- X2 – самые распространенные. Используются в бытовых приборах с номинальным напряжением сети до 250 В, выдерживают скачек до 2.5 кВ;
- Y1 – работают при номинальном сетевом напряжении до 250 В и выдерживают импульсное напряжение до 8 кВ;
- Y2 – довольно-таки распространенный тип, может быть использован при сетевом напряжении до 250 В и выдерживает импульсы в 5 кВ.
Допустимо применять отечественные пленочные конденсаторы К73-17 на 400 В (а лучше — на 630 В).
Сегодня широкое распространение получили китайские «шоколадки» (CL21), но в виду их крайне низкой надежности, очень рекомендую удержаться от соблазна применять их в своих схемах. Особенно в качестве балластных конденсаторов.
Внимание! Полярные конденсаторы ни в коем случае нельзя использовать в качестве балластных!
Итак, мы рассмотрели, как подключать светодиод к 220В (схемы и их расчет). Все приведенные в данной статье примеры хорошо подходят для одного или нескольких маломощных светодиодов, но совершенно нецелесообразны для мощных светильников, например, ламп или прожекторов — для них лучше использовать полноценные схемы, которые называются драйверами.
Простейшая однокомандная схема радиоуправления моделями (3 транзистора)
Для радиоуправления различными моделями и игрушками может быть использована аппаратура дискретного и пропорционального действия.
Основное отличие аппаратуры пропорционального действия от дискретной состоит в том, что она позволяет по командам оператора отклонять рули модели на любой требуемый угол и плавно изменять скорость и направление ее движения «Вперед» или «Назад».
Постройка и налаживание аппаратуры пропорционального действия достаточно сложны и не всегда под силу начинающему радиолюбителю.
Хотя аппаратура дискретного действия и имеет ограниченные возможности, но, применяя специальные технические решения, можно их расширить. Поэтому далее рассмотрим однокомандную аппаратуру управления, пригодную для колесных, летающих и плавающих моделей.
Схема передатчика
Для управления моделями в радиусе 500 м, как показывает опыт, достаточно иметь передатчик с выходной мощностью окьло 100 мВт. Передатчики радиоуправляемых моделей, как правило, работают в диапазоне 10 м.
Однокомандное управление моделью осуществляется следующим образом. При подаче команды управления передатчик излучает высокочастотные электромагнитные колебания, другими словами, генерирует одну несущую частоту.
Приемник, который находится на модели принимает сигнал, посланный передатчиком, в результате чего срабатывает исполнительный механизм.
Рис. 1. Принципиальная схема передатчика радиоуправляемой модели.
В итоге модель, подчинясь команде, меняет направление движения или осуществляет одно какое-нибудь заранее заложенное в конструкцию модели указание. Используя однокомандную модель управления, можно заставить модель осуществлять достаточно сложные движения.
Схема однокомандного передатчика представлена на рис. 1. Передатчик включает задающий генератор колебаний высокой частоты и модулятор.
Задающий генератор собран на транзисторе VT1 по схеме емкостной трех-точки. Контур L2, С2 передатчика настроен на частоту 27,12 МГц, которая отведена Госсвязьнадзором электросвязи для радиоуправления моделями.
Режим работы генератора по постоянному току определяется подбором величины сопротивления резистора R1. Созданные генератором высокочастотные колебания излучаются в пространство антенной, подключенной к контуру через согласующую катушку индуктивности L1.
Модулятор выполнен на двух транзисторах VT1, VT2 и представляет собой симметричный мультивибратор. Модулируемое напряжение снимается с коллекторной нагрузки R4 транзистора VT2 и подается в общую цепь питания транзистора VT1 высокочастотного генератора, что обеспечивает 100% модуляцию.
Управляется передатчик кнопкой SB1, включенной в общую цепь питания. Задающий генератор работает не непрерывно, а только при нажатой кнопке SB1, когда появляются импульсы тока, вырабатываемые мультивибратором.
Посылка в антенну высокочастотных колебаний, созданных задающим генератором, происходит отдельными порциями, частота следования которых соответствует частоте импульсов модулятора.
Детали передатчика
В передатчике использованы транзисторы с коэффициентом передачи тока базы Ь2іэ не менее 60. Резисторы типа МЛТ-0,125, конденсаторы — К10-7, КМ-6.
Согласующая антенная катушка L1 имеет 12 витков ПЭВ-1 0,4 и намотана на унифицированном каркасе от карманного приемника с подстроечным ферритовым сердечником марки 100НН диаметром 2,8 мм.
Катушка L2 бескаркасная и содержат 16 витков провода ПЭВ-1 0,8 намотанных на оправке 010 мм. В качестве кнопки управления можно использовать микропереключатель типа МП-7.
Детали передатчика монтируют на печатной плате из фольгированного стеклотекстолита. Антенна передатчика представляет собой отрезок стальной упругой проволоки 01…2 мм и длиной около 60 см, которая подключается прямо к гнезду XI, расположенному на печатной плате.
Все детали передатчика должны быть заключены в алюминиевый корпус. На передней панели корпуса располагается кнопка управления. В месте прохождения антенны через стенку корпуса к гнезду XI должен быть установлен пластмассовый изолятор, чтобы предотвратить касание антенны корпуса.
Налаживание передатчика
При заведомо исправных деталях и правильном монтаже передатчик не требует особой наладки. Необходимо только убедиться в его работоспособности и, изменяя индуктивность катушки L1, добиться максимальной мощности передатчика.
Для проверки работы мультивибратора надо включить высокоомные наушники между коллектором VT2 и плюсом источника питания. При замыкании кнопки SB1 в наушниках должен прослушиваться звук низкого тона, соответствующий частоте мультивибратора.
Для проверки работоспособности генератора ВЧ необходимо собрать волномер по схеме рис. 2. Схема представляет собой простой детекторный приемник, в котором катушка L1 намотана проводом ПЭВ-1 1…1,2 и содержит 10 витков с отводом от 3 витка.
Рис. 2. Принципиальная схема волномера для настройки передатчика.
Катушка намотана с шагом 4 мм на пластмассовом каркасе 025 мм. В качестве индикатора используется вольтметр постоянного тока с относительным входным сопротивлением 10 кОм/В или микроамперметр на ток 50…100мкА.
Волномер собирают на небольшой пластине из фольгированного стеклотекстолита толщиной 1,5 мм. Включив передатчик, располагают от него волномер на расстоянии 50…60 см. При исправном генераторе ВЧ стрелка волномера отклоняется на некоторый угол от нулевой отметки.
Настраивая генератор ВЧ на частоту 27,12 МГц, сдвигая и раздвигая витки катушки L2, добиваются максимального отклонения стрелки вольтметра.
Максимальную мощность высокочастотных колебаний, излучаемых антенной, получают вращением сердечника катушки L1. Настройка передатчика считается оконченной, если вольтметр волномера на расстоянии 1…1,2 м от передатчика показывает напряжение не менее 0,05 В.
Схема приемникаДля управления моделью радиолюбители довольно часто используют приемники, построенные по схеме сверхрегенератора. Это связано с тем, что сверхрегенеративный приемник, имея простую конструкцию, обладает очень высокой чувствительностью, порядка 10…20 мкВ.
Схема сверхрегенеративного приемника для модели приведена на рис. 3. Приемник собран на трех транзисторах и питается от батареи типа «Крона» или другого источника напряжением 9 В.
Первый каскад приемника представляет собой сверхрегенеративный детектор с самогаше-нием, выполненный на транзисторе VT1. Если на антенну не поступает сигнал, то этот каскад генерирует импульсы высокочастотных колебаний, следующих с частотой 60…100 кГц. Это и есть частота гашения, которая задается конденсатором С6 и резистором R3.
Рис. 3. Принципиальная схема сверхрегенеративного приемника радиоуправляемой модели.
Усиление выделенного командного сигнала сверхрегенеративным детектором приемника происходит следующим образом. Транзистор VT1 включен по схеме с общей базой и его коллекторный ток пульсирует с частотой гашения.
При отсутствии на входе приемника сигнала, эти импульсы детектируются и создают на резисторе R3 некоторое напряжение. В момент поступления сигнала на приемник продолжительность отдельных импульсов возрастает, что приводит к увеличению напряжения на резисторе R3.
Приемник имеет один входной контур L1, С4, который с помощью сердечника катушки L1 настраивается на частоту передатчика. Связь контура с антенной — емкостная.
Принятый приемником сигнал управления выделяется на резисторе R4. Этот сигнал в 10…30 раз меньше напряжения частоты гашения.
Для подавления мешающего напряжения с частотой гашения между сверхрегенеративным детектором и усилителем напряжения включен фильтр L3, С7.
При этом на выходе фильтра напряжение частоты гашения в 5… 10 раз меньше амплитуды полезного сигнала. Продетектированный сигнал через разделительный конденсатор С8 подается на базу транзистора VT2, представляющего собой каскад усиления низкой частоты, а далее на электронное реле, собранное на транзисторе ѴТЗ и диодах VD1, VD2.
Усиленный транзистором ѴТЗ сигнал выпрямляется диодами VD1 и VD2. Выпрямленный ток (отрицательной полярности) поступает на базу транзистора ѴТЗ.
При появлении тока на входе электронного реле, коллекторный ток транзистора увеличивается и срабатывает реле К1. В качестве антенны приемника можно использовать штырь длиной 70… 100 см. Максимальная чувствительность сверхрегенеративного приемника устанавливается подбором сопротивления резистора R1.
Детали и монтаж приемника
Монтаж приемника выполняют печатным способом на плате из фольгированного стеклотекстолита толщиной 1,5 мм и размерами 100×65 мм. В приемнике используются резисторы и конденсаторы тех же типов, что и в передатчике.
Катушка контура сверхрегенератора L1 имеет 8 витков провода ПЭЛШО 0,35, намотанных виток к витку на полистироловом каркасе 06,5 мм, с подстроечным ферритовым сердечником марки 100НН диаметром 2,7 мм и длиной 8 мм. Дроссели имеют индуктивность: L2 — 8 мкГн, a L3 — 0,07…0,1 мкГн.
Электромагнитное реле К1 типа РЭС-6 с обмоткой сопротивлением 200 Ом.
Настройка приемника
Настройку приемника начинают с сверхрегенеративного каскада. Подключают высокоомные наушники параллельно конденсатору С7 и включают питание. Появившийся в наушниках шум свидетельствует об исправной работе сверхрегенеративного детектора.
Изменением сопротивления резистора R1 добиваются максимального шума в наушниках. Каскад усиления напряжения на транзисторе VT2 и электронное реле особой наладки не требуют.
Подбором сопротивления резистора R7 добиваются чувствительности приемника порядка 20 мкВ. Окончательная настройка приемника производится совместно с передатчиком.
Если в приемнике параллельно обмотке реле К1 подключить наушники и включить передатчик, то в наушниках должен прослушиваться громкий шум. Настройка приемника на частоту передатчика приводит к пропаданию шума в наушниках и срабатыванию реле.
Литература: В.М. Пестриков. Энциклопедия радиолюбителя.
Схема простейших устройств управляемых светом (двигатель, реле)
Система телеуправления моделей с помощью светового луча наиболее простая, так как в качестве передатчика здесь можно использовать обычный карманный фонарик. Не так уж и сложен приемник такой модели. Такая телеаппаратура может быть установлена в различные электрофицированные игрушки, например, машинки с электродвигателем, питающимся от батарейки.
Рассмотрим вначале схему управления миниатюрного электрического моторчика с помощью транзистора. Простая схема такого управления представлена на рис. 22.1. При вращении оси переменного резистора Rl происходит изменение усиления транзистора, а отсюда и изменяется скорость вращения двигателя. Управление с помощью транзистора достаточно удобно и к тому же позволяет удлинить соединяющие провода между резистором и остальной частью схемы. Можно весь механизм, приводящий в движение игрушку, поместить внутри ее, а в руках держать переменный резистор, соединенный с ней длинными проводами. Хотя такая схема управления часто применяется на практике, более эффективным и современным является использование беспроводного управления.
Рис. 22.1. Принципиальная электрическая схема управления электродвигателем
Рис. 22.2. Принципиальная схема устройства управления электродвигателя лучом света
На рис. 22.2 приведена принципиальная схема беспроводного устройства, управляемого лучом света. С правой стороны от пунктирной линии находится обычная цепь моторчика с транзистором, а слева цепь с фотодиодом, которая заменила в предыдущей схеме управления переменный резистор R1. Если теперь осветить фотодиод лучом фонарика, то произойдет уменьшение его сопротивления. Это приведет к изменению сопротивления транзисторной цепи и вызовет быстрое вращение двигателя. Если теперь выключить свет, то двигатель остановится. Телеметрическое устройство собирается на небольшой монтажной планке, которая помещается внутри модели. Наверху модели, в удобном месте с точки зрения освещенности, крепится фотодиод. Модель с такой системой управления работает от луча света, направленного с расстояния до 1,3 м.
Автомат выключения уличного освещения
На таком же принципе можно построить и автомат включения уличного освещения в деревне цли загородном домике (рис. 22.3). Его датчиком служит фоторезистор типа ФС-К1, который, как и в схеме рис. 22.2, включен в цепь базы транзистора VT1. Темновое сопротивление фоторезистора составляет около 500…800 кОм, а коллекторный ток транзистора VT2 не превышает 3…4 мА, что недостаточно для срабатывания реле К1.
Рис. 22.3. Принципиальная схема устройства выключения уличного освещения
В это время контакты реле замкнуты и лампочка уличного освещения горит. С наступлением рассвета сопротивление фоторезистора постепенно уменьшается до 70…100 кОм, а ток в цепи базы транзистора VT1 увеличивается. Это приводит к повышению тока коллектора транзистора VT2 и срабатыванию реле К1, которое размыкает контакты К1.1 и лампа гаснет. Питание устройства построено по бестрансформаторной схеме с использованием гасящего конденсатора С2. В автомате использовано реле К1 типа РЭС-22 (паспорт РФ4.500.131). Конденсатор С2 типа МБГО на напряжение 600 В. Автомат смонтирован в корпусе из пластмассы размером 120x90x30 мм и настройки практически не требует. Для увеличения задержки времени выключения лампы следует уменьшить питающее напряжение до-15…16 В. Для этого вместо указанных на схеме типов стабилитронов, следует использовать один стабилитрон Д813 или два типа КС 175 (или ранних выпусков Д808).
Литература: В.М. Пестриков. Энциклопедия радиолюбителя.
Простые аддитивные схемы расчета — Справочник химика 21
Простые аддитивные схемы расчета [c.216]Один из примеров простых аддитивных схем расчета химических сдвигов представляет следующее уравнение (Грант и Пол), по которому можно определить химический сдвиг в спектроскопии ЯМР С для А-го углеродного атома б с в ацикличе- [c.32]
В опубликованной через два года работе [315] автор систематизировал при помощи своего метода ряд литературных данных по кинетике молекулярных реакций и сделал некоторые выводы о связи строения и реакционной способности соединений. При этом он показал, что применимость предложенной им в 1963 г. простой аддитивной схемы расчета энергии активации ограничивается превращениями, для которых справедливо правило аддитивности обычных химических связей. Исключение составляют молекулы с конденсированными соединениями и перфторированные молекулы. [c.129]
Энтропия (S°29s) этих окислов серы в газообразном состоянии равна соответственно 61,2, 59,29 и 53,05 кал (град моль), т. е. первая разность равна 1,9, а вторая 6,24 кал град моль). Поэтому простейшие аддитивные схемы, в которых каждому виду атомов (или ионов) приписывался постоянный инкремент, могли удовлетворять только в первый период накопления экспериментальных данных, пока точность их была еще невысока. Например, для энтропии возможная погрешность экспериментальных данных еще в 20-х годах достигала обычно нескольких кал град моль) и применение простой аддитивной схемы расчета во многих случаях не вносило существенной ошибки. [c.90]
Неприменимость в общем случае простых аддитивных схем расчета по инкрементам атомов или связей уже давно привела к введению инкрементов, относящихся к определенным группам атомов или связей (NO2, Nh3, СООН и др.). Не останавливаясь на ранних работах, отметим лишь системы групповых инкрементов теплот сгорания, разработанные Карашем ° и Кульбахом . [c.261]
В работе [293] на основании простой аддитивной схемы расчета получено значение —32 ккал/моль. Значение теплоты испарения изомеров СгНгСи при 298,15°К приводится в Справочнике Бюро стандартов США [3508]. [c.590]
В работе [293] на основании простой аддитивной схемы расчета получено ( 2HF I2, газ) = [c.591]
Простейший регулятор — Большая Энциклопедия Нефти и Газа, статья, страница 4
Простейший регулятор
Cтраница 4
На рис. 2.11 представлена принципиальная схема термостата с простейшим регулятором температуры. В термостат Т вставлен ртутный контактный термометр КТ. Контакты термометра должны быть установлены на делении его шкалы, совпадающем с требуемой температурой. При действии электрического нагревателя Я, находящегося в термостате, температура повышается, и высота столбика ртути в термометре увеличивается. Когда температура достигает требуемого значения, ртуть замыкает контакты термометра. При этом замыкается цепь постоянного тока, питающего катушку контактора К, а контактор выключает переменный ток, питающий нагреватель. [46]
В табл. 4 приводятся схемы различных функциональных блоков и простейших регуляторов, выполненных из элементов СЭГРА, на рис. 77 — схема ПИ-регулятора расхода, а на рис. 78 — схема пропорционального регулятора с дифференциальной приставкой для поддержания заданной производительности ленточного транспортера. [48]
Различие между статическим и астатическим регуляторами поясним с помощью рассмотрения простейшего регулятора напряжения, собранного по компенсационной схеме. [49]
Это наглядно видно из рис. 127, на котором представлена схема простейшего регулятора. [51]
Регулятор давления РД, схема которого представлена на рис. 62, является простейшим регулятором пневматического действия. [52]
Таким образом, автомат может поддерживать постоянную среднюю температуру объекта и выполнять функцию простейшего регулятора температуры. [54]
Возможность обеспечения высокой полноты сгорания высокосернистых мазутов с малыми избытками воздуха на базовых котлах путем применения простейших регуляторов, а в некоторых случаях даже и без них делает желательным выделение в такой режим работы большей части котельных агрегатов, что оправдывается также и с экономической точки зрения, поскольку такие котлы не нуждаются в сложных широкодиапазонных горелках со сравнительно высокими напорами воздуха, с повышенным давлением мазута и расходом пара для улучшения распыливания мазута. [55]
Иногда говорят, что помещения имеют хорошие динамические характеристики, имея в виду как раз возможность использовать простейшие регуляторы как наиболее надежные и дешевые. [56]
Кроме указанных регуляторов непрямого действия, применяемых для поддержания основных параметров, в системе автоматического регулирования используются простейшие регуляторы прямого действия. [57]
Примеры модулей МФСЗ приведены на рис. 6.1. Ввод информационных сигналов датчиков в АСР производится через кондуктивные разделители, а в простейших регуляторах непосредственно в регулирующее устройство. [58]
Такие системы управления, получившие название трансидинных, легко поддаются анализу, синтезу и иаладке благодаря тому, что вся система разбивается на простейшие регуляторы, каждый из которых контролирует свой параметр, причем выходной сигнал внешнего регулятора является сигналом задания для подчиненного внутреннего регулятора. [60]
Страницы: 1 2 3 4 5
ПРОСТЕЙШИЕ СХЕМЫ ВКЛЮЧЕНИЯ ЭЛЕКТРИЧЕСКИХ ПРИБОРОВ ЛИФТОВ
Лампу накаливания осветительную на схеме обозначают окружностью, перечеркнутой двумя взаимно перпендикулярными линиями (рис. 1. 1, а), если лампа сигнальная, то сегменты зачерненные (рис. 1.1, б). Выключатся имеет один из двух типов контактов: замыкающий или размыкающий (рис. 1.1, в, г).
Рис. 1.1. Схема цепи е лампой
Рис. 12 Контакты путевого выключателя и лампа, включенная двумя ШР
Схема лампы освещения с выключателем показана на рис. 1.1, д. На клеммах
есть напряжение, но лампа не горит — разомкнут контакт выключателя, в
цепи нет электрического тока. На рис. 1.1, е в цепи установлен контакт
выключателя размыкающий: в нормальном состоянии он замкнут, лампа
включена.
Выключатель имеет два фиксированных, т. е. устойчивых, положения: включено и выключено.
Особое значение имеют выключатели концевые и путевые. Они срабатывают (замыкают или размыкают цепь) под воздействием управляющих упоров-кулачков, когда механизм поворачивается или перемещается на определенное расстояние. Например, в шкафу управления установлена лампа освещения. При закрытой двери шкафа она выключена, так как контакт выключателя разомкнут. Когда открывают дверь шкафа, ее створка освобождает подвижный штифт выключателя, контакт замыкается и лампа загорается.
На рис 1 2, а показаны контакты путевого выключателя: замыкающий и размыкающий.
Можно включить лампу, вставляя штепсель в гнездо. Штепсель и гнездо образуют штепсельный разъем (рис. 1.2, б). Схема лампы, включенной с помощью двух штепсельных разъемов LUP, приведена на рис. 1.2, в. Штепсельные гнезда установлены в машинном помещении, на кабине, в приямке. Они позволяют включить переносной инструмент или лампу освещения, рассчитанные на 24 В переменного напряжения.
В кабине лифта находится кнопка вызова обслуживающего персонала КнВП, а в помещении дежурного — звонок ЗвВП. Схема их включения дана на рис. 1.3, а.
Пассажир нажимает на кнопку звонка: поскольку кнопка с самовозвратом, то как только он отпускает ее, пружина размыкает контакт,— звонка не слышно.
Кнопки с замыкающим контактом (рис. 1.3, б) установлены на лестничных площадках — кнопки вызова КнВ, и в кабине — кнопки приказа КнП. Нажимая на одну из них, пассажир включает этажное реле соответствующего этажа.
Кроме того, имеются кнопки с самовозвратом, у которых контакт постоянно замкнут (рис. 1.3, в) —это размыкающий контакт. Одна из них К-Стоп установлена в кабине, другая М-Стоп — в машинном помещении.
Кнопки с самовозвратом позволяют замкнуть или разомкнуть цепь, но на короткое время.
Рис. 1.3. Схема включения звонка вызова персонала и условное обозначение контактов кнопки с самовозвратом
Simply Scheme: Введение в информатику
Simply Scheme: Введение в информатику2 / e Авторские права (C) 1999 MIT
Ниже этого краткого содержания представлено расширенное содержание включая разделы в каждой главе. Щелкните название главы спрыгнуть. Вы также можете скачать полный текст каждой главы в формате PDF для элегантной печати или просмотрите версию HTML. Введение в детали включено в PDF-файл следующей главы.Проекты включены в PDF-файл предыдущей главы.
Примечание: эта книга все еще находится под защитой авторских прав и находится в печати. это размещены здесь для вашего личного использования, а не для перепродажи или распространения. Спасибо!
- Одна большая идея: символическое программирование
- Лисп и радикальная информатика
- Кому следует прочитать эту книгу
- Как читать эту книгу
- Списки и предложения
- Предложения и слова
- Перегрузка в текстовой абстракции
- Процедуры высшего порядка, лямбда и рекурсия
- Мутаторы и среды
- Разговор со схемой
- Восстановление после ошибок ввода
- Схема выхода
- Еще примеры
- Пример: аббревиатуры
- Пример: Свинья на латыни
- Пример: выбор мороженого
- Пример: комбинации из набора
- Пример: Факториал
- Играйте с процедурами
- Арифметика
- слов
- Домен и диапазон
- Другие типы: предложения и логические значения
- Наш любимый тип: функции
- Играй с ним
- Думая о том, что вы сделали
- Маленькие люди
- Результат замены
- Схемы сантехники
- Подводные камни
- Как определить процедуру
- Особые формы
- Функции и процедуры
- Имена аргументов в сравнении со значениями аргументов
- Процедура как обобщение
- Совместимость
- Модель замещения
- Подводные камни
- Селекторы
- Конструкторы
- Первоклассные слова и предложения
- Подводные камни
- Предикаты
- Использование предикатов
-
Если— особая форма - Так
ииили - Все, что не ложно, правда
- Решения, Решения, Решения
-
Еслиявляется составным - Подводные камни
- Как маленькие люди делают переменные
- Глобальные и локальные переменные
- Правда о подмене
-
Пусть - Подводные камни
-
Каждые - Пауза для размышлений
-
Сохранить -
Накопить - Объединение функций высшего порядка
- Выбор подходящего инструмента
- Функции первого класса и приговоры первого класса
-
Повторный - Подводные камни
- Процедуры, возвращающие процедуры
- Правда о
Определить - Правда о
Пусть - Конфликты имен
- Именованные и неназванные функции
- Подводные камни
- Предупреждение
- Технические термины в крестиках-ноликах
- Размышляя о структуре программы
- Первый шаг: тройки
- В поисках троек
- Использование
каждыес двухаргументными процедурами - Может ли компьютер победить в этом шаге?
- Если да, то в каком квадрате?
- Второй стих, такой же, как и первый
- Теперь стратегия усложняется
- В поисках точек поворота
- В наступлении
- Остатки
- Полный список программ
- Отдельная процедура для каждой длины
- Используйте то, что у вас есть, чтобы получить то, что вам нужно
- Обратите внимание, что они все одинаковы
- Обратите внимание, что они почти все одинаковые
- Базовые случаи и рекурсивные вызовы
- Свинья на латыни
- Проблемы, которые стоит попробовать
- Наши решения
- Подводные камни
- От метода комбинирования к прыжку веры
- Пример:
Реверс - Прыжок веры
- Базовый корпус
- Пример:
Факториал - Вероятные предположения для более мелких подзадач
- Пример:
Downup - Пример:
Evens - Упрощение базовых случаев
- Подводные камни
- Маленькие люди и рекурсия
- Отслеживание
- Подводные камни
-
Каждый узор - Шаблон
Keep - Шаблон
Accumulate - Объединение узоров
- Вспомогательные процедуры
- Как использовать рекурсивные шаблоны
- Проблемы, не подчиняющиеся шаблонам
- Подводные камни
- Пример:
Сортировка - Пример:
Исходное двоичное - Пример:
Сортировка слияний - Пример:
Подмножества - Подводные камни
- Описание проблемы
- Реализация: когда два предложения равны?
- Когда два предложения почти равны?
- Сопоставление с альтернативами
- Возврат
- Соответствие нескольких слов
- Объединение заполнителей
- Именование совпадающего текста
- Окончательная версия
- Абстрактные типы данных
- Отслеживание с возвратом и
известные значения - Как мы это писали
- Полный список программ
- Селекторы и конструкторы
- Программирование со списками
- Правда о приговорах
- Функции высшего порядка
- Другие примитивы для списков
- Списки ассоциаций
- Функции, принимающие переменные числа аргументов
- Рекурсия в произвольных структурированных списках
- Подводные камни
- Пример: мир
- Насколько велико мое дерево?
- Взаимная рекурсия
- Поиск датума в дереве
- Поиск датума на дереве
- Представление деревьев в виде списков
- Абстрактные типы данных
- Расширенный пример: анализ арифметических выражений
- Подводные камни
- Обобщающие шаблоны
- The
EveryPattern Revisited - Разница между
КартаиКаждые -
Фильтр -
НакопитьиУменьшить - Прочность
- Функции высшего порядка для структурированных списков
- The Zero-Trip Do Loop
- Подводные камни
- Печать
- Побочные эффекты и последовательность
- The
BeginSpecial Form - Это не функциональное программирование
- Не переходить на следующую строку
- Струны
- Процедура более высокого порядка для секвенирования
- Крестики-нолики Revisited
- Принятие пользовательского ввода
- Aesthetic Board Display
- Чтение и запись обычного текста
- Форматированный текст
- Последовательное программирование и порядок оценки
- Подводные камни
- Главный цикл
- Разница между процедурой и ее названием
- Список функций
- Проверка домена
- Намеренно путают функцию с ее именем
- Подробнее о функциях высшего порядка
- Больше прочности
- Полный список программ
- Порты
- Написание файлов для чтения
- Использование файла в качестве базы данных
- Преобразование строк файла
- Обоснование текста
- Сохранение интервала текста в файлах
- Объединение двух файлов
- Запись файлов для схемы для чтения
- Подводные камни
- Инди 500
- Векторы
- Использование векторов в программах
- Нефункциональные процедуры и состояние
- Перемешивание колоды
- Другие векторные инструменты
- Векторный шаблон рекурсии
- Векторы против списков
- Состояние, последовательность и эффекты
- Подводные камни
- Ограничения нашей электронной таблицы
- Команды электронной таблицы
- Перемещение выделения
- Ввод значений в ячейки
- Формулы
- Отображение значений формул
- Загрузка команд электронной таблицы из файла
- Прикладные программы и абстракции
- Ячейки, имена ячеек и идентификаторы ячеек
- Командный процессор
- Команды выбора ячейки
- Команда
Загрузить - Команда
Put - Переводчик формул
- Менеджер зависимостей
- Оценщик выражений
- Экранный принтер
- Менеджер ячейки
- Полный список программ
- Пример сеанса с нашей базой данных
- Как базы данных хранятся внутри
- Текущая база данных
- Реализация команд программы базы данных
- Дополнения к программе
- Дополнительная работа для хотшотов
- Лучшая книга по информатике
- За пределами SICP
- Стандартная схема
- Последние слова
Приложения
- Цикл разработки программы
- Комплексное редактирование
- Получение наших программ
- Настройка наших программ для вашей системы
- Загрузка наших программ
- Варианты схемы
- Стандарты схем
- Почему существует Common Lisp
- Определение процедур и переменных
- Соглашение об именах для предикатов
- Без слов и предложений
- Верно и неверно
- Файлы
- Массивы
- Эквиваленты примитивов схемы
- Отдельное пространство имен для процедур
-
Лямбда - Подробнее о
Функция - Написание процедур высшего порядка
[без возврата] резьба главы NEXT
Брайан Харви, bh @ cs.berkeley.edu Простая схемадля Android
Простая схема для AndroidПростая схема, для Android
Простая реализация Schem-подобного языка и редактора для Android
Доступно в Google Магазин игр.
Что и почему:
Я был в поезде, хотел написать код, и я подумал: « Интересно, есть ли хорошие реализации схемы для моего телефона? «я не нашел ни одного простого, удобного в использовании и эффективный (первый, который я установил, разбил мой Телефон).Я также хотел уметь писать графические и интерактивные программы легко (см. примеры изображений и / или большой взрыв / взаимодействие Примеры). Итак … я начал реализацию из всех основных функций, о которых я мог думать (см. традиционные формы схем и примеры, и приложение для полного списка поддерживаемые функции).
Выполнение должно быть хвостовой рекурсией, и даже нерекурсивные функции не должны запускаться не хватает места в стеке, поэтому я реализовал интерпретатор стиля с передачей продолжения с эффективная привязка и поиск.
Пока я пытался сохранить верность термину « Scheme-like «, я внес несколько изменений в язык (и реализация), чтобы сделать его немного легче для себя. По большей части изменения носят синтаксический характер, например, то, как литералы письменные и использование квадратных скобок для групповые условия и давай определения. (Этот поддерживается в Dr.Racket, но требуется в простой схеме ).
Основные отличия:
- Символьные литералы записываются в одинарные кавычки, возможно, ускользнул, например, ‘a’ или ‘\ n’
- Пары Cond (теперь необязательно) заключены в квадратные скобки:
(усл [(<3 4) "да"] [иначе «нет»]) - Пары привязки Let / Let * / LetRec (теперь также опционально) заключены в квадратные скобки:
(пусть ([x 10] [id (лямбда (а) а)]) (идентификатор x)) - То же самое для Let-Values / Let * -Values / LetRec-Values:
(let-values ([(x y) (values 10 12)] [(добавить) (лямбда (а б) (+ а б))]) (добавить x y))И результат выражение значений само по себе является многозначным значением, которое может быть развернутый (e.g., ограниченный let-values) потом. - Числа сопоставимы с длинными и двойными типами Java, т. Е. числа , а не точные (извините). Хотя вы можете использовать шестнадцатеричную и научную нотацию, например, 0x11 и 1.5e-5
Традиционные языковые формы, особенности, примеры:
Как и традиционная схема, Простая схема поддерживает define, define-struct, begin, let и многие другие формы / выражения.Ниже приведены несколько примеров:
Простые вещи ...
;; Комментарии, естественно, не выполняются
# |
Многострочные комментарии
Хотя они не вложены
| #
;; Определения значений
(определите два-пи (* 2 пи))
Определения функций ... ;; Факториал с IF (определить (факт n) (если (Определения структур...120 ;; Факториал с COND (определить (факт-условие)) (cond [( 720 ;; Взаимно-рекурсивные определения верхнего уровня (определите (даже n) (или (= n 0) (не (нечетное n)))) (определить (нечетное n) (или (= n 1) (даже (- n 1)))) (даже 5) ;; => ложь (даже 8) ;; => правда (нечетные 5) ;; => правда (нечетные 8) ;; => ложь
;; Точка: Число x Число
;; определяет: make-point, point-x, point-y и point?
(точка определения-структуры (x y))
(определить начало координат (точка создания 0 0))
(определить p (make-point 3 4))
(точка? p) ;; => правда
(точка-x p) ;; => 3
(точка-у п) ;; => 4
;; Расстояние между двумя точками
(определить (расстояние p1 p2)
(пусть ([dx (- (point-x p2) (point-x p1))]
[dy (- (point-y p2) (point-y p1))])
(sqrt (+ (* дх дх)
(* ды ды)))))
(исходное расстояние p) ;; => 5
Символы... Символы похожи на строковые литералы, но equlity
сравнение намного эффективнее
(символ =? vs. строка =?). Это
в значительной степени это.
;; Буквальный простой символ
(определите символ a-символа)
;; Преобразование и сравнение
(символ =? (строка-> символ "тест") 'тест) ;; => правда
(строка =? (символ-> строка 'тест) "тест") ;; => правда
Списки ... Списки могут быть созданы тремя
способами... cons / пусто, список
обозначение, или обозначение цитаты / '.
;; Использование минусов и пустых
(определите a-b-c (cons 'a (cons' b (cons 'c empty))))
;; Использование списка
(определите один-два-три (список 1 2 3))
;; Используя цитату / '
(определить смесь-1 (цитата (a (b) (1 2))))
(определить смесь-2 '(a (b) (1 2)))
Каждая нотация может создавать эквивалентные списки в этих случаях,
хотя выражения в кавычках / '
не оценивается.
;; Это эквивалентные
'((+ 2 3) (* 2 3))
(список (список '+ 2 3) (список' * 2 3))
;; И таковы эти
(список (+ 2 3) (* 2 3))
(список 5 6)
Конечно, у нас есть много функций, которые работают со списками...
(первый '(1 2 3)) ;; => 1
(второй '(1 2 3)) ;; => 2
(list-ref '(1 2 3) 2) ;; => 3
(список? a-b-c) ;; => правда
(пусто? a-b-c) ;; => ложь
(минусы? a-b-c) ;; => правда
(пусто? (rest (rest (rest a-b-c)))) ;; => правда
(длина a-b-c) ;; => 3
(добавить '(a b)' (c)) ;; => (список 'a' b 'c)
(переверните a-b-c) ;; => (список 'c' b 'a)
Простая схема также
включает карту, фолдр, фолдл,
и фильтр.
(map (lambda (n) (* n n)) '(1 2 3 4)) ;; => '(1 4 9 16)
(foldr string-append "" '("a" "b" "c")) ;; => "abc"
(foldl string-append "" '("a" "b" "c")) ;; => "cba"
(фильтр нечетный? '(1 2 3 4)) ;; => '(1 3)
(фильтровать даже? '(1 2 3 4)) ;; => '(2 4)
(andmap odd? '(2 4 6)) ;; => ложь
(andmap даже? '(2 4 6)) ;; => правда
(ormap odd? '(2 4 6)) ;; => ложь
(ormap odd? '(4 5 6)) ;; => правда
И, если у вас есть другие, которых не хватает, вы можете либо
напишите их или, если производительность важна, попросите, чтобы
Я их добавляю... например:
(определить (map2 f xs ys)
(cond [(или (empty? xs) (empty? ys)) empty]
[else (cons (f (сначала xs) (first ys))
(map2 f (rest xs) (rest ys)))]))
(map2 + '(1 2 3 4)' (2 4 6 8)) ;; => '(3 6 9 12)
(map2 * '(1 2 3 4)' (2 4 6 8)) ;; => '(2 8 18 32)
Последовательность и прочее ...
;; Печатает 'пять: 5 \ n', дает 20
(begin (выведите «пять:») (println 5) (* 4 5))
;; Печатает 'пять: 5 \ n', дает 20
(begin0 (* 4 5) (выведите «пять:») (println 5))
;; Дополнительные математические функции: mod, [in / de] crement
(% 13 5) ;; => 3
(++ 5) ;; => 6
(- 5) ;; => 4
;; Поразрядные функции: или, и, xor, сдвиги
(| 0xA 3) ;; => 11
(& 0xA 3) ;; => 2
(^ 0xA 3) ;; => 9
(>> 0xF 2) ;; => 3
(<< 0xF 2) ;; => 60
Значения и Let-значения:
Значения могут быть составными, а функции могут возвращать несколько значений.Но распаковывать их нужно специальным формы, т.е. let-значения, let * -values, или letrec-values.
(определить (перевести x y t)
(значения (+ x t) (+ y t)))
(определить (масштаб x y s)
(значения (* x s) (* y s)))
(определить (масштаб - & - перевести x y s t)
(let-values ([(nx ny) (scale x y s)])
(переведите nx ny t)))
(масштаб - & - перевести 3 4 10 2) ;; => (значения 32 42)
Простые макросы:
Простая схема поддерживает ограниченную форму макроса через синтаксис определения.Вы можете увидеть, как выглядит ваша программа после расширения с помощью новой кнопки расширения. Макрорасширение не полное, а там ограничены предупреждения / проверки. Я надеюсь улучшить синтаксис и функции, когда у меня будет время.
(определение-синтаксис foo-bar
(правила синтаксиса ()
[(фу-бар а) (+ а 2)]
[(фу-бар а б) (* а б)]))
(foo-bar 1) ;; Расширяется до (+ 1 2)
(foo-bar 2 20) ;; Заменяется до (* 2 20)
Если у вас только один случай, вы можете сократить его с помощью правила определения-синтаксиса
(определить-синтаксис-правило (добавить ко всем n lst)
(карта (лямбда (m) (+ n m)) lst))
(добавить ко всем 5 (список 1 2 3)) ;; => (список 6 7 8)
Вы не можете переопределить ключевые слова или стандартные формы, но вы можете учитывать идентификаторы символы в шаблонных выражениях (вместо имен привязок)
(определить-синтаксис сделать
;; add, sub и mult сопоставляются как литералы, а не как привязки
(правила синтаксиса (добавить дополнительный мульт)
[(добавить a b) (+ a b)]
[(do sub a b) (- a b)]
[(do mult a b) (* a b)]))
(добавить 2 4) ;; Расширяется до (+ 2 4)
(сделать мульт 5 10) ;; Заменяется до (* 5 10)
(сделать sub 7 5) ;; Расширяется до (- 7 5)
Но вы можете использовать let и другие привязки в своих макросах, и переменные будут переименованы, чтобы избежать конфликтов областей видимости.Вы также можете сделать так, чтобы ваш макрос ссылался на самого себя !. Предупреждение : Я не могу обещать гарантия, что вы всегда получите то, что хотите. Если вы обнаружите проблемы / странности, пожалуйста, сообщите я знаю, и я исправлю их, как только смогу! 🙂
;; Попробуйте и посмотрите, до чего он расширится!
(определение-синтаксис myor
(правила синтаксиса ()
[(myor a b c) (myor a (myor b c))]
[(myor a b) (let ([aa a]) (if aa aa b))]))
(мойор (<5 6) (= 6 3))
(мойор (<4 7) (> 5 3) (= 2 8))
Функции изображения и примеры:
Я реализовал библиотеку функций и формы (аналогично Racket's 2htdp / image и 2htdp / universe пакеты), которые поддерживают создание изображений и даже интерактивные игры / анимации.
Во-первых, цвета - это просто строки, которые называют цветные или специально отформатированы. Список поддерживаемые именованные цвета перечислены здесь. Кроме того, мы поддерживаем '#' шестнадцатеричные цвета с префиксом из 3, 4, 6 или 8 цифр. Например, "red" = "# F00" = "# FF0000". Для 4 и 8 цифр цвета, первая цифра (цифры) представляет цвет , альфа или непрозрачность. Итак, «# F00F» - непрозрачный синий цвет, «# 80F0» - частично прозрачный зеленый, а "# 11FF0000" почти полностью чистый красный.Конечно это в основном используется, когда вы начинаете наложение изображения ... но давайте сначала начнем с некоторых базовых изображений.
Создание простых изображений ...
(кружок 10 «сплошной» «# F00») ;; красный закрашенный круг
(круг 20 «контур» «# 00F») ;; синий круг границы
(эллипс 10 20 "твердый" "# 00FF00") ;; эллипс 10 x 20 с зеленой заливкой
(эллипс 20 10 "контур" "# 8F00") ;; красная, частично непрозрачная рамка эллипса 20 x 10
(прямоугольник 10 20 "сплошной" "# 5500FF00") ;; зеленый, в основном прозрачный, прямоугольник 10 x 20
(квадрат 10 «сплошной» «синий») ;; синий квадрат 10 х 10
(треугольник 20 «контур» «красный») ;; красная граница треугольника с радиусом 20
(звезда 20 «сплошной» «зеленый») ;; Пятиконечная звезда, радиус 20
(звезда 20 7 «сплошной» «зеленый») ;; 7-конечная звезда, радиус 20
(звездочка 20 10 7 «сплошная» «зеленая») ;; 7-конечная звезда, внешний радиус 20, внутренний радиус 10
(текст «Привет!» 30 «сплошной» «фиолетовый») ;; текстовое изображение фиолетового цвета, размер 30 пунктов
(строка 10 10 «желтый») ;; желтая линия под углом 45 градусов
(круглый прямоугольник 30 20 5 "контур" "серый") ;; Прямоугольник 30 x 20 с закругленными углами 5 пикселей
(круглый прямоугольник 30 20 6 4 "контур" "серый") ;; Прямоугольник 30 x 20 с углами эллипса 6 x 4
(многоугольник 20 6 "контур" "оранжевый") ;; оранжевый шестиугольник с радиусом 20
(make-color 0xA0) ;; "# FFA0A0A0"
(make-color 32 48 64) ;; "# FF203040"
(марка-цвет 16 32 48 64) ;; «# 10203040»
Свойства изображения...
(ширина изображения (квадрат 20 «контур» «зеленый»)) ;; => 20
(изображение-высота (круг 20 «контур» «зеленый»)) ;; => 40
Конечно, они мало что делают, пока вы не сможете отобразить их. . Вы можете показать свой изображение (я) с (show-image img-value ):
(шоу-изображение (звезда 200 9 "сплошной" "зеленый"))
Накладки : можно накладывать два (или более) изображения над одним и тем же центром, или overlay / xy два изображения с заданными x / y смещения (т.е.е., (оверлей / xy top-img смещение-x смещение-y бот-img ))
(показать изображение
(оверлей / xy (оверлей (квадрат 100 "сплошной" "# 800F")
(квадрат 200 "сплошной" "# 8FFF")
(квадрат 300 "сплошной" "# 8F00"))
0 310
(наложение (круг 50 "сплошной" "синий")
(круг 100 «сплошной» «белый»)
(кружок 150 "сплошной" "красный"))))
Сцены : Сцена особенная вид изображения с его происхождением на верхний левый.Их можно создать с помощью empty-scene и добавлен к использованию место-изображение и / или надстройка. Цвет по умолчанию - «белый», но вы также можете указать цвет как аргумент.
Обычно вам просто нужна пустая сцена размер текущего работающего устройства экран.
;; 100x200 пустая сцена, белая
(пустая сцена 100 200)
;; empty-scene (белый) размер экрана текущего устройства
(пустая сцена)
;; 100x200 пустая сцена, синий
(пустая сцена 100 200 «синие»)
;; empty-scene (черный) размер экрана текущего устройства
(пустая сцена "черная")
Когда у вас есть сцена, вы можете разместить изображения, (место-изображение img x y сцена ), или добавьте строки, (добавочная строка сцена x1 y1 x2 y2 цвет ).Оба функции возвращают результирующую сцену
;; Примечание: действительно будет только последнее шоу-изображение.
;; отображается ... так что разделите их, когда / если вы их запустите
(показать изображение
(место-изображение (треугольник 120 "сплошной" "# 8F00")
300 100
(изображение-место (квадрат 120 "сплошной" "# 800F")
200 100
(место-изображение (круг 50 "сплошной" "# 80F0")
100 100 (пустая сцена)))))
(показать изображение
(add-line (add-line (add-line (empty-scene) 10 10 200 100 «синий»)
10 10 200 200 «красный»)
10 10 100 200 "зеленых"))
Конечно, вы можете написать функции для генерации Изображения и сцены:
(определить (бычий глаз n x y радиус)
(если (= 0 n)
(пустая сцена)
(место-изображение (радиус круга "сплошной"
(если (= (% n 2) 0) «красный» «серый»))
х у
(бычий глаз (- n 1) x y (+ радиус 20)))))
(шоу-изображение (бычий глаз 8 275 400 30))
BigBang / Интерактивные формы и примеры:
Помимо функций изображения, я также реализованы некоторые функции Racket's большой взрыв форма.В частности, я реализовал:
- (on-tick tick-func rate )
tick-func должен иметь тип: World -> World
rate является необязательным, должен оцениваться как Number - (on-mouse mouse-func )
mouse-func должен иметь тип: Строка номера мира -> Сцена - (on-draw draw-func )
draw-func должен иметь тип: World -> Scene - (on-orient orient-func )
orient-func должен быть типа: World Number Number Number -> World
Следующая программа является рабочей пример большого взрыва, который использует Число как Мир , представляющий координата Y движущейся точки.
- Мир начинается как номер 0
- Для вытяжки мы создаем Сцена с синей точкой на Мир выс / у.
- При включении мы возвращаем обновил Мир , переместив точку вниз по экрану на 5 пикселей.
- Для мыши мы устанавливаем Мир будет высотой действие мыши / касания.
;; Мир - это число, которое представляет координату Y точки.
(определить (точка y)
(место-изображение (круг 20 «сплошной» «синий»)
275 лет
(пустая сцена)))
(большой взрыв 0
(точка рисования)
(на тике (лямбда (w) (+ 5 w)))
(на мыши (лямбда (ш х у что) у)))
Если вы запустите этот пример в Simple Схема , точка смещается к нижней части ваш экран.Когда вы касаетесь экрана, точка находится на высоте крана.
Немного сложнее ...
Мы можем масштабировать предыдущий пример с помощью определение структуры и более сложное функция галочки.
- Мир начинается в точке (275 200), с целевой точкой (275 200)
- Для рисования мы создаем сцену с синей точкой у World X / Y.
- Для on-tick возвращаем новый Мир , перемещая точку на десятую часть путь к целевой точке. Функция будет вызываться каждые 0,03 секунды
- Для мыши мы обновляем Целевая точка мира по X / Y действие мыши / касания. Возможные значения для 4 -й аргумент к на мыши функции: «кнопка вниз», «перетаскивание» или «кнопка вверх»
;; Мир - это точка, которая представляет собой X / Y точки.
;; и X / Y целевой точки
(точка определения-структуры (x y tx ty))
;; Нарисуйте точку на пустой сцене
(определить (точка d)
(место-изображение (круг 20 «сплошной» «синий»)
(точка-x d) (точка-y d)
(пустая сцена)))
;; Обновите целевую точку точки
(определить (мышь d x y что)
(cond [(string =? what "кнопка вниз")
(make-dot (dot-x d) (dot-y d) x y)]
[еще d]))
;; Переместите точку к целевой точке
(определить (шаг d)
(make-точка (+ (точка-x d) (/ (- (точка-tx d) (точка-x d)) 10.0))
(+ (точка-y d) (/ (- (точка-y d) (точка-y d)) 10.0))
(точка-TX г)
(точка-ты д)))
(большой взрыв (make-dot 275 200 275 200)
(точка рисования)
(шаг 0,03)
(мышь на мыши))
Если вы запустите этот пример в Simple Схема , при нажатии точка будет смещаться туда, куда вы нажимаете ... сначала быстро, затем замедление.
Использование событий ориентации устройства...
В качестве последнего примера мы будем использовать Simple Схема подключения к вашему Android-устройству события ориентации / акселерометра, чтобы повлиять на ваше Миры.
Это тоже немного более общее, так что тоже будет хорошо смотреться на вашем устройстве (ах) 🙂
- Мир начинается с нуля направление
- Для рисования мы создаем сцену с линией от центра (ширина / 2, высота / 2) в направлении последняя ориентация X / Y
- Для ориентации мы снимаем X и ориентация устройства по оси Y.The Y направление правильное из-за инверсии координат экрана ... но X должен быть перевернутый.
(определение-структура директория (x y))
(определить scn (пустая сцена))
(определить ширину / 2 (/ (ширина изображения scn) 2))
(определить высоту / 2 (/ (высота изображения scn) 2))
;; Проведите линию от центра
(определить (нарисовать линию w)
(ширина надстройки scn / высота 2 / высота 2
(+ ширина / 2 (* 20 (dir-x w)))
(+ высота / 2 (* 20 (dir-y w)))
"синий"))
(определить (ориентировать w x y z)
(make-dir (- x) y))
(большой взрыв (make-dir 0 0)
(линия на рисовании)
(по-восточному))
Если вы запустите этот пример в Simple Схема и перемещайте свое устройство, вы должен увидеть линию вниз (в сторону земли), длина которого пропорциональна насколько нивелировано устройство.
Надеюсь, этого хватит, чтобы начать возиться с вещами ... дайте мне знать, если найдете ошибки / опечатки в примерах.Наслаждайтесь!
Приложение: полный список поддерживаемых функций
Ниже приведен список всех поддерживаемых в настоящее время операторы с кратким описанием. Для большинства операторы, передавая двойное (десятичное число) как любое Аргумент преобразует результат в нецелочисленный результат.Многие из примитивов принимают любое число от 1 или больше аргументов, например, (- 6 3 1) равно 2.
- +: сложение, работает более чем с 1 аргументом (ами).
- -: Вычитание ...
- *: Умножение ..
- /: Деление ... Если все аргументы являются целыми числами, тогда результат будет целым числом, например, (/ 7 2) равно 3.
- %: остаток / мод, работает только с целыми числами
- ^: Побитовое исключающее ИЛИ, работает только с целыми числами
- | : Побитовое ИЛИ, работает только с целыми числами
- &: Побитовое И, работает только с целыми числами
- <<: Shift-влево, работает только с целыми числами
- >>: Sifth-right, работает только с целыми числами
- ++: приращение, работает только с целыми числами
- -: уменьшение, работает только с целыми числами
- =: Число, равное
- <: Число меньше
- >: число больше
- <=: Число меньше или равно
- > =: Число больше или равно
- not: логическое Not / Negation
- и: логическое И (сокращенное)
- или: логическое или (сокращенное)
Ниже приведен список всех поддерживаемых в настоящее время базовых функций с кратким описанием.
- print-base-functions: Распечатывает этот список в алфавитном порядке. Номер
- ? : Это число?
- число-> строка: преобразование числа в строку в десятичном формате
- лишнее? : Номер нечетный?
- даже? : Четное ли это число?
- max: максимум два значения
- мин: минимум два значения
- abs: Абсолютное значение
- этаж: Этаж данного номера, п.е., целая часть
- потолок: максимальное значение данного числа, например, для положительного числа округлить его до следующего целого числа
- round: округлить число до ближайшего целого
- cos: косинус
- sin: синус
- загар: касательный
- acos: Arccosine
- asin: Арксинус
- atan: Арктангенс
- журнал: База журнала e
- log10: База журнала 10
- exp: экспонента e, e. -й элемент списка
- rest: получает элементы после первого в списке, т.е.э., cdr
- take: возвращает первые n элементов списка, например, (take (list 1 2 3 4) 2) is (list 1 2)
- drop: возвращает оставшийся список после пропуска n элементов, например, (drop (list 1 2 3 4) 2) is (list 3 4)
- cons: добавляет элемент в начало списка Список
- ? : Это список?
- минусов? : Это непустой список?
- пусто? : Это пустой список?
- length: Получить длину списка Автомобиль
- : эквивалент первого
- cdr: эквивалент остатка
- cadr: эквивалент (car (cdr _))
- caddr: эквивалент (car (cdr (cdr _)))
- cadddr: эквивалент (car (cdr (cdr (cdr _))))
- cddr: эквивалент (cdr (cdr _))
- cdddr: эквивалент (cdr (cdr (cdr _)))
- cddddr: эквивалент (cdr (cdr (cdr (cdr _))))
- caar: эквивалент (автомобиль (автомобиль _))
- cadar: эквивалент (car (cdr (car _)))
- caddar: эквивалент (car (cdr (cdr (car _))))
- cdar: эквивалент (cdr (car _))
- cddar: эквивалент (cdr (cdr (car _)))
- cdddar: эквивалент (cdr (cdr (cdr (car _))))
- caaar: эквивалент (автомобиль (автомобиль (автомобиль _)))
- cadaar: эквивалент (car (cdr (car (car _))))
- cdaar: эквивалент (cdr (car (car _)))
- cddaar: эквивалент (cdr (cdr (car (car _)))) Карта
- : применяет данную функцию к каждому элементу в списке Фильтр
- : фильтрация списка с сохранением элементов, соответствующих предикату .
- foldl: сложите список слева направо
- foldr: сложите список справа налево
- build-list: строит список заданной длины с функцией, которая принимает индекс элемента.
- andmap: возвращает истину, если все элементы списка удовлетворяют предикату
- ormap: возвращает истину, если какой-либо из элементов списка удовлетворяет предикату
- append: объединяет два списка
- reverse: возвращает обратную сторону списка
- логическое =? : Логическое значение
- логическое? : Логическое значение?
- char-> string: преобразование символьного значения в строковое значение
- символов =? : Символ, равный
- знаков? : Это персонаж?
- image-width: получить ширину изображения
- image-height: получить ширину изображения
- make-color: создание цвета из значений R / G / B (двойной 0..1 или int 0..255)
- line: Построить линию Image
- круг: построить круг. Изображение Эллипс
- : построение эллипса Изображение Полигон
- : построение правильного многоугольника. Изображение . Треугольник
- : построить треугольник Image Звезда
- : Построить звезду Изображение Квадрат
- : Построение квадрата Изображение Прямоугольник
- : построить прямоугольник. Изображение
- round-rectangle: создать прямоугольник Изображение с закругленными углами
- текст: создать изображение текста Наложение
- : наложение изображений на основе их центральных точек
- overlay / xy: наложение двух изображений со смещением на основе их центральных точек
- повернуть: значение поворота изображения
- empty-scene: Создайте пустую сцену
- add-line: добавить строку в сцену (Scene, X1, Y1, X2, Y2)
- place-image: Поместите изображение в определенное X / Y (Изображение, X, Y, Сцена)
- show-image: Показать значение изображения или сцены
- строка-> список: преобразование строки в список символов
- список-> строка: преобразует список символов в строку
- строка-> символ: преобразование строки в соответствующий символ
- string-append: добавить два или более строковых значения
- string-downcase: преобразование строки в нижний регистр
- длина строки: получает длину строки
- ссылка на строку: получает n ^ -й символ строки
- string-upcase: преобразование строки в верхний регистр
- строка <=? : Строка меньше или равно, лексикографический порядок
- строка
- строка =? : Строковое равенство
- строка> =? : Строка больше или равно, лексикографический порядок
- строка>? : Строка больше, лексикографический порядок
- строка? : Строка? Подстрока
- : извлечь подстроку / диапазон индекса
- symbol-> string: преобразование символа в соответствующую строку
- символ =? : Тот же символ? Символ
- ? : Это символ?
- print: печатает (и возвращает) заданное значение
- println: печатает (и возвращает) заданное значение с новой строкой
Simply Scheme - 2-е издание: Введение в информатику: 9780262082815: Книги по информатике @ Amazon.com
Для тех, кто изучает язык программирования Scheme, второе издание Simply Scheme: Введение в информатику представляет собой очень удобоваримый вводный курс в стиле учебника по этому мощному и элегантному языку.По словам авторов, Simply Scheme задуман как «приквел» к другой книге, Structure and Interpretation of Computer Programs . Это последнее название было основным продуктом вводных курсов по информатике в течение многих лет, но оно предполагает определенную подготовку.
Simply Scheme упорно трудится, чтобы сделать несколько хитрые идеи Scheme доступными. В этом руководстве особое внимание уделяется небольшим разделам ключевых функций языка, от основных функций, переменных и далее до рекурсии и других концепций функционального программирования. В то время как такие языки, как C ++ и Java, используют объекты для моделирования данных, программисты Scheme разбивают проблему на функции. Искусство - и элегантность - решения проблем в Scheme происходит от применения рекурсии и других концепций дизайна.
Более длинные примеры кода в книге включают игру в крестики-нолики, примеры, которые работают с покером и бриджем, и демонстрацию рабочей электронной таблицы.На протяжении всей книги используется дружелюбный и свободный от жаргона подход к программированию. Эта книга как о , думая о как о Scheme, так и об основных моментах языка. Разделы по использованию программных шаблонов в Scheme помогают обновить эту новую редакцию.
Хотя Scheme и ее двоюродный брат Common Lisp (описанный в книге в приложении) не часто используются в бизнесе, они по-прежнему пользуются популярностью у компьютерных ученых, например, в исследованиях искусственного интеллекта. Простая схема позволяет сделать сложный язык программирования доступным и доступным. Это ценный ресурс для любого студента, изучающего информатику, который впервые принимает Scheme. - Ричард Драган
Охваченные темы : Основы языка схем, функции и функции высшего порядка, переменные, основы лямбда, рекурсия, абстракция, программные шаблоны в схеме, списки, деревья, последовательное программирование, работа с файлами, векторами , Common Lisp.
Авторы написали очень удобную книгу. Предложения и программы короткие; объяснения пошаговые.
- Choice... действительно потрясающее введение в программирование и компьютерные науки.
- Логин , Хвала за первое изданиеОб авторе
Брайан Харви - преподаватель отдела компьютерных наук Калифорнийского университета в Беркли.
Схема обозначена простейшая (12 двухрежимных элементов) портов...
Контекст 1
... мы собрали несколько десятков лучших оптических преобразований с количеством делителей, равным 12 и 13 (что для сравнения с общим случаем 10 (10 - 1) / 2 = 45 элементов). Оказалось, что все они являются лишь повторениями (вплоть до перестановок портов и перестановки фазовращателей) одной и той же схемы, представленной на рис. 2. Обратите внимание, что каждый прямоугольник на рисунке представляет собой двухмодовое преобразование (4) взятые при ϕ = 0 эллипсы обозначают одномодовые фазовые сдвиги (фактически, смену знака).Схема на рис.2 не является прямым результатом численного эксперимента, она была получена с помощью обширной аналитической постобработки (уменьшение фазовращателей и удаление ненужных ...
Контекст 2
... = 45 элементов ). Оказалось, что все они являются лишь повторениями (вплоть до перестановок портов и перестановки фазовращателей) одной и той же схемы, представленной на рис. 2. Обратите внимание, что каждый прямоугольник на рисунке представляет собой двухмодовое преобразование (4) взятые при ϕ = 0 эллипсы обозначают одномодовые фазовые сдвиги (фактически, смену знака).Схема на рис. 2 не является прямым результатом численного эксперимента, она была получена с помощью обширной аналитической постобработки (уменьшение фазовращателей и удаление ненужных пересечений оптического пути) и угадывания задействованных алгебраических чисел. Тем не менее, числовая обработка оказалась неоценимой в ее ...
Контекст 3
... на самом деле, установленная оптическая схема почти не пересекается и состоит из двух почти симметричных плеч, соединенных между собой через пару 45-ти разветвителей на выходе. .Соответствующее разложение, эквивалентное рис. 2 до перестановки входных портов, показано на рис. 3, где мы сохранили обычное расположение выходных портов 6 + 4 за счет, возможно, избыточного числа пересечений оптических путей. До конца текущего раздела мы сконцентрируемся на этом представлении, хотя оно кажется не самым ярким: мы рассуждаем ниже ...
Идентифицирована простейшая схема (12 двухрежимных элементов), порты ...
Контекст 1
... мы собрали несколько десятков лучших оптических преобразований с количеством делителей 12 и 13 (что сравнивается с общим случаем 10 (10 - 1) / 2 = 45 элементов). Оказалось, что все они являются лишь повторениями (вплоть до перестановок портов и перестановки фазовращателей) одной и той же схемы, представленной на рис. 2. Обратите внимание, что каждый прямоугольник на рисунке представляет собой двухмодовое преобразование (4) взятые при ϕ = 0 эллипсы обозначают одномодовые фазовые сдвиги (фактически, смену знака).Схема на рис.2 не является прямым результатом численного эксперимента, она была получена с помощью обширной аналитической постобработки (уменьшение фазовращателей и удаление ненужных ...
Контекст 2
... = 45 элементов ). Оказалось, что все они являются лишь повторениями (вплоть до перестановок портов и перестановки фазовращателей) одной и той же схемы, представленной на рис. 2. Обратите внимание, что каждый прямоугольник на рисунке представляет собой двухмодовое преобразование (4) взятые при ϕ = 0 эллипсы обозначают одномодовые фазовые сдвиги (фактически, смену знака).Схема на рис. 2 не является прямым результатом численного эксперимента, она была получена с помощью обширной аналитической постобработки (уменьшение фазовращателей и удаление ненужных пересечений оптического пути) и угадывания задействованных алгебраических чисел. Тем не менее, числовая обработка оказалась неоценимой в ее ...
Контекст 3
... на самом деле, установленная оптическая схема почти не пересекается и состоит из двух почти симметричных плеч, соединенных между собой через пару 45-ти разветвителей на выходе. .Соответствующее разложение, эквивалентное рис. 2 до перестановки входных портов, показано на рис. 3, где мы сохранили обычное расположение выходных портов 6 + 4 за счет, возможно, избыточного числа пересечений оптических путей. До конца текущего раздела мы сконцентрируемся на этом представлении, хотя оно кажется не самым ярким: рассуждаем ниже ...
Контекст 4
... мы собрали несколько десятков лучших оптических преобразований с количеством разделителей, равным 12 и 13 (что необходимо сравнить с общим случаем 10 (10 - 1) / 2 = 45 элементов).Оказалось, что все они являются лишь повторениями (вплоть до перестановок портов и перестановки фазовращателей) одной и той же схемы, представленной на рис. 2. Обратите внимание, что каждый прямоугольник на рисунке представляет собой двухмодовое преобразование (4) взятые при ϕ = 0 эллипсы обозначают одномодовые фазовые сдвиги (фактически, смену знака). Схема на рис. 2 не является прямым результатом численного эксперимента, она была получена с помощью обширной аналитической постобработки (уменьшение фазовращателей и удаление ненужных ...
Контекст 5
... = 45 элементов). Оказалось, что все они являются лишь повторениями (вплоть до перестановок портов и перестановки фазовращателей) одной и той же схемы, представленной на рис. 2. Обратите внимание, что каждый прямоугольник на рисунке представляет собой двухмодовое преобразование (4) взятые при ϕ = 0 эллипсы обозначают одномодовые фазовые сдвиги (фактически, смену знака). Схема на рис. 2 не является прямым результатом численного эксперимента, она была получена с помощью обширной аналитической постобработки (уменьшение фазовращателей и удаление ненужных пересечений оптического пути) и угадывания задействованных алгебраических чисел.Тем не менее, числовая обработка оказалась неоценимой в ее ...
Контекст 6
... на самом деле, установленная оптическая схема практически не пересекается и состоит из двух почти симметричных плеч, соединенных между собой через пару 45-ти разветвителей на выходе. . Соответствующее разложение, эквивалентное рис. 2 до перестановки входных портов, показано на рис. 3, где мы сохранили обычное расположение выходных портов 6 + 4 за счет, возможно, избыточного числа пересечений оптических путей.До конца текущего раздела мы сконцентрируемся на этом представлении, хотя оно кажется не самым ярким: мы рассуждаем ниже ...
Язык программирования схем
Язык программирования схемСхема - это статически ограниченный и правильно рекурсивный диалект язык программирования Lisp, изобретенный Гаем Льюисом Стилом-младшим и Джеральдом Джеем Сассманом. Он был разработан, чтобы иметь исключительно ясная и простая семантика и несколько различных способов формы выражения.Широкий спектр парадигм программирования, в том числе императивные, функциональные стили и стили передачи сообщений, удобные выражение в схеме.
Scheme был одним из первых языков программирования, в который были включены первые процедуры класса, как в лямбда-исчислении, тем самым доказывая полезность правил статической области видимости и блочной структуры в динамическом печатный язык. Схема была первым основным диалектом Лиспа, который различал процедуры из лямбда-выражений и символов, чтобы использовать один лексический окружение для всех переменных, и для оценки позиции оператора вызова процедуры точно так же, как и позицию операнда.Полностью полагаясь на вызовы процедур для выражения итерации, Scheme подчеркнули тот факт, что вызовы хвостовой рекурсии по сути, goto, которые передают аргументы. Scheme был первым широко используемым языком программирования, в котором впервые процедуры выхода из класса, из которых все ранее известные последовательные управляющие структуры могут быть синтезированы. Совсем недавно, опираясь на дизайн общей арифметики в Common Lisp, Scheme представили концепцию точного и неточного числа. Схема тоже первое программирование язык для поддержки гигиенических макросов, которые позволяют синтаксис блочно-структурированный язык для надежного расширения.
Схема MIT / GNU
Схема MIT / GNU - это полная среда программирования, работающая на многих платформы unix, а также Microsoft Windows и IBM OS / 2. Это имеет богатую библиотеку времени выполнения, мощный отладчик исходного уровня, компилятор машинного кода и встроенный редактор, подобный Emacs.
- Схема MIT / GNU доступен для машин с архитектурой Intel (x86) под управлением GNU / Linux, FreeBSD, IBM OS / 2 или Microsoft Windows 9x / ME / NT / 2000 / XP.
- СЗВЮЗ: 6.001 LA Руководство - как быть лаборантом вводного курса программирования в Массачусетском технологическом институте.
Документация
Другие реализации
- GUILE, GNU's Универсальный интеллектуальный язык для расширений - это библиотека реализация языка схем плюс различные удобные удобства. Он разработан так, что вы можете связать его с приложением или утилита, чтобы сделать его расширяемым.
- Кава компилирует схему в байт-коды Java.
- Схема PLT - это зонтик имя для семьи реализации Язык программирования схем.
- Псевдосхема встраивает схему в общее Лисп.
- Схема 48 - маленькая и портативная реализация на основе интерпретатора байтового кода. Он должен работать на любом 32-разрядная машина с байтовой адресацией, имеющая компилятор ANSI C и POSIX. служба поддержки.
- SCM - портативная схема реализация написана Обри Джаффером.
- Scsh, оболочка схемы, представляет собой среда системного программирования широкого спектра для Unix, встроенная в Схема R4RS. Работает на большинстве основных платформ Unix.
- Skij - частичный Реализация схемы, которая реализована и интегрирована с Java.
- STk - это версия схемы с интерфейсом Tk.
- VSCM - это переносимая реализация схемы, написанная Матиасом Блюмом из Принстона Университет.
- Проект Open Directory поддерживает список реализаций Scheme, предназначенный для всесторонний. Он включает бесплатное программное обеспечение, несвободное программное обеспечение и архаичные реализации, представляющие исторический интерес.
- David Pilo Mansion создал набор визуальных инструментов для Язык программирования схем вместе с базовым интерпретатором. В программа полностью написана на Java и предназначена как наглядное пособие для студентов, изучающих язык функционального программирования.
и т. Д.
Отправляйте отчеты об ошибках и другие сообщения, касающиеся схемы MIT, по адресу bug-cscheme на сайте zurich.ai.mit.edu
Последнее обновление 23 октября 2003 г.
Эта страница поддерживается Крисом Хэнсоном.Простая схема кодирования и декодирования кубита в неизвестном состоянии для различных топологических кодов
В этом разделе мы представляем общую процедуру кодирования и декодирования кубита (или нескольких кубитов) для кодов CSS на решетке и показываем, что она отлично работает, когда шум полностью отсутствует (т.е. подготовка и измерения идеальны и ошибок при хранении нет). Прежде чем вводить процедуру, мы кратко резюмируем формализм стабилизатора 9 и понятие кодов CSS.
CSS коды
Логическое кодовое пространство, то есть подпространство гильбертова пространства из N кубитов, с и -м кубитом, определенным в гильбертовом пространстве, натянуто на собственные векторы с собственным значением 1 элементов группы стабилизатора. Здесь S - абелева подгруппа группы Паули P N , где, где - оператор идентичности, а P N генерируется, где нижний индекс указывает на конкретный кубит i = {1,…, N }, верхний индекс A = { X , Y , Z } описывает одну из матриц Паули, задаваемых, и и. G ( S ), генератор S , всегда можно найти как набор эрмитовых взаимно коммутирующих операторов из группы Паули P N . Логические операторы кода - это операторы из P N , которые коммутируют со всеми операторами из G ( S ), но не генерируются ими. Поскольку S абелев, логические операторы определены по модулю G ( S ).Если обозначить через N - | G ( S ) | = D , где | G ( S ) | - количество элементов G (S), то мы можем написать и. Набор операторов, передвигающихся с S : { Z L , 1 , X L , 1 ,…, Z L64,9 D , X L , D , S }. Z L , i , X L , i создать пару дополнительных наблюдаемых (логических операторов), действующих на, то есть qu i -ый логический подсистема. Они подчиняются следующим коммутационным и антикоммутационным соотношениям: Z L , i X L , i = - X
Теперь рассмотрим один из N физических кубитов, который помечен индексом i ∈ [1,…, N ]. Без ограничения общности мы предполагаем, что он находится в состоянии α i | 0〉 i + β i | 1〉 i (где {| 0〉 i , | 1〉 i } - это набор собственных векторов Z i ), т.е. он не связан с другими кубитами.Мы определяем кодирование i -го кубита в i -й логический кубит, описываемый в системе как процесс, после которого i -й логический кубит находится в состоянии, где {| 0〉 L , i , | 1〉 L , i } - набор собственных векторов логического оператора Z L , i в подсистеме. Мы определяем декодирование как обратный процесс.
Поскольку точность квантового процесса зависит только от результатов измерений на двух дополнительных наборах входных состояний 23 , для доказательства правильности процедуры кодирования / декодирования достаточно показать, что она выполняет отображение между собственными состояниями X i , Z i (действующий) и X L , i , Z
Коды Кальдербанка-Шора-Стейна (CSS) 24,25,26 - это коды стабилизаторов, которые характеризуются тем, что их генератор содержит операторы из P N , которые являются только тензорным произведением идентичности. операторы I и X или Z операторы Pauli. Это означает, что логические операторы также имеют эту форму, поэтому нетривиальные элементы Z L , i включают только Z операторов, в то время как нетривиальные элементы X L , и выдаются только операторами X Pauli.Антикоммутационное отношение Z L , i X L , i = - X L L , i обеспечивается тем, что Z L , i и X L , 90d1479 i 90 количество физических кубитов (действуют на эти кубиты нетривиально).Очень полезным свойством кодов CSS является то, что исправление фазовых ошибок отделено от исправления битовых ошибок, поэтому их можно рассматривать отдельно. Ниже мы сосредоточимся на кодах CSS с локальными стабилизаторами, определенными на решетке.
Логические операторы, пересекающиеся на одном кубите
Мы представляем общую идею для кодирования неизвестного состояния в подсистему топологического кода CSS, где Z L , i и X L , i пересекаются на одном кубите, который мы обозначим как c i (рис.1 (а)). Используя тот факт, что в кодах CSS Z L , i ( X L , i ) является тензорным произведением Z ( X X ) операторов и идентификаторов отдельных кубитов, мы делаем четность операторов Z L , i ( X L , i ) зависимой только от состояния физического кубит c i .Для этого мы подготавливаем все остальные кубиты, на которых нетривиально действует Z L , i ( X L , i ), обозначенные здесь i как ( , k ) (( i , l )), в собственных состояниях, связанных с +1 собственными значениями Z i , k ( X i , л ).Поскольку мы предположили, что операторы Z L , i и X L , i пересекаются в одной точке, процедуры подготовки независимы. Мы будем использовать соглашение: Z i | 0〉 i = + | 0〉 i , Z i | 1〉 i = - | 1〉 i , X i | +〉 i = + | +〉 i , X
4 i i = - | -〉 i .Остальные кубиты (т.е. те, на которых логические операторы Z L , i и X L , i действуют тривиально) подготавливаются таким образом, чтобы кубиты которые нетривиально действуют, окружены кубитами в состояниях | 0〉 (| +〉). Заметим, что в бесшумном случае было бы достаточно подготовить остальные кубиты, кроме кубитов ( i , l ), в состояниях | 0〉.Тогда наша процедура не потребует решетчатой структуры, необходимой для определения окружения логических операторов. Однако подготовка всех кубитов, окружающих X L , i в состояниях | +〉, будет важна в шумном случае; см. раздел: Процедура кодирования / декодирования при наличии шума. Рисунок 1(a) Логические операторы, пересекающиеся на одном физическом кубите. (б) Логические операторы пересекаются на многих физических кубитах.Обратите внимание, что это схематическое изображение. В действительности логические операторы не обязательно должны быть строками, а коды не должны быть плоскими. Кубит c i , который мы хотим закодировать, помещен в одну из точек пересечения (черный крест). Подготавливаем другие кубиты, на которых нетривиально действует только один из логических операторов Z L , i и X L , i в состояниях i , k и | +〉 i , l соответственно.В случае большого количества точек пересечения мы разделим кубиты, на которых оба логических оператора действуют нетривиально (красные кресты), на пары и подготовим каждую пару в максимально запутанном состоянии (для простоты обозначено как | ϕ + 〉) в виде, где и обозначим кубиты, составляющие каждую пару.
Чтобы перевести состояние системы в подпространство, мы измеряем генераторы стабилизаторов и объединяем генераторы типа Z ( X -тип), которые дали результат -1, цепочками из операторов X ( Z ). .Цепочки X ( Z ), которые пересекают логические операторы Z L , i ( X L , i ) меняют свою четность. Однако, поскольку мы можем отслеживать, сколько раз это происходит, мы можем отменить это изменение четности, выполнив дополнительные X L , i ( Z L , i ), если это число нечетное.В конце концов, желаемое отображение реализуется, где | 0〉 L , i , | 1〉 L , i , | +〉 L , i , | -〉 L , i являются собственными векторами логических операторов Z L , i ,
Заметим, что многие коды в силу своих геометрических свойств не требуют выполнения дополнительных логических операций, так как всегда можно выбрать пути коррекции X ( Z ), проходящие через области решетки, которые не содержат логических операторов Z L , i ( X L , i ). Например, из-за соответствующих схем инициализации состояния (см.Рис. 2 (b), 3 (b), 4 (b), 6 (b)) это упрощение применяется к кодам CSS, рассматриваемым в следующем разделе.
Рисунок 2(а) Торический код Китаева. Каждая ссылка связана с кодовым кубитом. Код реализован в квадратном листе L × L на торе, следовательно, имеется 2 L 2 кодовых кубита. Генераторы-стабилизаторы типа X представлены звездами (тензорное произведение X , действующих на четыре кубита, образующих конкретную звезду), а типа Z плакетками (тензорное произведение Z , действующих на четыре кубита, которые сливаются в определенную табличку).Из-за периодических граничных условий имеется 2 ( L 2 - 1) независимых генератора-стабилизатора. Таким образом, можно закодировать 2 кубита. Примерные логические операторы, связанные с этими кубитами, отмечены на рисунке таким образом, что X L , i и Z L , i , где i = 1, 2. (б) Приготовление решетки. Кодируемые кубиты отмечены красными точками.Кубиты в зеленой и синей областях инициализируются в состояниях | 0〉 и | +〉 соответственно.
Рисунок 3(a) Плоский код с отверстиями. Ссылки обозначают кодовые кубиты. Звездочками обозначены генераторы-стабилизаторы типа X , а плакетками - генераторы-стабилизаторы типа Z . Топология модифицируется путем удаления некоторых кубитов и, как следствие, образования дыры. Звездные операторы с центром на краю отверстия превращаются в звездных операторов с 3 весами. Каждое отверстие связано с логическим кубитом (где Z L , i - любой замкнутый контур вокруг отверстия, а X L , i выходит из отверстия и заканчивается на границе).Мы используем эти два отверстия для определения одного логического кубита с Z L , 1 или Z L , 2 как Z L оператором и X L , 1 X L , 2 (строка X, соединяющая два отверстия) как X L . (б) Подготовка решетки. Кодируемый кубит отмечен красной точкой.Кубиты в зеленой и синей областях инициализируются в состояниях | 0〉 и | +〉 соответственно.
Рис. 4(a) Поверхностный код подсистемы с кубитами в вершинах. Есть два класса проверочных операторов, то есть 2-весовые операторы на границах (Z-тип расположены горизонтально, а X-тип - вертикально) и 6-весовые операторы проверки, состоящие из двух 3-весовых операторов треугольника, объединенных вместе (и расположенных по диагонали). в каждой ячейке для генераторов стабилизатора Z-типа и антидиагонально для X-типа).Логические операторы (черные линии) коммутируют со всеми стабилизаторами и антикоммутируют друг с другом. (б) Подготовка решетки. Кодируемый кубит отмечен красной точкой. Кубиты в зеленой и синей областях инициализируются в состояниях | 0〉 и | +〉 соответственно.
Рис. 5(a) Виртуальная решетка поверхностного кода подсистемы для исправления ошибок переворота битов. Каждый ромб (обозначающий 6-весовой стабилизатор Z-типа) помещается в центр каждой ячейки исходной решетки. Из каждого ромба возникает 6 строк, представляющих кодовые кубиты.2-весовые граничные проверочные операторы (связанные с кружками) замыкают решетку сверху и снизу. Черная жирная линия представляет логический оператор Z L . Код готовится так же, как на рис. 4 (б). (b) Виртуальная решетка поверхностного кода подсистемы для коррекции ошибки переворота фазы. Подготовка кода такая же, как на рис. 5 (а), но с решеткой, повернутой на 90 градусов. Ромбами и кружками обозначены стабилизаторы X-типа. Черная жирная линия представляет логический оператор X L .
Рисунок 6(a) Код Хааха. Каждая вершина связана с двумя кодовыми кубитами. Генераторы-стабилизаторы типов X и Z образуют кубы. Примерные логические операторы X L и Z L , связанные с синей и зеленой плоскостями, пересекаются на линии. (б) Подготовка решетки. Логические операторы X L и Z L (синяя и зеленая плоскости) пересекаются на линии.Из-за структуры кода в каждой вершине этой строки размещено по два кубита кода. Первый кубит каждой пары инициализируется в состоянии | 0〉. В центре толстой черной линии, состоящей из вторых кубитов каждой пары, вставлен красный кубит. Остальные кубиты, лежащие на этой строке, объединяются попарно, и каждая такая пара подготавливается в максимально запутанном состоянии | ϕ + 〉. Кубиты в зеленой и синей областях инициализируются в состояниях | 0〉 и | +〉 соответственно.
Процедура декодирования логического кубита, хранящегося в логическом подпространстве кода CSS, с Z L , i , X L , i логических операторов, пересекающихся с один физический кубит c i , состоит из выполнения измерения одного кубита в Z i , k ( X i , l , l на основе всех кубитов, где нетривиально определено Z L , i ( X L , i ), за исключением кубита c i (рис.1 (а)). По этим измерениям вычисляется четность оператора усеченного Z T , i ( X T , i ), где операторы усеченного вида - логические. операторы Z L , i и X L , i , с той лишь разницей, что они действуют на кубит c trivially .Если вычисленная четность нечетная, к кубиту, заданному на. Это выполняет требуемое отображение,,,.
Логические операторы, пересекающиеся на нечетном числе кубитов
Ниже мы представляем расширение процедуры кодирования / декодирования для CSS-кодов топологического стабилизатора, где логические операторы пересекаются более чем на одном кубите. Этот случай схематически проиллюстрирован на рис. 1 (b), где Z L , i , X L , i операторы действуют нетривиально на строке кубитов. .Однако следующие схемы применимы к кодам с произвольной структурой логических операторов. Кроме того, если логические операторы Z L , i и X L , i пересекаются на соседних кубитах, тогда наша кодировка будет локальной. Так обстоит дело с кодом Haah 22 , где Z L , i , X L , i - имеют нетривиальные размеры на поверхностях 3 прямоугольная решетка, каждая вершина которой занята двумя кубитами.Насколько нам известно, до сих пор не было предложено никакой схемы кодирования, применимой к важному классу кодов Хааха.
Первым шагом процедуры кодирования для кодов с логическими операторами, пересекающимися на одном физическом кубите, было обеспечение четности Z L , i , X L , i зависит только от состояния физического кубита, который мы хотим кодировать. Это было достигнуто путем помещения этого кубита на пересечение логических операторов и подготовки всех остальных кубитов ( i , k ) (( i , l )), на которых Z L , i ( X L , i ) действует нетривиально, в | 0〉 i , k (| +1479 , 9674 l ) состояния, стабилизированные Z i , k ( X i , l ).Это было критически важно для того, чтобы состояние N -кубитовой системы было собственным состоянием ± Z L , i и ± X L ,
Аналогично рассмотрим случай, когда логические операторы пересекаются на большем количестве физических кубитов. Кодируемый кубит находится в одной из точек пересечения и обозначается как c i .Как и раньше, мы подготавливаем все физические кубиты, на которых только один логический оператор действует нетривиально в соответствующем собственном состоянии операторов Паули с одним кубитом Z i , k (для Z L , i ) и X i , l (для X L , i ). Четное количество кубитов, на которых оба логических оператора действуют нетривиально (без учета кубита c i ) всегда можно разделить на пары, состоящие из кубитов, которые подготовлены в собственных состояниях и соответствуют собственным значениям. 1, п.е. максимально запутанные состояния, см. рис. 1 (б). Обратите внимание, что эти операторы коммутируют. Такая схема подготовки делает четность Z L , i ( X L , i ) зависимой только от собственного значения, как требуется. Мы вводим состояние системы, выполняя последовательность измерений и применяя соответствующие поправки (операции переворота битов и переворота фазы), которые либо не изменяют четность логических операторов (из-за соблюдаемых соотношений коммутации), либо меняют четность ( что можно исправить, применив к коду дополнительный логический оператор, как объяснялось ранее).
Процедура декодирования основана на измерении четности усеченных операторов Z T , i и X T , i . В случае кодов с логическими операторами, пересекающимися на одном кубите c i , четность усеченных операторов может быть вычислена из измерений одиночных кубитных операторов Паули, поскольку нет кубита, обеспечивающего соблюдение антикоммутационного отношения X , Z Измерения одиночного кубита типа .Процедура декодирования кодов с логическими операторами, пересекающимися на большем числе кубитов, основана на той же идее решения проблемы некоммутативности, что и кодирование: мы делим четное число кубитов, на которых оба усеченных оператора действуют нетривиально, и выполняем коммутирующие измерения и.


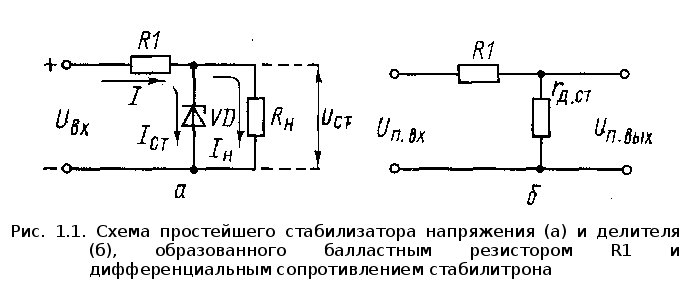 рис)
рис)