Логические схемы — Информатика — Уроки
Дата:
Предмет: информатика
Учитель:
Класс:
Тема урока: Логические схемы.
Цель урока: Формирование у обучающихся навыков построения логических схем для выражений.
Логические схемы
Над возможностями применения логики в технике ученые и инженеры задумывались уже давно. Например, голландский физик Пауль Эренфест (1880 — 1933), кстати, несколько лет, работавший в России, писал еще в 1910 году: «…Пусть имеется проект схемы проводов автоматической телефонной станции. Надо определить: 1) будет ли она правильно функционировать при любой комбинации, могущей встретиться в ходе деятельности станции; 2) не содержит ли она излишних усложнений. Каждая такая комбинация является посылкой, каждый маленький коммутатор есть логическое «или-или», воплощенное в эбоните и латуни; все вместе — система чисто качественных. .. «посылок», ничего не оставляющая желать в отношении сложности и запутанности… правда ли, что, несмотря на существование алгебры логики, своего рода «алгебра распределительных схем» должна считаться утопией?». Созданная позднее М.А.Гавриловым (1903 — 1979) теория релейно-контактных схем показала, что это вовсе не утопия.
.. «посылок», ничего не оставляющая желать в отношении сложности и запутанности… правда ли, что, несмотря на существование алгебры логики, своего рода «алгебра распределительных схем» должна считаться утопией?». Созданная позднее М.А.Гавриловым (1903 — 1979) теория релейно-контактных схем показала, что это вовсе не утопия.
Посмотрим на микросхему. На первый взгляд ничего того, что нас удивило бы, мы не видим. Но если рассматривать ее при сильном увеличении она поразит нас своей стройной архитектурой. Чтобы понять, как она работает, вспомним, что компьютер работает на электричестве, то есть любая информация представлена в компьютере в виде электрических импульсов. Поговорим о них.
С точки зрения логики электрический ток либо течет, либо не течет; электрический импульс есть или его нет; электрическое напряжение есть или его нет… В связи с этим поговорим о различных вариантах управления включением и выключением обыкновенной лампочки (лампочка также работает на электричестве).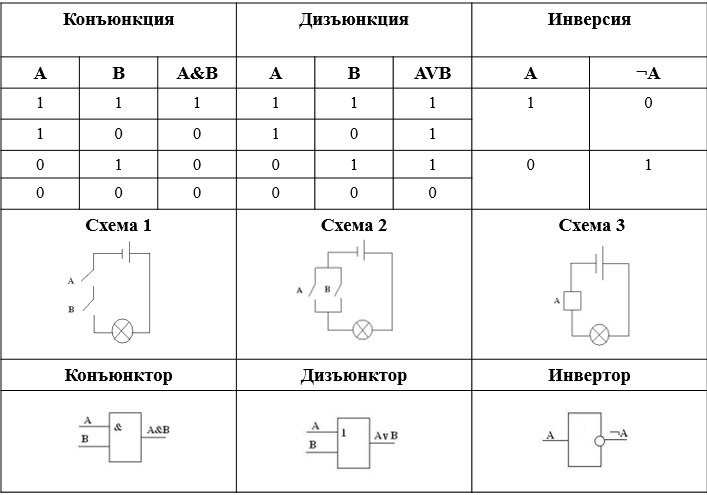 Для этого рассмотрим электрические контактные схемы, реализующие логические операции.
Для этого рассмотрим электрические контактные схемы, реализующие логические операции.
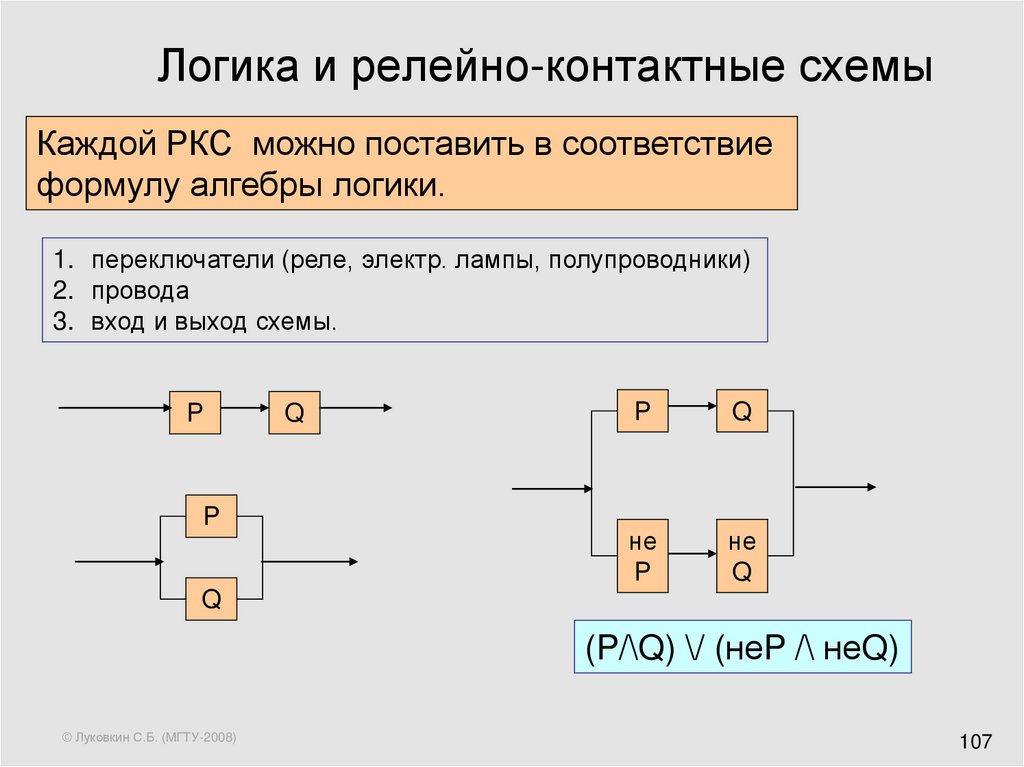
На рисунках контакты обозначены латинскими буквами А и В. Введем обозначения: 1 -контакт замкнут, 0 — контакт разомкнут. Цепь на схеме 1 с последовательным соединением контактов соответствует логической операции «И». Цепь на схеме 2 с параллельным соединением контактов соответствует логической операции «ИЛИ». Цепь на схеме 3 (электромагнитное реле) соответствует логической операции «НЕ».
Заполняем таблицу по ходу объяснения материала.
Конъюнкция | Дизъюнкция | Инверсия | ||||||
А 1 1 0 0 | В 1 0 1 0 | Результат 1 0 0 0 | А 1 1 0 0 | В 1 0 1 0 | Результат 1 1 1 0 | А 1 0 | ¬А 0 1 | |
Конъюнктор | Дизъюнктор | Инвертор | ||||||
Докажем это, рассмотрев состояния схем при различных состояниях контактов.
Схема 1 (составляем в основной таблице таблицу истинности).
Оба контакта в положении «включено». Тогда ток через лампочку идет и она горит.
Первый контакт в положении «включено» второй в положении «выключено». Ток не идет, лампочка не горит.
Обратная ситуация. Лампочка не горит.
Оба контакта в положении «выключено». Тока нет. Лампочка не горит.
Вывод: первая схема действительно реализует логическую операцию «И».
Схема 2 (составляем в основной таблице таблицу истинности).
Оба контакта в положении «включено». Тогда ток через лампочку идет и она горит.
Первый контакт в положении «включено» второй в положении «выключено». Ток идет, лампочка не горит.
Обратная ситуация. Лампочка горит.
Оба контакта в положении «выключено». Тока нет. Лампочка не горит.
Вывод: вторая схема действительно реализует логическую операцию «ИЛИ».
Схема 3 (составляем в основной таблице таблицу истинности).
В этом устройстве в качестве переключателя используется автоматический ключ. когда тока на нем нет, пластинка замыкает контакты и лампочка горит. если на ключ подать напряжение, то вследствие явления электромагнитной индукции пластинка прижимается и цепь размыкается. Лампочка не горит.
Вывод: третья схема действительно реализует логическую операцию «НЕ».
Недостатками контактных схем являлись их низкая надежность и быстродействие, большие размеры и потребление энергии. Поэтому попытка использовать такие схемы в ЭВМ не оправдала себя. Появление вакуумных и полупроводниковых приборов позволило создавать логические элементы с быстродействием от 1 миллиона переключений в секунду. Именно такие электронные схемы нашли свое применение в качестве элементной базы ЭВМ.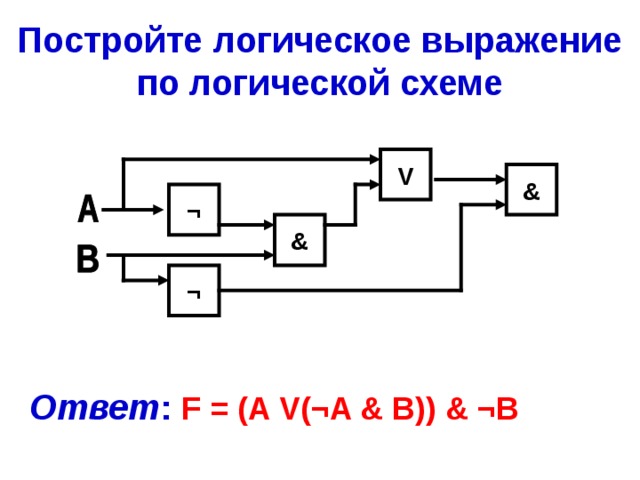 Вся теория, изложенная для контактных схем, была перенесена на электронные схемы. Элементы, реализующие базовые логические операции, назвали базовыми логическими элементами или вентилями и характеризуются они не состоянием контактов, а наличием сигналов на входе и выходе элемента. Их названия и условные обозначения являются стандартными и используются при составлении и описании логических схем компьютера.
Вся теория, изложенная для контактных схем, была перенесена на электронные схемы. Элементы, реализующие базовые логические операции, назвали базовыми логическими элементами или вентилями и характеризуются они не состоянием контактов, а наличием сигналов на входе и выходе элемента. Их названия и условные обозначения являются стандартными и используются при составлении и описании логических схем компьютера.
Почему необходимо уметь строить логические схемы?
Дело в том, что из вентилей составляют более сложные схемы, которые позволяют выполнять арифметические операции и хранить информацию. Причем схему, выполняющую определенные функции, можно построить из различных по сочетанию и количеству вентилей. Поэтому значение формального представления логической схемы чрезвычайно велико. Оно необходимо для того, чтобы разработчик имел возможность выбрать наиболее подходящий ему вариант построения схемы из вентилей. Процесс разработки общей логической схемы устройства (в том числе и компьютера в целом) таким образом, становится иерархическим, причем на каждом следующем уровне в качестве «кирпичиков» используются логические схемы, созданные на предыдущем этапе.
Алгебра логики дала в руки конструкторам мощное средство разработки, анализа и совершенствования логических схем. В самом деле, гораздо проще, быстрее и дешевле изучать свойства и доказывать правильность работы схемы с помощью выражающей ее формулы, чем создавать реальное техническое устройство. Именно в этом состоит смысл любого математического моделирования.
Логические схемы необходимо строить из минимально возможного количества элементов, что в свою очередь, обеспечивает большую скорость работы и увеличивает надежность устройства.
3. Построение логических схем
Правило построения логических схем:
Определить число логических переменных.
Определить количество базовых логических операций и их порядок.
Изобразить для каждой логической операции соответствующий ей вентиль.
Соединить вентили в порядке выполнения логических операций.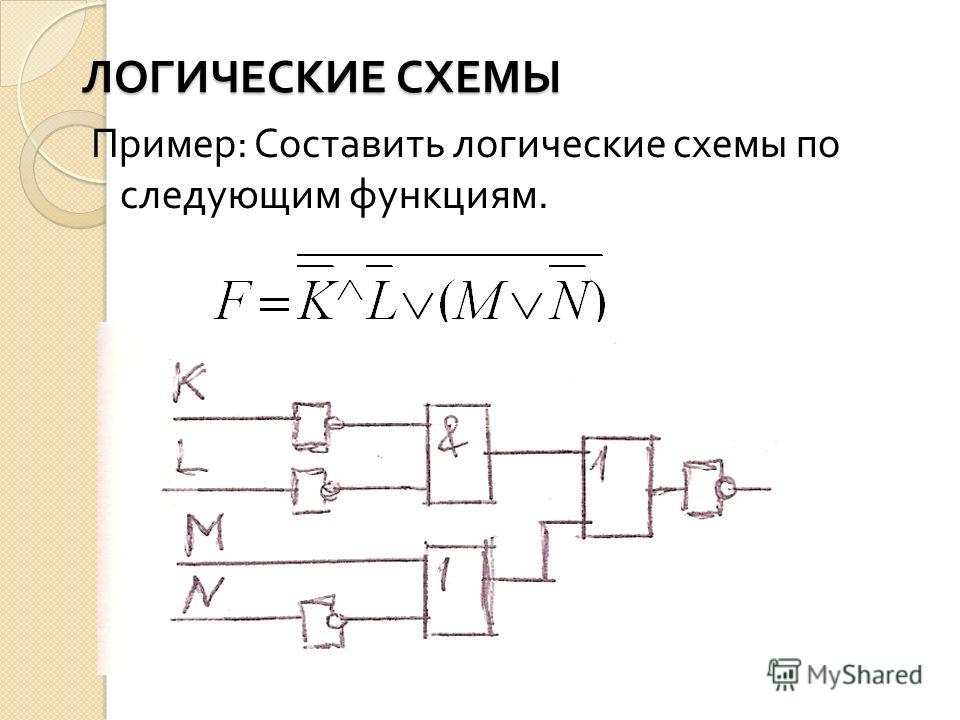
Пример 1
Пусть X = истина, Y = ложь. Составить логическую схему для следующего логического выражения: F = X v Y & X.
Две переменные — X и Y.
Две логические операции:
2 1
X v Y & X.
3) Строим схему:
Ответ: 1v 0 & 1 = 1.
Пример 2
Постройте логическую схему, соответствующую логическому выражению F=X&Yv¬(YvX). Найдите значение логического выражения для X=1, Y=0.
Переменных две: X и Y;
Логических операций четыре: конъюнкция, две дизъюнкции и инверсия:
1 4 3 2
X&Yv ¬ (YvX)
Схему строим слева направо в соответствии с порядком логических операций:
Вычислим значение выражения: F=1&0v ¬ (0v1) =0.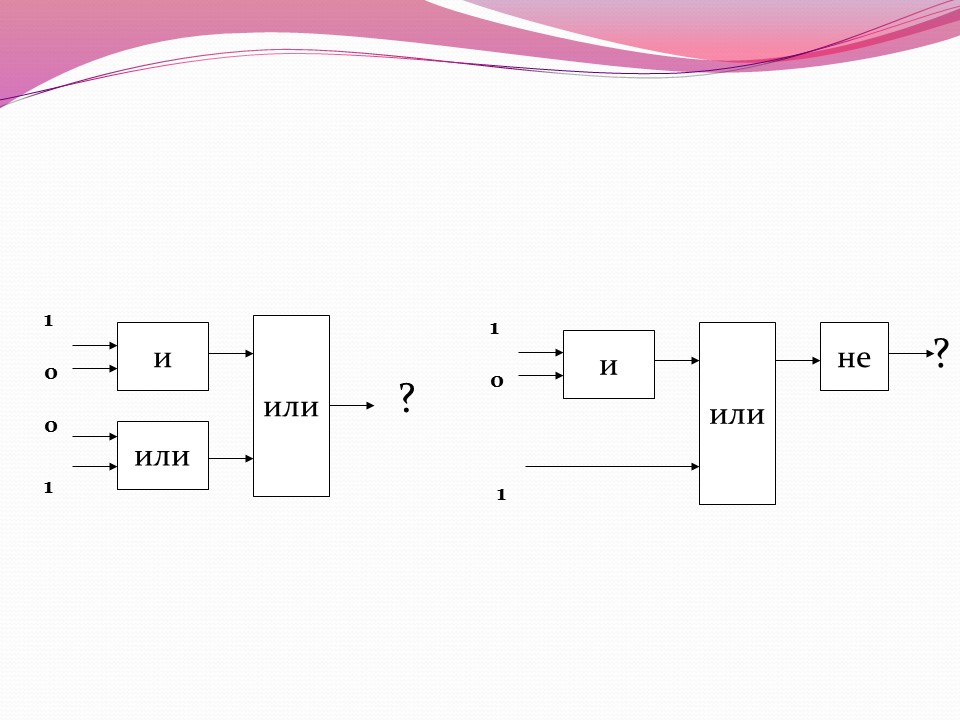
Закрепление изученного материала
Постройте логическое выражение по логической схеме:
А) | B) |
C ) А В С | D ) |
Логические схемы
Условное графическое изображение логических функций называется логической схемой.
Графическое изображение простой логической функции: дизъюнкции, конъюнкции, инверсии и некоторых других (И-НЕ, ИЛИ-НЕ, исключающее ИЛИ) называется элементом логических схем, или просто логическим элементом.
Любую
логическую функцию можно выразить с
помощью нескольких элементарных функций,
поэтому и любую логическую схему можно
представить в виде комбинаций логических
элементов.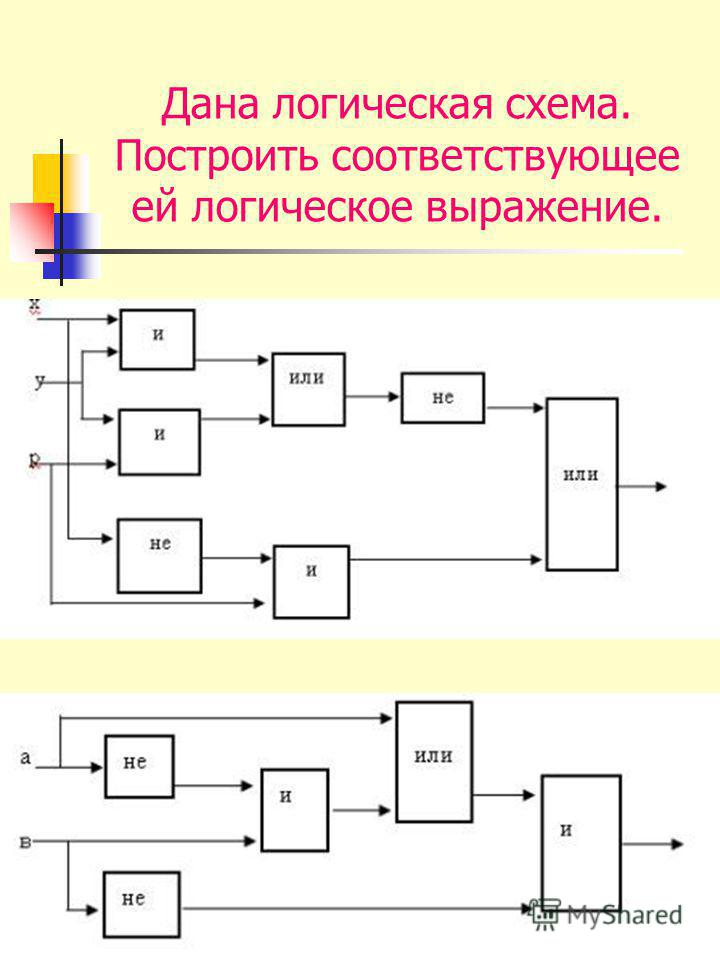 Таким образом, логические
схемы, это схемы, состоящие из логических
элементов.
Таким образом, логические
схемы, это схемы, состоящие из логических
элементов.
Логические элементы
1.Повторитель x=у
x y
2. Инвертор y= ┐x (схема НЕ)
x y
3.Дизъюнктор y=x1+x2 (схема ИЛИ)
x1 x2 | |
` |
4.Конъюнктор y=x1 x2 (схема И)
x1
x2
На основе этих элементов можно создать любое логическое устройство.
Функциональные схемы и логические схемы.
Функциональная
схема-это условное графическое изображение
реальных устройств или мысленных
абстракций с помощью специальных
символов. Каждый символ отображает
какую-то функцию, которую выполняет
элемент устройства или абстракции, и
называется функциональными элементом,
а функциональная схема состоит из
функциональных элементов.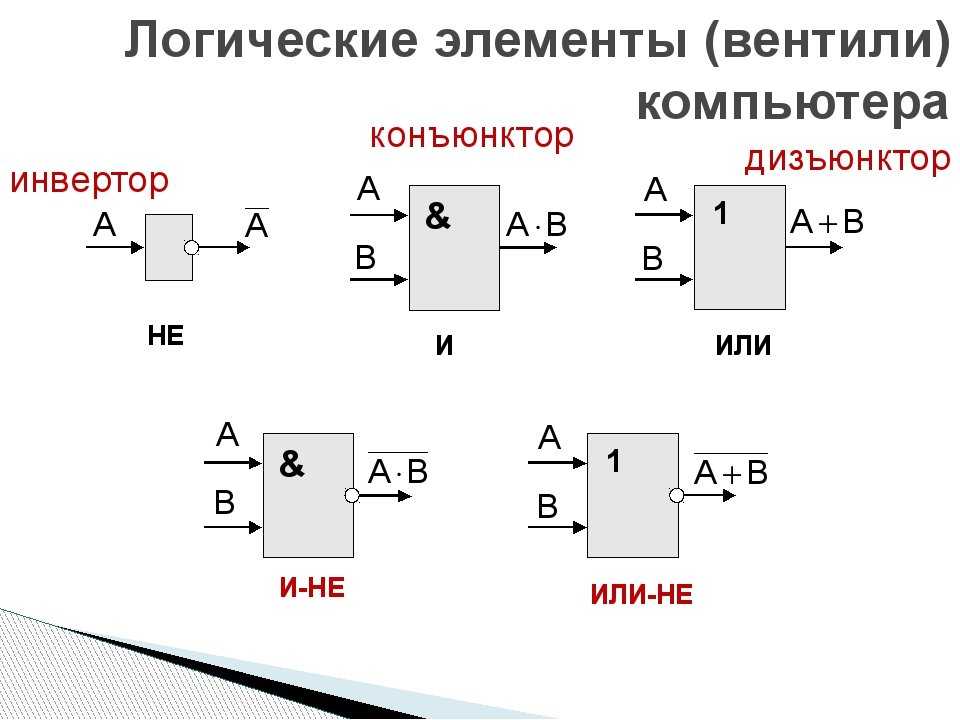
Логические схемы состоят из логических элементов, функциональных узлов и функциональных блоков. Перейдем непосредственно к логическим элементам, из которых состоят функциональные узлы, блоки и вообще все логические схемы.
Любую логическую функцию можно представить через элементарные операции. По этому любую логическую схему можно описать через элементарные логические элементы.
Функциональная схема, состоящая из функциональных элементов и описывающая какую-то более сложную функцию называется функциональным узлом. Каждый узел имеет тоже свое графическое изображение.
Функциональная схема, состоящая из функциональных узлов, называется функциональным блоком, который тоже может иметь свое графическое изображение. Логические схемы- частный случай функциональных схем, когда функциональные элементы изображают логические (булевы) функции.
Реальные
электронные и электрические цифровые
устройства, то есть устройства работающие
в режиме ВКЛ/ВЫКЛ, или в которых сигналы
могут иметь два дискретных уровня(
низкое/высокое напряжение )могут быть
описаны с помощью булевых логических
функций, и представлены в виде логических
(функциональных) схем.
В технике логический элемент это схема, выполняющая простые логические функции, а так же реальное устройство, реализующее простые логические операции-инверсия, дизъюнкция, конъюнкция, а логические схемы – это схемы электрических, электронных и других устройств, состоящих из логических элементов и выполняющих более сложные логические функции и операции, тоесть которые могут быть описаны логическими функциями.
Принципы построения функциональных узлов логических схем (примеры применения логических элементов)
В цифровых устройствах напряжения и токи могут принимать два значения: одному значению приписывается логический ноль, другому – логическая единица (например, u = 0B – логический ноль, u = 5B – логическая единица).
Второй вид дискретности в цифровых устройствах дискретность во времени. Считается, что все величины постоянны в течение такта и могут скачкообразно меняться на следующем такте.
Считается, что все
значения в схемах меняются в начале
тактового импульса.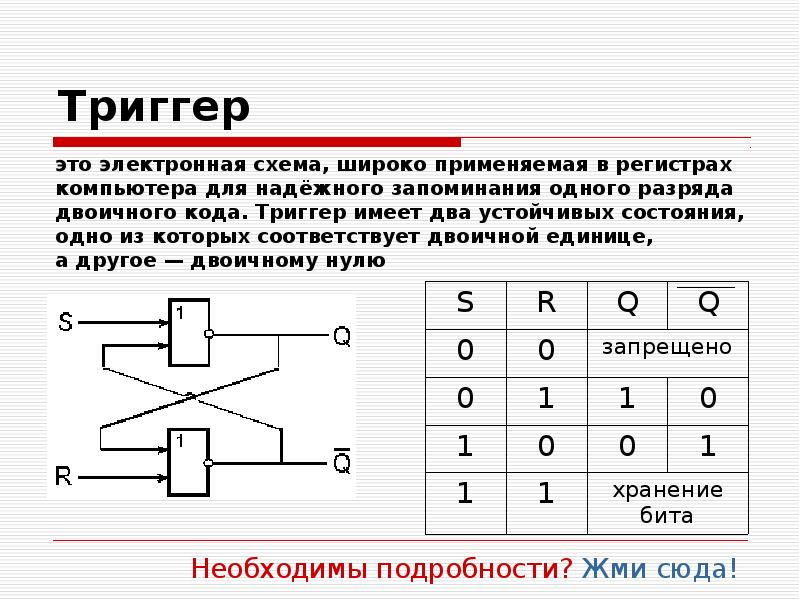 Хотя в реальности
изменение напряжения происходит с
некоторой задержкой относительно
переднего фронта тактового импульса.
Кроме того, некоторые устройства меняют
свое состояние после окончания тактового
импульса.
Хотя в реальности
изменение напряжения происходит с
некоторой задержкой относительно
переднего фронта тактового импульса.
Кроме того, некоторые устройства меняют
свое состояние после окончания тактового
импульса.
В качестве логического нуля или единицы выбирают определенный уровень напряжения или тока. Различают два подхода.
Импульсная логика: логический ноль – нет тока или напряжения, логическая единица – есть ток или напряжение.
Потенциальная логика: логический ноль – низкий уровень напряжения (потенциала), логическая единица – высокий уровень напряжения (потенциала). Наибольшее распространение получила потенциальная логика.
Логические элементы обеспечивают работу с 1 битом информации (ноль – единица).
Числа, адреса, команды представляются
в виде машинного слова, т. е. совокупности
нулей и единиц. Интерес представляет
обработка и передача не 1 бита, а их
совокупности, т.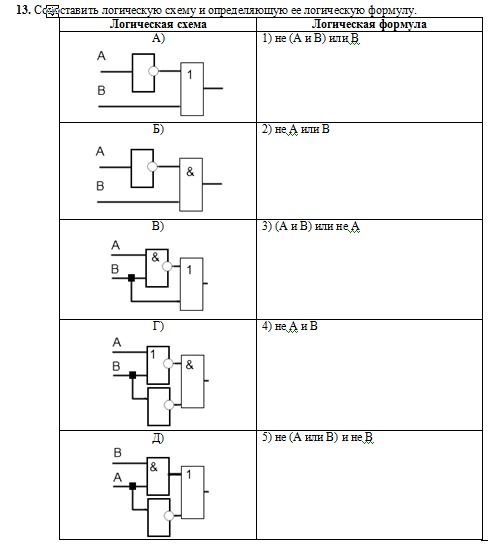
Совокупность логических (функциональных) элементов, часть логической (функциональной) схемы, описывающая одну или несколько логических функций, объединенных в одно целое, называется функциональным узлом.
Т. е. Функциональный узел – графическое изображение более сложной функции (по сравнению с функцией, описывающей логический элемент).
Функциональный узел – можно изобразить с помощью совокупности логических элементов или в виде одного графического символа.
Еще одно определение: функциональный узел – это совокупность логических элементов, обеспечивающих выполнение определенной операции.
Разновидности функциональных узлов.
Функциональные узлы могут быть одноразрядные, т. е. обрабатывающие
один разряд слова (например, сумматоры,
компараторы), и многоразрядными,
обрабатывающие слово целиком или 2
машинных слова или слога – ½ машинного
слова (все остальные узлы).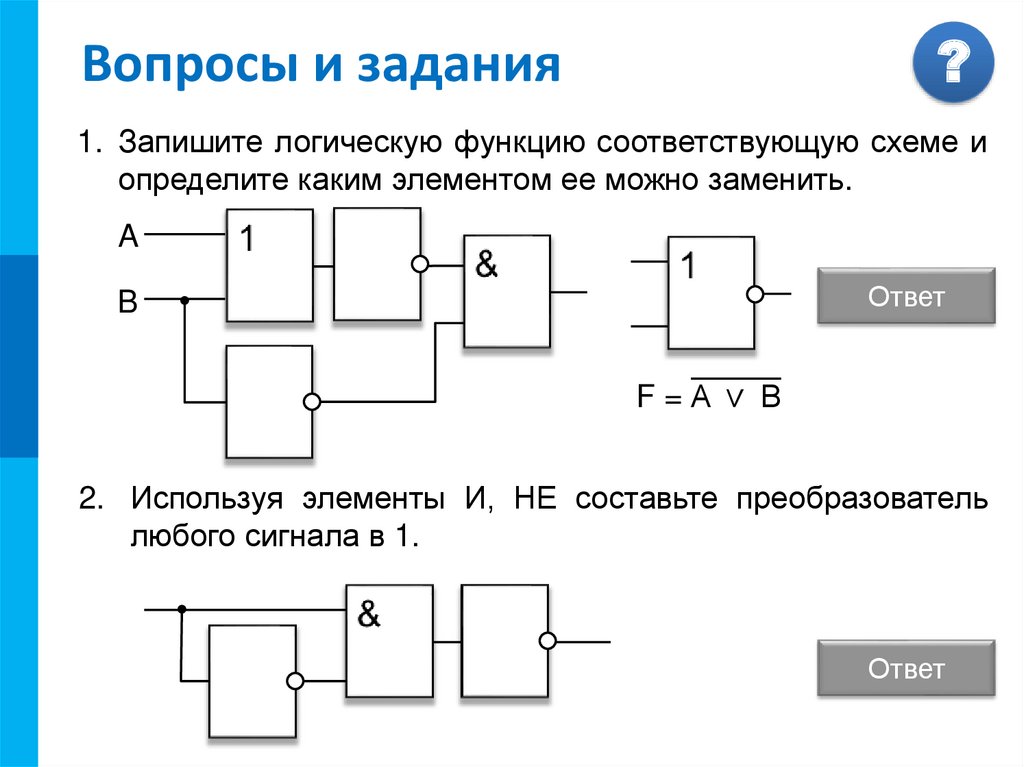
Функциональные многоразрядные узлы делятся на узлы параллельного типа и последовательного типа, т. е. работающие в параллельном или последовательном коде передачи информации.
Параллельный код – каждый временной такт используется для отображения одного разряда. Двоичный код слова – в виде временной последовательности. Причем слово передается по одной шине.
Параллельный код – все разряды слова передаются за один такт по отдельным шинам к отдельным элементам. При этом количество шин должно равняться количеству разрядов. Двоичный код слова — в виде пространственно разнесенной последовательности.
Последовательно-параллельный код – слово разбивается на слоги, каждый слог представляется в параллельном виде, а сами слоги передаются последовательно.
В последовательном коде могут работать
сумматоры, регистры сдвига, счетчики,
большинство же узлов работают в
параллельном коде.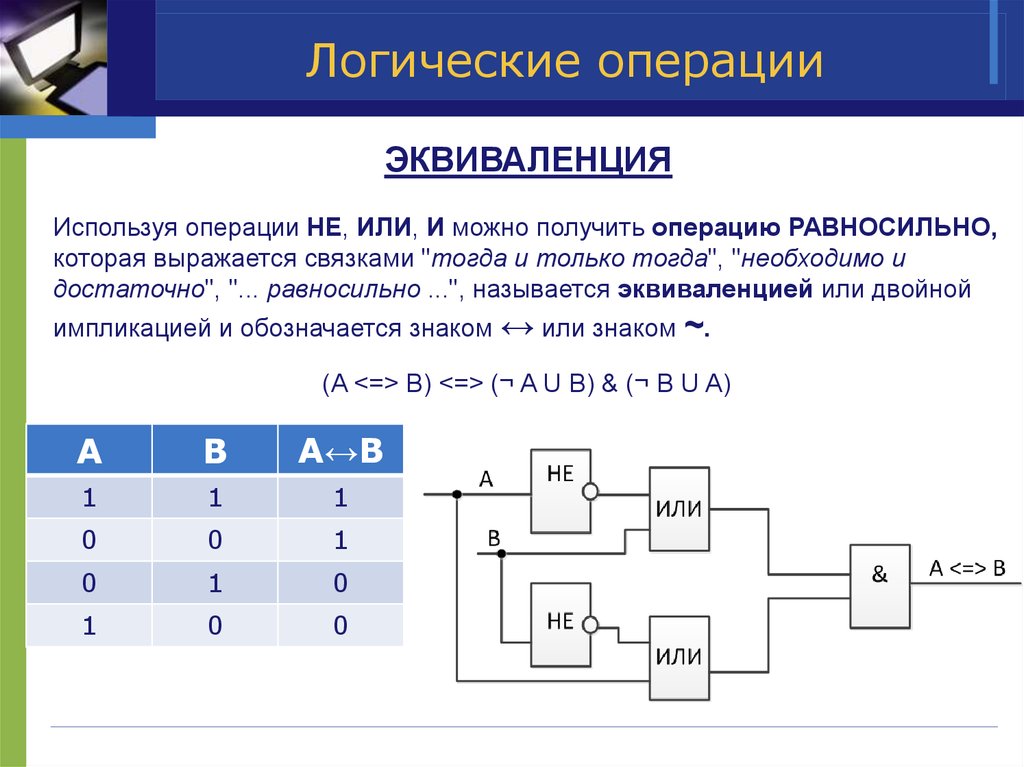
Кроме того передача информации может быть однофазной (по одной шине) и парафазной (по двум шинам), по одной передается сигнал, а по другой инвертированный сигнал.
Передача информации может быть асинхронной и синхронной (синхронизируемой).
Асинхронная (не синхронизированная) – сигналы передаются с небольшой задержкой от элемента к элементу. Элемент или узел срабатывает (меняет свое состояние) после прохода сигнала.
Синхронизируемая передача информации – элемент или узел срабатывает только после прихода синхроимпульса (т. е. в строго определенные моменты). Если на вход поступил сигнал, а синхроимпульс не подан, устройство не срабатывает. (т. е. должен поступить сигнал плюс синхроимпульс).
Комбинационные узлы (узлы
комбинационного типа) – функциональные
узлы, логическое состояние выходов
которых зависит только от комбинации
логических сигналов на входе в данный
момент времени, т.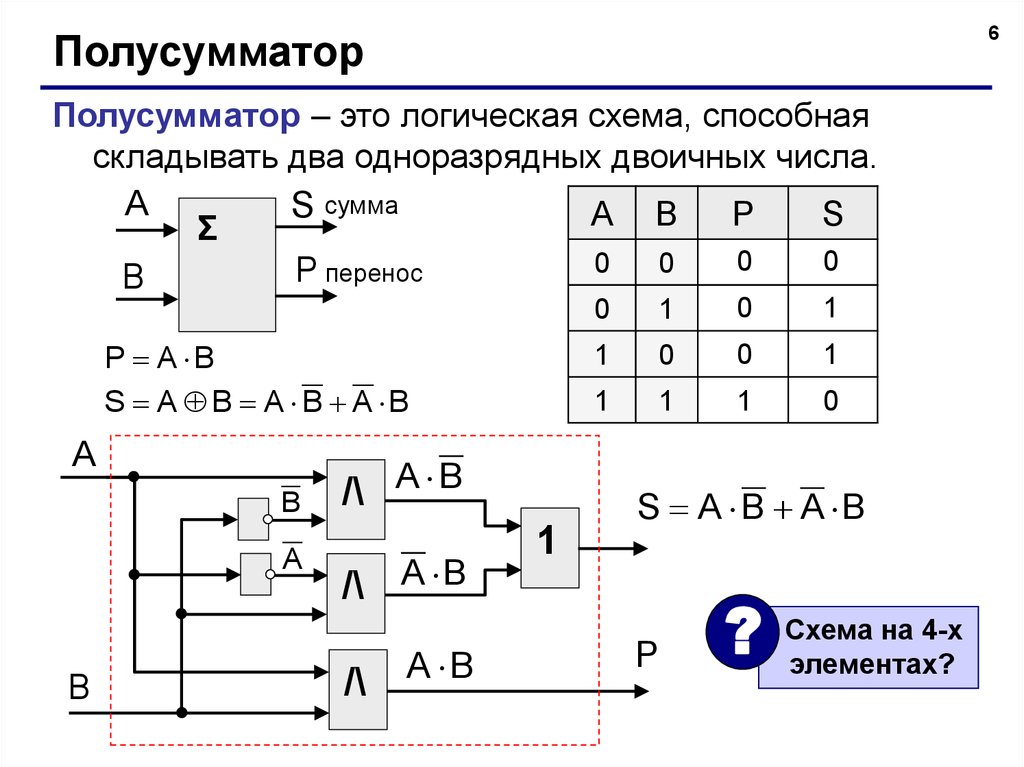
Последовательностные узлы (узлы последовательностного типа) – функциональные узлы, логическое состояние которых определяется последовательностью поступающих входных сигналов, т. е. логическое состояние определяется комбинацией входных сигналов не только в настоящий момент, но и в предыдущие моменты времени. Говорят, что такие узлы обладают памятью, например регистры, счетчики, генераторы кодов (распределители кодов). Узлы содержат элементы памяти – триггеры.
Другое название таких узлов — цифровые
автоматы Q(t+1)=f(Q(t),
x(t)). Различают
автомат Мили y(t)=(Q(t),
x(t)) и автомат
Мура y(t)=(Q(t)),
где Q(t) –
состояние узла, x(t),
y(t) – входные
и выходные сигналы.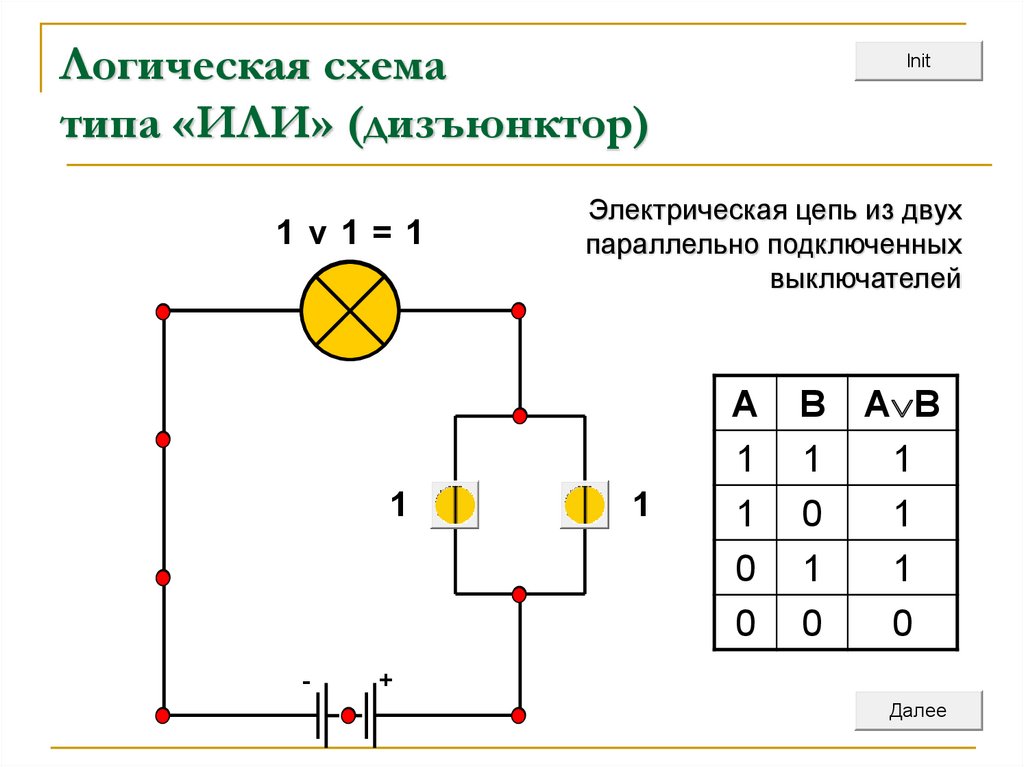
Вот простые примеры, показывающие как из логических элементов можно получить функциональные узлы последовательстного и комбинационного типа
Данные примеры показывают, почему Дискретную математику иногда называют Компьютерной математикой.
Обработка цифровой информации – сложение двоичных чисел
Двоичный сумматор — логическая схема, выполняющая арифметическое сложение чисел в двоичном коде, т.е. арифметическое сложение с помощью булевых операций.
Сложим два одноразрядных числа в двоичной системе:
0 + 0 = 0, 0 + 1 = 1, 1 + 0 = 1, 1 + 1 = 10.
a
b
P
S
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0
S – сумма в том же разряде, P – перенос в следующий разряд,
S = a b , P = a & b
a
b
S
P
1
&
a
b
S
P
1
&
a
b
S
P
1
&
a
b
S
P
1
&
a
a
a
b
b
b
S
S
S
P
P
1
1
1
&
&
P
&
1
&
S
P
a
b
Примеры цифровой логики
В этой статье д-р Тим Джексон рассматривает комбинаторную логику при проектировании систем.
Комбинаторная логика
Начнем со словесного описания того, чего мы хотим достичь. Мы вернемся к примеру, упомянутому в конце последнего задания, к расположению трех переключателей в блокировках для мощного лазера.
На фотографии показана лаборатория, используемая для изготовления тонких пленок новых электронных материалов. Большая серая рамка сзади — это лазер, излучающий 248 мкм импульсами длительностью 20 нс с энергией до 1 Дж в пучке площадью 2 см 9 .0013 2 . Это плотность энергии 5 кДж м 2 и плотность мощности 2,5 x 1011 Вт м -2 . Это УФ-излучение, достаточное для повреждения кожи, например, сильного солнечного ожога.
Для защиты персонала от лазерного луча может быть реализована система из трех переключателей, с переключателем S1 на двери в лабораторию, переключателем S2 на пластиковых крышках, которые видны над траекторией луча, и блокировкой S3 переключатель для всех этих блокировок, которыми может воспользоваться техник по техническому обслуживанию.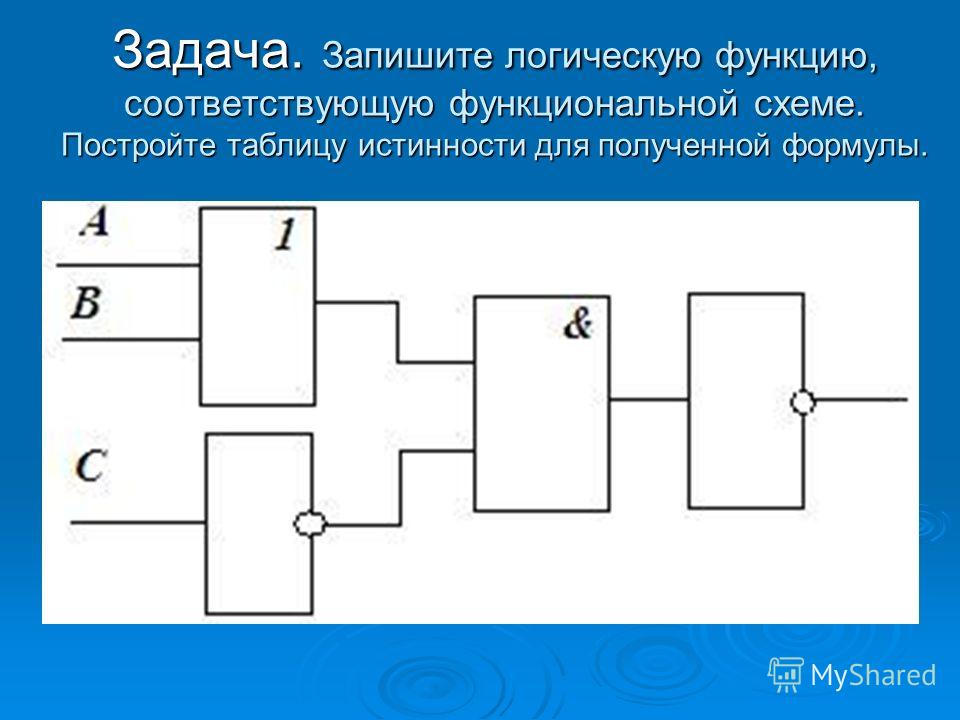 Чтобы запустить луч при обычном использовании, мы хотим, чтобы S1 и S2 были закрыты, а S3 открыта. Мы выбираем этот путь, потому что переключатели, активируемые дверью, обычно замыкаются (замыкают электрическую цепь), когда дверь закрыта. Когда переключатель замкнут, логический уровень низкий (см. шаг 3.4, цифровая электроника), поэтому это система Active-LOW.
Чтобы запустить луч при обычном использовании, мы хотим, чтобы S1 и S2 были закрыты, а S3 открыта. Мы выбираем этот путь, потому что переключатели, активируемые дверью, обычно замыкаются (замыкают электрическую цепь), когда дверь закрыта. Когда переключатель замкнут, логический уровень низкий (см. шаг 3.4, цифровая электроника), поэтому это система Active-LOW.
Наш план реализации начинается с описания физической системы.
«Лазер может быть активирован тогда и только тогда, когда S1 закрыт, S2 закрыт и S3 открыт».
Мы можем изобразить нашу цифровую сеть полностью символически, без деталей, как на рисунке 1. S1, S2 и S3 — двоичные переменные, представляющие состояние переключателей, а L — двоичная переменная, представляющая выход. сети.
Рисунок 1: Логическая сеть для лазерной системы безопасности (Нажмите, чтобы развернуть)
Логические элементы
Нам нужно получить соответствующий выход из возможных комбинаций входов, что мы достигаем с помощью логических элементов .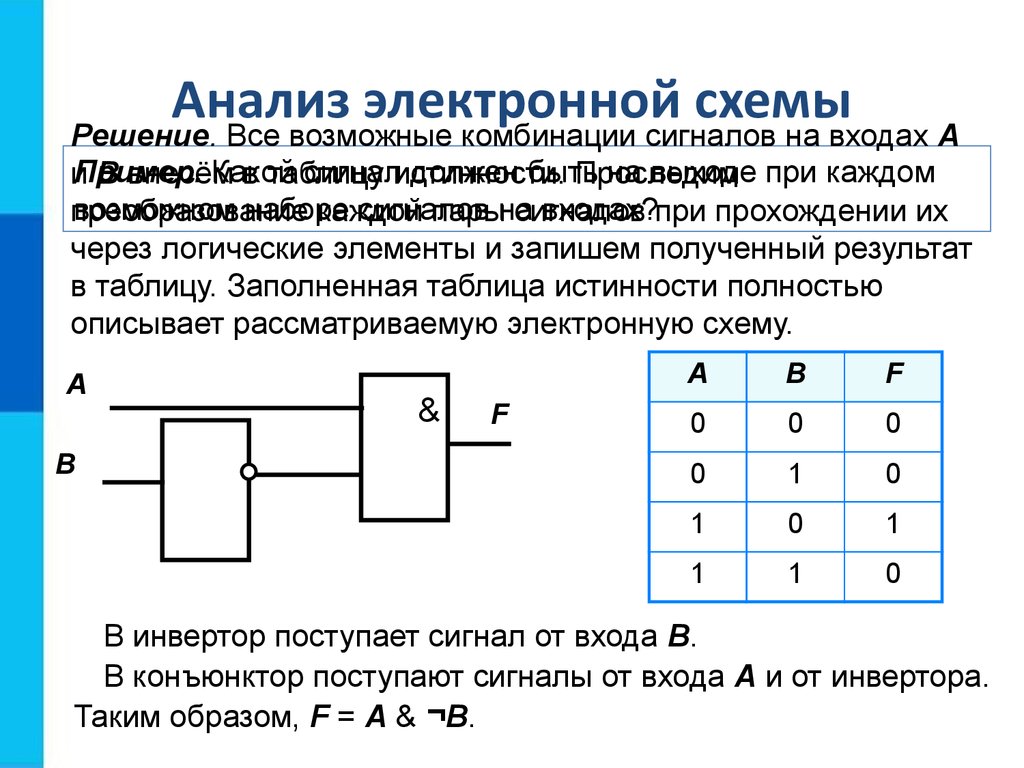 В таблице 1 показаны символы восьми логических вентилей, некоторые или все из которых вы можете распознать.
В таблице 1 показаны символы восьми логических вентилей, некоторые или все из которых вы можете распознать.
Таблица 1: Логические вентили (Нажмите, чтобы развернуть)
Таблица 2 ниже определяет каждый вентиль словами, а затем булевой логикой . Возможно, вы привыкли рисовать таблицы истинности для вентилей, но в сложных системах это становится очень неуклюжим, поэтому мы будем использовать здесь представление булевой логики.
| Ворота | Описание | Логическое представление |
|---|---|---|
| Буфер | Выход верен, только если вход верен | (К=А) |
| И | Вывод истинен тогда и только тогда, когда все входы истинны | (С=А∙В) |
| ИЛИ | Вывод истинен тогда и только тогда, когда хотя бы один вход верен | (С=А+В) |
| Исключительное ИЛИ | Выходные данные истинны тогда и только тогда, когда истинны один или другой вход, но не оба истинны | (С=А⊕В) |
| НЕ | Выход верен, только если ввод неверен | (C=фракция {}{A}) |
| НЕ-И | Выходные данные ложны тогда и только тогда, когда все входные данные верны | (C=фракция {}{(A∙B)}) |
| НО | Выход ложный тогда и только тогда, когда хотя бы один вход верен | (C=фракция {}{(A+B)}) |
| Исключительно НО | Выход верен, если оба входа ложны или оба входа верны | (C=фракция {}{(A⊕B)}) |
Таблица 2: Определения логических вентилей.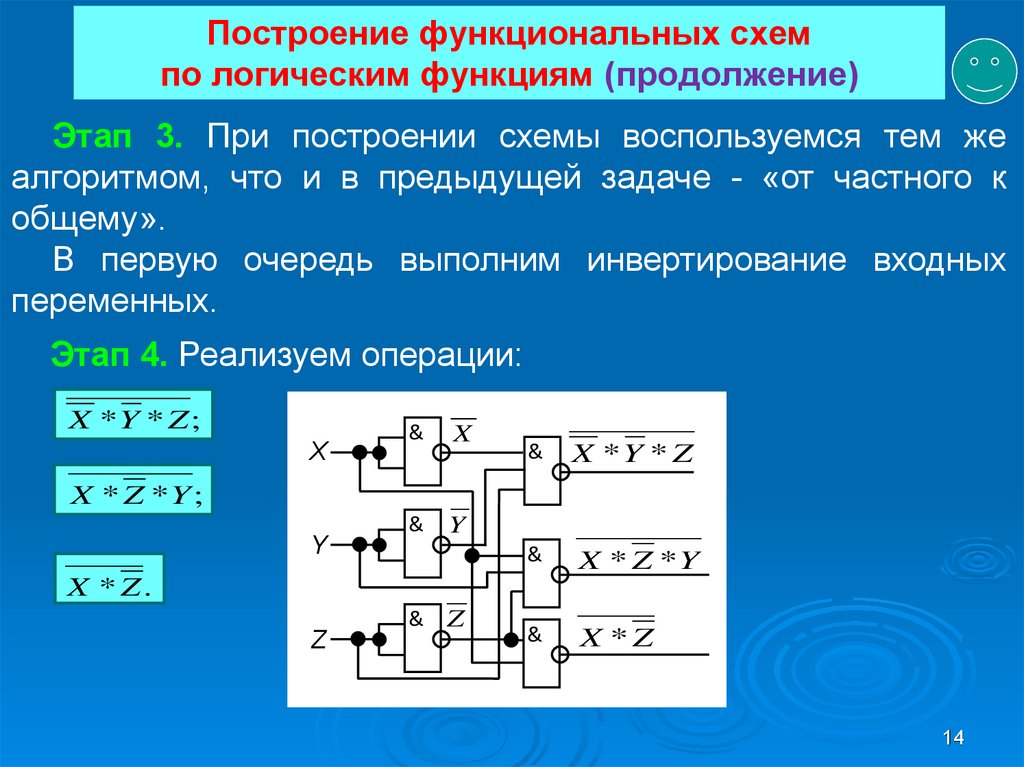
Теперь мы можем изложить наш план реализации на языке булевой логики . Помните, что active-LOW означает, что активное состояние переключателя равно 0 или FALSE. Мы можем сказать
«Лазер может быть запущен тогда и только тогда, когда S1 ЛОЖЬ, S2 ЛОЖЬ И S3 ИСТИНА».
Если «лазер может быть запущен», то мы хотим, чтобы L было ИСТИНА тогда и только тогда, когда S1 ЛОЖЬ И S2 ЛОЖЬ И S3 ИСТИНА»
Обратите внимание, что у нас не может быть комбинации двух входов FALSE и одного TRUE, мы должны быть конкретными.
Если мы начнем слева направо в нашем заявлении о дизайне, мы сначала потребуем, чтобы и S1, и S2 были ЛОЖНЫ. Булево уравнение для промежуточного выхода C будет иметь вид
[C:=frac{ }{S1}.frac{ }{S2}]
Если вы знаете «закон де Моргана» для упрощения логических выражений, то вы знаете, что
[C:=frac{ }{S1}.frac{ }{S2}=frac{ }{S1:+:S2}]
Из Таблицы 2 видно, что нам нужен вентиль ИЛИ-НЕ. Если бы вы не знали этой теоремы, вы могли бы получить тот же ответ, если бы по-другому выразили определение вентиля ИЛИ-НЕ; логический элемент ИЛИ-НЕ дает выход ИСТИНА только тогда, когда ни один из входов не является ИСТИНА.
Третий способ получить этот ответ — составить таблицу истинности для каждых ворот. Мы рассмотрим их в викторине, которая последует позже на этой неделе.
В любом случае, наш следующий шаг — объединить C с S3
[Л:=:Ккдот S3]
Этого можно добиться с помощью вентиля И. Итак, теперь мы можем нарисовать принципиальную схему нашей логической сети, как показано на рисунке 2.
Рисунок 2: Логическая сеть для лазерной безопасности (Нажмите, чтобы развернуть)
Могут быть и другие способы добиться того же результата. Для дизайнера самое простое часто оказывается лучшим, потому что меньше ошибок.
Почему мы предоставили подзаголовок Комбинаторная логика в этом разделе? Ответ заключается в том, что в этом примере нам не нужно беспокоиться о порядке, в котором переключатели открываются или закрываются. Нас беспокоит только нынешнее состояние системы. Нам нет дела до прошлого.
В последовательной логике выходы определяются последовательностью входов, которые приводят к текущему состоянию системы.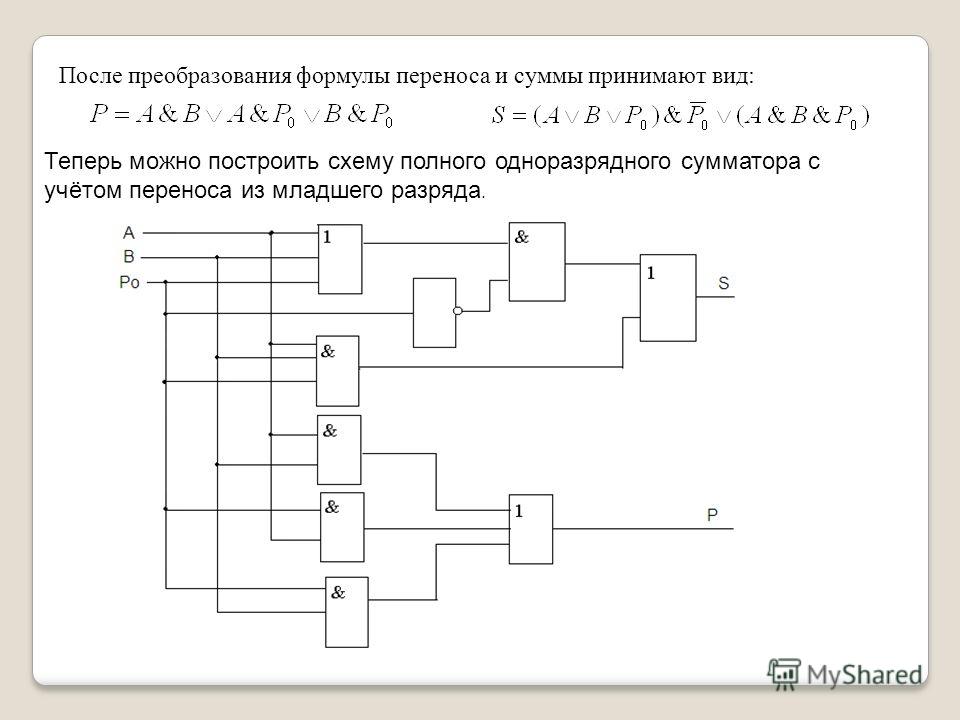 Нам нужна последовательная логика, когда важен порядок событий, способ, которым мы пришли к нашему нынешнему состоянию.
Нам нужна последовательная логика, когда важен порядок событий, способ, которым мы пришли к нашему нынешнему состоянию.
Существует два типа последовательной логики: синхронная, когда выходы обновляются только при получении импульсов от тактового сигнала, и асинхронная, когда выходы обновляются при получении любых входных сигналов.
Если бы мы хотели создать новую конструктивную особенность, например, которую нужно сначала закрыть, то нам понадобилась бы асинхронная логика.
Однако, даже если мы не возражаем против порядка событий, может быть причина использовать синхронную логику. В предыдущей статье мы говорили, что цифровые системы устойчивы к шуму, потому что они основаны на переходах, но мы рассматривали ВЫСОКИЙ и НИЗКИЙ уровни в наших схемах.
Чтобы представить последовательную логику, мы рассмотрим триггер типа D 9.0034 . Этот компонент копирует свои входные данные на свои выходные данные, когда на это указывает тактовый сигнал. Рисунок 3.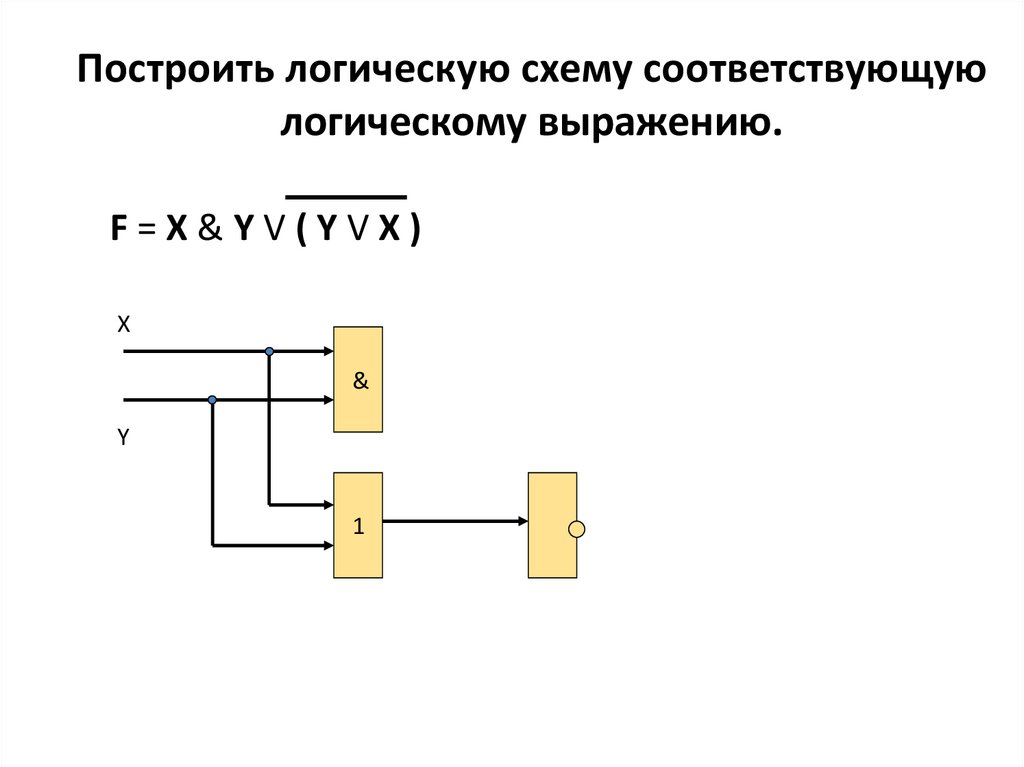 дает представление о том, как это работает.
дает представление о том, как это работает.
Рис. 3. Цифровые сигналы для выхода датчика двери, часов и триггера типа D (щелкните, чтобы развернуть)
На рис. 3 дверь изначально открыта, поэтому S1= ВЫСОКАЯ. Когда дверь закрыта и S1 = LOW, выход Q триггера фиксируется на новом входном значении только после поступления тактового импульса (CLK). Триггером для изменения является один из фронтов импульса, триггер типа D может запускаться по положительному или отрицательному фронту. На рис. 4 показан символ схемы для устройства, запускаемого положительным фронтом. Вход обычно обозначается буквой D. Инвертированный выход Q – предоставляется в дополнение к основному выходу Q. Выход триггера типа D копирует вход и, таким образом, удерживает или запоминает логический уровень. Выход Q заменит вход S1 на рисунках 1 и 2.
Рис. 4. Триггер типа D (щелкните, чтобы развернуть)
Представьте, что в цепях, обеспечивающих питание S1, есть помехи. Если нам не повезет, шум будет достаточно большим, чтобы заставить систему изменить состояние. Но мы будем реагировать на изменение состояния только в том случае, если есть еще и тактовый импульс. Обратите внимание на рис. 3, что тактовый сигнал имеет низкий коэффициент заполнения — он ВЫСОКИЙ в течение меньшего времени, чем НИЗКИЙ. Если тактовый импульс достаточно острый, шум будет пропущен. Наша система более надежна с синхронной логикой.
Но мы будем реагировать на изменение состояния только в том случае, если есть еще и тактовый импульс. Обратите внимание на рис. 3, что тактовый сигнал имеет низкий коэффициент заполнения — он ВЫСОКИЙ в течение меньшего времени, чем НИЗКИЙ. Если тактовый импульс достаточно острый, шум будет пропущен. Наша система более надежна с синхронной логикой.
Существуют и другие способы борьбы с шумом в воротах, но они выходят за рамки данного курса.
© University of Birmingham
Комбинационные логические схемы: определение, примеры и приложения
Поскольку область применения цифровых технологий и цифровых электронных схем распространяется на многие области, такие как программное обеспечение, здравоохранение, автоматизация, бизнес и многие другие, электронные представления логических функций, для представления этих цифровых сигналов используются многочисленные диапазоны логических вентилей. В сценарии с цифровой логикой выход полностью зависит от токового входа. В результате этого процесса логические элементы, которые используются для представления цифровых схем, классифицируются как последовательные логические схемы и комбинационные логические схемы.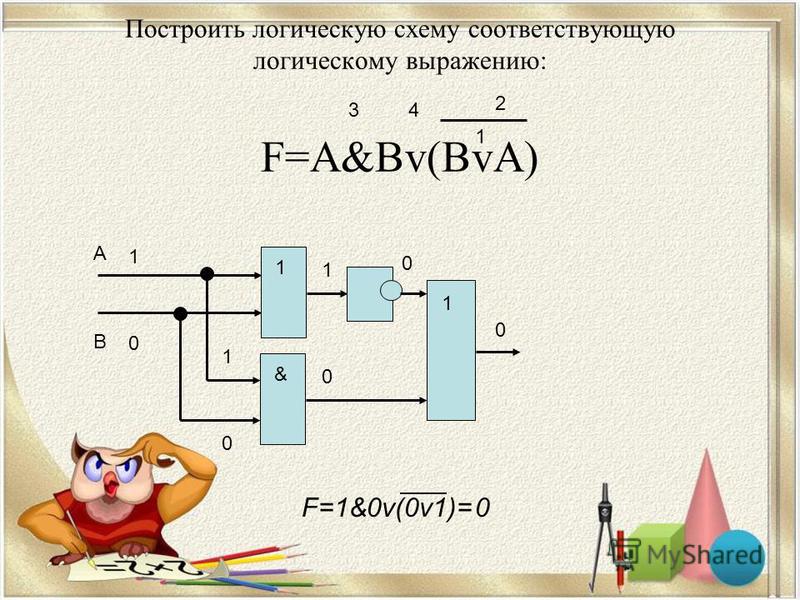 Поскольку реализация комбинационных логических схем присутствует во многих компьютерных схемах, давайте продолжим подробное обсуждение того, как они работают, и многих других концепций, связанных с этой концепцией.
Поскольку реализация комбинационных логических схем присутствует во многих компьютерных схемах, давайте продолжим подробное обсуждение того, как они работают, и многих других концепций, связанных с этой концепцией.
Что такое комбинационная логическая схема?
Комбинационная логическая схема, поскольку само название указывает на то, что это комбинация различных логических элементов. Комбинационная схема имеет характеристики:
- В любой момент времени вывод основан только на уровнях текущих входных клемм, а не на входах прошлого состояния.
- Этим схемам не нужны какие-либо состояния памяти или часы, поэтому прошлые входные данные не оказывают влияния на текущее состояние схемы.
- Комбинационная схема может принимать «n» входов и выдает только один выход.
Сложная или простая комбинационная логика может быть представлена через вентили «И-НЕ», «НЕ» или «НЕ-ИЛИ».
базовая комбинационная логическая схема
Представление комбинационных логических схем
Здесь мы обсудим три подхода к представлению комбинационных логических схем
- Логические элементы – это основные строительные блоки при разработке комбинационных логических схем.
 И-НЕ, NR, НЕ, ИЛИ, ИЛИ, И — все это логические элементы.
И-НЕ, NR, НЕ, ИЛИ, ИЛИ, И — все это логические элементы. - Булева алгебра – Это представление определяет связь между булевыми переменными и используется для проектирования цифровых схем через логические вентили. Каждая цифровая система в основном разработана с логическими элементами, поэтому булева алгебра является одним из основных подходов к представлению комбинационной логической схемы.
- Таблица истинности . Этот метод вычисляет операционные значения логических выражений для каждой комбинации значений, принимаемых их логическими переменными. Для каждого однобитового выхода в логическом блоке необходима таблица истинности для представления логики. Как правило, все выходные столбцы представлены в одной таблице.
Например, выражение, которое может быть представлено в трех вышеуказанных подходах следующим образом:
представление комбинационных логических схем
классификация комбинационных логических схем
комбинационные логические схемы классифицируются следующим образом
классификация комбинационных логических схем
Передовой реализацией комбинационной логической схемы является мультиплексор и демультиплексор. В них много входов или выходов находятся на одной линии, и логические вентили используются для декодирования соответствующего выхода для указанного входа.
В них много входов или выходов находятся на одной линии, и логические вентили используются для декодирования соответствующего выхода для указанного входа.
Примеры комбинационных логических схем
Широкая реализация комбинационных логических схем сегодня позволила нам обсудить большее количество примеров. Вот некоторые из реальных примеров:
Полусумматор
Это комбинационная логика, полученная с использованием двух входов и двух выходов. Схема позволила нам сложить два однобитных двоичных числа. Итак, основная цель использования полусумматора — сложение. С входами как A и B схема может быть спроектирована следующим образом
Блок-схема полусумматора
Таблица истинности
Вывод может быть получен следующим образом:
Входы | Выходы | ||
| А | Б | С | С |
| Л | л | л | л |
л | Х | Х | л |
| Н | л | Х | л |
| Н | Х | л | Х |
Принципиальная схема
Для получения выходных сумм и переносов схема подключается в следующем формате
схема схемы полусумматора
полный сумматор полный сумматор разработан.
 Он имеет возможность складывать два двоичных числа вместе с переносом ввода. Итак, это схема с тремя входами и двумя выходами.
Он имеет возможность складывать два двоичных числа вместе с переносом ввода. Итак, это схема с тремя входами и двумя выходами.Блок-схема полного сумматора
Таблица истинности
Вывод может быть получен следующим образом:
Входы | Выходы | |||
| А | Б | С в | С | С |
л | л | л | л | л |
| Л | л | Ч | Х | л |
л | Х | л | Х | л |
| Л | Х | Х | л | Х |
Х | л | л | Х | л |
| Н | л | Х | л | Х |
Х | Х | л | л | Х |
| Н | Х | Х | Х | Х |
Схема цепи
Для получения суммирования и переноса выходов схема подключается в следующем формате двоичные числа, во многих случаях нам нужно добавить n-битные числа вместе с переносом.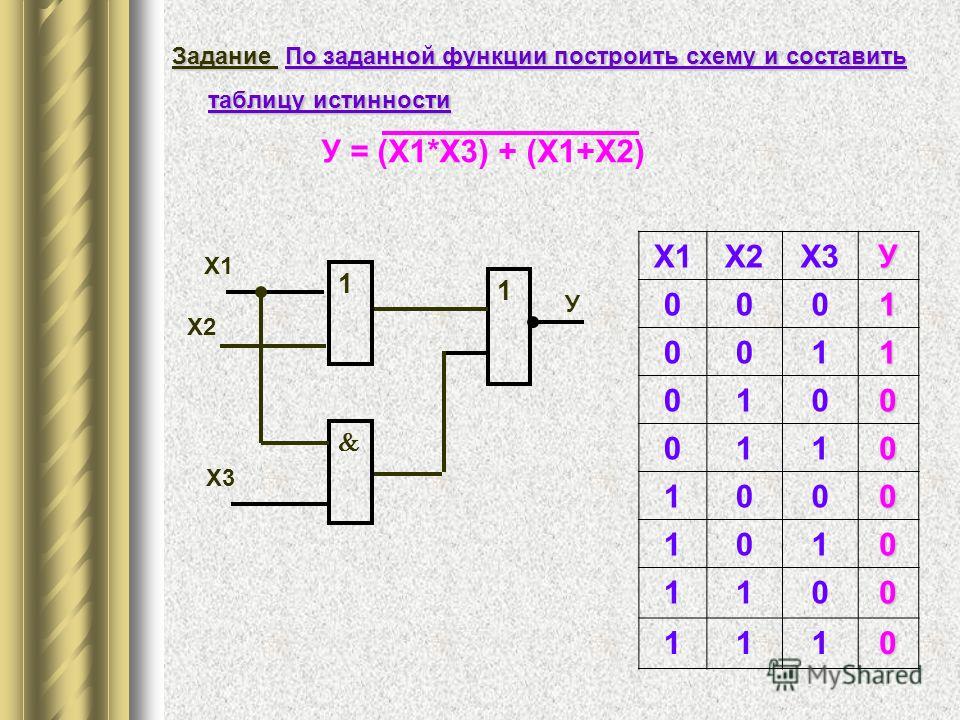 В этих случаях n-битный параллельный сумматор может складывать n-битные двоичные числа. Это комбинация многих полных сумматоров. Таким образом, выход переноса предыдущего сумматора подключается в качестве входа к следующему сумматору.
В этих случаях n-битный параллельный сумматор может складывать n-битные двоичные числа. Это комбинация многих полных сумматоров. Таким образом, выход переноса предыдущего сумматора подключается в качестве входа к следующему сумматору.
Полувычитатель
Принимая два двоичных числа «А» и «В» в качестве входных данных, полувычитатель получает на выходе заимствование и разность. «Разница» — это разница между двумя входными числами, а «Заем» — это тот, который содержит заимствование, если таковое имеется. В обоих входах A называется Minuend, а B называется Subtrahend.
Таблица истинности
Вывод может быть получен следующим образом:
Входы | Выходы | ||
| А | Б | Разница | Занять |
л | л | л | л |
| Л | Х | Х | Х |
Х | л | Х | л |
| Н | Х | л | л |
Принципиальная схема
Для получения выходов «Разница» и «Заимствование» схема подключается в следующем формате.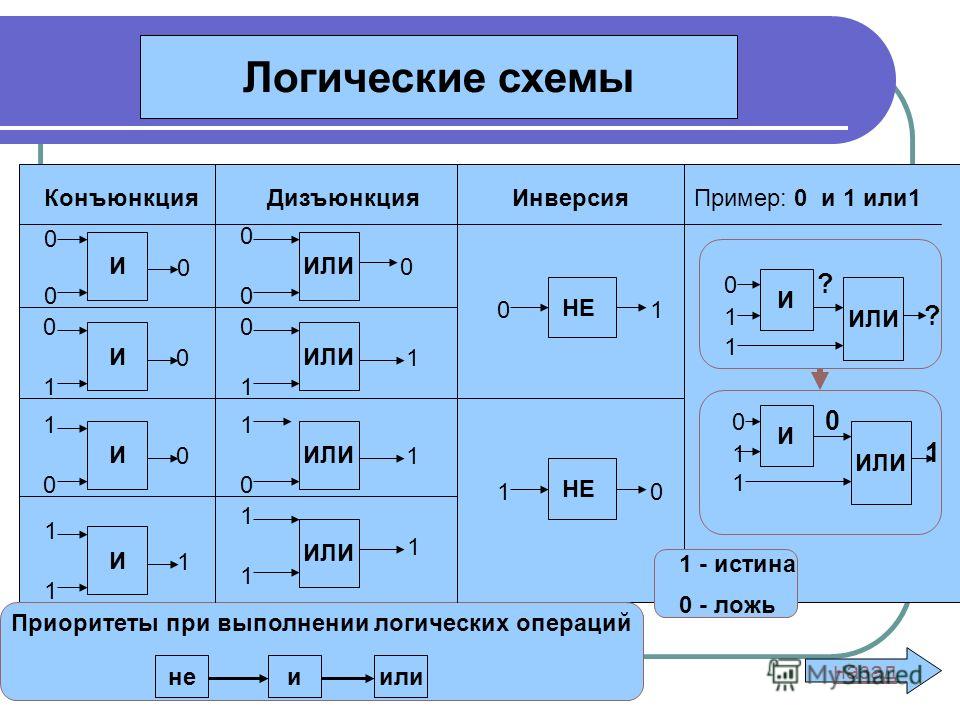
Принципиальная схема полувычитателя
Полный вычитатель разработан. Схема разработана с тремя входами, которые обеспечивают два выхода: «Разница» и «Заем». Где «Разница» — это разница между двумя входными данными, а «Заем» — это заимствование.
Таблица истинности
Результат полного вычитания следующий:
Входы | Выходы | |||
| А | Б | С в | А-Б-С | Занять |
л | л | л | л | л |
| Л | л | Ч | Х | Х |
л | Х | л | Х | Х |
| Л | Х | Х | л | Х |
Х | л | л | Х | л |
| Н | л | Х | л | л |
Х | Х | л | л | л |
| Н | Х | Х | Х | Х |
Принципиальная схема
Для получения выходов Разность и Заимство схема подключается в следующем формате число, которое нужно вычесть.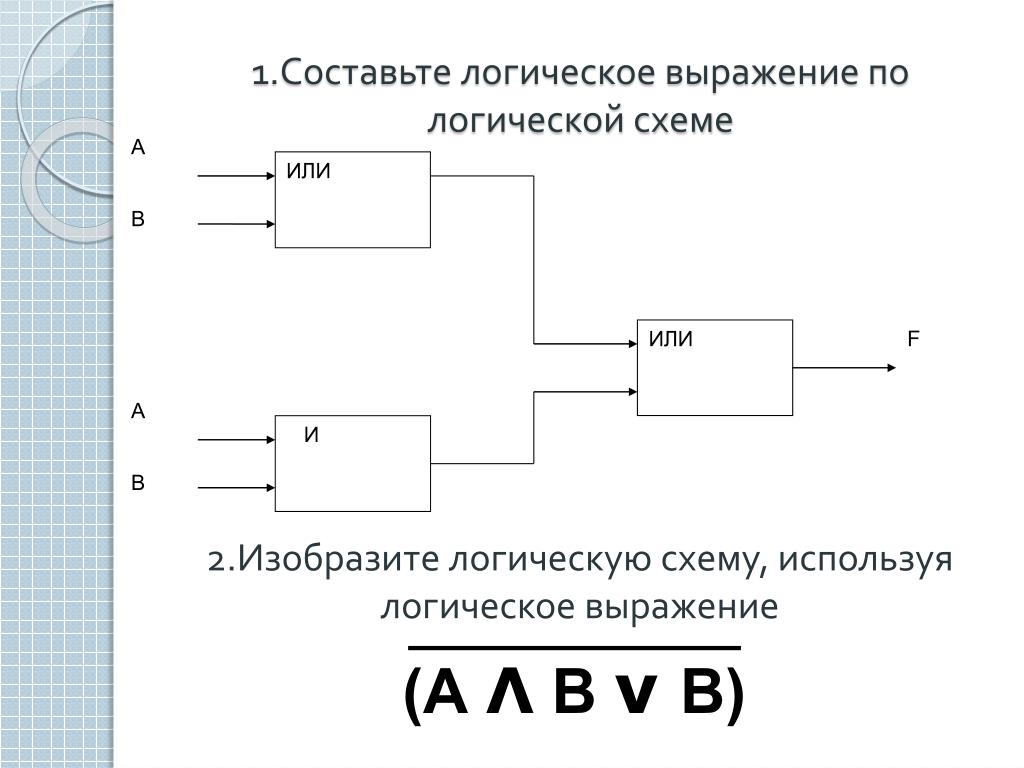 Например, мы можем выполнить A-B либо путем добавления 1 или 2 дополнения B к входу A. Итак, здесь мы используем двоичный сумматор для выполнения процесса вычитания.
Например, мы можем выполнить A-B либо путем добавления 1 или 2 дополнения B к входу A. Итак, здесь мы используем двоичный сумматор для выполнения процесса вычитания.
Подробно процесс можно описать так:
• Вычитаемое число должно быть пропущено через инвертор, чтобы получить его дополнение.
• Затем 4-битный сумматор складывает A и дополнение B и выдает результат вычитания.
• Когда A>B и C равно 0, а результат A-B в двоичном формате, тогда C = 1, а вывод находится в форме дополнения до 2.
На приведенной ниже схеме четко поясняется работа n-битного параллельного вычитателя.
Мультиплексор
Мультиплексор — это основное применение комбинационной логической схемы. Схема имеет «n» входов, «m» входов выбора с 2m = n и один выход. Это цифровая схема, которая выбирает один вход данных и направляет его на выход. Выбор входов осуществляется входами выбора. На основе нанесенного цифрового кода выбирается один из входов и адресуется выходу. Каскадная работа выполняется входом «E», который является активным входом с низким уровнем клеммы.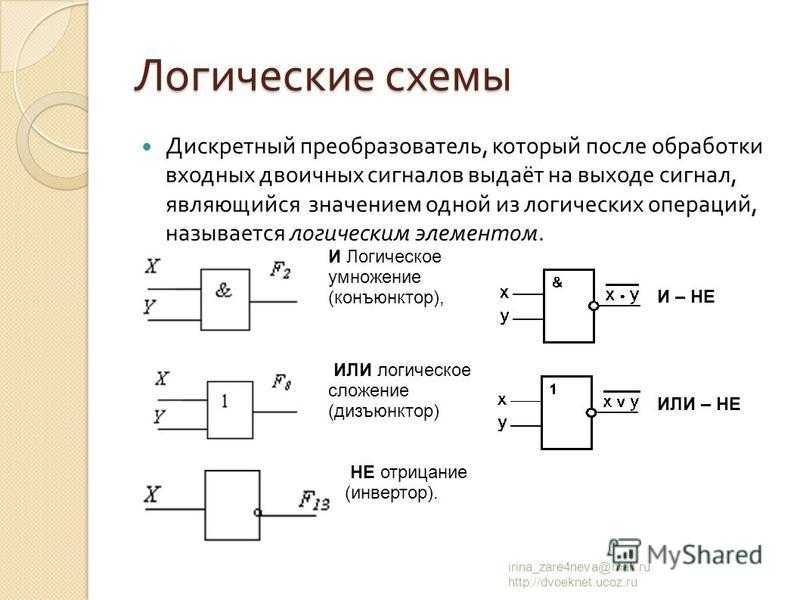 Блок-схема мультиплексора выглядит следующим образом
Блок-схема мультиплексора выглядит следующим образом
мультиплексор
Мультиплексоры используются во многих приложениях, поскольку они доступны как
- 2:1 Mux
- 4:1 Мультиплекс
- 16:1 Мультиплексор
- 32:1 Мультиплекс
Давайте разберемся с мультиплексором 2:1
Блок-схема – это базовая блок-схема работы мультиплексора 2:1
Мультиплексор 2-1 в комбинационной логической схеме
Таблица истинности Результат может быть получен, как показано ниже
Включить | Выберите | Выход |
Е | С | Д |
| Н | × | л |
Х | 0 | Д 0 |
| Н | Х | Д1 |
Демультиплексор
Демультиплексор выполняет операции, обратные операциям мультиплексора.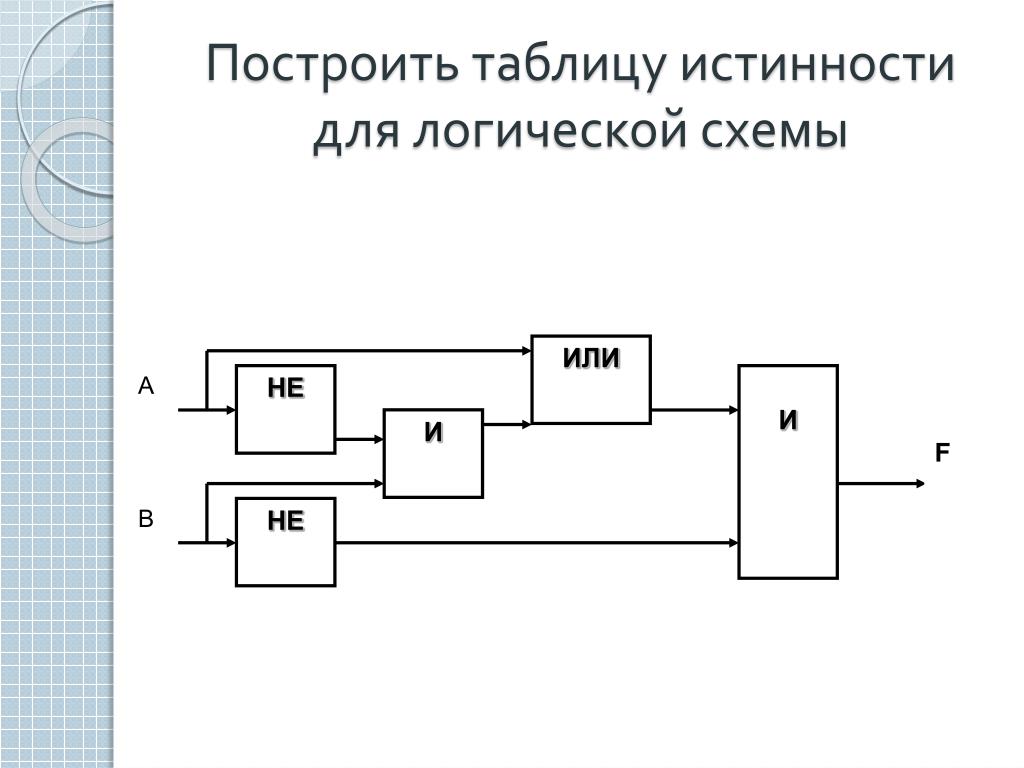 Он имеет только один вход и обеспечивает несколько выходов. Схема спроектирована с одним входом, m входами выбора и n выходами. В одном случае через входы выбора выбирается только один выход, и он направляется на выход. Демультиплексоры используются во многих приложениях, поскольку они доступны в виде
Он имеет только один вход и обеспечивает несколько выходов. Схема спроектирована с одним входом, m входами выбора и n выходами. В одном случае через входы выбора выбирается только один выход, и он направляется на выход. Демультиплексоры используются во многих приложениях, поскольку они доступны в виде
- 1:2 демультиплексор
- Демультиплексор 1:4
- демультиплексор 1:16
- демультиплексор 1:32
Давайте разберемся с демультиплексором 1:2
Блок-схема – это базовая блок-схема работы демультиплексора 1:2
Демультиплексор 1-2 в комбинационной логической схеме Вывод может быть получен, как показано ниже.
Включить | Выберите | Выход | |
Е | С | Д 0 | Д 1 |
| Л | × | л | л |
Х | л | л | D в |
| Н | Х | D в | л |
Декодеры, энкодеры, приоритетные энкодеры — все это примеры комбинационных логических схем.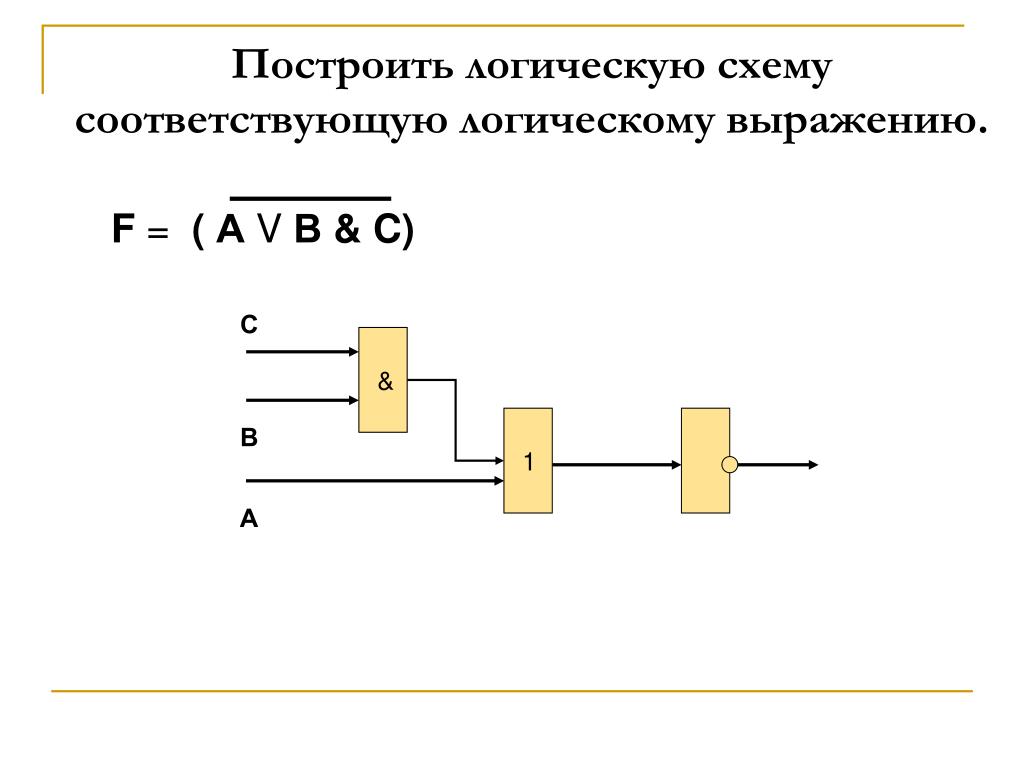
Перейдите по этой ссылке, чтобы узнать больше о схемах комбинационной логики MCQ
Применение схемы комбинационной логики
Схемы комбинационной логики являются основными строительными блоками цифровых систем. Они имеют широкий спектр применения. Они используются в
- Цифровые измерительные приборы
- Цифровая обработка
- Промышленная переработка
- Компьютеры
- Калькуляторы
- Цифровая связь
Схемы комбинационной логики, такие как арифметические и логические схемы, имеют применение как
- Компараторы
- Программируемые логические устройства
- Сумматоры и вычитатели
Комбинационные логические схемы в качестве цепей передачи данных применяются как
- Параллельные преобразователи в последовательные
- Маршрутизация данных
- Последовательно-параллельные преобразователи
- Битовое сжатие
- АЦП и ЦАП
- Кодировщики и декодеры
Схемы комбинационной логики в качестве схем преобразователя кода применяются как
- Преобразование двоичного кода в код Грея
- Преобразование серого в двоичный код
- BCD к Excess-3
- Превышение-3 к BCD
- Семисегментный код
Процедура проектирования комбинационной логической схемы
Следующие шаги ясно объясняют процедуру разработки схемы комбинационной логики
1. Идентификация необходимого количества входных и выходных переменных
Идентификация необходимого количества входных и выходных переменных
2. Символизация всех идентифицированных входных и выходных переменных
3. Выражение связи между этими переменными
4. По связи построить таблицу истинности
5. Вывести логическое выражение для всех выходов
6. Минимизировать логическое выражение, чтобы уменьшить сложность
7. Спроектировать логическую схему с помощью логических выражений
Для минимизации логических выражений используются различные подходы. K-map и Quinne-McCluskey являются наиболее популярными методами. Вышеизложенная процедура является упорядоченной и эффективной методикой. Благодаря этому конструкция цепей кажется полностью надежной.
Является ли мультиплексор комбинационной схемой?
Да, мультиплексор представляет собой комбинационную логическую схему, которая выводит несколько выходов из одного входа и разработана с помощью комбинации логических вентилей.
Является ли флип-флоп комбинационной схемой?
Нет, триггер — это пример последовательной схемы, которая генерирует выходные данные на основе выбранных входных данных и изменяет выходные данные через определенные промежутки времени, но не периодически.
Потребность в комбинационных схемах
Что ж, в наши дни сфера применения цифровой электроники приобрела огромное значение, а из многочисленных элементов большое значение получили комбинационные логические схемы. Эти схемы являются основными строительными блоками цифровых систем. Нам нужна реализация этих схем для повышения производительности, и они используются в операциях, которые работают с меньшим энергопотреблением. Кроме того, это независимые от времени и менее затратные схемы, и при обработке действий эта функция помогает больше всего.
Пожалуйста, перейдите по этой ссылке, чтобы узнать больше о Logic Gates MCQ
Часто задаваемые вопросы
1. Как используется булева алгебра?Этот метод используется для упрощения и анализа цифровой логики. Поскольку она работает с использованием битов 0 и 1, ее также называют двоичной алгеброй
2. Для чего используется K-карта? Устранение сложности, связанной с теоремами булевой алгебры, манипуляциями и уравнениями, k-карта является графическим представлением сокращения булевых выражений.
Имеются цифровые и аналоговые мультиплексоры. Опять же, они классифицируются как мультиплексирование с временным разделением (TDM), мультиплексирование с частотным разделением (FDM) и мультиплексирование с разделением по длине волны (WDM).
4. Что вы подразумеваете под мультиплексированием?Это процесс передачи нескольких потоков данных по каналу связи, после чего приемник восстанавливает отдельные сигналы.
5. Что такое логические операторы?Существует шесть булевых операторов. Это И, условное И, ИЛИ, условное ИЛИ, исключающее ИЛИ и НЕ. Каждый аргумент, передаваемый логическому оператору, должен быть логического типа данных, и выходные данные всегда имеют логический тип данных.
Перейдите по этой ссылке, чтобы узнать больше о MCQ Full Subtractor.
Воспользуйтесь всеми преимуществами комбинационных логических схем.


 И-НЕ, NR, НЕ, ИЛИ, ИЛИ, И — все это логические элементы.
И-НЕ, NR, НЕ, ИЛИ, ИЛИ, И — все это логические элементы.