Построение логических схем — Студопедия
Поделись
Знания из области математической логики можно использовать для конструирования электронных устройств. Нам известно, что 0 и 1 в логике не просто цифры, а обозначение состояний какого-то предмета нашего мира, условно называемых «ложь» и «истина». Таким предметом, имеющим два фиксированных состояния, может быть электрический ток. Устройства, фиксирующие два устойчивых состояния, называются бистабильными (например, выключатель, реле). Если вы помните, первые вычислительные машины были релейными. Позднее были созданы новые устройства управления электричеством — электронные схемы, состоящие из набора полупроводниковых элементов. Такие электронные схемы, которые преобразовывают сигналы только двух фиксированных напряжений электрического тока (бистабильные), стали называть логическими элементами.
На элементарном уровне конъюнкцию можно представить себе в виде последовательно соединенных выключателей, а дизъюнкцию — в виде параллельно соединенных выключателей:
Логические элементы имеют один или несколько входов и один выход, через которые проходят электрические сигналы, обозначаемые условно 0, если «отсутствует» электрический сигнал, и 1, если «имеется» электрический сигнал. Простейшим логическим элементом является инвертор, выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот. У этого элемента один вход и один выход. На функциональных схемах он обозначается:
Простейшим логическим элементом является инвертор, выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот. У этого элемента один вход и один выход. На функциональных схемах он обозначается:
Логический элемент, выполняющий логическое сложение, называется дизъюнктор. Он имеет, как минимум, два входа. На функциональных схемах он обозначается:
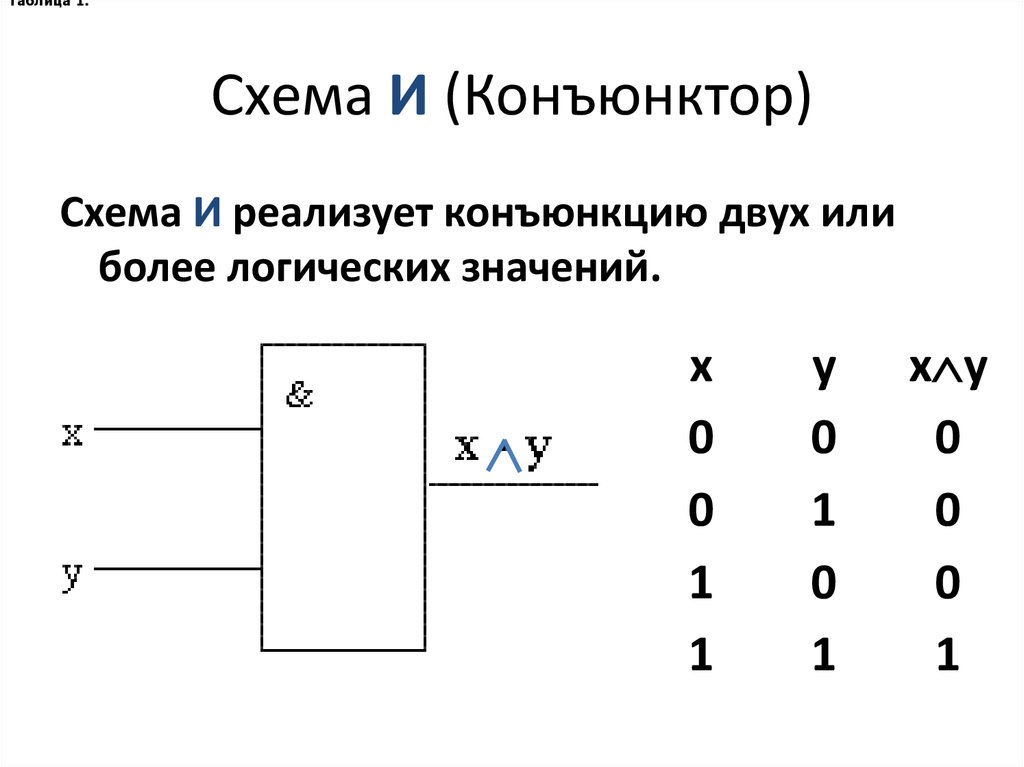
Логический элемент, выполняющий логическое умножение, называется конъюнктор.
Специальных логических элементов для импликации и эквивалентности нет, т.к. А => В можно заменить на А V В ; А <=> В можно заменить на (A & B)V(A & B).
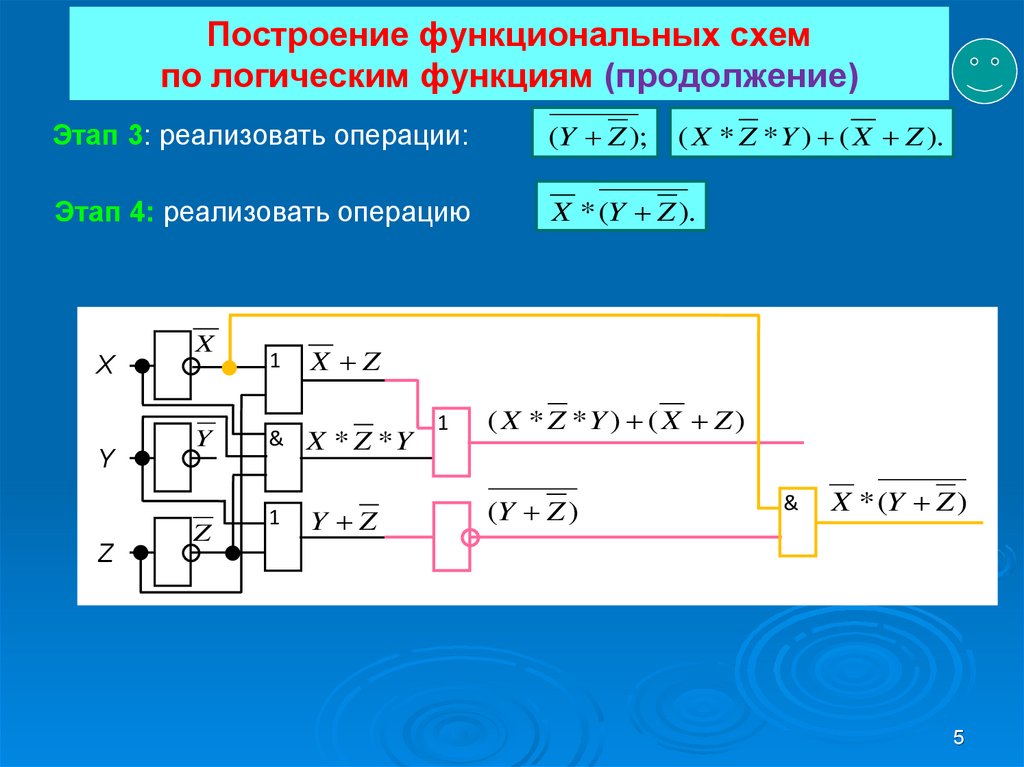
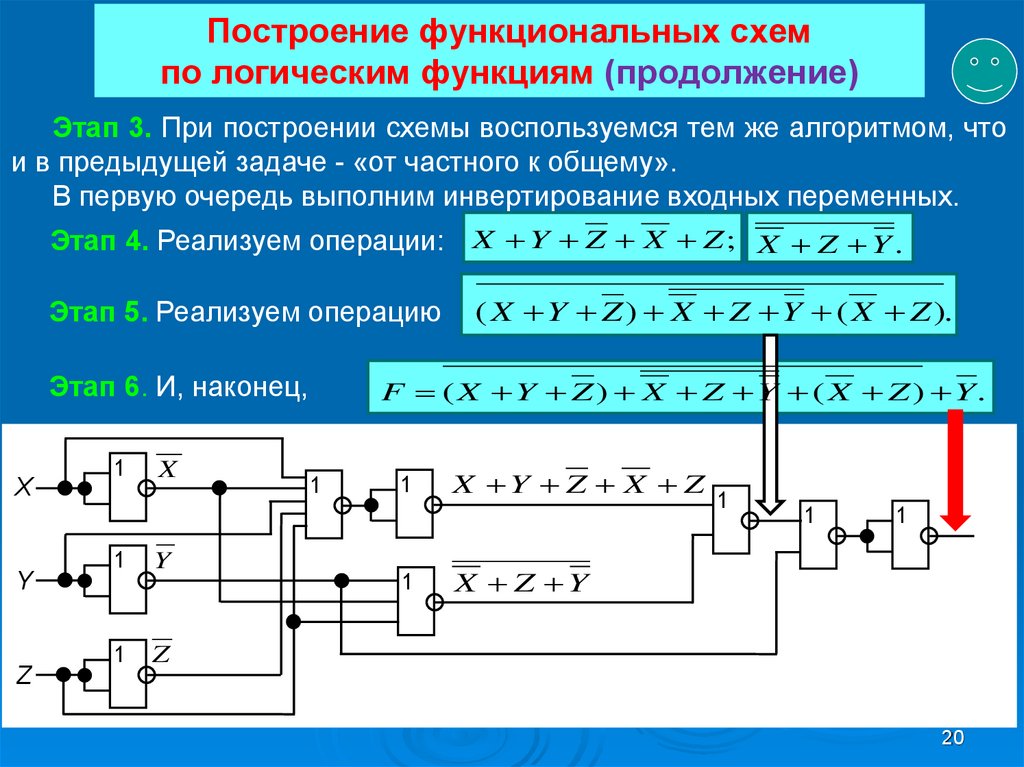
Другие логические элементы построены из этих трех простейших и выполняют более сложные логические преобразования информации. Сигнал, выработанный одним логическим элементом, можно подавать на вход другого элемента, это дает возможность образовывать цепочки из отдельных логических элементов.
Эта схема соответствует сложной логической функции F(A,B)= (А V В).
Попробуйте проследить изменения электрического сигнала в этой схеме. Например, какое значение электрического сигнала (0 или 1) будет на выходе, если на входе: А=1 и В=0.
Такие цепи из логических элементов называются логическими устройствами. Логические устройства же, соединяясь, в свою очередь образуют функциональные схемы (их еще называют структурными или логическими схемами). По заданной функциональной схеме можно определить логическую формулу, по которой эта схема работает, и наоборот.
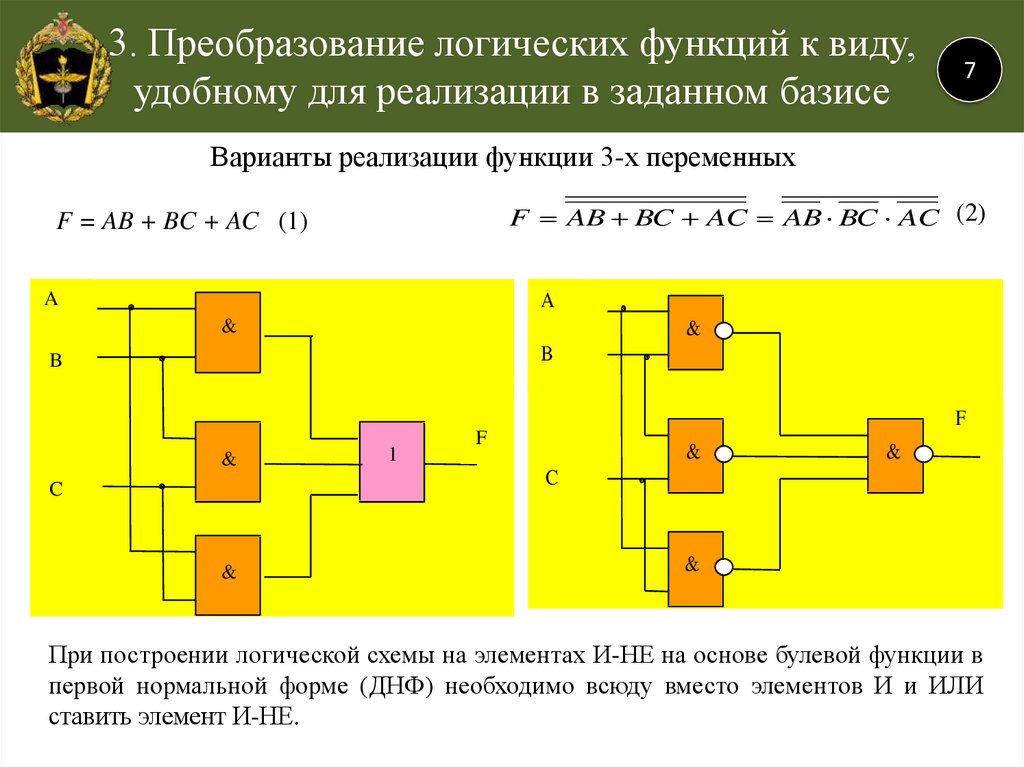
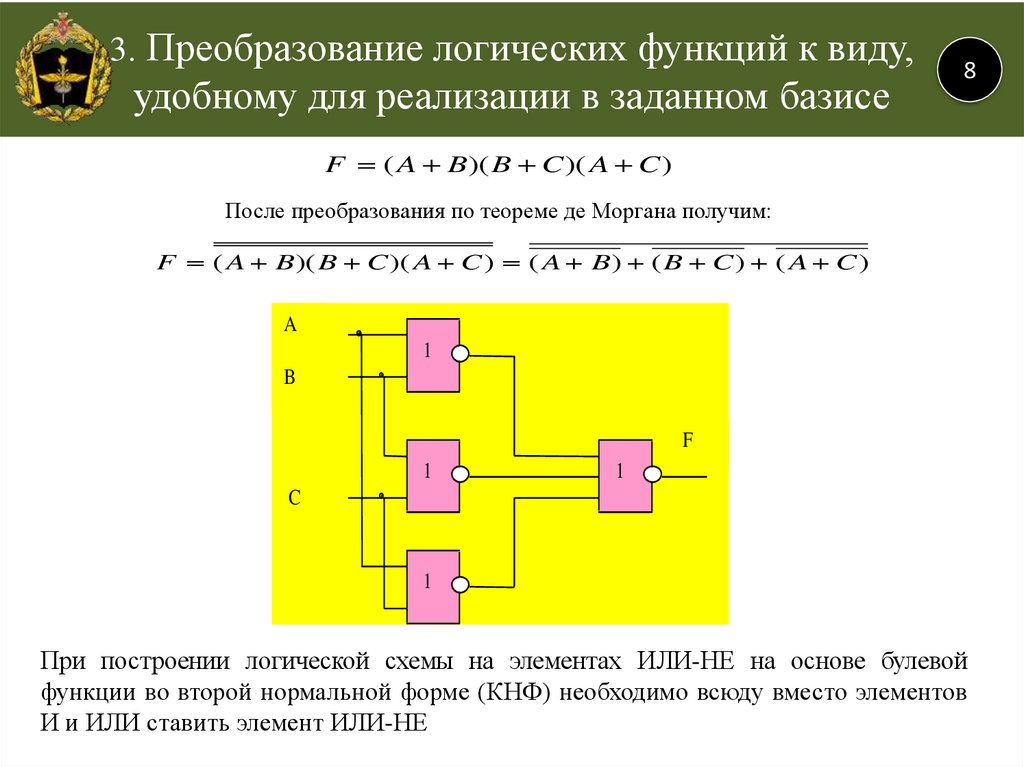
Пример 1. Логическая схема для функции будет выглядеть следующим образом:
Правила составления электронных логических схем по заданным таблицам истинности остаются такими же, как для контактных схем.
Пример 2. Составить логическую схему для тайного голосования трех персон A, B, C, условия которого определяются следующей таблицей истинности:
| A | ||||||||
| B | ||||||||
| C | ||||||||
| F |
Решение
По таблице построим СДНФ логической функции и упростим ее:
Правильность полученной формулы можно проверить, составив для нее таблицу истинности:
Значение полученной функции совпадает с исходным, что можно заметить, сравнивая таблицы.
Логическая схема полученной функции имеет вид:
Рассмотрим еще два логических элемента, которые играют роль базовых при создании более сложных элементов и схем.
Логический элемент И-НЕ состоит из конъюнктора и инвертора:
Выходная функция выражается формулой .
Логический элемент ИЛИ-НЕ состоит из дизъюнктора и инвертора:
Выходная функция выражается формулой .
я.
Вопросы для самоконтроля
1. Основные логические операции: конъюнкция, дизъюнкия (оба вида), отрицание, импликация, эквивалентность. Примеры логических выражений.
2. Таблица истинности. Примеры. A and not A; A or not A
3. Основные законы математической логики: перестановочное, сочетательное и распределительное
4. Законы де Моргана (закон отрицания).
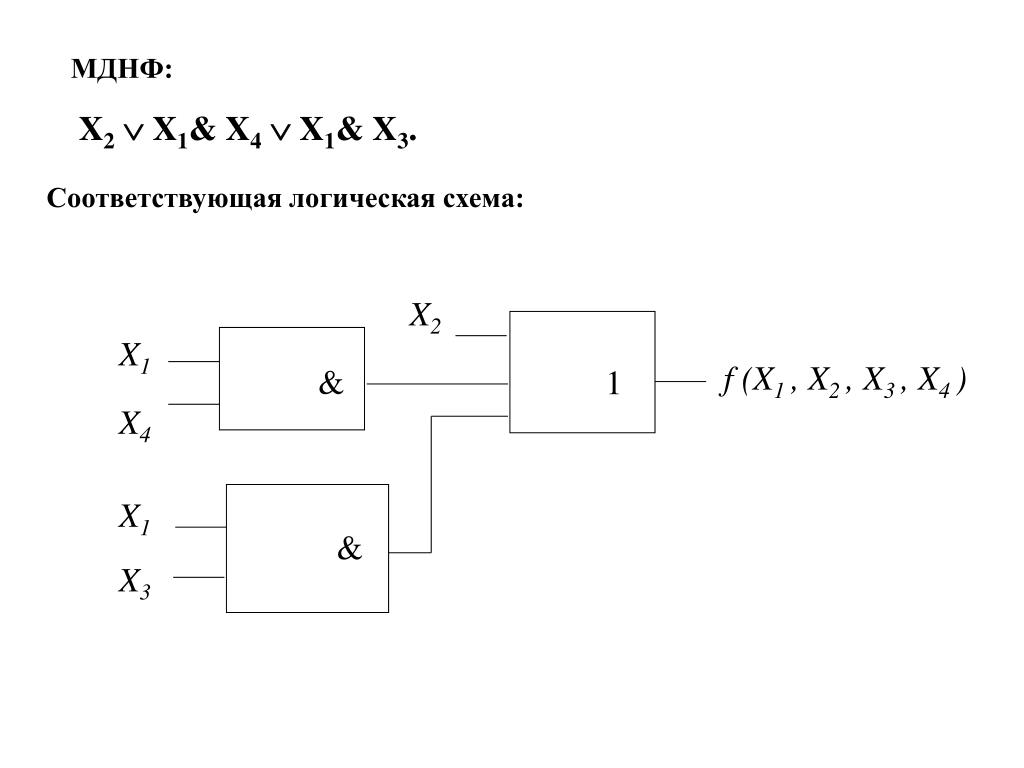
5. (Совершенная) дизъюнктивная нормальная форма. Пример
Лабораторная работа №2 (Вариант 9)
ФЕДЕРАЛЬНОЕ АГЕНСТВО СВЯЗИ
Ордена Трудового Красного Знамени
федеральное государственное бюджетное
образовательное учреждение высшего образования
«Московский Технический Университет Связи и Информатики» (МТУСИ)
Кафедра информатики
Дисциплина: МЛиТА
Лабораторная работа №2
«Логические схемы»
Выполнил:
Студент 2 курса
Факультета ЗОТФ
Группы БСТ-17хх
Иванов Иван
Вариант 09
Москва, 2018
Задание
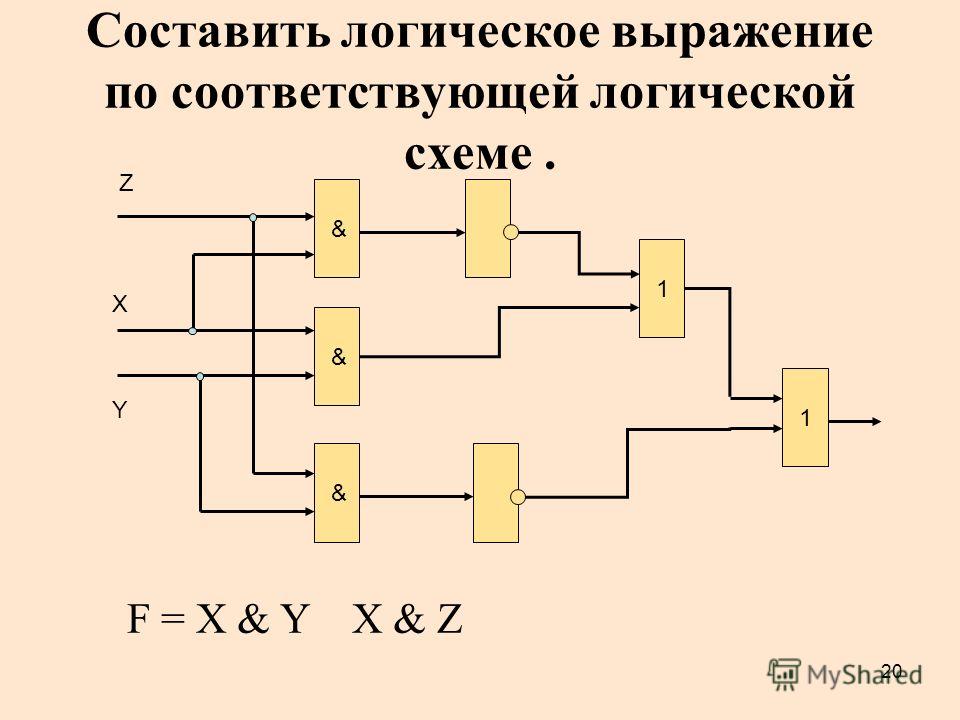
1. По логической схеме составить логическую
функцию
По логической схеме составить логическую
функцию
Ответ:
Задание 2. По логической схеме составить логическую функцию
Ответ:
Задание 3. По логической схеме составить логические функции
Ответ:
Задание 4. По логической схеме составить логическую функцию
Ответ:
Задание 5. По логической схеме составить логическую функцию
Ответ:
Задание 6. По логической схеме составить логическую функцию
Ответ:
Задание 7. По логической схеме составить логические функции
Ответ:
Задание 8. По логической схеме составить логическую функцию
Ответ:
Задача 9. Составить таблицу истинности логического выражения C
A | B | B&A | C | ||||
0 | 0 | 1 | 0 | 1 | 1 | 1 | |
0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
Задание
10. По логической функции составить
логическую схему
По логической функции составить
логическую схему
Задача 11. Построить логическую схему и таблицу истинности функции F(A,B)
A | B | A&B | F | |||
0 | 0 | 1 | 0 | 0 | 0 | 0 |
0 | 1 | 1 | 0 | 1 | 1 | 1 |
1 | 0 | 0 | 0 | 1 | 0 | 0 |
1 | 1 | 0 | 1 | 1 | 0 | 1 |
Задача
12.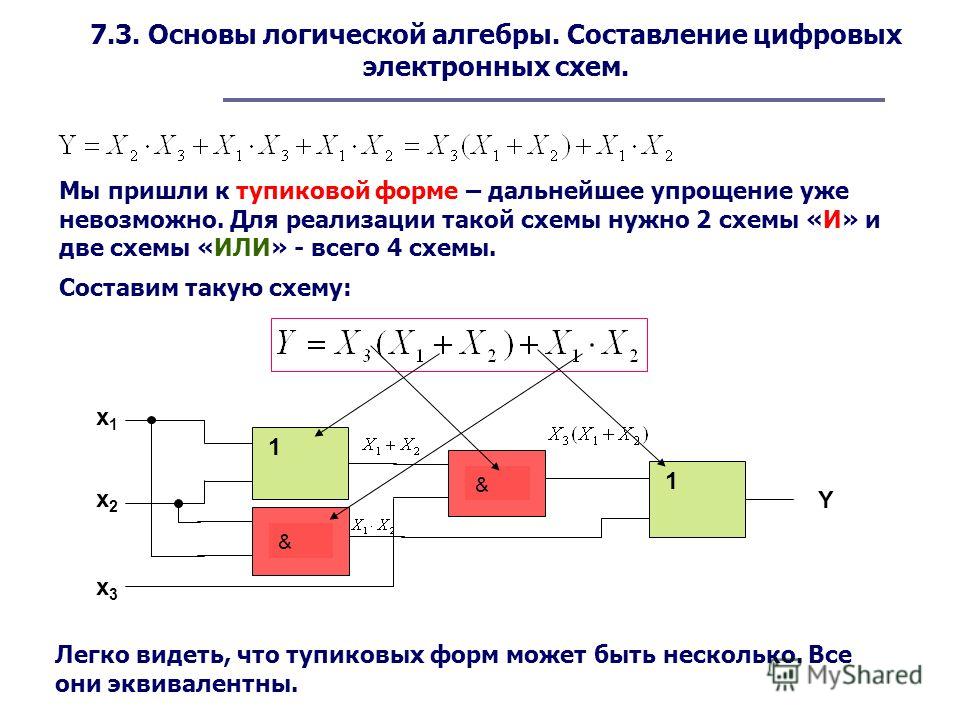 Построить логическую схему и таблицу
истинности функции F
Построить логическую схему и таблицу
истинности функции F
A | B | C | A&B | B&C | F | ||||
0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 |
1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
Логические функции — Tableau
Применяется к: Tableau Cloud, Tableau Desktop, Tableau Server
В этой статье представлены логические функции и их использование в Tableau. Он также демонстрирует, как создать логическое вычисление, используя пример.
Он также демонстрирует, как создать логическое вычисление, используя пример.
Зачем использовать логические вычисления
Логические вычисления позволяют определить, является ли определенное условие истинным или ложным (булева логика). Например, вы можете быстро узнать, были ли продажи в каждой стране, в которой вы распространяете свои товары, выше или ниже определенного порога.
Логический расчет может выглядеть примерно так:
СУММА(Продажи) > 1 000 000
Логические функции, доступные в Tableau:
Функция | Синтаксис | Описание |
| В | <выражение1> IN <выражение2> | Возвращает TRUE, если любое значение в Значения в Примеры: |
И | ЕСЛИ <выражение1> И <выражение2> ТО <затем> КОНЕЦ | Выполняет логическое соединение двух выражений. Пример: |
| КЕЙС | CASE <выражение> WHEN | Выполняет логические тесты и возвращает
соответствующие значения. Функция CASE оценивает CASE часто проще в использовании, чем IIF или IF THEN. ЕЩЕ. Обычно вы используете функцию ЕСЛИ для выполнения последовательности произвольных тестов,
и вы используете функцию CASE для поиска совпадения с выражением.
Но функцию CASE всегда можно переписать как функцию ЕСЛИ, хотя
функция CASE, как правило, будет более лаконичной. Много раз вы можете использовать группу, чтобы получить те же результаты, что и в сложном случае функция. Примеры: |
| ИНАЧЕ | IF | Проверяет ряд выражений, возвращающих значение Пример: |
| ЭЛЬСЕЙФ | IF | Проверяет ряд выражений, возвращающих значение Пример: |
| КОНЕЦ | IF | Проверяет ряд выражений, возвращающих значение Пример: |
| ЕСЛИ | IF | Проверяет ряд выражений, возвращающих значение Пример: |
| ЕСЛИ НУЛЬ | IFNULL(expr1, expr2) | Возвращает <выражение1>, если оно не равно нулю, в противном случае возвращает <выражение2>. Пример: |
| ИИФ | IIF(тест, затем, иначе, [неизвестно]) | Проверяет, выполнено ли условие, и возвращает одно значение, если оно TRUE, другое значение, если FALSE, и необязательное третье значение или NULL, если оно неизвестно. Пример: |
| ИСДАТА | ISDATE(строка) | Возвращает true, если заданная строка является допустимой датой. Пример: |
| НЕНУЛЬ | ISNULL (выражение) | Возвращает значение true, если выражение имеет значение NULL (не содержит допустимых данных). Пример: |
| МАКС | MAX(выражение) или Max(выражение1, выражение2) | Возвращает максимум одно выражение для всех записей или максимум два выражения для каждой записи. Пример: |
| МИН | МИН(выражение) или МИН(выражение1, выражение2) | Возвращает минимум выражения для всех записей или минимум двух выражений для каждой записи. Пример: |
| НЕ | ЕСЛИ НЕ <выражение> ТО <то> КОНЕЦ | Выполняет логическое отрицание выражения. Пример: |
| ИЛИ | ЕСЛИ <выражение1> ИЛИ <выражение2> ТО <тогда> КОНЕЦ | Выполняет логическое разъединение двух выражений. Пример: |
| ЗАТЕМ | IF | Проверяет ряд выражений, возвращающих значение Пример: |
| КОГДА | CASE | Находит первое Пример: |
| ЗН | ЗН(выражение) | Возвращает <выражение>, если оно не равно null, иначе возвращает ноль. Пример: |
Примечание . Некоторые из них на самом деле являются логическими операторами и отображаются черным, а не синим цветом. Дополнительные сведения см. в разделе Синтаксис оператора.
Создание логического вычисления
Следуйте инструкциям ниже, чтобы узнать, как создать логическое вычисление.
В Tableau Desktop подключитесь к сохраненному источнику данных Sample — Superstore , который поставляется с Tableau.
Перейти к рабочему листу.

Из области Data перетащите State на полку Rows.
На панели данных перетащите категорию на полку строк и поместите ее справа от состояния.
Из области Данные перетащите Продажи на полку Столбцы.
Выберите «Анализ» > «Создать вычисляемое поле».
В открывшемся редакторе расчетов выполните следующие действия:
Имя вычисляемого поля, KPI.
Введите следующую формулу:
СУММ([Прибыль]) > 0Это вычисление быстро проверяет, является ли член большим нуля.
 Если это так, он возвращает true; если нет, он возвращает ложь.
Если это так, он возвращает true; если нет, он возвращает ложь.Когда закончите, нажмите OK .
Новое вычисляемое поле появляется в разделе «Меры» на панели «Данные». Как и другие ваши поля, вы можете использовать его в одной или нескольких визуализациях.
На панели Данные перетащите KPI на Цвет на карточке Метки.
Теперь вы можете видеть, какие категории теряют деньги в каждом штате.
См. также
Визуализируйте ключевые индикаторы прогресса
Бесплатный видеоурок по логическим вычислениям
Функции в таблице
Табличные функции (по категориям)
Табличные функции (в алфавитном порядке)
Спасибо за отзыв!логических свойств и значений CSS — CSS: Каскадные таблицы стилей
Логические свойства и значения CSS — это модуль CSS, представляющий логические свойства и значения, которые обеспечивают возможность управления компоновкой с помощью логических, а не физических сопоставлений направлений и размеров.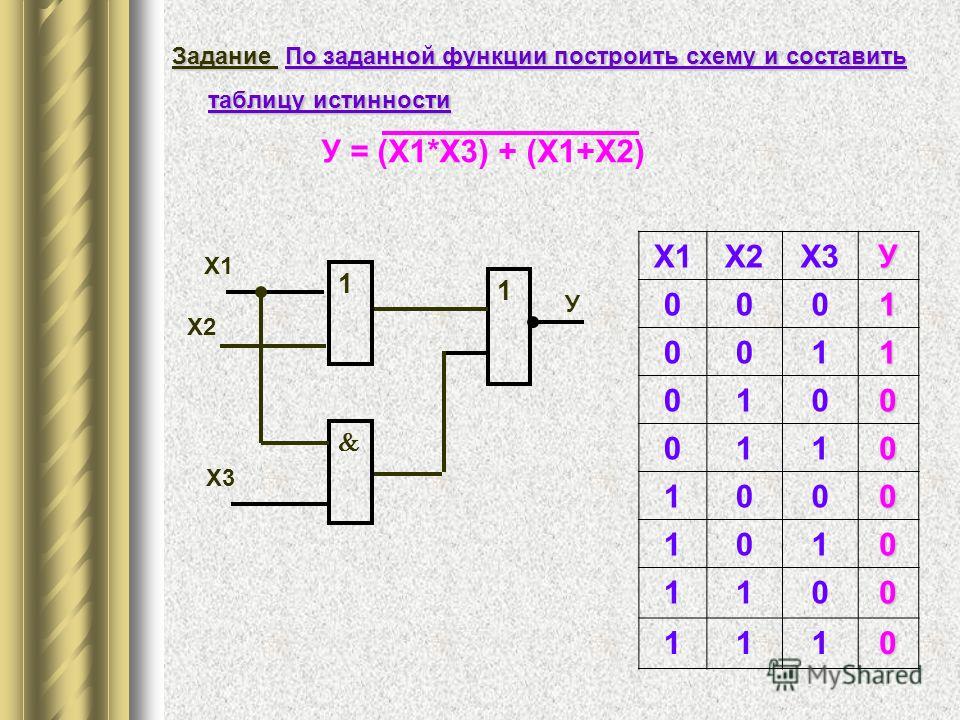
Модуль также определяет логические свойства и значения для свойств, ранее определенных в CSS 2.1. Логические свойства определяют относительные по направлению эквиваленты соответствующих им физических свойств.
Блочный и встроенный
Логические свойства и значения используют абстрактные термины блок и встроены в для описания направления, в котором они текут. Физический смысл этих терминов зависит от режима записи.
- Размер блока
Размер, перпендикулярный потоку текста в строке, т. е. вертикальный размер в режимах горизонтального письма и размер по горизонтали в режимах вертикального письма. Для стандартного английского текста это вертикальный размер.
- Внутренний размер
Размер, параллельный потоку текста внутри строки, т. е. размер по горизонтали в режимах горизонтального письма и размер по вертикали в режимах вертикального письма. Для стандартного английского текста это размер по горизонтали.

Свойства размеров
-
размер блока -
линейный размер -
максимальный размер блока -
максимальный встроенный размер -
мин. размер блока -
мин. встроенный размер
Свойства полей, границ и отступов
-
border-block -
цветной бордюр -
бордюр-блок-конец -
бордюр-блок-конечный цвет -
бордюрный блок-конец -
граница-блок-конец-ширина -
бордюр-блок-старт -
начальный цвет границы блока -
стартовый бордюрный блок -
начальная ширина граничного блока -
бордюрный блок -
ширина бордюрного блока -
цвет рамки -
бордюрный -
встроенный цвет границы -
граница-ряд-конец -
граница-инлайн-конечный цвет -
граница-инлайн-стиль конца -
граница-встроенная-конечная-ширина -
граница-инлайн-старт -
граница-встроенный-начальный цвет -
бордюр-инлайн-старт-стиль -
граница-встроенная-начальная-ширина -
встроенный бордюр -
встроенная ширина границы -
граница-начало-начало-радиус -
граница-начало-конец-радиус -
граница-конец-начало-радиус -
граница-конец-конец-радиус -
с каймой -
ширина границы -
поля(логическиеExpect behavior to change in the future."> Экспериментальный ключевое слово ) -
блок полей -
край-блок-конец -
старт блока полей -
встроенный в поля -
поле-встроенный-конец -
маржа-инлайн-старт -
заполнение(логическийЭкспериментальный ключевое слово ) -
набивочный блок -
конец подкладочного блока -
начальная прокладка -
встроенная прокладка -
внутренний конец -
дополнение-встроенное начало
Свойства для плавания и позиционирования
-
очистить(inline-endиinline-startключевые слова) -
float(inline-endиinline-startключевые слова) -
вставка -
вставной блок -
вставной блок-конец -
вставка-блок-старт -
врезной-врезной -
вставка-врезка-конец -
вставка-инлайн-старт
Свойства для ограничения размера
-
содержат-внутренний-размер-блока -
содержат встроенный встроенный размер
Другие свойства
-
заголовок-сторона(встроенный-конецивстроенный-началоключевые слова) -
блок перелива -
встроенный перелив -
overscroll-behavior-block -
overscroll-behavior-inline -
изменение размера(блокивстроенныеключевые слова) -
text-align(endиstartключевые слова)
Устаревшие свойства
-
offset-block-end


 .. ELSE <возврат по умолчанию> END
.. ELSE <возврат по умолчанию> END 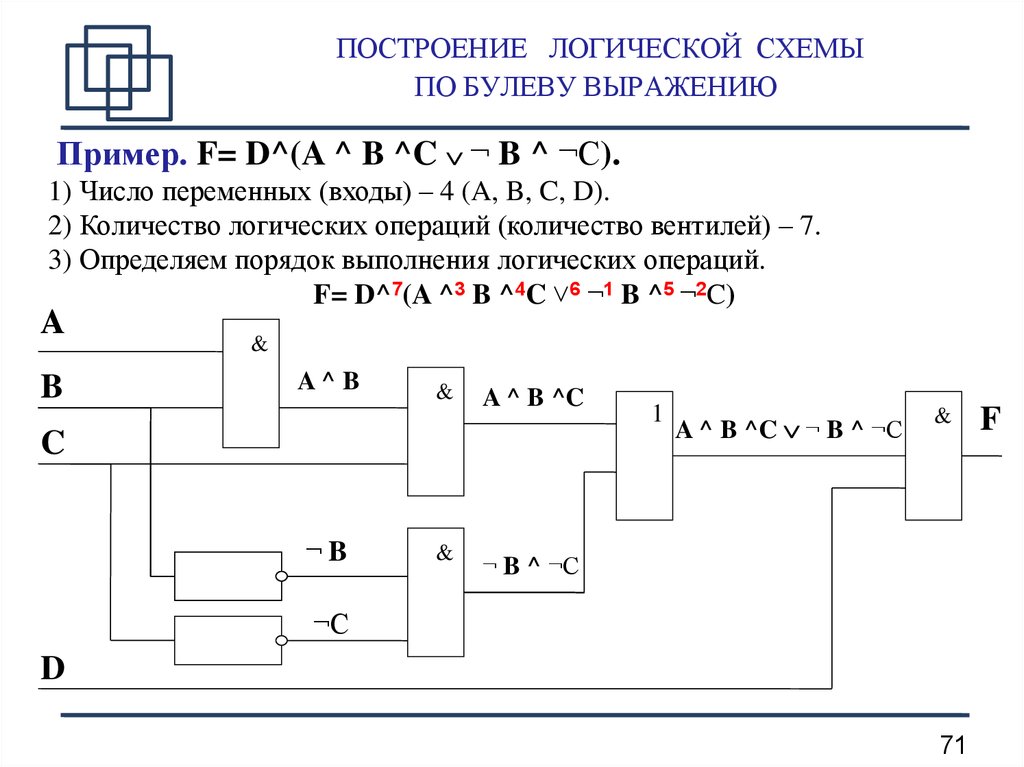
 ..] [ELSE
..] [ELSE 


 ..] [ELSE
..] [ELSE 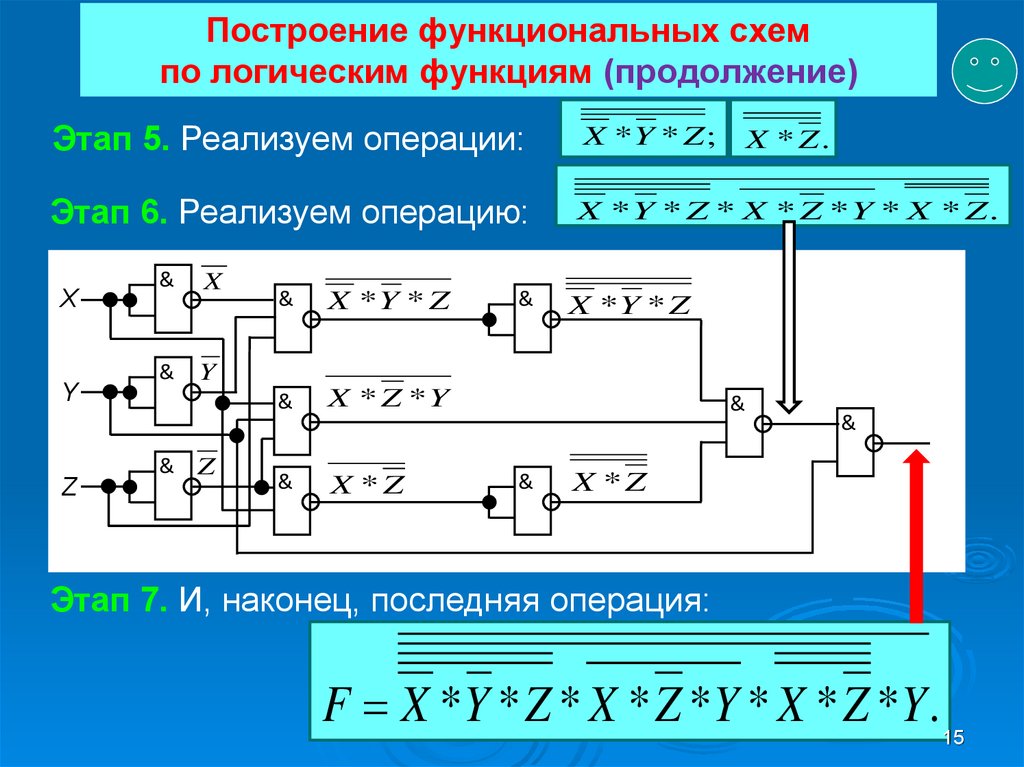

 Если это так, он возвращает true; если нет, он возвращает ложь.
Если это так, он возвращает true; если нет, он возвращает ложь.