Построение комбинационных схем

Определение 1

Построение комбинационных схем — это реализация схемы при помощи набора логических элементов на основе таблицы истинности.

Введение

Формирование выходного сигнала на основании обработки входных данных в любом компьютерном оборудовании выполняется формирователями или цифровыми автоматами двух типов:

1. Выполненными на основе комбинационных схем.
2. Выполненными на основе схем с памятью.

Комбинационными схемами называются схемы, у которых сигналы на выходе $Y = (у_1, у_2,…, у_m)$ в каждый дискретный временной промежуток единообразно задаются набором сигналов на входе $X = (x_1, х_2,…, х_n)$, поступивших в этот же временной момент t. Используемый в комбинационных схемах метод информационной обработки является комбинационным, так как итоги обработки имеют зависимость только лишь от комбинационного набора входных сигналов и они образуются сразу при появлении сигналов на входе. И это обстоятельство объясняет главное достоинство комбинационных схем, а именно высокое быстродействие. Информационные преобразования могут быть однозначно описаны функциями логики типа Y = f(X).

Готовые работы на аналогичную тему

Все виды логических функций и реализующие их комбинационные схемы делятся на регулярные и нерегулярные структуры. Регулярные структуры подразумевают формирование схем так, что все их выходы реализуются аналогично предыдущим. В нерегулярных структурах такой аналогии нет. В области практической реализации проектов компьютеров специалистами приобретён громадный опытный потенциал по синтезированию разнообразных схем. Большинство регулярных структурных построений заложено в основание реализации некоторых интегральных схем малой и средней интеграционной степени или функциональных составляющих больших и сверх больших интегральных схем. Самыми распространёнными комбинационными схемами являются шифраторы и дешифраторы, модули сравнения, комбинационные сумматоры и многие другие.

Дешифраторы

Дешифраторами являются комбинационные схемы, имеющие n входов и $т = 2^n$ выходов. Одиночный сигнал, сформированный на каком либо из m выходов, является однозначным соответствием комбинированного набора входных сигналов. К примеру, рассмотрим структуру дешифратора при n = 3, согласно таблице истинности, приведённой на рисунке ниже:

Рисунок 1. Таблица истинности. Автор24 — интернет-биржа студенческих работ

Дешифраторы повсеместно применяются в компьютерном оборудовании для того, чтобы выбрать информацию по заданному адресу, расшифровать код операции и так далее. Ниже приведены логические формулы данного дешифратора:

Рисунок 2. Логические формулы дешифратора. Автор24 — интернет-биржа студенческих работ

Данный дешифратор может быть реализован на основе логических элементов (И, НЕ), где кружки на выходе логических элементов обозначают логическое отрицание функций, которые реализуют элементы. Структурная схема дешифратора приведена на рисунке ниже и там же показано, как он отображается на принципиальной схеме электронной вычислительной машины:

Рисунок 3. Схема ЭВМ. Автор24 — интернет-биржа студенческих работ

Шифраторы осуществляют решение задачи, обратной дешифрации, то есть по нумерации сигнала на входе выполняется формирование однозначного комбинационного набора сигналов на выходе.

Сумматоры

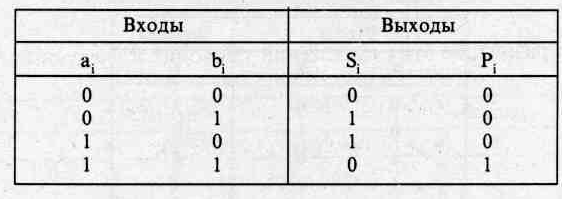
Комбинационные сумматоры тоже считаются часто применяемым в компьютерном оборудовании элементом. Структурная организация и принцип действия сумматора определяются законами бинарного сложения. Принцип работы многоразрядного сумматора базируется на правилах одноразрядного суммирования двоичных чисел. Рассмотрим пример сумматора, который выполняет суммирование двух одноразрядных чисел аi и bi при отсутствии переноса из предыдущих разрядов. То есть, это может быть, к примеру, суммирование младшего разряда в бинарном коде. Таблица истинности для такой операции суммирования, приведена ниже:

Рисунок 4. Таблица истинности. Автор24 — интернет-биржа студенческих работ

Логические формулы сумматора:

Рисунок 5. Логические формулы сумматора. Автор24 — интернет-биржа студенческих работ

Здесь $S_i$ является функцией суммы одного разряда, а $Р_i$ является функцией наличия переноса. Она принимает значение, равное единице, то есть присутствует перенос в следующий разряд, когда $a_i = 1$ и $b_i = 1$.

Схема такого полусумматора (а) и его обозначение в схеме компьютера (б) представлены на следующем рисунке:

Рисунок 6. Схема полусумматора. Автор24 — интернет-биржа студенческих работ

Формулы, заложенные в основание одноразрядных сумматоров, применяются и при реализации сумматоров, рассчитанных на большое количество разрядов. Отличие таблиц истинности одноразрядного сумматора (полусумматора) от таблицы истинности сумматоров, которые учитывают переносы, заключается в наличии дополнительного входа р, являющегося обозначением переноса из предыдущего разряда.

Схемы с памятью

Схемы с памятью считаются более сложными информационными преобразователями. Присутствие элемента памяти в схемной организации даёт возможность запоминания промежуточных состояний работы с сигналами и учёта их величин при последующих действиях. Формирование выходных сигналов $Y = (y_1,y_2,…,y_m)$ в таких схемных организациях осуществляется, помимо учёта набора входных сигналов $X = (х_1,х_2,…,х_п)$, ещё и с учётом набора состояний схем памяти $Q = (q_1,q_2,…,q_k)$. Для правильного учёта этого обстоятельства, вводится отличие текущего дискретного момента времени t и следующего временного момента (t+1). Обобщённая структурная организация схемы, имеющей внутреннюю память, представлена на рисунке ниже.

Рисунок 7. Обобщённая структурная организация схемы, имеющей внутреннюю память. Автор24 — интернет-биржа студенческих работ

Осуществление передачи величины Q между временными моментами t и (t+1) выполняется, как правило, с использованием памяти, имеющей две ступени, и специальных синхроимпульсов. Простейшим элементом памяти в компьютерном оборудовании являются триггерные схемы. В своё время эти компоненты заменили в электронных вычислительных машинах запоминающие элементы памяти, работающие на основе остаточной намагниченности ферритовых сердечников.

Рассмотрим пример построения элемента памяти на триггерной основе, который имеет два входа:

1. R (Reset, что означает сброс), предназначенный для сброса триггера в исходное состояние.
2. S (Set, что означает установка), предназначенный для перевода триггера в состояние запоминания единицы.

Если на триггер не поступают входные сигналы, то он обязан в том же состоянии до момента, пока не поступит сигнал на один из входов. На рисунке а) показана схема триггера, на рисунке б) обозначение на общих схемах и на рисунке в) диаграмма работы триггера.

Рисунок 8. Схемы и диаграмма. Автор24 — интернет-биржа студенческих работ

Проектирование комбинационных схем (стр. 1 из 2)

Тема реферата «Проектирование комбинационных схем».

Комбинационной схемой (КС) называется схема из логических (переключательных) элементов, реализующая булеву функцию или совокупность булевых функций. В общем случае КС можно представить схемой, приведенной на рис. 1, где х₁, х₂,….х_n — входы КС, f₁, f₂,…,f_m — ее выходы.

Рисунок. 1

Под логическим (переключательным) элементом чаще всего понимают техническое устройство, реализующее одну элементарную булеву функцию.

Прикладная теория цифровых автоматов не рассматривает физические явления, лежащие в основе разработки и функционирования логических элементов. Обычно логический элемент понимается как «черный ящик» и учитывается только реализуемая элементом булева функция. Примеры логических элементов ИЛИ — НЕ, И — НЕ, реализующих соответствующие булевые функции двух переменных, представлены на рис. 2.

Рисунок 2

Под глубиной (числом уровней) КС понимается максимальное число логических элементов, расположенных на пути следования сигнала от входов КС к ее выходу. Глубина КС оказывает существенное влияние на быстродействие КС, так как каждый логический элемент обладает внутренней задержкой распространения сигнала. Одно- и двухуровневые КС обладают максимальным быстродействием. Однако они не всегда могут быть использованы, поскольку число входов реальных логических элементов в интегральном исполнении ограничено.

Если КС реализует одну булеву функцию, то она называется одновыходовой КС (рис. 3). Если КС реализует совокупность булевых функций, то она называется многовыходовой КС.

Рисунок 3

Комбинационным схемам соответствуют схемы без обратных связей (под обратной связью понимается соединение выхода некоторого логического элемента со своим входом, возможно, через цепочку других логических элементов (рис. 4)).

Рисунок 4

Логические элементы, используемые для построения КС, характери-зуются определенными техническими парамет-рами, среди которых наиболее важные коэффи-циент объединения по входу І; коэффициент объединения по выходу U(коэффи- циент разветвления) и задержка сигнала ∆ τ в логическом элементе.

Система функций, реализуемая выбранной для синтеза схем совокупностью логических элементов, всегда должна быть функционально полной, т. е. допускать реализацию любой булевой функции на основе принципа суперпозиции. Если в качестве системы функций выбраны функции И, ИЛИ, НЕ, то считают, что реализован булев базис. Проектирование КС в булевом базисе наиболее просто, так как методы минимизации булевых функций в основном ориентированы на него. Поэтому, как правило, на первом этапе КС проектируется в булевом базисе с последующим переходом в заданный базис. Если выбраны функции И-НЕ или ИЛИ-НЕ, то считают, что реализуется универсальный или монофункциональный базис. Для удобства проектирования в различных системах элементов возможна реализация и смешанного базиса.

Конструктивно логические элементы объединяются в единые корпуса — интегральные микросхемы (ИМС). В общем случае, под интегральной микросхемой понимается микроэлектронное изделие, имеющее высокую плотность упаковки элементов и соединений между ними; при этом все элементы выполнены нераздельно и электрически соединены между собой таким образом, что с точки зрения спецификации, испытаний, поставки и эксплуатации изделие рассматривается как единое.

Число логических элементов, объединяемых в один корпус ИМС, характеризует степень интеграции логических элементов. Степень интеграции влияет на надежность, габаритные размеры, энергопотребляемость проектируемых КС. Различают ИМС малой, средней, большой и сверхбольшой степени интеграции.

В настоящее время используютоценки: до 100 000 вентилей — БИС, более 100000 вентилей—СБИС.

Коэффициент объединения І по входу логического элемента ИМС задает максимальное число логических элементов, выходы которых могут быть объединены на входе данного элемента.

Коэффициент объединения U по выходу (коэффициент разветвления) логического элемента ИМС задает максимальное число входов логических элементов, которые могут быть соединены с выходом данного логического элемента без нарушения режима его работы.

Если некоторый логический элемент КС оказался перегруженным по выходу (после окончания проектирования КС), то необходимо произвести эквивалентное преобразование структуры КС с целью его разгрузки. Это преобразование сводится либо к введению в КС специальных усилителей-формирователей, либо к дублированию данного логического элемента.

Задержка ∆ τ логического элемента характеризует промежуток времени между моментами установления сигналов на входах и выходах логического элемента. Распространение сигнала по КС в зависимости от задержек логических элементов, через которые он проходит, характеризует быстродействие КС. Прохождение сигналов по различным путям в КС вызывает появление различных задержек, что может послужить причиной неустойчивого функционирования КС.

Современные средства вычислительной техники собираются из ИМС, типовых как по физическим принципам функционирования, так и по выполняемым логическим функциям.

Основные требования к комплекту ИМС следующие:

1) ИМС комплекта должны обеспечивать возможность построения различных устройств и систем обработки цифровой информации;

2) число различных типов ИМС должно быть оптимальным, чтобы обеспечивалась простота эксплуатации сложных систем и взаимозаменяемость их частей;

3) в комплекте должны быть предусмотрены ИМС, которые не выполняют логических функций, а согласуют нагрузочные характеристики логических элементов и обеспечивают формирование электрических сигналов;

4) ИМС комплекта должны быть технологичными в изготовлении и удобными для проверки их электрических параметров;

5) комплект ИМС должен быть функционально полным;

6) комплект ИМС должен содержать специальные ИМС, предназначенные для построения управляющих цепей, запоминающих устройств, цепей связи запоминающих и логических устройств, согласования электромеханических устройств (реле, переключателей, механизмов перфорации и печати) и логических устройств, связи различных устройств с устройствами ввода-вывода информации, индикации информационных состояний и генерации высокостабильных тактовых сигналов.

В процессе реализации конкретных схем решаются задачи обеспечения необходимых характеристик надежности. В общем случае эти характеристики могут быть рассчитаны, исходя из надежностных характеристик элементов и конкретной схемы (это касается не только комбинационных схем). В тех случаях, когда расчетная надежность не удовлетворяет исходным требованиям, применяются специальные методы повышения надежности. Среди них наиболее интересными, с точки зрения теории цифровых автоматов, являются методы контроля работы схем с использованием помехоустойчивых кодов.

Таким образом, на этапе структурного синтеза решается задача построения комбинационной схемы, реализующей заданную совокупность булевых функций и удовлетворяющей заданным требованиям быстродействия и надежности.

2.Проектирование комбинационных схем в булевом и монофункциональном базисах

При проектировании КС на логических элементах И, ИЛИ, НЕ и отсутствии ограничений на число входов элементов пользуются изложенными ранее методами минимизации булевых функций. При наличии ограничений наиболее простым методом является применение специальных ИМС, называемых расширителями и имеющихся в комплектах ИМС. Расширители позволяют увеличить, в случае необходимости, число входов логического элемента путем включения дополнительного (точно такого же) логического элемента на один из входов основного.

а) б)

в) г)

Рисунок 5

Рассмотрим переход от реализации булевой функции в булевом базисе, т. е. на логических элементах И, ИЛИ, НЕ к схемам в монофункциональном базисе, т. е. реализованных на логических элементах ИЛИ — НЕ либо И — НЕ. Такие логические элементы широко используются в имеющихся на практике комплектах ИМС. Заметим, что если булева функция в базисе И, ИЛИ, НЕ реализована двухуровневой КС в соответствии с рис. 5, а. б, то переход к реализации в базисе И — НЕ либо ИЛИ—НЕ может быть осуществлен заменой всех элементов КС (рис. 5 а) на логические элементы ИЛИ—НЕ, и элементов КС (рис. 5.б) на логические элементы ИЛИ—НЕ с сохранением как переменных, поданных на входы элементов, так и связей между ними. Преобразованные КС представлены на рис. 5. в., г. В приведенных на рисунках схемах полагается, что на входы КС переменные поступают как с отрицанием, так и без отрицания, т. е. элемент НЕ на входах КС не учитывается.

Порядок проектирования комбинационных схем — Студопедия

При проектировании схем, выполняющих ту или иную логическую функцию, необходимо обеспечить минимизацию аппаратных затрат на реализацию этих схем, а также во многих случаях необходимо сократить номенклатуру используемых логических элементов. Последнее требование реализуется путем выбора соответствующей системы элементов. В настоящее время основные серии интегральных логических схем включают в себя элементы, составляющие некоторый функционально полный логический базис, а также дополнительные элементы, реализующие часто встречающиеся логические функции [ 1 ] . В качестве функционально полных базисов используются, как правило, одноэлементные базисы «И-НЕ» либо «ИЛИ-НЕ».

Рассмотрим этапы проектирования комбинационных логических схем на одноэлементном базисе «И-НЕ» без использования каких-либо дополнительных логических элементов на примере проектирования одноразрядного комбинационного сумматора. Такой сумматор является основой построения многоразрядной суммирующей схемы, выполняющей операции над числами, представленными в том или ином коде.

Пример выполнения операции суммирования чисел, представленных в обратном коде:

X^ок=0.1011

Y^ок=1.0110

₊0.1011

1.0110

₊1.0.0001

_______1

0.0010

Из примера видно, что в каждом разряде происходит суммирование соответствующих разрядов операндов и переноса, поступающего из предыдущего разряда (для младшего разряда – циклический перенос из знакового разряда). При этом вырабатывается значение суммы в этом разряде и перенос в следующий разряд.

Условно-графическое обозначение элемента, выполняющего эти действия, приведено на рис. 13.4.

Рис. 13.4.Условно-графическое обозначение одноразрядого сумматора

Рассмотрим основные этапы проектирования такой схемы.

Этап 1. Представление функции, выполняемой проектируемой схемой, в каноническом виде, то есть в виде таблицы истинности или одной из совершенных нормальных форм записи. Обычно на этом этапе функцию легче описать таблицей истинности. Так как проектируется двухвыходная логическая схема, то необходимо представить таблицу истинности для каждого ее выхода (табл. 13.6).

Таблица 13.6.
Входы	Выходы
Xi	Yi	Pi	Si	Pi+1

Этап 2. Минимизация логической функции. На этом этапе можно использовать любые методы минимизации [ 5 ] . Специфика минимизации многовыходных функций – необходимость получения устройства, имеющего минимальный общий состав оборудования, то есть следует проводить минимизацию одной функции с учетом возможного использования части полученного оборудования для минимизации другой функции. В нашем примере не будем рассматривать эту особенность и проведем автономную минимизацию каждой функции. Минимизацию логических функций можно проводить различными методами: методом Квайна, его модификацией – методом Квайна – Мак-Класки, методом диаграмм Вейча. Метод диаграмм Вейча удобно использовать для минимизации функций от небольшого (до четырех) числа переменных. Диаграмма Вейча для функции S

i представлена в табл. 13.7.

Таблица 13.7. Диаграмма Вейча для функции суммы одноразрядного сумматора
	yi	yi
xi
xi
	pi	pi	pi

Из диаграммы видно, что минимальная дизъюнктивная нормальная форма для функции суммы одноразрядного сумматора совпадает с ее совершенной дизъюнктивной нормальной формой:

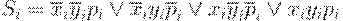
Диаграмма Вейча для функции P_i+1 представлена в табл. 13.8.

Таблица 13.8. Диаграмма Вейча для функции переноса одноразрядного сумматора
	yi	yi
xi
xi
	pi	pi	pi

Минимальная дизъюнктивная нормальная форма для этой функции имеет вид:

Этап 3. Перевод функции в базис, в котором будет строиться схема. В выбранном варианте это базис «Штрих Шеффера»:

Этап 4. Составление схемы на элементах, реализующих функции выбранного базиса. Для более наглядного отображения этого этапа выше обозначены номера элементов, которые будут реализовывать ту или иную часть функции. Полученные схемы представлены на рис.13.5 и 13.6.

Рис. 13.5.Схема, реализующая функцию суммы одноразрядного сумматора

Рис. 13.6.Схема, реализующая функцию переноса одноразрядного сумматора

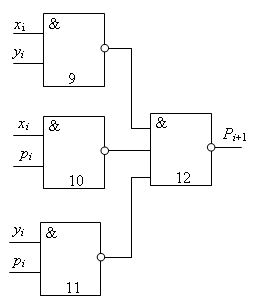
Значит так.
Таблица истиннности такая:

x1 x2 x3 y
0 0 0 1
0 0 1 1
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 0

теперь рисуем собственно диаграмму:

x2 x2 !x2 !x2
x1 1 0 1 0
!x1 0 0 1 1
!x3 x3 x3 !x3

То есть расставляем 1 туда, где они стоят в таблице истинности (! — не, то есть отрицание) Первая ячейка — x1 = 1, x2 = 1, x3 = 0. Подпись показывает, где какое значение переменной должно быть. Там, где ! — соответствующая переменная = 0, где его нет — 1.

Теперь строим функцию. Все 1 должны быть закрыты соответствующим произведением, причем 2, 4 или 8 рядом стоящих 1 можно объединять и закрыть одним произведением или даже одной переменной. Таблица не плоская, она свернута по длинной стороне, то есть 1-я колонка соприкасается с 4-й, однако в данном случае нас это не интересует — таких соприкосновений нет. Каждая 1 должна быть закрыта.

Пишем. Имеем 2 пары 1, стоящих рядом (строка 2 столбцы 3,4 и столбец 3) и 1 единица отдельно. Соответственно, имеем функцию:

y = x1^x2^!x3 V !x2^x3 V !x1^!x2, поскольку:
— отдельная единица зависит от всех переменных
— пара в столбце 3 не зависит от значения x1
— пара в строке 2 не зависит от значения x3

Если бы было 4 единицы рядом (строка или квадрат), они дали бы член, состоящий только из 1 переменной, поскольку не зависиле бы от 2 других.

Построение комбинационных схем на логических элементах. Технологии минимизации комбинационных схем. Использование диаграмм Вейча для минимизации фал.

Схемы, выходное состояние которых однозначно определяется только комбинацией входных сигналов, называют комбинационными. Закон функционирования КС определяется системой переключательных (логических) функций:

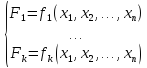
Синтез (построение) комбинационной схемы состоит в построении схемы на основе заданного закона ее функционирования в виде системы переключательных функций (ПФ) или таблиц истинности. При синтезе комбинационной схемы чаще всего необходимо построить схему с использованием минимального числа элементов в заданном элементном базисе, например, на элементах И-НЕ.

Комбинационные схемы строятся из элементарных логических элементов И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и других. Соединяют эти элементы так, как это следует из логической формулы, т.е. вход одного элемента, в котором часть аргументов обработана как указано в формуле, подключается ко входу другого, где выполняется дальнейшая обработка логической функции. В схеме не должно быть обратных связей, т.е. соединения выходов последующих схем со входами предыдущих.

Пример: Пусть дана логическая функция

Комбинационная схема представлена на рисунке.

Этапы синтеза:

1. Задание логической функции словесно, с помощью таблиц истинности или булевых выражений.

2. Минимизация логической функции с помощью алгебраического или графического метода (диаграммы Вейча, карты Карно).

3. Запись булевого выражения минимизированной переключательной функции.

4. Преобразование булевого выражения минимизированной ПФ для реализации её в заданном базисе И-НЕ или ИЛИ-НЕ.

5. Составление функциональной схемы, т.е. изображение нужных логических элементов и связей между ними.

Технологии минимизации. Минимизацией называют процедуру упрощения аналитического выражения, представляющего переключательную (логическую) функцию, направленную на то, чтобы булево выражение ПФ содержало минимальное количество членов с минимальным числом переменных. Способы минимизации: алгебраический; с помощью диаграмм Вейча (карт Карно).

Алгебраический способ минимизации ПФ — используя тождества и теоремы булевой алгебры.

Пример 1. Исходное булево выражение: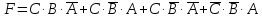

Применяя теорему склеивания 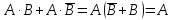, получим булево выражение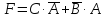, которое равносильно (эквивалентно) исходному, но значительно проще его.

Диаграммы Вейча построены так, что их соседние клетки содержат члены исходной ПФ, отличающиеся значением одной переменной: один член содержит эту переменную в прямой форме, а другой – в инверсной. Благодаря этому возникает наглядное представление о различных вариантах склеивания смежных членов.

Исходным продуктом для применения диаграмм Вейча является представление ПФ таблицей истинности, в которой возможные наборы переменных упорядочены по возрастанию или по убыванию их десятичных эквивалентов.

Вид диаграмм Вейча зависит от числа переменных минимизируемой ПФ — n и от того, как упорядочены наборы переменных в таблице. Если наборы упорядочены по возрастанию их десятичных эквивалентов, то диаграммы Вейча для n=2,3,4 имеют вид, приведенный на рисунке.

Число клеток диаграммы равно количеству наборов переменных: Nкл=Nнаб=2ⁿ.

Каждая клетка соответствует определенному набору переменных и имеет номер, одинаковый с номером набора.

Строки и столбцы диаграммы, помеченные чертой, определяют наборы, в которых переменные принимают единичные значения (входят в прямой форме). Строки и столбцы, не помеченные чертой, соответствуют наборам, в которых те же переменные принимают нулевые значения (входят в инверсной форме). В клетки записываются значения ПФ на соответствующем наборе (нулевое или единичное). Если на каком-то наборе функция не определена, то в клетке диаграммы ставится прочерк (или x).

ПФ считается неопределенной, если:

1) данный набор переменных в реальном логическом устройстве невозможен;

2) значение функции на данном наборе безразлично.

После заполнения диаграммы можно приступить непосредственно к минимизации, которую производят по единицам или нулям. В первом случае результатом минимизации будет булево выражение в ДНФ, а во втором – в КНФ.

Краткий алгоритм:

1. Функция, выраженная в СДНФ (СКНФ), записывается в диаграмму Вейча путём проставления единиц (нулей) в соответствующие координаты.

2. Производится объединение единиц (нулей), стоящих рядом, в так называемые m-кубы. Можно объединять единицы (нули), которые образуют правильный прямоугольник, содержащий 2, 4, 8, 16 единиц (нулей).

Замечание. Необходимо объединять максимально возможное количество смежных клеток, содержащих единицы (нули).

Замечание. Одна и та же единица (нуль) может охватываться несколько раз разными кубами.

Замечание. Верхняя и нижняя строки – смежные (можно объединить). Левый и правый столбцы – смежные. Угловые клетки – тоже смежные (диаграмму можно мысленно свернуть в тор).

Замечание. Перед выполнением минимизации в клетки, содержащие прочерки (где ПФ не определена), можно записать дополнительные единицы (нули), что способствует получению более простого конечного булевого выражения. При этом следует помнить, что хотя бы один раз необходимо объединить лишь основные единицы (нули). Дополнительные единицы (нули) могут увеличивать суммарное число единиц (нулей), входящих в куб, то есть уменьшать число переменных в результирующих конъюнкциях (дизъюнкциях).

3. Выписываются координаты получившихся m-кубов.

Объединённая дизъюнкция (конъюнкция) конъюнктивных (дизъюнктивных) координат всех m-кубов и есть минимальная форма.

Целью минимизации является получение минимальной ДНФ или КНФ, содержащей минимум членов с минимальным количеством входящих в них переменных.

Преобразование из базисов СДНФ и СКНФ в базис «Штрих Шеффера» и «Стрелка Пирса» (проверить, работает ли это как для Шеффера, так и для Пирса, сам алгоритм расписан вроде как только для Шеффера):

1. Проставляются скобки;

2. Все знаки конъюнкции и дизъюнкции заменяются на Штрих Шеффера.

Исключение: если вся функция состоит из одной импликанты, то она берётся с отрицанием.

Исключение: В состав функции входит импликанта из одной буквы – эта импликанта берётся с отрицанием.

7.3. Методы построения безопасных комбинационных схем

Методы синтеза безопасных схем зависят от свойств элементов схемы. С точки зрения надежности можно выделить два класса элементов: элементы с несимметричными отказами, у которых вероятность возникновения отказа одного вида (0→1 или 1→0) настолько мала, что ею можно пренебречь; элементы с симметричными отказами, у которых отказы обоих видов примерно равновероятны и ими нельзя пренебречь.

Примером элемента первого класса является замыкающий, фронтовой контакт железнодорожных реле типов НМШ и РЭЛ. У этих реле можно пренебречь вероятностью сваривания контакта (отказ типа 0→1). Несимметричность отказов достигается специальными мерами. В данном случае применены контактные материалы, которые практически не свариваются (графит – серебро). Примером элемента второго класса служит рассмотренный транзисторный логический элемент (см. рис. 7.6), у которого отказы «Обрыв» и «Короткое замыкание» равновероятны. Большинство логических элементов и реле общепромышленного назначения являются элементами с симметричными отказами. Элементы с несимметричными отказами создают специально для решения проблемы безопасности. В дальнейшем элементы, у которых вероятность отказов типа 0→1 мала, будем называть h₁—надежными.

В h₁-надежных схемах замена сигналов типа 0→1 на выходе не допускается, но возможна замена 1→0. Поэтому наиболее экономичные схемы могут быть получены с использованием h₁-надежных элементов, у которых нет отказов типа 0→1.

Рассмотрим правила построения h₁-надежных схем на h₁-надежных элементах. Пусть имеется произвольная схема S (рис. 7.9), содержащая h₁-надежные элементы Э1, Э2,…,Э_s, каждый из которых реализует некоторую ФАЛ f₁, f₂,…,f_s. Присвоим каждому элементу свой ранг. Первый ранг имеют элементы, соединенные только со входами схемы, ранг r – элементы, входы которых соединены с выходами элементов с рангом не выше, чем r–1. Первый ранг имеют элементы Э1 и Э2, второй – Э3, третий – Э4, четвертый – Э5 и т. д.

Рис. 7.9. Схема на h₁-надежных элементах

Теорема 7.1. Неизбыточная логическая схема S, построенная на h₁-надежных элементах, является h₁-надежной тогда и только тогда, когда все ее элементы ранга k ≥ 2 реализуют монотонные ФАЛ.

На рис. 7.10, а приведена схема на h₁-надежных элементах И, ИЛИ, НЕ, для которой не выполняется требование теоремы 7.1. В ней элемент 4, являющийся элементом третьего ранга, реализует немонотонную функцию (инверсию). Схема реализует функцию

. (7.4)

Рис. 7.10. Логические схемы, не удовлетворяющая (а) и удовлетворяющая (б) требованиям теоремы 7.1

Рассмотрим работу схемы на двоичном наборе х₁ = 1; х₂ = 0; х₃ = 0; f = 0. Пусть происходит отказ элемента 3 типа 1→0. Элемент 4 инвертирует вид отказа, т. е. на его входе будет происходить изменение сигнала 0→1. Это же изменение сигнала будет и на выходе схемы. Следовательно, схема не является h₁-надежной. Для выполнения требования теоремы 7.1, преобразуем формулу (7.4), применив правило де Моргана:

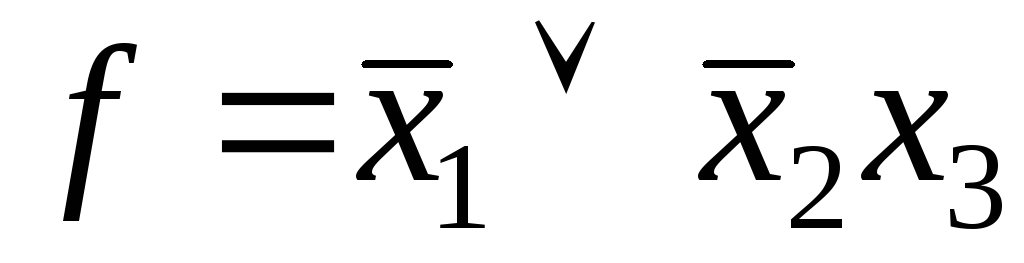. (7.5)

Формула (7.5) в отличие от формулы (7.4) имеет знаки отрицания только над переменными. Это означает, что в соответствующей ей схеме (рис. 7.10, б) элементы, реализующие немонотонную ФАЛ (инверсию), являются только элементами первого ранга. Если все инверторы подключены только к входам схемы, изменение сигнала 1→0, на какой-либо внутренней линии схемы не может перейти в изменение сигнала 0→1 и схема является h₁-надежной.

Теорема 7.1 накладывает весьма жесткие ограничения на способы построения h₁-надежных схем. В самом деле, единственными формами представления ФАЛ, у которых немонотонная операция (инверсия) применяется только к переменным функции, являются дизъюнктивная (ДНФ) и конъюнктивная (КНФ) нормальные формы, а также скобочные формы, полученные из них преобразованиями на основе сочетательного, переместительного и распределительного законов алгебры логики (такие скобочные формы будем обозначать СДНФ и СКНФ). Из этого факта и теоремы 7.1 следует теорема 7.2.

Теорема 7.2. Схемная реализация ФАЛ на h₁-надежных элементах является h₁-надежной тогда и только тогда, когда она осуществлена по одной из четырех форм представления функции: ДНФ, КНФ, СДНФ и СКНФ.

Учебный курс «Информатика»

Алгебра логики

Логические элементы

Построение комбинационных схем

Арифметико-логическое устройство

Моделирование памяти. Триггер

Вопросы и упражнения

    Комбинационные схемы строятся из элементарных логических элементов И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и др., нами не рассмотренных. Соединяют эти элементы так, как это следует из логической формулы, т.е. вход одного элемента, в котором часть аргументов обработана как указано в формуле, подключается ко входу другого, где выполняется дальнейшая обработка логической функции. В схеме не должно быть обратных связей, т.е. соединения выходов последующих схем со входами предыдущих.     Двигаясь от начала схемы, на входе каждого элемента записывается буквенное выражение входного сигнала. Входы подаются на условное обозначение логических элементов, на выходе которых записывается логическая формула начала обработки входных сигналов, а затем их выходы соединяются так, как указано в заданной логической функции, и на выходе всей комбинационной схемы записывается выражение выполненной логической функции.     Пример: Пусть дана логическая функция

    Требуется составить комбинационную схему.
    Прежде чем перейдём к рисованию схемы, полезно выяснить следующие вопросы:
    

Какие операции используются в логической функции?
    

Как заданные операции условно обозначаются?
    

Каков порядок выполнения операций?

    Ответив на все эти вопросы, не составит большого труда нарисовать комбинационную схему:

    Другой класс логических схем составляют схемы с внутренней памятью. Такие схемы называют последовательностными. Только анализируя логические схемы можно понять, как работает то или иное логическое устройство

3.2. Комбинационные схемы

Обработка входной информации X в выходную У (см. рис. 2.1) в любых схемах ЭВМ обеспечивается преобразователями или цифро­выми автоматами двух видов: комбинационными схемами и схемами с памятью.

Комбинационные схемы (КС) — это схемы, у которых выходные сигналы Y = (у₁, у₂,…, у_т) в любой момент дискретного времени од­нозначно определяются совокупностью входных сигналов X=(x_1, х₂,…, х_n), поступающих в тот же момент времени t. Реализуемый в КС способ обработки информации называется комбинационным по­тому, что результат обработки зависит только от комбинации вход­ных сигналов и формируется сразу же при поступлении входных сиг­налов. Поэтому одним из достоинств комбинационных схем является их высокое быстродействие. Преобразование информации однознач­но описывается логическими функциями вида Y = f(X).

Логические функции и соответствующие им комбинационные схе­мы подразделяют на регулярные и нерегулярные структуры. Регу­лярные структуры предполагают построение схемы таким образом, что каждый из ее выходов строится по аналогии с предыдущими. В нерегулярных структурах такая аналогия отсутствует. Примером построения нерегулярной структуры может служить разработка схе­мы в примере 2.16.

В практике проектирования ЭВМ накоплен огромный опыт по син­тезу различных схем. Многие регулярные структуры положены в ос­нову построения отдельных ИС малой и средней степени интеграции или отдельных функциональных частей БИС и СБИС. Из регуляр­ных комбинационных схем наиболее распространены дешифраторы,

шифраторы, схемы сравнения, комбинационные сумматоры, комму­таторы и др. •

Рассмотрим принципы построения подобных регулярных струк­тур.

Дешифраторы (ДШ) — это комбинационные схемы с п входами и т = 2ⁿ выходами. Единичный сигнал, формирующийся на одном из т выходов, однозначно соответствует комбинации входных сигна­лов. Например, разработка структуры ДШ для n=3 согласно мето­дике, изложенной в п. 2.4, позволяет получить таблицу истинности (табл. 3.1) и логические зависимости.

Таблица 3.1 Таблица истинности дешифратора

Дешифраторы широко используются в ЭВМ для выбора информа­ции по определенному адресу, для расшифровки кода операции и др. Логические зависимости дешифратора:

На рис. 3.2 представлены структурная схема ДШ, построенная в базисе (И, НЕ), и условное ее обозначение на принципиальных элект­рических схемах ЭВМ. Кружочки у линий, выходящих из логических элементов, указывают на инверсию функций, реализуемых элемен­тами.

Шифратор (ШР) решает задачу, обратную схемам ДШ, т. е. по номеру входного сигнала формирует однозначную комбинацию вы­ходных сигналов. Пример по-строения ШР иллюстрируется таблицей истинности (табл. 3.2) и схемами на рис. 3.3.

Рис. 3.2. Структурная схема дешифратора (а) и обозначение дешифратора на принципиальных электрических схемах (б)

Таблица 3.2 Таблица истинности шифратора

Логические зависимости шифратора:

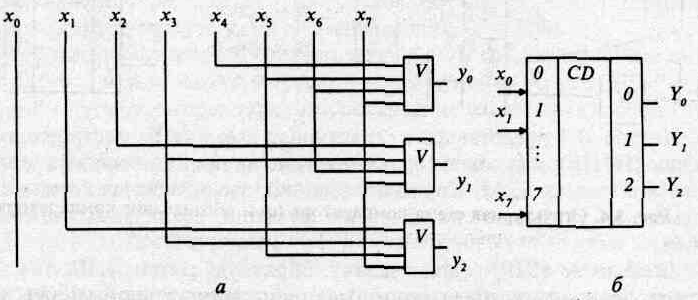
Рис. 3.3. Структурная схема шифратора (а) и обозначение шифратора на принципиальных электрических схемах (б)

Обратим внимание, что табл. 3.1 и 3.2 во многом похожи, входы и выходы в них поменялись местами. Состояния входов табл. 3.2 содер­жат только по одному единичному элементу. Другие произвольные комбинации входов недопустимы.

Схемы сравнения, или компаратор, обычно строятся как пораз­рядные. Они широко используются и автономно, и в составе более сложных схем, например при построении сумматоров.

Таблица истинности (табл. 3.3) отражает логику работы i-го раз­ряда схемы сравнения при сравнении двух векторов — А и В. На рис. 3.4 показана структурная схема компаратора.

Таблица 3.3 Таблица истинности компаратора

Логическая зависимость компаратора:

На схеме 3.4, помимо выхода Y₂, фиксирующего равенство значе­ний разрядов, показаны выходы Y_l и Y₃ соответствующие сигналам «больше» и «меньше».

Рис. 3.4. Структурная схема компаратора (а) и обозначение компаратора на принципиальных электрических схемах (б)

Комбинационный сумматор. Принципы построения и работы сум­матора вытекают из правил сложения двоичных цифр (см. п. 2.3). Схема сумматора также является регулярной и широко используется в ЭВМ. При сложении одноразрядных двоичных цифр можно выявить закономерности в построении и многоразрядных сумматоров.

Сначала рассмотрим сумматор, обеспечивающий сложение двух двоичных цифр а₁ и b₁ считая, что переносы из предыдущего разряда не поступают. Этой логике отвечает сложение младших разрядов дво­ичных чисел. Процесс сложения описывается таблицей истинности (табл. 3.4) и логическими зависимостями (3.2), где S_i — функция одно­разрядной суммы и Р_i — функция формирования переноса. Перенос формируется в том случае, когда а₁=1 и b_l=1.

Таблица 3.4 Таблица истинности комбинационного полусумматора

Логические зависимости:

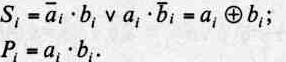
Зависимости (3.2) соответствуют логике работы самого младше­го разряда любого сумматора. Структурная схема одноразрядного сумматора (полусумматора) представлена на рис. 3.5.

Рис. 3.5. Структурная схема полусумматора (а) и обозначение полусумматора(б)

Логические зависимости полусумматора Si и компаратора (3.1) очень похожи, так как они инверсны по отношению друг к другу.

Уравнения, положенные в основу одноразрядного сумматора, ис­пользуются и при построении многоразрядных сумматоров. Логика работы каждого разряда сумматора описывается табл. 2.2, которую можно считать его таблицей истинности.

Таблица истинности сумматора, учитывающего сигналы перено­са, отличается от таблицы полусумматора (см. табл. 3.4) дополни­тельным входом р — переносом из предыдущих разрядов.

Исходные логические зависимости, формируемые по табл. 2.2, имеют следующие совершенные ДНФ:

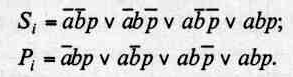
Преобразование этих выражений приводит к следующим зависи­мостям:

В приведенных выражениях индексы у переменных в правых час­тях уравнений опущены.

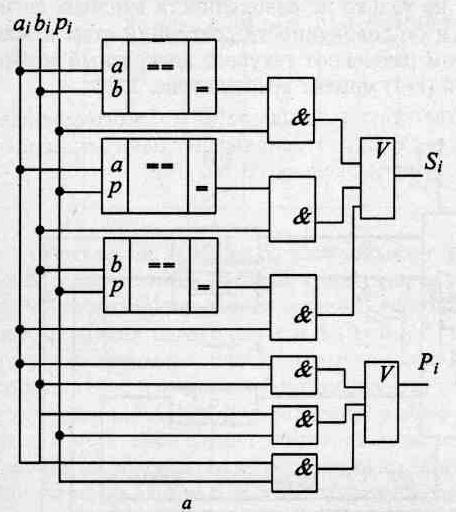
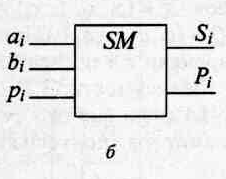
Рис. 3.6. Структурная схема одного разряда комбинационного сумматора: а — структурная схема одного разряда; 6 — условное изображение

Из анализа логических зависимостей видно, что структурная схе­ма i-го разряда сумматора требует включения в свой состав трех схем сравнения для формирования разрядной суммы и шести схем совпаде­ния (рис. 3.6).

Структурная схема многоразрядного комбинационного суммато­ра на электрических схемах изображена на рис. 3.7.

Рис. 3.7. Структурная схема многоразрядного комбинационного сумматора

DIGITAL BASIC — 1.4: Комбинационные схемы | Концепции СБИС

Введение

Цифровые схемы бывают двух типов:

• Комбинационные схемы (также известные как независимая от времени логика)
• Комбинационные цифровые схемы — это схемы, выход которых является функцией только текущего входа.
• Последовательные схемы
• Вывод зависит не только от текущего ввода, но и от истории ввода

Давайте обсудим эти схемы в формате сравнительной таблицы.

Нет памяти (блок памяти не требуется)	Есть память (требуется блок памяти)
Выход — функция текущего входа.	Выход является функцией текущего + предыдущего входов. Выход = ƒ (In, предыдущий In)
Для проектирования базовых вентилей (AND, OR, NOT) или универсальных вентилей (NAND, NOR) используются	Используются для создания конечных автоматов, базового строительного блока во всех цифровых схемах, а также схемах памяти и других устройствах.
Примеры комбинационных цифровых схем: полусумматор, полный сумматор, полувычитатель, полный вычитатель, преобразователь кода, декодер, мультиплексор, демультиплексор, кодировщик, ПЗУ и т. Д.	Примеры последовательных цифровых цепей: регистры, регистр сдвига, Счетчики пр.
Построение комбинационной логики обычно выполняется одним из двух методов: Сумма произведений (СОП) Произведение сумм (POS)	Построение последовательной логики обычно выполняется с использованием таблиц состояний.
Быстрее, потому что задержка между входом и выходом из-за задержки распространения только ворот	Медленнее, чем комбинационные схемы
	Проектировать сравнительно сложнее

Классификация комбинационных логических схем:

• Арифметические и логические функции
• Сумматоры
• Вытяжные устройства
• Сравнители
• PLD
• Передача данных
• Мультиплексоры
• Демультиплексоры
• Декодеры
• Энкодеры
• Преобразователи кода
• Двоичный преобразователь
• Преобразователь BCD
• 7-сегментный дисплей

Классификация последовательных цепей

• Синхронных цепей
• Асинхронные схемы

Синхронные последовательные цепи	Асинхронные последовательные цепи
Элементы памяти синхронизируются триггером	Элементы памяти либо разблокированы Триггеры, либо элементы временной задержки
Изменение входного сигнала может повлиять на элементы памяти при активации тактового сигнала.	Изменение входного сигнала может повлиять на элементы памяти в любой момент времени.
Максимальная рабочая скорость часов зависит от задействованной временной задержки.	Из-за отсутствия часов асинхронные схемы могут работать быстрее, чем синхронные схемы.
состояние устройства изменяется только в дискретные моменты времени в ответ на тактовый сигнал	схемы состояние устройства может измениться в любое время в ответ на изменение входов

Комбинационные схемы:

Давайте обсудим некоторые детали комбинационной схемы (например, блок-схему, принципиальную схему и таблицу истинности).Я не буду здесь подробно обсуждать принципиальную схему, потому что она очень проста. В некоторых случаях, если у вас возникла путаница, вы можете сослаться на любые книги по базовой электронике. Или вы можете использовать K-карту, чтобы выяснить уравнения, которые упоминаются либо на блок-схеме, либо на принципиальной схеме.

Важные моменты:

• Полусумматор можно преобразовать в Полувычитатель с помощью дополнительного инвертора.
• Полный сумматор может быть реализован с использованием двух полусумматоров и логического элемента ИЛИ.
• Полный вычитатель может быть реализован с использованием двух полувычитателей и логического элемента ИЛИ.
• Полный сумматор может быть преобразован в полный вычитатель с помощью дополнительного инвертора.
• Сумматор полный 2 типа
• Сумматор переноса пульсации.
• Сумматор Carry Look- Ahead
• Четырехбитный двоичный параллельный сумматор может быть построен с использованием
• 3 полных сумматора и 1 полусумматор или
• 4 полных сумматора с входным переносом для младшего разряда. Полный сумматор равен нулю.

4 Bit FA: Использование 4 полных сумматоров (бит переноса LSB FA = 0)

4-битный FA: 3 полных сумматора + 1 полусумматор

Важные моменты:

• Декодер
• Преобразует двоичную информацию из «n» входных строк в максимум 2 ⁿ уникальных выходных строк.
• Например. 2х4 строчный декодер (его еще называют одним четырехстрочным декодером)
• Активные декодеры с высокой выходной мощностью построены с логическим элементом И.
• Активные декодеры с низким выходом сконструированы с логическими элементами NAND.
• Декодер от 3 до 8 строк также называется двоично-восьмеричным декодером или преобразователем. Его также называют декодером 1 из 8, потому что одновременно активен только один из 8 выходов.
Декодеры
• широко используются в системе памяти компьютера, где они реагируют на ввод адресного кода от ЦП, чтобы активировать место хранения в памяти, указанное адресным кодом.

В следующей части комбинационных схем мы подробно обсудим мультиплексор с несколькими примерами.Причина в том, что я обсуждаю MUX отдельно, потому что у него есть несколько важных вещей, о которых обычно спрашивают в интервью. Также это очень важно с точки зрения проектирования СБИС. ,

Комбинационные схемы — Скачать PDF бесплатно

Транскрипция

1 Комбинационные схемы Комбинационные схемы без сохранения состояния Выходы являются функциями только входов Входы Комбинационная схема Выходы 3 Четверг, 2 сентября 3

2 Схема активатора (вид высокого уровня) Схема активатора имеет данные 2 входов (может быть несколько бит, но пока немного примеров) включить / отключить (т.е.е., вкл. / выкл.) Включить цепь: выход = данные, Включить цепь выключить: выход обнулен (например, выходной сигнал — все с) (включен) (отключен) Включить / выключить Включить / отключить DATA DATA DATA 4 Четверг, сентябрь 2, 3

3 Схема мультиплексора (высокий уровень) k Значения данных вводятся в качестве входных данных Селектор выбирает, какой из них выходит 2 ДАННЫЕ ДАННЫЕ ДАННЫЕ2 ДАННЫЕ2 ДАННЫЕ3 5 Четверг, 2 сентября 3

4 Схема декодера (общий вид) Нет Входы DATA 2 кбитовых выхода Вход селектора выбирает, какой выход =, все остальные выходы = 2 выхода out2 out3 6 Четверг, 2 сентября, 3

5 Построение больших схем: Иерархическое проектирование 3-4 AN MX B Big Circuit AB MX N ME EA 2 B 2 A 3 B 3 MX MX N 2 N 3 (a) Разработка небольших схем для использования в больших схемах A i Меньшие схемы B i MX N i NNN 2 N 3 ME E (b) (c) 28 Pearson Education, Inc.М. Моррис Мано и Чарльз Р. Кайм ОСНОВЫ ЛОГИЧЕСКОГО И КОМПЬЮТЕРНОГО ДИЗАЙНА, 4e 7 Четверг, 2 сентября 3

6 Обозначение: Эмуляция логического элемента с k-входом через 2 входа Каждый каскад в схеме сокращает количество вентилей на половину k входной вентиль, эмулируемый схемами логических элементов с 2 входами глубины log2 k Тот же процесс работает и для ИЛИ, И ИСКЛЮЧАЮЩЕЕ ИЛИ 8 Четверг, 2 сентября 3

7 Цепи активатора: бит Ввод данных A 3-5 Сокращенная таблица истинности (входные данные указаны в выходных данных). ) XA EN (a) F EN FA EN 28 Pearson Education, Inc.М. Моррис Мано и Чарльз Р. Кайм ОСНОВЫ ЛОГИКИ И ДИЗАЙНА КОМПЬЮТЕРА, 4e XA (b) Для обеих схем активатора, описанных выше, выход включается (F = X) только при подаче входного сигнала ENABLE (EN =). Обратите внимание на другой вывод при ОТКЛЮЧЕНИИ F EN FA 9 Четверг, 2 сентября 3

8 Схемы на основе декодера Преобразует n-битовый вход в m-битный выход, где n <= m <= 2 n ABC 3: 8 декодер Стандартный декодер : i th output =, all others =, где i - двоичное представление input () Четверг, 2 сентября, 3

9 Схемы на основе декодера Преобразует n-битовый вход в m-битовый выход, где n <= m <= 2 н е.g., = (i = 5) AB 3: 8 декодер C Стандартный декодер: i th output =, all others =, где i - двоичное представление input () четверг, 2 сентября 3

10 Decoder (: 2) Внутренний дизайн 3-7 ADDDAADA (a) (b) 28 Pearson Education, Inc. М. Моррис Мано и Чарльз Р. Кайм ОСНОВЫ ЛОГИКИ И КОМПЬЮТЕРНОГО ДИЗАЙНА, 4e 2 Четверг, 2 сентября 3

11 Декодер (2: 4) 3-8 AAADDD 2 D 3 ADAADAA (a) D 2 AA (b) D 3 AA Стандартный декодер: i-й вывод =, все остальные =, где i — двоичное представление ввода 28 Pearson Education, Inc.М. Моррис Мано и Чарльз Р. Кайм ОСНОВЫ ЛОГИЧЕСКОГО И КОМПЬЮТЕРНОГО ДИЗАЙНА, 4e 3 Четверг, 2 сентября 3

12 Иерархический дизайн декодера (декодер 2: 4) b: 2 декодер ‘bb’ b’a ‘ba a: 2 decoder ‘aa b’a ba Декодер 2: 4 Может построить декодер 2: 4 из двух: 2 декодера (и некоторые дополнительные схемы) 4 Четверг, 2 сентября, 3

13 Декодер (3: 8) Иерархическая структура: использование небольшие декодеры для создания больших входов декодера И 8 2-входные И ADDAD 2 Декодер 2-в-4 D 3 D 4 A Декодеры 2-в-2 D 5 D 6 D 7 Примечание. A2 выбирает, будет ли декодер строки до 4 активен в верхней половине (A2 =) или в нижней (A2 =) строке декодера от 3 до 8 28 Pearson Education, Inc.М. Моррис Мано и Чарльз Р. Кайм ОСНОВЫ ЛОГИЧЕСКОГО И КОМПЬЮТЕРНОГО ДИЗАЙНА, 4e 5 Четверг, 2 сентября 3

14 Энкодеры 6 Инверсия декодера: преобразует m-битовый вход в n-битный выход, где n <= m < = 2 n 28 Pearson Education, Inc. М. Моррис Мано и Чарльз Р. Кайм ОСНОВЫ ЛОГИКИ И КОМПЬЮТЕРНОГО ДИЗАЙНА, 4e T 3-7 ТАБЛИЦА 3-7 Таблица истинности для выходов восьмерично-двоичного кодировщика D 7 D 6 D 5 D 4 D 3 D 2 DDA 2 AA Четверг, 2 сентября 3

15 Декодеры и кодеры n {Decoder} 2 n значений BCD Однократное кодирование n {n Encoder} 2 Примечание: для кодировщиков — предполагается, что ввод один, остальные s 7 четверг, 2 сентября 3

16 Priority Encoder T 3-8 Предназначен для любой комбинации входов ТАБЛИЦА 3-8 Таблица истинности входов приоритетных выходов энкодера D 3 D 2 DDAAVXXXXXXXX 28 Pearson Education, Inc.М. Моррис Мано и Чарльз Р. Кайм ОСНОВЫ ЛОГИЧЕСКОГО И КОМПЬЮТЕРНОГО ДИЗАЙНА, 4e 8 Четверг, 2 сентября 3

17 Общее преобразование кода: схема, которая покрывает некоторые входы на выходы 3-3 afbegdc (a) Обозначение сегмента (b) Числовое обозначение для отображения 28 Pearson Education, Inc. М. Моррис Mano & Чарльз Р. KIME LOGIC и компьютерный дизайн Основ, 4e 9 четверг, 2 сентября, 3

18 Код преобразования Вход Выход afegdbc Va WXYZ abcdefgl XXXXXXXXXXXXXXXXXXXXX XXXXXXXXXXXXXXXXXXXXX XXXXXX 2 четверг, 2 сентября 3

19 fe Преобразование кода abgcd e.g., какие выходы загораются при входе V = 4? Input Output Va W X Y Z a b c d e f g l X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X X 2, четверг, 2 сентября 3

20 {Преобразование кода Input Output a f e b g c d f = Для каких значений загорается? {XXXXXX {Z = Y = {X = Va WXYZ abcdefgl XXXXXXXXXXXXXXXXXXXXXX XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX22 ) Z + XY W = {XXXXXX {X = {Z = WX f YZ 23 четверг, 2 сентября, 3

22 Мультиплексоры Комбинационная схема, которая выбирает двоичную информацию из одной из многих входных линий и направляет ее на одну выходную линию n 2 входа Биты выбора выхода n указывают (в двоичном формате), какой вход подается на выход 24 Четверг, 2 сентября 3

23 Пример мультиплексора II I2 I3 I 4 I5 I6 I7 I5 25 Четверг, 2 сентября 3

24 Мультиплексоры и демультиплексоры n {2 Mux 2 ^ n входов n {n-битное двоично-десятичное значение вывода axxxxxxxaxbxxxxxxbxxc xxxxxcxxxdxx xxdxxxxexxxexxxxxfxxf xxxxxxgxgxxxxxxxhh 26 четверг, 2 сентября 3

25 мультиплексоров и демультиплексоров, называемых управляющей логикой Mux Demux merge fork 27 четверг, 2 сентября 3

26 демультиплексоров Demux n} 2 n {входное n-битное значение BCD 2 ^ ndeeff 28 Четверг, 2 сентября, 3

27 Внутренняя организация мультиплексора 3-26 Логика выбора (выбирает, какой вход проходит) S Логика активатора декодера (принимает входы) S 4 2 И-ИЛИ S Декодер SIIY Или вентиль проходит через ненулевой Ii YI 2 Только ворота И проходят через ворота I 3 И ворота обнуляют невыбранные Ii 28 Pearson Education, Inc.М. Моррис Мано и Чарльз Р. Кайм ОСНОВЫ ЛОГИЧЕСКОГО И КОМПЬЮТЕРНОГО ДИЗАЙНА, 4e 29 Четверг, 2 сентября 3

28 Представление функций с помощью декодеров и мультиплексоров, например, F = AC + BC ABC minterm FA BC 3-to-8 Decoder 8 -to- MUX Decoder: ИЛИ minterms, для которых F должен оценивать до ABC MUX: Введите значение F для каждого minterm 3 Четверг, 2 сентября 3

29 Slick MUX trick Можно использовать меньший MUX с небольшим трюком e ,g., F = AC + BC Примечание для строк, парных ниже, A&B имеет одинаковые значения, C выполняет итерацию между & Для пары строк F либо равно ,, C, либо CABC minterm F}}}} F = F = CF = CF = C 4-to-MUX AB AB AB AB AB 3 Четверг, 2 сентября 3,

30 Уловка Slick MUX: пример, например, F = AC + BC + AC ABC minterm F}}} F = F = CF = C} F = CC 4-to- MUX AB AB AB AB AB 32 Четверг, 2 сентября 3

,

Комбинационные функции и схемы — Скачать PDF бесплатно

Комбинированный логический дизайн

Двухуровневая логика с использованием вентилей NAND

CSE140: Компоненты и методы проектирования цифровых систем Реализация двух- и многоуровневой логики Tajana Simunic Rosing 1 Двухуровневая логика с использованием вентилей NND Заменить вентили minterm ND вентилями NND Разместите

Дополнительная информация

БУЛЕВА АЛГЕБРА И ЛОГИЧЕСКИЕ ВОРОТА

БУЛЕВА АЛГЕБРА И ЛОГИЧЕСКИЕ ВОРОТА Логические вентили — это электронные схемы, которые можно использовать для реализации самых элементарных логических выражений, также известных как булевы выражения.Логический вентиль самый простой

Дополнительная информация

Sistemas Digitais I LESI — 2º ano

Sistemas Digitais I LESI — 2º ano Урок 6 — Практики комбинированного дизайна Проф. Жуан Мигель Фернандес ([email protected]), Информационный отдел UNIVERSIDADE DO MINHO ESCOLA DE ENGENHARIA — PLD (1) —

Дополнительная информация

КОМБИНАЦИОННЫЕ ЦЕПИ

КОМБИНАЦИОННЫЕ ЦЕПИ http: // www.tutorialspoint.com/computer_logical_organization/combinational_circuits.htm Авторские права tutorialspoint.com Комбинированная схема — это схема, в которой мы объединяем различные

Дополнительная информация

Элементарные логические ворота

Элементарные логические элементы Название Символ Инвертор (NOT Gate) ND Gate OR Таблица истинности ворот Логическое уравнение = = = = = + C. E. Комбинационная логическая схема Страуда (/ 6) Другие элементарные логические элементы NND Gate NOR Gate

Дополнительная информация

Комбинационные схемы

Комбинационные схемы Комбинационные схемы не имеют состояния Выходы являются функциями только входов Входы Комбинационная схема Выходы 3 Четверг, 2 сентября, 3 Схема включения (общий обзор)

Дополнительная информация

3.Базовые комбинации ворот

3. Базовые комбинации затворов 3.1 Затвор TTL NAND В логических схемах транзисторы играют роль переключателей. Для тех, кто находится в затворе TTL, проводящее состояние (включено) возникает, когда сигнал базового эмиттера высокий, и

Дополнительная информация

[4] Логические символы и таблица истинности

[4] Логика и таблица истинности 1. Как читать таблицу логики MIL-типа 1.1 показаны логические символы типа MIL, используемые для высокоскоростных ИС CMO. Эта логическая схема основана на MIL-TD-806. Тактовый инвертор и трансмиссия

Дополнительная информация

Реализация NAND и NOR

University of Wisconsin — Madison EE / omp ci 352 Основы цифровых систем harles R. Kime ection 2 Fall 200 hapter 2 Комбинационные логические схемы Часть 7 harles Kime & Thomas Kaminski Реализация NND и NOR

Дополнительная информация

Понимание логического дизайна

В приложении «Понимание логического дизайна» к вашему учебнику нет необходимой справочной информации.Этот документ дополняет его. Когда вы пишете add DD R0, R1, R2, вы представляете что-то вроде этого: R1

Дополнительная информация

ПРОЕКТИРОВАНИЕ ВОРОТНЫХ СЕТЕЙ

ПРОЕКТИРОВАНИЕ ШЛЮЗОВЫХ СЕТЕЙ ПРОЕКТИРОВАНИЕ ДВУХУРОВНЕВЫХ СЕТЕЙ: и / или и или / и СЕТИ МИНИМАЛЬНЫЕ ДВУХУРОВНЕВЫЕ СЕТИ ПРОЦЕДУРА МИНИМИЗАЦИИ КАРНАУГСКИХ КАРТ И ОГРАНИЧЕНИЯ ИНСТРУМЕНТОВ ДВУХУРОВНЕВЫХ СЕТЕЙ ПРОЕКТИРОВАНИЕ ДВУХУРОВНЯ

Дополнительная информация

6.БУЛЕВОЙ ЛОГИЧЕСКИЙ ДИЗАЙН

6. OOLEN LOGI DESIGN 89 Темы: oolean алгебра, переход между oolean алгеброй и логическими вентилями и релейной логикой. Примеры логики. Цели: уметь упростить дизайн с oolean algebra 6. ВВЕДЕНИЕ

Дополнительная информация

ОБНАРУЖЕНИЕ И ИСПРАВЛЕНИЕ ОШИБОК

Приложение к «Основам логики и компьютерного дизайна», 3-е издание 1 ОБНАРУЖЕНИЕ И ИСПРАВЛЕНИЕ ОШИБОК Предоставлены отдельные темы, не охваченные в третьем издании «Основ логики и компьютерного дизайна»

Дополнительная информация

Мультипликаторы.Введение

Множители Введение Множители играют важную роль в современной цифровой обработке сигналов и различных других приложениях. С развитием технологий многие исследователи пытались и пытаются

Дополнительная информация

Справочное руководство по логике

Руководство по выбору логики Расширенные микроустройства ВВЕДЕНИЕ В этом сборнике данных и руководстве по проектированию мы предполагали, что вы имеете хорошее практическое знание логики.К сожалению, всегда приходит время

Дополнительная информация

Глава 3 Основы цифровых технологий

Глава 3 Цифровые asics Мы завершаем наш обзор основных понятий обзором тем из цифровой электроники. Мы ограничиваем наше внимание аспектами, которые важны для понимания простого

Дополнительная информация

Счетчики и декодеры

Physics 3330 Эксперимент № 10 Осень 1999 г. Назначение счетчиков и декодеров В этом эксперименте вы спроектируете и сконструируете 4-битный сквозной десятичный счетчик с десятичным дисплеем.Такой счетчик

Дополнительная информация

Пример оформления: счетчики. Пример оформления: счетчики. 3-битный двоичный счетчик. 3-битный двоичный счетчик. Другие полезные счетчики:

Пример дизайна: ers er: последовательная схема, которая повторяет заданную последовательность выходных сигналов после тактовых импульсов. A, B, C, Z. G, O, T, E, R, P, S,! 7 ,,,,,,,. ,,,,,,,,,,,. Двоичный счетчик: следует за двоичным

Дополнительная информация

ДЕСЯТИЧНОЕ ЧИСЛО с двоичным кодом: B.CD.

ДЕСЯТИЧНОЕ ЧИСЛО С ДВОИЧНЫМ КОДОМ: B.C.D. ДРУГОЙ СПОСОБ ПРЕДСТАВЛЕНИЯ ДЕСЯТИЧНЫХ ЧИСЕЛ ПОЛЕЗНО, ПОТОМУ ЧТО ПРОЦЕСС МНОГИХ ЦИФРОВЫХ УСТРОЙСТВ + ОТОБРАЖЕНИЕ НОМЕРОВ В ДЕСЯТКАХ В BCD КАЖДЫЙ НОМЕР ОПРЕДЕЛЕН ДВОИЧНЫМ КОДОМ ИЗ 4 БИТОВ.

Дополнительная информация

(См. Время слайда: 00:01:16 мин)

Организация цифровых компьютеров Проф. П. К. Бисвас, Департамент электронной и электротехнической инженерии, Индийский технологический институт, Харагпур, Лекция No.# 04 Дизайн процессора: Tirning & Control

Дополнительная информация

Лабораторная работа 1: Исследование ворот и шлепанцев.

1.1 Цель лабораторной работы 1: Изучение вентилей и триггеров Ознакомиться с реализациями схем с использованием ИС и проверить поведение различных логических вентилей и триггеров. 1.2 Требования к оборудованию a. Оборудование —

Дополнительная информация

Ч А П Т Е Р.Логические схемы

К А П Т Е Р Логические схемы Многие важные функции естественным образом вычисляются с помощью прямолинейных программ, программ без циклов или ветвлений. Такие вычисления удобно описывать схемами

Дополнительная информация

Основы цифровых технологий

Основы цифровых технологий Десятое издание Глава 1 Флойда, 2009 г., Pearson Education, Upper 2008 Pearson Saddle River, Education NJ 07458.Все права защищены. Аналоговые величины. Наиболее естественные величины, которые мы видим.

. Дополнительная информация

Организация и работа ЦП

Организация и работа CPU Цикл Fetch-Execute Работа CPU 1 обычно описывается в терминах цикла Fetch-Execute. 2 Fetch-Execute Cycle Получить инструкцию Увеличить программу

Дополнительная информация

(1) / 30 (2) / 30 (3) / 40 ИТОГО / 100

Ваше имя: Номер SI: УНИВЕРСИТЕТ КАЛИФОРНИИ В БЕРКЛИ БЕРКЛИ АВИС ИРВИН ЛОС-АНДЖЕЛЕС РИВЕРСИ САН ИЕГО САН-ФРАНЦИСКО Кафедра электротехники и компьютерных наук САНТА-БАРБАРА САНТА

Дополнительная информация

Модуль 3: Флойд, Основы цифровых технологий.

Модуль 3: Лектор: Юншэн Гао Комната: Технология — 3.25 Электронная почта: [email protected] Структура: 6 лекций 1 Учебная оценка: 1 Лаборатория (5%) 1 Тест (20%) Учебник: Floyd, Digital Fundamental

Дополнительная информация

Основы цифровых технологий

Основы цифровых технологий Десятое издание Флойд глава 8 2009 г. Pearson Education, Upper 2008 Pearson Saddle River, Education NJ 07458. Все права защищены. Подсчет в двоичном формате Как вы знаете, последовательность двоичного счета

Дополнительная информация

ГЛАВА 16 ЦЕПИ ПАМЯТИ

ГЛАВА 6 ЦЕПИ ПАМЯТИ Краткое содержание главы 6.Чипы и триггеры 6. Память полупроводников: типы и архитектура 6.3 Ячейки RM с произвольным доступом 6.4 Сенсорные усилители и декодеры адреса 6.5 Только для чтения

Дополнительная информация ,

Разница между комбинационными и последовательными схемами со сравнительной таблицей

Когда доходит до понимания основных концепций цифровой электроники, то комбинационные и последовательные схемы — это две концепции, которые необходимо понимать целиком.

Комбинированные и последовательные схемы

Таблица сравнения

Основание разницы	Комбинированные логические схемы	Схемы последовательной логики
Выход	Выход представляет собой функции токовых входов или логику, не зависящую от времени.	Выходные данные представлены в виде функций, относящихся к часам, текущим входам, а также предыдущим состояниям данной системы.
Хранение данных и распределение места в памяти	Комбинационные схемы не могут хранить данные (состояние). Они не содержат никаких элементов памяти.	Последовательные схемы имеют пространство памяти, необходимое для хранения текущих состояний, отправленных в качестве управляющих входов (разрешения) для следующего набора операций.Они содержат элементы памяти, которые хранят данные в цифровых схемах.
Требование обратной связи	Они не нуждаются в вводе. Комбинационные схемы обычно выводят вход в соответствии с разработанной логикой.	Этим схемам требуется обратная связь от выхода, чтобы сохранить входные данные в области памяти для следующего набора операций.
Основное использование	В основном используется для логических и арифметических операций.Схемы представлены с помощью булевой алгебры; они дополнительно упрощаются за счет использования фундаментальных и универсальных логических вентилей.	Используется для хранения данных и поэтому используется в оперативной памяти.
Элементарные строительные блоки	Основными строительными блоками комбинационных схем являются логические вентили.	Элементарными строительными единицами последовательных логических схем являются триггеры (двоичные запоминающие устройства).
Зависимость от часов	Комбинационные схемы не зависят от часов; следовательно, запуск не важен для их работы.	Последовательные логические схемы синхронизируются, и поэтому они запускаются для работы с помощью электронных импульсов. Триггеры, если они срабатывают, называются синхронными последовательными цепями. Цепи, которые не запускаются, называются асинхронными последовательными цепями.
Пример схем	Сумматор [1 + 0 = 1; зависимость только от текущих входов, т.е. 1 и 0].	Счетчик [Предыдущий O / P + 1 = Текущий O / P; зависимость от текущих входных данных и предыдущего состояния информации.]
Приложение	Эти схемы используются вместе с кодировщиками, сумматорами, декодерами, вычитателями, мультиплексорами и т. Д.	Последовательные схемы используются в случае триггеров и защелок.В этих схемах защелки считаются простейшими элементами, используемыми для сохранения более раннего состояния. Защелки также известны как шлепки.
Определение	Комбинационная логическая схема — это цифровая логическая схема, в которой выход может быть определен с помощью логических функций, связанных с входами текущего состояния.	Последовательная логическая схема — это цифровая логическая схема, в которой выход может быть определен с использованием логической функции, относящейся к входам текущего состояния, а также входам предыдущего состояния.
Хранение состояния в цепи	Комбинационные схемы не могут сохранять в себе какое-либо состояние.	Последовательные цепи способны сохранять свое более раннее состояние на основе текущих входов, а также предыдущих состояний.

Комбинированная схема

Комбинационные логические схемы, называемые независимой от времени логикой, которые связаны с набором различных вентилей, которые генерируют выход текущих входов, принадлежащих этому моменту.Основными строительными единицами комбинационных схем являются И, ИЛИ, НЕ, а универсальными вентилями являются И-И и И-И-И.

В большинстве случаев в схемах комбинационной логики выходные линии следуют за линиями тока. Эти схемы реализуются через логические схемы, в которых выход является чистой функцией только текущих входов. Декодер — типичный пример комбинационной схемы; он используется для преобразования данных двоичного кода в данные десятичного кода.

В случае схем комбинационной логики генерируемый выход в любой момент времени зависит от токовых входов в любой конкретный момент.Есть три типа комбинационных логических схем — передача данных, арифметические и логические функции и преобразователи кода. Примерами схем передачи данных являются мультиплексоры, кодеры, демультиплексоры, декодеры и т. Д. Сумматоры, компараторы, PLD, вычитатели и т. Д. Являются экземплярами арифметических и логических схем. Примерами схем преобразователя кода являются двоично-десятичный код, семь сегментов и т. Д. В общем случае комбинированные схемы содержат m двоичных выходов и n двоичных входов. Они полезны для реализации всех важнейших функций цифровых компьютеров.

Характеристики комбинационных схем

• Графические символы: Они изображают связанную схему логических вентилей.
• Логические уравнения: В этих уравнениях выходные сигналы изображены как булевы функции различных входных сигналов.
• Таблица истинности: Эта таблица дает «двоичные выходные сигналы, необходимые для набора 2-х входных сигналов.
• Эти не зависящие от времени схемы легко спроектировать, они быстрые и независимые от предыдущих входов для генерации выходных данных.

Последовательный контур

Последовательные логические схемы — это особая категория схем, в которых выход зависит как от значения текущих входов, так и от последовательности прошлых выходов. В последовательных схемах выходной сигнал изменяется в соответствии с серией вставленных данных. Другими словами, последовательные логические схемы содержат пространство памяти для хранения немедленных результатов. Например, последовательные схемы хранят запись того, был ли логический уровень 0 или 1 подключен к данному входу; тот же факт применяется к полученным таким образом выходным данным.Устройства памяти обычно состоят из простых логических элементов ИЛИ.

Последовательные схемы реализуются с помощью различных устройств, таких как защелки, триггеры, регистры и т. Д. Входы, требуемые последовательными логическими схемами, меняются из одного из двух состояний по мере необходимости. Есть два типа последовательных схем — асинхронные и синхронные. Последовательная логическая схема помечается как одновременная, когда внутреннее состояние устройства изменяется в определенное время и управляется часами.Схемы последовательной логики спроектированы так, чтобы их было сложно обрабатывать по сравнению с комбинационными схемами. Эти зависящие от времени медленные схемы нуждаются в пути обратной связи, который существует между их входами и выходами. Последовательные схемы в основном используются для хранения данных и способны сохранять любое состояние или сохранять свое предыдущее состояние. Эти схемы требуют запуска, поскольку они зависят от часов.

Ключевые различия между последовательными и комбинационными схемами

• Комбинационным схемам требуются новейшие входы для генерации выходных данных.С другой стороны, входы, относящиеся к последовательным цепям, принимают решение о производстве (предоставленных входов) после рассмотрения всех предыдущих выходных данных вместе с текущими входами.
• Комбинационная схема неспособна хранить данные, тогда как последовательные схемы способны хранить заданный объем данных в областях памяти, выделенных для этой цели. Напротив, примеры комбинационных схем включают сумматоры, вычитатели, декодеры, кодеры и т. Д. Модели последовательных схем лучше всего определять как триггеры, защелки и регистры.
• Часы не используются в случае комбинационных схем, тогда как последовательные схемы имеют часы для запуска своих функций.
• В то время как комбинационная схема не нуждается в какой-либо обратной связи для своего функционирования, последовательные схемы требуют того же всегда.

Заключение

Короче говоря, цифровые устройства, состоящие из комбинационных схем, не нуждаются в предварительном выводе для их успешной работы. В случае последовательных логических схем для получения точных результатов требуются как предыдущий выход, так и текущие входы.Мы хотели бы получить известие от вас, если у вас есть дополнительные входы для комбинационных схем по сравнению с последовательными схемами. Напишите нам в разделе комментариев ниже. Мы будем ждать ответа от вас.

,