2.13.2. Одноразрядный сумматор

Сумматоры выполняют арифметическое сложение чисел, которое производится начиная с младших разрядов чисел. В каждом разряде сумматора выполняются одинаковые действия, т. е. суммируются две двоичные цифры в со­ответствии с правилами сложе­ния двоичных цифр.

При сложении двух единиц возникает единица переноса в старший разряд, которую нужно учесть при сложении цифр следующего разряда. Поэтому в каждом разряде сумматора необходимо предусмотреть возможность суммирования трех цифр: двух цифр слагаемых и единицы переноса из младшего разряда. В свою очередь, в каждом разряде необходимо сформировать не только значение одного разряда суммы, но и значение единицы переноса в соседний старший разряд. Таким образом, сумматор для сложения многоразрядных чисел можно построить из одинаковых схем, каждая из которых выполняет сложение двух цифр слагаемых и переноса из младшего разряда. Такая схема называется одноразрядным сумматором. Одноразрядный сумматор представляет собой комбинационную схему с тремя входами и двумя выходами, логика работы которой соответствует следующей таблице истинности (табл.

2.13).

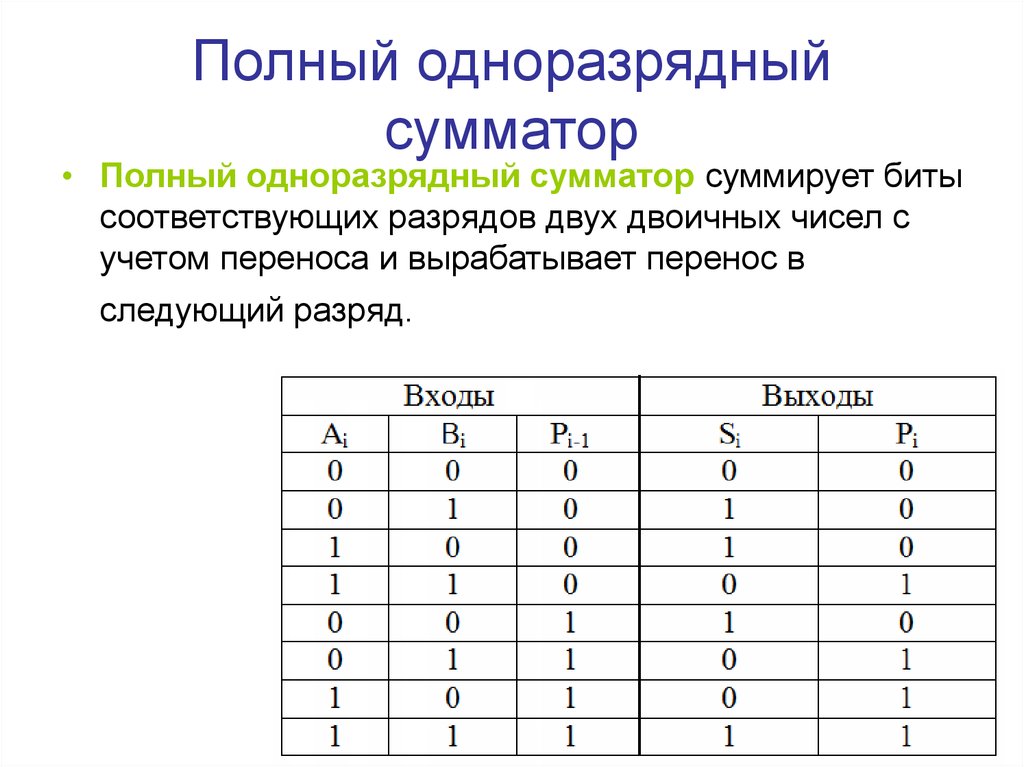
Таблица 2.13. Логика одноразрядного сумматора

Входы			Выходы
ai	bi	pi-1	si	pi
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

В соответствии с таблицей истинности уравнения выходов после минимизации имеют следующий вид:

Схемы одноразрядного сумматора и его условное графическое обозначение показаны на рис.

2.25.

Рис. 2.25. Одноразрядные сумматоры:

а – схема сумматоров на элементах И-НЕ;

б – схема сумматора с использованием элементов сложения по модулю 2;

в – условное графическое обозначение

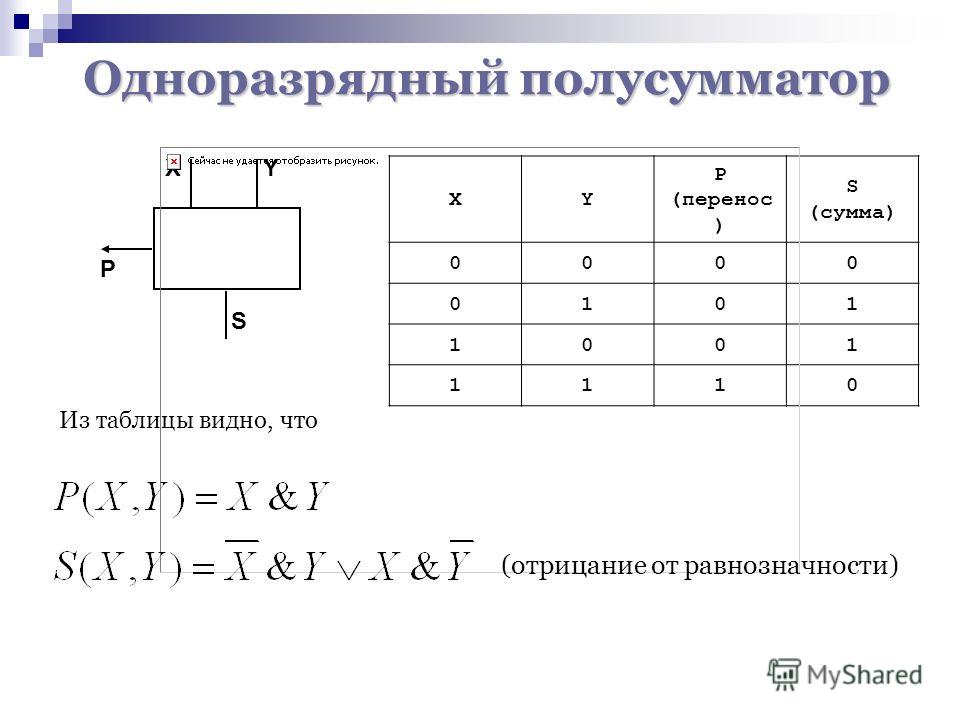
Полусумматором или одноразрядным сумматором на два входа, называется схема с двумя входами и двумя выходами, которая реализует следующие функции:

где – значение суммы в данном разряде; – значение переноса из данного разряда; и – одноименные разряды слагаемых.

Полусумматоры могут быть использованы для построения схем одноразрядных сумматоров на три входа, а также схем ускорения умножения. Варианты схемы полусумматора и его условное графическое обозначение приведены на рис. 2.26.

Рис. 2.26. Полусумматор:

а – схема; б – условное графическое обозначение;

в – схема одноразрядного сумматора на основе полусумматоров

§3.

3. Логические основы устройства компьютера

Планирование уроков на учебный год (по учебнику Н.Д. Угриновича, профильный уровень)

Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 10 классы | Планирование уроков на учебный год (по учебнику Н.Д. Угриновича, профильный уровень) | §3.3. Логические основы устройства компьютера

Содержание урока

3.3.1. Базовые логические элементы

3.3.2. Сумматор двоичных чисел

Полусумматор

Полный одноразрядный сумматор

Контрольные вопросы. Компьютерный практикум

3.3.3. Триггер

Полный одноразрядный сумматор

Рассмотрим схему сложения двух n-разрядных двоичных чисел а_n …а_iа_i-1…а₀ и b_n .

..b_ib_i-1…b₀:

При сложении цифр i-го разряда складываются a_i и b_i, а также p_i-1 — перенос из i-1-го разряда. Результатом будет s_i — сумма и p_i — перенос в старший разряд. Одноразрядный двоичный сумматор — это устройство с тремя входами и двумя выходами.

Таким образом, полный одноразрядный сумматор должен иметь три входа: А, В — слагаемые и Р₀ — перенос из младшего разряда и два выхода: сумму S и перенос Р. Таблица сложения в этом случае будет иметь следующий вид (табл. 3.15).

Таблица 3.15. Таблица сложения одноразрядных двоичных чисел с учетом переноса из младшего разряда

Идея построения полного сумматора точно такая же, как и полусумматора. Из таблицы сложения видно, что перенос (логическая переменная Р) принимает значение 1 тогда, когда хотя бы две входные логические переменные одновременно принимают значение 1.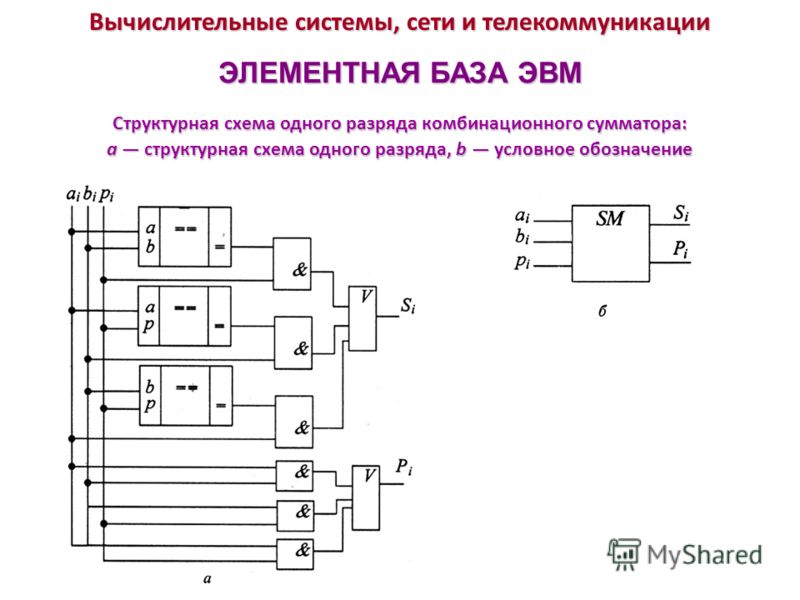 Таким образом, перенос реализуется путем логического сложения результатов попарного логического умножения входных переменных А, В, Р₀

. Формула переноса получает следующий вид:

Р = (А & В) ∨ (А & P₀) ∨ (В & Р₀).

Для получения значения суммы (логическая переменная S) необходимо результат логического сложения входных переменных А, В, Р₀ умножить на инвертированный перенос P:

S=(A ∨ B ∨ P₀) & P.

Данное логическое выражение дает правильные значения суммы во всех случаях, кроме одного, когда все входные логические переменные принимают значение 1. Действительно:

Р = (1 & 1) ∨ (1 & 1) ∨ (1 & 1) = 1

,

S = (1 ∨ 1 ∨ 1) & P = 1 & 0 = 0.

Для получения правильного значения суммы (для данного случая переменная S должна принимать значение 1) необходимо сложить полученное выше выражение для суммы с результатом логического умножения входных переменных А, В, Р₀.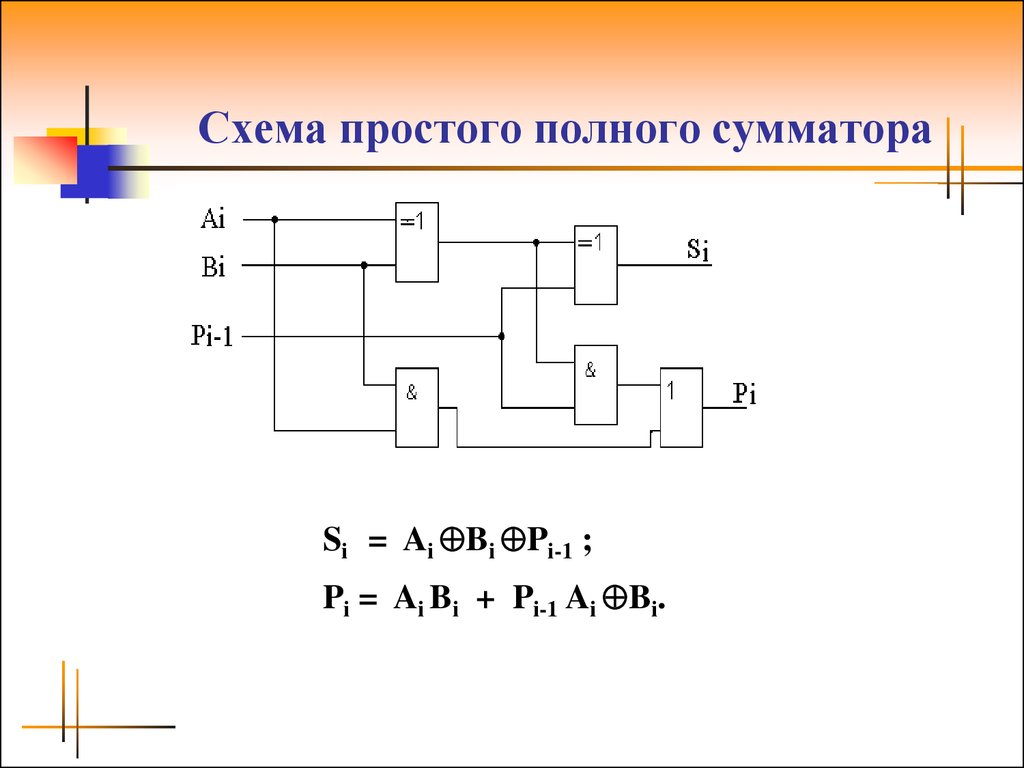 В результате логическое выражение для вычисления суммы в полном сумматоре принимает следующий вид:

S = (A ∨ В ∨ P₀) & P₀ ∨ (A & В & Р₀).

Теперь можно построить логическую схему полного одноразрядного сумматора (рис. 3.15).

Рис. 3.15. Сумматор двоичных чисел

Многоразрядный сумматор процессора состоит из полных одноразрядных сумматоров. На каждый разряд ставится одноразрядный сумматор, причем выход (перенос) сумматора младшего разряда подключен ко входу сумматора старшего разряда.

Следующая страница Контрольные вопросы. Компьютерный практикум

Cкачать материалы урока

сумматоров | CircuitVerse

Оглавление

1. Полусумматор
2. Введение
3. Блок-схема
4. Таблица истинности
5. Принципиальная схема
6. Полусумматор от универсальных вентилей
7. Полный сумматор
8. Введение
9. Блок-схема
10. Таблица истинности
11. Принципиальная схема
12. Полный сумматор из 2 полусумматоров
13. Полный сумматор из универсальных вентилей
14. Сумматор переноса пульсаций
15. Полувычитатели
16. Введение
17. Таблица истинности
18. Принципиальная схема
19. Полувычитатель из универсальных ворот
20. Полные вычитатели
21. Введение
22. Таблица истинности
23. Принципиальная схема
24. Полный вычитатель из универсальных ворот
25. N-битный параллельный сумматор и вычитатель
26. Введение
27. 4-битный параллельный сумматор
28. Блок-схема
29. N-битный параллельный вычитатель
    1. 4-битный параллельный вычитатель
    2. Блок-схема
    3. 8-битный полный сумматор и вычитатель

Половинный сумматор

Введение

Полусумматор представляет собой комбинационную логическую схему с двумя входами и двумя выходами.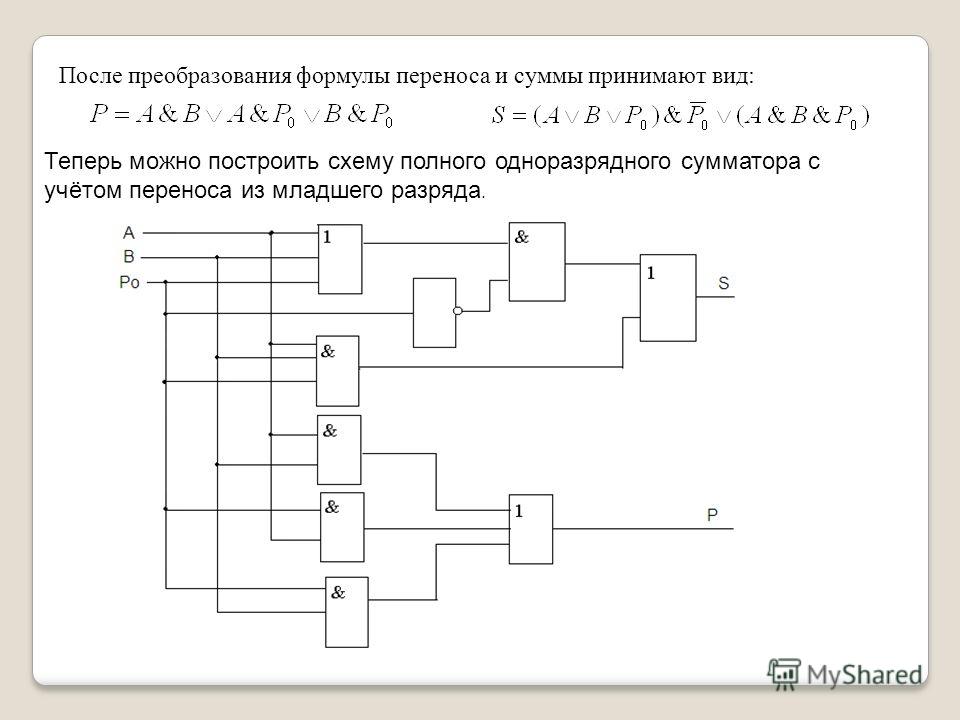 Схема полусумматора предназначена для сложения двух одноразрядных двоичных чисел А и В. Это основной строительный блок для сложения двух однобитных чисел. Эта схема имеет два выхода , несущие и , суммирующие 9.0078 .

Блок-схема

Таблица истинности

Принципиальная электрическая схема

Полусумматор из универсальных ворот

Полный сумматор

Введение

Полный сумматор разработан для преодоления недостатка схемы полусумматора. Он может складывать два однобитовых числа A и B и передавать c. Полный сумматор представляет собой комбинационную схему с тремя входами и двумя выходами.

Блок-схема

Таблица истинности

Принципиальная электрическая схема

Полный сумматор из 2 полусумматоров

Полный сумматор из универсальных вентилей

Сумматор переноса пульсации

Полувычитатели

Введение

Полувычитатель представляет собой комбинированную схему с двумя входами и двумя выходами (разность и заимствование).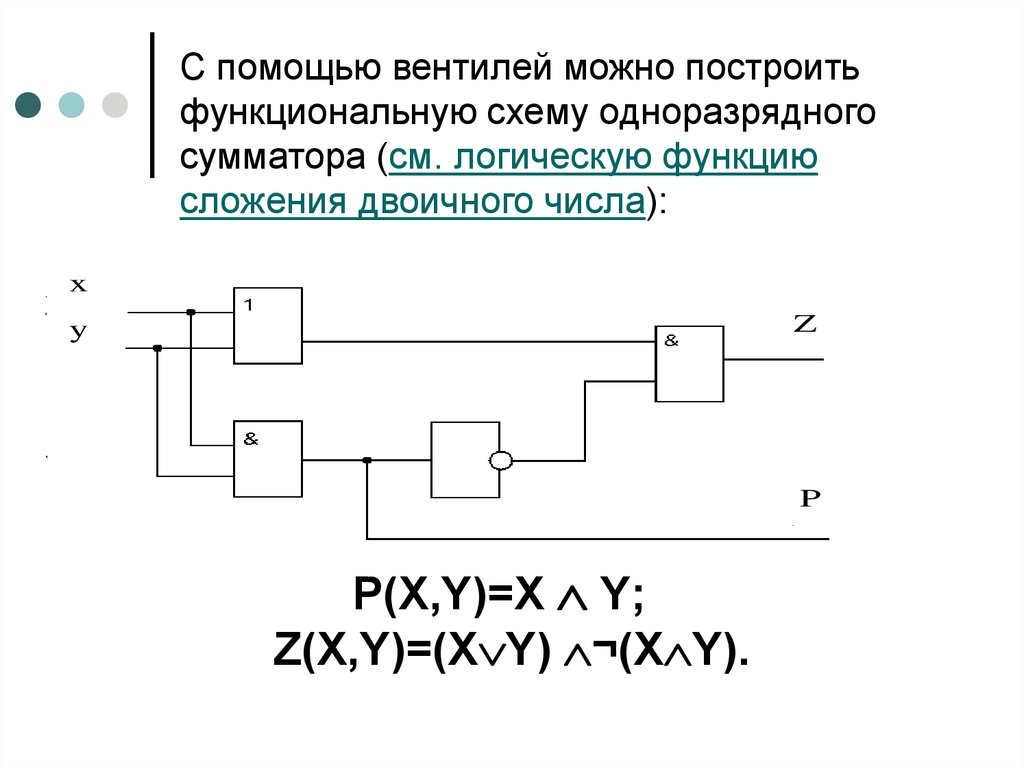 Он производит разницу между двумя двоичными битами на входе, а также создает выход (Заимствование), чтобы указать, была ли заимствована 1. В вычитании (A-B) A называется уменьшаемым битом, а B называется вычитаемым битом.

Таблица истинности

Принципиальная электрическая схема

Полувычитатель из универсальных ворот

Полные вычитатели

Введение

Недостаток половинного вычитателя преодолевается полным вычитателем. Полный вычитатель представляет собой комбинационную схему с тремя входами A, B, C и двумя выходами D и C’. A — «уменьшаемое», B — «вычитаемое», C — «заимствование», полученное на предыдущем этапе, D — разностный выход, а C — выходной результат заимствования.

Таблица истинности

Принципиальная электрическая схема

Полный вычитатель из универсальных ворот

N-битный параллельный сумматор и вычитатель

Введение

Полный сумматор может складывать только два однозначных двоичных числа вместе с вводом переноса. Но на практике вам нужно добавить двоичные числа, которые намного длиннее одного бита. Чтобы сложить два n-битных двоичных чисел, вам нужно использовать n-битный параллельный сумматор. Он использует несколько полных сумматоров в каскаде. Выход переноса предыдущего полного сумматора подключается к входу переноса следующего полного сумматора.

4-битный параллельный сумматор

На блок-диаграмме A0 и B0 представляют младший разряд четырехбитных слов A и B.

Следовательно, Full Adder-0 является младшим этапом. Следовательно, его Cin навсегда стал равным 0. Остальные соединения такие же, как у n-разрядного параллельного сумматора, показанного на рис. Четырехразрядный параллельный сумматор является очень распространенной логической схемой.

Блок-схема

Вычитание может быть выполнено путем добавления до 1 или 2 вычитаемого числа. Например, вы можете выполнить вычитание (A-B), добавив либо 1, либо 2-е дополнение B к A. Это означает, что вы можете использовать двоичный сумматор для выполнения двоичного вычитания.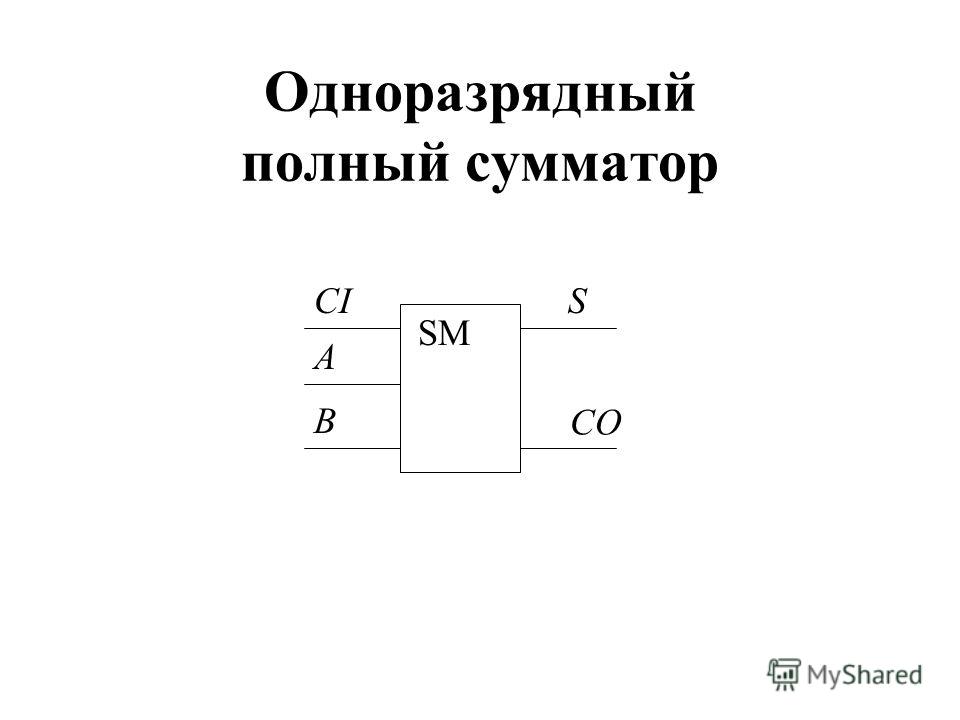

4-битный параллельный вычитатель

Вычитаемое число (B) сначала проходит через инверторы для получения дополнения до 1. Затем 4-битный сумматор складывает A и дополнение B до 2 для получения вычитания. S3 S2 S1 S0 представляет результат двоичного вычитания (AB), а выход переноса Cout представляет полярность результата. Если A > B Cout = 0 и результат в двоичной форме (AB), то Cout = 1, и результат находится в форме дополнения до 2.

Блок-схема

8-битный полный сумматор и вычитатель

1. Рассмотрим схему полусумматора — для какого из следующих входов A, B выход суммы (S) одинаков?
   1. 0,0
      • 0,1
      • 1,0
   2. 1,1
2. Используя только какие из следующих логических элементов в минимальном количестве, может быть реализована схема полусумматора?
   1. НО
      • И
      • ИЛИ
      • НЕ
3. Что из перечисленного ниже является 4-битным полным сумматором IC?
   1. 74LS83
      • 7474
      • 7408
      • 7432
4. Какая из следующих схем называется n-битным параллельным сумматором?
   1. Сумматор переноса пульсации
      • Полусумматор
      • Полувыталкиватель
      • Полный сумматор
5. В каком из следующих случаев сумматор можно использовать в качестве первичного элемента?
   1. Арифмологическое устройство (ALU)
   2. Цифровой калькулятор
      • Блок памяти
      • Циклическая операция

Включите JavaScript для просмотра комментариев с помощью Disqus.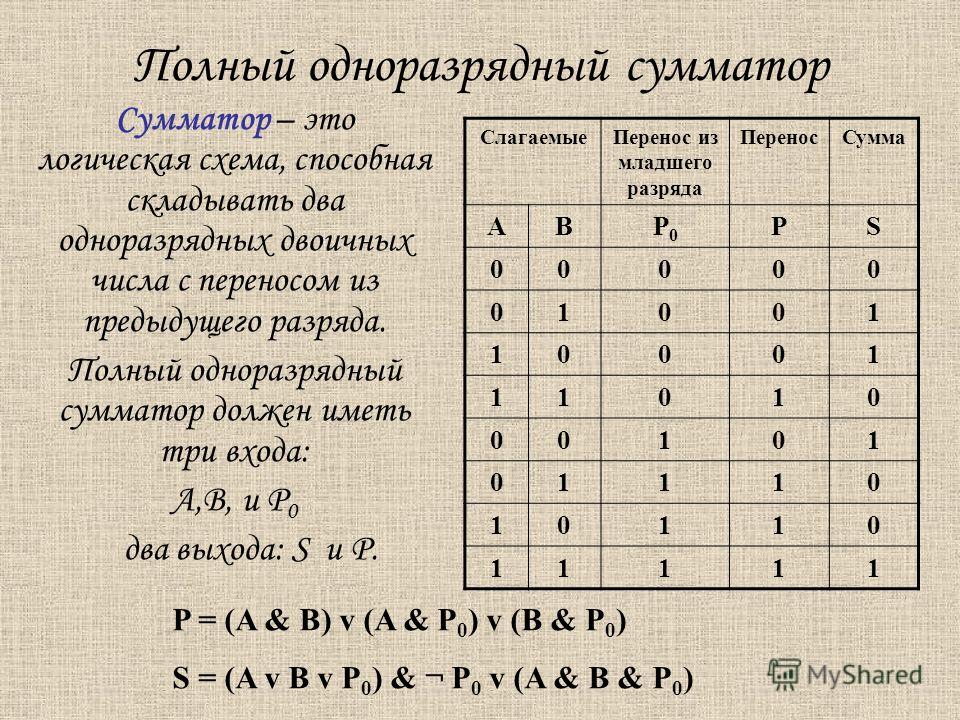

---

Половинные и полные сумматоры

Половинные и полные сумматоры
Далее: Мультиплексоры и декодеры Вверх: Комбинационная логика Предыдущая: Сигнальная гонка

Из базовых вентилей мы разработаем полную схему сумматора, которая добавляет два двоичные числа. Рассмотрите возможность добавления двух 2-битных двоичных чисел и . , где бит переноса. Таблица истинности для всех комбинаций и показана на таблица 7.5.

 
Таблица 7.5:  Двоичное сложение двух 2-битных чисел. столбец.

Из таблицы истинности

Механизация этих двух уравнений показана на рис. рисунок 7.7.

 
Рис. 7.7:  Механизация полусумматора с использованием EOR и вентиль AND.

Эта схема известна как полусумматор. Он не может обрабатывать сложение любых двух произвольных чисел, потому что не позволяет вводить бит переноса из добавления двух предыдущие цифры. Схема, которая может обрабатывать эти три входа, может выполнять сложение любых двух двоичных чисел.

Таблица истинности для трех входных переменных показана на рисунок 7.8.

 
Рисунок 7.8:  Двоичное сложение двух 2-битных чисел. столбец.

Из таблицы истинности

Это известно как логика большинства. И мажоритарный детектор показан на рисунке 7.9.

 
Рисунок 7.9:  Механизация мажоритарного детектора.

Следующее устройство (рисунок 7.10) известно как полный сумматор. и может добавить три отдельных бита информации и вернуть сумму бит и вынос бит.

 
Рисунок 7.10:  Полная механизация сумматора.

Схема, показанная на рисунке 7.11, способна добавить любые два цифры любого размера. Входы и , и выход .

 
Рисунок 7.11:  Схема, способная складывать два 3-битных числа.

Пример: Если вход схемы на рисунке 7. 12 записан как число ABCD , напишите девять цифр, которые дадут настоящую В .

 
Рисунок 7.12:  Типичная логическая функция.

 
Таблица 7.6: Таблица истинности для типичного примера логической функции.

ABCD =(2,3,6,7,11,12,13,14,15) дает Q верно.

Пример: Используя соглашение о дополнении до 2, 3-битное число ABC может представляют числа от -3 до 3, как показано в таблице 7.7. (игнорировать -4). Предполагая, что A, B, C и доступны в качестве входных данных, цель состоит в том, чтобы разработать схему, которая даст 2-битный выходной EF, который является абсолютным значением числа ABC. Ты имеют только двух- и трехвходовые элементы И и ИЛИ.

1. Заполнить таблицу истинности битами ABC и EF .

   Таблица истинности показана в таблице 7.7.

    
   Таблица 7.7:  Таблица истинности для ABC и EF биты.
   

2. Напишите выражение булевой алгебры для E и для F .

3. Механизируйте эти выражения.

   Механизированные выражения показаны на рисунке 7.13.

    
   Рисунок 7.13:  Механизация долот ABC и EF.
   

Пример: Предположим, что 2-битное двоичное число AB должно быть передано между устройств в шумной обстановке. Чтобы уменьшить количество необнаруженных ошибок введенный передачей, дополнительный бит P часто включается в добавить избыточность информации. Предположим, что P имеет значение true или false по мере необходимости, чтобы получить нечетное количество истинных битов в результирующем 3-битное число АВР . Когда число получено, логические схемы требуется для генерации сигнала ошибки E всякий раз, когда нечетное число условие битов не выполняется.

1. Разработайте таблицу истинности E в терминах A , B и P .