Таблицы истинности.Логические схемы презентация, доклад
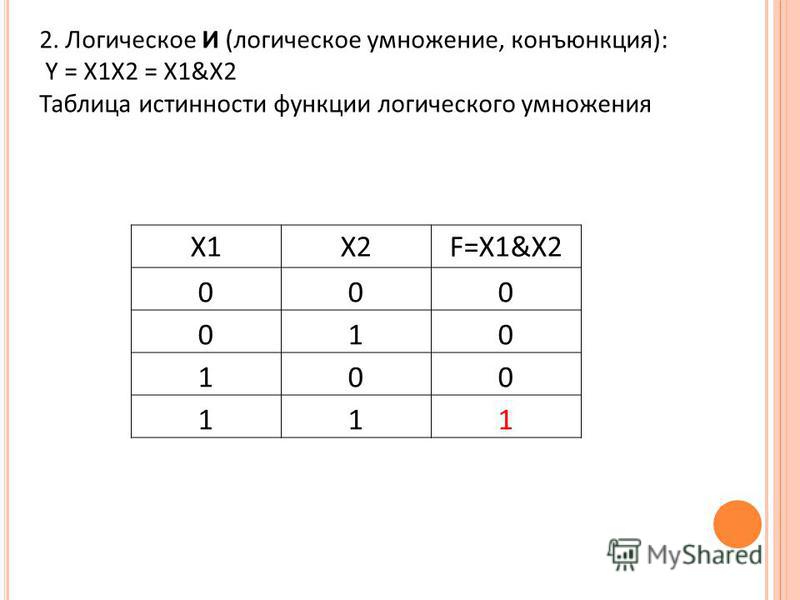
Таблицы истинности.
Логические схемы
Урок информатики.
10 класс.
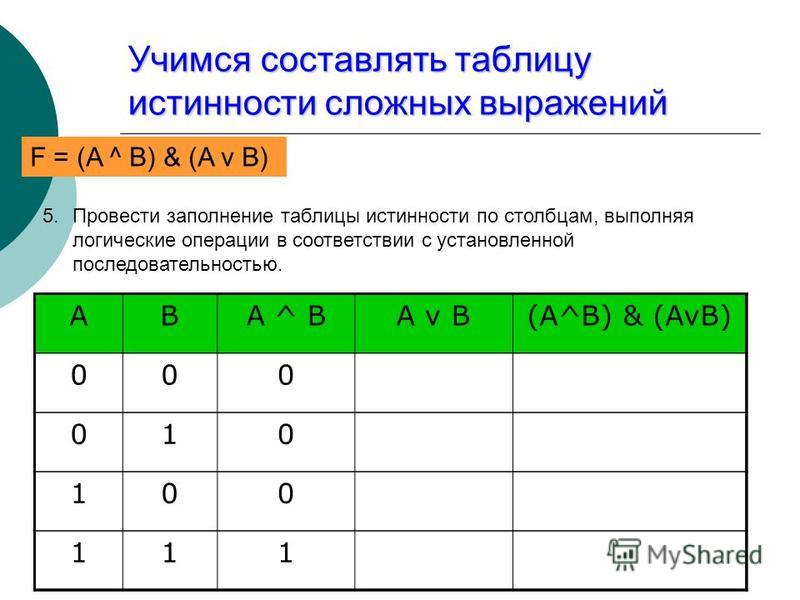
Построим таблицу истинности для выражения F = (AvB)&(¬Av¬B).
Количество строк = 22 (2 переменных) + 1 (заголовки столбцов) = 5.
Количество столбцов = 2 логические переменные (А, В) + 5 логических операций (v, &, ¬, v,) = 7.
Расставим порядок выполнения операций:
1 5 2 4 3
(A v B) & (•A v•B)
Построим таблицу истинности для выражения: F = (AvB)&(¬Av¬B).
:
И
ИЛИ
НЕ
Логические схемы
Конъюнкция
А
В
0
0
0
И
Устимкина Л.
И., ББСОШ №1
Дизъюнкция
А
В
ИЛИ
Инверсия
А
1
0
Таблица истинности
Построение логических схем
Определить число логических переменных.
Определить количество базовых логических операций и их порядок.
Изобразить для каждой логической операции соответствующий вентиль.
Соединить вентили в порядке выполнения логических операций.
Х
Y
1
0
0
1
1
Пример 1
Пусть X = истина, Y = ложь. Составить логическую схему для следующего логического выражения: F = X v Y & X.
Две переменные — X и Y.
Две логические операции:
2 1
X v Y & X.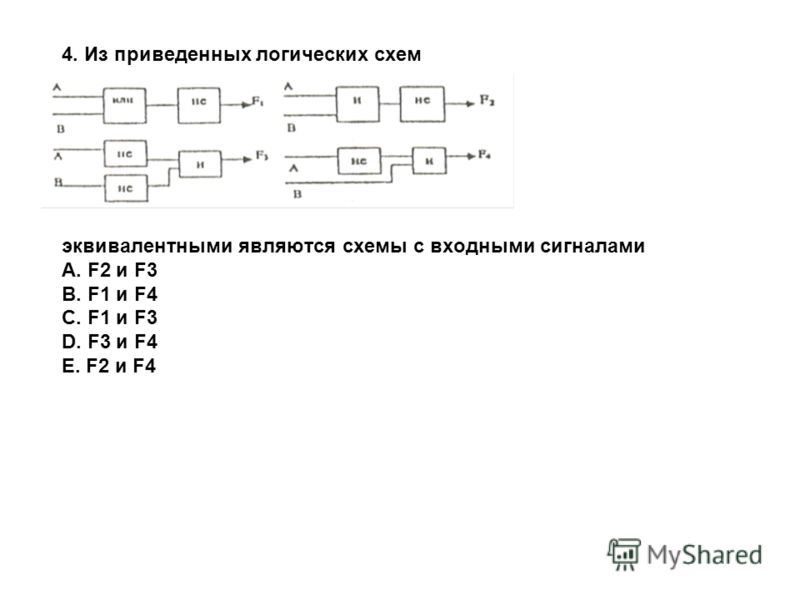
Ответ: 1v 0 & 1 = 1.
Пример 2
Постройте логическую схему, соответствующую логическому выражению F=X&Yv¬(YvX). Найдите значение логического выражения для X=1, Y=0.
Переменных две: X и Y;
Логических операций четыре: конъюнкция, две дизъюнкции и инверсия:
1 4 3 2
X&Yv ¬ (YvX)
Схему строим слева направо в соответствии с порядком логических операций
0
№1
Составьте таблицы истинности для следующих логических выражений:
F=(X&•Y)vZ.
F=X&YvZ.
F= ¬ (XvY) & (YvX).
F= ¬ ((XvY) & (ZvX)) & (ZvY).
F= A&B&C&•D.
F= (AvB) & (•BvAvB).
№3
Постройте логическое выражение по логической схеме:
А
В
¬
¬
№4
Постройте логическую схему, соответствующую логическому выражению, и найдите значение логического выражения:
F = AvB& •C, если А = 1, В=1, С=1 (1).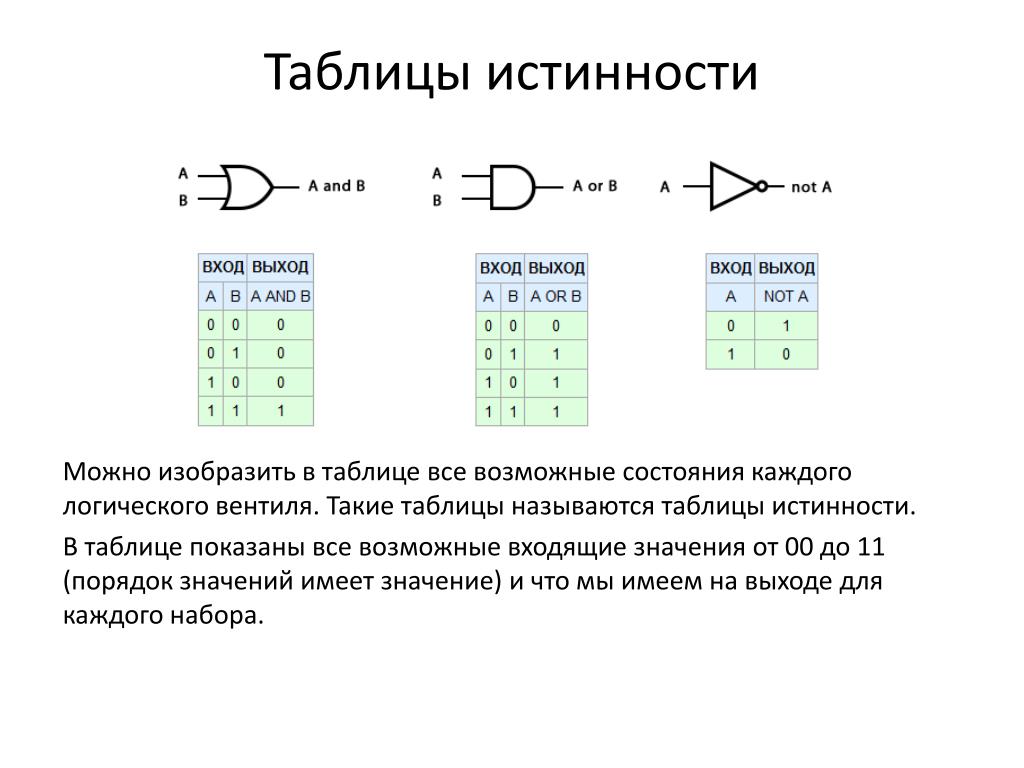
F = ¬ (AvB&C), если А=0, В=1, С=1 (1).
F = •AvB&C, если А=1, В=0, С=1 (0).
F = (AvB) & (CvB), если А=0, В=1, С=0 (1).
F = ¬ (А&В&С), если А=0, В=0, С=1 (1).
F = ¬ (A&B&C) v (B & C v•A), если А=1, В=1, С=0 (1).
F = B&•Av•B&A, если А=0, В=0 (0).
Домашнее задание
№1
Составьте таблицы истинности и определите истинность формулы:
1) F = ((Av •B)→B)&(•AvB).
2)F = ¬(AvB)≡(•AvB).
F = ¬ ((А →В) ≡ (•B →Ā)).
№2
Составьте логические схемы к следующим логическим выражениям:
A) F = Bv(C&•A) v (A&B).
B) F= ¬ (A&B) vC&D.
№3
Постройте логические выражения к логическим схемам:
C
D
&
&
1
&
&
&
1
Презентация «Логические выражение — Таблицы истинности
Слайд 1
Обобщающий урок по теме: «ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ, ТАБЛИЦЫ ИСТИННОСТИ, ЛОГИЧЕСКИЕ СХЕМЫ»
1
0
1
0
1
0
1
0
1
0
10
1
0
10
1
0
10
1
1
0
1
0
1
0
1
0
1
0
10
1
0
10
1
0
10
1
Искандарова А.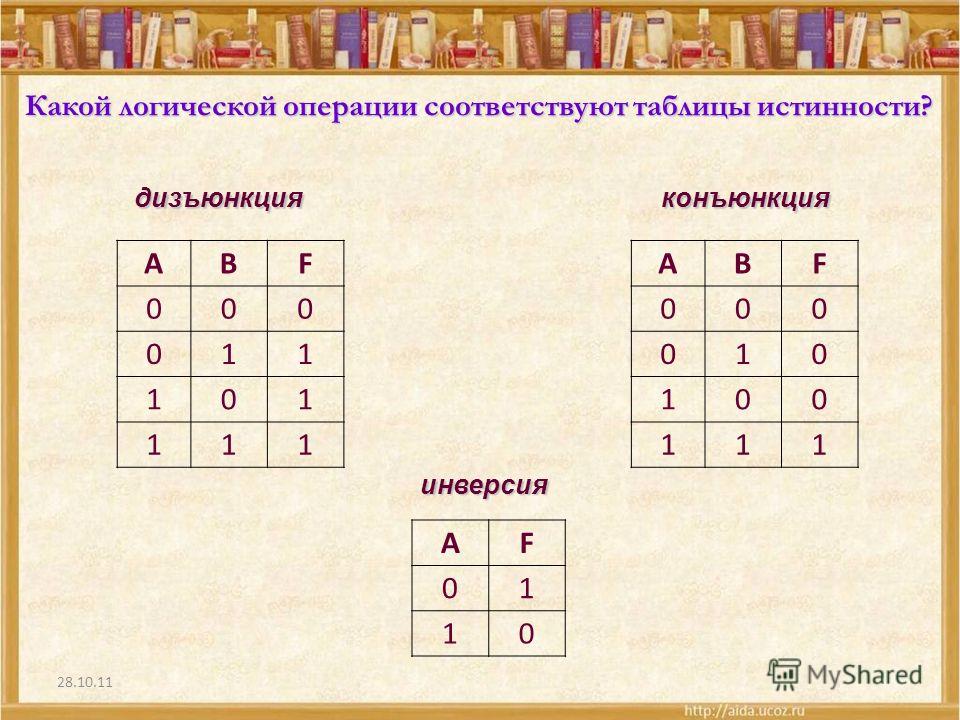
Р. г. Уфа
Слайд 2
Вопросы для повторения
Что понимают под высказыванием?
Высказывание(суждение) – это повествовательное предложение, в котором что-либо утверждается или отрицается. Высказывание может быть либо истинно, либо ложно.
Привести примеры простых высказываний.
Кошка является домашним животным.
Процессор – это устройство обработки информации.
Привести примеры сложных высказываний.
Петя и Вася играют в шахматы.
Принтер является устройством вывода информации или сканер устройством ввода информации.
1
0
1
0
1
0
1
0
1
0
10
1
0
10
1
0
10
1
Слайд 3
Вопросы для повторения
Что понимают под логическим выражением?
Логическая формула (логическая выражение) – формула, содержащая лишь логические переменные и знаки логических операций.
Какие значения могут принимать логические переменные?
Логические переменные могут принимать лишь два значения: «истина» (1) и «ложь» (0).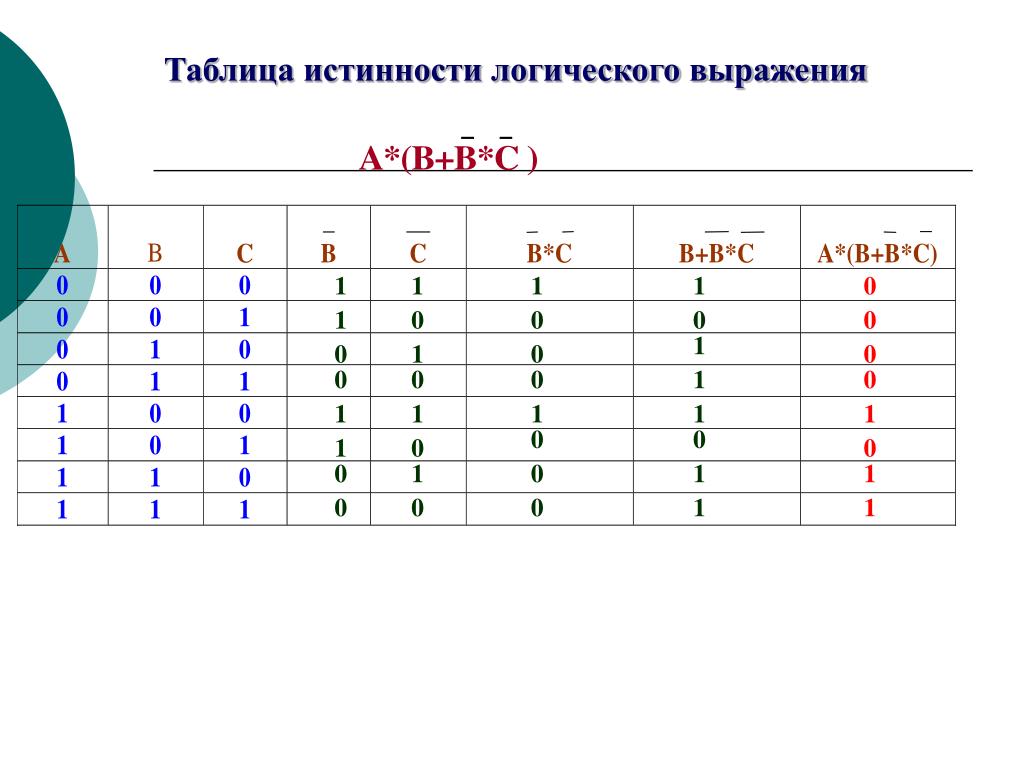
Назовите основные логические операции.
Конъюнкция, дизъюнкция, отрицание.
Каков порядок выполнения логических операций?
Отрицание, конъюнкция, дизъюнкция.
1
0
1
0
1
0
1
0
1
0
10
1
0
10
1
0
10
1
Слайд 4
Таблицы истинности
А В А & В А v B ¬ A ¬ B
Найдите значение выражений:
1 and (0 or not 0)=
not(0 or 1) and 1=
1
0
1
0
1
0
1
0
1
0
10
1
0
10
1
0
10
1
Слайд 5
Таблицы истинности
А В А & В А v B ¬ A ¬ B
0 0 0 0 1 1
0 1 0 1 1 0
1 0 0 1 0 1
1 1 1 1 0 0
Найдите значение выражений:
1 and (0 or not 0)=1*(0+1)=1
not(0 or 1) and 1=0*1=0
1
0
1
0
1
0
1
0
1
0
10
1
0
10
1
0
10
1
Слайд 6
Базовые логические элементы
Конъюнктор
Инвертор
Дизъюнктор
НЕ
1
0
1
0
1
0
1
0
1
0
10
1
0
10
1
0
10
1
Слайд 7
Базовые логические элементы
Конъюнктор
Инвертор
Дизъюнктор
НЕ
1
0
1
0
1
0
1
0
1
0
10
1
0
10
1
0
10
1
Слайд 8
1
Выполните вычисления по схемам
1
0
1
0
1
0
1
0
1
0
10
1
0
10
1
0
10
1
&
1
0
1
0
1
&
&
1
0
1
1
1)
2)
Слайд 9
Выполните вычисления по схемам
1
0
1
0
1
0
1
0
1
0
10
1
0
10
1
0
10
1
&
1
0
1
0
1
&
&
1
0
1
1
1)
2)
0
1
1
1
0
Слайд 10
F = A v ¬В & С
Построить таблицу истинности по данному логическому выражению.
Построить логическую схему.
A B C
1
0
1
0
1
0
1
0
1
0
10
1
0
10
1
0
10
1
Слайд 11
F = A v ¬В & С
Построить таблицу истинности по данному логическому выражению.
Построить логическую схему.
A B C ¬В ¬В & С A V ¬В & С
0 0 0 1 0 0
0 0 1 1 1 1
0 1 0 0 0 0
0 1 1 0 0 0
1 0 0 1 0 1
1 0 1 1 1 1
1 1 0 0 0 1
1 1 1 0 0 1
1
0
1
0
1
0
1
0
1
0
10
1
0
10
1
0
10
1
Слайд 12
F = A v ¬В & С
Построить таблицу истинности по данному логическому выражению.
Построить логическую схему.
1
0
1
0
1
0
1
0
1
0
10
1
0
10
1
0
10
1
Слайд 13
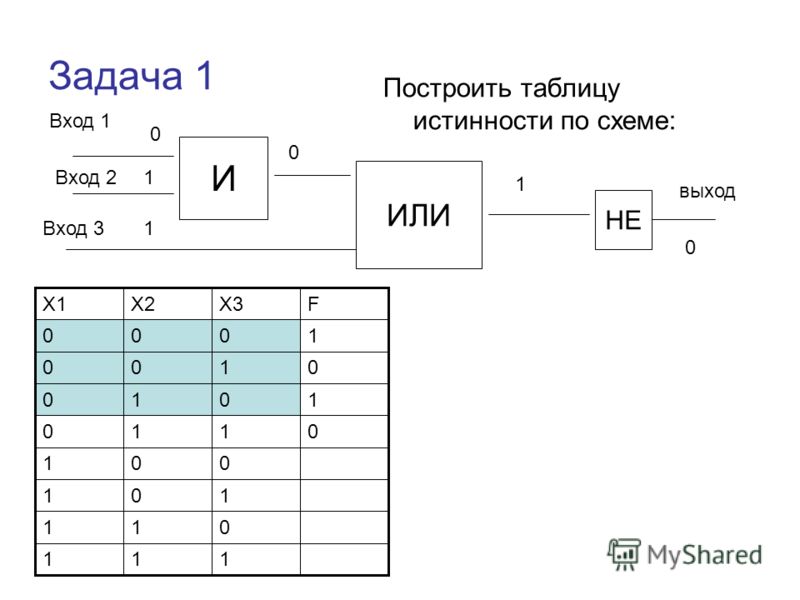
По заданной логической схеме записать логическое выражение
x
y
z
1
1
&
Построить таблицу истинности двумя способами.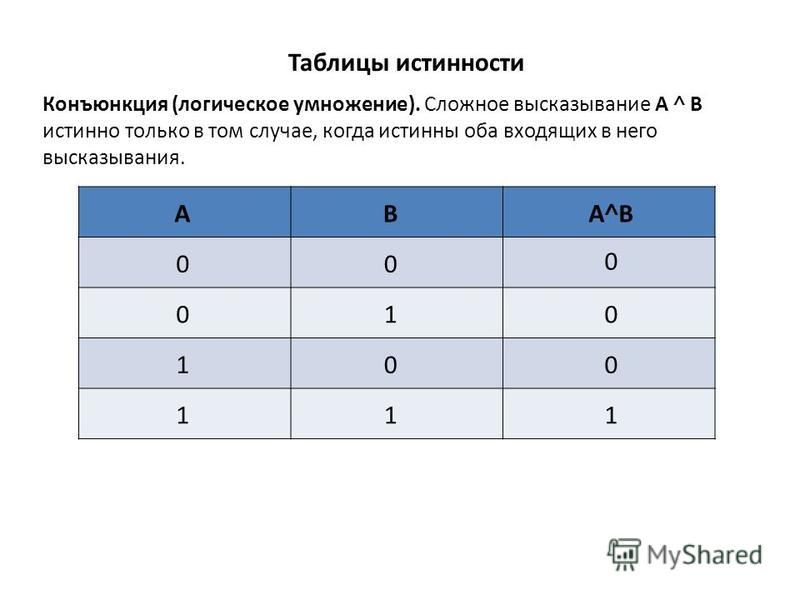
1
0
1
0
1
0
1
0
1
0
10
1
0
10
1
0
10
1
Слайд 14
По заданной логической схеме записать логическое выражение
x
y
z
1
1
&
Построить таблицу истинности двумя способами:
в тетрадях;
в MS Excel.
1
0
1
0
1
0
1
0
1
0
10
1
0
10
1
0
10
1
F(x,y,z)=(¬(X v Y) v z) & x
Слайд 15
Проверка
x y z x+y ¬(x+y) ¬(x+y)+z
(¬(x+y)+z)*x
0 0 0 0 1 1 0
0 0 1 0 1 1 0
0 1 0 1 0 0 0
0 1 1 1 0 1 0
1 0 0 1 0 0 0
1 0 1 1 0 1 1
1 1 0 1 0 0 0
1 1 1 1 0 1 1
1
0
1
0
1
0
1
0
1
0
10
1
0
10
1
0
10
1
Слайд 16
Список литературы:
Информатика и ИКТ. Профильный уровень: учебник для 10 класса . Н.Д. Угринович. М.: БИНОМ. Лаборатория знаний, 2010.
Информатика.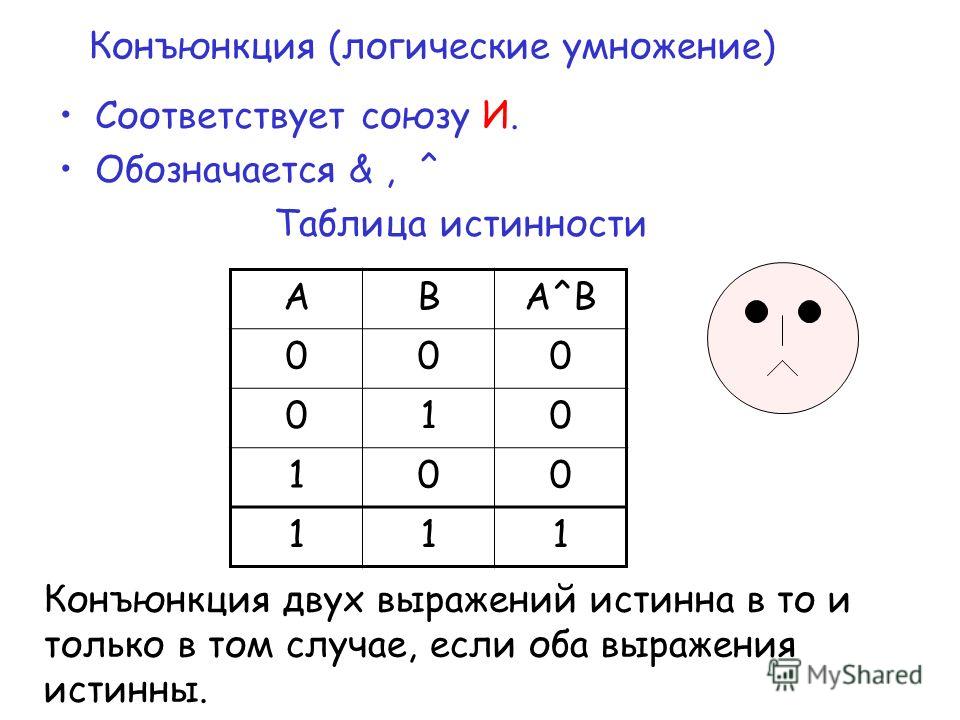
Задачник-практикум в 2 т. / Под ред. И.Г. Семакина, Е.К. Хеннера: Том 1. – М.: БИНОМ. Лаборатория знаний, 2010.
для цифровой логики Таблицы истинности
для цифровой логикиТаблица истинности показывает, как выход логической схемы реагирует на различные комбинации входов, используя логическую 1 для истинного и логический 0 для ложного. Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов.
| Индекс Концепции электроники Цифровые схемы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
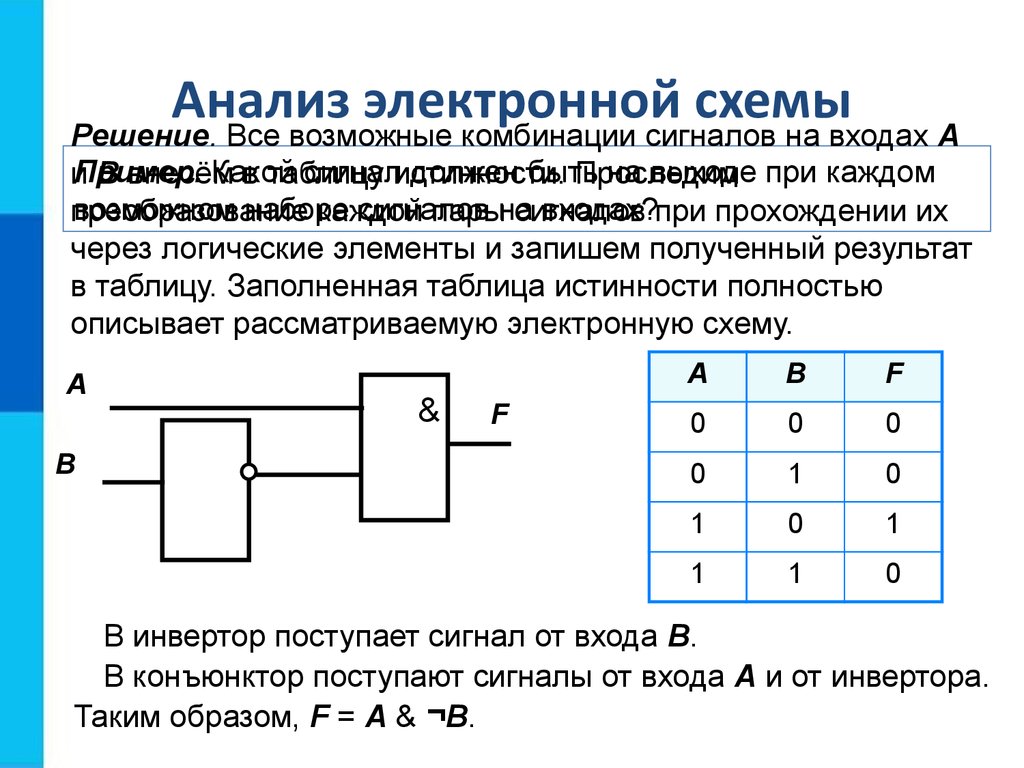
Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов.
Все перестановки входов перечислены слева, а выход схемы указан справа. Желаемый результат может быть достигнут комбинацией логических вентилей. Показана таблица истинности для двух входов, но ее можно расширить до любого количества входов. Входные столбцы обычно строятся в порядке двоичного счета с количеством битов, равным количеству входов.
