Курс физики. Том II. Учение об электричестве

Курс физики. Том II. Учение об электричестве

Путилов К.А. Курс физики. Том II. Учение об электричестве. Учебное пособие. — М.: Гостехтеориздат, 1954 г. Данный трёхтомный курс физики предназначается в качестве учебного пособия для высших учебных заведений с расширенной программой физики. В первом томе изложены физические основы механики, акустика, молекулярная физика и термодинамика, во втором — учение об электричестве, в третьем — оптика и атомная физика. Главное внимание уделено достижениям экспериментальной физики, разъяснению основных законов физики и характеристике технических применений физики. Приведены исторические сведения и рассмотрены некоторые философские вопросы физики. Оглавление ЧАСТЬ ТРЕТЬЯ. УЧЕНИЕ ОБ ЭЛЕКТРИЧЕСТВЕ § 2. Количество электричества. Закон Кулона § 3. Атомное строение электричества § 4. Напряженность электрического поля § 5. Теорема Острогдадского — Гаусса § 6. Вектор электрической индукции § 7. Примеры применения теоремы Остроградского — Гаусса § 8. Потенциал электрического поля § 9. Формулы электростатики в практической системе единиц ГЛАВА II. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ § 10. Распределение электричества по поверхностй заряженных проводников § 11. Электризация проводников в поле и деформация поля проводниками § 12. Контактная разность потенциалов § 13. Электроемкость § 14. Расчет электроемкости конденсаторов § 15. Электрическая энергия § 16. Энергия поля § 17. Электрометры § 18. О природе электрических явлений ГЛАВА III. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ § 19. Дипольная и электронная поляризация диэлектриков. Сегнетоэлектрики § 20. Деформация поля диэлектриками § 21. Электрическая восприимчивость § 22. Электронная теория диэлектриков § 23. Пьезоэлектрические и пироэлектрические явления § 24. Электроконвекционные явления (электрофорез, электроэндосмос и др.) ГЛАВА IV. ПОСТОЯННЫЙ ТОК § 25. Величина тока. Электродвижущая сила и напряжение § 26. Закон Ома. Законы Кирхгофа § 27. Закон Джоуля — Ленца § 28. Дифференциальная форма законов Ома и Джоуля — Ленца. Соотношение аналогии между проводимостью и емкостью ГЛАВА V. ТОК В МЕТАЛЛАХ § 29. Сведения об электропроводности. Термометры сопротивления, болометры, тензометры § 30. Закон Видемана — Франца. Теория электропроводности металлов § 31. Сверхпроводимость § 32. Термоэлектрические явления и их применение § 33. Зависимость термоэлектродвижущей силы от температуры спаев. Явление Пельтье ГЛАВА VI. ТОК В ПОЛУПРОВОДНИКАХ § 34. Полупроводники § 35. Понятие о зонной теории электропроводности § 36. Применения полупроводников ГЛАВА VII. ТОК В ЭЛЕКТРОЛИТАХ § 37. Электролиз. Законы Фарадея. Электрохимические эквиваленты. Потенциалы разложения § 38. Вторичные реакции на электрэдах. Применения электролиза § 39. Подвижность ионов и электропроводность растворов § 40. Гальванические элементы. Электрохимическая природа коррозии § 41. Электродные потенциалы § 42. Аккумуляторы § 43. Свободная энергия гальванической цепи. Концентрационные элементы ГЛАВА VIII. ТОК В ГАЗАХ § 44. Ионизация и электропроводность газов § 45. Типы и механизм разряда в газах § 46. Катодные и анодные лучи § 47. Тлеющий разряд § 48. Дуговой разряд § 49. Искровой разряд. Молния ГЛАВА IX. ТОК ЭЛЕКТРОННОЙ ЭМИССИИ. ЭЛЕКТРОННЫЕ ЛАМПЫ § 50. Термоэлектронная эмиссия. Формула Ричардсона — Дёшмена § 51. Торможение электронного потока. Рентгеновы трубки § 52. Пустотные выпрямители тока (диоды, кенотроны) § 53. Усилительные электронные лампы (триоды) § 54. Фотоэлектрический эффект. Фотоэлементы. Фотореле § 55. Вторичная электронная эмиссия. 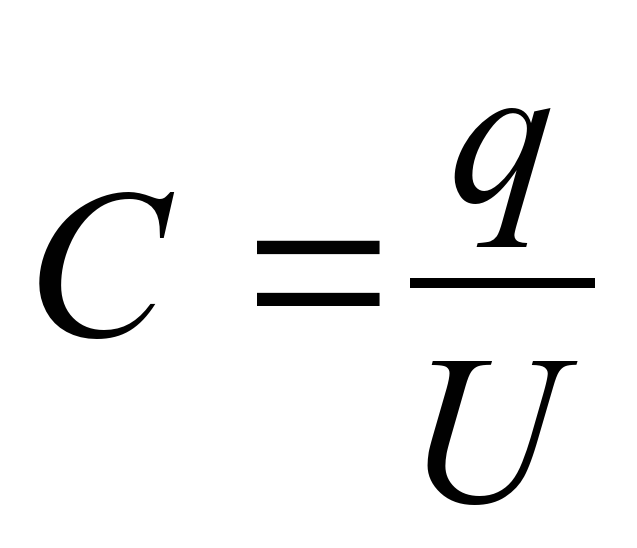Электронные умножители § 56. Динатронный эффект. Экранированные радиолампы ГЛАВА X. МАГНИТНОЕ ПОЛЕ § 57. Исторические сведения. Закон Кулона для магнитных полюсов § 58. Магнитные величины и соотношения, аналогичные электрическим § 59. Магнитное поле Земли § 60. Магнитное поле тока § 61. Закон Био и Савара § 62. Магнитодвижущая сила. Поток индукции электромагнита § 63. Магнитные свойства веществ и их использование § 64. Электронная теория магнетизма ГЛАВА XI. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ТОК § 65. Формула Ампера и ее трактовка по Фарадею § 66. Работа, производимая током при перемещении проводника в магнитном поле. Электромоторы § 67. Отклоняющее действие магнитного поля на электронный поток (в вакууме и в металле) § 68. Электродинамические измерительные приборы. Гальванометры, Осциллографы § 69. Формулы электродинамики в практической системе единиц ГЛАВА XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ § 70. Понятие об электромагнитном поле. Электромагнитная индукция § 71. Закон Ленца. Картина электромагнитного поля по Фарадею § 72. Закон Фарадея. Индукционное измерение магнитного потока и магнитодвижущей силы. Вихревые токи § 73. Явление самоиндукции. Индуктивность. Законы нарастания и спада тока при включении и выключении цепи § 74. Энергия магнитного поля тока. Индуктивность и энергия электромагнита. Индуктивность кабеля § 75. Взаимная индуктивность. Энергия взаимодействия токов. Коэффициент взаимной индукции катушек с общим сердечником § 76. Уравнения Максвелла и уравнения Лорентца § 77. Электромагнитное происхождение массы электрона ГЛАВА XIII. ПЕРЕМЕННЫЙ ТОК § 78. Генерирование переменного тока § 79. Работа генератора электрической энергии на нагрузку Эффективные значения напряжения и величины тока § 80. Емкостное сопротивление и индуктивное сопротивление § 81. Активные и реактивные токи. Коэффициент мощности (cos f). Потери (tg b) § 82. Обобщенный закон Ома § 83. Электрический резонанс § 84. Трансформация тока § 85. Трехфазный ток. Синхронные и асинхронные моторы ГЛАВА XIV. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ И ИХ ПРИМЕНЕНИЕ § 86. Индуктор § 87. Колебательный контур § 88. Вибратор Герца (возбуждение колебательного контура индуктором). Токи Тесла § 89. Электромагнитные волны. Вектор Умова — Пойнтинга § 90. Излучение электрического диполя. Волны в двухпроводной линии. Антенны § 91. Распространение электромагнитных волн. Роль ионосферы. «Радиоокно» в космос § 92. Ламповые генераторы электрических колебаний § 93. Модуляция электрических колебаний § 94. Прием, детектирование и усиление радиосигналов. Супергетеродины § 95. Преобразование звуковых колебаний в электрические и электрических в звуковые. Электрозапись и воспроизведение звука § 96. Телевидение § 97. Сантиметровые волны и их распространение в волноводах § 98. Радиолокация. Генерирование ультракоротких волн (клистроны и магнетроны)

Понятие электроемкости и конденсаторов, расчет электроемкости

Если двум, находящимся на некотором расстоянии друг от друга, проводникам сообщить электрические заряды (q1 и q2), между ними появится электрическое поле. Разность потенциалов (Δφ) в нём будет определяться величинами сообщённых зарядов и формой, которую имеют проводники. Разность потенциалов между 2 точками постоянного во времени и однородного электрического поля называют напряжением (U).

Заряды, сообщённые проводникам, могут быть оба положительными, оба отрицательными или иметь разные знаки. Последний случай при равных абсолютных значениях зарядов нашёл в физике и электротехнике наибольшее применение и поэтому нам особенно интересен.

Электроемкость

Определение 1

Под конденсатором понимают систему из нескольких (чаще всего двух) находящихся близко друг от друга проводников, отделённых друг от друга слоем диэлектрика.

В подавляющем большинстве случаев его толщина много меньше размеров обкладок.

Определение 2

Электрической ёмкостью (C) между двумя проводниками называется скалярная величина, прямо пропорциональная абсолютной величине заряда одного из проводников и обратно пропорциональная разности потенциалов и напряжению между ними.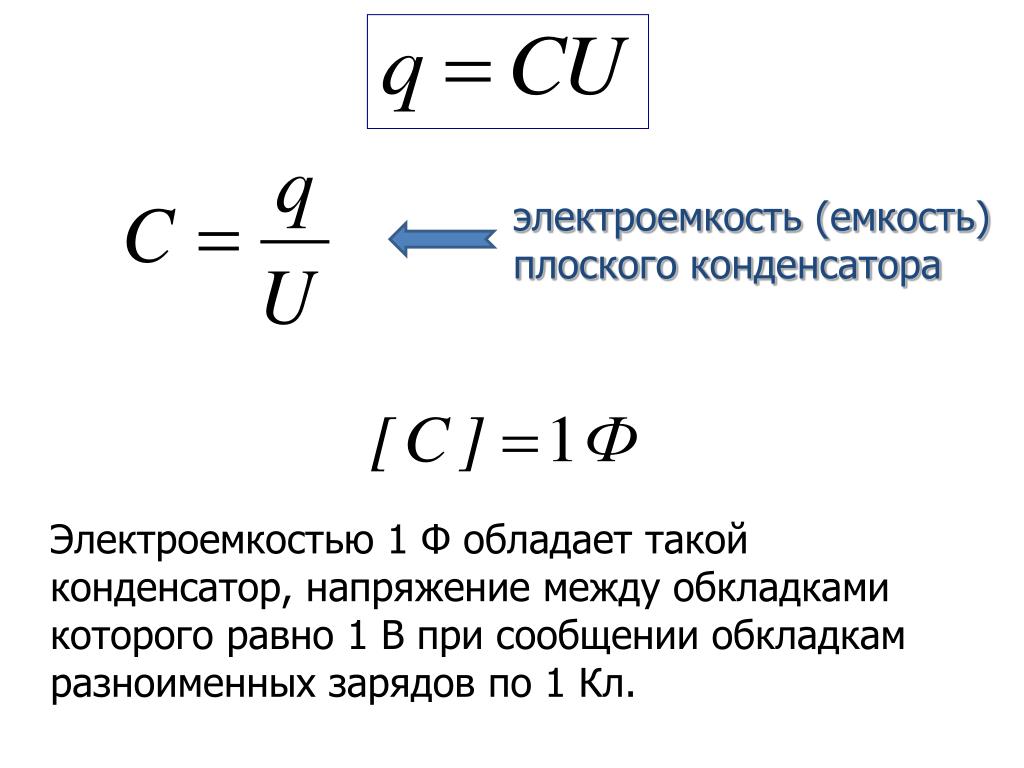

В виде формулы данное определение можно записать следующим образом:

\[C=(q / \Delta \varphi)=(q / U)\]

В системе СИ электроёмкость измеряют в Фарадах. Один Фарад равен электроемкости конденсатора, при которой заряд, равный 1 Кулону, создаёт между его пластинами напряжение в 1 Вольт.

\[1 \Phi=\frac{1 \mathrm{~Kл}}{1 \mathrm{~B}}\]

Ёмкость в 1 Фарад – величина очень большая. На практике чаще всего используют мили фарады (одна тысячная фарада), микрофарады (одна миллионная), нанофарады (одна миллиардная), пикофарады (10 в минус 12-й степени).

Определение 3

Плоским называют конденсатор, образованный двумя плоскими, параллельно расположенными по отношению друг к другу пластинами. Если роль диэлектрика между ними играет воздух, то такой конденсатор называют воздушным.

Определение 4

Электрическое поле в плоском конденсаторе сосредотачивается главным образом между пластинами, однако часть его выходит за их пределы. Это вышедшее поле называют полем рассеяния. {2}}{R_{2}-R_{1}}\].

Цилиндрический конденсатор

Определение 6

Им называют систему находящихся один в другом цилиндров.

Для упрощения расчётов расположим их на одной оси.

Если пренебречь краевыми эффектами, то \[\varphi_{1}-\varphi_{2}=\frac{\lambda}{2 \pi \varepsilon \varepsilon_{0}} \ln \left(\frac{r_{2}}{r_{1}}\right)=\frac{q}{2 \pi \varepsilon \varepsilon_{0} l} \ln \left(\frac{r_{2}}{r_{1}}\right)\]

\[C=\frac{q}{\varphi_{1}-\varphi_{2}}=\frac{2 \pi \varepsilon_{0}}{\ln \left(\frac{r_{2}}{r_{1}}\right)}\].

Теперь вы знаете, чему равна электроемкость конденсатора, давайте рассмотрим их соединения в электрической цепи.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Расчёт электроемкости батареи конденсаторов

Определение 7

Батареей статических конденсаторов называют группу конденсаторов, связанных между собой электрическим соединением. {2}\right)=\mathrm{const}\].

Электроемкость конденсатора, энергия которого известна, из приведённых формул вычисляется достаточно легко:

C=Q²/(2W-LI²)

В контуре станут происходить гармонические колебания, общее их уравнение \[\ddot{Q}+\frac{1}{L C} Q=0\].

Его решение: \[Q(t)=Q_{m} \cos \omega_{0} t\]

Для силы тока и напряжения получим

\[I=\frac{d Q}{d t}=-\omega_{0} Q_{m} \sin \omega_{0} t=I_{m} \cos \left(\omega_{0} t+\frac{\pi}{2}\right)\], \[U_{C}=\frac{Q}{C}=\frac{Q_{m}}{C} \cos \omega_{0} t=U_{m} \cos \omega_{0} t\].

Чтобы получить формулу электроемкости конденсатора колебательного контура в любой момент времени, следует обе части

\[U_{C}=\frac{Q}{C}=\frac{Q_{m}}{C} \cos \omega_{0} t\]

Умножить на C и поделить на Uc.

В результате получим: \[C=\frac{Q_{m}}{U_{C}} \cos \omega_{0} t\].

19.5 Конденсаторы и диэлектрики – College Physics

Глава 19 Электрический потенциал и электрическое поле

Резюме

• Опишите действие конденсатора и определите емкость.
• Расскажите о конденсаторах с плоскими пластинами и их емкостях.
• Обсудите процесс увеличения емкости диэлектрика.
• Определить емкость при данных заряде и напряжении.

Конденсатор — это устройство, используемое для накопления электрического заряда. Применение конденсаторов варьируется от фильтрации статического электричества в радиоприеме до накопления энергии в сердечных дефибрилляторах. Как правило, коммерческие конденсаторы имеют две проводящие части, расположенные близко друг к другу, но не соприкасающиеся, как показано на рис. 1. (Большую часть времени между двумя пластинами используется изолятор для обеспечения разделения — см. обсуждение диэлектриков ниже.) Когда клеммы батареи подключены к изначально незаряженному конденсатору, равные количества положительного и отрицательного заряда, [латекс]{+Q}[/латекс] и [латекс]{-Q}[/латекс], разделены на две его пластины. Конденсатор в целом остается нейтральным, но в этом случае мы называем его хранящим заряд [латекс]{Q}[/латекс].

Конденсатор

Конденсатор — это устройство, используемое для накопления электрического заряда.

Рисунок 1. Оба показанных здесь конденсатора были изначально разряжены перед подключением к батарее. Теперь у них есть отдельные заряды + Q и – Q на две половины. а) Конденсатор с плоскими пластинами. (b) Свернутый конденсатор с изоляционным материалом между двумя его проводящими листами.

Сумма заряда [латекс]{Q}[/латекс] a , который может хранить конденсатор , зависит от двух основных факторов: приложенного напряжения и физических характеристик конденсатора, таких как его размер.

Количество заряда

Q  Конденсатор может хранить

Количество заряда [латекс]{Q}[/latex], который может хранить конденсатор , зависит от двух основных факторов: приложенного напряжения и физических характеристик конденсатора. , например, его размер.

Система, состоящая из двух одинаковых параллельных проводящих пластин, разделенных расстоянием, как показано на рисунке 2, называется конденсатором с параллельными пластинами. Легко увидеть взаимосвязь между напряжением и накопленным зарядом для плоского конденсатора, как показано на рисунке 2. Каждая линия электрического поля начинается с отдельного положительного заряда и заканчивается отрицательным, так что поле будет больше. линии, если есть больше заряда. (Рисовать одну силовую линию для каждого заряда — это только для удобства. Мы можем нарисовать много силовых линий для каждого заряда, но их общее число пропорционально количеству зарядов.) Таким образом, напряженность электрического поля прямо пропорциональна [латексной ]{Q}[/латекс]

Рисунок 2. Линии электрического поля в этом плоском конденсаторе, как всегда, начинаются с положительных зарядов и заканчиваются с отрицательными зарядами. Поскольку напряженность электрического поля пропорциональна плотности силовых линий, она также пропорциональна количеству заряда на конденсаторе.

Поле пропорционально заряду:

[латекс]{E \propto Q},[/латекс]

, где символ [латекс]{\пропто}[/латекс] означает «пропорционально». Из обсуждения в главе 19.2 Электрический потенциал в однородном электрическом поле, мы знаем, что напряжение на параллельных пластинах равно [латекс]{V = Ed}[/латекс]. Таким образом,

[латекс] {V \propto E}.[/латекс]

Отсюда следует, что [latex]{V \propto Q}[/latex], и наоборот,

[латекс]{Q \propto V}.[/латекс]

В общем случае это верно: чем больше напряжение, приложенное к любому конденсатору, тем больший заряд в нем хранится.

Различные конденсаторы сохраняют различное количество заряда при одном и том же приложенном напряжении в зависимости от их физических характеристик. Мы определяем их емкость [латекс]{C}[/латекс] так, чтобы заряд [латекс]{Q}[/латекс], хранящийся в конденсаторе, был пропорционален [латексу]{С}[/латексу]. Заряд, хранящийся в конденсаторе, равен 9.0005

[латекс]{Q = CV}. [/латекс]

Это уравнение выражает два основных фактора, влияющих на количество накопленного заряда. Этими факторами являются физические характеристики конденсатора, [латекс]{C}[/латекс], и напряжение, ВВ . Преобразовывая уравнение, мы видим, что емкость [латекс]{C}[/латекс]  – это количество накопленного заряда на вольт, или

.

[латекс] {C =} [/латекс] [латекс] {\ гидроразрыва {Q} {V}}. [/латекс]

Емкость

Емкость [латекс]{C}[/латекс] — это количество заряда, накопленного на вольт, или

[латекс] {C =} [/латекс] [латекс] {\ гидроразрыва {Q} {V}}. [/латекс]

Единицей измерения емкости является фарад (Ф), названный в честь Майкла Фарадея (1791–1867), английского ученого, внесшего вклад в области электромагнетизма и электрохимии. Поскольку емкость — это заряд на единицу напряжения, мы видим, что фарад — это кулон на вольт, или

.

[латекс] {1 \;\textbf{F} =}[/латекс] [латекс]{\ гидроразрыва {1 \;\текст{C}}{1 \;\текст{V}}}. {-3} \;\textbf{F})}[/latex].

На рис. 3 показаны некоторые распространенные конденсаторы. Конденсаторы в основном изготавливаются из керамики, стекла или пластика, в зависимости от назначения и размера. Как обсуждается ниже, в их конструкции обычно используются изоляционные материалы, называемые диэлектриками.

Рисунок 3. Некоторые типовые конденсаторы. Размер и значение емкости не обязательно связаны. (кредит: Уинделл Оскей)

Конденсатор с параллельными пластинами, показанный на рисунке 4, имеет две идентичные проводящие пластины, каждая из которых имеет площадь поверхности [латекс]{A}[/латекс], разделенную расстоянием [латекс]{d}[/латекс] (без материала между тарелки). Когда к конденсатору прикладывается напряжение [латекс]{V}[/латекс], он накапливает заряд [латекс]{Q}[/латекс], как показано на рисунке. Мы можем увидеть, как его емкость зависит от [латекс]{А}[/латекс] и [латекс]{d}[/латекс], рассматривая характеристики кулоновской силы. Мы знаем, что одинаковые заряды отталкиваются, разноименные притягиваются, а сила между зарядами уменьшается с расстоянием. Поэтому кажется вполне разумным, что чем больше пластины, тем больше заряда они могут хранить, потому что заряды могут распространяться дальше. Таким образом, [латекс]{C}[/латекс] должен быть больше для большего [латекса]{А}[/латекс]. Точно так же, чем ближе пластины друг к другу, тем сильнее притяжение к ним противоположных зарядов. Таким образом, [латекс]{C}[/латекс] должен быть больше для меньшего [латекса]{d}[/латекс].

Рисунок 4. Конденсатор с параллельными пластинами с пластинами, разделенными расстоянием d . Каждая пластина имеет площадь A .

Можно показать, что для конденсатора с плоскими пластинами есть только два фактора ([латекс]{А}[/латекс] и [латекс]{d}[/латекс]), которые влияют на его емкость [латекс]{С}[ /латекс]. Емкость конденсатора с плоскими пластинами в виде уравнения равна

.

[латекс] {C = {\ varepsilon}_0} [/латекс] [латекс] {\ гидроразрыва {A} {d}}. [/латекс] 92}[/латекс]. Небольшое числовое значение [латекс] {{\ varepsilon}_0} [/латекс] связано с большим размером фарада. Плоский конденсатор должен иметь большую площадь, чтобы иметь емкость, приближающуюся к фарадам. (Обратите внимание, что приведенное выше уравнение справедливо, когда параллельные пластины разделены воздухом или свободным пространством. Когда между пластинами помещается другой материал, уравнение модифицируется, как описано ниже.)

Пример 1. Емкость и заряд в конденсаторе с параллельными пластинами

93 \;\text{V}}[/latex] применяется к нему?

Стратегия

Нахождение емкости [латекс]{С}[/латекс] является прямым применением уравнения [латекс]{С = {\varepsilon}_0 А/д}[/латекс]. Как только [латекс]{C}[/латекс] найден, накопленный заряд можно найти с помощью уравнения [латекс]{Q = CV}[/латекс].

Решение для (a)

Ввод данных значений в уравнение для емкости плоского конденсатора дает

[латекс]\begin{array}{r @{{}={}} l} { C} & {\varepsilon}_0 \frac{A}{d} = (8,85 \times 10^{-12} \;\frac{F}{m}) \frac{1,00 \;\text{m} ^2}{1. {-9} \;\textbf{F} = 8,85 \;\text{nF}}. \end{array}[/latex]

Обсуждение для (a)

Это маленькое значение емкости показывает, насколько сложно сделать устройство с большой емкостью. Помогают специальные методы, такие как использование тонкой фольги очень большой площади, расположенной близко друг к другу.

Решение для (b)

Заряд, хранящийся в любом конденсаторе, определяется уравнением [латекс]{Q = CV}[/латекс]. Ввод известных значений в это уравнение дает 96 \;\text{V} / \text{m}}[/latex], на этом конденсаторе нельзя накопить больше заряда за счет увеличения напряжения.

Еще один интересный биологический пример, связанный с электрическим потенциалом, обнаружен в плазматической мембране клетки. Мембрана отделяет клетку от окружающей среды, а также позволяет ионам избирательно входить и выходить из клетки. На мембране существует разность потенциалов около -70 мВ. Это связано с наличием в клетке в основном отрицательно заряженных ионов и преобладанием положительно заряженного натрия (Na 96 \;\text{V} / \text{m}}. [/latex]

Этого электрического поля достаточно, чтобы вызвать пробой воздуха.

Предыдущий пример подчеркивает сложность сохранения большого количества заряда в конденсаторах. Если [латекс]{d}[/латекс] уменьшить для получения большей емкости, то максимальное напряжение должно быть уменьшено пропорционально, чтобы избежать пробоя (поскольку [латекс]{E = V/d}[/латекс]). Важное решение этой проблемы состоит в том, чтобы поместить изолирующий материал, называемый диэлектриком, между пластинами конденсатора и сделать [латекс]{d}[/латекс] как можно меньше. Мало того, что меньший [латекс]{d}[/латекс] увеличивает емкость, многие изоляторы могут выдерживать более сильные электрические поля, чем воздух, прежде чем разрушиться.

Использование диэлектрика в конденсаторе имеет еще одно преимущество. В зависимости от используемого материала емкость больше, чем указанная уравнением [латекс] {C = {\ varepsilon} _0 \ frac {A} {d}} [/ латекс], на коэффициент [латекс] {\ каппа} [/latex] , называемая диэлектрической проницаемостью . Емкость плоского конденсатора с диэлектриком между пластинами равна

.

[латекс] {C = \ каппа {\ varepsilon} _0} [/ латекс] [латекс] {\ гидроразрыва {A} {d}} [/ латекс] [латекс] {{\ текст {параллельный конденсатор с диэлектриком} )}.[/латекс]

Значения диэлектрической проницаемости [латекс]{\каппа}[/латекс] для различных материалов приведены в таблице 1. Обратите внимание, что [латекс]{\каппа}[/латекс] для вакуума точно равен 1, поэтому приведенное выше уравнение действует и в этом случае. Если используется диэлектрик, возможно, путем помещения тефлона между пластинами конденсатора в примере 1, то емкость увеличивается в [латекс] {\ каппа} [/латекс], что для тефлона составляет 2,1.

Самостоятельный эксперимент: изготовление конденсатора

Насколько большой конденсатор можно сделать из обертки от жевательной резинки? Пластины будут алюминиевой фольгой, а перегородка (диэлектрик) между ними будет бумагой. 96}[/латекс] Вода 80 — Таблица 1. Диэлектрическая проницаемость и диэлектрическая прочность для различных материалов при 20ºC

Также обратите внимание, что диэлектрическая проницаемость воздуха очень близка к 1, так что конденсаторы, заполненные воздухом, действуют так же, как конденсаторы с вакуумом между пластинами , за исключением , что воздух может стать проводящим, если напряженность электрического поля становится слишком большой . (Напомним, что [латекс]{E = V/d}[/латекс] для конденсатора с плоскими пластинами.) В таблице 1 также показаны максимальные значения напряженности электрического поля в В/м, называемые диэлектрической прочностью, для нескольких материалов. Это поля, выше которых материал начинает разрушаться и проводить. Диэлектрическая прочность накладывает ограничение на напряжение, которое может быть приложено для данного разделения пластин. Например, в примере 1 расстояние составляет 1,00 мм, поэтому предел напряжения для воздуха равен 94 \;\text{V})} \\[1em] & {1. 1 \;\text{mC}.} \end{массив}[/latex]

Это в 42 раза больше заряда того же воздушного конденсатора.

Диэлектрическая прочность

Максимальная напряженность электрического поля, выше которой изоляционный материал начинает разрушаться и проводить ток, называется диэлектрической прочностью.

Каким образом диэлектрик увеличивает емкость под микроскопом? В этом виновата поляризация изолятора. Чем легче он поляризуется, тем больше его диэлектрическая проницаемость [латекс] {\ каппа} [/латекс]. Вода, например, является полярной молекулой, потому что один конец молекулы имеет небольшой положительный заряд, а другой конец имеет небольшой отрицательный заряд. Полярность воды приводит к тому, что она имеет относительно большую диэлектрическую проницаемость, равную 80. Эффект поляризации можно лучше всего объяснить с точки зрения характеристик кулоновской силы. На рис. 5 схематично показано разделение заряда в молекулах диэлектрического материала, помещенного между заряженными пластинами конденсатора. Кулоновская сила между ближайшими концами молекул и зарядом на пластинах притягивает и очень велика, так как они очень близко друг к другу. Это притягивает к пластинам больше заряда, чем если бы пространство было пустым, а противоположные заряды находились на расстоянии [латекс]{d}[/латекс].

Рис. 5. (а) Молекулы изоляционного материала между пластинами конденсатора поляризуются заряженными пластинами. Это создает слой противоположного заряда на поверхности диэлектрика, который притягивает больше заряда к пластине, увеличивая ее емкость. (b) Диэлектрик снижает напряженность электрического поля внутри конденсатора, что приводит к меньшему напряжению между пластинами при том же заряде. Конденсатор сохраняет тот же заряд при меньшем напряжении, что означает, что он имеет большую емкость из-за диэлектрика.

Другой способ понять, как диэлектрик увеличивает емкость, — рассмотреть его влияние на электрическое поле внутри конденсатора. На рис. 5(b) показаны силовые линии электрического поля с установленным диэлектриком. Поскольку силовые линии заканчиваются на зарядах в диэлектрике, их меньшее количество проходит от одной стороны конденсатора к другой. Таким образом, напряженность электрического поля меньше, чем если бы между пластинами был вакуум, хотя на пластинах находится тот же заряд. Напряжение между пластинами равно [латекс]{V = Ed}[/латекс], так что диэлектрик тоже снижает его. Таким образом, существует меньшее напряжение [латекс]{V}[/латекс] для того же заряда [латекс]{Q}[/латекс]; поскольку [латекс]{С = Q/V}[/латекс], емкость [латекс]{С}[/латекс] больше.

Диэлектрическая проницаемость обычно определяется как [латекс]{\каппа = E_0/E}[/латекс] или отношение электрического поля в вакууме к электрическому полю в диэлектрическом материале, и она тесно связана с поляризуемостью материал.

Вещи большие и малые

Субмикроскопическое происхождение поляризации

Поляризация — это разделение зарядов внутри атома или молекулы. Как уже отмечалось, планетарная модель атома изображает его как имеющее положительное ядро, вращающееся вокруг отрицательно заряженных электронов, подобно планетам, вращающимся вокруг Солнца.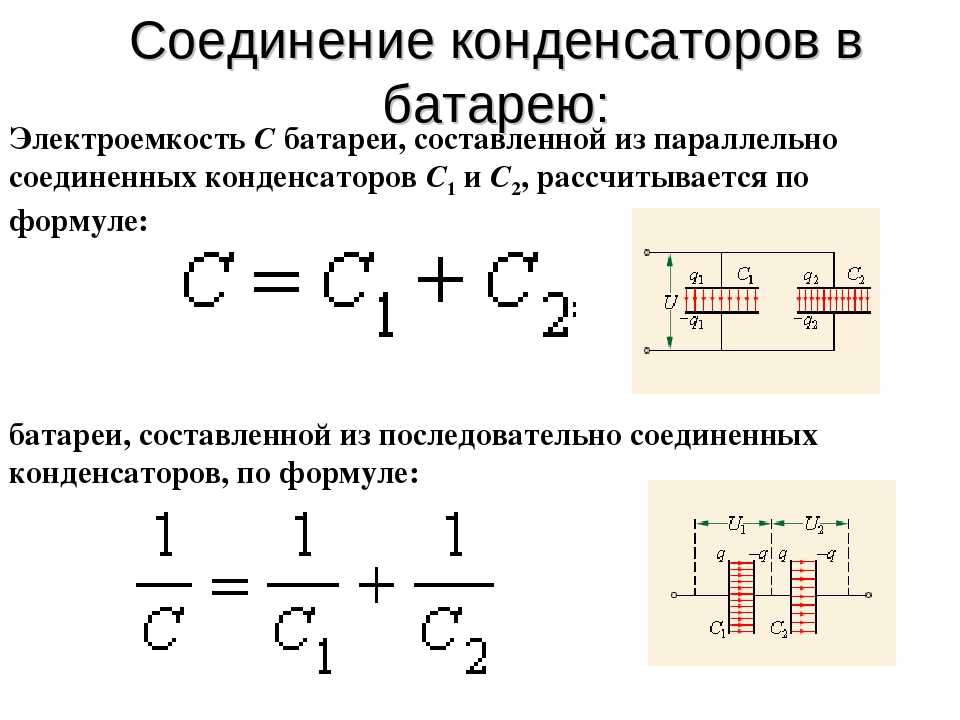 Хотя эта модель не совсем точна, она очень полезна для объяснения широкого круга явлений и будет уточнена в другом месте, например, в главе 30 «Атомная физика». Субмикроскопическое происхождение поляризации можно смоделировать, как показано на рис. 6.9.0005 Рис. 6. Представление художника о поляризованном атоме. Орбиты электронов вокруг ядра немного смещены внешними зарядами (показаны преувеличенно). Возникающее в результате разделение зарядов внутри атома означает, что он поляризован. Обратите внимание, что противоположный заряд теперь ближе к внешним зарядам, вызывая поляризацию.

В главе 30 «Атомная физика» мы найдем, что орбиты электронов правильнее рассматривать как электронные облака с плотностью облака, связанной с вероятностью нахождения электрона в этом месте (в отличие от определенных местоположений и путей планет в их орбиты вокруг Солнца). Это облако смещается кулоновской силой так, что атом в среднем имеет разделение заряда. Хотя атом остается нейтральным, теперь он может быть источником кулоновской силы, поскольку заряд, поднесенный к атому, будет ближе к одному типу заряда, чем к другому.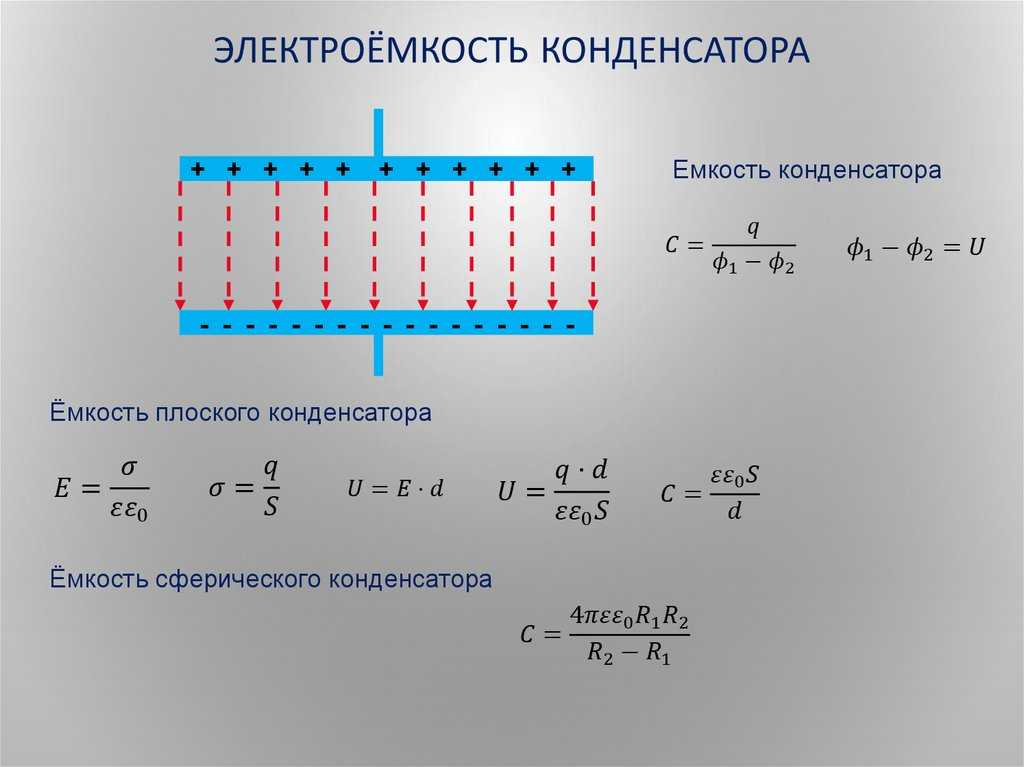

Некоторым молекулам, например молекулам воды, присуще разделение зарядов, поэтому их называют полярными молекулами. Рисунок 7 иллюстрирует разделение заряда в молекуле воды, которая имеет два атома водорода и один атом кислорода [латекс]{\textbf{H}_2 \textbf{O}}[/latex]. Молекула воды несимметрична — атомы водорода отталкиваются в одну сторону, придавая молекуле форму бумеранга. Электроны в молекуле воды более сконцентрированы вокруг более сильно заряженного ядра кислорода, чем вокруг ядер водорода. Это делает кислородный конец молекулы слегка отрицательным, а водородный конец оставляет слегка положительным. Присущее полярным молекулам разделение зарядов облегчает их согласование с внешними полями и зарядами. Поэтому полярные молекулы проявляют больший поляризационный эффект и имеют большую диэлектрическую проницаемость. Те, кто изучает химию, обнаружат, что полярная природа воды имеет множество эффектов. Например, молекулы воды намного эффективнее собирают ионы, потому что они имеют электрическое поле и разделение зарядов для притяжения зарядов обоих знаков. Кроме того, как показано в предыдущей главе, полярная вода обеспечивает защиту или экранирование электрических полей в сильно заряженных молекулах, представляющих интерес в биологических системах.

Рисунок 7. Представление художника о молекуле воды. Существует неотъемлемое разделение зарядов, поэтому вода является полярной молекулой. Электроны в молекуле притягиваются к ядру кислорода и оставляют избыток положительного заряда вблизи двух ядер водорода. (Обратите внимание, что схема справа представляет собой грубую иллюстрацию распределения электронов в молекуле воды. На ней не показано фактическое количество протонов и электронов, участвующих в структуре.)

PhET Explorations: Capacitor Lab

Узнайте, как работает конденсатор! Измените размер пластин и добавьте диэлектрик, чтобы увидеть влияние на емкость. Измените напряжение и увидите заряды на пластинах. Наблюдайте за электрическим полем в конденсаторе. Измерьте напряжение и электрическое поле.

Рис. 8. Конденсаторная лаборатория

• Конденсатор — это устройство, используемое для накопления заряда.
• Количество заряда [латекса]{Q}[/латекса], которое может хранить конденсатор, зависит от двух основных факторов: приложенного напряжения и физических характеристик конденсатора, таких как его размер.
• Емкость [латекс]{C}[/латекс] представляет собой количество накопленного заряда на вольт , или

  [латекс] {C =} [/латекс] [латекс] {\ гидроразрыва {Q} {V}}. [/латекс]

• Емкость плоского конденсатора равна [латекс]{C = {\varepsilon}_0 \;\frac{A}{d}}[/латекс], когда пластины разделены воздухом или свободным пространством. [latex][{\varepsilon}_0}[/latex] называется диэлектрической проницаемостью свободного пространства.
• Емкость плоского конденсатора с диэлектриком между пластинами определяется выражением

  [латекс] {C = \ каппа {\ varepsilon} _0} [/ латекс] [латекс] {\ гидроразрыва {A} {d}}, [/латекс]

  , где [латекс]{\каппа}[/латекс] — диэлектрическая проницаемость материала.

• Максимальная напряженность электрического поля, выше которой изоляционный материал начинает разрушаться и проводить ток, называется диэлектрической прочностью.

 

 

конденсатор

устройство, накапливающее электрический заряд

емкость

количество накопленного заряда на единицу вольта

диэлектрик

изоляционный материал

диэлектрическая прочность

максимальное электрическое поле, выше которого изоляционный материал начинает разрушаться и проводить

плоский конденсатор

две одинаковые проводящие пластины, разделенные расстоянием

полярная молекула

молекула с присущим разделением зарядов

 

Как работают конденсаторы как измерить накопленный заряд формулы

Конденсаторы

30. 01.2022 | Просмотров: 2799 | Схемы | от: ELECTRONOOBS

Доля

Сегодня я буду использовать конденсатор с плоскими пластинами для некоторых экспериментов. Сегодня мы начнем с первого класса и речь пойдет о конденсаторах. Я хочу показать вам, как они работают, некоторые связанные уравнения с конденсаторами, какие типы у нас есть и как площадь, диэлектрик и расстояние между пластинами могут повлиять на характеристики конденсатора. Кроме того, мы увидим, как измерить накопленный заряд внутри конденсатора, используя несколько классных формул.

Часть 1. Как работают конденсаторы?

Итак, как работает доза конденсатора? Что ж, самое простое представление конденсатора — это две проводящие пластины, подобные приведенным ниже, расположенные рядом друг с другом, но никогда не касаются , и обычно между ними находится какой-то диэлектрик , и мы увидим, какой диэлектрик находится в данный момент. С другой стороны, мы знаем, что электроны имеют отрицательный заряд. Отрицательное с отрицательным будет отталкивать друг друга, а положительное с отрицательным притягиваться, все благодаря электрическим полям. Идея конденсатора состоит в том, чтобы хранить эти электроны на своих металлических пластинах. Но вы видите, вы не можете добавить больше электронов к металлу, потому что они будут вытеснены другими электронами, которые уже есть в металле. Если только вы не нанесете положительный заряд на другую сторону, чтобы они притянулись. Эта сила притяжения (электрическое поле) могла бы преодолеть толкающую силу, создаваемую электронами, отталкивающими друг друга, и, таким образом, на металлических пластинах конденсатора накапливался бы больший заряд. Чем больше это электрическое поле, тем больше заряда мы можем передать металлической пластине.

Для создания отрицательного и положительного заряда мы прикладываем к пластинам дифференциальное напряжение , но пластины никогда не касаются друг друга. С помощью этой разницы потенциалов мы теперь можем выталкивать электроны на правую пластину и высасывать их из левой пластины, создавая положительный заряд. Поскольку металлические пластины не соприкасаются, электроны не могут перейти на другую сторону, чтобы заполнить положительные отверстия. Но между положительным и отрицательным зарядом существует электрическая сила, и эта сила удерживает их вместе. Так что даже если я отключу подачу напряжения, так как заряду некуда деться, конденсатор сохранит свой заряд. Вот как мы можем хранить энергию внутри конденсатора.

Часть 2 — Типы конденсаторов

А что, если я подключу аккумулятор наоборот. У этого идеального конденсатора левая и правая металлические пластины одинаковы, поэтому он будет работать без проблем. Но в зависимости от материалов, которые мы используем для изготовления конденсаторов, это может быть проблемой, и это может случиться с вашим конденсатором. Видите ли, есть несколько типов материалов, которые мы могли бы использовать для изготовления конденсаторов, таких как керамика , тантал, электролит, полимер, слюда, пленка или кремний 9. 0025, и у каждого из них есть свои особенности.

Например, для электролитических и танталовых конденсаторов эти материалы делают их поляризованными, и мы используем такие символы, чтобы обозначить их как поляризованные или неполяризованные. Мы можем видеть электролитический или танталовый конденсатор с линией, указывающей на отрицательный контакт. Если вы разместите их задом наперёд, они могут не сработать или даже взорваться. Посмотрите видео ниже и посмотрите, как взрываются конденсаторы !

Часть 3 — Диэлектрик

Итак, это была основная часть о конденсаторах. До сих пор между металлическими пластинами у нас был воздух. Мы называем материал между пластинами диэлектриком , а в электромагнетизме это электрический изолятор, который может поляризоваться электрическим полем. Воздух — это диэлектрик, пластик — еще один диэлектрик, резина может быть диэлектриком, стекло или даже дерево — диэлектриком для конденсаторов. Но в зависимости от используемого материала для диэлектрика свойства конденсатора будут меняться. Единицей измерения конденсаторов является емкость, которая измеряется в фарадах в честь Майкла Фарадея. Эта емкость идеально равна площади пластин, деленной на расстояние между пластинами и умноженной на электростатическую постоянную. Эта константа равна эпсилон 0, умноженному на эпсилон r, где эпсилон 0 — диэлектрическая проницаемость пустоты, а эпсилон r — диэлектрическая проницаемость используемого материала. Таким образом, очевидно, что на емкость конденсатора влияет материал, из которого изготовлен диэлектрик.

Ниже приведена таблица с различными материалами и каждой соответствующей диэлектрической проницаемостью. Как вы можете видеть, воздух имеет диэлектрическую проницаемость 1. Но стекло, например, имеет диэлектрическую проницаемость от 5 до 10, поэтому очевидно, используя формулу выше, если расстояние и площадь остаются прежними, но мы меняем диэлектрик с воздуха на стекла, емкость должна быть выше.

Часть 4 — Расстояние между пластинами

Из той же формулы мы также можем видеть, что емкость может меняться в зависимости от расстояния. Чем меньше расстояние между пластинами, тем выше будет емкость. Опять же, я измеряю емкость этих двух металлических пластин. Теперь я уменьшаю расстояние между ними. Как видите, емкость теперь выше. И он станет ниже, если я увеличу расстояние. Чтобы получить очень высокие значения, производители используют очень тонкие материалы, свернутые вместе, чтобы проводящий материал всегда был изолирован. Таким образом, у нас есть огромная площадь и очень небольшое расстояние между ними, что приводит к высоким значениям емкости.

Часть 5 — Площадь конденсатора

Чем больше общая площадь, тем выше будет емкость. В этом примере, когда я сдвигаю одну пластину в сторону, общая площадь становится меньше, поэтому, как вы можете видеть, емкость уменьшается. На самом деле, мы можем видеть это с переменными конденсаторами, такими как этот здесь. Вращением ручки можно разделить большую или меньшую площадь, поэтому значение становится выше или ниже. И, как я уже говорил вам ранее, чтобы получить наибольшую площадь и минимальный объем, производители упаковывают конденсаторы вот так, где проводник и диэлектрик свернуты вместе в цилиндре.

Часть 6. Расчет накопленного заряда

Другая формула состоит в том, что электрическое поле равно приложенному напряжению, деленному на расстояние. Электрическое поле должно быть постоянным, так что произойдет, если я увеличим расстояние с тем же напряжением. Что ж, еще один эксперимент, который мы можем провести с этими пластинами, — вычислить накопленный заряд внутри конденсатора. Что нам нужно сделать, так это зарядить пластины, скажем, до 12 В, когда расстояние составляет 1 мм, а затем отключить источник питания.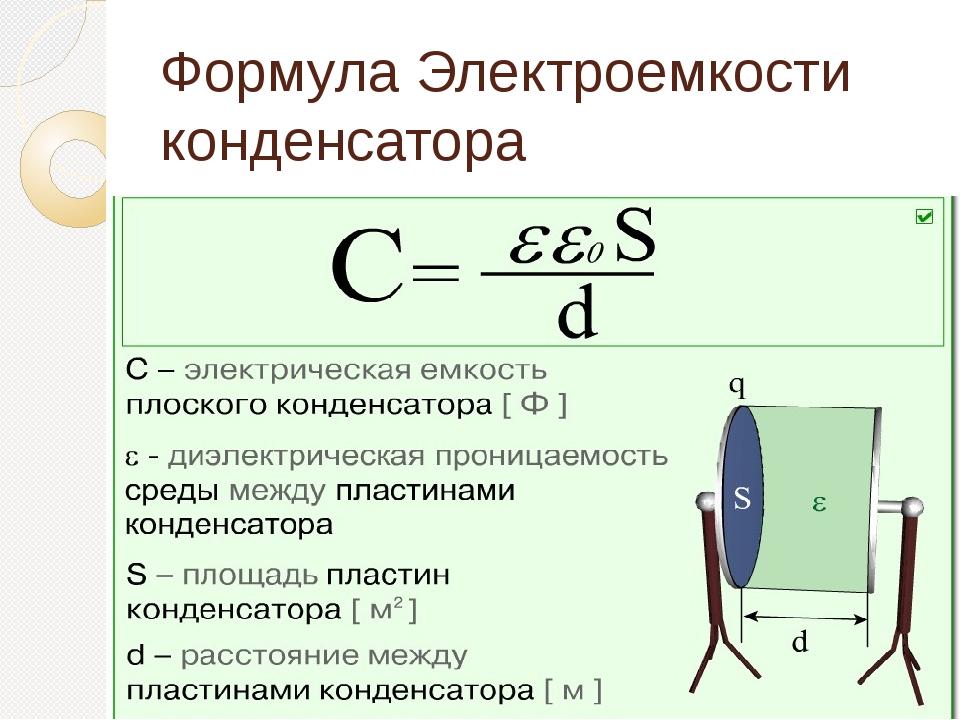 Затем увеличиваем расстояние при измерении напряжения и расстояния, и по формуле ранее, так как поле должно быть постоянным, напряжение должно увеличиваться. Мы можем сделать замеры и составить таблицу, где у нас есть напряжение и расстояние в мм. Затем мы передаем эти значения в инвертированные значения, то есть 1 делим на напряжение и 1 делим на расстояние. Мы наносим эти значения на график и делаем линейную регрессию этой линии в Excel. Это даст уравнение, которое мы могли бы использовать, в приведенном ниже примере y = 0,0545x + 0,0336.

Это уравнение на самом деле представляет 1/V = a * 1/d + b. Теперь мы получаем это 0,0545 и называем его, например, «а». Затем из этих двух других формул и предыдущего уравнения мы можем получить, что Q, который представляет собой накопленный заряд, равен эпсилону 0, умноженному на площадь конденсатора, деленному на это число «а». Поскольку мой конденсатор круглый, площадь в моем случае равна пи R в квадрате, где R — радиус моей металлической пластины, и мы можем легко это измерить.