Логические элементы для зануд

Зануд не любят, но все мы ими бываем. Мимо самоделки, сделанной родственной душой, я пройти не смог. Глядите, какая необычная.
Считается, что логические элементы, содержащие инверторы — И-НЕ, ИЛИ-НЕ и исключающее ИЛИ-НЕ — невозможно выполнить на одних только диодах и резисторах. Но автор Hackaday под очень прикольным ником Dr. Cockroach (представьте себе таракана с фонендоскопом — смешно?) проявил немного занудства и сделал вывод, что светодиод — разновидность диода, а фоторезистор — разновидность резистора. Ага, значит, всё-таки можно!
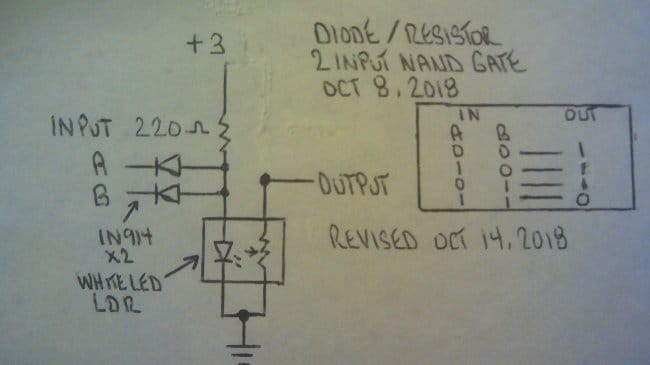
Вначале он изготовил оптопару из светодиода и фоторезистора, после чего включил её в такую схему:
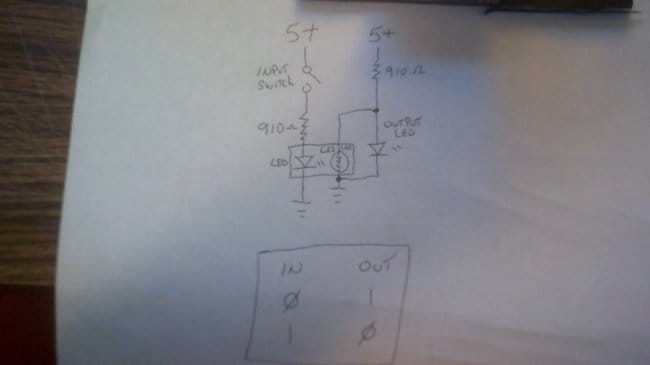
Индикаторный светодиод — тот, который не входит в состав оптопары, а виден пользователю — он подключил не последовательно с фоторезистором, а параллельно ему. Когда включён светодиод оптопары, сопротивление фоторезистора становится меньше сопротивления резистора, через который питается индикаторный светодиод. То, что при этом происходит, по-научному называется шунтированием. Индикаторный светодиод выключается. А если выключить светодиод оптопары, индикаторный, наоборот, включится, поскольку шунтирование прекратится. Значит, получился инвертор на одних диодах и резисторах. Первый логический элемент для зануд заработал!
Но оптопара, конечно, громоздкая получилась. Сейчас Dr. Cockroach это исправит.

Теперь компактнее. Только свет снаружи проникать будет. В общем, не просто так люди изобрели термоусадку. Она как раз пригодится!

Вместо индикаторного светодиода к выходу инвертора можно подключить светодиод другой оптопары, то есть, из таких логических элементов можно составлять сложные схемы. Но на одних инверторах далеко не уедешь. Понимая это, мастер добавил обычные, несветящиеся диоды и сделал симпатичный элемент И-НЕ:

Если в этой схеме переполюсовать обычные диоды и исключить левый резистор, получится элемент ИЛИ-НЕ. Теперь, когда сами элементы разработаны, мастер задумывается о том, где их применить, и делает такую штуку:

Это — RS-триггер. Два элемента И-НЕ в нём применены в качестве инверторов (оба входа соединены), два других таких же — по прямому назначению. Посмотрите на схему:
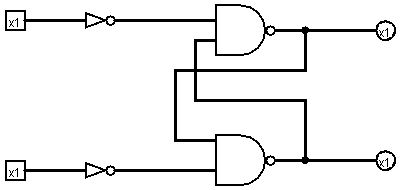
«Доктор Таракан» проверяет её:
Работает, как и подобает RS-триггеру.
Разобрав несколько ночников, Dr. Cockroach обнаружил в каждом из них по фоторезистору и маленькой плате с SMD-светодиодом. Из них он тоже сделал оптопары, а потом подумал: зачем для каждого логического элемента делать довольно крупную плату, если резисторы и обычные диоды можно очень компактно разместить, используя объёмный монтаж? Сравните новые логические элементы со старыми — разница в габаритах значительная!

Выводы у них расположены так:

Испытания в полном разгаре, и судя по отсутствию криков и ударов кулаком об стол, всё работает как задумывалось:
На обычных логических элементах строят не только триггеры, но и мультивибраторы. На «занудных», оказывается, тоже можно. И на не-SMD-шных:
И на SMD-шных:
Помню, был фантастический фильм про роботов, размножающихся разборкой разных железок и сборкой из их деталей себе подобных. Очень похоже на одного из них:

Руководствуясь электрической и логической схемами, вы тоже можете повторить эксперимент мастера:
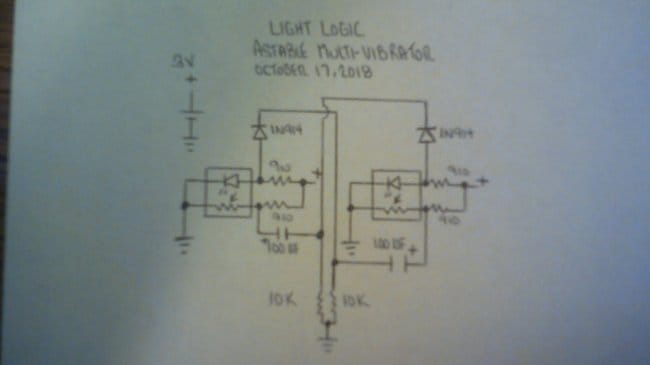
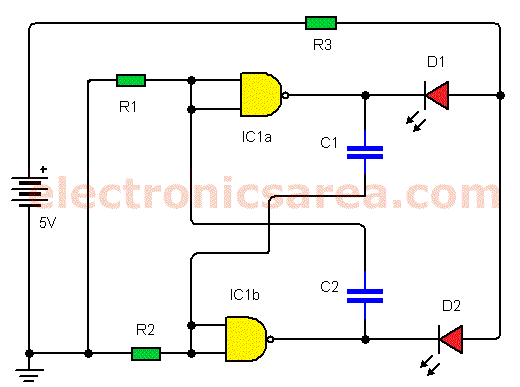
Обратите внимание, что на первой из схем Dr. Cockroach не показал индикаторные светодиоды и резистор для них.
Затем мастер посмотрел на схему элемента И-НЕ ещё раз и понял: подтягивающий резистор на выходе не обязателен, потому что он есть на входе следующего такого же элемента. Разумеется, если следующий элемент — ИЛИ-НЕ, где подтягивающего резистора нет как раз на входе, работать ничего не будет. Но элементы ИЛИ-НЕ «Доктор Таракан» решил больше не применять, потому что в них происходит некоторая потеря напряжения логического уровня. Элементы ИЛИ всегда можно сделать из инверторов и элементов И-НЕ, которые теперь устроены так:
Так работает цепь из мультивибратора и элемента И-НЕ:
И решил мастер: а не замахнуться ли ему на целый JK-триггер?
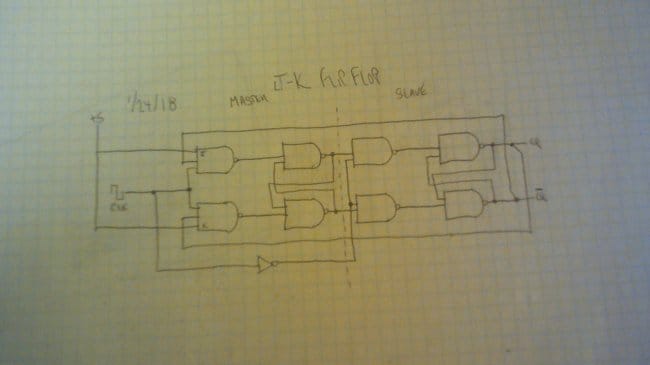
А чтобы получилось брутальнее и нагляднее, собрал всё это Dr. Cockroach из логических элементов хоть и с SMD-шными оптопарами, но на переходных платах:

Так оно работает при тактировании мультивибратором. Схема очень критична к напряжению питания.
Ну а элемент в не-SMD-шном варианте он, наоборот, сделал миниатюрным, с применением объёмного монтажа, и придал ему вертикальную форму, чтобы было похоже на транзистор:
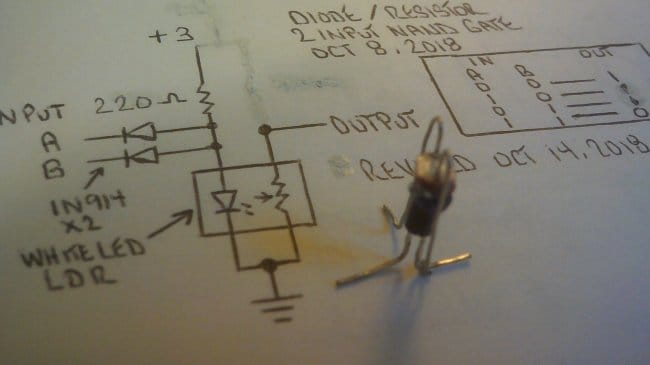
По поведению такая оптопара тоже подобна транзистору, и не полевому, а биполярному. Ибо управляется током.
Эти логические элементы работают на низких частотах, поэтому за их работой удобно наблюдать при помощи программного осциллографа на компьютере или смартфона. Dr. Cockroach для начала попробовал теоретически рассчитать форму сигнала на выходах мультивибратора при частоте в 43 Гц и точном подборе напряжения питания:
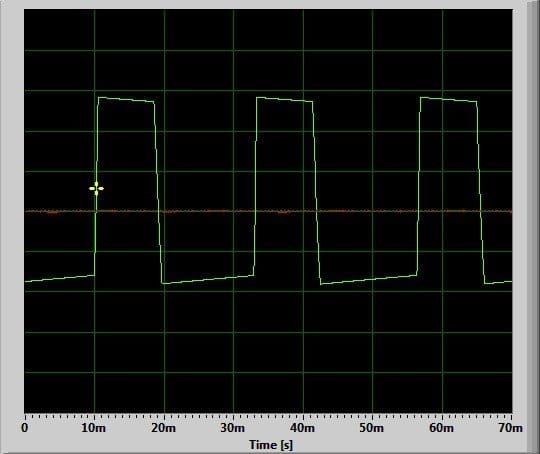
Реальный сигнал при 19,8 Гц:
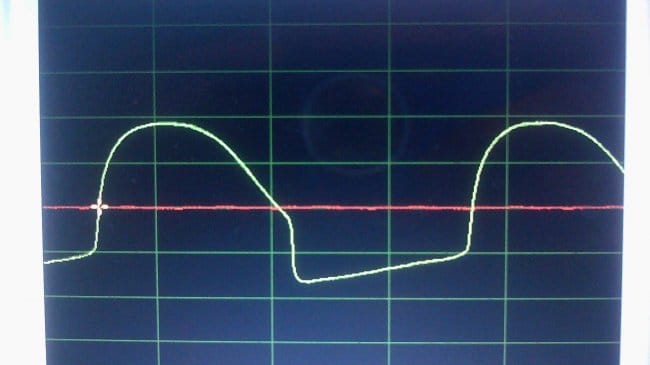
Он же, после инвертирования:
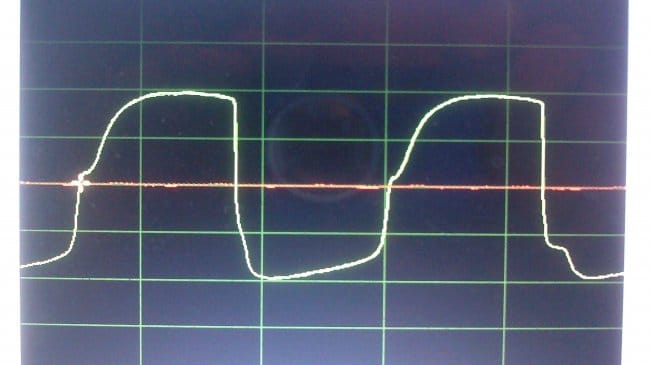
А вот что будет, если частоту увеличить до 42,2 Гц:
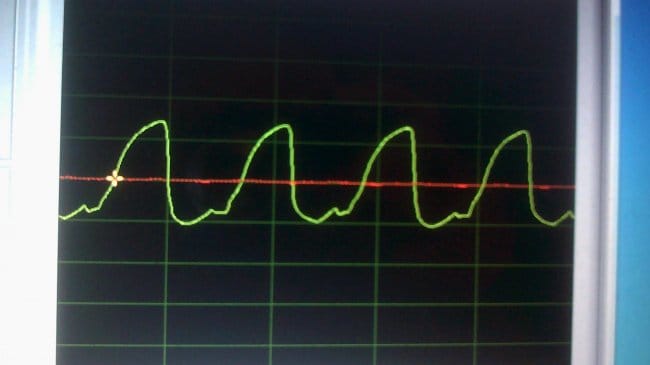
«Доктор Таракан» пришёл к выводу, что искажают форму сигнала паразитные ёмкости в фоторезисторе.
Мастер экспериментирует со светодиодами габарита 0402. Они так малы, что любой из них по сравнению с фоторезистором — крошка:

И всё работает:
Но поскольку логический элемент вновь собран не объёмным монтажом…

Мастер приделал к JK-триггеру другой мультивибратор и любуется результатом:
А теперь он делится схемами элементов НЕ, И-НЕ и ИЛИ-НЕ, причём в третьем оптопара содержит два светодиода. Непонятно, правда, как это согоасуется с тем, что ранее он хотел от ИЛИ-НЕ отказаться вообще.
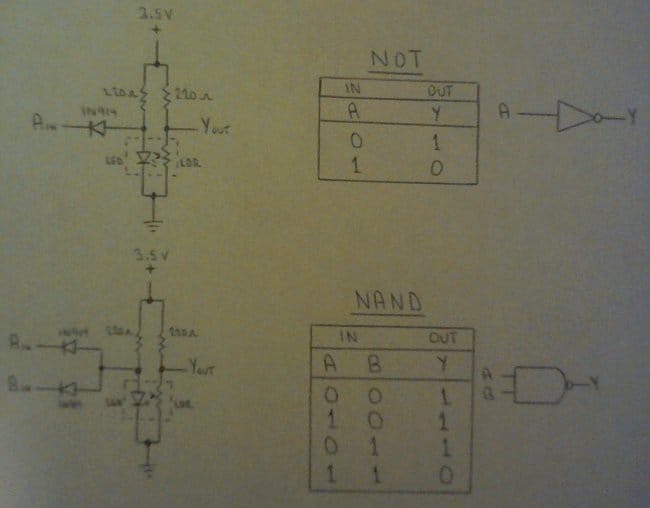
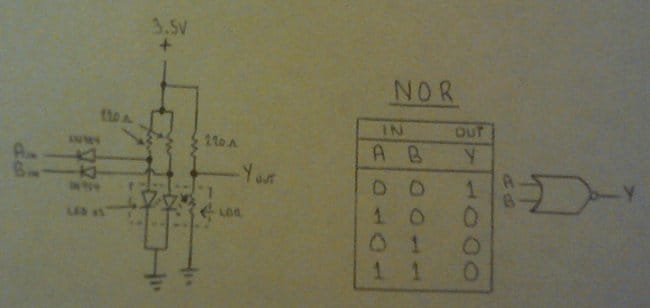
Dr. Cockroach решил попробовать сделать на оптопаре линейный усилитель — не всё же логическими элементами ограничиваться. Получился именно усилитель — с ним при одной и той же амплитуде входного сигнала звук громче, чем без него. Только никогда так не делайте — если в схеме есть источник постоянной составляющей, источник сигнала надо подключать не напрямую, а через конденсатор.
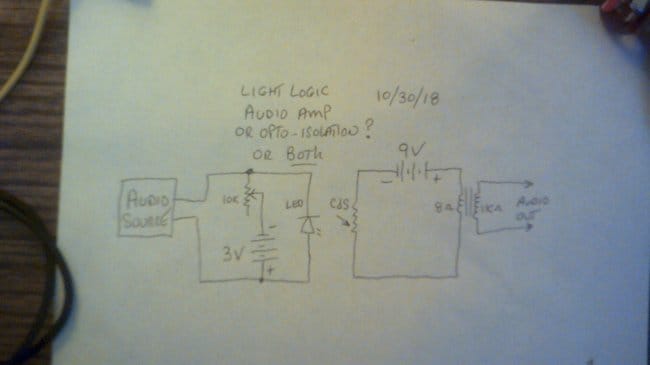
А это — микросхема, точнее, микросборка с четырьмя элементами И-НЕ, прямо как в нашей любимой К155ЛА3!

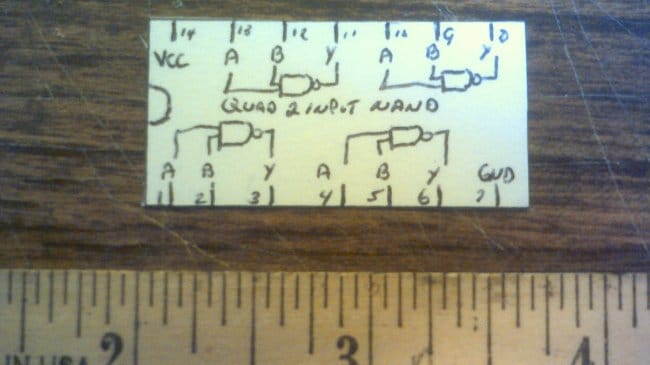
Где аналог К155ЛА3, там и D-триггер — для него требуются как раз четыре логических элемента И-НЕ. Как и микросхему-прототип, самодельную микросборку можно превратить в такой триггер добавлянием только одних проводов.

Чтобы управлять триггером, мастер построил неказистый, но отлично работающий пульт. На этот раз, конечно, снова всё получилось:
RS-триггер может быть значительно упрощён, если не составлять его из логических элементов, а применить знакомый каждому электрику принцип самоблокирующегося реле. Только чуть видоизменённый, так что сразу на обе кнопки нажимать нельзя — источник питания закоротите:
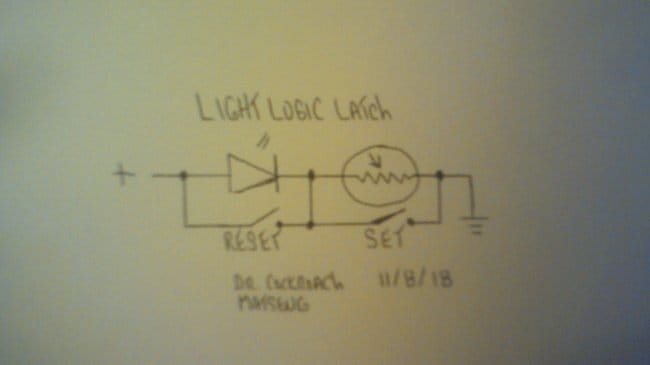
Свободен от этого недостатка другой триггер, чуть более сложный. В нём снова на один и тот же фоторезистор направлены сразу два светодиода:
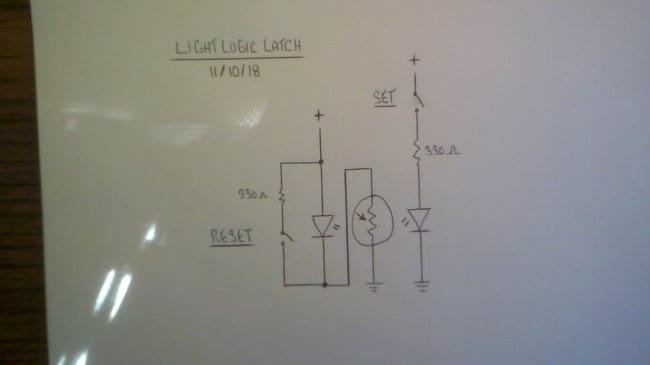
Чтобы у триггера был выход, «Доктор Таракан» ещё несколько усложнил схему (где теперь, наоборот, один светодиод светит сразу на два фоторезистора) и добавил инвертор:
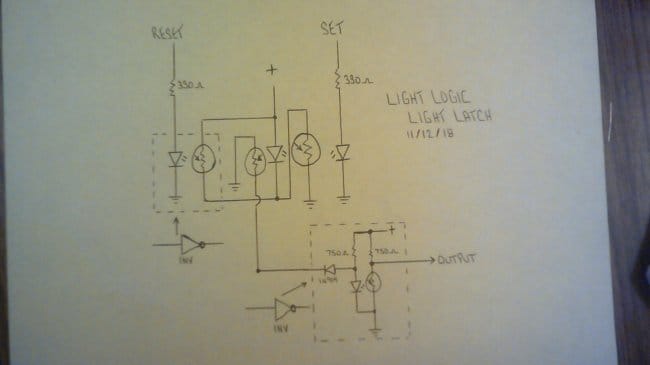
Снова всё работает:
Чтобы сделать одновибратор с нерегулируемой длительностью импульса на выходе, Dr. Cockroach подаёт на один вход элемента И входной сигнал непосредственно, а на другой — тот же сигнал, но пропущенный через цепочку из трёх инверторов. Что, в общем-то, эквивалентно одному инвертору, только задержка более длительная:
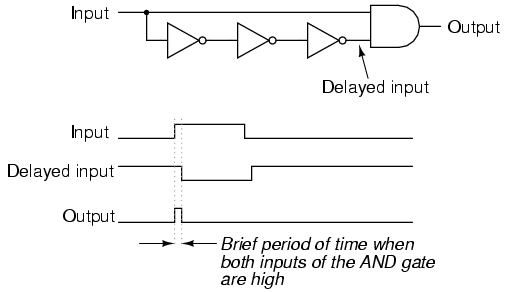
Ну вот, на вход поступают длинные импульсы, на выходе получаются короткие. То, что надо!
Ну а впереди у мастера — целый счётчик из триггеров, только он пока не готов:
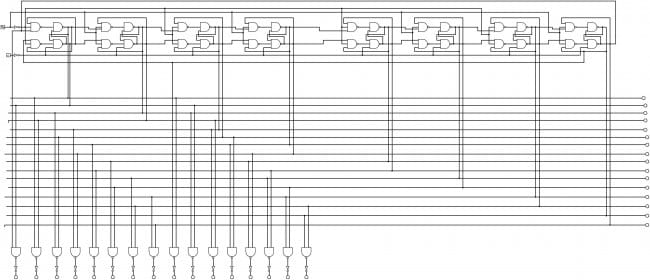
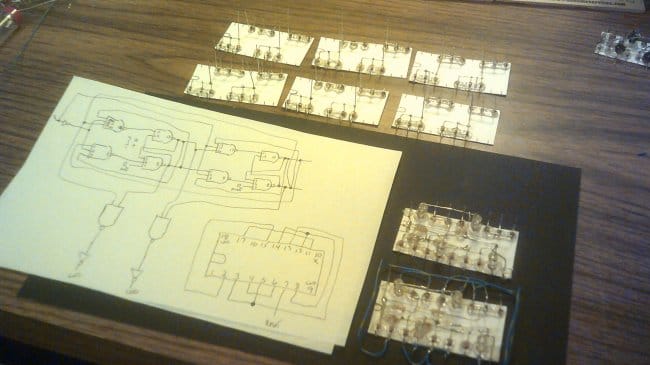
Надеюсь, теперь читатель будет чуточку лояльнее относиться к занудам. Один из которых доказал, что инвертирующие логические элементы на одних диодах и резисторах возможны, если светодиод считать бродом, а фоторезистор — резистором. И столько всего сделал интересного. А этот счётчик у него тоже обязательно получится.
В общем, быть занудой — это здорово!
Источник
 Доставка новых самоделок на почту
Доставка новых самоделок на почтуПолучайте на почту подборку новых самоделок. Никакого спама, только полезные идеи!
*Заполняя форму вы соглашаетесь на обработку персональных данных
Становитесь автором сайта, публикуйте собственные статьи, описания самоделок с оплатой за текст. Подробнее здесь.§21. Элементы схемотехники. Логические схемы
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 10 классы | Планирование уроков на учебный год (ФГОС) | Элементы схемотехники. Логические схемы

 |
21.1. Логические элементы |  |
||
| Элементы схемотехники. Логические схемы |  |
21.2. Сумматор |

21.1. Логические элементы
 Логический элемент — это устройство с л входами и одним выходом, которое преобразует входные двоичные сигналы в двоичный сигнал на выходе.
Логический элемент — это устройство с л входами и одним выходом, которое преобразует входные двоичные сигналы в двоичный сигнал на выходе.
Работу любого логического элемента математически удобно описать как логическую функцию, которая упорядоченному набору из нулей и единиц ставит в соответствие значение, также равное нулю или единице.
В схемотехнике широко используются логические элементы, представленные в таблице 4.2.
Таблица 4.2
Условные обозначения типовых логических элементов
Логический элемент И (конъюнктор) реализует операцию логического умножения. Единица на выходе этого элемента появится тогда и только тогда, когда на всех входах будут единицы.
Опишите подобным образом логические элементы ИЛИ (дизъюнктор), НЕ (инвертор), И-НЕ, ИЛИ-НЕ.
Однотипность сигналов на входах и выходах позволяет подавать сигнал, вырабатываемый одним элементом, на вход другого элемента. Это позволяет из двухвходовых элементов «собирать» многовходовые элементы (рис 4.7), а также синтезировать произвольные комбинационные схемы, соединяя в цепочки отдельные логические элементы.
Рис. 4.7. Схема и обозначение четырёхвходового конъюнктора
Пример. По заданной логической функции F(A, В) = & В v А & построим комбинационную схему (рис. 4.8).
Построение начнём с логической операции, которая должна выполняться последней. В данном случае такой операцией является логическое сложение, следовательно, на выходе логической схемы должен быть дизъюнктор. На него сигналы подаются с двух конъюнкторов, на которые в свою очередь подаются один входной сигнал нормальный и один инвертированный (с инверторов).
Рис. 4.8. Комбинационная схема функции F(A, В) = & В v А &
Cкачать материалы урока
Логические элементы и их релейные эквиваленты
С помощью логических элементов довольно легко реализуются функции алгебры логики, которая является костяком устройств автоматики и вычислительных машин. Логические элементы могут реализовываться огромным количеством способов в зависимости от надобности и состоять из полупроводниковых, релейных, интегральных, пневматических и других элементов и схем.
Между величинами, входящими и выходящими из логического элемента, существует определенная зависимость, которая называется функциональной и обозначается как y = f(x) для устройств с одной переменной и как y = f(x1, x2) для устройств с двумя переменными величинами. В этой записи Х называют независимую переменную или аргумент, а Y – зависимая переменная, так как ее значение напрямую зависит от значения аргумента Х.
Ниже показана таблица логических элементов и эквивалентных им положений контактов реле:

Функция повторения
Реализуется логическим элементом повторителем (пункт 1 в таблице). Повторитель можно сравнить с нормально открытым контактом реле. При открытом контакте Х=0 и, соответственно Y=0, то есть цепь находится в непроводящем состоянии, а при закрытом наоборот Х=1 и Y=1, то есть цепь находится в проводящем состоянии.
Функция отрицания
Реализует данную функцию логический элемент НЕ или как его часто называют – инвертор (пункт 2 в таблице). Его сравнивают с нормально закрытым контактом реле, когда при отсутствии напряжения на катушке управления (Х=0) его контакт находится в проводящем состоянии (Y=1). При подаче напряжения на катушку (Х=1) контакт размыкается и разрывает цепь (Y=0).
Функция логического сложения
В схемотехнике носит название дизъюнкция или функция ИЛИ (пункт 3 в таблице). Реализуема эта функция логическим элементом дизъюнктором. Суть данной операции заключается в логическом суммировании входных сигналов X для получения результирующего сигнала на выходе Y. Описывается данная зависимость простой формулой X1 + X2 = Y. Вот примеры – 0+0=1, 1+0=1,0+1=1,1+1=1. На примере обычного реле – это два параллельно подключенных нормально разомкнутых контакта. Если один контакт разомкнут, то проводимость цепи обеспечит второй, замкнутый контакт. Для того что бы цепь оказалась разорванной, необходимо разомкнуть оба контакта.
Функция логического умножения
В схемотехнике носит название конъюнкция или функция И (пункт 4 в таблице). Реализует ее специальный логический элемент – конъюктор. Данная функция – логическое перемножение сигналов:

Если сравнить с реле – то это два последовательно включенные нормально открытые контакты. А при таком подключении контактов реле проводимость можно получить только в случае, когда оба контакта замкнуты.
Функция равнозначности
Имеет следующий вид — X1≡X2 = Y или в виде логических символов: 0≡0 =1; 1≡0 = 0; 0≡1 = 0; 1≡1 = 1.
Значения 1 будет только при условии, что X1 = X2. Эквивалентом в релейной схеме будет два последовательно включенных переключающихся контакта (пункт 5 в таблице).
Функция неравнозначности
Противоположная функции равнозначности (пункт 6 в таблице) и часто носит название функции сложности по модулю m2:

Таблица истинности. Базовые логические элементы.
Так же, как и стандартные Булевы выражения, информация на входах и выходах различных логических элементов или логических схем может быть собрана в единую таблицу – таблицу истинности.
Таблица истинности дает наглядное представление о системе логических функций. В таблице истинности отображаются сигналы на выходах логических элементов при всех возможных комбинациях сигналов на их входах.
В качестве примера, рассмотрим логическую схему с двумя входами и одним выходом. Входные сигналы отметим как «А» и «В», а выход «Q». Есть четыре (2²) возможных комбинаций входных сигналов, которые можно подать на эти два входа («ON — наличие сигнала» и «OFF — отсутствие сигнала»).
Однако, когда речь идет о логических выражениях и, особенно о таблице истинности логических элементов, вместо общего понятия «наличие сигнала» и «отсутствие сигнала» используют битные значения, которые представляют собой логический уровень «1» и логический уровень «0» соответственно.
Тогда четыре возможные комбинации «А» и «В» для 2-входного логического элемента можно представить в следующем виде:
- «OFF» — «OFF» или (0, 0)
- «OFF» — «ON» или (0, 1)
- «ON» — «OFF» или (1, 0)
- «ON» — «ON» или (1, 1)
Следовательно, у логической схемы имеющей три входа будет восемь возможных комбинаций (2³) и так далее. Для обеспечения легкого понимания сути таблицы истинности, мы будем изучать ее только на простых логических элементах с числом входов не превышающим двух. Но, несмотря на это, принцип получения логических результатов для многовходных элементов схемы остается таким же.
Практически, таблица истинности состоит из одного столбца для каждой из входных переменных (например, А и В), и один последний столбец для всех возможных результатов логической операции (Q). Следовательно, каждая строка таблицы истинности содержит один из возможных вариантов входных переменных (например, A = 1, B = 0), и результат операции с этими значениям.
Таблица истинности
Элемент «И»
Для логического элемента «И» выход Q будет содержать лог.1, только если на оба входа («А» и «В») будет подан сигнал лог.1
Микросхемы, содержащие логический элемент «И»:
- К155ЛИ1, аналог SN7408N
- К155ЛИ5 с открытым коллектором, аналог SN74451N
- К555ЛИ1, аналог SN74LS08N
- К555ЛИ2 с открытым коллектором, аналог SN74LS09N
Элемент «ИЛИ»
Выход Q, элемента «ИЛИ», будет иметь лог.1, если на любой из двух входов или же на оба входа сразу подать лог.1
Микросхемы, содержащие логический элемент «ИЛИ»:
- К155ЛЛ1, аналог SN7432N
- К155ЛЛ2 с открытым коллектором, аналог SN75453N
- К555ЛЛ1, аналог SN74LS32N
Элемент «НЕ»
В данном случае выход Q, логического элемента «НЕ», будет иметь сигнал противоположный входному сигналу.
Микросхемы, содержащие логический элемент «НЕ»:
- К155ЛН1, аналог SN7404N
- К155ЛН2 с открытым коллектором, аналог SN7405N
- К155ЛН3, аналог SN7406N
- К155ЛН5 с открытым коллектором, аналог SN7416N
- К155ЛН6, аналог SN7466N
Элемент «И-НЕ»
На выходе Q элемента «И-НЕ» будет лог.1 если на обоих входах одновременно отсутствует сигнал лог.1
Микросхемы, содержащие логический элемент «И-НЕ»:
- К155ЛА3, аналог SN7400N
- К155ЛА8, аналог SN7401N
- К155ЛА9 с открытым коллектором, аналог SN7403N
- К155ЛА11 с открытым коллектором, аналог SN7426N
- К155ЛА12 с открытым коллектором, аналог SN7437N
- К155ЛА13 с открытым коллектором, аналог SN7438N
- К155ЛА18 с открытым коллектором, аналог SN75452N
Элемент «ИЛИ-НЕ»
Только если на оба входа логического элемента «ИЛИ-НЕ» подать лог.0 мы получим на его выходе Q сигнал соответствующий лог.1
Микросхемы, содержащие логический элемент «ИЛИ-НЕ»:
- К155ЛЕ1, аналог SN7402N
- К155ЛЕ5, аналог SN7428N
- К155ЛЕ6, аналог SN74128N
Элемент «Исключающее ИЛИ»
В данном случае выход Q будет содержать лог.1, если на вход элемента «Исключающее ИЛИ» поданы два противоположных друг другу сигнала.
Микросхемы, содержащие логический элемент «Исключающее ИЛИ»:
- К155ЛП5, аналог SN7486N
Подведем итог, собрав все полученные ранее результаты работы логических элементов в единую таблицу истинности:
Логические основы устройства компьютера. Базовые логические элементы
Тема урока: «Логические основы устройства компьютера. Базовые логические элементы»
Цель урока: общение и систематизация знаний, полученных при изучении раздела основы логики. формирование представления о логических элементах, познакомить со схематическим способом представления логических выражений.
Задачи урока:
общеобразовательные:
обобщить и систематизировать знания по основным понятиям: высказывание, умозаключение, логические операции – логическое сложение, логическое умножение, логическое отрицание, таблицы истинности;
повторить основные базовые операции;
познакомить с основными логическими элементами;
научить строить логические схемы по логическим выражениям и наоборот.
развивающие:
развитие логического мышления учащихся;
формирование умений анализировать, обобщать, делать выводы, формализовать задачи;
развитие интереса к информатике.
воспитательные:
формирование научного мировоззрения.
Тип урока: комбинированный (систематизация знаний, объяснение нового материала, практическая работа)
Требования к знаниям и умениям учащихся на момент проведения урока:
Учащиеся должны знать:
основные логические операции (конъюнкция – логическое умножение, дизъюнкция – логическое сложение, инверсия – логическое отрицание), импликацию и эквивалентность;
обозначения логических операций;
приоритет выполнения логических операций;
Учащиеся должны уметь:
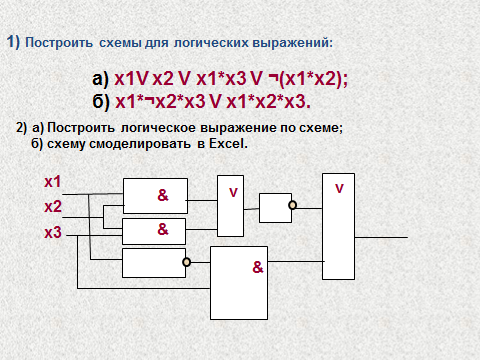
строить схемы логических выражений;
записывать логические выражения по логическим схемам.
Наглядное пособие: презентация, подготовленная в PowerPoint
Ход урока
1. Организационный момент – объявляется тема, цели урока, его этапы.
2. Актуализация опорных знаний.
— Основные логические операции.
— Таблицы истинности логических операций.
— Приоритет логических операций.
— Логическая формула ЕСЛИ в электронных таблицах.
Задания для устной работы.
Чему равно значение логического выражения
 , если А=0, В=0, С=1?
, если А=0, В=0, С=1?Чему равно значение логического выражения
 , если А=1, В=0, С=1?
, если А=1, В=0, С=1?Чему равно значение логического выражения
 , если А=1, В=1, С=0 ?
, если А=1, В=1, С=0 ?
3. Объяснение нового материала (кратко)
Компьютер – это устройство, состоящее из различных электронных элементов, представляющих собой простейшие электрические схемы. Каким образом происходит обработка электрического сигнала и его преобразование в цифровой код? Наличие электрического сигнала в цепи соответствует логической единице (истине), отсутствие тока – логическому нолю (ложь). А логические операции осуществляют логические элементы, которые технически реализуются с помощью переключательных схем. Поскольку любая логическая операция может быть представлена в виде трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов. Дискретный преобразователь, после обработки на входе двоичных сигналов на выходе дает сигнал – значение логической операции. Базовые логические элементы реализуют три основные логические операции: «И», «ИЛИ», «НЕ».
Каким логическим операциям соответствуют логические элементы?
&



x1
y2



x1
y
&
Vли


x
¬¬

F=x&y
F=xvy
F= ¬x
Базовые логические элементы также еще называют вентилями.
Вентиль «И» – конъюнктор. Реализует конъюнкцию.
Вентиль «ИЛИ» – дизъюнктор. Реализует дизъюнкцию.
Вентиль «НЕ» – инвертор. Реализует инверсию.
Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс – 1, нет – 0. На входы логического элемента поступают сигналы – значения аргументов, на выходе появляется сигнал – значение функции.
При демонстрации презентации ученики определяют, какой логической операции соответствует каждая из электрических схем. Делаются выводы: конъюнкцию реализуют последовательно соединённые переключатели, дизъюнкцию – параллельно соединённые переключатели, последовательно подключенные к участку цепи.
Задание: смоделируйте в электронной таблице Excel схемы логических элементов – конъюнкции, дизъюнкции, инверсии.
Соединив логические элементы в соответствии с логическим выражением, получим логическую схему, реализующую данное выражение. Булево выражение – описание логической схемы. Ученикам предлагаются задания на построение логических схем по логическому выражению и составление логического выражения по схеме (см. презентацию).
Для закрепления изученного материала учащиеся устно и письменно выполняют упражнения различного типа:
определение базового логического элемента на схеме 1;
определение значения выходного сигнала при заданных входных сигналах на схеме 2;
1. 2.
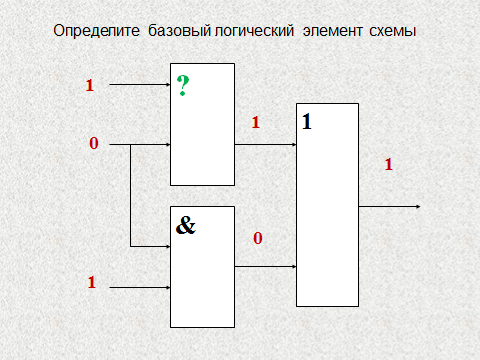
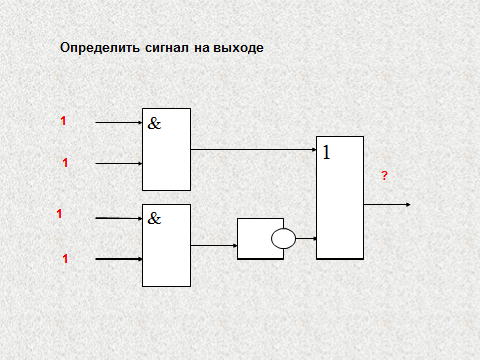
определение невозможных комбинаций входных сигналов при заданном выходном сигнале (учащиеся работают самостоятельно в тетрадях).
Какие комбинации входных сигналов невозможны для указанных схем?
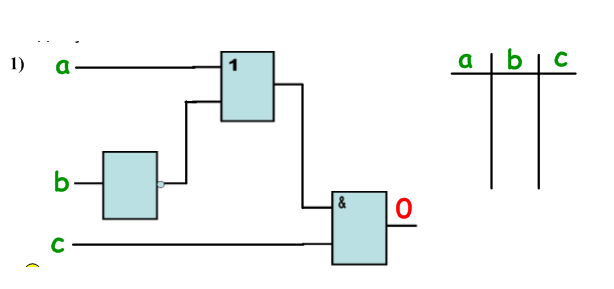
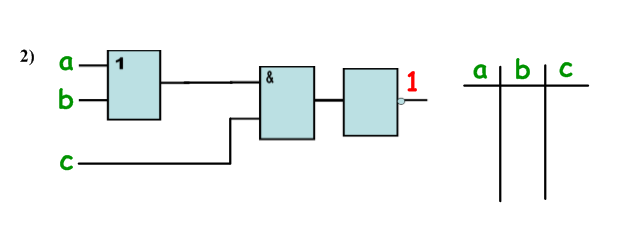
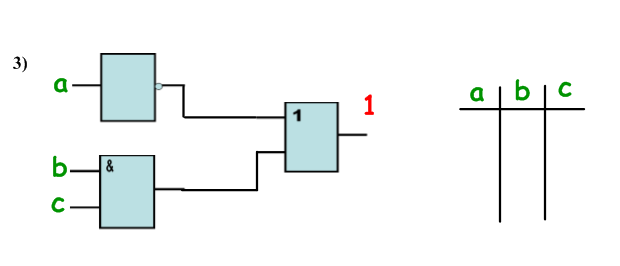
Подводятся итоги урока и задается домашнее задание.
4.Домашнее задание:
п. 3.3.1.


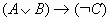 , если А=0, В=0, С=1?
, если А=0, В=0, С=1?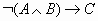 , если А=1, В=0, С=1?
, если А=1, В=0, С=1?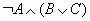 , если А=1, В=1, С=0 ?
, если А=1, В=1, С=0 ?