Простая физика — EASY-PHYSIC
Электромагнитные колебания в контуре — одна из сложных тем ЕГЭ. Энергия переходит из одной формы в другую и концентрируется то в конденсаторе, то в катушке. Период колебаний энергии — вдвое меньше, чем период колебаний в контуре (энергия колеблется с двойной частотой).
Задача 1.
Колебательный контур состоит из катушки индуктивности и двух одинаковых конденсаторов, включенных параллельно. Период собственных колебаний в контуре мкс. Чему будет равен период ‚ если конденсаторы включить последовательно?
Емкость цепи равна , так как конденсаторы включены параллельно. Тогда период колебаний:
Теперь, если мы включим конденсаторы последовательно, то емкость будет равна
Тогда
То есть подкоренное выражение стало меньше в 4 раза, а значит, период стал меньше вдвое.
Ответ: мкс.
Задача 2.
В колебательном контуре емкость конденсатора мкФ, индуктивность катушки Гн, амплитуда напряжения на конденсаторе В. В некоторый момент времени напряжение на конденсаторе В. Найдите энергию магнитного поля в этот момент.
В некоторый момент времени напряжение на конденсаторе В. Найдите энергию магнитного поля в этот момент.
Амплитуда напряжения позволяет найти полную энергию:
Так как напряжение на конденсаторе в некоторый момент времени равно 1 В, то в этот момент его энергия равна
Следовательно, энергия магнитного поля равна
Ответ: мкДж
Задача 3.
Чему равен период свободных электрических колебаний в контуре, если максимальный заряд конденсатора Кл, а максимальная сила тока в контуре А?
Полная энергия поля равна
Откуда
Тогда период равен
Ответ: c.
Задача 4.
Колебательный контур состоит из конденсатора емкостью пФ и катушки индуктивности мГн (см. рис.). Какова амплитуда колебаний силы тока , если амплитуда колебаний напряжения В?
К задаче 4
Определим угловую частоту:
Ток может быть найден по формуле:
Ответ: 0,12 А
Задача 5.
Колебательный контур состоит из конденсатора емкостью 1 мкФ и катушки индуктивности 4 Гн. Амплитуда колебаний заряда конденсатора 100 мкКл. Напишите уравнение зависимости напряжения на конденсаторе от времени .
Общий вид зависимости напряжения от времени
То есть нужно определить угловую частоту и амплитуду напряжения.
Полная энергия поля равна
Откуда
Тогда
Записываем зависимость напряжения от времени:
Задача 6.
Два конденсатора мкФ, мкФ и катушка индуктивности Гн соединены по схеме (см. рис.). В начальный момент ключ в цепи конденсаторов разомкнут, конденсатор не заряжен, ток в катушке отсутствует, хотя конденсатор заряжен до напряжения В. Какова амплитуда силы тока в катушке при установившихся колебаниях после замыкания ключа?
К задаче 6
На конденсаторе накоплен заряд, которым он «поделится» с конденсатором . «Дележ» произойдет так, что
Но напряжение на конденсаторах одно и то же:
Тогда
Откуда:
То есть .
Определяем ток:
Емкость двух конденсаторов, соединенных параллельно, равна мкФ.
Ответ: 0,01 А.
Задача 7.
По условию предыдущей задачи определите период изменения энергии магнитного поля катушки. Он вдвое меньше периода колебаний.
Ответ: c
Задача 8.
Конденсатор емкостъю 1 мкФ зарядили до максимапьного заряда 4 мкКл и замкнули на катушку с индуктивностью 0,12 Гн. Пренебрегая активным сопротивлением соединительных проводов контура, определите, каким будет мгновенное значение тока в контуре в тот момент, когда энергия контура будет распределена между электическим и магнитным полем в соотношении .
Определим амплитуду напряжения:
Полная энергия поля равна
Откуда
Ответ: 0,01 А
Ответы на вопросы «Постоянный электрический ток. § 12. Расчет силы тока и напряжения в электрических цепях»
1. Найдите разность потенциалов на резисторах, сопротивление которых 2 0м и 4 0м, в схеме, изображенной на рисунке 39.
 [2 В, 8 В]
[2 В, 8 В]Дано:
Решение:
Найдем полное сопротивление цепи RП (см. рисунок):
1. Найдите разность потенциалов на резисторах, сопротивление которых 2 0м и 4 0м, в схеме, изображенной на рисунке 39.
[2 В, 8 В]Дано:
Решение:
Найдем полное сопротивление цепи RП (см. рисунок):
в 2 раза больше, чем
следовательно по
пойдет вдвое
меньший ток.
Ответ:
2. В вашем распоряжении три резистора: 3 0м, 5 0м и 6 0м. Какие возможные сопротивления можно получить, комбинируя или используя отдельно эти резисторы? Нарисуйте со
Ответствующие схемы соединений. [0,7 Ом; 1,9 Ом; 2,0 Ом; 2,4 Ом; 2,7 Ом; 3 Ом; 3,2 Ом; 3,4 Ом; 5 Ом; 5,7 Ом; 6 Ом; 7 Ом; 7,9 Ом; 8 Ом; 9 Ом; 11 Ом; 14 Ом]Дано:
Найти: все комбинации
Комбинации из 3-х резисторов:
Комбинации из 2-х резисторов:
Комбинации из 1-ого резистора:
3.
 Три резистора 40 Ом, 60 Ом и 120 Ом соединены параллельно в группу, которая включена последовательно резисторам сопротивлениями 15 0м и 25 0м. ЭДС источника
240 В. Найдите: 1)силу тока, протекающего через сопротивление 25 0м; 2) разность потенциалов на параллельной группе; 3) напряжение на сопротивлении 15 0м; 4) силу тока через сопротивление 60 Ом; 5) силу тока через сопротивление 40 Ом. [1) 4 А; 2) 80 В; 3) 60 В; 4) 1,34 А; 5) 2 А]
Три резистора 40 Ом, 60 Ом и 120 Ом соединены параллельно в группу, которая включена последовательно резисторам сопротивлениями 15 0м и 25 0м. ЭДС источника
240 В. Найдите: 1)силу тока, протекающего через сопротивление 25 0м; 2) разность потенциалов на параллельной группе; 3) напряжение на сопротивлении 15 0м; 4) силу тока через сопротивление 60 Ом; 5) силу тока через сопротивление 40 Ом. [1) 4 А; 2) 80 В; 3) 60 В; 4) 1,34 А; 5) 2 А]Дано:
Решение:
R1, R2, R3 соединены параллельно, следовательно
Ответ:
4. Найдите заряд на конденсаторе, включенном в электрическую схему, изображенную на рисунке 40. Все величины, указанные на схеме известны. Внутренним сопротивлением источника тока пренебречь.[q = 3CU/4]
Дано:
Решение:
Найдем эквивалентное сопротивление цепи (см. рисунок) без учета конденсатора:
Обозначим напряжение в точке А как
а в точке
Тогда в
точке С напряжение будет таким же, как и в точке А, а в точке D,
IR/2 — сила тока, который идет через верхний резистор.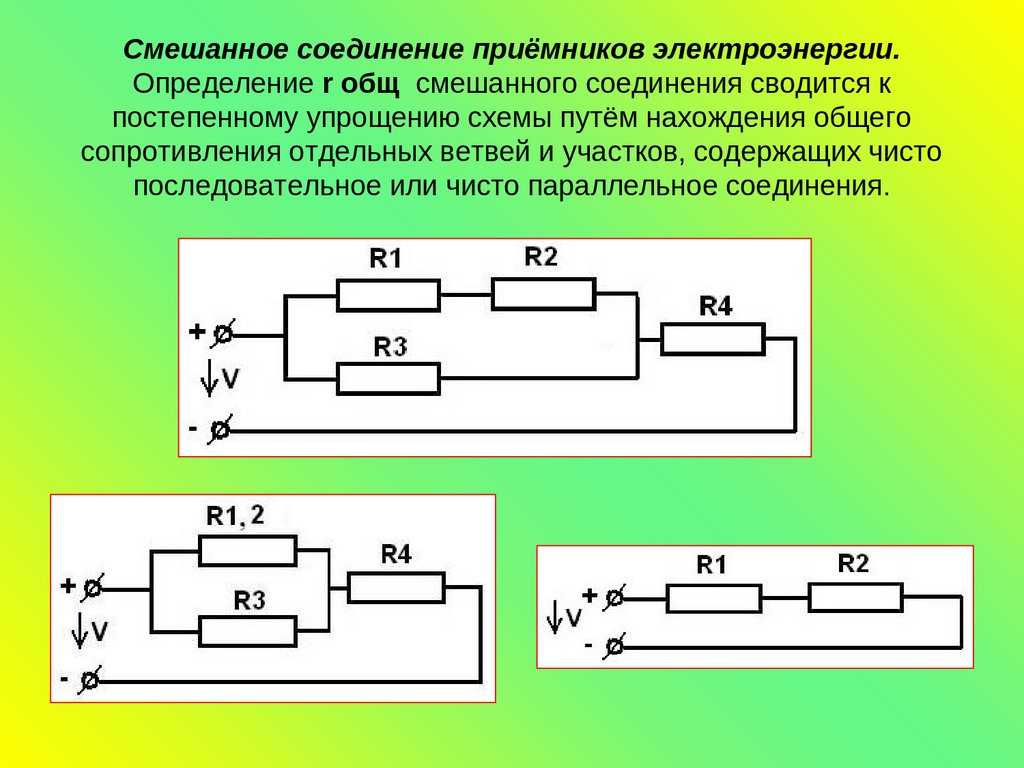 )
)
Заряд на конденсаторе найдем по формуле
Ответ:
5. Рассчитайте разность потенциалов U
ab в электрической схеме, показанной на рисунке 41. Внутренним сопротивлением источника тока пренебречь.[0,05 U]Дано:
Решение:
Решается аналогично предыдущей задаче.
Ответ:
Источник:
Решебник
по
физике
за 11 класс (Касьянов В.А., 2002 год),
к главе «Постоянный электрический ток. § 12. Расчет силы тока и напряжения в электрических цепях».
Все задачи
← 5. Источник тока с ЭДС ε и внутренним сопротивлением r замкнут на реостат с переменным сопротивлением R. Постройте графики зависимости I(R) от U(R).
Ответы на вопросы «Постоянный электрический ток. § 13. Измерение силы тока и напряжения» →
Объяснение урока: Конструкция омметра
В этом объяснении мы научимся описывать сочетание гальванометра с постоянными и переменными резисторами для проектирования омметра постоянного тока.
Омметр — это прибор, используемый для измерения сопротивления резистора. Используя закон Ома, мы знаем, что можем найти сопротивление цепи, разделив напряжение на силу тока: 𝑅=𝑉𝐼.
Давайте рассмотрим, как мы можем найти эти значения, подключив гальванометр к цепи с резистором в ней.
Напомним, что гальванометры измеряют ток. Если посмотреть на стрелку гальванометра, большее отклонение означает больший ток, что означает меньшее сопротивление. Меньшее отклонение означает большее сопротивление.
Если счетчик показывает нулевой ток, это означает, что сопротивление цепи бесконечно, поэтому она всегда должна отклоняться, пусть даже незначительно. Чтобы увидеть, происходит ли отклонение, гальванометр обычно модифицируют, чтобы он начинался с нуля, а не с отрицательных значений тока.
Максимальное значение тока, которое может быть измерено гальванометром, равно 𝐼. Таким образом, каждая точка на циферблате представляет собой долю тока: половинное отклонение означает ток 𝐼2, четверть отклонения — 𝐼4 и так далее.
В идеале мы хотим добавить к гальванометру определенное сопротивление, чтобы общее сопротивление составляло ток 𝐼. Мы делаем это, устанавливая два разных резистора: постоянный резистор 𝑅 и переменный резистор 𝑅. Это, в сочетании с собственным сопротивлением гальванометра 𝑅, составляет все сопротивления в цепи, прежде чем что-либо добавить.
Эти сопротивления таковы, что, когда в цепи нет другого сопротивления, тока достаточно, чтобы вызвать максимальное отклонение счетчика, 𝐼. Это означает, что мы хотим связать общее сопротивление построенного омметра 𝑅 с 𝐼 следующим образом: 𝑅=𝑉𝐼,, где полное сопротивление омметра равно 𝑅=𝑅+𝑅+𝑅.
Мы можем настроить переменный резистор на определенное значение, точное значение связано с другими значениями. Чтобы показать это, мы должны начать с соотношения закона Ома с полным сопротивлением омметра: 𝑅=𝑉𝐼.
Мы можем заменить 𝑅 его составными частями следующим образом: 𝑅+𝑅+𝑅=𝑉𝐼.
Теперь мы можем найти 𝑅, вычитая 𝑅 и 𝑅 из обеих частей:
𝑅+𝑅+𝑅−𝑅−𝑅=𝑉𝐼−𝑅−𝑅𝑅=𝑉𝐼−𝑅−𝑅.
Давайте рассмотрим пример, использующий это уравнение.
Пример 1: Регулировка переменного сопротивления омметра
Показана схема, которую можно использовать в качестве омметра. В схеме используется гальванометр с сопротивлением 50 Ом, который имеет полный ток отклонения 0,5 мА. В схему также входят источник постоянного тока напряжением 3,5 В, постоянный резистор сопротивлением 2,5 кОм и переменный резистор. Сопротивление переменного резистора регулируют до тех пор, пока плечо гальванометра не окажется в положении полного отклонения. Какое сопротивление установлено на переменном резисторе? Ответ с точностью до ома.
Ответ
Резистор слева представляет переменный резистор.
Давайте посмотрим на уравнение 𝑅=𝑉𝐼−𝑅−𝑅.
Напряжение 3,5 В, сопротивление гальванометра 𝑅 50 Ом. Для других значений нам нужно сначала преобразовать их в базовые единицы. В 1 кОм 1 000 Ом: 10001,Ом, поэтому 10001×2,5=2500.ОмкОмкОм
Следовательно, постоянный резистор равен 2 500 Ом.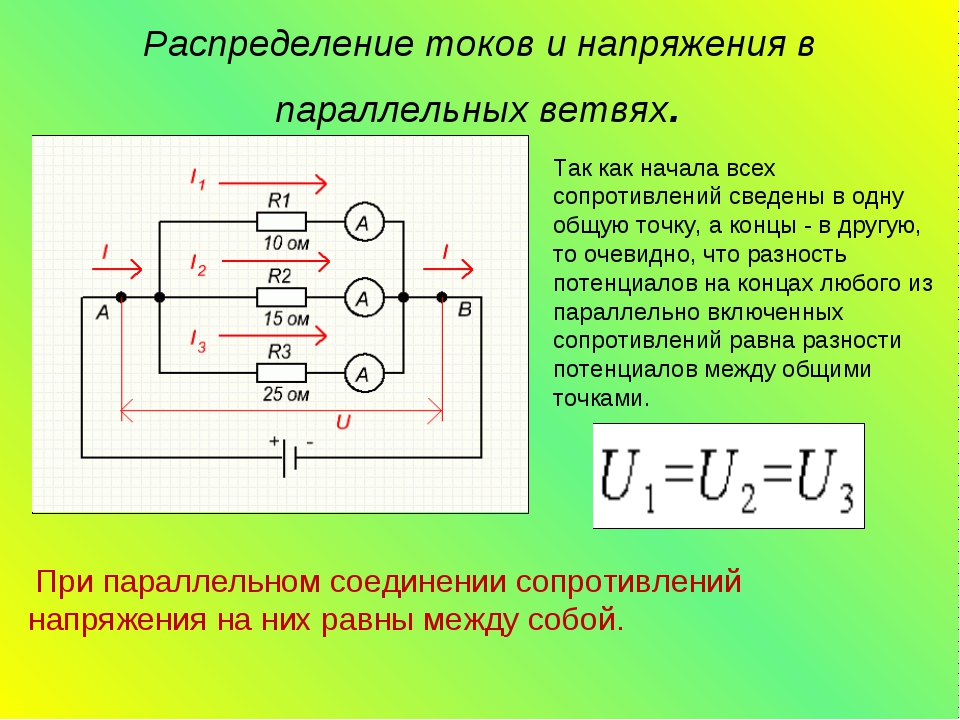
Теперь посмотрим на ампер. В 1 А 1 000 мА: 10001, мАА так 11000×0,5=0,0005. АмАмАА
Полное отклонение тока, 𝐼, составляет 0,0005 ампер.
Таким образом, мы можем подставить эти значения в уравнение для переменного резистора: 𝑅=(3,5)(0,0005)−2500−50,VAΩΩ
Вольт на ампер дает единицы измерения Ом, что дает значение переменного сопротивления 7000−2500−50=4450.ΩΩΩΩΩ
Таким образом, с точностью до Ома значение этого переменного резистора должно быть установлено равным 4 450 Ом.
Теперь, когда мы знаем, как настроить омметр, давайте посмотрим, как более точно рассчитывается шкала гальванометра. Если счетчик начинает с нулевого тока и доходит до 𝐼, то мы можем связать ток с общим сопротивлением в цепи следующим образом: 𝐼=𝑉𝑅.всего
Это означает, что шкала гальванометра начинается с бесконечного сопротивления, затем отклоняется, пока не достигнет 0 на дальнем конце.
В сочетании с резисторами получается наш омметр. Чтобы измерить неизвестный резистор, он должен быть включен последовательно с другими частями омметра.
Давайте рассмотрим пример.
Пример 2: Как должен быть подключен неизвестный резистор
Показана схема, которую можно использовать в качестве омметра. В схеме используются гальванометр, источник постоянного тока с известным напряжением, постоянный резистор и переменный резистор. Сопротивление переменного резистора регулируют до тех пор, пока плечо гальванометра не окажется в положении полного отклонения. Схема предназначена для нахождения сопротивления резистора с неизвестным сопротивлением. Резистор с неизвестным сопротивлением должен быть подключен к цепи. Каким из следующих способов должен быть подключен резистор?
- Последовательно со всеми остальными компонентами
- Параллельно с переменным резистором
- Параллельно с источником постоянного тока
- Параллельно с постоянным резистором
- Параллельно с гальванометром
Ответ
Если 9 компонент, будь то гальванометр, источник постоянного тока, переменный или постоянный резистор, подключен параллельно, он не будет измерять правильно. Единственный способ, которым омметр с его переменным резистором, отрегулированным на полное отклонение, правильно измерит неизвестный резистор, — это включить неизвестный резистор последовательно.
Единственный способ, которым омметр с его переменным резистором, отрегулированным на полное отклонение, правильно измерит неизвестный резистор, — это включить неизвестный резистор последовательно.Правильный ответ: A.
Способ, которым мы измеряем сопротивление с помощью этого омметра, заключается в пропорциональном отклонении стрелки гальванометра, причем большее отклонение означает больший ток и, следовательно, меньшее сопротивление.
Давайте рассмотрим пример.
Пример 3. Определение сопротивления с использованием определенного отклонения стрелки
Показана схема, которую можно использовать в качестве омметра. В схеме используются гальванометр, источник постоянного тока с известным напряжением, постоянный резистор и переменный резистор. Угол 𝜃 — это полный угол отклонения гальванометра. Два резистора 𝑅 и 𝑅 подключены к омметру так, чтобы их сопротивления можно было измерить омметром. Угол отклонения гальванометра уменьшается на угол 𝜙 при подключении 𝑅, а его угол отклонения уменьшается на угол 𝛼 при подключении 𝑅; 𝛼>𝜙.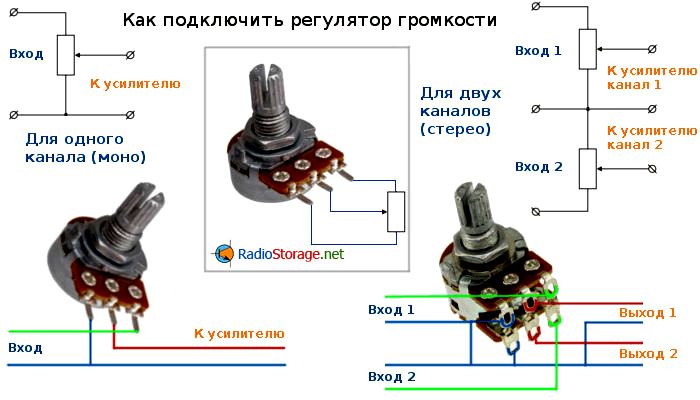 Что из следующего правильно связывает сопротивления 𝑅 и 𝑅?
Что из следующего правильно связывает сопротивления 𝑅 и 𝑅?
- 𝑅 = 𝑅
- 𝑅𝑅
- 𝑅> 𝑅
Ответ
. Большее сопротивление будет показано на счетчике в качестве меньшего относительного отклонения и меньшего сопротивления в качестве большего отклонения. Эти углы, на которые отклоняются стрелки, относятся к одному и тому же омметру, откалиброванному одинаково, поэтому, поскольку между ними есть разница, 𝑅 не может равняться 𝑅. Так что А не то.
Таким образом, угол с наибольшим отклонением будет иметь наименьшее сопротивление. Поскольку 𝛼>𝜙, а 𝛼 представляет 𝑅, 𝑅 — меньшее значение сопротивления, чем 𝑅. Таким образом, правильный ответ C, 𝑅>𝑅.
Если в цепь добавляется неизвестный резистор и стрелка отклоняется наполовину, это означает, что добавленное сопротивление равно сопротивлению омметра, 𝑅. Таким образом, мы можем обновить маркировку сопротивления на гальванометре, чтобы показать это соотношение в центре.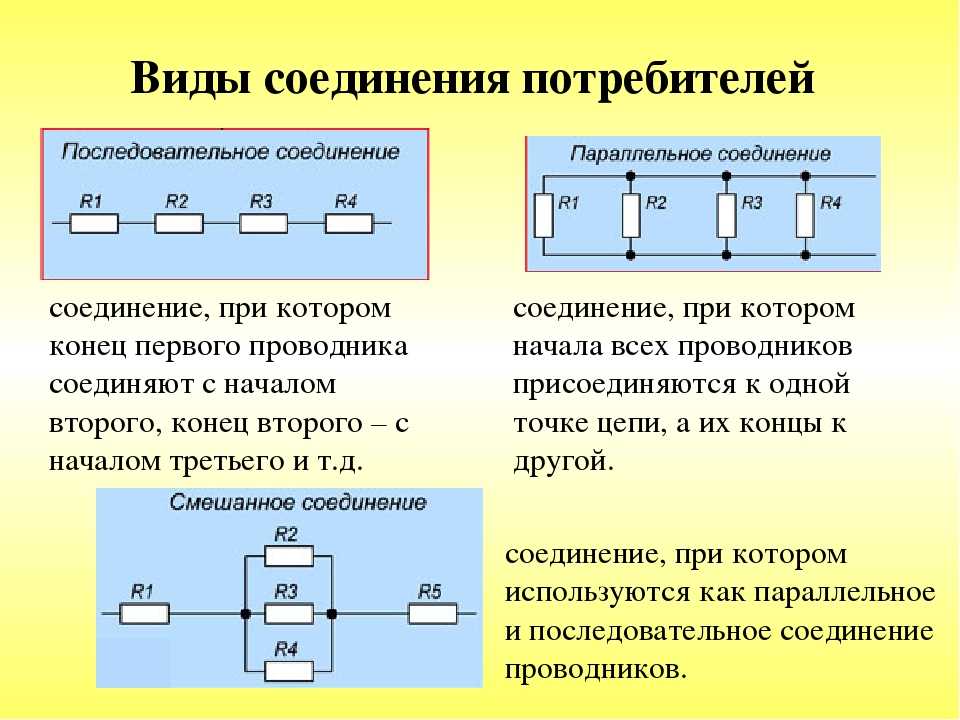
Прогиб обратно пропорционален сопротивлению. Эта позиция на полпути между центром и правой стороной метра равна 𝑅2, а между центром и левой стороной — 2𝑅, и так далее.
4𝑅 находится на полпути между точкой слева и точкой 2𝑅, 8𝑅 находится на полпути между ней и 4𝑅 и так далее. Каждый дополнительный ом обеспечивает все меньшее и меньшее отклонение стрелки по мере приближения к стороне бесконечности. Отклонение иглы нелинейно. Чтобы увидеть точное соотношение, давайте посмотрим на пропорцию отклонения.
Обозначим пропорцию отклонения стрелки 𝑟, которая является долей текущего отклонения к максимальному отклонению: 𝑟=.currentdeflectionmaximumdeflection
Отклонение стрелки обычно измеряется в градусах, что при таком делении становится просто пропорцией. Затем это отклонение можно связать с фактическим значением неизвестного сопротивления, сравнив его с сопротивлением омметра.
Если мы разделим сопротивление омметра, 𝑅, на эту пропорцию, а затем вычтем сопротивление омметра, это даст значение неизвестного резистора:
𝑅=𝑅𝑅−𝑅. неизвестно
неизвестно
Давайте рассмотрим несколько примеров.
Пример 4. Определение сопротивления с помощью отклонения стрелки наполовину
На схеме показана шкала омметра, используемого для измерения неизвестного сопротивления. Сопротивление омметра 25 кОм. Угол полного отклонения омметра 𝜙=60∘. Угол отклонения плеча омметра 𝜃=30∘. Что такое неизвестное сопротивление? Ответ с точностью до килоома.
Ответ
Полное отклонение этого омметра при 60° составляет 0 Ом, а при 0° — ∞.
Средняя точка между ними равна сопротивлению омметра, которое нам дано. Таким образом, неизвестное сопротивление равно просто 25 кОм, но давайте также найдем его с помощью уравнения.
Коэффициент отклонения равен 0,5, поэтому мы подставляем эти значения в уравнение, чтобы получить 𝑅=250,5−2550−25=25.unknownkΩkΩkΩkΩkΩ
Итак, неизвестное сопротивление равно 25 кОм.
Пример 5: Определение сопротивления с помощью определенного отклонения стрелки
На схеме показана шкала омметра, используемого для измерения неизвестного сопротивления.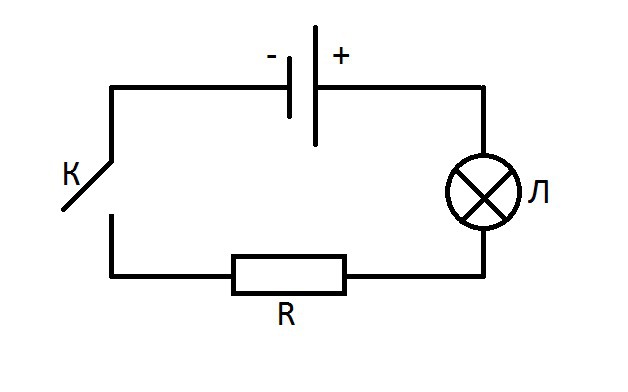 Сопротивление омметра 25 кОм. Угол полного отклонения омметра 𝜙=60∘. Угол отклонения плеча омметра 𝜃=48∘. Что такое неизвестное сопротивление? Ответ с точностью до килоома.
Сопротивление омметра 25 кОм. Угол полного отклонения омметра 𝜙=60∘. Угол отклонения плеча омметра 𝜃=48∘. Что такое неизвестное сопротивление? Ответ с точностью до килоома.
Ответ
Полное отклонение этого омметра при 60° составляет 0 Ом, а при 0° — ∞. Сопротивление омметра 𝑅 равно 25 кОм. 4860=0,8.
Используя эту пропорцию в уравнении, 𝑅=250,8−2531,25−25=6,25.unknownkΩkΩkΩkΩkΩ
Таким образом, с точностью до килоом неизвестное сопротивление равно 6 кОм.
Пример 6. Определение сопротивления по малому отклонению стрелки
На схеме показана шкала омметра, используемого для измерения неизвестного сопротивления. Сопротивление омметра 25 кОм. Угол полного отклонения омметра 𝜙=60∘. Угол отклонения плеча омметра 𝜃=6∘. Что такое неизвестное сопротивление? Ответ с точностью до килоома.
Ответ
Полное отклонение этого омметра при 60° составляет 0 Ом, а при 0° — ∞. Сопротивление омметра 𝑅 равно 25 кОм. 660=0,1.
Используя эту пропорцию в уравнении,
𝑅=250,1−25250−25=225.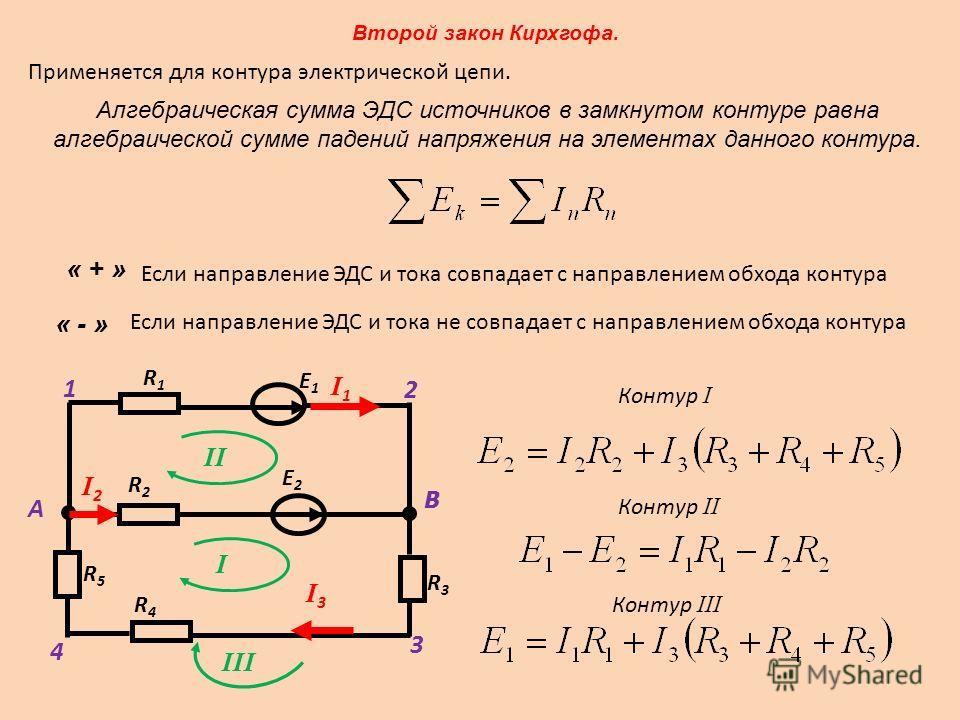 unknownkΩkΩkΩkΩkΩ
unknownkΩkΩkΩkΩkΩ
Таким образом, с точностью до килоом неизвестное сопротивление составляет 225 кОм.
Давайте подытожим то, что мы узнали из этого объяснения.
Ключевые моменты
- Омметр можно создать, последовательно соединив постоянный резистор, переменный резистор и гальванометр.
- Для калибровки гальванометра номиналы постоянного и переменного резисторов должны быть выбраны таким образом, чтобы ток был равен полному отклонению гальванометра.
- Омметры имеют нелинейную шкалу отклонения стрелки от ∞ до 0 Ом.
Выбор типа резистора: постоянный или переменный
Резисторы бывают двух основных видов: фиксированные и переменные. Оба типа обычно используются в электронных схемах. Вот краткая информация о каждом типе и почему вы должны выбрать тот или иной:
A Постоянный резистор обеспечивает постоянное сопротивление, определенное на заводе. Вы используете его, когда хотите ограничить ток в пределах определенного диапазона или разделить напряжение определенным образом.
 В схемах со светодиодами используются постоянные резисторы для ограничения тока, что защищает светодиод от повреждения.
В схемах со светодиодами используются постоянные резисторы для ограничения тока, что защищает светодиод от повреждения.Переменный резистор , , обычно называемый потенциометром (сокращенно pot ), позволяет регулировать сопротивление практически от нуля до заданного на заводе максимального значения. Вы используете потенциометр, когда хотите изменить величину тока или напряжения, подаваемого на часть вашей цепи. Несколько примеров того, где вы можете найти потенциометры, — это переключатели диммера, регуляторы громкости для аудиосистем и датчики положения, хотя цифровые элементы управления в значительной степени заменили потенциометры в бытовой электронике.
Присмотритесь к постоянным и переменным резисторам. На следующем рисунке показаны символы схемы, которые обычно используются для обозначения постоянных резисторов, потенциометров и другого типа переменного резистора, называемого реостатом . Зигзагообразный рисунок должен напоминать вам, что резисторы затрудняют прохождение тока, так же как изгиб шланга затрудняет прохождение воды.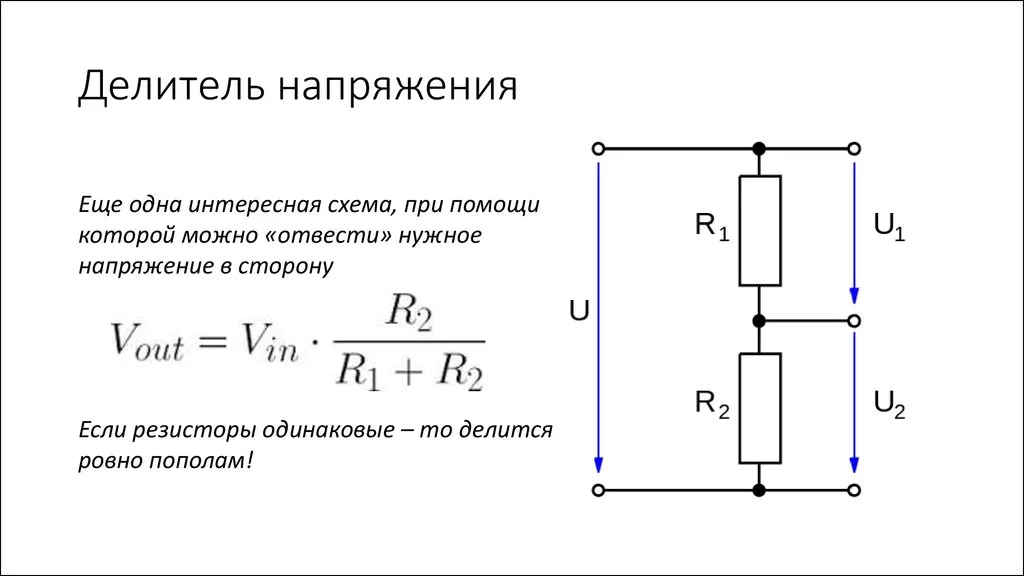
Символы цепи для постоянного резистора (слева), потенциометра (в центре) и реостата (справа).
Постоянные резисторы рассчитаны на определенное сопротивление, но фактическое сопротивление любого данного резистора может отличаться (в большую или меньшую сторону) от его номинального значения на некоторый процент, известный как допуск резистора .
Допустим, вы выбрали
с допуском 5%. Фактическое сопротивление, которое он обеспечивает, может составлять от
Ом.(потому что 5% от 1000 равно 50). Можно сказать, что сопротивление
.плюс-минус 5%.
Постоянные резисторы бывают двух категорий:
Резисторы стандартной точности могут варьироваться от 2% до 20% от их номинальных значений. Маркировка на корпусе резистора покажет вам, насколько далеко может быть фактическое сопротивление (например, +/–2 %, +/–5 %, +/–10 % или +/–20 %). Вы используете резисторы стандартной точности в большинстве хобби-проектов, потому что (чаще всего) вы используете резисторы для ограничения тока или деления напряжения в пределах допустимого диапазона.
 Резисторы с допуском 5% или 10% обычно используются в электронных схемах.
Резисторы с допуском 5% или 10% обычно используются в электронных схемах.Высокоточные резисторы имеют погрешность всего 1% от их номинальной стоимости. Вы используете их в схемах, где вам нужна исключительная точность, например, в точной синхронизации или в цепи опорного напряжения.
Постоянные резисторы часто поставляются в цилиндрическом корпусе с двумя торчащими выводами, чтобы их можно было подключать к другим элементам схемы. Не стесняйтесь вставлять постоянные резисторы в свои схемы любым способом — в этих маленьких устройствах с двумя контактами нет ни левого, ни правого, ни верхнего, ни нижнего, ни туда, ни обратно.
Большинство постоянных резисторов имеют цветовую маркировку с их номинальным значением и допуском, но некоторые резисторы имеют свои значения, выбитые прямо на крошечной упаковке вместе с кучей других букв и цифр, которые гарантированно вызовут путаницу. Если вы не уверены в значении конкретного резистора, вытащите мультиметр, настройте его на измерение сопротивления в омах и поместите его щупы на резистор (в любом случае), как показано на рисунке.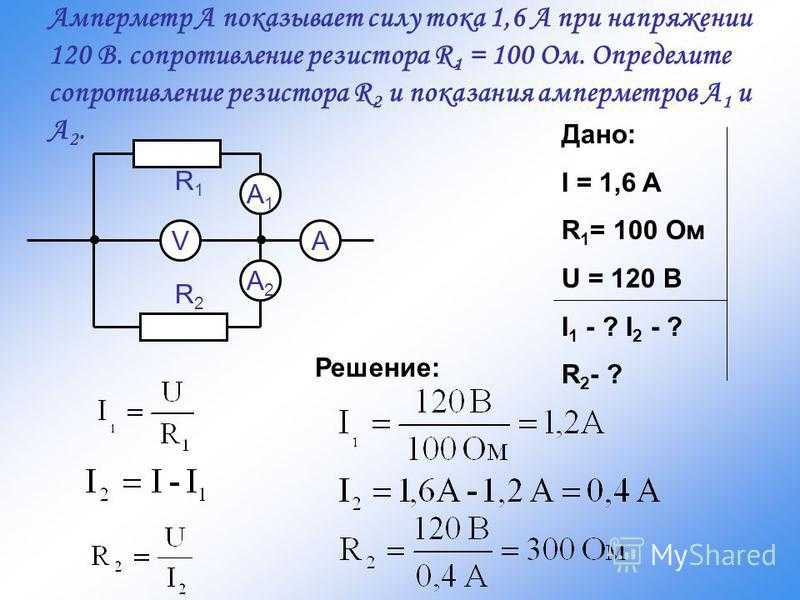


 В схемах со светодиодами используются постоянные резисторы для ограничения тока, что защищает светодиод от повреждения.
В схемах со светодиодами используются постоянные резисторы для ограничения тока, что защищает светодиод от повреждения. Резисторы с допуском 5% или 10% обычно используются в электронных схемах.
Резисторы с допуском 5% или 10% обычно используются в электронных схемах.