Пример решения задачи (резистивная цепь с конденсаторами и катушками)
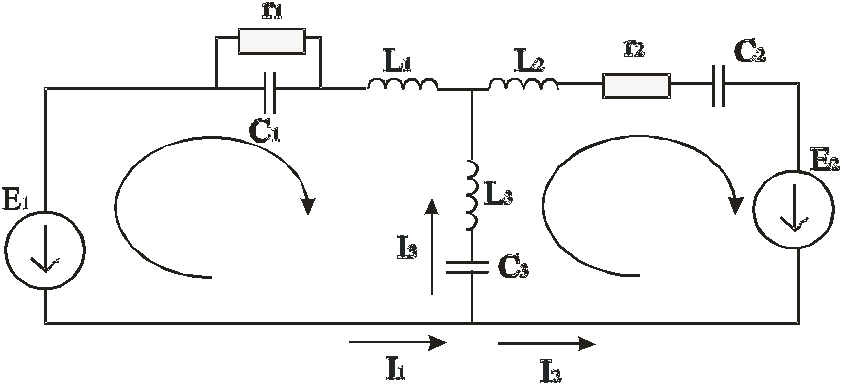
Дано:
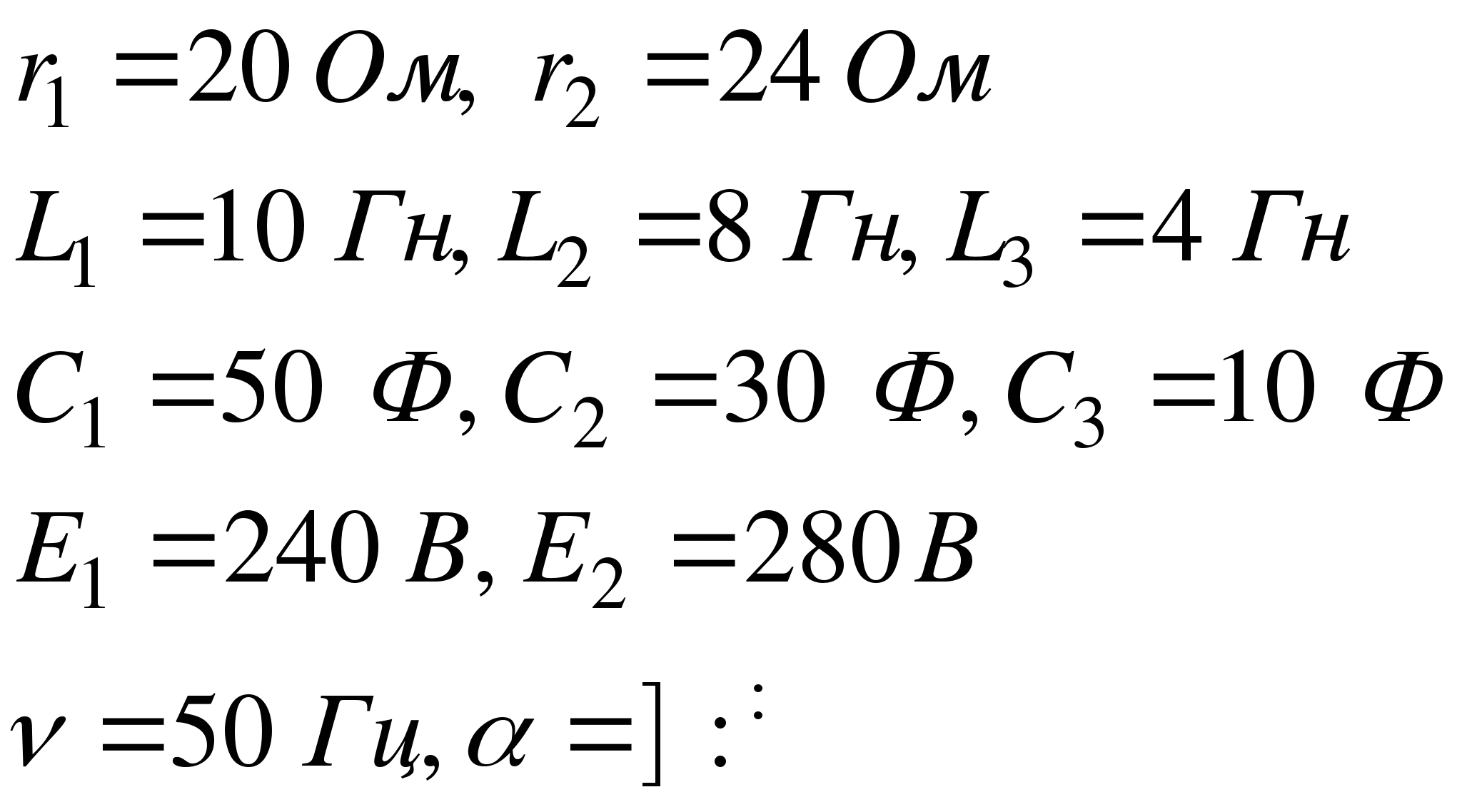
Найти:
токи во всех ветвях по методу контурных токов и классическим, с помощью законов Кирхгофа
проверить баланс мощностей
построить векторную диаграмму для внешнего контура
Согласно заданию, напряжения на источниках питания меняются по закону:
 , где
, где 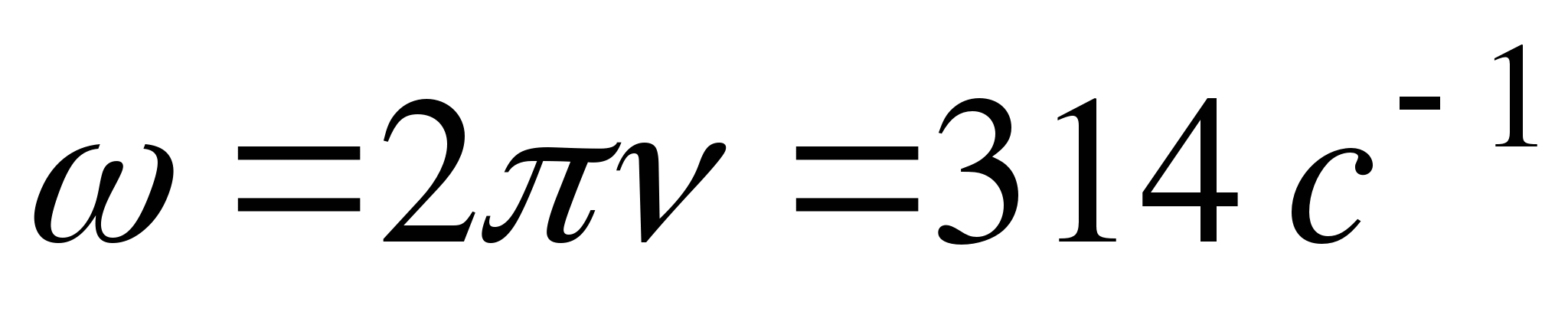 .
.
Составим эквивалентную схему замещения и определим комплексные сопротивления элементов:
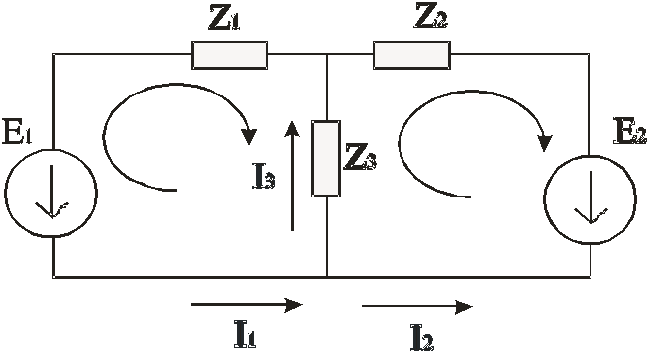

Запишем уравнения Кирхгофа для левого и правого контуров в схеме замещения:
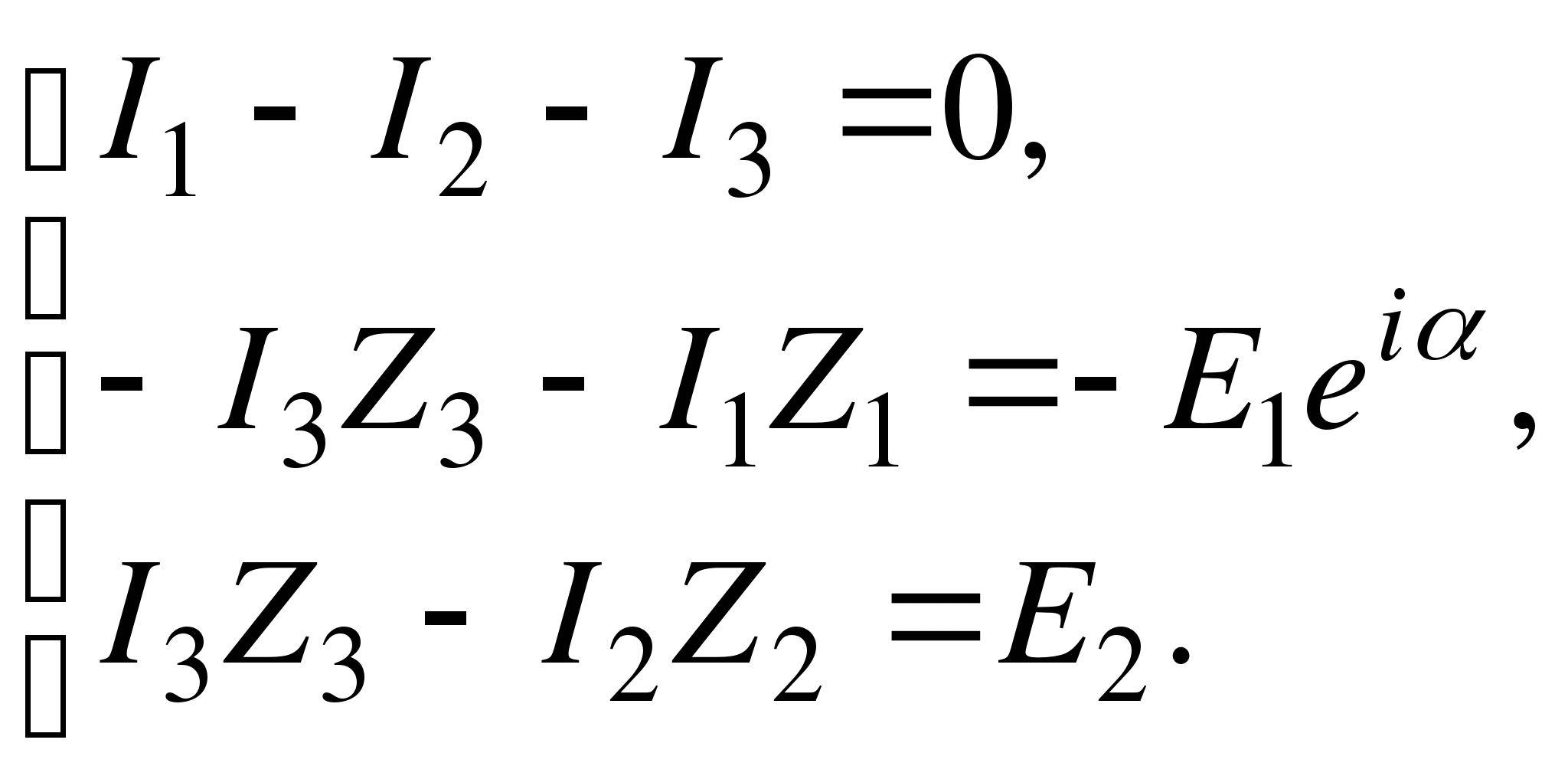
Ток I1 втекает в узел, поэтому ставим знак «+», а I2 и I3 – вытекают, поэтому перед ними знак «–».
Токи I1, I3, а также ЭДС направлены против обхода контура, поэтому «–».
Ток I3 и E2 направлены вдоль обхода контура, поэтому «+», I2 – против обхода, поэтому «–» .
Решением системы уравнений являются токи:
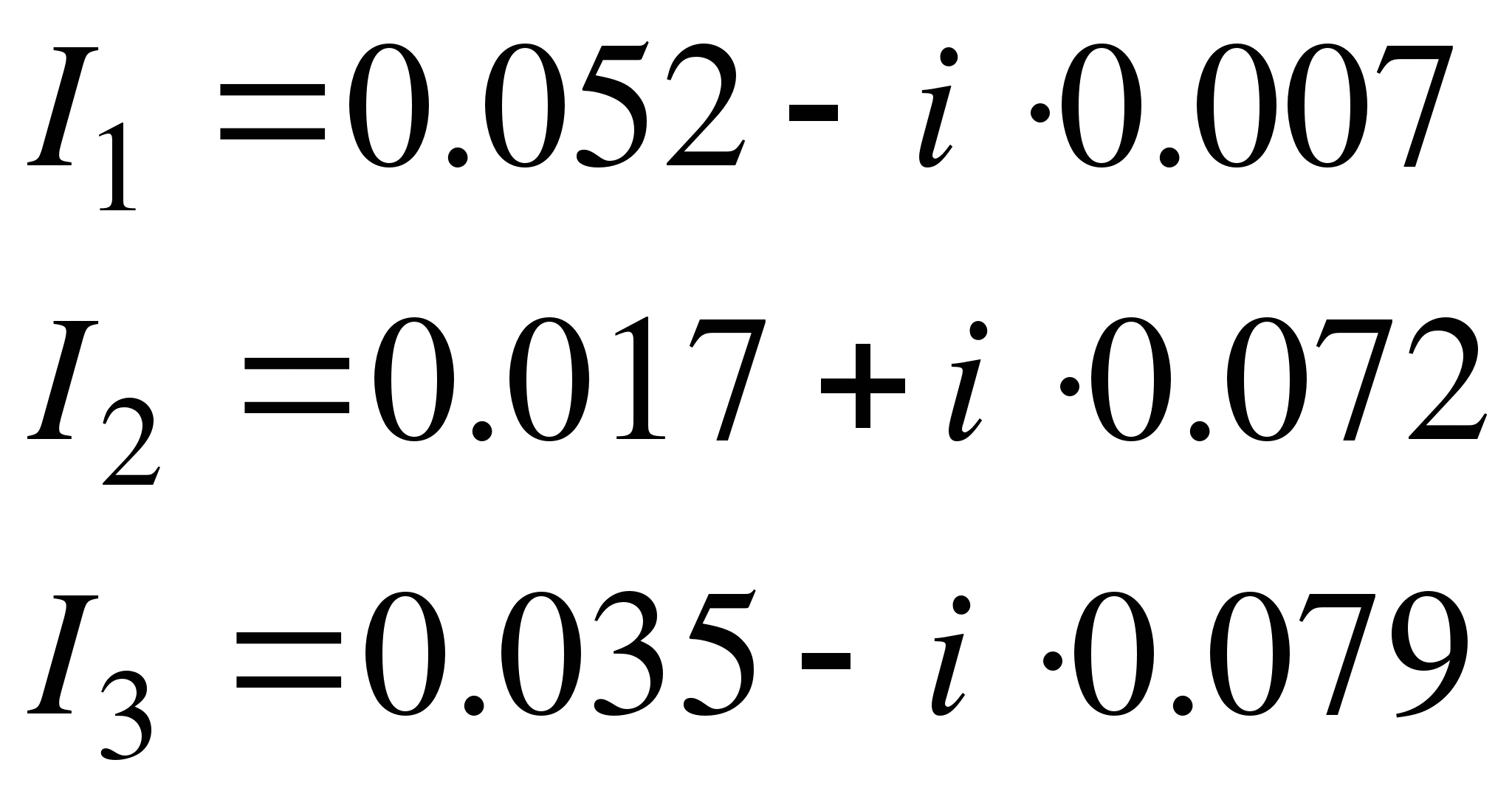 (1)
(1)
Проверим теперь, сходится ли баланс мощностей (мощность, генерируемая источниками ЭДС, должна быть равна мощности, потребленной резисторами 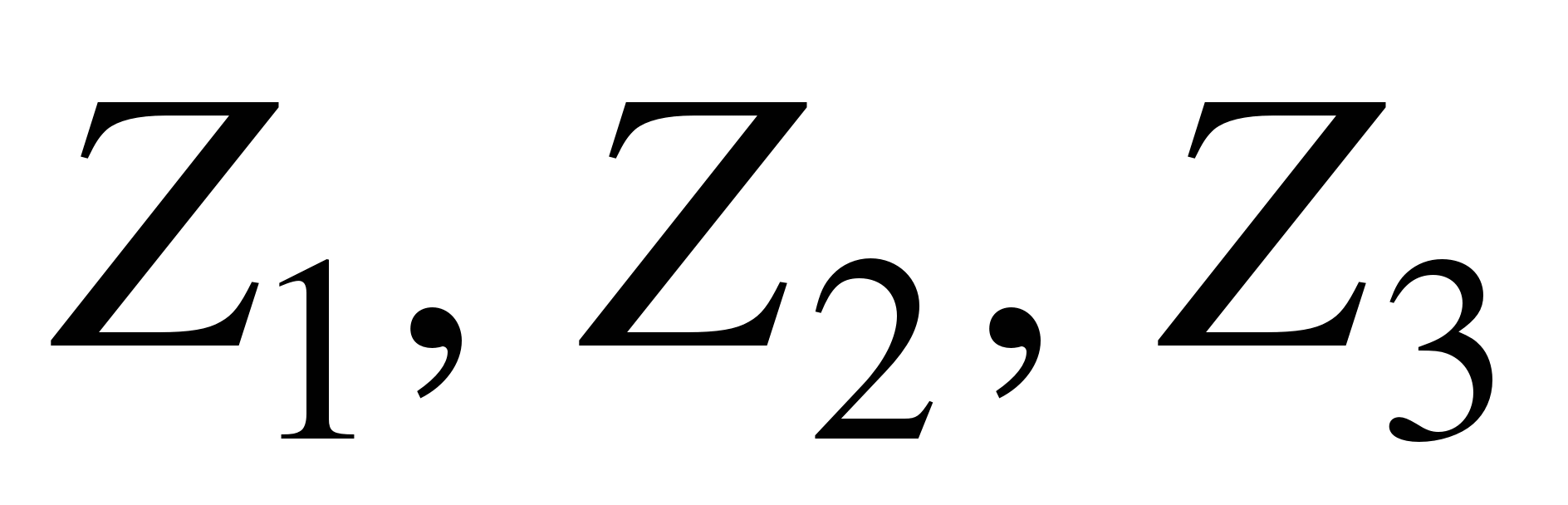 ), т.е. выполняется ли равенство
), т.е. выполняется ли равенство 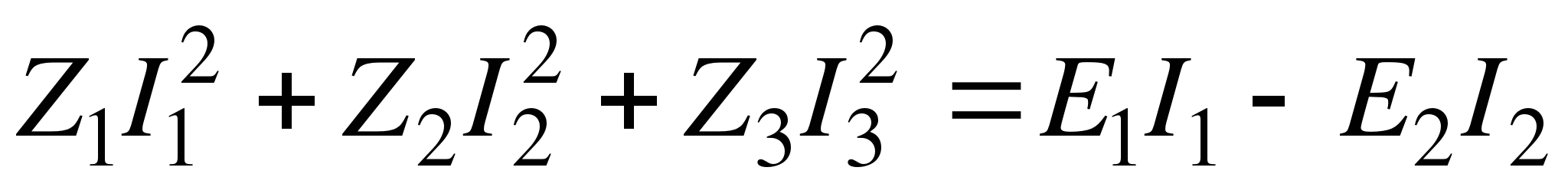
Левая часть этого уравнения равна:
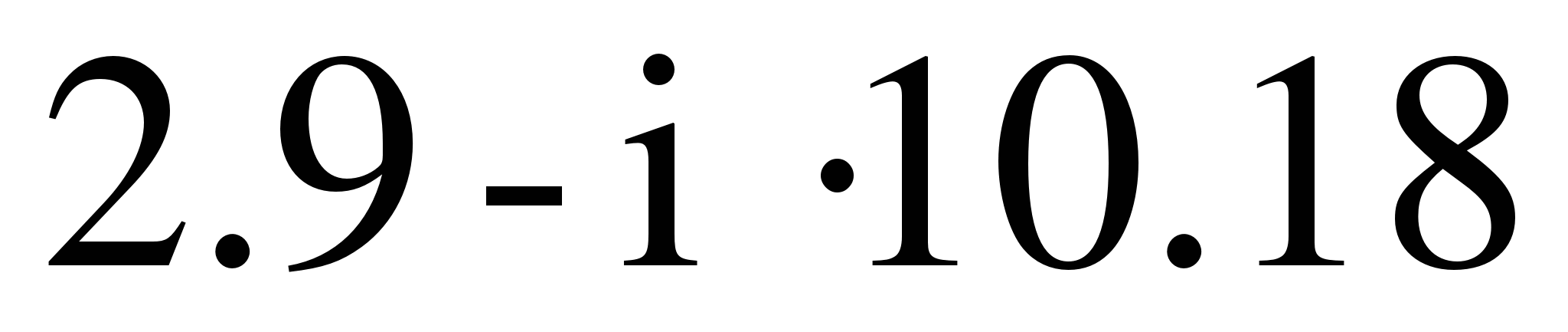
Правая часть уравнения равна:
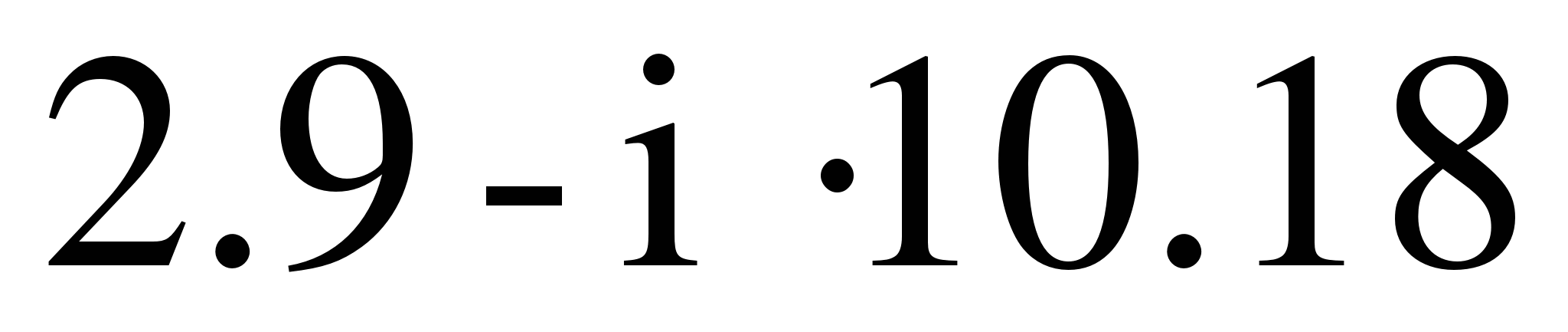
Таким образом, баланс мощностей сходится, значит, задача решена верно.
Ту же схему запишем по методу контурных токов, согласно которому в каждом контуре течет независимый контурный ток (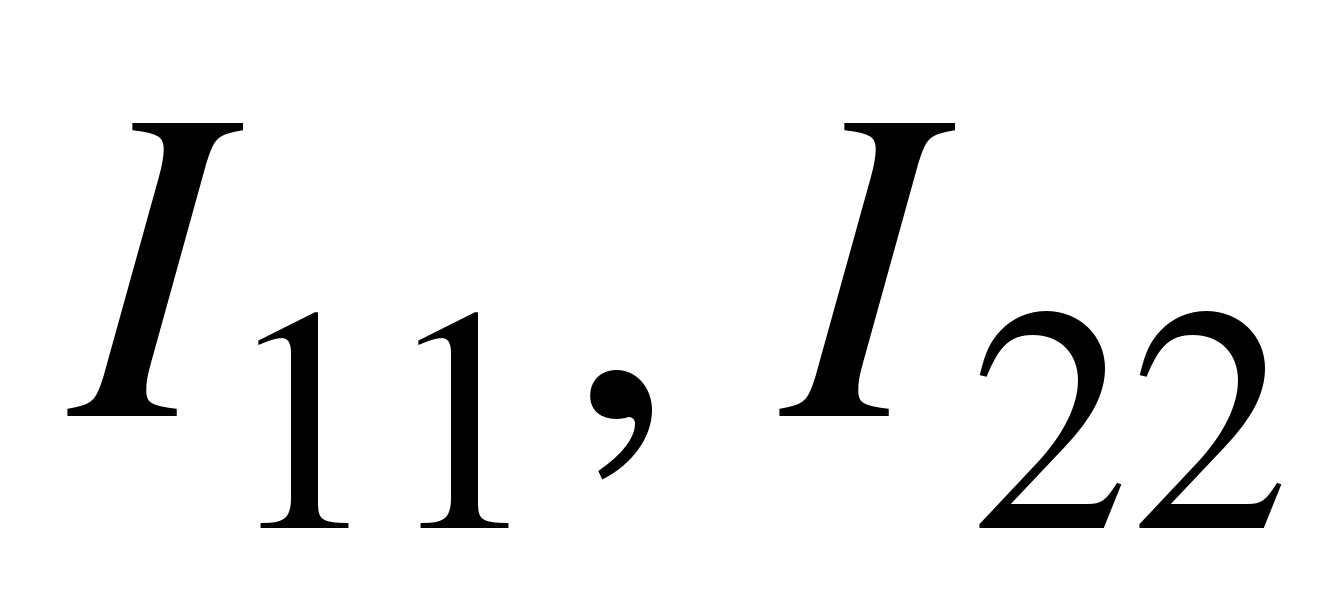
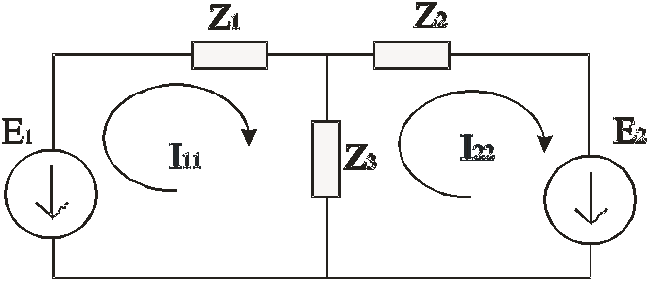
По сравнению с методом Кирхгофа здесь на одно уравнение и на одну неизвестную меньше, что ускоряет расчеты. В средней ветви течет ток 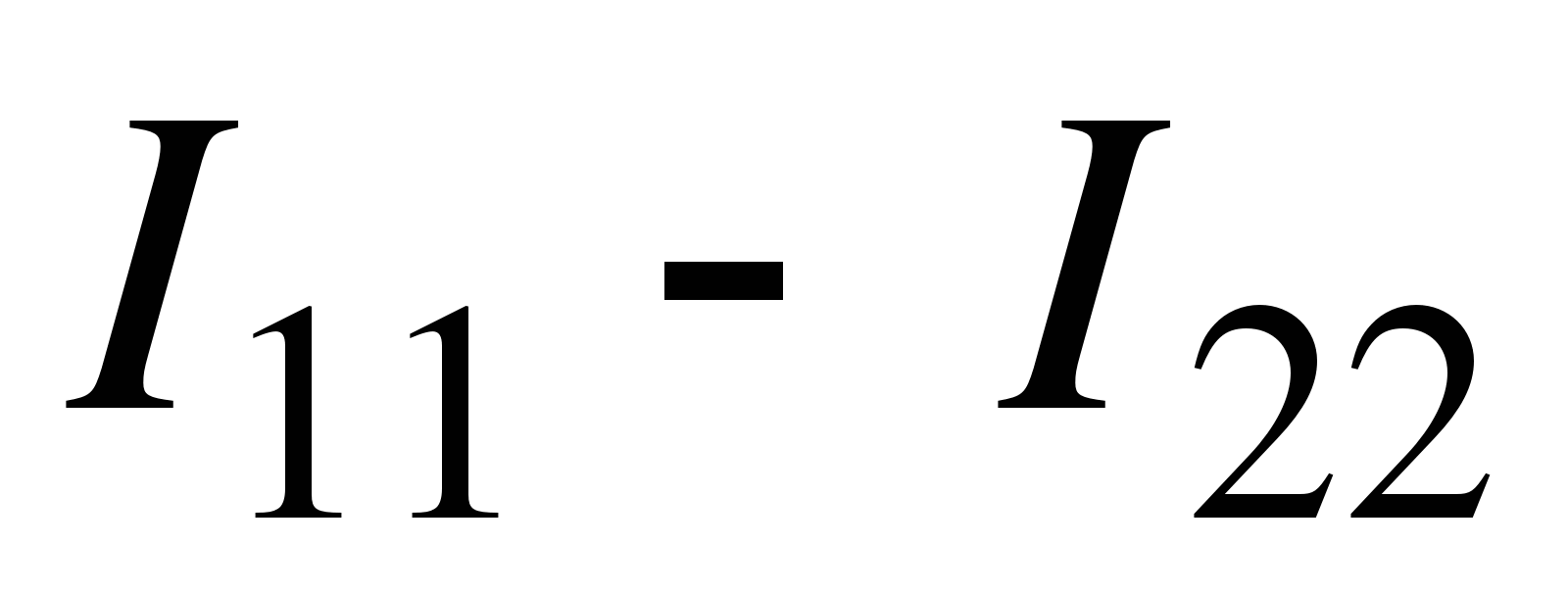 , направленный вниз (на рисунке не показан). Пусть обходы контуров совпадают с направлениями контурных токов. Тогда, согласно правилу Кирхгофа, получим:
, направленный вниз (на рисунке не показан). Пусть обходы контуров совпадают с направлениями контурных токов. Тогда, согласно правилу Кирхгофа, получим:
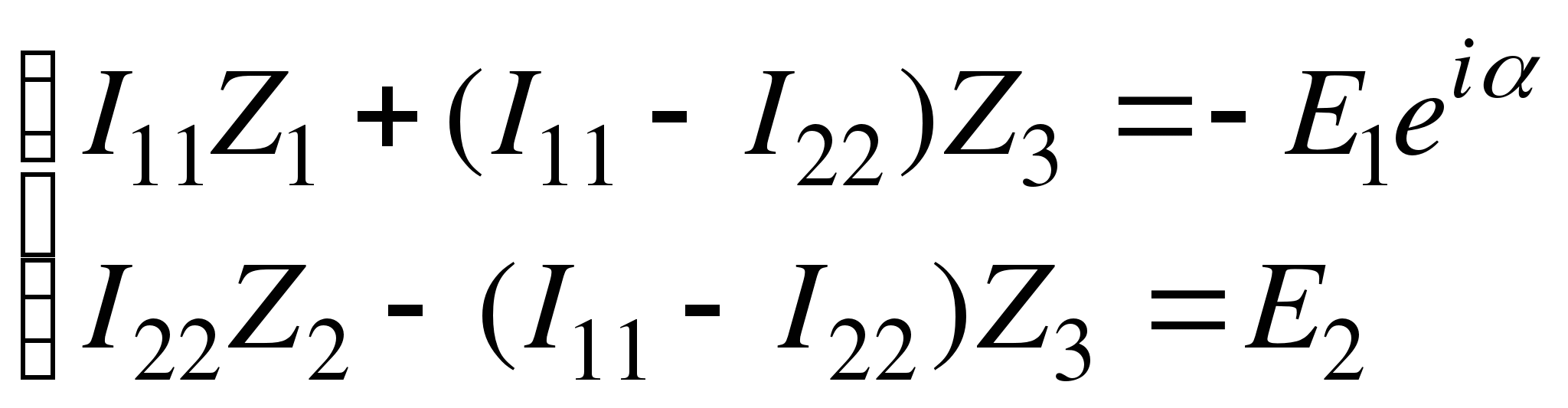
ЭДС берется со знаком «+», если увеличение потенциала источника совпадает с направлением контурного тока. Ток в средней ветви определяется как разница токов I11 и I22.
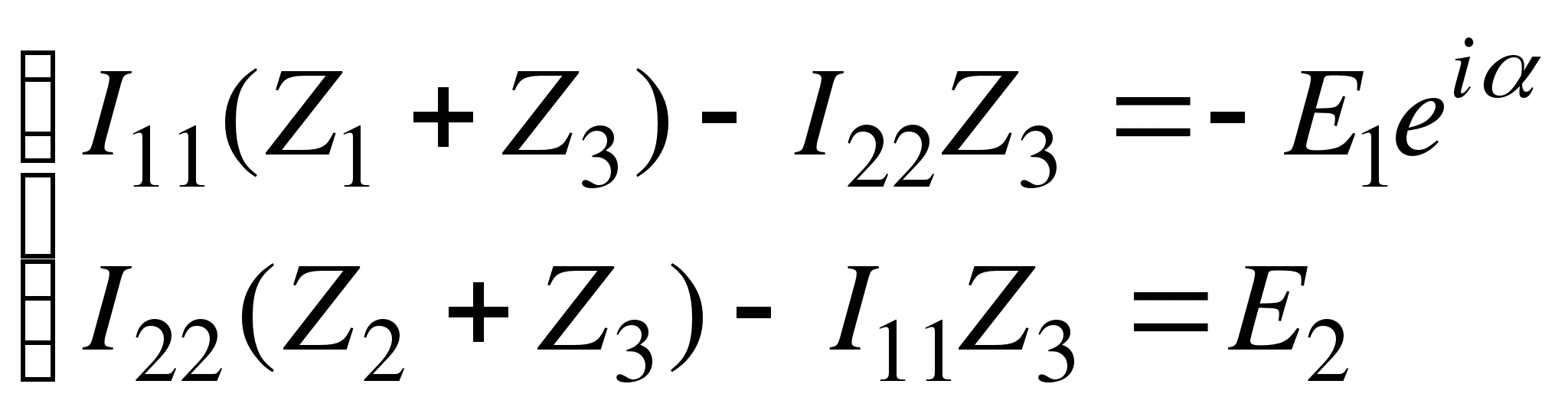
Решением системы уравнений являются контурные токи
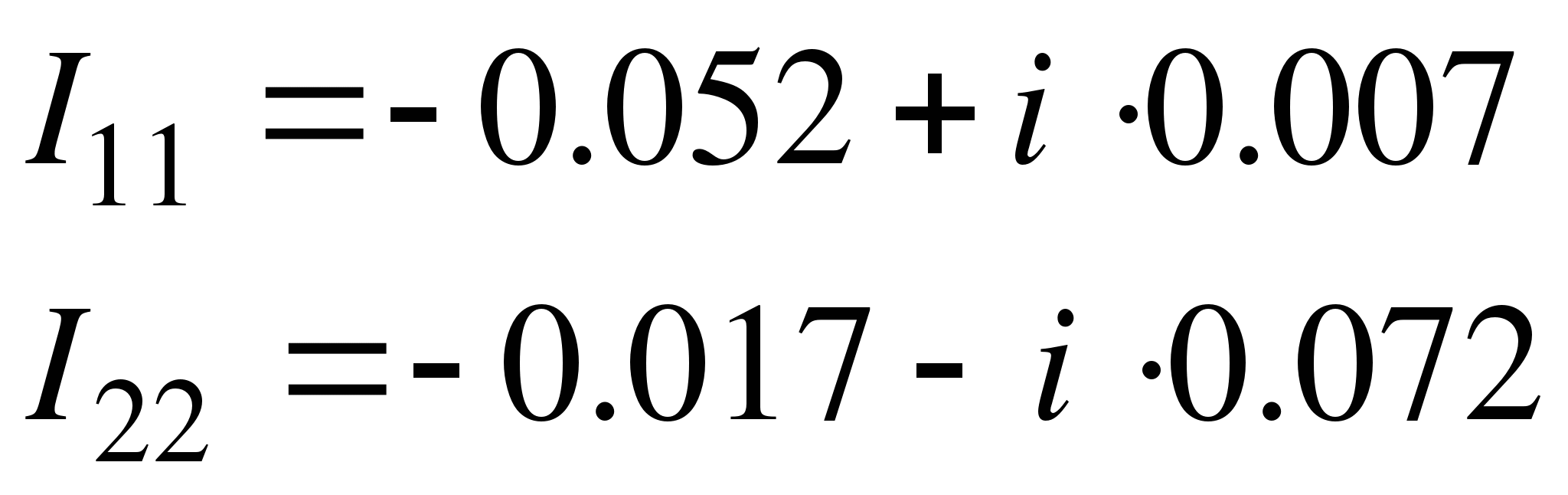 (2)
(2)
Находим ток в средней ветви 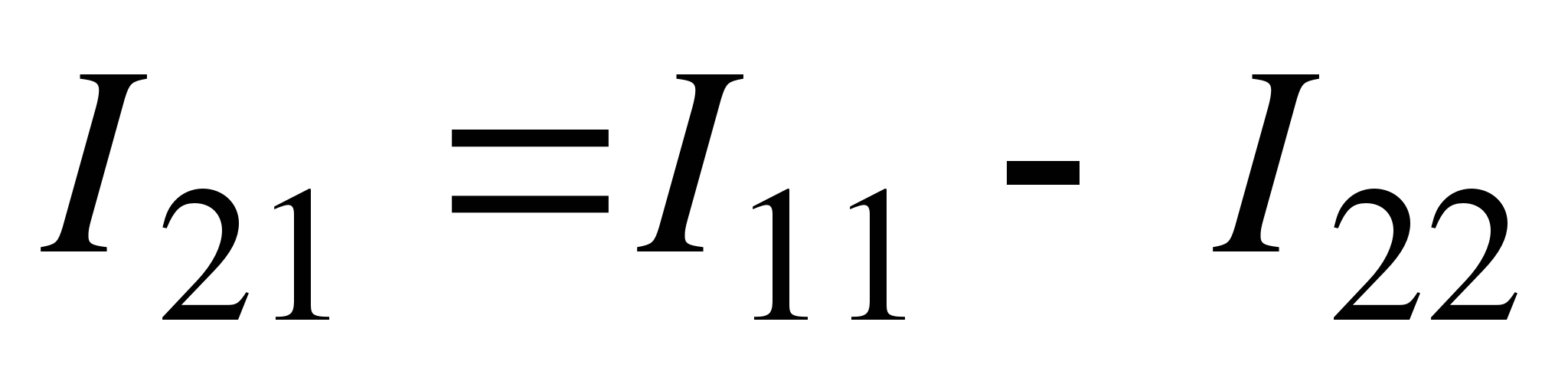
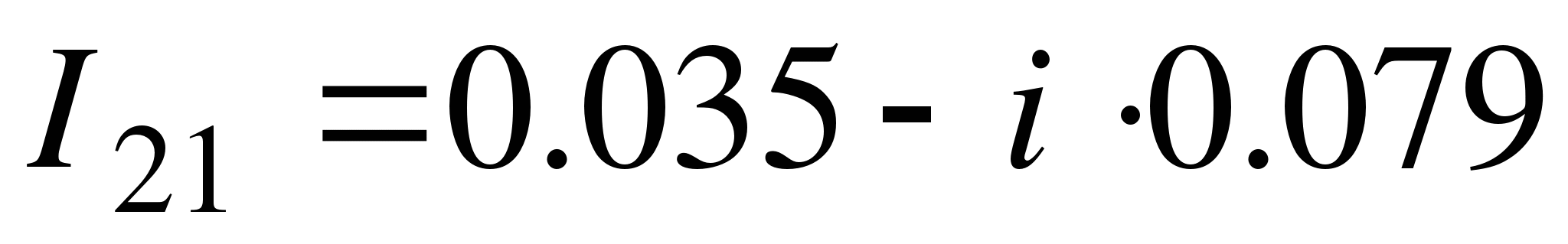
Как видим, решение (2) с точностью до знака совпадает с решением (1).
Проверим теперь, сходится ли баланс мощностей, т.е. выполняется ли тождество: 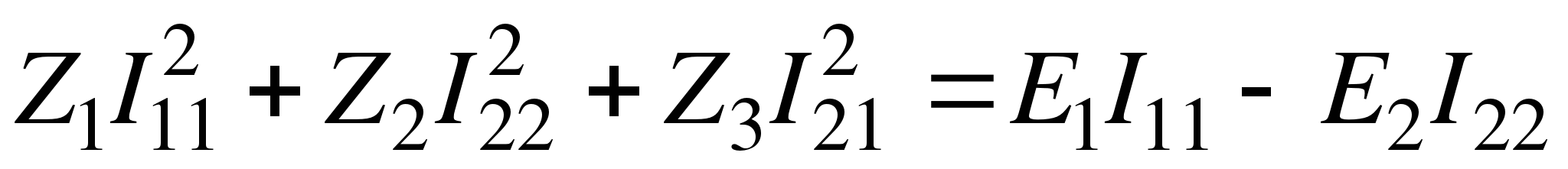 .
.
Левая часть тождества равна 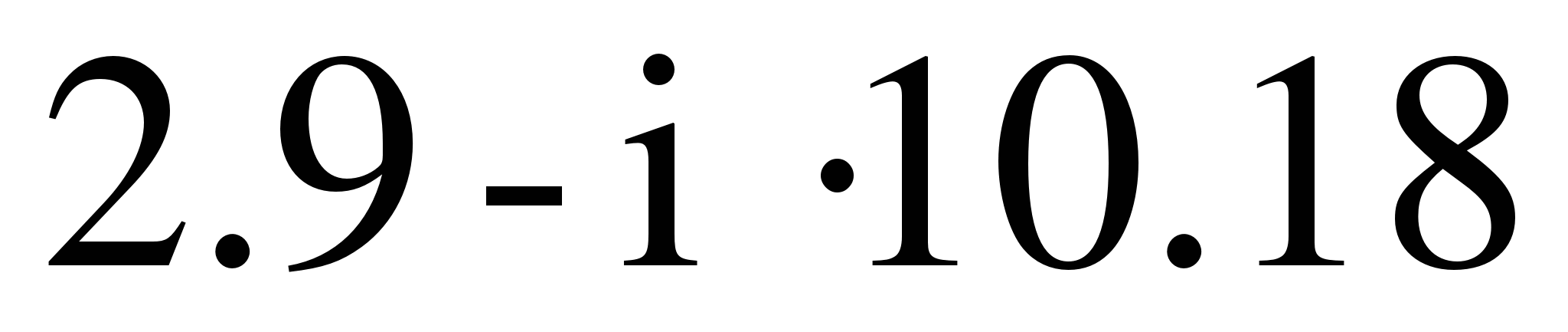 ;
;
Правая часть тождества равна 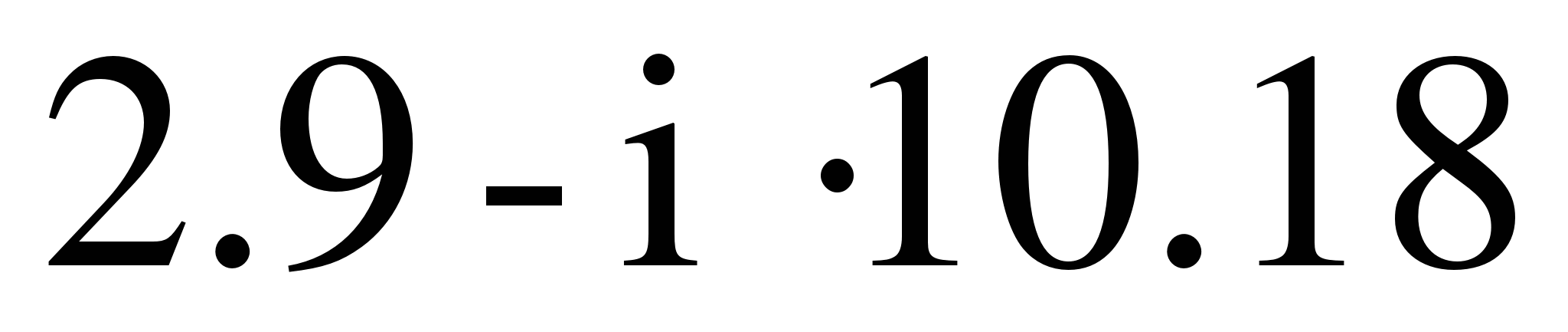
Таким образом, баланс мощностей сходится.
Построим теперь векторную диаграмму для внешнего контура цепи.
Воспользуемся рисунком, на котором указаны направления токов в ветвях (из решения задачи первым способом).
Выберем точку в контуре, потенциал которой примем равным нулю (пусть это будет т.О на рисунке).
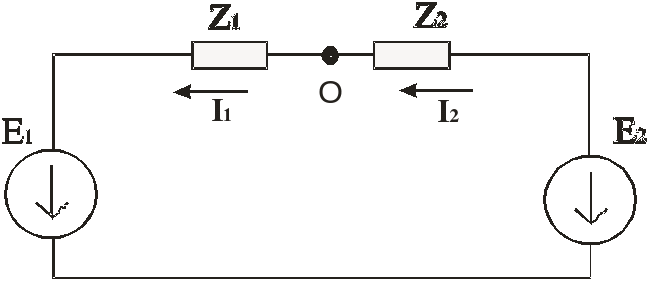
Вычислим падения напряжения на каждом из элементов (будем вычислять модули и фазовые сдвиги)

Вычислим модули и аргументы этих величин
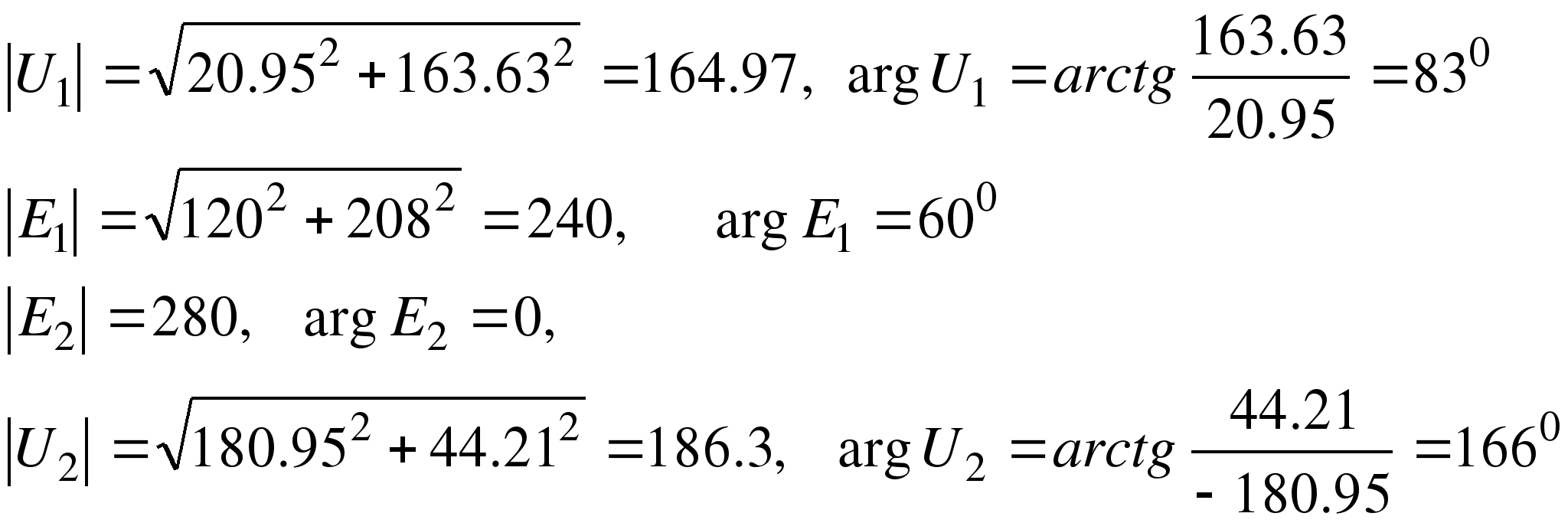
На основе этих данных построим векторную диаграмму, начиная от точки О и двигаясь вдоль контура по часовой стрелке, при этом будем учитывать направление обхода контура и направление уменьшения потенциалов.
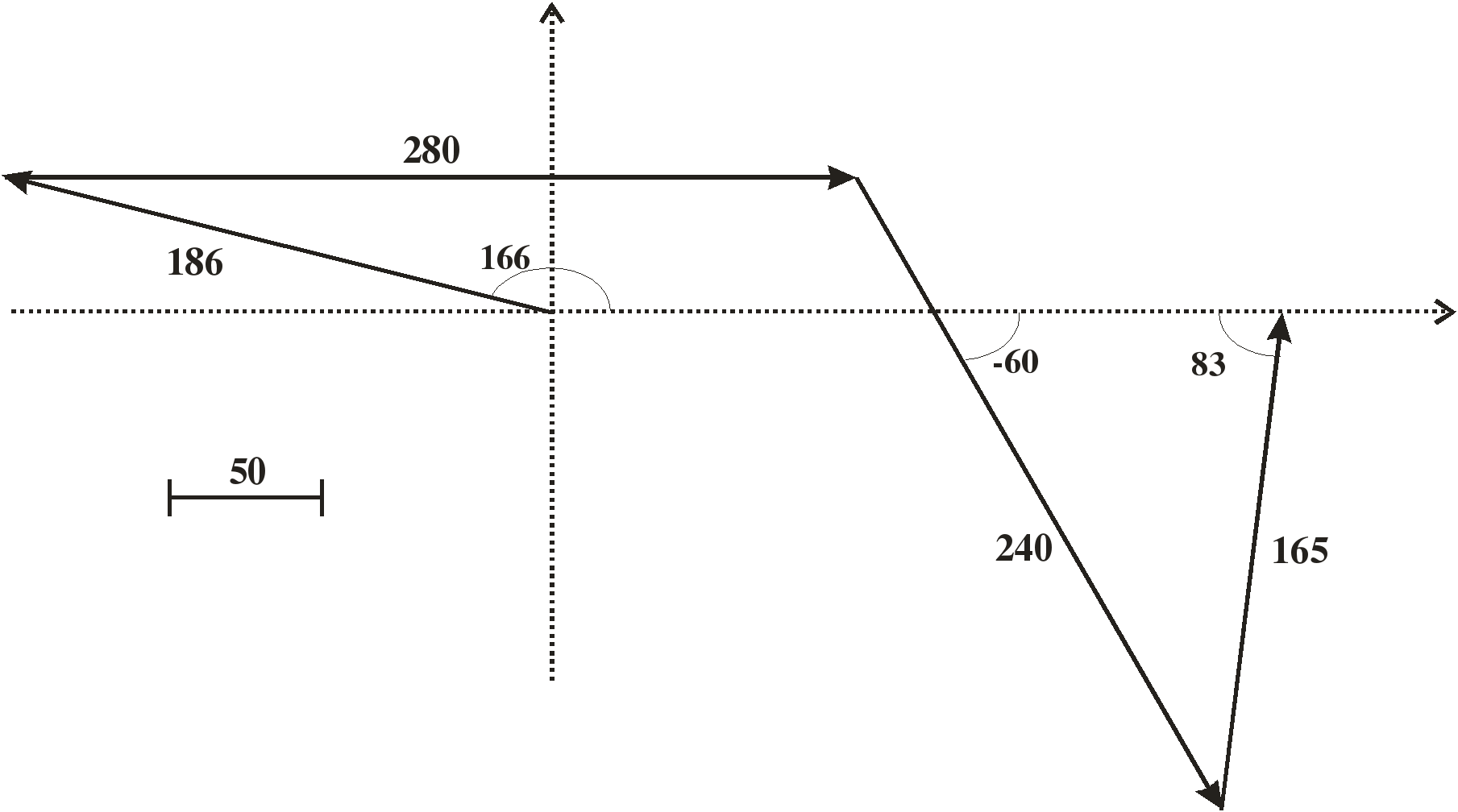
Резисторы, конденсаторы, катушки индуктивности, дроссели, трансформаторы, их использование в электрооборудовании автомобилей.
Пассивные элементы– элементы, которые выполняют пассивное (не усиливают) преобразование параметров цепей и электронных схем. К ним относятся
Резисторы (сопротивления)– наиболее распространенные компоненты электронной аппаратуры, с помощью которых осуществляется регулирование и распределение электроэнергии между цепями и элементами схем. Различаются по назначению, конструкции, материалам и пр.
Конденсаторы (емкости)
У конденсаторов различают номинальную и фактическую емкость. Номинальная емкость указывается на маркировке конденсатора, а фактическая зависит от внешних условий (температура, частота).
Катушки (индуктивности) и их разновидности –дроссели, содержащие магнитопровод из ферромагнитного материала, имеют в электронных схемах более ограниченное применение ввиду их относительно больших габаритов, обладая, вместе с тем, рядом специфических достоинств (например, высокая температурная стойкость).
Дросселем называется разновидность катушки индуктивности, представляющая собой катушку с магнитопроводом, выполненным, как правило, из пластин электротехнической стали, что позволяет увеличить индуктивность. Главное конструктивное отличие дросселя от трансформатора – небольшой воздушный зазор (0,1 мм) в цепи магнитопровода.
Трансформаторы– статические устройства, обеспечивающие преобразование параметров переменных напряжений. Используются в электронных схемах главным образом для преобразования напряжения сети в напряжение, необходимое для питания электронных устройств.
Принцип действия электромагнитного трансформатора основан на преобразовании энергии электрического поля в энергию магнитного поля и обратно.
Вопрос 5
Перечислите основные причины изменения технического состояния автомобилей. Опишите последствия основных факторов изменения технического состояния автомобиля и влияние технического состояния автомобиля на его ходовые качества.
Основные причины изменения ТС и конструктивных параметров: нагружение элементов, взаимное перемещение элементов, воздействие тепловой и электр. энергии, воздействие хим. активных компонентов, воздействие внешней среды (влаги, ветра, температуры, солнечной радиации), воздействие оператора.
Последствия и формы изменения конструктивных параметров времени: изнашивание, коррозия, усталостные разрушения и изменения, старение и др.
Изнашивание. Процесс изнашивания возникает под действием трения , зависящего от материала и качества обработки поверхности и теплового режима работы сопряжения. Изнашивание – процесс разрушения и отделения материала с поверхности детали и накопления ёё остаточной деформации при трении, проявляющийся в постепенном изменении размеров и формы детали. Результат изнашивания, определяемый в установленных единицах, называется – износом, который может быть линейным, объёмным, массовым. Интенсивность изнашивания- это относительные величины износа.
Пластическая деформация и разрушении. Такие повреждения связаны с достижением и повышением пределов текучести или прочности у вязких или хрупких материалов.
Усталостные разрушения. Эти виды разрушений возникают при циклическом приложении нагрузок, превышающих предел выносливости металла детали.
Коррозия. Это явление происходит вследствие агрессивного воздействия среды на детали, приводящего к окислению металла детали и, как следствие , к уменьшению прочности и ухудшению внешнего вида. Она в основном поражает детали кузова, кабины, рамы.
Старение. Техническое состояние деталей и экспл. материалов изменяется под действием окружающей среды. В процессе эксплуатации свойства смазочных материалов и эксплуатационных жидкостей ухудшаются в результате накопления в них продуктов износа, изменения вязкости и потери свойств прсадок.
Влияние условии эксплуатации. Влияние условий эксплуатаций при которых экспл. а\м влияют на режимы работы агрегатов, ускоряют или замедляют изменения параметров их тех. состояния.
— дорожные условия – определяющие реж. работы а\м. Режим работы влияет на износ его дет., износ и разрущение дорожного покрытия сокращяет надёжностя а\м на 14-30%
— условия движения
— условия перевозки
— природно — климатические условия
Эквивалентная схема замещения конденсатора.
Эквивалентная
схема замещения конденсатора представлена
на рис 1 и представляет собой последовательное
соединение собственной емкости
конденсатора С,
индуктивности пластин и выводов
конденсатора 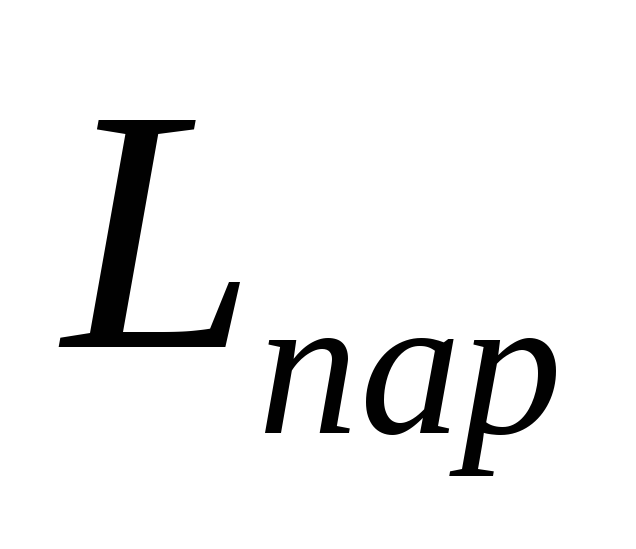 и активного сопротивления выводов,
контактного узла и сопротивления
обкладок конденсатора
и активного сопротивления выводов,
контактного узла и сопротивления
обкладок конденсатора
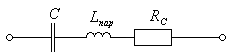
Рис.1. Упрощенная эквивалентная схема замещения конденсатора.
Модуль
полного сопротивления 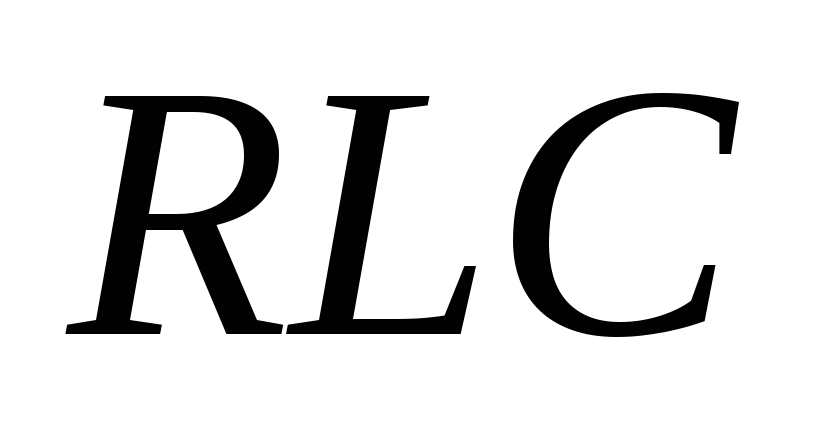 — цепи
определяется по формуле
— цепи
определяется по формуле
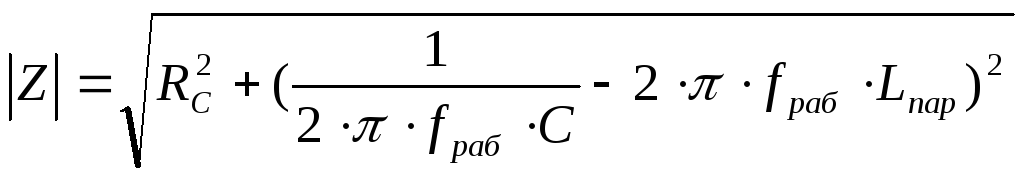 4
4
где С собственная емкость конденсатора;
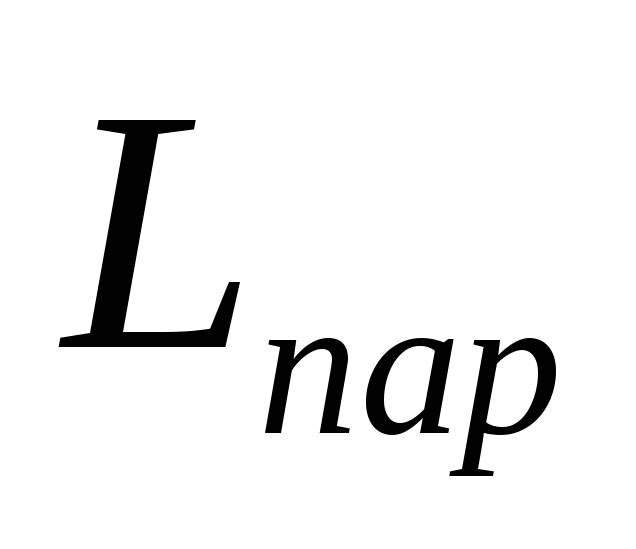 индуктивность
пластин и выводов конденсатора;
индуктивность
пластин и выводов конденсатора;
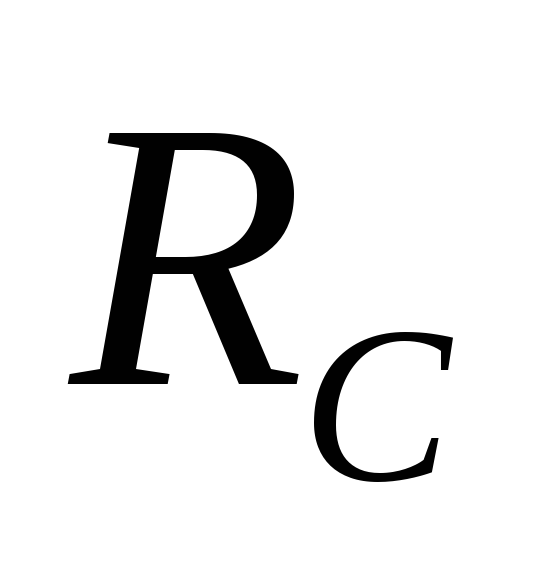 активное
сопротивление выводов контактного узла
и сопротивление обкладок конденсатора;
активное
сопротивление выводов контактного узла
и сопротивление обкладок конденсатора;
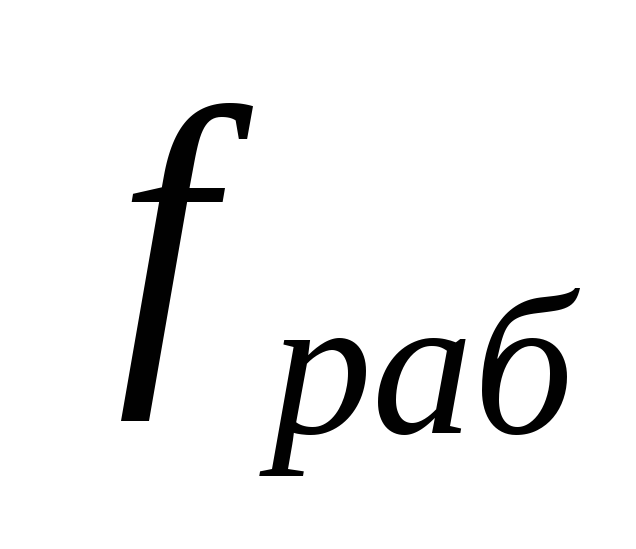 рабочая
частота
рабочая
частота
Из формулы (4) видно, что модуль полного сопротивления такой цепи зависит от частоты, на которой работает конденсатор. На рис.2 представлена зависимость полного сопротивления RLC — цепи от частоты.
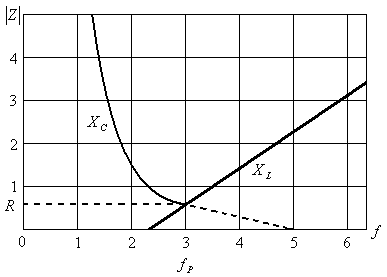
Рис. 2 Зависимость модуля полного сопротивления RLC -цепи от частоты.
Из формулы (4) и рис.2 видно, что модуль полного сопротивления на резонансной частоте имеет минимальное значение и носит шюто активный характер. Резонансная частота такой цепи определяется по формуле
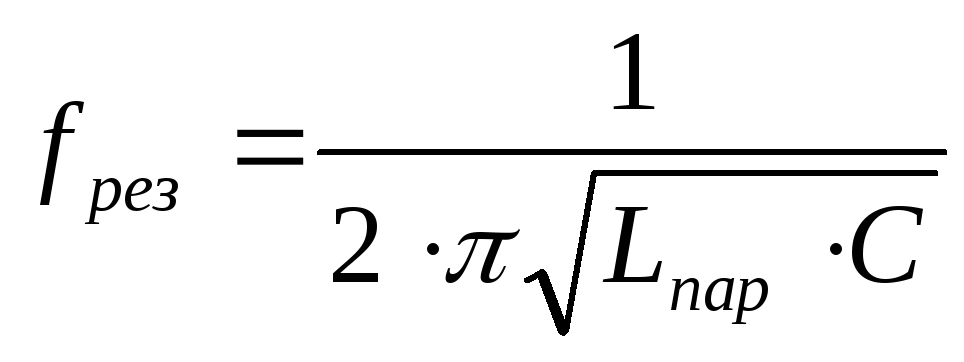 5
5
На
частоте ниже резонансной модуль полного
сопротивления RLC цепи носит емкостный характер, а на
частоте выше резонансной — индуктивный.
Это приводит к изменению эквивалентной
схемы замещения для различных частот.
Достаточно рассмотреть три случая когда
конденсатор используется на резрнансной
частоте 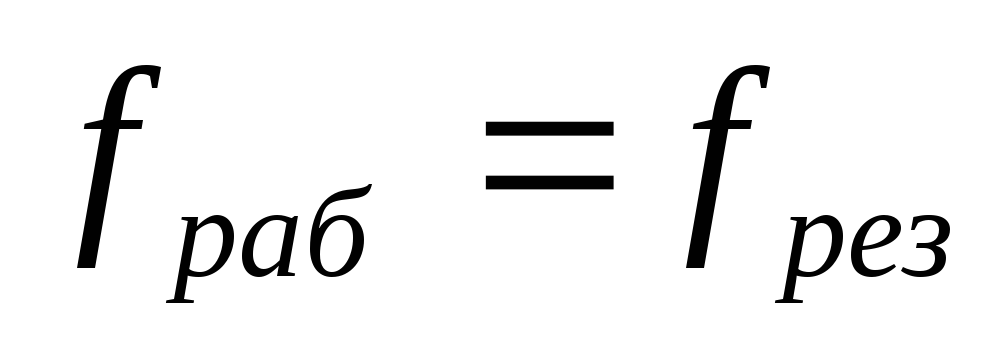 ,
,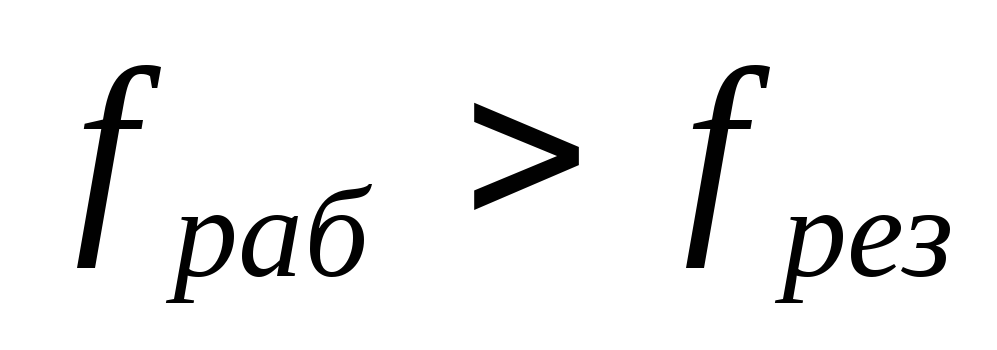 и
и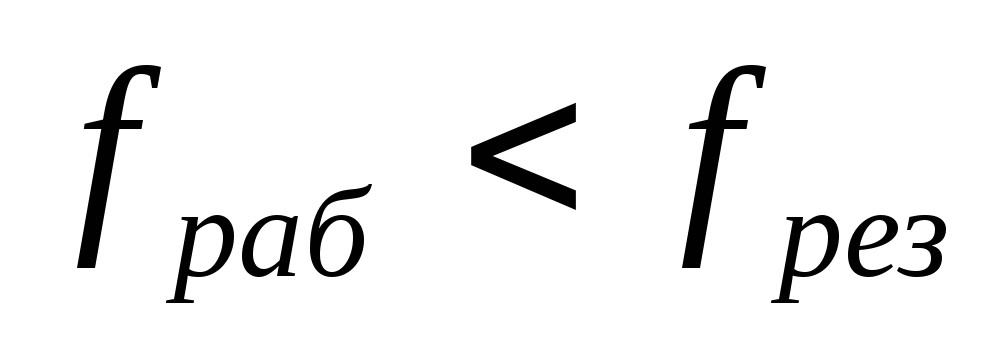 чтобы представить переходные процессы,
происходящие в нем.
чтобы представить переходные процессы,
происходящие в нем.
Для
случая, когда рабочая частота совпадает
с резонансной, т.е. 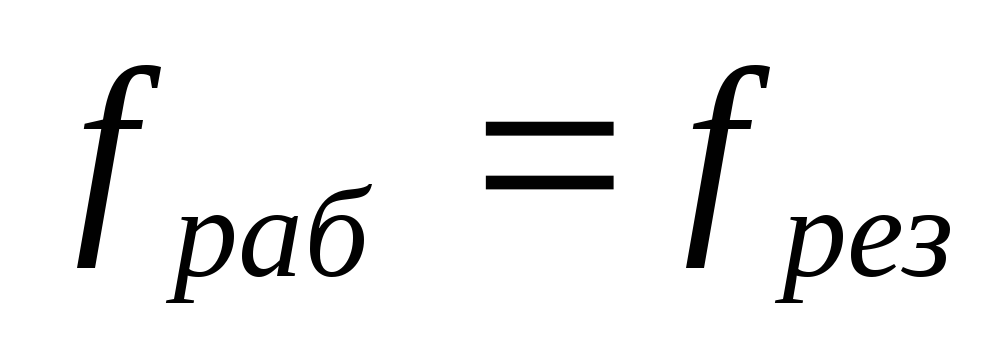 емкостная и индуктивные составляющие
в выражении (4) равны и модуль полного
сопротивления носит чисто активный
характер, причем это сопротивление
минимально и определяется из выражения
емкостная и индуктивные составляющие
в выражении (4) равны и модуль полного
сопротивления носит чисто активный
характер, причем это сопротивление
минимально и определяется из выражения
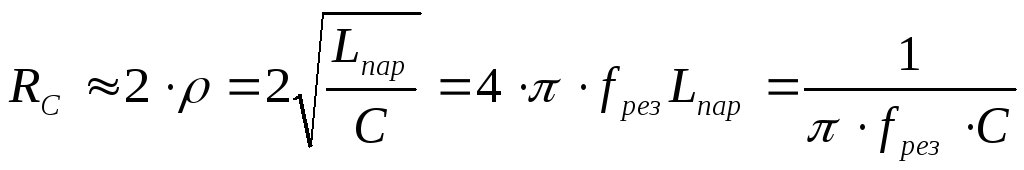 6
6
Резонансная частота такого контура без учета потерь определяется формулой (5), а добротность контура равна
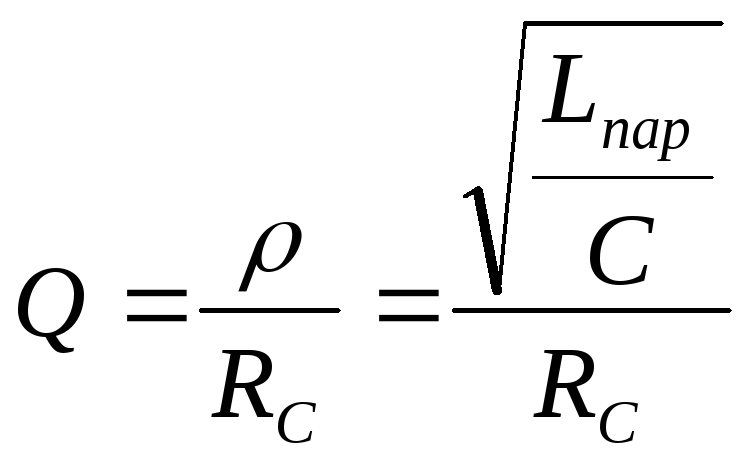 7
7
где  волновое
сопротивление контура;
волновое
сопротивление контура;
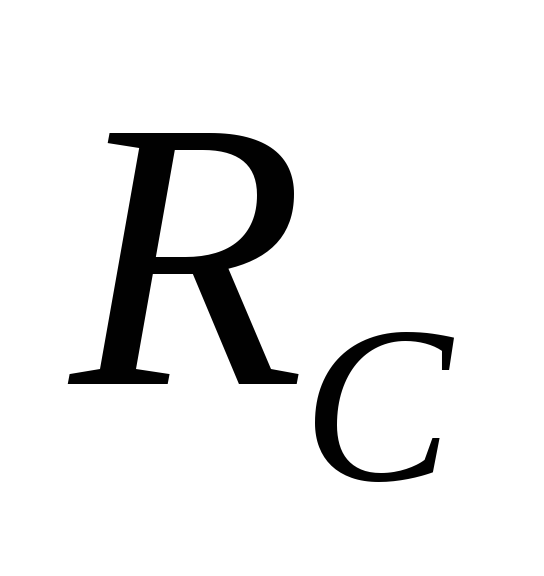 сопротивление
контура на резонансной частоте.
сопротивление
контура на резонансной частоте.
Полоса пропускания такого контура находится из следующего выражения
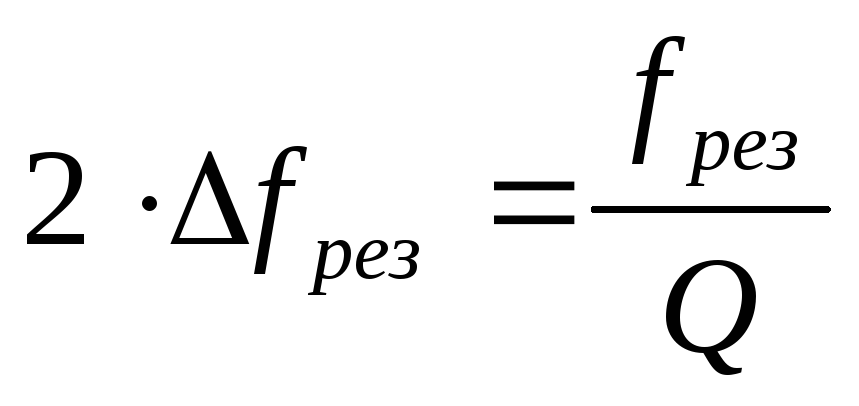 8
8
В полосе пропускания контура, с достаточной степенью точности, можно считать, что эквивалентная схема замещения конденсатора состоит из чисто активного сопротивления, поэтому переходные процессы, происходящие в активном сопротивлении, от частоты не зависят.
Для
случая когда рабочая частота больше
резонансной частоты контура (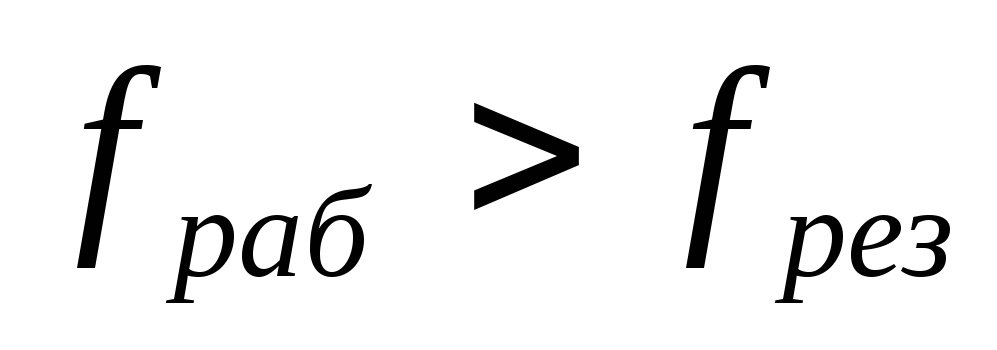 ),
т.е. когда
),
т.е. когда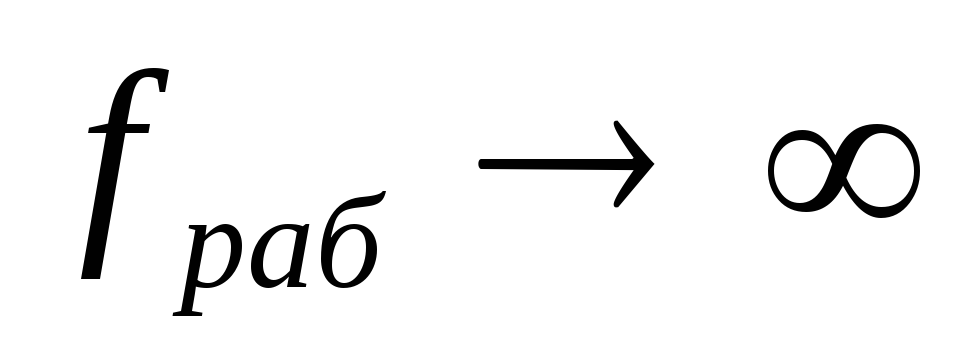 составляющая в выражении (4) стремится
к нулю. Модуль полного сопротивления
конденсатора носит индуктивный характер
и, соответственно, эквивалентная
схема замещения конденсатора для
рассматриваемого случая, несколько
видоизменяется.. Она представлена на
рис. 3.
составляющая в выражении (4) стремится
к нулю. Модуль полного сопротивления
конденсатора носит индуктивный характер
и, соответственно, эквивалентная
схема замещения конденсатора для
рассматриваемого случая, несколько
видоизменяется.. Она представлена на
рис. 3.
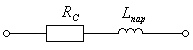
Рис.3. Эквивалентная схема замещения конденсатора для частот выше резонансной частоты.
Модуль полного сопротивления RLC — цепи, представленной на рис.3, определяется выражением
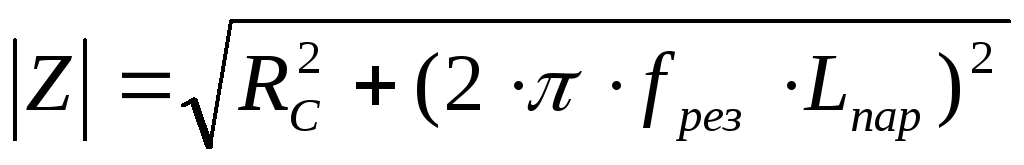 9
9
Наличие
индуктивности в рассматриваемой цепи
приводит к частотной зависимости
модуля полного сопротивления конденсатора
на частотах 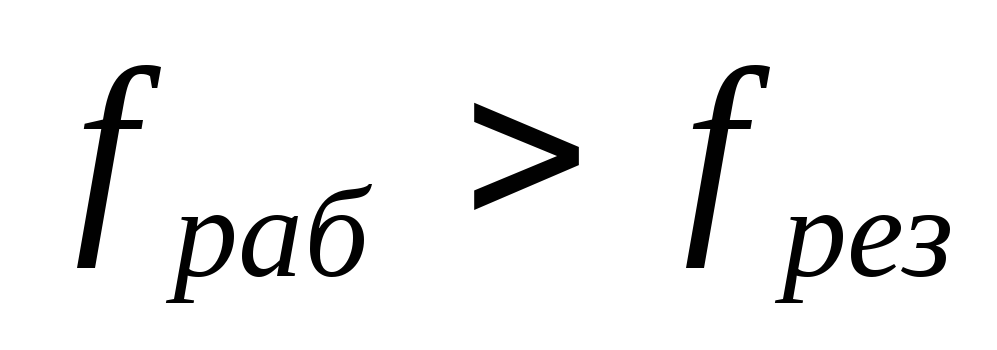 .
Переходные процессы происходящие вRL —
цепи при коммутации подробно рассмотрены
в лабораторной работе №1,
поэтому здесь не рассматриваются.
.
Переходные процессы происходящие вRL —
цепи при коммутации подробно рассмотрены
в лабораторной работе №1,
поэтому здесь не рассматриваются.
Для
случая когда рабочая частота ниже
резонансной 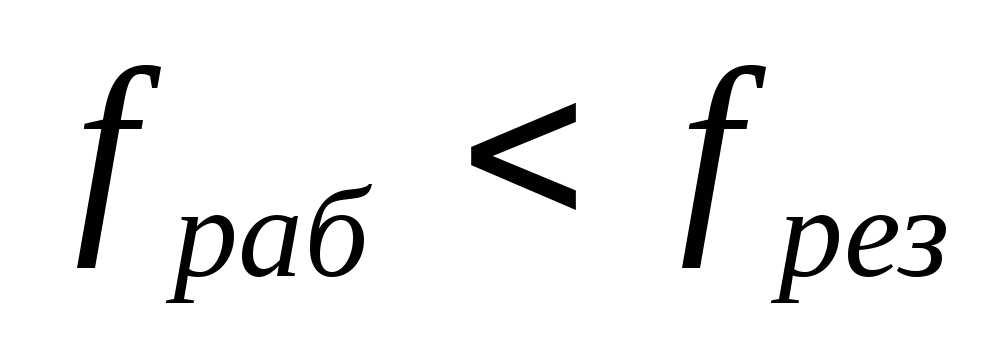 ,
т.е. когда
,
т.е. когда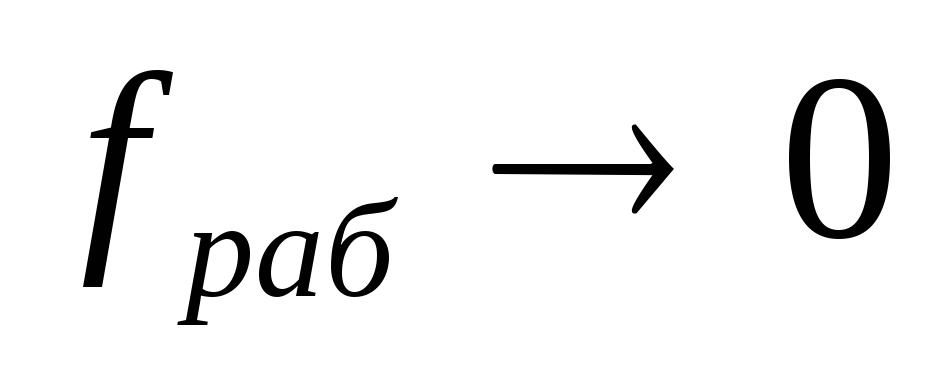 индуктивная составляющая в выражении
(4) стремится к нулю (
индуктивная составляющая в выражении
(4) стремится к нулю (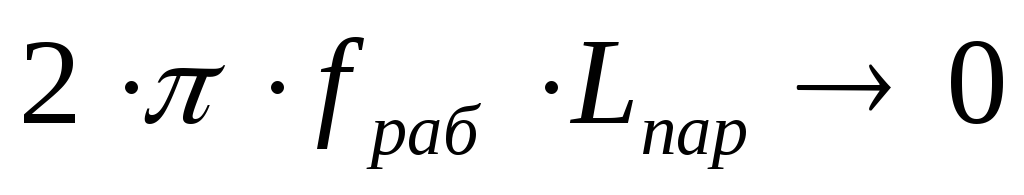 )
поэтому модуль полного сопротивления
конденсатора носит емкостный характер
и, соответственно, эквивалентная схема
замещения конденсатора для рассмотриваемого
случая несколько видоизменяется. Она
представлена на рис.4.
)
поэтому модуль полного сопротивления
конденсатора носит емкостный характер
и, соответственно, эквивалентная схема
замещения конденсатора для рассмотриваемого
случая несколько видоизменяется. Она
представлена на рис.4.
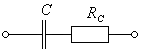
Рис. 4. Эквивалентная схема замещения конденсатора для частот ниже резонансной частоты.
Модуль полного сопротивления RC — цепи, представленной на рис.4, определяется выражением
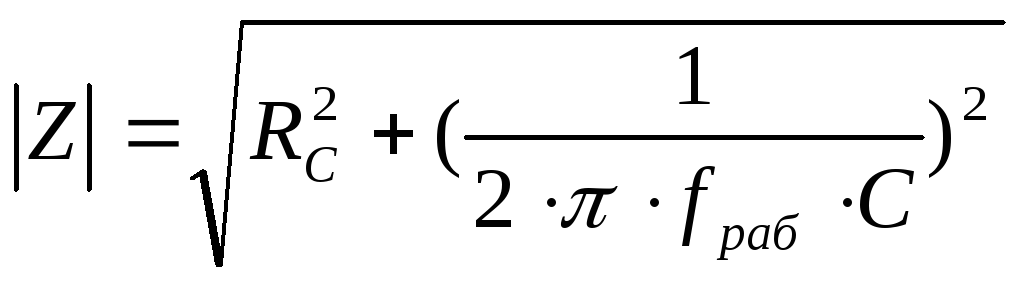 10
10
Наличие
емкости в
рассматриваемой
цепи приводит к частотной зависимости
модуля полного сопротивления конденсатора
на частотах 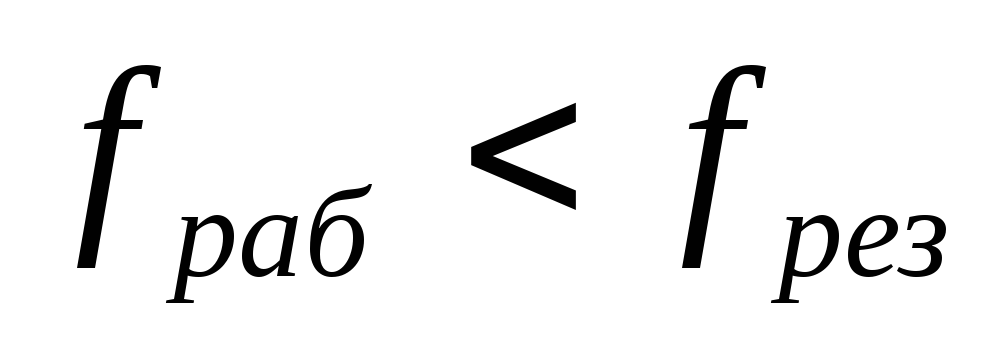 .
.
Рассмотрим переходные процессы, происходящие в RC — цепи при подключении её к источнику постоянной э.д.с. Схема включения RC — цепи к источнику постоянной э.д.с. представлена на рис.5.
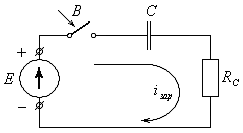
Рис. 5.
В RC — цепях рекомендуется вначале найти
напряжение на конденсаторе, а затем
ток е
цепи.
Из рис.5 видно, что при замыкании
выключателя В в момент 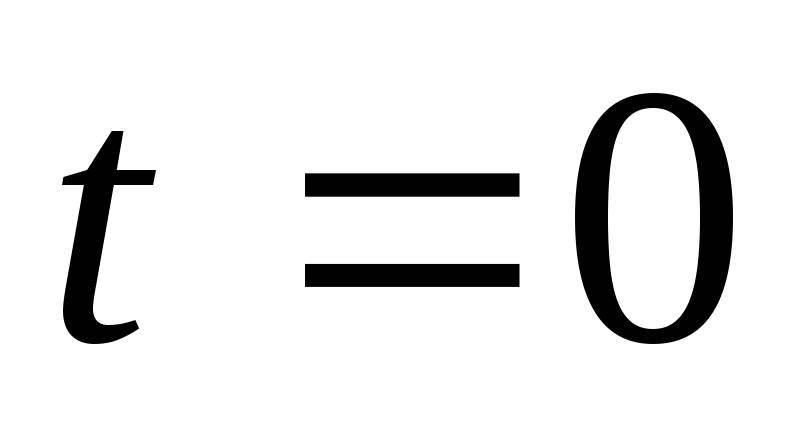 источник
постоянной э.д.с. подключается к RC — цепи. В момент скачка входного напряжения
сопротивления конденсатора равно
нулю, так как согласно второму закону
коммутации напряжение на нем мгновенно
измениться не может, поэтому в
начальный момент напряжение источника
целиком оказывается приложенным к
резистору
источник
постоянной э.д.с. подключается к RC — цепи. В момент скачка входного напряжения
сопротивления конденсатора равно
нулю, так как согласно второму закону
коммутации напряжение на нем мгновенно
измениться не может, поэтому в
начальный момент напряжение источника
целиком оказывается приложенным к
резистору 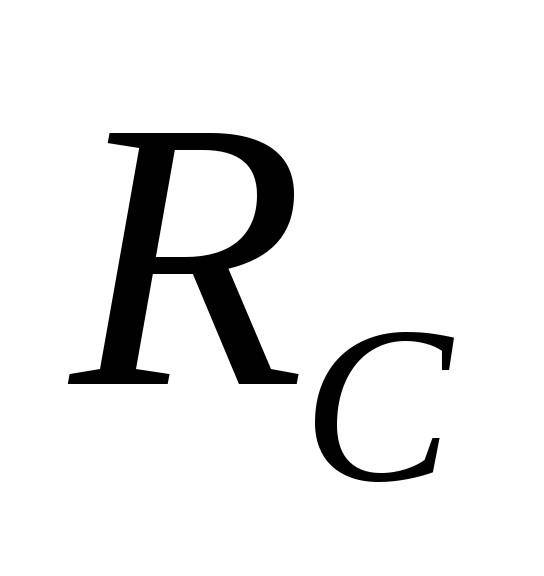 .
Затем конденсатор начинает заряжаться,
на его обкладках накапливается заряд
и напряжение между ними постепенно
возрастает. В соответствии со вторым
законом Кирхгофа (сумма падений напряжений
на резисторе
.
Затем конденсатор начинает заряжаться,
на его обкладках накапливается заряд
и напряжение между ними постепенно
возрастает. В соответствии со вторым
законом Кирхгофа (сумма падений напряжений
на резисторе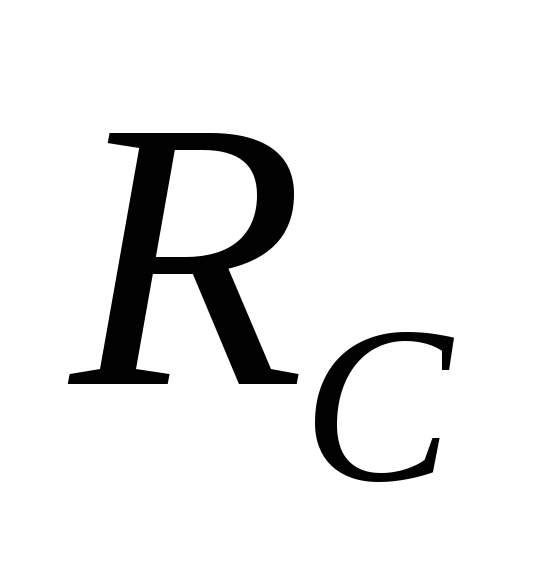 и конденсатораС уравновешивается внешней э.д.с.) и для
и конденсатораС уравновешивается внешней э.д.с.) и для 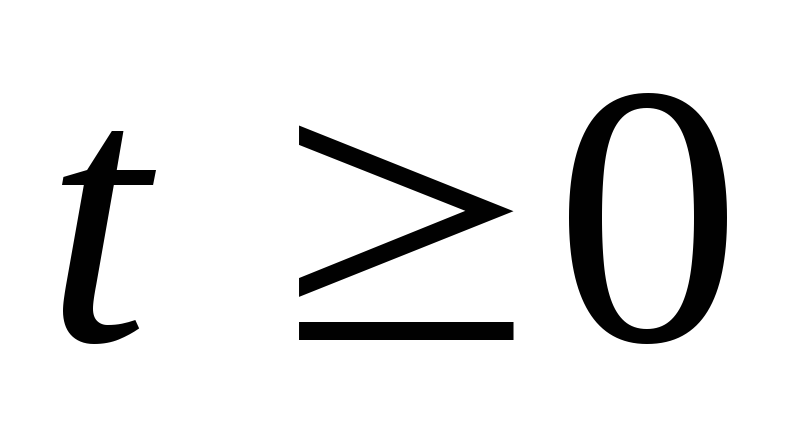 запишем уравнение
запишем уравнение
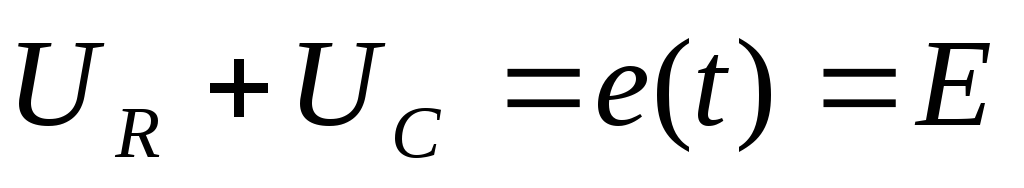 11
11
Учитывая
уравнение (11), можно утверждать, что при
увеличении напряжения 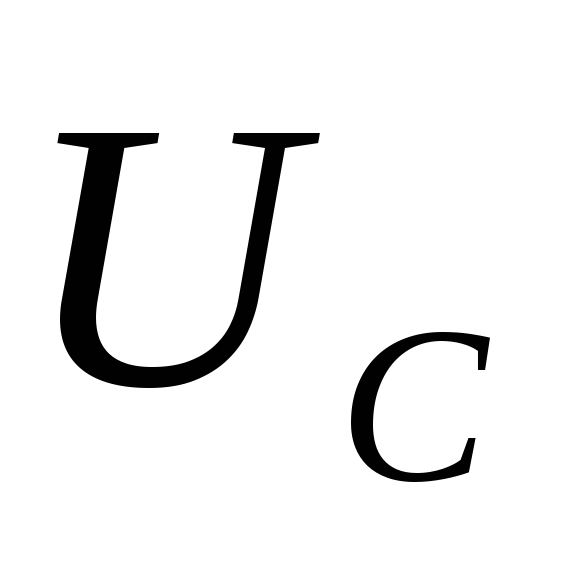 падение напряжения на резисторе
падение напряжения на резисторе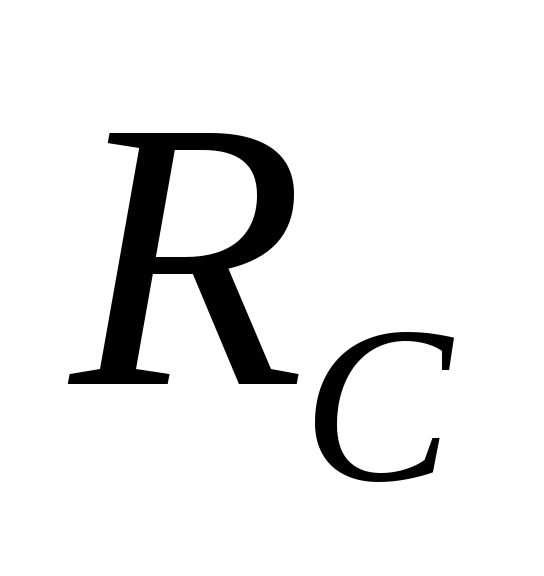 уменьшается,
а, следовательно, ток в RC — цепи уменьшается. Наконец, напряжение
на конденсаторе
уменьшается,
а, следовательно, ток в RC — цепи уменьшается. Наконец, напряжение
на конденсаторе 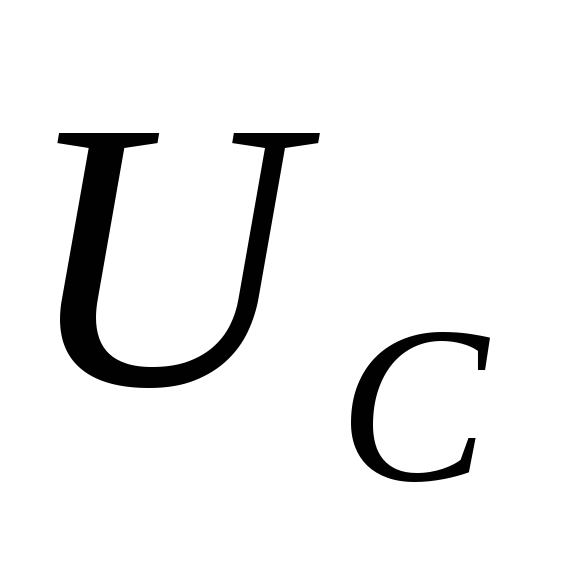 становится
равным з.д.с. источника
становится
равным з.д.с. источника 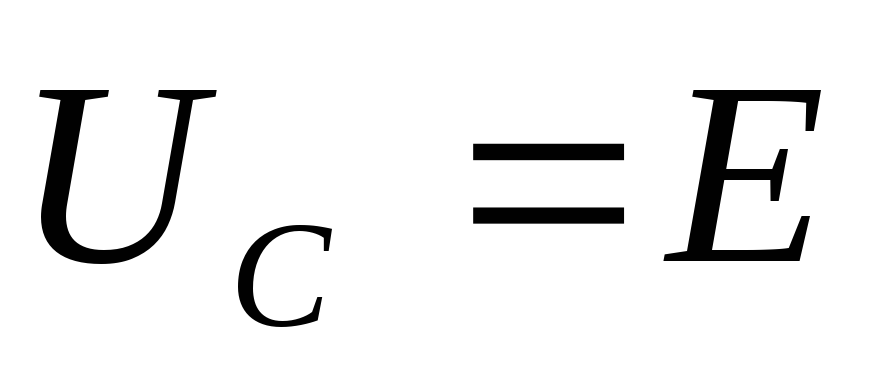 и процесс заряда конденсатора
заканчивается, ток вRC – цепи становится равным нулю. Очевидно,
что напряжение на конденсаторе изменяется
от нуля до Е. Для определения переходного
процесса RC — цепи выразим напряжение на резисторе
и процесс заряда конденсатора
заканчивается, ток вRC – цепи становится равным нулю. Очевидно,
что напряжение на конденсаторе изменяется
от нуля до Е. Для определения переходного
процесса RC — цепи выразим напряжение на резисторе 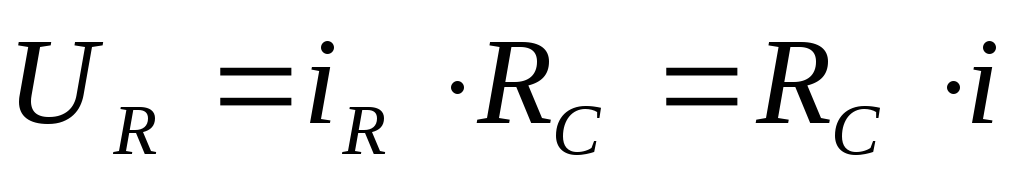 через
через 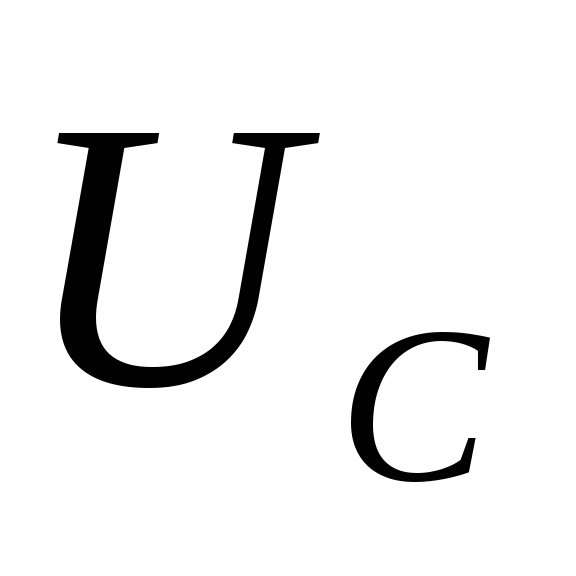 .
.
Учитывая,
что при последовательном соединении R и С ток в любом участке RС — цепи одинаков и равен 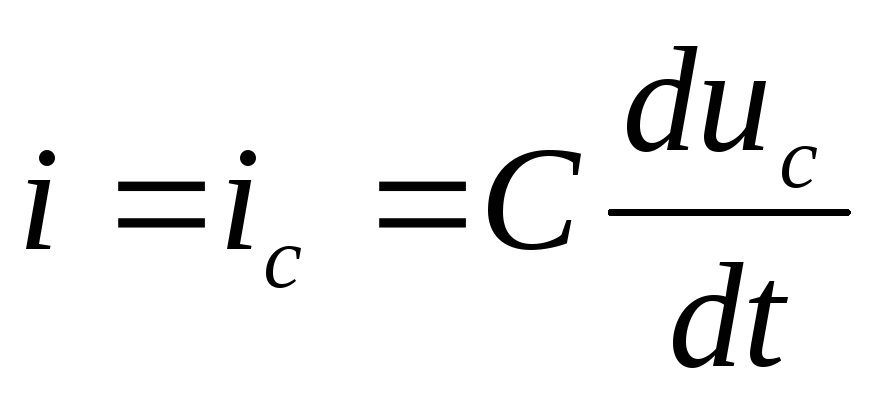 можно записать
можно записать
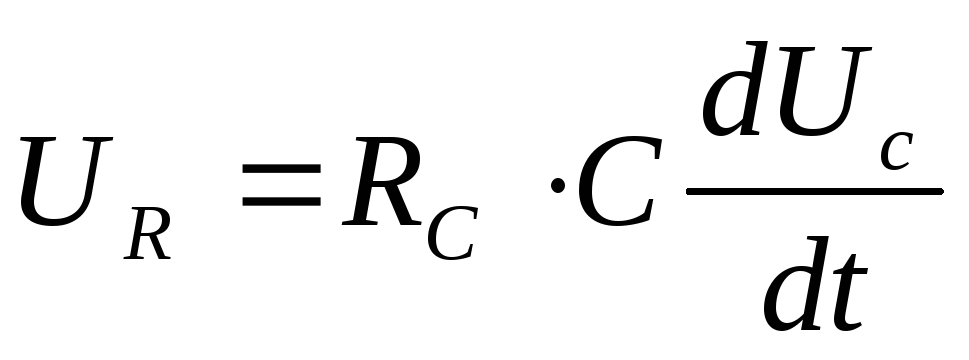 12
12
подставляя
значение 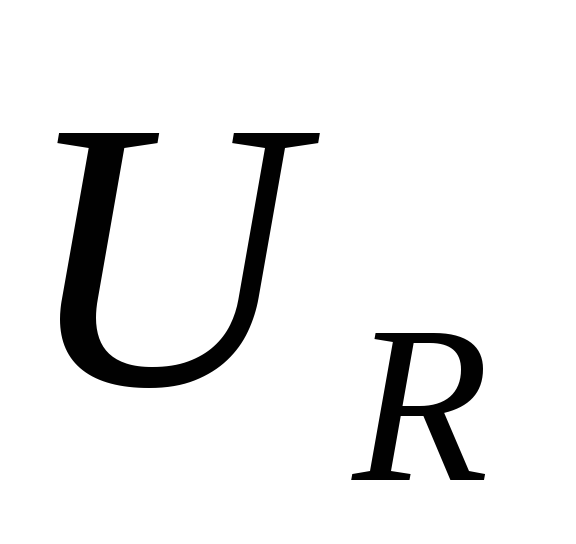 из (12) в уравнение (11) получим
из (12) в уравнение (11) получим
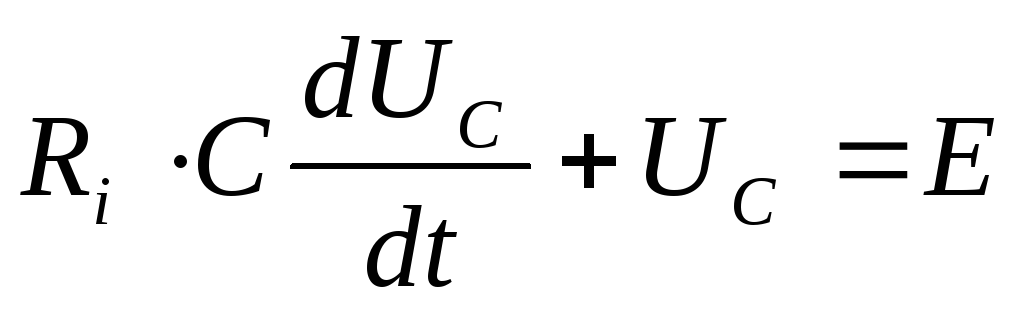 13
13
Это
выражение представляет собой
дифференциальное уравнение первого
порядка, в котором неизвестной функцией
является напряжение 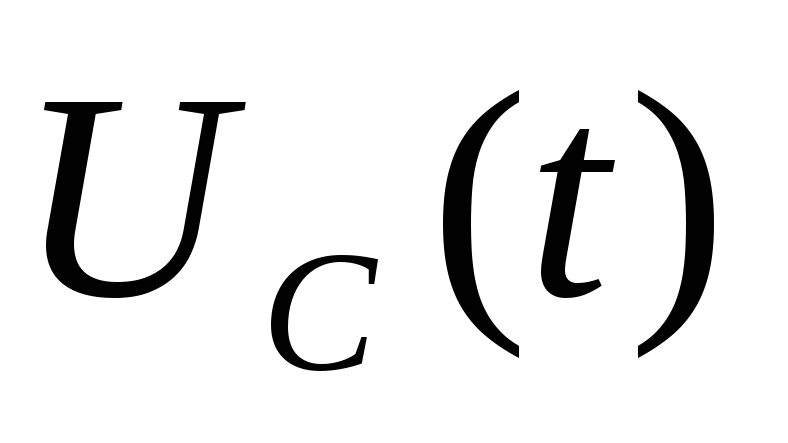 .
При использовании «классического»
метода решения напряжение
.
При использовании «классического»
метода решения напряжение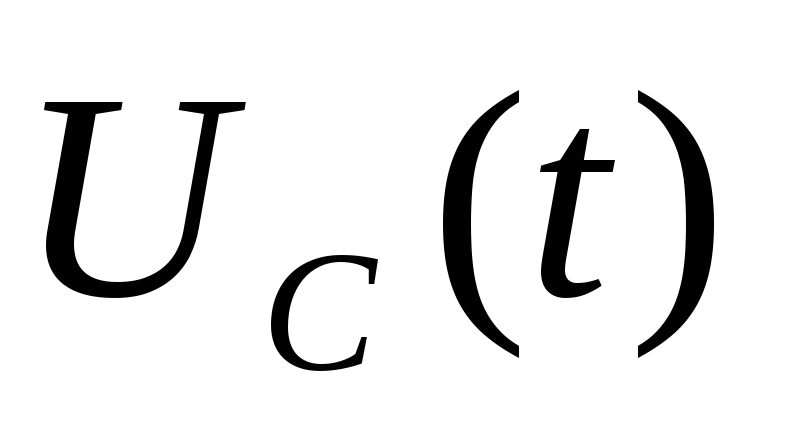 следует искать в виде суммы вынужденной
следует искать в виде суммы вынужденной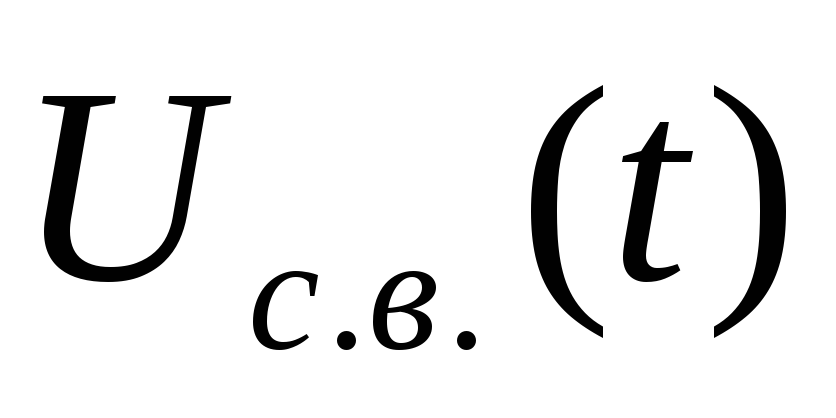 и свободной
и свободной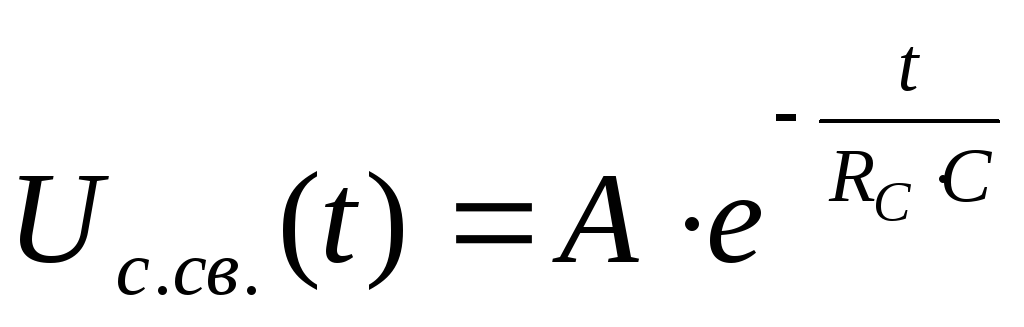 составляющих. Исходя из этого запишем
составляющих. Исходя из этого запишем
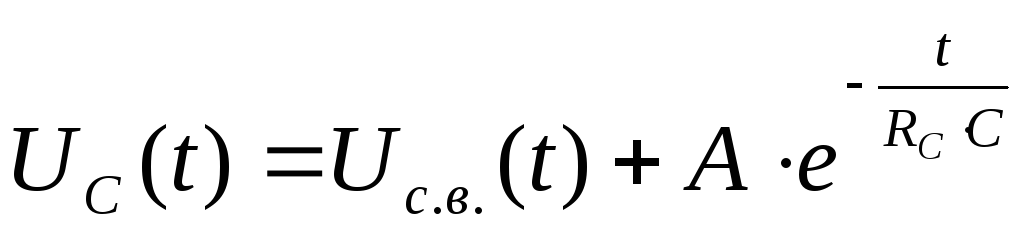 14
14
Вынужденная
составляющая напряжения, очевидно,
равна 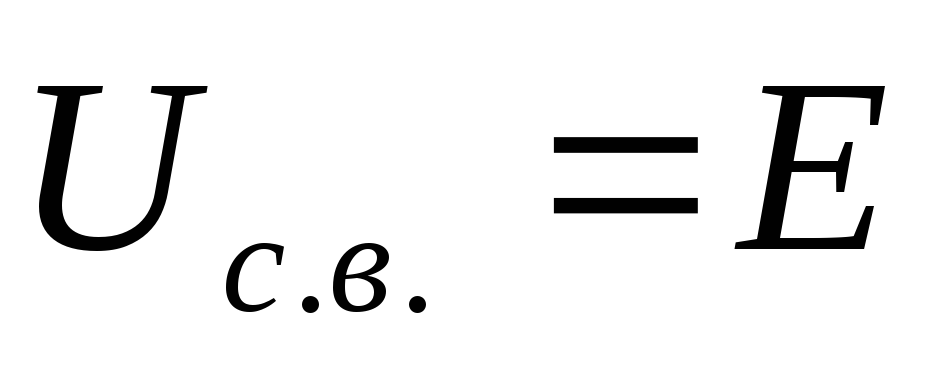 ,
поскольку в установившимся режиме
конденсатор заряжен до э.д.с. внешнего
источника питания.
,
поскольку в установившимся режиме
конденсатор заряжен до э.д.с. внешнего
источника питания.
Тогда согласно выражению (14) можно записать
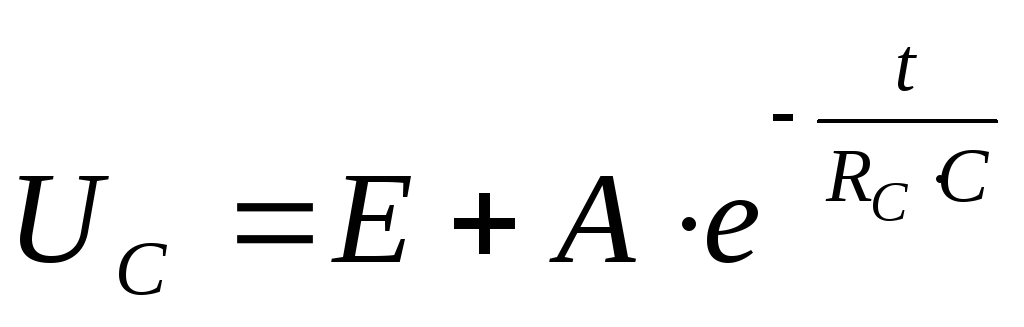 15
15
Чтобы
определить постоянную А,
воспользуемся начальными условиями,
состоящими в том, что к моменту коммутации
конденсатор был разряжен, т.е. 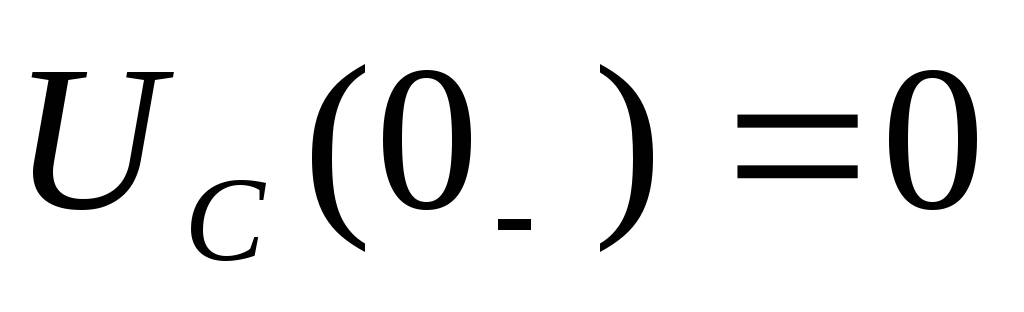 .
Из выражения (15) для момента
.
Из выражения (15) для момента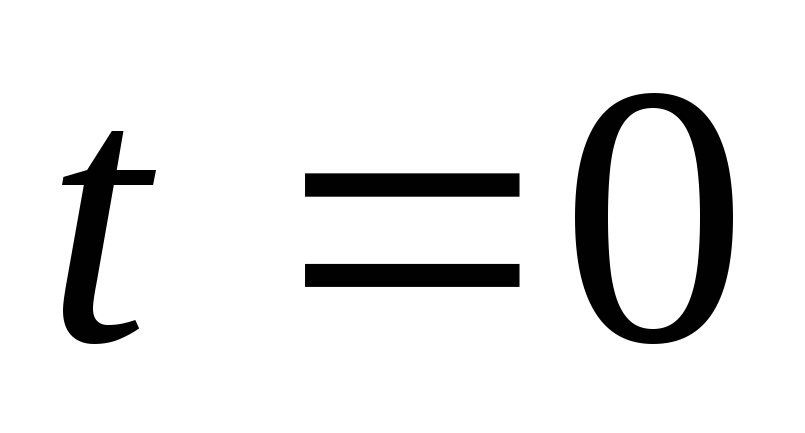 имеем
имеем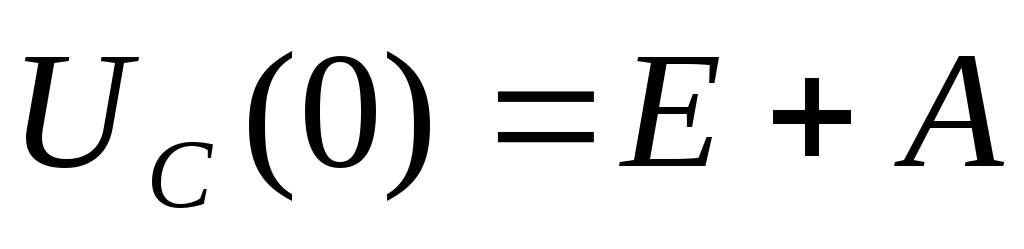 .
С другой стороны, согласно второму
закону коммутации напряжение
.
С другой стороны, согласно второму
закону коммутации напряжение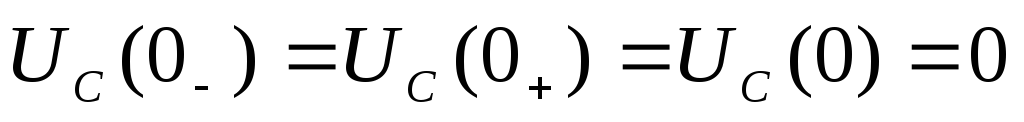 . Из этих двух отношений находим
. Из этих двух отношений находим .
Таким образом, свободная составляющая
напряжения на конденсаторе равна
.
Таким образом, свободная составляющая
напряжения на конденсаторе равна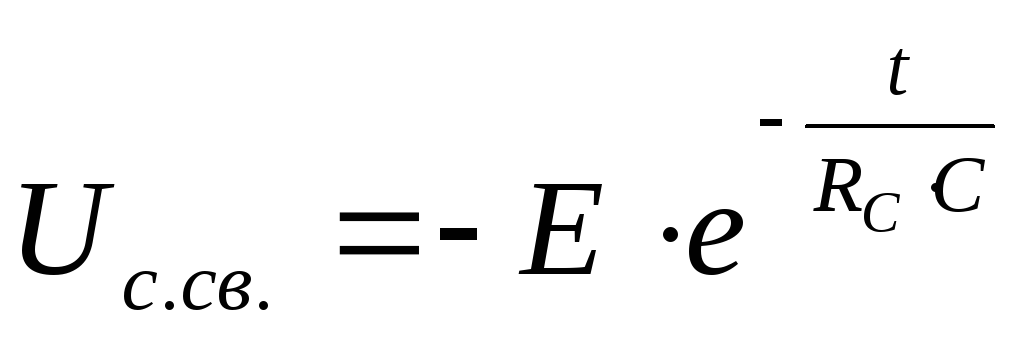 ,
а полное напряжение на конденсаторе в
процессе его заряда изменяется во
времени согласно выражению
,
а полное напряжение на конденсаторе в
процессе его заряда изменяется во
времени согласно выражению
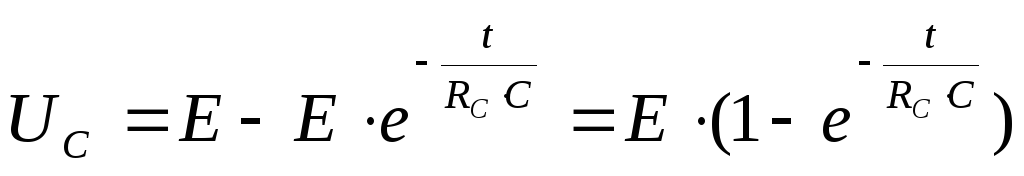 16
16
по экспоненциальному закону, стремясь к Е.
На
рис. 6а. приведены графики полного
напряжения на конденсаторе, а также
вынужденной и свободной составляющих.
Обратим внимание, что в момент 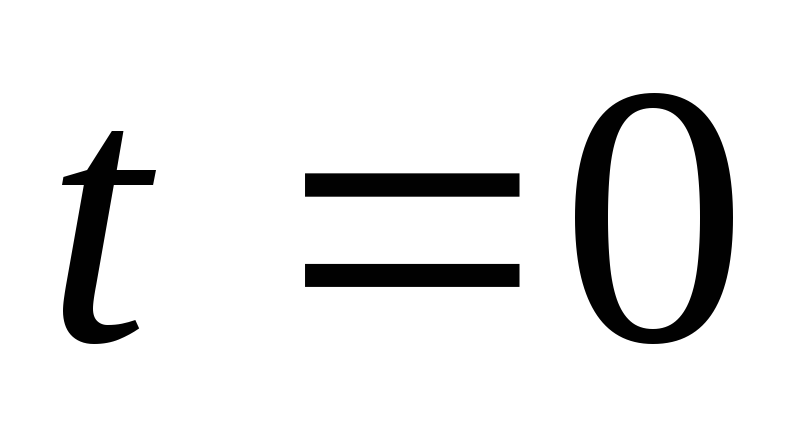 сумма напряжений
сумма напряжений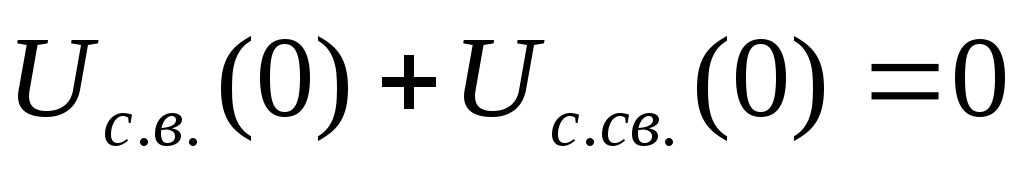 ,
чем обеспечивается выполнение начальных
условий. При значениях
,
чем обеспечивается выполнение начальных
условий. При значениях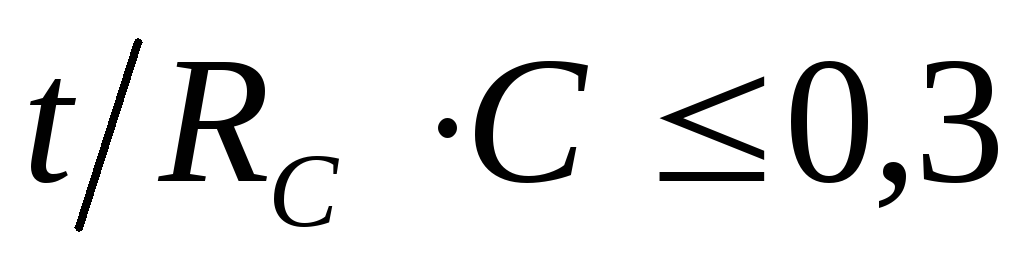 т.е. начальном этапе переходного процесса,
функция
т.е. начальном этапе переходного процесса,
функция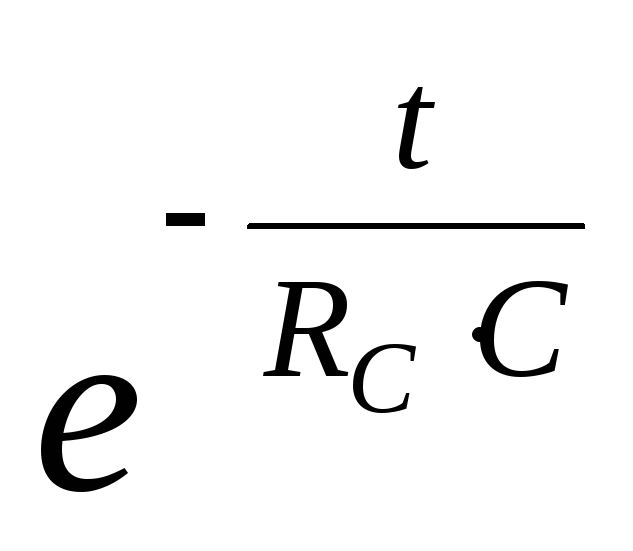 с удовлетворительной для практических
целей точностью при
с удовлетворительной для практических
целей точностью при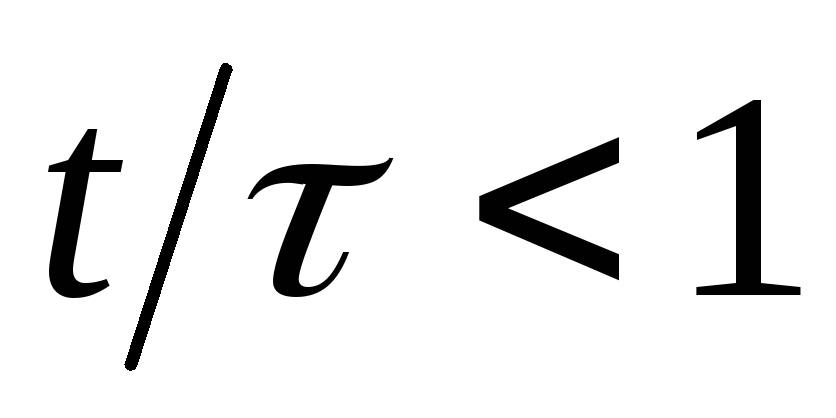 может быть аппроксимирована рядом
разложения
может быть аппроксимирована рядом
разложения
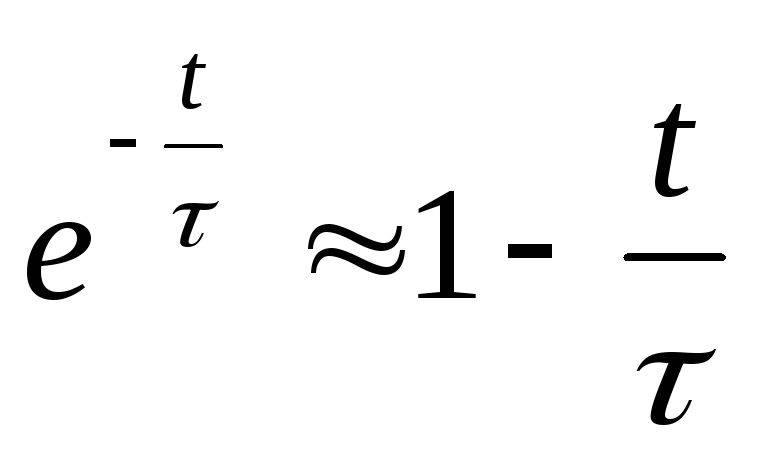
Тогда
для напряжения 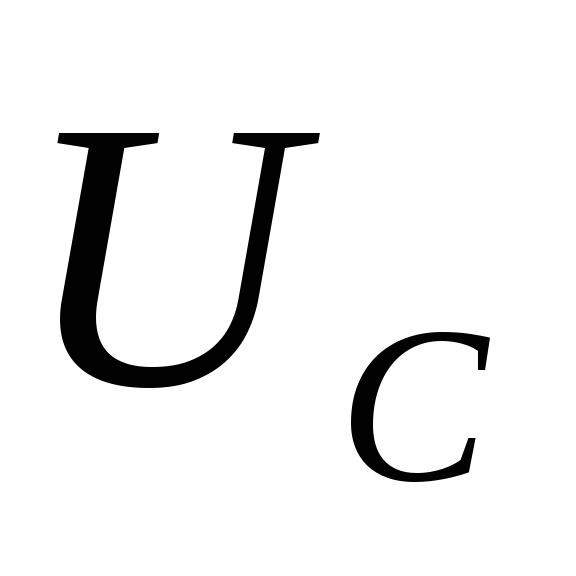 получим выражение
получим выражение
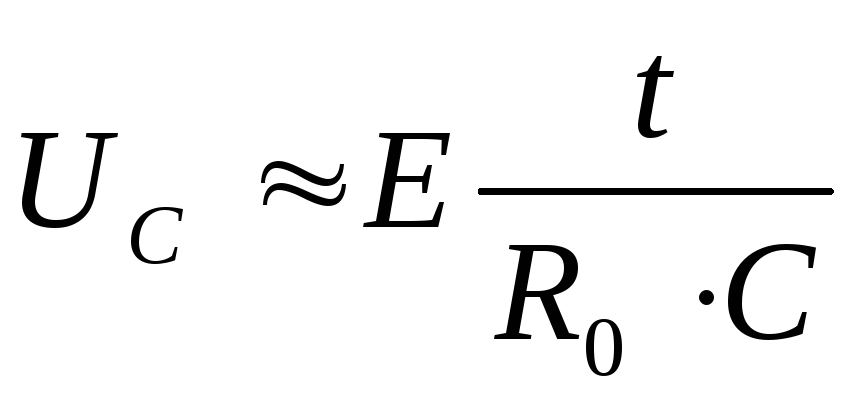 17
17
из которого следует, что нарастание напряжения на конденсаторе в начале процесса происходит по линейному закону.
Ток
в RC-цепи
(ток заряда конденсатора) может быть
найден дифференцированием выражения
(16) для 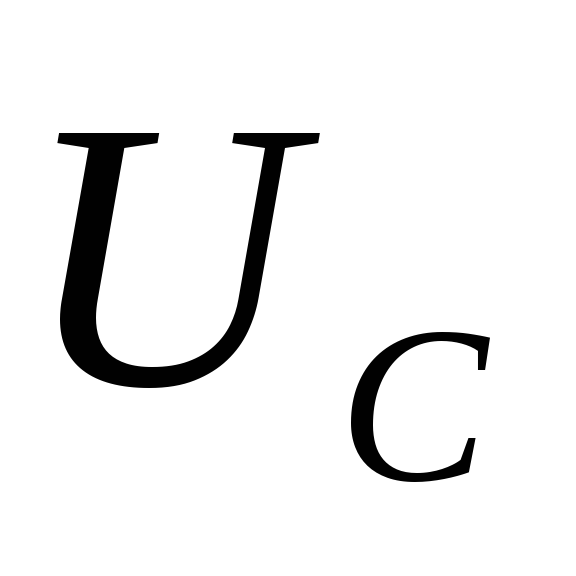 . Очевидно,
он должен содержать только свободную
составляющую, так как в установившемся
режиме ток в цепи равен нулю.
. Очевидно,
он должен содержать только свободную
составляющую, так как в установившемся
режиме ток в цепи равен нулю.
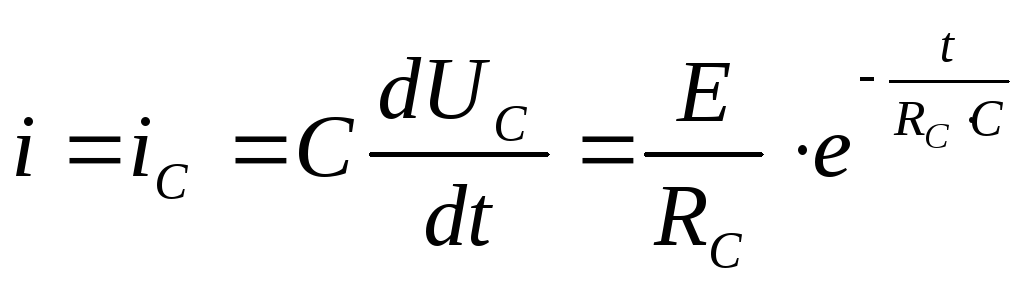 18
18
Падение
напряжения на резисторе 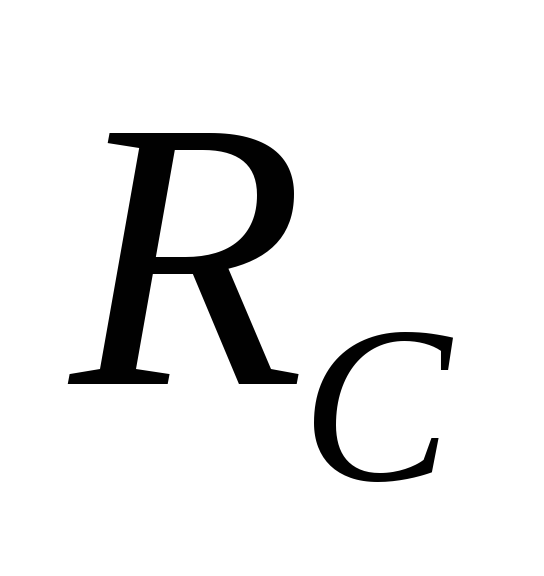
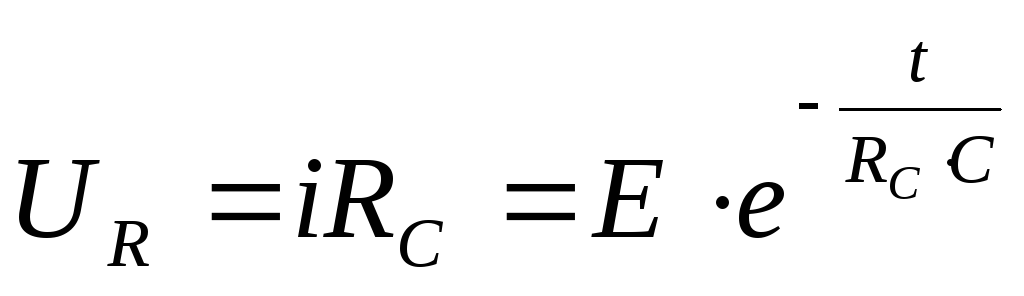 19
19
Ток
в RC —
цепи и напряжение на 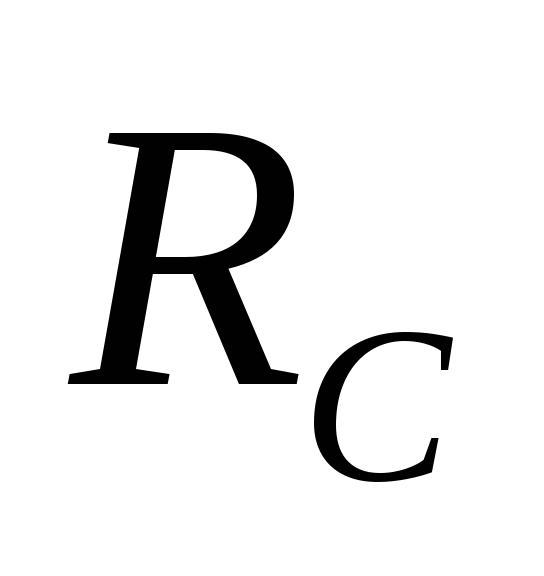 с течением времени убывают по одинаковому
экспоненциальному закону. Этот ток
максимален в начальный момент, причем
его начальная величина ограничена
только сопротивлением
с течением времени убывают по одинаковому
экспоненциальному закону. Этот ток
максимален в начальный момент, причем
его начальная величина ограничена
только сопротивлением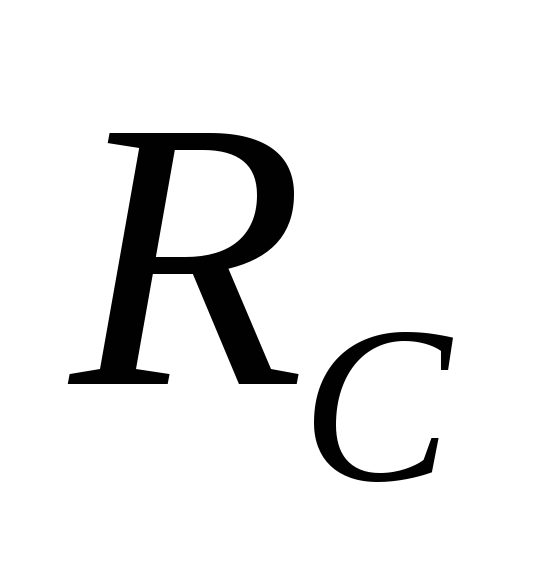 .
График кривой тока показан на рис. 6.б.
.
График кривой тока показан на рис. 6.б.
Заметим, что в момент включения ток конденсатора изменяется скачком от нуля до максимального значения; это физически возможно, так как скачек тока в RC — цепи не приводит к скачкообразному изменению запаса энергии в электрическом поле конденсатора.
Произведение RC для данной цепи постоянно (поскольку
значения 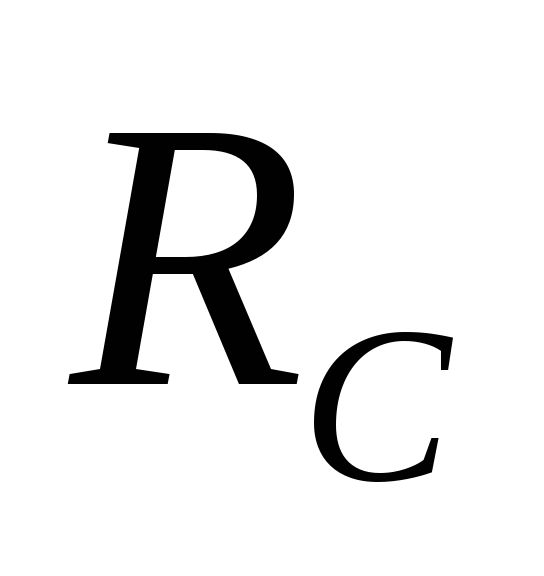 и С не изменяются). Это произведение
обозначается буквой
и С не изменяются). Это произведение
обозначается буквой 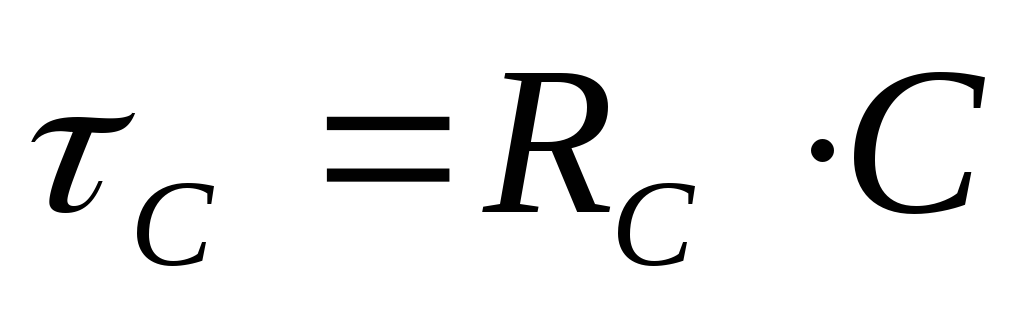 и называется постоянной времениRC — цепи.
и называется постоянной времениRC — цепи.
Длительность
переходного процесса зависит от
постоянной времени. Чем больше
сопротивление 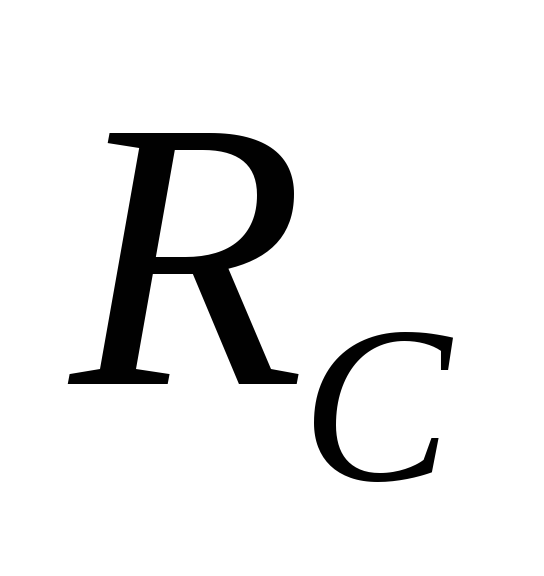 ,
тем медленнее заряжается конденсаторС.
Чем больше емкость конденсатора С,
тем больше заряд надо .накопить на
пластинах конденсатора для получения
напряжения Е.
Таким образом, чем больше постоянная
времени цепи, тем больше продолжительность
переходного процесса. Величина
,
тем медленнее заряжается конденсаторС.
Чем больше емкость конденсатора С,
тем больше заряд надо .накопить на
пластинах конденсатора для получения
напряжения Е.
Таким образом, чем больше постоянная
времени цепи, тем больше продолжительность
переходного процесса. Величина 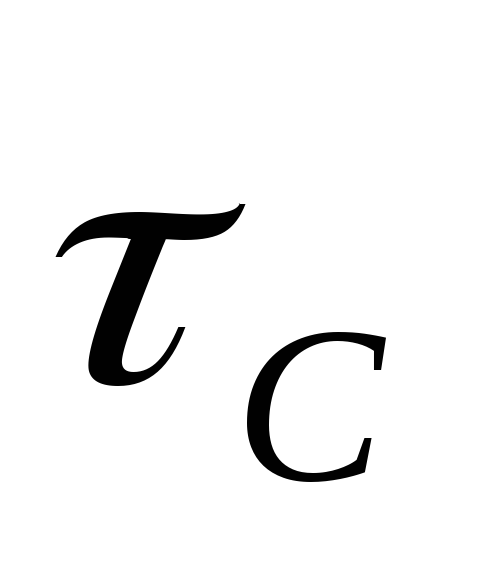 позволяет сравнивать между собой
различные конденсаторы в отношении
времени установления стационарного
режима. Физически постоянная времени
представляет время, в течение которого
свободные составляющие тока и напряжения
в цепи уменьшаются вe раз.
позволяет сравнивать между собой
различные конденсаторы в отношении
времени установления стационарного
режима. Физически постоянная времени
представляет время, в течение которого
свободные составляющие тока и напряжения
в цепи уменьшаются вe раз.
По
истечении времени 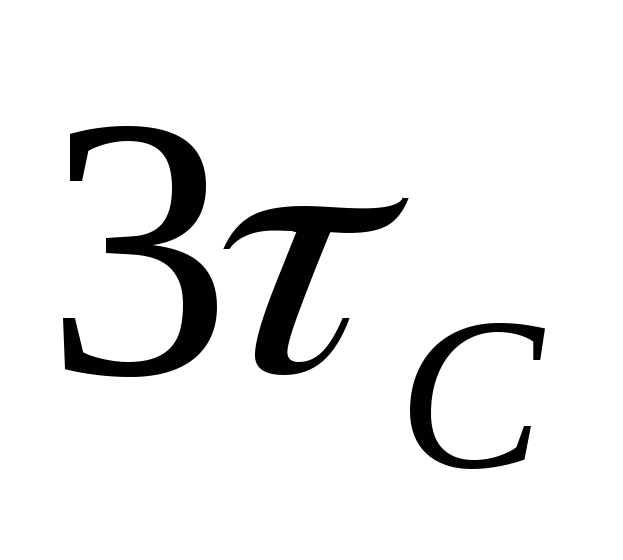 ,
которое называется временем установления,
переходной процесс принято считать
закончившимся, напряжение на
конденсаторе становится равным0,95E,
а ток в цепи уменьшается до 0,05Е.
,
которое называется временем установления,
переходной процесс принято считать
закончившимся, напряжение на
конденсаторе становится равным0,95E,
а ток в цепи уменьшается до 0,05Е.
Чтобы
получить представление о скорости
нарастания напряжения 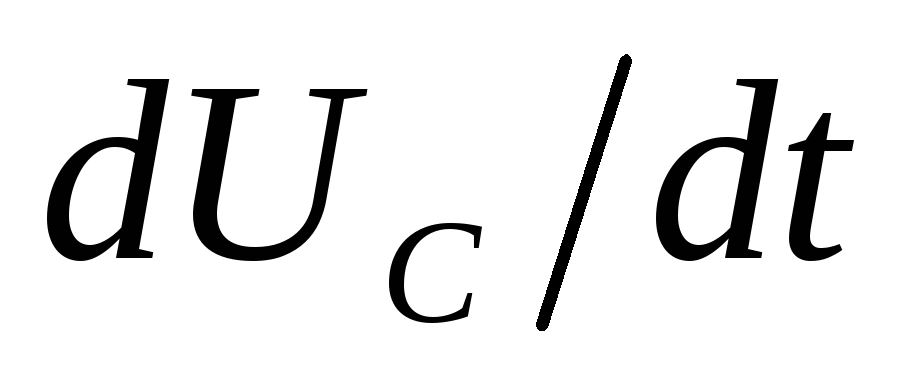 нa
конденсаторе, из уравнения (13) найдем
производную
нa
конденсаторе, из уравнения (13) найдем
производную
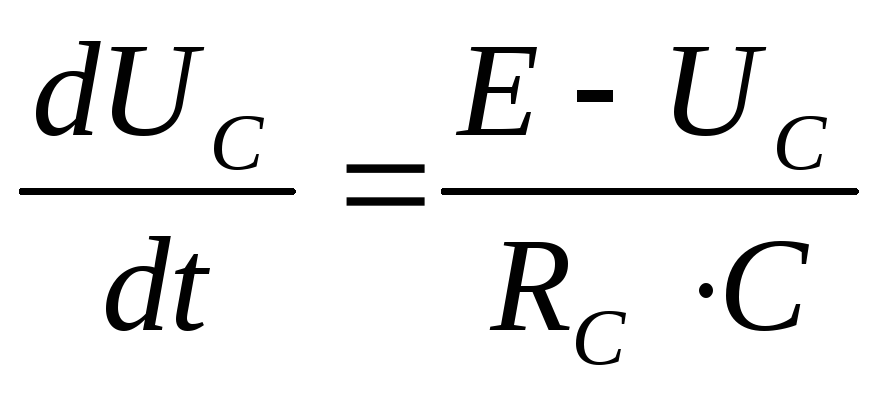 20
20
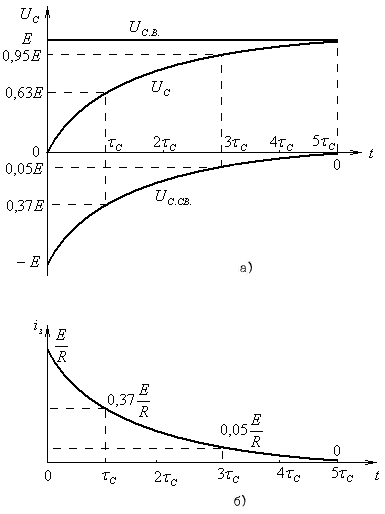
Рис.6. Кривые изменения напряжения на конденсаторе (а) и тока (б) в RC-цепи при включении постоянной э.д.с.
Величина 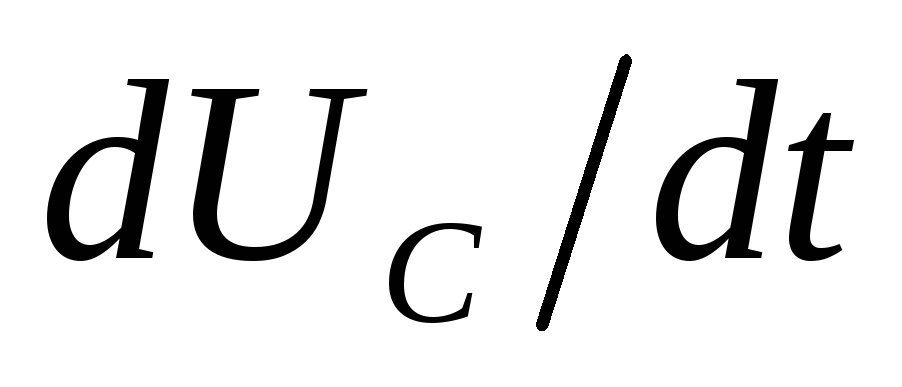 обратно
пропорциональна постоянной времени RC-цепи.
Скорость нарастаний напряжения уменьшения
по мере того, как само напряжение
увеличивается, т.е. по мере заряда
конденсатора, в начальный момент,
когда
обратно
пропорциональна постоянной времени RC-цепи.
Скорость нарастаний напряжения уменьшения
по мере того, как само напряжение
увеличивается, т.е. по мере заряда
конденсатора, в начальный момент,
когда 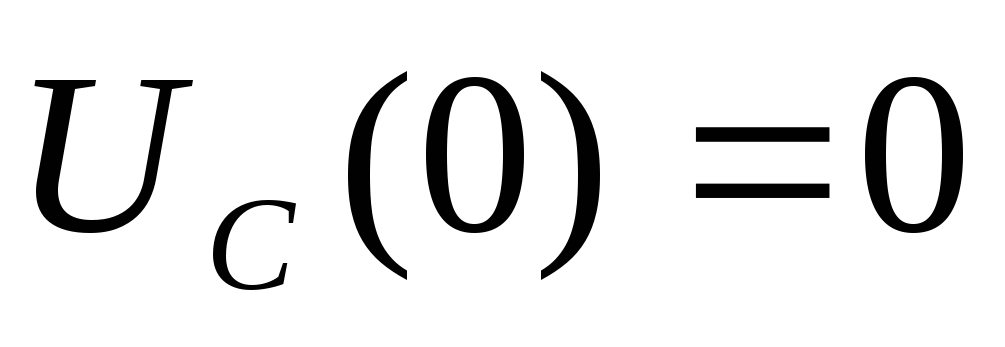 ,
имеет максимальное значение
,
имеет максимальное значение
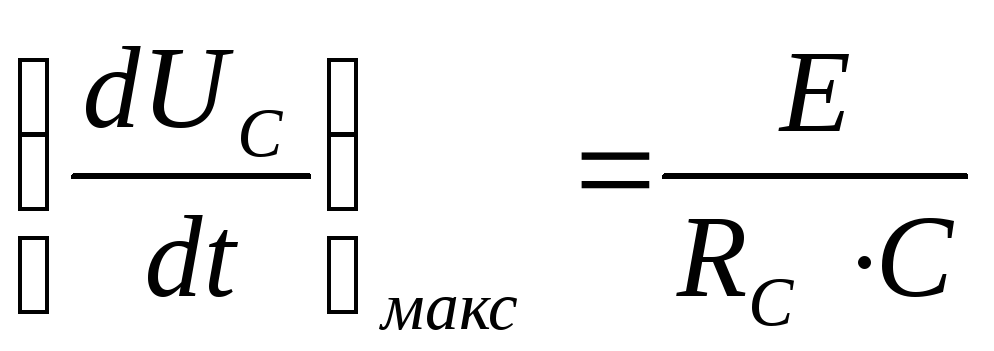
Такие выводы не являются неожиданными и вытекают из свойств экспоненциальной функции, которая в данном случае определяет закон нарастания напряжения на конденсаторе.
Во
время переходного процесса в электрическом
поле конденсатора происходит
непрерывное накопление энергии, которая
в установившемся режиме 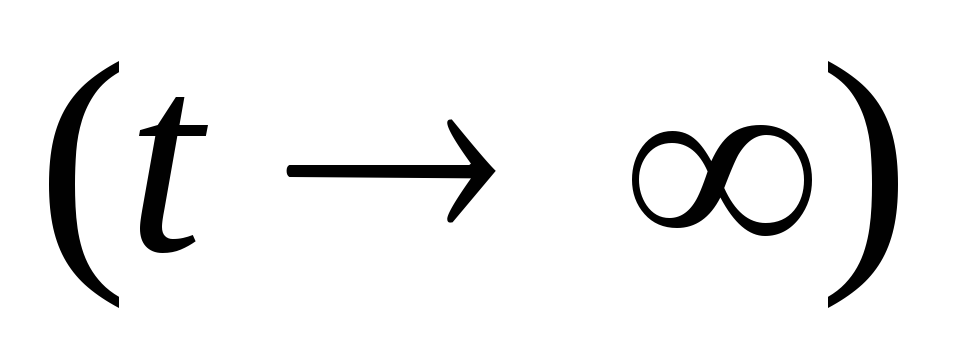 равна
равна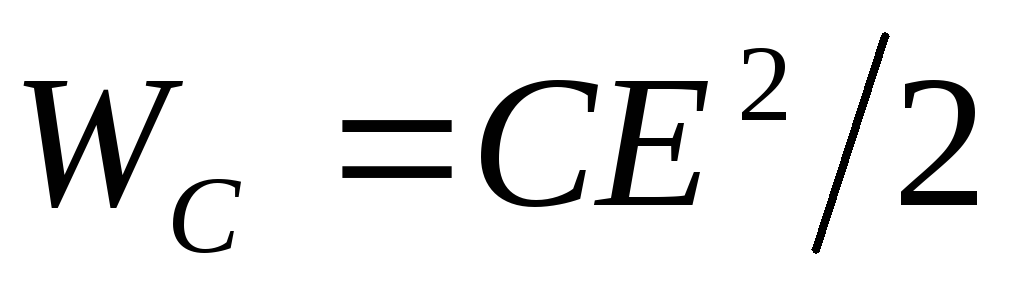 .
Одновременно часть энергии, отдаваемой
источником, выделяется в виде тепла в
резисторе. Эта энергия может быть
вычислена по формуле
.
Одновременно часть энергии, отдаваемой
источником, выделяется в виде тепла в
резисторе. Эта энергия может быть
вычислена по формуле
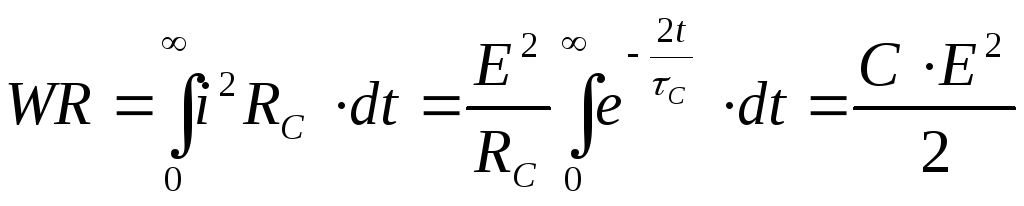
Энергия 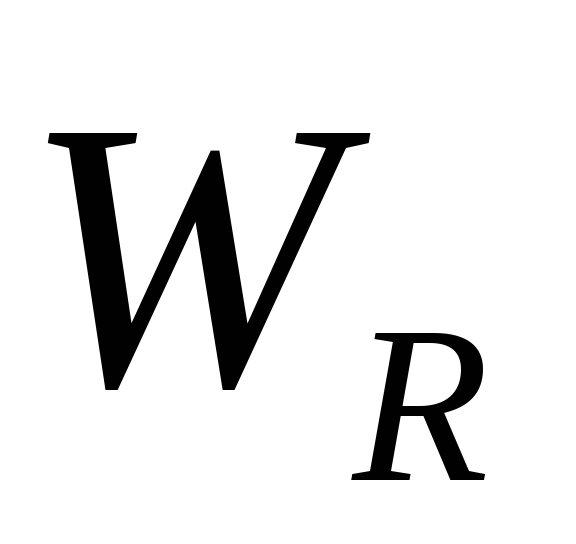 ,
теряемая в
,
теряемая в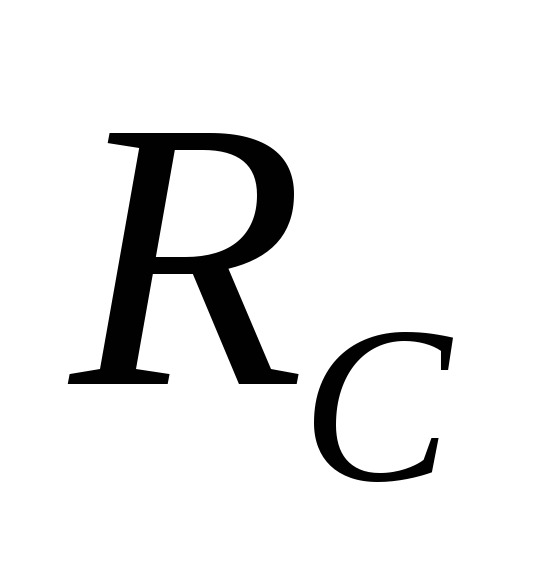 , не
зависит от величины сопротивления и
равна энергии, запасаемой в электрическом
поле конденсатора. Таким образом, к.п.д.
процесса заряда конденсатора от источника
постоянного напряжения равен 50%.
, не
зависит от величины сопротивления и
равна энергии, запасаемой в электрическом
поле конденсатора. Таким образом, к.п.д.
процесса заряда конденсатора от источника
постоянного напряжения равен 50%.
Рассмотрим переходные процессы, происходящие в RC — цепи, при ее закорачивании (конденсатор заряжен).
На рис.7 представлена RC — цепь, которая закорачивается при замыкании выключателя В.
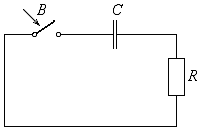
Рис.7.
На
рис. 7 представлена RC — цепь, в которой ток отсутствует, а
конденсатор С заряжен до напряжения Е.
Если в момент 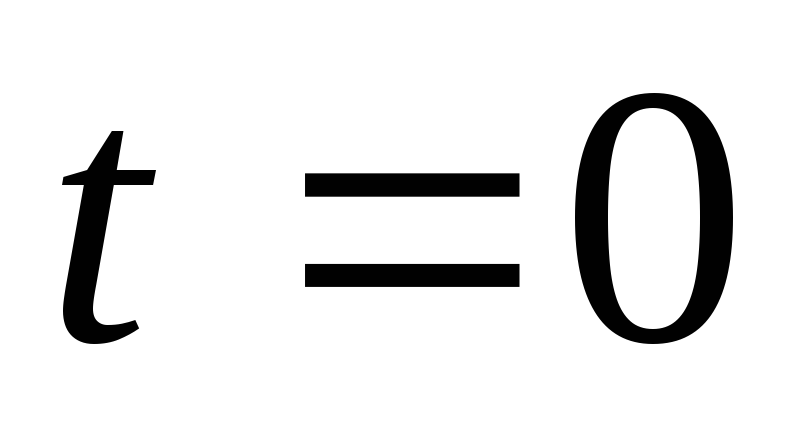 перевести выключательВ во включенное состояние, то конденсатор
окажется замкнутым на резистор и в RС — цепи возникнет ток, который будет
поддерживаться за счет запаса энергии,
накопленной в электрическом поле
конденсатора. С течением времени энергия электрического
поля рассеивается, превращаясь в
тепло е
резисторе,
ток разряда уменьшается и со временем
становится равным нулю. Эта задача с не
нулевыми начальными условиями.
Полагая в выражении (13), что его правая
часть равна нулю, получим однородное
дифференциальное уравнение для напряжения
на конденсаторе
перевести выключательВ во включенное состояние, то конденсатор
окажется замкнутым на резистор и в RС — цепи возникнет ток, который будет
поддерживаться за счет запаса энергии,
накопленной в электрическом поле
конденсатора. С течением времени энергия электрического
поля рассеивается, превращаясь в
тепло е
резисторе,
ток разряда уменьшается и со временем
становится равным нулю. Эта задача с не
нулевыми начальными условиями.
Полагая в выражении (13), что его правая
часть равна нулю, получим однородное
дифференциальное уравнение для напряжения
на конденсаторе
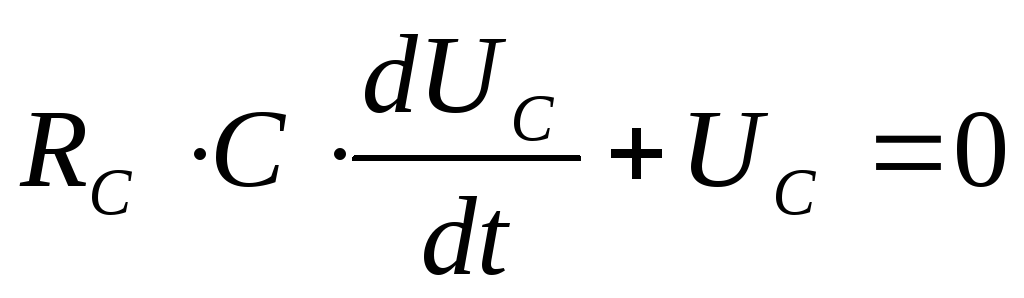 21
21
Внешнее
воздействие в цепи отсутствует, поэтому
искомое решение для напряжения 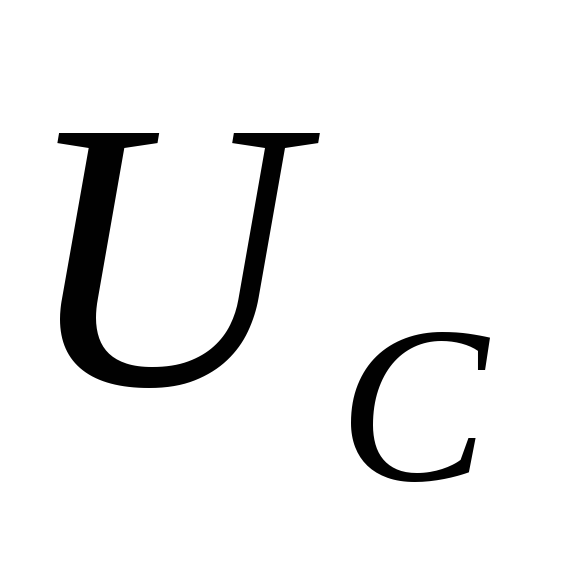 в выражении (14) будет иметь только
свободную составляющую.
в выражении (14) будет иметь только
свободную составляющую.
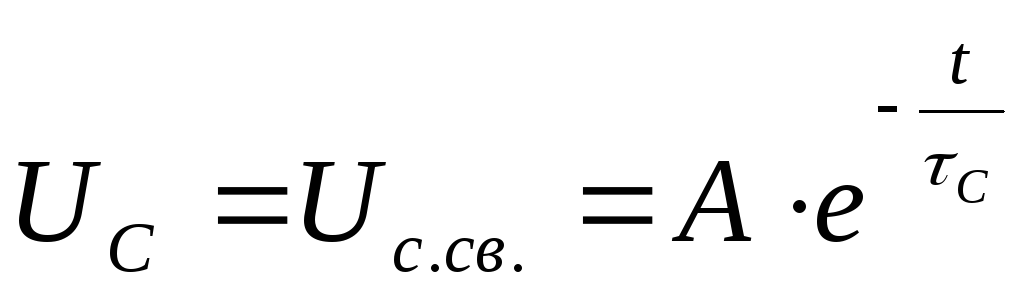 22
22
Для
определения постоянной А воспользуемся начальными условиями.
Из уравнения (22) при 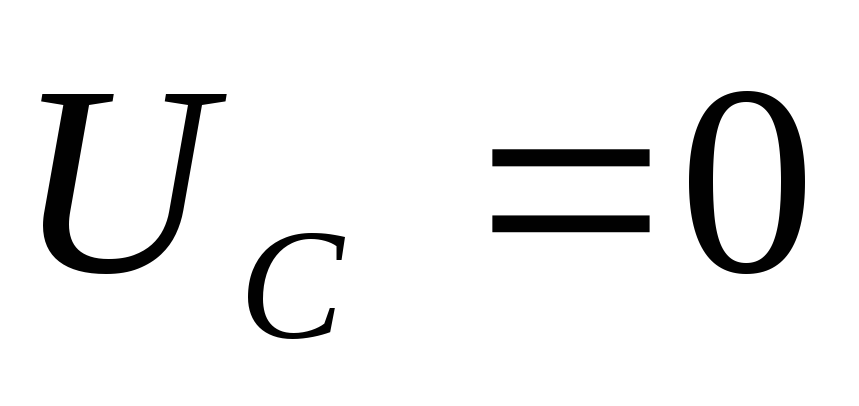 ,
,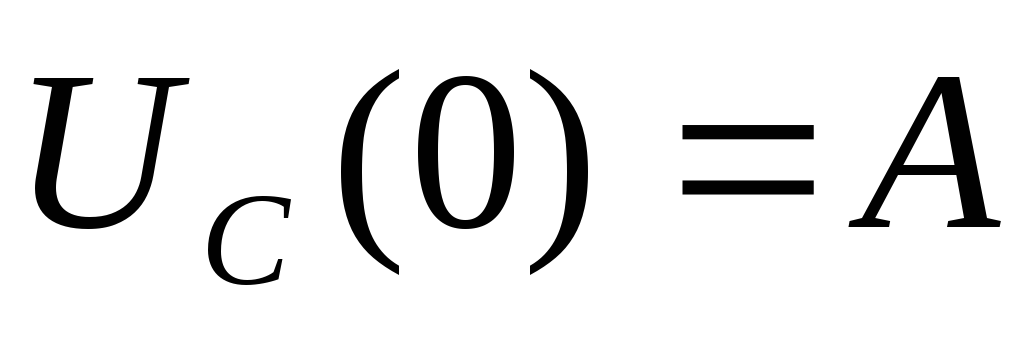 .
Кроме того, согласно второму закону
коммутации
.
Кроме того, согласно второму закону
коммутации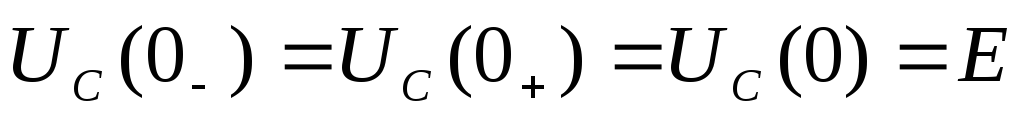 ,
так как конденсатор к моменту коммутации
был заряжен до напряженияЕ.
Следовательно, А = Е и напряжение на конденсаторе согласно
уравнению (22)
,
так как конденсатор к моменту коммутации
был заряжен до напряженияЕ.
Следовательно, А = Е и напряжение на конденсаторе согласно
уравнению (22)
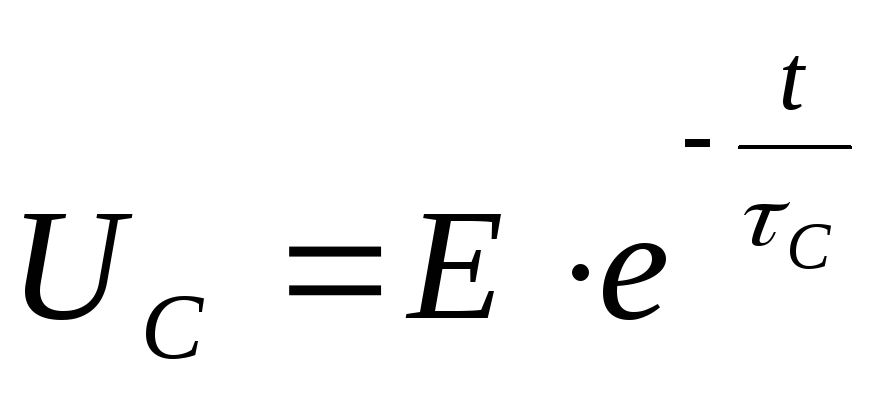 23
23
изменяется по экспоненциональному закону.
Величина разрядного тока равна
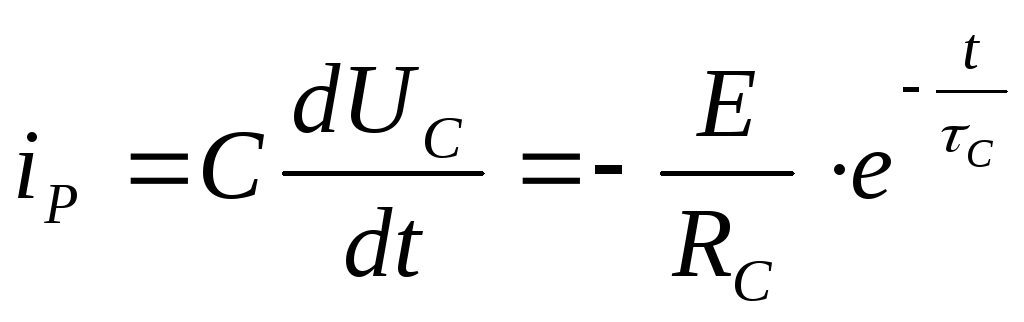 24
24
Падение напряжения на резисторе равно
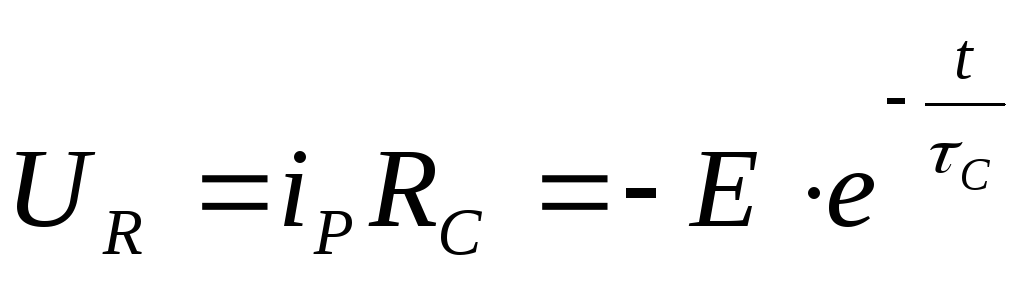 25
25
Отрицательный
знак в выражении (24) для 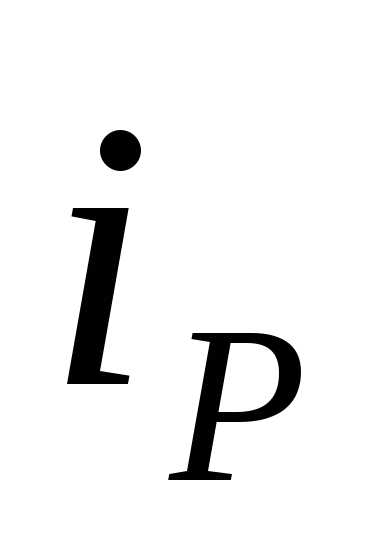 указывает на то, что направление
разрядного тока противоположно
направлению зарядного тока, условно
принятому за положительное (рис.5).
Максимальная величина разрядного тока
указывает на то, что направление
разрядного тока противоположно
направлению зарядного тока, условно
принятому за положительное (рис.5).
Максимальная величина разрядного тока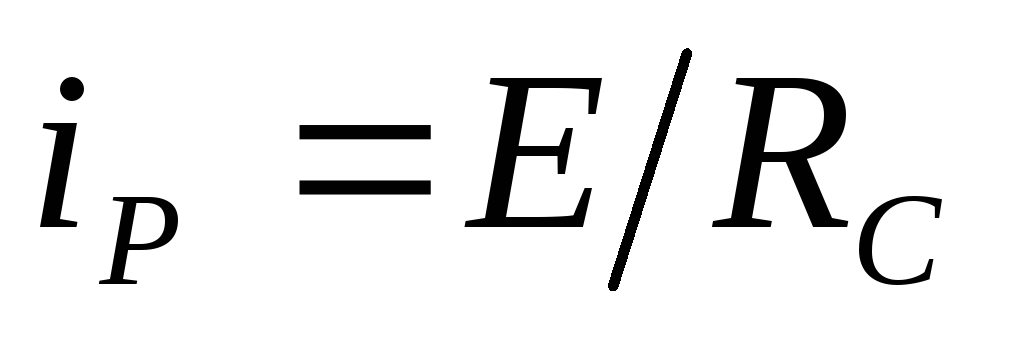 ограничивается лишь активным сопротивлениемRС —
цепи. Если сравнить выражения (24) и (18)
для разрядного и зарядного токов, то
можно заключить, что оба тока в RС —
цепи изменяются одинаково, но имеют
противоположные направления.
ограничивается лишь активным сопротивлениемRС —
цепи. Если сравнить выражения (24) и (18)
для разрядного и зарядного токов, то
можно заключить, что оба тока в RС —
цепи изменяются одинаково, но имеют
противоположные направления.
Продолжительность
переходного процесса определяется
постоянной времени 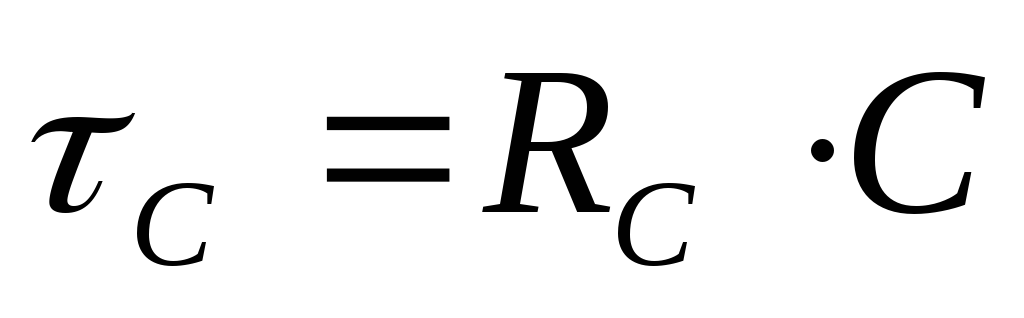 .
Чем больше емкость конденсатора и
сопротивление резистора, тем,
соответственно, больше накопленный
заряд на пластинах и меньше разрядный
ток и тем медленнее разряжается
конденсатор.
.
Чем больше емкость конденсатора и
сопротивление резистора, тем,
соответственно, больше накопленный
заряд на пластинах и меньше разрядный
ток и тем медленнее разряжается
конденсатор.
С энергетической точки зрения процесс короткого замыкания RС-цепи характеризуется тем, что энергия, которая до коммутации была запасена в электрическом поле конденсатора, целиком превращается в тепло в резисторе.
При проектировании приборных устройств весьма часто возникает необходимость передавать через RС — цепи импульсный сигнал.
Рассмотрим
воздействие импульсного сигнала на RC-цепь.
Предположим, что на RC — цепь воздействует сигнал, представляющий
прямоугольный импульс напряжения 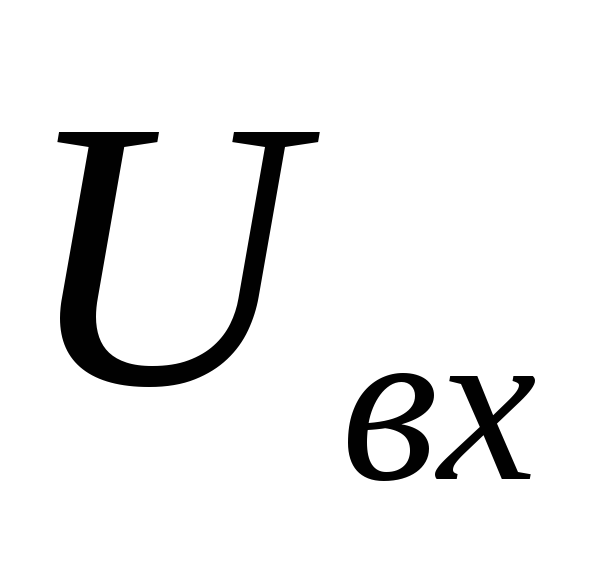 .
Его можно представить следующим
соотношением:
.
Его можно представить следующим
соотношением:
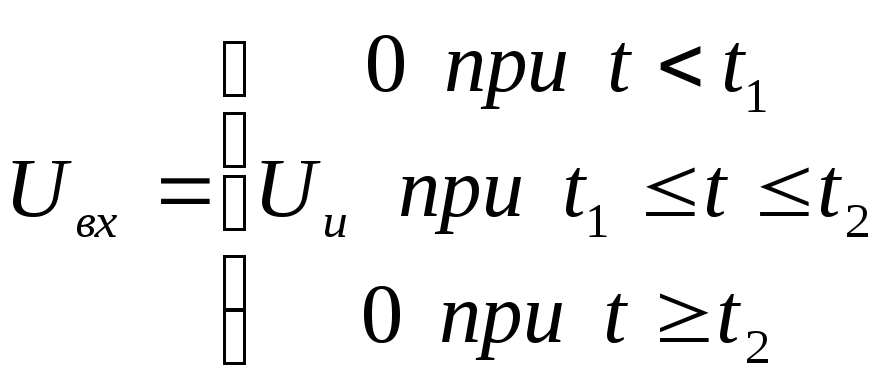 26
26
Схема включения RС — цепи к генератору импульсов представлена на рис.8.
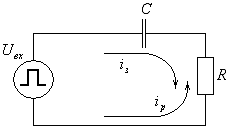
Рис.8.
В
интервале времени 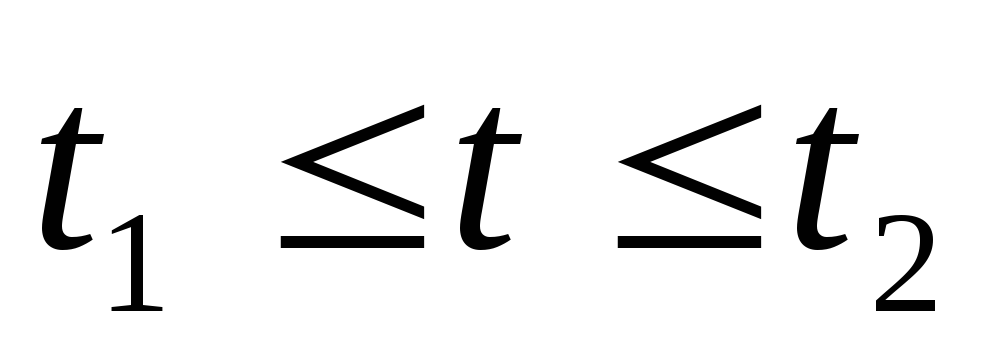 RC-цепь
подвергается воздействию ступенчатого
напряжения, поэтому ток в RС — цепи, падение напряжения на резисторе
и конденсаторе изменяются по тем же
законам, как и при воздействии на RС — цепь постоянной э.д.с.
RC-цепь
подвергается воздействию ступенчатого
напряжения, поэтому ток в RС — цепи, падение напряжения на резисторе
и конденсаторе изменяются по тем же
законам, как и при воздействии на RС — цепь постоянной э.д.с.
При 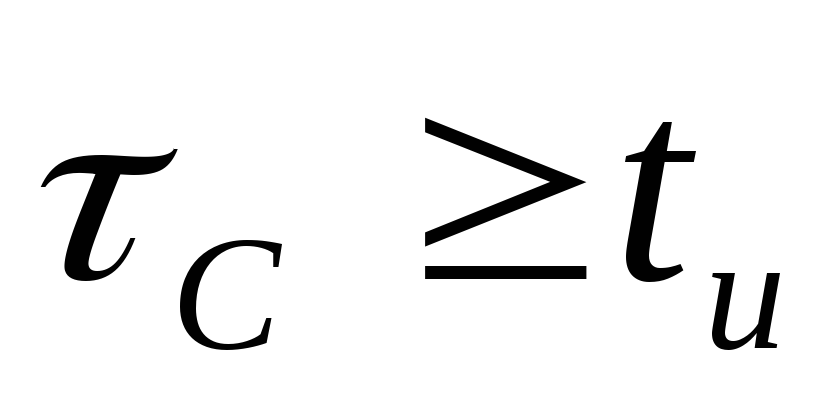 конденсатор за время действия импульса
почти не заряжается (рис.9.а). Напряжение
на выходеRС
— цепи (падение напряжения на резисторе)
в соответствии со вторым законом Кирхгофа
равно.
конденсатор за время действия импульса
почти не заряжается (рис.9.а). Напряжение
на выходеRС
— цепи (падение напряжения на резисторе)
в соответствии со вторым законом Кирхгофа
равно.
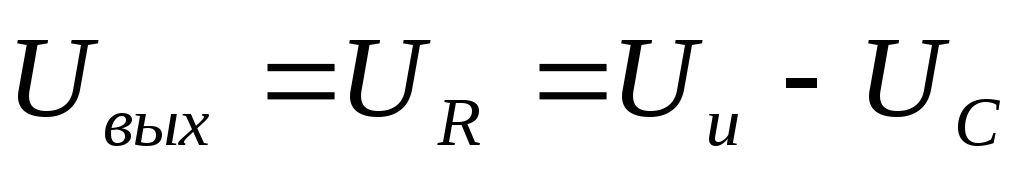 27
27
В
течение действия импульса в электрическом
поле конденсатора накапливается
незначительное количество знергии,
поэтому после окончания действия
импульса при 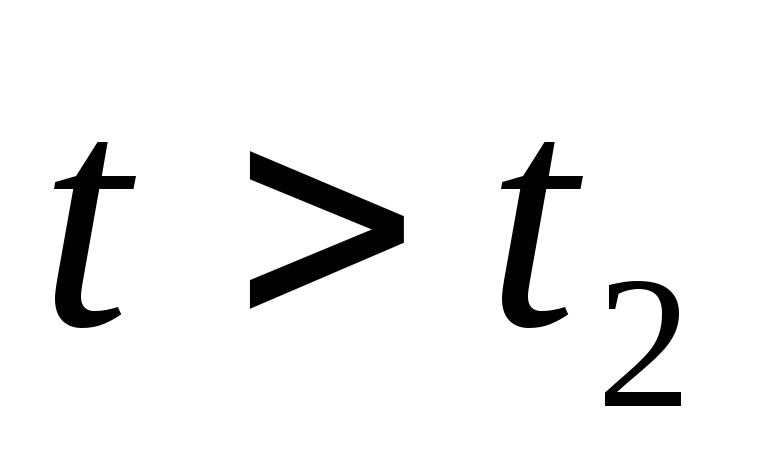 вRC — цепи практически не возникает переходный
процесс (рис.9.а).
вRC — цепи практически не возникает переходный
процесс (рис.9.а).
Когда
постоянная времени RС-цепи
соизмерена с длительностью импульса,
т.е. 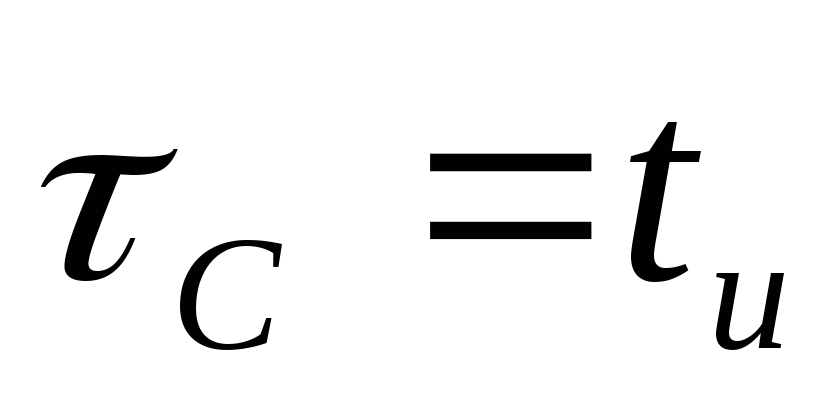 (рис.9.б), то за время действия импульса
конденсатор успевает зарядиться до
величины
(рис.9.б), то за время действия импульса
конденсатор успевает зарядиться до
величины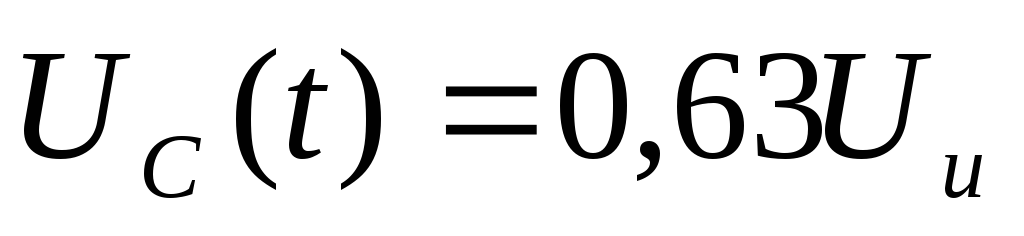 .
Поэтому выходное напряжение в течение
длительности непрерывно уменьшается
и в конце импульса определяется следующим
выражением
.
Поэтому выходное напряжение в течение
длительности непрерывно уменьшается
и в конце импульса определяется следующим
выражением
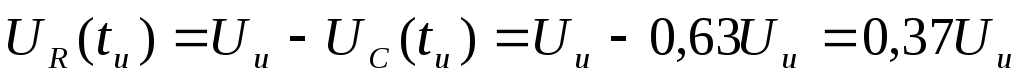 28
28
После
окончания действия входного импульса
при 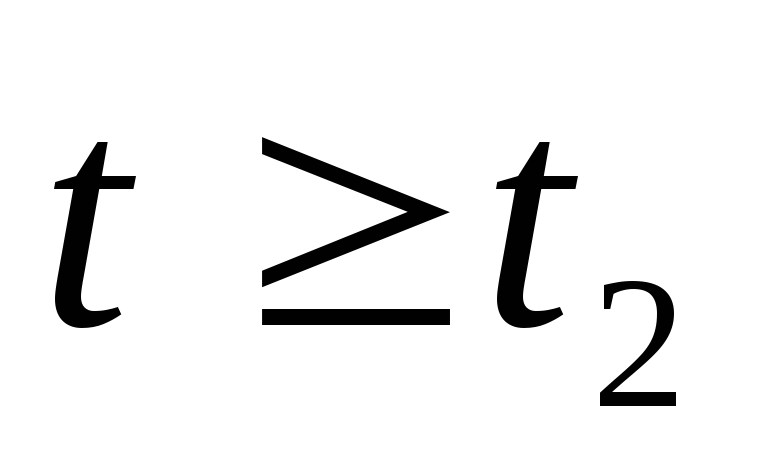 вRC — цепи возникает переходной процесс,
обусловленный рассеянием энергии,
запасенной в электрическом поле
конденсатора. В RC — цепи появляется разрядный ток
конденсатора, направление которого
противоположно зарядному току, а на
выходе возникает отрицательный импульс
(рис.9.б).
вRC — цепи возникает переходной процесс,
обусловленный рассеянием энергии,
запасенной в электрическом поле
конденсатора. В RC — цепи появляется разрядный ток
конденсатора, направление которого
противоположно зарядному току, а на
выходе возникает отрицательный импульс
(рис.9.б).
В
случае когда постоянная времени RС — цепи значительно меньше длительности
импульса (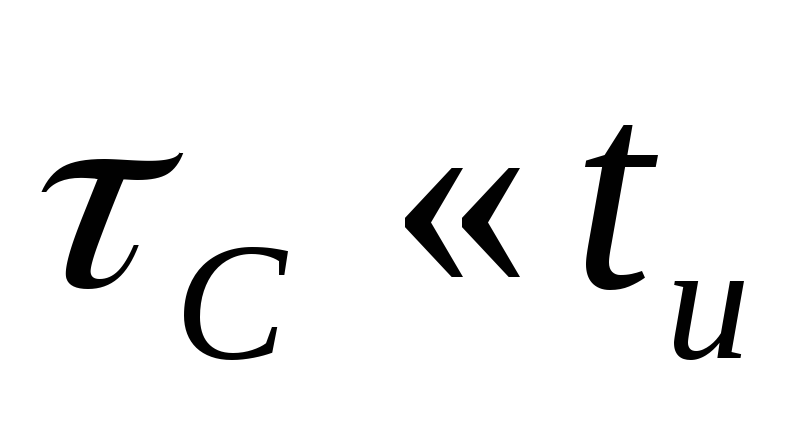 )
конденсатор успевает полностью разрядится
в
самом
начале импульса
)
конденсатор успевает полностью разрядится
в
самом
начале импульса 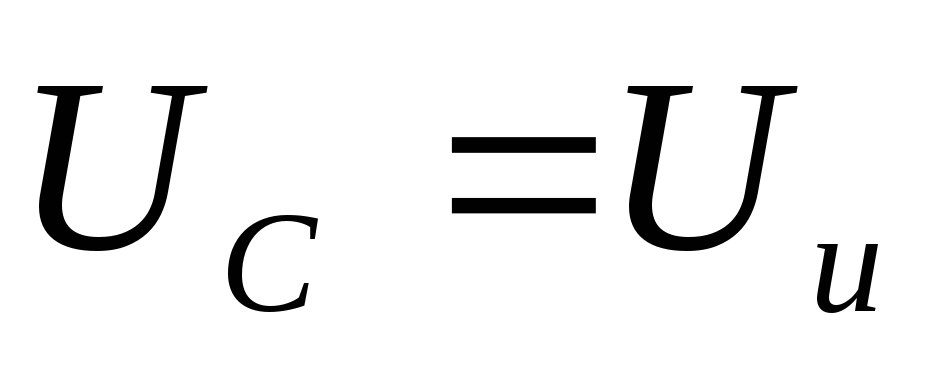 .
После чего выходное напряжение (падение
напряжения на резисторе) станет равным
нулю, т.е.
.
После чего выходное напряжение (падение
напряжения на резисторе) станет равным
нулю, т.е.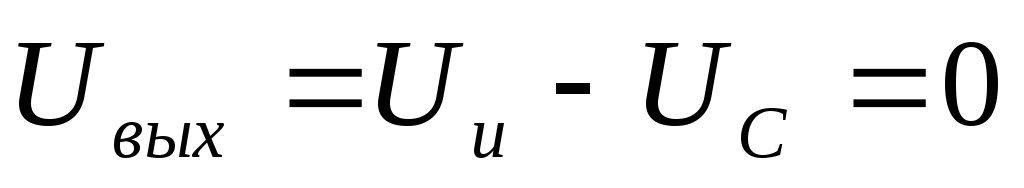 .
На выходе появится короткий импульс
положительной полярности (см.рис.9.в)
обусловленный
протеканием зарядного тока, с
амплитудой равной
.
На выходе появится короткий импульс
положительной полярности (см.рис.9.в)
обусловленный
протеканием зарядного тока, с
амплитудой равной 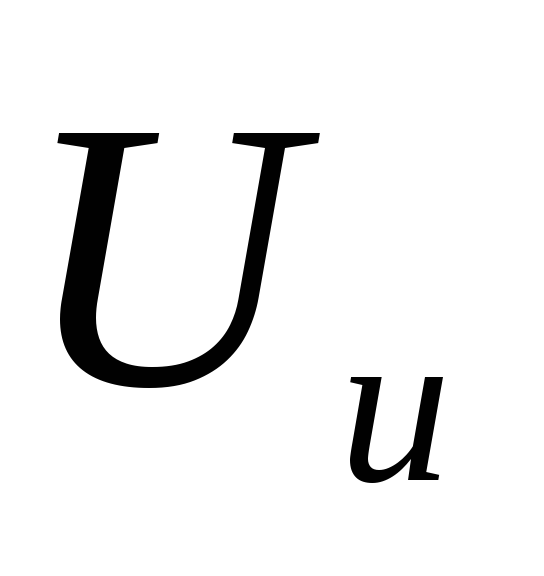 .
.
В
момент окончания входного импульса,
т.е. 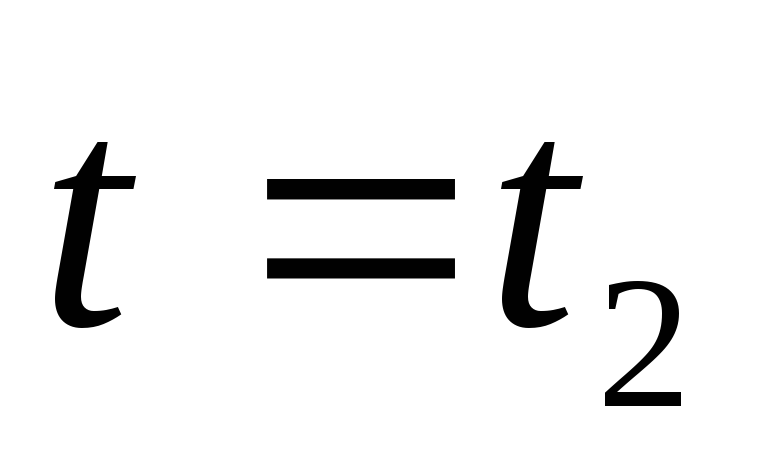 ,
вRC — цепи возникает ток разряда конденсатора
и на выходе RC — цепи появляется короткий отрицательный
импульс с амплитудой равной
,
вRC — цепи возникает ток разряда конденсатора
и на выходе RC — цепи появляется короткий отрицательный
импульс с амплитудой равной 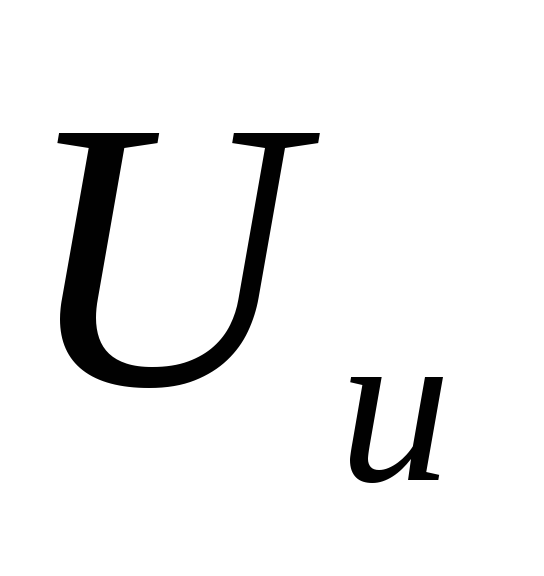 (рис.9.в).
(рис.9.в).
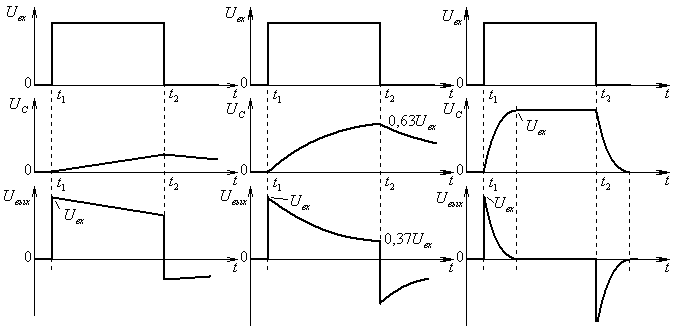
Рис.9. Прохождение импульса через RC — цепь:
а
— эпьюры напряжений при 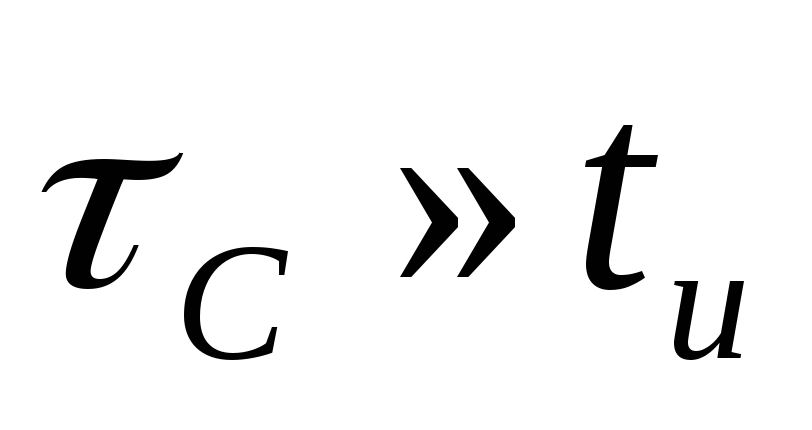
б
– тоже при 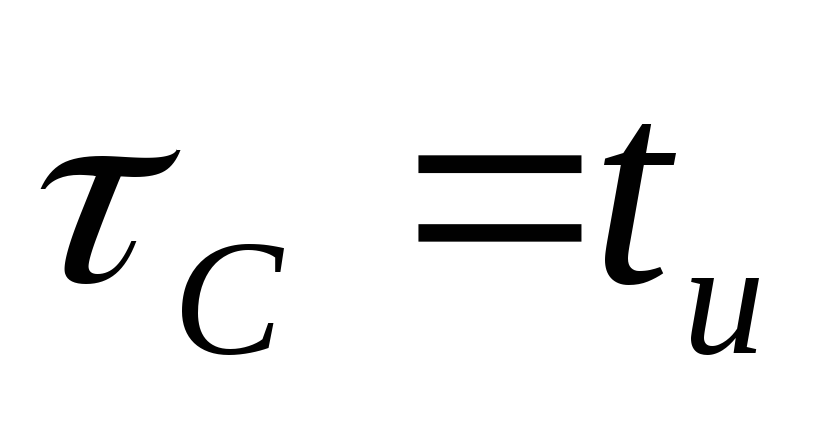
в
– тоже при 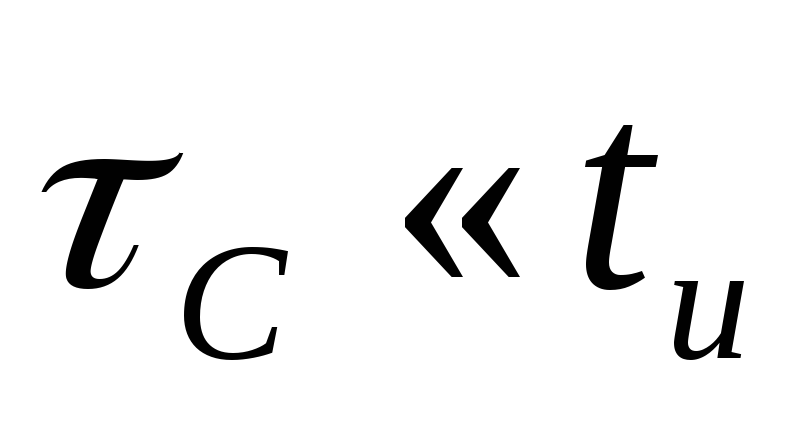
Схемы замещения реальных элементов электрической цепи
26 | 1. Основные положения |
1.2.3.1. Активные элементы
Как видно из рис. 1.11 и 1.12 ВАХ идеальных источников ЭДС и тока не пересекают оси тока и напряжения соответственно. Это говорит о том, что идеальный источник ЭДС не может находится в режиме короткого замыкания (в этом случае мы получим iкз = ∞, откуда p = ui = ∞, что не имеет физического смысла), а идеальный источник тока в режиме холостого хода (в этом случае мы получим uхх = ∞, откуда p = ui = ∞, что не имеет физического смысла).
Таким образом, для моделирования источника напряжения (так, обычно, называют реальный источник ЭДС) нам необходимо добавить последовательно включённый с источником ЭДС резистивный элемент с сопротивлением Rвн (который характеризует внутреннее сопротивление источника), ограничивающий ток через источник ЭДС, а для моделирование реального источника тока нам необходимо добавить параллельно включённый с источником тока резистивный элемент с проводимостью Gвн (характеризует внутреннюю проводимость источника), ограничивающий падение напряжения на источнике тока.
Схемы замещения реальных источников напряжения и тока и их ВАХ приведены на рис. 1.13 и 1.14.
Источник напряжения используется в качестве схемы замещения источников электрической энергии, внутреннее сопротивление которых много меньше сопротивления нагрузки (Rвн Rн, это наиболее распостранённый случай, соответствующий, например, гальваническим элементам и индуктивным генераторам), противном случае (Rвн Rн, характерно для емкостных генераторов и полупроводниковых устройств, работающих в соответствующих режимах) используется источник тока.
Следует отметить, что при анализе электрической цепи широко практикуется взаимное преобразование источников тока и напряжения. Целью этих преобразований является исключительно упрощение математических расчётов и они не несут в себе физического смысла.
1.2. Элементы электрической цепи замещения | 27 |
1.2.3.2. Пассивные элементы
Схема замещения реального элемента электрической цепи характеризует протекающие в нём физические процессы, т. е. является математической моделью элемента. Сложность схемы замещения определяется необходимой точностью расчётов, конструктивными особенностями реального элемента и характером протекающего тока. Обычно в качестве основного критерия выступает частота тока –– чем выше частота, тем выше роль процессов связанных с преобразованием энергии электрического и магнитного полей и сложнее схема замещения. Выбор схемы замещения является весьма сложной задачей, требующей глубокого понимания процессов протекающих не только в самом элементе, но и их влияния на цепь в целом.
Рассмотрим схемы замещения наиболее распространённых пассивных элементов: резистора, конденсатора и катушки индуктивности.
Резистор
Характеристики идеального резистора будут соответствовать резистивному элементу схемы замещения.
Реальные резисторы, в основной массе случаев, достаточно хорошо отвечают этой модели, однако при необходимости более точных расчётов, особенно на высоких частотах, становится необходимым учитывать индуктивность проволоки (для проволочных резисторов), а также её барьерную ёмкость (рис. 1.15). На сверхвысоких частотах резко возрастает роль индуктивности и ёмкости выводов резистора.
Если резистор выполнен в виде катушки, то индуктивная составляющая будет играть значительную роль уже на сравнительно низких частотах.
Конденсатор
Характеристики идеального конденсатора будут соответствовать емкостному элементу схемы замещения.
Реальные конденсаторы, в основной массе случаев, достаточно хорошо отвечают этой модели, однако при необходимости более точных расчётов, особенно на высоких напряжениях, становится необходимым учитывать неидеальность диэлектрика, находящегося между обкладками конденсатора, которая характеризуется током утечки и на схеме
28 |
|
| 1. Основные положения | |||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
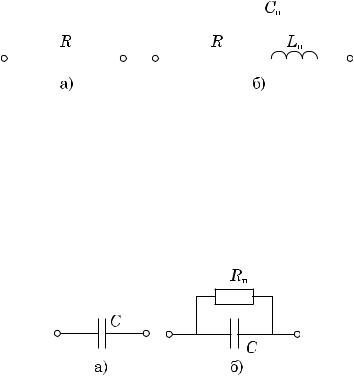
Рис. 1.15. Схема замещения резистора а –– на низких частотах; б –– на высоких частотах
Cп и Lп –– паразитные емкостная и индуктивная составляющие
замещения представлена в виде резистивного элемента, подключенного параллельно к емкостному (рис. 1.16). На сверхвысоких частотах резко возрастает роль индуктивности и ёмкости выводов конденсатора.
Рис. 1.16. Схема замещения конденсатора
а–– на низких частотах; б –– на высоких частотах Rп –– паразитная резистивная составляющие
Катушка индуктивности
Характеристики идеальной катушки индуктивности будут соответствовать индуктивному элементу схемы замещения.
Реальные катушки индуктивности намотаны из провода, имеющего ненулевое удельное сопротивление, таким образом, чем больше витков содержит катушка, тем будет выше её активное сопротивление, которое, обычно, необходимо учитывать во всём диапазоне частот (следует отметить, что на постоянном токе индуктивная составляющая катушки будет равна нулю, и в качестве схемы замещения можно ис-
6. Цепи синусоидального тока с резисторами, конденсаторами и катушками индуктивности
Эксперименты данного раздела касаются взаимодействия резисторов, конденсаторов и катушек индуктивности при переменном синусоидальном напряжении.
Цель состоит в измерении и расчете токов, напряжений и их фазовых сдвигов, также как и эквивалентных параметров цепей при параллельном и последовательном соединении резисторов, конденсаторов и катушек.
Действующие значения и фазы соответствующих величин могут быть показаны на векторных диаграммах или на осциллограммах.
На векторной диаграмме каждая синусоидальная функция времени (ток или напряжение) представляется вектором, длина которого соответствует в выбранном масштабе амплитуде или действующему значению, а направление определяется начальной фазой, отсчитываемой от выбранного начала отсчета углов. Например, напряжение u = Um sin (t+) изображается вектором длинойUmилиUm/2, расположенным под угломк горизонтали. Векторные изображения синусоидальных величин в дальнейшем будут подчеркиваться.
6.1. Последовательное соединение резистора и конденсатора
6.1.1. Общие сведения
Когда к цепи (рис. 6.1.1) с последовательным соединением резистора и конденсатора подается переменное синусоидальное напряжение, один и тот же синусоидальный ток имеет место в обоих компонентах цепи.
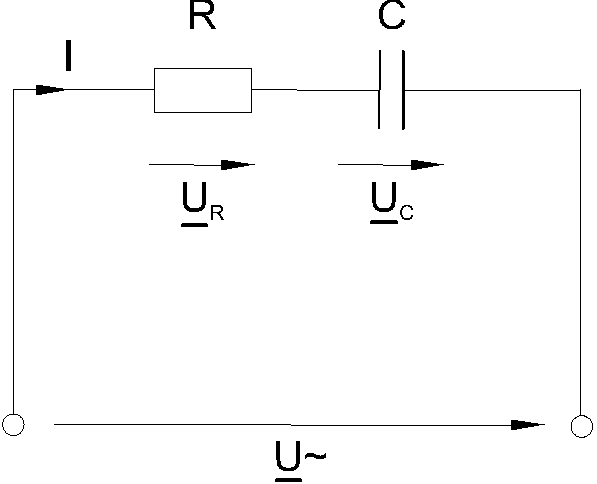
Рис. 6.1.1
Между напряжениями UR, UC иU существуют фазовые сдвиги, обусловленные емкостным реактивным сопротивлениемXCконденсатора. Они могут быть представлены с помощью векторной диаграммы напряжений (рис. 6.1.2
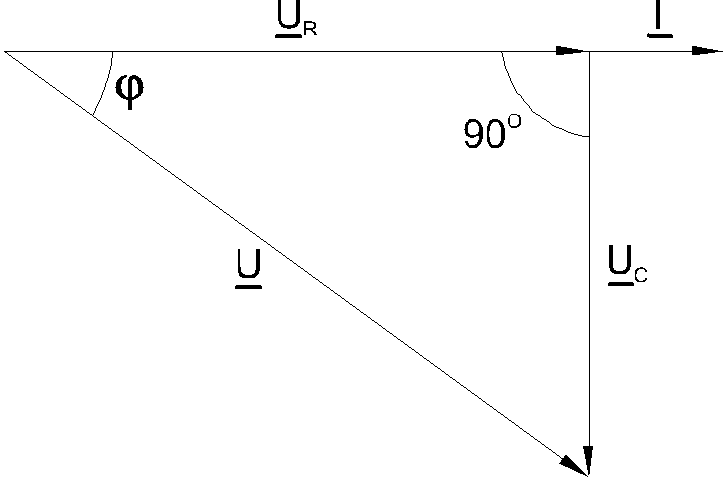
Рис. 6.1.2
Фазовый сдвиг между током I и напряжением на резистореUR отсутствует, тогда как сдвиг между этим током и падением напряжения на конденсатореUCравен -900 (т.е. ток опережает напряжение на 900). При этом сдвиг между полным напряжением цепиU и токомIопределяется соотношением между сопротивлениями XCиR.
Если каждую сторону треугольника напряжений разделить на ток, то получим треугольник сопротивлений (рис.6.1.13). В треугольнике сопротивлений Zпредставляет собой так называемое полное сопротивление цепи.
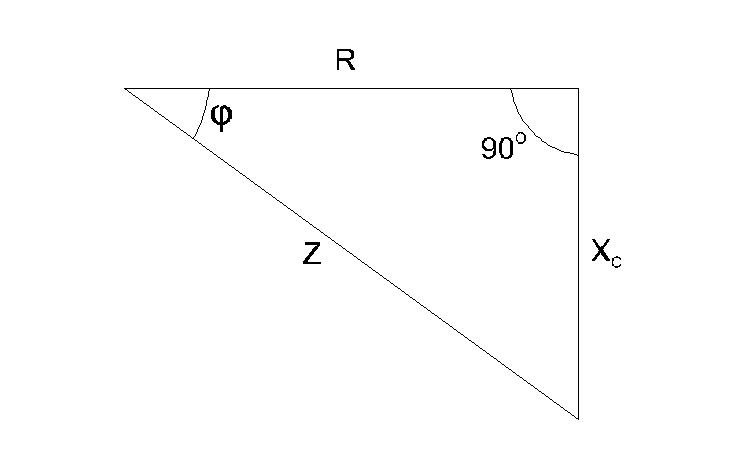
Рис. 6.1.3
Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение действующих или амплитудных значений напряжений на отдельных элементах цепи невозможно. Невозможно и сложение разнородных (активных и реактивных) сопротивлений. Однако, в векторной форме
U = UR +UC.
Действующее значение полного напряжения цепи, как следует из векторной диаграммы
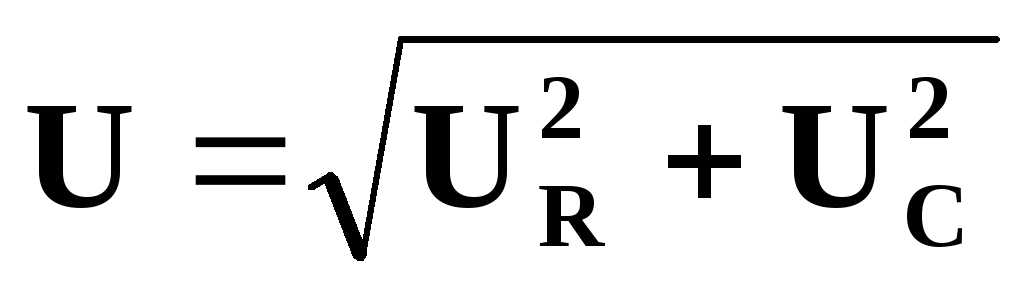 = Z I
= Z I
Полное сопротивление цепи
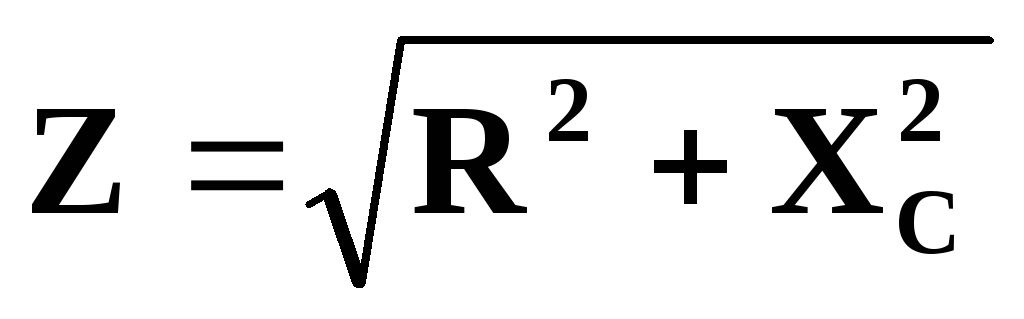 = U I
= U I
Активное сопротивление цепи
R = Z cos
Емкостное реактивное сопротивление цепи
XC = Z sin
Угол сдвига фаз
= arctg (-UC UR) = arctg (-ХC R)
6.1.2. Экспериментальная часть Задание
Для цепи с последовательным соединением резистора и конденсатора измерьте и вычислите действующие значения падений напряжения на резисторе URи конденсатореUC, токI, угол сдвига фаз, полное сопротивление цепиZи емкостное реактивное сопротивлениеXCи активной сопротивлениеR.
Порядок выполнения работы
Соберите цепь согласно схеме (рис. 6.1.4), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U= 5 В,f= 1 кГц.
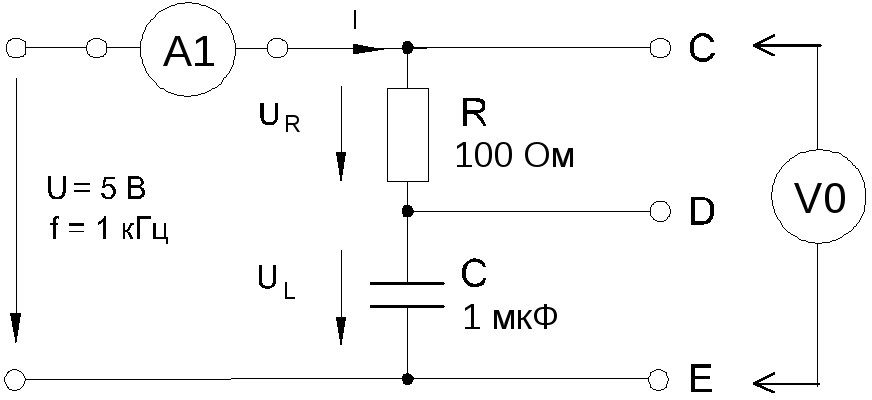
Рис. 6.1.4
Выполните мультиметрами или виртуальными приборами измерения действующих значений тока и напряжений, указанных в табл. 6.1.1. При измерениях напряжений подключайте мультиметр или канал V0 коннектора к зажимамC-E,C-D,D-E:
Таблица 6.1.1.
U,B
UR, B
UC, B
I, мА
, град
R, Ом
XC, Ом
Z, Ом
Примечание
Расчет
Вирт. Изм
Фазовый угол
= arctg (UC UR) =
Полное сопротивление цепи
Z = U I =
Активное сопротивление цепи
R = Z cos
Емкостное реактивное сопротивление цепи
XC = Z sin
Если вы работаете с виртуальными приборами, то измерьте с помощью блока «Приборы II»R, , XC, Z и запишите их значения также в таблицу 6.1.1 под рассчитанными величинами. Сравните результаты.
Рис. 6.1.5 Рис. 6.1.6
Измерение параметров электрических цепей на переменном токе. Измерение параметров конденсатора с помощью моста переменного тока, страница 5
Реактивные компоненты электрических цепей (конденсаторы и катушки индуктивности) проявляют себя, как комплексные сопротивления, обладающие кроме реактивной составляющей активным сопротивлением, которое характеризует потери активной энергии и называется сопротивлением потерь. Для учета вклада этого сопротивления в общий импеданс, которым обладают реактивные компоненты, их представляют в виде схем замещения (см. рис 4).
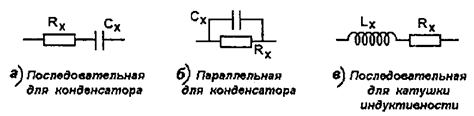
Рис.4 Схемы замещения
Если конденсатор обладает малыми потерями, его схему замещения удобно представить в виде последовательного соединения идеального конденсатора и сопротивления потерь, а импеданс такого соединения выражается формулой
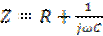 ,
,
Конденсатор со значительными потерями описывается параллельной схемой замещения, импеданс и комплексная проводимость которой выражается формулами :
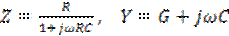 , где G=1/R
, где G=1/R
Для катушек индуктивности принята последовательная схема замещения с импедансом :
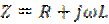
Активные потери в конденсаторе и катушке индуктивности приводят к тому, что фазовый сдвиг между напряжением и током в реальном реактивном компоненте электрической цепи отличается от π/2 на угол δ. Общепринятой характеристикой потерь конденсаторов является тангенс этого угла: tgδ Для катушек индуктивности характеристикой потерь является добротность, но в ряде случаев и для них используется tgδ .
Для рассмотренных схем замещения tgδ выражается формулами (в порядке их представления):
tgδ=ωRC; tgδ=1/ωRC=G/ωC; tgδ=R/ωL=1/ωGL
6.2. Мосты переменного тока
|
|
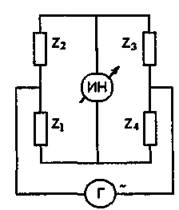
Одним из наиболее эффективных средств измерения параметров электрических цепей являются мосты постоянного и переменного тока, которые широко применяются и в качестве образцовых средств при поверке мер электрических величин. Мосты переменного тока позволяют производить измерения емкости, индуктивности и связанных с ними параметров: тангенса угла потерь конденсаторов, добротности катушек индуктивности, а также активного сопротивления с погрешностью от единиц до тысячных долей процента. Конкретное значение погрешности определяется погрешностью элементов, из которых составлен мост, а также чувствительностью индикатора равновесия моста. Принципиальная схема моста переменного тока может быть представлена в виде эквивалентной схемы, состоящей из четырех комплексных сопротивлений Z1 — Z4 (рис. 5).
Источником питания моста переменного тока является генератор синусоидального напряжения Г. Индикатор равновесия моста ИН включен в измерительную диагональ моста. Как известно, ток и напряжение в измерительной диагонали моста равны нулю, если выполняется условие равновесия:
Z1xZ3 = Z2xZ4. (1)
|
Рис. 5. Мост переменного тока |
Если в одно из плеч моста включено комплексное сопротивление, значение которого необходимо измерить, например Z1, то, изменяя сопротивления других плеч, можно добиться отсутствия тока или напряжения в измерительной диагонали и, зная сопротивления плеч Z2-Z4, рассчитать значение неизвестного сопротивления. Комплексному условию равновесия моста (1) соответствуют два вещественных равенства, которые получают покомпонентным приравниванием действительных и мнимых частей комплексных сопротивлений Z=R+jX:
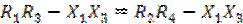
(2)
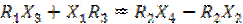
Полагая 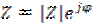 имеем
имеем
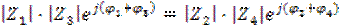
Последнее соотношение можно выразить двумя равенствами :
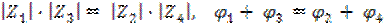 ,
,
Таким образом, мостовые цепи переменного тока в отличие от мостовых цепей постоянного тока, могут быть уравновешены только при одновременном выполнении двух условий равновесия. Для этого необходима регулировка, по крайней мере, двух параметров.
В качестве индикаторов равновесия удобно использовать электроннолучевой осциллограф, который позволяет разделить признаки неуравновешенности моста по амплитуде и по фазе благодаря схеме его включения. Если фазы напряжения питания и напряжения в диагонали моста различны, то на экране осциллографа будет изображаться эллипс, а при равенстве фаз — прямая, наклон которой определяется амплитудой напряжения в диагонали моста: с уменьшением амплитуды наклон прямой уменьшается. По мере приближения к равновесию наклон большой оси эллипса и его малая ось будут уменьшаться, и при достижении равновесия эллипс вырождается в горизонтальную прямую.
2.13. Параллельное соединение активного сопротивления, индуктивности и емкости
Рассмотрим схему, состоящую из параллельно соединенных активного и реактивных элементов (рис. 2.31, а).
Требуется по известным G, ВL, ВC, U рассчитать токи. Как и прежде, задачу будем решать двумя методами.
1. М е т о д в е к т о р н ы х д и а г р а м м.
Токи
ветвей находятся сразу: 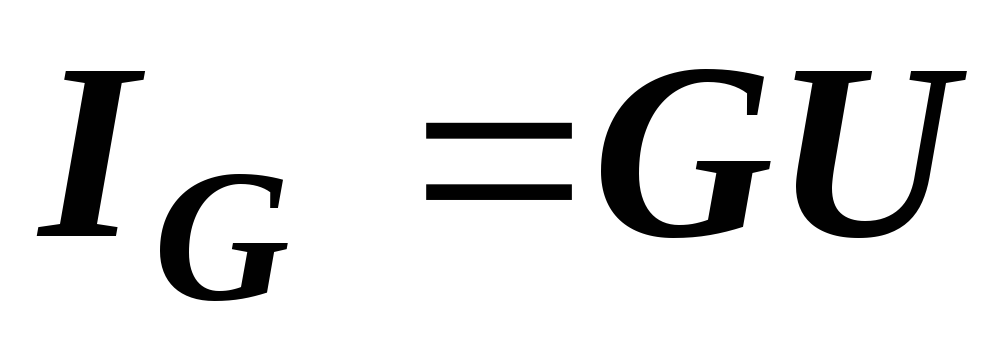 ,
, 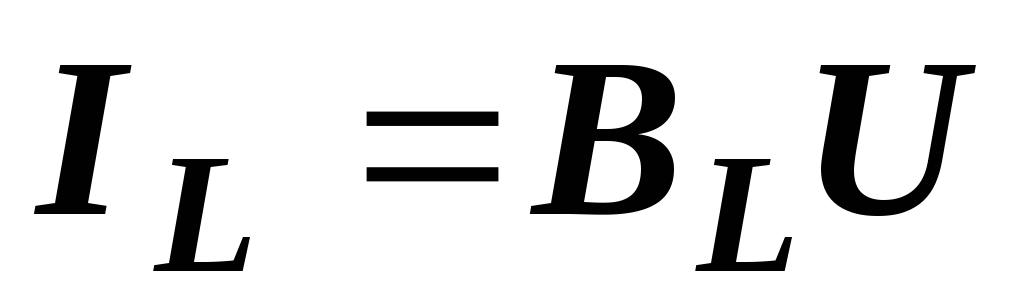 ,
, 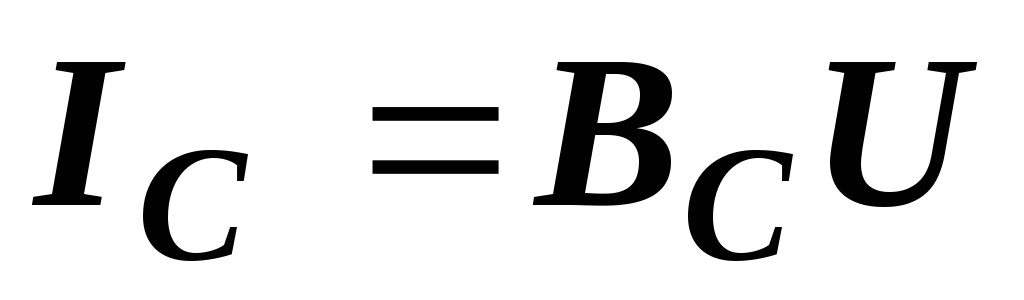 .
.
Для
определения общего тока 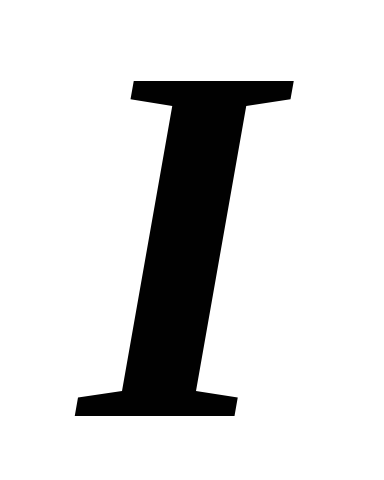 необходимо построить векторную диаграмму
(рис. 2.31, б).
Построение начинаем с вектора напряжения,
так как оно является общим для всех
ветвей. Из векторной диаграммы имеем
необходимо построить векторную диаграмму
(рис. 2.31, б).
Построение начинаем с вектора напряжения,
так как оно является общим для всех
ветвей. Из векторной диаграммы имеем
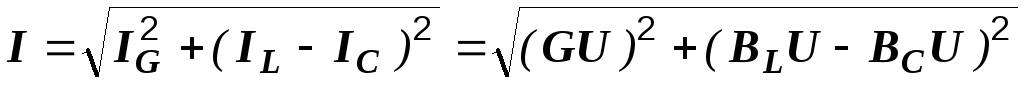
или 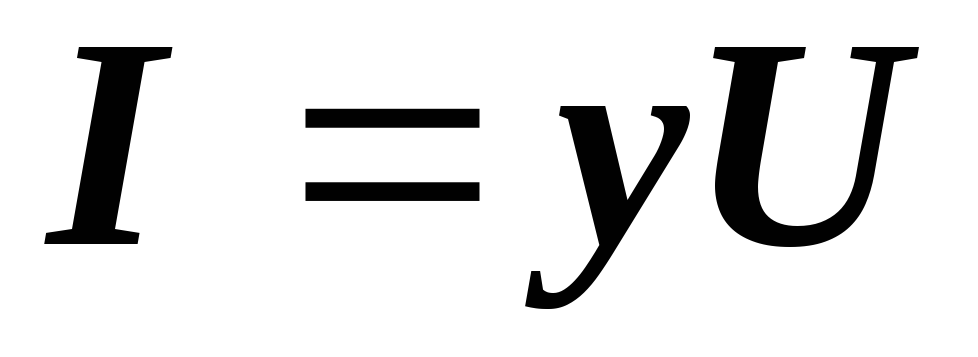 ,
,
где  – полная проводимость цепи, равная
– полная проводимость цепи, равная
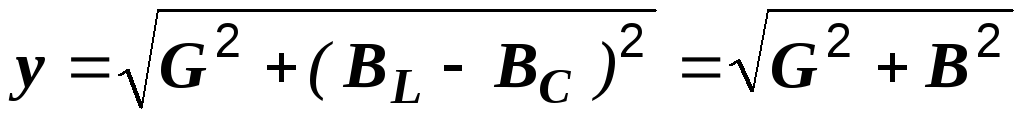 .
.
Разность индуктивной
и емкостной проводимостей представляет
собой общую реактивную проводимость
цепи 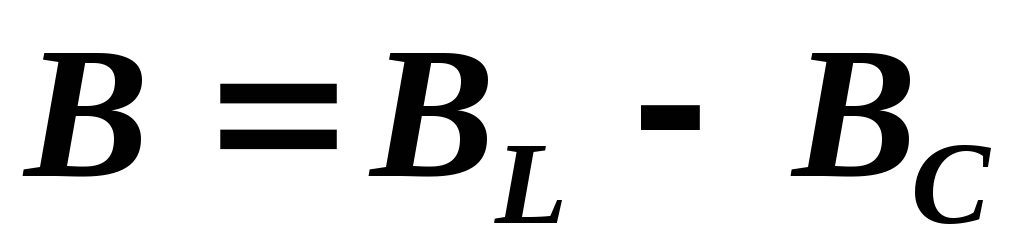 .
.
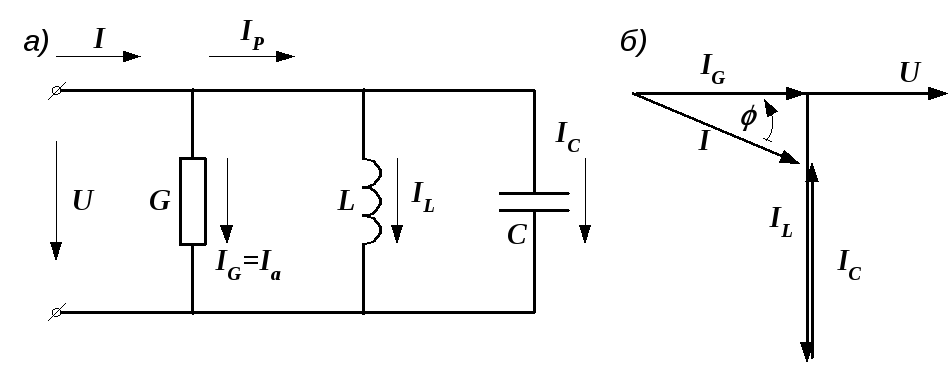 Рис.
2.31. Электрическая цепь и ее векторная
диаграмма
Рис.
2.31. Электрическая цепь и ее векторная
диаграмма
Векторы
токов на диаграмме образуют треугольник
токов. Его горизонтальный катет,
представляющий проекцию вектора тока
на вектор напряжения, называется активной
составляющей тока и равен току в активном
элементе цепи: 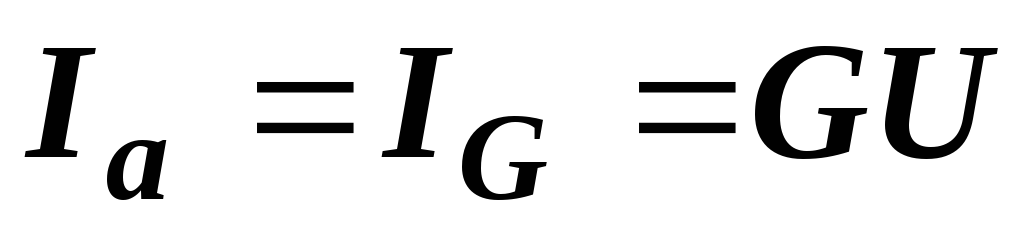 (рис. 2.32, а).
Проекция вектора тока на направление,
перпендикулярное напряжению,
– это реактивная составляющая тока.
Она равна суммарному току реактивных
элементов
(рис. 2.32, а).
Проекция вектора тока на направление,
перпендикулярное напряжению,
– это реактивная составляющая тока.
Она равна суммарному току реактивных
элементов 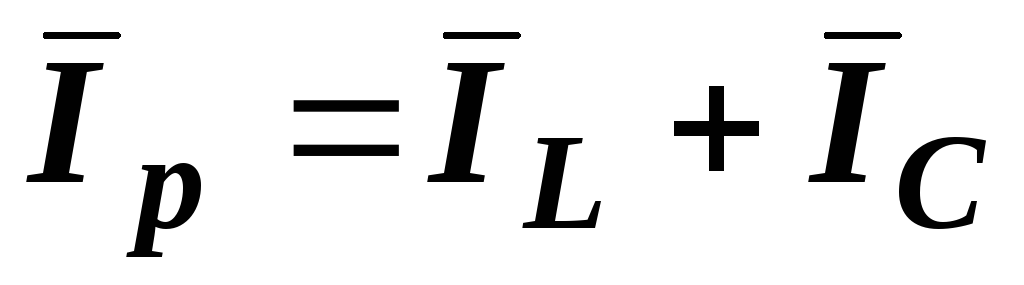 и определяется как разность
длин векторов:
и определяется как разность
длин векторов: 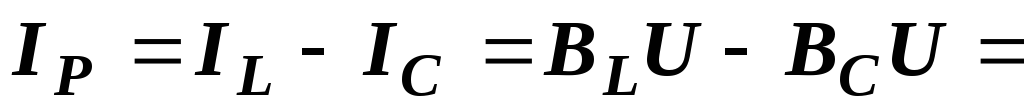
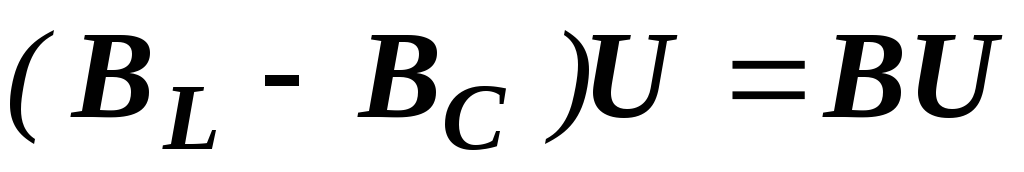 (см. рис. 2.31,б и 2.32, а).
(см. рис. 2.31,б и 2.32, а).
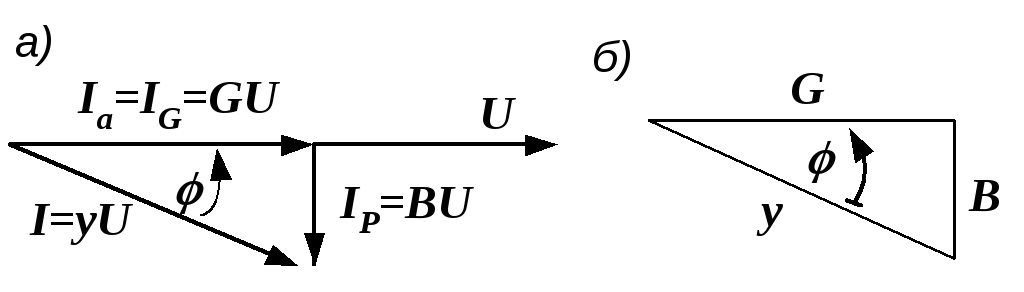
Рис. 2.32. Треугольники токов и проводимостей
Разделив
все стороны треугольника токов на  ,
получим треугольник проводимостей
(рис. 2.32, б),
стороны которого связаны следующими
соотношениями:
,
получим треугольник проводимостей
(рис. 2.32, б),
стороны которого связаны следующими
соотношениями:
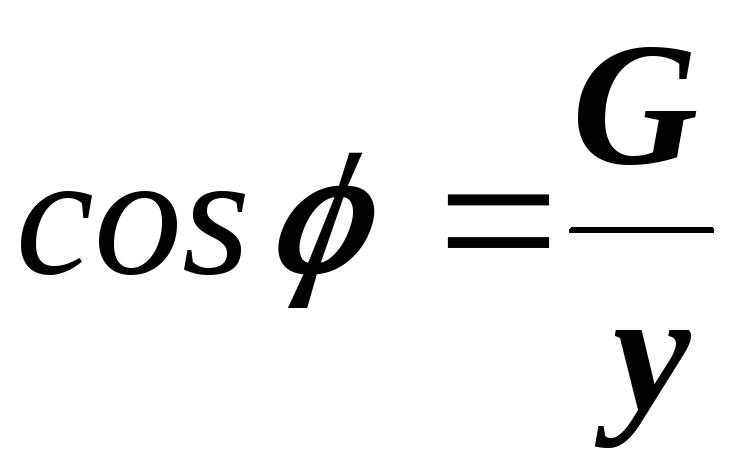 ,
, 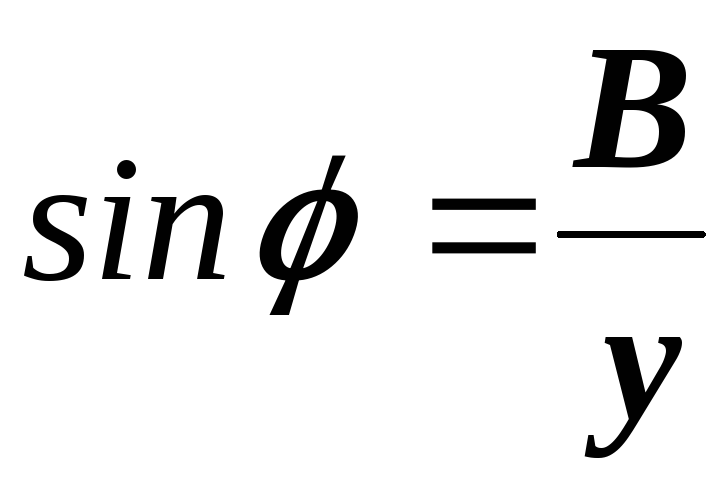 ,
, 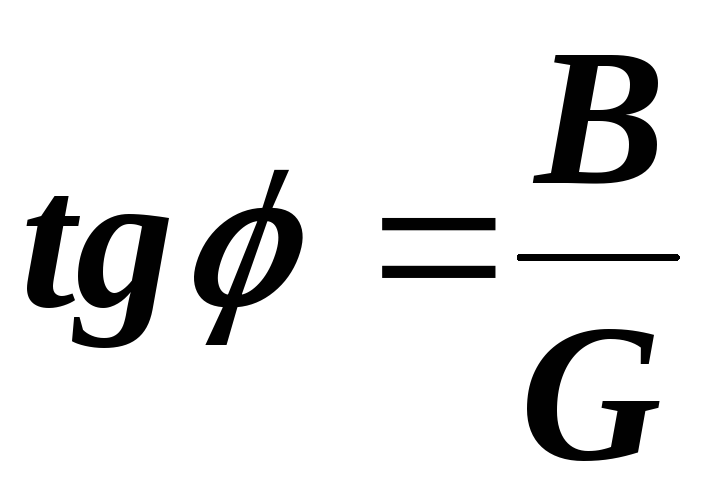 ,
, 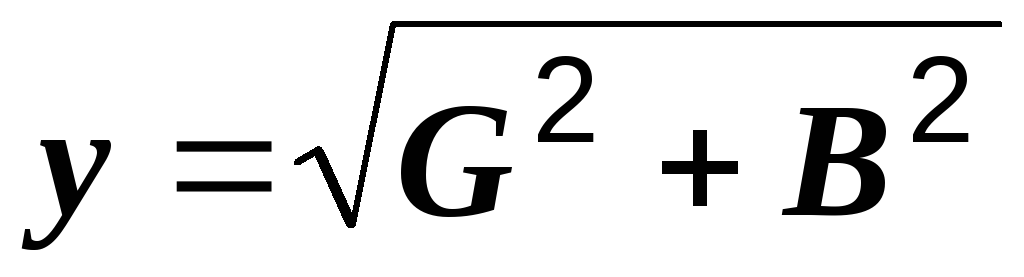 . (2.29)
. (2.29)
2. С и м в о л и ч е с к и й м е т о д.
Раньше были получены следующие формулы:
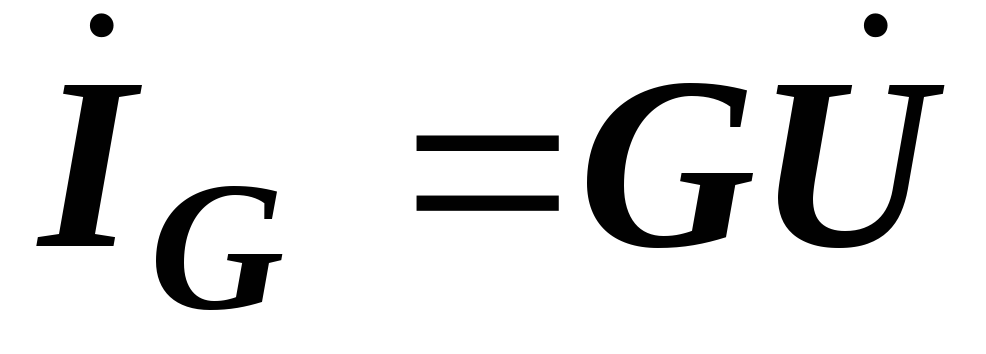 ,
, 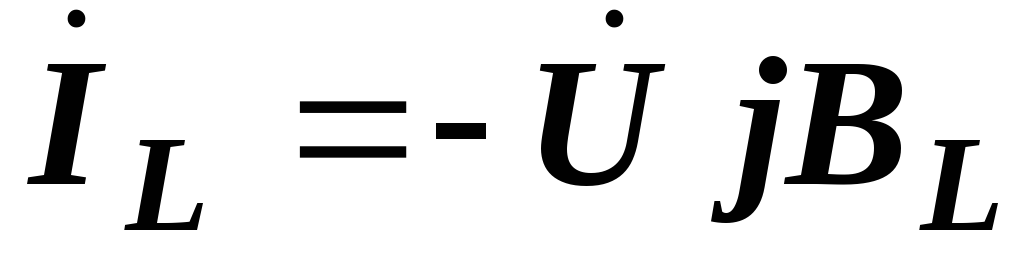 ,
, 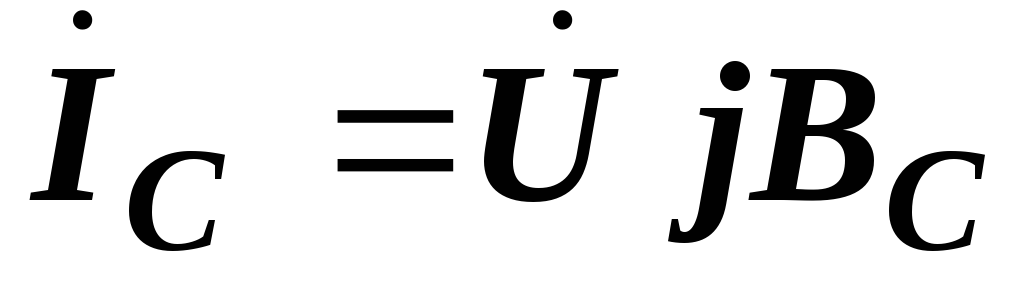 .
.
Подставляя их в уравнение первого закона Кирхгофа, получаем:
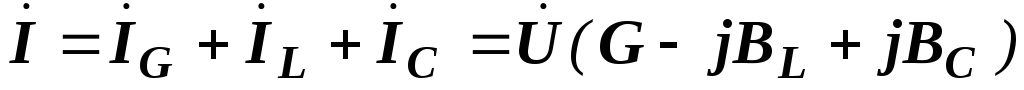 или
или 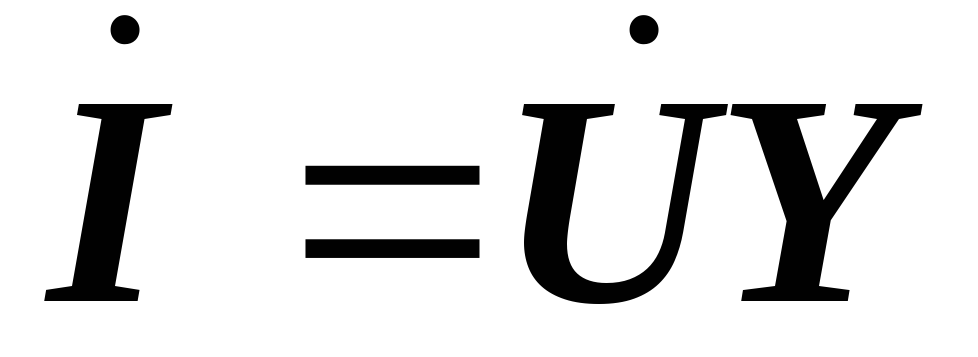 ,
,
где  – комплексная проводимость цепи, равная
– комплексная проводимость цепи, равная
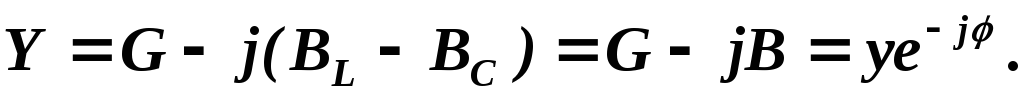
Пример
2.12. Для цепи, показанной на рис. 2.33, а,
рассчитать токи, угол сдвига фаз между
током и напряжением на входе цепи,
построить векторную диаграмму. Числовые
значения параметров цепи: 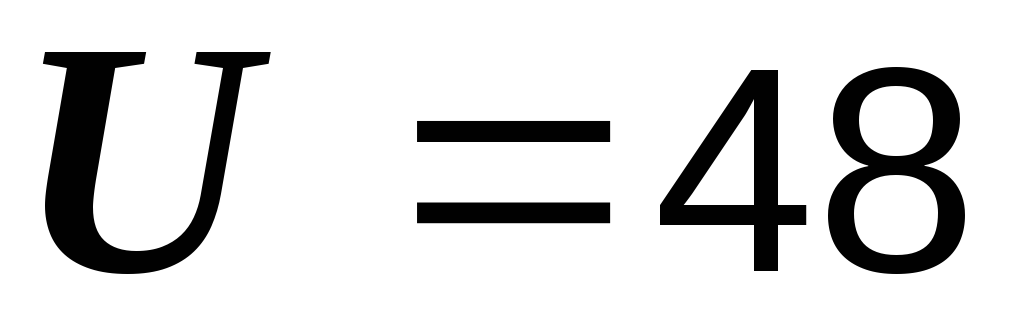 В,
В, 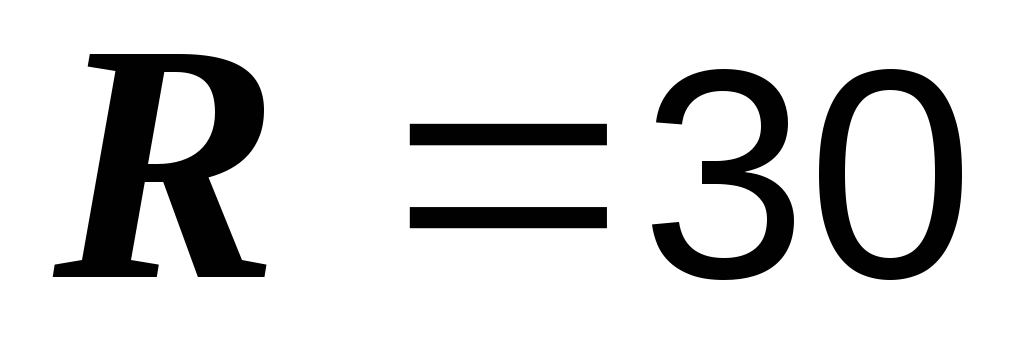 Ом,
Ом, 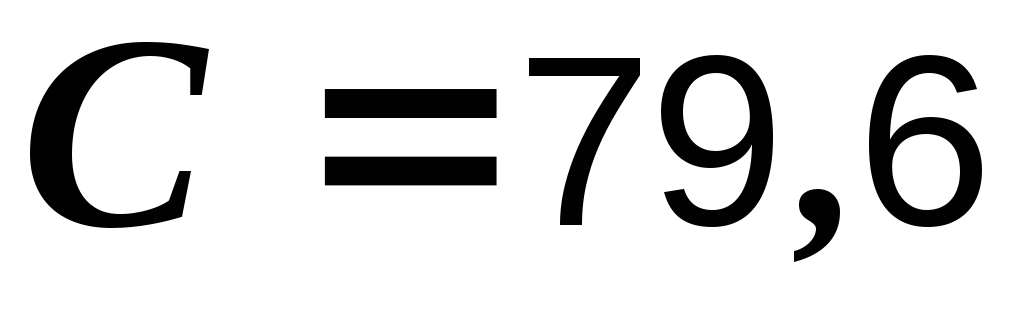 мкФ,
мкФ, 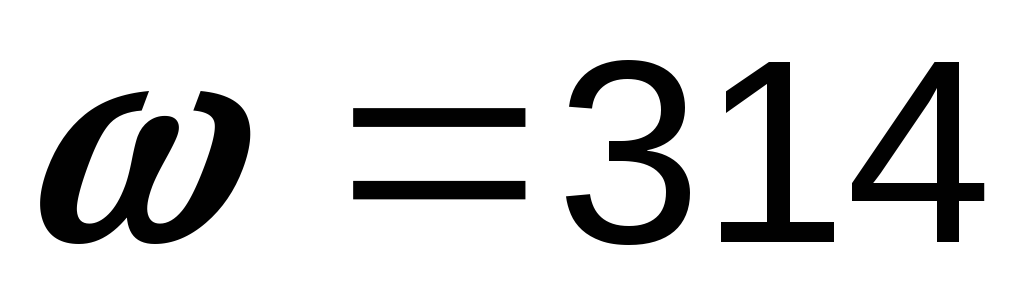 с-1.
с-1.
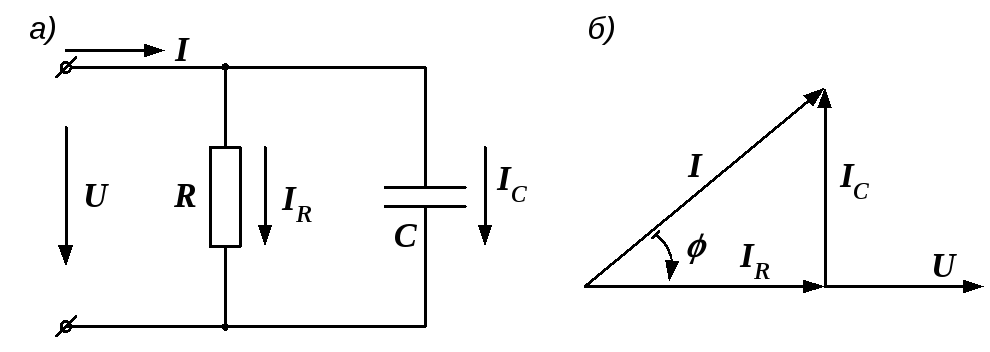 Рис.
2.33. Электрическая цепь и ее векторная
диаграмма
Рис.
2.33. Электрическая цепь и ее векторная
диаграмма
Р е ш е н и е.
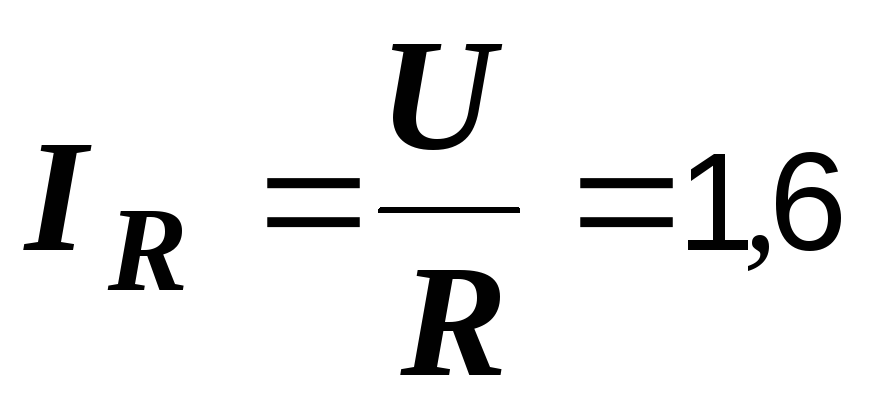 А,
А,  Ом,
Ом,
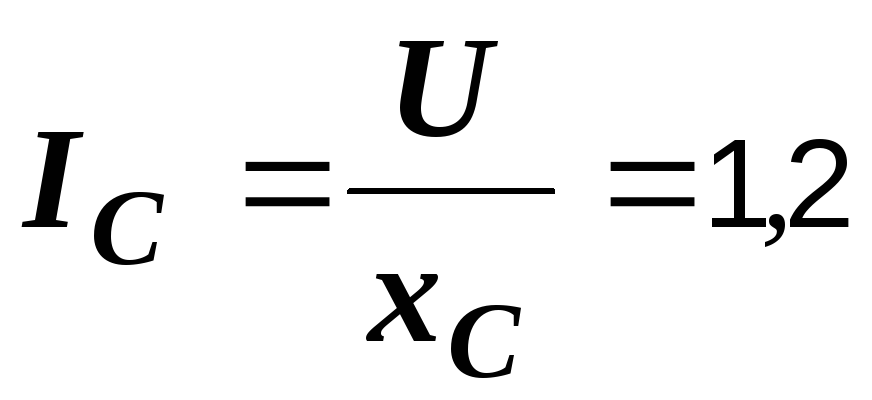 А,
А, 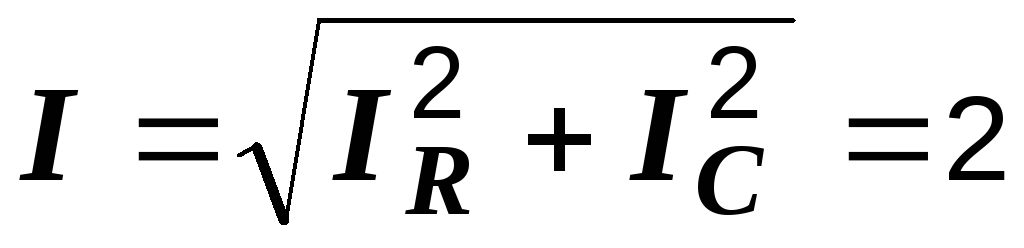 А.
А.
Векторная диаграмма приведена на рис. 2.33, б.
Угол
сдвига фаз 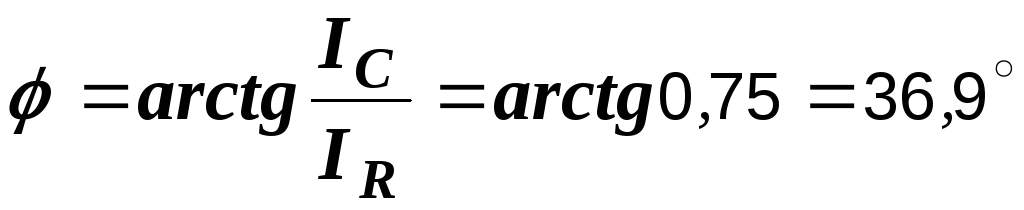 .
.
Величину общего тока можно найти иначе:
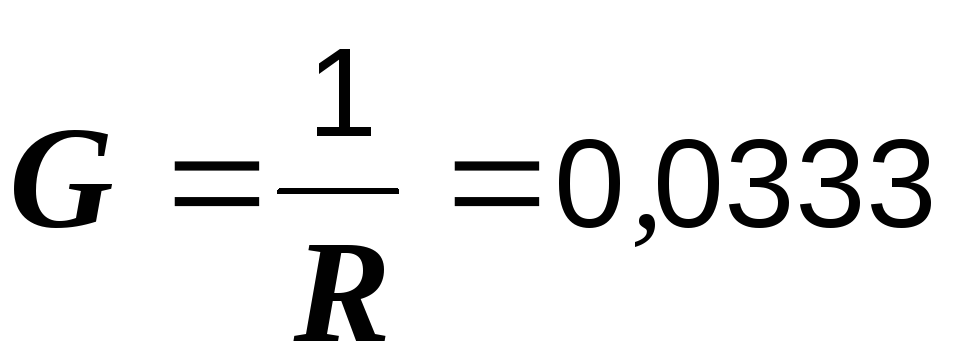 См,
См, 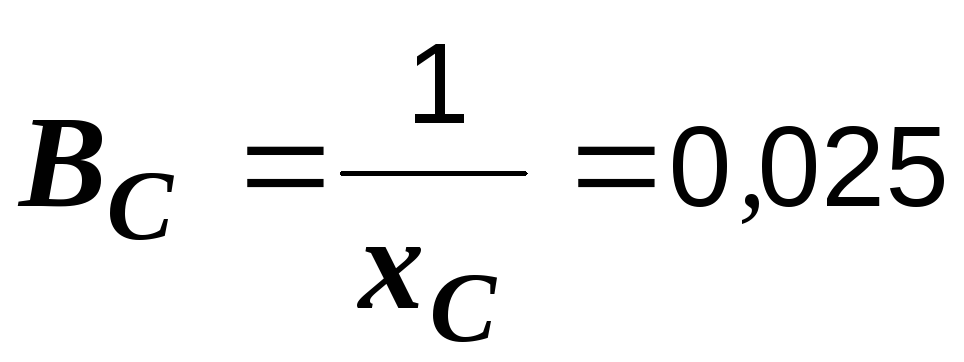 См,
См,
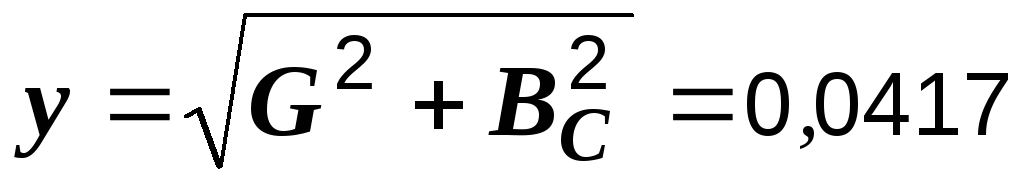 См,
См, 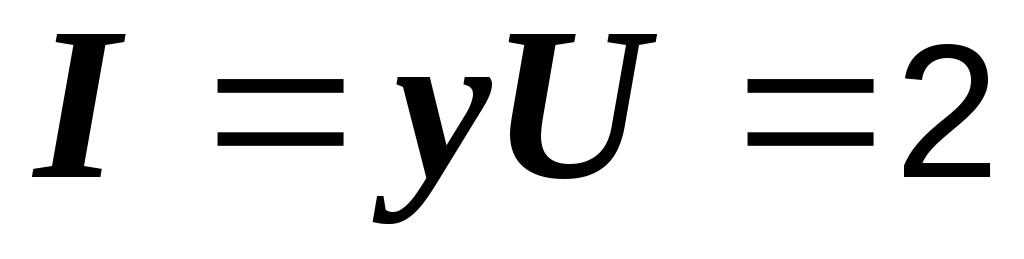 А.
А.
Пример 2.13. Начертить цепь, векторная диаграмма которой изображена на рис. 2.34, а.
Р е ш е н и е задачи показано на рис. 2.34, б.
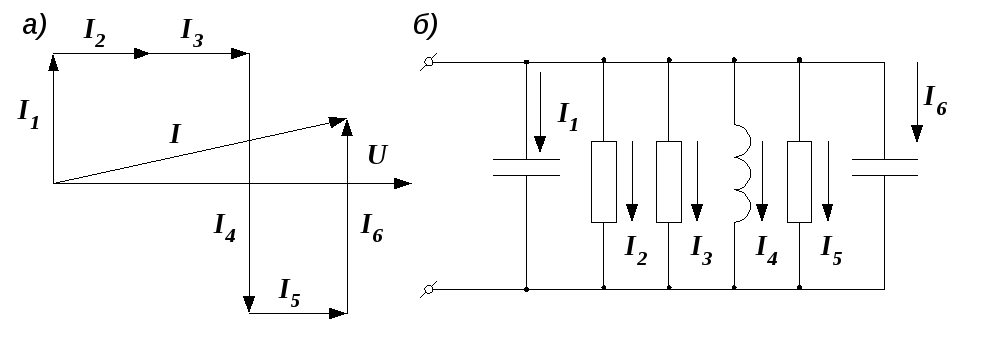
Рис. 2.34. Векторная диаграмма и соответствующая ей электрическая цепь
Пример 2.14. Чему равно показание амперметра А на входе цепи в схемах рис. 2.35, если амперметры А1 и А2 во всех случаях показывают соответственно 4 и 3 А?
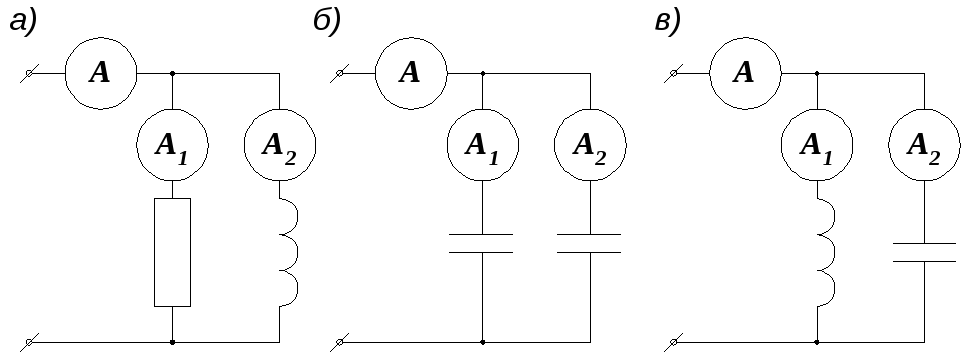
Рис. 2.35. Измерение тока в электрической цепи
Предлагаем для каждого случая самостоятельно построить векторную диаграмму и убедиться в правильности приведенных ответов: а) 5А, б) 7А, в) 1А.
2.14. Пассивный двухполюсник в цепи синусоидального тока.Эквивалентные сопротивления и проводимости
На
рис. 2.36 показан пассивный двухполюсник,
состоящий из активных и реактивных
элементов. Действующие значения
напряжения  ,
тока
,
тока 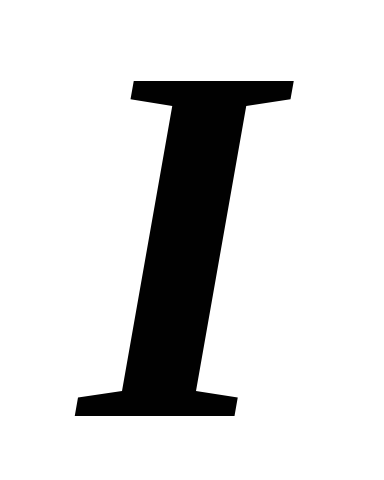 и угол сдвига фаз между ними
и угол сдвига фаз между ними  известны.
известны.
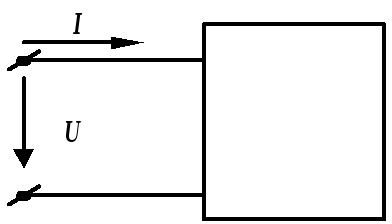
Рис. 2.36. Пассивный двухполюсник
Построим по этим значениям векторную диаграмму и, спроектировав вектор напряжения на вектор тока и перпендикулярное к нему направление, получим треугольник напряжений, образованный сторонами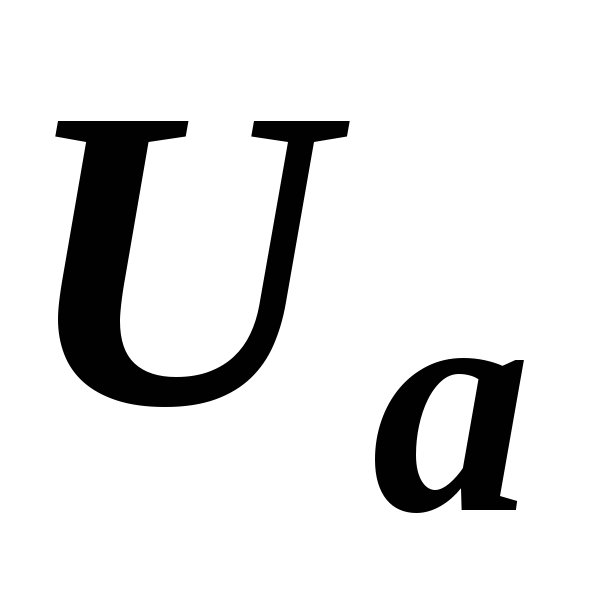 ,
, 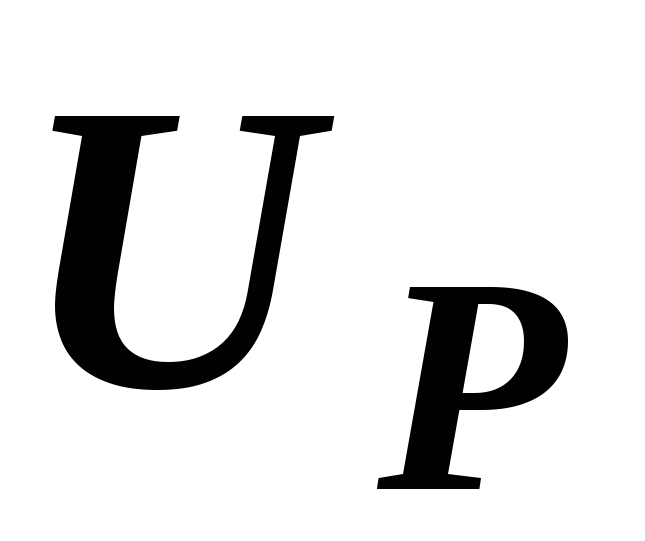 и
и  (рис. 2.37, а).
(рис. 2.37, а). Как
и раньше, 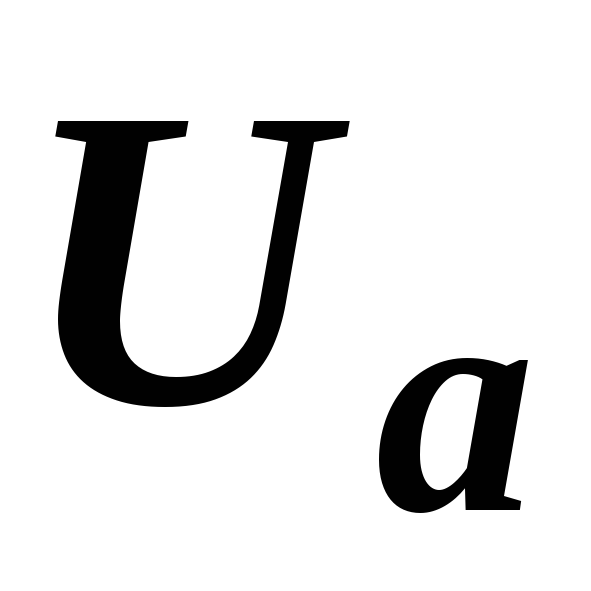 и
и 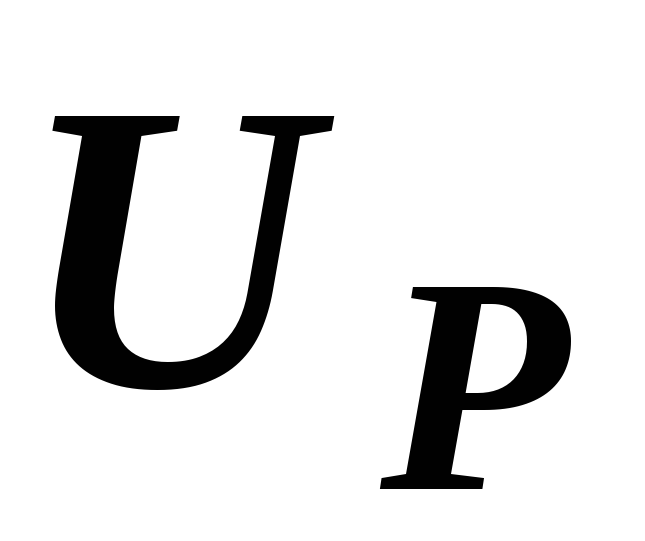 будем называть активной и реактивной
составляющими напряжения. Изображенная
в таком виде диаграмма соответствует
схеме, показанной на рис. 2.37, б.
Действительно, для нее
будем называть активной и реактивной
составляющими напряжения. Изображенная
в таком виде диаграмма соответствует
схеме, показанной на рис. 2.37, б.
Действительно, для нее 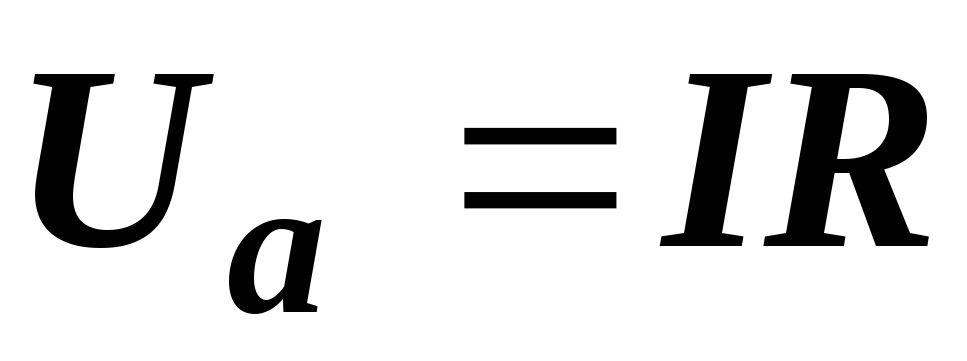 ,
, 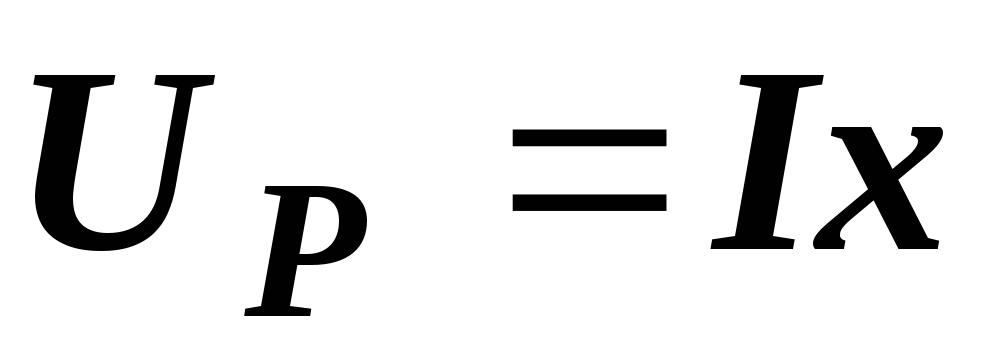 и
и 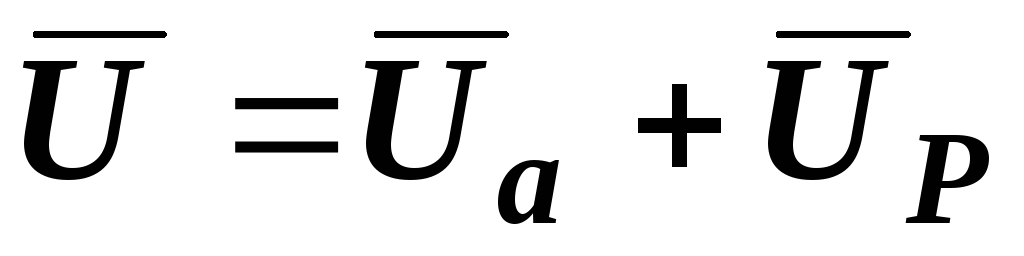 .
Схема называется последовательной
схемой замещения или последовательной
эквивалентной схемой пассивного
двухполюсника, а ее параметры
.
Схема называется последовательной
схемой замещения или последовательной
эквивалентной схемой пассивного
двухполюсника, а ее параметры  ,
,  и
и  – эквивалентными сопротивлениями
двухполюсника.
– эквивалентными сопротивлениями
двухполюсника.
Рис. 2.37. Векторная диаграмма и соответствующая ей последовательная эквивалентная схема
Треугольник,
образованный сторонами  ,
,  и
и  и подобный треугольнику напряжений,
представляет собой треугольник
сопротивлений (рис. 2.28, б),
для которого справедливы формулы (2.27).
и подобный треугольнику напряжений,
представляет собой треугольник
сопротивлений (рис. 2.28, б),
для которого справедливы формулы (2.27).
Теперь
разложим в е к т о р т о к а на две
составляющие – активную 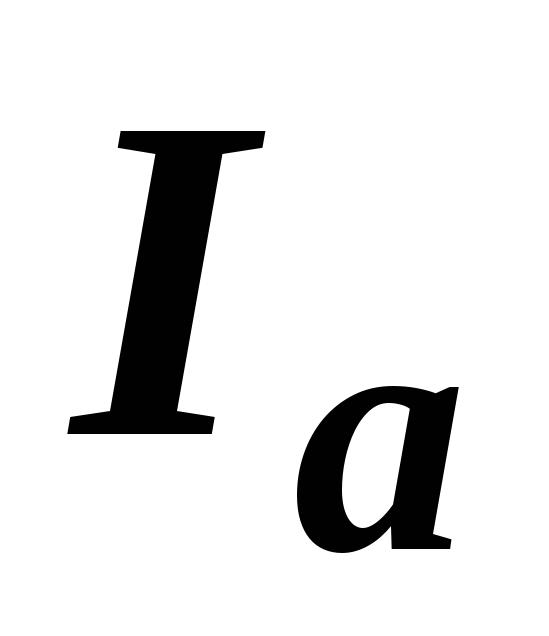 ,
направленную по вектору напряжения, и
реактивную
,
направленную по вектору напряжения, и
реактивную 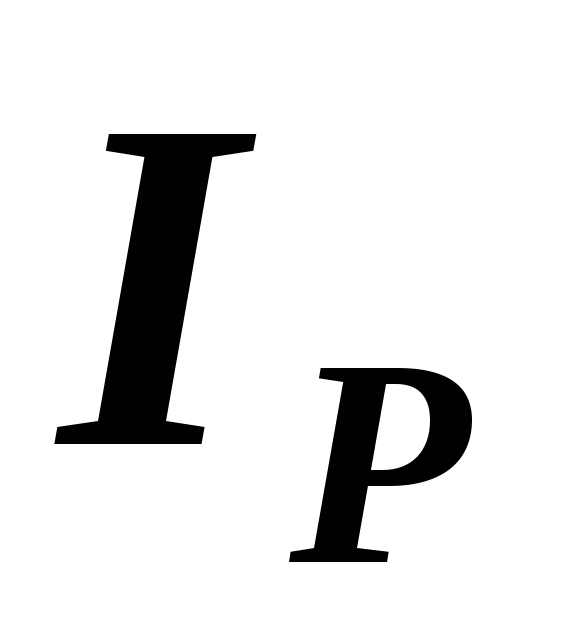 ,
перпендикулярную к нему (рис. 2.38, а).
Такой векторной диаграмме соответствует
параллельная схема замещения двухполюсника
(рис. 2.38, б).
Ее
параметры
,
перпендикулярную к нему (рис. 2.38, а).
Такой векторной диаграмме соответствует
параллельная схема замещения двухполюсника
(рис. 2.38, б).
Ее
параметры  ,
,  и
и  называются эквивалентными проводимостями.
Токи в элементах
называются эквивалентными проводимостями.
Токи в элементах  и
и  мы и представляем как активную и
реактивную составляющие общего тока:
мы и представляем как активную и
реактивную составляющие общего тока: 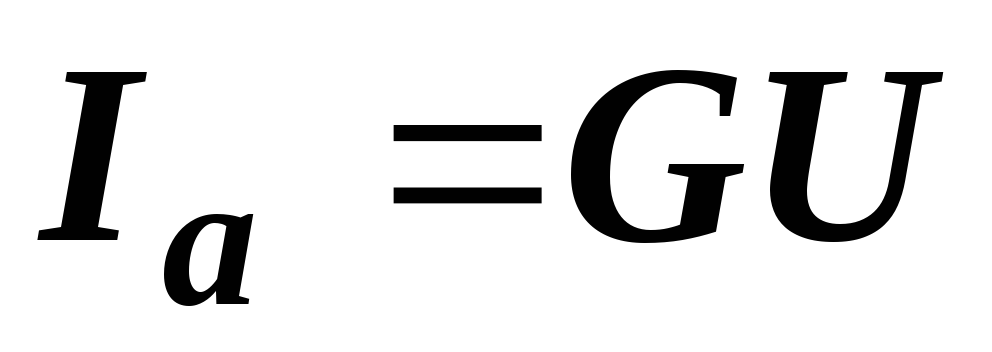 ,
, 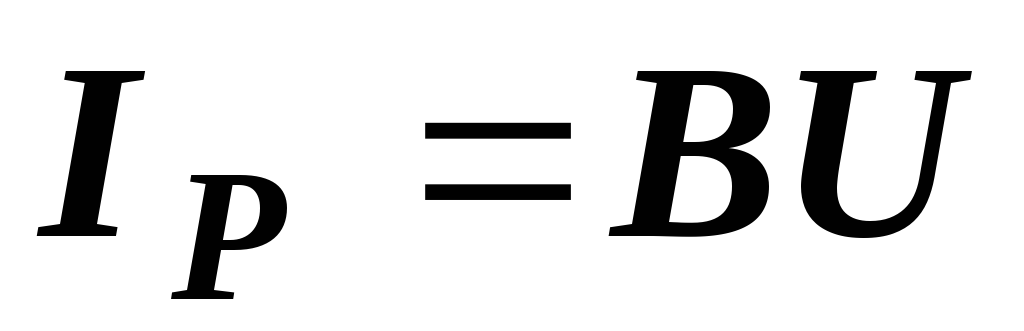 .
Из треугольника токов (рис. 2.38, а)
получается треугольник проводимостей (рис. 2.32, б),
стороны которого связаны между собой
формулами (2.29).
.
Из треугольника токов (рис. 2.38, а)
получается треугольник проводимостей (рис. 2.32, б),
стороны которого связаны между собой
формулами (2.29).
а) б)
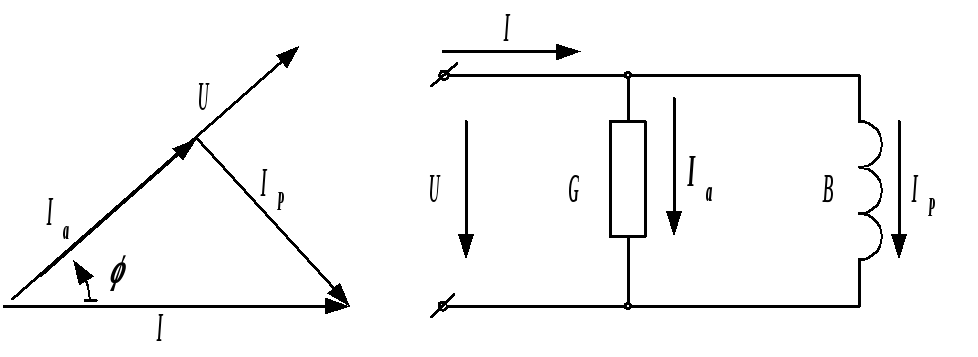
Рис. 2.38. Параллельная эквивалентная схема и ее векторная диаграмма
Получим условия эквивалентности приведенных схем.
Для
последовательной цепи 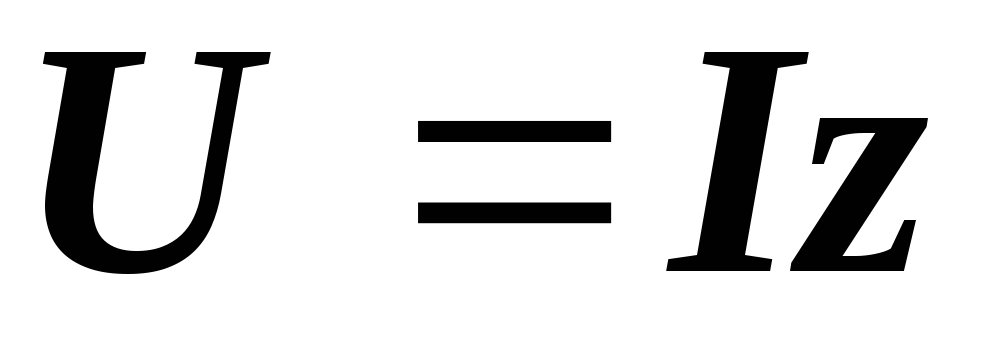 ,
для параллельной
,
для параллельной 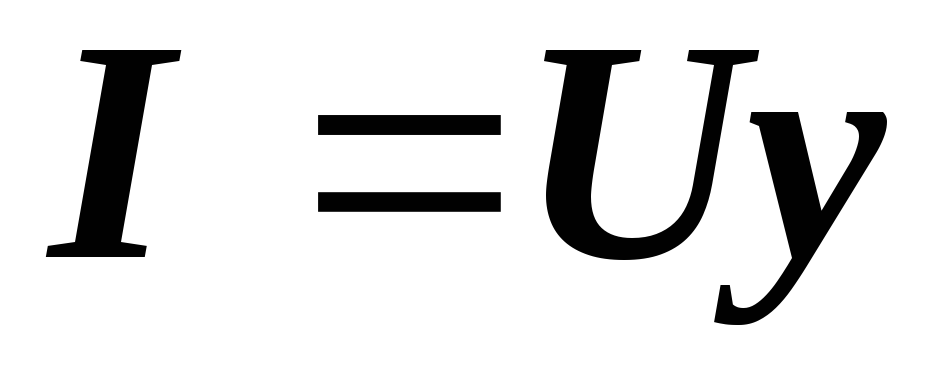 ,
а так как токи и напряжения в обеих
схемах одинаковы, то
,
а так как токи и напряжения в обеих
схемах одинаковы, то
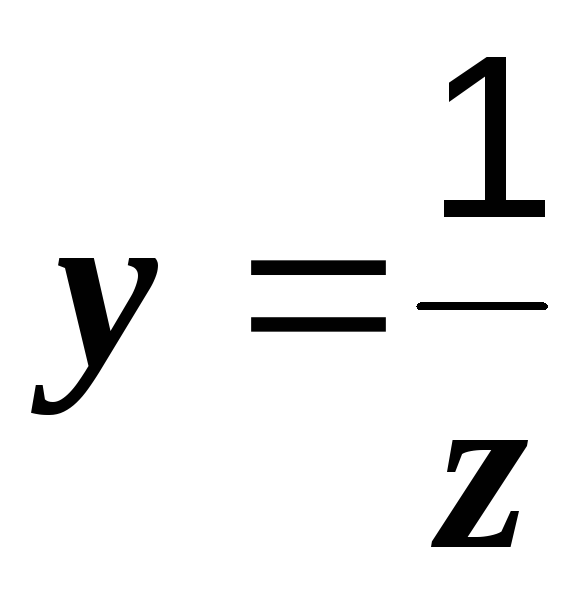 и
и 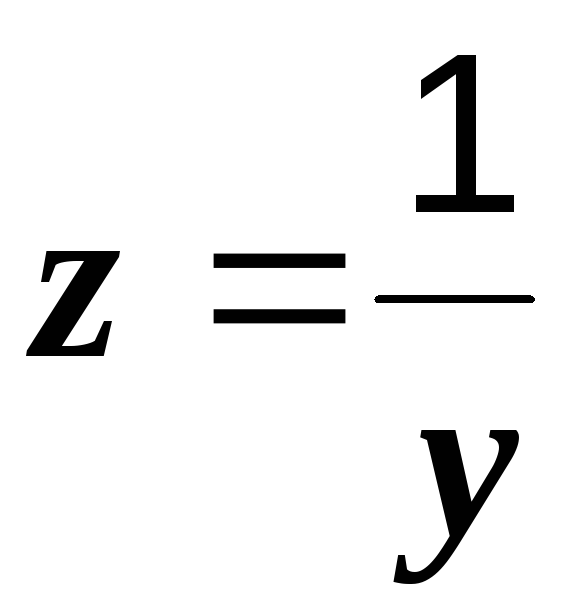 ,
(2.30)
,
(2.30)
т.е. в любой электрической цепи полная проводимость есть величина, обратная полному сопротивлению.
Из сопоставления формул (2.27) и (2.29) можно записать:
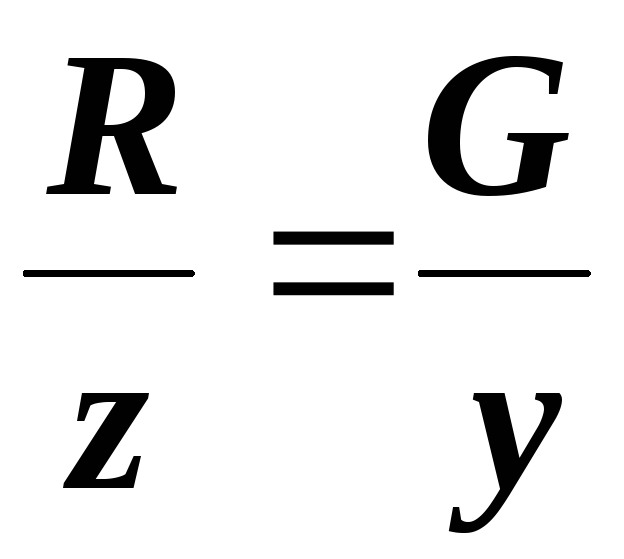 и
и 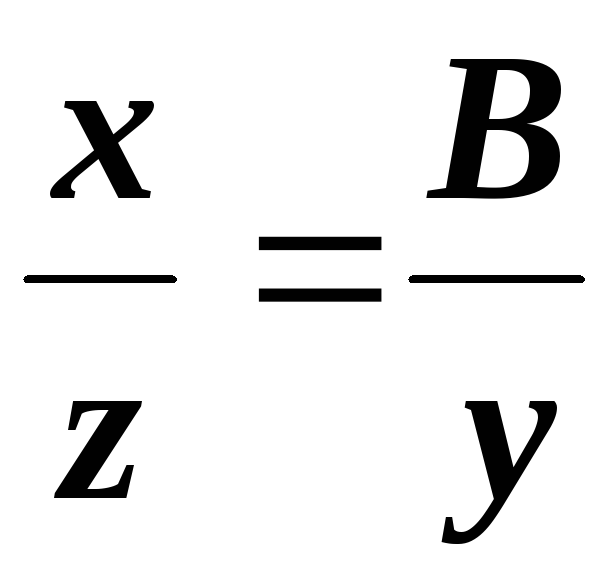 .
.
Рассматривая последние выражения совместно с (2.30), можно получить две группы формул:
Формулы перехода от последовательной эквивалентной схемы к параллельной: | Формулы перехода от параллельной эквивалентной схемы к последовательной: |
| |
Обращаем внимание на то, что каждая из проводимостей G и B зависит от обоих сопротивлений – активного и реактивного. В свою очередь, каждое из сопротивлений определяется обеими проводимостями. Соотношения G = 1/R и B = 1/x справедливы только в частном случае, первое – при х = 0, второе – при R = 0.
Следует отметить, что активная и реактивная составляющие напряжения и тока физически не существуют, измерить их нельзя. Они относятся только к соответствующим эквивалентным схемам замещения и находятся расчетом. Более того, проектируя, например, вектор тока на различные напряжения, мы получим для него разные составляющие.
Пример 2.15. Найти общее сопротивление цепи, состоящей из параллельно соединенных активного R = 30 Ом и индуктивного х = 40 Ом сопротивлений (рис. 2.39, а).
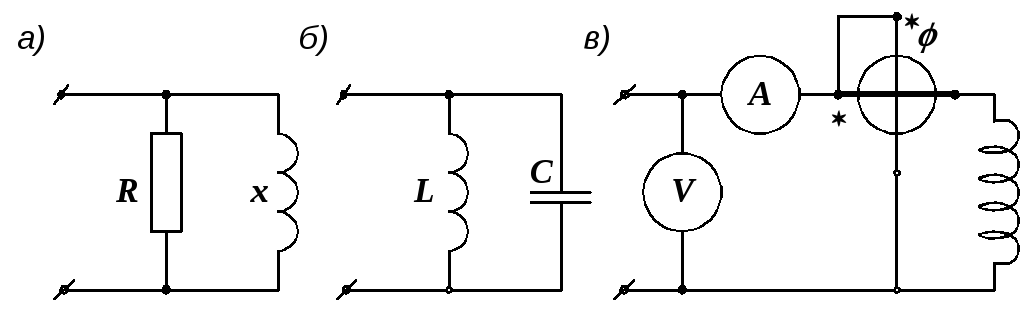
Рис. 2.39. Схемы к примерам 2.15–2.17
Р
е ш е н и е. Так как в левой ветви реактивного
сопротивления нет, то ее проводимость
в соответствии с (2.31) равна G
= 1/R.
Аналогично, во второй ветви B
= 1/x.
Полная
проводимость цепи 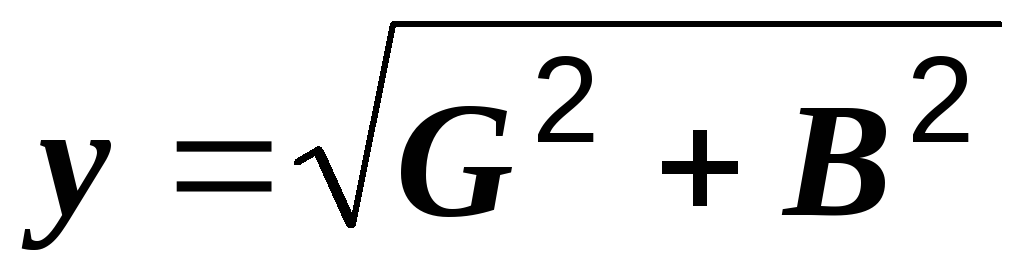 .
В соответствии с (2.30) полное сопротивление
цепи
.
В соответствии с (2.30) полное сопротивление
цепи
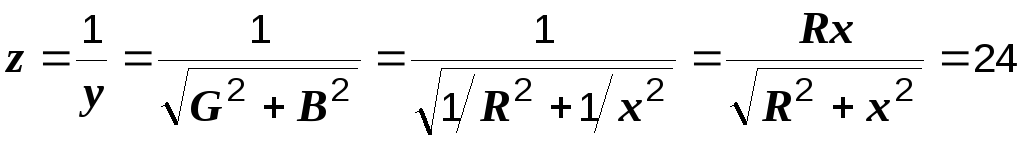 Ом.
Ом.
Пример 2.16. Рассчитать общее сопротивление цепи, состоящей из параллельно соединенных индуктивности L = 0,478 Гн и емкости С = 31,85 мкФ (рис. 2.39, б). Частота питающего напряжения f = 50 Гц.
Р е ш е н и е. Определяем сопротивления ветвей:
 Ом,
Ом,
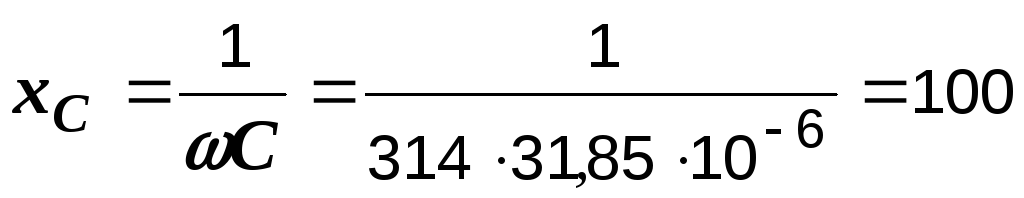 Ом.
Ом.
Так как в ветвях отсутствуют активные сопротивления, то их проводимости соответственно равны BL = 1/xL и BC = 1/xС. Полная эквивалентная проводимость цепи не содержит активной составляющей и равна
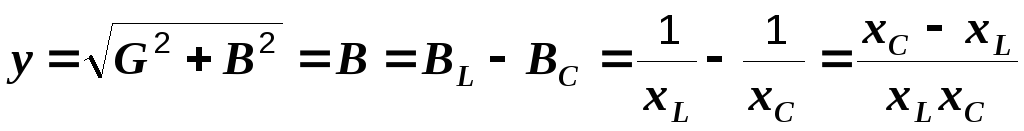 .
.
Полное эквивалентное сопротивление
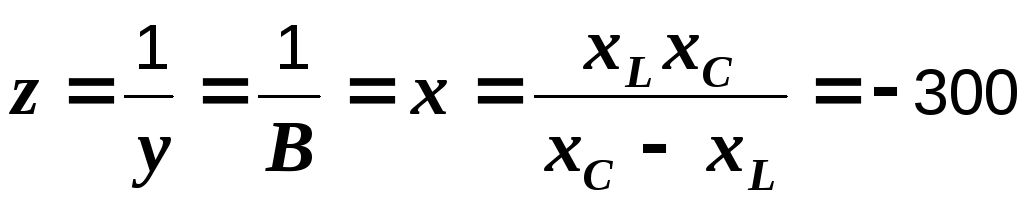 Ом.
Ом.
В рассматриваемой цепи активных элементов нет, она носит чисто реактивный характер. Он может быть индуктивным или емкостным. Знак минус в ответе свидетельствует о последнем, т.е. вся цепь может быть заменена конденсатором емкостью
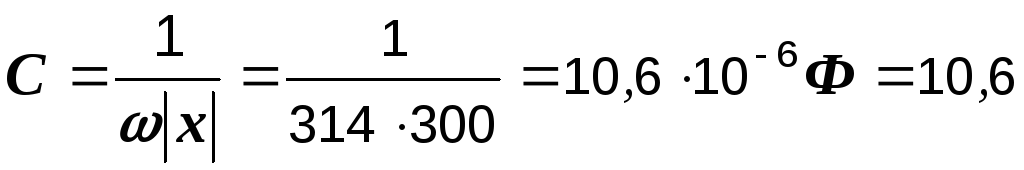 мкФ.
мкФ.
Пример 2.17. Амперметр А, вольтметр V и фазометр , включенные в цепь катушки (рис. 2.39, в), дали следующие показания: U = 220 В, I = 4,4 А, cos = 0,8. Частота питающего напряжения 50 Гц. Определить параметры последовательной и параллельной схем замещения катушки.
Р е ш е н и е. Находим параметры последовательной эквивалентной схемы:
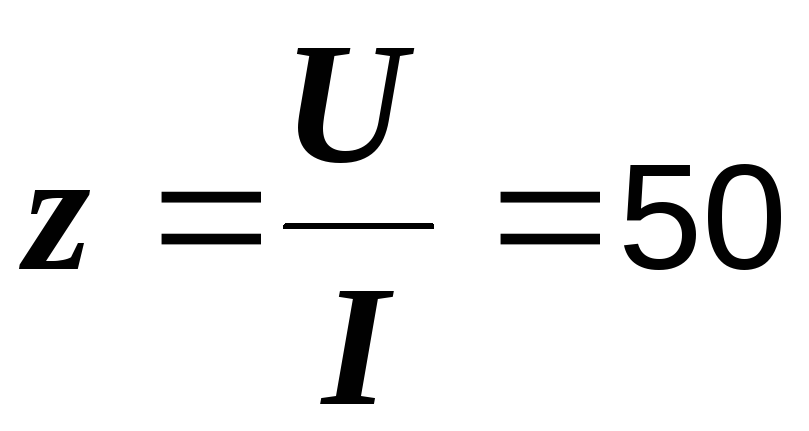 Ом,
Ом, 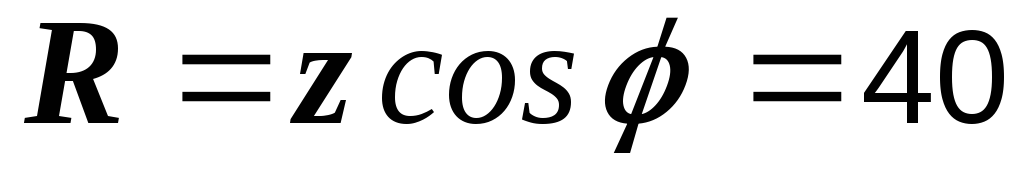 Ом,
Ом,
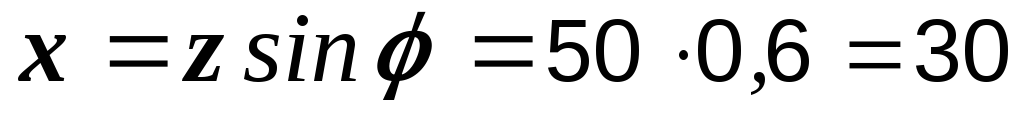 Ом.
Ом.
Рассчитываем элементы параллельной эквивалентной схемы:
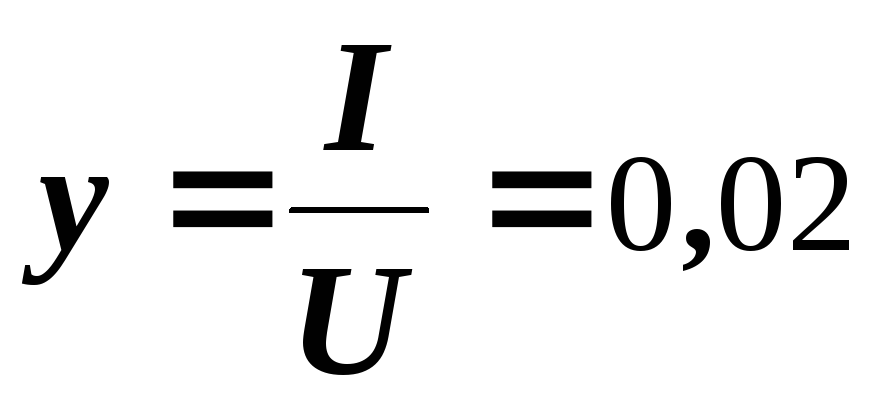 См,
См, 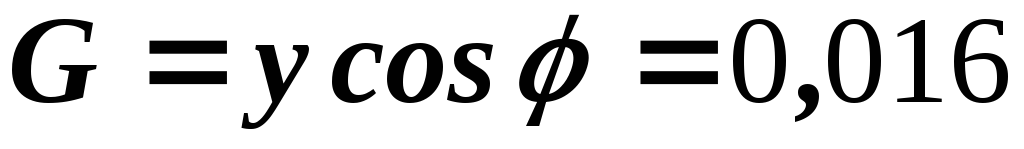 См,
См,
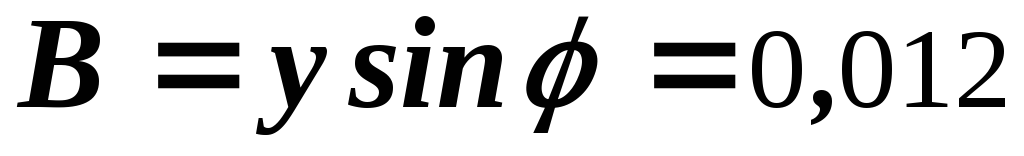 См.
См.
После определения эквивалентных сопротивлений эквивалентные проводимости можно было найти иначе, по формулам (2.31):
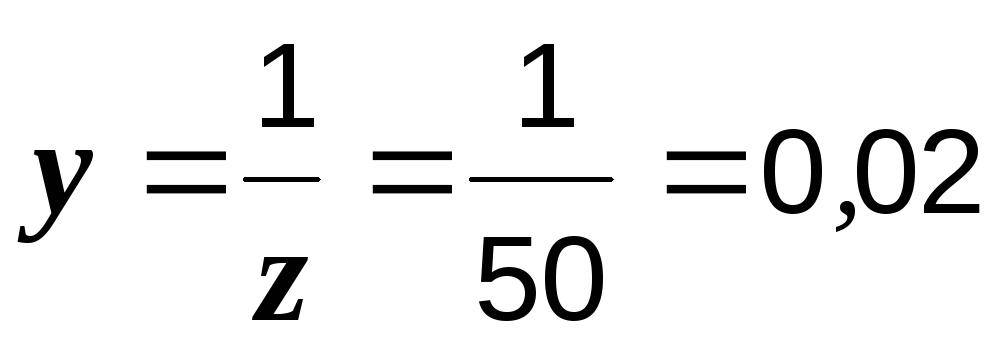 См,
См, 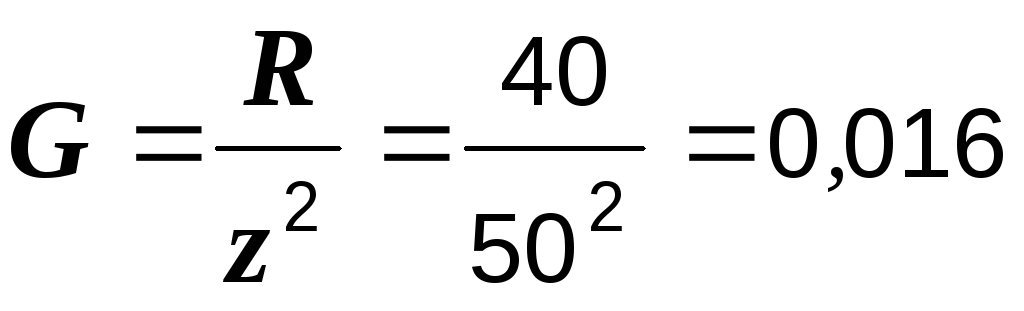 См,
См,
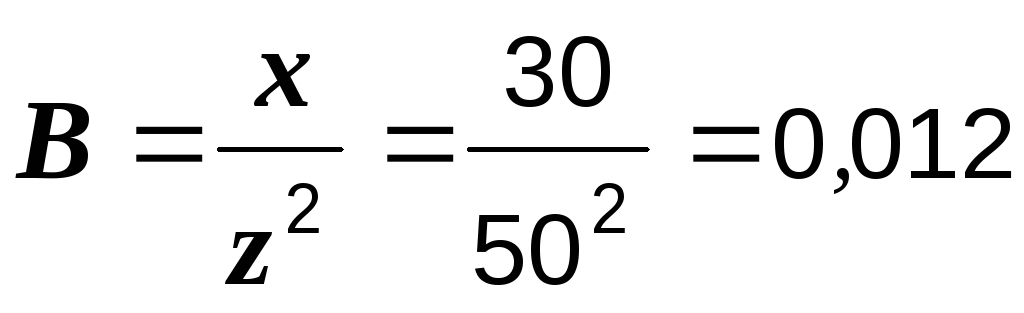 См.
См.
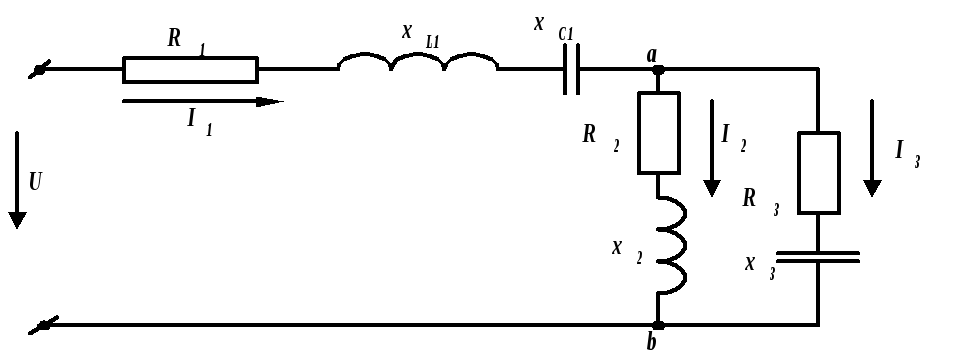
Рис. 2.40. Расчетная схема
Пример 2.18. Рассчитать токи в схеме, приведенной на рис. 2.40. 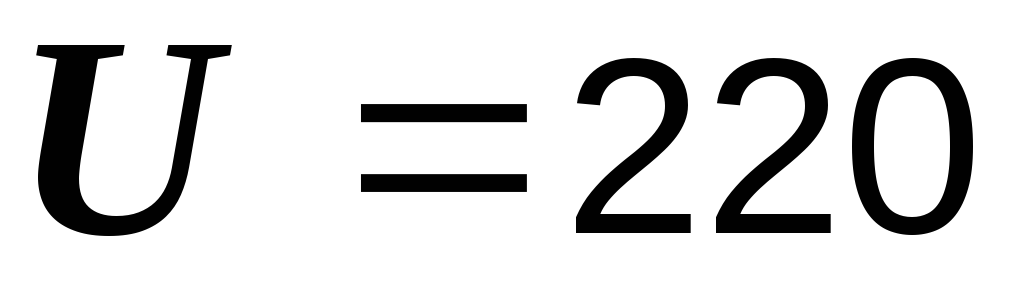 В,
В,
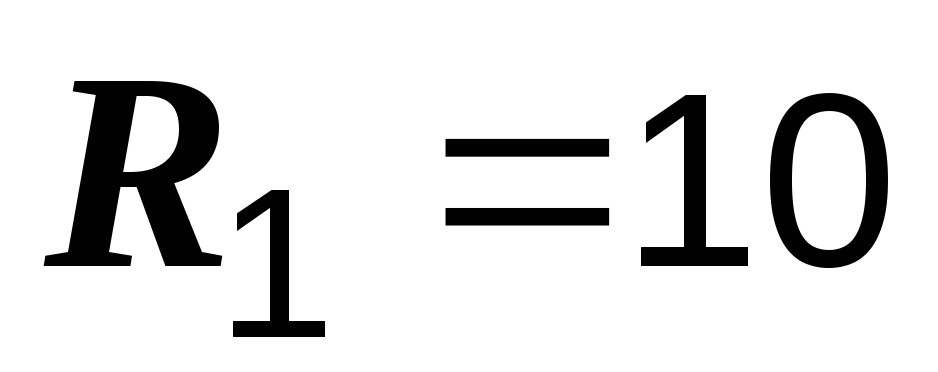 Ом,
Ом,
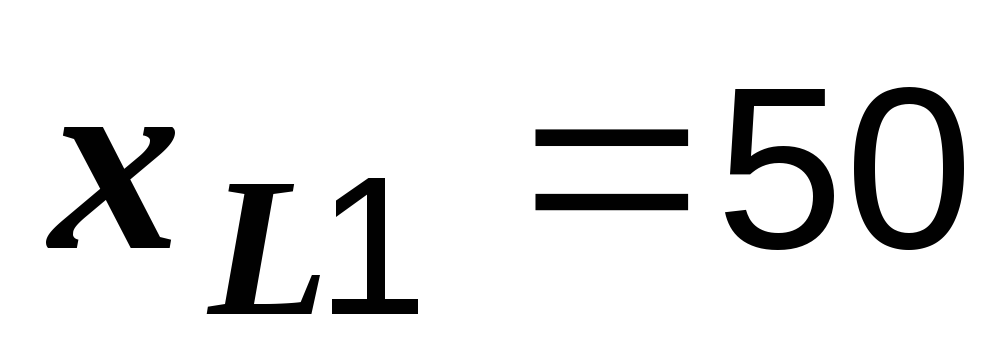 Ом,
Ом,
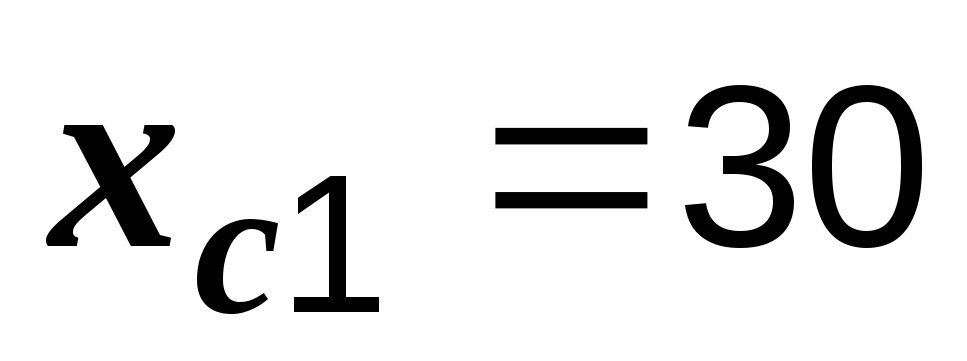 Ом,
Ом,
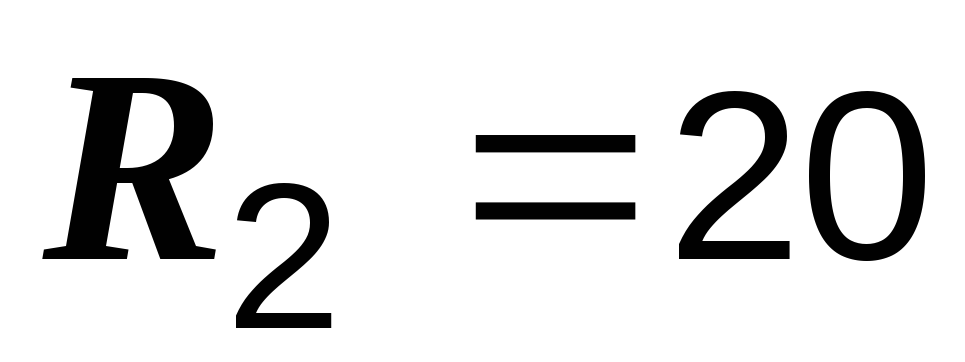 Ом,
Ом,
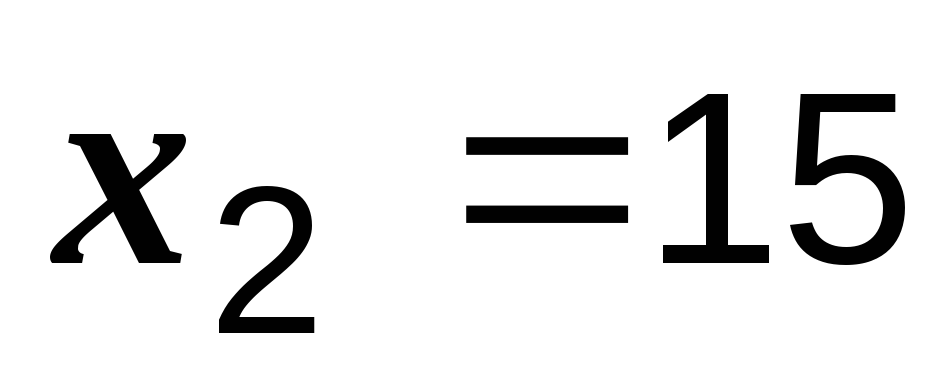 Ом,
Ом,
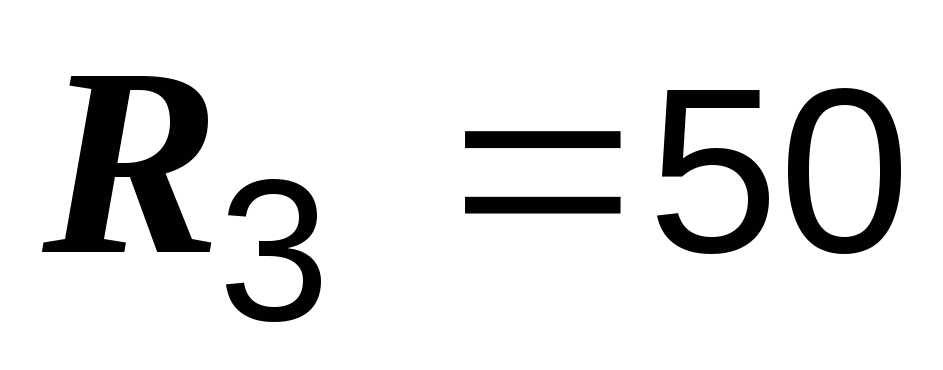 Ом,
Ом,
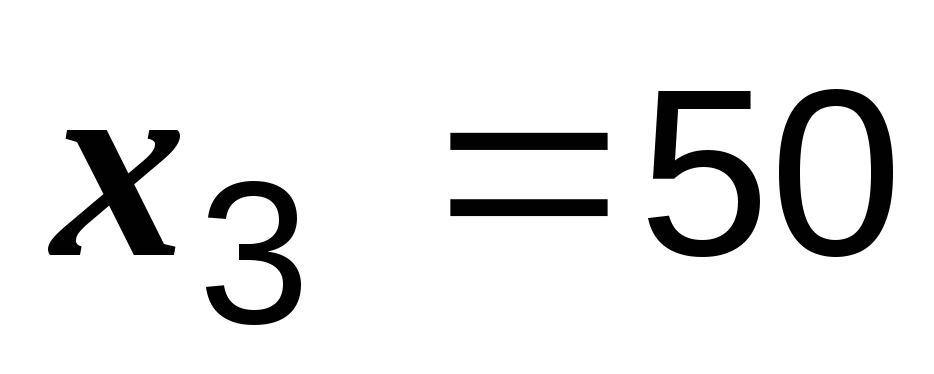 Ом.
Ом.
Р е ш е н и е. Определяем полные сопротивления второй и третьей ветвей:
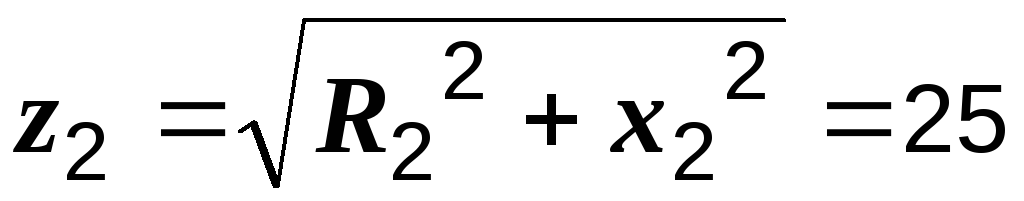 Ом,
Ом, 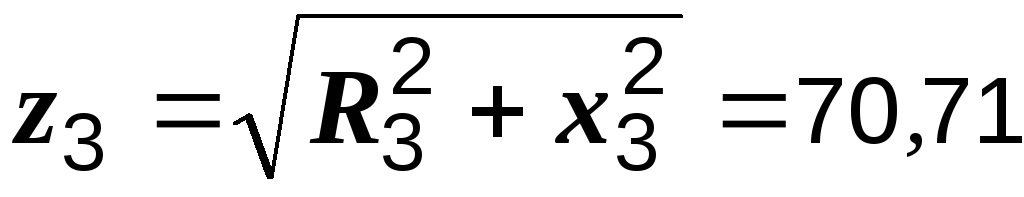 Ом.
Ом.
Преобразуем эти ветви в эквивалентные параллельные (рис. 2.41, а).
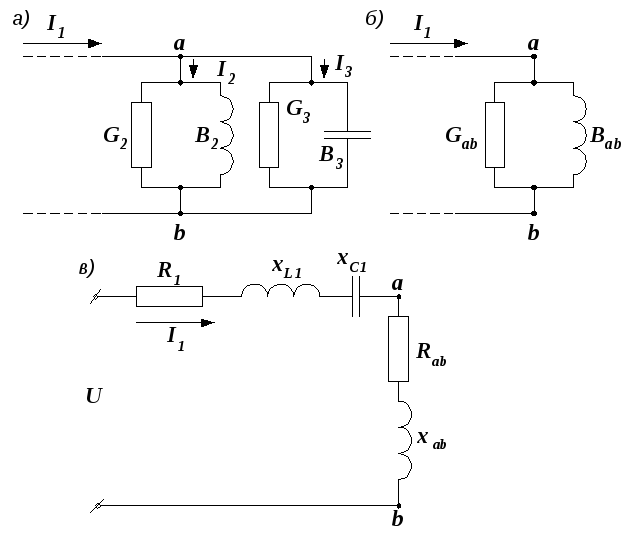
Рис. 2.41. Преобразования электрической цепи
Их проводимости:
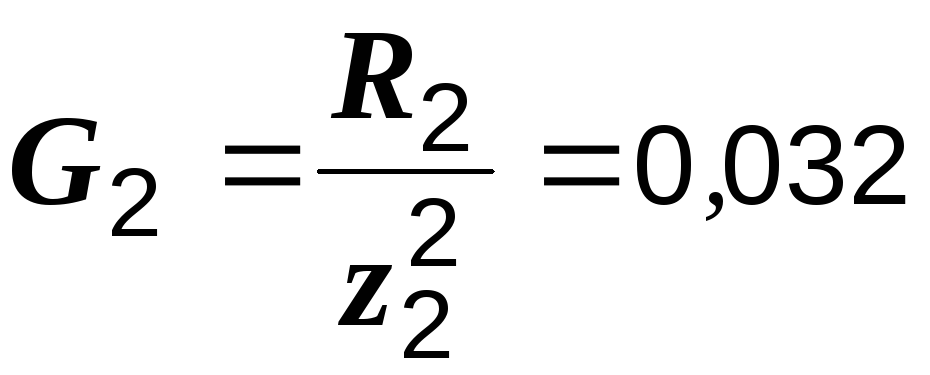 См,
См, 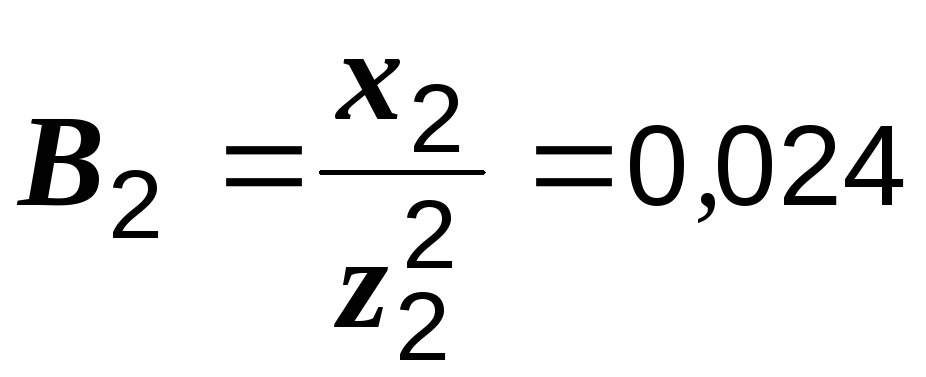 См,
См,
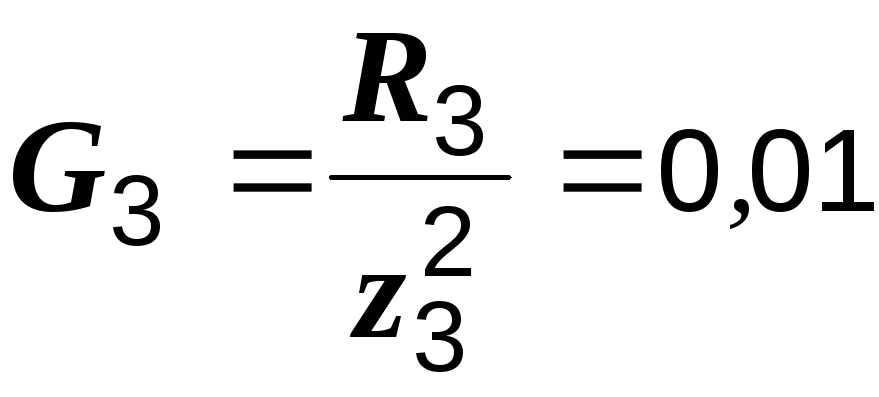 См,
См, 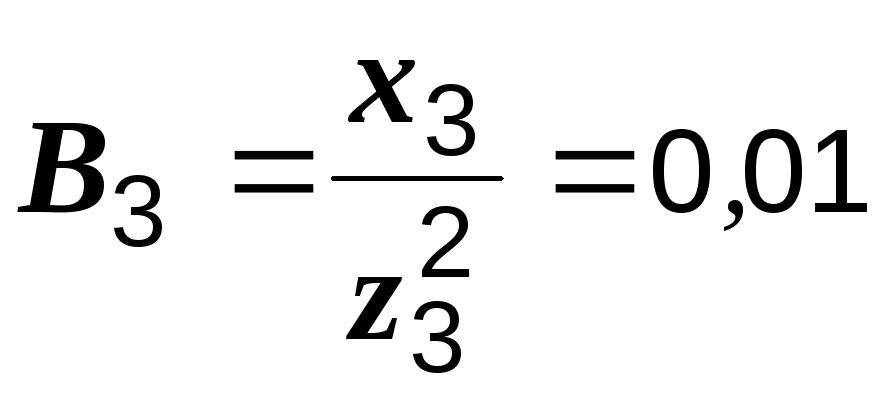 См.
См.
Суммируем
активные и реактивные проводимости
параллельных ветвей: 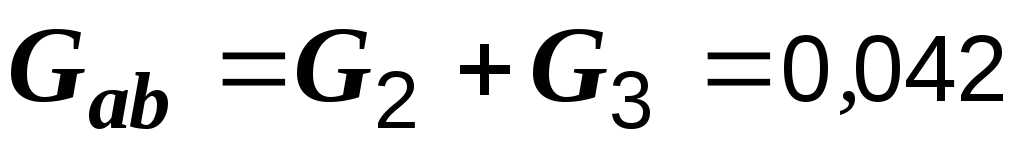 См,
См, 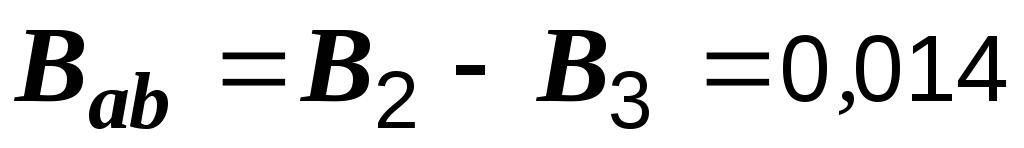 См
(см. рис. 2.41, б).
См
(см. рис. 2.41, б).
Определяем
эквивалентные сопротивления участка  (рис. 2.41, в):
(рис. 2.41, в):
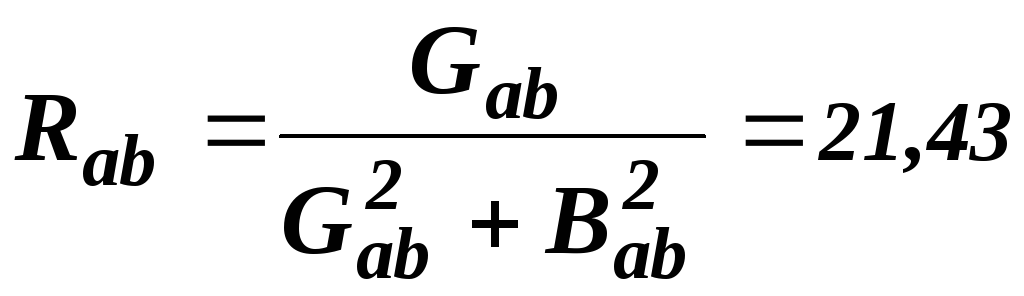 Ом, Ом,
Ом, Ом,
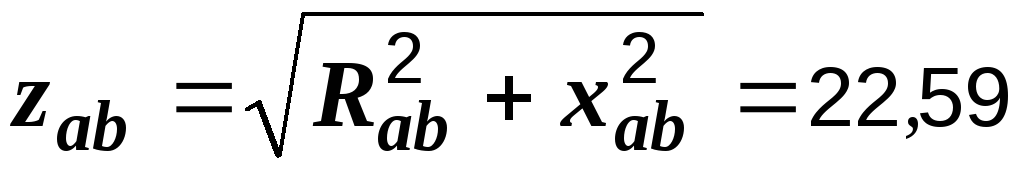 Ом,
Ом,
и полное сопротивление цепи:
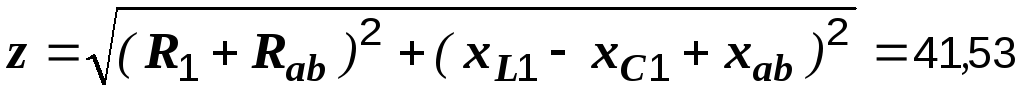 Ом.
Ом.
Ток на входе цепи I1 = U/z = 220/41,53 = 5,297 A.
Напряжение
на участке  Uab= I1zab=
119,7 В.
Uab= I1zab=
119,7 В.
Токи второй и третьей ветвей:
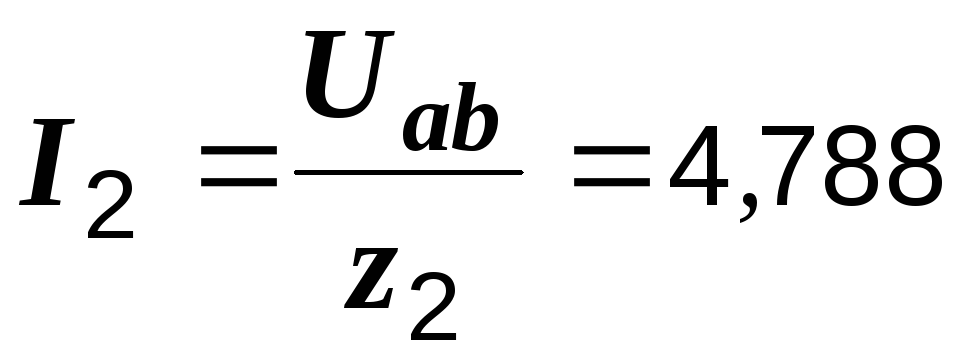 А,
А, 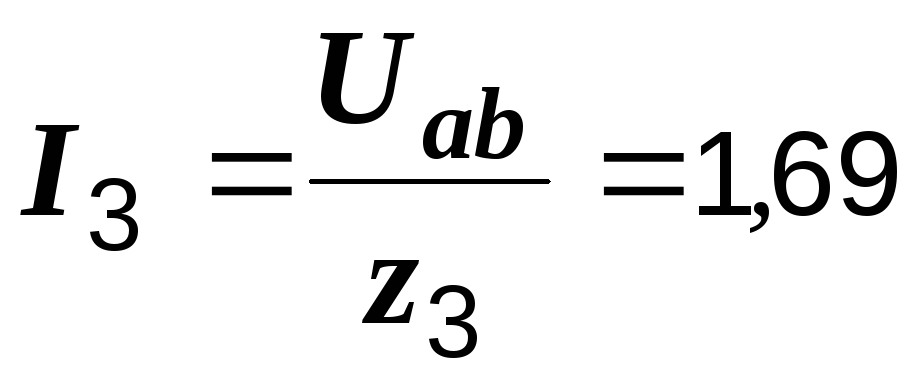 А.
А.
Еще
раз напоминаем, что для численных
значений токов и напряжений законы
Кирхгофа неприменимы: 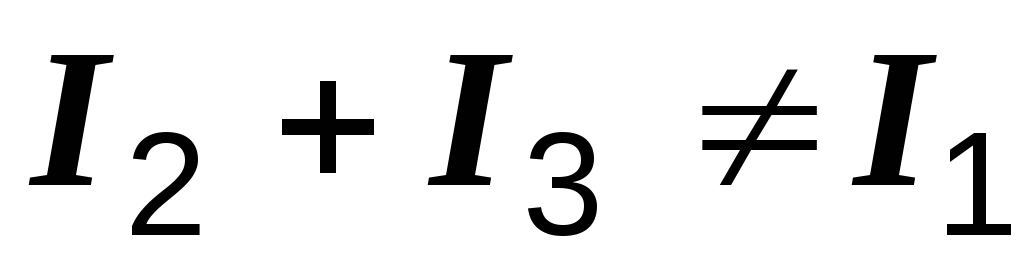 .
.


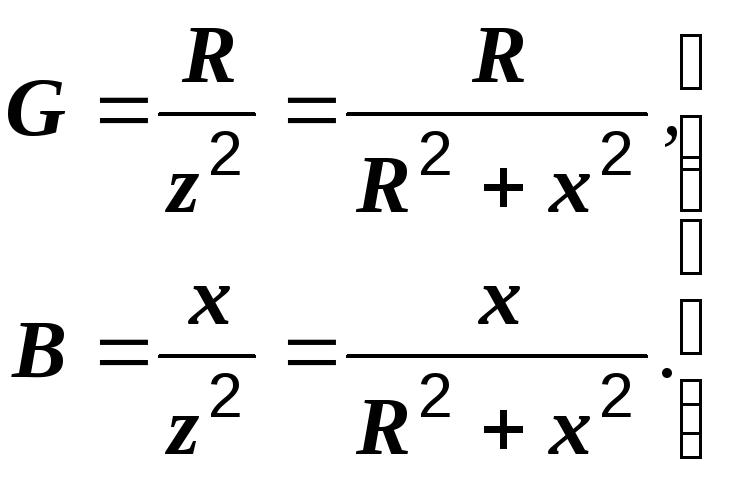 (2.31)
(2.31)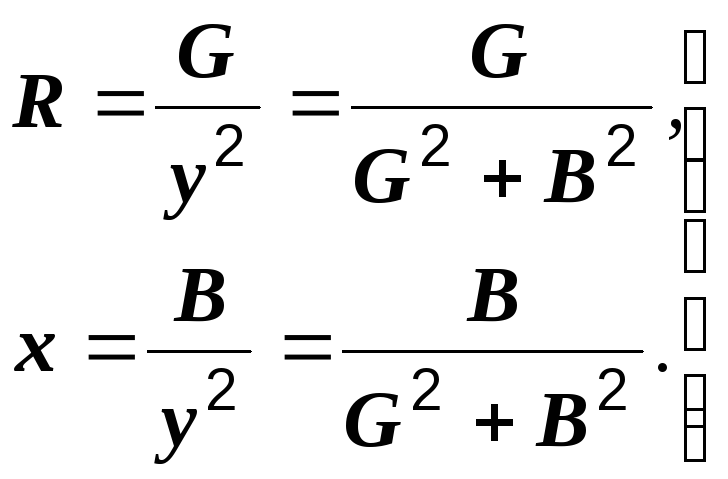 (2.32)
(2.32)