LC-цепь • ru.knowledgr.com

LC-цепь, также названная резонирующей схемой, схемой бака, или настроенной схемой, является электрической цепью, состоящей из катушки индуктивности, представленной письмом L и конденсатором, представленным письмом C, связанным вместе. Схема может действовать как электрический резонатор, электрический аналог настраивающейся вилки, храня энергию, колеблющуюся в резонирующей частоте схемы.

LC-цепи используются или для создания сигналов в особой частоте или для выбирания сигнал в особой частоте от более сложного сигнала. Они — ключевые компоненты во многих электронных устройствах, особенно радиооборудовании, используемом в схемах, таких как генераторы, фильтры, тюнеры и миксеры частоты.

LC-цепь — идеализированная модель, так как она предполагает, что нет никакого разложения энергии из-за сопротивления. Любое практическое внедрение LC-цепи будет всегда включать потерю, следующую из маленького но сопротивления отличного от нуля в пределах компонентов и соединяющую провода. Цель LC-цепи состоит в том, чтобы обычно колебаться с минимальным демпфированием, таким образом, сопротивление сделано максимально низким. В то время как никакая практическая схема не без потерь, это, тем не менее, поучительно, чтобы изучить эту идеальную форму схемы, чтобы получить понимание и физическую интуицию. Для модели схемы соединяющееся сопротивление см. схему RLC.

Терминология

LC-цепь с двумя элементами, описанная выше, является самым простым типом конденсаторной катушкой индуктивности сети (или сети LC). Это также упоминается как вторая LC-цепь заказа, чтобы отличить его от более сложного (более высокий заказ) сети LC с большим количеством катушек индуктивности и конденсаторов. У таких сетей LC больше чем с двумя реактансами может быть больше чем одна резонирующая частота.

Заказ сети — заказ рациональной функции, описывающей сеть в сложной переменной частоты s. Обычно заказ равен числу L и элементов C в схеме и в любом случае не может превысить это число.

Операция

LC-цепь, колеблющаяся в ее естественной резонирующей частоте, может сохранить электроэнергию. Посмотрите мультипликацию в праве. Конденсатор хранит энергию в электрическом поле (E) между его пластинами, в зависимости от напряжения через него, и катушка индуктивности хранит энергию в своем магнитном поле (B), в зависимости от тока через него.

Если заряженный конденсатор будет связан через катушку индуктивности, то ток начнет течь через катушку индуктивности, создавая магнитное поле вокруг этого и уменьшая обвинение, и поэтому напряжение, на конденсаторе. В конечном счете все обвинение на конденсаторе закончится, и напряжение через него достигнет ноля. Однако ток продолжится неизменный в соответствии с законом Фарадея индукции, которая требует, чтобы для тока, чтобы измениться в катушке индуктивности, напряжение было применено к нему (это походит на Первый Закон Ньютона для скорости, массы и силы). Никакая энергия не требуется для этого, если ток остается постоянным. Однако в то время как ток продолжает течь, конденсатор повторно приобретет обвинение противоположного знака, и его предельное напряжение повысится снова с обратной полярностью. Это применяет напряжение к катушке индуктивности, которая является теперь против ее тока, таким образом, ток теперь падает. Снова это в соответствии с Законом Фарадея. Падающий ток катушки индуктивности и возрастающее конденсаторное напряжение указывают на передачу энергии с катушки индуктивности на конденсатор. Это походит на движущуюся массу, сталкивающуюся с весной и сжимающую его. То, когда магнитное поле полностью рассеяло ток, на мгновение остановится, и обвинение будет снова сохранено в конденсаторе с полярностью напротив ее оригинальной. Это закончит половину цикла колебания. Процесс тогда начнется снова наоборот с током, текущим в противоположном направлении через катушку индуктивности.

Обвинение течет назад и вперед между пластинами конденсатора через катушку индуктивности. Энергия колеблется назад и вперед между конденсатором и катушкой индуктивности до (если не пополненный от внешней схемы), внутреннее сопротивление заставляет колебания вымереть. В большинстве заявлений настроенная схема — часть большей схемы, которая применяет переменный ток к нему, стимулируя непрерывные колебания. Если они будут в естественной колебательной частоте (Естественная частота), то резонанс произойдет. Действие настроенной схемы, известное математически как гармонический генератор, подобно маятнику, качающемуся назад и вперед или воде, хлюпающей назад и вперед в баке; поэтому схему также называют схемой бака.. Это формально походит на массово-весенний генератор; посмотрите Конденсаторную аналогию. Естественная частота (то есть, частота, в которой это будет колебаться, когда изолировано от любой другой системы, как описано выше) определены ценностями емкости и индуктивности. В типичных настроенных схемах в электронном оборудовании колебания очень быстры, тысячи к миллиардам времен в секунду.

Эффект резонанса

Резонанс происходит, когда LC-цепь ведут из внешнего источника в частоте, в которой индуктивные и емкостные реактансы равны в величине. Частоту, в которой это равенство держится для особой схемы, называют резонирующей частотой.

Резонирующая частота LC-цепи —

::

где L — индуктивность в henries, и C — емкость в farads. У угловой частоты есть единицы радианов в секунду.

Эквивалентная частота в единицах герц —

::

LC-цепи часто используются в качестве фильтров; отношение L/C — один из факторов, который определяет их «Q» и так селективность. Для ряда резонирующая схема с данным сопротивлением, чем выше индуктивность и ниже емкость, тем более узкий полоса пропускания фильтра. Для параллельной резонирующей схемы применяется противоположное. Позитивные отклики вокруг настроенной схемы («регенерация») могут также увеличить селективность (см. множитель Q и Регенеративную схему).

Колеблитесь настройка может обеспечить приемлемо широкую аудио полосу пропускания, все же хорошую селективность.

Заявления

У

эффекта резонанса LC-цепи есть много важных применений в обрабатывающих системах сигнала и коммуникационных системах.

1. Наиболее распространенное применение схем бака настраивает радио-передатчики и приемники. Например, когда мы настраиваем радио на особую станцию, LC-цепи установлены в резонансе для той особой несущей частоты.
2. Ряд резонирующая схема обеспечивает усиление напряжения.
3. Параллельная резонирующая схема обеспечивает текущее усиление.
4. Параллельная резонирующая схема может использоваться в качестве импеданса груза в выходных цепях усилителей RF. Из-за высокого импеданса, выгода усилителя максимальна в резонирующей частоте.
5. Обе параллели и ряд резонирующие схемы используются в нагревании индукции.

LC-цепи ведут себя как электронные резонаторы, которые являются ключевым компонентом во многих заявлениях:

• Приемный-Seeley дискриминатор

Решение для временного интервала

Законы Кирхгоффа

Согласно закону о напряжении Кирхгоффа, напряжение через конденсатор, V, плюс напряжение через катушку индуктивности, V должно равняться нолю:

::

Аналогично, согласно действующему законодательству Кирхгоффа, ток через конденсатор равняется току через катушку индуктивности:

::

От учредительных отношений для элементов схемы мы также знаем это

::

и

::

Отличительное уравнение

Реконструкция и замена дают второе уравнение дифференциала заказа

::

Параметр ω, резонирующая угловая частота, определен как:

::

Используя это может упростить отличительное уравнение

::

Связанный полиномиал —

::

Таким образом,

::

или

::

:::: где j — воображаемая единица.

Решение

Таким образом полное решение отличительного уравнения —

::

и может быть решен для A и B, рассмотрев начальные условия.

Так как показательное сложно, решение представляет синусоидальный переменный ток.

Начиная с электрического тока я — физическое количество, это должно быть с реальным знаком. В результате можно показать, что константы A и B должны быть сложными, спрягается:

::

Теперь, позвольте

::

Поэтому,

::

Затем, мы можем использовать формулу Эйлера, чтобы получить реальную синусоиду с амплитудой I, угловая частота ω = (LC), и угол фазы.

Таким образом получающееся решение становится:

::

и

::

Начальные условия

Начальные условия, которые удовлетворили бы этот результат:

::

и

::

Серийная LC-цепь

В серийной конфигурации LC-цепи катушка индуктивности L и конденсатор C связаны последовательно, как показано здесь. Полное напряжение v через открытые терминалы является просто суммой напряжения через катушку индуктивности и напряжения через конденсатор. Ток i в положительный терминал схемы равен току и через конденсатор и через катушку индуктивности.

:

:

Резонанс

Индуктивная величина реактанса увеличения как частота увеличиваются, в то время как емкостная величина реактанса уменьшается с увеличением частоты. В одной особой частоте эти два реактанса равны в величине, но напротив в знаке; ту частоту называют резонирующей частотой для данной схемы.

Следовательно, в резонансе:

:

:

Решая для, у нас есть

:

который определен как резонирующая угловая частота схемы.

Преобразовывая угловую частоту (в радианах в секунду) в частоту (в герц), у каждого есть

:

В серийной конфигурации, X и X уравновешивают друг друга. В реальных, а не идеализированных компонентах ток отклонен, главным образом сопротивлением катушки windings. Таким образом ток, поставляемый ряду резонирующая схема, является максимумом в резонансе.

• В пределе, поскольку ток максимален. Импеданс схемы минимален. В этом государстве схему называют кругом получателей.
• Для

• Поскольку. Следовательно, схема индуктивная.

Импеданс

В серийной конфигурации происходит резонанс, когда сложный электрический импеданс схемы приближается к нолю.

Сначала рассмотрите импеданс серийной LC-цепи. Полный импеданс дан суммой индуктивных и емкостных импедансов:

::

Написание индуктивного импеданса как Z = jωL и емкостного импеданса как Z = (jωC) и замена дает

::.

Написание этого выражения под общим знаменателем дает

::.

Наконец, определяя естественную угловую частоту как

::

импеданс становится

::.

Нумератор подразумевает, что в пределе как, полный импеданс Z будет нолем и иначе отличный от нуля. Поэтому серийная LC-цепь, когда связано последовательно с грузом, будет действовать как полосовой фильтр, имеющий нулевой импеданс в резонирующей частоте LC-цепи.

Параллельная LC-цепь

В параллельной конфигурации катушка индуктивности L и конденсатор C связаны параллельно, как показано здесь. Напряжение v через открытые терминалы равно и напряжению через катушку индуктивности и напряжению через конденсатор. Общий ток я текущий в положительный терминал схемы равен сумме тока, текущего через катушку индуктивности и ток, текущий через конденсатор.

:

:

Резонанс

Позвольте R быть внутренним сопротивлением катушки. Когда X равняется X, реактивные токи ветви равны и противоположны. Следовательно они уравновешивают друг друга, чтобы дать ток минимума в главной линии. Так как общий ток минимален в этом государстве, полный импеданс максимален.

Резонирующая частота, данная:.

Обратите внимание на то, что любой реактивный ток ветви не минимален в резонансе, но каждому дает отдельно, деля исходное напряжение (V) реактанс (Z). Следовательно I=V/Z, согласно закону Ома.

• В f ток линии минимален. Полный импеданс максимален. В этом государстве схему называют rejector схемой.
• Ниже f схема индуктивная.
• Выше f схема емкостная.

Импеданс

Тот же самый анализ может быть применен к параллельной LC-цепи. Полным импедансом тогда дают:

::

и после замены и и упрощение, дает

::

который далее упрощает до

::

где

::

Отметьте это

::

но поскольку все другие ценности импеданса конечно. Параллельная LC-цепь, связанная последовательно с грузом, будет действовать как заграждающий фильтр, имеющий бесконечный импеданс в резонирующей частоте LC-цепи. Параллельная LC-цепь, связанная параллельно с грузом, будет действовать как полосовой фильтр.

История

Первые доказательства, что конденсатор и катушка индуктивности могли произвести электрические колебания, были обнаружены в 1826 французским ученым Феликсом Савари. Он нашел, что, когда Лейденская фляга была освобождена от обязательств через проводную рану вокруг железной иглы, иногда иглу оставили намагниченной в одном направлении и иногда в противоположном направлении. Он правильно вывел, что это было вызвано заглушенным колеблющимся током выброса в проводе, который полностью изменил намагничивание иглы назад и вперед, пока это не было слишком маленьким, чтобы иметь эффект, оставив иглу намагниченной в случайном направлении. Американский физик Джозеф Генри повторил эксперимент Савари в 1842 и пришел к тому же самому заключению, очевидно независимо. Британский ученый Уильям Томсон (лорд Келвин) в 1853 показал математически, что выброс Лейденской фляги через индуктивность должен быть колебательным, и получил свою резонирующую частоту. Британский радио-исследователь Оливер Лодж, освобождая от обязательств большую батарею Лейденских фляг через длинный провод, создал настроенную схему с ее резонирующей частотой в диапазоне звуковых частот, который произвел музыкальный тон из искры, когда это было освобождено от обязательств. В 1857 немецкий физик Беренд Вильгельм Феддерсен сфотографировал искру, произведенную резонирующей Лейденской схемой фляги во вращающемся зеркале, представив видимые свидетельства колебаний. В 1868 шотландский физик Джеймс клерк Максвелл вычислил эффект применения переменного тока к схеме с индуктивностью и емкостью, показав, что ответ максимален в резонирующей частоте. Первый пример электрической кривой резонанса был издан в 1887 немецким физиком Генрихом Херцем в его новаторской статье об открытии радиоволн, показав длину искры, доступной от его промежутка искры датчики резонатора LC как функция частоты.

Одной из первых демонстраций резонанса между настроенными схемами был Лодж «syntonic фляги» эксперимент приблизительно в 1889. Он поместил две резонирующих схемы друг рядом с другом, каждый состоящий из Лейденской фляги, связанной с приспосабливаемой катушкой с одним поворотом с промежутком искры. Когда высокое напряжение от катушки индукции было применено к одной настроенной схеме, создав искры и таким образом колеблющийся ток, искры были взволнованы в другой настроенной схеме только, когда схемы были приспособлены к резонансу. Лодж и некоторые английские ученые предпочли термин «syntony» для этого эффекта, но термин «резонанс», в конечном счете прикрепленный. Первое практическое применение для LC-цепей было в 1890-х в передатчиках радио промежутка искры, чтобы позволить приемнику и передатчику быть настроенным на ту же самую частоту. Первый патент для системы радиосвязи, которая позволила настраиваться, был подан Лоджем в 1897, хотя первые практические системы были изобретены в 1900 итальянским радио-пионером Гульельмо Маркони.

См. также

• ЕМКОСТНО-РЕЗИСТИВНАЯ схема

Внешние ссылки

То

---

Резонанс в последовательном и параллельном LC контуре. » Хабстаб

Чтобы понять причину возникновения резонанса необходимо разобраться как течёт ток через конденсатор и катушку индуктивности.
При протекании тока через катушку индуктивности напряжение опережает ток. Давайте рассмотрим этот процесс подробнее, когда напряжение на концах катушки максимально, ток через катушку не течет, по мере уменьшения напряжения, ток увеличивается и когда напряжение на концах катушки равно нулю, ток через катушку максимален. Далее, напряжение уменьшается и достигает минимума, ток при этом равен нулю. Из этого можно сделать вывод, что ток через катушку максимален, когда напряжение на её концах равно нулю и ток равен нулю, когда напряжение на её концах максимально. Таким образом, если сопоставить графики изменения напряжения и тока , создаётся впечатление, что напряжение опережает ток на 90 градусов. Это можно увидеть на рисунке ниже.

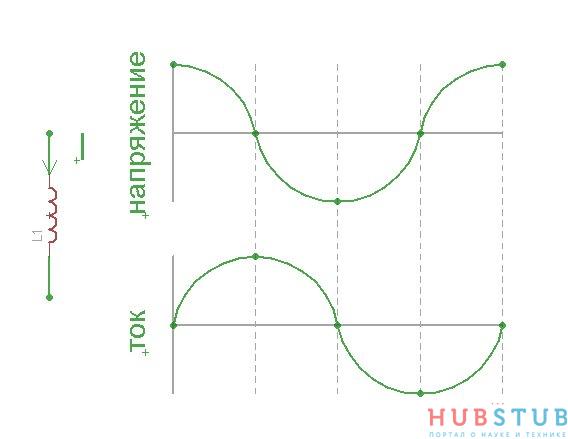
Совсем противоположно катушке индуктивности ведет себя конденсатор. Когда напряжение на концах конденсатора равно нулю, ток через него максимален, по мере зарядки конденсатора ток через него уменьшается, это связано с тем, что разность потенциалов между конденсатором и источником напряжения уменьшается, а чем меньше разность потенциалов, тем меньше ток. Когда конденсатор полностью заряжен ток через него не течет так, как нет разности потенциалов. Напряжение начинает уменьшаться и становится равно нулю, при этом ток максимален только течет в другом направлении, далее напряжение достигает минимума и ток через конденсатор снова не течет. Делаем вывод, что ток через конденсатор максимальный когда напряжение на его обкладках равно нулю и ток равен нулю когда напряжение на конденсаторе минимально. Если сопоставить графики изменения тока и напряжение, создается впечатление, что ток опережает напряжение на 90 градусов. Это можно увидеть на рисунке ниже.

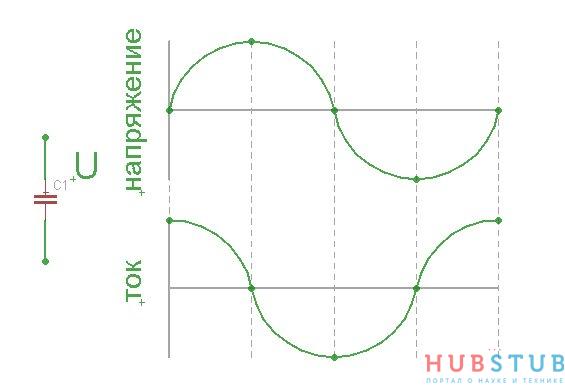
На резонансной частоте для контура, состоящего из конденсатора и катушки индуктивности, неважно параллельный он или последовательный, их сопротивления равны и сдвиг фаз между напряжением и током равен нулю. Ведь действительно если подумать, то в конденсаторе ток опережает напряжение на 90 градусов, то есть +90 градусов, а в катушке индуктивности ток отстает от напряжения на 90 градусов, то есть -90 градусов и если сложить их получится нуль. Для пары, конденсатор и катушка индуктивности параллельный и последовательный резонанс возникают на одной и той же частоте.

Давайте рассмотрим резонанс в последовательном колебательном контуре.

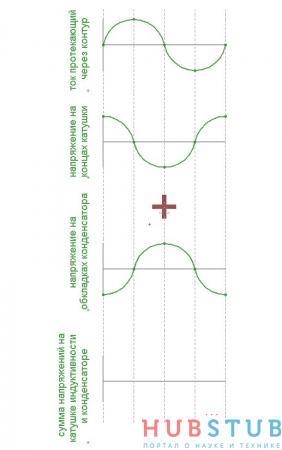
На верхнем графике изображена зависимость тока от времени, протекающего через контур, ниже два графика это напряжения, на конденсаторе и катушке, самый нижний это сумма напряжений на катушке и конденсаторе. Видно, что суммарное напряжение на конденсаторе и катушке индуктивности равно нулю, также говорят, что сопротивление последовательного колебательного контура на резонансной частоте стремится к нулю.
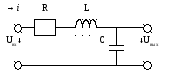
Давайте соберем простую схему, изображенную на рисунке.

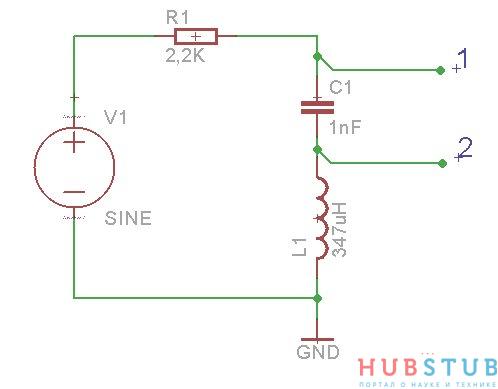
Сопротивление резистора должно быть больше выходного сопротивления генератора, то есть больше 50 Ohm, я взял первый попавшийся.
Расчетная резонансная частота такого контура 270 KHz, но так как номиналы имеют определенный допуск, который обычно указывается в процентах, придется ее подобрать. Подбирать будем исходя из того, что сопротивления катушки индуктивности и конденсатора на резонансной частоте равны, а так как они соединены последовательно, то равны и падения напряжений. Первый канал показывает напряжение на контуре, второй канал напряжение на катушке, канал Math показывает разность между первым и вторым каналом, а по сути напряжение на конденсаторе. Причина по которой, я не подключил щуп осциллографа параллельно конденсатору, будет подробно описана в следующей статье. Если кратко, то есть правило подключать земляной крокодил только к земле, если осциллограф и исследуемая схема питаются от бытовой сети и имеют заземление. Делается это, для того чтобы не спалить исследуемую схему и осциллограф.


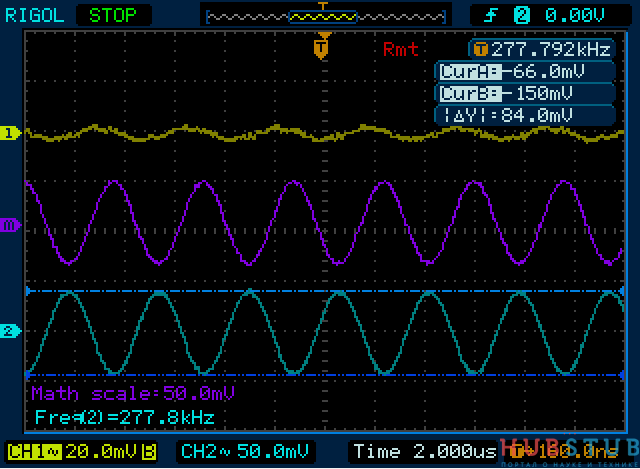
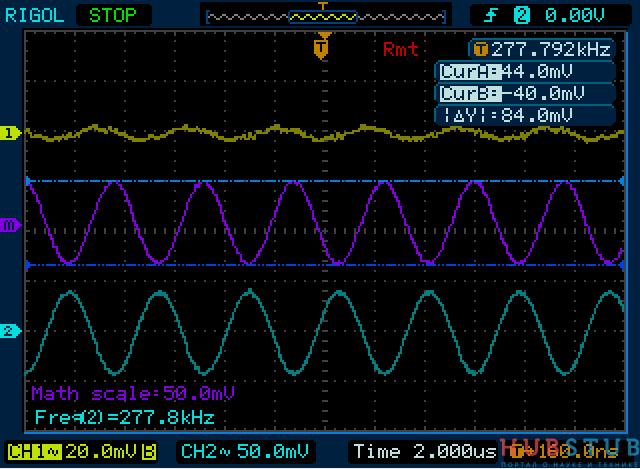
На осциллограммах видно, что на резонансной частоте падение напряжения на катушке и конденсаторе равны и противоположны по знаку, а суммарное падение напряжения на контуре стремится к нулю. В последовательном колебательном контуре на резонансной частоте напряжение на катушке и конденсаторе выше чем на генераторе. Давайте увеличим частоту и посмотри что изменится.

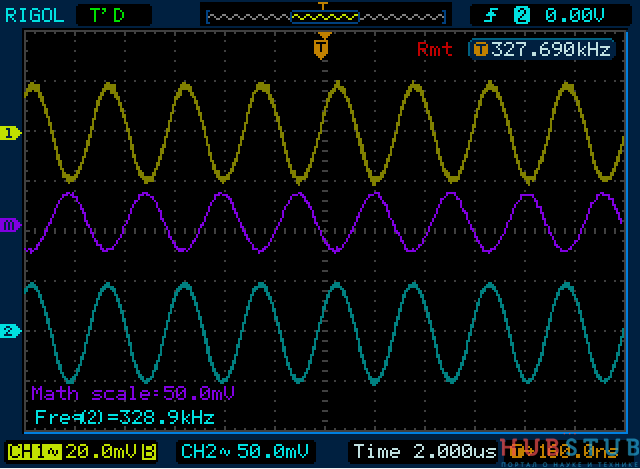
Видим, что напряжение на катушке увеличилось потому, что увеличилось её сопротивление, так как оно прямо пропорционально зависит от частоты. Напряжение на конденсаторе уменьшилось потому, что его сопротивление с ростом частоты уменьшается. Теперь уменьшим частоту.

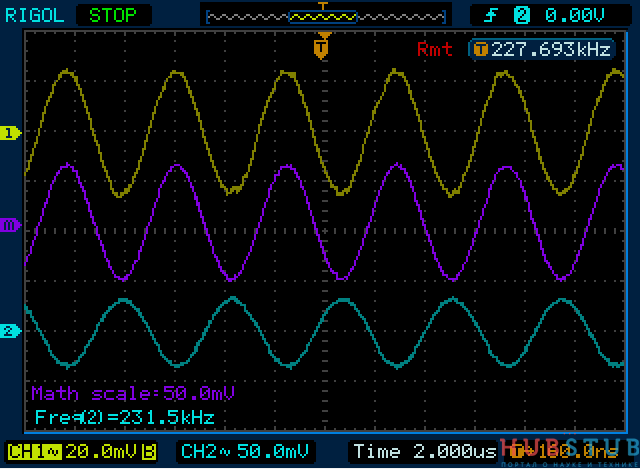
Видим, что напряжение на конденсаторе увеличилось, а на катушке уменьшилось, также надо отметить, что разность фаз между сигналами равна 180 градусам.

Давайте теперь рассмотрим резонанс в параллельном контуре, ситуация аналогичная с последовательным контуром, только в последовательном мы рассматривали напряжения, а в параллельном будем рассматривать токи.

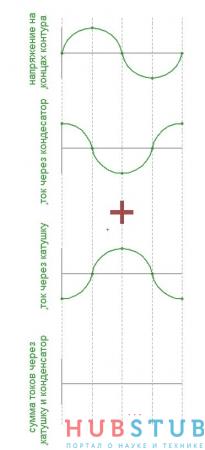
Видим, что токи сдвинуты относительно друг друга на 180 градусов, а их сумма равна нулю, то есть ток через контур не течет, а его сопротивление стремится к бесконечности. Параллельный колебательный контур используют как полосно-заграждающий фильтр, радиолюбители называют его фильтр- пробка. Он не пропускает напряжение частота которого равна его резонансной частоте. Давайте соберем простую схему, изображенную на картинке ниже и посмотрим как будет изменяться напряжение на концах контура в зависимости от частоты.

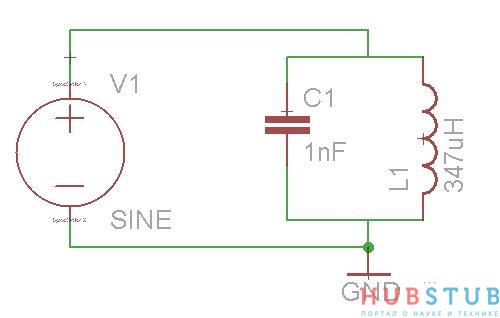
Так как конденсатор и индуктивность те же, что и в прошлом эксперименте резонансная частота контура та же.

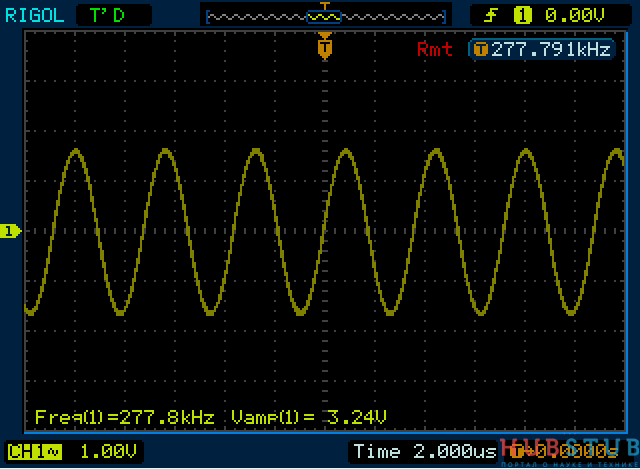
На резонансной частоте сопротивление контура стремится к бесконечности, следовательно и напряжение будет максимально. Давайте уменьшим частоту.

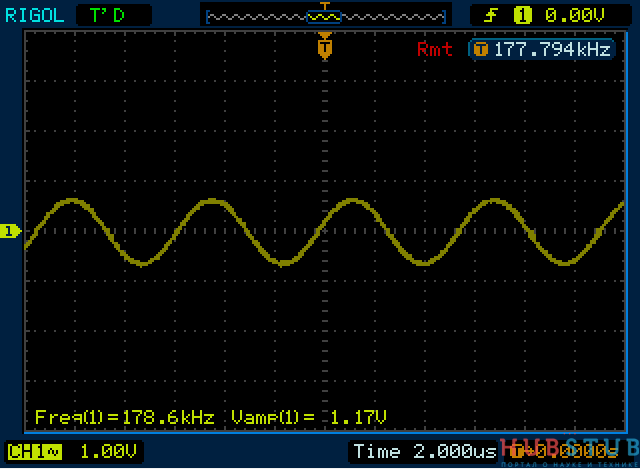
Видим, что напряжение на контуре уменьшилось, произошло это потому, что сопротивление катушки уменьшилось и она зашунтировала конденсатор.
Теперь давайте увеличим частоту.

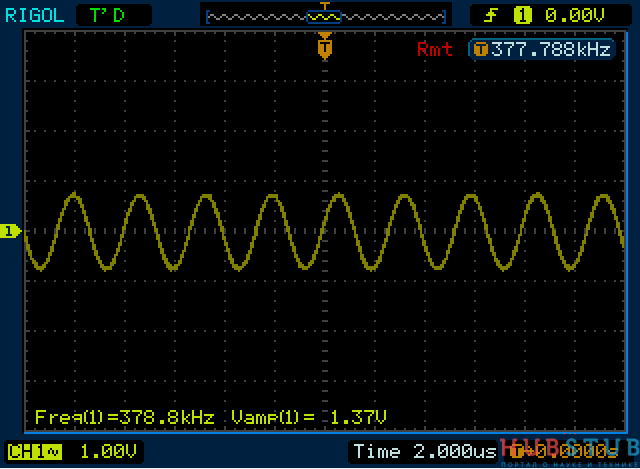
С ростом частоты сопротивление конденсатора уменьшилось и он зашунтировал катушку.
Пожалуй, это всё, что хотелось рассказать про резонанс.

Тема занятия 5: Колебательный контур.

5.1 Идеальный колебательный контур.

Колебательный контур называется идеальным, если он состоит из катушки и емкости и в нем нет сопротивления потерь.

Р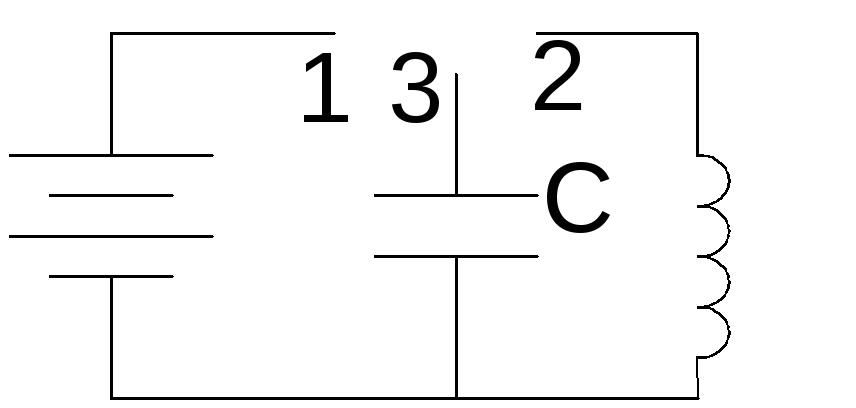ассмотрим физические процессы в следующей цепи:

1 Ключ стоит в положении 1. Конденсатор начинает заряжаться, от источника напряжения и в нем накапливается энергия электрического поля,

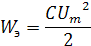
т.е.конденсатор становится источником электрической энергии.

2. Ключ в положении 2. Конденсатор начнет разряжаться. Электрическая энергия, запасенная в конденсаторе переходит в энергию магнитного поля катушки.

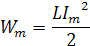
Ток в цепи достигает максимального значения(точка 1). Напряжение на обкладках конденсатора уменьшается до нуля.

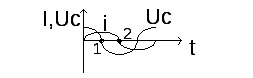
В период от точки 1 до точки 2 ток в контуре уменьшается до нуля, но как только он начинает уменьшатся , то уменьшается магнитное поле катушки и в катушке индуцируется ЭДС самоиндукции, который противодействует уменьшению тока, поэтому он уменьшается до нуля не скачкообразно, а плавно. Так как возникает ЭДС самоиндукции, то катушка становится источником энергии. От этой ЭДС конденсатор начинает заряжаться, но с обратной полярностью (напряжение конденсатора отрицательное) (в точке 2 конденсатор вновь заряжается).

Вывод: в цепи LC происходит непрерывное колебание энергии между электрическим и магнитным полями, поэтому такая цепь называется колебательным контуром.

Получившиеся колебания называются свободнымиилисобственными, поскольку они происходят без помощи постороннего источника электрической энергии, внесенной ранее в контур (в электрическое поле конденсатора). Так как емкость и индуктивность идеальны (нет сопротивления потерь) и энергия из цепи не уходит, амплитуда колебаний с течением времени не меняется и колебания будут

незатухающими.

Определим угловую частоту свободных колебаний:

Используем равенство энергий электрического и магнитного полей

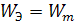
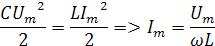
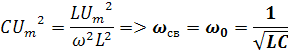
,где ώ угловая частота свободных колебаний.

[ ώ

]=1/с

f0=ώ/2π [Гц].

Период свободных колебаний Т0=1/f.

Частоту свободных колебаний называют частотой собственных колебаний контура.

Из выражения: ώ²LC=1получимώL=1/Cώ, следовательно, при токе в контуре с частотой свободных колебаний индуктивное сопротивление равно емкостному сопротивлению.

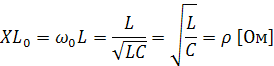
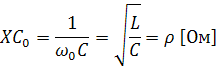
Характеристические сопротивления.

Индуктивное или емкостное сопротивление в колебательном контуре при частоте свободных колебаний называется

характеристическим сопротивлением.

Характеристическое сопротивление вычисляется по формулам:

5.2 Реальный колебательный контур

Реальный колебательный контур обладает активным сопротивлением, поэтому при воздействии в контуре свободных колебаний энергия предварительно заряженного конденсатора постепенно тратится, преобразуясь в тепловую.

Свободные колебания в контуре являются затухающими, так как в каждый период энергия уменьшается и амплитуда колебаний в каждый период будет уменьшаться.

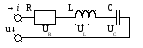
Рисунок — реальный колебательный контур.

Угловая частота свободных колебаний в реальном колебательном контуре :

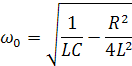
Если R=2… , то угловая частота равна нулю, следовательно свободные колебания в контуре не возникнут.

Таким образом колебательным контуромназывается электрическая цепь состоящая из индуктивности и емкости и обладающая малым активным сопротивлением, меньшим удвоенного характеристического сопротивления, что обеспечивает обмен энергией между индуктивностью и емкостью.

В реальном колебательном контуре свободные колебания затухают тем быстрее, чем больше активное сопротивление.

Для характеристики интенсивности затухания свободных колебаний используется понятие «затухание контура» — отношение активного сопротивления к характеристическому.

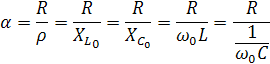
На практике используют величину, обратную затуханию – добротность контура.

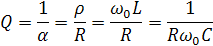
Для получения незатухающих колебаний в реальном колебательном контуре необходимо в течение каждого периода колебаний пополнять электрическую энергию на активном сопротивлении контура в такт с частотой собственных колебаний. Это осуществляется с помощью генератора.

Если подключить колебательный контур к генератору переменного тока, частота которого отличается от частоты свободных колебаний контура, то в цепи протекает ток с частотой равной частоте напряжения генератора. Эти колебания называют вынужденным.

Если частота генератора отличается от собственной частоты контура, то такой колебательный контур является ненастроенным относительно частоты внешнего воздействия, если же частоты совпадают, то настроенным.

Задача: Определить индуктивность , угловую частоту контура, характеристическое сопротивление, если емкость колебательного контура 100 пФ, частота свободных колебаний 1,59 МГц.

Решение:

Тестовые задания:

Добротность колебательного контура определяется по формуле:	Отношение активного сопротивления к характеристическому Величина обратная затуханию
Какие колебания называются свободными	непрерывные колебания энергии между электрическим и магнитным полями колебания, амплитуда которых в каждый период времени уменьшается

Тема занятия 8: РЕЗОНАНС НАПРЯЖЕНИЙ

Резонанс напряжений – явление возрастания напряжений на реактивных элементах, превышающих напряжение на зажимах цепи при максимальном токе в цепи, которое совпадает по фазе с входным напряжением.

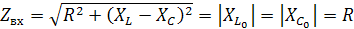
Условия возникновения резонанса:

1. Последовательное соединение LиCс генератором переменного тока;

2. Частота генератора должна быть равна частоте собственных колебаний контура , при этом характеристические сопротивления равны;

3. Сопротивление должно быть меньше, чем 2ρ, так как только в этом случае в цепи возникнут свободные колебания, поддерживаемые внешним источником.

Полное сопротивление цепи:

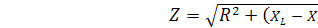=R,

так как равны характеристические сопротивления. Следовательно, при резонансе цепь носит чисто активный характер, значит, входное напряжение, и ток в момент резонанса совпадают по фазе. Ток принимает максимальное значение.

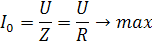
При максимальном значении тока напряжение на участках L и C будут большими и равными между собой.

Напряжение на зажимах цепи:

.

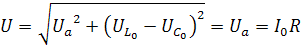Рассмотрим следующие соотношения:

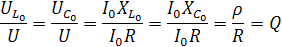, следовательно

.

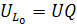
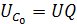Q –добротность контура –при резонансе напряжения показывает, во сколько раз напряжение на реактивных элементах больше входного напряжения генератора, питающего цепь. При резонансе коэффициент передачи последовательного колебательного контура

резонанса.

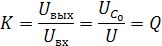
Пример:

Если добротность равна 100, напряжение на зажимах 1В, то

Uc=Ul=QU=100В,

то есть напряжение на зажимах меньше напряжений на емкости и индуктивности. Это явление называется резонансом напряжений

При резонансе, коэффициент передачи равен добротности.

Построим векторную диаграмму напряжения

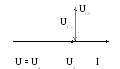
Напряжение на емкости равно напряжению на индуктивности, следовательно напряжение на сопротивлении равно напряжению на зажимах и совпадает по фазе с током.

Рассмотрим энергетический процесс в колебательном контуре:

В цепи имеется обмен энергии между электрическим полем конденсатора и магнитным полем катушки. К генератору энергия катушки не возвращается. От генератора в цепь поступает такое количество энергии, которое тратится на резисторе. Это необходимо для того, чтобы в контуре наблюдались незатухающие колебания. Мощность в цепи только активная.

Докажем это математически:

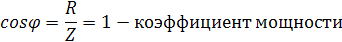
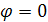
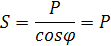, полная мощность цепи, которая равна активной мощности.

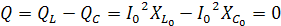, реактивная мощность.

8.1 Резонансная частота. Расстройка.

В цепи, содержащей реактивные элементы, произойдет резонанс, если цепь имеет резистивный характер:

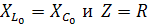
Lώ=l/ώC, следовательно

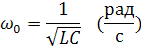
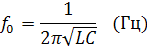, угловая резонансная частота.

Из формулы видно, что резонанс наступает, если частота питающего генератора равна собственным колебаниям контура.

При работе с колебательным контуром необходимо знать, совпадает ли частота генератора и частота собственных колебаний контура. Если частоты совпадают, то контур остается настроенным в резонанс, если не совпадает – то в контуреприсутствует расстройка.

Настроить колебательный контур в резонанс можно тремя способами:

1 Изменять частоту генератора , при значениях емкости и индуктивности const, то есть изменяя частоту генератора мы подстраиваем эту частоту под частоту колебательного контура

2 Изменять индуктивность катушки, при частоте питания и емкости const;

3 Изменять емкость конденсатора , при частоте питания и индуктивности const.

Во втором и третьем способе изменяя частоту собственных колебаний контура, подстраиваем ее под частоту генератора.

При ненастроенном контуре частота генератора и контура не равны, то есть присутствует расстройка.

Расстройка – отклонение частоты от резонансной частоты.

Существует три вида расстройки:

1. Абсолютная – разность между данной частотой и резонансной

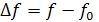
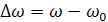
2. Обобщенная – отношение реактивного сопротивления к активному:

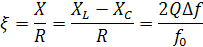
3. Относительная – отношение абсолютной расстройки к резонансной частоте:

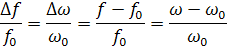
При резонансе все расстройки равны нулю, если частота генератора меньше частоты контура, то расстройка считается отрицательной,

Если больше – положительной.

Таким образом добротность характеризует качество контура, а обобщенная расстройка- удаленность от резонансной частоты.

8.2 Построение зависимостейX, X_L, X_C отf.

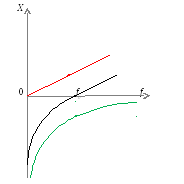
Задачи:

1. Сопротивление контура 15 Ом, индуктивность 636 мкГн, Емкость 600 пФ, напряжение питающей сети 1,8 В. Найти собственную частоту контура, затухание контура, характеристическое сопротивление, ток, активную мощность, добротность, напряжение на зажимах контура.

Решение:

2. Напряжение на зажимах генератора 1 В, частота питающей сети 1 МГц, добротность 100, емкость 100 пФ. Найти: затухание, характеристическое сопротивление, активное сопротивление, индуктивность, частоту контура, ток, мощность, напряжения на емкости и индуктивности.

Решение:

Тестовые задания:

Отношение реактивного сопротивления к активному это :	А) Абсолютная расстройка; Б) Обобщенная расстройка; В) Относительная расстройка.

Тема занятия 9 : Входные и передаточные АЧХ и ФЧХ последовательного колебательного контура.

9.1 Входные АЧХ и ФЧХ.

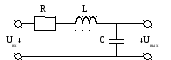
В последовательном колебательном контуре:

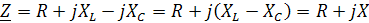, где

R – активное сопротивление;

X – реактивное сопротивление.

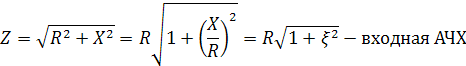
Учитывая, ч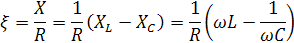то

,то

ώ=0 ζ=-∞ Z=∞

ώ=ώ۪۪ζ=0 Z=R

ώ=∞ ζ=∞ Z=∞, следовательно график имеет вид:

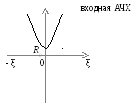
Из графика видно, что контур обладает наименьшим сопротивлением на резонансной частоте, при увеличении расстройки сопротивление увеличивается.

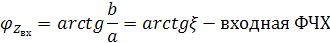
ζ=0 φ=0 R

ζ=1 φ=45° RL

ζ=-1 φ=-45° RC

ζ=∞ φ=90° L

ζ=-∞ φ=-90° C.

Построим график:

На участке ζ=[-1;1]

ФЧХ имеет линейный

характер.

1. На участке ζ=[-∞;0] — цепь носит активно-емкостной характер;

2. На участке ζ=[0;∞]- цепь носит frnbdyj-индуктивный характер;

3. При ζ=0 — цепь носит активный характер;

2. Передаточные АЧХ и ФЧХ

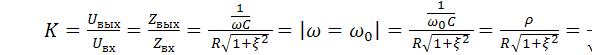
передаточная характеристика АЧХ

ζ=-∞ k=0

ζ=0 k=Q

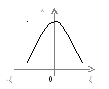ζ=∞ k=0

Построим график зависимости:

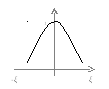
Разделим k∕kои получим передаточную

характеристику АЧХ в относительных

единицах, которая имеет вид:

Чтобы построить передаточную ФЧХ необходимо: построить входную ФЧХ, взять её зеркальное ее отображение и сместить на -90°.

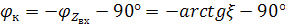
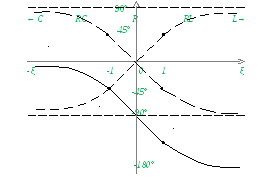
На участке ζ=[-1;1] – передаточная ФЧХ носит линейный характер.

Калькулятор расчёта полосно-заграждающих режекторных фильтров на LC цепях

Что такое режекторный фильтр (он же полосно-заграждающий, он же — фильтр-пробка) и с чем его едят, мы определились на предыдущей странице, рассматривая пассивные и активные режекторные RC-фильтры.

Так же, как и в случаях с НЧ, ВЧ и полосовыми собратьями, LC режекторные фильтры обладают рядом достоинств, таких как: высокая стабильность, низкий уровень собственных шумов, а также возможность работы с широким спектром сигналов, включая СВЧ диапазоны.

Простейший представитель режекторного LC-фильтра 2-го порядка представлен на Рис.1.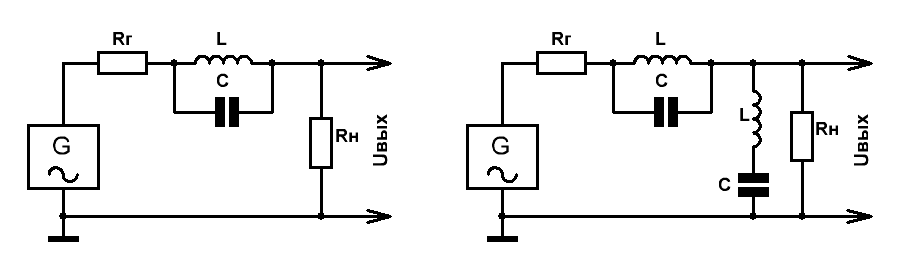

Рис.1 Рис.2

Логика работы такого фильтра предельно проста.
На резонансной частоте fо= 1/2π√LС сопротивление параллельного колебательного контура, образованного катушкой индуктивности L и конденсатором C, принимает максимальное значение, соответственно максимальное значение принимает и коэффициент подавления сигнала на этой частоте.
Глубина режекции (подавления частоты fo) этого фильтра при работе на согласованную нагрузку, равную характеристическому сопротивлению колебательного контура ρ = √L/C , достигает 45 дБ.

На Рис.2 представлена схема Г-образного режекторного фильтра 4-го порядка.
Принцип работы этого фильтра основан на использовании резонансов напряжений и токов в последовательных и параллельных колебательных контурах. На частоте резонанса сопротивление параллельного плеча оказывается максимальным, а последовательного – минимальным, что и соответствует наибольшему затуханию цепи.
Глубина режекции в данной схеме уже может составлять величину 90 дБ.

Приведём таблицу для расчёта элементов этих фильтров.
Не забываем, что характеристическое сопротивление фильтра ρ должно равняться Rг =Rн.

ТАБЛИЦА РАСЧЁТА ЭЛЕМЕНТОВ РЕЖЕКТОРНЫХ LC- ФИЛЬТРОВ 2-го и 4-го ПОРЯДКОВ

Для получения больших значений подавления центральной частоты (глубины режекции) используют два или более Г-образных звеньев, соединяя их последовательно, чтобы образовать Т-образное звено, или П-образное звено.
На Рис.3 приведены схемы типовых полосно-заграждающих LC-фильтров 6-го порядка Т-образной (слева) и П-образной (справа) структур с глубиной режекции — около 130 дБ.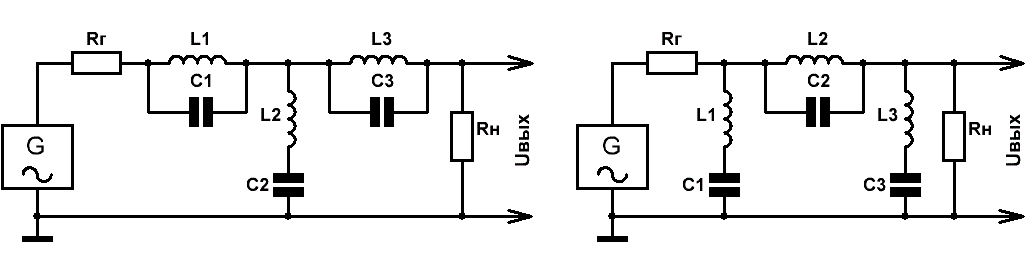

Рис.3

Ничего не изменилось — последовательная ветвь обладает минимальным полным сопротивлением и оказывает шунтирующее воздействие на центральной частоте диапазона. Ее полное сопротивление начинает увеличиваться по обе стороны от частоты резонанса.
Параллельная же ветвь на центральной частоте имеет максимальное сопротивление, и оно уменьшается по обе стороны резонанса.

Центральная частота режекции равна fо= 1/2π√LС, характеристическое сопротивление ρ = √L/C , а значения частотозадающих элементов рассчитываются исходя из следующих равенств:
L₁ = L₃ = L/2,  L₂ = L,  C₁ = C₃ = C×2,  C₂ = C для Т-образного фильтра,
L₁ = L₃ = L×2,  L₂ = L,  C₁ = C₃ = C/2,  C₂ = C для П-образного фильтра.

Приведём таблицу для расчёта элементов и этих фильтров.

ТАБЛИЦА РАСЧЁТА ЭЛЕМЕНТОВ РЕЖЕКТОРНЫХ Т- и П-образных LC- ФИЛЬТРОВ

Ширина полосы задержания представленных режекторных LC-фильтров составляет величину, примерно равную 50% от значения центральной частоты fo.

 

lc-цепочка 🎓 ⚗ перевод с русского на английский

Цепочка уравнений Боголюбова — (цепочка ББГКИ, иерархия ББГКИ, цепочка уравнений Боголюбова  Борна  Грина  Кирквуда  Ивона)  система уравнений эволюции системы, состоящей из большого числа тождественных взаимодействующих частиц, заключенных в некотором …   Википедия

Цепочка ББГКИ — Цепочка уравнений Боголюбова (цепочка ББГКИ, ББГКИ иерархия, цепочка уравнений Боголюбова  Борна  Грина  Кирквуда  Ивона)  система уравнений эволюции системы, состоящей из большого числа тождественных взаимодействующих частиц, заключенных в… …   Википедия

Цепочка ценности — (англ. Value chain)  это инструмент стратегического анализа, направленный на подробное изучение деятельности организации с целью стратегического планирования. Идея цепочки ценности была предложена Майклом Портером в книге «Конкурентное… …   Википедия

ЦЕПОЧКА — ЦЕПОЧКА, цепочки, жен. 1. Маленькая и тонкая цепь. Цепочка для часов. 2. Группа бойцов, двигающихся друг за другом в какой нибудь линии (воен.). Цепочка конных разъездов. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 …   Толковый словарь Ушакова

Цепочка снов — явление, при котором человек видит несколько снов, пронизанных одной сюжетной линией, с одними и теми же персонажами, в одних и тех же или разных условиях. Может происходить в течение одного периода сна, например ночью. В отличие от обычного… …   Википедия

цепочка — 1. цепка (прост.) 2. см. вереница Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Александрова. 2011. цепочка сущ. • …   Словарь синонимов

Цепочка — см. Цепь, цепочка, оковы, узы …   Библейская энциклопедия Брокгауза

Цепочка доказательств — Ein Mann wie eine Waffe Жанр триллер Режиссёр Майкл Роуитц Автор сценария Тимо Берндт В главных ролях Клаус Лёвич Дженифер Нитч Майкл Бренднер Оливье Коритт …   Википедия

Цепочка на ноге — Цепочка на ногe и кольцо на пальце Цепочка на ноге  разновидность украшения, в частности ювелирного, которое носят на лодыжке. Цепочки на лодыжке и кольца на пальцах ноги, а также их комбинация многие века используются женщинами в Египте и… …   Википедия

Цепочка стоимости — (added value chain) вновь созданные на каждом этапе воспроизводственного процесса стоимости (чистая продукция, добавленная стоимость). Подробнее см. Стоимостная цепочка …   Экономико-математический словарь

цепочка стоимости — Вновь созданные на каждом этапе воспроизводственного процесса стоимости (чистая продукция, добавленная стоимость). Подробнее см. Стоимостная цепочка. [http://slovar lopatnikov.ru/] Тематики экономика EN added value chain …   Справочник технического переводчика

Цепочка пор. Линейная пористость — Группа пор в сварном шве, расположенная в линию, параллельно оси сварного шва, рис. А.41 Источник: РД 03 606 03: Инструкция по визуальному и измерительному контролю Цепочка пор. Линейная пористость (2014) Группа пор в сварном шве, расположенная в …   Словарь-справочник терминов нормативно-технической документации

Цепочка —  Цепочка  ♦ Сhaоne    Традиционная метафора для обозначения непрерывной серии. Именно это имеет в виду Декарт, упоминая в своем «Рассуждении о методе» «длинные цепочки простых и ясных доводов, которыми так любят пользоваться геометры». Об этом же …   Философский словарь Спонвиля

Цепочка «производство — потребности потребителя» — Цепочка производство потребности …   Словарь терминов антикризисного управления

ЦЕПОЧКА — ЦЕПОЧКА, и, жен. 1. Маленькая тонкая цепь (в 1 знач.), а также вообще изделие, имеющее вид цепи. Золотая ц. Ц. для часов. Дверная ц. (запор, позволяющий слегка приоткрыть дверь). 2. Ряд, вереница людей, предметов. Растянуться в цепочку. Идти… …   Толковый словарь Ожегова

ЦЕПОЧКА ЦЕННОСТИ — ЦЕПОЧКА ЦЕННОСТИ, совокупность видов деятельности фирмы (основных и поддерживающих), направленных на создание потребительской ценности, благодаря которой покупатель приобретает товар или услугу. Концепция цепочки ценности была предложена… …   Энциклопедический словарь

цепочка — это… Что такое LC-цепочка?

Цепочка уравнений Боголюбова — (цепочка ББГКИ, иерархия ББГКИ, цепочка уравнений Боголюбова  Борна  Грина  Кирквуда  Ивона)  система уравнений эволюции системы, состоящей из большого числа тождественных взаимодействующих частиц, заключенных в некотором …   Википедия

Цепочка ББГКИ — Цепочка уравнений Боголюбова (цепочка ББГКИ, ББГКИ иерархия, цепочка уравнений Боголюбова  Борна  Грина  Кирквуда  Ивона)  система уравнений эволюции системы, состоящей из большого числа тождественных взаимодействующих частиц, заключенных в… …   Википедия

Цепочка ценности — (англ. Value chain)  это инструмент стратегического анализа, направленный на подробное изучение деятельности организации с целью стратегического планирования. Идея цепочки ценности была предложена Майклом Портером в книге «Конкурентное… …   Википедия

ЦЕПОЧКА — ЦЕПОЧКА, цепочки, жен. 1. Маленькая и тонкая цепь. Цепочка для часов. 2. Группа бойцов, двигающихся друг за другом в какой нибудь линии (воен.). Цепочка конных разъездов. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 …   Толковый словарь Ушакова

Цепочка снов — явление, при котором человек видит несколько снов, пронизанных одной сюжетной линией, с одними и теми же персонажами, в одних и тех же или разных условиях. Может происходить в течение одного периода сна, например ночью. В отличие от обычного… …   Википедия

цепочка — 1. цепка (прост.) 2. см. вереница Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Александрова. 2011. цепочка сущ. • …   Словарь синонимов

Цепочка — см. Цепь, цепочка, оковы, узы …   Библейская энциклопедия Брокгауза

Цепочка доказательств — Ein Mann wie eine Waffe Жанр триллер Режиссёр Майкл Роуитц Автор сценария Тимо Берндт В главных ролях Клаус Лёвич Дженифер Нитч Майкл Бренднер Оливье Коритт …   Википедия

Цепочка на ноге — Цепочка на ногe и кольцо на пальце Цепочка на ноге  разновидность украшения, в частности ювелирного, которое носят на лодыжке. Цепочки на лодыжке и кольца на пальцах ноги, а также их комбинация многие века используются женщинами в Египте и… …   Википедия

Цепочка стоимости — (added value chain) вновь созданные на каждом этапе воспроизводственного процесса стоимости (чистая продукция, добавленная стоимость). Подробнее см. Стоимостная цепочка …   Экономико-математический словарь

цепочка стоимости — Вновь созданные на каждом этапе воспроизводственного процесса стоимости (чистая продукция, добавленная стоимость). Подробнее см. Стоимостная цепочка. [http://slovar lopatnikov.ru/] Тематики экономика EN added value chain …   Справочник технического переводчика

цепочка — это… Что такое LC-цепочка?

Цепочка уравнений Боголюбова — (цепочка ББГКИ, иерархия ББГКИ, цепочка уравнений Боголюбова  Борна  Грина  Кирквуда  Ивона)  система уравнений эволюции системы, состоящей из большого числа тождественных взаимодействующих частиц, заключенных в некотором …   Википедия

Цепочка ББГКИ — Цепочка уравнений Боголюбова (цепочка ББГКИ, ББГКИ иерархия, цепочка уравнений Боголюбова  Борна  Грина  Кирквуда  Ивона)  система уравнений эволюции системы, состоящей из большого числа тождественных взаимодействующих частиц, заключенных в… …   Википедия

Цепочка ценности — (англ. Value chain)  это инструмент стратегического анализа, направленный на подробное изучение деятельности организации с целью стратегического планирования. Идея цепочки ценности была предложена Майклом Портером в книге «Конкурентное… …   Википедия

ЦЕПОЧКА — ЦЕПОЧКА, цепочки, жен. 1. Маленькая и тонкая цепь. Цепочка для часов. 2. Группа бойцов, двигающихся друг за другом в какой нибудь линии (воен.). Цепочка конных разъездов. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 …   Толковый словарь Ушакова

Цепочка снов — явление, при котором человек видит несколько снов, пронизанных одной сюжетной линией, с одними и теми же персонажами, в одних и тех же или разных условиях. Может происходить в течение одного периода сна, например ночью. В отличие от обычного… …   Википедия

цепочка — 1. цепка (прост.) 2. см. вереница Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Александрова. 2011. цепочка сущ. • …   Словарь синонимов

Цепочка — см. Цепь, цепочка, оковы, узы …   Библейская энциклопедия Брокгауза

Цепочка доказательств — Ein Mann wie eine Waffe Жанр триллер Режиссёр Майкл Роуитц Автор сценария Тимо Берндт В главных ролях Клаус Лёвич Дженифер Нитч Майкл Бренднер Оливье Коритт …   Википедия

Цепочка на ноге — Цепочка на ногe и кольцо на пальце Цепочка на ноге  разновидность украшения, в частности ювелирного, которое носят на лодыжке. Цепочки на лодыжке и кольца на пальцах ноги, а также их комбинация многие века используются женщинами в Египте и… …   Википедия

Цепочка стоимости — (added value chain) вновь созданные на каждом этапе воспроизводственного процесса стоимости (чистая продукция, добавленная стоимость). Подробнее см. Стоимостная цепочка …   Экономико-математический словарь

цепочка стоимости — Вновь созданные на каждом этапе воспроизводственного процесса стоимости (чистая продукция, добавленная стоимость). Подробнее см. Стоимостная цепочка. [http://slovar lopatnikov.ru/] Тематики экономика EN added value chain …   Справочник технического переводчика