Логические схемы — презентация онлайн
1. ЛОГИЧЕСКИЕ СХЕМЫ
ТихомировАлександр Николаевич
учитель информатики
гимназия № 528
Санкт-Петербург
2. ЛОГИЧЕСКИЕ СХЕМЫ
Алгебра логики лежит в основеанализа и проектирования
логических схем.
Логические схемы состоят из
логических элементов,
осуществляющих
логические операции.
3. ЛОГИЧЕСКИЕ СХЕМЫ
Проектирование логических схем –это реализация
заданных логических функций с
помощью логических элементов.
Анализ логических схем выяснение того, какие логические
сигналы появятся на выходе схемы
после подачи определенных
входных сигналов.
4. ЛОГИЧЕСКИЕ СХЕМЫ
Логические элементы реализуютлогические функции.
A
A
&
A
f (A,B)
1
f (A,B)
B
B
f (A,B) = A * B
f (A,B) = A + B
f (A)
A
f (A)
A
f (A,B)
B
f (A) = A
f (A,B) = A B
5. ЛОГИЧЕСКИЕ СХЕМЫ
Логические схемы реализуют логическиевыражения.

Дана логическая функция
от логических переменных X,Y,Z:
f (X,Y,Z) = ( (X * Y) (Y + Z) ) * (X Z)
Построить логическую схему (диаграмму),
реализующую данную логическую функцию.
6. ЛОГИЧЕСКИЕ СХЕМЫ
f (X,Y,Z) = ( (X * Y) (Y + Z) ) * (X Z)X
&
Y
&
Y
Z
1
X
Z
f (X,Y,Z)
7. ЛОГИЧЕСКИЕ СХЕМЫ
f (X,Y,Z) = ( (X * Y) (Y + Z) ) * (X Z)&
8. ЛОГИЧЕСКИЕ СХЕМЫ
f (X,Y,Z) = ( (X * Y) (Y + Z) ) * (X Z)&
X
Z
9. ЛОГИЧЕСКИЕ СХЕМЫ
f (X,Y,Z) = ( (X * Y) (Y + Z) ) * (X Z)&
Y
1
X
Z
Z
10. ЛОГИЧЕСКИЕ СХЕМЫ
f (X,Y,Z) = ( (X * Y) (Y + Z) ) * (X Z)X
&
Y
Y
&
1
X
Z
Z
11. ЛОГИЧЕСКИЕ СХЕМЫ
f (X,Y,Z) = ( (X * Y) (Y + Z) ) * (X Z)X
&
Y
&
Y
Z
1
X
Z
f (X,Y,Z)
12. ЛОГИЧЕСКИЕ СХЕМЫ
f (X,Y,Z) = ( (X * Y) (Y + Z) ) * (X Z)X
&
Y
&
Y
Z
1
X
Z
f (X,Y,Z)
13.
 ЛОГИЧЕСКИЕ СХЕМЫf (X,Y,Z) = ( (X * Y) (Y + Z) ) * (X Z)
ЛОГИЧЕСКИЕ СХЕМЫf (X,Y,Z) = ( (X * Y) (Y + Z) ) * (X Z)X
&
Y
&
Y
Z
1
X
Z
f (X,Y,Z)
14. ЛОГИЧЕСКИЕ СХЕМЫ
f (X,Y,Z) = ( (X * Y) (Y + Z) ) * (X Z)X
&
Y
&
Y
Z
1
X
Z
f (X,Y,Z)
15. ЛОГИЧЕСКИЕ СХЕМЫ
f (X,Y,Z) = ( (X * Y) (Y + Z) ) * (X Z)X
&
Y
&
Y
Z
1
X
Z
f (X,Y,Z)
16. ЛОГИЧЕСКИЕ СХЕМЫ
f (X,Y,Z) = ( (X * Y) (Y + Z) ) * (X Z)Инверсия
значения
элемента
X
&
Инверсия
значения
функции
Y
&
Y
1
X
Z
Инверсия
значения
функции
Z
f (X,Y,Z)
17. ЛОГИЧЕСКИЕ СХЕМЫ
Анализ логических схем — выяснение того, какие логические сигналыпоявятся на выходе схемы после подачи определенных входных сигналов.
f (X,Y,Z) = ( (X * Y) (Y + Z) ) * (X Z)
X
&
Y
&
Y
Z
1
X
Z
f (X,Y,Z)
18.
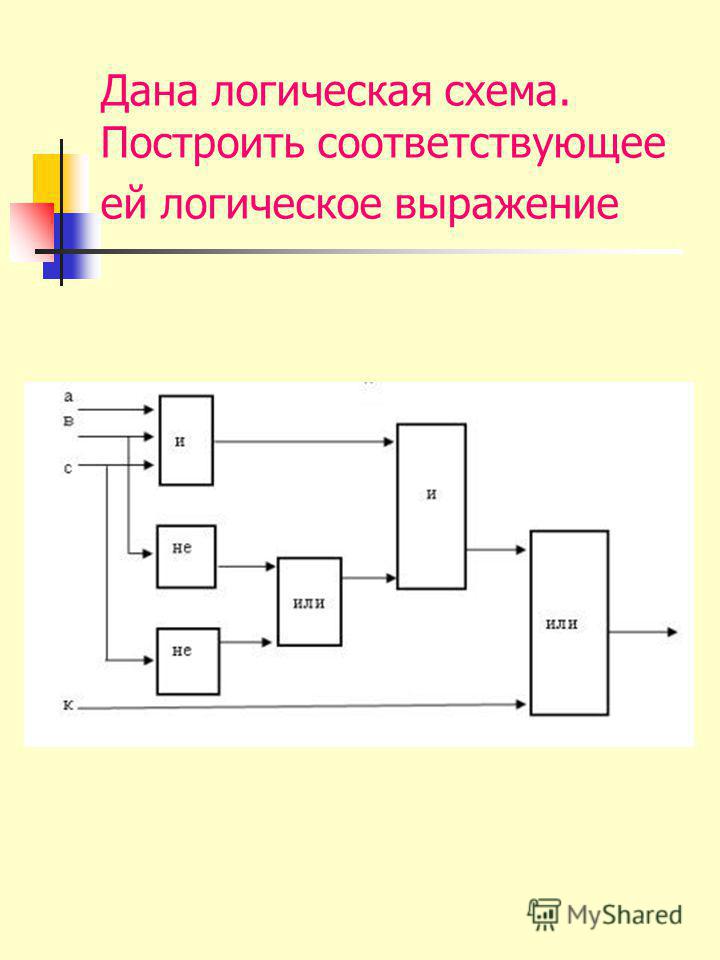 ЛОГИЧЕСКИЕ СХЕМЫНайти значение f (X,Y,Z) при X=1, Y=0, Z=1.
ЛОГИЧЕСКИЕ СХЕМЫНайти значение f (X,Y,Z) при X=1, Y=0, Z=1.f (X,Y,Z) = ( (X * Y) (Y + Z) ) * (X Z)
X
&
Y
&
Y
Z
1
X
Z
f (X,Y,Z)
19. ЛОГИЧЕСКИЕ СХЕМЫ
Найти значение f (X,Y,Z) при X=1, Y=0, Z=1.f (X,Y,Z) = ( (1 * 0) (0 + 1) ) * (1 1)
1
&
0
&
0
1
1
1
1
f (X,Y,Z)
20. ЛОГИЧЕСКИЕ СХЕМЫ
Найти значение f (X,Y,Z) при X=1, Y=0, Z=1.f (X,Y,Z) = ( (1 * 0) (0 + 1) ) * (1 1)
1
&
1
1
0
1
&
0
1
1
1
0
1
0
1
1
0
f (X,Y,Z)
21. ЛОГИЧЕСКИЕ СХЕМЫ
Дана логическая схема (диаграмма).X
Y
&
&
f (X,Y,Z)
Z
Z
Y
1
X
Построить логическую функцию f (X,Y,Z),
реализованную данной логической схемой.
22. ЛОГИЧЕСКИЕ СХЕМЫ
XY
&
&
f (X,Y,Z)
Z
Z
Y
1
X
f (X,Y,Z) = ( ( ( X Y ) * Z ) * ( Z + Y ) ) X
23.
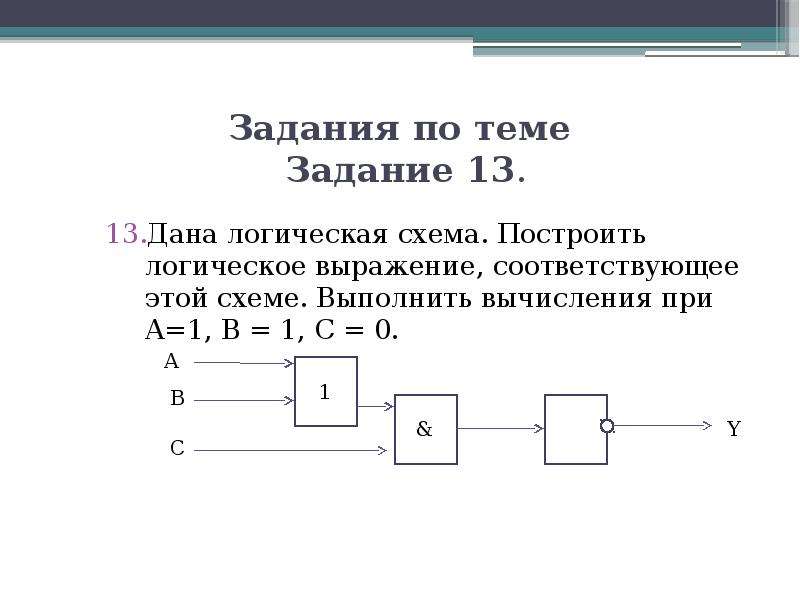 ЛОГИЧЕСКИЕ СХЕМЫДана логическая схема (диаграмма).
ЛОГИЧЕСКИЕ СХЕМЫДана логическая схема (диаграмма).1
1
1
0
&
0
1
&
0
0
0
1
1
1
0
1
1
f (X,Y,Z)
0
X
Построить логическую функцию f (X,Y,Z),
реализованную данной логической схемой.
Учебный курс «Информатика»
Учебный курс «Информатика»|
Комбинационные схемы строятся из элементарных логических элементов И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и др.
Требуется составить комбинационную схему.
Ответив на все эти вопросы, не составит большого труда нарисовать комбинационную схему:
Другой класс логических схем составляют схемы с внутренней памятью. |
|
||
2007 © Copyright by L.Gazizova (E-mail: [email protected]), WebMasters N.Woit, R.Akzamutdinov, A. Sabirova |
Хотя запрошенный вами набор примечаний представлен ниже, он не обновлялся с января 2003 года.
Спасибо за интерес к этому учебнику. Пожалуйста, не стесняйтесь, пишите мне по электронной почте на tarnoff etsu.edu, если у вас есть какие-либо вопросы или комментарии. — Дэйв Тарнофф Представьте себе цепь лампочки, которая управляется нажатием кнопки. Состояния следующие:
Это кажется ужасно сложной диаграммой состояний для таких простая процедура, но она учла все возможности для конструкция этой схемы. Теперь нам нужно спроектировать схему. На рисунке ниже представлена временная диаграмма образца для работы
эта схема. Это всего лишь один из способов, которым схема может работать для конкретного
последовательность нажатий кнопок. Во-первых, обратите внимание, что точки — это то, что я добавил в Рисунок, чтобы помочь вам понять процесс конечного автомата. Каждый период начинается, когда что-то вынуждает состояние измениться, либо сброс или передний фронт к часам. Это означает, что состояние система меняется только тогда, когда тактовый импульс переводит нас в следующее состояние или перезагрузка заставляет нас вернуться в исходное состояние. В период 1 сигнал сброса вернул состояние система в состояние 1. Выход лампочки в этот момент выключен. Когда возникает тактовый импульс, он перемещает нас в период 2. Глядя на
нашу диаграмму состояний, мы видим, что единственное, что
который выводит нас из состояния 1, если пользователь
нажимает кнопку. Когда часы поднимаются между периодом 1 и 2,
кнопка отпущена, поэтому мы остаемся в состоянии 1.
Лампочка по-прежнему выключена. Для следующего тактового импульса, перемещающего нас в период 3, кнопка нажал. Из нашей диаграммы состояний мы видим, что это переместит нас в состояние 2. Результат в этом состоянии горит лампочка. Следующий тактовый импульс переводит нас в период 4. Кнопка по-прежнему нажата, поэтому мы остаемся в состоянии 2. В периоде 5 тактовый импульс увеличивается при отпускании кнопки. Это переводит нас в состояние 3. на выходе из этого состояния горит лампочка. В периоде 6 часы идут вверх, пока кнопка еще не нажата. Единственное, что выводит нас из состояния 3, это нажимаем на кнопку, поэтому мы остаемся в состоянии 3. Тактовый импульс, который перемещает нас от периода 6 к периоду 7, происходит, когда кнопка нажата. Проверка состояния 3 на нашей диаграмме состояний показывает, что это переместит нас в Состояние 4, на выходе которого лампочка выключена. Обзор триггеров9R — Во время обычной работы этот сигнал имеет высокий уровень. Единственный
время, когда мы его используем, — это понизить его, чтобы заставить Q выйти на логический нуль. Единственный
время, когда мы его используем, — это понизить его, чтобы заставить Q выйти на логический нуль.Использование триггеров для определения наших состоянийДавайте начнем с нумерации наших состояний, чтобы мы могли найти для них логическое представление.
Из этой таблицы видно, что для представления требуется 2 цифры. Таблицы истинности следующего состоянияСледующий шаг на пути к разработке логики для эта система должна принимать информацию, которую мы имеем на диаграмме состояний и превратить его в таблицу истинности. Как и все наши предыдущие таблицы истинности, левые столбцы будут для наших входных данных и правые столбцы будут для выходов. есть крупный дополнение к нашим таблицам истинности здесь: «следующее состояние» будет добавлено как один из выходов таблицы. Другими словами, из определенного набора входных данных, мы должны знать, каким будет следующее состояние конечного автомата. Например, если текущее состояние равно 1 и кнопка ввода отпущена, следующее состояние — 2. Таблица для нашего примера показана ниже. Обратите внимание, что ввод кнопки равен 0 для отпускания и 1 для
нажимается и Выход равен 0 для выключенной лампы и 1 для включенной.
Отлично! Теперь у нас есть таблица истинности.
Теперь мы можем преобразовать каждую из этих таблиц в карту Карно. Затем делаем наши прямоугольники. А из них мы можем вывести выражения SOP. Наконец, это дает нам логическую схему ниже. Copyright © 2001 Дэвид Л. Тарнофф. Все права защищены. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Нарисуйте логическую диаграмму для следующего логического выражения $Y=(\\overline{\\text{A}}+B)\\centerdot (A+\\overline{\\text{B}})$. Также напишите таблицу истинности
Ответ
ПодтвержденоБолее 300 тысяч просмотров
Подсказка: Чтобы нарисовать логическую диаграмму приведенного выше логического выражения, нам сначала нужно знать символы локусов для различных логических операций. Нам также нужно знать, как функционируют операции, чтобы мы соответственно вводили входные данные.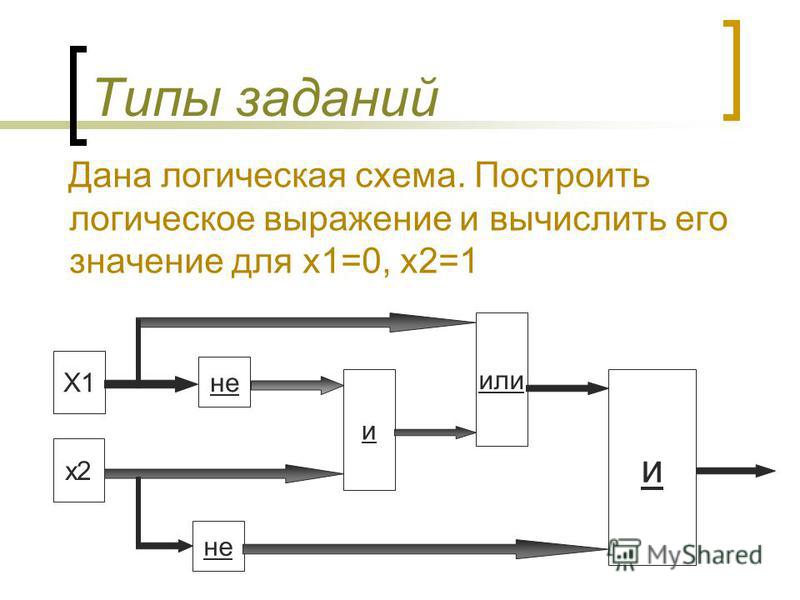 Как только мы узнаем операции и логические символы логических выражений, мы можем написать таблицу истинности, а также нарисовать логическую диаграмму для данного логического выражения.
Как только мы узнаем операции и логические символы логических выражений, мы можем написать таблицу истинности, а также нарисовать логическую диаграмму для данного логического выражения. Полный ответ:
Есть три основных логических элемента. Первый и основной НЕ ворота. Выход из-за этого логического элемента является не чем иным, как дополнением входного сигнала. Предположим, что наш входной сигнал равен Y, тогда выходной сигнал X определяется как $X=\overline{Y}$. Эти ворота обозначены символом, приведенным ниже.
Следующие ворота, которые мы собираемся обсудить, — ворота ИЛИ. Этот вентиль имеет в основном два входа и один выход. Операция, выполняемая над двумя входными сигналами, такова, что выходной сигнал затвора равен сумме двух входных сигналов. Предположим, что двумя входными данными являются A и B. Тогда выход C определяется выражением 9.0015 $C=A+B$ .Логический символ ворот приведен ниже.
Последним основным элементом является логический элемент И. Этот вентиль также имеет два входа и один выход. Операция, выполняемая над двумя входными сигналами, такова, что выходной сигнал затвора равен произведению двух входных сигналов. Предположим, что два входа — это A и B. Тогда выход C определяется как $C=A\centerdot B$. Логический символ для ворот приведен ниже.
Этот вентиль также имеет два входа и один выход. Операция, выполняемая над двумя входными сигналами, такова, что выходной сигнал затвора равен произведению двух входных сигналов. Предположим, что два входа — это A и B. Тогда выход C определяется как $C=A\centerdot B$. Логический символ для ворот приведен ниже.
Входы логического элемента в основном равны либо единице, либо нулю. Допустим, мы строим логический вентиль для приведенного выше выражения, т.е. $Y=(\overline{\text{A}}+B)\centerdot (A+\overline{\text{B}})$. Допустим, A и B — два входа, а Y — выход. Давайте сначала определим таблицу истинности приведенного выше логического уравнения таким образом, чтобы мы брали различные возможности входных данных A и B.
| A | B | $\overline{A}$ | $\overline{B}$ | $\overline{A}+B$ | 9000 4 $A+\overline{B}$$Y=(\overline{A}+B)\centerdot (A+\overline{B})$ | |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 |
Теперь из символы, которые мы знаем, позволяют нам построить логический элемент, имеющий входы A и B и выход как Y.


 , нами не рассмотренных. Соединяют эти элементы так, как это следует из логической формулы, т.е. вход одного элемента, в котором часть аргументов обработана как указано в формуле, подключается ко входу другого, где выполняется дальнейшая обработка логической функции. В схеме не должно быть обратных связей, т.е. соединения выходов последующих схем со входами предыдущих.
Двигаясь от начала схемы, на входе каждого элемента записывается буквенное выражение входного сигнала. Входы подаются на условное обозначение логических элементов, на выходе которых записывается логическая формула начала обработки входных сигналов, а затем их выходы соединяются так, как указано в заданной логической функции, и на выходе всей комбинационной схемы записывается выражение выполненной логической функции.
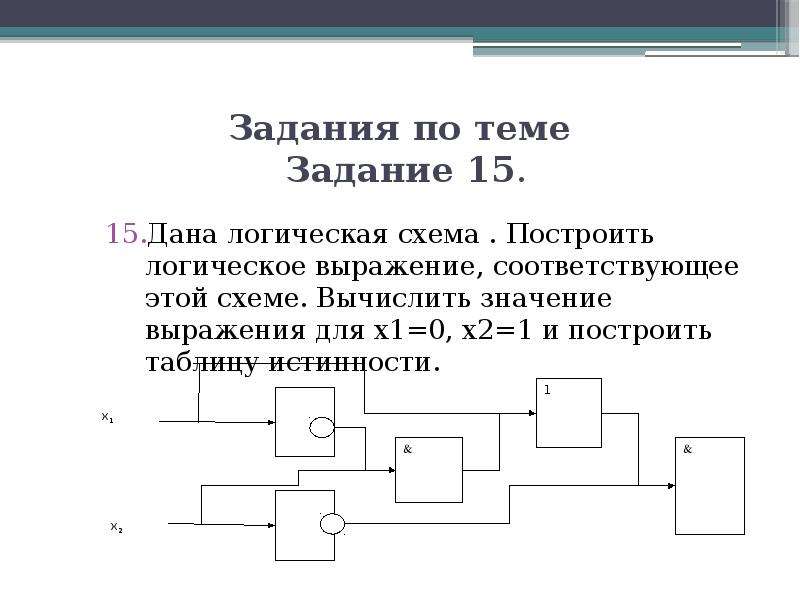
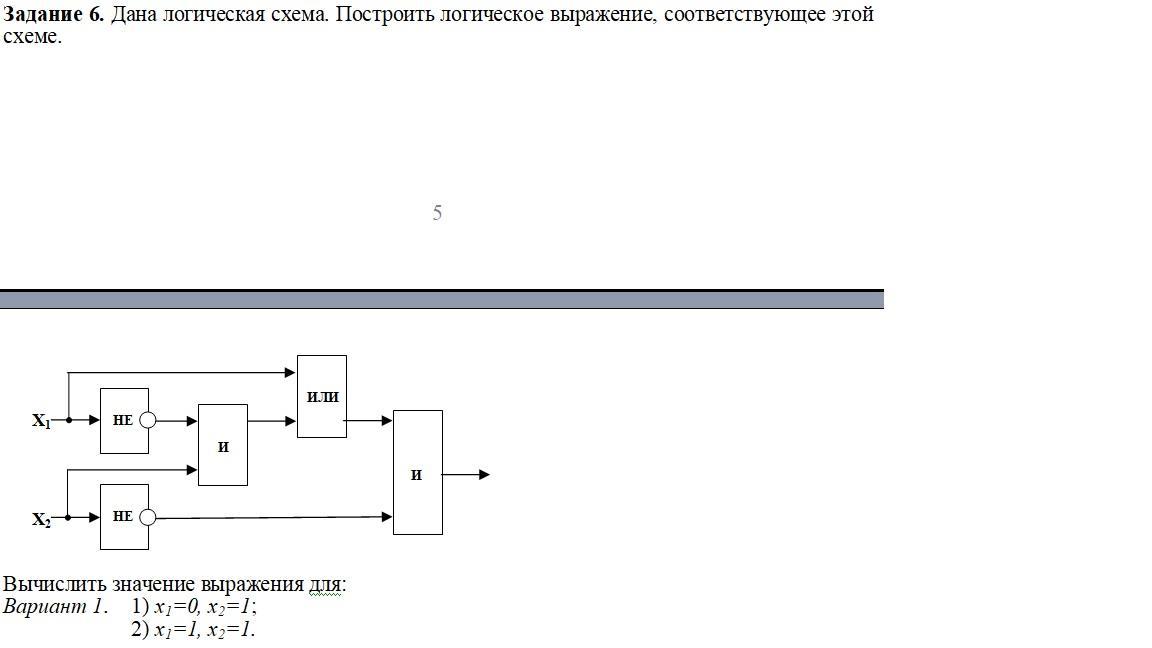
Пример: Пусть дана логическая функция
, нами не рассмотренных. Соединяют эти элементы так, как это следует из логической формулы, т.е. вход одного элемента, в котором часть аргументов обработана как указано в формуле, подключается ко входу другого, где выполняется дальнейшая обработка логической функции. В схеме не должно быть обратных связей, т.е. соединения выходов последующих схем со входами предыдущих.
Двигаясь от начала схемы, на входе каждого элемента записывается буквенное выражение входного сигнала. Входы подаются на условное обозначение логических элементов, на выходе которых записывается логическая формула начала обработки входных сигналов, а затем их выходы соединяются так, как указано в заданной логической функции, и на выходе всей комбинационной схемы записывается выражение выполненной логической функции.
Пример: Пусть дана логическая функция
 кнопка. Вы нажимаете на кнопку, и лампочка загорается.
Отпустите его, он останется включенным. Нажмите кнопку второй раз и
лампочка гаснет. Отпустите кнопку, и он останется выключенным. Этот
«улучшенная» диаграмма состояния лампочки показана ниже.
кнопка. Вы нажимаете на кнопку, и лампочка загорается.
Отпустите его, он останется включенным. Нажмите кнопку второй раз и
лампочка гаснет. Отпустите кнопку, и он останется выключенным. Этот
«улучшенная» диаграмма состояния лампочки показана ниже.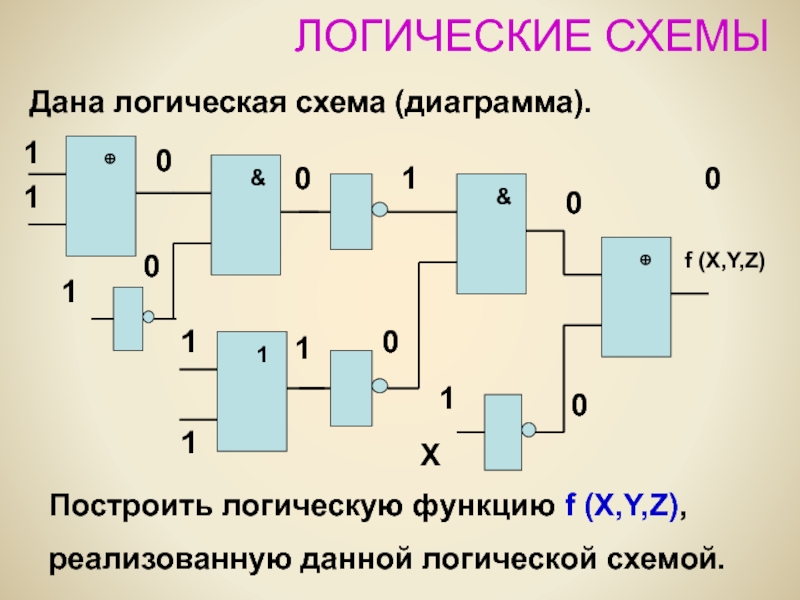
 Я представляю его здесь для тех из вас, у кого есть
проблемы с пониманием потока диаграммы состояний.
Я представляю его здесь для тех из вас, у кого есть
проблемы с пониманием потока диаграммы состояний.
 все штаты. Это означает, что мы можем использовать два триггера для представления
состояние машины. На рисунках ниже показано каждое возможное состояние
представлен двумя триггерами.
все штаты. Это означает, что мы можем использовать два триггера для представления
состояние машины. На рисунках ниже показано каждое возможное состояние
представлен двумя триггерами. )
) На самом деле, у нас есть
три таблицы истинности: одна для бита 1 следующего состояния, одна для бита 0 следующего
состояния и один для вывода.
На самом деле, у нас есть
три таблицы истинности: одна для бита 1 следующего состояния, одна для бита 0 следующего
состояния и один для вывода. (Пауза, пока я жду, пока стихнет коллективный стон…) Заметьте, что
Я изменил входную переменную для кнопки на букву Б .
(Пауза, пока я жду, пока стихнет коллективный стон…) Заметьте, что
Я изменил входную переменную для кнопки на букву Б .