Двоичная, восьмеричная и шестнадцатеричная системы счисления. 10 класс
Похожие презентации:
Пиксельная картинка
Информационная безопасность. Методы защиты информации
Электронная цифровая подпись (ЭЦП)
Этапы доказательной медицины в работе с Pico. Первый этап
История развития компьютерной техники
От печатной книги до интернет-книги
Краткая инструкция по CIS – 10 шагов
Информационные технологии в медицине
Информационные войны
Моя будущая профессия. Программист
1. Двоичная, восьмеричная и шестнадцатеричная системы счисления
Урок для 10-го классаРазработала Т.Л.Маслова, учитель
информатики гимназии №114
Разберем понятия позиционная и непозиционная система счисления:
Позиционная (десятичная) и непозиционная (римская) системы счисления.
Люди издавна используют десятичную систему счисления.
Разбирается пример получения многоразрядного десятичного числа и разложение
о
по степеням основания, т.
05
101
Ученики самостоятельно переводят заданные учителем
десятичные числа в двоичный код табличным способом.
4. Восьмеричная система счисления
Использование восьмеричной системы счисления связано с необходимостьюсократить и визуально упростить двоичные записи, так как при передаче
двоичной информации между людьми, велика вероятность искажения
информации.
В восьмеричной системе счисления используются числа от 0 до 7
000-0
001-1
010-2
011-3
100-4
101-5
110-6
111-7
Одна восьмеричная цифра заменяет три двоичных разряда, поэтому
запись двоичного числа уменьшается в длину в 3 раза.
Способы перевода:
1) Можно использовать для перевода промежуточную двоичную систему
счисления, разбив двоичную запись на триады:
85—1 010 101——1258
2) Можно применить последовательное деление на основание системы
счисления, в которую переводим число, т.е. на 8:
85 8
-80 10 8
5
-8
2
Получили число 1258
1
6.
Шестнадцатеричная система счисления.Используется, так же, как и восьмеричная, для сокращения ивизуального упрощения двоичных записей, но двоичный код разбивается
уже на тетрады, т. е. группы по 4 разряда.
В 4- разрядах могут быть закодированы цифры от 0 (0000) до 15 (1111),
но, так как цифр 10 – 15 в десятичной системе нет, то было предложено
использовать буквы латинского (английского) алфавита от A до F
Таким образом: 0000- 0
0001- 1
0111- 7
1101- D
0010- 2
1000- 8
1110- E
0011- 3
1001- 9
1111- F
0100- 4
1010- A
0101- 5
1011- B
0110- 6
1100- C
Одна шестнадцатеричная цифра заменяет четыре двоичных разряда,
поэтому запись двоичного числа уменьшается в длину в 4 раза.
Способы перевода:
1) Можно использовать для перевода промежуточную двоичную систему
счисления, разбив двоичную запись на триады:
85— 101 0101——5516
2) Можно применить последовательное деление на основание системы
счисления, в которую переводим число, т.
е. на 8:85 16
-80 5
5
Получили число 5516
8. Системы счисления с произвольным основанием
Аналогично разобранному выше, можно сделать вывод,что существует бесконечное множество систем счисления
с любым, произвольным основанием.
Теоретически, мы сами можем изобрести систему, с основанием,
например,
14, весь вопрос только в том, какие знаки мы выберем в качестве
цифр от 10 до 13
Например: 10 –
11 12 –
13 —
English Русский Правила
Двоичная, восьмеричная, шестнадцатеричная системы счисления.
Двоичная система счисления
Восьмери́чная систе́ма счисле́ния — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.
Восьмеричная
система часто используется в областях,
связанных с цифровыми устройствами.
Характеризуется лёгким переводом
восьмеричных чисел в двоичные и обратно,
путём замены восьмеричных чисел на
триплеты двоичных. Ранее широко
использовалась в программировании и
вообще компьютерной документации,
однако в настоящее время почти полностью
вытеснена шестнадцатеричной.
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 1010 до 1510, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
Широко
используется в низкоуровневом
программировании и компьютерной
документации, поскольку в современных
компьютерах минимальной единицей памяти
является 8-битный байт, значения которого
удобно записывать двумя шестнадцатеричными
цифрами. Такое использование началось
с системы IBM/360, где вся документация
использовала шестнадцатеричную систему,
в то время как в документации других
компьютерных систем того времени (даже
с 8-битными символами, как, например,
PDP-11 или БЭСМ-6) использовали восьмеричную
систему.
Правило деления-умножения
Для преобразования целых чисел используется правило деления, а для преобразования правильных дробей — правило умножения. Для преобразования смешанных чисел используются оба правила соответственно для целой и дробной частей числа.
Проверим, не ошиблись ли мы в процессе преобразования? Для этого преобразуем получившееся двоичное
число в десятичную систему по обычной формуле разложения:1248.
1×82+7×81+4×80=6410+5610+410=124
Таблица 1. Таблица соответствия восьмеричных цифр и двоичного кода
Десятичныйэквивалент | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Двоичныйкод | 0 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
Восьмеричнаяцифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Используя
эту таблицу можно просто заменить каждую
восьмеричную цифру тремя двоичными
битами.
Три двоичных бита обычно называют
триадой или трибитом. Теперь давайте
переведём восьмеричное число 174
Аналогично можно выполнить перевод числа из двоичной системы в восьмеричную. Для этого двоичное число разбивают на триады относительно крайнего правого разряда (или двоичной запятой) и, используя таблицу , каждой триаде ставят в соответствие восьмеричную цифру.
10101001,101112 | 010 | 101 | 001, | 101 | 1102 | =251,568 |
2 | 5 | 1 | 5 | 6 |
Аналогичным
образом можно выполнить перевод числа
из шестнадцатеричной формы в двоичную
и обратно.
В этом случае для представления
шестнадцатеричной цифры потребуется
четыре двоичных разряда. Четыре двоичных
разряда обычно называют тетрадой
Таблица 2. Таблица соответствия шестнадцатеричных цифр и двоичного кода
Двоичный код | шестнадцатеричная цифра | Десятичный эквивалент |
0000 | 0 | 0 |
0001 | 1 | 1 |
0010 | 2 | 2 |
0011 | 3 | 3 |
0100 | 4 | 4 |
0101 | 5 | 5 |
0110 | 6 | 6 |
0111 | 7 | 7 |
1000 | 8 | 8 |
1001 | 9 | 9 |
a | 10 | |
1011 | b | 11 |
1100 | c | 12 |
1101 | d | 13 |
1110 | e | 14 |
1111 | f | 15 |
10101001,101112 | 1010 | 1001, | 1011 | 10002 | =A9,B816 | |
A | 9 | B | 8 |
Восьмеричная система счисления: определение, преобразование, таблица, примеры
Что такое восьмеричная система счисления?
Восьмеричная система счисления — это система счисления с основанием 8.
Система счисления — это система представления чисел. Система счисления — это способ представления чисел с помощью набора символов и указаний. Наиболее часто используемой системой счисления является десятичная система счисления, которая имеет основание 10 и использует десять цифр от 0 до 9 для формирования других чисел.
Вот таблица, показывающая различные системы счисления и количество цифр, используемых в каждой системе.
Восьмеричная система счисления представляет собой систему счисления с основанием 8 и использует цифры от 0 до 7. Это означает, что имеется только 8 символов или цифр (0, 1, 2, 3, 4, 5, 6, 7), используемых для образуют другие числа.
Основное преимущество использования восьмеричной системы счисления заключается в том, что в ней используется меньше цифр, чем в десятичной и шестнадцатеричной системах счисления. Таким образом, у него меньше вычислений и, следовательно, меньше ошибок в расчетах.
Определение восьмеричной системы счисления
Система счисления с основанием 8 называется восьмеричной системой счисления.
Позиция каждой цифры имеет значение, равное степени 8. Число в восьмеричной системе счисления представлено числом 8 в основании, например 9.0006 $512_8,\; 56_8$ , и т.д.
Теперь давайте разберемся, как осуществляются взаимопреобразования между этими системами.
Связанные игры
Преобразование восьмеричных чисел в двоичные
Основание восьмеричной системы счисления равно 8. Основание двоичной системы счисления равно 2. Чтобы преобразовать восьмеричное число в двоичное, нам нужно преобразовать каждое число из восьмеричного числа к двоичному числу. Взгляните на приведенную ниже таблицу преобразования восьмеричных чисел в двоичные:
| Восьмеричное значение | Двоичный эквивалент |
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 90 038 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 | 7 | 111 |
Каждая цифра должна быть преобразована в 3-битное двоичное число.
Таким образом, мы получаем двоичный эквивалент числа. Давайте разберемся в этом с помощью примера.
Пример: Преобразуйте $(16)_8$ в двоичное число.
Решение: $(16)_8$ — восьмеричное число.
С помощью приведенной выше таблицы преобразования мы можем записать
$1_8 = 001_2$ и $6_8 = 110_2$
Таким образом, $(16)_8 = (001110)_2$
Связанные рабочие листы
Преобразование восьмеричных чисел в десятичные
Преобразование восьмеричных чисел в десятичные — простой процесс!
Число в восьмеричной системе расширяется по основанию восемь, где каждая цифра умножается на степень 8 в зависимости от ее положения.
После преобразования восьмеричного числа в десятичное оно имеет основание 10.
Поясним это на примере:
Пример: Преобразуйте $(321)_8$ в десятичную форму.
90)$
$= (3\times64) + (2\times8) + (1\times1)$
$= 192 + 16 + 1$
$= 20 9_{10}$
Таким образом, $( 321)_8 = (209)_{10}$
| Восьмеричная основание 8 | Десятичное число основание 10 |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 | 90 045
| 7 | 7 |
| 10 | 8 |
| 11 | 9 | 900 45
| 12 | 10 |
| 13 | 11 |
| 14 | 12 | 15 | 13 |
| 16 | 14 |
Преобразование десятичного числа в восьмеричное
При этом преобразовании десятичное число делится на 8 каждый раз, когда из предыдущей цифры получается напоминание.
Давайте разберемся с этим преобразованием на примере.
Пример: Преобразование $416_{10}$ в восьмеричное число.
Разделить 416 на восьмеричное основание, 8.
| Разделить на 8 | Частное | 9 0005 Остаток |
|---|---|---|
| $416\div8$ | 52 | 0 |
| $52\div8$ | 6 | 90 269 4|
| $6\div8$ | 0 | 6 |
Останавливаемся когда значение частного становится равным 0. Записав остатки в обратном порядке, мы получим эквивалентное восьмеричное число. Таким образом, восьмеричное представление числа 416 равно 640.
Следовательно, $(416)_{10} = (640)_8$
Преобразование восьмеричного числа в шестнадцатеричное
Шестнадцатеричная система счисления имеет основание 16 и использует шестнадцать символов. В нем используются цифры от 0 до 9 и буквы от A до F.
| Восьмеричный | Шестнадцатеричный | |||||||
| 0 | 0 | |||||||
| 1 | 1 | |||||||
| 2 | 2 | |||||||
| 3 | 3 | |||||||
| 4 | 4 | |||||||
| 5 | 5 9 0038 | |||||||
| 6 | 6 | |||||||
| 7 | 7 | |||||||
| 10 | 8 | 9 0045|||||||
| 11 | 9 | |||||||
| 12 | А | |||||||
| 13 | В | 900 45|||||||
| 14 | C | |||||||
| 15 | D | |||||||
| 16 | E | |||||||
| Ф | ||||||||
| 20 | 10 |
Преобразование десятичного числа в шестнадцатеричное | $\times$ | 0 | 1 | 2 9 0006 | 3 | 4 | 5 | 6 | 7 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 9004 5
| 2 | 0 | 2 | 4 | 6 | 10 | 12 | 14 | 16 |
| 3 | 0 | 3 | 6 | 11 90 038 | 14 | 17 | 22 | 25 |
| 4 | 0 | 4 | 10 | 14 | 20 | 24 | 30 | 34 | 9004 5
| 5 | 0 | 5 | 12 | 17 | 24 | 31 | 9 0475 3643 | |
| 6 | 0 | 6 | 14 | 22 | 9 0475 3036 | 44 | 52 | |
| 7 | 0 | 7 | 16 | 25 | 34 | 43 | 52 | 61 | 9004 5
Альтернативный тег: Восьмеричная таблица умножения
Факты о восьмеричной системе счисления
- В 1801 г.
Джеймс Андерсон критиковал французов за то, что они основывают метрическую систему на десятичной арифметике. Он предложил основание 8 и ввел термин восьмеричное число.
Джеймс Андерсон критиковал французов за то, что они основывают метрическую систему на десятичной арифметике. Он предложил основание 8 и ввел термин восьмеричное число.- Основное преимущество использования восьмеричных чисел заключается в том, что в них используется меньше цифр, чем в десятичной и шестнадцатеричной системах счисления. Таким образом, у него меньше вычислений и меньше вычислительных ошибок.
- Восьмеричная система счисления широко используется в компьютерных приложениях и цифровых системах счисления. Восьмеричное число также используется в авиации в виде кода.
- Восьмеричная система аналогична шестнадцатеричной, поскольку обе они легко преобразуются в двоичную, где восьмеричная соответствует трехзначной двоичной, а шестнадцатеричная — четырехзначной двоичной.
Заключение
В этой статье мы узнали о восьмеричной системе счисления и взаимопреобразованиях между восьмеричной, двоичной, шестнадцатеричной и десятичной.
Давайте решим несколько примеров на основе понятий, которые мы рассмотрели.
Решенные примеры в восьмеричной системе счисления
Пример 1. Преобразование $(242)_8$ в двоичное число
Решение:
$(242)_8$is восьмеричное число.
С помощью таблицы преобразования восьмеричной системы в двоичную имеем:
$2_8 = 010_2$ и $4_8 = 100_2$
$(242)_8 = (010100010)_2$
Следовательно, $(242) _8 = (010100010)_2$
Пример 2. Преобразование десятичного числа 33 в восьмеричное. 90)$
$= (5\times64) + (6\times8) + (0\times1)$
$= 320 + 48 + 0$
$= 368$
Таким образом, $(560)_8 = (368)_{10}$
Пример 4. Преобразование $725_{10}$ в восьмеричное число.
Решение:
Разделить данное число 725 на 8.
| Разделить на 8 5 Частное | Остаток | |
|---|---|---|
| $725\div8$ | 90 | 5 |
| $90\div8$ | 11 | 2 |
| $11\div8$ | 1 | 3 |
| $1\div8$ | 0 | 1 |
Записав остатки в обратном порядке, получим эквивалентное восьмеричное число.
Таким образом, восьмеричное представление числа 725 равно 1325.
Следовательно, $(725)_{10} = (1325)_8$
Пример 5. Преобразование восьмеричного числа 90$
$= 4\times64 + 5\times8 + 2\times1$
$= 256 + 40 + 2$
$(452)_8 = (298)_{10}$
Следовательно, десятичная дробь число $(298)_{10}$.
Теперь мы можем узнать шестнадцатеричное число, разделив 298 на 16, пока остаток не станет меньше 16.
$\frac{298}{16} = 18$, остаток $= 10$
$\frac{18 }{16} = 1$, остаток $= 2$
$\frac{1}{16} = 0$, остаток $= 1$
Используя таблицу преобразования десятичных чисел в шестнадцатеричные, мы имеем $10 = A$
Запишите остатки в обратном порядке.
$(452)_8 = (12A)_{16}$
Таким образом, $(452)_8 = (12A)_{16}$
Практические задачи по восьмеричной системе счисления
1Система счисления с его основанием как _________ известен как восьмеричная система счисления.
16
8
2
10
Правильный ответ: 8
Восьмеричная система счисления, или для краткости восьмеричная, имеет основание 8.
Часто задаваемые вопросы о восьмеричной системе счисления
Для чего используется восьмеричная система счисления?
Восьмеричная система счисления обеспечивает удобный способ преобразования больших двоичных чисел в более компактные и меньшие группы. Однако восьмеричная система счисления менее популярна. Поскольку базовое значение восьмеричной системы счисления равно 8, их максимальное числовое значение равно 7 и не может быть больше 7.
Как преобразовать двоичное число в восьмеричное?
Сгруппируйте все 1 и 0 в двоичном числе в наборы по три, начиная с крайнего правого. Добавьте нули слева от последней цифры, если у вас недостаточно цифр, чтобы составить набор из трех. Сравните свои наборы двоичных чисел с этой восьмеричной таблицей преобразования.
Давайте разберем это преобразование на примере:
Преобразование $(11100100)_2$ в восьмеричное число.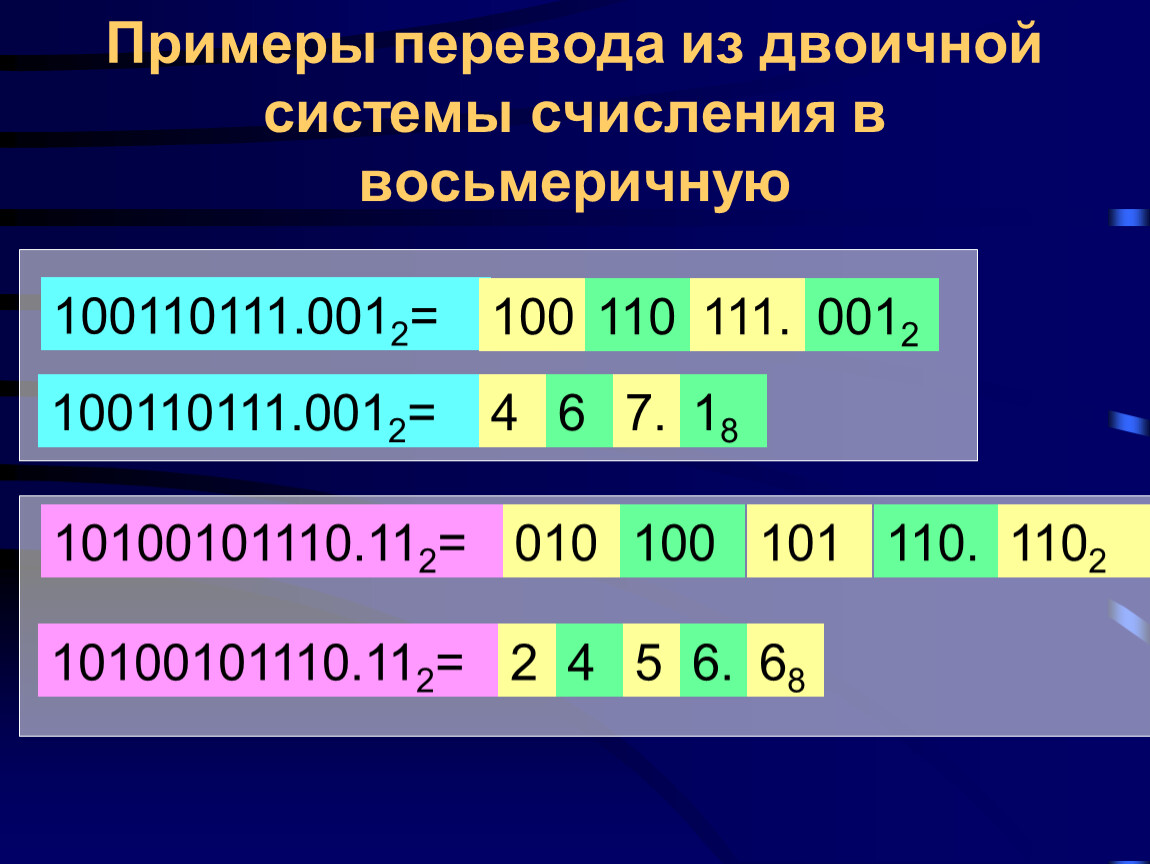
$(011100100)_2 = 011 | 100 | 100 = 344$
Следовательно, $(11100100)_2 = (344)_8$
Каковы недостатки восьмеричной системы счисления?
Основным недостатком восьмеричной системы счисления является то, что компьютер ее не понимает. Поэтому для цифровых систем требуется дополнительная схема, преобразующая восьмеричное число в двоичное. Восьмеричная система счисления используется в миникомпьютерах.
Как сложить восьмеричные числа?
Существуют различные способы сложения восьмеричных чисел. Одним из способов является преобразование добавляемых чисел в десятичные числа и нахождение суммы в виде десятичного числа. Наконец, преобразуйте результат обратно в восьмеричное число. Другой способ — использовать восьмеричную таблицу сложения. Это дает мгновенный результат и не требует расчетов,
Что следует за цифрой 7 в восьмеричном счете?
Восьмеричное число после 7 равно 10. Десятичное число 8 представлено как 10 в восьмеричной системе счисления.
В восьмеричной системе счисления нет ни 8, ни 9.
Двоичный, восьмеричный и шестнадцатеричный | Введение в математику колледжа |
Модуль 3: Система счисления
В современной вычислительной технике и цифровой электронике наиболее часто используются десятичные (по основанию 10), двоичные (по основанию 2), восьмеричные (по основанию 8) и шестнадцатеричные (по основанию 16). Если мы конвертируем между двумя основаниями, отличными от десятичных, нам обычно нужно преобразовать число в основание 10, а затем преобразовать это число во второе основание. Однако мы можем легко преобразовать напрямую из двоичного в восьмеричное и наоборот, а также из двоичного в шестнадцатеричное и наоборот.В этом видео представлено основное введение в эти преобразования:
Для другого описания это больше похоже на лекцию по математике:
youtube.com/embed/2UwxdCLFW70?feature=oembed» allowfullscreen=»»> три цифры по основанию два. В базе восемь эти числа представлены одной цифрой.
| Базовый 2 (двоичный) номер | Основание 10 (десятичное), эквивалент | Основание 8 (восьмеричное) число |
|---|---|---|
| 000 | 0 | 0 |
| 001 | 1 | 1 |
| 010 | 2 | 2 |
| 011 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
по основанию 2 для представления этих же чисел:| Число по основанию 2 | Эквивалент | с основанием 10Базовый номер 8 |
|---|---|---|
| 1000 | 8 | 10 = 1 × 8 + 0 × 1 |
| 1001 | 9 | 11 = 1 × 8 + 1 × 1 |
| 1010 | 10 | 12 = 1 × 8 + 2 × 1 |
| … | … | … |
| 111100 | 60 | 74 = 7 × 8 + 4 × 1 |
| 111101 | 61 | 75 = 7 × 8 + 5 × 1 |
| 111110 | 62 | 76 = 7 × 8 + 6 × 1 |
| 111111 | 63 | 77 = 7 × 8 + 7 × 1 |
Вы видите здесь закономерность? Для одной цифры в базе 8 нам нужно до трех цифр в базе 2. Для двух цифр в базе 8 нам нужно 4, 5 или 6 цифр в базе 2. Для трех цифр в базе 8 нам нужно 7, 8 , или 9цифры в базе 2. Для каждой дополнительной цифры в базе 8 нам нужно до трех пробелов, чтобы представить ее в базе 2. Вот способ запомнить это: 2 3 = 8, поэтому нам нужно три пробела. Здесь поможет пара примеров.
- Преобразуйте число 6157 8 в основание 2. Мы разделим каждую цифру по основанию 8 на три цифры по основанию 2, используя трехзначный эквивалент по основанию 2, поэтому 6 8 = 110 2 , 1 8 = 001 2 и т. д.
- Преобразуйте число 10111011001010 2 в число с основанием 8. Разделите это число на наборы по три, , начиная с крайней правой цифры , а затем преобразуйте каждый набор из трех в его эквивалент в формате с основанием 8.
Для шестнадцатеричного (основание 16) нам нужно до четырех двоичных цифр для представления каждой отдельной цифры.
Запомните это, вспомнив, что 2 4 = 16, поэтому нам нужно четыре цифры.
Вы можете распечатать копии этих листов, чтобы помочь вам с преобразованием между двоичным и восьмеричным или шестнадцатеричным:
- Преобразование из двоичного в восьмеричный
- Преобразование двоичного формата в шестнадцатеричный
Если вы хотите проверить себя в преобразовании чисел от 0 до 255 в двоичные, восьмеричные и шестнадцатеричные (и между этими основаниями), вот ссылка на представления этих чисел: Двоичные, восьмеричные и шестнадцатеричные числа.
Лицензии и атрибуты
Лицензионный контент CC, оригинальный
- Математика для гуманитарных наук I. Предоставлено : Институт расширенного обучения муниципального колледжа Северной Вирджинии. Расположен по адресу : https://online.nvcc.edu/. Лицензия : CC BY: Атрибуция
Все права защищены.
Автор : MyWhyU.
