Меню сайтаРасчет геометрических характеристик сечений он-лайн NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.
Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной
сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн. Расчет рам, ферм балок он-лайн NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы. Лекции — теория, практика, задачи… Примеры решения задач
Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое. Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое). Форум сопромата и механики Книги — разная литература по теме. Заказать задачу Друзья сайта (ссылки) WIKIbetta Разработчикам (сотрудничество) Веб-мастерам (партнёрка) О проекте, контакты Подпроекты |
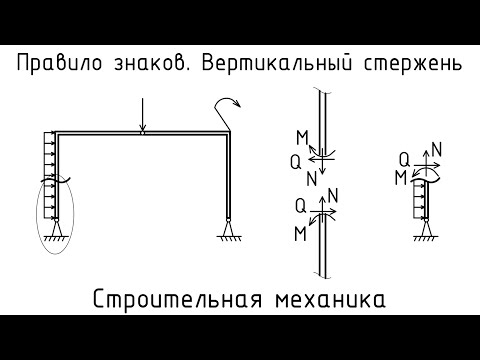
Базовый курс лекций по сопромату, теория, практика, задачи.::Оглавление:: 3.4. Правило знаков для изгибающих моментов и поперечных сил. Поперечная сила в сечении балки mn (рис. 3.7, а) считается положительной, если равнодействующая внешних сил слева от сечения направлена снизу вверх, а справа — сверху вниз, и отрицательной — в противоположном случае (рис. Изгибающий момент в сечении балки, например в сечении mn (рис. 3.8, а), считается положительным, если равнодействующий момент внешних сил слева от сечения направлен по часовой стрелке, а справа — против часовой стрелки, и отрицательным в противоположном случае (рис. 3.8, б). Моменты, изображенные на рис. 3.8, а, изгибают балку выпуклостью вниз, а моменты, изображенные на рис. 3.8, б, изгибают балку выпуклостью вверх. Это можно легко проверить, изгибая тонкую линейку. Отсюда следует другое, более удобное для запоминания правило знаков для изгибающего момента. Изгибающий момент считается положительным, если в рассматриваемом сечении балка изгибается выпуклостью вниз. Далее будет показано, что волокна балки, расположенные в вогнутой части, испытывают сжатие, а в выпуклой — растяжение. Таким образом, условливаясь откладывать положительные ординаты эпюры М вверх от оси, мы получаем, что эпюра оказывается построенной со стороны сжатых волокон балки. |
СообществоПоиск людей ВходРешение задач
Заказать задачу Расчет редукторов
Расчет редуктора он-лайн Для Android (рекомендую)NEWMobile Beam 2.0 Java 2 ME |
Правила знаков в механике
Правила знаков для внешних сил, моментов, внутренних силовых факторов, напряжений и перемещений принятые в сопромате, теоретической и технической механике при решении задач.
При растяжении-сжатии
Внутренняя продольная сила N, которая стремится растянуть рассматриваемую часть бруса, считается положительной. Сжимающая продольная сила имеет отрицательный знак.
Положительное направление внутренней продольной силы N
Видео по правилам знаков:
Другие видео
При кручении
Внутренний скручивающий момент T считается положительным, если он стремится повернуть рассматриваемую часть бруса против хода часовой стрелки, при взгляде на него со стороны внешней нормали.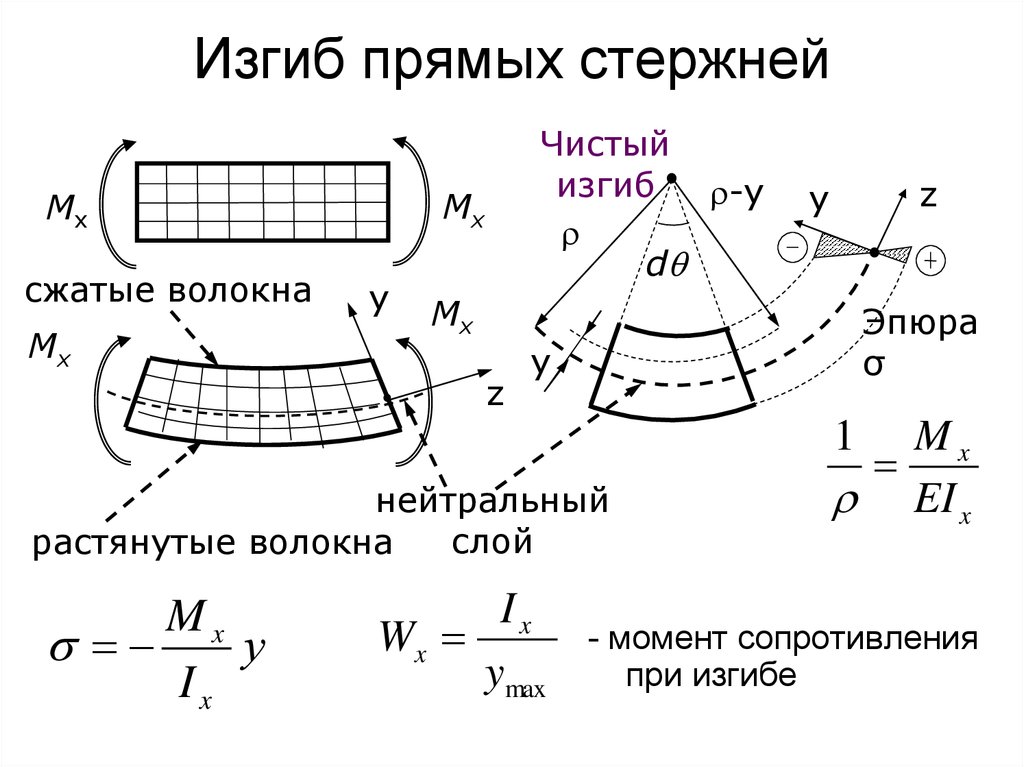
Положительное направление внутреннего скручивающего момента T
При изгибе
Внутренняя поперечная сила Q считается положительной, в случае, когда она стремится повернуть рассматриваемую часть бруса по ходу часовой стрелки.
Положительное направление внутренней поперечной силы Q
Внутренний изгибающий момент M положителен, когда он стремится сжать верхние волокна бруса.
Положительное направление внутреннего изгибающего момента M
Примечание: Величина и знак внутренних сил и моментов зависит от вызывающих их внешних усилий, поэтому указанные правила знаков в том же виде справедливы и для внешних нагрузок.
Правило знаков при внецентренном нагружении
Положительными принимаются внешние усилия стремящиеся вызвать растяжение первой четверти сечения.
Положительное направление действия внешних нагрузок
Нормальные напряжения σ положительны, если они растягивают выделенный элемент бруса.
Положительные нормальные напряжения
Касательные напряжения τ будут положительными, если они стремятся повернуть рассматриваемый элемент бруса по ходу часовой стрелки.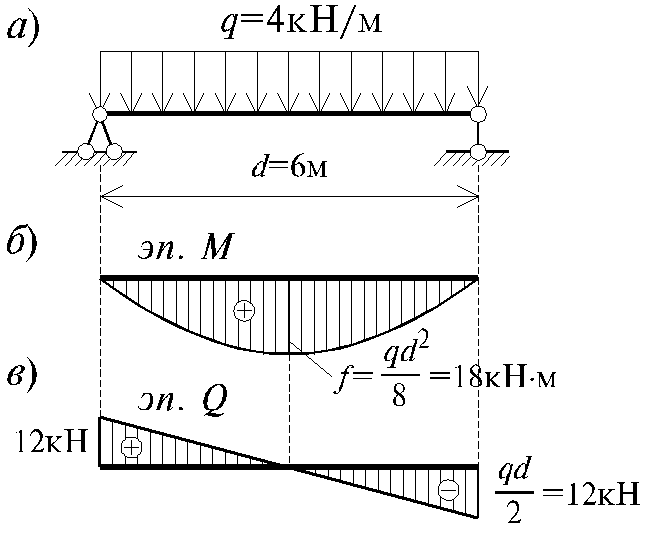
Положительные касательные напряжения
Правило знаков для деформаций и перемещений
Деформация при растяжении-сжатии Δl считается положительной, если длина стержня при этом увеличивается.
Положительная деформация при продольном нагружении
При плоском поперечном изгибе
Вертикальное перемещение сечения бруса принимается положительным, если оно направлено вверх от начального положения.
Положительные перемещения сечений балки при изгибе
Для проекций сил на оси системы координат
Проекции внешних сил на оси системы координат принимаются положительными, если их направление совпадает с положительным направлением соответствующей оси.
Для моментов
Сосредоточенные моменты и моменты сил в уравнениях статики записываются с положительным знаком, если они стремятся повернуть рассматриваемую систему против хода часовой стрелки.
При составлении уравнений равновесия статичных (неподвижных) систем (например, при определении опорных реакций), последние два правила упрощаются до вида:
Проекции сил и моменты, имеющие одинаковое направление записываются с одинаковыми знаками, соответственно проекции сил и моменты обратного направления – с противоположными.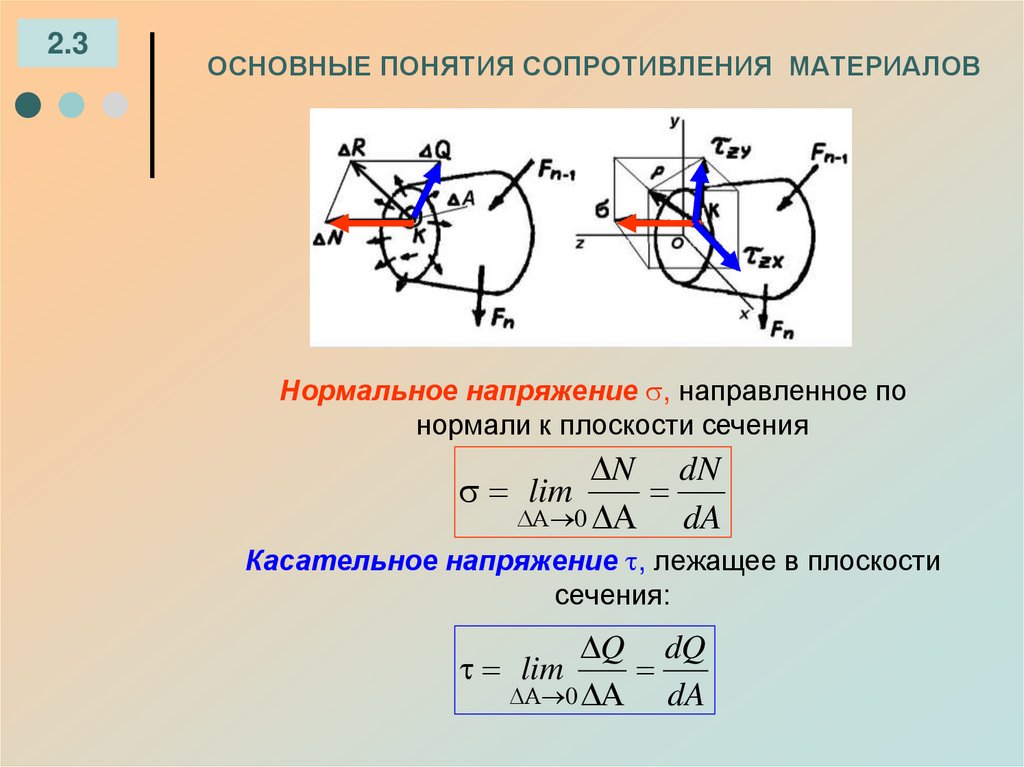
Метод сечений >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Подробнее
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ
На нашем сайте можно бесплатно скачать:
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Сохранить или поделиться с друзьями
Помощь с решением
ВЫБЕРИТЕ РАЗДЕЛ МЕХАНИКИ
- Техническая механика (техмех)
- Теоретическая механика (теормех)
- Сопротивление материалов (сопромат)
- Строительная механика (строймех)
- Теория механизмов и машин (ТММ)
- Детали машин и ОК (ДМ)
Поддержать сайт
Реакции и диаграммы балок – Приложение по сопротивлению материалов для энергетики
Основной корпус
Диаграммы
Цели обученияПо окончании этой главы вы должны уметь:
- Определять реакции свободно опертых, выступающих и консольных балок
- Рассчитайте и начертите диаграммы поперечной силы и изгибающего момента для балок, подверженных сосредоточенным нагрузкам, равномерным распределенным нагрузкам и их комбинациям.

Обзор балок
Балки – это конструктивные элементы различного инженерного назначения, такие как крыши, мосты, механические узлы и т. д. В общем случае балка представляет собой тонкую, прямую, жесткую конструкцию, изготовленную из изотропных материалов и, что наиболее важно, подвергается нагрузкам, перпендикулярным их продольной оси. Если бы вместо перпендикулярных нагрузок тот же элемент конструкции подвергался бы продольным нагрузкам, его называли бы колонной или стойкой. Если бы тот же элемент подвергался крутящему моменту, его называли бы и рассматривали как вал. Поэтому при идентификации механических или конструктивных компонентов очень важно учитывать способ нагрузки.
Обратите внимание, что когда дело доходит до ориентации, балки могут быть горизонтальными, вертикальными или с любым промежуточным наклоном (как погруженные в воду пластины, анализируемые в гидромеханике)… при условии, что нагрузка перпендикулярна их главной оси.
Опоры балки:
| Тип опоры | Похоже на | Символ | Реакции |
Ролик, также называемый
|
|
| |
Закрепленный, также называемый
|
| ||
| Фиксированный |
|
Нагрузки на балку
| Нагрузки | Символ | Примеры | Крытый |
Точка, также называемая
|
| Да | |
| Униформа Распределенная |
| Да | |
| Переменная Распределенная |
| Да | |
| Концентрированные моменты |
| № |
Типы балок:
| Типы | Схема | Примеры | Крытый |
| Простые балки или просто поддерживаемые |
| Да | |
| Нависающие балки |
| Да | |
| Консольные балки |
| Да | |
| Составные балки |
| № | |
| Неразрезные балки |
| № |
Решение для балочных реакций
При нахождении реакций рекомендуются следующие шаги:
- Нарисуйте схему тела без балки
- Заменить равномерную распределенную нагрузку (если есть) эквивалентной точечной нагрузкой
- Решить ΣM A = 0 (сумма моментов относительно опоры A).
 Это даст вам R B (реакция на поддержке B).
Это даст вам R B (реакция на поддержке B). - Решите ΣM B = 0. Это даст вам R A .
- Используя R A и R B , найденные на шагах 3 и 4, проверьте, выполняется ли ΣV = 0 (сумма всех вертикальных сил).
- Обратите внимание, что шаги 4 и 5 можно поменять местами.
- Для консольной балки используйте ΣV = 0, чтобы найти вертикальную реакцию на стене, и ΣM , стена = 0, чтобы найти реакцию момента на стене. Нет никакого другого уравнения для проверки ваших результатов.
Диаграммы поперечных сил и изгибающих моментов
Обратите внимание:«Сдвиговые силы — это внутренние силы, возникающие в материале балки для уравновешивания внешних сил, чтобы обеспечить равновесие всех частей балки.
Изгибающие моменты — это внутренние моменты, возникающие в материале балки, чтобы уравновесить стремление внешних сил вызвать вращение любой части балки».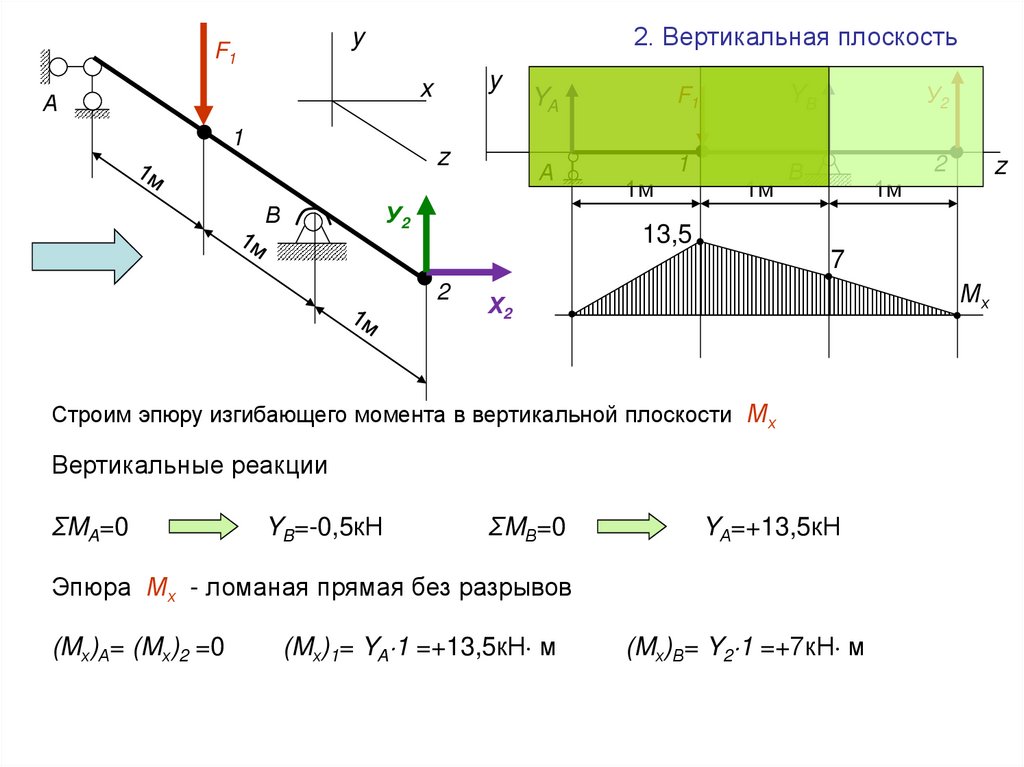 [3]
[3]
Перерезывающую силу в любом сечении балки можно найти путем суммирования всех вертикальных сил слева или справа от рассматриваемого сечения.
Аналогично, изгибающий момент в любом сечении балки можно найти, сложив моменты слева или справа рассматриваемого сечения. Опорной точкой момента является рассматриваемое местоположение.
По соглашению внутренние силы сдвига, действующие вниз, считаются положительными. Они противодействуют восходящим внешним силам. Следовательно, при представлении поперечных сил их можно рисовать в направлении внешних сил. Это визуально проще, чем следовать соглашению о знаках.
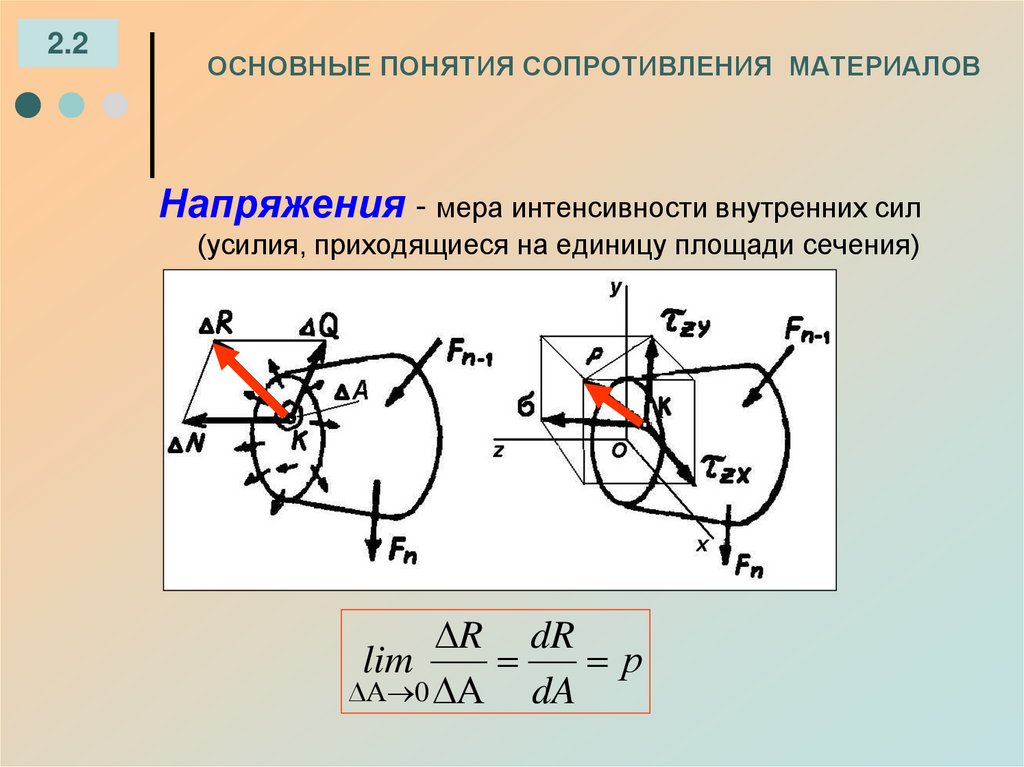
Моменты по часовой стрелке обычно считаются отрицательными, а моменты против часовой стрелки считаются положительными. При представлении изменения изгибающего момента обратитесь к следующей таблице, показывающей качественные кривые изгибающего момента в зависимости от формы графиков поперечной силы.
.
При построении диаграмм поперечной силы и изгибающего момента, несмотря на то, что соглашение о знаках важно, постоянство имеет решающее значение. Например, рассмотрим простую балку, нагруженную точечной нагрузкой, приложенной к нагрузке UD. Запустив диаграммы на опоре А, глядя на страницу, вы получите следующее:
Теперь переверните луч по горизонтали на 180º (или измените точку наблюдения, глядя на луч с противоположной стороны) и нарисуйте диаграммы, начиная с той же точки A. Диаграммы будут выглядеть следующим образом:
Обратите внимание, что хотя диаграммы поперечной силы выглядят как зеркальные изображения (перевернутые по горизонтали), диаграмма изгибающего момента не затрагивается. Кроме того, наиболее важный результат этого анализа показывает, что максимальная сила сдвига и величина изгибающего момента всегда будут одинаковыми.
Контрольные точки диаграммы направленностиПри построении диаграммы направленности учитывайте следующее:
Диаграммы поперечной силы:
- На концах свободно опертой балки поперечная сила равна нулю.

- На стенке консольной балки поперечная сила равна вертикальной реакции на стене. На свободном конце балки поперечная сила равна нулю.
- На любом сегменте балки, к которому не приложены нагрузки, поперечная сила остается постоянной (горизонтальная линия).
- Точечная нагрузка или реакция на диаграмме поперечной силы вызывает резкое изменение графика в направлении приложенной нагрузки.
- Равномерная распределенная нагрузка, действующая на балку, представлена прямолинейной поперечной силой с отрицательным или положительным наклоном, равной нагрузке на единицу длины.
Диаграмма изгибающих моментов:
- На концах свободно опертой балки изгибающие моменты равны нулю.
- На стенке консольной балки изгибающий момент равен реакции момента. На свободном конце изгибающий момент равен нулю.
- В месте, где поперечная сила пересекает нулевую ось, соответствующий изгибающий момент имеет максимальное значение.

- Форма кривой изгибающего момента между двумя точками балки показана в двух приведенных выше таблицах.
- Изменение изгибающего момента между двумя точками на балке равно площади под диаграммой поперечной силы между теми же двумя точками.
Приведенные выше рекомендации помогут вам в создании диаграмм пучков; они также служат проверкой.
При решении диаграмм балок в классе и дома вы можете проверить свои ответы с помощью этого бесплатного онлайн-калькулятора балок: SkyCiv Cloud Engineering Software
Задача 1: Укажите максимальные значения поперечной силы и изгибающего момента.
Задача 2: Укажите максимальные значения поперечной силы и изгибающего момента.
Задача 3: Балка длиной 24 м свободно поддерживается на расстоянии 3 м от каждого конца. Балка несет точечную нагрузку 18 кН на левом конце и 22 кН на правом конце балки.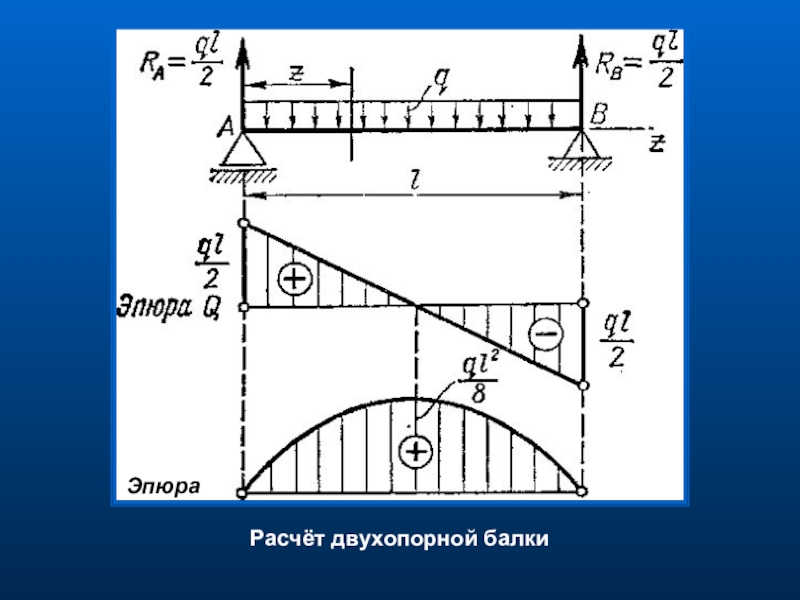 Балка весит 400 кг/м. Нарисуйте диаграммы балок и определите место на балке, где изгибающий момент равен нулю.
Балка весит 400 кг/м. Нарисуйте диаграммы балок и определите место на балке, где изгибающий момент равен нулю.
Задача 4: Простая нависающая балка длиной 112 футов выступает над левой опорой на 14 футов. Балка несет сосредоточенную нагрузку в 90 тысяч фунтов на расстоянии 12 футов от правого конца и равномерно распределенную нагрузку в 12 тысяч фунтов на фут на высоте 40 футов. участок с левого конца. Нарисуйте диаграммы балки и определите поперечную силу и изгибающий момент в сечении на расстоянии 50 футов от левого конца.
Проблема 5: Предложите улучшение этой главы.
- Нажмите на схему, чтобы развернуть ↵
УСЛОВИЯ ЗНАКОВ ДЛЯ ДИАГРАММЫ ИЗГИБАЮЩЕЙ СИЛЫ И ИЗГИБАЮЩЕГО МОМЕНТА
Знак условные обозначения для поперечной силы Предположим, что у нас есть одна балка AB, и у нас есть
предполагается один раздел XX, как показано на следующем рисунке.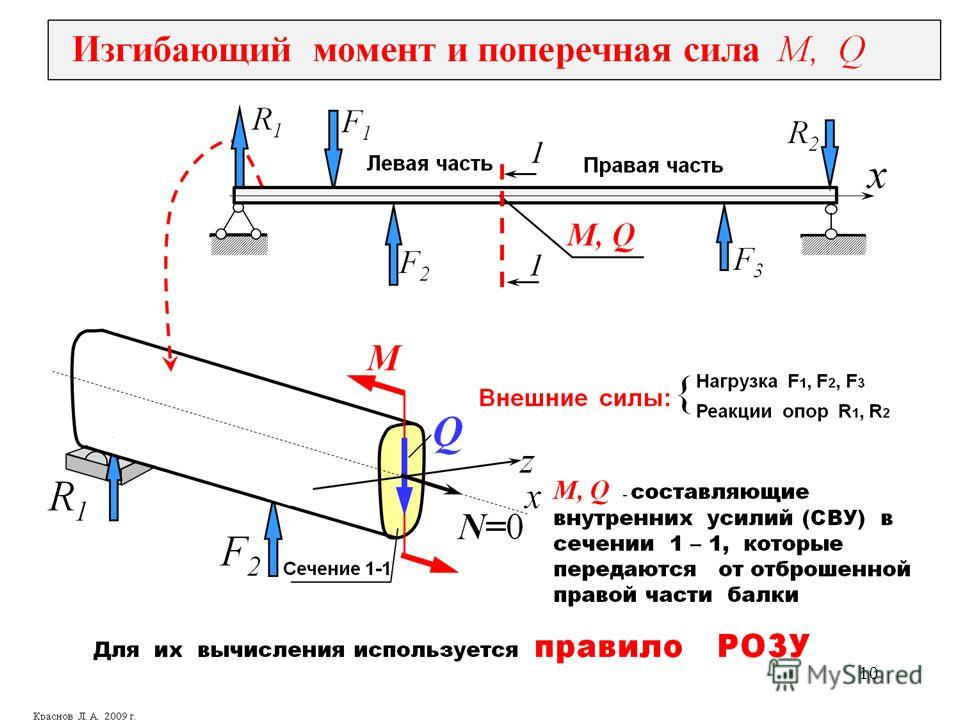 Теперь мы поймем
здесь то, какие условные знаки будут использоваться здесь для поперечной силы.
Теперь мы поймем
здесь то, какие условные знаки будут использоваться здесь для поперечной силы.
Перерезывающую силу в сечении будем считать положительна, если равнодействующая сил слева от сечения направлена вверх направление.
Перерезывающую силу в сечении будем считать положительна, если равнодействующая сил справа от сечения направлена вниз.
Сдвиг сила в сечении будет отрицательнойПеререзывающая сила в сечении будет считаться отрицательной если равнодействующая сил слева от сечения направлена вниз.
Перерезывающая сила в сечении будет считаться отрицательной если равнодействующая сил справа от сечения направлена вверх.
Знак правила гибки Предположим, что у нас есть один луч AB и у нас есть
предполагается один раздел XX, как показано на следующем рисунке. Теперь мы поймем
здесь то, какие условные знаки будут использоваться здесь для изгибающего момента.
Теперь мы поймем
здесь то, какие условные знаки будут использоваться здесь для изгибающего момента.
Изгибающий момент в сечении будем считать положительный, если изгибающий момент слева от сечения направлен по часовой стрелке а изгибающий момент справа от сечения направлен против часовой стрелки.
Такой тип изгибающего момента будет также называться провисающий изгибающий момент.
Другими словами, мы также можем сказать, что изгибающий момент при сечение считается положительным, если изгибающий момент в этом сечении будет стремиться изогнуть балку по кривизне с вогнутостью в верхней части.
Гибка момент на участке будет отрицательным Изгибающий момент в сечении будем считать отрицательным
если изгибающий момент слева от сечения направлен против часовой стрелки и
изгибающий момент справа от сечения направлен по часовой стрелке.
Такой тип изгибающего момента также называется скребком. изгибающий момент.
Точно так же мы можем также сказать, что изгибающий момент в сечение будет считаться отрицательным, если изгибающий момент в этом сечении будет стремиться изогнуть балку по кривизне, имеющей выпуклость наверху.
На рисунке выше показано состояние положительного изгибающий момент и отрицательный изгибающий момент. Легко видеть, что в случае положительный изгибающий момент, балка будет изгибаться по кривизне с вогнутостью в Топ.
Мы также можем видеть, что в случае отрицательного балка изгибающего момента будет изгибаться по кривизне с выпуклостью вверху.
Мы увидим еще одну важную тему, а именно основы диаграммы поперечной силы и изгибающего момента в категории прочности материала.
У вас есть предложения? Пожалуйста, напишите в поле для комментариев
Ссылка: Прочность материала, Р.



 3.7, б).
3.7, б).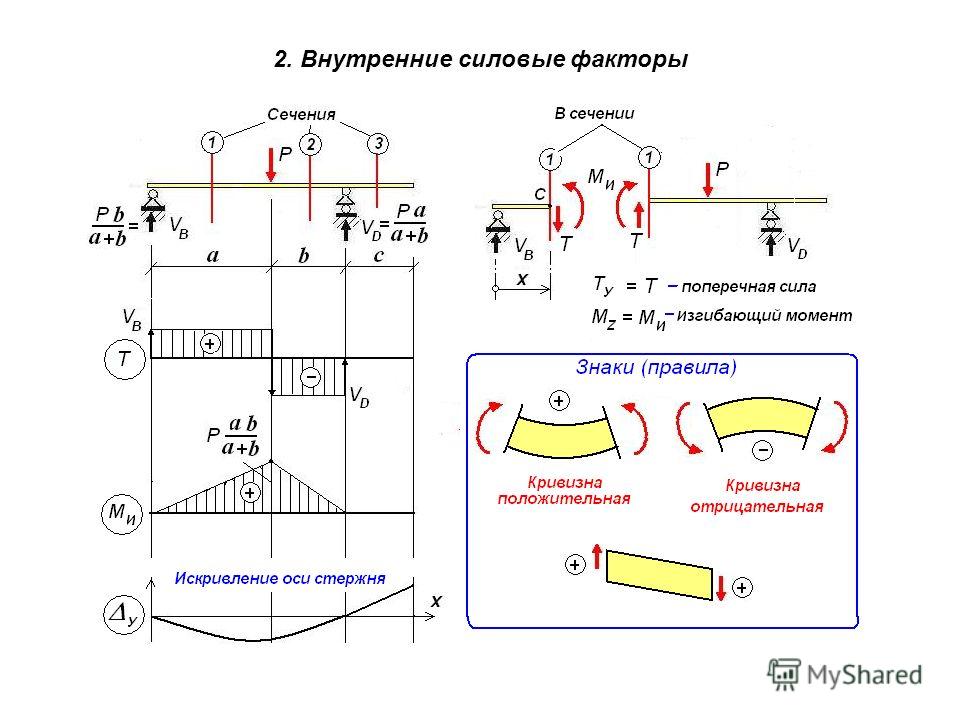
 Это даст вам R B (реакция на поддержке B).
Это даст вам R B (реакция на поддержке B).