Site Loader
Posted on 18.09.1991

Угловая частота ω в записанном выражении для мгновенного значения напряжения определяется в зависимости от заданной частоты источника переменного тока

ω = 2πf = 2 ∙ 3,14 ∙ 50 = 314 1/с .

Индуктивные сопротивления

xL1 = ω L1 = 314 ∙ 63,8 ∙ 10–3 = 20 Ом,

xL2 = ω L2 = 314 ∙ 47,8 ∙ 10–3 = 15 Ом,

xL3 = ω L3 = 314 ∙ 63,7 ∙ 10–3 = 20 Ом.

Ёмкостные сопротивления

xС2 =1/(ω С2) = 1/(314 ∙ 318 ∙ 10–6) = 10 Ом,

xС3 =1/(ω С3) = 1/(314 ∙ 212,3 ∙ 10–6) = 15 Ом.

Полное сопротивление участков цепи в комплексной форме

Преобразованная цепь изображена на рисунке 6,

a.

Чтобы не загромождать рисунок, в преобразованной схеме исключены измерительные приборы, которые на расчёт токов и напряжений не влияют.

По аналогии с цепью постоянного тока осуществляем эквивалентные преобразования цепи, представленные на рисунках 6, би в.

Рисунок 6 – Эквивалентная (а) и упрощенные (б, в) схемы цепи

Параллельно соединенные элементы z2, z3, z

4 заменяем одним эквивалентным z234

Последовательно соединенные элементы z1 и z234 заменяем одним эквивалентным

2. Для упрощенной схемы, представленной на рисунке 6, в, по закону Ома определим действующее значение комплексного тока I1 в неразветвленной части цепи

Далее определяем падение напряжения на участках:

Комплексное падение напряжения на параллельном участке:

Токи в ветвях после разветвления:

Если разветвленный участок имеет только две ветви, включенные параллельно, то токи в ветвях после разветвления можно определять без расчета Ucd,используя формулу разброса.

3. Модули показательной формы выражений для токов есть действующие значения реальных токов ветвей, которые фиксируют приборы электромагнитной системы. Следовательно, амперметр в первой ветви покажет 6,764 А.

Вольтметр, включенный параллельно емкостному элементу, покажет падение напряжения на нем.

Так как падение напряжения на участке есть произведение тока участка на значение его сопротивления, то получаем:

,

где zV– полное комплексное сопротивление участка, на котором определяется падение напряжения.

Так как в примере находим падение напряжения на емкостном элементе с сопротивлением xС3, то

Показание вольтметра есть модуль выражения

UV, т. е.UV= 51,97 В.

Ваттметр, включенный на входе цепи, показывает активную мощность, потребляемую всей схемой. Эта мощность будет действительной частью выражения комплекса полной мощности Sна входе, которае имеет вид

Активная мощность Рист = 956,34 Вт, реактивная мощность Qист = 1140,04 вар, значит показание ваттметра Рw = 956,34 Вт

4. Для проверки результатов расчета необходимо составить баланс активных и реактивных мощностей. Эти балансы показывают, что активные и реактивные мощности на входе должны быть равны сумме соответственно активных и реактивных мощностей всех потребителей.

Активная мощность на входе определена, а активные мощности отдельных потребителей рассчитывают как произведение активного сопротивления участка на квадрат действующего значения тока этого участка. В рассматриваемой схеме два активных потребителя r1 иr2. Суммарная активная мощность нагрузки

Относительная ошибка вычислений для активной мощности

Ошибка менее одного процента допускается. Она возникает из-за округ-

ления числовых данных при расчете.

Реактивную мощность потребителей определяют как произведение квадрата тока реактивного элемента на его сопротивление. Причем реактивная мощность катушки индуктивности положительна, а конденсатора отрицательна.

Формула циклической частоты колебаний в физике

Формула циклической частоты колебаний в физике

Определение и формула циклической частоты колебаний

Определение

Циклическая частота — это параметр, характеризующий колебательные движения. Обозначают эту скалярную величину как $\omega $, иногда ${\omega }_0$.

Напомним, что уравнение гармонических колебаний параметра $\xi $ можно записать как:

\[\xi \left(t\right)=A{\cos \left({\omega }_0t+{\varphi }_0\right)\ }\left(1\right),\]

где $A={\xi }_{max}$ — амплитуда колебаний величины $\xi $; $\left({\omega }_0t+{\varphi }_0\right)$=$\varphi $ — фаза колебаний; ${\varphi }_0$ — начальная фаза колебаний.

Циклическую частоту при гармонических колебаниях определяют как частную производную от фазы колебаний ($\varphi $) по времени ($t$):

\[{\omega }_0=\frac{?\varphi }{\partial t}=\dot{\varphi }\left(2\right).

\]

Циклическая частота колебаний связана с периодом ($T$) колебаний формулой:

\[{\omega }_0=\frac{2\pi }{T}\left(3\right).\]

Циклическую частоту с частотой $?$$?$ связывает выражение:

\[{\omega }_0=2\pi \nu \ \left(4\right).\]

Формулы для частных случаев нахождения циклической частоты

Пружинный маятник совершает гармонические колебания с циклической частотой равной:

\[{\omega }_0=\sqrt{\frac{k}{m}}\left(5\right),\]

$k$ — коэффициент упругости пружины; $m$ — масса груза на пружине.

Гармонические колебания физического маятника происходят с циклической частотой равной:

\[{\omega }_0=\sqrt{\frac{mga}{J}}\left(6\right),\]

где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние между центром масс маятника и точкой подвеса; $m$ — масса маятника.

Частным случаем физического маятника является математический маятник (физический маятник, масса которого сосредоточена в точке), циклическая частота его колебаний может быть найдена как:

\[{\omega }_0=\sqrt{\frac{g}{l}}\left(7\right),\]

где $l$ — длина подвеса, на которой находится материальная точка.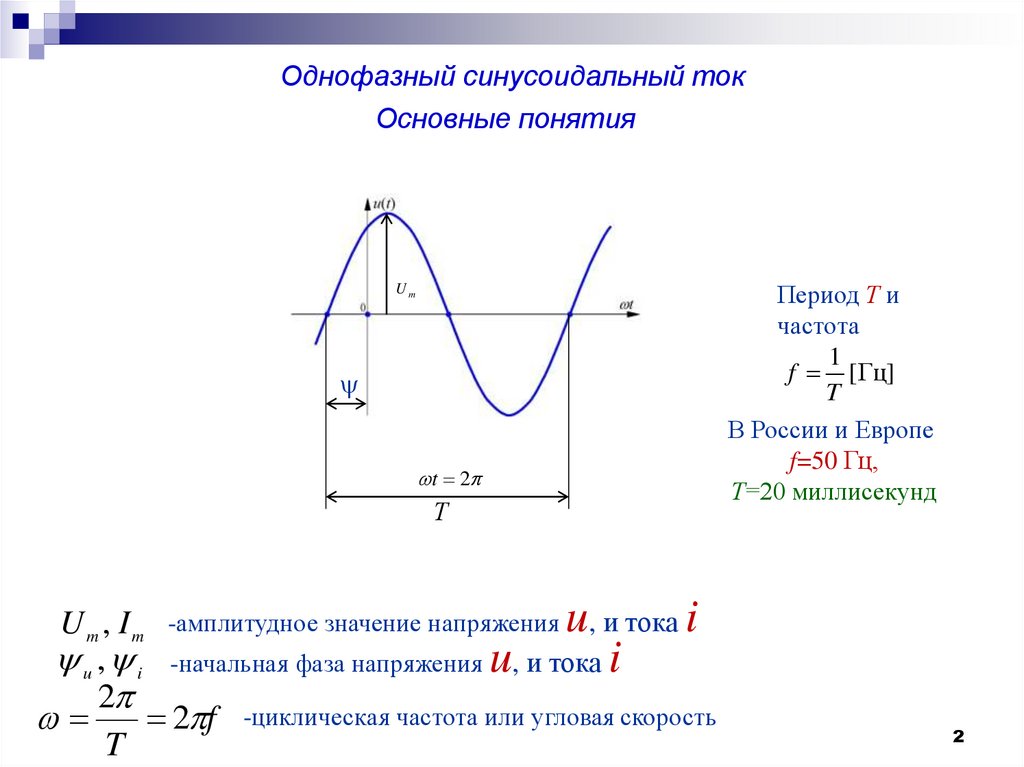 2S_1S_2}}$

Пример 2

Задание. Чему равна циклическая частота гармонических колебаний материальной точки, если амплитуда скорости точки равна ${\dot{x}}_{max}=v_0$, амплитуда ее ускорения: ${\ddot{x}}_{max}=a_0$? Начальная фаза колебаний равна нулю.

Решение. Из контекста условий задачи понятно, что колебания совершает координата $x$, поэтому уравнение колебаний (в общем виде) запишем как:

\[x\left(t\right)=A{\cos \left({\omega }_0t+{\varphi }_0\right)=\ }A{\cos \left({\omega }_0t\right)\ }\left(2.1\right),\]

По условию задачи ${\varphi }_0$=0. Тогда уравнение для скорости изменения параметра $x\left(t\right)$ имеет вид:

\[\dot{x}\left(t\right)=v\left(t\right)=-A{\omega }_0{\sin \left({\omega }_0t\right)\left(2.2\right).\ }\]

Из выражения (2.2) следует, что:

\[{\dot{x}}_{max}=v_0=A{\omega }_0\left(2. 2 \end{array} \right.\left(2.6\right).\]

Найдем отношение $\frac{a_0}{v_0}$, получим:

\[\frac{a_0}{v_0}={\omega }_0.\]

Ответ. ${\omega }_0=\frac{a_0}{v_0}$

Читать дальше: формула частоты колебаний пружинного маятника.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

[Решено] Угловая частота переменного тока в цепи L-C-R

Угловая частота переменного тока в цепи L-C-R составляет 100 рад/с. Подключенные компоненты показаны на рисунке. Найдите значение индуктивности катушки и емкости конденсатора.

  1. 1,33 ч и 250 мкл
  2. 1,33 ч и 150 мкл
  3. 0,8 ч и 150 мкл
  4. 0,8 ч и 250 мкл

Вариант 4: 0,8 ч и 250 мкф

свободно

.0002 JEE Mains Предыдущий документ 1 (проведен: 12 апреля 2019 г. , смена 2)

16,2 тыс. пользователей

90 вопросов

360 баллов

180 минут

КОНЦЕПЦИЯ:

→Потенциал конденсатора записывается как;

В C  = IX C

Здесь «I» — ток, а X C — емкостное реактивное сопротивление.

→Для индуктора потенциал записывается как;

В Л  = IX L

Здесь «I» — ток, а X L — индуктивное сопротивление.

→ Емкостное сопротивление записывается как;

 \(X_C= \frac{1}{ω C}\)

Здесь C – емкость, \(ω\) и ​​– угловая частота.

Индуктивное сопротивление записывается как;

X L = ωL

Здесь C — емкость, ω — угловая частота.

РАСЧЕТ:

Дано: Угловая частота , ω = 100 рад/с

Согласно закону Ома, V = IR

I = \(\frac{V}{R}\)

⇒I = \(\frac{15}{60 }\) = \(\frac{1}{2}\) A

Теперь потенциал конденсатора записывается как;

VC = IX C    —-(1)

и \(X_C= \frac{1}{ω C}\)

⇒ \(X_C= \frac{1}{100C}\)

и ток в конденсаторе I = \(\frac{1}{4}\) A

Теперь, подставив это значение в уравнение (1), мы имеем;

В C  = \(\frac{1}{4} \times \frac{1}{100C}\) ⇒10 = \(\frac{1}{400C}\) или,  C = \(\frac{ 1}{4000}\) = 250 мкФ

Теперь потенциал катушки индуктивности записывается как;

V L  = IX L     —-(1)

и XL = ωL

⇒XL = 100L

и ток I = \(\frac{20 }{40} \(\frac{1}{2}\) A

, а ток в катушке = \(\frac{1}{2} — \frac{1}{4}\) = \(\frac{1 }{4}\) A

Теперь, подставив это значение в уравнение (1), мы имеем;

V L  = \(\frac{1}{4} \times 100L\)

⇒ 20 = 25 L

⇒ L = 0,8 H

Следовательно, вариант 4) является правильным ответом.

Скачать решение PDF

Поделиться в WhatsApp

Последние основные обновления JEE

Последнее обновление: 22 сентября 2022 г.

Национальное агентство по тестированию (NTA) опубликовало отметку JEE Mains 2022 Cut Off Marks для бумаги I. Работа I проводилась в два этапа. Сессия 1 проводилась с 24 по 30 июня 2022 г., а сессия 2 — с 25 по 30 июля 2022 г. Всего 24 кандидата набрали 100 баллов NTA в JEE Main 2022. Национальное агентство по тестированию список лучших и количество кандидатов, прошедших квалификацию JEE Advanced 2022.

Калькулятор угловой частоты колебаний в RLC-цепи

Калькулятор угловой частоты колебаний в RLC-цепи вычислит:

  1. Угловую частоту незатухающих колебаний в RLC-цепи
  2. Угловую частоту затухающих колебаний в RLC-цепи

    3. Расчетные параметры: Токопроводящий провод цепи и материал, из которого изготовлена ​​катушка индуктивности, однородны и везде имеют одинаковую толщину; источник подает переменный ток

    Angular Frequency of Oscillations in RLC Circuit Calculator
    🖹 Normal View🗖 Full Page View
    Calculator Precision (Decimal Places)0123456789101112131415
    Resistance of the RLC circuit (R) Ω
    Inductance RLC-цепи (L) H
    Емкость RLC-цепи (C) F

    6664. Индуктивность RLC-цепи (L) Гн [Генри]
    Угловая частота колебаний RLC-цепи Результаты калькулятора (подробные расчеты и формула ниже)
    Угловая частота незатухающих колебаний в RLC-цепи рад/с [радиан в секунду]
    Угловая частота затухающих колебаний в RLC-цепи рад/с [радиан в секунду]
    Angular frequency of undamped oscillations in a RLC circuit calculation
    ω = 1 / √ L × C
    ω = 1 / √ ×
    ω = 1 / √
    ω = 1 /
    ω =
    Angular frequency of damped oscillations in a RLC circuit
    ω ‘ = √ 1 / L × C — ( R / 2L ) 2
    ω ‘ = √ 1 / × — ( / 2 × ) 2
    ω ‘ = √ 1 / — ( / ) 2
    ω ‘ = √ — 2
    ω ‘ = √ —
    ш ‘ = √
    ω ‘ =
    Угловая частота колебаний в RLC Suppulator
    Емкость RLC-цепи (C) Ф [Фарад]

    Обратите внимание, что формулы для каждого расчета вместе с подробными расчетами доступны ниже. Когда вы вводите конкретные коэффициенты каждой угловой частоты колебаний в расчете цепи rlc, калькулятор угловой частоты колебаний в цепи RLC автоматически вычисляет результаты и обновляет элементы формулы физики с каждым элементом угловой частоты колебаний в расчете цепи rlc. . Затем вы можете отправить по электронной почте или распечатать эту угловую частоту колебаний в расчете схемы rlc, если это необходимо для дальнейшего использования.

    Мы надеемся, что Калькулятор угловой частоты колебаний в цепях RLC оказался полезным для вашей версии физики. Если да, мы просим вас оценить этот калькулятор физики и, если у вас есть время, поделиться им в своей любимой социальной сети. Это позволяет нам распределять будущие ресурсы и сохранять эти калькуляторы по физике и учебные материалы бесплатными для всех по всему миру. Мы считаем, что у всех должен быть бесплатный доступ к учебным материалам по физике. Делясь с вами, вы помогаете нам охватить всех студентов-физиков и тех, кто интересуется физикой по всему миру.

    ★ ★ ★ ★ ★ [23 голоса]

    Связанные физики Секция 15: Секция

    . : Электроника

    Раздел 22: Космология

    Угловая частота незатухающих колебаний в RLC-цепи Формула и расчет

    ω = 1 / √ L × C

    Угловая частота демпфированных колебаний в схеме RLC и расчете

    ω ‘ = √ 1 / 1 / 1 /

    02010202010201020102010201020101010101010101010109тели 1 / 1 / . / 2L ) 2

    This formula derives from

    ω ‘ = √ ω 2 — ( R / 2L ) 2

    , где ω ‘ — Угловая частота демпфированных колебаний и

    ω = 1 / √ L × C 9000.

alexxlab

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *