Плюс в кружке — что он означает в математике — Журнал «Код»

Иногда в некоторых задачах и формулах можно встретить странный знак — плюс в кружке: ⨁. Рассказываем, что он означает в математике и информатике.

Информатика: исключающее или (XOR)

В статье про сложение двух чисел с помощью транзистора мы говорили о логических операциях — И, ИЛИ и НЕ. Они работают с битами, то есть с нулями и единицами. Например, логическая операция НЕ меняет значение бита на противоположное — 1 меняет на 0 и наоборот. 

Другие логические операции работают уже с двумя битами, они называются бинарными — например, логическое И, которое мы используем в половине наших проектов. Логика такая:

если оба числа — это единицы, то результат тоже будет единица, а во всех остальных случаях он будет равен нулю.

Логическое исключающее ИЛИ — это бинарная логическая операция, которая возвращает истину только тогда, когда одно из чисел — 1, а второе — 0. Обозначается так —  XOR:

0 XOR 0 = 0

0 XOR 1 = 1

1 XOR 0 = 1

1 XOR 1 = 0

В информатике эту операцию ещё называется сложением по модулю 2, когда от результата откидывается всё, что кратно двум:

0 ⨁ 0 = 0

0 ⨁ 1 = 1

1 ⨁ 0 = 1

1 + 1 = 2 ← кратно двум, поэтому отбрасываем, и получается 1 ⨁ 1 = 0

Чтобы было понятнее, как это работает, посчитаем 12 ⨁ 9 с точки зрения ИТ. Если непонятно, как из одного числа получается другое из нолей и единиц, почитайте нашу статью про двоичное счисление:

1. Переводим 12 в двоичный вид: 1100
2. Переводим 9 в двоичный вид: 1001
3. Побитово применяем XOR к каждому разряду и получаем 0101
4. Переводим 0101 в десятичный вид: 5
5. 12 ⨁ 9 = 5

Математика: некий алгоритм расчёта

Иногда на собеседованиях дают такие задания на проверку логики:

4 ⨁ 2 = 26

8 ⨁ 1 = 79

6 ⨁ 5 = 111

Чему равно 7 ⨁ 3?

Если попробовать посчитать это как XOR, то результат не совпадёт с тем, что в ответах. Это значит, что плюсом в кружке обозначается некий алгоритм расчёта, в котором нам и нужно разобраться, чтобы решить задачу. 

Алгоритм расчёта при этом может быть любым и включать в себя сколько угодно действий. В нашем случае он выглядит так:

Сначала из левого числа вычитается правое — так получается первое число в ответе: 

4 − 2 = 2

8 − 1 = 7

6 − 5 = 1

А затем, наоборот, правое число складывается с левым — так получается второе число в ответе:

4 + 2 = 6

8 + 1 = 9

6 + 5 = 11

Получается, что правильное решение будет таким: 7 ⨁ 3 = 410

Ещё математика: это прямая сумма

Ещё плюсом в кружке в математике обозначается прямая сумма — когда по определённым правилам из векторных пространств или групп создаются новые математические объекты.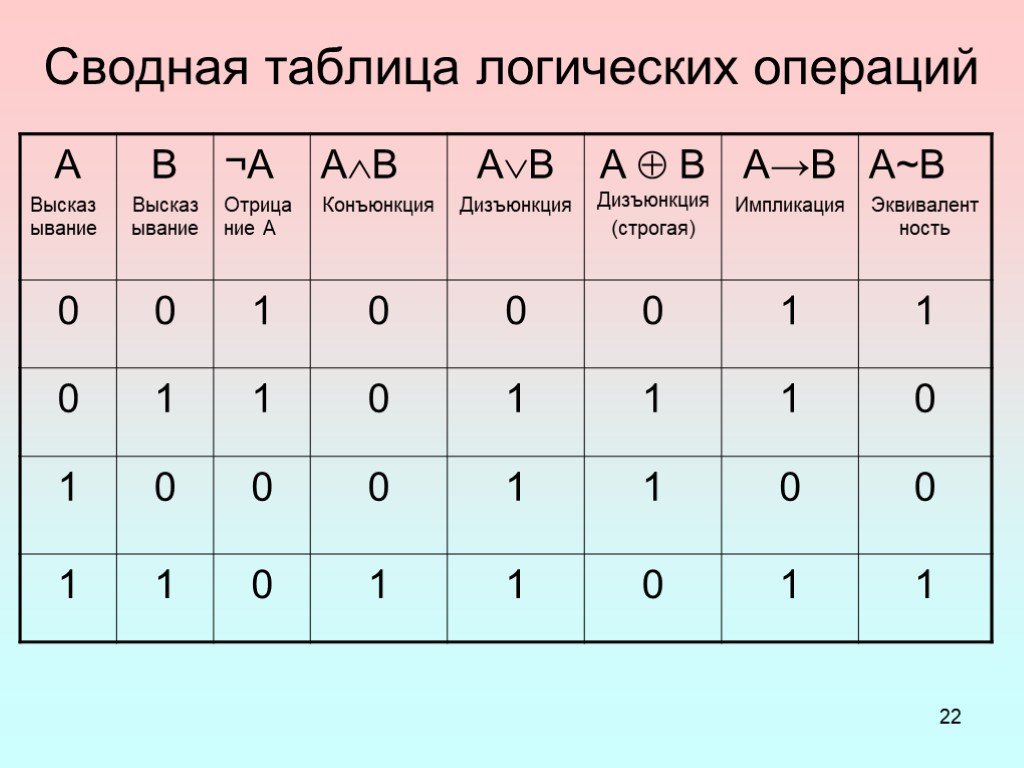 Если вы не математик, то, скорее всего, вам это никогда не пригодится, но теперь вы сможете блеснуть знаниями на очередном созвоне с коллегами.

Знакомимся с вектором

👉 Короче: 

Если вы встретили в задаче плюс в кружке, сразу уточните, что именно здесь имеется в виду: исключающее ИЛИ (XOR), некий алгоритм расчёта или прямая сумма.

Текст:

Михаил Полянин

Редактор:

Максим Ильяхов

Художник:

Даня Берковский

Корректор:

Ирина Михеева

Вёрстка:

Кирилл Климентьев

Соцсети:

Алина Грызлова

Python | Условные выражения

Последнее обновление: 13.11.2022

Ряд операций представляют условные выражения. Все эти операции принимают два операнда и возвращают логическое значение, которое в Python представляет тип bool. Существует только два логических значения — True (выражение истинно) и False (выражение ложно).

Операции сравнения

Простейшие условные выражения представляют операции сравнения, которые сравнивают два значения. Python поддерживает следующие операции сравнения:

• ==

  Возвращает True, если оба операнда равны. Иначе возвращает False.

• !=

  Возвращает True, если оба операнда НЕ равны. Иначе возвращает False.

• > (больше чем)

  Возвращает True, если первый операнд больше второго.

• < (меньше чем)

  Возвращает True, если первый операнд меньше второго.

• >= (больше или равно)

  Возвращает True, если первый операнд больше или равен второму.

• <= (меньше или равно)

  Возвращает True, если первый операнд меньше или равен второму.

Примеры операций сравнения:

a = 5
b = 6
result = 5 == 6  # сохраняем результат операции в переменную
print(result)  # False - 5 не равно 6
print(a != b)  # True
print(a > b)  # False - 5 меньше 6
print(a < b)  # True

bool1 = True
bool2 = False
print(bool1 == bool2)  # False - bool1 не равно bool2

Операции сравнения могут сравнивать различные объекты — строки, числа, логические значения, однако оба операнда операции должны представлять один и тот же тип.

Логические операции

Для создания составных условных выражений применяются логические операции. В Python имеются следующие логические операторы:

• Оператор and (логическое умножение) применяется к двум операндам:

  x and y

  Сначала оператор and оценивает выражение x, и если оно равно False, то возвращается его значение. Если оно равно True, то оценивается второй операнд — y и возвращается значение y.

  age = 22
  weight = 58
  result = age > 21 and weight == 58
  print(result)  # True
  

  В данном случае оператор and сравнивает результаты двух выражений: age > 21 weight == 58. И если оба этих выражений возвращают True, то оператор and также возвращает True (формально возвращается значение последнего операнда).

  Но операндами оператора and необязательно выступают значения True и False. Это могут быть любые значения. Например:

  result = 4 and "w"
  print(result)  # w, так как 4 равно True, поэтому возвращается значение последнего операнда
  
  result = 0 and "w"
  print(result)  # 0, так как 0 эквивалентно False
  

  В данном случае число 0 и пустая строка «» расматриваются как False, все остальные числа и непустые строки эквивалентны True

• or (логическое сложение) также применяется к двум операндам:

  x or y

  Сначала оператор or оценивает выражение x, и если оно равно True, то возвращается его значение. Если оно равно False, то оценивается второй операнд — y и возвращается значение y. Например

  age = 22
  isMarried = False
  result = age > 21 or isMarried
  print(result)  # True, так как выражение age > 21 равно True
  

  И также оператор or может применяться к любым значениям. Например:

  result = 4 or "w"
  print(result)  # 4, так как 4 эквивалентно True, поэтому возвращается значение первого операнда
  
  result = 0 or "w"
  print(result)  # w, так как 0 эквивалентно False, поэтому возвращается значение последнего операнда
  

• not (логическое отрицание)

  Возвращает True, если выражение равно False

  age = 22
  isMarried = False
  print(not age > 21)  # False
  print(not isMarried)  # True
  print(not 4)  # False
  print(not 0)  # True
  

Оператор in

Оператор in возвращает True если в некотором наборе значений есть определенное значение. Он имеет следующую форму:

значение in набор_значений

Например, строка представляет набор символов. И с помощью оператора in мы можем проверить, есть ли в ней какая-нибудь подстрока:

message = "hello world!"
hello = "hello"
print(hello in message)  # True - подстрока hello есть в строке "hello world!"

gold = "gold"
print(gold in message)  # False - подстроки "gold" нет в строке "hello world!"

Если нам надо наоборот проверить, нет ли в наборе значений какого-либо значения, то мы може использовать модификацию оператора — not in. Она возвращает True, если в наборе значений НЕТ определенного значения:

message = "hello world!"
hello = "hello"
print(hello not in message)  # False

gold = "gold"
print(gold not in message)  # True

НазадСодержаниеВперед

Какие символы в основном используются в программировании? | по plabs.id | PLABS.ID

Опубликовано в

·

Чтение: 4 мин.

·

13 октября 2021 г.

Команду построения в программировании, безусловно, нельзя отделить от «символа». Символы в компьютерном программировании — это примитивные типы данных, экземпляры которых имеют уникальную удобочитаемую форму. В программировании мы используем вызываемый символ как «оператор». Эти символы можно использовать в качестве идентификаторов, имеющих определенное назначение для каждого символа. Используется несколько символов, но это основные символы, которые используются в программировании:

1. Скобки или скобки ()

Скобки имеют особое назначение. Это часто используется для управления порядком операций в выражении и для предоставления вложенных параметров функции или метода.

Пример использования квадратных скобок в коде Python

2. Фигурные скобки или фигурные скобки {}

Скобки используются для группировки операторов и объявлений и в большинстве языков программирования C и C++. В операторах фигурные скобки входят в оператор if, цикл (пока, для и делать/пока), функции, условные операторы или операторы переключения. За открывающей фигурной скобкой { всегда должна следовать закрывающая скобка }. Эти фигурные скобки относятся к состоянию, когда сбалансирован. Если он несбалансирован (например, просто открытая фигурная скобка ‘{‘), это может привести к непроницаемым ошибкам компилятора, которые иногда трудно отследить в больших программах. Из-за разнообразия использования фигурные скобки также очень важны для синтаксиса программы. Перенос фигурных скобок на одну или две строки обычно существенно влияет на смысл программы.

Пример использования словаря в Python Code

3. Квадратные скобки []

Квадратные скобки используются для определения использования массива или, можно сказать, для индексации элементов в массиве, а также строк. В массиве индексы начинаются с нуля 0, так что первый элемент массива 1 является массивом [0] и [9] является элементом числа 10.

Пример использования квадратных скобок в Python Code

4. Точка с запятой ;

Этот символ сообщает компилятору, что он достиг конца команды или оператора. Если в предложении истории, это будет похоже на точку, чтобы просто закончить строку кода.

Пример использования точки с запятой в коде Python.

Пример использования равенства в коде Python

6. Равно… ==

Это используется для проверки равенства значений двух операндов, если да (они одинаковы), то условие становится истинным.

Например, a == 10 неверно (не то же самое)

Пример использования is equal в Python Code

7. Is Not Equal to.. !=

Используется для проверки значения двух операнов равны или нет, если значения не равны, то условие становится истинным.

Пример использования is not equal to в коде Python

8. Одинарные кавычки ‘ ‘ и двойные кавычки » »

Эти два используются одинаково, оба используются для указания того, что вы вводите символы непосредственно в код . Вы можете использовать любой из них в зависимости от ваших предпочтений. Но главный недостаток одинарной кавычки (») не поддерживается JSON.

Пример использования одинарных и двойных кавычек в коде Python

9. Математические символы +-*/%

Это символы, используемые для выполнения арифметических операций.

+ для сложения (добавляет два операнда)

— для вычитания (вычитает второй операнд)

* для умножения (умножает оба операнда)

/ для деления (делит числитель на числитель)

% для модуля (это дает остаток от деления между знаками)

Пример использования математических символов в Python Code

Математическая логика. Логика использовалась для тысяч… | Брэндон Скеррит | Заметки по информатике

Фото Michał Grosicki на Unsplash Опубликовано в

·

Чтение: 9 мин.

·

25 ноября 2017 г.

искусственный интеллект. Логика связана с истинностью и ложностью утверждений. Логика, которую мы будем изучать, будет отвечать на вопрос: «когда утверждение следует из набора утверждений?»

Ранее я уже писал здесь о логике, поэтому эта статья будет относительно короткой, когда дело доходит до объяснения все про логику. Если вы хотите понять логику, пожалуйста, прочитайте статью, которую я написал о логике. Это просто расширение того, что мы узнали.

Предложения могут быть только истинными или ложными.

Интерпретация присваивает пропозициональному утверждению истинностное значение Истина или Ложь. True или False могут быть представлены как 0 и 1 соответственно.

Существует около 500 000 способов представления логических символов, вот наиболее распространенные способы

Символ в логике 9или И или ,

Символ в электронике

Что он делает

Принимает >1 входных данных, и если оба входных значения истинны, выдает истинные значения.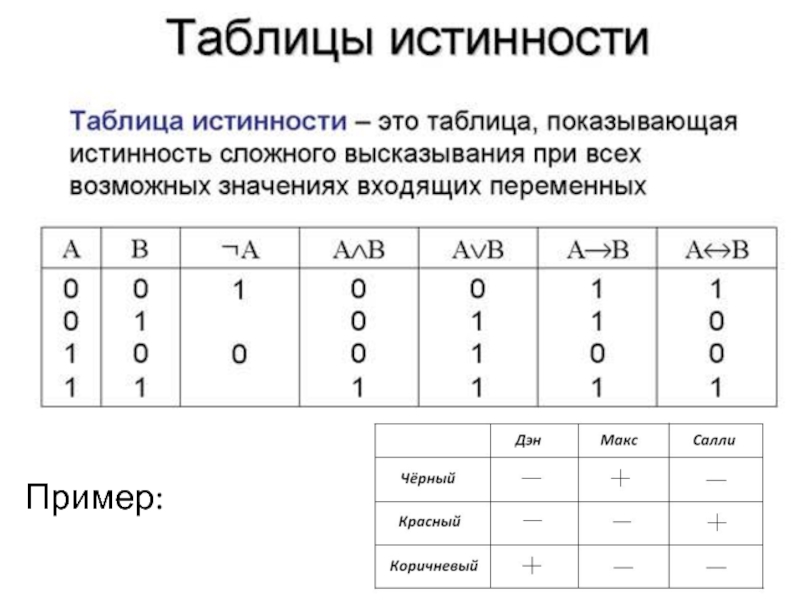

Таблица истинности

Символ в логике

V или «ИЛИ»

Символ в электронике

Что это делает

Принимает >

1 вводов, если любой из вводов верен чем вывод верен.

Таблица истинности

Символ в логике <=> или ≡

Символ в электронике Нет, это концепция, а не ворота.

Что он делает A и B должны принимать одно и то же значение истинности

Таблица истинности

A B A <=> B 1 1 = 1 0 1 = 0 1 0 = 0 0 0 = 1

Символ в Логика => или «если a, то b»

Символ в электронике Нет

Что делает Если A верно, то верно и B

Таблица истинности

Имея интерпретацию I, мы можем вычислить истинностное значение любой формулы P при I. То есть, имея версию формулы, мы можем вычислить истинностное значение.

если I(P) = 1, то мы говорим, что P истинно при интерпретации I. если I(P) = 0, то мы говорим, что P ложно при интерпретации I.

Этот раздел может помочь читателю разобраться в логических головоломках. .

На острове есть два вида жителей: рыцари, которые всегда говорят правду, и лжецы, которые всегда лгут. Вы отправляетесь на остров и встречаете А и Б. А говорит, что «Б — рыцарь» Б говорит, что «Мы двое противоположных типов»

Что такое А и Б?

Итак, у нас есть 2 варианта, р: «А — рыцарь»; и q: «B — рыцарь»

У нас есть 2 варианта, потому что один из них должен быть рыцарем. Либо и A, и B — лжецы, что делает B рыцарем, поскольку он сказал правду, значит, он солгал, либо A — рыцарь и говорит правду, что B — рыцарь.

Варианты для лица A p истинно, то есть утверждение «A — рыцарь» истинно. P => Q p ложно, то есть утверждение «A — рыцарь» ложно. ¬P => ¬Q

Варианты для человека B q истинно, тогда q => ¬p q ложно, тогда ¬q => ¬p

Теперь нам просто нужно построить таблицу истинности для этих значений

p q ¬p ¬q p => q ¬p => ¬q q => ¬p ¬q => ¬p 0 0 1 1 1 1 1 1 = 1

Тогда мы остановимся здесь, потому что мы нашли удовлетворительную интерпретацию, согласно которой они оба являются лжецами.

Примечание. Слайды лекций для этого не помогли, и для этого нет звука. Пожалуйста, напишите мне, что это такое.

Современные компьютеры используют для работы логические вентили. Вы должны иметь представление о логических элементах из приведенного выше.

Никогда не объединяйте два входных провода

Если есть 2 отдельных входа, A и B, вы не можете объединить их в один провод.

Один входной провод можно разделить на части и использовать как вход для двух отдельных ворот

Если у вас есть один вход A, его можно разделить на 2 отдельных провода.

Выходной провод можно использовать как входной

Выход провода можно использовать как вход.

Ни один выходной сигнал логического элемента не может в конечном итоге вернуться к этому логическому элементу.

Имея таблицу, подобную приведенной ниже, как бы мы построили для нее логическую схему?

Сначала вычисляем, где оно равно 1 (истинно), а затем уже оттуда формализуем его в математической логике, из математической логики мы можем вывести для него схему. Иногда проще сразу догадаться, какие логические вентили используются.

Две схемы эквивалентны, если они производят одинаковый результат при одинаковых входных данных.

2 формулы эквивалентны, если они содержат одно и то же значение истинности при всех возможных интерпретациях.

Символ «≡» используется для обозначения отношения эквивалентности.

Факты

≡ рефлексивно ≡ транзитивно ≡ симметрично

Есть несколько правил, которые мы можем использовать для упрощения пропозициональных формул.

Коммуникативное право

AB = BA, A + B = B + A

Примеры: 6 * 2 = 12 и 2 * 6 = 12 3 + 4 = 7 и 4 + 3 = 7

Ассоциационный закон

A (BC) = AB (C) = ABC

Примеры: ((BC) = AB (C) = ABC

: ( 2 + 4) + 5 = 6 + 5 = 11 2 + (4 + 5) = 2 + 9 = 11

Распределительный закон

a(b+c) = ab + ac

Пример: 3 × ( 2 + 4) = 3 * 6 = 18 3 × 2 + 3 × 4 = 6 + 12 = 18

Законы Деморгана

(A ∪ B)’ = (A)’ ∩ (B)’ Первый закон гласит, что дополнением объединения двух множеств является пересечение дополнений.

(A ∩ B)’ = (A)’ ∪ (B)’ Второй закон гласит, что дополнение пересечения двух множеств есть объединение дополнений.

Чтобы получить хороший пост в блоге о понимании этих законов, нажмите (здесь)[https://brilliant.org/wiki/de-morgans-laws/]

Прочие правила

Not Not A = A A или A и B = A A или не A и B = A и B (A или B) (A или C) = A или B и C

Что делать дальше С этого момента превратите схему в логическое выражение и упростите ее используя приведенные выше правила. 9, v или ¬.

В этом разделе мы еще немного познакомимся с логическими вентилями, рассмотрев семейство неисключающих вентилей.

Символ в логике

Нет

Символ в электронике

Что он делает узел. Выход вентиля XOR истинен только в том случае, если один из его входов отличается от другого входа.

Таблица истинности

Символ в логике

Нет

Символ в электронике

Что он делает

Логический элемент И-НЕ принимает >1 входов, а выход противоположен вентилю И.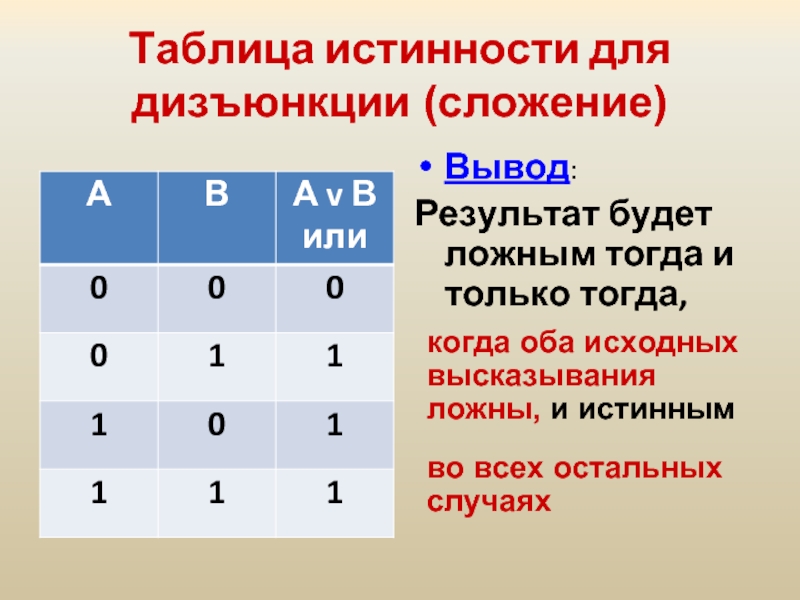 Вывод истинен, когда один или несколько, но не все входные данные ложны.

Таблица истинности

Все логические функции могут быть созданы с использованием вентилей XOR или NAND.

Двоичная система счисления, состоящая из 0 и 1.

Преобразование десятичного числа в двоичное

В качестве альтернативы вы можете запомнить степени 2. 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024… А затем, чтобы преобразовать число в двоичное, давайте скажем, 6, вы строите это из разных сил. Итак, 6 — это 011, а затем переверните это, 110

Двоичное сложение

Кое-что, что вам нужно знать о двоичном коде 0 + 0 = 0 1 + 0 = 1 0 + 1 = 1 1 + 1 = 10

Как только вы узнаете эти основные правила, вы можете складывать любые числа в двоичном формате так же, как вы можете складывать обычные числа. Попробуйте это упражнение

011

полусумматор

Полусумматор — это тип двоичного сумматора в электронике, который складывает два одиночных двоичных разряда и обеспечивает вывод плюс значение переноса.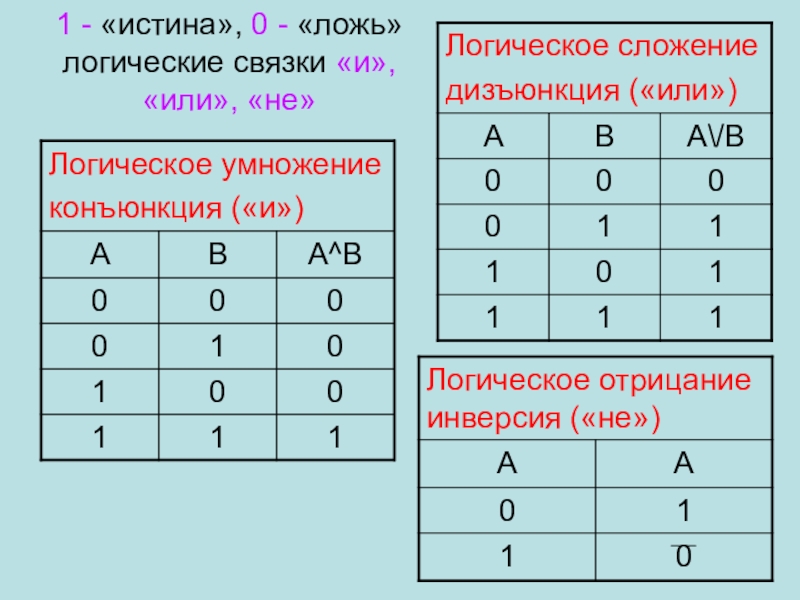

Примечание. Полусумматор Бориса слишком сложен, вы можете добиться того же, заменив 3 его логических элемента одним элементом XOR.

Таблица истинности

Полный сумматор

Полный сумматор позволяет выполнять перенос и перенос.

Посмотрите это видео для лучшего понимания

Обозначение черного ящика

Мы можем представить полный сумматор в виде черного ящика, нам не нужно знать, что происходит внутри это, только входы и выходы.

4-битный сумматор

Используя запись черного ящика, мы можем создать 4-битный сумматор

http://www.electronics-tutorials.ws/combination/comb_7.html

Компьютерное представление отрицательных целых чисел 016

Для представления целых чисел используется фиксированное количество битов: 8, 16, 32 или 64 бита. Беззнаковое целое может занимать все доступное пространство.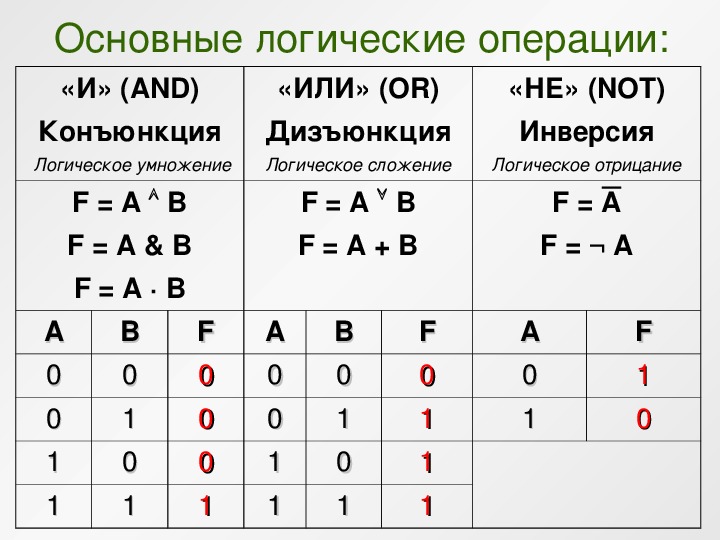

Вы можете «подписать» двоичное число, чтобы указать, отрицательное оно или нет. Например, число 10 может быть представлено в 8-битном виде как 00001010, а -10 может быть представлено в 8-битном виде как 10001010

. Но иногда это вызывает проблемы, например, 10000000 представляет -0. Чтооо?? Отрицательный 0? Да! Это верно, и это именно та проблема, которую это вызывает.

Здесь в игру вступает дополнение 2.

Дополнение до двух

Преобразование десятичной дроби в дополнение до двух

1) Преобразовать число в двоичное, игнорируя пока знак. Таким образом, 5 — это 0101, а -5 — это 0101.

2) Если число положительное, то все готово, дальше ничего не нужно. Иначе…

3) Если число отрицательное, то:

• Найдите дополнение (например, преобразуйте все 0 в 1 и все 1 в 0)
• Добавьте 1 к дополнению

Итак, инвертируйте все цифры и добавьте 1 . Простой.

Если вы хотите узнать, почему это работает, нажмите здесь

Сложение в двоичном виде, пересмотренный вариант

Перенос, выходящий за пределы конца, часто можно игнорировать, например:

-1 + -3 1111

• 1101 1100 с переносом 1, который идет до конца к влево можно не обращать внимания.