Единицы измерения массы — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 июля 2019; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 июля 2019; проверки требуют 2 правки.Исторически многие меры массы были кратны эталону — массе зерна (семени) различных растений: пшеницы, ячменя (см. гран), некоторых бобовых, риса, просо, горчицы, некоторых кактусов (в Америке)[1].
Популярной мерой веса выступали монеты: были «под рукой» и имели нормированный вес. Откуда критерий цены «дороже золота/серебра».
Метрическая система[править | править код]
Первоначально единицей измерения массы в метрической системе единиц являлся грамм, определявшийся как масса 1 см³ дистиллированной воды при температуре 4 °C и давлении в 1 атмосферу.
В настоящее время в Международной системе единиц (СИ) в качестве единицы измерения массы принят килограмм, являющийся одной из семи основных единиц СИ, а грамм представляет собой дольную единицу килограмма, равную 1/1000 килограмма. По определению, действовавшему до 2019 года, «
Кроме того, килограмм является единицей массы и относится к числу основных единиц в системах МКС, МКСА, МКСК, МКСГ, МКСЛ, МКГСС[4].
В настоящее время
- Тонна — 106 (1 000 000) граммов, или 1000 килограммов.
- Центнер — 105 (100 000) граммов, или 100 килограммов.
- Карат — 0,2 грамма.
Единицы массы в науке[править | править код]
- Атомная единица массы (а. е. м., дальтон) = 1,660 538 921(73)⋅10
- Солнечная масса M☉ = 1.98847(7)⋅1030 кг[6][7].
- Электронвольт, 1 эВ = 1,782 661 845(39)⋅10−36 кг[8][9]; применяются также кратные (килоэлектронвольт, кэВ; мегаэлектронвольт, МэВ, гигаэлектронвольт, ГэВ; тераэлектронвольт, ТэВ) и дольные (миллиэлектронвольт, мэВ) единицы.
- Масса электрона me = 9,109 382 91(40)⋅10
- Масса протона mp = 1,672 621 777(74)⋅10−27кг[11].
- Планковская единица массы MPl = 2,176 51(13)⋅10−8 кг[12].
Американская система[править | править код]
(см. также Английская система мер)
- Стоун — 14 фунтов, или 6,35029318 кг
- фунт — 453,59237 г (точное и официальное значение)
- Унция — 1/16 фунта, или 1/224 стоуна, или 28,349523125 г
- Драхма (единица измерения массы, США) — 1/16 унции, или 1/256 фунта, или 1/3584 стоуна, или 1,7718451953125 г
- Гран — 1/98000 стоуна, или 1/7000 фунта, или 1/437,5 унции, или 1/27,34375 драхмы, или 64,79891 мг
- Короткая тонна = 20 коротких хандредвейтов = 2000 фунтов = 0,90718474 т
- Короткий хандредвейт = 100 фунтов = 45,359237 кг
Британская аптечная система[править | править код]
(см. также Английская система мер)
- Тройский фунт (единица измерения), или аптечный фунт = 373,2417216 грамма
- Тройская унция = 1/12 тройского фунта, или 31,1034768 грамма
- Драхма (единица измерения массы, Великобритания) = 1/8 тройской унции, или 1/96 тройского фунта, или 3,8879346 грамма
- Скрупул = 1/3 драхмы, или 1/288 тройского фунта, или 1,2959782 грамма
- Гран = 1/20 скрупула, или 0,06479891 г
Русская система мер[править | править код]
- Берковец = 164 килограмма
- Пуд = 1/10 берковца = 40 фунтам = 1280 лотам = 3840 золотникам = 368 640 долям = 16,3804815 кг
- Фунт = 409,5120375 граммов
- Лот = 1/32 фунта = 3 золотникам = 288 долям = 12,797 251 191 395 300 грамма
- Золотник = 1/96 фунта = 4,26575417 г
- Доля = 1/96 золотника = 44,435 миллиграмма
Европейские меры массы[править | править код]
(см. также Английская система мер)
- Аса — Германия, Голландия = 0,048063 г
- Английская тонна (или длинная) = 1,016 т
- Марка — единица веса серебра или золота в средневековой Западной Европе, приблизительно равная 8 тройским унциям (249 г). Позднее марка стала использоваться как денежная единица в Англии, Шотландии, Германии и скандинавских странах.
- Тод — Англия = 12 торговых фунтов = 5,44310844 кг
- Феркин — Англия = 56 фунтов = 25,40117272 кг или = 64 фунтов = 29,02991168 кг
- Хандредвейт — Англия = 112 торговых фунтов = 50,80234544 кг
- Хогсхед — Англия = 1000 фунтов = 453,6 кг
Античные единицы массы[править | править код]
В странах Юго-Восточной Азии[править | править код]
Древнееврейские единицы массы[править | править код]
Арабские единицы массы[править | править код]
как обозначается масса тела в физике
В физике все обозначается первыми буквами от английского (или латинского) m — mass (масс) p — pressure (давление) V- volume (объем) T — temperature (температура) v — velocite (скорость) t — time (время)
Мю — Википедия
| Буква греческого алфавита мю | |
|---|---|
| Μμ | |
Изображение
| |
| Μ: greek capital letter mu μ: greek small letter mu | |
| Юникод | Μ: U+039C μ: U+03BC |
| HTML-код | Μ: μ: |
| UTF-16 | Μ: 0x39C μ: 0x3BC |
| Μ: %CE%9C μ: %CE%BC | |
| Мнемоника | Μ: Μμ: μ |
Μ, μ (название: мю, греч. μι, др.-греч. μῦ) — 12-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 40. Происходит от финикийской буквы 
— мем. От буквы мю произошли латинская буква M и кириллическая М.
Новогреческое название — ми (μι [miː]).
Строчная буква μ широко используется во многих отраслях науки, в отличие от заглавной Μ, которая совпадает по написанию с латинской или кириллической буквами.
В математике[править | править код]
В физике[править | править код]
Молярная масса — Википедия
Моля́рная ма́сса — характеристика вещества, отношение массы вещества к его количеству. Численно равна массе одного моля вещества, то есть массе вещества, содержащего число частиц, равное числу Авогадро. Молярная масса, выраженная в г/моль, численно совпадает с молекулярной массой, выраженной в а. е. м., и относительной молекулярной массой. Однако надо чётко представлять разницу между молярной массой и молекулярной массой, понимая, что они равны лишь численно и отличаются по размерности[1].
Молярные массы сложных молекул можно определить, суммируя молярные массы входящих в них элементов. Например, молярная масса воды h3O{\displaystyle {\ce {h3O}}} есть
- M(h3O)=2⋅M(H)+M(O)=2⋅1 g/mol+16 g/mol=18 g/mol{\displaystyle M({\ce {h3O}})=2\cdot M({\ce {H}})+M({\ce {O}})=2\cdot 1~{\rm {{g/mol}+16~{\rm {{g/mol}=18~{\rm {g/mol}}}}}}}
Например, молярная масса кислорода как элемента M(O)=16{\displaystyle M\left({\ce {O}}\right)=16} г/моль, а в виде простого вещества, состоящего из молекул O2{\displaystyle {\ce {O2}}}, M(O2)=32{\displaystyle M\left({\ce {O2}}\right)=32} г/моль.
В Международной системе единиц (СИ) единицей измерения молярной массы является килограмм на моль (русское обозначение: кг/моль; международное: kg/mol), но из-за того, что когда молярная масса выражена в г/моль, её численное значение совпадает с относительной молекулярной массой, исторически сложилось, что молярную массу, как правило, выражают в г/моль.
Молярную массу в формулах обычно обозначают заглавной буквой M{\displaystyle M}.
Молярная масса некоторых веществ и смесей[править | править код]
Округлённые до целого числа молекулярные массы некоторых веществ и смесей приведены в таблице.
Средняя молярная масса M¯{\displaystyle {\bar {M}}} смеси нескольких индивидуальных веществ с разными молярными массами M1,M2…Mn{\displaystyle M_{1},M_{2}…M_{n}} может быть вычислена через мольные доли x1,x2…xn{\displaystyle x_{1},x_{2}…x_{n}} веществ в смеси как среднее арифметическое взвешенное мольных долей[2]:
- M¯=∑i=1nxiMi∑i=1nxi=∑i=1nxiMi,{\displaystyle {\bar {M}}={\frac {\sum _{i=1}^{n}x_{i}M_{i}}{\sum _{i=1}^{n}x_{i}}}=\sum _{i=1}^{n}x_{i}M_{i},}
так как ∑i=1nxi=1.{\displaystyle \sum _{i=1}^{n}x_{i}=1.}
Если состав вещества задан через массовые доли w1,w2…wn{\displaystyle w_{1},w_{2}…w_{n}} индивидуальных веществ, то средняя молярная масса определяется через среднее гармоническое взвешенное массовых долей[2]:
- M¯=∑i=1nwi∑i=1nwi/Mi=1∑i=1nwi/Mi.{\displaystyle {\bar {M}}={\frac {\sum _{i=1}^{n}w_{i}}{\sum _{i=1}^{n}w_{i}/M_{i}}}={\frac {1}{\sum _{i=1}^{n}w_{i}/M_{i}}}.}
Средняя молярная масса важна для смесей газов, так как входит в термодинамические уравнения состояния газовых смесей.
Например, молярная масса воздуха Ma¯{\displaystyle {\bar {M_{a}}}}, в предположении, для простоты пренебрегаем другими газами, что он состоит на 23,2 масс. % (21 об. %) из кислорода, 75,4 масс. % (78 об. %) азота и 1,4 масс. % (1 об. %) аргона (молярные массы 32; 28 и 40 г/моль соответственно) даёт для средней молярной массы воздуха:
- Ma¯=21⋅32+78⋅28+1⋅40100=10075,4/28+23,2/32+1,4/40=28,96{\displaystyle {\bar {M_{a}}}={\frac {21\cdot 32+78\cdot 28+1\cdot 40}{100}}={\frac {100}{75,4/28+23,2/32+1,4/40}}=28,96} г/моль.
Более точный расчет средней молярной массы сухого воздуха дает 28,97 г/моль[3].
Для высокомолекулярных веществ, состоящих из молекул с разной молярной массой, например, полимеров, иногда указывают среднюю молярную массу или диапазон молярных масс.
Глинка Н. Л. Общая химия: Учеб. пособие для вузов /Под ред. А. И. Ермакова. — 30-е изд., испр. — М.: ИНТЕГРАЛ-ПРЕСС, 2005. — 728 с.: ил. — ISBN 5-89602-017-1.
| Символ (TeX) | Символ (Unicode) | Название | Значение | Пример |
|---|---|---|---|---|
| Произношение | ||||
| Раздел математики | ||||
| ⇒ → ⊃ | Импликация, следование | означает «если верно, то также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒, или для обозначения надмножества, см. ниже.). | верно, но неверно (так как также является решением). | |
| «влечёт» или «если…, то» | ||||
| везде | ||||
| ⇔ | Равносильность | означает « верно тогда и только тогда, когда верно». | ||
| «если и только если» или «равносильно» | ||||
| везде | ||||
| ∧ | Конъюнкция | истинно тогда и только тогда, когда и оба истинны. | , если — натуральное число. | |
| «и» | ||||
| Математическая логика | ||||
| ∨ | Дизъюнкция | истинно, когда хотя бы одно из условий и истинно. | , если — натуральное число. | |
| «или» | ||||
| Математическая логика | ||||
| ¬ | Отрицание | истинно тогда и только тогда, когда ложно . | ||
| «не» | ||||
| Математическая логика | ||||
| ∀ | Квантор всеобщности | обозначает « верно для всех ». | ||
| «Для любых», «Для всех» | ||||
| Математическая логика | ||||
| ∃ | Квантор существования | означает «существует хотя бы один такой, что верно » | (подходит число 5) | |
| «существует» | ||||
| Математическая логика | ||||
| = | Равенство | обозначает « и обозначают одно и то же значение». | 1 + 2 = 6 − 3 | |
| «равно» | ||||
| везде | ||||
| := :⇔ | Определение | означает « по определению равен ». означает « по определению равносильно » | (Гиперболический косинус) (Исключающее или) | |
| «равно/равносильно по определению» | ||||
| везде | ||||
| { , } | Множество элементов | означает множество, элементами которого являются , и . | (множество натуральных чисел) | |
| «Множество…» | ||||
| Теория множеств | ||||
| { | } { : } | Множество элементов, удовлетворяющих условию | означает множество всех таких, что верно . | ||
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
| ∅ {} | Пустое множество | и означают множество, не содержащее ни одного элемента. | ||
| «Пустое множество» | ||||
| Теория множеств | ||||
| ∈ ∉ | Принадлежность/непринадлежность к множеству | означает « является элементом множества » означает « не является элементом множества » | ||
| «принадлежит», «из» «не принадлежит» | ||||
| Теория множеств | ||||
| ⊆ ⊂ | Подмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является подмножеством», «включено в» | ||||
| Теория множеств | ||||
| ⊇ ⊃ | Надмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является надмножеством», «включает в себя» | ||||
| Теория множеств | ||||
| ⊊ | Собственное подмножество | означает и . | ||
| «является собственным подмножеством», «строго включается в» | ||||
| Теория множеств | ||||
| ⊋ | Собственное надмножество | означает и . | ||
| «является собственным надмножеством», «строго включает в себя» | ||||
| Теория множеств | ||||
| ∪ | Объединение | означает множество элементов, принадлежащих или (или обоим сразу). | ||
| «Объединение … и …», «…, объединённое с …» | ||||
| Теория множеств | ||||
| ⋂ | Пересечение | означает множество элементов, принадлежащих и , и . | ||
| «Пересечение … и … », «…, пересечённое с …» | ||||
| Теория множеств | ||||
| \ | Разность множеств | означает множество элементов, принадлежащих , но не принадлежащих . | ||
| «разность … и … », «минус», «… без …» | ||||
| Теория множеств | ||||
| → | Функция | означает функцию с областью определения и областью прибытия (областью значений) . | Функция , определённая как | |
| «из … в», | ||||
| везде | ||||
| ↦ | Отображение | означает, что образом после применения функции будет . | Функцию, определённую как , можно записать так: | |
| «отображается в» | ||||
| везде | ||||
| N или ℕ | Натуральные числа | означает множество или реже (в зависимости от ситуации). | ||
| «Эн» | ||||
| Числа | ||||
| Z или ℤ | Целые числа | означает множество | ||
| «Зед» | ||||
| Числа | ||||
| Q или ℚ | Рациональные числа | означает | ||
| «Ку» | ||||
| Числа | ||||
| R или ℝ | Вещественные числа, или действительные числа | означает множество всех пределов последовательностей из | ( — комплексное число: ) | |
| «Эр» | ||||
| Числа | ||||
| C или ℂ | Комплексные числа | означает множество | ||
| «Це» | ||||
| Числа | ||||
| < > | Сравнение | обозначает, что строго меньше . означает, что строго больше . | ||
| «меньше чем», «больше чем» | ||||
| Отношение порядка | ||||
| ≤ или ⩽ ≥ или ⩾ | Сравнение | означает, что меньше или равен . означает, что больше или равен . | ||
| «меньше или равно»; «больше или равно» | ||||
| Отношение порядка | ||||
| ≈ | Приблизительное равенство | с точностью до означает, что 2,718 отличается от не больше чем на . | с точностью до . | |
| «приблизительно равно» | ||||
| Числа | ||||
| √ | Арифметический квадратный корень | означает неотрицательное действительное число, которое в квадрате даёт . | ||
| «Корень квадратный из …» | ||||
| Числа | ||||
| ∞ | Бесконечность | и суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел. | ||
| «Плюс/минус бесконечность» | ||||
| Числа | ||||
| | | | Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества | обозначает абсолютную величину . обозначает мощность множества и равняется, если конечно, числу элементов . | ||
| «Модуль»; «Мощность» | ||||
| Числа и Теория множеств | ||||
| ∑ | Сумма, сумма ряда | означает «сумма , где принимает значения от 1 до », то есть . означает сумму ряда, состоящего из . | ||
| «Сумма … по … от … до …» | ||||
| Арифметика, Математический анализ | ||||
| ∏ | Произведение | означает «произведение для всех от 1 до », то есть | ||
| «Произведение … по … от … до …» | ||||
| Арифметика | ||||
| ! | Факториал | означает «произведение всех натуральных чисел от 1 до включительно, то есть | ||
| « факториал» | ||||
| Комбинаторика | ||||
| ∫ | Интеграл | означает «интеграл от до функции от по переменной ». | ||
| «Интеграл (от … до …) функции … по (или d)…» | ||||
| Математический анализ | ||||
| df/dx f'(x) | Производная | или означает «(первая) производная функции от по переменной ». | ||
| «Производная … по …» | ||||
| Математический анализ | ||||
| Производная -го порядка | или (во втором случае если — фиксированное число, то оно пишется римскими цифрами) означает «-я производная функции от по переменной ». | |||
| «-я производная … по …» | ||||
| Математический анализ |
Килограмм — Википедия
Килогра́мм (русское обозначение: кг; международное: kg) — единица измерения массы, одна из семи основных единиц Международной системы единиц (СИ). Кроме того, является единицей массы и относится к числу основных единиц в системах МКС, МКСА, МКСК, МКСГ, МКСЛ, МКГСС[1]. Килограмм является единственной из основных единиц системы СИ, которая используется с приставкой («кило», обозначение «к»).
XXVI Генеральная конференция по мерам и весам (13—16 ноября 2018 года) одобрила[2] определение килограмма
, основанное на фиксации численного значения постоянной Планка. Решение вступило в силу 20 мая 2019 года.
Килограмм, обозначение кг, является единицей массы в СИ; его величина устанавливается фиксацией численного значения постоянной Планка h равной в точности 6,62607015⋅10-34, когда она выражена единицей СИ Дж⋅с, которая эквивалентна кг⋅м2⋅с−1, где метр и секунда определены через c и ΔνCs.[3][4]
Действовавшее до мая 2019 года определение килограмма было принято III Генеральной конференцией по мерам и весам (ГКМВ) в 1901 году и формулировалось так[5][6]:
Килограмм — единица массы, равная массе международного прототипа килограмма.
До 20 мая 2019 года килограмм оставался последней единицей СИ, определенной на основе изготовленного человеком объекта. После принятия нового определения с практической точки зрения величина килограмма не изменилась, но существующий «прототип» (эталон) более не определяет килограмм, а является очень точной гирькой с потенциально измеримой погрешностью.
Международный прототип (эталон) килограмма хранится в Международном бюро мер и весов (расположено в Севре близ Парижа) и представляет собой цилиндр диаметром и высотой 39,17 мм из платино-иридиевого сплава (90 % платины, 10 % иридия).
Современный международный эталон килограмма был выпущен Генеральной конференцией по мерам и весам (ГКМВ) в 1889 году на основе Метрической конвенции (1875) и передан на хранение Международному бюро мер и весов (МБМВ), действующему от имени ГКМВ. Международный эталон килограмма практически не подвергается какому-либо перемещению или использованию. Его копии хранятся в национальных метрологических учреждениях по всему миру. В 1889, 1948, 1989 и 2014 годах проводились верификации копий с эталоном с целью обеспечить единство измерений массы относительно эталона[7]. Поскольку были обнаружены изменения масс копий эталона, Международный комитет мер и весов (МКМВ) рекомендовал переопределить килограмм с помощью фундаментальных физических свойств.
Связь между массой и постоянной Планка с теоретической точки зрения определяется двумя формулами[8]. Эквивалентность массы и энергии связывает энергию E{\displaystyle E} и массу m{\displaystyle m}:
- E=mc2,{\displaystyle \ E=mc^{2},}
где c{\displaystyle c} — скорость света в вакууме. Постоянная Планка h{\displaystyle h} связывает квантовое и традиционное понятия энергии:
- E=hν,{\displaystyle E=h\nu ,}
где ν{\displaystyle \nu } — частота.
Эти две формулы, найденные в начале XX века, устанавливают теоретическую возможность измерения массы через энергию индивидуальных фотонов, но практические эксперименты, позволяющие связать массу и постоянную Планка, появились лишь в конце XX века.
Весы Киббла использовались с середины 1970-х годов для измерения величины постоянной Планка. Сотрудники Национального института стандартов США П. Мор (англ. Peter Mohr) и Б. Тэйлор (англ. Barry Taylor) в 1999 году предложили, наоборот, зафиксировать величину постоянной Планка и определять с помощью этих весов массу. Посмертно названные в честь изобретателя, Б. Киббла (англ.)русск., весы Киббла — это усовершенствование токовых весов, они представляют собой электромеханический инструмент, где масса вычисляется через электрическую мощность:
- U1I2=mgv1,{\displaystyle U_{1}I_{2}=mgv_{1},}
где U1I2{\displaystyle U_{1}I_{2}} — произведение электрического тока I2{\displaystyle I_{2}} во время балансирования массы и напряжения U1{\displaystyle U_{1}} в процессе калибровки, gv1{\displaystyle gv_{1}} — произведение ускорения свободного падения g{\displaystyle g} и скорости катушки v1{\displaystyle v_{1}} во время калибровки весов. Если gv1{\displaystyle gv_{1}} независимо замерено с высокой точностью (практические особенности эксперимента также требуют высокоточного замера частоты[9]), предыдущее уравнение по сути определяет килограмм в зависимости от величины ватта (или наоборот). Индексы у U1{\displaystyle U_{1}} и I2{\displaystyle I_{2}} введены с тем, чтобы показать, что это виртуальная мощность (замеры напряжения и тока делаются в разное время), избегая эффектов от потерь (которые могли бы быть вызваны, например, наведёнными токами Фуко)[10].
Связь между ваттом и постоянной Планка использует эффект Джозефсона и квантовый эффект Холла[9][11]:
- поскольку I2=U2R{\displaystyle I_{2}={\frac {U_{2}}{R}}}, где R{\displaystyle R} — электрическое сопротивление, U1I2=U1U2R{\displaystyle U_{1}I_{2}={\frac {U_{1}U_{2}}{R}}};
- эффект Джозефсона: U(n)=nf(h3e){\displaystyle U(n)=nf\left({\frac {h}{2e}}\right)};
- квантовый эффект Холла: R(i)=1i(he2){\displaystyle R(i)={\frac {1}{i}}\left({\frac {h}{e^{2}}}\right)},
где n{\displaystyle n} и i{\displaystyle i} — целые числа (первое связано со ступенькой Шапиро, второе — фактор заполнения плато квантового эффекта Холла), f{\displaystyle f} — частота из эффекта Джозефсона, e{\displaystyle e} — заряд электрона. После подстановки выражений для U{\displaystyle U} и R{\displaystyle R} в формулу для мощности и объединения всех целочисленных коэффициентов в одну константу C{\displaystyle C}, масса оказывается линейно связанной с постоянной Планка:
- m=Cf1f2hgv1{\displaystyle m=Cf_{1}f_{2}{\frac {h}{gv_{1}}}}.
Поскольку все остальные величины в этом уравнении могут быть определены независимо от массы, оно смогло быть принято за определение единицы массы после фиксации значения 6,62607015×10−34 Дж·с для постоянной Планка.[12]
Слово «килограмм» произошло от французского слова «kilogramme», которое в свою очередь образовалось из греческих слов «χίλιοι» (хилиои), что означает «тысяча», и «γράμμα» (грамма), что означает «маленький вес»[13] Слово «kilogramme» закреплено во французском языке в 1795 году[14]. Французское написание слова перешло в Великобританию, где впервые оно было использовано в 1797 году[15], в то время как в США слово стало использоваться в форме «kilogram», позднее ставшее популярным и в Великобритании[16][К 1]Положение о мерах и весах (англ. Weights and Measures Act) в Великобритании не запрещает использование обоих написаний[17].
В XIX веке французское сокращение «kilo» было заимствовано в английский язык, где стало применяться для обозначения как килограммов[18], так и километров[19].
Идея использовать заданный объём воды для определения единицы измерения массы была предложена английским философом Джоном Уилкинсом в его эссе 1668 года как способ связать массу и длину[20][21].
7 апреля 1795 года грамм был принят во Франции как «абсолютный вес объёма чистой воды, равного кубу [со стороной] в сотую часть метра, и при температуре тающего льда»[22][23]. В это же время была поручена работа с необходимой точностью определить массу кубического дециметра (литра) воды[К 2][22].
Поскольку торговля и коммерция обычно имеют дело с предметами, чья масса намного значительней одного грамма, и поскольку стандарт массы, изготовленный из воды, был бы неудобен в обращении и сохранении, было предписано отыскать способ практической реализации такого определения. В связи с этим был изготовлен временный эталон массы в виде металлического предмета в тысячу раз тяжелее, чем грамм, — 1 кг.
Французский химик Луи Лефёвр-Жино (англ. Louis Lefèvre-Gineau) и итальянский натуралист Джованни Фабброни (англ. Giovanni Fabbroni) после нескольких лет исследований решили переопределить наиболее устойчивую точку воды: температура, при которой вода имеет наибольшую плотность, которая была определена в 4 °C[К 3][24]. Они решили, что 1 дм³ воды при своей максимальной плотности эквивалентен 99,9265 % массы временного эталона килограмма, изготовленного четыре года назад[К 4]. Интересно, что масса 1 м³ дистиллированной воды при 4 °C и атмосферном давлении, принятая за ровно 1000 килограммов в историческом определении 1799 года, согласно современному определению тоже составляет приблизительно 1000,0 килограммов[25].
Временный эталон был изготовлен из латуни и постепенно покрылся бы патиной, что было нежелательно, поскольку его масса не должна была меняться. В 1799 году под руководством Лефёвра-Жено и Фабброни был изготовлен постоянный эталон килограмма из пористой платины, которая химически инертна. С этого момента масса эталона стала основным определением килограмма. Сейчас этот эталон известен как kilogramme des Archives (с фр. — «архивный килограмм»)[25].
Копия эталона 1 кг, хранится в США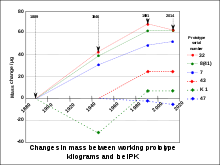
Дрейф массы копий эталонаЗа XIX век технологии измерения массы значительно продвинулись. В связи с этим, а также в преддверии создания в 1875 году Международного бюро мер и весов, специальная международная комиссия запланировала переход к новому эталону килограмма. Этот эталон, называемый «международный прототип килограмма», был изготовлен из платиново-иридиевого сплава (более прочного, чем чистая платина) в виде цилиндра высотой и диаметром 39 мм[26], и с тех пор он хранится в Международном бюро мер и весов. В 1889 году было принято международное определение килограмма как массы международного прототипа килограмма[25]; это определение действовало до 2019 года.
Были изготовлены также копии международного прототипа килограмма: шесть (на данный момент) официальных копий; несколько рабочих эталонов, используемых, в частности, для отслеживания изменения масс прототипа и официальных копий; и национальные эталоны, калибруемые по рабочим эталонам[25]. Две копии международного эталона были переданы России[26], они хранятся во ВНИИ метрологии им. Менделеева.
За время, прошедшее с изготовления международного эталона, его несколько раз сравнивали с официальными копиями. Измерения показали рост массы копий относительно эталона в среднем на 50 мкг за 100 лет[27][28]. Хотя абсолютное изменение массы международного эталона не может быть определено с помощью существующих методов измерения, оно определённо должно иметь место[27]. Для оценки величины абсолютного изменения массы международного прототипа килограмма приходилось строить модели, учитывающие результаты сравнений масс самого прототипа, его официальных копий и рабочих эталонов (при этом, хотя обычно участвующие в сравнении эталоны обычно предварительно промывали и чистили, но не всегда), что дополнительно усложнялось отсутствием полного понимания причин изменений масс. Это привело к пониманию необходимости ухода от определения килограмма на основе материальных предметов[25].
В 2011 году XXIV Генеральная конференция по мерам и весам приняла Резолюцию, в которой предложено в будущей ревизии Международной системы единиц (СИ) продолжить переопределение основных единиц таким образом, чтобы они были основаны не на созданных человеком артефактах, а на фундаментальных физических постоянных или свойствах атомов[29]. В частности предлагалось, что «килограмм останется единицей массы, но его величина будет установлена путём фиксации численного значения постоянной Планка в точности равным 6,626 06X⋅10−34, когда она выражается единицей СИ м2·кг·с−1, которая равна Дж·с». В Резолюции отмечается, что сразу после предполагаемого переопределения килограмма масса его международного прототипа будет равна 1 кг, но это значение приобретёт погрешность и впоследствии будет определяться экспериментально. Такое определение килограмма стало возможным благодаря прогрессу физики в XX веке.
В 2014 году было проведено внеочередное сравнение масс международного прототипа килограмма, его официальных копий и рабочих стандартов; на результатах этого сравнения основаны рекомендованные значения фундаментальных постоянных CODATA 2014 и 2017 годов, на которых, в свою очередь, основывается новое определение килограмма.
Рассматривалось также альтернативное определение килограмма, основанное на результатах работы проекта «Авогадро» (англ. The Avogadro Project). Команда проекта, создав сферу из кристалла моноизотопного кремния 28Si массой 1 кг и рассчитав количество атомов в ней, предполагает описать килограмм как определённое количество атомов данного изотопа кремния[30]. Однако Международное бюро мер и весов не стало использовать такой вариант определения килограмма[29][31].
XXVI Генеральная конференция по мерам и весам в ноябре 2018 года одобрила[2] новое определение килограмма, основанное на фиксации численного значения постоянной Планка. Решение вступило в силу во Всемирный день метрологии 20 мая 2019 года.
На практике, взвешивание на весах Киббла — это чрезвычайно сложный эксперимент, и потому Генеральная конференция по мерам и весам в 2011 году рекомендовала создать набор вторичных стандартов в виде привычных гирек, включая как существующие платино-иридиевые эталоны, так и новые сферы из кремния, которые будут далее использоваться для распространения эталона по миру[9].
По историческим причинам, название «килограмм» уже содержит десятичную приставку «кило», поэтому кратные и дольные единицы образуют, присоединяя стандартные приставки СИ к названию или обозначению единицы измерения «грамм» (которая в системе СИ сама является дольной: 1 г = 10−3 кг).
Вместо мегаграмма (1000 кг), как правило, используют единицу измерения «тонна».
В определениях мощности атомных бомб в тротиловом эквиваленте вместо гигаграмма применяется килотонна, вместо тераграмма — мегатонна.
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 101 г | декаграмм | даг | dag | 10−1 г | дециграмм | дг | dg |
| 102 г | гектограмм | гг | hg | 10−2 г | сантиграмм | сг | cg |
| 103 г | килограмм | кг | kg | 10−3 г | миллиграмм | мг | mg |
| 106 г | мегаграмм | Мг | Mg | 10−6 г | микрограмм | мкг | µg |
| 109 г | гигаграмм | Гг | Gg | 10−9 г | нанограмм | нг | ng |
| 1012 г | тераграмм | Тг | Tg | 10−12 г | пикограмм | пг | pg |
| 1015 г | петаграмм | Пг | Pg | 10−15 г | фемтограмм | фг | fg |
| 1018 г | эксаграмм | Эг | Eg | 10−18 г | аттограмм | аг | ag |
| 1021 г | зеттаграмм | Зг | Zg | 10−21 г | зептограмм | зг | zg |
| 1024 г | иоттаграмм | Иг | Yg | 10−24 г | иоктограмм | иг | yg |
| применять не рекомендуется не применяются или редко применяются на практике | |||||||
- Комментарии
- ↑ Написание kilogram является современной формой, используемой Международным бюро мер и весов, Национальным институтом стандартов и технологий (NIST), Национальным метрологическим бюро (англ. National Measurement Office) Великобритании, Национальным научно-исследовательским советом Канады, и Национальным институтом измерений (англ. National Measurement Institute) Австралии.
- ↑ Эта же директива определила литр как «единицу измерения объёма как для жидкостей, так и для твёрдых тел, которая равна объёму куба [со стороной] в десятую часть метра». Оригинальный текст: «Litre, la mesure de capacité, tant pour les liquides que pour les matières sèches, dont la contenance sera celle du cube de la dixièrne partie du mètre.»
- ↑ Современные измерения показывают, что температура, при которой вода имеет наибольшую плотность, составляет 3,984 °C. Однако учёные конца XVIII века использовали значение 4 °C.
- ↑ Временный эталон килограмма был изготовлен в соответствии с единственным неточным измерением плотности воды, сделанным ранее Антуаном Лавуазье и Рене Жюст Гаюи, которое показало, что один кубический дециметр дистиллированной воды при 0 °C имеет массу в 18 841 гран согласно французской системе мер (англ. Units of measurement in France), которой скоро предстояло исчезнуть. Более новое и аккуратное измерение, проведённое Лефёвром-Жино и Фабброни, показало, что масса кубического дециметра воды при температуре 4 °C составляет 18 827,15 гран
- Источники
- ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 61. — 240 с. — ISBN 5-7050-0118-5.
- ↑ 1 2 Historic Vote Ties Kilogram and Other Units to Natural Constants
- ↑ Draft Resolution A «On the revision of the International System of units (SI)» to be submitted to the CGPM at its 26th meeting (2018), <https://www.bipm.org/utils/en/pdf/CGPM/Draft-Resolution-A-EN.pdf>
- ↑ Decision CIPM/105-13 (October 2016). The day is the 144th anniversary of the Metre Convention.
- ↑ Unit of mass (kilogram) (англ.). SI Brochure: The International System of Units (SI) [8th edition, 2006; updated in 2014]. BIPM. Дата обращения 11 ноября 2015.
- ↑ Положение о единицах величин, допускаемых к применению в Российской Федерации (неопр.) (недоступная ссылка). Федеральный информационный фонд по обеспечению единства измерений. Росстандарт. Дата обращения 28 февраля 2018. Архивировано 18 сентября 2017 года.
- ↑ Verifications (англ.). Resolution 1 of the 25th CGPM (2014). BIPM. Дата обращения 8 октября 2015.
- ↑ Kilogram: Mass and Planck’s Constant (англ.). NIST. Дата обращения 18 ноября 2018.
- ↑ 1 2 3 Ernst O. Goebel, Uwe Siegner. Quantum Metrology: Foundation of Units and Measurements. John Wiley & Sons, 2015. (англ.) С. 165—167.
- ↑ Robinson I. A., Schlamminger S. The watt or Kibble balance: a technique for implementing the new SI definitionof the unit of mass (англ.) // Metrologia. — 2016. — Vol. 53. — P. A46—A74. — DOI:10.1088/0026-1394/53/5/A46.
- ↑ Michael Stock. The watt balance: determination of the Planck constant and redefinition of the kilogram Архивная копия от 1 сентября 2012 на Wayback Machine // Royal Society Discussion Meeting: The new SI, January 2011. (англ.) С. 10.
- ↑ Алексей Понятов. Последним сдался килограмм (рус.) // Наука и жизнь. — 2019. — № 3. — С. 3—7.
- ↑ Fowler, HW; Fowler, F. G. The Concise Oxford Dictionary (англ.). — Oxford: Oxford University Press, 1964.
- ↑ Décret relatif aux poids et aux mesures du 18 germinal an 3 (7 avril 1795) (фр.). Grandes lois de la République. Digithèque de matériaux juridiques et politiques, Université de Perpignan. Дата обращения 3 ноября 2011. Архивировано 10 мая 2013 года.
- ↑ Kilogram (неопр.) (недоступная ссылка). Oxford English Dictionary. Oxford University Press. Дата обращения 3 ноября 2011. Архивировано 10 мая 2013 года.
- ↑ Kilogram (неопр.). Oxford Dictionaries. Дата обращения 3 ноября 2011. Архивировано 10 мая 2013 года.
- ↑ Spelling of «gram», etc (неопр.). Weights and Measures Act 1985. Her Majesty’s Stationery Office (30 октября 1985). Дата обращения 6 ноября 2011. Архивировано 10 мая 2013 года.
- ↑ «kilo (n1)», Oxford English Dictionary (2nd ed.), Oxford: Oxford University Press, 1989, <http://www.oed.com/viewdictionaryentry/Entry/103394>. Проверено 8 ноября 2011.
- ↑ «kilo (n2)», Oxford English Dictionary (2nd ed.), Oxford: Oxford University Press, 1989, <http://www.oed.com/viewdictionaryentry/Entry/103395>. Проверено 8 ноября 2011.
- ↑ An Essay towards a Real Character and a Philosophical Language (Reproduction) (неопр.) (PDF). Дата обращения 3 апреля 2011. Архивировано 10 мая 2013 года.
- ↑ An Essay towards a Real Character and a Philosophical Language (Transcription) (неопр.) (PDF). Дата обращения 3 апреля 2011. Архивировано 10 мая 2013 года.
- ↑ 1 2 Decree on weights and measures (фр.) (7 avril 1795). — «Gramme, le poids absolu d’un volume d’eau pure égal au cube de la centième partie du mètre, et à la température de la glace fondante.». Архивировано 10 мая 2013 года.
- ↑ Gattel C. M. Nouveau Dictionnaire portatif de la Langue Françoise. — 1797. — Vol. 2. — P. 695.
- ↑ L’histoire du mètre, la détermination de l’unité de poids (неопр.). Архивировано 10 мая 2013 года.
- ↑ 1 2 3 4 5 Richard S. Davis, Pauline Barat and Michael Stock. A brief history of the unit of mass: continuity of successive definitions of the kilogram // Metrologia. — 2016. — Vol. 53. — P. A12–A18. — DOI:10.1088/0026-1394/53/5/A12.
- ↑ 1 2 Килограмм / К. П. Широков // Кварнер — Конгур. — М. : Советская энциклопедия, 1973. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 12).
- ↑ 1 2 Why change the SI? (англ.) на сайте Международного бюро мер и весов
- ↑ Towards a redefinition of the kilogram (англ.). The BIPM watt balance. BIPM. Дата обращения 10 октября 2015.
- ↑ 1 2 On the future revision of the International System of Units, the SI (англ.). Resolution 1 of the 24th CGPM (2011). BIPM. Дата обращения 11 ноября 2015.
- ↑ The Avogadro Project (неопр.) (недоступная ссылка). Дата обращения 8 октября 2015. Архивировано 7 апреля 2014 года.
- ↑ On the future revision of the International System of Units, the SI (англ.). Resolution 1 of the 25th CGPM (2014). BIPM. Дата обращения 11 ноября 2015.
- Смирнова Н. А. Единицы измерений массы и веса в Международной системе единиц. — М, 1966.
