Сферические зеркала :: Класс!ная физика

Пример изображения в выпуклом зеркале.
Художник Пармиджанино. Автопортрет в выпуклом зеркале.
1524г. Вена

___

В жизни вы часто видели своё искаженное отражение на выпуклой поверхности, например, никелированного чайника или кастрюли. Интересно наблюдать за изменением своего отражения в обыкновенной полированной ложке, если поворачивать ее то вогнутой, то выпуклой стороной.

Сферическое зеркало представляет собой часть поверхности шара и может быть вогнутым или выпуклым. Хотя принято считать, что зеркала должны быть стеклянными, на практике сферические зеркала чаще делают металлическими.

Как же формируется изображение предмета в сферических зеркалах?

Изображение предметв в вогнутом зеркале.

Точка фокуса зеркала ( F )расположена в середине отрезка, соединяющего центр кривизны сферической поверхности зеркала ( O ) и вершину зеркала точку M.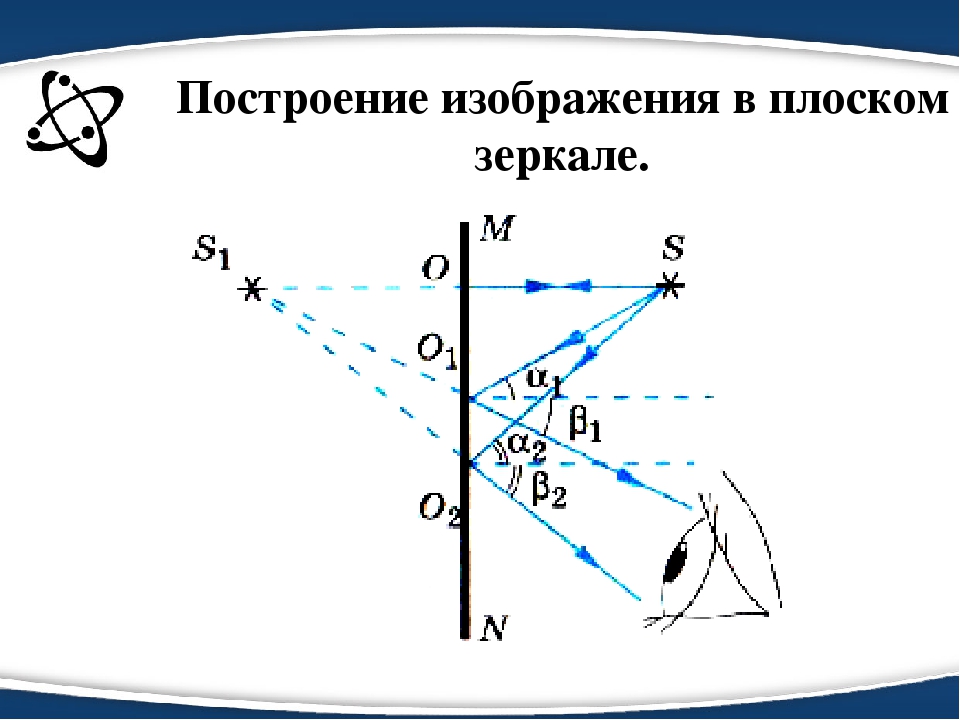

Фокусное расстояние зеркала равно f = R/2.

Пучок лучей, падающий на вогнутое зеркало параллельно оптической оси, после отражения собирается в точке фокуса.

Если предмет находится на расстояниях от вогнутого зеркала, превышающих фокусное расстояние, изображение предмета действительное и перевернутое.

Если предмет расположен между фокусом и вершиной зеркала, то его изображение получается мнимым, прямым и увеличенным. Оно будет находиться за зеркалом.

Изображение предмета в выпуклом зеркале.

Пучок лучей, падающий на выпуклое зеркало параллельно оптической оси, отражается так, как будто все лучи выходят из точки фокуса, находящейся за зеркалом на расстоянии R/2.

Независимо от расположения предмета его изображение в выпуклом зеркале является мнимым, уменьшенным и прямым.

Примеры применения сферических зеркал.

В оптических приборах применяются зеркала с различной отражающей поверхностью: плоские, сферические и более сложных форм. Неплоские зеркала подобны линзам, имеющим свойство увеличивать или уменьшать изображение предмета по сравнению с оригиналом.

Вогнутые зеркала.

В наше время вогнутые зеркала чаще используются для освещения. В карманном электрическом фонарике стоит крошечная лампочка всего в несколько свечей. Если бы она посылала свои лучи во все стороны, то от такого фонарика было бы мало пользы: его свет не проникал бы дальше одного-двух метров. Но за лампочкой поставлено маленькое вогнутое зеркальце. Поэтому луч света от карманного фонаря прорезывает темноту на десять метров вперед. Однако, в фонаре имеется еще и маленькая линза — перед лампочкой. Зеркальце и линза помогают друг другу создавать направленный луч света.

Так же устроены и автомобильные фары и прожекторы, рефлектор синей медицинской лампы, корабельный фонарь на верхушке мачты и фонарь маяка. В прожекторе светит мощная дуговая лампа. Но если бы вынули из прожектора вогнутое зеркало, то свет лампы бесцельно разошелся бы во все стороны, она светила бы не на семьдесят километров, а всего на один-два…

Особенно сложно устроен фонарь маяка. В древности самым мощным маяком был Александрийский маяк — последнее из чудес света, связанное с именем Александра Македонского. Согласно легенде, на Александрийском маяке находилось огромное зеркало, при помощи которого можно было видеть корабли, отплывавшие из Греции. Маяк находился в городе Александрия, основанном в 332 году до н.э. в дельте Нила. На подходе к городу на острове Фарос было решено построить маяк. Маяк получился в виде трехэтажной башни высотой 120 метров. На башне находилось множество остроумных технических приспособлений: флюгера, астрономические приборы, часы. На третьем этаже, в круглой, обнесенной колоннами ротонде, горел вечно громадный костер. Но и большой костер дает не так уж много света. К тому же свет его расходился бы во все стороны и должен был бы быстро терять свою силу. Можно предположить, что огонь костра отражался с помощью большого вогнутого металлического зеркала с линзой. Вогнутое зеркало отбрасывало все лучи в одном направлении, и благодаря этому свет маяка значительно усиливался. Дрова для костра доставлялись наверх по спиральной лестнице, такой пологой и широкой, что по ней на стометровую высоту въезжали повозки, запряженные ослами.
С падением римской империи он перестал светить, обвалилась верхняя башня, а стены нижнего этажа разрушились после землетрясения в 14 веке. Руины древнего маяка были встроены в турецкую крепость и в ней существуют поныне.

___

Английский ученый Исаак Ньютон использовал вогнутое зеркало в телескопе. И в современных телескопах также используются вогнутые зеркала.

А вот вогнутые антенны радиотелескопов очень большого диаметра состоят из множества отдельных металлических зеркал. Например, антенна телескопа РАТАН-600 состоит из 895 отдельных зеркал, расположенных по окружности. Конструкция этого телескопа позволяет одновременно наблюдать несколько участков неба

Выпуклые зеркала.

Такие выпуклые небьющиеся зеркала часто можно увидеть на улицах города и в общественных местах.

Установка дорожных зеркал на дорогах с ограниченной видимостью позволяет обезопасить автотранспорт и людей. Эти зеркала оснащены по контуру светоотражающими элементами и светятся в темноте, отражая свет фар автомашин.

Купольные зеркала для помещений представляют собой зеркальную полусферу, с углом обзора, достигающим 360 градусов. При этом зеркало крепится в основном на потолке.

Обзорные зеркала используются как на улицах, так и в помещениях. Так, например, в магазине обзорное показывает персоналу кто и что делает в проходах между стеллажами, а на тяжелом участке автостоянки позволяет автовладельцам выполнять маневры без столкновений.

Примеры установки и угол обозрения:

для купольного зеркала.

Другие страницы по теме « Страна «Зазеркалье»»

Древние металлические зеркала
Старинные стеклянные зеркала
Сигнальное зеркало

Секрет Этрусских зеркал
Волшебные зеркала
Ещё о волшебных зеркалах
Перископ
Зеркало разведчика
Зеркало художника
Цилиндрические зеркала
Как делают зеркала
Зеркала Архимеда
Сферические зеркала
Зеркала для развлечений
Опыты с зеркалами
Калейдоскоп
Необычные зеркала
«Зеркальные»предрассудки
Зеркало, которое не врет
Вогнутые зеркалa
Антизеркало для видимого света

Устали? — Отдыхаем!

Вверх

Зеркала

Плоское зеркало представляет собой простейшее способное создавать изображение предмета оптическое устройство.

Получаемое с помощью него изображение некоторого объекта формируется за счет отражаемых от зеркальной поверхности лучей.

Определение 1

По причине его образования вследствие пересечения «мнимых» продолжений, а не непосредственно самих лучей подобные изображения носят название мнимых (рис 3.2.1).

Рисунок 3.2.1. Ход лучей при отражении от плоского зеркала. Точка S’ является мнимым изображением точки S.

Мнимое изображение предмета расположено симметрично относительно плоскости зеркальной поверхности вследствие закона отражения света. Размер изображения эквивалентен размеру отражаемого объекта.

Виды зеркал

Определение 2

Обладающую формой сферического сегмента зеркально отражающую поверхность называют сферическим зеркалом.

Определение 3

Оптическим центром зеркала называют использованный в процессе вырезания в качестве необходимого материала центр сферы.

Определение 4

Полюсом является вершина сферического сегмента.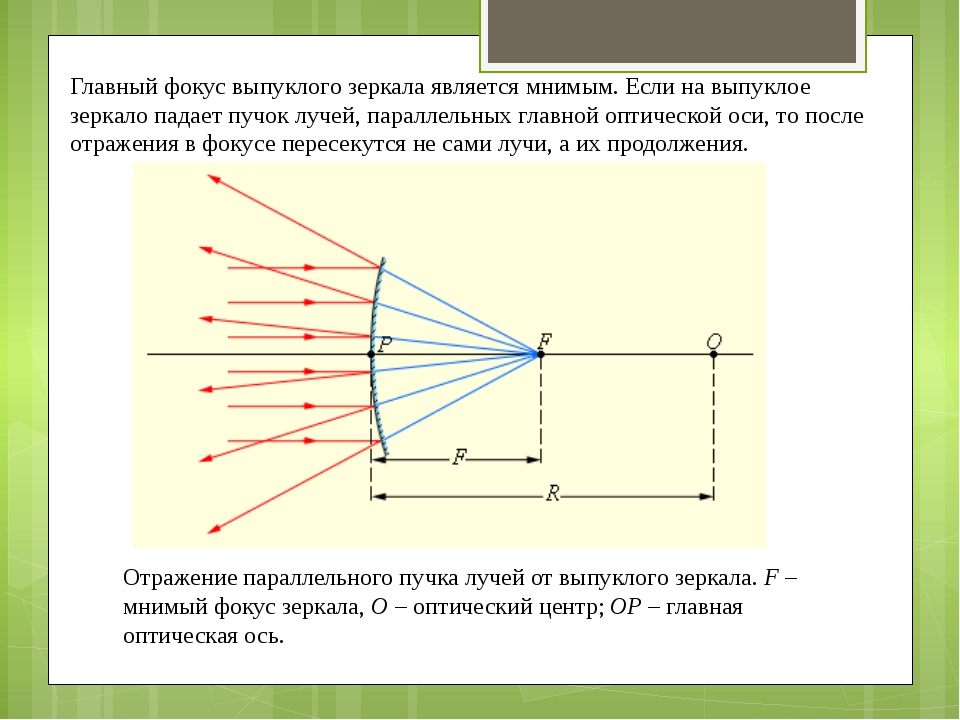

Определение 5

Проходящая через оптический центр и полюс зеркала прямая, называется главной оптической осью сферического зеркала.

Главная оптическая ось выделена из всех других проходящих через оптический центр прямых только тем, что она является осью симметрии зеркала.

Сферические зеркала делятся на вогнутые и выпуклые.

Определение 6

Если на вогнутое сферическое зеркало падает параллельный главной оптической оси пучок лучей, то, отразившись от зеркала, лучи пересекутся в точке, которая носит название главного фокуса F зеркала.

Типы изображений в зеркалах

Определение 7

Расстояние от фокуса до полюса зеркала называют фокусным расстоянием. Оно, как главный фокус, обозначается буквой F.

У вогнутого сферического зеркала главный фокус является действительным. Он расположен в середине между центром и полюсом зеркала, как это проиллюстрировано на рисунке зеркала 3.2.2.

Рисунок 3. 2.2. Отражение параллельного пучка лучей от вогнутого сферического зеркала. Точки O – оптический центр, P – полюс, F – главный фокус зеркала; OP – главная оптическая ось, R – радиус кривизны зеркала.

Замечание 1

Стоит учитывать, что отраженные лучи пересекаются примерно в одной точке только тогда, когда падающий параллельный пучок, так называемый параксиальный пучок, достаточно узок.

Главный фокус выпуклого зеркала мнимый. В случае, если на выпуклое зеркало падает параллельный главной оптической оси пучок лучей, то, отразившись в фокусе, пересекаются продолжения лучей (рисунок 3.2.3).

Рисунок 3.2.3. Отражение параллельного пучка лучей от выпуклого зеркала. F – мнимый фокус зеркала, O – оптический центр, OP – главная оптическая ось.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Фокусные расстояния сферических зеркал характеризуются определенным знаком: в случае вогнутого зеркала F=R2, выпуклого же –  F=-R2, где R представляет собой радиус кривизны зеркала.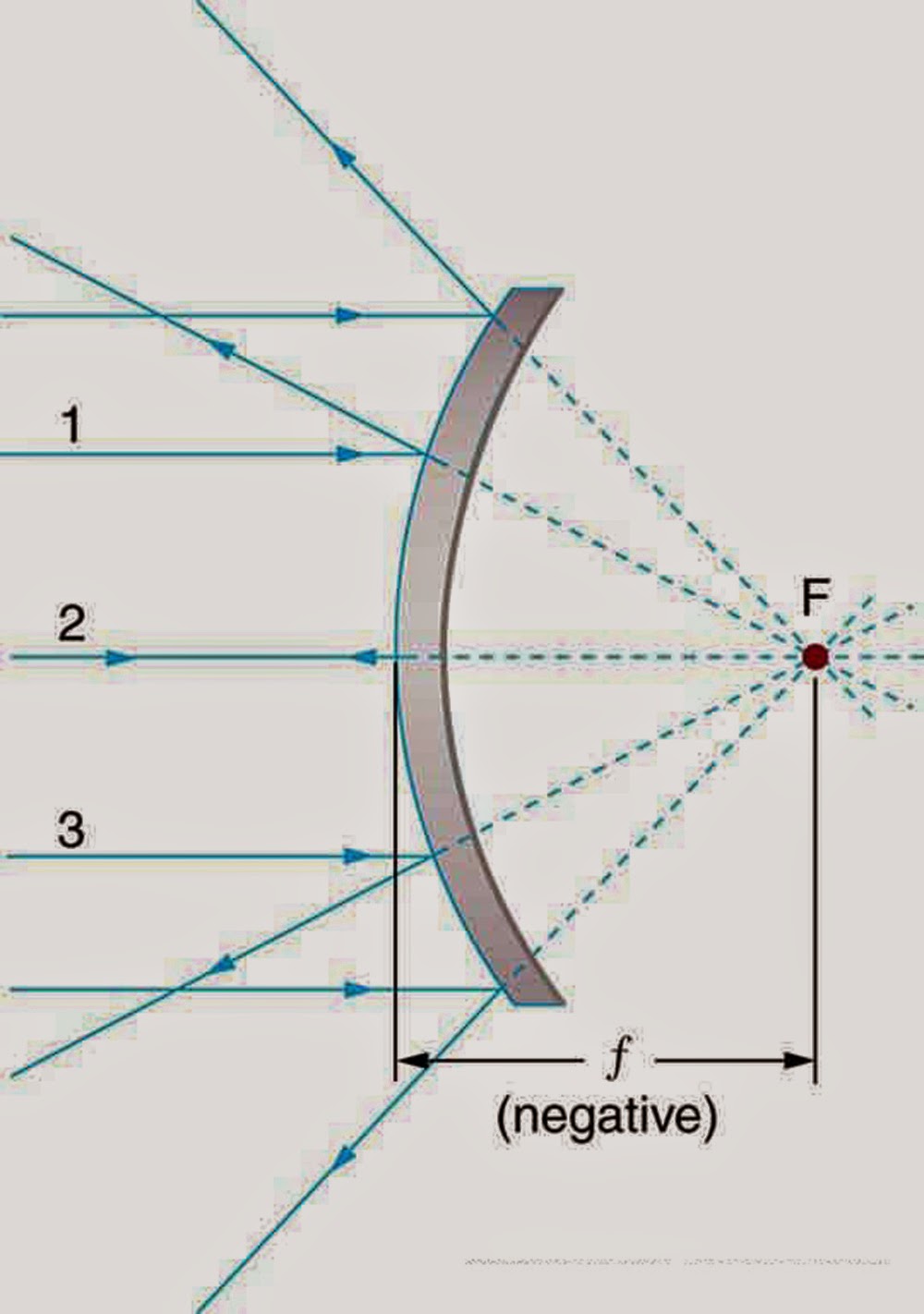

Изображение каждой конкретной точки A предмета в сферическом зеркале может быть построено благодаря любой паре стандартных лучей:

1. Луч AOC, который проходит сквозь оптический центр зеркала. Отраженный луч COA идет по этой же прямой;
2. Луч AFD, проходящий через фокус зеркала. Отраженный луч параллелен главной оптической оси;
3. Луч AP, падающий на полюс зеркала. Отраженный луч относительно главной оптической оси симметричен с падающим.
4. Параллельный главной оптической оси луч AE. Отраженный луч EFA1 проходит через принадлежащий зеркалу фокус.

Приведенные в списке выше стандартные лучи на рисунке 3.2.4 проиллюстрированы для случая вогнутого зеркала. Данные лучи проходят через являющуюся изображением точки A точку A’. Оставшиеся отраженные лучи тоже проходят через точку A’.

Определение 8

Такой ход лучей, при котором все вышедшие из одной точки лучи пересекаются в другой точке, называется стигматическим.

Отрезок A’B’ представляет собой изображение объекта AB.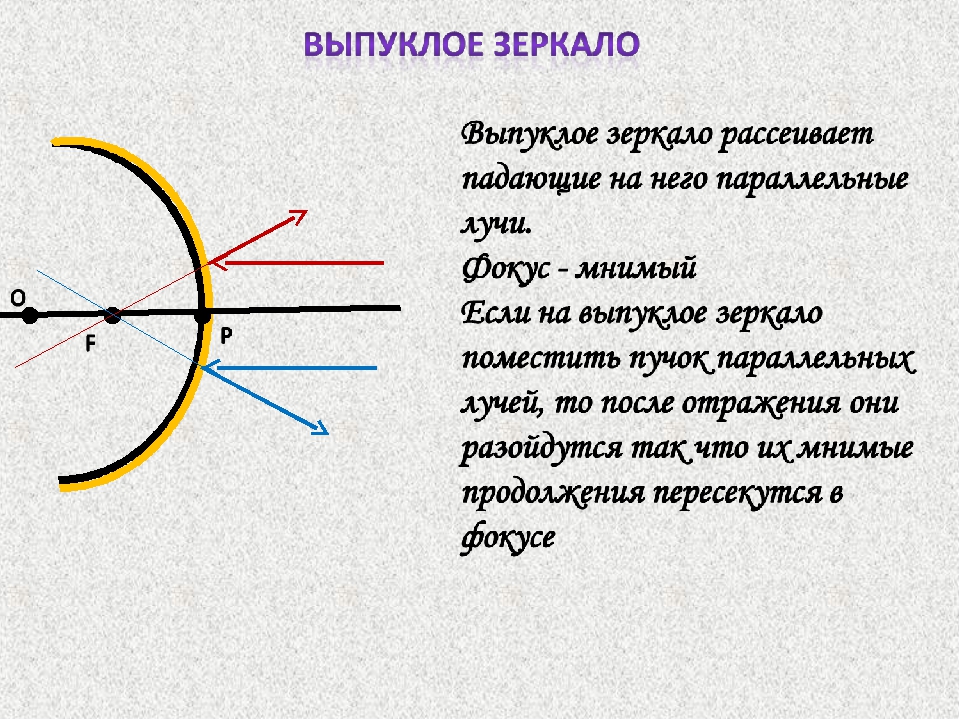 Аналогичны построения и для случая с выпуклым зеркалом.

Рисунок 3.2.4. Построение изображения в вогнутом сферическом зеркале.

С помощью формулы сферического зеркала могут быть определены размер и положение изображения объекта: 

1d+1f=1F.

В данном соотношении d играет роль расстояния от предмета до зеркала, а f представляет собой расстояние от зеркала до изображения. Величины d и f подчиняются определенному правилу знаков:

1. d>0 и f>0 – для действительных изображений и предметов;
2. d<0 и f<0 – для мнимых изображений и предметов.

Для проиллюстрированного на рисунке 3.2.4 случая мы имеем: F>0, то есть зеркало вогнутое; d=3F>0 (действительный предмет).

Из формулы сферического зеркала получаем: f=32F>0, соответственно, изображение является действительным.

Если вместо вогнутого зеркала взять выпуклое, с аналогичным по модулю фокусным расстоянием, мы получим приведенный ниже результат:

F<0, d=–3F>0, f=34F<0 – изображение мнимое.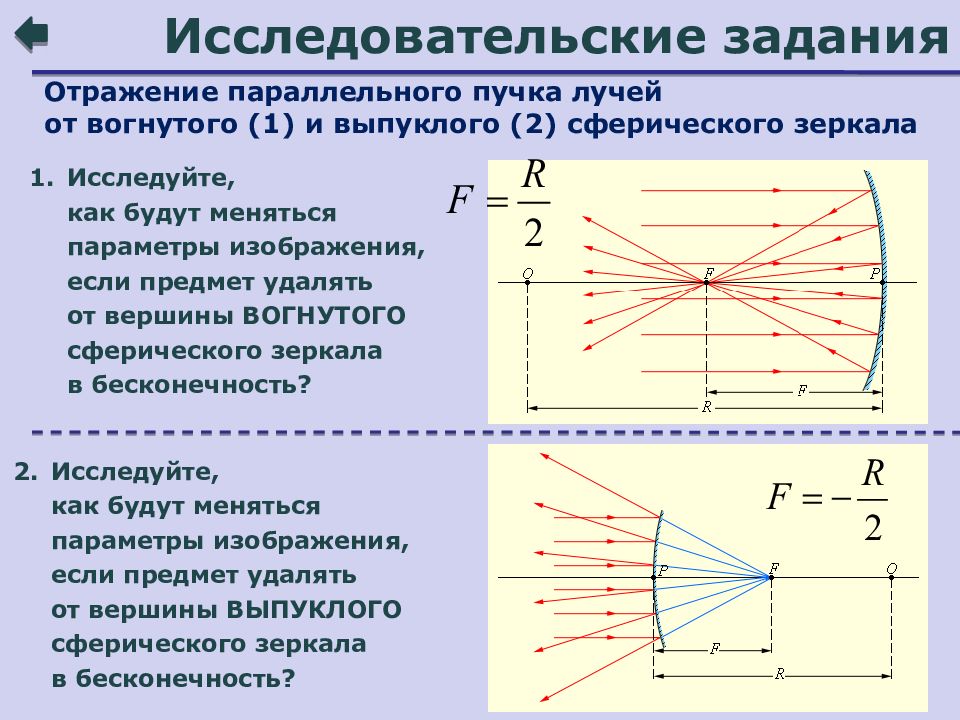

Величина линейного увеличения, принадлежащая сферическому зеркалу, может быть определена в виде отношения линейных размеров предмета h и изображения h’.

В зависимости от того, является ли изображение перевернутым или прямым, h’ приписывают определенный знак, (h'<0) минус в первом случае и плюс во втором (h’>0). Величина h всегда считается положительной. В случае подобного определения линейное увеличение сферического зеркала выражается в виде формулы, легко получаемой из рисунка 3.2.4: 

Г=h’h=-fd.

В первом из рассмотренных ранее примеров Г=-12<0 – соответственно, изображение является перевернутым, уменьшенным в 2 раза. Во втором Г=14>0 – то есть изображение прямое и уменьшенное в 4 раза.

Рисунок 3.2.5. Модель изображения в плоском зеркале.

Рисунок 3.2.6. Модель сферического зеркала.

Вогнутое зеркало – simulation, animation – eduMedia

Вогнутое зеркало – simulation, animation – eduMedia

⚠ eduMedia will be under maintenance on June 12, 2021

Краткое содержание

Во­гну­тое зер­ка­ло и вы­гну­тое зер­ка­ло яв­ля­ют­ся дву­мя раз­но­вид­но­стя­ми сфе­ри­че­ско­го зер­ка­ла.

Ха­рак­те­ри­сти­ки сфе­ри­че­ских зер­кал ни­же­сле­дую­щие:

• Центр С (центр сфе­ры),
• Вер­ши­на S (точ­ка пе­ре­се­че­ния, ле­жа­щая ме­ж­ду зер­ка­лом и оп­ти­че­ской осью)
• Ра­ди­ус кри­виз­ны R (ра­ди­ус сфе­ры). В фор­му­лах оп­ти­ки, ра­ди­ус кри­виз­ны яв­ля­ет­ся ал­геб­раи­че­ской ве­ли­чи­ной. R яв­ля­ет­ся по­ло­жи­тель­ным для во­гну­то­го зер­ка­ла и от­ри­ца­тель­ным для вы­пук­ло­го.
• Фо­кус  F — точ­ка, в ко­то­рой схо­дят­ся все лу­чи, ко­то­рые рас­про­стра­ня­ют­ся в на­прав­ле­нии, па­рал­лель­ном к оп­ти­че­ской оси (ус­ло­вие Га­ус­са=стиг­ма­тизм вбли­зи).
• Дли­на/фо­кус­ное рас­стоя­ние Lf — дли­на FS. Она со­став­ля­ет по­ло­ви­ну ра­диу­са кри­виз­ны. Lf=R/2 

Соз­да­ние изо­бра­же­ния в со­от­вет­ст­вии с ус­ло­вия­ми Га­ус­са (ма­лые уг­лы), уп­ро­ща­ет­ся при по­строе­нии ос­нов­ных лу­чей:

• Па­рал­лель­но­го лу­ча к оп­ти­че­ской оси, от­ра­жён­но­го при про­хо­ж­де­нии че­рез фо­кус F. 
• Луч, про­хо­дя­щий че­рез точ­ку С, от­ра­жён­ный на са­мо­го се­бя.
• Луч, про­хо­дя­щий че­рез фо­кус F, от­ра­жа­ет­ся па­рал­лель­но оп­ти­че­ской оси.

Два из этих лу­чей по­зво­ля­ют соз­дать изо­бра­же­ние.

Для во­гну­то­го зер­ка­ла, изо­бра­же­ние яв­ля­ет­ся мни­мым, ко­гда пред­мет на­хо­дит­ся ме­ж­ду F и S. Изо­бра­же­ние ста­но­вит­ся дей­ст­ви­тель­ным, ко­гда пред­мет рас­по­ло­жен даль­ше, чем F.

Нажать, а затем сместить свечу вдоль оптической оси.

Нажать, а затем переместить по вертикали пламя от свечи для того, чтобы изменить его размер.

Цели обучения

• Построить изображение предмета в вогнутом зеркале.

Поделиться ×

100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА

В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.

— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?

— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.

Зарегистрироваться можно будет электронно на сайте Национального центра тестирования. Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.

Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.

— Расскажите поподробнее?

— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.

— Система оценивания останется прежней?

— Количество предметов остается прежним — три обязательных предмета и два на выбор. Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.

Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Максимальное количество баллов остается прежним — 140.

— А апелляция?

— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.

— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?

— Мы решили оставить прежнее время — 240 минут. Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.

— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?

— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.

— На сколько процентов будет обновлена база вопросов?

— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.

— По вашему мнению система справится с возможными хакерскими атаками, взломами?

— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.

Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.

— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?

— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.

— Сколько человек будет сидеть в одной аудитории?

— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.

— Будут ли ужесточены требования по дисциплине, запрещенным предметам?

— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.

Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.

— А наблюдатели будут присутствовать во время сдачи тестирования?

— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.

— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?

— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.

Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.

— Сколько средств выделено на проведение ЕНТ в этом году?

Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. Они будут, но несущественные.

— Все-таки почему именно в 2021 году было принято решение проводить ЕНТ в электронном формате. Это как-то связано с пандемией?

— Это не связано с пандемией. Просто нужно переходить на качественно новый уровень. Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.

Физика линз и оптических зеркал

Вогнутые зеркала

Вогнутое зеркало дает сходящийся пучок лучей. Все лучи, падающие на такое зеркало параллельно его главной оси, после отражения сходятся в точке, называемой фокусом. Расстояние между фокусом и и зеркалом — это фокусное расстояние зеркала. Чем меньше фокусное расстояние, тем сильнее увеличение. Фокусное расстояние зависит от кривизны зеркала. Зеркало со значительной кривизной обладает коротким фокусным расстоянием и большим увеличением.

Выпуклые зеркала

Выпуклое зеркало дает расходящийся пучок лучей. Когда параллельные лучи падают на выпуклое зеркало, отраженные лучи расходятся. Фокус выпуклого зеркала расположен позади него, в точке, из которой эти лучи кажутся исходящими. Чем меньше фокусное расстояние, тем меньше отраженное изображение. Выпуклые зеркала формируют прямые (не перевернутые) изображения.

Увеличение и поле зрение

Обычные плоские зеркала формируют неискаженные изображения, соответствующие реальным пропорциям отраженного объекта. У вогнутого зеркала того же размера поле зрения уже, поэтому оно формирует изображение уменьшенного участка объекта, зато во много раз увеличенное по сравнению с оригиналом. Благодаря способности создавать увеличенное изображение вогнутые зеркала позволяют подробно рассмотреть отдельный небольшой участок объекта. Вот почему у вогнутого зеркала удобно бриться или накладывать косметику на лицо.

Ось симметрии зеркала или линзы называется ее главной (или оптической) осью. Любой луч, падающий на вогнутое зеркало параллельное его главной оси, после отражения проходит через точку, именуемую главным фокусом зеркала.

Выпуклые зеркала имеют более широкое поле зрение, чем плоские, но формируют уменьшенные изображения. Это очень удобно, если необходимо обеспечить панорамный обзор. На стенках многих крупных магазинов, высоко над головами покупателей, установлены большие выпуклые зеркала. В сочетании с видеокамерами они позволяют службе безопасности наблюдать даже за за теми уголками помещения, которые обычно скрыты от глаз. Зеркала заднего вида в автомобилях тоже слегка выпуклый. Обзор у водителя шире, чем был бы при плоском зеркале.

Вогнутые и выпуклые поверхности кривых зеркал в комнатах смеха создают забавные эффекты, растягивая, сужая или переворачивая изображения.

Оптические линзы

Преломление светового луча при переходе из воздуха в стекло используется в оптических приборах, например в линзах. Физика линзы состоит в построении изображение объекта, находящегося за ней.

Линзы обычно имеют круглую форму. Выпуклые линзы толще посередине, чем по краям. У вогнутых линз середина тоньше, чем края. Световой луч преломляется сначала на поверхность линзы, а затем лучи преломляются вновь, выходя наружу с противоположной стороны линзы. Линзы, предназначенные для работы в ультрафиолетовой области спектра, изготавливают из кристаллов кварца, флюорита, фтористого лития, в инфракрасной — из особых сортов стекла, кремния, германия, фтористого лития, йодистого цезия.

Вогнутые линзы

Вогнутые, или рассеивающие, линзы превращают параллельные лучи в расходящиеся. Фокус вогнутой линзы — это точка позади линзы, из которой лучи кажутся исходящими. Объекты выглядят меньше, если их наблюдать через вогнутую линзу. Увеличение кривизны сокращает фокусное расстояние вогнутой линзы и еще сильнее уменьшает изображения объектов.

На схеме показан ход лучей через вогнутую линзу. Вогнутая линза создает уменьшенное изображение, заставляя световые лучи расходиться от оптической оси.

Вогнутые линзы используют в очках для близоруких людей, в объективах фотоаппаратов, в телескопах и микроскопах. Их точно подгоняют к криволинейным поверхностям выпуклых линз и других материалов. Составные линзы снижают хроматическую аберрацию, то есть, нечеткость изображений, вызванную тем, что для света с разной длиной волны увеличения слегка различается.

Выпуклые линзы

Выпуклые, или собирающие, линзы собирают световые лучи, параллельные главной оптической оси, в одну точку, называемую главным фокусом. Фокусное расстояние — это расстояние между линзой и главным фокусом.

На схеме показан ход лучей через выпуклую линзу. Выпуклая линза создает увеличенное изображение, заставляя световые лучи сходится к оптической оси линзы.

Выпуклая линза может сфокусировать свет от объекта на экране. Изображение окажется перевернутым.

Выпуклые линзы применяются в увеличительных стеклах (лупах) и очках для дальнозорких людей. Поскольку выпуклая линза собирает солнечный свет в главном фокусе, с ее помощью можно зажечь бумагу или другой легко воспламеняющейся материал.

Выпуклая линза в проекторе формирует увеличенное изображение слайда в проекторах. Это изображение действительное, потому что изображение проходит сквозь него, и его можно спроецировать на экран.

Физики сфокусировали свет с помощью плоского зеркала на эффекте фотонной струи

Симуляция распространения отраженных от зеркала волн при угле падения 60°

Minin et. al. / Scientific Reports, 2020

Физики создали плоское диэлектрическое зеркало, которое способно фокусировать свет в отраженном пучке. Его принцип работы основан на эффекте фотонной струи, согласно которому микрочастицы в материале могут выполнять функцию линз, фокусируя излучение в субволновом диапазоне. Результаты работы, опубликованные в журнале Scientific Reports, помогут создать приборы для оптической визуализации с более высоким разрешением изображения.

Обычные сферические зеркала преломляют свет благодаря своей изогнутой форме. Лучи света в таких зеркалах проходят различный путь в зависимости от места падения, из-за чего на выходе они теряют параллельность и собираются в фокусе. У плоских зеркал лучи в фокусе не собираются, а сохраняют параллельность на выходе из-за отсутствия искривления поверхности. Отраженные от таких зеркал лучи, шедшие до этого параллельно друг другу, не собираются в одной точке. Не так давно исследователям удалось создать плоские зеркала, которые имеют фокус. Они представляют собой слоистую структуру из диэлектрических материалов или комплекс метал-изолятор-метал и способны фокусировать свет при определенном угле падения вблизи поверхности линзы. 

Физики под руководством Олега Минина (Oleg V. Minin) из Томского государственного университета разработали плоское зеркало, работающее по совершенно другому принципу. Принцип его работы основан на эффекте фотонной струи, который заключается в фокусировке отдельными диэлектрическими частицами падающего света. Каждая такая микрочастица по-своему преломляет попадающий на нее свет и собирает его в своем фокусе на небольшом расстоянии от поверхности. В зависимости от формы частицы будет отличаться и вид фотонной струи — потока излучения, который образуется на теневой стороне частицы после преломления падающего на нее света.

Изображения отраженных от зеркала пучков излучения. (a), (b), (c) — для диэлектрического зеркала и углов падения соответственно 45°, 60° и 75°; (d) — для кремниевой подложки под углом падения 45°.

Igor V. Minin et. al. / Scientific Reports 2020

Созданное учеными зеркало представляет собой слой полидиметилсилоксана — органического полимера, содержащего атомы кремния и кислорода — на кремниевой подложке. Молекулы внутри этого материала собираются в микрочастицы различной формы, граничащие друг с другом. Изготовленное исследователями зеркало имеет форму квадрата размером 10×10 микрометров толщиной всего один микрометр. Его поместили на кремниевую подложку, после чего освещали излучением с тремя длинами волн из разных частей видимого спектра под углами от 30 до 75 градусов.

В результате авторы выяснили ключевые особенности фотонной струи нового фокусирующего плоского зеркала. В частности, они установили точку ее максимальной интенсивности. Ученые также показали, что с увеличением угла освещения интенсивность излучения в фокусе отраженного пучка уменьшается. При этом падают и линейные параметры пучка.

Из-за того, что фокусные расстояния нового материала находятся в микрометровом диапазоне, авторы предлагают использовать его для создания небольших фотонных устройств, в которых свет распространяется между элементами без дифракции. Также такое фокусирующее плоское зеркало найдет применение в приборах для оптической визуализации, где позволит существенно повысить получаемое при съемке разрешение.

Кроме твердых зеркал бывают еще и жидкие. Ранее ученые из Имперского колледжа Лондона использовали две несмешивающиеся жидкости и наночастицы золота, чтобы создать зеркало с переменным коэффициентом отражения, который можно контролировать с помощью электрического тока.

От редактора

Изначально в заметке руководителем коллектива назывался Чэн-Ян Лю (Cheng-Yang Liu). Но настоящий руководитель коллектива — Олег Минин. Мы внесли исправления в текст заметки. Приносим свои извинения.

Никита Шевцев

Плоское зеркало. Построение изображений в плоском зеркале

юя D 8 7 8 : 0

Каждый день по нескольку раз вы смотрите в зеркало и видите в нем своё изображение. Попробуем ответить на вопросы: где и на каком расстоянии от зеркала находится изображение? Какие его размеры по сравнению с размерами самого предмета? И как оно образуется?

Чтобы ответить на эти вопросы, проделаем такой опыт. На столе расположим вертикально стеклянную пластинку и зажжённую свечу. Стеклянная пластинка будет выполнять роль плоского зеркала.

Как видим, в стекле хорошо видно изображение свечи. Однако, заглянув за пластинку, мы свечи там не обнаружим.

Теперь возьмём такую же по размерам, но незажжённую свечу и будем перемещать с другой стороны пластинки вдоль линейки до тех пор, пока она не совместится с изображением, то есть не будет казаться зажжённой. По линейке определим расстояния от пластинки до свечи и до её изображения. Не трудно заметить, что эти расстояния оказались равными. А так как незажжённая свеча совместилась с изображением по высоте, то можно сделать вывод, что размеры изображения равны размерам предмета.

Если передвинуть свечу ближе к стеклянной пластинке, то её изображение тоже приблизится, причём ровно на столько же, на сколько приблизилась свеча.

Положение изображения не изменится, если вместо стеклянной пластинки использовать плоское зеркало.

Из проведённых опытов следует, что в плоском зеркале глаз видит изображение таких же размеров, что и предмет, и на таком же расстоянии за зеркалом.

Но что значит: «Глаз видит изображение»? Как глаз определяет местоположение предмета или его изображения? Чтобы ответить на возникшие вопросы, давайте рассмотрим, как получается изображение предмета в плоском зеркале. Итак, пусть перед зеркалом находится источник света S. Из множества лучей выделим два, например, SA и SB, падающих на зеркало. Пользуясь законом отражения света, построим отражённые лучи/

Не трудно заметить, что пучок света, ограниченный отражёнными лучами, будет расходящимся. Он то и попадает в глаз наблюдателя.

Если продолжить отражённые лучи за плоскость зеркала, то они пересекутся в точке S’. Глаз воспринимает отражённые лучи так, как будто они исходят из этой точки, которая является изображением светящейся точки S. То есть глазу кажется, что светящаяся точка находиться именно там. Такое изображение называют мнимым.

Мнимое изображение — изображение, получаемое на пересечении не самих отражённых (или преломлённых) лучей, а их продолжений.

Следовательно, плоское зеркало даёт мнимое изображение.

Теперь построим изображение протяжённого предмета, например, свечи в плоском зеркале. Для этого нам необходимо построить изображение двух её крайних точек. Для этого можно использовать любые два луча. Итак, пусть первый луч от точки А падает на зеркало в точку О перпендикулярно плоскости зеркала. Значит, угол падения равен 0^о. Следовательно, отражённый луч пойдёт вдоль падающего, но в обратном направлении, так как, согласно закону отражения света, угол падения и угол отражения равна.

Второй луч направим к зеркалу под некоторым углом. От зеркала он отразиться под таким же углом.

Из полученного рисунка видно, что отражённые лучи не пересекаются. Но пересекаются их продолжения в точке A’. Следовательно, эта точка и есть изображение точки A причём, как вы уже догадались, мнимое изображение.

Аналогично можно построить изображение любой точки предмета, в том числе и точки B.

Пользуясь признаками равенства треугольников, нетрудно доказать, что треугольники ACO и A’CO.

Это ещё раз подтверждает, что изображение предмета за зеркалом, находится на таком же расстоянии от него, как и сам предмет.

Важно запомнить, что предмет и его изображение в плоском зеркале представляют собой не тождественные, а симметричные фигуры. Например, посмотрим на изображение человека в зеркале. Правая рука на этом изображении расположена так, как будто это рука левая. То есть в зеркале «право» и «лево» меняются местами.

Таким образом, из опытов и построений следует, что изображение предмета в плоском зеркале является мнимым, прямым (то есть не перевёрнутым), по размерам равным предмету, находится на таком же расстоянии за зеркалом, на котором расположен предмет перед зеркалом и симметрично предмету.

Зеркала применяются в различных сферах жизнедеятельности человека: в быту, в медицине, на транспорте и в космической сфере.

Плоское зеркало используется и в перископе. Этот прибор устанавливают, например, на подводных лодках. Он позволяет с лодки, находящейся под водой, увидеть, что происходит на поверхности воды. Перископ представляет собой трубу, состоящую из трёх секций: двух горизонтальных и одной вертикальной. В местах соединения горизонтальных и вертикальной секций расположены зеркала. Зеркала взаимно параллельны и составляют угол сорок пять градусов с горизонталью.

Принцип работы перископа следующий. На верхнее зеркало падают горизонтальные лучи света от предмета, например, от корабля. После отражения от зеркала лучи изменят своё направление на вертикальное и попадут на второе зеркало. После отражения в нём лучи света вновь изменят направление на девяносто градусов и попадут в глаз наблюдателя.

Пример решения задач.

Задача. В системе двух зеркал глаз увидел изображение светящейся точки благодаря лучам 1 и 2. Где оно расположено? Где находится сама светящаяся точка? Сколько всего будет изображений?

Зеркала | Безграничная физика

Отражение изображения плоским зеркалом

Зеркало — это отражающая поверхность, которая отражается от света, создавая реальное или виртуальное изображение.

Цели обучения

Описать взаимодействие света с зеркальной поверхностью

Основные выводы

Ключевые моменты

• Отраженные изображения могут быть реальными или виртуальными. В плоском зеркале изображения виртуальны.
• Виртуальные изображения в плоском зеркале имеют инверсию влево-вправо.
• Рисование лучевой диаграммы — это способ предсказать, как будет выглядеть отраженное изображение.

Ключевые термины

• виртуальное изображение : виртуальное изображение возникает, когда лучи света на самом деле не встречаются на изображении

Плоские зеркала и отражение

Зеркало — это отражающая поверхность, которая не пропускает свет и вместо этого отражает его, создавая изображение. Чаще всего используются плоские зеркала, называемые плоскими. Эти зеркала изготавливаются путем нанесения тонкого слоя нитрата серебра или алюминия за плоский кусок стекла.

Когда вы помещаете объект перед зеркалом, вы видите изображение того же объекта в зеркале. Объект является источником падающих лучей, а изображение формируется отраженными лучами. Изображение, образованное отражением, может быть реальным или виртуальным. «Настоящее» изображение возникает, когда световые лучи фактически пересекаются на изображении и становятся перевернутыми или перевернутыми. «Виртуальное» изображение возникает, когда лучи света на самом деле не встречаются на изображении. Вместо этого вы «видите» изображение, потому что ваш глаз проецирует световые лучи назад.Вас обманом заставили увидеть изображение! Виртуальное изображение находится правой стороной вверх (вертикально).

В плоских или плоских зеркалах изображение представляет собой виртуальное изображение и находится на том же расстоянии за зеркалом, что и объект перед зеркалом. Изображение также имеет тот же размер, что и объект. Эти изображения также инвертированы по четности, что означает, что они имеют инверсию влево-вправо.

Лучевые диаграммы

Мы можем предсказать, как будет выглядеть отражение, нарисовав диаграмму лучей. Эти диаграммы можно использовать для определения положения и размера изображения, а также для определения того, является ли это изображение реальным или виртуальным.Вот шаги, которые вы выполняете, чтобы нарисовать диаграмму лучей:

1. Нарисуйте плоское зеркало в виде прямой линии на главной оси. Главная ось — это воображаемая линия, проведенная перпендикулярно зеркалу.
2. Нарисуйте объект в виде стрелки перед зеркалом.
3. Нарисуйте изображение объекта, используя принцип, согласно которому изображение располагается за зеркалом на том же расстоянии, что и объект перед зеркалом. Размер изображения также совпадает с размером объекта.показывает эти первые три шага.
4. Поставьте точку в том месте, где находится глаз.
5. Укажите одну точку на изображении и нарисуйте отраженный луч, который проходит к глазу, когда он видит эту точку. Не забудьте добавить стрелку.
6. Нарисуйте падающий луч для света, идущего от соответствующей точки на объекте к зеркалу, так, чтобы соблюдался закон отражения.
7. Продолжайте движение до других крайних точек на объекте (т. Е. Кончика и основания стрелки). Завершенная диаграмма лучей показана в
.

Угол, под которым луч света падает на зеркало, совпадает с углом, под которым он будет отражаться обратно.Если, например, луч света покидает верхнюю часть объекта, движущегося параллельно главной оси, он ударяется о зеркало под углом 0 градусов и отражается обратно под углом 0 градусов. Когда это происходит, мы говорим, что луч обычно попадает в зеркало. Если луч света попадет на объект под углом 30 градусов, он отразится обратно под углом 30 градусов.

Формирование изображения сферическими зеркалами: условные обозначения отражения и знака

Зеркало — это отражающая поверхность, через которую не проходит свет, сделанная из слоя нитрата серебра или алюминия за куском стекла.

Цели обучения

Отличительные свойства вогнутых и выпуклых зеркал

Основные выводы

Ключевые моменты

• Изображения в зеркалах могут быть как настоящими, так и виртуальными.
• Краткое описание свойств вогнутых зеркал показано ниже: сходящееся реальное изображение перевернутое изображение перед зеркалом.
• Краткое описание свойств выпуклых зеркал показано ниже: расходящееся виртуальное изображение вертикальное изображение за зеркалом.

Ключевые термины

• вогнутая : изогнутая, как внутренняя поверхность сферы или чаши
• выпуклый : изогнутый или изогнутый наружу, как внешняя часть чаши, сферы или круга

Обзор

Зеркало — это отражающая поверхность, через которую свет не проходит, а отражается от нее, и это создает изображение. Зеркала изготавливаются путем нанесения тонкого слоя нитрата серебра или алюминия за плоский кусок стекла.

Когда вы помещаете объект перед зеркалом, вы видите тот же объект в зеркале.Это изображение, которое кажется позади зеркала, называется изображением. Объект является источником падающих лучей, а изображение формируется отраженными лучами. Изображение, образованное отражением, может быть реальным или виртуальным. Настоящее изображение возникает, когда световые лучи фактически пересекаются на изображении и переворачиваются или перевернуты. Виртуальное изображение возникает, когда лучи света на самом деле не встречаются на изображении. Вместо этого вы «видите» изображение, потому что ваш глаз проецирует световые лучи назад. Виртуальное изображение находится правой стороной вверх (вертикально).

В этом разделе рассматриваются сферические зеркала. Сферические зеркала могут быть как вогнутыми, так и выпуклыми. Центр кривизны — это точка в центре сферы, которая описывает, насколько велика сфера. Эти концепции показаны на.

Сферические зеркала : На этом рисунке показана разница между вогнутым и выпуклым зеркалом.

Вогнутые зеркала

В вогнутом зеркале главная ось — это линия, перпендикулярная центру зеркала.Самый простой способ визуализировать, как будет выглядеть изображение в этом типе зеркала, — это диаграмма лучей. Прежде чем это можно будет сделать, сначала необходимо определить фокус. Эта точка находится на полпути между зеркалом и центром кривизны на главной оси. Расстояние до фокальной точки от зеркала называется фокусным расстоянием. Как видно из рисунка, это фокусное расстояние также равно половине радиуса кривизны. показана лучевая диаграмма вогнутого зеркала.

Диаграмма вогнутых лучей : Это диаграмма лучей вогнутого зеркала.Шаги, необходимые для рисования, такие же, как и в плоском зеркале.

Краткое описание свойств вогнутых зеркал показано ниже:

• сходящаяся
• реальное изображение
• перевернутое
• изображение перед зеркалом

Зеркала выпуклые

У выпуклых зеркал главная ось такая же, как у плоского или вогнутого зеркала, перпендикулярна центру зеркала. В этом случае фокус находится за зеркалом. Выпуклое зеркало из-за этого имеет отрицательное фокусное расстояние.Точка фокусировки находится на том же расстоянии от зеркала, что и в вогнутом зеркале. Это показано на.

Диаграмма луча выпуклого зеркала : Выпуклое зеркало с тремя лучами, нарисованными для определения положения изображения. Каждый падающий луч отражается в соответствии с законом отражения. Отраженные лучи расходятся. Если отраженные лучи вытянуты за зеркалом, то их пересечение дает расположение изображения за зеркалом. Для выпуклого зеркала изображение виртуальное и прямое.

Краткое описание свойств выпуклых зеркал показано ниже:

• расходящиеся
• виртуальный образ
• прямая
• изображение за зеркалом

Учебное пособие по физике: Уравнение зеркала

Диаграммы

могут использоваться для определения местоположения, размера, ориентации и типа изображения, формируемого объектами, когда они помещаются в заданном месте перед вогнутым зеркалом.Использование этих диаграмм было продемонстрировано ранее в Уроке 3. Лучевые диаграммы предоставляют полезную информацию о взаимоотношениях объекта и изображения, но не предоставляют информацию в количественной форме. Хотя лучевая диаграмма может помочь определить приблизительное местоположение и размер изображения, она не предоставит числовой информации о расстоянии до изображения и размере объекта. Чтобы получить этот тип числовой информации, необходимо использовать уравнение Mirror Equation и уравнение увеличения .Уравнение зеркала выражает количественную зависимость между расстоянием до объекта (d _o ), расстоянием до изображения (d _i ) и фокусным расстоянием (f). Уравнение формулируется следующим образом:

Уравнение увеличения связывает отношение расстояния до изображения и расстояния до объекта с отношением высоты изображения (h _i ) и высоты объекта (h _o ). Уравнение увеличения указано следующим образом:

Эти два уравнения можно объединить для получения информации о расстоянии до изображения и высоте изображения, если известны расстояние до объекта, высота объекта и фокусное расстояние.

Чтобы продемонстрировать эффективность уравнения зеркала и уравнения увеличения, рассмотрим следующий пример задачи и ее решение.

Пример проблемы № 1

Лампочка высотой 4,00 см помещена на расстоянии 45,7 см от вогнутого зеркала с фокусным расстоянием 15,2 см. Определите расстояние до изображения и размер изображения.

Как и все проблемы в физике, начните с выявления известной информации.

h o = 4,0 см

d o = 45,7 см

f = 15,2 см

Затем определите неизвестные величины, которые вы хотите найти.

Для определения расстояния до изображения необходимо использовать уравнение зеркала. Следующие строки представляют решение для расстояния до изображения; показаны замены и алгебраические шаги.

1 / f = 1 / do + 1 / d _и

1 / (15,2 см) = 1 / (45,7 см) + 1 / d _i

0,0658 см ^-1 = 0,0219 см ^-1 + 1 / d _i

0,0439 см ^-1 = 1 / d _i

Числовые значения в приведенном выше решении были округлены при записи, но не округленные числа использовались во всех расчетах. Окончательный ответ округляется до третьей значащей цифры.

Для определения высоты изображения необходимо уравнение увеличения. Поскольку три из четырех величин в уравнении (без учета M) известны, четвертая величина может быть вычислена. Решение показано ниже.

h _i / h _o = — d _i / d _o

h _i /( 4,0 см) = — (22,8 см) / (45,7 см)

h _i = — (4,0 см) • (22,8 см) / (45,7 см)

Отрицательные значения высоты изображения указывают на то, что изображение является перевернутым.Как это часто бывает в физике, отрицательный или положительный знак перед числовым значением физической величины представляет информацию о направлении. В случае высоты изображения отрицательное значение всегда указывает на перевернутое изображение.

Из расчетов в этой задаче можно сделать вывод, что если объект высотой 4,00 см поместить на 45,7 см от вогнутого зеркала с фокусным расстоянием 15,2 см, то изображение будет перевернуто, высотой 1,99 см и расположением 22,8 см. от зеркала.Результаты этого расчета согласуются с принципами, рассмотренными ранее в этом уроке. В этом случае объект расположен на за центром кривизны (который будет на два фокусных расстояния от зеркала), а изображение расположено между центром кривизны и точкой фокусировки. Это относится к категории случая 1: объект расположен за пределами C.

Теперь давайте попробуем второй пример задачи:

Пример проблемы № 2

А 4.Лампочка высотой 0 см помещается на расстоянии 8,3 см от вогнутого зеркала с фокусным расстоянием 15,2 см. (ПРИМЕЧАНИЕ: это тот же объект и то же зеркало, только на этот раз объект расположен ближе к зеркалу.) Определите расстояние до изображения и размер изображения.

Опять же, начнем с определения известной информации.

h o = 4,0 см

d o = 8.3 см

f = 15,2 см

Затем определите неизвестные величины, которые вы хотите найти.

Для определения расстояния до изображения необходимо использовать уравнение зеркала. Следующие строки представляют решение для расстояния до изображения; показаны замены и алгебраические шаги.

1 / f = 1 / do + 1 / d _и

1 / (15,2 см) = 1 / (8.3 см) + 1 / д _и

0,0658 см ^-1 = 0,120 см ^-1 + 1 / d _i

-0,0547 см ^-1 = 1 / d _i

Числовые значения в приведенном выше решении были округлены при записи, но не округленные числа использовались во всех расчетах. Окончательный ответ округляется до третьей значащей цифры.

Для определения высоты изображения необходимо уравнение увеличения.Поскольку три из четырех величин в уравнении (без учета M) известны, четвертая величина может быть вычислена. Решение показано ниже.

h _i / h _o = — d _i / d _o

h _i /( 4,0 см) = — (-18,2 см) / (8,3 см)

h _i = — (4,0 см) • (-18,2 см) / (8,3 см)

Отрицательное значение расстояния до изображения указывает, что изображение является виртуальным изображением, расположенным за зеркалом.Опять же, отрицательный или положительный знак перед числовым значением физической величины представляет информацию о направлении. В случае расстояния до изображения отрицательное значение всегда означает за зеркалом. Также обратите внимание, что высота изображения — положительное значение, что означает вертикальное изображение. Любое изображение, расположенное вертикально и расположенное за зеркалом, считается виртуальным изображением.

Из расчетов во втором примере задачи можно сделать вывод, что если поместить объект высотой 4,0 см 8.3 см от вогнутого зеркала с фокусным расстоянием 15,2 см, тогда изображение будет увеличено, вертикально, высотой 8,8 см и расположено на 18,3 см позади зеркала. Результаты этого расчета согласуются с принципами, рассмотренными ранее в этом уроке. В этом случае объект находится перед точкой фокусировки (т.е. расстояние до объекта меньше фокусного расстояния), а изображение располагается за зеркалом. Это относится к случаю 5: объект расположен напротив F.

Знаки +/-

Условные обозначения для указанных величин в уравнении зеркала и уравнениях увеличения следующие:

• f = +, если зеркало вогнутое
• ф — если зеркало выпуклое зеркало
• d _i — это +, если изображение является реальным и расположено на стороне зеркала со стороны объекта.
• d _i is — если изображение виртуальное и находится за зеркалом.
• h _i равно +, если изображение является вертикальным (и, следовательно, также виртуальным)
• h _i is — если изображение перевернутое изображение (а значит, тоже реальное)

Как и во многих других математических задачах в физике, этот навык можно приобрести только через личную практику. Возможно, вы захотите потратить некоторое время, чтобы попытаться решить проблемы в разделе «Проверьте свое понимание» ниже.

Мы хотели бы предложить … Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействовать — это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием наших интерактивных приложений Optics Bench Interactive или Name That Image Interactive. Вы можете найти это в разделе Physics Interactives на нашем сайте.Optics Bench Interactive предоставляет учащимся интерактивную среду для изучения формирования изображений с помощью линз и зеркал. Интерактивное приложение Name That Image Interactive предлагает учащимся интенсивную умственную тренировку по распознаванию характеристик изображения для любого заданного местоположения объекта перед изогнутым зеркалом.

Проверьте свое понимание

1. Определите расстояние до изображения и высоту изображения для 5.Объект высотой 00 см, расположенный на расстоянии 45,0 см от вогнутого зеркала с фокусным расстоянием 15,0 см.

2. Определите расстояние до изображения и высоту изображения для объекта высотой 5,00 см, помещенного на 30,0 см от вогнутого зеркала с фокусным расстоянием 15,0 см.

3. Определите расстояние до изображения и высоту изображения для объекта высотой 5 см, помещенного на 20.0 см от вогнутого зеркала с фокусным расстоянием 15,0 см.

4. Определите расстояние до изображения и высоту изображения для объекта высотой 5,00 см, помещенного на 10,0 см от вогнутого зеркала с фокусным расстоянием 15,0 см.

5. Увеличенное перевернутое изображение находится на расстоянии 32,0 см от вогнутого зеркала с фокусным расстоянием 12.0 см. Определите расстояние до объекта и определите, является ли изображение реальным или виртуальным.

ZINGER : 6. Перевернутое изображение увеличивается в 2 раза, когда объект помещается на 22 см перед вогнутым зеркалом. Определите расстояние до изображения и фокусное расстояние зеркала.

Веб-сайт класса физики

Отражение и зеркала: обзор набора проблем

Этот набор из 26 задач нацелен на вашу способность использовать закон отражения, понимать взаимосвязь между расстоянием до изображения и расстоянием до объекта для плоских зеркал, а также использовать уравнение зеркала и коэффициент увеличения для решения проблем, которые связывают характеристики объекта и изображения с фокусным расстоянием. длина вогнутых и выпуклых зеркал.Проблемы варьируются по сложности от очень простых и простых до очень сложных и сложных. Более сложные задачи обозначены цветом , синие задачи .

Закон отражения

Когда дело доходит до отражения от плоской зеркальной поверхности, световые лучи следуют довольно предсказуемой схеме. Угол, под которым луч света приближается к поверхности зеркала, равен углу, под которым он отходит от зеркала.Это известно как закон отражения. В физике углы приближения измеряются относительно нормали к поверхности. Нормальная линия — это воображаемая линия, которая перпендикулярна зеркалу в точке, где луч света падает на зеркало. Угол между нормальной линией и приближающимся или падающим лучом известен как угол падения. Точно так же угол между отраженным лучом и той же нормальной линией известен как угол отражения. По закону отражения угол падения равен углу отражения.Более подробное и исчерпывающее обсуждение закона отражения и связанных с ним терминов можно найти в Учебнике по физике.

Характеристики плоских зеркальных изображений

Объекты, помещенные перед плоскими зеркалами, будут иметь соответствующее изображение, расположенное за зеркалом. Расстояние от изображения до зеркала всегда идентично расстоянию от предмета до зеркала. Так что если человек стоит 2.0 метров перед зеркалом, то изображение будет располагаться на идентичных 2,0 метра за зеркалом. Такой образ — виртуальный образ; при просмотре такого виртуального изображения в зеркале может показаться, что свет исходит с расстояния 2,0 метра за зеркалом. Если бы вы подошли к зеркалу и посмотрели на это так называемое виртуальное изображение, там не было бы ничего физического. Наблюдателю только кажется, что мысленный свет исходит из этого места в глаз при просмотре изображения человека в зеркале.Более подробное и исчерпывающее обсуждение характеристик плоского зеркального изображения можно найти в учебном пособии по физике.

Математика изогнутого зеркала

Большинство задач в этом наборе задач относятся к изогнутым зеркалам — как вогнутой, так и выпуклой разновидности. Два уравнения, относящихся к этим задачам, — уравнение зеркала и уравнение увеличения. Уравнение зеркала связывает расстояние до изображения с расстоянием до объекта и фокусным расстоянием.Уравнение зеркала

1 / f = 1 / d _o + 1 / d _i

Переменная d _o представляет собой расстояние до объекта или расстояние между зеркальной поверхностью и объектом. Переменная d _i представляет собой расстояние до изображения или расстояние между зеркальной поверхностью и изображением. Переменная f обозначает фокусное расстояние зеркала. В некоторых задачах фокусное расстояние не указывается; скорее указан радиус кривизны сферического зеркала.Радиус кривизны (R) просто вдвое больше значения фокусного расстояния (R = 2 • f). Как и любое уравнение в физике, уравнение зеркала можно использовать для решения неизвестной переменной с помощью алгебраической замены и перестановки. Учитывая, что в уравнении зеркала присутствуют три величины, две из них должны быть известны, чтобы найти третью неизвестную величину.

Изогнутое зеркало обычно увеличивает или уменьшает размер изображения по сравнению с размером объекта.Коэффициент увеличения — это число, которое выражает степень увеличения или уменьшения. Коэффициент увеличения — это просто отношение размера изображения к размеру объекта. Часто рассчитывается по формуле

.

M = h _i / h _o

В этом уравнении переменная M представляет увеличение, переменная h _i представляет высоту изображения, а переменная h _o представляет высоту объекта. В итоге отношение изображения к высоте объекта эквивалентно отношению изображения к расстоянию до объекта.Поэтому уравнение увеличения часто записывается как

M = h _i / h _o = — d _i / d _o

Отрицательный знак в приведенном выше уравнении относится к тому, что может быть наиболее проблемным аспектом этого набора проблем. Переменные в этих двух уравнениях могут быть как положительными, так и отрицательными. Положительный и отрицательный характер определяется фактическими характеристиками формируемых изображений и зеркал, которые используются в конкретных задачах.В таблице ниже приведены так называемые условные обозначения для шести переменных этих двух уравнений.

Переменная	Подписать Конвенцию
д или	Для наших целей расстояние до объекта (d o ) всегда будет положительным.
ч o	Для наших целей высота объекта (h o ) всегда будет положительной.
d i	Положительное расстояние до изображения (d i ) соответствует положению изображения на той же стороне зеркала, что и объект. Отрицательное расстояние до изображения (d i ) соответствует изображению, расположенному за зеркалом. Таким образом, реальные изображения всегда будут характеризоваться положительными значениями d i ; виртуальные образы будут иметь отрицательные значения d i
ч i	Высота положительного изображения (h i ) соответствует вертикальному изображению.Высота отрицательного изображения (h i ) соответствует инвертированному изображению. Поскольку все вертикальные изображения (положительные значения h и ) являются виртуальными изображениями, расположенными за зеркалом; вертикальные изображения, таким образом, будут виртуальными изображениями с отрицательными значениями d и . Точно так же инвертированные изображения с их отрицательными значениями hi являются реальными изображениями, которые имеют положительные значения d i .
из	Вогнутое зеркало будет иметь положительное фокусное расстояние (f), а выпуклое зеркало — отрицательное фокусное расстояние (f).
M	Значения увеличения положительны, если высота изображения (h i ) положительна. Таким образом, положительные значения M соответствуют вертикальным виртуальным изображениям, расположенным за зеркальной поверхностью. А отрицательные значения M соответствуют перевернутым, реальным изображениям, расположенным на стороне зеркала объекта.

При чтении проблемы важно обращать внимание на подсказки внутри проблемы, чтобы определить знак данной величины.Например, часто указывается расстояние от фокуса до зеркала. Это просто значение расстояния, соответствующее абсолютному значению фокусного расстояния. Положительное или отрицательное фокусное расстояние зависит от того, является ли зеркало вогнутым или выпуклым. Внимательное прочтение проблемы и понимание соглашения о знаках относительно фокусного расстояния (как указано в таблице выше) позволяет принять решение о знаке на f. В качестве второго примера некоторые проблемы описывают изображение, находящееся на указанном расстоянии от изогнутого зеркала.Указанное значение — это просто абсолютное значение расстояния до изображения. Положительное или отрицательное значение d _i зависит от того, находится ли изображение перед зеркалом или за ним. Внимательное прочтение постановки задачи вместе с пониманием соглашения о знаках для расстояния между изображениями (как указано в таблице выше) позволяет принять решение о знаке на d _i . Эти типы решений имеют решающее значение для вашего успеха в решении этой задачи. Принятие правильных решений не имеет ничего общего с вашими математическими способностями; скорее, они являются проверкой вашего концептуального понимания и вашей готовности внимательно прочитать проблему и уделить внимание деталям, которые могут быть важны.

В этом наборе задач есть несколько примеров, в которых зеркальное уравнение должно использоваться для решения неизвестной переменной, но известно только одно из двух других значений переменных. Такие проблемы обычно имеют формулировку эффекта: «изображение реальное и в три раза больше объекта». Такое заявление раскрывает информацию об увеличении изображения. Поскольку отношение изображения к высоте объекта равно (отрицательному) отношению расстояния изображения к расстоянию до объекта, мы можем сказать, что размер и высота могут рассматриваться как синонимы.Заявление о том, что изображение в три раза превышает размер объекта, означает, что отношение h _i / h _o равно +3 или -3. Определение того, является ли h _i / h _o +3 или -3, требует понимания условных обозначений (как описано в приведенной выше таблице). Значение h _o всегда положительно (для наших целей). Значение h _i является положительным для вертикальных изображений и отрицательным для инвертированных изображений. Поскольку это утверждение утверждает, что изображение является реальным (и, следовательно, инвертированным), коэффициенту h _i / h _o должно быть присвоено значение -3.Поскольку hi / ho равно -d _i / d _o , значение -3 может быть приравнено к -d _i / d _o . Этот поток логики позволяет записать выражение для d _i через d _o . Это выражение для d _i через d _o можно подставить в уравнение зеркала, чтобы преобразовать его в одно уравнение с одной неизвестной. Затем можно выполнить обычные алгебраические манипуляции, чтобы найти d _i или d _o .

В таблице ниже кратко описан процесс преобразования словесного утверждения в математическое уравнение, которое в конечном итоге используется для замены в зеркальное уравнение.

Устное заявление	Математический эквивалент	Выражение d i через d o
«… изображение реальное и в три раза больше объекта ».	ч i / ч o = -3 = -d i / d o	d i = + 3d o или d o = (+1/3) • d i

Привычки эффективно решать проблемы

Эффективный решатель проблем по привычке подходит к физическим проблемам таким образом, чтобы отражать набор дисциплинированных привычек.Хотя не все эффективные специалисты по решению проблем используют один и тот же подход, все они имеют общие привычки. Эти привычки кратко описаны здесь. Эффективное решение проблем …

• … внимательно читает задачу и создает мысленную картину физической ситуации. При необходимости они набрасывают простую схему физической ситуации, чтобы помочь визуализировать ее.
• … идентифицирует и регистрирует известные и неизвестные количества в организованном порядке.Приравнивает заданные значения к символам, используемым для представления соответствующей величины — например, d _o = 24,2 см; d _i = 16,8 см; f = ???.
• … строит стратегию решения неизвестной величины; стратегия, как правило, сосредоточена вокруг использования физических уравнений и во многом зависит от понимания принципов физики.
• … определяет подходящую (ые) формулу (ы) для использования, часто записывая их. При необходимости они выполняют необходимое преобразование количеств в правильные единицы.
• … выполняет подстановки и алгебраические манипуляции, чтобы найти неизвестную величину.

Подробнее …

Дополнительная литература / Учебные пособия:

Следующие страницы Учебного пособия по физике могут быть полезны для того, чтобы помочь вам в понимании концепций и математики, связанных с этими проблемами.

Набор задач «Отражение и зеркала»

Просмотреть набор задач

Решения с аудиогидом для отражения и зеркал

Просмотрите решение проблемы с аудиогидом:
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26

Физика того, как зеркало создает виртуальный мир

Здесь зеленая стрелка просто представляет какой-то случайный объект.Это могло быть что угодно. Теперь свет падает на этот объект и отражается во всех направлениях. Я нарисовал две стрелки, чтобы обозначить лишь часть отраженных световых лучей. Оба этих световых луча движутся к зеркалу и отражаются от него таким образом, что угол отражения равен углу падения.

Понял? Свет в комнате отражается от объекта, а затем отражается от зеркала к вашему глазу. Обратите внимание, что после того, как два луча отражаются от зеркала, они никогда не пересекаются. Вы можете нарисовать столько световых лучей, сколько захотите, но они не пересекутся после отражения от зеркала.

Теперь наши человеческие глаза тупые. Они не могут точно сказать, откуда пришел свет. Вместо этого наши глаза и мозг прослеживают свет обратно туда, откуда он, по-видимому, исходит. Здесь появляются две пунктирные линии. Это проекции световых лучей на точку за зеркалом, где линии сходятся.

Нашим немым глазом это выглядит точно на , как будто есть такая же зеленая стрелка с другой стороны зеркала — но, конечно, это просто изображение.Поскольку на самом деле лучи света там не встречаются, на самом деле его и нет. Это просто виртуальный образ. Также обратите внимание, что виртуальное изображение стоит вертикально, как и объект. Это будет верно для всех виртуальных изображений — они имеют ту же ориентацию, что и объект. А как насчет зеркал заднего вида влево и вправо? Это другой вопрос, но вот ответ.

А как насчет того реального изображения? Чтобы создать реальное изображение, нам понадобится нечто иное, чем простое плоское зеркало. Вот где пригодится зеркало для макияжа.Увеличительная сторона зеркала для макияжа не плоская, а параболическая. Когда параллельные световые лучи попадают в параболическое зеркало, все они отражаются в одну и ту же точку — точку фокусировки.

Расположение этой точки фокуса зависит от кривизны зеркала, но сейчас это не очень важно. Так что же произойдет, если вы поднесете лицо к зеркалу для макияжа? Вот диаграмма световых лучей, на которой ваше лицо представлено зеленой стрелкой. Простите за это.

Physics Mirrors — Physics Видео от Brightstorm

Итак, давайте теперь поговорим о зеркалах и формировании изображения, прежде чем я буду слишком углубляться в это. Я действительно хочу поговорить о том, что значит быть изображением.Итак, что происходит: мы берем объект и помещаем его перед зеркалом, свет отражается от этого объекта, затем идет и отражается от зеркала, а затем важно то, что происходит со светом после того, как он отражается от зеркала. . Хорошо, идея в том, что иногда этот свет отражается от зеркала, а затем снова объединяется, так что это означает, что он будет преобразовывать то же изображение. Он будет выглядеть так же, как когда он отражался от объекта, и это то, что мы подразумеваем под изображением, оно выглядит как объект.Теперь, если свет действительно проходит через изображение, отражаясь, возвращается и воссоединяется, то мы называем это изображение реальным. Хорошо, это изображение реальное, если, с другой стороны, оно просто выглядит так, как будто есть изображение, и на самом деле свет вообще не воссоздается, тогда это изображение будет называться виртуальным, хорошо.

Мы обнаружим, что если вы используете только одно зеркало или один объектив, то реальные изображения всегда инвертируются, что означает, что они всегда перевернуты, поэтому вы смотрите через объектив, объект находится правой стороной вверх, изображение перевернуто правильно.С другой стороны, виртуальные изображения всегда будут вертикальными или правильными, если есть одно зеркало или один объектив. И тогда, конечно, у нас может быть увеличение, увеличение всегда определяется отношением расстояния до изображения от зеркала к тому, насколько далеко находится объект от зеркала. Хорошо, давайте сделаем это очень быстро с помощью простейшего случая — плоского зеркала. Хорошо, плоское зеркало выглядит так, у нас есть свет, исходящий от объекта, и он просто отражается прямо назад, так что есть одно из них.Давайте нарисуем еще один, ну, у меня есть свет от объекта, а затем он просто отражается, и запомните, что угол отражения равен углу падения, поэтому он будет таким.

Теперь вот вопрос, собираются ли когда-нибудь эти два луча рекомбинировать? Ну, это определенно не похоже на то, что они просто отдаляются друг от друга. Итак, что я имел в виду под изображением? Я имею в виду, что я стою перед плоским зеркалом, я вижу изображение, вот идея: когда я стою перед плоским зеркалом, я вижу эти два световых луча, но мой мозг автоматически не думает о том, что зеркало находится там, он просто говорит хорошо, вот эти два световых луча.Таким образом, он экстраполирует световые лучи обратно, как если бы зеркала там не было, и так смотрите, и как это выглядит. Похоже, что свет исходит отсюда, посмотрите на это, на том же расстоянии за зеркалом, на котором находился объект перед зеркалом, такого же размера, как и объект, являющийся изображением. Обратите внимание на то, что изображение расположено прямо вверх, оно того же размера и на таком же расстоянии. Итак, у нас есть виртуальное изображение, потому что на самом деле света здесь никогда не было, если я пойду и посмотрю за зеркало, я ничего там не увижу, верно? Хорошо, я посмотрю стену, хорошо.Итак, идея состоит в том, что на самом деле здесь не было света, поэтому виртуальное прямое изображение на том же расстоянии от зеркала, что и объект, с увеличением 1, хорошо, что означает, что он не увеличивается.

Хорошо, давайте рассмотрим несколько более сложные случаи, связанные с изогнутыми зеркалами. Но нам нужно делать это осторожно, есть 3 основных случая: вогнутое зеркало 2 случая этого и выпуклое зеркало только 1 случай, так что это будет хорошо. Хорошо, давайте сначала посмотрим на вогнутое зеркало, хорошо, если объект находится далеко от зеркала, насколько далеко это зависит от того, насколько оно вогнуто, насколько оно изогнуто.Но если объект находится далеко, давайте нарисуем пару этих лучей, давайте нарисуем 1 к вершине, хорошо, он будет отражаться под тем же углом, под которым попал. Хорошо, а затем мы сделаем 1 прямо, так что мы сделаем 1 точно так же, и он будет отражаться под тем же углом, под которым попал, но помните, что угол измеряется от нормали. Итак, я должен был нарисовать себя немного нормальным, хорошо, а затем я должен был нарисовать отражатель и посмотреть на него, у нас действительно есть эти лучи, рекомбинирующие. Таким образом, это дает нам реальное изображение, но обратите внимание, что реальное изображение перевернуто, хорошо, так что это даст мне настоящее перевернутое изображение, хорошо, это будет ближе, увеличение будет меньше 1, хорошо, и вот что происходит.Теперь давайте подумаем, что будет, если я начну перемещать этот объект.

Оказывается, что когда объект приближается к зеркалу, изображение перемещается все дальше и дальше. Хорошо, эти две вещи будут совпадать на расстоянии, равном радиусу круга, который получился бы, если бы вы сделали круг, он называется радиусом кривизны, насколько он изогнут, хорошо, чем более плоский он является, тем больше этот радиус. Чем он более изогнутый, тем меньше радиус, поэтому эти две вещи будут накладываться друг на друга, а затем они будут двигаться вот так.Изображение уйдет в бесконечность, когда объект переместится в определенное место перед зеркалом, называемое фокусным расстоянием. Хорошо, и это будет обсуждаться более подробно в разделе, посвященном уравнению объектива. Хорошо, а что будет, если я подойду ближе, чем фокусное расстояние? Что ж, давайте еще раз посмотрим, что мы нарисуем 2 луча, один, а затем давайте нарисуем другой, нарисуем этот зеленым. Итак, мы пойдем прямо, а затем вспомним, что я должен дать себе свое обычное хорошо, а эти 2 на самом деле нет, извините, эти 2 на самом деле не будут перекрываться, они никогда не будут рекомбинировать, хорошо, поэтому я должен продолжить их в обратном направлении чтобы увидеть, где мое изображение.

И мое изображение здесь намного выше, виртуально и прямолинейно, так что это виртуальное, прямое. Итак, в основном идея состоит в том, что с вогнутым зеркалом объект приближается к зеркалу.У меня есть реальное перевернутое изображение, которое удаляется от зеркала, две вещи совпадают на короткое время и имеют одинаковый размер, но одна из них реальная, ну, объект очевидно реально. Изображение будет реальным и перевернутым, а затем изображение исчезнет и продолжит уходить в бесконечность, как только объект достигнет этой определенной точки, которую мы переходим сюда.И изображение появляется с другой стороны, теперь оно виртуальное и прямое, и по мере того, как объект приближается к зеркалу, изображение также приближается к зеркалу. Хорошо, это вогнутая, это самый сложный случай. Хорошо, теперь давайте сделаем более простой случай, давайте сделаем выпуклую, хорошо выпуклую, вот так, а затем снова мне нужна моя маленькая нормаль вот так. Хорошо, так что есть один, давайте сделаем еще один, вот мы и спустимся вот так. Обратите внимание, что эти два, очевидно, никогда не собираются рекомбинировать правильно, так что это означает, что у нас есть виртуальное изображение, мы можем определить, где оно находится, продолжая эти геометрические линии и посмотрев, что мы получим в итоге.

Мы заканчиваем тем, что здесь происходило, поэтому проблема в том, что здесь у нас всегда есть прямое виртуальное изображение, которое находится дальше от зеркала, чем объект. В этом случае у нас всегда есть прямое виртуальное изображение, которое ближе к зеркалу, чем объект. Эти зеркала очень, очень полезны, например, в магазинах, потому что все имеет небольшое увеличение на 1, а это означает, что если вы используете одно из этих выпуклых зеркал, вы можете видеть больше, вы можете видеть больше происходящего, вы можете увидеть весь магазин на один раз правильно, чего нельзя сказать о вогнутых зеркалах.Вогнутые зеркала на самом деле используются для увеличения предметов, так что это некоторые качественные идеи о том, как работают зеркала и формирование изображения.

Mirrors — Physics LibreTexts

Зеркало — это устройство, которое содержит поверхность, используемую для отражения света.

Поскольку зеркала обычно не поглощают много света, большая часть света перенаправляется при контакте с зеркалом, и общее качество объекта обычно сохраняется в новом изображении.

Зеркала изготавливаются из разных материалов и имеют множество применений.

САМОЛЕТ СЕРЕБРЯНЫЕ ЗЕРКАЛА

Обычно так делают повседневные зеркала.

Во-первых, это зеркало сделано из прозрачного плоского стекла. Стекло почти прозрачное, чтобы пропускать большую часть света.

Во-вторых, стекло покрыто тонким слоем серебра. Твердое серебро, образующееся на стекле, образуется в результате восстановления жидкого нитрата серебра, который изначально прилипает к стеклу.Серебро поглощает очень мало света и отражает около 95% его. Когда свет падает на серебро, он отражается под тем же углом, что и на серебро.

Наконец, световые лучи в конечном итоге встречаются и формируется виртуальное изображение. (Это видео на YouTube демонстрирует эту концепцию: http://www.youtube.com/watch?v=0T3CVPlv1D8)

Серебро очень часто используется, потому что это лучший отражатель видимого света среди обычных металлов. Он отражает около 95% видимого света в спектрах видимого света (400–700 нм).Хотя серебро стоит дорого, слоя серебра толщиной 100 нм обычно достаточно для достижения полной отражательной способности серебра.

Помимо описанного выше серебряного зеркала, зеркала также могут быть изготовлены из других материалов. Полезность материала зависит от его стоимости и эффективности отражения имеющихся длин волн света.

Алюминиевые зеркала

Алюминий часто заменяют серебром. На это есть две основные причины.Во-первых, алюминий сохраняет высокую отражающую способность в ультрафиолетовом диапазоне. Это делает его особенно полезным для космических приложений. Во-вторых, алюминий намного дешевле серебра.

Алюминий сохраняет отражающую способность 88-92% в видимой области спектра.

Алюминиевые зеркала обычно изготавливаются путем прикрепления алюминия к стеклу с помощью вакуума и последующего покрытия алюминия несколькими слоями защитной краски.

Зеркала с золотым покрытием

Зеркала из золота очень дороги в изготовлении.Однако они очень полезны для отражения инфракрасного излучения. Золотые зеркала могут улавливать 96% излучения в спектре от 800 нм до 20 мкм. Однако они в основном бесполезны ниже 500 нм.

Зеркала могут принимать не только разные покрытия, но и разные формы.

Зеркала могут быть плоскими (см. Описание вверху), вогнутыми или выпуклыми.

Формы зеркал:

Зеркала вогнутые

Вогнутое зеркало используется для фокусировки изображения близко к зеркалу.Изображения перед зеркалом или за ним в зависимости от того, насколько далеко изображение находится от точки фокусировки. Для получения дополнительной информации посетите: http://www.physicsclassroom.com/class/refln/u13l3e.cfm

Зеркала выпуклые

Выпуклые зеркала используются для создания виртуальных образов, которые формируются по другую сторону зеркала. Эти зеркала используются в качестве боковых зеркал автомобилей. Для получения дополнительной информации посетите: http://www.physicsclassroom.com/class/refln/u13l4a.cfm

Использование зеркал:

Самым распространенным зеркалом является плоское зеркало, используемое для того, чтобы смотреть на себя.Другие распространенные зеркала включают выпуклые зеркала, используемые на боковых зеркалах для автомобилей, и плоское зеркало, используемое в качестве заднего зеркала для автомобилей. Менее распространенные, но очень важные, повседневные зеркала включают зеркала, расположенные в телевизорах и проекторах.

Возьмем, к примеру, зеркало DLP, разработанное Texas Instruments: http://www.ti.com/lsds/ti/analog/dlp…dlp-works.page. Это набор из миллионов микрозеркал, которые тщательно направляют свет, чтобы на экране он отображался в высоком разрешении.

Другой очень важный пример зеркал — зеркала телескопа Хаббла.Ниже приведено полезное изображение с http://hubblesite.org/the_telescope/hubble_essentials/image.php?image=light-path:

.

Последний, но интересный пример использования зеркал — это солнечная площадка Иванпа, расположенная в пустыне Мохаве. http://news.nationalgeographic.com/news/energy/2013/07/130725-ivanpah-solar-energy-mojave-desert/

Это система, в которой сотни или зеркала окружают водонапорную башню. Днем зеркала отражают свет в водонапорную башню в центре системы.Это нагревает воду. В конечном итоге вода собирается для получения энергии.

2.3: Сферические зеркала — Physics LibreTexts

Цели обучения

К концу этого раздела вы сможете:

• Опишите формирование изображения сферическими зеркалами.
• Используйте лучевые диаграммы и уравнение зеркала для расчета свойств изображения в сферическом зеркале.

Изображение в плоском зеркале имеет тот же размер, что и объект, находится в вертикальном положении и находится на том же расстоянии за зеркалом, что и объект перед зеркалом.С другой стороны, изогнутое зеркало может формировать изображения, которые могут быть больше или меньше, чем объект, и могут формироваться либо перед зеркалом, либо за ним. В общем, любая изогнутая поверхность образует изображение, хотя некоторые изображения могут быть настолько искажены, что их невозможно распознать (подумайте о зеркалах в стиле забавных домиков). Поскольку изогнутые зеркала могут создавать такое богатое разнообразие изображений, они используются во многих оптических устройствах, которые находят множество применений. Мы сконцентрируемся на сферических зеркалах по большей части, потому что их легче изготовить, чем зеркала, такие как параболические зеркала, и поэтому они более распространены.

Изогнутые зеркала

Мы можем определить два основных типа сферических зеркал. Если отражающей поверхностью является внешняя сторона сферы, зеркало называется выпуклым зеркалом . Если внутренняя поверхность является отражающей поверхностью, она называется вогнутым зеркалом .

Симметрия — один из основных отличительных признаков многих оптических устройств, включая зеркала и линзы. Ось симметрии таких оптических элементов часто называют главной осью или оптической осью.Для сферического зеркала оптическая ось проходит через центр кривизны зеркала и вершину зеркала, как показано на рисунке \ (\ PageIndex {1} \).

Рисунок \ (\ PageIndex {1} \). Сферическое зеркало формируется путем вырезания части сферы и посеребрения внутренней или внешней поверхности. Вогнутое зеркало имеет посеребрение на внутренней поверхности (вспомните «пещера»), а выпуклое зеркало имеет серебрение на внешней поверхности.

Рассмотрим лучи, параллельные оптической оси параболического зеркала, как показано на рисунке \ (\ PageIndex {2a} \).Следуя закону отражения, эти лучи отражаются так, что они сходятся в точке, называемой фокусной точкой . На рисунке \ (\ PageIndex {2b} \) показано сферическое зеркало, которое больше по сравнению с его радиусом кривизны. В этом зеркале отраженные лучи не пересекаются в одной и той же точке, поэтому зеркало не имеет четко определенной точки фокусировки. Это называется сферической аберрацией и приводит к нечеткому изображению протяженного объекта. На рисунке \ (\ PageIndex {2c} \) показано сферическое зеркало, которое мало по сравнению с его радиусом кривизны.Это зеркало является хорошим приближением параболического зеркала, поэтому лучи, приходящие параллельно оптической оси, отражаются в четко определенную точку фокусировки. Расстояние по оптической оси от зеркала до фокальной точки называется фокусным расстоянием зеркала.

Рисунок \ (\ PageIndex {2} \): (a) Параллельные лучи, отраженные от параболического зеркала, пересекаются в одной точке, называемой фокусной точкой F. (b) Параллельные лучи, отраженные от большого сферического зеркала, не пересекаются в одной общей точке. . (c) Если сферическое зеркало мало по сравнению с его радиусом кривизны, оно лучше приближается к центральной части параболического зеркала, поэтому параллельные лучи по существу пересекаются в общей точке.Расстояние по оптической оси от зеркала до фокуса — это фокусное расстояние f зеркала.

Выпуклое сферическое зеркало также имеет точку фокусировки, как показано на рисунке \ (\ PageIndex {3} \). Падающие лучи, параллельные оптической оси, отражаются от зеркала и, кажется, исходят из точки \ (F \) на фокусном расстоянии \ (f \) за зеркалом. Таким образом, точка фокусировки виртуальна, потому что на самом деле через нее не проходят никакие настоящие лучи; они только кажутся исходящими от него.

Рисунок \ (\ PageIndex {3} \): (a) Лучи, отраженные выпуклым сферическим зеркалом: падающие лучи света, параллельные оптической оси, отражаются от выпуклого сферического зеркала и, кажется, исходят из четко определенной фокальной точки в фокусное расстояние f на противоположной стороне зеркала.Фокус является виртуальным, потому что через него не проходят настоящие лучи. (б) Фотография виртуального изображения, образованного выпуклым зеркалом. (кредит b: модификация работы Дженни Даунинг)

Как фокусное расстояние зеркала соотносится с радиусом кривизны зеркала? На рисунке \ (\ PageIndex {4} \) показан единственный луч, который отражается сферическим вогнутым зеркалом. Падающий луч параллелен оптической оси. Точка, в которой отраженный луч пересекает оптическую ось, является точкой фокусировки. Обратите внимание, что все падающие лучи, параллельные оптической оси, отражаются через точку фокусировки — для простоты мы показываем только один луч.Мы хотим выяснить, как фокусное расстояние \ (FP \) (обозначается \ (f \)) соотносится с радиусом кривизны зеркала \ (R \), длина которого составляет

.

\ [R = CF + FP. \ label {eq31} \]

Закон отражения говорит нам, что углы \ (\ angle OXC \) и \ (\ angle CXF \) одинаковы, а поскольку падающий луч параллелен оптической оси, углы \ (\ angle OXC \) и \ (\ angle XCP \) тоже такие же. Таким образом, треугольник \ (CXF \) является равнобедренным треугольником с \ (CF = FX \). Если угол \ (θ \) мал, то

\ [\ sin θ≈ θ \ label {sma} \]

, который называется «малоугловым приближением »), затем \ (FX≈FP \) или \ (CF≈FP \).Подставляя это в уравнение \ ref {eq31} для радиуса \ (R \), мы получаем

\ [\ begin {align} R & = CF + FP \ nonumber \\ [4pt] & = FP + FP \ nonumber \\ [4pt] & = 2FP \ nonumber \\ [4pt] & = 2f \ end {align } \]

Другими словами, в малоугловом приближении фокусное расстояние \ (f \) вогнутого сферического зеркала составляет половину его радиуса кривизны, \ (R \):

\ [f = \ dfrac {R} {2}. \]

В этой главе мы предполагаем, что малоугловое приближение (также называемое параксиальным приближением ) всегда справедливо.В этом приближении все лучи являются параксиальными лучами, что означает, что они составляют небольшой угол с оптической осью и находятся на расстоянии намного меньшем, чем радиус кривизны от оптической оси. В этом случае их углы отражения \ (θ \) малы, поэтому

\ [\ sin θ≈ \ tan θ≈ θ. \ label {smallangle} \]

Рисунок \ (\ PageIndex {4} \): Отражение в вогнутом зеркале. В малоугловом приближении луч, параллельный оптической оси CP, отражается через фокальную точку F зеркала.

Использование трассировки лучей для поиска изображений

Чтобы найти местоположение изображения, сформированного сферическим зеркалом, мы сначала используем трассировку лучей, которая представляет собой метод рисования лучей и использование закона отражения для определения отраженных лучей (позже для линз мы используем закон преломления для определения преломленных лучей). В сочетании с некоторой базовой геометрией мы можем использовать трассировку лучей, чтобы найти фокус, местоположение изображения и другую информацию о том, как зеркало управляет светом. Фактически, мы уже использовали трассировку лучей выше, чтобы определить фокус сферических зеркал или расстояние до изображения плоских зеркал.Чтобы найти изображение объекта, вы должны найти как минимум две точки изображения. Для определения местоположения каждой точки необходимо провести по крайней мере два луча из точки на объекте и построить их отраженные лучи. Точка пересечения отраженных лучей в реальном или виртуальном пространстве — это место, где находится соответствующая точка изображения. Чтобы упростить трассировку лучей, мы сконцентрируемся на четырех «основных» лучах, отражения которых легко построить.

На рисунке \ (\ PageIndex {5} \) показаны вогнутое и выпуклое зеркало, перед каждым из которых находится объект в форме стрелки.Это объекты, изображения которых мы хотим найти с помощью трассировки лучей. Для этого мы рисуем лучи из точки \ (Q \), которая находится на объекте, но не на оптической оси. Мы выбираем рисовать наш луч от кончика объекта. Главный луч 1 идет из точки \ (Q \) параллельно оптической оси. Как обсуждалось выше, отражение этого луча должно проходить через точку фокусировки. Таким образом, для вогнутого зеркала отражение главного луча 1 проходит через фокальную точку \ (F \), как показано на рисунке \ (\ PageIndex {5b} \).Для выпуклого зеркала обратное продолжение отражения главного луча 1 проходит через точку фокусировки (т.е. виртуальный фокус). Главный луч 2 сначала проходит по линии, проходящей через точку фокусировки, а затем отражается обратно по линии, параллельной оптической оси. Главный луч 3 движется к центру кривизны зеркала, поэтому он падает на зеркало при нормальном падении и отражается обратно вдоль линии, откуда он пришел. Наконец, главный луч 4 попадает в вершину зеркала и отражается симметрично относительно оптической оси.

Рисунок \ (\ PageIndex {5} \): четыре главных луча, показанные для (а) вогнутого зеркала и (б) для выпуклого зеркала. Изображение формируется там, где пересекаются лучи (для реальных изображений) или где их обратные продолжения пересекаются (для виртуальных изображений).

Четыре главных луча пересекаются в точке \ (Q ′ \), где находится изображение точки \ (Q \). Чтобы найти точку \ (Q ′ \), достаточно провести любые два из этих главных лучей. Таким образом, мы можем выбрать любой из основных лучей, по нашему желанию, для определения местоположения изображения.Иногда полезно рисовать более двух основных лучей, чтобы проверить правильность трассировки лучей.

Чтобы полностью найти расширенное изображение, нам нужно найти вторую точку на изображении, чтобы мы знали, как изображение ориентировано. Для этого мы прослеживаем основные лучи от основания объекта. В этом случае все четыре основных луча бегут вдоль оптической оси, отражаются от зеркала, а затем возвращаются назад вдоль оптической оси. Сложность в том, что, поскольку эти лучи коллинеарны, мы не можем определить единственную точку их пересечения.Все, что мы знаем, это то, что основание изображения находится на оптической оси. Однако, поскольку зеркало симметрично сверху вниз, оно не меняет вертикальную ориентацию объекта. Таким образом, поскольку объект вертикальный, изображение должно быть вертикальным. Следовательно, изображение основания объекта находится на оптической оси непосредственно над изображением кончика, как показано на рисунке.

Для вогнутого зеркала расширенное изображение в этом случае формируется между точкой фокусировки и центром кривизны зеркала.Он перевернут по отношению к объекту, является реальным изображением и меньше самого объекта. Если бы мы переместили объект ближе или дальше от зеркала, характеристики изображения изменились бы. Например, в следующем упражнении мы покажем, что объект, помещенный между вогнутым зеркалом и его точкой фокусировки, приводит к виртуальному изображению, которое находится в вертикальном положении и больше, чем объект. Для выпуклого зеркала расширенное изображение формируется между точкой фокусировки и зеркалом. Он расположен вертикально по отношению к объекту, представляет собой виртуальное изображение и меньше самого объекта.

Правила трассировки лучей

Трассировка лучей очень полезна для зеркал. Правила трассировки лучей приведены здесь для справки:

• Луч, идущий параллельно оптической оси сферического зеркала, отражается вдоль линии, проходящей через точку фокусировки зеркала (луч 1 на рисунке \ (\ PageIndex {5} \)).
• Луч, проходящий по линии, проходящей через точку фокусировки сферического зеркала, отражается вдоль линии, параллельной оптической оси зеркала (луч 2 на рисунке \ (\ PageIndex {5} \)).
• Луч, проходящий по линии, проходящей через центр кривизны сферического зеркала, отражается обратно по той же линии (луч 3 на рисунке \ (\ PageIndex {5} \)).
• Луч, попадающий в вершину сферического зеркала, отражается симметрично относительно оптической оси зеркала (луч 4 на рисунке \ (\ PageIndex {5} \)).

Мы используем трассировку лучей, чтобы проиллюстрировать, как изображения формируются зеркалами, и получить числовую информацию об оптических свойствах зеркала.Если мы предположим, что зеркало мало по сравнению с его радиусом кривизны, мы также можем использовать алгебру и геометрию, чтобы вывести уравнение зеркала, что мы и сделаем в следующем разделе. Комбинирование трассировки лучей с уравнением зеркала — хороший способ анализа зеркальных систем.

Формирование изображения путем отражения — уравнение зеркала

Для плоского зеркала мы показали, что сформированное изображение имеет ту же высоту и ориентацию, что и объект, и находится на том же расстоянии за зеркалом, что и объект перед зеркалом.Хотя для изогнутых зеркал ситуация немного сложнее, использование геометрии приводит к простым формулам, связывающим расстояние до объекта и изображения с фокусными расстояниями вогнутых и выпуклых зеркал.

Рисунок \ (\ PageIndex {6} \): Изображение, сформированное вогнутым зеркалом.

Рассмотрим объект \ (OP \), показанный на рисунке \ (\ PageIndex {6} \). Центр кривизны зеркала обозначен \ (C \) и находится на расстоянии \ (R \) от вершины зеркала, как показано на рисунке. Расстояние до объекта и изображения обозначено \ (d_o \) и \ (d_i \), а высота объекта и изображения обозначена \ (h_o \) и \ (h_i \), соответственно.Поскольку углы \ (ϕ \) и \ (ϕ ′ \) являются альтернативными внутренними углами, мы знаем, что они имеют одинаковую величину. Однако они должны отличаться по знаку, если мы измеряем углы от оптической оси, поэтому \ (ϕ = −ϕ ′ \). Аналогичный сценарий имеет место для углов \ (θ \) и \ (θ ′ \). Закон отражения говорит нам, что они имеют одинаковую величину, но их знаки должны отличаться, если мы измеряем углы от оптической оси. Таким образом, \ (θ = −θ ′ \). Взяв тангенс углов \ (θ \) и \ (θ ′ \) и используя свойство \ (\ tan (−θ) = — \ tan θ \), мы получим

\ [\ left.\ begin {array} {rcl} \ tanθ = \ dfrac {h_o} {d_o} \\ \ tanθ ′ = — \ tanθ = \ dfrac {h_i} {d_i} \ end {array} \ right \} = \ dfrac { h_o} {d_o} = — \ dfrac {h_i} {d_i} \ label {eq51} \]

или

\ [- \ dfrac {h_o} {h_i} = \ dfrac {d_o} {d_i}. \ Label {eq52} \]

Аналогично, касательная к \ (ϕ \) и \ (ϕ ′ \) дает

\ [\ left. \ begin {array} {rcl} \ tanϕ = \ dfrac {h_o} {d_o-R} \\ \ tanϕ ′ = — \ tanϕ = \ dfrac {h_i} {R-d_i} \ end {array} \ right \} = \ dfrac {h_o} {d_o-R} = — \ dfrac {h_i} {R-d_i} \]

или

\ [- \ dfrac {h_o} {h_i} = \ dfrac {d_o-R} {R-d_i}.\ label {eq55} \]

Объединение уравнения \ ref {eq51} и \ ref {eq55} дает

\ [\ dfrac {d_o} {d_i} = \ dfrac {d_o-R} {R-d_i}. \]

После небольшой алгебры получается

.

\ [\ dfrac {1} {d_o} + \ dfrac {1} {d_i} = \ dfrac {2} {R}. \ label {eq57} \]

Для этого результата не требуется приближения, поэтому он является точным. Однако, как обсуждалось выше, в малоугловом приближении фокусное расстояние сферического зеркала составляет половину радиуса кривизны зеркала, или \ (f = R / 2 \).Вставка этого в уравнение \ ref {eq57} дает уравнение зеркала :

\ [\ underbrace {\ dfrac {1} {d_o} + \ dfrac {1} {d_i} = \ dfrac {1} {f}} _ {\ text {зеркальное уравнение}}. \ label {зеркальное уравнение} \]

Уравнение зеркала связывает расстояние до изображения и объекта с фокусным расстоянием и действительно только в малоугловом приближении (уравнение \ ref {sma}). Хотя он был получен для вогнутого зеркала, он также справедлив и для выпуклых зеркал (доказательство этого оставлено в качестве упражнения). Мы можем расширить уравнение зеркала на случай плоского зеркала, отметив, что плоское зеркало имеет бесконечный радиус кривизны.Это означает, что точка фокусировки находится на бесконечности, поэтому уравнение зеркала упрощается до

\ [d_o = −d_i \]

, которое представляет собой то же уравнение, полученное ранее.

Обратите внимание, что мы очень внимательно относились к знакам при выводе уравнения зеркала. Для плоского зеркала расстояние до изображения имеет знак, противоположный расстоянию до объекта. Кроме того, реальное изображение, сформированное вогнутым зеркалом на рисунке \ (\ PageIndex {6} \), находится на противоположной стороне оптической оси по отношению к объекту.В этом случае высота изображения должна иметь знак, противоположный высоте объекта. Чтобы отслеживать знаки различных величин в уравнении зеркала, мы теперь вводим соглашение о знаках.

Условные обозначения для сферических зеркал

Использование согласованного соглашения о знаках очень важно в геометрической оптике. Он присваивает положительные или отрицательные значения для величин, характеризующих оптическую систему. Понимание соглашения о знаках позволяет описывать изображение без построения лучевой диаграммы.В этом тексте используется следующее соглашение о знаках:

.

1. Фокусное расстояние \ (f \) положительно для вогнутых зеркал и отрицательно для выпуклых зеркал.
2. Расстояние до изображения \ (d_i \) положительно для реальных изображений и отрицательно для виртуальных изображений.

Обратите внимание, что правило 1 означает, что радиус кривизны сферического зеркала может быть положительным или отрицательным. Что значит иметь отрицательный радиус кривизны? Это просто означает, что радиус кривизны выпуклого зеркала определяется как отрицательный.

Увеличение изображения

Давайте воспользуемся соглашением о знаках для дальнейшей интерпретации вывода зеркального уравнения. При выводе этого уравнения мы обнаружили, что высота объекта и изображения связаны соотношением

\ [- \ dfrac {h_o} {h_i} = \ dfrac {d_o} {d_i}. \ label {eq61} \]

См. Уравнение \ ref {eq52}. И объект, и изображение, сформированное зеркалом на рисунке \ (\ PageIndex {6} \), реальны, поэтому расстояния между объектом и изображением положительны. Самая высокая точка объекта находится над оптической осью, поэтому высота объекта положительна.Однако изображение находится ниже оптической оси, поэтому высота изображения отрицательная. Таким образом, это соглашение о знаках согласуется с нашим выводом уравнения зеркала.

Уравнение \ ref {eq61} фактически описывает линейное увеличение (часто называемое просто « увеличение ») изображения с точки зрения расстояния до объекта и изображения. Таким образом, мы определяем безразмерное увеличение \ (м \) следующим образом:

\ [\ underbrace {m = \ dfrac {h_i} {h_o}} _ {\ text {линейное увеличение}}.\ label {mag} \]

Если \ (m \) положительный, изображение вертикальное, а если \ (m \) отрицательное, изображение инвертируется. Если \ (| m |> 1 \), изображение больше, чем объект, а если \ (| m | <1 \), изображение меньше, чем объект. При таком определении увеличения мы получаем следующее соотношение между вертикальным и горизонтальным объектом и расстояниями между изображениями:

\ [m = \ dfrac {h_i} {h_o} = — \ dfrac {d_i} {d_o}. \]

Это очень полезное соотношение, потому что оно позволяет вам получить увеличение изображения от объекта и расстояния до изображения, которые вы можете получить из уравнения зеркала.

Пример \ (\ PageIndex {1} \): Солнечная электрическая генерирующая система

Одна из солнечных технологий, используемых сегодня для выработки электричества, включает устройство (называемое параболическим желобом или концентрирующим коллектором), которое концентрирует солнечный свет на почерневшей трубе, содержащей жидкость. Эта нагретая жидкость перекачивается в теплообменник, где тепловая энергия передается другой системе, которая используется для генерации пара и, в конечном итоге, вырабатывает электричество посредством обычного парового цикла.На рисунке \ (\ PageIndex {7} \) показана такая рабочая система в южной Калифорнии. Настоящее зеркало представляет собой параболический цилиндр с фокусом на трубе; однако мы можем приблизительно представить зеркало как ровно четверть кругового цилиндра.

Рисунок \ (\ PageIndex {7} \): Коллекторы с параболическим желобом используются для выработки электроэнергии в южной Калифорнии. (кредит: «kjkolb» / Wikimedia Commons)

1. Если мы хотим, чтобы солнечные лучи фокусировались на расстоянии 40,0 см от зеркала, каков радиус зеркала?
2. Какое количество солнечного света сконцентрировано на трубе на метр длины трубы при условии, что инсоляция (падающее солнечное излучение) составляет 900 Вт / м ² ?
3. Если трубка для жидкости имеет 2.Диаметр 00 см, каково повышение температуры жидкости на метр трубы за 1 минуту? Предположим, что все солнечное излучение, падающее на отражатель, поглощается трубой, а жидкость представляет собой минеральное масло.

Стратегия

Сначала определите задействованные физические принципы. Часть (а) относится к оптике сферических зеркал. Часть (b) включает небольшую математику, в первую очередь геометрию. Часть (c) требует понимания тепла и плотности.

Решение

а.2 (1,00 \, м) \ nonumber \\ [4pt] & = 0,251 \, кг \ end {align *} \]

Следовательно, повышение температуры за одну минуту равно

\ [\ begin {align *} \ Delta T & = \ dfrac {Q} {mc} \ nonumber \\ [4pt] & = \ dfrac {(1130 \, W) (60.0 \, s)} {(0.251 \ , кг) (1670 \, Дж⋅кг / ° C)} \ nonumber \\ [4pt] & = 162 ° \ end {align *} \]

Значение

Массив таких труб в калифорнийской пустыне может обеспечить тепловую мощность 250 МВт в солнечный день, при этом температура жидкости достигает 400 ° C.Мы рассматриваем здесь только один метр трубы и игнорируем тепловые потери по трубе.

Пример \ (\ PageIndex {2} \): изображение в выпуклом зеркале

Кератометр — это устройство, используемое для измерения кривизны роговицы глаза, особенно для подгонки контактных линз. Свет отражается от роговицы, которая действует как выпуклое зеркало, и кератометр измеряет увеличение изображения. Чем меньше увеличение, тем меньше радиус кривизны роговицы.Если источник света находится на расстоянии 12 см от роговицы, а увеличение изображения составляет 0,032, каков радиус кривизны роговицы?

Стратегия

Если вы найдете фокусное расстояние выпуклого зеркала, образованного роговицей, то вы знаете его радиус кривизны (это в два раза больше фокусного расстояния). Расстояние до объекта d _o = 12 см, увеличение m = 0,032. Сначала найдите расстояние до изображения \ (d_i \), а затем найдите фокусное расстояние \ (f \).

Решение

Начните с уравнения увеличения (Equation \ ref {mag}), решите для \ (d_i \) и вставьте заданные значения, чтобы получить

\ [d_i = −m d_o = — (0.{−1} \\ [4pt] & = — 40,0 \, см \ end {align *} \]

Радиус кривизны в два раза больше фокусного расстояния, поэтому

\ [R = 2f = −0,80 \, см \]

Значение

Фокусное расстояние отрицательное, поэтому фокус виртуальный, как и ожидалось для вогнутого зеркала и реального объекта. Найденный здесь радиус кривизны приемлем для роговицы. Расстояние от роговицы до сетчатки у взрослого глаза составляет около 2,0 см. На практике роговица может не иметь сферической формы, что усложняет подбор контактных линз.Обратите внимание, что расстояние до изображения здесь отрицательное, что соответствует тому факту, что изображение находится за зеркалом. Таким образом, изображение виртуально, потому что на самом деле через него не проходят лучи. В задачах и упражнениях вы покажете, что для фиксированного расстояния до объекта меньший радиус кривизны соответствует меньшему увеличению.

СТРАТЕГИЯ РЕШЕНИЯ ПРОБЛЕМ: СФЕРИЧЕСКИЕ ЗЕРКАЛА

• Шаг 1. Сначала убедитесь, что задействовано формирование изображения сферическим зеркалом.
• Шаг 2.Определите, требуется ли трассировка лучей, уравнение зеркала или и то, и другое. Скетч очень полезен, даже если трассировка лучей не требуется специально для этой задачи. Напишите на эскизе символы и известные значения.
• Шаг 3. Определите, что именно необходимо определить в проблеме (определите неизвестные).
• Шаг 4. Составьте список того, что дано или может быть выведено из проблемы, как указано (определить известные).
• Шаг 5. Если требуется трассировка лучей, используйте правила трассировки лучей, перечисленные в начале этого раздела.
• Шаг 6. Большинство количественных задач требуют использования зеркального уравнения. Используйте примеры в качестве руководства для использования уравнения зеркала.
• Шаг 7. Проверьте, имеет ли ответ смысл. Соответствуют ли знаки расстояния до объекта, расстояния до изображения и фокусного расстояния тому, что ожидается от трассировки лучей? Знак увеличения правильный? Разумны ли расстояния между объектом и изображением?

Отклонение от малоугловой аппроксимации

Приближение малых углов (Equation \ ref {smallangle}) является краеугольным камнем вышеупомянутого обсуждения формирования изображения сферическим зеркалом.При нарушении этого приближения изображение, создаваемое сферическим зеркалом, искажается. Такое искажение называется аберрацией. Здесь мы кратко обсудим два конкретных типа аберраций: сферическую аберрацию и кому.

Сферическая аберрация

Рассмотрим широкий пучок параллельных лучей, падающих на сферическое зеркало, как показано на рисунке \ (\ PageIndex {8} \). Чем дальше от оптической оси падают лучи, тем хуже сферическое зеркало приближается к параболическому зеркалу.Таким образом, эти лучи не фокусируются в той же точке, что и лучи, которые находятся около оптической оси, как показано на рисунке. Из-за сферической аберрации изображение протяженного объекта в сферическом зеркале будет размытым. Сферические аберрации характерны для зеркал и линз, которые мы рассмотрим в следующем разделе этой главы (для устранения сферических аберраций необходимы более сложные зеркала и линзы).

Рисунок \ (\ PageIndex {8} \): (a) При сферической аберрации лучи, которые находятся дальше от оптической оси, и лучи, которые находятся ближе к оптической оси, фокусируются в разных точках.Обратите внимание, что аберрация усиливается для лучей, удаленных от оптической оси. (b) При коматической аберрации параллельные лучи, не параллельные оптической оси, фокусируются на разной высоте и на разных фокусных расстояниях, поэтому изображение содержит «хвост», как у кометы (что на латыни означает «кома»). Обратите внимание, что цветные лучи предназначены только для облегчения просмотра; цвета не указывают на цвет света.

Кома или коматическая аберрация

Кома похожа на сферическую аберрацию, но возникает, когда падающие лучи не параллельны оптической оси, как показано на рисунке \ (\ PageIndex {8b} \).Напомним, что малоугловое приближение справедливо для сферических зеркал, малых по сравнению с их радиусом. В этом случае сферические зеркала являются хорошим приближением параболических зеркал. Параболические зеркала фокусируют все лучи, параллельные оптической оси в фокусной точке. Однако параллельные лучи, которые расположены на , а не на параллельны оптической оси, фокусируются на разной высоте и на разных фокусных расстояниях, как показано на рисунке \ (\ PageIndex {8b} \). Поскольку сферическое зеркало симметрично относительно оптической оси, различные цветные лучи на этом рисунке создают круги соответствующего цвета на фокальной плоскости.

Хотя сферическое зеркало показано на рисунке \ (\ PageIndex {8b} \), коматическая аберрация возникает также и для параболических зеркал — она ​​не является результатом нарушения в приближении малых углов (уравнение \ ref {smallangle}). Однако сферическая аберрация возникает только для сферических зеркал и является результатом нарушения в малоугловом приближении. Мы обсудим и кому, и сферическую аберрацию позже в этой главе в связи с телескопами.

Авторы и авторство

• Сэмюэл Дж.Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

.