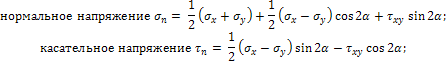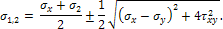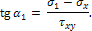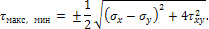6. Напряжение в точке. Полное, нормальное, касательное напряжения. Размерности напряжения.

Напряжение – мера распределения внутренних сил по сечению.

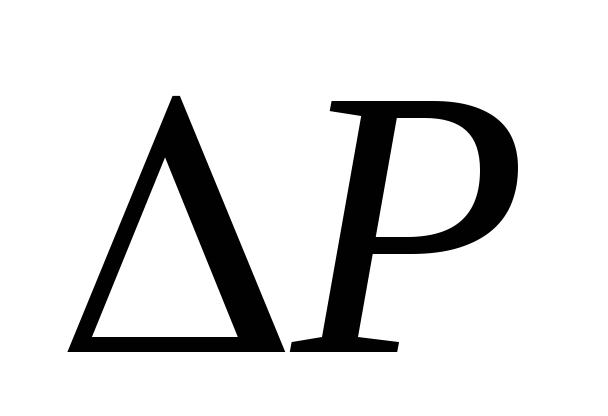, где— внутренняя сила, выявленная на площадке.

Полное напряжение .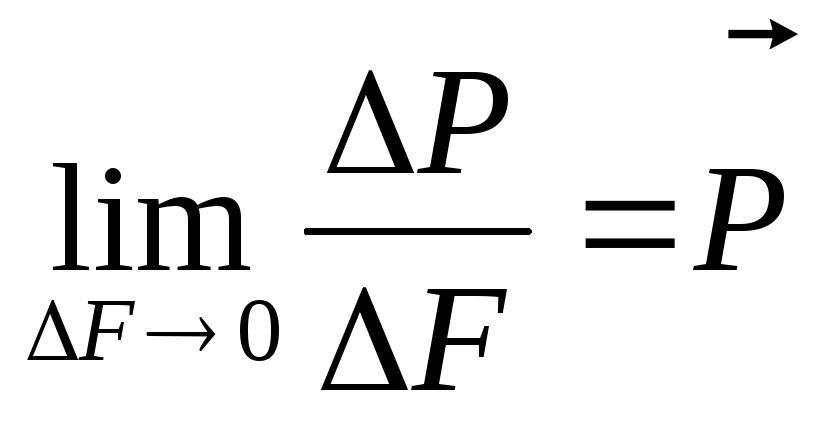

Нормальное напряжение – проекция вектора полного напряжения на нормаль обозначается через σ. 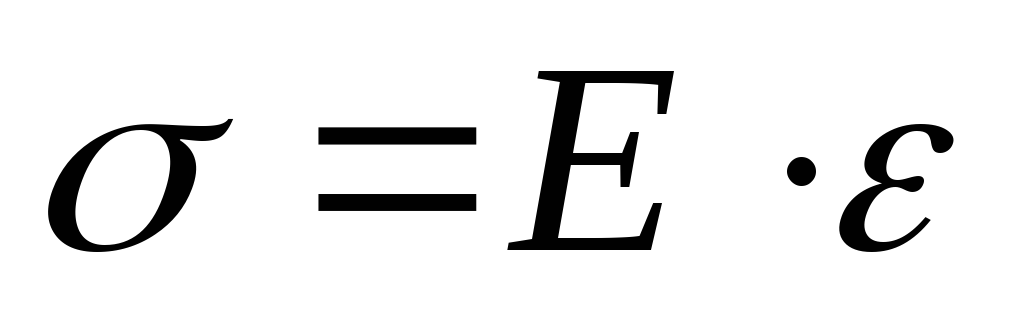, где Е – модуль упругости I рода, ε – линейная деформация. Нормальное напряжения вызывается только изменением длин волокон, направлением их действий, а угол поперечных и продольных волокон не искажается.

Касательное напряжение – составляющие напряжения в плоскости сечения. 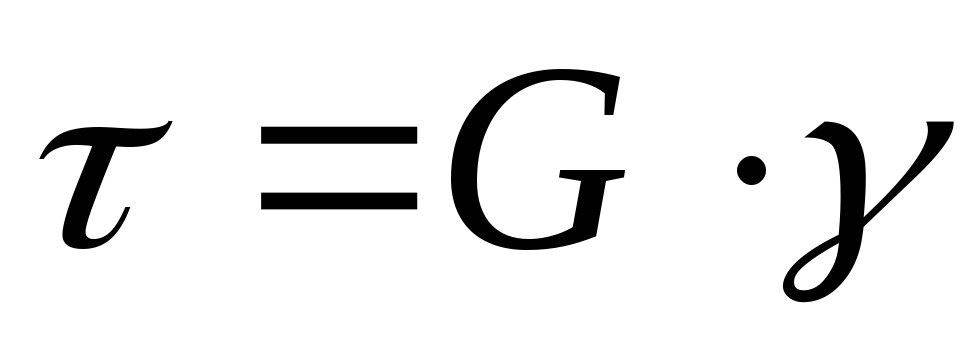, где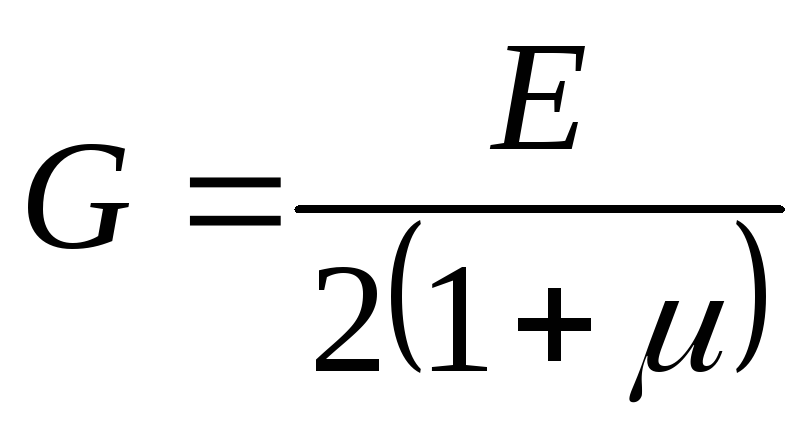(для изотропного материала) – модуль сдвига (модуль упругости II рода), μ – коэффициент Пуассона (=0,3), γ – угол сдвига.

7. Закон Гука для одноосного напряжённого состояния в точке и закон Гука для чистого сдвига. Модули упругости первого и второго рода, их физический смысл, математический смысл и графическая интерпретация. Коэффициент Пуассона.

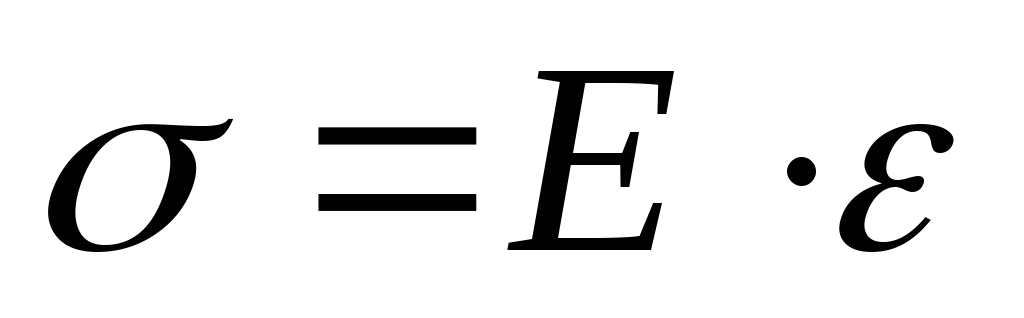— закон Гука для одноосного напряжённого состояния в точке.

Е – коэффициент пропорциональности (модуль упругости I рода). Модуль упругости является физической константой материала и определяется экспериментально. Величина Е измеряется в тех же единицах, что и σ, т.е. в кГ/см².

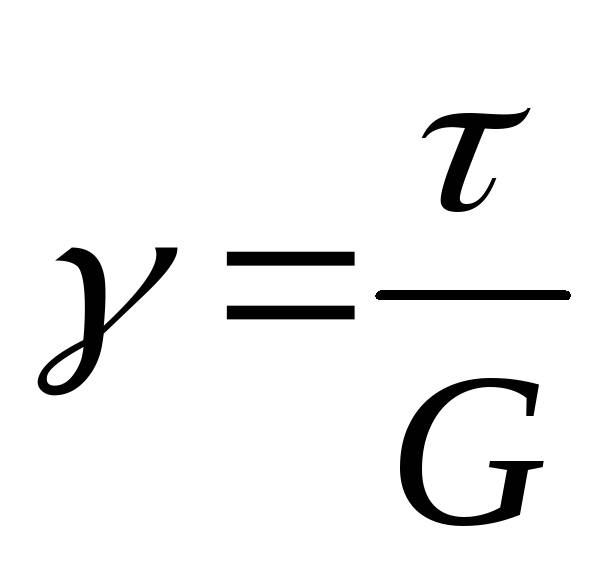— закон Гука для сдвига.

G– модуль сдвига (модуль упругости II рода). Размерность модуляGтакая же, как и у модуля Е, т.е. кГ/см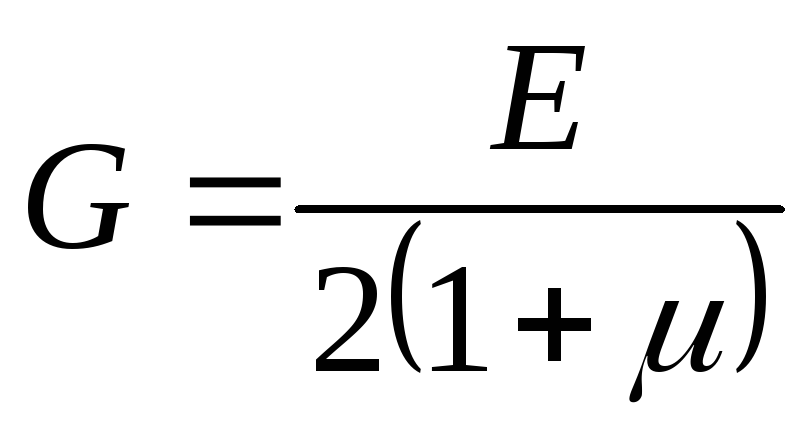

2..

μ – коэффициент Пуассона (коэффициент пропорциональности). 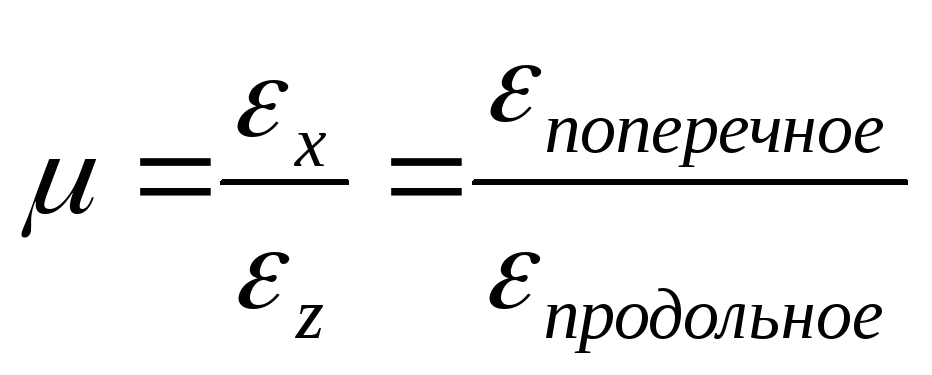. Безразмерная величина, характеризующая свойства материала и определяющаяся экспериментально и лежит в интервале от 0,25 до 0,35 и не могут превышают 0,5 (для изотропного материала).

8. Центральное растяжение (сжатие) прямого бруса. Определение внутренних продольных сил методом сечений. Правило знаков для внутренних продольных сил. Привести примеры расчёта внутренних продольных сил.

Брус испытывает состояние центрального растяжения (сжатия) в том случае, если в его поперечных сечениях возникают центральные продольные силы N_z(т.е. внутренняя сила, линия действия которой направлена по осиz), а остальные 5 силовых факторов равны нулю (Q_x=Q_y=M_x=M_y=M_z=0).

Правило знаков для N_z: истинная растягивающая сила – «+», истинная сжимающая сила – «-».

9. Центральное растяжение (сжатие) прямого бруса. Постановка и решение задачи об определении напряжений в поперечных сечениях бруса. Три стороны задачи.

Центральное напряжение (сж.) прямого бруса см. в вопросе 8.

Постановка: Прямой брус из однородного материала, растянутый (сжатый) центральными продольными силами N. Определить напряжение, возникающее в поперечных сечениях бруса, деформации и перемещения поперечных сечений бруса в зависимости от координатzэтих сечений.

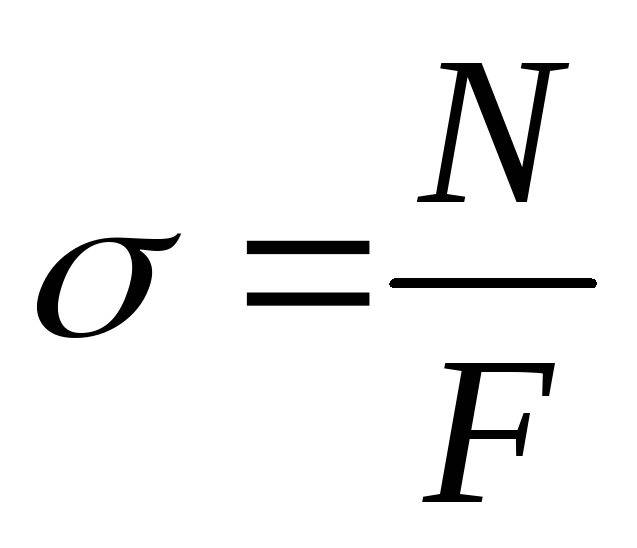
10. Центральное растяжение (сжатие) прямого бруса. Определение деформаций и перемещений. Жёсткость бруса при растяжении (сжатии). Привести примеры соответствующих расчётов.

Центральное напряжение (сж.) прямого бруса см. в вопросе 8.

.

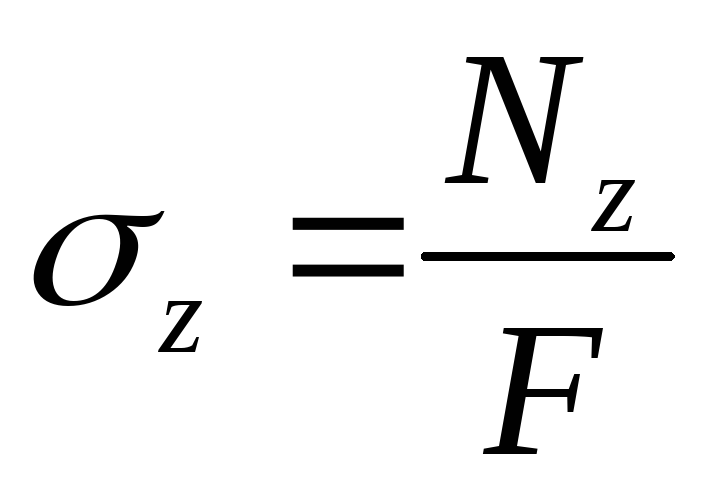При центральном растяжении (сж.) бруса в поперечном направлении в сечении возникает только нормальное напряжение σ_z, постоянное во всех точках поперечного сечения и равноеN_z/F.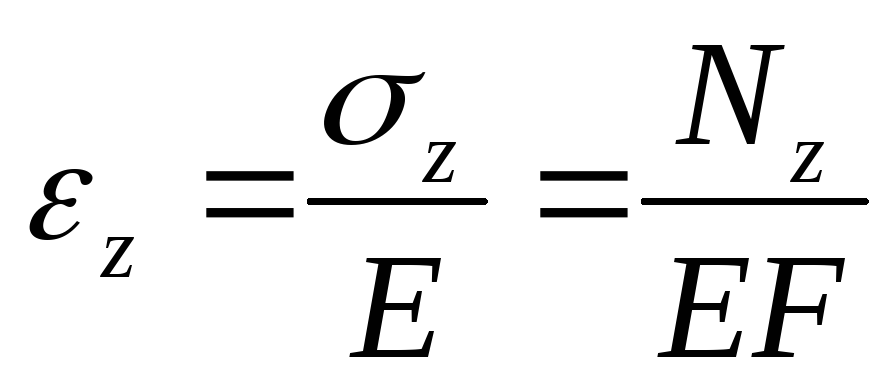, гдеEF– жёсткость бруса при растяжении (сжатии). Чем больше жёсткость бруса, тем меньше деформируется бус при одной и той же силе. 1/(EF) – податливость бруса при растяжении (сжатии).

11. Центральное растяжение (сжатие) прямого бруса. Статически неопределимые системы. Раскрытие статической неопределимости. Влияние температурного и монтажного факторов. Привести примеры соответствующих расчётов.

Центральное напряжение (сж.) прямого бруса см. в вопросе 8.

Если число линейно-независимых уравнений статики меньше числа неизвестных, входящих в систему этих уравнений, то задача по определению этих неизвестных становится статически неопределимой. 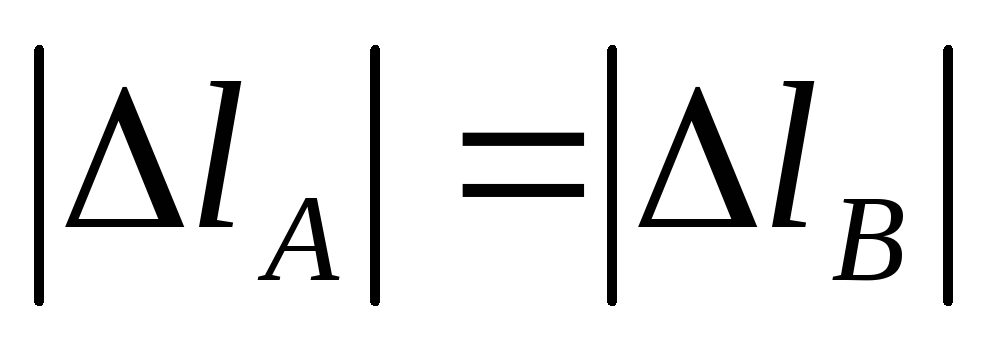(На сколько удлинится одна часть, на столько сожмётся вторая).

Нормальные условия — 20º С. 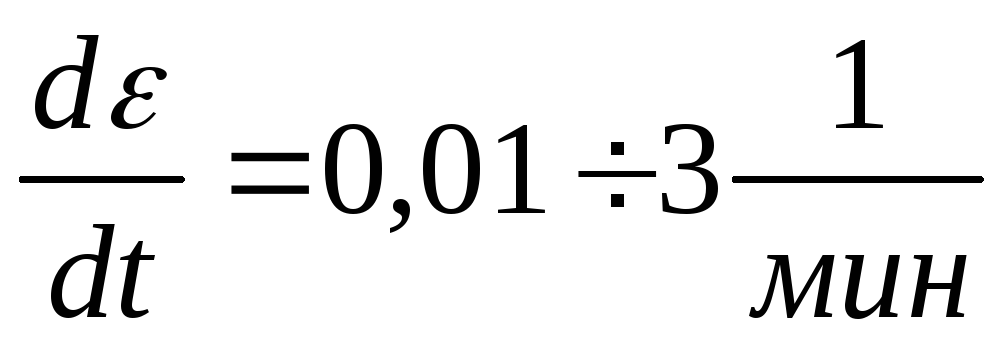.f(σ,ε,tº,t)=0 – функциональная зависимость между 4 параметрами.

12. Опытное изучение механических свойств материалов при растяжении (сжатии). Принцип Сен-Венана. Диаграмма растяжения образца. Разгрузка и повторное нагружение. Наклёп. Основные механические, прочностные и деформационные характеристики материала.

Механические свойства материалов вычисляют с помощью испытательных машин, которые бывают рычажными и гидравлическими. В рычажной машине усилие создаётся при помощи груза, действующего на образец через систему рычагов, а в гидравлической – с помощью гидравлического давления.

Принцип Сен-Венана: Характер распределения напряжения в поперечных сечениях достаточно удалённых (практически на расстояния, равные характерному поперечному размеру стержня) от места приложения нагрузок, продольных сил не зависит от способа приложения этих сил, если они имеют один и тот же статический эквивалент. Однако в зоне приложения нагрузок закон распределения напряжения может заметно отличаться от закона распределения в достаточно удалённых сечениях.

Если испытуемый образец, не доводя до разрушения, разгрузить, то в процессе разгрузки зависимость между силой Р и удлинением Δlобразец получит остаточное удлинение.

Если образец был нагружен на участке, на котором соблюдается закон Гука, а затем разгружен, то удлинение будет чисто упругим. При повторном нагружении пропадёт промежуточная разгрузка.

Наклёп (нагартовка) – явление повышения упругих свойств материала в результате предварительного пластического деформирования.

Предел пропорциональности – наибольшее напряжение, до которого материал следует закону Гука.

Предел упругости – наибольшее напряжение, до которого материал не получает остаточных деформаций.

Предел текучести – напряжение, при котором происходит рост деформации без заметного увеличения нагрузки.

Предел прочности – максимальное напряжение, которое может выдержать образец, не разрушаясь.

13. Физический и условный пределы текучести материалов при испытании образцов на растяжение, предел прочности. Допускаемые напряжения при расчёте на прочность центрально растянутого (сжатого) бруса. Нормативный и фактический коэффициенты запаса прочности. Привести числовые примеры.

В тех случаях, когда на диаграмме отсутствует явно выраженная площадка текучести, за предел текучести принимается условно величина напряжения, при котором остаточная деформация ε_ост=0,002 или 0,2%. В некоторых случаях устанавливается предел ε_ост=0,5%.

max|σ_z|=[σ].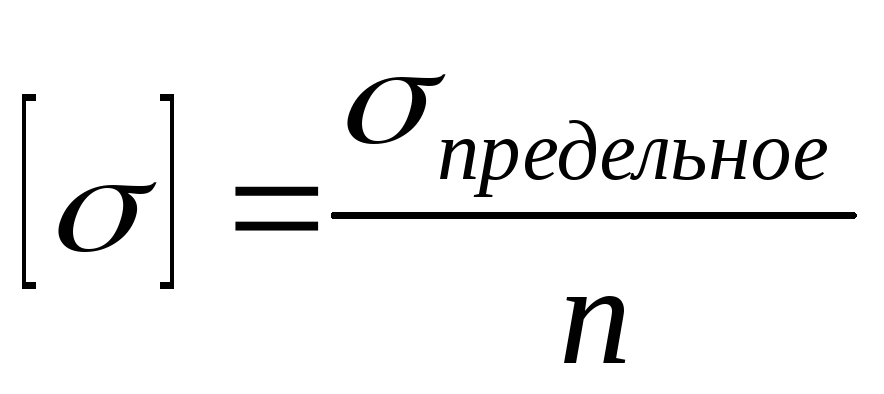

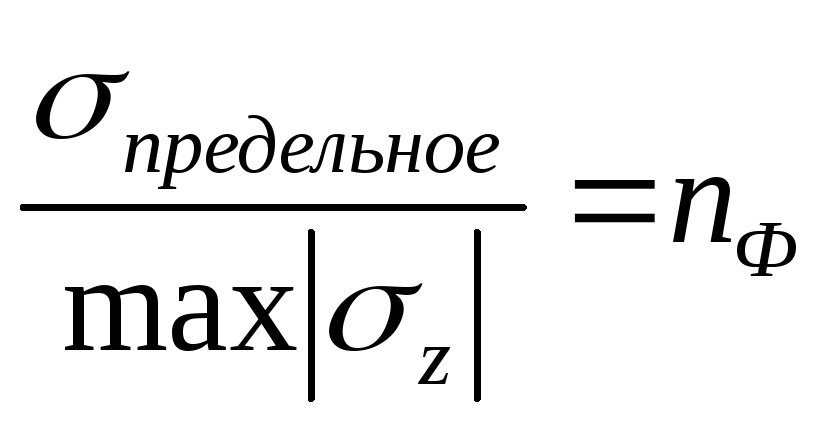,n>1(!) – нормативный коэффициент запаса прочности.

— фактический коэффициент запаса прочности.n>1(!).

max|σ_z|_растяж≤[σ]_растяж;max|σ_z|_сжатия≤[σ]_сжатия.

14. Центральное растяжение (сжатие) прямого бруса. Расчёты на прочность и жёсткость. Условие прочности. Условие жёсткости. Три типа задач при расчёте на прочность.

Центральное напряжение (сж.) прямого бруса см. в вопросе 8.

max|σ_z|_растяж≤[σ]_растяж

;max|σ_z|_сжатия≤[σ]_сжатия.

15.Обобщённый закон Гука для трёхосного напряжённого состояния в точке. Относительная объёмная деформация. Коэффициент Пуассона и его предельные значения для однородного изотропного материала.

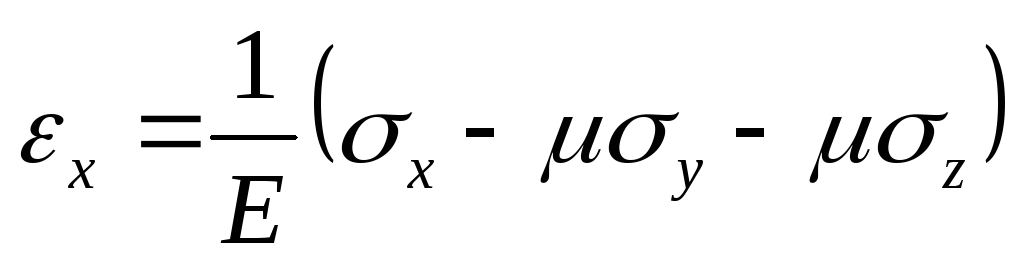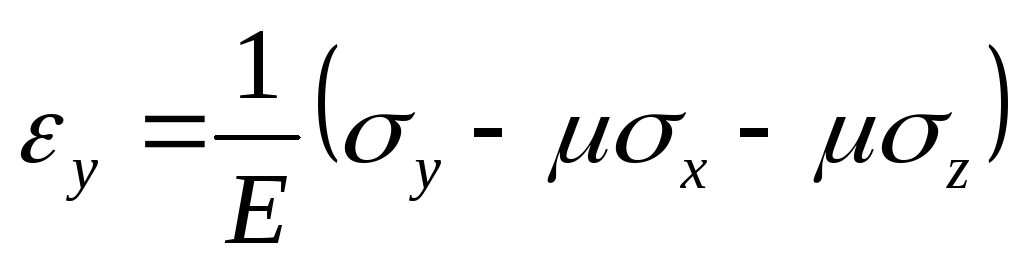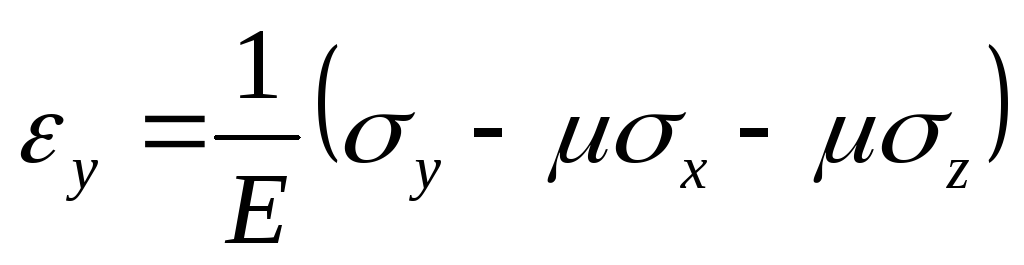,,. Сложив эти уравнения, получим выражение объёмной деформации: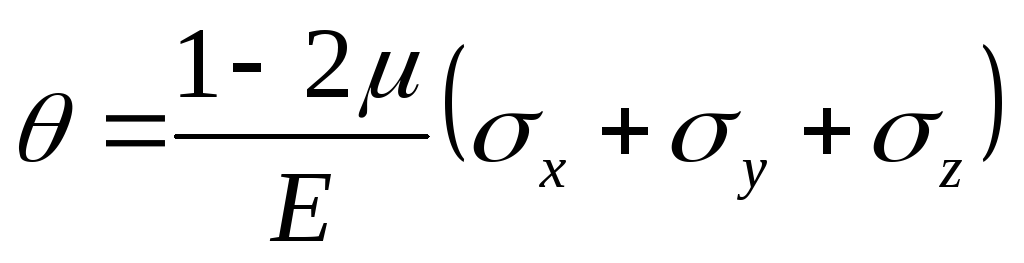. Это выражение позволяет определить предельное значение коэффициента Пуассона для любого изотропного материала. Рассмотрим случай, когда σ_x=σ_y=σ_z=р. В этом случае:. При положительном р величина θ должна быть также положительной, при отрицательном р изменение объёма будет отрицательным. Это возможно только в том случае, когда μ≤1/2. Следовательно, значение коэффициента Пуассона для изотропного материала не может превышать 0,5.

16. Соотношение между тремя упругими постоянными для изотропного материала (без вывода формулы).

,,.

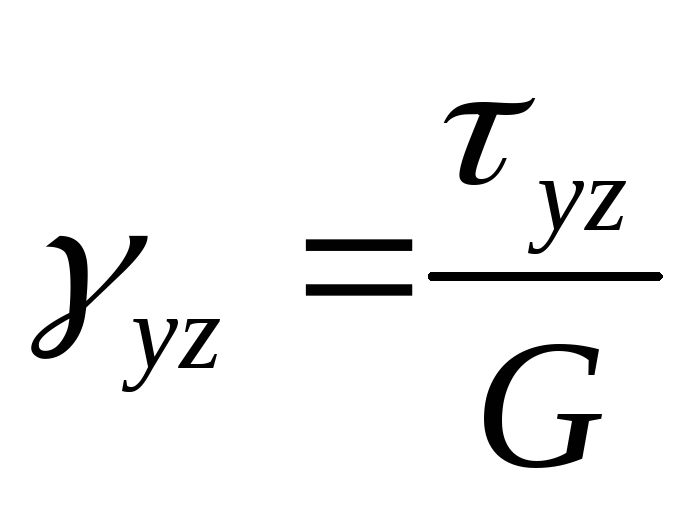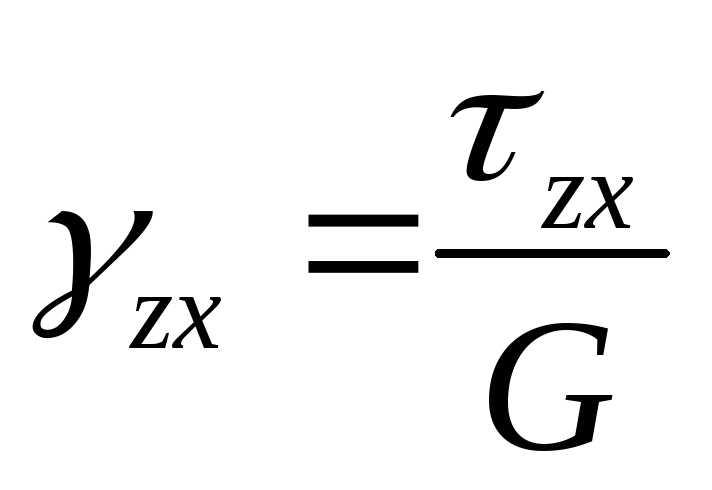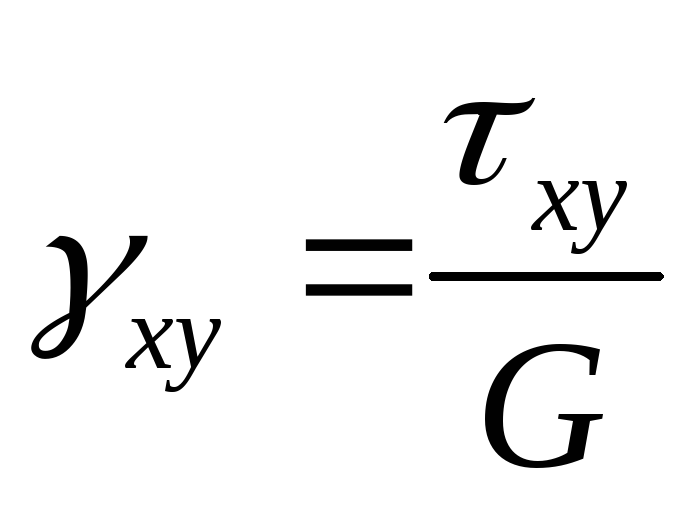17. Исследование напряжённо-деформированного состояния в точках центрально-растянутого (сжатого) прямого бруса. Закон парности касательных напряжений.

,.

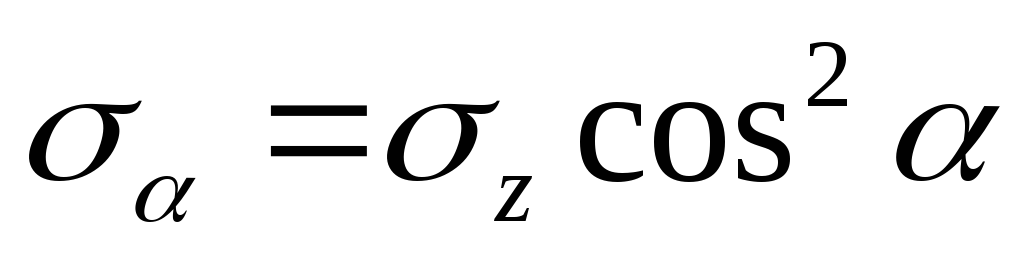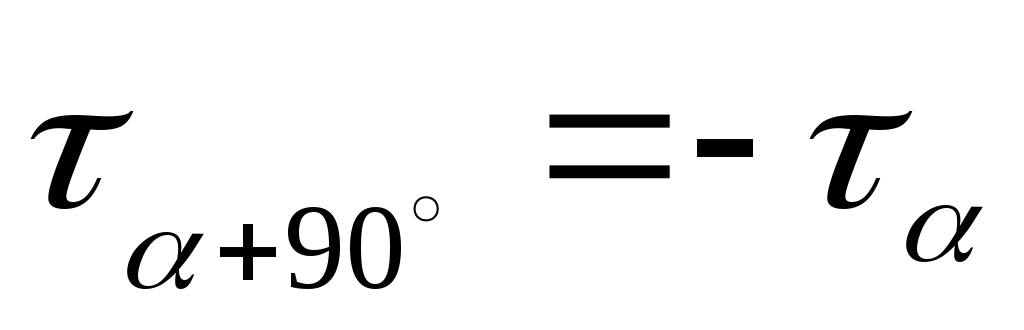— закон парности касательных напряжений.

18. Центральное растяжение (сжатие) бруса из линейно-упругого материала. Потенциальная энергия упругой деформации бруса и её связь с работой внешних продольных сил, приложенных к брусу.

А=U+K. (В результате работы накапливается потенциальная энергия деформированного телаU, кроме того, работа идёт на совершение скорости массе тела, т.е. преобразуется в кинетическую энергию).

Если центральное растяжение (сжатие) бруса из линейно-упругого материала производится очень медленно, то скорость перемещения центра масс тела будет весьма малой. Такой процесс нагружения называется статическим. Тело в любой момент находится в состоянии равновесия. В этом случае А=U, и работа внешних сил целиком преобразуется в потенциальную энергию деформации.,,.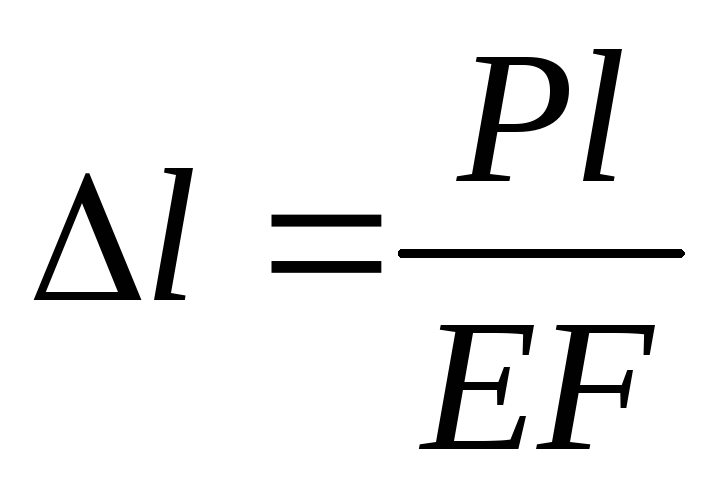

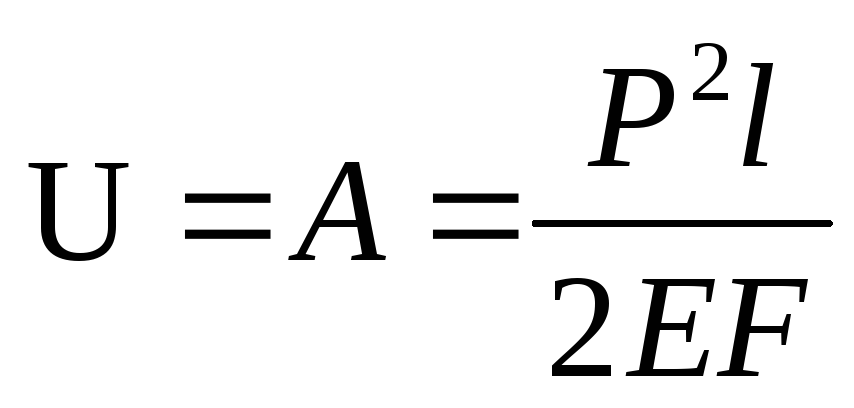Лекции и примеры решения задач технической механики

Мерой интенсивности распределения внутренних сил R в окрестности точки в пределах данного сечения площадью A являются напряжения p, измеряемые в единицах силы, отнесенной к единице площади dA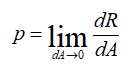
Полные напряжения в точке
Единица измерения напряжений — Паскаль (Н/м²=Па).
Рассмотрим подробнее:

Система приложенных к телу внешних нагрузок, приводит к возникновению в его сечениях внутренней силы R и момента M

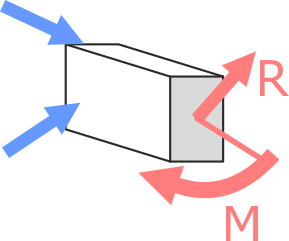Внутренние сила и момент в сечении бруса

При этом надо понимать что внутренняя сила и внутренний момент воздействуют на всё сечение бруса в целом.

Выделим в рассматриваемом сечении элементарную площадку dA бесконечно малой площади.

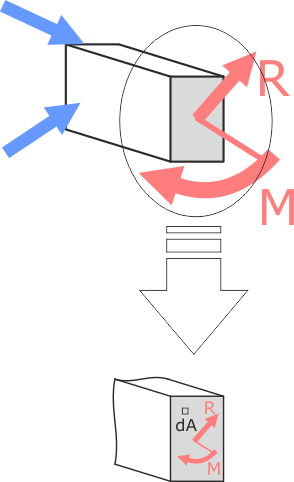Элементарная площадка в сечении бруса

Полное напряжение – часть внутренних усилий, приходящаяся на конкретную точку сечения.

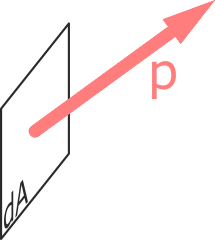Вектор полного напряжения в точке

Обозначение полного напряжения в точке – p.
Единица измерения – Паскаль [Па] (Н/м²).

Ввиду того, что большинство конструкционных материалов обладает высокой прочностью часто напряжения, возникающие в них, измеряются в кратных величинах, например мегапаскаль [МПа].

В общем случае вектор полного напряжения в точке может располагаться под любым углом к сечению. В таких случаях для существенного упрощения расчетов его удобно раскладывать на составляющие (проекции):

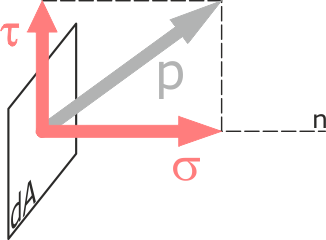Нормальное и касательное напряжения

Проекция вектора полного напряжения p на нормаль к сечению называется нормальным напряжением и обозначается через σ, а проекция вектора полного напряжения на плоскость сечения называется касательным напряжением и обозначается через τ.

Разложение вектора полного напряжения на две указанные составляющие имеет конкретный физический смысл – с нормальным напряжением связано разрушение путем отрыва, а с касательным – разрушение путем сдвига или среза.

В частных случаях (например при растяжении-сжатии и кручении) в поперечных сечениях бруса имеют место только нормальные и только касательные напряжения соответственно.

При решении таких задач, величина нормальных и касательных напряжений сравнивается с соответствующими допустимыми значениями напряжений.

Примеры расчета напряжений >>

1. Общие понятия и основные положения

1.Основные гипотезы в сопротивлении материалов.

В сопротивлении материалов принимаются гипотезы о сплошном, однородном, изотропном и линейно упругом теле.

Материал конструкции принимается однородным и сплошным, при этом не учитывается анатомическая структура или молекулярное строение тела. Свойства материала не зависят от формы и размеров тела и одинаковы во всех его точках.

Материал конструкции изотропен, т. е. его свойства по всем направлениям одинаковы.

Материал конструкции является идеально упругим и способен полностью восстанавливать первоначальные форму и размеры, после устранения причин, вызвавших деформацию.

2.Внешние силы и их классификация.

Все силы могут быть разделены на объемные и поверхностные. К объемным относятся силы тяжести, силы инерции и т. п.

Если внешние силы являются результатом контактного взаимодействия, то они относятся к поверхностным силам.

Поверхностные силы могут быть разделены на сосредоточенные и распределенные силы.

Сосредоточенные силы передаются на конструкцию через небольшую площадку, поэтому условно считают, что они приложены в точке.

Распределенная сила (нагрузка) передается на конструкцию через определенную площадь.

По времени действия на конструкцию различают постоянные и временные нагрузки.

Постоянной называют нагрузку, действующую непрерывно в течении всего срока службы сооружения (собственный вес конструкции).

Временная нагрузка имеет ограниченную продолжительность действия (ветровая нагрузка, вес снега).

3.Основные объекты, изучаемые в сопромате.

1) Брус – элемент конструкции, одно из измерений которого существенно больше двух других.

2) Стержень – брус с прямолинейной геометрической осью

3) Балка – горизонтальный или наклонный стержень, работающий на изгиб

4) Пластина – плоский элемент конструкции, отличающийся тем, что толщина ее мала по сравнению с двумя другими размерами

5) Оболочка – в отличие от пластины ее внешние контуры образованы не плоскостями, а криволинейными поверхностями.

6) Массивное Тело – элемент конструкции, основные размеры которого достаточно велики и одного и того же порядка

4.Понятие о расчетной схеме.

 Расчетная схема конструкции — это  его упрощенная схема, освобожденная от не­существенных в данном случае особенностей. Удачно выбранная расчетная схема даст результаты расчета, близкие к реальным. При неудачном выборе – результаты расчетов окажутся далеки от истины, что может привести к плачевным последствиям. Выбор расчетной схемы конструкции в сопротивлении материалов производят в соответствии с гипотезами (допущениями).

5.Внутренние силы. Метод мысленных сечений. Напряжение полное, нормальное и касательное. Размерность напряжения.

Внутренние силы – силы взаимодействия между отдельными элементами сооружения или отдельными частями элемента, возникающие под действием внешних сил.

Для определения внутренних усилий применяется метод сечений. В общем случае на рассчитываемый элемент конструкции, находящийся в равновесии действует произвольная система сил. Мысленно проводим плоскость (для бруса обычно проводится перпендикулярно его продольной оси) и рассекаем на две части рассматриваемый элемент. Левую часть мысленно отбрасываем, а правую оставляем в рассмотрении. Действие отброшенной левой части учитываем внутренними усилиями.

Если все внутренние усилия приводятся к:

1. N (продольная сила) – простое растяжение или сжатие

2. Qx,Qy (поперечные силы) – сдвиг

3. Mz (крутящий момент) – кручение

4. Mx, My (изгибающие моменты) – изгиб

Интенсивность нормальных сил называется нормальным напряжением σ

Касательных сил— касательным напряжением τ.

Нормальное и касательное напряжение являются составляющими полного напряжения p в рассматриваемой точке. Полное напряжение может быть определено также по формуле: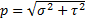

15.Напряжения. Виды напряжения, виды деформации. Правила знаков. Примеры расчета плоского напряженного состояния.

Напряжением называется интенсивность действия внутренних сил в точке тела, то есть, напряжение — это внутреннее усилие, приходящееся на единицу площади. По своей природе напряжение — это поверхностная нагрузка, возникающая на внутренних поверхностях соприкасания частей тела.

 Деформацией называется изменение размеров и формы тела под действием приложенных сил.

Напряжением называется отношение действующего усилия к площади поперечного сечения тела или образца σ = P/F.     В зависимости от направления действия силы нормальные напряжения подразделяют на растягивающие и сжимающие. Различают временные и остаточные напряжения.     Временные напряжения возникают под действием внешней нагрузки и исчезают после ее снятия, остаточные — остаются в теле после прекращения действия нагрузки.

Если после прекращения действия внешних сил изменения формы, структуры и свойств тела полностью устраняются, то такая деформация называется упругой.

При возрастании напряжений выше предела упругости деформация становится необратимой. При снятии нагрузки устраняется лишь упругая составляющая деформации, оставшаяся часть называется пластической деформацией.

Норм напряжение:

Составляющая напряжений, направленных по нормали к площадке ее действия.

Касат напряжение:

Составляющая напряжений, лежащих в плоскости сечения.

Правила знаков:

Нормальные напряжения σ принимаются положительными (т.е. σ>0), если они растягивают выделенный элемент бруса.

Касательные напряжения τ принимаются положительными (т.е. τ>0), если они стремятся повернуть рассматриваемый элемент бруса по ходу часовой стрелки.

При растяжении-сжатии

Внутренняя продольная сила N, которая стремится растянуть рассматриваемую частьбруса, считается положительной. Сжимающая продольная сила имеет отрицательный знак.

При кручении

Внутренний скручивающий момент T считается положительным, если он стремится повернуть рассматриваемую часть бруса против хода часовой стрелки, при взгляде на него со стороны внешней нормали.

При изгибе

Внутренняя поперечная сила Q считается положительной, в случае, когда она стремится повернуть рассматриваемую часть бруса по ходу часовой стрелки.

Внутренний изгибающий момент M положителен, когда он стремится сжать верхние волокна бруса.

Деформация при растяжении-сжатии Δl считается положительной, если длина стержняпри этом увеличивается.

При плоском поперечном изгибе

Вертикальное перемещение сечения бруса принимается положительным, если оно направлено вверх от начального положения.

Правило знаков при составлении уравнений статики

— для проекций сил на оси системы координат

Проекции внешних сил на оси системы координат принимаются положительными, если их направление совпадает с положительным направлением соответствующей оси.

— для моментов

Сосредоточенные моменты и моменты сил в уравнениях статики записываются с положительным знаком, если они стремятся повернуть рассматриваемую систему против хода часовой стрелки.

Правило знаков при составлении уравнений статики для неподвижных систем

При составлении уравнений равновесия статичных (неподвижных) систем (например, приопределении опорных реакций), последние два правила упрощаются до вида:

Проекции сил и моменты, имеющие одинаковое направление принимаются положительными, а соответственно проекции сил и моменты обратного направления – отрицательными.

ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ

Если все векторы напряжений параллельны одной и той же плоскости, напряженное состояние называется плоским (рис. 1). Иначе: напряженное состояние является плоским, если одно из трех главных напряжений равно нулю.

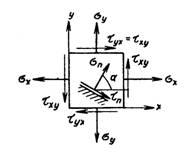
Рисунок 1.

Плоское напряженное состояние реализуется в пластине, нагруженной по ее контуру силами, равнодействующие которых расположены в ее срединной плоскости (срединная плоскость — плоскость, делящая пополам толщину пластины).

Направления напряжений на рис. 1 приняты за положительные. Угол α положителен, если он откладывается от оси х к оси у. На площадке с нормалью n:

(1)

при .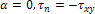

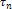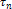Нормальное напряжение σ_n положительно, если оно растягивающее. Положительное напряжение показано на рис. 1. Правило знаков дляпо формуле (1) то же самое, что для напряженийпо формуле (1).

Данное здесь правило знаков относится к наклонным площадкам. В статье «Объёмное напряженное состояние» сформулировано правило знаков для компонентов напряжений в точке, т. е. для напряжений на площадках, перпендикулярных осям координат. Это правило знаков принято в теории упругости.

Главные напряжения на площадках, перпендикулярных плоскости напряжений:

(2)

(Поскольку здесь рассматриваются только два главных напряжения, они обозначены через σ₁ и σ₂, хотя может оказаться, что σ₂<0, т. е. σ₂ не будет средним из трех главных напряжений). Угол α₁ составляемый нормалью к первой главной площадке с осью х, находится из равенства:

(3)

Наибольшее  и  наименьшее  касательные напряжения

(4)

Эти напряжения действуют на площадках, расположенных под углом 45° к первой и второй главным площадкам.

Если главные напряжения σ₁ и σ₂ имеют одинаковый знак, то наибольшее касательное напряжение действует на площадке, расположенной под углом 45° к плоскости напряжений (плоскости ху). В этом случае:

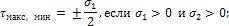
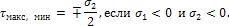
В стенке балки (здесь имеется в виду обычная балка, а не балка-стенка)  при ее изгибе силами реализуется частный случай плоского напряженного состояния. В стенках балки одно из нормальных напряжений σ_y равно нулю. В этом случае напряжения получатся по формулам (1), (2) и (4), если в этих формулах положить σ_y=0. Положение первой главной площадки определяется формулой (3).

РАСТЯЖЕНИЕ ПО ДВУМ НАПРАВЛЕНИЯМ (рис 2):

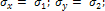
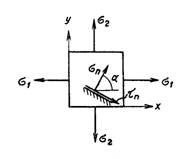
Рисунок 2.

При σ₁>0 и σ₂<0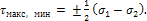 

При σ₁>0 и σ₂>0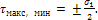 

При σ₁<0 и σ₂<0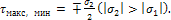 

ЧИСТЫЙ СДВИГ (рис. 3)

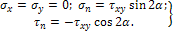
Напряжение (сопромат)

Напряженное состояние в точке тела является ключевым понятием в сопромате. Необходимость введения понятия напряжения в точке для суждения об интенсивности внутренних сил в некоторой точке сечения стержня вызвана неравномерным распределением внутренних сил по длине и поперечному сечению в общем случае нагружения.

Напряжение в точке тела K (обозначено буквой p) – это интенсивность внутренней силы , возникающей на бесконечно малой площадке в окрестности данной точки (рис. 1.4, а).

В количественном выражении .

Понятие о напряжении в точке твердого тела в некотором смысле напоминает понятие о давлении, действующем, например, внутри жидкости. Однако давление в точке жидкости одинаково во всех направлениях. Если проведем через точку K тела другое сечение, иной будет внутренняя сила. Следовательно, иным будет и напряжение, хотя оно возникает в той же самой точке K.

Напряжение в точке тела в разных направлениях (на разных площадках, проходящих через данную точку тела) может быть различным (в частности, оно может возникать только в одном направлении).

Понятие о напряжении в точке деформируемого твердого тела ввел в 1822 г. французский ученый Огюстен Луи Коши.

Основную роль в расчетах прочности играет не полное напряжение p, а его проекции на оси координат x, y и z: нормальное напряжение ( – сигма), направленное по перпендикуляру к площадке (параллельно оси z), и касательные напряжения ( – тау), лежащие в плоскости сечения и направленные, соответственно, вдоль осей x и y (рис. 1.4, б). Первый индекс у касательных напряжений характеризует нормаль к площадке z, на которой они возникают.

Между полным (), нормальным () и касательными напряжениями ( и ) существует зависимость:

.

Касательные напряжения служат мерой тенденции одной части сечения смещаться (или скользить) относительно другой его части.

Единицы нормальных и касательных напряжений в СИ – паскаль (Па). Один паскаль – это напряжение, при котором на площадке в один квадратный метр возникает внутренняя сила, равная одному ньютону (то есть равная, приблизительно, весу одного яблока). Как мы увидим в дальнейшем, эта единица напряжения мизерно мала. В сопромате чаще используются другие единицы:

1 МПа = 106 Па; 1 кН/см2 = 107 Па.

В технической системе единиц напряжения измеряются в килограммах силы на миллиметр (сантиметр) в квадрате (кгс/мм2 или кгс/см2) . Следует запомнить, что 1 кН/см2 » 1 кгс/мм2.

Сопромат.in.ua: Напряжения

Напряжением называется интенсивность действия внутренних сил в точке тела, то есть, напряжение — это внутреннее усилие, приходящееся на единицу площади. По своей природе напряжение — это поверхностная нагрузка, возникающая на внутренних поверхностях соприкасания частей тела. Напряжение, так же как и интенсивность внешней поверхностной нагрузки, выражается в единицах силы, отнесенных к единице площади:Па=Н/м² (МПа = 10⁶ Н/м², кгс/см²=98 066 Па ≈ 10⁵Па, тс/м² и т. д.).

Рассечем тело произвольным сечением Выделим небольшую площадку ∆A. Внутреннее усилие, действующее на нее, обозначим [math]∆\vec{R}[/math]. Полное среднее напряжение на этой площадке [math]\vec{р} = ∆\vec{R}/∆A [/math]. Найдем предел этого отношения при [math]∆A \to 0[/math] . Это и будет полным напряжение на данной площадке (точке) тела.

\textstyle \vec{p} = \lim_{\Delta A \to 0} {\Delta\vec{R}\over \Delta A}

Полное напряжение [math]\vec p[/math], как и равнодействующая внутренних сил, приложенных на элементарной площадке, является векторной величиной и может быть разложено на две составляющие: перпендикулярное к рассматриваемой площадке – нормальное напряжение σ_n и касательное к площадке – касательное напряжение [math]\tau_n[/math]. Здесь n – нормаль к выделенной площадке.

Касательное напряжение, в свою очередь, может быть разложено на две составляющие, параллельные координатным осям x, y, связанным с поперечным сечением – [math]\tau_{nx}, \tau_{ny}[/math]. В названии касательного напряжения первый индекс указывает нормаль к площадке,второй индекс — направление касательного напряжения.

$$\vec{p} = \left[\matrix{\sigma _n \\ \tau _{nx} \\ \tau _{nx}} \right]$$

Отметим, что в дальнейшем будем иметь дело главным образом не с полным напряжением [math]\vec p [/math], а с его составляющими [math]σ_x,\tau _{xy}, \tau _{xz} [/math] . В общем случае на площадке могут возникать два вида напряжений: нормальное σ и касательное τ.

Тензор напряжений

При анализе напряжений в окрестности рассматриваемой точки выделяется бесконечно малый объемный элемент (параллелепипед со сторонами dx, dy, dz), по каждой грани которого действуют, в общем случае, три напряжения, например, для грани, перпендикулярной оси x (площадка x) – [math]σ_x,\tau _{xy}, \tau _{xz} [/math]

Компоненты напряжений по трем перпендикулярным граням элемента образуют систему напряжений, описываемую специальной матрицей – тензором напряжений

$$ T _\sigma = \left[\matrix{
\sigma _x & \tau _{yx} & \tau _{zx} \\
\tau _{xy} & \sigma _y & \tau _{zy} \\ \tau _{xz} & \tau _{yz} & \sigma _z
}\right]$$

Здесь первый столбец представляет компоненты напряжений на площадках,
нормальных к оси x, второй и третий – к оси y и z соответственно.

При повороте осей координат, совпадающих с нормалями к граням выделенного
элемента, компоненты напряжений изменяются. Вращая выделенный элемент вокруг осей координат, можно найти такое положение элемента, при котором все касательные напряжения на гранях элемента равны нулю.

Площадка, на которой касательные напряжения равны нулю, называется главной площадкой.

Нормальное напряжение на главной площадке называется главным напряжением

Нормаль к главной площадке называется главной осью напряжений .

В каждой точке можно провести три взаимно-перпендикулярных главных площадки.

При повороте осей координат изменяются компоненты напряжений, но не меняется напряженно-деформированное состояние тела (НДС).

Связь внутренних усилий и напряжений

Внутренние усилия есть результат приведения к центру поперечного сечения внутренних сил, приложенных к элементарным площадкам. Напряжения – мера, характеризующая распределение внутренних сил по сечению.

Предположим, что нам известно напряжение в каждой элементарной площадке. Тогда можно записать:

Продольное усилие на площадке dA: dN = σ_zdA
Поперечная сила вдоль оси х: dQ _x = [math]\tau {zx}[/math] dA
Поперечная сила вдоль оси y: dQ _y = [math]\tau {zy}[/math] dA
Элементарные моменты вокруг осей x,y,z: $$\begin{array}{lcr} dM _x = σ _z dA \cdot y \\ dM _y = σ _z dA \cdot x \\ dM _z = dM _k = \tau _{zy} dA \cdot x — \tau _{zx} dA \cdot y \end{array}$$

Выполнив интегрирование по площади поперечного сечения получим:

То есть, каждое внутренне усилие есть суммарный результат действия напряжений по всему поперечному сечению тела.

---

---

Связанные статьи

метки: напряжения

1.3. Внутренние силы и напряжения

Числовой мерой распределения внутренних сил по сечению является напряжение.

Рассмотрим сечение А некоторого тела (рис. 5). В окрестности точки K выделим элементарную площадку , в пределах которой выявлена внутренняя сила. За среднее напряжение на площадкеAF принимаем отношение

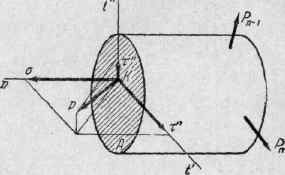
Рис. 5

Будем уменьшать площадку , стягивая ее в точкуК. Поскольку среда непрерывна, возможен предельный переход при .

Векторная величина представляет собой полное напряжение в точ­ке К в сечении А. Напряжение имеет размерность силы, деленной на площадь

Полное напряжение может быть разложено на три составляю­щие по нормали к плоскости сечения и по двум осям в плоскости сечения (рис. 5). Проекция вектора полного напряжения на нормаль обозначается через и называетсянормальным напряжением. Со­ставляющие в плоскости сечения называются касательными напря­жениями и обозначаются через . В зависимости от расположения и наименования осей обозначения и снабжаются системой ин­дексов, порядок которых будет установлен в дальнейшем.

Сово­купность напряжений для множества площадок, проходящих через точку, образует напряженное состояние в точке, которое опреде­ляется шестью числовыми величинами и является в сопротивлении материалов одним из наиболее важных понятий.

1.4. Перемещения и деформации

При нагружении тел внешними силами или при изменении температуры происходит их деформация. При деформи­ровании тела его точки, а также мысленно проведенные линии или сечения перемещаются в плоскости или в пространстве относи­тельно своего исходного положения.

Под нагрузкой в твердом теле возникают внутренние силы взаимодействия между частицами, оказывающие противодействие внешним силам и стремящиеся вернуть частицы тела в положение, которое те занимали до деформации.

Деформации бывают упругие, т. е. исчезающие после прекраще­ния действия вызвавших их сил, и пластические, или остаточные,— не исчезающие.

С увеличением внешних сил внутренние силы также увеличи­ваются до известного предела, зависящего от свойств ма­териала. Наступает момент, когда тело уже не в состоянии сопро­тивляться дальнейшему увеличению внешних сил. Тогда оно раз­рушается. В большинстве случаев для величины деформаций эле­ментов конструкции устанавливают определенные ограничения.

В сопротивлении материалов изучают следующие основные виды деформаций стержня: растяжение и сжатие, сдвиг (срез), кручение и изгиб и более сложные деформации, получаю­щиеся в результате сочетания нескольких основных.

Основным объектом, рассматриваемым в сопротивлении матери­алов, является стержень с прямолинейной осью.

Растяжение или сжатие возникает, например, в случае, когда к стержню по его оси приложены противоположно направленные силы (рис. 6). При этом про­исходит перемещение сечений вдоль оси стержня, который при растяжении удлиняется, а при сжатии укорачивается.

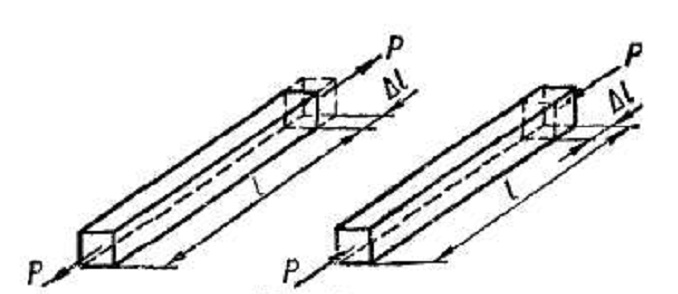
Рис. 6

Изменение первоначальной длиныl стержня называют абсолютным удлинением при растяжении или абсолютным укорочением при сжатии. От­ношение абсолютного удлинения (укорочения) к первоначальной длине стержня называют средним относительным удлинением на длине и обозначают обычно буквой е_ср:

На растяжение или сжатие работают многие элементы конструк­ций: стержни ферм, колонны, штоки паровых машин и поршневых насосов, стяжные винты и другие детали.

Сдвиг (срез) возникает, когда внешние силы смещают два па­раллельных плоских сечения стержня одно относительно другого при неизменном расстоянии между ними (рис. 7).

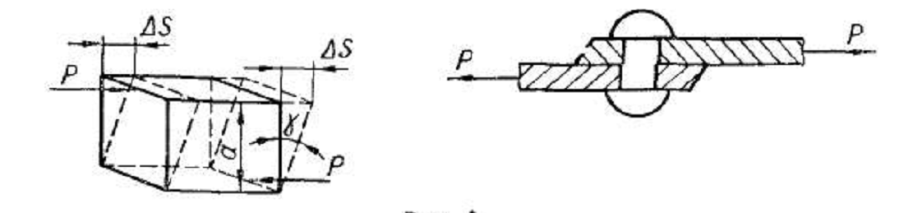
Рис 7.

Величина сме­щения называется абсолютным сдвигом.

Относительным сдвигом называют отношение абсолютного сдвига к расстоянию а между смещающимися плоскостями (тангенс угла ). Вследствие малости угла при упругих деформациях его тангенс принимают равным углу перекоса рассматриваемого элемента. Следовательно, относитель­ный сдвиг

Относительный сдвиг является угловой деформацией, характери­зующей перекос элемента. На сдвиг или срез работают, например, заклепки и болты, скрепляющие элементы, которые внешние силы стремятся сдвинуть один относительно другого.

Кручение возникает при действии на стержень внешних сил, об­разующих момент относительно оси стержня (рис. 8).

Рис 8

Деформация кручения сопровождается поворотом поперечных сечений стержня относительно друг друга вокруг его оси. Угол поворота одного се­чения стержня относительно другого, находящегося на расстоянии l, называют углом закручивания на длине l.

Oтносительным углом закручи­вания называют отношение угла за­кручивания к длинеl

На кручение работают валы, шпин­дели токарных и сверлильных стан­ков и другие детали.

Деформация изгиба (рис. 9) заключается в искривлении оси прямого или кривого стержня.

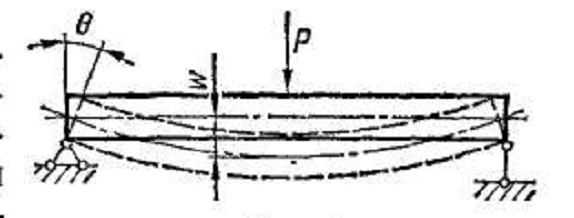
Рис 9.

Происходящее при этом перемещение какой-либо точки оси стерж­ня выражается вектором, начало которого совмещено с первона­чальным положением точки, а конец — с положением той же точки в деформированном стержне. В прямых стержнях перемещения то­чек, направленные перпендикулярно к начальному положению оси, называют прогибами и обозначают буквой w. При изгибе происхо­дит также поворот сечений стержня вокруг осей, лежащих в плос­костях сечений. Углы поворота сечений относительно их начальных положений обозначаются буквой .

На изгиб работают, например, оси железнодорожных вагонов, листовые рессоры, зубья шестерен, спицы колес, балки междуэтажных перекрытий, рычаги и многие другие детали.

В результате одновременного дей­ствия на тело сил, вызывающих раз­личные виды указанных основных де­формаций, возникает более сложная деформация.

Для определения деформации в какой-либо точке A (рис. 10) проведем в недеформированном теле отрезок прямой АВ, исходя­щий из этой точки в произвольном направлении и имеющий длину S

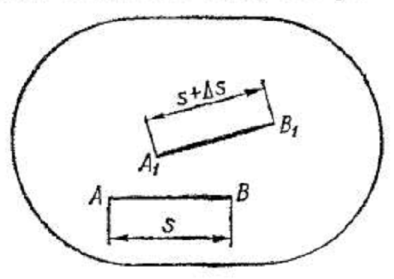
Рис. 10

После деформации точки А и В переместятся и займут положения и соответственно, а расстояние S между ними изменится на величину . Отношение

называется средней относительной линейной деформацией отрезка АВ. Приближая точку В к точ­ке A, т. е. уменьшая длину отрезка s, в пределе получим

Величина представляет собой относительную линейную де­формацию в точке А по направлению АВ. Если , то рас­стояние между точкамиА и В увели­чивается, (относитель­ным удлинении), при наблюдается относительным уко­рочение.

В точке А относи­тельные линейные деформации по раз­личным направлениям могут быть различны. В выбранной прямоуголь­ной системы координат ОХУZ относительные линейные деформа­ции в точке A обозначают соответственно через .

Для полной характеристики деформации в точке вводят еще и угловые деформации. Если до деформации тела из точки А (рис. 11) провести два отрезка АВ и AС, образующих прямой угол, то после перемещения точек вследствие дефор­мации тела отрезки займут положения и а угол между ними изме­нитсяна величину .

Приближая точки В и С к точке А, в пределе получим изменение первона­чально прямого угла на величину

Это изменение прямого угла, выра­женное в радианах, называется

относительной угловой деформаци­ей в точке А в плоскости, где лежат отрезки

АВ и АС. В точке А относительные угловые деформации в трех взаимно перпендикулярных координатных плоско­стях различны и обозначаюся соответственно —

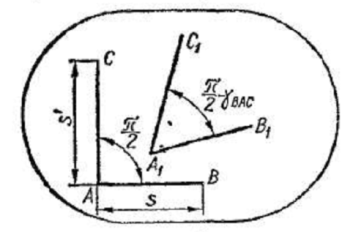
Рис. 11

Деформированное состояние в точке тела полностью определяет­ся шестью компонентами деформации — тремя относительными ли­нейными деформациями и тремя относительными угло­выми деформациями .